陀螺仪的基本特性
陀螺仪的基本特性

3.2 陀螺仪的基本特性双自由度陀螺的两个基本特性是:进动性和定轴性。
3.2.1 陀螺仪的进动性简单的说陀螺的进动性是指当陀螺受到外力矩的作用时,所产生的一种复合扭摆运动,其进动角速度的方向垂直于外力矩的方向,其进动角速度的大小正比与外力矩,或者说,陀螺进动的方向为角动量以最短距离导向外力矩的方向。
为了便于理解,我们以二自由度的框架陀螺为例,其进动表现为:外力矩如沿着内框轴作用时,则陀螺仪绕外框转动;若外力矩沿外框轴作用时,则陀螺绕内框转动。
3.2.2 陀螺仪的定轴性陀螺的定轴性是指转子绕自转轴高速旋转时,如果不受外力矩的作用,自转轴将相对于惯性空间保持方向不变。
换言之,双自由度陀螺具有抵抗干扰力矩,力图保持转子轴相对惯性空间的方位稳定的特性。
在实际的陀螺仪中,由于结构和工艺的不尽完善,总是不可避免的存在干扰力矩,因此,考查陀螺仪的定轴性,更有实际意义的是考查有干扰情况下,在有限的时间内,自转轴保持方位稳定的能力。
由陀螺仪的进动性可以知道,在干扰力矩的作用下,陀螺将产生进动,使得自转轴偏离原有的方位,这种方位偏差就称为漂移。
一般说来,框架陀螺仪的漂移较大,从几度每小时到几十度每小时不等,这就是为什么框架式陀螺测斜仪在测量前要求标桩对北,测量结束后还必须校北的原因。
3.3 陀螺仪的表观进动由于陀螺仪自转轴相对于惯性空间保持方位不变(当陀螺仪的漂移足够小;同地球自转引起的地球相对惯性空间方位变化比较,可近似的认为陀螺仪相对惯性空间的方位不变),而地球以其自转角速度绕极轴相对惯性空间转动,所示观察者若以地球为参考基准,将会看到陀螺仪自转轴相对地球转动,这种相对运动称为陀螺仪的表观运动。
表观运动的实质是陀螺仪可以跟踪测量地球自转角速度。
例如在地球任意纬度处,放置一个高精度的二自由度陀螺仪,并使其自转轴处于当地垂线位置,如图所示,可以看到陀螺的自转轴将逐渐偏离当地的地垂线,而相对地球作圆锥面轨迹的表观进动,每24小时进动一周。
旋转质量陀螺仪及其力学分析
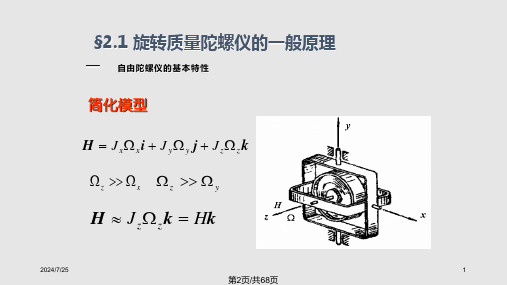
陀螺力矩所产生的这种外环稳定效应,称为陀螺动力 稳定效应,简称陀螺动力效应。
2024/7/25
10
第11页/共68页
一 自由陀螺仪的基本特性
3.陀螺力矩与陀螺效应
陀螺动力稳定效应对内框架无效!
2024/7/25
11
第12页/共68页
一 自由陀螺仪的基本特性
3.陀螺力矩与陀螺效应
当基座绕垂直于自转轴的
方向转动时,轴承带动自
转轴改变方向,强迫转子
进动。强迫进动所产生的
陀螺力矩,将引起自转轴
两端轴承的附加压力,压
力过大时,造成转轴弯曲
F
或轴承损坏。
2024/7/25
第13页/共68页
F
12
二 单自由度陀螺的运动方程与动力学分析
1.单自由度陀螺感受转动的特性
ωy
FA
My
ω
FA
2024/7/25
13
第14页/共68页
转子角动量在框架坐标系中表示为:
Hc Je (x )i Je (y cos z sin ) j Jz ( z cos y sin )k
2024/7/25
19
第20页/共68页
3.单自由度陀螺的运动方程
(3) 组件
组件的角动量 H B H b H c
H B (J e Jbx )(x )i (J e Jby )( y cos z sin ) j [J z (J z Jbz )(z cos y sin )]k
2024/7/25
31
第32页/共68页
1.利用欧拉动力学方程列写陀螺运动微分方程
二自由度陀螺的广义坐标:
转子轴绕外环轴的转角
转子轴绕内环轴的转角
陀螺仪原理1基本特性

陀螺仪原理1基本特性陀螺仪是一种测量和操控物体旋转姿态和角速度的仪器。
它的原理基于陀螺的力矩和角动量守恒。
陀螺仪主要由陀螺和测量装置组成,其中陀螺是陀螺仪的核心部件,而测量装置用于测量陀螺的角速度和姿态。
陀螺的基本特性如下:1.稳定性:陀螺具有很高的稳定性,不受外力的干扰。
这是因为陀螺在转动过程中,会生成一个力矩,使得它的旋转轴保持不变。
这种稳定性使得陀螺仪能够准确地测量物体的旋转姿态和角速度。
2.精度:陀螺仪具有很高的精度,能够测量微小的角度变化和角速度。
3.抗干扰性:陀螺仪具有很强的抗干扰能力,可以排除外界的振动和加速度干扰。
这是通过使用惯性测量装置和滤波算法来实现的。
4.快速响应:陀螺仪能够快速地响应外界的变化,准确地反映物体的旋转姿态和角速度变化。
陀螺仪的工作原理如下:1.陀螺力矩:当陀螺旋转时,其转动轴总是保持不变。
这是因为旋转产生了一个力矩,使得陀螺的旋转轴始终与外界力矩的方向相同。
这个力矩称为陀螺力矩,它使得陀螺能够保持稳定的旋转。
2.角动量守恒:根据角动量守恒定律,陀螺的角动量大小和方向在没有外力作用下保持不变。
这意味着陀螺的旋转轴在转动过程中保持不变。
3.测量装置:测量装置通过测量陀螺的角速度和姿态来获取物体的旋转信息。
常见的测量装置包括陀螺仪芯片、加速度计、磁力计等。
这些装置能够感知陀螺的角速度和加速度,并通过信号处理和滤波算法将其转化为测量结果。
陀螺仪在许多领域都有广泛的应用,包括航空航天、导航、汽车行驶控制、无人机、手机电子稳定器等。
它的基本特性和工作原理使得其成为一种重要的测量和控制工具,可以提高系统的稳定性和精度。
随着技术的不断发展,陀螺仪的性能和应用范围还将进一步扩大。
陀螺仪基本特性试验

陀螺仪基本特性试验陀螺仪基本特性试验一、实验目的1.用实验的方法观察并验证陀螺仪的基本特性——定轴性,进动性和陀螺力矩效应。
2.学习使用陀螺实验用主要设备——转台。
3.利用线性回归方法进行数据处理。
二、实验设备1.TZS-74陀螺仪表综合试验转台。
2.双自由度陀螺仪。
3.砝码。
4.实验用电源:交流220V,50~(转台用)36V,400~三相电源。
三、实验内容和步骤(一)定轴性实验1.陀螺马达不转时,开动转台,观察陀螺仪是否有定轴性。
2.接通电源,几下陀螺转子的转速方向,开动转台观察转子转动时陀螺仪的定轴性。
(二)进动性实验1.外加力矩,观察进动现象。
根据进动规律判断角动量H的方向,并和上面记下的转速方向做一比较。
2.测量进动角速度和外加力矩的关系:(1)在加力杆的前后标尺上分别加不同重量的砝码,记录进动的角度与实践,列表并计算出对应于每一外加力矩的进动角速度值,画出实验曲线。
(2)根据进动规律x Mω=(H J=Ω)计算出对应于每一外加H力矩的进动角速度,画出理论曲线。
(3)将实验曲线与理论曲线进行比较并说明产生误差的原因。
(4)用线性回归的方法进行数据处理,并通过求回归系数的方法求出角动量H的值。
3.测量进动角速度和角动量的关系在同一外力矩作用下,测量陀螺马达在额定转速下和断电一分钟后的进动角速度(断电一分钟后马达转速低于额定转速)。
根据实验结果说明进动角速度和角动量的关系。
(三)陀螺力矩实验1.开动转台,使双自由度陀螺仪基座转动,观察有无陀螺力矩效应,并说明原因。
2.观察双自由度陀螺仪在进动时的陀螺力矩效应。
用手对内框架加力矩,用手的感觉来测量陀螺力矩的大小和方向。
说明陀螺力矩产生的原因。
3.拧紧固定外框架的螺钉。
用手对内框架加力矩。
观察此时转子轴的运动方向。
用手感觉此时对手是否有陀螺力矩作用,加以分析。
4.测量陀螺力矩和进动角速度的关系为了达到测量陀螺力矩的目的,我们拧紧固定外框架的螺钉,是陀螺仪成为单自由度陀螺仪。
陀螺仪转动自由度与角动量守恒

陀螺仪转动自由度与角动量守恒陀螺仪转动自由度与角动量守恒陀螺仪是一种常见的物理实验装置,通过旋转陀螺仪本体,可以观察到许多有趣的现象。
在陀螺仪的旋转过程中,我们可以发现其具有转动自由度和角动量守恒的特性。
首先,陀螺仪的转动自由度是指其可以在三个不同的方向上自由旋转。
通常情况下,陀螺仪可以在水平面内绕其重心旋转,这被称为陀螺仪的倾斜自由度。
此外,陀螺仪还可以绕垂直于水平面的轴旋转,这被称为陀螺仪的预cession自由度。
最后,陀螺仪还可以绕其自身的轴旋转,这被称为陀螺仪的自旋自由度。
这些自由度的存在使得陀螺仪的运动变得更加复杂和有趣。
其次,陀螺仪的角动量守恒是指在陀螺仪旋转过程中,其角动量的大小和方向保持不变。
根据角动量守恒定律,当陀螺仪开始旋转时,其自身的角动量将保持不变,直到受到外力或摩擦力的作用。
这意味着陀螺仪在旋转过程中,其自身的旋转速度和角动量将保持恒定,不会发生变化。
陀螺仪转动自由度和角动量守恒的特性对于我们理解陀螺仪的运动以及相关的物理现象都具有重要意义。
例如,在陀螺仪的旋转过程中,我们可以发现一些奇特的现象,比如陀螺仪在倾斜自由度和预cession自由度下的复杂运动轨迹。
这些现象可以通过运用转动动力学理论以及角动量守恒定律来解释和理解。
此外,陀螺仪的转动自由度和角动量守恒的特性还在许多实际应用中得到了广泛的利用。
比如,在导航系统中,陀螺仪可以用来测量飞机或船只的方向和姿态,从而实现航行的导航控制。
另外,陀螺仪还可以用于惯性导航系统中,为导弹、飞行器等提供精确的导航信息。
综上所述,陀螺仪的转动自由度和角动量守恒是其独特而重要的特性。
通过研究和理解陀螺仪的转动自由度和角动量守恒,我们可以更好地认识和应用陀螺仪的运动规律,同时也可以更好地理解和解释其他相关的物理现象。
陀螺仪作为一种常见的实验装置,在科学研究和实际应用中都有着广泛的应用前景。
陀螺罗经指北原理综述

U2
X
在哪个轴上? N ?只能加于水平
轴(oY )上。
E
V2
?原则:必须人为施加水平轴控制力矩(M y),产生一个u2
使其与v2大小相等,方向相反,才能克服? 2影响。
陀螺罗经指北原理概述
(一)下重式罗经的控制力矩
1. 下重式罗经灵敏(指北)部分的结构:
陀螺转子
Z
核心-液浮、双转子陀螺球
(252mm )
量矩H 矢端以捷径趋向外力矩 M 矢端,作进动运动或
旋进运动。( H →M ) z
例: 1 - 1
M
?p? H
? py M y
P4 Fig1-4
? pz M z
o
y
My
F
H
进动方向: 右手定则
xF
二、 陀螺仪及其特性
陀螺罗经指北原理概述
?
pz
?
My H
;
?
py
?
?
Mz H
陀螺罗经指北原理概述
(一)地球自转产生的影响
液体连通器式:
My 产生方式: 重心下移
液体连通器某端 容器多余液体
M y 指向: 总是指北
总是指南
H指向: X轴正方向
X轴负方向
M y算式: M y ? ? M?
M y ? M?
u2 ? M y ? ? M?
u2 ? ? My ? ? M?
u2 ? ? M?
陀螺罗经指北原理概述
1 )主轴指北端投影图: (下重式罗经为例 )
4 )椭圆运动轨迹的特征:
Z。N的N点不断向W移 动。 南纬?反之
PS
陀螺罗经指北原理概述
?
e
? ?
陀螺仪的定义

陀螺仪的定义
陀螺仪的定义
陀螺仪的定义:陀螺仪是测定飞机飞行姿态用的一种仪表,它是测量载体的方位或角速度的核心元件,由一个高速旋转的转子和保证转子的旋转轴能在空间自由转动的支承系统组成。
主要利用惯性原理工作,具有定轴性与进动性这两个重要特性。
经典陀螺仪具有高速旋转的转子,能够不依赖任何外界信息而测出飞机等飞行器的运动姿态。
现代陀螺仪的外延有所增大,已经推广到没有转子而功能与经典陀螺仪相同的仪表上。
陀螺仪根据支承方式的不同可分为:由框架支承的框架陀螺仪,利用静电场支承的静电陀螺仪,利用液体或气体润滑膜支承的液浮或气浮陀螺仪,利用弹性装置支承的挠性陀螺仪;也可根据转子旋转轴的不同自由度分为单自由度和双自由度陀螺仪。
1852年,法国科学家傅科制作了一套能显示地球转动的仪器,命名为陀螺仪。
1914年陀螺仪开始作为惯性基准构成飞机的电动陀螺稳定装置。
20世纪20年代起,陀螺仪广泛应用于船舶、飞机的自动控制、导航系统。
直到50年代,陀螺仪在构造原理上改进不大,测量度不高。
50年代之后,随着静电悬浮、挠性支撑技术的出现,陀螺仪的构造得到很大改善,精度大为提高。
1975年,激光陀螺仪研制成功,它可靠性高,不受重力加速度的影响,在飞机的惯性导航中得到广泛应用。
陀螺仪基本知识惯性导航

电子信息工程学院
30
将大地水准体用 一个有确定参数的 旋转椭球体来逼近 代替(如椭球面与 真实大地水准面之 间的高度差的偏差 平方和最小),这 种旋转椭球体称为 参考椭球体,简称 参考椭球。
电子信息工程学院
31
国际通用参考椭球体
电子信息工程学院
32
WGS-84坐标系基本参数
(1)椭球长半径 (a) 6378137 2m;
电子信息工程学院
38
5.机体坐标系 OX BY(BMZBobile Frame,Body Frame )
机体坐标系与飞机固连,
用表示OX BYB,Z坐B 标原点 机O纵与轴飞一机致重,心重O与合Z飞,B 机O竖X与B轴飞
一致, O与Y飞B 机横轴一致。Fra bibliotekZB YB
XB
电子信息工程学院
39
6.平台坐标系OX pYpZ(pPlatform frame )
电子信息工程学院
33
二、惯性系统中常用的坐标系
在地球上进行导航,所定义的坐标系要将惯导系统 的测量值与地球的主要方向联系起来。因此涉及到了 各种不同的坐标系,主要有以下几类:
陀螺坐标系 地理坐标系 惯性坐标系 地球坐标系 载体坐标系
电子信息工程学院
34
1.陀螺坐标系oxyz
x轴:与陀螺内环轴一致,固连于内环上; z轴:与陀螺转子轴一致,固连于内环上;但不随转子转动; y轴:与oxy平面平行,大方向与外环一致,但一般不与外环轴一致
2.传感器:输出与被测量参数成一定关系的电信号 。如陀螺航向传感器,角速度传感器。
3.本身作为一个元部件,与其它自动控制元部件 组成各种陀螺装置。如陀螺稳定平台,惯性导 航系统等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.2 陀螺仪的基本特性
双自由度陀螺的两个基本特性是:进动性和定轴性。
3.2.1 陀螺仪的进动性
简单的说陀螺的进动性是指当陀螺受到外力矩的作用时,所产生的一种复合扭摆运动,其进动角速度的方向垂直于外力矩的方向,其进动角速度的大小正比与外力矩,或者说,陀螺进动的方向为角动量以最短距离导向外力矩的方向。
为了便于理解,我们以二自由度的框架陀螺为例,其进动表现为:外力矩如沿着内框轴作用时,则陀螺仪绕外框转动;若外力矩沿外框轴作用时,则陀螺绕内框转动。
3.2.2 陀螺仪的定轴性
陀螺的定轴性是指转子绕自转轴高速旋转时,如果不受外力矩的作用,自转轴将相对于惯性空间保持方向不变。
换言之,双自由度陀螺具有抵抗干扰力矩,力图保持转子轴相对惯性空间的方位稳定的特性。
在实际的陀螺仪中,由于结构和工艺的不尽完善,总是不可避免的存在干扰力矩,因此,考查陀螺仪的定轴性,更有实际意义的是考查有干扰情况下,在有限的时间内,自转轴保持方位稳定的能力。
由陀螺仪的进动性可以知道,在干扰力矩的作用下,陀螺将产生进动,使得自转轴偏离原有的方位,这种方位偏差就称为漂移。
一般说来,框架陀螺仪的漂移较大,从几度每小时到几十度每小时不等,这就是为什么框架式陀螺测斜仪在测量前要求标桩对北,测量结束后还必须校北的原因。
3.3 陀螺仪的表观进动
由于陀螺仪自转轴相对于惯性空间保持方位不变(当陀螺仪的漂移足够小;同地球自转引起的地球相对惯性空间方位变化比较,可近似的认为陀螺仪相对惯性空间的方位不变),而地球以其自转角速度绕极轴相对惯性空间转动,所示观察者若以地球为参考基准,将会看到陀螺仪自转轴相对地球转动,这种相对运动称为陀螺仪的表观运动。
表观运动的实质是陀螺仪可以跟踪测量地球自转角速度。
例如在地球任意纬度处,放置一个高精度的二自由度陀螺仪,并使其自转轴处于当地垂线位置,如图所示,可以看到陀螺的自转轴将逐渐偏离当地的地垂线,而相对地球作圆锥面轨迹的表观进动,每24小时进动一周。
若使得自转轴处于当地子午线位置,此时将看到陀螺仪自转轴逐渐偏离当地子午线,也相对地球作圆锥面轨迹的表观进动,每24小时一周。
3.4 坐标系
在对地球角速度进行测量时,我们首先需要了解几种主要的坐标系:惯性坐标系和地理坐标系。
l 惯性坐标系:通常以日心惯性坐标系代表惯性空间,其坐标原点选在太阳中心,坐标轴指向恒星。
l 地球坐标系:地理坐标系与地球固联,随着地球一起转动。
坐标原点为地球的中心,轴与地球自转轴重合,轴指向本初子午面与赤道平面交线,轴构成右手坐标系。
l 地理坐标系:在设定地理坐标系时,原点为仪器的中心或地球表面是的一点,和在当地水平面内,沿当地地垂线指向上方。
习惯上我们以“东、北、天”或“北、西、天”为顺序构成右手坐标系。
因此,地球的自转可以看作是地球坐标系相对惯性坐标系的转动,在设定了地理坐标系后,我们就可以计算当地地理坐标系的绝对角速度。
若我们以“北、西、天”为地理坐标系,则地球坐标系相对惯性坐标系的转动角速度在地理坐标系
上的投影为:
如图所示:
,
,
可见地球角速度只在北向分量和天顶向上有分量,或者说,具有水平分量和垂直分量。
3.5 陀螺测斜仪的测量原理
使用陀螺测斜仪进行测量目的是根据各测量点的方位、倾斜角来确定井眼轴线的空间位置,同时为了与钻具配合,必须随时得到工具面角。
在进行测量时,我们选取如下的两个坐标系:地理坐标系(北西天)和探管坐标系,最初两坐标系各相应的轴彼此重合。
方位角、倾斜角和工具面角分别对应于坐标系的相位旋转:
l 首先系绕轴负方向旋转角度A,此即方位角,得到系;
l 然后系绕轴负方向旋转角度I,此即倾斜角,得到系;
l 最后系绕的负方向旋转角度T,此即工具面角,得到系;
根据上述规定的各坐标系之间的相对转角关系可以得到地
理坐标系与探管坐标系之间的方位角余弦矩阵,使得有如下关系成立:
(1)地球自转角速度与重力加速度在地理坐标系中的分量是已
知的,根据前面的分析,可以得到:
(2)因而可以得到地球自转角速度和重力加速度在探管坐标系中的各个分量:
(3)
(4)
(5)
(6)
(7)
(8)
其中:
———为地球自转角速度的水平分量
———为地球自转角速度的垂直分量
———为当地纬度
由(3)~(8)式我们可以求出、、:
(9)
(10)
(11)。
