人教版高中数学选修(1-2)-1.2典型例题:一道独立性检验考题及变式
人教新课标版数学高二(人教A)选修1-2试题 1.2独立性检验的基本思想及其初步应用

1. 2一、选择题1.假设有两个分类变量X 与Y ,它们的可能取值分别为{x 1,x 2}和{y 1,y 2},其2×2列联表为:( ) A .a =5,b =4,c =3,d =2 B .a =5,b =3,c =4,d =2 C .a =2,b =3,c =4,d =5 D .a =2,b =3,c =5,d =4 [答案] D[解析] 可以由公式K 2=n (ad -bc )2(a +b )(c +d )(a +c )(b +d )分别计算K 2的观测值k 的值,用k 的大小来决定X 与Y 有关系的可能性的大小. .3.某卫生机构对366人进行健康体检,阳性家族史者糖尿病发病的有16人,不发病的有93人;阴性家族史者糖尿病发病的有17人,不发病的有240人,有______的把握认为糖尿病患者与遗传有关系.( )A .99.9%B .99.5%C .99%D .97.5%[答案] D[解析] 可以先作出如下列联表(单位:人):糖尿病患者与遗传列联表k =366×(16×240-17×93)2109×257×33×333≈6.067>5.024.故我们有97.5%的把握认为糖尿病患者与遗传有关系. 4.下列关于K 2的说法中正确的是( )A .K 2在任何相互独立问题中都可以用来检验有关还是无关B .K 2的值越大,两个事件的相关性就越大C .K 2是用来判断两个分类变量是否有关系的随机变量,只对于两个分类变量适合D .K 2的观测值k 的计算公式为k =n (ad -bc )(a +b )(c +d )(a +c )(b +d )[答案] C[解析] K 2值是用来判断两个分类变量是否有关系的一个随机变量,并不是适应于任何独立问题的相关性检验.5.在吸烟与患肺病这两个分类变量的计算中,下列说法正确的是( )A .若K 2的观测值为k =6.635,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病B .从独立性检验可知,有99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有99%的可能患有肺病C .若从统计量中求出有95%的把握认为吸烟与患肺病有关系,是指有5%的可能性使得推判出现错误D .以上三种说法都不正确 [答案] C[解析] 通过k 2的观测值对两个变量之间的关系作出的判断是一种概率性的描述,是一种统计上的数据,不能把这种推断结果具体到某一个个体上.7.某班主任对全班50名学生进行了作业量多少的调查,数据如下表:A .99%B .95%C .90%D .无充分依据[答案] B[解析] 由表中数据得k =50×(18×15-8×9)226×24×27×23≈5.059>3.841.所以约有95%的把握认为两变量之间有关系.9.某调查机构调查教师工作压力大小的情况,部分数据如表:( ) A .0.01 B .0.05 C .0.10D .0.005[答案] B [解析]K 2=n (ad -bc )2(a +b )(a +c )(c +d )(d +b )=100(53×1-12×34)287×13×65×35≈4.9>3.841,因此,在犯错误的概率不超过0.05的前提下,认为工作压力大与不喜欢教师职业有关系.10.在一次独立性检验中,根据计算结果,认为A 与B 无关的可能性不足1%,那么K 2一个可能取值为( )A .6.635B .5.024C .7.897D .3.841[答案] A二、填空题11.统计推断,当________时,有95%的把握认为事件A 与B 有关;当________时,认为没有充分的证据显示事件A 与B 是有关的.[答案] K 2>3.84,K 2≤2.70612.某高校“统计初步”课程的教师随机调查了选该课的一些学生情况,具体数据如下表:K 2=50×(13×20-10×7)223×27×20×30≈4.844,因为K 2≥3.841,所以判定主修统计专业与性别有关系,那么这种判断出错的可能性为________.[答案] 5%[解析] ∵k >3.841,所以有95%的把握认为主修统计专业与性别有关,出错的可能性为5%.14.调查者通过随机询问72名男女中学生喜欢文科还是理科,得到如下列联表(单位:名)性别与喜欢文科还是理科列联表) [答案] 有 [解析]通过计算K 2的观测值k =72×(16×8-28×20)236×36×44×28≈8.42>7.879.故我们有99.5%的把握认为中学生的性别和喜欢文科还是理科有关系.。
人教版高二数学选修1-2备选题库 1-2 独立性检验的基本思想及其应用

1.下列关于等高条形图的叙述正确的是()
A.从等高条形图中可以精确地判断两个分类变量是否有关系
B.从等高条例形图中可以看出两个变量频数的相对大小
C.从等高条形图可以粗略地看出两个分类变量是否有关系
D.以上说法都不对
C
在等高条形图中仅能粗略判断两个分类变量的关系,故A 错.在等高条形图中仅能找出频率,无法找出频数,故B错.2.对两个分类变量进行独立性检验的主要作用是()
A.判断模型的拟合效果
B.对两个变量进行相关分析
C.给出两个分类变量有关系的可靠程度
D.估计预报变量的平均值
C
独立性检验的目的就是明确两个分类变量有关系的可靠程度.3.在吸烟与患肺病这两个分类变量的计算中,下列说法中正确的是()
A.若随机变量K2的观测值k>6.635,我们有99%的把握说吸烟与患肺病有关,则某人吸烟,那么他有99% 的可能患有肺病B.若利用随机变量K2求出有99%的把握说吸烟与患肺病有关,则在100个吸烟者中必有99个患肺病
C.若利用随机变量K2求出有95%的把握说吸烟与患肺病有关,则是指有5%的可能性使得推断错误
D.以上说法均有错误
C
在独立性检验中得到的概率是两个分类变量有关系的概率.。
高中数学选修1-2(人教A版)第一章统计案例1.2知识点总结含同步练习及答案

为研究不同的给药方式(口服或注射)和药的效果(有效与无效)是否有关,进行了相应的抽样调查,调查结果 如表所示.根据所选择的
193
个病人的数据,能否作出药的效果与给药方式有关的结论? 有效 口服 注射 合计
58 64 122
无效
40 31 71
合计
98 95 193
解:提出假设
H 0 :药的效果与给药方式没有关系.
) 的前提下,认为"爱好该项运动与性别有关" 的前提下,认为"爱好该项运动与性别无关"
以上的把握认为"爱好该项运动与性别有关" 以上的把握认为"爱好该项运动与性别无关"
0.01 = 1% 1%
的机会错误,即有
99%
以上的把握认为“爱好这项运动与性别有
关”.同时,在犯错误的概率不超过
的前提下,认为“爱好该项运动与性别有关”.
答案: C 解析: 由题意
K 2 = 7.8 > 6.635 ,有 0.01 = 1% 的机会错误,即有 99% 以上的把握认为“爱好这项运 动与性别有关”.同时,在犯错误的概率不超过 1% 的前提下,认为“爱好该项运动与性别有关”;
高考不提分,赔付1万元,关注快乐学了解详情。
≈ 7.8
附表:
P (K 2 ⩾ k) k 0.050 3.841 0.010 6.635 0.001 10.828
参照附表,得到的正确结论是( A.在犯错误的概率不超过 B.在犯错误的概率不超过 C.有 D.有 解:C 由题意
K 2 = 7.8 > 6.635 ,有 99% 99% 0.1% 0.1%
答案: A
B.①③
C.②③
D.①②③
3. 分类变量 X 和 Y 的列联表如下:
则下列说法中正确的是 (
高中数学 专题1.2 独立性检验的基本思想及初步应用练习(含解析)新人教A版选修1-2(2021年

2016-2017学年高中数学专题1.2 独立性检验的基本思想及初步应用练习(含解析)新人教A版选修1-2编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2016-2017学年高中数学专题1.2 独立性检验的基本思想及初步应用练习(含解析)新人教A版选修1-2)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2016-2017学年高中数学专题1.2 独立性检验的基本思想及初步应用练习(含解析)新人教A版选修1-2的全部内容。
独立性检验的基本思想及初步班级:姓名:_____________1。
与表格相比,能更直观地反映出相关数据总体状况的是()A。
列联表 B.散点图C。
残差图D。
等高条形图2.分类变量X和Y的列联表如下:Y1Y2总计X1a b a+bX2c d c+d总计a+c b+d a+b+c+d则下列说法中正确的是()A。
ad—bc越小,说明X与Y关系越弱B。
ad—bc越大,说明X与Y关系越强C。
(ad-bc)2越大,说明X与Y关系越强D。
(ad—bc)2越接近于0,说明X与Y关系越强【解析】选C.因为K2=,所以(ad—bc)2越大,则K2越大,X与Y关系越强,故选C.3。
下面是2×2列联表。
y1y2总计x1332154x2a1346总计b34则表中a,b处的值应为( )A.33,66B.25,50 C。
32,67 D.43,56【解析】选A。
由2×2列联表知a+13=46,所以a=33,又b=a+33,所以b=33+33=66。
4。
研究生毕业的一个随机样本给出了关于所获取学位类别与学生性别的分类数据如表所示:硕士博士总计男16227189女1438151总计30535340根据以上数据,则( )A.性别与获取学位类别有关B.性别与获取学位类别无关C。
高中数学选修1-2《1.2 独立性检验的基本思想及其初步应用》课后作业本(人教A版,pdf版,含答案)

认为性 别 与 喜 欢 饮 酒 有 关 的 正 确 性 的 概 率 为
若两个分类变量 # 与 $ 的列联表为 ( !
独立性检验的基本思想及其初步应用 第一章 统计案例 下表 是 某 地 区 的 一 种 传 染 病 与 饮 用 水 的 调 0 查表
已知 ' !
)
/ 0 +" * * * "% '! 0
)
" 根 据 表 中 的 数 据 计 算% 得到 # * / ) / * * #% *
&% - / ! # (% )) 0 * .
)
!
) " ) + *3 ! # * #3) *5# ) !3! " 则 # + "% # ) ) "3. "3# ! .3# ! !
独立性检验的基本思想及其初步应用 第一章 统计案例
第三课时
班级 姓名 时间 ! " 分钟 某班主任对全班" # *名学生进行了作业量的 数据如下表 ( 调查 %
认为作业多 男生 女生 总计 # / / ) . 认为作业不多 + # " ) ! 总计 ) 0 ) " *
试作统计分析推 断 得 病 是 否 与 饮 用 不 干 净 水 有关
#
)
总计 ) " " . / #
# )
总计
# * ! * " *
# " # . #
则* 这个结论出错的可能 # 与$ 之间有关系 + 性为 列表 ( "
'! ) ! * " * *" ! *
最新整理最新数学:新人教A版选修1-2 1.2独立性检验的基本思想及其初步应用(同步练习).doc

1. 2 独立性检验的基本思想及其初步应用例题:1.三维柱形图中柱的高度表示的是( )A .各分类变量的频数B .分类变量的百分比C .分类变量的样本数D .分类变量的具体值 解析: 三维柱形图中柱的高度表示图中各个频数的相对大小.选A2. 统计推断,当______时,有95 %的把握说事件A 与B 有关;当______时,认为没有充分的证据显示事件A 与B 是有关的.解析:当841.3>k 时,就有95 %的把握说事件A 与B 有关,当076.2≤k 时认为没有充分的证据显示事件A 与B 是有关的.3.为了探究患慢性气管炎与吸烟有无关系,调查了却339名50岁以上的人,结果如下表所示,据此数据请问:50岁以上的人患慢性气管炎与吸烟习惯有关系吗?2分析:有表中所给的数据来计算2K 的观测值k,再确定其中的具体关系. 解:设患慢性气管炎与吸烟无关.a=43,b=162,c=13,d=121,a+b=205,c+d=134, a+c=56,b+d=283,n=339所以2K 的观测值为469.7))()()(()(2==+++-=d b c a d c b a bc ad n k .因此635.6>k ,故有99%的把握认为患慢性气管炎与吸烟有关. 课后练习:1. 在三维柱形图中,主对角线上两个柱形高度的乘积与副对角线上的两个柱形的高度的乘积相差越大两个变量有关系的可能性就( )A.越大B.越小C.无法判断D.以上都不对 2.下列关于三维柱形图和二维条形图的叙述正确的是: ( ) A .从三维柱形图可以精确地看出两个分类变量是否有关系B .从二维条形图中可以看出两个变量频数的相对大小,从三维柱形图中无法看出相对频数的大小C .从三维柱形图和二维条形图可以粗略地看出两个分类变量是否有关系D .以上说法都不对3.对分类变量X 与Y 的随机变量2K 的观测值K ,说法正确的是() A . k 越大," X 与Y 有关系”可信程度越小; B . k 越小," X 与Y 有关系”可信程度越小; C . k 越接近于0," X 与Y 无关”程度越小 D . k 越大," X 与Y 无关”程度越大4. 在吸烟与患肺病这两个分类变量的计算中,下列说法正确的是( )A.若K 2的观测值为k=6.635,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病;B.从独立性检验可知有99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有99%的可能患有肺病;C.若从统计量中求出有95% 的把握认为吸烟与患肺病有关系,是指有5% 的可能性使得推判出现错误;D.以上三种说法都不正确.5.若由一个2*2列联表中的数据计算得k 2=4.013,那么有 把握认为两个变量有关系6.某高校“统计初步”课程的教师随机调查了选该课的一些学生情况,具体数据如下表:250(1320107) 4.84423272030k ⨯⨯-⨯=≈⨯⨯⨯因为23.841K ≥,所以判定主修统计专业与性别有关系,那么这种判断出错的可能性为 ____;7.在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人。
人教版高中数学选修1-2 练习:独立性检验的基本思想及其初步应用练习:
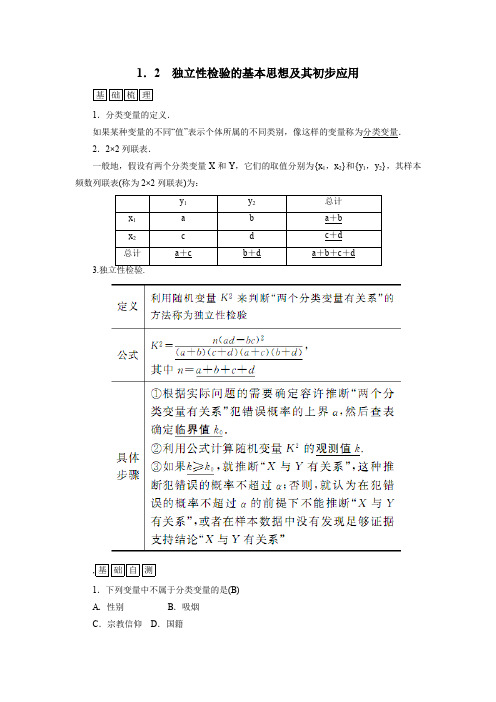
1.2独立性检验的基本思想及其初步应用基础梳理1.分类变量的定义.如果某种变量的不同“值”表示个体所属的不同类别,像这样的变量称为分类变量.2.2×2列联表.一般地,假设有两个分类变量X和Y,它们的取值分别为{x1,x2}和{y1,y2},其样本频数列联表(称为2×2列联表)为:3.,基础自测1.下列变量中不属于分类变量的是(B)A.性别B.吸烟C.宗教信仰D.国籍解析:“吸烟”不是分类变量,“是否吸烟”才是分类变量.故选B.2.下面是一个2×2列联表则表中a、bA.94、96 B.52、50C.52、54 D.54、52解析:由a+21=73,得a=52,由b+46=100,得b=54.3.某高校“统计初步”课程的教师随机调查了选修该课程的一些学生情况,具体数据如下表:为了判断主修统计专业是否与性别有关系,根据表中的数据,得到K2=50×(13×20-10×7)2≈4.844>3.841,所以判定主修统计专业与性别有关系,那么这种判断23×27×20×30出错的可能性为____________.解析:P(K2>3.841)=0.05,判断出错的可能性为5%.答案:5%(一)重点通过案例理解分类变量、列联表、独立性检验的含义,利用列联表的独立性检验进行估计.(二)难点独立性检验的基本思想,随机变量K2的含义.(三)知识结构图(三)思维总结(1)直观分析的两种方法. ①频率分析.通过对样本的每个分类变量的不同类别和事件发生的频率的大小比较来分析变量之间是否有关系,通常通过列联表列出两个分类变量进行分析.一般地,假设有两个分类变量X 和Y ,它们的取值分别为{x 1,x 2}和{y 1,y 2},其样本频数列联表(称为2×2列联表)为:-bc|越小,说明两个分量之间的关系越弱;|ad -bc|越大,说明两个分类变量之间的关系越强.②图形分析.利用等高条形图来分析两分类变量之间是否具有相关关系,形象、直观地反映两个分类变量之间的总体状态和差异大小,进而推断它们之间是否有关系.a .绘制等高条形图时,列联表的行对应的是高度,两行的数据不相等,但对应的条形图的高度是相同的,两列的数据对应不同颜色.b .等高条形图中有两个高度相同的矩形,每一个矩形中都有两种颜色,观察下方颜色区域的高度,如果两个高度相差比较明显⎝⎛⎭⎫即a a +b 和c c +d 相差很大,就判断两个分类变量之间有关系. (2)独立性检验及其基本思想. ①独立性检验.利用随机变量K 2来确定在多大程度上可以认为“两个分类变量有关系”的方法称为两个分类变量的独立性检验.利用上诉公式求出K 2的观测值为k=n(ad-bc)2(a+b)(c+d)(a+c)(b+d).再得出X与Y有关系的程度,通常用到以下数据:(i)如果k>6.635,在犯错误的概率不超过0.01的前提下认为X与Y有关系;(ii)如果k>2.706,在犯错误的概率不超过0.1的前提下认为X与Y有关系;值得注意的是:观察值k越大,越有利于结论“X和Y有关系”,越小越有利于结论“X 和Y没有关系”.因此,可以建立一定的规则:当k≥k0时就说X与Y有关系,k<k0时就说X和Y没有关系,故求得观测值后只要与建立的规则进行比较即可得出结论.②独立性检验的基本思想.独立性检验的基本思想是要确认“两个分类变量有关系”这一结论成立的可信程度,首先假设该结论不成立,即假设“两个分类变量没有关系”成立,在该假设下我们构造的随机变量K2应该很小,如果由观察数据计算得到K2的观测值k很大,则在一定程度上说明假设不合理,根据随机变量K2的含义,可以通过P(k≥6.635)≈0.01来评价假设不合理的程度,由实际计算出k>6.635,说明假设不合理的程度约为99%,即两个分类变量有关系这一结论成立的可信度为99%,不合理的程度可查下表得出:1.独立性检验是对两个分类变量间是否有关系的一种案例分析方法,其分析方法有:等高条形图法和利用假设的思想方法,计算出某一个随机变量K2的观测值来进行判断.2.在等高条形图中,可以估计满足条件X=x1的个体中具有Y=y1的个体所占的比例为aa+b,也可以估计满足条件X=x2的个体中具有Y=y2的个体所占的比例为cc +d ,两个比例的值相差越大,两个分类变量相关的可能性就越大.3.独立性检验的一般步骤: (1)根据样本数据制成2×2列联表;(2)根据公式K 2=n (ad -bc )2(a +b )(a +c )(b +d )(c +d )计算K 2的观测值;(3)比较K 2与临界值的大小关系作统计推断.1.在等高条形图形中,下列哪两个比值相差越大,“两个分类变量有关系”成立的可能性越大(C )A .a a +b 与d c +dB .c a +b 与a c +dC .a a +b 与c c +dD .a a +b 与c b +c2.通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表;由K 2=n (ad -bc )(a +b )(c +d )(a +c )(b +d )算得,K 2=110(40×30-20×20)260×50×60×50≈7.8.附表:A .有99%以上的把握认为“爱好该项运动与性别有关”B .有99%以上的把握认为“爱好该项运动与性别无关”C .在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”D .在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”3.某高校“统计初步”课程的教师随机调查了选该课的一些学生的情况,具体数据如下表:k =50(13×20-10×7)220×30×23×27≈4.844,因为k >3.841,所以确定主修统计专业与性别有关系,那么这种判断出错的可能性为________.解析:∵k =4.844>3.841,∴有95%的把握可以确定主修统计专业与性别有关,那么这种判断出错的可能性为5%.答案:5%1.在研究两个分类变量之间是否有关系时,可以粗略地判断两个分类变量是否有关的是(B )A .散点图B .等高条形图C .2×2列联表D .以上均不对2.对分类变量X 与Y 的随机变量K 2的观测值k ,说法正确的是(B ) A .k 越大,“X 与Y 有关系”可信程度越小 B .k 越小,“X 与Y 有关系”可信程度越小 C .k 越接近0,“X 与Y 无关”程度越小 D .k 越大,“X 与Y 无关”程度越大 3.下面是一个2×2列联表:则表中a 、b 的值分别是A .94、96 B .25、21 C .25、27 D .27、254.分类变量x 和y 的列联表如下,则(C )A.ad-bcB.ad-bc越大,说明x与y的关系越弱C.(ad-bc)2越大,说明x与y的关系越强D.(ad-bc)2越小,说明x与y的关系越强解析:由K2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d)知,(ad-bc)2越大,K2值越大,说明x与y的关系越强.5.某班主任对全班50名学生进行了作业量多少的调查,数据如下表:A.99% B.95%C.90% D.无充分依据解析:由表中数据计算K2=50×(18×15-8×9)226×24×27×23≈5.059,而K2=5.059>3.841,所以约有95%的把握认为两变量之间有关.6.为了探究电离辐射的剂量与人体的受损程度是否有关,用两种不同剂量的电离辐射照射小白鼠,在照射后14天内的结果如下表所示:解析:根据独立性检验的基本思想,可知其类似反证法,即要确认“两个分类变量有关系”这一结论成立的可信程度,首先假设结论不成立,即假设结论“两个分类变量没有关系”成立,对本题,进行统计分析时的统计假设应是“小白鼠的死亡与剂量无关”.答案:小白鼠的死亡与剂量无关7.(2013·韶关二模)以下四个命题中:①在一次试卷分析中,从每个试室中抽取第5号考生的成绩进行统计,是简单随机抽样;②样本数据3,4,5,6,7的方差为2;③对于相关系数r。
高中数学选修1-2独立性检验 例题解析2

独立性检验例题解析2【例1】为研究大气污染与人的呼吸系统疾病是否有关,对重污染地区和轻污染地区作跟踪调查,得出以下数据:请根据统计数据,作出合适的判断分析.【解】假设H:大气污染与人的呼吸系统疾病无关由公式得22()()()()()n ad bca b c d a c b dχ-=++++23000(1031487139713)72.636116288415001500⨯-⨯=≈⨯⨯⨯因为72. 636>10.828,所以拒绝H, 即我们有99.9%的把握认为大气污染与人的呼吸系统疾病有关.【点评】由于2χ≈72. 635远大于10.828,所以“大气污染与人的呼吸系统疾病无关”几乎不可能发生,判断二者有关的准确性很高,也可以说大气污染与人的呼吸系统疾病紧密相关.【例2】在国家未实施西部开发战略前,一新闻单位在应届大学毕业生中随机抽取1000人问卷,只有80人志愿加入西部建设,而国家公布实施西部开发战略后,随机抽取1200名应届大学毕业生问卷,有400人志愿加入国家西部建设.问:实施西部开发战略的公布是否对应届大学毕业生的选择产生了影响.解:据题意信息列出2×2列联表:假设西部开发战略的公布实旋未起作用(零假设H).由公式计算卡方:22()()()()()n ad bca b c d a c b dχ-=++++22200(80800920400)205.22 480172010001200⨯-⨯=≈⨯⨯⨯因为205.22>10.828,所以由小概率原理判断拒绝H.因此我们有99.9%的把握认为西部开发战略的实施起了作用【点评】即使不利用独立性检验我们也能正确地判断“开发战略”起了作用,但利用卡方通过数据信息更有说服力,还可说明实施西部开发战略的公布具有强大的带动作用.【例3】巴西医生马廷思收集犯有各种贪污、受贿罪的官员与廉洁官员寿命的调查资料:500名贪官中有348人的寿命小于平均寿命、152人的寿命大于或等于平均寿命;590名廉洁官员中有93人的寿命小于平均寿命、497人的寿命大于或等于平均寿命这里,平均寿命是指“当地人均寿命”试分析官员在经济上是否清廉与他们寿命的长短之间是否独立?【解】据题意列2×2列联表如下:假设H:官员是否清白与他们的寿命长短无关,由公式22()()()()()n ad bca b c d a c b dχ-=++++21090(34849715293)325.635 500590441649⨯-⨯=≈⨯⨯⨯因为325.635>10.828,所以我们有的99.9%的把握拒绝H.即我们有99.9%的把握认为官员在经济上是否清廉与他们的寿命长短有密切关系.【点评】这是社会学调查研究中常用的方式,从数据分析来看,两事物不仅相关,而且紧密相关,我们可以有99 .9%以上的把握说不清廉的官员易过早死亡且这一结论的正确性远大于99.9%。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一道独立性检验考题及变式
独立性检验是通过K2统计量,运用假设检验的方法,研究了两个“变量”的关系问题.独立性检验在医学、社会经济、生活、科学技术等方面的应用十分广泛,在处理社会问题时得到得数据中,也常常用到独立性检验.
例.(2010年高考辽宁理)为了比较注射A, B两种药物后产生的皮肤疱疹的面积,选200只家兔做试验,将这200只家兔随机地分成两组,每组100只,其中一组注射药物A,另一组注射药物B。
(Ⅰ)甲、乙是200只家兔中的2只,求甲、乙分在不同组的概率;
(Ⅱ)下表1和表2分别是注射药物A和B后的试验结果.(疱疹面积单位:mm2)
表1:注射药物A后皮肤疱疹面积的频数分布表
(ⅰ)完成下面频率分布直方图,并比较注射两种药物后疱疹面积的中位数大小;
(ⅱ)完成下面2×2列联表,并回答能否有99.9%的把握认为“注射药物A后的疱疹面积与注射药物B后的疱疹面积有差异”.
表3:
分析 (1)根据各组的频数分布表计算出各组的频率,再除以组距5,此即频率分布直方图中各组的小矩形的高,据此画出频率分布直方图;(2)根据给出的频数分布表和列联表的要求,即可写出列联表,然后根据给出的公式进行计算,再与临界值表进行比较.作出结论.
解:(Ⅰ)甲、乙两只家兔分在不同组的概率为
991981002002100199
C P C == (Ⅱ)(i )
图Ⅰ注射药物A 后皮肤疱疹面积的频率分布直方图 图Ⅱ注射药物B 后皮肤疱疹面积的频率分布直方图
可以看出注射药物A 后的疱疹面积的中位数在65至70之间,而注射药物B 后的疱疹面积的中位数在70至75之间,所以注射药物A 后疱疹面积的中位数小于注射药物B 后疱疹面积的中位
数。
……8分
(ii )表3:。
