离散数学课程作业(2)
2020年春季学期课程作业离散数学第2次13979-重庆大学网络教育学院-参考资料

重庆大学网络教育学院-2020年春季学期课程作业离散数学第2次-参考资料请认真阅读一下说明然后下载:题库有可能会换,不保证全部都有!请仔细核对是不是您需要的题目再下载!!!!本文档的说明:如果题目顺序和你的试卷不一样,按CTRL+F在题库中逐一搜索每一道题的答案,预祝您取得好成绩百!一、单项选择题 (共 30 题、0 / 90 分 )1、一棵有向树,如果恰有一个节点的入度为0,其余所有节点的入度都为1,则称为()。
A、根树B、普通树C、树根D、树节点参考答案是:A2、设有向图(a)、(b)、(c)、(d)如下图所示,则下列结论成的是()A、(a)是强连通的B、(b)是强连通的C、(c)是强连通的D、(d)是强连通的参考答案是:A3、P:今天下雨。
Q:明天下雨。
上述命题的合取为()。
(符号表示)A、┐P∧┐QB、┐P∨QC、┐P∨┐QD、P∧Q参考答案是:D4、设有向图D为欧拉图,则图D中每个结点的入度()出度。
A、等于B、大于C、小于D、不能确定参考答案是:A5、下列关系中哪些能构成函数?()A、{〈x,y〉|x,y∈ N,x+y<10}B、{〈x,y〉|x,y∈ N,x+y=10}C、{〈x,y〉|x,y∈ R,|x|=y}D、{〈x,y〉|x,y∈ R,x=|y|}参考答案是:C6、设〈G , *〉是一个独异点, 并且对于G中的每一个元素a都有( ),则〈G , * 〉是一个阿贝尔群。
A、a * a= aB、a * a= eC、a * e= eD、e* a= e参考答案是:B7、张三或李四都可以做这件事。
设P:张三可以做这件事。
Q:李四可以做这件事。
则命题符号化为()。
A、┐P∧┐QB、┐P∨QC、┐P∨┐QD、参考答案是:D8、在一个具有n个节点的图中,则任何简单路的长度均不大于()。
A、nB、n-1C、n+1D、2n参考答案是:B9、欧拉公式的原型为()。
A、v+e+r=2B、v-e+r=2C、v-e-r=2D、v+e-r=2参考答案是:B10、下面关于广群,半群,独异点,群的关系正确的是()。
奥鹏地大21年春季 《离散数学》在线作业二.doc

1.A.(1)正确B.(2)正确C.(3)正确D.(4)正确【参考答案】: D2.设无向图G有16条边且每个顶点的度数都是2,则图G有( )个顶点A.10B.4C.8D.16【参考答案】: D3.若一棵完全二元(叉)树有2n-1个顶点,则它()片树叶A.nB.2nC.2n-1D.2【参考答案】: A4.A.(1)正确B.(2)正确C.(3)正确D.都不正确【参考答案】: A5.设谓词P(x):x是奇数,Q(x):x是偶数,谓词公式x(P(x)Q(x))在哪个个体域中为真?( )A.自然数B.实数C.复数D.(1)--(3)均成立【参考答案】: A6.A.选项A对B.选项B对C.选项C对D.选项D对【参考答案】: A7.A.(1)正确B.(2)正确C.(3)正确D.(4)正确【参考答案】: D8.下列哪一种图不一定是树()A.无简单回路的连通图B.有n个顶点n-1条边的连通图C.每对顶点间都有通路的图D.连通但删去一条边便不连通的图【参考答案】: C9.A.(1)正确B.(2)正确C.(3)正确D.(4)正确【参考答案】: B10.每个无限循环群有()个生成元A.1B.2C.3D.4【参考答案】: B11.集合A={1,2,…,10}上的关系R={<x,y>|x+y=10,x,y A},则R 的性质为()A.自反的B.对称的C.传递的,对称的D.传递的【参考答案】: B12.A.单射而非满射B.满射而非单射C.双射D.既不是单射也不是满射【参考答案】: D13.图的构成要素是()A.结点B.边C.结点与边D.结点、边和面【参考答案】: C14.A.(1)正确B.(2)正确C.(3)正确D.(4)正确【参考答案】: A15.每个非平凡的无向树至少有()片树叶A.1B.2C.3D.4【参考答案】: B16.A.(1)正确B.(2)正确C.(3)正确D.(4)正确【参考答案】: D17.A.(1)正确B.(2)正确C.(3)正确D.(4)正确【参考答案】: B18.量词的约束范围称为量词的()A.定义域B.个体域C.辖域D.值域【参考答案】: C19.A.A正确B.B正确C.C正确D.D正确【参考答案】: D20.设G是连通简单平面图,G中有11个定点,5个面,则G中的边是()A.10B.12C.14D.16【参考答案】: C21.判断下列命题哪个为真?( )A.A-B=B-A => A=BB.空集是任何集合的真子集C.空集只是非空集合的子集D.若A的一个元素属于B,则A=B【参考答案】: A22.下面给出的集合中,哪一个是前缀码?( )A.{0,10,110,101111}B.{01,001,000,1}C.{b,c,aa,ab,aba}D.{1,11,101,001,0011}【参考答案】: B23.A.(1)正确B.(2)正确C.(3)正确D.(4)正确【参考答案】: D24.A.选项A正确B.选项B正确C.选项C正确D.选项D正确【参考答案】: D25.设无向图G有18条边且每个顶点的度数都是3,则图G有( )个顶点A.10B.4C.8D.12【参考答案】: D26.A.文字B.短语C.子句D.合取范式E.析取范式【参考答案】: CDE27.设R是任意集合A上的空关系,则R是()A.自反的B.反自反的C.对称的D.反对称的E.传递的【参考答案】: ABCDE28.存在欧拉通路的有向欧拉图都是单向连通图( )A.错误B.正确【参考答案】: B29.同一谓词公式,指定不同的论域,其真值不一定相同( )A.错误B.正确【参考答案】: B30.A.错误B.正确【参考答案】: B31.若无向图中恰有两个度为奇数的结点,则这两个结点必连通( )A.错误B.正确【参考答案】: B32.设G为简单平面图,则n-m+r=2,其中n,m,r分别为G的顶点数、边数和面数( )A.错误B.正确【参考答案】: A33.“北京与天津的距离很近”是复合命题( )A.错误B.正确【参考答案】: A34.A.错误B.正确【参考答案】: A35.A.错误B.正确【参考答案】: B。
离散数学形成性考核作业(二)
离散数学形成性考核作业(二) 图论部分本课程形成性考核作业共4次,内容由中央电大确定、内容由中央电大确定、统一布置。
统一布置。
本次形考作业是第二次作业,大家要认真及时地完成图论部分的形考作业,字迹工整,次作业,大家要认真及时地完成图论部分的形考作业,字迹工整,抄写题目,抄写题目,抄写题目,解答题有解答解答题有解答过程。
过程。
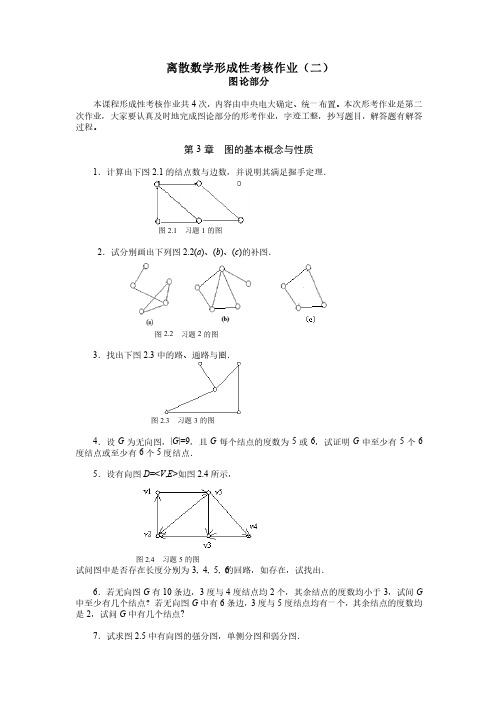
第3章 图的基本概念与性质1.计算出下图2.1的结点数与边数,并说明其满足握手定理.的结点数与边数,并说明其满足握手定理.图2.1 习题1的图的图2.试分别画出下列图2.2(a )、(b )、(c )的补图.的补图.图2.2 习题2的图的图3.找出下图2.3中的路、通路与圈.中的路、通路与圈.图2.3 习题3的图的图4.设G 为无向图,|G |=9,且G 每个结点的度数为5或6,试证明G 中至少有5个6度结点或至少有6个5度结点.度结点.5.设有向图D =<V ,E >如图2.4所示,所示,图2.4 习题5的图的图 试问图中是否存在长度分别为3, 4, 5, 6的回路,如存在,试找出.的回路,如存在,试找出.的回路,如存在,试找出.6.若无向图G 有10条边,3度与4度结点均2个,其余结点的度数均小于3,试问G中至少有几个结点?若无向图G 中有6条边,3度与5度结点均有一个,其余结点的度数均是2,试问G 中有几个结点? 7.试求图2.5中有向图的强分图,单侧分图和弱分图.中有向图的强分图,单侧分图和弱分图.的图图2.5 习题7的图8.试说明图2.6中G1和G2同构.同构.G1G2图2.6 习题8的图9.试求图2.7中的邻接矩阵与可达矩阵.中的邻接矩阵与可达矩阵.图2.7 习题9的图10.有n个结点的无向完全图的边数为个结点的无向完全图的边数为 .11.图中度数为奇数的结点为数个. .图中度数为奇数的结点为 数个.12.已知图G的邻接矩阵为的邻接矩阵为,有( ).则G有(A.5点,8边B.6点,7边C.5点,7边D.6点,8边第4章几种特殊图1.试分别构造满足下列条件的无向欧拉图.试分别构造满足下列条件的无向欧拉图(1)有偶数个结点,奇数条边.)有偶数个结点,奇数条边.)有偶数个结点,偶数条边.(2)有偶数个结点,偶数条边.)有奇数个结点,偶数条边.(3)有奇数个结点,偶数条边.)有奇数个结点,奇数条边.(4)有奇数个结点,奇数条边.2.分别构造满足下列条件的四个汉密尔顿图.分别构造满足下列条件的四个汉密尔顿图)偶数个结点,奇数条边.(1)偶数个结点,奇数条边.(2)有偶数个结点,偶数条边.)有偶数个结点,偶数条边.)有奇数个结点,偶数条边.(3)有奇数个结点,偶数条边.(4)有奇数个结点,奇数条边.)有奇数个结点,奇数条边.3.试画出一个没有一条欧拉回路,但有一条汉密尔顿回路的图..试画出一个没有一条欧拉回路,但有一条汉密尔顿回路的图. 4.如图2.8是否为欧拉图?试说明理由.是否为欧拉图?试说明理由.判断是否为欧拉图图2.8 判断是否为欧拉图5.如图2.9是否为汉密尔顿图?试说明理由.是否为汉密尔顿图?试说明理由.判断是否为汉密尔顿图图2.9 判断是否为汉密尔顿图6.试分别说明图4.3(a)、(b)与(c)是否为平面图.)是否为平面图.判断是否为平面图图2.10 判断是否为平面图7.试分别求出图2.11(a)、(b)与(c)的每个图的面的次数.)的每个图的面的次数.求面的次数图2.11 求面的次数8.试利用韦尔奇·鲍威尔算法分别对图2.12(a)、(b)与(c)着色.)着色.图2.12 图的着色中那些是树,那些是森林,并说明理由..试指出图2.13中那些是树,那些是森林,并说明理由.图2.13 习题1的图中的一个生成树,并说明其中的树枝、弦,以及对应生成树的补.中的一个生成树,并说明其中的树枝、弦,以及对应生成树的补.图2.14 习题2的图的所有不同构的生成树.的完全图K5 的所有不同构的生成树.图2.15 习题3的图中的最小生成树及其权值.中的最小生成树及其权值.图2.16 习题4的图结点?结点?A.1 B.2 C.3 D.4 7.无向树T有3个3度结点,2个4度结点,其余的都是树叶,则T(有( )片树叶?)片树叶?A.3 B.7 C.9 D.11 8.无向树T有1个2度结点,3个3度结点,4个4度结点,1个5度结点,其余的都是树叶,)片树叶?有( )片树叶?则T有(A.12 B.14 C.16 D.20 9.无向树T有9片树叶,5个3度结点,其余的都是4度结点,则T有几个4度结点?度结点?A.0 B.1 C.2 D.3 。
电大离散数学作业2

离散数学集合论部分形成性考核书面作业本课程形成性考核书面作业共3次,内容主要分别是集合论部分、图论部分、数理逻辑部分的综合练习,基本上是按照考试的题型(除单项选择题外)安排练习题目,目的是通过综合性书面作业,使同学自己检验学习成果,找出掌握的薄弱知识点,重点复习,争取尽快掌握.本次形考书面作业是第一次作业,大家要认真及时地完成集合论部分的综合练习作业.要求:学生提交作业有以下三种方式可供选择:1. 可将此次作业用A4纸打印出来,手工书写答题,字迹工整,解答题要有解答过程,完成作业后交给辅导教师批阅.2. 在线提交word文档3. 自备答题纸张,将答题过程手工书写,并拍照上传.一、填空题1.设集合{1,2,3},{1,2}A B==,则P(A)-P(B )= {{3}, {1,2,3}, {1, 3 }, {2,3}} ,A⨯B= {<1,1>,<1,2>,<2,1>,<2,2>,<3,1>,<3,2>} .2.设集合A有10个元素,那么A的幂集合P(A)的元素个数为1024 .3.设集合A={0, 1, 2, 3},B={2, 3, 4, 5},R是A到B的二元关系,R⋂∈y∈x<且=且>∈x{B,,AAyyBx}则R的有序对集合为{<2, 2>,<2, 3>,<3, 2>},<3, 3> .4.设集合A={1, 2, 3, 4 },B={6, 8, 12},A到B的二元关系R=}x∈y∈><y=2,,,{ByxAx那么R-1={<6,3>,<8,4>} .5.设集合A={a, b, c, d},A上的二元关系R={<a, b>, <b, a>, <b, c>, <c, d>},则R具有的性质是反自反性,反对称性.6.设集合A={a, b, c, d},A上的二元关系R={<a, a >, <b, b>, <b, c>, <c, d>},若在R中再增加两个元素<c, b>, <d, c>,则新得到的关系就具有对称性.7.如果R1和R2是A上的自反关系,则R1∪R2,R1∩R2,R1-R2中自反关系有 2 个.8.设A={1, 2}上的二元关系为R={<x, y>|x∈A,y∈A, x+y =10},则R的自反闭包为{<1, 1>, <2, 2>} .9.设R是集合A上的等价关系,且1 , 2 , 3是A中的元素,则R中至少包含<1, 1>, <2, 2>, <3, 3> 等元素.10.设A={1,2},B={a,b},C={3,4,5},从A到B的函数f ={<1, a>, <2, b>},从B到C的函数g={< a,4>, < b,3>},则Ran(g︒ f)= {3,4} .二、判断说明题(判断下列各题,并说明理由.)1.若集合A = {1,2,3}上的二元关系R={<1, 1>,<2, 2>,<1, 2>},则(1) R是自反的关系;(2) R是对称的关系.解:(1)错误,R不是自反关系,因为没有有序对<3,3>.(2)错误,R不是对称关系,因为没有有序对<2,1>2.设A={1,2,3},R={<1,1>, <2,2>, <1,2> ,<2,1>},则R是等价关系.解:错误, 即R不是等价关系.因为等价关系要求有自反性x R x, 但<3, 3>不在R中.3.若偏序集<A,R>的哈斯图如图一所示,则集合A的最大元为a,最小元不存在.οοοοab cd图一οοοg e fh ο解:错误.集合A的最大元不存在,a是极大元.4.设集合A={1, 2, 3, 4},B={2, 4, 6, 8},,判断下列关系f是否构成函数f:A→,并说明理由.B(1) f={<1, 4>, <2, 2,>, <4, 6>, <1, 8>};(2) f={<1, 6>, <3, 4>, <2, 2>};(3) f={<1, 8>, <2, 6>, <3, 4>, <4, 2,>}.解:(1) f不能构成函数.因为A中的元素3在f中没有出现.(2) f不能构成函数.因为A中的元素4在f中没有出现.(3) f可以构成函数.因为f的定义域就是A,且A中的每一个元素都有B中的唯一一个元素与其对应,满足函数定义的条件.三、计算题1.设}4,2{=CB==E,求:A},5,4,3,2,1{=},5,2,1{4,1{},(1) (A⋂B)⋃~C;(2) (A⋃B)-(B⋂A) (3) P(A)-P(C);(4) A⊕B.解:(1)因为A∩B={1,4}∩{1,2,5}={1},~C={1,2,3,4,5}-{2,4}={1,3,5}所以(A∩B ) ⋃~C={1}⋃{1,3,5}={1,3,5}(2)(A⋃B)-(B⋂A)= {1,2,4,5}-{1}={2,4,5}(3)因为P(A)={φ,{1}, {4}, {1,4}}P(C)={φ,{2},{4},{2,4}}所以P(A)-P(C)={ φ,{ 1},{ 4},{ 1,4}}-{φ,{ 2},{ 4},{2,4 }}(4) 因为A⋃B={ 1,2,4,5}, A⋂B={ 1}所以A⊕B=A⋃B-A⋂B={1,2,4,5}-{1}={2,4,5}2.设A={{1},{2},1,2},B={1,2,{1,2}},试计算(1)(A-B);(2)(A∩B);(3)A×B.解:(1)A-B ={{1},{2}}(2)A∩B ={1,2}(3)A×B={<{1},1>,<{1},2>,<{1},{1,2}>,<{2},1>,<{2},2>,<{2},{1,2}>,<1,1>,<1,2>,<1, {1,2}>,<2,1>,<2,2>,<2, {1,2}>}3.设A={1,2,3,4,5},R={<x,y>|x∈A,y∈A且x+y≤4},S={<x,y>|x∈A,y∈A且x+y<0},试求R,S,R•S,S•R,R-1,S-1,r(S),s(R).解:R={<1,1>,<1,2>,<1,3>,<2,1>,<2,2>,<3,1>}, \R-1={<1,1>,<2,1>,<3,1>,<1,2 >,<2,2>,<1, 3>}S=φ, S-1 =φr(S)={<1,1>,<2,2>,<3,3>,<4,4>,<5,5>}s(R)= {<1,1>,<1,2>,<1,3>,<2,1>,<2,2>,<3,1>}R •S=φS •R=φ4.设A ={1, 2, 3, 4, 5, 6, 7, 8},R 是A 上的整除关系,B ={2, 4, 6}.(1) 写出关系R 的表示式; (2 )画出关系R 的哈斯图;(3) 求出集合B 的最大元、最小元.解:R={<1,1>,<1,2>,<1,3>,<1,4,<1,5>,<1,6>,<1,7>,<1,8>,<2,2>,<2,4>,<2,6>,<2,8>,<3,3>,<3,6>,<4,4>,<4,8>,<5,5>,<6,6>,<7,7>,<8,8>}(2)关系R 的哈斯图如图(3)集合B 没有最大元,最小元是:2四、证明题1.试证明集合等式:A ⋃ (B ⋂C )=(A ⋃B ) ⋂ (A ⋃C ).证明:设,若x ∈A ⋃ (B ⋂C ),则x ∈A 或x ∈B ⋂C , 即 x ∈A 或x ∈B 且 x ∈A 或x ∈C .即x ∈A ⋃B 且 x ∈A ⋃C ,即 x ∈T =(A ⋃B ) ⋂ (A ⋃C ),所以A ⋃ (B ⋂C )⊆ (A ⋃B ) ⋂ (A ⋃C ).反之,若x ∈(A ⋃B ) ⋂ (A ⋃C ),则x ∈A ⋃B 且 x ∈A ⋃C ,即x ∈A 或x ∈B 且 x ∈A 或x ∈C ,即x ∈A 或x ∈B ⋂C ,7即x∈A⋃ (B⋂C),所以(A⋃B) ⋂ (A⋃C)⊆ A⋃ (B⋂C).因此.A⋃ (B⋂C)=(A⋃B) ⋂ (A⋃C).2.试证明集合等式A⋂ (B⋃C)=(A⋂B) ⋃ (A⋂C).证明:设S=A∩(B∪C),T=(A∩B)∪(A∩C),若x∈S,则x∈A且x∈B∪C,即x∈A且x∈B或x∈A且x∈C,也即x∈A∩B或x∈A∩C,即x∈T,所以S⊆T.反之,若x∈T,则x∈A∩B或x∈A∩C,即x∈A且x∈B 或x∈A且x∈C也即x∈A且x∈B∪C,即x∈S,所以T⊆S.因此T=S.3.对任意三个集合A, B和C,试证明:若A B = A C,且A,则B = C.证明:设x∈A,y∈B,则<x,y>∈A⨯B,因为A⨯B = A⨯C,故<x,y>∈ A⨯C,则有y∈C,所以B⊆ C.设x∈A,z∈C,则<x,z>∈ A⨯C,因为A⨯B = A⨯C,故<x,z>∈A⨯B,则有z∈B,所以C⊆B.故得B=C.4.试证明:若R与S是集合A上的自反关系,则R∩S也是集合A上的自反关系.证明:R1和R2是自反的,∀x∈A,<x, x> ∈R1,<x, x> ∈R2,则<x, x> ∈R1∩R2,所以R1∩R2是自反的.。
离散数学第一第二次作业

第1部分命题逻辑一、单项选择题1.下列哪个语句是真命题()。
(A) 我正在说谎(B) 如果1+2 = 3,则雪是黑色的(C)如果1+2 = 5,则雪是黑色的(D)上网了吗2.命题公式为()→→()。
P Q P(A)重言式(B) 可满足式(C)矛盾式(D)等值式3.设命题公式P∧(Q→⌝P),记作G,则使G的真值指派为1的P,Q 的取值是()。
(A) (0,0) (B) (0,1) (C) (1,0) (D) (1,1)4.与命题公式P→(Q→R)等值的公式是()。
(A)(P∨Q)→R (B)(P∧Q)→R (C)(P→Q)→R (D)P→(Q∨R)5.命题公式(P∧Q)→P是()。
(A) 永真式(B) 永假式(C) 可满足式(D) 合取范式二、填空题1.P,Q为两个命题,当且仅当时,P Q∧的真值为1,当且仅当时,P Q∨的真值为0。
2.给定两个命题公式A,B,若时,则称A和B是等值的,记为A B⇔。
3.任意两个不同极小项的合取为式,全体极小项的析取式必为式。
4.设P:天下雨,Q:我们去郊游。
则⑴命题“如果天不下雨,我们就去郊游”可符号化为。
⑵命题“只有天不下雨,我们才去郊游”可符号化为。
⑶命题“我们去郊游,仅当天不下雨”可符号化为 。
5.设命题公式G =P ∧(⌝Q ∨R ),则使G 取真值为1的指派是 , , 。
6.已知命题公式为G =(⌝P ∧Q )→R ,则命题公式G 的析取范式是三、计算题1.将下列命题符号化:⑴ 李强不是不聪明,而是不用功;⑵ 如果天不下雨,我们就去郊游;⑶ 只有不下雨,我们才去郊游。
2.给出下列公式的真值表⑴ ()P Q R P Q R ∧→→∧∧⌝⑵ ()()()P Q Q R P R ⌝∨∧→→⌝∧⌝3.给P 和Q 指派真值1,给R 和S 指派真值0,试求出下列命题的真值:⑴ ()P Q R ∨∧ ⑵ ()()P R Q S →∧⌝→4.判断下列命题公式的类型:⑴()↔→⌝∨P Q P QP P Q R→∨∨⑵()()5.化简命题公式(()())→↔⌝→⌝∧。
离散数学II课程实验题(代数部分)上机作业

离散数学A(II)课程实验题(代数) hj120828一、基本要求:1、可选用C或C++等编程语言或平台进行编程实验,不可直接选用非自编算法库内容。
2、实验内容可在课程提供的实验题中选,或自己设计问题与相关算法题。
3、按时间及任务要求提交实验中完成的程序代码、可执行程序、程序开发说明文档,内容包括实验数据与结果等。
二、代数结构部分题1、设V1=<{a1, a2}, max >和V2=<{b1, b2}, min >是两个数系统, 其中max (x, y)表示x与y 中较大的数;min (x, y)表示x与y中较小的数。
max和min可以看作二元运算。
输入a1, a2, b1, b2为整数, 考虑积代数V1 × V2.(1)设积代数中的二元运算为*运算,输出它的运算表(2)输出积代数的单位元和零元2、设代数系统V1=<A, •>、V2=<A, ∗>、 V3=<A, ⊙>、 V4=<A, △>,A={ x|x∈Z,1≤x≤20},a•b= 2a+b,a∗b=max(a, b),a⊙b=(a+b) mod8 + 2,a△b=min(a-b),试设计算法并编程实验,要求:(1)试判断V1、V2、V3、V4是否为代数系统。
(2)试判断这些代数系统是否有左单位元与右单位元、零元,如存在,请求出。
(3)试分别判断代数系统中的运算是否满足交换律、结合律、幂等律、分配律、吸收律。
(4)试判断这些代数系统之间是否可以建立同态、同构映射,如存在,试建立。
3、设Klein四元群<G, *>,其中G={e,a,b,c},*运算表示如下,试设计算法并编程验证<G, *>是群。
*e a b cE e a b ca a e c bb bc e aC c b a e4、试设计算法并编程求出模6加群<Z6,+6>的子群。
国家开放大学电大本科《离散数学》网络课形考任务2作业及答案

国家开放大学电大本科《离散数学》网络课形考任务2作业及答案此任务2 g选择题题目1 无向完全图K4是()、选择一项:A、树 B、欧拉图 C、汉密尔顿图 D、非平面图题目2 已知一棵无向树T中有8个顶点,4度、3度、2度的分支点各一个,T 的树叶数为()、选择一项: A、4 B、8 C、3 D、5 题目3 设无向图G的邻接矩阵为 011111 0 0111 0 0 0 011 0 011 01 0 则G 的边数为( 选择一项: A、7 B、14 C、6 D、1 题目4 如图一所示,以下说法正确的是()、选择一项: A、 ((a, e), (b, c)}是边割集 B、{(a, e)}是边割集 C、{(d, e)}是边割集 D、((a, e)}是割边题目5 以下结论正确的是()、选择一项: A、有n个结点n-l条边的无向图都是树B、无向完全图都是平面图 C、树的每条边都是割边 D、无向完全图都是欧拉图题目6 若G是一个欧拉图,则G一定是()、选择一项: A、汉密尔顿图 B、连通图 C、平面图 D、对偶图题目7 设图G=, vGV,则下列结论成立的是()、选择一项:A、云 d做、)=2|% B、2>“ = |司 w C、 deg(v)=2|S| D、deg(v)=|E| 题目8 图G如图三所示,以下说法正确的是()、选择一项: A、(b, d}是点割集 B、{c}是点割集 C、{b, c}是点割集 D、 a是割点题目9 设有向图(a)、(b)、(c)与(d)如图五所示,则下列结论成立的是()、选择一项: (a)是费连通的 B、 (d)是强连通的 C、 (c)是强连通的D、 (b)是强连通的题目10 设有向图(a)、(b)、(c)与(d)如图六所示,则下列结论成立的是()、选择一项: A、 (b)只是弱连通的 B、 (c)只是弱连通的 C、 (a)只是弱连通的 D、 (d)只是弱连通的判断逝题目11 设图G是有6个结点的连通图,结点的总度数为18,则可从G中删去4条边后使之变成树、()选择一项:对错题目12 汉密尔顿图一定是欧拉图、()选择一项:对错题目13 设连通平面图G的结点数为5,边数为6,则面数为4、()选择一项:对错题目14 设G是一个有7个结点16条边的连通图,则G为平面图、()选择一项:对错题目15 如图八所示的图G存在一条欧拉回路、()选择一项:对错题目16 设图G如图七所示,则图G的点割集是{f}、()选择一项:对错题目172>瞒)=2圜设G是一个图,结点集合为V,边集合为E,则代衫()选择一项:对错题目18 设图G是有5个结点的连通图,结点度数总和为10,则可从G中删去6条边后使之变成树、()选择一项:对错题目19 如图九所示的图G不是欧拉图而是汉密尔顿图、()选择一项:对错题目20 若图 G=,其中 V=( a, b, c, d }, E={ (a, b), (a, d), (b, c), (b, d)},则该图中的割边为(b, c)、()选择一项:对。
国家开放大学电大本科《离散数学》网络课形考任务2作业及答案

A. 有n个结点n-1条边的无向图都是树
B. 无向完全图都是平面图
C. 树的每条边都是割边
D. 无向完全图都是欧拉图
题目6
若G是一个欧拉图,则G一定是( ).
选择一项:
A. 汉密尔顿图
B. 连通图
C. 平面图
D. 对偶图
题目7
设图G=<V, E>,v∈V,则下列结论成立的是 ( ) .
选择一项:
选择一项:
对
错
题目17
设G是一个图,结点集合为V,边集合为E,则 ( )
选择一项:
对
错
题目18
设图G是有5个结点的连通图,结点度数总和为10,则可从G中删去6条边后使之变成树.( )
选择一项:
对
错
题目19
如图九所示的图G不是欧拉图而是汉密尔顿图.( )
选择一项:
对
错
题目20
若图G=<V, E>,其中V={ a, b, c, d },E={ (a, b), (a, d),(b, c), (b, d)},则该图中的割边为(b, c).( )
题目8
图G如图三所示,以下说法正确的是 ( ).
选择一项:
A. {b, d}是点割集
B. {c}是点割集
C. {b, c}是点割集
D. a是割点
题目9
设有向图(a)、(b)、(c)与(d)如图五所示,则下列结论成立的是( ).
选择一项:
A. (a)是强连通的
B. (d)是强连通的
C. (c)是强连通的
选择一项:
对
错
题目12
汉密尔顿图一定是欧拉图.( )
选择一项:
对
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《离散数学》课程作业(2)-------数理逻辑部分
一、 填空题
1. 将几个命题联结起来,形成一个复合命题的逻辑联结词主要有否定、 、 、 和等值。
2、命题公式G=(P ∧Q )→R ,则G 共有 个不同的解释;把G 在其所有解释下所
取真值列成一个表,称为G 的 ;解释(⌝P ,Q ,⌝R )或(0,1,0)使G 的真值为 。
3、 已知命题公式R Q P G →∧⌝=)(,则G 的析取范式是 。
4、 求公式)()(R P Q P ∧⌝∨∧的主析取范式 。
5、 设命题公式)(R Q P G →⌝→=,则使公式G 为假的解释是 、 和 。
6、在谓次词逻辑中将下面命题符号化:在北京工作的人未必都是北京人(提示:设F (x ):x
在北京工作。
G (x ):x 是北京人。
) 。
7、将公式化成等价的前束范式,=→∃→⌝∃∃)))()((),((x R z zQ y x yP x 。
8、设谓词的定义域为},,{c b a ,将表达式)()(x xS x xR ∃∧∀中的量词消除,写成与之等价的
命题公式是 。
二、 单项选择题
1、下列语句中,( )是命题。
A .下午有会吗?
B .这朵花多好看呀!
C .2是常数。
D .请把门关上。
2、一个公式在等价意义下,下面哪个写法是唯一的( )。
A .析取范式
B .合取范式
C .主析取范式
D .以上答案都不对
3、设命题公式P Q P G →∧=)(,则G 是( )。
A. 恒假的
B. 恒真的
C. 可满足的
D. 析取范式
4、设命题公式)(),
(P Q P H Q P G ⌝→→=→⌝=,则G 与H 的关系是( )。
以上都不是。
.;.;.;.D H G C G H B H G A =⇒⇒
5、已知命题))((R Q P G ∧→⌝=,则所有使G 取真值1的解释是( )。
A (0,0,0),(0,0,1),(1,0,0)
B (1,0,0),(1,0,1),(1,1,0)
C (0,1,0),(1,0,1),(0,0,1)
D (0,0,1),(1,0,1),(1,1,1)
6、设I 是如下一个解释,0
101),(),(),()
,(},,{b b P a b P b a P a a P b a D =, 则在解释I 下取真值为1的公式是( )。
),(.);,(.);,(.);,(.y x yP x D x x xP C y x yP x B y x yP x A ∃∀∀∀∀∀∃
7、下面给出的一阶逻辑等价式中,( )是错的。
)).
(()(.));
(()(.);
()())()((.);
()())()((.x B A x x xB A D x A x x xA C x xB x xA x B x A x B x xB x xA x B x A x A →∀=∀→⌝∃=⌝∀∀∨∀=∨∀∃∨∃=∨∃
三、 计算题 1. 求命题公式⌝(P ∨Q )↔(P ∧Q )的析取范式与合取范式。
2、通过求主析取范式判断下列命题公式是否等值。
(1)(P∧Q)∨(⌝P∧Q∧R);
(2)(P∨(Q∧R))∧(Q∨(⌝P∧R));
3、用真值表判断下列公式是恒真?恒假?可满足?
(1)(P∧⌝P)↔Q
(2)⌝(P→Q)∧Q
(3)((P→Q)∧(Q→R))→(P→R)
4、设解释I为:
(1)定义域D={-2,3,6};
(2)F(x):x≤3;
G(x):x>5。
在解释I下求公式∃x(F(x)∨G(x))的真值。
5、设I 是如下一个解释:
1
)3,3(1)2,3(1)3,2(1)2,2(1)3(0)2(2)3(3)2(2},3,2{G G G G F F f f a D =,试求下列公式在I 下的真值:
))).
(,())((()2));,()(()1x f x G x f F x a x G x F x ∧∃∧∀
6、设F (x ,y ):x 对y 过敏;M (x ):x 是人;G (y ):y 是食物。
试将命题“某些人对某些
食物过敏”符号化。
四。
证明题
1. 利用基本等价式证明下列命题公式为恒真公式。
((P →Q )∧(Q →R ))→(P →R )
((P ∨Q )∧⌝(⌝P ∧(⌝Q ∨⌝R )))∨(⌝P ∧⌝Q )∨(⌝P ∧⌝R )
2. 证明等价式R R P R Q R Q P =∧∨∧∨∧⌝∧⌝)()())((。
3. 利用形式演绎法证明:{P →Q , R →S ,P ∨R }蕴涵Q ∨S 。
4. 利用形式演绎法证明:},
,,,{T R S T S R P Q P ⌝→⌝→⌝→∨蕴涵Q 。
5 .判断下面推理是否正确,并证明你的结论。
如果小王是理科生,他的数学成绩必好。
如果小王不是文科生,他必为理科生。
小王没学好数学(即数学成绩不好)。
所以,小王是文科生。
(提示:先将命题符号化,再用形式演绎法推出正确与否。
)
6. 利用一阶逻辑的基本等价式,证明:
∀x∀y(F(x)→G(y))=∃xF(x)→∀yG(y)
(注:可编辑下载,若有不当之处,请指正,谢谢!)。
