中环杯五年级试题
第十三届中环杯五年级初赛试题附答案分析 2
第十三届“中环杯”小学生思维能力训练活动五年级选拔赛1.计算:31.3×7.7+11×8.85+0.368×230=()。
2.宠物商店有狃狸犬和西施犬共2012只,其中母犬1110只,狐狸犬1506 只,公西施犬202只。
那么母狐狸犬有_( )只。
3.一个数A为质数,并且A+14, A+18, A+32, A+36也是质数。
那A的值是( )4.一个口袋中有50个编上号码的相同的小球,其中编号为1,2,3,4,5的小球分别有2,6,10,12,20个。
任意从口袋中取球,至少要取出()个小球,才能保证其中至少有7个号码相同的小球。
5.表格中定义了关于“*”的运算,如3*4=2。
(1*2)*(1*2)*……(1*2)=()。
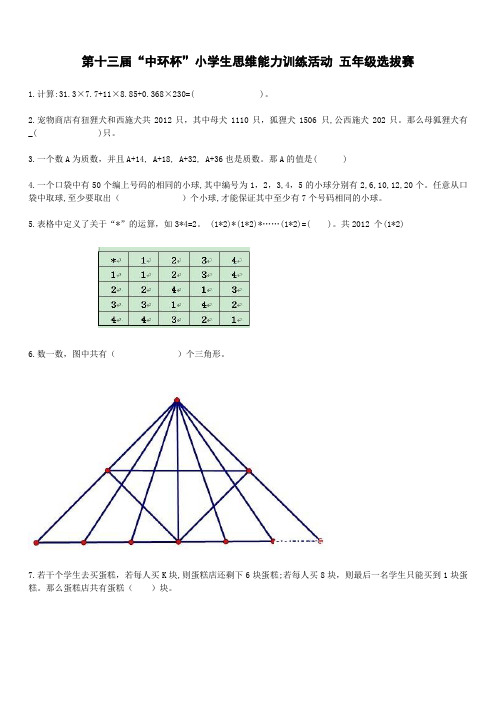
共2012 个(1*2)6.数一数,图中共有()个三角形。
7.若干个学生去买蛋糕,若每人买K块,则蛋糕店还剩下6块蛋糕;若每人买8块,则最后一名学生只能买到1块蛋糕。
那么蛋糕店共有蛋糕()块。
8.—张正方形纸,如图所示折叠后,构成的图形中,角x的度数是()。
9.A、B两地相距66千米,甲、丙两人从A地向B地行走,乙从B地向AI地行走。
甲每小时行12千米,乙每小时行10千米,丙每小时行8千米。
三人同时出发()小时后, 乙刚好走到甲、丙两人距离的中点。
10.有()个形如abcdabcd的数能被18769 整除。
11.小明带24个自制的纪念品去伦敦奥运会卖。
早上每个纪念品卖7英镑,卖出的纪念品不到总数的一半。
下午他对每个纪念品的价格进行打折,折后的价格仍是—个整数。
下午他卖完了剩下的纪念品。
全天共收入120英镑。
那么早上他卖出了()个纪念品。
12.如图,在一个四边形ABCD中,AC,BD相交于点O。
作三角形DBC的高DE,联结AE。
若三角形ABO的面积与三角形DCO的面积相等,且DC=17厘米,DE=15厘米,则阴影部分的面积为( )平方厘米。
13.五名选手在一次数学竞赛中共得414分;毎人得分互不相等且都是整数,并且其中得分最高的选手得了92分,那么得分最低的选手至少得()分,最多得()分。
中环杯五年级试题

第十三届“中环杯”五年级决赛考题1、我们有下列的公式:2、有一类四位数,除以5余1,除以7余4,除以11余9。
这类四位数中最小的一个是几。
3、有A,B,C,D,E五个人,其中每个人永远说谎话或者永远说真话,并且他们彼此都互相知道对方的行为。
A说B是说谎话者,B说C是说谎者,C说D是说谎者,D说E是说谎者。
那么,这五个人中最多有几位说谎者。
4、在1-200之间有几个数,其所有不同的素因数之和为16(比如:12的所有不同的素因数为2,3,其和为2+3=5)。
5、某次数学比赛,计分方法有两种,分别是:第一种,答对一题给5分,答错不给分,不答给2分,第二种,先给39分,然后答对一题给3分,答错扣1分,不答不给分。
某个考生完成所有题目后,用两种方法计分,都得71分。
则这个考生未答得题目有几题。
6、在右图的数字谜中,每个字母代表了一个数字。
不同的字母代表了不同的数字,相同的字母代表了相同的数字。
则T=()7、平行四边形ABCD中,点P,Q,R,S分别为边AB,BC,CD,DA的中点,而点T 为线段SR的中点。
已知四边形ABCD的面积为120平方厘米,则三角形PQT面积为()平方厘米。
8、已知一个筛子的六个面上分别写了六个不同的正整数,这六个正整数的和为60。
现在对这个筛子进行这样的操作:每次操作选取正方体的一个顶点,将包含这个顶点的三个面上的数字都加1,经过多次的操作后,这个正方形的所有面上的数字都相同了。
满足条件的不同的筛子有()种(六个面的数字选定后就算一种,不考虑这六个数字如何放在筛子上)。
9、定义an=1+3+32+……3n(n为正整数),比如:a4=1+3+32+……34。
那么a1,a2……a2013中,有()各数是7的倍数。
11、有一对四位数对(2025,3136),拥有如下的特点:每个数都是完全平方数,并且第二个四位数的每个数码比第一个四位数的对应数码都大1。
请找出所有满足这个个点的五位数数对。
第九届中环杯五年级初赛

( 3、 6.1 6.3 6.5 9.9 6.2 6.4 6.6 9.8
)。
4、如下图,3 个“△”和 1 个“◇”与 10 个“*”平衡,1 个“◇”与 1 个“◇”和 2 个“*” 平衡,那么( )个“*”和 1 个“◇”平衡。
5、老师带的钱买 14 支铅笔和 12 本练习本,正好用完。如果买 20 支铅笔和 10 本练习本也 正好用完,如果老师把带的钱全部买铅笔,可以买( )支。
置叠加的立方体个数, 则这个几何体的表面积是多少。 并画出主视图。 5. 如图,编号为 1~7 的七块拼板都是由 5 个 11 的小正方形组成的。请你从中选出 5 块, 拼成一个如“答题图” 5 5 的大正方形。请你在“答题图”上画出你的拼法(要求描线清 晰) ,并标上所用拼板的编号,每个拼板只能用一次(拼板正,反面可翻转拼搭)
第九届“中环杯”小学生思维能力训练活动五年级初赛
一、填空题9 ( 1、已知 A * B AB A B, 则 1*9*9*9
共10次运算
) 。
2、在正整数 1,2,3,4„..中,第 311 个不能被 5 整除的数是(
) 。
答题图
6、某人从某地向前走 16 米,原地向右转 18 ,再向前走 16 米,再向右转 18 这样走 下去,他第一次回到出发点时,一共走了( )米。
7、 一只船被发现漏水时, 已经进了一些水, 水匀速进入船内。 如果 10 人淘水, 3 小时淘完; 如果 5 人淘水,8 小时淘完,如果要求 2 小时淘完,需要安排( )人淘水。 8、红星小学组织学生划船。若乘坐大船,除 1 条船坐 6 人外,其余每船均坐 17 人。若乘坐 小船,则除 1 船坐 2 人外,其余每船均坐 10 人。如果学生的人数超过 100 人,不到 200, 那么学生共有( )人。 9、甲,乙两人从 A,B 两地同时出发相向而行,甲每分钟行 70 米,乙每分钟行 50 米。出发一 段时间后,两人在距中点 100 米处相遇。如果甲出发后在途中某地停留了一会儿,两人还将 在距中点 250 米处相遇。那么甲在途中停留了( )分钟。 10、某个大于 1 的自然数分别除 442,297,210,得到相同的余数,则该自然数为( ) 。 二、动手动脑题: (每题 10 分,共 50 分) 1、A,B 两地相距 27 千米。甲,丙两人从 A 地向 B 地行走,乙从 B 地向 A 地行走.甲每小时 行 4 千米,乙每小时行 3 千米,丙每小时行 2 千米。三人同时出发,问几小时后甲刚好走到 乙,丙两人距离的中点?要求写出关键的解题推理。 2、已知△ABC 的面积为 5,且 BD=2DC,AE=ED.求阴影部分面积。要求写出关键的解题推理过 程。
第九届中环杯数学思维能力训练五年级决赛解析

)。
【考点】约数与倍数、质因数分解 【解析】设 a, b m , a Am , b Bm ,那么 a b 185 可化简成
3
A3m3 Bm 185 ,即 m A3m2 B 185 5 37 ,所以 m 5 , 25 A3 B 37 ,
第九届“中环杯”小学生思维能力训练活动 五年级决赛
一、填空题: 1、 99
999 的尾数为(
99
)。
99
【考点】周期问题 【解析】9 的幂的尾数周期是:9,1。 99 是奇数,所以 99
999 的尾数是 9。 b c b c b c b c 注:幂运算需要注意的地方: a a a , a a a ,
那么从费用上来考虑应选择丙队。
4、如图,三角形 ABC 、三角形 ACD 与三角形 AEF 均为等边三角形, AE BC ,
AF CD , GH AE 。如果三角形 ABC 的面积是 10cm2 ,那么三角形 EGH 的面积是
多少?
A
A
B E D G C F
H
D
C
B
【考点】直线型面积的计算,平行线比例关系 【解析】在直角三角形 AEG 中, EAG 30 ,所以有 EG
所以 285 头牛可以吃 840 285 180 8 天。
2
【答案】8 天 10、 A 、 B 、 C 三人进行小口径步枪射击比赛,每个人射击 6 次,并且都得了 71 分,三人共 18 次的得分情况从小到大排列为:1、1、1、2、2、3、3、5、5、10、10、10、20、20、20、25、 25、 50。 已知 A 首先射击两次, 共得 22 分; 请根据条件判断, 是 ( ) C 第一次射击只得 3 分, (填 A 、 B 或 C )击中了靶心(击中靶心得 50 分) 。 【考点】逻辑推理 【解析】 A 得 71 分,且前两次得到 22 分,那么 A 不可能有一次得到 50 分,且 22 2 20 , 后四次得到 71 22 49 分,如果其中没有 25 分,那么最多还有 2 个 20 分,不管取多少 个 20 分,都不可能取到 49 分,所以 49 25 20 3 1 。 再考虑 C ,后面 5 次要拿到 68 分,如果其中有一次 50 分,那么剩下 4 次要拿到 18 分,只 能是18 10 5 2 1 。所以 C 可能击中靶心。 最后考虑 B ,如果 B 击中了靶心,那么他其余 5 次要拿到 21 分,那么还剩下的 20 分和 25 分只能是 C 拿, 3 个 10 分页必须至少由 C 拿 2 个,71 3 20 25 10 10 3 ,C 还 得拿 1 个 3 分,但是 3 分已经没有了,矛盾。 【答案】 C 二、动手动脑题: 1、50 个数排成一行,除了第 1 个数以外,每个数的 3 倍加 1 恰好等于它后面那个数。这一行 最左边的几个数是这样的:0、1、4、13 ,那么,最右边的数除以 7 余几? 【考点】周期问题,余数定理 【解析】利用余数加法定理和乘法定理,可得到这些数除以 7 的余数,依次为:0、1、4、 6、5、2、0、1、4、6、5、2,不难看出其中的周期性,以“0、1、4、6、5、2”为一 个周期。 50 6 8 2 ,所以最右边的数除以 7 余 1。 【答案】1 2、甲、乙两人的信纸一样多,信封也一样多,甲写一封信用一张信纸,乙写一封信用三张信 纸。结果甲的信封用完时还剩 40 张信纸,乙的信纸用完时还剩 60 个信封。原来他们各有多少 个信封和多少张信纸? 【考点】盈亏问题 【解析】每封信: 1 张信纸 多 40 张信纸 3 张信纸 多 60 个信封 第二个条件可以转化为 每封信: 3 张信纸,少 60 3 180 张信纸 所以信封有 40 180 3 1 110 个,信纸有110 1 40 150 张。 【答案】信封有 110 个,信纸有 150 张。
第十五届中环杯初赛五年级试题解析

第十五届中环杯初赛五年级试题解析Coca-cola standardization office【ZZ5AB-ZZSYT-ZZ2C-ZZ682T-ZZT18】第十五届“中环杯”小学生思维能力训练活动五年级选拔赛1、已知2468135713572468m n++++++-=++++++,其中 m,,n 是两个互质的正整数,则10______m n +=。
【考点】分数计算【答案】110 分析:2016910920110162020=-=⨯+=原式。
2、D 老师家里有五个烟囱,这五个烟囱正好从矮到高排成一排,相邻两个烟囱之间的高度差为 2 厘米,其中最高的烟囱又正好等于最矮的两个烟囱的高度之和,则五个烟囱的高度之和是________厘米。
【考点】等差数列,方程【答案】50分析:设这五个烟囱分别为 x-4,x-2,x ,x+2,x+4,则 x+4=x-2+x-4,x=10, 和为 5x=50。
3、已知()()22332014a b c d =+⨯-,其中 a 、b 、c 、d 是四个正整数,请你写出满足条件的一个乘法算式:___________。
【考点】数的拆分,分解质因数【答案】答案不唯一 分析:2014=1×2014=2×1007=19×106=38×53()()22335932+⨯-4、一个长方体的长、宽分别为 20 厘米、15 厘米,其体积的数值与表面积的数值相等,则它的高为______厘米(答案写为假分数)。
【考点】立体几何,方程 【答案】6023分析:设高为 h ,则 ()60201520152015223h h h h ⨯⨯=⨯++⨯=,则。
5、一次中环杯比赛,满分为 100 分,参赛学生中,最高分为 83 分,最低分为 30 分(所有的分数都是整数),一共有 8000 个学生参加,那么至少有_____个学生的分数相同。
【考点】抽屉原理【答案】149分析:833015480005414881481149-+=÷=+=,…,。
第7届中环杯五年级初赛

3. 下图是一个正方形,请你将它划分成 10 个小正方形。
4. 下图是一张边长为 5 厘米的方格纸,借助没有刻度的直尺,一共能在这张方格纸上画出 ( )种不同大小的正方形(正方形的面积必须是整平方厘米数) ,它们的面积分 别是( )平方厘米。
5. 请补全下列各图,使之成为关于给定直线的轴对称图形。
第七届“中环杯”小学生思维能力训练活动五年级复赛
一、填空题: (请把正确答案填在括号内,每题 5 分,共 50 分) 1. 5.6 2.7 0.48 7.4 0.12 37 0.28 9 ( )
2. 1111 2222 2222 3333 3333 4444 4444 5555 (
)
3. 121122 123 124 2004 2005 2006 的乘积的末尾有( 4.已知: 1 2 6,3 4 14,5 7 24, 那么, 10 20 ( ) 。
)个零。
5. 如图是由 15 块同样大小的长为 28 厘米的长方形地砖铺成的图形。这个图形的周长是 ( )厘米,面积是( )平方厘米。
6.左、中、右三棵树上分别停着同样多的麻雀,后来从中间树上飞走了一些麻雀,停在左右 两边的树上去了。 这时左边树上的麻雀比中间树上多 9 只, 右边树上的麻雀比左边的少 3 只, 且正好是中间树上麻雀的 3 倍。原来三棵树上共停了( )只麻雀。 7.小明有个三层书架,在一次大扫除时,他把这个书架上的书全部搬了出来,整理完以后又 平均放入每一层。 爸爸回来一看, 发现第一层的书是原来的 1.2 倍, 第二层的书比原来少了 7 本,第三层的书比原来多了 1 本。这个书架上共有书( )本。 8.李经理要从公司到分厂去开会。他以 75 千米 小时 的车速开了 5 分钟后发现,按此速前进 将要迟到 10 分钟。于是他加速到 90 千米 小时 继续开,结果反而提前 5 分钟到达。那么,公 司到分厂的距离是( )千米。
五年级中环杯竞赛试题
第九届“中环杯”小学生思维能力训练活动区 学校 班姓名 准考证号 907999.99799.9979.997.998.9989.99899.998999.99()+++++++=201020102008200820082010⨯-⨯=( )。
将自然数按下图从1开始,2处拐弯,4处拐弯,7、11、16 处拐弯。
第20次拐弯的数是( )。
161514131222222221234520052006+++++++ 的和的末位数是( )。
如果32347;454567830∆=+=∆=++++=,按此规律计算:①74=( )∆② 321,x x ∆==()。
一艘客船在两个码头之间航行,顺水5小时行完全程,逆水7小时行完全程。
水速每小时5千米,那么两码头之间的距离是()千米。
一只魔袋里装有30种不同颜色的魔球各30只,现在请你闭上眼睛到袋中去摸球,每次限摸3只。
要使摸出的球至少有三种颜色是不少于3只的,那么至少要摸( )次。
将从8开始的11个连续自然数填入下图中的圆圈内,要使每边上的三个数字和都相等,共有( )种填法。
三角形ABC和三角形D EF是两个完全一样的直角三角形,如下图,把它们重叠在一起,那么阴影部分的面积为()2cm。
F2005年小明家养了一只大母羊,第二年春天它生了2只小公羊和3只小母羊。
每只小母羊从出生的第三年起也生了2只小公羊和3只小母羊。
那么到2010年,小明家共有()只羊。
下图两个完全一样的图形都是由5个小正方形组成的,请把它们分成四块,拼成一个大正方形,在原图上画出划分方法,并在空白处画出所拼的大正方形。
下图是由五个同样的正方形组成的图形,请你将它平均分成3份,要使每份的形状、大小完全一样。
下图是边长为2的三个完全一样的正方形,将它分成形状大小完全一样的四块,再拼成一个长方形,在下图上作图表示如何分法,并在空白处画出所拼的长方形。
并求这个长方形的周长。
“中环杯”-5年级-第11届-初赛
第十一届中环杯五年级初赛填空题:(每题7分,共56分)1.计算3.6 X 42.3 X3.75 – 12.5 X 0.423 X 28 =2.3支铅笔和5支圆珠笔的价钱一共是A元,6支铅笔和3支圆珠笔的价钱一共是B元,那么一支铅笔和一只圆珠笔的价钱一共是()元(用含有A、B的式子表示)。
3.将自然数按从小到大都顺序无间隔地排成一列:123456789101112……,则左起第2010位上的数字是()。
4.一个长42厘米,宽24厘米,高36厘米的长方体木块,表面涂上红漆,再把它锯成若干个相同大小的小正方形且没有废料。
则表明没有涂上红漆的小正方体至少有()块。
5.如图,小正方形的3/5被阴影部分覆盖,大正方形的7/8被阴影部分覆盖。
大正方形的阴影部分面积比小正方形的阴影部分面积大11平方米,那么小正方形的面积是()平方米6.小明站在一条直行的铁道旁,从远处向小明驶来的火车拉响汽笛,过了一会儿,小明听见汽笛声,再过27秒钟,火车行驶到他面前。
已知火车的速度是34米/秒,音速是340米/秒,那么火车拉响汽笛时距离小明()米远。
7.某校五年级的同学,每人订阅了《青少年科技》、《小朋友》、《故事大王》、《少年科学》、《少年文艺》中的至少2种刊物。
那么,这个年级至少要有()名学生,才能保证他们中至少有10人订的报刊杂志完全相同。
8.李师傅某天生产了一批零件,把他们分成甲、乙两堆摆放。
如果从甲堆零件中拿出15个放到乙堆中,则两堆零件的个数相等;如果从乙堆零件中拿出15个放到甲堆中,则甲堆的零件个数是乙堆的4倍。
甲堆原有零件()个,李师傅这天共生产了()个零件。
动手动脑题:1.快、中、慢三辆车同时从同一地点出发,沿着同一条公路追赶前面的一个骑车人。
已知这三辆车分别是每小时54千米,22千米、12千米,快车和中车分别用2小时、6小时追上了骑车人。
那么慢车要用多少时间追上骑车人?(本题10分)2.有7张卡片,上面分别写着1、2、3、4、5、6、7这七个数字。
第十五届“中环杯”初赛五年级 试题解析
第十五届“中环杯”小学生思维能力训练活动五年级选拔赛1、已知2468135713572468m n++++++-=++++++,其中 m,,n 是两个互质的正整数,则10______m n +=。
【考点】分数计算【答案】110 分析:2016910920110162020=-=⨯+=原式。
2、D 老师家里有五个烟囱,这五个烟囱正好从矮到高排成一排,相邻两个烟囱之间的高度差为 2 厘米,其中最高的烟囱又正好等于最矮的两个烟囱的高度之和,则五个烟囱的高度之和是________厘米。
【考点】等差数列,方程【答案】50分析:设这五个烟囱分别为 x-4,x-2,x ,x+2,x+4,则 x+4=x-2+x-4,x=10, 和为 5x=50。
3、已知()()22332014a b c d =+⨯-,其中 a 、b 、c 、d 是四个正整数,请你写出满足条件的一个乘法算式:___________。
【考点】数的拆分,分解质因数【答案】答案不唯一 分析:2014=1×2014=2×1007=19×106=38×53()()22335932+⨯-4、一个长方体的长、宽分别为 20 厘米、15 厘米,其体积的数值与表面积的数值相等,则它的高为______厘米(答案写为假分数)。
【考点】立体几何,方程 【答案】6023分析:设高为 h ,则 ()60201520152015223h h h h ⨯⨯=⨯++⨯=,则。
5、一次中环杯比赛,满分为 100 分,参赛学生中,最高分为 83 分,最低分为 30 分(所有的分数都是整数),一共有 8000 个学生参加,那么至少有_____个学生的分数相同。
【考点】抽屉原理【答案】149分析:833015480005414881481149-+=÷=+=,…,。
6、对 35个蛋黄月饼进行打包,一共有两种打包规格:大包袋里每包有9 个月饼,小包装里每包有 4个月饼。
五年级中环杯历届试题
五年级中环杯历届试题五年级中环杯历届试题导语:在所有好的,不好的情绪里,毫无预兆地想念你,是我不可告人的隐疾。
以下小编为大家介绍五年级中环杯历届试题文章,欢迎大家阅读参考!五年级中环杯历届试题一、单项选择题(在下列每题的四个选项中,只有一个选项是符合试题要求的。
请把答案填入答题框中相应的题号下。
每小题1分,共23分)1. 健康牛的体温为( )。
A. 38~39.5°CB. 37~39°CC. 39~41°CD. 37.5~39.5°C2. 动物充血性疾病时,可视黏膜呈现( )。
A. 黄染B. 潮红C. 苍白D. 发绀3. 心肌细胞脂肪变性是指( )。
A. 心肌间质脂肪浸润B. 心肌脂肪组织变性C. 心外膜脂肪细胞堆积D. 心肌细胞胞质中出现脂滴4. 化脓菌入血、生长繁殖、产生毒素、形成多发性脓肿,该病是( )。
A. 脓毒血症B. 毒血症C. 败血症D. 菌血症5. 细胞坏死过程中,核变小、染色质浓聚,被称之为( )。
A. 核溶解B. 核分裂C. 核固缩D. 核碎裂6. 在慢性炎症组织中,最多见的炎症细胞是( )。
A.中性粒细胞 B.嗜酸性粒细胞C.淋巴细胞 D.肥大细胞7. 商品蛋鸡中暑时的胸肌颜色( )。
A.暗红色 B.鲜红色 C.浅白色 D.基本正常8. 甲硝唑主要用于下列哪种情况( )。
A. 大肠杆菌病B. 抗滴虫和厌氧菌C. 需氧菌感染D. 真菌感染9. 下列动物专用抗菌药是( )。
A.环丙沙星 B.氧氟沙星 C.强力霉素 D.泰乐菌素10.被病毒污染的场地,进行消毒时,首选的消毒药是( )。
A.烧碱 B.双氧水 C.来苏儿 D.新洁尔灭11.解救弱酸性药物中毒时加用NaHCO3的目的是( )。
A. 加快药物排泄B. 加快药物代谢C. 中和药物作用D. 减少药物吸收12.国家强制免疫的动物疫病不含( )。
A.禽流感 B.蓝耳病 C.猪瘟 D.新城疫13.鸭传染性浆膜炎的病原为( )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014中环杯五年级试题
一、填空题(每小题5分,共50分)
1. 计算:++1/2x(32-12)=_________
2. 420x814x1616除以13的余数为__________
3. 五年级有甲乙两班,甲班学生人数是乙班学生人数的5/7,如果从乙班调3人去甲班,甲班学生人数就是乙班学生人数的4/5,甲班原有学生_________人
4. 已知990x991x992x993=966428A91B40
AB=
5. 如图,△ABC面积为60,E、F分别为AB和AC上的点,满足AB=3AE,AC=3AF,点D 是线段BC上的动点,设△FBD的面积为S1, △EDC的面积为S2,则S1x S2的最大值为__________.
6.如图,在每个方框中填入一个数字,使得乘法竖式成立,则这个算式乘积的最大值和最小值的之差为__________.
8. 有15位选手参加一个围棋锦标赛,每两个人之间需要比赛一场,赢一场得2分,平一场各得1分,输一场得0分,如果一位选手的得分不少于20分,他就能获得一份奖品,那么,最多有_______位选手获得奖品。
9. 在一场1000米的比赛中,一个沙漏以相同的速率在漏沙了,漏出来的沙子都掉入
一个杯中(这个沙漏是在比赛进行了一段时间后才开始漏沙的),小明以匀速进行
跑动,当他跑到200米的时候,第a颗沙子正好掉入杯中,当他跑到300米的时候,第be颗沙子正好掉入杯中, 当他跑到400米的时候,第de颗沙子正好掉入杯中, 当他跑到500米的时候,第fg颗沙子正好掉入杯中(a、b、c、d、e、f、g都是0-9的数字,
并且它们的值可以相等),我们发现:(1)a是2的倍数,(2)be是一个质数;(3)de是5的倍数;(4)fg是3的倍数,那么四位数debe=__________(如果有多个解,需要将多个解都写在横线上)。
10. 如图a,7个汉字写在图中的7个圆圈中,要求从某一个圆圈开始,沿着线段一笔
画这个图形(所有圆圈都要走到,而且只能走一次),将这个一笔画路径上的字连
成字串(如图b,从“中”开始一笔画,得到的字串为“中环难杯真的好”)。
那么
能够组成的不同字串有_________个。
11. 如图两个正方形ABEG,GECD的面积为m平方厘米,阴影部分的面积为n平方厘米,已知m、n都是正整数,则正方形ABEG的边长为_______厘米。
二、动手动脑题(每小题10分,共50分,除第15题外请给出详细解题步骤)
12. 两人同时从AB两地出发,相向而行,甲每小时行千米,乙每小时行10千米,甲
行30分钟,到达恒生银行门口,想起来自己的信用卡没有带,所以他原速返回A地去拿卡,找到卡后,甲又用元素返往B地,结果当乙达到A地时,甲还需要15分钟到达B 地,那么A、B间的距离是多少厘米?
13. 如果一个数的奇约数个数有2m个(m为自然数),则我们称这样的数为“中环数”,比如3的奇约数有1,3,一共2=21,所以3是一个“中环数”。
再比如21的奇约数有
1,3,7,21,4=22,所哟21 也是一个中环数。
我们希望能找到n个连续的中环数。
求n 的最大值。
14. 下左图是一个奇怪的黑箱子,这个额黑箱子有一个输入口,一个输出口,我们在输入口输入一个数字,那么在输出口就会产生一个数字结果,其遵循的规则是:(1)如果输入的是奇数k输出的是,4k+1
(2)如果输入的是偶数k,输出的是,k+2
比如输入的是数字8,那么输出的就是8+2=10, 输入的是数字3,那么输出的就是3x4+1=13. 现在将3个这样的黑箱子串联起来,如下右图,这样第一个黑箱子的输出成为第二个黑箱子的输入,依次类推,比如输入的数字16,经过第一个黑箱子,得到的结果是8,这个8就作为第二个黑箱子的输入,经过第二个黑箱子,得到结果4,这个4就作为第三个黑箱子的输入,经过第三个黑箱子,得到结果2,这个2结果就是最后的输出了。
我们可以用16-8-4-2来表示这样的过程。
现在,美羊羊,喜羊羊,懒羊羊,羊爸爸在这个串联的黑箱子输入串输入不同的正整数,其中羊爸爸输入的数字最大,得到的4个最终输出结果竟然是相同的,当这个输出结果最小时,求:羊爸爸的输入值是多少?
15. 如果我们将很多边长为1的正方形放入等腰△ABC中,BC边上的高为AH,AB和BC 的长度都是正整数,要求所有小正方形都有两条边与BC平行(如图所示),先放最下面一层,从两边往中间放(最靠边的小正方形的一个顶点正好在三角形的边上,直到中间的空隙放不下一个小正方形为止,依次类推,不断地往上面叠放小正方形,
点到无法往上叠为止,我们发现,每层的中间都没产生空隙,而且BC/AH<8,最后整个△ABC内一共放了330个小正方形,求BC长度的最大值
15.(1)你能将下面的长方形图纸分隔成全等的4个图形吗(如参考图)?请给出不同于参考图的另外三种分隔方法。
(2)画一个封闭的环,水平或竖直穿过相邻的单元格,环不能交叉或重叠,下图就是一些不允许出现的情况。
下图中有数字的单元格不能作为环的一部分,单元格内的数字表示其周围八个相邻的单元格内被环占住的个数,请在图中画出这个环。
答案
本文来源于爱教网:上海中考微信(shzhongkao1)为广大家长及孩子提供:上海初中阶段相关信息,包括初中数学、初中英语、初中物理、初中化学等科目的学习方法,还提供中考政策、考试说明、中考择校等中考最新资讯。
