工程力学第十章答案高斌
大学《工程力学》课后习题解答-精品
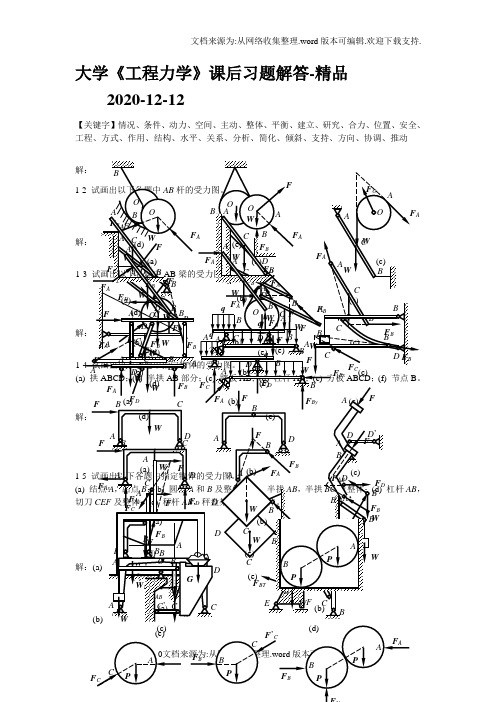
大学《工程力学》课后习题解答-精品2020-12-12【关键字】情况、条件、动力、空间、主动、整体、平衡、建立、研究、合力、位置、安全、工程、方式、作用、结构、水平、关系、分析、简化、倾斜、支持、方向、协调、推动(e)(c)(d)(e)’CD2-2 杆AC 、BC 在C 处铰接,另一端均与墙面铰接,如图所示,F 1和F 2作用在销钉C 上,F 1=445 N ,F 2=535 N ,不计杆重,试求两杆所受的力。
解:(1) 取节点(2) AC 与BC 2-3 水平力F A 和D 处的约束力。
解:(1) 取整体(2) 2-4 在简支梁,力的大小等于20KN ,如图所示。
若解:(1)(2)求出约束反力:2-6 如图所示结构由两弯杆ABC 和DE 构成。
构件重量不计,图中的长度单位为cm 。
已知F =200 N ,试求支座A 和E 的约束力。
解:(1) 取DE (2) 取ABC2-7 在四连杆机构ABCD 试求平衡时力F 1和F 2解:(1)取铰链B (2) 取铰链C 由前二式可得:F FF ADF2-9 三根不计重量的杆AB,AC,AD在A点用铰链连接,各杆与水平面的夹角分别为450,,450和600,如图所示。
试求在与O D平行的力F作用下,各杆所受的力。
已知F=0.6 kN。
解:(1)间汇交力系;(2)解得:AB、AC3-1 已知梁AB 上作用一力偶,力偶矩为M ,梁长为l ,梁重不计。
求在图a ,b ,c 三种情况下,支座A 和B 的约束力解:(a) (b) (c) 3-2 M ,试求A 和C解:(1) 取 (2) 取 3-3 Nm ,M 2解:(1)(2) 3-5 大小为AB 。
各杆 解:(1)(2)可知:(3) 研究OA 杆,受力分析,画受力图:列平衡方程:AB A3-7 O1和O2圆盘与水平轴AB固连,O1盘垂直z轴,O2盘垂直x轴,盘面上分别作用力偶(F1,F’1),(F2,F’2)如题图所示。
工程力学课后习题答案第10章题解g

( ) ∑ M B
= 0 , FC
= − Me l
↓
77
CA 段
M
=
−
Me l
x1
⎜⎛ 0 ⎝
≤
x1
<
l 2
⎟⎞ ⎠
AB 段
M
=
−
Me l
x2
+
Me
⎜⎛ ⎝
l 2
<
x2
≤
l
⎟⎞ ⎠
CA
段 ⎜⎛ 0 ⎝
≤
x1
<
l 2
⎟⎞ ⎠
AB
段 ⎜⎛ ⎝
l 2
<
x2
≤
l ⎟⎞ ⎠
EIw1′′ =
−
Me l
x1
EIw1′
=
3d × (3d )3
12
=
81d 4 12
;设钢丝绳每股横截面为 d × d ,则 9 股钢丝绳的惯
性矩为 I 2
= 9× d ×d3 12
=
9d 4 12
=
1 9
I1
,故钢丝绳要柔软得多。
10-4 用叠加法求梁的位移时,应满足哪些条件? 答 小变形。
10-5 提高梁的弯曲刚度的主要措施有哪些?与提高梁强度的措施有何不同? 答 提高梁的弯曲刚度的主要措施有 (1)调整加载方式,改善结构设计; (2)减小梁的跨度,增加支承约束; (3)增大梁的弯曲刚度 EI。
)
=
3 8
qlx2
−
ql 2
⎜⎛ ⎝
x2
−
l 4
⎟⎞ ⎠
⎜⎛ ⎝
l 2
≤
x2
≤
l ⎟⎞ ⎠
工程力学高斌第九章答案

15kN . m
5kN . m
15kN . m
-
Q qa/2 +
-
qa/2 + x
qa/2
M q a 2/8 +
-
x
q a 2/8
5. 设梁的剪力图如图所示,试作弯矩图及载荷图。已知梁上设有作用集中力偶。 (a)
4kN q=1kN/m
3kN
Q
3kN
2kN
3kN
1kN
A
B
1kN
C
D
x
5
3kN 2m 2m 4m
3
2
⎡ 50 × 2003 ⎤ 150 × 503 Iz = ⎢ + 50 × 200 × 53.62 + + 50 × 150 × 71.4 2 ⎥ mm 4 12 ⎣ 12 ⎦ = 10180 cm 4
根据弯曲正应力强度条件
M
0.8p
σ max
M = ymax ≤ [σ ] , M≤[σ].Iz/ymax Iz
解:梁的弯矩图如图, 弯矩的两个极值分别为
µ1 = 0.8P , MA =2P×1.4 - P×2= 0.8P µ2 = 0.6 P , MC = -0.6 P
截面对形心轴的惯性矩为
8
(Iz =bh /12 + Ah1 , h1 腹 = 153.6–100=53.6mm ,h1 翼 =200-153.6+25 =71.4mm )
实心圆截面梁的最大应力
σ max =
空心圆截面最大应力
′ = σ max
空心圆截面梁比实心圆截面梁的最大正应力减少了
′ σ max − σ max 159 − 93.6 = = 41.1% σ max 159
工程力学_修订版__课后答案(高斌_著)_湖南大学出版社

由
∑M
A
�� ( F ) = 0 得:
( −4 × 2 × 1 + 10 − 40 ×
2 2 × 1 − 40 × × 4 + RB sin 30� × 4 = 0 (40 应为 4 ) 2 2 = - 8 + 10 - 2√2 – 8 √2 + 2 RB RB = 5√2 – 1 = 6.07 kN
思考题:1. √;2. ×;3. ×;4. ×;5. √;6. ×;7. ×;8. ×;9. √. 习题二 1. 平面力系由三个力和两个力偶组成,它们的大小和作用位置如图示,长度单位为 cm,求此力 系向 O 点简化的结果,并确定其合力位置。 解:设该力系主矢为 R′ ,其在两坐标轴上的投影分别为 Rx 、 Ry 。由合力投影定理有: 角 Rx =
A B A B A B
解得: YB = 10.125 kN, X A = −18.5 kN, X B = 18.5 kN (解法 2) 解: (1)取整体为研究对象,画受力图,列平衡方 程
∑Yi = 0, YA + YB – Q = 0 YA + YB = Q = 10 kN (1) ∑Xi = 0 , XA + XB = 0 (2) ∑ MD = 0 ,XB .6 - YA .8 -YB .8 – Q.3.1 = 0 XB = 111/6 = 18.5 kN 代入(2)式,得 XA = - 18.5 kN 取 ACD 杆为研究对象,画受力图 ∑MD = 0 , - YA ×8 – Q × 0.1 = 0 YA = - 10×0.1/8 = - 0.125 kN 代入(1) ,得 Y = - Y + 10 = 10.125 kN
F
F NB b
《工程力学》课后习题解答

z
A
F
B 45o
FAB
60o FAD
O
D
y
45o
C
FAC
x
解:(1) 取整体为研究对象,受力分析,AB、AB、AD 均为二力杆,画受力图,得到一个空 间汇交力系;
(2) 列平衡方程:
Fx 0 FAC cos 45o FAB cos 45o 0 Fy 0 F FAD cos 60o 0 Fz 0 FAD sin 60o FAC sin 45o FAB sin 45o 0
FA
FB
M l
FB
M l
(c) 受力分析,画受力图;A、B 处的约束力组成一个力偶;
FA A
M
l/2 l
B
θ
FB
9
《工程力学》习题选解
列平衡方程:
M 0 FB l cos M 0
FA
FB
l
M cos
FB
l
M cos
3-2 在题图所示结构中二曲杆自重不计,曲杆 AB 上作用有主动力偶,其力偶矩为 M,试求 A 和 C 点处的约束力。
解得:
FAD 2F 1.2 kN AB、AC 杆受拉,AD 杆受压。
FAC FAB
6 4
FAD
0.735
kN
8
《工程力学》习题选解
3-1 已知梁 AB 上作用一力偶,力偶矩为 M,梁长为 l,梁重不计。求在图 a,b,c 三种情 况下,支座 A 和 B 的约束力
M
l/2
A
B
l
(a)
M
l/3
A
30o
B
C
M2
M1
O
解:(1) 研究 BC 杆,受力分析,画受力图:
工程力学材料力学答案-第十章

10-1试计算图示各梁指定截面(标有细线者)的剪力与弯矩。
解:(a)(1) 取A +截面左段研究,其受力如图;由平衡关系求内力0SA A F F M ++==(2) 求C 截面内力;取C 截面左段研究,其受力如图;由平衡关系求内力2SC C Fl F F M ==(3) 求B -截面内力截开B -截面,研究左段,其受力如图;由平衡关系求内力SB B F F M Fl ==qB(d)(b)A(a)SA+M A+SCM CASBM B(b)(1) 求A 、B 处约束反力eA B M R R l==(2) 求A +截面内力;取A +截面左段研究,其受力如图;eSA A A e M F R M M l++=-=-= (3) 求C 截面内力;取C 截面左段研究,其受力如图;22e e SC A A e A M Ml F R M M R l +=-=-=-⨯= (4) 求B 截面内力;取B 截面右段研究,其受力如图;0eSB B B M F R M l=-=-= (c)(1) 求A 、B 处约束反力eM A+M CB R BMBA B Fb FaR R a b a b==++ (2) 求A +截面内力;取A +截面左段研究,其受力如图;0SA A A FbF R M a b++===+ (3) 求C -截面内力;取C -截面左段研究,其受力如图;SC A C A Fb FabF R M R a a b a b--===⨯=++ (4) 求C +截面内力;取C +截面右段研究,其受力如图;SC B C B Fa FabF R M R b a b a b++=-=-=⨯=++ (5) 求B -截面内力;取B -截面右段研究,其受力如图;0SB B B FaF R M a b--=-=-=+ (d)(1) 求A +截面内力取A +截面右段研究,其受力如图;A RSA+M A+ RA SC-M C- B R BM C+B R B M qBM233 22248SA A l ql l l ql F q M q ++=⨯==-⨯⨯=-(3) 求C -截面内力;取C -截面右段研究,其受力如图;222248SC C l ql l l ql F q M q --=⨯==-⨯⨯=-(4) 求C +截面内力;取C +截面右段研究,其受力如图;222248SC C l ql l l ql F q M q ++=⨯==-⨯⨯=-(5) 求B -截面内力;取B -截面右段研究,其受力如图;0 0SB B F M --==10-2.试建立图示各梁的剪力与弯矩方程,并画剪力与弯矩图。
工程力学习题 及最终答案

——————————————工程力学习题——————————————第一章绪论思考题1) 现代力学有哪些重要的特征?2) 力是物体间的相互作用。
按其是否直接接触如何分类?试举例说明。
3) 工程静力学的基本研究内容和主线是什么?4) 试述工程力学研究问题的一般方法。
第二章刚体静力学基本概念与理论习题2-1 求图中作用在托架上的合力F R。
习题2-1图2-2 已知F 1=7kN ,F 2=5kN, 求图中作用在耳环上的合力F R 。
2-3 求图中汇交力系的合力F R 。
2-4 求图中力F 2的大小和其方向角α。
使 a )合力F R =1.5kN, 方向沿x 轴。
b)合力为零。
2习题2-2图(b)F 1F 1F 2习题2-3图(a )F 1习题2-4图2-5 二力作用如图,F 1=500N 。
为提起木桩,欲使垂直向上的合力为F R =750N ,且F 2力尽量小,试求力F 2的大小和α角。
2-6 画出图中各物体的受力图。
F 12习题2-5图(b)(a)(c)(d)AC2-7 画出图中各物体的受力图。
(f)(g) 习题2-6图(b)(a )DC2-8 试计算图中各种情况下F 力对o 点之矩。
(d)习题2-7图习题2-8图 P(d)(c)(a ) A2-9 求图中力系的合力F R 及其作用位置。
习题2-9图( a )1F 3 ( b )F 3F 2( c) 1F /m( d )F 32-10 求图中作用在梁上的分布载荷的合力F R 及其作用位置。
2-11 图示悬臂梁AB 上作用着分布载荷,q 1=400N/m ,q 2=900N/m, 若欲使作用在梁上的合力为零,求尺寸a 、b 的大小。
( a )q 1=600N/m2( b )q ( c )习题2-10图B习题2-11图第三章静力平衡问题习题3-1 图示液压夹紧装置中,油缸活塞直径D=120mm,压力p=6N/mm2,若α=30︒, 求工件D所受到的夹紧力F D。
工程力学课后习题答案【整理版】

工程力学 静力学与材料力学 (单辉祖 谢传锋 著) 高等教育出版社 课后答案 1-1试画出以下各题中圆柱或圆盘的受力图。
与其它物体接触处的摩擦力均略去。
解� 1-2 试画出以下各题中A B 杆的受力图。
BA OW(a ) B A O WF(b ) OW (c ) AAO W(d ) BA O W (e ) BFB FABO W (a ) BA OW F(b ) F A F BAO W(c )FA FO AO W (d ) F B F A A O W (e ) BF B FA A WC B (c ) D(a ) AW CEB (b ) AW C DB《工程力学》习题选解 。
工程力学 静力学与材料力学 (单辉祖 谢传锋 著) 高等教育出版社 课后答案解�1-3试画出以下各题中A B 梁的受力图。
ABF (d ) CABW (e ) CAB W (e ) C FB FA AB F(d ) CFB F A (a ) FD FB FE DAW CEB (b ) AW CD B F D FB FA (c ) A WC B FB FA AWCB(a ) W ABCD(c ) AB Fq D (b ) C CABFW DA’ D ’ B’ (d ) AB Fq (e )解�1-4 试画出以下各题中指定物体的受力图。
(a ) 拱A B C D �(b ) 半拱A B 部分�(c ) 踏板A B �(d ) 杠杆A B �(e ) 方板A B C D �(f ) 节点B 。
解� A WCB(a ) FB FAA BFqD(b ) FC FD W ABC(c ) FC FB CAB F WD(d ) FB FA FD ABFq(e ) FB x FB y FA AB F (a ) D C WAF(b ) DB (c ) F ABD D ’ A B F(d ) C DW A B CD(e ) W A BC(f ) A BF(a ) D CWFA x FA y FD AF (b ) B FB FA (c ) FA B DF B FD1-5 试画出以下各题中指定物体的受力图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
σ3
τ
σ3 σ1
80
σ3 σ3
σ1
a0
(0,20)
B
80
40
2a
0
A
20
C
a0
(f)
σ1 σ3
�
w. c
60°
om
σ
40
求载荷 P。已知 E = 210GN / m , µ = 0.28 。 解: (1)绕 A 点取一单元体, 应力状态如图:
2
ww
σ 60� = σ −30�
(2)由广义虎克定律得:
50 + 30 50 − 30 + cos 60° 2 2
20
30°
50 50
50
解析法求解:
(a)
σ 45° =
w.
50
50 50 + cos 90° − 20sin 90° 2 2
50
kh
D1 (0,50)
(2)图解法:
后 答
��� � ⎧σ 1 = OA = 50ΜΡa ⎪ ��� � ⎨ σ = OB = −50ΜΡa ⎪ ⎩ 3
(3)
应力分析
18 号槽钢 (P388)
A = 29.29 × 2cm 2
(4)强度分析:
为什么小车位于 AC 的中点时 AC 杆的弯矩最大: (1)由截面法可知:小车左侧剪力为 YC>0,右侧为 YC-P<0, 故小车 P 的作用点为弯矩图直线升、降区间的转折点,该截面 由∑MA=0,P×(L-x)-YC.L=0,得 YC=(L-x)P/L 即 x=L/2 时,弯矩 M 值最大.
w. c
Yc Xc
WZ = 2 ×152.2cm3
om
X
N AB
30°
网
案
弯矩最大。求小车位于距 C 端为 x 截面上的弯矩:
p
1.75m
1.75m
3.手摇式提升机如图示,已知轴的直径 d=30mm,材料为 Q235 钢, [σ ] = 80Mpa ,试按第三强度 理论求最大起重载荷 Q。 解: (1)轴的外力
m
课
My:
3 M D1 = P2 × 150 4
Mz
562.5N.m
750N.m
= 1125 KN.mm
1 M C 2 = × 1125 3 = 375 KN.mm
MY
1125N.m
M: M C = 562.52 + 3752
= 676.1 KN.mm
M D = 11252 + 187.52
= 1140.5 KN.mm
ε 60� =
后 答
1 ⎡σ � − µσ −30� ⎤ ⎦ E ⎣ 60 σ 2.72 = σ [3 − µ ] = 4E 4E
案
网
σ σ 3 − cos120� = σ 2 2 4 σ σ 1 = − cos(−60� ) = σ 2 2 4
w.
l
l
kh
da
6.图示一钢质圆杆,直径 D=200mm,已知 A 点在与水平线 60 方向上的正应变 ε 60� = 4.1× 10 , 试
∑ M C (F ) = 0 :
N AB sin 30°× 3.5 − P ×1.75 = 0 N AB = P = 40 kN
∑ FY = 0 :
YC + N AB sin30° − P = 0 YC = P = 20 kN 2 ∑ FX = 0 :
1
Xc
课
后 答
(
30 − 50 2 ) + 202 = 22.36 Mpa 2
Q 向轴简化为 Q—弯曲
力偶 M n = 200 Q = T —扭转 (2)内力—见图 危险截面位中点:
课
M n = 200 Q M max =
QL 4 Q × 600 = = 150Q (Nmm) 4
2
后 答
由 YC 对小车作用点之矩:M= YC•x=(L-x)P/L•x=-Px /L+Px,当 M’=-2Px/L+P=0 时,
主平面位置
σ1
σ3
40
课
(d)解:作应力图
��� � σ 1 = OA = 55 MPa ��� � σ 3 = OB = −35 MPa ���� � τ max = CD1 = 45 MPa 2α 0 = 27
�
45°
σ3
σ1
(d)
τ
35
55
(e)解:作应力图
a
40
D1(-30,20)
��� � σ 1 = OA = 45 MPa ��� � σ 3 = OB = −45 MPa ���� τ max = OD = 45 MPa
案
600 ×103 Mn τ= = = 70.63ΜΡα 2πγ 2δ 2 × π × 262 × 2
1 = × 63.66 + 70.63sin(−120� ) 4 = −45.5ΜΡα σ τ −60� = sin(−120� ) − 70.63cos(−120� ) 2 = 8.1ΜΡα
(3)
ww
∆σ 121 − 120 = = 8.3 × 10−3 = 0.83% < 5% 满足要求(分母应为 [σ] ) ∆ 120 [ ]
w.
kh
(σ拉+α弯 max = N/A + Mmax /wz,二应力均为拉应力 )
da
′′ = 34.64 × 103 /(29.29 × 2 × 100) + 35 × 106 /(2 ×152.2 ×103 ) = 121ΜΡα σ max = σ ′ + σ max
轮 D 的直径为 d D =150mm,其上作用着水平切向力 P2 =10kN。若[ σ ]=100Mpa,试用第四强度理论求轴 的直径。 解: (1)外力分析, 将P 1, P 2 向 AB 轴简化,如图
A C
da kh
D
P2
dc 300 m=P = 5× 1• 2 2
= 750 KN.mm
(2)内力分析:
σ
m p A
30°
d
p
σ
da kh
σ1
m
解: (1)绕 A 点取单元体,应力为:
ww
网
σ=
20 ×103 P 20 ×103 = = = 63.66ΜΡα A π dδ π × 50 × 2
w.
σ3
a
(2) σ −60� =
后 答
σ σ + cos(−120� ) + τ sin(−120�σ )1 2 2
案
网
(3)图
kh
N AB p
1.75m 1.75m
σ min =
30+50 30-50 2 ) + 202 − ( 2 2 = 17.64ΜΡα 2 × (−20) tg2α ° = − = −2 30 − 50
da
30+50 30+50 2 + ( ) + 202 2 2 = 62.36ΜΡα
σ2
网
= 5 MPa 50 τ 45° = sin 90° + 20 cos 90° 2 = 25 MPa
ww
da
B
0
= 45 MPa 50 − 30 τα = sin 60° = 8.66 MPa 2
w. c
(b)
A(50,0)
45°
案
(c)
D2 (0,-50)
τ max = OD1 = 50 MPa
w. c
σ1
om
31.72°
X C = N AB cos 30° = 34.64 kN
(2)内力分析:见轴力图,弯矩图。AC 梁为压,弯组合变形,危险截面位于 AC 中点。
M max = 20 × 1.75 (=YC ×3.5/2)
= 35 kN.m
N
X
(-)
3 4 .6 4 k N
M
35KN.M
2
(
T = 200Q)
Mn
200Q
X
轴发生弯曲与扭转组合变形 (3)强度计算:
σ xd3 =
M 2 n + M 2 max WZ
(Mn
应为 T)
M
150Q
( 2002 + 1502 ) × Q = ≤ [σ ] 0.1× 303
Q≤
0.1× 303 × 80 150 + 200
2 2
X
= 860 N ∴ 最大起重载为 860N.
2τ 2 × (−70.63) =− =2.22 σ 63.66
2α 0 = 65.74�
α 0 = 32.87�
课
后 答
案
网
ww
w.
7
kh
da
w. c
om
σ max = σ min =
σ 1 =109.3ΜΡα
课
63.66 63.66 2 σ σ + ( )2 + τ 2 = + ( ) + 70.632 = 109.3 ΜΡα 2 2 2 2
σ σ 63.66 63.66 2 − ( )2 + τ 2 = − ( ) + 70.632 = −45.6 ΜΡα 2 2 2 2 σ 3 =-45.6ΜΡα
工程力学习题答案
第十章 组合变形 1. 已知单元体应力状态如图示(应力单位为 ΜΡα ) ,试求: (1)指定斜截面上的正应力和剪应 力; (2)主应力的大小、主平面位置; (3)在单元体上画出平面位置和主应力方向; (4)最大剪应力. 解: (1) α = 30 斜截面上的应力:
