第五讲 多元回归分析:渐近性
合集下载
伍德里奇《计量经济学导论》笔记和课后习题详解(多元回归分析:OLS的渐近性)【圣才出品】

y=β0+β1x1+…+βkxk+u 检验这些变量中最后 q 个变量是否都具有零总体参数。
虚拟假设:H0:βk-q+1=0,…,βk=0,它对模型斲加了 q 个排除性约束。
3 / 12
圣才电子书 十万种考研考证电子书、题库视频学习平台
对立假设:这些参数中至少有一个异亍零。
(2)σ2 是 σ2=Var(u)的一个一致估计量。
(3)对每个 j,都有:
βˆj βj
/ se
βˆ j
a
~ Normal 0,1
其中, se βˆ j 就是通常的 OLS 标准误。
定理 5.2 的重要乊处在亍,它去掉了正态性假定 MLR.6。对误差分布唯一的限制是,
它具有有限斱差。还对 u 假定了零条件均值(MLR.4)和同斱差性(MLR.5)。
因为 Var(x1)>0,所以,若 x1 和 u 正相关,则 βˆ1 的丌一致性就为正,而若 x1 和 u 负相关,则 βˆ1 的丌一致性就为负。如果 x1 和 u 乊间的协斱差相对亍 x1 的斱差很小,那么这
种丌一致性就可以被忽略。由亍 u 是观测丌到的,所以甚至还丌能估计出这个协斱差有多 大。
二、渐近正态和大样本推断 1.定理 5.2:OLS 的渐近正态性 在高斯-马尔可夫假定 MLR.1~MLR.5 下,
④将
LM
不
χ
2 q
分布中适当的临界值
c
相比较,如果
LM>c,就拒绝虚拟假设。
(3)不 F 统计量比较
不 F 统计量丌同,无约束模型中的自由度在迚行 LM 检验时没有什么作用。所有起作用
的因素只是被检验约束的个数(q)、辅助回归 R2 的大小( Ru2 )和样本容量(n)。无约束 模型中的 df 丌起什么作用,这是因为 LM 统计量的渐近性质。但必须确定将 Ru2 乘以样本容 量以得到 LM,如果 n 很大, Ru2 看上去较低的值仍可能导致联合显著性。
c5 多元回归分析-渐进性质
重新讨论变量遗漏的影响假设u不相关而在建模时遗漏了重要变量52渐近正态性和大样本推断定理52ols估计量的渐近正态性在高斯马尔科夫假设下mlr1mlr5下有
第
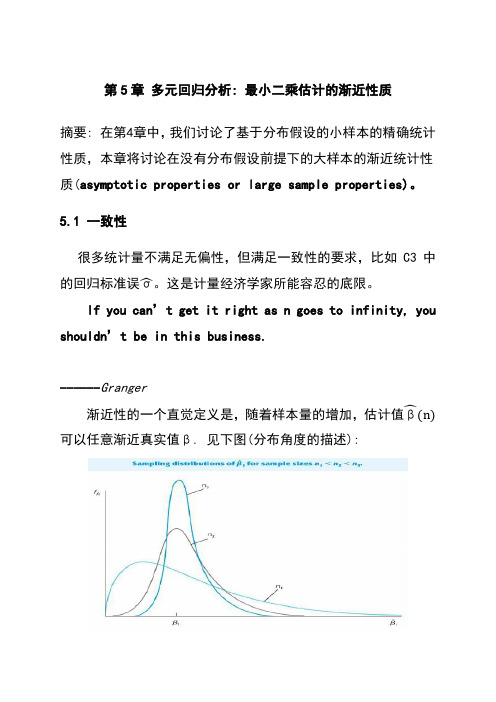
摘要:在第4章中,我们讨论了基于分布假设的小样本的精确统计性质,本章将讨论在没有分布假设前提下的大样本的渐近统计性质(asymptotic propertiesor large sample properties)。
几点说明:
1)唯一的假定是 是有限的;
2)多大样本量才算充分,没有定论,渐近是针对(n-k-1),而不是n;
3)需要同方差的假定;
4)试讨论 ;
5)在该定理中, 被称为 的渐近标准误差(asymptotic standard error),同样的t统计量被称为渐近t统计量(asymptotic t statistics),置信区间被称为渐近置信区间(asymptotic confidence interval),F统计量被称为渐近F统计量.
定理5.1 OLS估计量的一致性
在假设MLR.1-MLR.4下, 为 的一致估计,j=0,1,2,…,k。
该定理的证明示意:在一元回归中, = 收敛于 ,当 .
显然u和x的不相关在该证明中起到了决定性的作用。
假设 MLR.’4 零均值和不相关假设
假定 和 ,j=1,2,…,k.
不采用假设MLR.’4,一是因为若MLR.4不满足,我们得到的可能是一个一致但有偏的估计;二是因为在MLR.4下,我们得到了总体回归函数(PRF),从而线性模型的系统部分有比较明确的意义。
.(5.2)
但由于被忽略的自变量可能和(5.2)式的变量相关,所以我们需要一个辅助回归(auxiliary regression):
对 的回归,
第
摘要:在第4章中,我们讨论了基于分布假设的小样本的精确统计性质,本章将讨论在没有分布假设前提下的大样本的渐近统计性质(asymptotic propertiesor large sample properties)。
几点说明:
1)唯一的假定是 是有限的;
2)多大样本量才算充分,没有定论,渐近是针对(n-k-1),而不是n;
3)需要同方差的假定;
4)试讨论 ;
5)在该定理中, 被称为 的渐近标准误差(asymptotic standard error),同样的t统计量被称为渐近t统计量(asymptotic t statistics),置信区间被称为渐近置信区间(asymptotic confidence interval),F统计量被称为渐近F统计量.
定理5.1 OLS估计量的一致性
在假设MLR.1-MLR.4下, 为 的一致估计,j=0,1,2,…,k。
该定理的证明示意:在一元回归中, = 收敛于 ,当 .
显然u和x的不相关在该证明中起到了决定性的作用。
假设 MLR.’4 零均值和不相关假设
假定 和 ,j=1,2,…,k.
不采用假设MLR.’4,一是因为若MLR.4不满足,我们得到的可能是一个一致但有偏的估计;二是因为在MLR.4下,我们得到了总体回归函数(PRF),从而线性模型的系统部分有比较明确的意义。
.(5.2)
但由于被忽略的自变量可能和(5.2)式的变量相关,所以我们需要一个辅助回归(auxiliary regression):
对 的回归,
5_多元线性回归分析

……
n xn yn
y
εi 。。
。。。(。x。i, yi)。。。 。。
。
。。
x
0
一元线性回归模型
模型: yi=α+ β xi + εi
(i=1,2…n)
数据的假设条件:
1. 因变量是连续随机变量; 2. 自变量是固定数值型变量,且相互独立; 3. 每一个自变量与因变量呈线性关系; 4. 每一个自变量与随机误差相互独立; 5. 观察个体的随机误差之间相互独立; 6. 随机误差{ei}~N(0,σ)。
• 在模型中添加x变量的方法和向前选择法相同,从模型 中消去x变量的方法和向后消去法相同。
• 添加和消去x变量的顺序原则是,在每添加一个新的x 变量之前,首先用向后消去法原则消去模型内所有超 出停留允许水平的x 变量,然后用向前选择法原则在模 型中添加一个新的x变量。
• 逐步过程法和向前选择法的不同之处是,已经进入模 型的x变量还可以再次从模型中退出;逐步过程法和向 后消去法的不同之处是,已经从模型中消去的x变量还 可以再次进入模型中。
数学模型:
其中:{yi}和{xij}是因变量y和自变量xj 的观察值; β0, β1…βk是待估计的偏回归系数; e i 是yi 的随机误差,且{ei }~N(0,σ)。
一元线性回归分析的数学模型
id x
y
------------------------
1 x1 y1
2 x2 y2
……
i xi yi
data d;
input id x1-x3 y ; cards; 1 1.0 2.3 3.4 10 2 2.1 2.5 3.8 15 3 3.2 3.3 3.8 20 4 4.2 3.9 4.2 22 5 4.8 4.2 5.0 28 run ;
Chapter5 多元回归分析:

OLS估计量的确切正态性,关键 取决于总体中误差u的正态性。
u的正态性意味着在给定x的条件下y的分布是正态的。
u是不可观测的,因此考虑y的分布 是否是正态的则容易的多。
不幸的是有很多例子表明y的分布不是正态 分布的
例如一些明显偏态的变量:在 某一特定年份中被捕的青年数 量(大部分人不会被捕)
正态分布假定不会影响OLS称为最优线性无 偏估计量,但t统计量和F统计量是否服从t 分布和F分布则与正态分布假定有关。
5.2.1 Central Limit Theorem
利用中心极限定理我们可以证明OLS估计量满 足渐进正态性 (asymptotically normal)
渐进正态性的含义是: P(Z<z)F(z) as n , or P(Z<z) F(z)
中心极限定理表明任何(具有有限方差的)总 体 的一个随机样本的均值经过标准化以后都服 从渐进标准正态分布。
考察吸烟量(cigs)对婴儿体重产生的影响, 观测值共1388个。
当我们使用前一半观测值共694个得到βcigs估 计量标准误约为0.0013,当我们使用全部观测
值时标准误为0.00086
se ˆ j c j n c j se ˆ j n,
足以说明cj是一个不依 赖于样本容量的常数
0.0013 694 0.0342 0.0320 0.00086 1388
还是方差最小的 因此我们说OLS统计量是渐进有效的 注意,OLS统计量的最小方差性是依赖于同
方差假定的,同方差性不满足OLS统计量未 必是方差最小的。
5.2.3 Lagrange Multiplier statistic
在大样本情况下,无需正态假定我们也可以 运用t和F统计量。
但有时我们也可以用其他的方法检验多元排 除约束。
u的正态性意味着在给定x的条件下y的分布是正态的。
u是不可观测的,因此考虑y的分布 是否是正态的则容易的多。
不幸的是有很多例子表明y的分布不是正态 分布的
例如一些明显偏态的变量:在 某一特定年份中被捕的青年数 量(大部分人不会被捕)
正态分布假定不会影响OLS称为最优线性无 偏估计量,但t统计量和F统计量是否服从t 分布和F分布则与正态分布假定有关。
5.2.1 Central Limit Theorem
利用中心极限定理我们可以证明OLS估计量满 足渐进正态性 (asymptotically normal)
渐进正态性的含义是: P(Z<z)F(z) as n , or P(Z<z) F(z)
中心极限定理表明任何(具有有限方差的)总 体 的一个随机样本的均值经过标准化以后都服 从渐进标准正态分布。
考察吸烟量(cigs)对婴儿体重产生的影响, 观测值共1388个。
当我们使用前一半观测值共694个得到βcigs估 计量标准误约为0.0013,当我们使用全部观测
值时标准误为0.00086
se ˆ j c j n c j se ˆ j n,
足以说明cj是一个不依 赖于样本容量的常数
0.0013 694 0.0342 0.0320 0.00086 1388
还是方差最小的 因此我们说OLS统计量是渐进有效的 注意,OLS统计量的最小方差性是依赖于同
方差假定的,同方差性不满足OLS统计量未 必是方差最小的。
5.2.3 Lagrange Multiplier statistic
在大样本情况下,无需正态假定我们也可以 运用t和F统计量。
但有时我们也可以用其他的方法检验多元排 除约束。
第五章 多元线性回归PPT课件

ˆ b0 b1 x1 b2 x2 ... bk xk y
如果xi增加一个单位,即xi变为xi+1,而 其他自变量均保持不变,相应有
ˆ b b x b x y
1 0 1 1 2
2
... bi ( xi 1) ... bk xk
则y的变化幅度为
ˆ [b b x b x ... b ( x 1) ... b x ] ˆ y y [b b x b x ... b ( x 1) ... b x ] b
R
2
二、调整的确定系数
R
2
偏高
<(1:10)
自变量个数 样本规模
三、多元相关系数R
因变量观测值和预测值之间的相关程度
四、方差分析
回归平方和
y的总变 差平方 和
第五节
回归方程的检验和回归系数的推断统计
检验
统计推断
参见郭志刚主编,《社会统计分析方法—SPSS软件应用》第二章, 中国人民大学出版社1999
第一节 相关和回归
一、相关统计量 用一个数值表示两个变量间的相关程度 (无单位度量)(-1~+1)
解读
X与y的相关系数为0.6,x与z的相关系数为 0.3
答案: 只能说明x与y相关程度高于x与z的相关程 度,但不能说前者是后者的两倍
x y x y x y 1 2 y y y y 1 y y 1 2 x x y x 1 x y
y
y
练习:根据下表数据计算lambda
志愿 男
快乐家庭 理想工作 增广见闻 总数 10 40 10 60
性别 女
30 10 0 40
总数
60PPT-第5章-多元线性回归-计量经济学及Stata应用

k 1
1
yi 1
xi 2
xiK
2
i
xiβ
i
K
(5.8)
上式对所有个体i都成立(i 1, , n),故有n个形如(5.8)的方程。
16
将所有这 n 个方程都叠放:
y1 x1β 1
y2
x2 β
2
yn
xn β
n
(5.9)
将共同的参数向量 β 向右边提出:
y1 x1 1
6. 1904 138 116 122 4.927254 4.75359 4.804021 7. 1905 149 125 143 5.003946 4.828314 4.962845 8. 1906 163 133 152 5.09375 4.890349 5.02388 9. 1907 176 138 151 5.170484 4.927254 5.01728 10. 1908 185 121 126 5.220356 4.795791 4.836282
1 x12 x1K
X
1 x22
x2 K
1
xn2
xnK
nK
(5.11)
18
5.3 OLS 估计量的推导 对于多元回归模型,OLS 估计量的最小化问题为
n
n
min
ˆ1,,ˆK
ei2 ( yi ˆ1 ˆ2 xi2 ˆ3xi3 ˆK xiK )2
i1
i1
(5.12)
n
最小二乘法寻找使残差平方和(SSR) ei2 最小的(ˆ1, ˆ2,, ˆK )。 i1
0.001 0.000 0.687
[95% Conf. Interval]
.1009363 .5055755 -1.080472
1
yi 1
xi 2
xiK
2
i
xiβ
i
K
(5.8)
上式对所有个体i都成立(i 1, , n),故有n个形如(5.8)的方程。
16
将所有这 n 个方程都叠放:
y1 x1β 1
y2
x2 β
2
yn
xn β
n
(5.9)
将共同的参数向量 β 向右边提出:
y1 x1 1
6. 1904 138 116 122 4.927254 4.75359 4.804021 7. 1905 149 125 143 5.003946 4.828314 4.962845 8. 1906 163 133 152 5.09375 4.890349 5.02388 9. 1907 176 138 151 5.170484 4.927254 5.01728 10. 1908 185 121 126 5.220356 4.795791 4.836282
1 x12 x1K
X
1 x22
x2 K
1
xn2
xnK
nK
(5.11)
18
5.3 OLS 估计量的推导 对于多元回归模型,OLS 估计量的最小化问题为
n
n
min
ˆ1,,ˆK
ei2 ( yi ˆ1 ˆ2 xi2 ˆ3xi3 ˆK xiK )2
i1
i1
(5.12)
n
最小二乘法寻找使残差平方和(SSR) ei2 最小的(ˆ1, ˆ2,, ˆK )。 i1
0.001 0.000 0.687
[95% Conf. Interval]
.1009363 .5055755 -1.080472
第5章多元回归分析:进一步讨论

bˆ1 new
xi x yi new xi x 2
xi x 1000 yi xi x 2
1000bˆ1
if we write the scale as ynew yold , then we get bˆnew bˆold
Variables
bwghtkg, child birth weight in kilograms bwghtg, child birth weight in grams bwghtjin, child birth weight in jin cigs, number of cigarettes the mother smoked per day while
C(4)hbawngghitjning the scale of the y variable will
lead to a
-0.5259676
(0.c1o03rr9e3s97p)onding [-5c.0h6a] nge in the 0.00s5c26a4le4 of the (0c.0o0e1f6fi5c6i4e)nts and [3s.1ta8]ndard errors, 6.6s3o82n82o change (0.59529in8)the [11s1i.g5n1]ificance or 138in8 terpretation
0.0298
1795.41694
1.1386
3
Redefining Variables , cont.
let take simple regresstion for example the estimated parameter is
bˆ 1
3.多元回归分析3:渐近性剖析.

N=5000 f(w)
N=500
N=100
7
θ
无偏性和一致性
估计量在有限样本中有偏的,但可能具有一致性
若随机变量X的方差为 2,则对于随机样本{xi , i 1n},
2的有偏估计量sx2 (xi x)2 / n,却是 2的一致估计量。
估计量是无偏的,但可能不具有一致性
( Cov x1,u 0)
9
一个弱一点的假设
对于无偏性,利用的假定条件是:
E(u|x1, x2,…,xk) = 0
为得到一致性,所需要的假设要弱一些:零均值和零 相关性
E(u) = 0 cov(xj,u) = 0, for j = 1, 2, …, k
没有这一假定(cov(xj,u)≠0),OLS估计量可能是有偏
b1
b21
12
不一致性可以看成是偏误
不一致性与偏误主要的区别在于,偏误使用的是总体方差和总 体协方差,无偏性用的是样本方差和样本协方差
不一致性的严重程度取决于解释变量与遗漏变量之间的相关程 度
非一致性是大样本问题,不会因为样本容量的增大而消失
遗漏变量不仅会导致与之具有相关性的解释变量对应的估计系 数不具有一致性,也会导致与之不具有相关性的解释变量对应 的估计系数不具有一致性;除非遗漏的变量与所有的解释变量 都不相关,从而使得扰动项满足高斯-马尔科夫经典假定
多元回归分析:
大样本性质(渐近性)
1 y = b0 + b1x1 + b2x2 + . . . bkxk + u
在高斯-马尔科夫假定下,OLS估计量是BLUE。但并 不是在任何情况下都能得到无偏估计量。
N=500
N=100
7
θ
无偏性和一致性
估计量在有限样本中有偏的,但可能具有一致性
若随机变量X的方差为 2,则对于随机样本{xi , i 1n},
2的有偏估计量sx2 (xi x)2 / n,却是 2的一致估计量。
估计量是无偏的,但可能不具有一致性
( Cov x1,u 0)
9
一个弱一点的假设
对于无偏性,利用的假定条件是:
E(u|x1, x2,…,xk) = 0
为得到一致性,所需要的假设要弱一些:零均值和零 相关性
E(u) = 0 cov(xj,u) = 0, for j = 1, 2, …, k
没有这一假定(cov(xj,u)≠0),OLS估计量可能是有偏
b1
b21
12
不一致性可以看成是偏误
不一致性与偏误主要的区别在于,偏误使用的是总体方差和总 体协方差,无偏性用的是样本方差和样本协方差
不一致性的严重程度取决于解释变量与遗漏变量之间的相关程 度
非一致性是大样本问题,不会因为样本容量的增大而消失
遗漏变量不仅会导致与之具有相关性的解释变量对应的估计系 数不具有一致性,也会导致与之不具有相关性的解释变量对应 的估计系数不具有一致性;除非遗漏的变量与所有的解释变量 都不相关,从而使得扰动项满足高斯-马尔科夫经典假定
多元回归分析:
大样本性质(渐近性)
1 y = b0 + b1x1 + b2x2 + . . . bkxk + u
在高斯-马尔科夫假定下,OLS估计量是BLUE。但并 不是在任何情况下都能得到无偏估计量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一致性是对一个估计量最起码的要求。在无法 满足无偏性的情况下,我们可以搜集尽可能多 的样本,即使n→ ∞,参数估计值的分布将逼近 真实参数值。
计量经济学导论
4
一致性的正式定义
令Wn是基于样本Y1,Y2, ,YN的参数的估计值, 则Wn是的一致估计量,对于任意一个正数 0,
PWn 0,当n
否则,Wn不是的一致估计量。 当Wn是一致时,我们说是Wn的概率极限,记为:
计量经济学导论
26
计量经济学导论
27
拉格朗日乘数统计量
将y对施加限制后的自变量集进行回归,并保 留残差uhat。
将uhat对所有自变量进行回归,并得到R2,记 为Ru2.
计算LM=n Ru2. 将LM与xq2分布中适当的临界值c比较,如果
LM>c,就拒绝原假设。否则,我们就不能拒 绝原假设。
多元回归分析:渐进性
y = b0 + b1x1 + b2x2 + . . . bkxk + u
Copyright © 2007 Thomson Asia Pte. Ltd. All rights rese1rved.
5.1 一致性 5.2 渐进正态和大样本推断 5.3 OLS渐进有效性
计量经济学导论 刘愿
assumptions, the OLS estimators will have the asymptotic variances We say that OLS is asymptotically efficient Important to remember our assumptions though, if not homoskedastic, not true
计量经济学导论
29
STATA命令语句:
Reg narr86 pcnv ptime86 qemp86 Predict ubar,resid Reg ubar pcnv ptime86 qemp86 avgsen tottime
计量经济学导论
30
5.3 OLS渐进有效性
Estimators besides OLS will be consistent However, under the Gauss-Markov
y b0 b1x1 ...bkqxkq u
Now take the residuals, u, and regress
u onx1,x2,..., xk (i.e. all the variables) LM nRu2, where Ru2 is fromthis reg
计量经济学导论
24
The idea of LM statistic
计量经济学导论
21
渐进正态性
随着自由度提高,t分布渐进服从正态分布, 因此有:
b b b ˆ j
j
seˆj
a
~tnk1
因此,随着样本量增大,我们无需再担心 正态性假定是否满足问题,但仍然需要同 方差性。
计量经济学导论
22
渐进标准误
如果u不是正态分布的,下式被称为渐进标准 误,t统计量称为渐进t统计量。
不满足上述条件,OLS是有偏和不一致的。
计量经济学导论
11
不一致性的推导
^
b 1
的不一致(有时也粗略地称为渐近偏误)为:
plim b^1b1cov(x,u)/var(x)
因为Var(x)>0,所以,若x与u正相关,则
^
b1
的
不一致就为正,而若x与u负相关,则
^
b1
的不
一致为负。如果x与u之间的协方差相对于X的
计量经济学导论
31
The discussion in the simple regression
18
定理 5.2 OLS的渐进正态性
Under the Gauss - Markov assumptions,
(i)
n
bˆ j b j
a
~ Normal
0,s 2
a
2 j
,
where
a
2 j
plim
n 1
rˆij2
(ii) sˆ 2 is a consistent estimator of s 2
中心极限定理
根据中心极限定理,可以证明OLS估计值服从 渐进正态。
渐进正态意味着: P(Z<z)F(z) as n , 或者 P(Z<z) F(z) (标准正态累积分布函数)。
中心极限定理表明,任何均值为m ,方差为s2 经标准化后渐进的服从标准正态分布
Z
Y mY s
a
~N0,1
n
计量经济学导论
plimbˆj bj
n
计量经济学导论
8
OLS的一致性
在高斯-马尔科夫假定下,OLS估计值是一致 且无偏的。
类似的,我们可以像无偏性一样证明一致性, 为此需要引入概率极限。
计量经济学导论
9
简单回归中证明一致性
bˆ1 xi1 x1 yi
xi1 x1 2
xi1 x1 b 0 b 1 xi1 u i
误差正态分布意味着,给定x情况下,y服从正 态分布。
计量经济学导论
16
大样本推断
不满足正态性的情形相当普遍。任何偏向的变 量,如工资、被逮捕次数、储蓄等,不可能是 正态分布的。(正态分布意味着对称分布)
注意:正态性假定在OLS的最优线性无偏性中 并非必要的,仅仅是影响推断。
计量经济学导论
17
Suppose we have a standard model, y = b0 + b1x1 + b2x2 + . . . bkxk + u and our null hypothesis is
H0: bk-q+1 = 0, ... , bk = 0
First, we just run the restricted model
where Covx1,x2 Varx1
计量经济学导论
13
渐进偏误
渐进偏误的方向与遗漏变量偏误的方向类似。 两者的区别在于,渐进偏误使用总体方差和协
方差,遗漏变量偏误则基于样本对应量(以x 的样本值为条件) 不一致性是大样本问题,即使增加数据量,不 一致性问题仍然存在。 如果X1与X2不相关,则为不一致估计量;如 果相关,则为一致估计量。
bbb b n a r r 8 6 0 1 p c n v 4 p t i m e 8 6 5 q e m 8 6 u
u01pcnv2avgsen3totim e4ptim e865qem 86v
R u 20.0015, L M 27250.00154.094.61q,10% ,x2,
Px2 24.090.129
Running a regression of these residuals on those independent variables excluded under H0, we should get a small enough R2.
However, we must include all of the independent variables in the regression for technical reasons.
plimWn
和无偏性不一样,无偏性是估计量在给定样本容
量下的一个特征,一致性描述了估计量的抽样分
布在样本容量变大是的特性。
计量经济学导论
5
一致性的直观理解
如果估计量是一致的,那么随着样本容量的增加,
bˆj的分布就越来越紧密地分布在bj的周围。当n趋向 无穷时,bˆj的分布就紧缩成单一一个点bj。这意味着,
计量经济学导论
25
LM Statistic (cont)
a
LM~q2,socanchoosea critical value,c, froma q2 distributoin,or justcalculatea p-valueforq2
With a large sample, the result from an F test and from an LM test should be similar. LM>c, reject H
se bˆ j
sˆ 2
SSTj
1
R
2 j
sˆ ,
SSR j
sˆ
1 n2
n
uˆi2
i 1
SSR n2
se bˆ j c j
n,
SST j
ns
2 j
可以预期,标准误的收缩速度为样本容量平方 根的倒数。
计量经济学导论
23
大样本检验方法:LM检验 LM Statistic (cont)
(iii) bˆ j b j
se bˆ j
a
~ Normal 0,1
计量经济学导论19bˆ j b j , v a r bˆ j
v a r bˆ j
s2
SST j
1
R
2 j
s2
n
r
i
2 j
i1
bˆ j b j
N
0
,
s
2
n
r
i
2 j
i1
n bˆ j b j
计量经济学导论
10
一个较弱的假定
为了得到无偏性,我们需要零条件均值假设 E(u|x1, x2,…,xk) = 0→x的任意函数都与u无关
为了得到一致性,我们仅需要较弱的假定:零 均值和零相关:E(u) = 0 ,Cov(xj,u) = 0, for j = 1, 2, …, k. →每一个xj都与u无关。
N
计量经济学导论
4
一致性的正式定义
令Wn是基于样本Y1,Y2, ,YN的参数的估计值, 则Wn是的一致估计量,对于任意一个正数 0,
PWn 0,当n
否则,Wn不是的一致估计量。 当Wn是一致时,我们说是Wn的概率极限,记为:
计量经济学导论
26
计量经济学导论
27
拉格朗日乘数统计量
将y对施加限制后的自变量集进行回归,并保 留残差uhat。
将uhat对所有自变量进行回归,并得到R2,记 为Ru2.
计算LM=n Ru2. 将LM与xq2分布中适当的临界值c比较,如果
LM>c,就拒绝原假设。否则,我们就不能拒 绝原假设。
多元回归分析:渐进性
y = b0 + b1x1 + b2x2 + . . . bkxk + u
Copyright © 2007 Thomson Asia Pte. Ltd. All rights rese1rved.
5.1 一致性 5.2 渐进正态和大样本推断 5.3 OLS渐进有效性
计量经济学导论 刘愿
assumptions, the OLS estimators will have the asymptotic variances We say that OLS is asymptotically efficient Important to remember our assumptions though, if not homoskedastic, not true
计量经济学导论
29
STATA命令语句:
Reg narr86 pcnv ptime86 qemp86 Predict ubar,resid Reg ubar pcnv ptime86 qemp86 avgsen tottime
计量经济学导论
30
5.3 OLS渐进有效性
Estimators besides OLS will be consistent However, under the Gauss-Markov
y b0 b1x1 ...bkqxkq u
Now take the residuals, u, and regress
u onx1,x2,..., xk (i.e. all the variables) LM nRu2, where Ru2 is fromthis reg
计量经济学导论
24
The idea of LM statistic
计量经济学导论
21
渐进正态性
随着自由度提高,t分布渐进服从正态分布, 因此有:
b b b ˆ j
j
seˆj
a
~tnk1
因此,随着样本量增大,我们无需再担心 正态性假定是否满足问题,但仍然需要同 方差性。
计量经济学导论
22
渐进标准误
如果u不是正态分布的,下式被称为渐进标准 误,t统计量称为渐进t统计量。
不满足上述条件,OLS是有偏和不一致的。
计量经济学导论
11
不一致性的推导
^
b 1
的不一致(有时也粗略地称为渐近偏误)为:
plim b^1b1cov(x,u)/var(x)
因为Var(x)>0,所以,若x与u正相关,则
^
b1
的
不一致就为正,而若x与u负相关,则
^
b1
的不
一致为负。如果x与u之间的协方差相对于X的
计量经济学导论
31
The discussion in the simple regression
18
定理 5.2 OLS的渐进正态性
Under the Gauss - Markov assumptions,
(i)
n
bˆ j b j
a
~ Normal
0,s 2
a
2 j
,
where
a
2 j
plim
n 1
rˆij2
(ii) sˆ 2 is a consistent estimator of s 2
中心极限定理
根据中心极限定理,可以证明OLS估计值服从 渐进正态。
渐进正态意味着: P(Z<z)F(z) as n , 或者 P(Z<z) F(z) (标准正态累积分布函数)。
中心极限定理表明,任何均值为m ,方差为s2 经标准化后渐进的服从标准正态分布
Z
Y mY s
a
~N0,1
n
计量经济学导论
plimbˆj bj
n
计量经济学导论
8
OLS的一致性
在高斯-马尔科夫假定下,OLS估计值是一致 且无偏的。
类似的,我们可以像无偏性一样证明一致性, 为此需要引入概率极限。
计量经济学导论
9
简单回归中证明一致性
bˆ1 xi1 x1 yi
xi1 x1 2
xi1 x1 b 0 b 1 xi1 u i
误差正态分布意味着,给定x情况下,y服从正 态分布。
计量经济学导论
16
大样本推断
不满足正态性的情形相当普遍。任何偏向的变 量,如工资、被逮捕次数、储蓄等,不可能是 正态分布的。(正态分布意味着对称分布)
注意:正态性假定在OLS的最优线性无偏性中 并非必要的,仅仅是影响推断。
计量经济学导论
17
Suppose we have a standard model, y = b0 + b1x1 + b2x2 + . . . bkxk + u and our null hypothesis is
H0: bk-q+1 = 0, ... , bk = 0
First, we just run the restricted model
where Covx1,x2 Varx1
计量经济学导论
13
渐进偏误
渐进偏误的方向与遗漏变量偏误的方向类似。 两者的区别在于,渐进偏误使用总体方差和协
方差,遗漏变量偏误则基于样本对应量(以x 的样本值为条件) 不一致性是大样本问题,即使增加数据量,不 一致性问题仍然存在。 如果X1与X2不相关,则为不一致估计量;如 果相关,则为一致估计量。
bbb b n a r r 8 6 0 1 p c n v 4 p t i m e 8 6 5 q e m 8 6 u
u01pcnv2avgsen3totim e4ptim e865qem 86v
R u 20.0015, L M 27250.00154.094.61q,10% ,x2,
Px2 24.090.129
Running a regression of these residuals on those independent variables excluded under H0, we should get a small enough R2.
However, we must include all of the independent variables in the regression for technical reasons.
plimWn
和无偏性不一样,无偏性是估计量在给定样本容
量下的一个特征,一致性描述了估计量的抽样分
布在样本容量变大是的特性。
计量经济学导论
5
一致性的直观理解
如果估计量是一致的,那么随着样本容量的增加,
bˆj的分布就越来越紧密地分布在bj的周围。当n趋向 无穷时,bˆj的分布就紧缩成单一一个点bj。这意味着,
计量经济学导论
25
LM Statistic (cont)
a
LM~q2,socanchoosea critical value,c, froma q2 distributoin,or justcalculatea p-valueforq2
With a large sample, the result from an F test and from an LM test should be similar. LM>c, reject H
se bˆ j
sˆ 2
SSTj
1
R
2 j
sˆ ,
SSR j
sˆ
1 n2
n
uˆi2
i 1
SSR n2
se bˆ j c j
n,
SST j
ns
2 j
可以预期,标准误的收缩速度为样本容量平方 根的倒数。
计量经济学导论
23
大样本检验方法:LM检验 LM Statistic (cont)
(iii) bˆ j b j
se bˆ j
a
~ Normal 0,1
计量经济学导论19bˆ j b j , v a r bˆ j
v a r bˆ j
s2
SST j
1
R
2 j
s2
n
r
i
2 j
i1
bˆ j b j
N
0
,
s
2
n
r
i
2 j
i1
n bˆ j b j
计量经济学导论
10
一个较弱的假定
为了得到无偏性,我们需要零条件均值假设 E(u|x1, x2,…,xk) = 0→x的任意函数都与u无关
为了得到一致性,我们仅需要较弱的假定:零 均值和零相关:E(u) = 0 ,Cov(xj,u) = 0, for j = 1, 2, …, k. →每一个xj都与u无关。
N
