fluent瞬态问题
Fluent学习总结
FLUENT学习总结1 概述：FLUENT是目前处于世界领先地位的商业CFD软件包之一，最初由FLUENT Inc.公司发行。
2006年2月ANSYS Inc.公司收购FLUENT Inc.公司后成为全球最大的CAE软件公司。
FLUENT是一个用于模拟和分析复杂几何区域内的流体流动与传热现象的专用软件。
FLUENT提供了灵活的网格特性，可以支持多种网格。
用户可以自由选择使用结构化或者非结构化网格来划分复杂的几何区域，例如针对二维问题支持三角形网格或四边形网格；针对三维问题支持四面体、六面体、棱锥、楔形、多面体网格；同时也支持混合网格。
用户可以利用FLUENT提供的网格自适应特性在求解过程中根据所获得的计算结果来优化网格。
FLUENT是使用C语言开发的，支持并行计算，支持UNIX和Windows等多种平台，采用用户/服务器的结构，能够在安装不同操作系统的工作站和服务器之间协同完成同一个任务。
FLUENT通过菜单界面与用户进行交互，用户可以通过多窗口的方式随时观察计算的进程和计算结果。
计算结果可以采用云图、等值线图、矢量图、剖面图、XY散点图、动画等多种方式显示、存贮和打印，也可以将计算结果保存为其他CFD软件、FEM软件或后处理软件所支持的格式。
FLUENT还提供了用户编程接口，用户可以在FLUENT的基础上定制、控制相关的输入输出，并进行二次开发。
1.1 FLUENT软件包的组成针对不同的计算对象，CFD软件都包含有3个主要功能部分：前处理、求解器、后处理。
其中前处理是指完成计算对象的建模、网格生成的程序；求解器是指求解控制方程的程序；后处理是指对计算结果进行显示、输出的程序。
FLUENT软件是基于CFD软件的思想设计的。
FLUENT软件包主要由GAMBIT、Tgrid、Filters、FLUENT几部分组成。
（1）前处理器。
包括GAMBIT、Tgrid和Fliters。
其中GAMBIT是由FLUENT Inc.公司自主开发的专用CFD前置处理器，用于模拟对象的几何建模以及网格生成。
Fluent经典问题答疑
Fluent经典问题答疑8 什么叫边界条件？有何物理意义？它与初始条件有什么关系？边界条件与初始条件是控制⽅程有确定解的前提。
边界条件是在求解区域的边界上所求解的变量或其导数随时间和地点的变化规律。
对于任何问题，都需要给定边界条件。
初始条件是所研究对象在过程开始时刻各个求解变量的空间分布情况，对于瞬态问题，必须给定初始条件，稳态问题，则不⽤给定。
对于边界条件与初始条件的处理，直接影响计算结果的精度。
在瞬态问题中，给定初始条件时要注意的是：要针对所有计算变量，给定整个计算域内各单元的初始条件；初始条件⼀定是物理上合理的，要靠经验或实测结果确定。
10 在数值计算中，偏微分⽅程的双曲型⽅程、椭圆型⽅程、抛物型⽅程有什么区别？很多描述物理问题的控制⽅程最终就可以归结为偏微分⽅程，描述流动的控制⽅程也不例外。
从数学⾓度，⼀般将偏微分⽅程分为椭圆型（影响域是椭圆的，与时间⽆关，且是空间内的闭区域，故⼜称为边值问题），双曲型（步进问题，但依赖域仅在两条特征区域之间），抛物型（影响域以特征线为分界线，与主流⽅向垂直；具体来说，解的分布与瞬时以前的情况和边界条件相关，下游的变化仅与上游的变化相关；也称为初边值问题）；从物理⾓度，⼀般将⽅程分为*衡问题（或稳态问题），时间步进问题。
两种⾓度，有这样的关系：椭圆型⽅程描述的⼀般是*衡问题（或稳态问题），双曲型和抛物型⽅程描述的⼀般是步进问题。
⾄于具体的分类⽅法，可以参考⼀般的偏微分⽅程专著，⾥⾯都有介绍。
关于各种不同*似⽔*的流体控制⽅程的分类，可以参考张涵信院⼠编写《计算流体⼒学—差分⽅法的原理与应⽤》⾥⾯讲的相当详细。
三种类型偏微分⽅程的基本差别如下：1）三种类型偏微分⽅程解的适定性（即解存在且唯⼀，并且解稳定）要求对定解条件有不同的提法；2）三种类型偏微分⽅程解的光滑性不同，对定解条件的光滑性要求也不同；椭圆型和抛物型⽅程的解是充分光滑的，因此对定解条件的光滑性要求不⾼。
FLUENT知识点解读
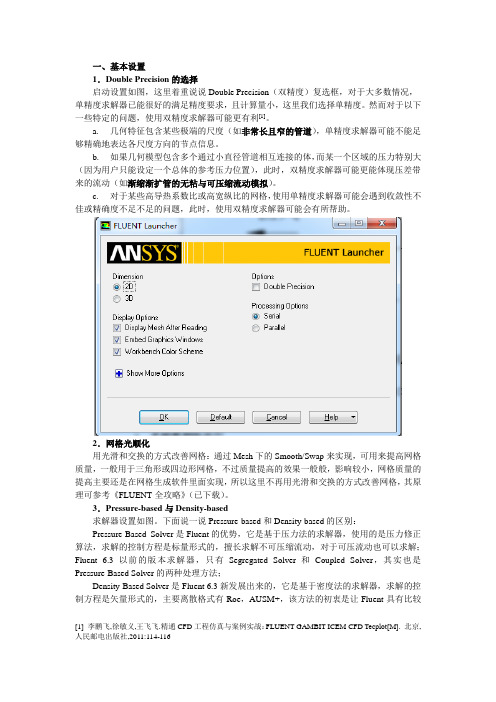
一、基本设置1．Double Precision的选择启动设置如图，这里着重说说Double Precision（双精度）复选框，对于大多数情况，单精度求解器已能很好的满足精度要求，且计算量小，这里我们选择单精度。
然而对于以下一些特定的问题，使用双精度求解器可能更有利[1]。
a.几何特征包含某些极端的尺度（如非常长且窄的管道），单精度求解器可能不能足够精确地表达各尺度方向的节点信息。
b.如果几何模型包含多个通过小直径管道相互连接的体，而某一个区域的压力特别大（因为用户只能设定一个总体的参考压力位置），此时，双精度求解器可能更能体现压差带来的流动（如渐缩渐扩管的无粘与可压缩流动模拟）。
c.对于某些高导热系数比或高宽纵比的网格，使用单精度求解器可能会遇到收敛性不佳或精确度不足不足的问题，此时，使用双精度求解器可能会有所帮助。
2．网格光顺化用光滑和交换的方式改善网格：通过Mesh下的Smooth/Swap来实现，可用来提高网格质量，一般用于三角形或四边形网格，不过质量提高的效果一般般，影响较小，网格质量的提高主要还是在网格生成软件里面实现，所以这里不再用光滑和交换的方式改善网格，其原理可参考《FLUENT全攻略》（已下载）。
3．Pressure-based与Density-based求解器设置如图。
下面说一说Pressure-based和Density-based的区别：Pressure-Based Solver是Fluent的优势，它是基于压力法的求解器，使用的是压力修正算法，求解的控制方程是标量形式的，擅长求解不可压缩流动，对于可压流动也可以求解；Fluent 6.3以前的版本求解器，只有Segregated Solver和Coupled Solver，其实也是Pressure-Based Solver的两种处理方法；Density-Based Solver是Fluent 6.3新发展出来的，它是基于密度法的求解器，求解的控制方程是矢量形式的，主要离散格式有Roe，AUSM+，该方法的初衷是让Fluent具有比较[1] 李鹏飞,徐敏义,王飞飞.精通CFD工程仿真与案例实战：FLUENT GAMBIT ICEM CFD Tecplot[M]. 北京,人民邮电出版社,2011:114-116好的求解可压缩流动能力，但目前格式没有添加任何限制器，因此还不太完善；它只有Coupled的算法；对于低速问题，他们是使用Preconditioning方法来处理，使之也能够计算低速问题。
fluent瞬态中间时刻计算结果
当谈到计算结果的中间时刻，fluent瞬态模拟是一个非常重要的主题。
在工程领域中，fluent瞬态模拟被广泛应用于流体动力学、传热、化学反应等领域。
而在这些领域中，对于计算结果的中间时刻也具有非常重要的意义。
在本文中，我们将针对fluent瞬态模拟中计算结果的中间时刻进行全面评估和探讨，以便更深入地理解这一主题。
让我们来理解什么是fluent瞬态模拟。
fluent是一种流体动力学计算软件，它能够模拟流体流动、传热、物质传输等现象。
而瞬态模拟则是指在一定的时间范围内对这些现象进行数值模拟，从而得到计算结果。
在瞬态模拟中，中间时刻的计算结果往往对于理解流体运动、温度分布等物理现象至关重要。
那么，为什么需要关注fluent瞬态模拟中的中间时刻计算结果呢？中间时刻的计算结果可以帮助我们更加全面地了解流体运动和传热现象。
在很多工程设计和科学研究中，我们需要对流体运动过程中的各个时刻进行详细分析，以便更好地优化设计或者理解物理规律。
中间时刻的计算结果也可以为我们提供更多的信息，帮助我们更准确地预测未来的发展趋势。
在一些特定的工程问题中，对于流体流动或者传热过程的预测非常关键，而中间时刻的计算结果能够提供更加可靠的预测依据。
在实际的fluent瞬态模拟中，如何获取准确且有意义的中间时刻计算结果也是一个挑战。
我们需要选择合适的时间步长和计算方法，以保证计算结果的准确性和稳定性。
我们需要注意数值耗散和数值扩散等问题，这些数值误差可能会对中间时刻的计算结果产生较大影响。
在一些特定的工程问题中，如何处理边界条件、网格剖分等也会对中间时刻的计算结果产生影响。
在进行fluent瞬态模拟时，我们需要全面考虑这些因素，以获得可靠且有意义的中间时刻计算结果。
对于fluent瞬态模拟中的中间时刻计算结果，我个人认为需要更加强调其在工程应用中的重要性。
在很多工程问题中，我们往往需要对流体流动、传热等现象进行详细的分析和预测，而中间时刻的计算结果可以为我们提供更多的信息和更可靠的依据。
fluent松散耦合的共轭传热 瞬态求解
【fluent松散耦合的共轭传热瞬态求解】01. 引言在本文中，我们将探讨fluent软件中的松散耦合的共轭传热瞬态求解。
这是一个复杂而又具有挑战性的主题，但通过逐步分析和讨论，我们将一步步深入了解这一概念。
通过本文的阅读，读者将能够全面、深刻并且灵活地理解fluent软件中的松散耦合的共轭传热瞬态求解。
02. fluent软件中的热传导在开始探讨松散耦合的共轭传热瞬态求解之前，我们先了解一下fluent软件中的热传导。
热传导是指物质内部由于温度差而引起的热量传递过程。
在fluent中，通过建立几何模型、设定边界条件和选择适当的求解方法，可以对热传导进行模拟和求解。
03. 共轭传热共轭传热是指在传热过程中不同的传热机制相互影响，产生耦合作用的现象。
在流体流动中，传热可以通过对流和热传导进行耦合传递。
在fluent中，可以通过设置不同的传热模型和参数，对共轭传热进行模拟和求解。
04. 松散耦合在fluent中，我们可以选择进行松散耦合的传热求解。
松散耦合是指在求解过程中，系统的不同部分之间存在一定程度的耦合作用，但是这种耦合作用并不会对整体的求解过程产生显著影响。
通过松散耦合的传热求解，可以更加高效地进行模拟和分析。
05. 瞬态求解与稳态求解不同，瞬态求解是指在一定的时间范围内对系统的变化进行求解。
在fluent中，通过瞬态求解可以对系统在时间上的变化进行模拟和分析，从而更好地理解系统的动态特性。
06. 深入研究通过对fluent软件中的松散耦合的共轭传热瞬态求解的概念和基本原理的介绍，我们可以进一步深入研究这一主题。
可以通过案例分析和模拟实验，对松散耦合的共轭传热瞬态求解进行具体的应用和验证。
07. 个人观点对于fluent软件中的松散耦合的共轭传热瞬态求解，我认为这是一个非常具有挑战性和前沿性的主题。
通过不断学习和研究，我们可以更好地掌握这一求解方法，为工程和科学领域的发展做出更大的贡献。
08. 总结与回顾通过本文的阐述，我们对fluent软件中的松散耦合的共轭传热瞬态求解有了更加全面、深刻和灵活的理解。
fluent常见问题
1、流场数值计算的目的是什么？主要方法有哪些？其基本思路是什么？各自的适用范围是什么？答：这个问题的范畴好大啊。
简要的说一下个人的理解吧：流场数值求解的目的就是为了得到某个流动状态下的相关参数，这样可以节省实验经费，节约实验时间，并且可以模拟一些不可能做实验的流动状态。
主要方法有有限差分，有限元和有限体积法，好像最近还有无网格法和波尔兹曼法（格子法）。
基本思路都是将复杂的非线性差分/积分方程简化成简单的代数方程。
相对来说，有限差分法对网格的要求较高，而其他的方法就要灵活的多。
2、可压缩流动和不可压缩流动，在数值解法上各有何特点？为何不可压缩流动在求解时反而比可压缩流动有更多的困难？答：注：这个问题不是一句两句话就能说清楚的，大家还是看下面的两篇小文章吧，摘自《计算流体力学应用》，读完之后自有体会。
3、可压缩Euler及Navier-Stokes方程数值解描述无粘流动的基本方程组是Euler方程组，描述粘性流动的基本方程组是Navier-Stokes 方程组。
用数值方法通过求解Euler方程和Navier-Stokes方程模拟流场是计算流体动力学的重要内容之一。
由于飞行器设计实际问题中的绝大多数流态都具有较高的雷诺数，这些流动粘性区域很小，由对流作用主控，因此针对Euler方程发展的计算方法，在大多数情况下对Navier-Stokes方程也是有效的，只需针对粘性项用中心差分离散。
用数值方法求解无粘Euler方程组的历史可追溯到20世纪50年代，具有代表性的方法是1952年Courant等人以及1954年Lax和Friedrichs提出的一阶方法。
从那时开始，人们发展了大量的差分格式。
Lax和Wendroff的开创性工作是非定常Euler(可压缩Navier-Stokes)方程组数值求解方法发展的里程碑。
二阶精度Lax-Wendroff格式应用于非线性方程组派生出了一类格式，其共同特点是格式空间对称，即在空间上对一维问题是三点中心格式，在时间上是显式格式，并且该类格式是从时间空间混合离散中导出的。
fluent中time step size
fluent中time step size
在 Fluent 中，时间步长（time step size）是指在每个迭代步骤中模拟的时间区间。
时间步长的大小会影响仿真的精度和模拟的稳定性。
时间步长的选择是一个关键的决策，可以通过以下几种方式来确定合适的时间步长大小：
1. 收敛性：通过在多个时间步骤上执行仿真并观察结果的变化情况，可以确定模拟是否已经达到收敛状态。
如果结果在连续的时间步长下相对稳定，那么相应的时间步长可以被视为合适的大小。
2. 稳定性限制：有时候，模拟的稳定性可能受到时间步长的限制。
一般来说，流动问题通常受到 Courant-Friedrichs-Lewy (CFL) 数量的限制，该数量可以通过以下公式计算：CFL = U * Δt / Δx，其中 U 是流动的最大速度，Δx 是网格大小，Δt 是时间步长。
保持 CFL 数量在一定范围内可以确保模拟的稳定性。
3. 物理现象：对于具体的物理现象，一些特定的时间尺度可能会指导时间步长的选择。
例如，对于瞬态流动问题，可以根据关注的时间尺度选择相应的时间步长大小。
在 Fluent 中，可以通过在求解器控制台中设置时间步长参数来调整时间步长的大小。
常用的参数包括时间步长大小、最大时间步长、Courant 数量限制等。
通过进行多次仿真实验以及
分析结果的稳定性和精度，可以逐渐调整时间步长大小，以获得满意的模拟结果。
fluent瞬态计算残差曲线
瞬态计算残差曲线1. 瞬态计算的介绍瞬态计算是一种针对瞬时电力系统运行状态进行分析的方法，通常用于分析系统在故障发生、开关操作等瞬时事件下的动态响应。
在这种计算中，残差曲线是一种重要的分析工具，用来反映系统在瞬时事件后的电压、电流等各种变量的变化过程，对系统的稳定性和可靠性具有重要的参考价值。
2. 瞬态计算的重要性瞬态计算可以帮助电力系统工程师快速准确地了解系统在瞬时事件后的运行状态，为系统的优化设计和故障分析提供重要依据。
通过对残差曲线的分析，可以发现系统中可能存在的振荡、过电压、欠电压等问题，为改进系统的稳定性和可靠性提供重要参考。
3. 残差曲线的计算方法残差曲线通常是通过瞬态计算软件进行模拟计算得到的。
在进行瞬态计算时，需要考虑系统的各种参数和组件的动态特性，如发电机、变压器、线路、负荷等。
通过对系统进行仿真计算，得到系统在不同瞬时事件下的电压、电流等变化情况，然后绘制残差曲线进行分析。
4. 残差曲线的分析方法在得到残差曲线后，需要对其进行深入的分析。
首先需要比较残差曲线与基准曲线的差异，进而找出系统的动态响应特点。
同时还需要分析残差曲线上可能存在的振荡、过电压、欠电压等现象，并进一步确定系统的稳定性和可靠性。
在分析时需要考虑系统的动态特性、结构特点以及各种电气设备的特性。
5. 残差曲线的应用残差曲线的应用范围非常广泛，包括电网规划、电气设备设计、电力系统运行等方面。
通过对残差曲线的分析，可以及时发现系统中可能存在的问题并进行改进优化，保障系统的安全稳定运行。
在系统故障分析和故障定位中，残差曲线也具有重要的作用，可以帮助工程师快速准确地分析和定位故障。
6. 结语瞬态计算残差曲线是一种重要的分析工具，对电力系统的稳定性和可靠性具有重要的参考价值。
通过对残差曲线的计算和分析，可以及时发现系统中可能存在的问题并进行改进优化，为系统的安全稳定运行提供重要支持。
在今后的工作中，我们需要进一步加强对残差曲线的研究和应用，提高电力系统的稳定性和可靠性。