数值分析3-插值方法
数值分析-计算方法-插值a
500 5
18
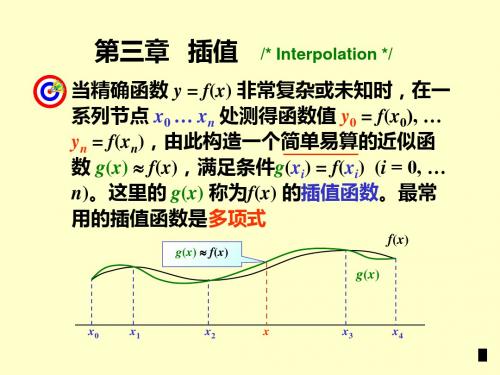
解: n = 1 分别利用x0, x1 以及 x1, x2 计算
x0
x1
x2
利用
x0 6 , x1 4
L 1 (x ) x /6 /4 /4 1 2 x /4 /6 /6 1 2
sin
而
50 0
Lf1内要( (5端1x 8插计)点 ) 通算s,0 常的i.x 7插n 7 优x6值12 2 所于4效,在外果R 1 的推(x 较) 区。f 好(f x 间选)2 ( 。 ! 的择x s )(x ix ,n 6 f)x (( x 4 )) 4 s 2 |( ix x n , 6 )x x ( ( 4 6 )|, 4)
Ln ( xi ) yi , i 0, ... , n
条件:无重合节点,即 i j xi xj
n=1
线性插值
已称知为x拉0 氏, x基1 ;函y0数, y1/*,La求graL n1 g(exB)asa is0 */,a1x 使得
L满1( 足x0 )条 件y0 l,i(Lx1j)(=x1 )ij/*yK1 ronecker Delta */
f(x)L (x) n
f ( ) (n1)
ni
i
项式是唯一存在的。
证明: 由插值条件可知,插值多项式Ln(x)的系数ai满足线性
方程组
1
x 0
xn 0
a0
y 0
1
x 1
xn 1
a1
y 1
1
x n
“数值分析”中的三次样条插值实践教学探讨

性、 主动性、 灵活性得不到充分发挥 , 难以提高探索 和 获取样 条 知识 的能力 。
三是 对案 例教 学 中的数 据缺乏 背 景 了解 。虽 然 在个 别教 材 中 , 添加 了三次样 条实 际应 用案 例 , 但仅 靠课 堂讲 授和上 机 实验是 无法 让学 生对 案例 中 的实
“ 数值 分 析 " 中的 三次 样 条 插值 实践 教 学 探 讨 木
徐 圣 兵
( 广东工业大学应用数学学 院 , 广东 广州 , 106 50 0 ) 摘 要: 文章 阐述 了“ 数值 分析” 中的三次样条插值教学 中加入 实践教 学环 节的必要性 , 通过具体 实例介绍 了作 并 者在 三次样条插值教 学中进行 了实践教 学的尝试和探 讨 , 旨在对今后 的三次样条插 值 的教 学起到一定 的
等方面要符合培养 目标的要求 , 要和相关课程相匹 配 。实践 教学是 专 业 教学 的重 要 组 成部 分 , 培养 是
学生 自学 、 独立 分析 问 题 和 解 决 问题 能 力 的 主要 手 段 , 实践性 较 强课程 的一 种重 要教 学手段 。 是
环 节 已成为 当务 之急 。
一
二 、实 践 教 学
针 对 上述 问题 , 了培 养学 生 自主分 析 问题 、 为 解
、
三次样 条插值教 学 中存在 的 问题
决 问题 的 能力 , 发 学生学 习三次样 条插 值 的兴趣 , 激 加 深他 们对 三次 样 条 知识 的理 解 和认 识 , 文提 出 本
了在三 次样 条教 学 中加 入 实践教 学环 节 的想法 。 实 践教 学 的含 义包 括 实验 、 习 、 会 实 践 、 实 社 课
数值分析插值法

数值分析插值法插值法是数值分析中的一种方法,用于通过已知数据点的函数值来估计介于这些数据点之间的未知函数值。
插值法在科学计算、数据处理、图像处理等领域中得到广泛应用。
插值法的基本思想是通过已知数据点构造一个函数,使得该函数逼近未知函数,并在已知数据点处与未知函数值相等。
插值法的关键是选择适当的插值函数,以保证估计值在插值区间内具有良好的近似性质。
常用的插值法有拉格朗日插值法、牛顿插值法和埃尔米特插值法等。
以下将分别介绍这些插值法的原理及步骤:1. 拉格朗日插值法:拉格朗日插值法通过构造一个多项式函数来逼近未知函数。
假设已知n+1个数据点(x0, y0), (x1, y1), ..., (xn, yn),其中x0, x1, ..., xn为给定的节点,y0, y1, ..., yn为对应的函数值。
拉格朗日插值多项式的一般形式为:L(x) = y0 * l0(x) + y1 * l1(x) + ... + yn * ln(x)其中l0(x), l1(x), ..., ln(x)为拉格朗日基函数,定义为:li(x) = (x - x0)(x - x1)...(x - xi-1)(x - xi+1)...(x - xn) / (xi - x0)(xi - x1)...(xi - xi-1)(xi - xi+1)...(xi - xn)拉格朗日插值法的步骤为:a. 计算基函数li(xi)的值。
b.构造插值多项式L(x)。
c.计算L(x)在需要估计的插值点上的函数值f(x)。
2.牛顿插值法:牛顿插值法通过构造一个差商表来逼近未知函数。
差商表的第一列为已知数据点的函数值,第二列为相邻数据点的差商,第三列为相邻差商的差商,以此类推。
最终,根据差商表中的数值,构造一个差商表与未知函数值相等的多项式函数。
牛顿插值法的步骤为:a.计算差商表的第一列。
b.计算差商表的其他列,直至最后一列。
c.根据差商表构造插值多项式N(x)。
数值分析中的插值理论及应用

数值分析中的插值理论及应用数值分析是一门研究数学运算方法在计算机上实现的学科。
在数值分析中,插值是一种常用的数值近似方法,用于估计或预测在给定数据点之间的未知数值。
本文将介绍插值理论的基本概念和常见方法,并探讨其在实际应用中的作用和意义。
一、插值理论的概念插值是指通过已知数据点之间的数值关系,计算得出新的数据点的数值。
在数值分析中,插值主要用于以下两个方面:1. 数据重建:在给定的数据点上,通过插值方法得到相应函数的近似曲线。
这样可以对已知数据进行补充和估计,使数据更加完整。
2. 函数逼近:在某个区间内,通过数据点之间的插值方法得到一个与原函数相似的函数,以便分析和处理。
二、常见的插值方法以下是数值分析中常见的几种插值方法:1. 线性插值:线性插值是最简单的插值方法之一,其思想是通过已知数据点的连线来估计新数据点的数值。
线性插值适用于数据点之间变化较为平缓的情况。
2. 拉格朗日插值:拉格朗日插值是一种多项式插值方法,通过已知数据点和一个构造的拉格朗日多项式,计算新数据点的数值。
拉格朗日插值适用于任意数据分布的情况。
3. 牛顿插值:牛顿插值是一种基于差商的插值方法,通过已知数据点和一个构造的牛顿插值多项式,计算新数据点的数值。
牛顿插值适用于数据点较为密集的情况。
4. 样条插值:样条插值是一种光滑插值方法,通过已知数据点和一个构造的光滑曲线,计算新数据点的数值。
样条插值适用于数据点较为离散和分段光滑的情况。
三、插值方法的应用插值方法在各个领域都有广泛的应用,以下是一些典型的应用场景:1. 数学建模:在数学建模中,常常需要通过已知数据点进行函数逼近和数值预测。
插值方法可以用来构建逼近函数和预测模型,为建模提供支持。
2. 图像处理:在图像处理中,插值方法可以用于图像的放大、缩小和重建。
通过已知像素点之间的插值,可以获得新的像素点的数值,从而改变图像的大小和清晰度。
3. 数据分析:在大数据分析中,常常需要对缺失数据进行估计和填补。
常用数值分析方法3插值法与曲线拟合

p1(x)y1yx2 2 xy11(xx1)(变形)
xx1xx22y1xx2xx11y2
A1(x)
A2(x)
插值基函数
X.Z.Lin
3.2.3 抛物线插值
已知:三点(x1,y1)、(x2,y2)、(x3,y3) 求:其间任意 x 对应的 y 值
y (x3, y3)
y=f(x) (x2, y2) y=p2(x)
(1)算术平均值
n
xi
x i1 n
(2)标准偏差
n xi2 N xi 2 n
i1
i1
n1
(3)平均标准偏差
E
n
(4)剔出错误数据??可可疑疑数数 据据
Q 数据排序(升):x1,x2,…,xn;
最大与最小数据之差;
值 可疑数据与其最邻近数据之间的差
法 求Q值:
Qxnxn1 或 Qx2x1
3.1 实验数据统计处理
3.1.1 误差
系统误差 经常性的原因
影响比较恒定
偶然误差
偶然因素
正态分布规律
校正
过失误差
统计分析
-3σ -2σ -σ 0 σ 2σ 3σ 图6.1 平行试验数据的正态分布图
操作、计算失误
错误数据
剔出
21:39 07.02.2021
2/37
X.Z.Lin
3.1.2 数据的统计分析
A3(x)(x(x3 xx11))((xx3xx22))
21:39 07.02.2021
9/37
X.Z.Lin
3.2.4 Lagrange插值的一般形式
已知:n点(x1,y1)、(x2,y2)……(xn,yn) 求:其间任意 x 对应的 y 值
数值分析三次样条插值

0
2
1
n1
1
n2
2 n1
M d 0
MM dd n2 M d 2
1 1 2 2
n1 n1 n n
di f xi2, xi1, xi
华长生制作
7
2、 三弯矩构造法
三次样条插值函数 S( x) 可以有多种表达式,有时用二阶导数
值S( xi) Mi (i 0,1,, n)
Mi
xi
表示时,使用更方便。 在力学上解释
为细M梁i 在 S处( x的) 弯矩,并且得到的弯矩与相邻两个弯矩有关,故
称用由于表S(示x)在区间的算[x法i , x为i三1](弯i 矩0,算1,法,。n 1) 上是三次多项式,
hn
n1 3
Mn
f
x0 , x1 f
xn1, xn
其中
0
h1 h1h n
1
0 ,
hn , 0 hnh0
d1
6(
f
[
x
,
0
x1]
f
x[ , n1
x
n])(h1
h
n)
1
.
可解出 M i (i 0,1,, n) ,方程组的矩阵形式为
2
hi
min hi
,M4
max x[a,b]
f (4) (x)
1in
华长生制作
16
精品课件!
精品课件!
可见S(x), S(x)和S(x)在[a,b]上一致收敛到f (x), f (x)和f (x)
数值分析插值法

-
K
(
x)
n
(t
-
xi
)
推广:若 ( x0 ) = ( x1 ) = ( x2 ) = 0
0 ( x0 , x1 ), 1 i (=0x1 , x2 )
(x)有 n使+2得个不(同0 )的= 根(x10)…= 0xn x (0 ,1(n)使1) (得x ) =0(, )=x 0 (a, b)
有 余
娜
原
创
多项式插值----polynomial interpolation
Problem I. 给定y=f(x)的函数表, xi[a,b]
Interpolation interval
Interpolation points
求 次数不超过 n 的多项式
Pn ( x) = a0 a1 x an x n
1 h4 max | 24 x0xx3
f
4(x) |
手 有 余 娜 原 创
证明
n
(1) xikli (x) = xk , k = 0,1, 2, n i=0
n
(2) (xi - x)k li (x) = 0,k = 0,1, 2, n i=0
(3) p(x)是任一最高次项系数为1的n+1次多项式,则
Interpolation polynomial
(2.1)
Interpolation condition
使得
P ( x ) = y , i = 0, ... , n
ni
i
(2.2)
条件:无重合节点,即 i j xi x j
手 有 余 娜 原 创多项式 Nhomakorabea值的几何意义 Pn(x) f(x)
数值分析中的插值算法及其应用

数值分析中的插值算法及其应用数值分析是研究解决数学问题的数值方法的一门学科。
其中,插值算法是数值分析中重要的方法之一。
插值是指在给定一些数据点的情况下,用一些方法建立一个函数,该函数可以在给定区间内的任何一点上计算出函数值。
插值方法有很多种,其中比较常用的有拉格朗日插值法、牛顿插值法和埃尔米特插值法。
1. 拉格朗日插值法拉格朗日插值法是一种将一个多项式函数p(x)与一系列已知数据点相联系的方法。
假设给定n个数据点(x1, y1), (x2, y2), ..., (xn, yn),其中x1 < x2 < ... < xn,那么可以构造一个次数小于等于n-1的多项式函数p(x)满足p(xi) = yi,i=1,2,...,n。
设p(x)的表达式为:p(x) = Σyi li(x)其中,li(x)为拉格朗日基函数。
每个基函数都满足:li(xi) = 1, li(xj) = 0, j≠i基函数的表达式为:li(x) = Π[j≠i] (x - xj) / (xi - xj)利用拉格朗日插值法,可以在给定数据点的情况下,快速计算函数在其他点上的值。
2. 牛顿插值法牛顿插值法是一种利用差商的方法建立插值多项式的方法。
相比于拉格朗日插值法,牛顿插值法更注重于递推计算。
给定n个数据点(x1, y1), (x2, y2), ..., (xn, yn),牛顿插值法可以建立一个关于x的n次多项式。
首先,定义一个差商:f[xi] = yif[xi, xi+1, ..., xj] = (f[xi+1, ..., xj] - f[xi, ..., xj-1]) / (xj - xi)差商f[xi, xi+1, ..., xj]是由区间(xi, xj)内的函数值f(xi), f(xi+1), ..., f(xj)所计算得到的。
定义一个新的多项式qk(x),其中:qk(x) = f[x0, x1, ..., xk] + (x - xk) qk-1(x)其中q0(x) = f[x0]。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
特殊情况
误差的事后估计
基本假设与依据是 假设 f″(x)在[a,b]内改变不大
事后估计法
y
x x2 x1 x2
y1
x x1 x2 x1
y2
y
y1
x x1 x2 x1
( y2
y1 )
埃特金算法的迭代原理
x 0 x1x 2
f (x)
x x2 x1 x2
x0x1
f1 ( x1 )
插值余项
设节点 a x0 x1 xn b ,且 f 满足条件 f C n[a,b] , f (n1)在[a , b]内存在, 考察截断误差
Rn( x ) f ( x ) pn( x )
罗尔定理 : 若 (x) 在[x0 , x1 ]连续,在 (x0, x1)充分光滑,
且 ( x0 ) ( x1 ) 0 存在 (x0, x1)使得 。
又因为
l0 (x0 ) 1
则
c
( x0
x1)( x0
1 x2 )(x0
xn )
基函数的一般形式
即
l0 (x)
(x x1)(x x2 )(x xn ) (x0 x1)(x0 x2 )(x0 xn )
1 jn
x xj x0 x j
l1 ( x)
(x x0 )(x x2 )(x xn ) (x1 x0 )(x1 x2 )(x1 xn )
算插值公式。 2 埃特金算法虽具有承袭性,但算法是递推
型的,不便于进行理论上的分析 3 牛顿公式具有承袭性并且理论推导严密
pn pm g( x )
插商(均差)及其性质
可建立关于系数 a0,a1,…,an的线性方程组
a0 a1 x0 a2 x02 an x0n y0 a0 a1 x1 a2 x12 an x1n y1 a0 a1 xn a2 xn2 an xnn yn
插值问题的可解性
克莱姆法则
xi
Di D
范德蒙行列式
1 x0 x02 x0n
( ) 0
推广:若 ( x0 ) ( x1 ) ( x2 ) 0
0 ( x0 , x1 ), 1 ( x1 , x2 )
使得 (0 ) (1 ) 0
(0 , 1 ) 使得 ( ) 0
如何推导插值余项
pn ( x )
pn ( x )
插值余项
插值误差举例
插值误差举例
拉格朗日插值的几点问题
要使得 则要求
pn (x0 ) y0
l0 (x0 ) 1 l1(x0 ) 0 ln (x0 ) 0
依此类推要满足初始条件,所有基函数必须满足下列条件。
基函数表
x
x0 x1 xn
l0 (x) 1 0 0
l1(x) 0 1 0
ln (x) 0 0 1
构造基函数
由已知条件,假设
l0 (x) c(x x1)(x x2 )(x xn )
f
(
x
)
pn (
x
)
f n1( ) (
( n 1 )!
x
x0
)n1
式中 ξ界于 x0与 x之间,因而 ξ∈[a,b].
拉格朗日插值
问题2 求作 n 次多项式 pn(x),使满足条件
pn(xi)= yi,i = 0,1,…,n
(2)
这就是所谓拉格朗日( Lagrange)插值.
线性插值
f(x) (x1 ,y1) P1(x)
x0x2
x x1 x2 x1
f1( x2 )
x0x1 x k-1xi
x 0x1 x k2x k-1
x0x1 xk-2xi
fk ( xi )
x xi xk xi
fk1( xk1 )
x xk1 xi xk1
fk1( xi )
埃特金算法
1.5 牛顿插值公式
提出的原因: 1 拉格朗日插值每增加一个新点都要重新计
床加工等方面)
泰勒插值
pn ( x)
f ( x0 )
f ( x0 )( x x0 )
f
( x0 2!
)
(
x
x0
)2
f
(n) ( x0 n!
)
(x
x0 )n
条件: pn(k ) (x0 ) f (k ) (x0 ),
k 0,1,, n
泰勒插值余项
定理 1 假设 f(x)在含有点 x0的区间[a,b]内有直 到 n +1阶导数,则当 x∈[a,b]时,对于由式(1) 给出的 pn(x),成立
0 jn j 1
x xj x1 x j
ln (x)
(x x1)(x x2 )(x xn1) (xn x1)(xn x2 )(xn xn1)
1 jn1
x xj xn x j
基函数插值的一般表达式
lk ( x )
n j 0
x xj xk - x j
jk
n
pn ( x ) lk ( x ) yk k 0
1 v
x1
x12
x1n
1i
(
j
x
j
xi )
1 xn xn2 xnn
多项式插值定理
定理 (唯一性) 满足 P( xi ) yi , i 0, ... , n 的 n 阶插值一般形式
pn (x) l0(x) y0 l1(x) y1 ln (x) yn
第一章 插值方法
插值方法的意义
插值方法的应用
对于早期的插值问题来说,f(x)通常是已 知函数,比如对数函数,指数函数,三角 函数等,并且已经有了这些函数值列表, 插值法可以用来计算那些不在表中的点处 的函数值。对于这一类问题来说,现在已 经不需要用插值方法来计算。
插值方法的应用
对于现在的许多实际问题来说,我们并不 知道f(x)的具体形式,所对应的函数值可 能是由测量仪器或其他物理设备中直接读 出来的,f(x)只是一个数学概念意义下的 函数。 (比如:图像的方法处理,天气预报,机
(x0 ,y0)
x0
x1
可见 P1(x) 是过 ( x0 , y0 ) 和 ( x1, y1 ) 两点的直线。
抛物线插值
p2(x) f(x)
f(x)
x0
x1
x2
因过三点的二次曲线为抛物线,故称为抛物插值。
插值问题的可解性
设所求的插值多项式为 pn ( x) a0 a1 x a2 x2 an xn 待定系数法
问题: •对于相同的插值公式,内插与外推哪一个的精度高。 •插值点越多得到插值公式的精度越高? •拉格朗日插值对于不同的初始函数,在相同点上的插 值公式也不同。 •多项式插值是唯一的插值方式? •基函数的形式只和插值点的x坐标相关,和y值无关。 •由n个点插值得到的基函数的次数必定是n-1次的多项 式
