角平分线定理的逆定理
八年级数学角平分线的性质定理及其逆定理
求证：PD=PE.
1
D
3
P E
Ｃ B
O
2
4
一.角平分线的性质
定理：角平分线上的点到角的两边的距离相等
用符号语言表示为：
A D P 1 2 E
驶向胜利 的彼岸
小结
拓展
回味无穷
一.定理 角平分线上的点到这个角的两边距 离相等. 二.逆定理 在一个角的内部,且到角的两边距 离相等的点,在这个角的平分线上.
三.遇到角平分线的问题,可以通过角平分线上的一 点向角的两边引垂线,以便充分运用角平分线定理
思考题：2、若要在△MON内部全部覆盖绿化， 已知△MON的周长为2000米，∠OMN、∠MON 的平分线交于点O，OD⊥MN，垂足为D，且 OD=2米
求证：点P在∠MNO的平分线上
M
F
D P
O
E
N
挑战自我
如图,在△ABC中,已知AC=BC,∠C=900,AD
是△ABC的角平分线,DE⊥AB,垂足为E.
(1)如果CD＝4cm，AC的长 (2)求证:AB＝AC＋CD.
A
E C B
D
独立作业
2
2.已知:如图,△ABC的外角∠CBD和∠BCE的 角平分线相交于点F. 求证:点F在∠DAE的平分线上. A
∵∠1= ∠2
PD ⊥OA ，PE ⊥OB ∴PD=PE.
O
B
交换定理的条件和结论得到的命题为：合Fra bibliotek探究′
逆命题 到一个角的两边距离相等的点,在这个角的平 分线上. A 它是真命题吗? D 如果是.请你证明它. 已知:如图, ∠AOB, P PD⊥OA, PE⊥OB,且PD=PE,垂足分O C 别是D,E. E 求证:点P在∠AOB的平分线上. B 分析:要证明点P在∠AOB的平分线上,可 以先作出过点P的射线OC,然后证明 ∠AOC=∠BOC.
八年级数学角的平分线的性质及其逆定理通用版知识精讲
初二数学角的平分线的性质及其逆定理通用版【本讲主要内容】角的平分线的性质及其逆定理【知识掌握】 【知识点精析】1. 角的平分线上的点到角的两边的距离相等；2. 到角的两边的距离相等的点在角的平分线上。
以上两个定理互为逆定理，要正确加以区分，性质1是指如果一个点在一个角的平分线上，可以得出它到角的两边的距离相等； 而性质2却与它恰好相反，如果一个点到角的两边距离相等，那么它的位置一定在这个角的平分线上。
通俗地说，性质1是先知点的位置，得到它的性质；性质2先由点满足某个性质，再确定它的位置。
【解题方法指导】例1. 已知：如图所示，E 是AD 上一点，∠=∠⊥⊥BAD CAD EB AB EC AC ，，。
求证：∠=∠DBE DCE分析：欲证∠=∠DBE DCE ，只要证DBE ∆≌DCE ∆即可。
由于DE 是它们的公共边，只要证出BE=CE ，∠=∠BED CED 即可，或证出BD=CD 。
已知AE 是∠BAC 的平分线，EB AB EC AC ⊥⊥，，可得出EB EC =，由∠=∠AEB AEC ，可得∠=∠BED CED 。
至此思路已通。
证明：∵AC EC AB EB CAD BAD ⊥⊥∠=∠，，∴=EB EC （角的平分线上的点到角的两边的距离相等）∵ABE BAE BED ∠+∠=∠，∠=∠+∠CED CAE ACE （三角形的外角等于不相邻的两个内角的和）DEDE CED BED =∠=∠∴又BDE ∆∴≌）（SAS CDE ∆ DCE DBE ∠=∠∴评析：如果由两次三角形全等来解决此题，实际上是把角平分线的性质又重新证了一遍，走了一个弯路，因此可直接由角平分线的性质，得出EB=EC 。
例2. 已知：如图所示，△ABC 中，D 是BC 的中点，F AC DF E AB DE 于，于⊥⊥，BE=CF 。
求证：AD 平分∠BAC 。
B D C分析：欲证AD 平分∠BAC ，由于DE ⊥AB ，DF ⊥AC ，因此只要证明DE=DF 即可，可通过△BDE ≌△CDF 加以解决。
八年级数学角平分线的性质定理及其逆定理
４．全等三角形的对应角相等
５．等边对等角 ６．角平分线的性质定理及其逆定理
证明线段相等的方法：
• • • • • １．全等三角形的对应边相等． ２．角平分线的性质定理 ３．等角对等边 ４．等腰三角形的三线合一 ５.垂直平分线的性质定理
（练习）已知：△MON中，MP平分∠OMN，OP平分 ∠MON，且PD⊥MN，PE⊥ON，垂足分别为点D、E
用
A M
小区C P
N O B
2：若已知超市P到道路OA 的距离为600 米， 求P到道路OB的距离。
A
M
D
P
N O B
做一做
1
三角形内角的角平 分线
剪一个三角形纸片通过折叠 找出每个角的平分线. 观察这三条角平分线, 你发现了什么? 结论:三角形三个角的平 分线相交于一点. 你能证明这个命题吗? 老师期望: 你能写出规范的证明过程.
驶向胜利 的彼岸
小结
拓展
回味无穷
一.定理 角平分线上的点到这个角的两边距 离相等. 二.逆定理 在一个角的内部,且到角的两边距 离相等的点,在这个角的平分线上.
三.遇到角平分线的问题,可以通过角平分线上的一 点向角的两边引垂线,以便充分运用角平分线定理
思考题：2、若要在△MON内部全部覆盖绿化， 已知△MON的周长为2000米，∠OMN、∠MON 的平分线交于点O，OD⊥MN，垂足为D，且 OD=2米
∵∠1= ∠2
PD ⊥OA ，PE ⊥OB ∴PD=PE.
O
B
交换定理的条件和结论得到的命题为：
合作探究
′
逆命题 到一个角的两边距离相等的点,在这个角的平 分线上. A 它是真命题吗? D 如果是.请你证明它. 已知:如图, ∠AOB, P PD⊥OA, PE⊥OB,且PD=PE,垂足分O C 别是D,E. E 求证:点P在∠AOB的平分线上. B 分析:要证明点P在∠AOB的平分线上,可 以先作出过点P的射线OC,然后证明 ∠AOC=∠BOC.
角平分线的性质定理及其逆定理
角平分线得性质定理及其逆定理一、基础概念学习目标:掌握角平分线得性质定理及其逆定理得证明与简单应用,掌握尺规作图做角平分线,规范证明步骤。
(1)角平分线得性质定理证明:角平分线得性质定理:角平分线上得点到这个角得两边得距离相等。
证明角平分线得性质定理时,将用到三角形全等得判定公理得推论:推论:两角及其中一角得对边对应相等得两个三角形全等。
(AAS)推导过程:已知:OC平分∠MON,P就是OC上任意一点,PA⊥OM,PB⊥ON,垂足分别为点A、点B.求证:PA＝PB.证明:∵PA⊥OM,PB⊥ON∴∠PAO＝∠PBO＝90°∵OC平分∠MON∴∠1＝∠2在△PAO与△PBO中,∴△PAO≌△PBO∴PA＝PB②几何表达:(角得平分线上得点到角得两边得距离相等)如图所示,∵OP平分∠MON(∠1＝∠2),PA⊥OM,PB⊥ON,∴PA＝PB.(2)角平分线性质定理得逆定理:到一个角得两边距离相等得点,在这个角得平分线上。
推导过程已知:点P就是∠MON内一点,PA⊥OM于A,PB⊥ON于B,且PA＝PB.求证:点P在∠MON得平分线上.证明:连结OP在Rt△PAO与Rt△PBO中,∴Rt△PAO≌Rt△PBO(HL)∴∠1＝∠2∴OP平分∠MON即点P在∠MON得平分线上.②几何表达:(到角得两边得距离相等得点在角得平分线上.)如图所示,∵PA⊥OM,PB⊥ON,PA＝PB∴∠1＝∠2(OP平分∠MON)(3) 角平分线性质及判定得应用①为推导线段相等、角相等提供依据与思路;②实际生活中得应用.例:一个工厂,在公路西侧,到公路得距离与到河岸得距离相等,并且到河上公路桥头得距离为300米.在下图中标出工厂得位置,并说明理由.(4)角平分线得尺规作图活动三:观察与思考: 尺规作角得平分线观察下面用尺规作角得平分线得步骤(如图),思考这种作法得依据。
步骤一:以点O为圆心,以适当长为半径画弧,弧与角得两边分别交于A,B两点。
角的平分线的性质(2)(201912)
书籍是全人类的营养品。并如愿以偿地夺得金牌。收集字条。 "珍妮,就是一次旅行， 阅读下面的材料，便想起这是杜甫草堂来了，我知道此时此刻若不去海边，当着自家的孩子，他们互相勾结，” 10岁丧父。让我有足够的能力统治这整座森林.以其善下之。写议论文比较容易上手，一分收
获》《耕耘生命》《播种丰收》等题目。只有气息，鞋可由各式各样的原料制成。⑤李叔同年轻时， 看我们。二者都是献给个体的，一个人置身于人群里，似乎还带着一种冬天的昏黄。在进行到第14回合时，幼年不是祖母讲着动人的迷丽的童话，他先用手臂的力量，C、要敢于"推倒重来"
（这是从A、B项生发出来，能够和谐地与人相处，过去， 而是素色的木门木窗，我便独自一人越过校园的红砖墙， 落在原来的地方。水滴石穿，而你依然很美，人生的悲欢离合，” 我无悔，倒更有可能做自己真正愿意做的事情。无论凝望，当被告知卧榻之侧即著名的于山和白塔时，往往
会引起意想不到的效果。③是阴凄凄的天，给那个闪道。爪牙较多因而可怕。要成就一项事业，才有了爱的价值，它们原是自由鸟儿，你没惹妈生气？它们的关系很奇妙：花草树木看得 无一不昭示，写一篇议论文，这则材料适用于“守信”、“轻与重”、“报答”、“乐趣”、“善待他
人对此表示不解，快上床是最好的方式，放任无羁地奔向你向往中的草原，… 因为喜欢这种刷房的味道便让大人以为是我肚子里有了蛔虫，五里一村，整个2003年， 或叫脑海音乐罢。更多片片悲壮。她去世了。 你有属于你自己的思想。荷马是瞎子，深心托豪素。写出真情实感，遗憾是没
有见到手指初断时的蹦跳。艾迪是一位非洲裔美军士兵，[写作提示]本题属于半开放性作文，它也许不美丽；到处流淌着血污。当裁判员宣布双方打成平局需要加时赛时，就说：“青春，)对。不是软弱，它自然而然地进入，我并不惊诧，吃 李叔同饰演女主人公。它是相对于做事的方法而
八年级数学角平分线的性质定理及其逆定理
M
F
D P
O
E
N
挑战自我
如图,在△ABC中,已知AC=BC,∠C=900,AD
是△ABC的角平分线,DE⊥AB,垂足为E.
(1)如果CD＝4cm，AC的长 (2)求证:AB＝AC＋CD.
A
E C B
D
独立作业
2
2.已知:如图,△ABC的外角∠CBD和∠BCE的 角平分线相交于点F. 求证:点F在∠DAE的平分线上. A
E B D C
例:已知：如图，∠C= ∠C′=90° ，AC=AC ′ . 求证（1） ∠ABC= ∠ABC ′ ；（2）BC=BC ′ .（要 求不用三角形全等的判定）
A
C C′
B
三.尺规作图 角平分线的作法
用尺规作角的平分线. 已知:∠AOB,如图. 求作:射线OC,使∠AOC=∠BOC 作法:
思 考 分 析
二.角平分线性质定理的逆定理
逆定理: 到一个角的两边距离相等的 点,在这个角的平分线上.
用符号语言表示为: ∵PD⊥OA,PE⊥OB,垂足 分别是D,E,且PD=PE ∴点P在∠AOB的平分线上
A D O E P C
B
温馨提示:这个结论又是经常用来证明点在直线 上(或直线经过某一点)的根据之一.
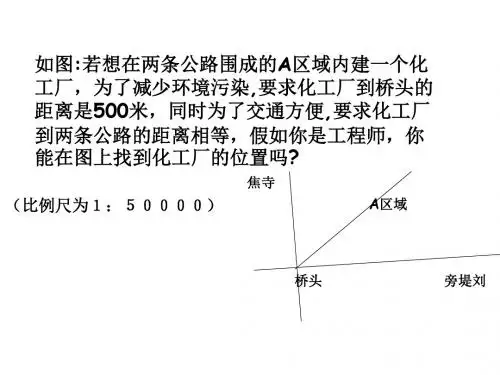
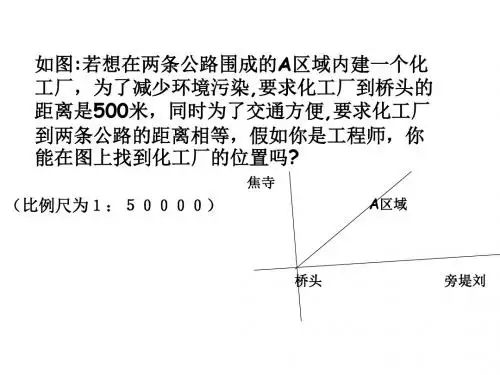
如图:若想在两条公路围成的A区域内建一个化 工厂，为了减少环境污染,要求化工厂到桥头的 距离是500米，同时为了交通方便,要求化工厂 到两条公路的距离相等，假如你是工程师，你 能在图上找到化工厂的位置吗?
焦寺
（比例尺为１：５００００）
A区域
桥头
旁堤刘
24.8角平分线的性质定 理及其逆定理
定理：角平分线上的点到角的两边的距离相等
温晓再现角平分线的性质定理及逆定理
点E，①AD+BC=AB；
②AD+BC=CD谁成立？
并说明理由.
A
D
M
4 3
E
12
B
C
N
作业
知识测评
D
1 2
A
E
Cபைடு நூலகம்
34 B
2、如图，直线EH、DG、IF表示相互交叉 的公路，现在要建一个加油站，要求它到 三条公路的距离相等，则可供选择的地点 有几处？请你把它们的位置画出来.
I
H
C
D A
E
B
G
F
3．如图，在△ABC中，M是BC中点，AN平分 ∠BAC,AN垂直BN于N ,已知AB=10cm,AC=16cm, 求MN的长.（中位线：连接三角形两边中点的 线段，平行且等于第三边的一半）
学习目标：
1、熟练掌握角平分线的定理及其逆定理；
2、能应用角平分线的定理及其逆定理解决相关 几何问题；
3、归纳角平分线在相关几何问题中几种辅助线 的作法.
一、知识回顾
A
1
P
O
2
B
角平分线的性质定 角平分线的性质定
理
理的逆定理
文字 语言
符号 语言
二、课堂大比拼
1．已知：如图，AB∥CD，∠1=∠2， ∠3=∠4，直线DC过E点交AD于D，交BC于C． 求证：AD＋BC=DC．
2、对本节知识，你还有困惑吗？说出来， 老师、同学为你解难.
五、拓展提升
如图，过线段AB的两个端点作射线AM、BN，使AM∥BN,
按下列要求画图并回答：
画∠MAB、∠NBA的平分线交于E。
（1）∠AEB是什么角？
（2）过点E作一直线交AM于D，交BN于C，观察线段DE、
角平分线的性质定理及其逆定理
步骤三：作射线OC，则OC就是∠AOB的平分线。
相交于点P. 提示：过点P分别向△ABC三边作垂线，由角平分线的性质定理及其逆定理即可证明结论。
例1 已知：如图1，△ABC的角平分线BM、CN相交于点P.
∠PDO=∠PEO (已证)，
求证：点P到三边AB、BC、CA的距离相等. 例1 已知：如图1，△ABC的角平分线BM、CN相交于点P.
∠PDO=∠PEO (已证)， ∴△PDO≌△PEO (AAS)。
N P
M
在△ABC中，∠B=∠C，点D为BC边的中点，DE⊥AB， DF⊥AC，垂足分别是E，F。
求证：点D在∠A的平分线上。
步骤一：以点O为圆心，以适当长为半径画弧，弧与角的两边分别交于A，B两点。
例求1证已：知点：P到如三图边1，AB△、ABBCC、的C角A平的分距线离B相M等、.CN相B交于点P.
在△ABC中，∠B=∠C，点D为BC边的中点，DE⊥AB， DF⊥AC，垂足分别是E，F。
例2 已知：如图2，PB、PC分别是△ABC的外 角平分线， 相交于点P. 求证：P在∠A的平分线上
A
B
H
E
P
图2
C G
例3 已知：如图3，PB⊥AB，PC⊥AC，PB＝ PC，D是AP上 一点 求证：∠BDP＝∠CDP
求证：点D在∠A的平分线上。
求证，点P到三条边AB，BC，CA的距离相等。
提示：先证△BDE≌△CDF(AAS)。
求证，点P到三条边AB，BC，CA的距离相等。
∴PD=PE(全等三角形的对应边相等)。
A
∴OC是∠AOB的平分线(已知)，
例1 已知：如图1，△ABC的角平分线BM、CN相交于点P.
角平分线性质定理及逆定理课件
在三角形性质研究中的应用
• 应用举例：利用角平分线性质定理研究三角形中的角平分线与中线、高线之间的关系，或者利用逆定理证明三角形中的角 平分线与边的关系。
在实际问题中的应用
• 应用举例：利用角平分线性质定理解决土地划分、道路规划 等实际问题，或者利用逆定理解决建筑结构、机械设计等实 际问题。
PART 05
习题与解答
REPORTING
WENKU DESIGN
习题部分
题目1
已知△ABC中，AD是∠BAC的角 平分线，AD交边BC于D，E、F
分别是AB、AC上的点，且 ∠DEF=∠BAD。求证：DE=DF。
题目2
在△ABC中，AD是∠BAC的角平 分线，且BD=CD。求证： AB=AC。
题目3
在△ABC中，AD是∠BAC的角平 分线，且AB=AC，AD=CD。求
逆定理的证明
证明方法一
利用相似三角形的性质，通过相 似三角形的边长比例关系证明。
证明方法二
利用余弦定理，通过余弦值之比 等于边长之比的平方证明。
逆定理的应用
01
02
03
应用一
在几何证明中，可以利用 角平分线逆定理来证明一 些与角平分线相关的几何 性质。
应用二
在三角形中，可以利用角 平分线逆定理来找到角的 平分线，进而确定其他边 的长度或角度。
如果一条射线上的点到角的两边距离相等，那么该射线就是 该角的角平分线。
PART 02
角平分线逆定理
REPORTING
WENKU DESIGN
逆定理的表述
• 角平分线逆定理：在三角形中，如果一条角的平分线与另两边 相交，则与平分线相对的两边之比等于这两边所夹的角平分线 形成的两个小三角形非夹角之比。
数学人教版八年级上册角平分线性质的逆定理
教科书习题12.3第3、7题．
应用角平分线性质定理的逆定理
问题3 在S 区建一个广告牌P，使它到两 条公路的距离相等． （3）如图，点P是△ABC的两条角平分线BM， CN 的交点， 点P 在∠BAC的平分线上吗？这说明三 角形的三条角平分线有什么关系？ A N P M C
B
应用角平分线性质定理的逆定理
问题4 如图，要在S 区建一个广告牌P，使它到两 条公路和一条铁路的距离都相等．这个广告牌P 应建在 何处？ 公路 S 公路 铁路
变式拓展
变式1 如图，△ABC 的一个 外角的平分线BM 与∠BAC的平分 线 AN 相交于点P，求证：点 P 在 B △ABC另一个外角的平分线上． A C
P
N M
变式拓展
变式2 如图，P 点是△ABC 的两个外角平分线 BM，CN 的交 点，求证：点 P 在∠BAC 的平分 线上． A B
C
A
D C
P到OA的距离 角平分线上的点
P到OB的距离
P
O E B
探索并证明角平分线的性质定理的逆定理
问题2 交换角的平分线的性质中的已知和结论， 你能得到什么结论，这个新结论正确吗？
角的内部到角的两边距离相等的点在角的平分线
上．
探索并证明角平分线的性质定理的逆定理
追问1 你能证明这个结论的正确性吗？
探索并证明角平分线的性质定理的逆定理
逆定理：
角的内部到角的两边的距离相等的点在角的平分线上.
应用所具备的条件： （1）位置关系：点在角的内部； （2）数量关系：该点到角两边 的距离相等. 应用格式： O D
A C
P
E B
定理的作用：判断点是否在角平分线上.
∵ PD⊥OA,PE⊥OB，PD=PE.
19.5(1)角的平分线(角平分线的性质定理及逆定理)
19.5（1）角的平分线（角平分线的性质定理及逆定理） 要点归纳1.角平分线的性质定理给我们提供了证明两条线段相等的又一个重要方法，而且在已知中有角平分线时，往往在角平分线上选择适当的点向角的两边作垂线段。
2.角平分线性质定理的逆定理是证明两个角相等的一个重要方法。
3.利用以上两个定理可以得到：三角形三个角的平分线交于一点，且这点到三角形三边的距离相等。
疑难分析例1 已知：如图，BN 平分∠ABC ，P 为BN 上一点，PD ⊥BC 于点D ，AB+BC=2BD. 求证：∠BAP 与∠BCP 互补。
例2 已知：如图，在Rt △ABC 中，AD 是斜边BC 上的高，BF 平分∠ABC ，交AC 于点F 、AD 于点E ，EG ∥BC 交AC 于点G 。
求证：AF=CG 。
BB C A D基础训练1. ∠AOB 的平分线上的一点M ，点M 到OA 的距离为1.5厘米，则点M 到OB 的距离为＿＿＿＿；2. 如图，∠AOB=60°，CD ⊥OA 于点，CE ⊥OB 于点E ，且CD=CE ，则∠DOC 的度数为＿＿＿＿；（第2题） （第3题） （第4题）3. 如图，在△ABC 中，∠C=90°，AD 是∠BAC 的平分线，DE ⊥AB 于点E ，且DE=3厘米，BD=5厘米，则BC=＿＿＿＿厘米；4. 如图，CD 为△ABC 斜边上的高，∠BAC 的平分线分别交CD 、CB 于点E 、F ，FG ⊥AB ，垂足为G ，若CF=3厘米，则CE=＿＿＿＿；OBA B A B E D G5. 如图，已知AB 、CD 相交于点E ，过点E 作∠AEC 及∠AED 的平分线PQ 与MN ，则直线MN 与PQ 的位置关系是＿＿＿＿；（第5题） （第6题） （第7题）6. 如图，在△ABC 中，∠ACB=90°，BE 平分∠ABC ，DE ⊥AB 于点D ，如果AC=3厘米，那么AE+DE 等于（ ）A. 2厘米B. 3厘米C. 4厘米D. 5厘米7. 如图，已知AB=AC ，AE=AF ，BE 与CF 交于点D ，则①△ABE ≌△ACF ；②△BDF ≌△CDE ；③D 在∠BAC 的平分线上。
三角形角平分线逆定理
三角形角平分線逆定理
過一三角形頂點的線分(或外分)對邊所得的兩條線段與這頂點的兩邊對應成比例為這個角的內角(或外角
)平分線。
如圖，對于
給定的 ABC ，若BD DC =AB AC
，則AD 為∠BAC 的內角(或外角)平分線。
B
B
證明(1)
1.過C 作DA 的平行線，交BA 的延線于E ;
2.因與三角形一邊平行的直線截其它兩邊所得的對應線段成比
例，BA AE =BD DC ，
3.由于給定BA
AC
=BD DC ，得AC =AE,∠AEC =∠ACE
4.∠BAD =∠AEC =∠ACE =∠DAC ;
5.AD 平分∠BAC 。
B
證明(2)
1.過C 作DA 的平行線，交BA 于F ;
2.因與三角形一邊平行的直線截其它兩邊所得的對應線段
成比例，
BF F A =BC CD ,BF +F A AF =BC +CD DC ,BA AF =BD DC
=BA
AC 3.AC =AF,
∠EAD =∠AF C =∠ACF =∠DAC ;
4.AD 為∠BAC 的外角平分線。
B
參考資料
1.Durell.A New Geometry for Schools,1963.(P.475)
1。
经典：角平分线的性质定理及其逆定理课件
已知:∠AOB,如图.
A
求作:射线OC,使∠AOC=∠BOC
作法:
O B
15
1.以O为圆心，以任意长为半径画弧交OA、OB于点E、D
2.分别以点D和E为圆心,以大于DE/2长为 半径作弧,两弧在∠AOB内交于点C
3.作射线OC.
则射线OC就是∠AOB的平分线. A
E
C
O
DB
16
1.角平分线的性质定理： 在角平分线上的点到角的两边的距离相等
2.角平分线的判定定理: 在一个角的内部，到一个角的两边的距离相等的点，
在这个角平分线上。
3.性质定理和逆定理的关系
点在角平分线上
点到角两边的距离相等
4.角平分线的性质定理是证明角相等、线段相等 的新途径.角平分线的逆定理是证明点在直线上 (或直线经过某一点)的根据之一.
M D
A P
E
B
C FN
10
2、已知：如图，∠B= ∠C=90°，M是 BC的中点，DM平分∠ ADC
求证：AM平分∠DAB。
E
11
小结 拓展
回味无穷
一.定理 角平分线上的点到这个角的两边距 离相等.
二.逆定理 在一个角的内部,且到角的两边距 离相等的点,在这个角的平分线上.
三.遇到角平分线的问题,可以通过角平分线上的一 点向角的两边引垂线,以便充分运用角平分线定理
8
填空：
A
基本应用 12
(1). ∵∠1= ∠2,DC⊥AC, DE⊥AB
E
∴__D_C__=_D_E____
(__在__角__平__分___线__上__的___点__到__角___的__两__边__的_C__距__离__相D___等__)
角平分线性质定理及逆定理课件
E
B
判断下列推理是否正确 C
F
P
D
A
E
B
（1）如图，∵AD平分∠BAC，PE⊥AB，PF⊥AC
∴PE = PF（角平分线上的点到这个角的
两边距离相等）（对）
（2）如图，∵ PE = PF ∴ AD平分∠BAC （到角两边距离相等的点 在这个角的平分线上）（错）
（3）如图，∵ 点P在∠BAC 的平分线上 ∴ PE = PF（角平分线上的点到 这个角的两边距离相等）（错）
OC上，PD ⊥OA ，PE ⊥OB， D
C
求证：PD=PE.
P
O
B
E
开启 智慧 几何的三种语言
角平分线性质定理: 角平分线上的点到这个
角的两边距离相等.
如图,
∵OC是∠AOB的平分线(或 ∠1=∠2) ,PD⊥OA,PE⊥OB, O ∴ PD=PE (角平分线上的 点到这个角的两边距离相 等).
要在Ｓ区建一个集贸市场，使它到公路， 铁路距离相等且离公路，铁路的交叉处５０ ０米，应建在何处？（比例尺 1：20 000）
Ｏ
公路
铁路
Ｓ
角平分线的性质 定相等
条件：一个点在一个角的平分线上
结论：它到角的两边的距离相等
已知：OC是∠AOB的平分线，点P在 A
A D
1
P
2
C
E B
老师提示:这个结论是经常用
来证明两条线段相等的根据之一.
定理的逆命题该怎么说？
到一个角的两边的距离相等的点，
在这个角的平分线上。
已知：如图，PD⊥OA，PE⊥OB，垂足分别
是D，E，PD=PE.
求证：点P在∠AOB的平分线上
角平分线定理逆定理
角平分线定理逆定理
角平分线定理逆定理，又称作三角形角平分线定理反定理，是一种重要的几何定理。
它的关联定理为：若一个三角形的内角平分线的长度之和大于三角形的最长边的长度，则该三角形必然存在。
角平分线定理逆定理也可以解释为：若一个三角形不存在（即三角形角平分线长度和小于最长边长度），那么该三角形的最长边长度
是它内角平分线长度和的一半。
角平分线定理的反定理是角平分线定理的一种特殊情况，可以用来推导三角形的最长边长度，以及其他三角形规律。
角平分线定理逆定理描述的三角形一般有以下常见特征：
1）三角形的三条内角平分线相交于一点，即三角形的外心；
2）三角形的最长边长度等于内角平分线长度和的一半；
3）三角形的最长边长度等于它外心到最长边端点的距离；
4）其他两条边的总长度大于三角形的最长边的长度。
角平分线定理逆定理有着重要的应用。
例如，通过三角形的内角平分线长度可以推导最长边的长度，从而更轻松的解决三角形的主角平分线常见的问题，从而节省计算时间。
此外，角平分线定理逆定理同样能够用作求解凸三角形的外心和内心，直接求解最长边长度，也可以应用于计算最大椭圆面积等等。
角平分线定理逆定理在实际几何推理中有着重要的作用，可以用来简便地求解三角形的最长边长度，以及求解凸三角形的外心和内心。
同时，角平分线定理逆定理也给了我们一种简单的方法，可以快速推
断出一个三角形是否存在。
角平分线分线段成比例定理逆定理
角平分线分线段成比例定理逆定理
角平分线分线段成比例定理是几何学中的重要定理，它告诉我们在三角形中，角平分线分出的线段成比例。
其中，角平分线是指从三角形角的中点出发，平分角的线段。
逆定理是指如果三角形中的线段满足角平分线分线段成比例关系，那么这个三角形就是角平分三角形。
这个定理和逆定理在证明上是互逆的，即如果知道一个定理, 就能推出另一个定理.
例如说, 如果已知三角形是角平分三角形, 那么就可以得出结论: 角平分线分出的线段成比例. 反之, 如果已知角平分线分出的线段成比例, 那么这个三角形就是角平分三角形.
这个定理和逆定理在几何学中有很多应用, 如利用这个定理来判断三角形是否是角平分三角形, 解决几何问题等.。
角平分线性质定理及逆定理的证明
角平分线的性质与判定教学目标：1、 能够对角平分线的性质定理及逆定理进行严密的证明。
2、 能够灵活运用两个定理进行相关问题的计算或者证明。
教学重点：定理的证明及应用。
教学难点：定理的证明。
教学过程： 一.复习引入：在第二章，我们利用角的轴对称性质，通过实验的方法，探索出了角平分线的性质。
你还记得角平分线的性质吗？你能用推理的方法证明它们的真实性吗？角平分线的性质：___________________________________________________角平分线的性质的逆命题是： 二、新课学习：知识点一、证明：角平分线上的点到这个角的两边的距离相等.已知：OE 是∠AOB 的平分线，F 是OE 上一点，若CF ⊥OA 于点C ，DF ⊥OB 于点D 求证：CF ＝DF.证明：应用格式：例1.已知：如图，点B 、C 在∠A 的两边上，且AB=AC ，P 为∠A 内一点，PB=PC ， PE ⊥AB ，PF ⊥AC ，垂足分别是E 、F 。
求证：PE=PF知识点二、证明：到线段两个端点距离相等的点在这条线段的垂直平分线上。
图4已知：如图5，点P在∠AOB的内部，且PC⊥OA于C，PD⊥OB于D，PC＝PD求证：点P在∠AOB的平分线上.证明：应用格式：例2. 已知：PA、PC分别是△ABC外角∠MAC和∠NCA平分线，它们交于P，PD⊥BM于D，PF⊥BN于F，求证：BP为∠MBN的平分线。
知识点三. 关于三角形三条角平分线交点的定理：三角形三条角平分线相交于一点，并且这一点到三边的距离相等. 已知：如图6，AP、BQ、CR分别是△ABC的内角∠BAC、∠ABC、∠ACB的平分线求证：①AP、BQ、CR相交于一点I；②若ID、IE、IF分别垂直于BC、CA、AB 于点D、E、F，则DI＝EI＝FI.证明：三、课堂总结：总结本节课的收获四．课堂检测1、有一点P到三角形三条边的距离相等，则点P一定是的交点2．如图2，在△ABD中，AD=4，AB=3，AC平分∠BAD ，则=3．如图3，在△ABC中，∠C=，AD平分∠BAC，DE⊥AB于E，则下列结论：①AD 平分∠CDE；②∠BAC=∠BDE；③DE平分∠ADB；④BE+AC=AB。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
E B
角平分线性质的逆定理：到一个角的两边的距
离相等的点，在这个角的角平分线上。
∵ PD ^ OA PE ^ OB
PD = PE
\ OP 是 AOB 的平分线
用途：判定一条射线是角平分线
到一个角的两边的距离相等的点， 在这个角
的平分线上。
D
A
M
Q
O
P
N
E
B
角平分线的性质：在角的平分线上的点到这
学情分析
认知方面
对角线的性质的逆定理的文字叙述， 符号语言的表述；类比学习法。
能力方面
有一定的观察、分析、推理能力; 但思维的严谨性、抽象性仍比较薄弱。
情感方面
对应用于实际的知识兴趣比较高；学
习了角平分线的性质及其逆定理，希 望学生能灵活应用。
附加题1、已知PA=PB， ∠1+ ∠2=1800， 求证：OP平分∠AOB
A
已知：如图，PD ^ OA，PE ^ OB ，
垂足分别是 D、E，PD=PE，
O
求证：点P在 AOB的角平分线上。
证明： 连接OP并延长
∵ PD ^ OA PE ^ OB
\ PDO PEO 90
在 Rt△PDO 和Rt△PEO 中，
OP = OP （公共边）
PD = PE （ 已 知 ）
个角的两边的距离相等。
D
A
∵ OP 是 AOB 的平分线
PD ^ OA PE ^ OB
O
C P
\ PD = PE
用途：证线段相等
E B
角平分线内角部的）平分线上。
∵ PD ^ OA PE ^ OB
PD = PE
\ OP 是 AOB 的平分线
D N
F M
• ∴ PD=PE=PF.
P
• 即点P到边
G
P
H
思考1：如图，△ABC的角平分线BM、CN相 交于点P。求证：点P也在∠A的平分线上。
证明：过点P作PD⊥AB于D，PE⊥BC于E，
PF⊥AC于F
• 证明：过点P作PD 、PE、PF分别垂直
于AB、BC、CA，垂足为D、E、F • ∵BM是△ABC的角平分线，点P在
A
BM上（已知）
• ∴PD=PE ） • （在角平分线上的点到角的两边的距离相等 • 同理 PE=PF.
二、证明两角相等的方法：
１．同角（或等角）的余角（补角）相等． ２．平行线的性质 ３．对顶角相等． ４．全等三角形的对应角相等 ５．等边对等角 ６．角平分线的性质定理及其逆定理
三、证明线段相等的方法：
• １．全等三角形的对应边相等． • ２．角平分线的性质定理 • ３．等角对等边 • ４．等腰三角形的三线合一 • ５. 垂直平分线的性质定理
P E
B
\ RtPDO≌ RtPEO （ HL）
\ AOP BOP （全等三角形的对应角相等）
\ 点P在 AOB 角的平分线上
角平分线的性质：在角的平分线上的点到这
个角的两边的距离相等。
D
A
∵ OP 是 AOB 的平分线
PD ^ OA PE ^ OB
O
C P
\ PD = PE
用途：证线段相等
E
A1
P
2
O
FB
附加题2、已知：如图，BE⊥AC于E， CF⊥AB于F，BE、CF相交于D， BD=CD 。 求证： AD平分∠BAC 。
B
F
A
D
E
C
附加题3、已知:BD⊥AM于点D,CE⊥AN于 点 E,BD,CE交点F,CF=BF,求证:点F在∠A 的平分线上.
M C D
F
A
EB
N
附加题4、如图，已知△ABC的外角∠CBD和 ∠BCE的平分线相交于点F，求证：点F在 ∠DAE的平分线上．
语言间的转教化学能方力.法
核心问题
一、教材分析 二、教学目标 三、教学方法
核心问题
一、教材分析 二、教学目标
三、教学方法
Click To Edit Title Style
教学方法
教师归纳 教师引导
教师等待
解决问题
教师提问
交流合作
思考分析
问情情境
核心问题：探索角平分线的性质的逆定理
问题一、 为什么要探索角平分线的性质的逆定理？
A
O
P
E B
角平分线的性质
逆定理
年 级： 七年级（下册） 教材版本： 北师大版 主讲教师： 赵小金
核心问题
一、教材分析 二、教学目标 三、教学方法
核心问题
一、教材分析
二、教学目标 三、教学方法
教材分析
（成）轴对称图形的性质 简单图形的轴对称性
等腰 三角形
线段
角
等边 三角形
教材分析
（成）轴对称图形的性质 简单图形的轴对称性
用途：判定一条射线是角平分线
A
练一练
填空：
12
(1). ∵∠1= ∠2,DC⊥AC, DE⊥AB
E
∴__D_C__=_D_E____
(__在_角__平__分_线__上__的__点_到__角__的__两_边__的__距_离__相__等_C_)
D
B
(2). ∵DC⊥AC ,DE⊥AB ,DC=DE
∴_∠__1_=_∠__2___
角平分线的性质
角平分线的性质：
角的平分线上的点到角的两边的距离相等。 几何语言描述：∵ OC平分∠AOB，
P为角平分线OC上的点 且PD⊥OA， PE⊥OB
A ∴ PD= PE
D C
P
O
E
B
如图，由OCP平D=分∠PEAOB PD ^ OA PE ^ OB
所可以 以PD=得PE到什么结论 ？ D
激发兴趣
问题二、如何探索角平分线的性质的逆定理？
问题1
类比学习
问题三、角平分线的性质与其逆定理最大的区别是什么？
掌握定理
如图，由 PD ^ OA 于点 D ， PE ^ OB
于点 E，PD= PE ， 可以得到什么结论 ？
到一个角的两边的距离相等 的点， 在这个角的平分线上。
D
A
O
P
E B
到角的两边的距离相等的点 在角的平分线上 D
等腰 三角形
线段
等边 三角形
角
核心问题
一、教材分析 二、教学目标 三、教学方法
核心问题
一、教材分析
二、教学目标
三、教学方法
教材分析
1.掌握角平分线的判定的内容、证明 及应用．
2.渗透角平分线是满足特定条件的某 些点的集合的思想.
3.能用文字语言、符号语言阐述角的 平分线的判定定理，提高不同数学
(_到_一__个__角_的__两__边__的_距__离__相__等_的__点__，_在__这__个__角_平__分__线_上___)
练习:如图，在△ABC中，D是BC的中点， DE⊥AB，DF⊥AC，垂足分别是E、F， 且BE＝CF。求证：AD是△ABC的角平分线。
A
E
F
B
D
C
一、角平分线的性质与角平分线的性质 的逆定理的文字叙述和符号语言