北师大版九年级数学上册期末复习压轴题专题训练试题
北师大版九年级数学上期末备考压轴题专项培优：特殊的平行四边形(解析版)
期末备考压轴题专项培优：特殊的平行四边形1．如图，四边形ABCD是正方形，△ABE是等边三角形，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM．设点N 的坐标为（m，n）．（1）若建立平面直角坐标系，满足原点在线段BD上，点B（﹣1，0），A（0，1）．且BM＝t（0＜t≤2），则点D的坐标为（1，0），点C的坐标为（0，﹣1）；请直接写出点N纵坐标n的取值范围是0＜n≤；（2）若正方形的边长为2，求EC的长，以及AM+BM+CM的最小值．（提示：连结MN：＝+1，＝﹣1）解：（1）如图1，以直线BD为x轴，直线AC为y轴，建立平面直角坐标系，∵四边形ABCD是正方形，∴OA＝OB＝OC＝OD，∵点B（﹣1，0），A（0，1），∴D（1，0），C（0，﹣1）；过N作NH⊥BD于h，∴∠NHB＝90°，∵将BM绕点B逆时针旋转60°得到BN，∴∠NBH＝60°，BM＝BN，∴NH＝BN＝t，∵0＜t≤2，∴点N纵坐标n的取值范围是0＜n≤；故答案为：（1，0），（0，﹣1）；0＜n≤；（2）如图所示，连接MN，过E作EH⊥BC，交CB的延长线于H，由旋转可得，BM＝BN，∠NBM＝60°，∴△BMN是等边三角形，∴MN＝BM，∵△ABE是等边三角形，∴BE＝BA，∠ABE＝60°，∴∠ABM＝∠EBN，∴△ABM≌△EBN（SAS），∴AM＝EN，∴AM+BM+CM＝EN+MN+CM，∴当E，N，M，C在同一直线上时，AM+BM+CN的最小值是CE的长，又∵∠ABE＝60°，∠ABH＝90°，∴∠EBH＝30°，∴Rt△EBH中，EH＝EB＝×2＝1，∴BH＝＝＝，∴CH＝2+，∴Rt△CEH中，CE＝＝＝＝；∴AM+BM+CM的最小值为+．2．如图，在▱ABCD中，∠BAD的平分线交BC于点E，交DC的延长线于F，以EC、CF为邻边作▱ECFG．（1）证明▱ECFG是菱形；（2）若∠ABC＝120°，连结BD、CG，求∠BDG的度数；（3）若∠ABC＝90°，AB＝6，AD＝8，M是EF的中点，求DM的长．解：（1）证明：，∵AF平分∠BAD，∴∠BAF＝∠DAF，∵四边形ABCD是平行四边形，∴AD∥BC，AB∥CD，∴∠DAF＝∠CEF，∠BAF＝∠CFE，∴∠CEF＝∠CFE，∴CE＝CF，又∵四边形ECFG是平行四边形，∴四边形ECFG为菱形；（2）∵四边形ABCD是平行四边形，∴AB∥DC，AB＝DC，AD∥BC，∵∠ABC＝120°，∴∠BCD＝60°，∠BCF＝120°由（1）知，四边形CEGF是菱形，∴CE＝GE，∠BCG＝∠BCF＝60°，∴CG＝GE＝CE，∠DCG＝120°，∵EG∥DF，∴∠BEG＝120°＝∠DCG，∵AE是∠BAD的平分线，∴∠DAE＝∠BAE，∵AD∥BC，∴∠DAE＝∠AEB，∴∠BAE＝∠AEB，∴AB＝BE，∴BE＝CD，∴△BEG≌△DCG（SAS），∴BG＝DG，∠BGE＝∠DGC，∴∠BGD＝∠CGE，∵CG＝GE＝CE，∴△CEG是等边三角形，∴∠CGE＝60°，∴∠BGD＝60°，∵BG＝DG，∴△BDG是等边三角形，∴∠BDG＝60°；（3）如图2中，连接BM，MC，∵∠ABC＝90°，四边形ABCD是平行四边形，∴四边形ABCD是矩形，又由（1）可知四边形ECFG为菱形，∠ECF＝90°，∴四边形ECFG为正方形．∵∠BAF＝∠DAF，∴BE＝AB＝DC，∵M为EF中点，∴∠CEM＝∠ECM＝45°，∴∠BEM＝∠DCM＝135°，在△BME和△DMC中，∵，∴△BME≌△DMC（SAS），∴MB＝MD，∠DMC＝∠BME．∴∠BMD＝∠BME+∠EMD＝∠DMC+∠EMD＝90°，∴△BMD是等腰直角三角形．∵AB＝6，AD＝8，∴BD＝10，∴DM＝BD＝5．3．如图，在正方形ABCD中，对角线AC、BD相交于点O，以AD为边向外作等边△ADE，连接CE，交BD于F．（1）如图1，若AE＝，求DF的长；（2）如图2，点M为AB的延长线上一点，连接CM，连接FM且FM平分∠AMC，求证：CM＝MF﹣AM．解：（1）如图1，连接OE，∵四边形ABCD是正方形，∴AD＝CD，∠ADC＝90°，OA＝OD＝OB＝OC∵△ADE是等边三角形∴AD＝DE＝AE＝，∠ADE＝60°∴CD＝AD＝，OD＝OB＝∵AE＝DE，OD＝OA∴OE垂直平分AD即OE⊥AD，DH＝AH∴OE＝OH+EH＝+＝，∵∠ADC＝∠DHE＝90°∴CD∥OE∴△CDF∽△EOF∴＝，即DF＝OF∵DF+OF＝OD＝∴OF＝﹣DF∴DF＝（﹣DF），解得：DF＝﹣1．（2）如图2，连接EO，过点F作PQ⊥CD交EO于N，在MA上截取MT＝MC，连接FT，设正方形边长为a，∵四边形ABCD是正方形，△ADE是等边三角形∴AD＝AB＝CD＝DE＝a，∠ADC＝∠DAB＝90°∠ADE＝60°易证OE⊥AD∴OE＝a，OD＝a，由（1）知△CDF∽△EOF∴＝，即a•DF＝a•OF∵DF+OF＝a∴OF＝a﹣DF∴a•DF＝a（a﹣DF）∴DF＝a，∵△DPF是等腰直角三角形∴DP＝PF＝DF＝a，∴FQ＝a﹣a＝a＝CP，∵FM平分∠AMC，∴∠CMF＝∠AMF在△MCF和△MTF中∴△MCF≌△MTF（SAS）∴CF＝FT∴Rt△CFP≌Rt△FTQ（HL）∴QT＝PF＝a，∵AQ＝DP∴AQ＝QT∵BM+AB﹣AT＝MT＝CM∴CM﹣BM＝AB﹣AT＝a﹣2×a＝a，CM+BM＝MT+BM＝BT+2BM＝a﹣2×a+2BM＝a+2BM∴CM2﹣BM2＝（CM﹣BM）（CM+BM）＝a（a+2BM）∵CM2﹣BM2＝BC2＝a2，∴a（a+2BM）＝a2，∴BM＝a在Rt△BCM中，tan∠BMC＝＝＝，∴∠BMC＝60°∴∠AMF＝30°∴＝cos∠AMF＝cos30°＝∴2MQ＝MF∵2MQ＝2BM+2BQ＝2BM+2BT+2QT＝（BM+BT）+（BM+BT+AT）＝CM+AM ∴CM+AM＝MF即CM＝MF﹣AM．4．在菱形ABCD中，∠ABC＝60°，BD为菱形的一条对角线．（1）如图1，过A作AE⊥BC于点E，交BD于点F，若EF＝2，求菱形ABCD的面积；（2）如图2，M为菱形ABCD外一点，过A作AN⊥BM交BM的延长线于点N，连接AM，DM，AG⊥DM于点G，且∠AMN＝∠AMD，求证：DM＝BM+AM．（1）解：如图1中，∵四边形ABC都是菱形，∠ABC＝60°，∴∠ABD＝∠DBC＝30°，∵AE⊥BC，∴∠BEF＝90°，∵EF＝2，∴BF＝2EF＝4，∠BFE＝60°，∵∠BFE＝∠ABF+∠F AB，∴∠ABF＝∠F AB＝30°，∴BF＝AF＝4，∴AE＝AF+EF＝6，∴AB＝＝4，∴BC＝AB＝4，∴S＝BC•AE＝24．菱形ABCD（2）证明：如图2中，∵∠AMN＝∠AMG，AN⊥MN，AG⊥DM，∴AN＝AG，∵∠MNA＝∠MGA＝90°，AM＝AM，AN＝AG，∴Rt△MAN≌Rt△MAG（HL），∴NM＝MG，∵∠ANB＝∠AGD＝90°，AN＝AG，AB＝AD，∴Rt△ANB≌Rt△AGD（HL），∴∠ABN＝∠ADG，BN＝DG，∴∠BMD＝△BAD＝120°，∴∠NMG＝60°，∴∠AMN＝∠AMG＝30°，∴DM﹣BM＝MG+DG﹣（BN﹣MN）＝2MN＝AM，∴DM＝BM+AM．5．如图，点A、B、C、D在同一条直线上，点E、F分别在直线AD的两侧，且AE＝DF，∠A＝∠D，AB＝DC．（1）求证：四边形BFCE是平行四边形；（2）若AD＝12，DC＝3，∠EBD＝60°，则BE＝6时，四边形BFCE是菱形．（只需完成填空，不需写出具体过程．）（1）证明：∵在△ABE和△DCF中，∴△ABE≌△DCF（SAS），∴BE＝FC，∠ABE＝∠DCF，∴∠EBC＝∠FCB，∴BE∥FC，∴四边形BFCE是平行四边形；（2）解：当四边形BFCE是菱形，则BE＝EC，∵AD＝12，DC＝3，AB＝DC，∴BC＝6，∵∠EBD＝60°，EB＝EC，∴△EBC是等边三角形，∴BE＝6．故答案为：6．6．已知：如图，在▱ABCD中，G、H分别是AD、BC的中点，E、O、F分别是对角线BD上的四等分点，顺次连接G、E、H、F．（1）求证：四边形GEHF是平行四边形；（2）当▱ABCD满足AB⊥BD条件时，四边形GEHF是菱形；（3）若BD＝2AB，①探究四边形GEHF的形状，并说明理由；②当AB＝2，∠ABD＝120°时，直接写出四边形GEHF的面积．（1）证明：连接AC，如图1所示：∵四边形ABCD是平行四边形，∴OA＝OC，OB＝OD，∴BD的中点在AC上，∵E、O、F分别是对角线BD上的四等分点，∴E、F分别为OB、OD的中点，∵G是AD的中点，∴GF为△AOD的中位线，∴GF∥OA，GF＝OA，同理：EH∥OC，EH＝OC，∴EH＝GF，EH∥GF，∴四边形GEHF是平行四边形；（2）解：当▱ABCD满足AB⊥BD条件时，四边形GEHF是菱形；理由如下：连接GH，如图2所示：则AG＝BH，AG∥BH，∴四边形ABHG是平行四边形，∴AB∥GH，∵AB⊥BD，∴GH⊥BD，∴GH⊥EF，∴四边形GEHF是菱形；故答案为：AB⊥BD；（3）解：①四边形GEHF是矩形；理由如下：由（2）得：四边形GEHF是平行四边形，∴GH＝AB，∵BD＝2AB，∴AB＝BD＝EF，∴GH＝EF，∴四边形GEHF是矩形；②作AM⊥BD于M，GN⊥BD于N，如图3所示：则AM∥GN，∵G是AD的中点，∴GN是△ADM的中位线，∴GN＝AM，∵∠ABD＝120°，∴∠ABM＝60°，∴∠BAM＝30°，∴BM＝AB＝1，AM＝BM＝，∴GN＝，∵BD＝2AB＝4，∴EF＝BD＝2，∴△EFG的面积＝EF×GN＝×2×＝，∴四边形GEHF的面积＝2△EFG的面积＝．7．如图，边长为6的正方形ABCD中，E，F分别是AD，AB上的点，AP⊥BE，P为垂足．（1）如图1，AF＝BF，AE＝2，点T是射线PF上的一个动点，当△ABT为直角三角形时，求AT的长；（2）如图2，若AE＝AF，连接CP，求证：CP⊥FP．（1）解：在正方形ABCD中，可得∠DAB＝90°．∵在Rt△BAE中，tan∠ABE＝＝＝，∴∠ABE＝30°．点T是射线PF上的一个动点，当△ABT为直角三角形时，分三种情况：①当点T在AB的上方，∠ATB＝90°，显然此时点T和点P重合，即AT＝AP＝AB＝3；②当点T在AB的下方，∠ATB ＝90°，如图①所示．在Rt△APB中，由AF＝BF，可得：AF＝BF＝PF＝3，∴∠BPF＝∠FBP＝30°，∴∠BFT＝60°．在Rt△ATB中，TF＝BF＝AF＝3，∴△FTB是等边三角形，∴TB＝3，AT＝＝3；③当点T在AB的下方，∠ABT＝90°时，如图②所示．在Rt△FBT中，∠BFT＝60°，BF＝3，BT＝BF•tan60°＝3．在Rt△ATB中：AT＝＝3．综上所述：当△ABT为直角三角形时，AT的长为3或3或3；（2）证明：如图③所示，∵四边形ABCD是正方形，∴AB＝AD＝BC，AD∥BC，∠DAB＝90°，∴∠3＝∠4．∵在Rt△EAB中，AP⊥BE，∴∠1+∠2＝90°，∠3+∠2＝90°，∴∠1＝∠3，∴∠1＝∠3＝∠4，∵tan∠1＝，tan∠3＝，∴＝，∵AE＝AF，AB＝BC，∴＝，∴△PBC∽△P AF，∴∠5＝∠6．∵∠6+∠7＝90°，∴∠5+∠7＝90°，即∠CPF＝90°，∴CP⊥FP．8．已知：如图，在▱ABCD中，G、H分别是AD、BC的中点，AE⊥BD，CF⊥BD，垂足分别为E、F．（1）求证：四边形GEHF是平行四边形；（2）已知AB＝5，AD＝8．求四边形GEHF是矩形时BD的长．（1）证明：∵四边形ABCD是平行四边形，∴AD∥BC，AD＝BC，∴∠GDE＝∠FBH，∵G、H分别是AD、BC的中点，AE⊥BD，CF⊥BD，∴在Rt△AED和Rt△CFB中，EG＝AD＝GD，FH＝BC＝HB，∴EG＝FH，∠GED＝∠GDE，∠FBH＝∠BFH，∴∠GED＝∠BFH，∴EG∥FH，∴四边形GEHF是平行四边形；（2）解：连接GH，当四边形GEHF是矩形时，∠EHF＝∠BFC＝90°，∵∠FBH＝∠BFH，∴△EFH∽△CBF，∴＝，由（1）可得：GA∥HB，GA＝HB，∴四边形GABH是平行四边形，∴GH＝AB＝5，∵在矩形GEHF中，EF＝GH，且AB＝5，AD＝8，∴＝，解得：BF＝，∴BE＝BF﹣EF＝﹣5＝，在△ABE和△CDF中∴△ABE≌△CDF（AAS），∴BE＝DF＝，∴BD＝BF+DF＝+＝．9．如图，点M是正方形ABCD的边BC上一点，连接AM，点E是线段AM上一点，∠CDE的平分线交AM延长线于点F．（1）如图1，若点E为线段AM的中点，BM：CM＝1：2，BE＝，求AB的长；（2）如图2，若DA＝DE，求证：BF+DF＝AF．解：（1）设BM＝x，则CM＝2x，BC＝3x，∵BA＝BC，∴BA＝3x．在Rt△ABM中，E为斜边AM中点，∴AM＝2BE＝2．由勾股定理可得AM2＝MB2+AB2，即40＝x2+9x2，解得x＝2．∴AB＝3x＝6．（2）延长FD交过点A作垂直于AF的直线于H点，过点D作DP⊥AF于P点．∵DF平分∠CDE，∴∠1＝∠2．∵DE＝DA，DP⊥AF∴∠3＝∠4．∵∠1+∠2+∠3+∠4＝90°，∴∠2+∠3＝45°．∴∠DFP＝90°﹣45°＝45°．∴AH＝AF．∵∠BAF+∠DAF＝90°，∠HAD+∠DAF＝90°，∴∠BAF＝∠DAH．又AB＝AD，∴△ABF≌△ADH（SAS）．∴AF＝AH，BF＝DH．∵Rt△F AH是等腰直角三角形，∴HF＝AF．∵HF＝DH+DF＝BF+DF，∴BF+DF＝AF．10．在四边形ABCD中，对角线AC、BD相交于点O，过点O的两条直线分别交边AB、CD、AD、BC于点E、F、G、H．【感知】如图①，若四边形ABCD是正方形，且AG＝BE＝CH＝DF，则S四边形AEOG＝ S 正方形ABCD ；【拓展】如图②，若四边形ABCD 是矩形，且S 四边形AEOG ＝S 矩形ABCD ，设AB ＝a ，AD ＝b ，BE ＝m ，求AG 的长（用含a 、b 、m 的代数式表示）；【探究】如图③，若四边形ABCD 是平行四边形，且AB ＝3，AD ＝5，BE ＝1，试确定F 、G 、H 的位置，使直线EF 、GH 把四边形ABCD 的面积四等分．解：【感知】如图①，∵四边形ABCD 是正方形，∴∠OAG ＝∠OBE ＝45°，OA ＝OB ，在△AOG 与△BOE 中，， ∴△AOG ≌△BOE ，∴S 四边形AEOG ＝S △AOB ＝S 正方形ABCD ；故答案为：；【拓展】如图②，过O 作ON ⊥AD 于N ，OM ⊥AB 于M ，∵S △AOB ＝S 矩形ABCD ，S 四边形AEOG ＝S 矩形ABCD ，∴S △AOB ＝S 四边形AEOG ，∵S △AOB ＝S △BOE +S △AOE ，S 四边形AEOG ＝S △AOG +S △AOE ， ∴S △BOE ＝S △AOG ， ∵S △BOE ＝BE •OM ＝mb ＝mb ，S △AOG ＝AG •ON ＝AG •a ＝AG •a ， ∴mb ＝AG •a ，∴AG ＝；【探究】如图③，过O作KL⊥AB，PQ⊥AD，则KL＝2OK，PQ＝2OQ，∵S平行四边形ABCD＝AB•KL＝AD•PQ，∴3×2OK＝5×2OQ，∴＝，∵S△AOB ＝S平行四边形ABCD，S四边形AEOG＝S平行四边形ABCD，∴S△AOB ＝S四边形AEOG，∴S△BOE ＝S△AOG，∵S△BOE ＝BE•OK＝×1×OK，S△AOG＝AG•OQ，∴×1×OK＝AG•OQ，∴＝AG＝，∴当AG＝CH＝，BE＝DF＝1时，直线EF、GH把四边形ABCD的面积四等分．11．如图，在矩形ABCD中，AB＝8cm，BC＝16cm，点P从点D出发向点A运动，运动到点A停止，同时，点Q从点B出发向点C运动，运动到点C即停止，点P、Q 的速度都是1cm/s．连接PQ、AQ、CP．设点P、Q运动的时间为ts．（1）当t为何值时，四边形ABQP是矩形；（2）当t为何值时，四边形AQCP是菱形；（3）分别求出（2）中菱形AQCP的周长和面积．解：（1）∵在矩形ABCD中，AB＝8cm，BC＝16cm，∴BC＝AD＝16cm，AB＝CD＝8cm，由已知可得，BQ＝DP＝tcm，AP＝CQ＝（16﹣t）cm，在矩形ABCD中，∠B＝90°，AD∥BC，当BQ＝AP时，四边形ABQP为矩形，∴t＝16﹣t，得t＝8，故当t＝8s时，四边形ABQP为矩形；（2）∵AP＝CQ，AP∥CQ，∴四边形AQCP为平行四边形，∴当AQ＝CQ时，四边形AQCP为菱形即＝16﹣t时，四边形AQCP为菱形，解得t＝6，故当t＝6s时，四边形AQCP为菱形；（3）当t＝6s时，AQ＝CQ＝CP＝AP＝16﹣6＝10cm，则周长为4×10cm＝40cm；面积为10cm×8cm＝80cm2．12．如图，在四边形ABCD中，AB＝AD，CB＝CD，E是CD上的点，BE交AC于点F，连接DF．（1）求证：∠BAF＝∠DAF，∠AFD＝∠CFE；（2）若AB∥CD，试证明：四边形ABCD是菱形；（3）在（2）的条件下，试确定点E的位置，使得∠EFD＝∠BCD，并说理由．证明：（1）在△ABC和△ADC中，，∴△ABC≌△ADC，∴∠BAC＝∠DAC，在△ABF和△ADF中，∴△ABF≌△ADF，∴∠AFB＝∠AFD，∵∠CFE＝∠AFB，∴∠AFD＝∠CFE，∴∠BAF＝∠DAC，∠AFD＝∠CFE；（2）∵AB∥CD，∴∠BAC＝∠ACD，∵∠BAC＝∠DAC，∴∠BAC＝∠ACD，∴∠DAC＝∠ACD，∴AD＝CD，∵AB＝AD，CB＝CD，∴AB＝CB＝CD＝AD，∴四边形ABCD是菱形；（3）∵四边形ABCD是菱形，∴BC＝CD，∠BCF＝∠DCF，∵CF＝CF，∴△BCF≌△DCF，∴∠CBF＝∠CDF，∵BE⊥CD，∴∠BEC＝∠DEF＝90°，∴∠EFD＝∠BCD．13．如图，在△ABC中，点O是边AC上一个点，过点O作直线MN∥BC分别交∠ACB、外角∠ACD的平分线于点E、F．（1）若CE＝8，CF＝6，求OC的长；（2）连接AE、AF．问：当点O在边AC上运动到什么位置时，四边形AECF是矩形？证明你的结论．（1）证明：∵EF交∠ACB的平分线于点E，交∠ACB的外角平分线于点F，∴∠OCE＝∠BCE，∠OCF＝∠DCF，∵EF∥BC，∴∠OEC＝∠BCE，∠OFC＝∠DCF，∴∠OEC＝∠OCE，∠OFC＝∠OCF，∴OE＝OC，OF＝OC，∴OE＝OF；∵∠OCE+∠BCE+∠OCF+∠DCF＝180°，∴∠ECF＝90°，在Rt△CEF中，由勾股定理得：EF＝＝10，∴OC＝OE＝EF＝5；（2）当点O在边AC上运动到AC中点时，四边形AECF是矩形．理由如下：当O为AC的中点时，AO＝CO，∵EO＝FO，∴四边形AECF是平行四边形，∵∠ECF＝90°，∴平行四边形AECF是矩形．14．如图，菱形ABCD的对角线AC、BD相交于点O，过点D作DE∥AC且DE＝AC，连接CE、OE，连接AE交OD于点F．（1）求证：OE＝CD；（2）若菱形ABCD的边长为2，∠ABC＝60°．求AE的长．（1）证明：在菱形ABCD中，OC＝AC．∴DE＝OC．∵DE∥AC，∴四边形OCED是平行四边形．∵AC⊥BD，∴平行四边形OCED是矩形．∴OE＝CD．（2）在菱形ABCD中，∠ABC＝60°，∴AC＝AB＝2．∴在矩形OCED中，CE＝OD＝．在Rt△ACE中，AE＝．15．如图，以△ABC的各边，在边BC的同侧分别作三个正方形ABDI，BCFE，ACHG．（1）求证：△BDE≌△BAC；（2）求证：四边形ADEG是平行四边形．（3）直接回答下面两个问题，不必证明：①当△ABC满足什么条件时，四边形ADEG是矩形？②当△ABC满足什么条件时，四边形ADEG是正方形？（1）证明：∵四边形ABDI、四边形BCFE、四边形ACHG都是正方形，∴AC＝AG，AB＝BD，BC＝BE，∠GAC＝∠EBC＝∠DBA＝90°．∴∠ABC＝∠EBD（同为∠EBA的余角）．在△BDE和△BAC中，，∴△BDE≌△BAC（SAS），（2）∵△BDE≌△BAC，∴DE＝AC＝AG，∠BAC＝∠BDE．∵AD是正方形ABDI的对角线，∴∠BDA＝∠BAD＝45°．∵∠EDA＝∠BDE﹣∠BDA＝∠BDE﹣45°，∠DAG＝360°﹣∠GAC﹣∠BAC﹣∠BAD＝360°﹣90°﹣∠BAC﹣45°＝225°﹣∠BAC∴∠EDA+∠DAG＝∠BDE﹣45°+225°﹣∠BAC＝180°∴DE∥AG，∴四边形ADEG是平行四边形（一组对边平行且相等）．（3）①当四边形ADEG是矩形时，∠DAG＝90°．则∠BAC＝360°﹣∠BAD﹣∠DAG﹣∠GAC＝360°﹣45°﹣90°﹣90°＝135°，即当∠BAC＝135°时，平行四边形ADEG是矩形；②当四边形ADEG是正方形时，∠DAG＝90°，且AG＝AD．由①知，当∠DAG＝90°时，∠BAC＝135°．∵四边形ABDI是正方形，∴AD＝AB．又∵四边形ACHG是正方形，∴AC＝AG，∴AC＝AB．∴当∠BAC＝135°且AC＝AB时，四边形ADEG是正方形．。
初中数学 北师大版 九年级上学期期末备考压轴题专项习题：反比例函数(含答案)
数学九年级（北师大版）上学期期末备考压轴题专项习题：反比例函数1．如图，O为坐标原点，点B在x轴的正半轴上，四边形OACB是平行四边形，OA＝10，sin∠AOB＝，反比例函数y＝kx﹣1（k＞0）在第一象限内的图象经过点A，与BC交于点F．（1）求反比例函数的表达式；（2）若点F为BC的中点，求△OBF的面积．2．如图，已知一次函数y＝kx+b的图象交反比例函数的图象于点A（2，﹣4）和点B（n，﹣2），交x轴于点C．（1）求这两个函数的表达式；（2）求△AOB的面积；（3）请直接写出使一次函数值大于反比例函数值的x的范围．3．如图，A（4，3）是反比例函数y＝在第一象限图象上一点，连接OA，过A作AB∥x 轴，截取AB＝OA（B在A右侧），连接OB，交反比例函数y＝的图象于点P．（1）求反比例函数y＝的表达式；（2）求点B的坐标及OB所在直线解析式；（3）求△OAP的面积．4．如图，在平面直角坐标系中，四边形ABCD为正方形，已知点A（﹣6，0）、D（﹣7，3），点B、C在第二象限内．（1）点B的坐标；（2）将正方形ABCD以每秒2个单位的速度沿x轴向右平移t秒，若存在某一时刻t，使在第一象限内点B、D两点的对应点B'、D'正好落在某反比例函数的图象上，请求出此时t的值以及这个反比例函数的解析式；（3）在（2）的情况下，问是否存在y轴上的点P和反比例函数图象上的点Q，使得以P、Q、B'、D'四个点为顶点的四边形是平行四边形？若存在，请直接写出符合题意的点P、Q的坐标；若不存在，请说明理由．5．如图，直线y＝x与反比例函数y＝（x＞0）的图象相交于点D，点A为直线y＝x上一点，过点A作AC⊥x轴于点C，交反比例函数y＝（x＞0）的图象于点B，连接BD．（1）若点B的坐标为（8，2），则k＝，点D的坐标为；（2）若AB＝2BC，且△OAC的面积为18，求k的值及△ABD的面积．6．如图，已知反比例函数y＝与一次函数y＝x+b的图象在第一象限相交于点A（1，﹣k+4）．（1）试确定这两个函数的表达式；（2）求△AOB的面积；（3）直接写出一次函数值大于反比例函数值的自变量x的取值范围．7．如图，在平面直角坐标系中，△ABC的顶点A在x轴负半轴上，顶点C在x轴正半轴上，顶点B在第一象限，过点B作BD⊥y于点D，A（﹣6，0），C（6，0），tan∠ACB ＝2，∠BAC＝45°（1）则AC＝；（2）反比例函数y＝的图象经过点B，求k的值；（3）在线段OD上是否存在点P，使以P，B，D为顶点的三角形与以P，O，A为顶点的三角形相似？若存在，请直接写出满足条件的点P的坐标（不用写过程）；若不存在，请说明理由．8．“凡此变数中函彼变数者，则此为彼之函数”这是我国著名数学家李善兰给出的“（function）函数”翻译，一次函数、二次函数、反比例函数是初中阶段必须掌握的三大初等函数．（1）已知一次函数y＝kx+b与反比例函数相交于A（1，6），B（n，2）两点，求这两个函数的解析式及由坐标系原点O，A，B围成的三角形的面积；（2）已知实数m，n（m＜n）在二次函数y＝x2+3x﹣4对称轴的同一侧，当m≤x≤n时，y的取值范围为，求出m，n的值；（3）已知直线y＝2tx﹣2和抛物线y＝（t2﹣1）x2﹣1在y轴左边相交于A，B两点，点C是线段AB的中点，经过C，D（﹣2，0）的直线交y轴于点H（0，h），求h取值范围．9．如图，在平面直角坐标系中，OA⊥OB，AB⊥x轴于点C，点A（，1）在反比例函数y＝的图象上．（1）求反比例函数y＝的表达式；（2）求△AOB的面积；（3）在坐标轴上是否存在一点P，使得以O、B、P三点为顶点的三角形是等腰三角形若存在，请直接写出所有符合条件的点P的坐标：若不存在，简述你的理由．10．如图，点A（a，b）是双曲线y＝（x＞0）上的一点，点P是x轴负半轴上的一动点，AC⊥y轴于C点，过A作AD⊥x轴于D点，连接AP交y轴于B点．（1）△P AC的面积是；（2）当a＝2，P点的坐标为（﹣2，0）时，求△ACB的面积；（3）当a＝2，P点的坐标为（x，0）时，设△ACB的面积为S，试求S与x之间的函数关系．11．直线y＝kx+b与反比例函数（x＞0）的图象分别交于点A（m，4）和点B（8，n），与坐标轴分别交于点C和点D．（1）求直线AB的解析式；（2）观察图象，当x＞0时，直接写出的解集；（3）若点P是x轴上一动点，当△COD与△ADP相似时，求点P的坐标．12．已知一次函数y＝kx+b的图象与反比例函数y＝的图象交于点A，与x轴交于点B（5，0），若OB＝AB，且S＝．△OAB（1）求反比例函数与一次函数的表达式；（2）若点P为x轴上一点，△ABP是等腰三角形，求点P的坐标．13．如图，双曲线y＝（x＞0）经过△AOB的点顶A（2，3），AB∥x轴，OB交双曲线于点C，且OB＝3OC（1）求k的值；（2）连接AC，求点C的坐标和△ABC的面积．14．如图，在平面直角坐标系xOy中，菱形ABCD的对角线AC与BD交于点P（﹣1，2），AB⊥x轴于点E，正比例函数y＝mx的图象与反比例函数y＝的图象相交于A，P两点．（1）求m，n的值与点A的坐标；（2）求证：△CPD∽△AEO；（3）求sin∠CDB的值．15．如图，已知一次函数y＝mx﹣4（m≠0）的图象分别交x轴，y轴于A（﹣4，0），B两点，与反比例函数y＝（k≠0）的图象在第二象限的交点为C（﹣5，n）（1）分别求一次函数和反比例函数的表达式；（2）点P在该反比例函数的图象上，点Q在x轴上，且P，Q两点在直线AB的同侧，若以B，C，P，Q为顶点的四边形是平行四边形，求满足条件的点P和点Q的坐标．参考答案1．解：（1）如图，过点A 作AH ⊥OB 于H ， ∵sin ∠AOB ＝，OA ＝10， ∴AH ＝8，OH ＝6， ∴A 点坐标为（6，8），代入反比例函数y ＝kx ﹣1（k ＞0）可得：k ＝6×8＝48， ∴反比例函数解析式：y ＝；（2）如图，过点F 作FM ⊥x 轴于M ， ∵四边形AOBC 是平行四边形， ∴AO ∥BC ，AO ＝CB ＝10， ∴∠AOB ＝∠FBM ， ∵sin ∠AOB ＝， ∴sin ∠FBM ＝， ∵点F 为BC 的中点， ∴BF ＝5，∵AH ＝8，OH ＝6， ∴FM ＝4，BM ＝3， ∴S △BFM ＝6，∵F 在反比例函数图象上， ∴S △OFM ＝24，∴S △OBF ＝S △OFM ﹣S △BFM ＝18．2．解：（1）把A（2，﹣4）的坐标代入得：，∴4﹣2m＝﹣8，反比例函数的表达式是；把B（n，﹣2）的坐标代入得，解得：n＝4，∴B点坐标为（4，﹣2），把A（2，﹣4）、B（4，﹣2）的坐标代入y＝kx+b得，解得，∴一次函数表达式为y＝x﹣6；（2）当y＝0时，x＝0+6＝6，∴OC＝6，∴△AOB的面积＝×6×4﹣×6×2＝6；（3）由图象知，一次函数值大于反比例函数值的x的范围为0＜x＜2或x＞4．3．解：（1）将点A（4，3）代入y＝（k≠0），得：k＝12，则反比例函数解析式为y＝；（2）如图，过点A作AC⊥x轴于点C，则OC＝4、AC＝3，∴OA＝＝5，∵AB∥x轴，且AB＝OA＝5，∴点B的坐标为（9，3）；设OB所在直线解析式为y＝mx（m≠0），将点B（9，3）代入得m＝，∴OB所在直线解析式为y＝x；（3）联立解析式：解得：，可得点P坐标为（6，2），过点P作PD⊥x轴，延长DP交AB于点E，连接AP，则点E坐标为（6，3），∴AE＝2，PE＝1，PD＝2，则△OAP的面积＝×（2+6）×3﹣×6×2﹣×2×1＝5．4．解：（1）如图，过点B、D分别作BH⊥x轴、DG⊥x轴交于点H、G，∵点A（﹣6，0）、D（﹣7，3），∴OA＝6，OG＝7，DG＝3，∴AG＝OG﹣OA＝1，∵∠DAG+∠BAH＝90°，∠DAG+∠GDA＝90°，∴∠GDA＝∠BAH，又∠DGA＝∠AHB＝90°，AD＝AB，∴△DGA≌△AHB（AAS），∴DG＝AH＝3，BH＝AG＝1，∴点B坐标为（﹣3，1）；（2）由（1）知，B（﹣3，1），∵D（﹣7，3）∴运动t秒时，点D'（﹣7+2t，3）、B'（﹣3+2t，1），设反比例函数解析式为y＝，∵点B'，D'在反比例函数图象上，∴k＝（﹣7+2t）×3＝（﹣3+2t）×1，∴，k＝6，∴反比例函数解析式为；（3）存在，理由：由（2）知，点D'（﹣7+2t，3）、B'（﹣3+2t，1），t＝，∴D'（2，3）、B'（6，1），由（2）知，反比例函数解析式为y＝，设点Q（m，），点P（0，s），以P、Q、B'、D'四个点为顶点的四边形是平行四边形，∴①当PQ与B'D'是对角线时，∴（0+m）＝（2+6），（s+）＝（3+1），∴m＝8，s＝，∴Q（8，），P（0，），②当PB'与QD'是对角线时，∴（0+6）＝（2+m），（s+1）＝（+3），∴m＝4，s＝，∴Q（4，），P（0，）．③当PD'与QB'是对角线时，∴（0+2）＝（m+6），（s+3）＝（+1），∴m＝﹣4，s＝﹣，∴Q（﹣4，﹣），P（0，﹣），综上：Q（8，），P（0，）或Q（4，），P（0，）或Q（﹣4，﹣），P（0，﹣）．5．解：（1）把B（8，2）代入y＝得：k＝2×8＝16，∴反比例函数的关系式为y＝，由题意得：解得：，（舍去）∴点D的坐标为（4，4）故答案为：16，（4，4）（2）过点D作DE⊥OC，DF⊥AC，垂足为E、F，如图所示：∵点A在第一象限y＝x上，∴AC＝OC，又∵△OAC的面积为18，∴AC＝OC＝6，∵AB＝2BC，∴AB＝4，BC＝2，∴点B（6，2），代入y＝得，k＝12；设点D（a，a）代入y＝得，a＝（a＞0）∴D （，），即OE ＝DE ＝，∴DF ＝EC ＝OC ﹣OE ＝6﹣，∴△ABD 的面积＝AB •DF ＝×4×（6﹣）＝12﹣；因此k 的值为12，∴△ABD 的面积为12﹣．6．解：（1）∵已知反比例函数y ＝与一次函数y ＝x +b 的图象在第一象限相交于点A （1，﹣k +4）， ∴﹣k +4＝k ， 解得k ＝2，故反比例函数的解析式为y ＝，又知A （1，2）在一次函数y ＝x +b 的图象上， 故2＝1+b ， 解得b ＝1，故一次函数的解析式为y ＝x +1； （2）由题意得：，解得x ＝﹣2或1， ∴B （﹣2，﹣1），令y ＝0，得x +1＝0，解得x ＝﹣1， ∴C （﹣1，0）， ∴S △AOB ＝S △AOC +S △COB ＝×1×2+×1×1 ＝1+ ＝1.5；（3）由图象可知，当一次函数的值大于反比例函数值时，x的取值范围是x＞1或﹣2＜x ＜0．7．解：（1）6﹣（﹣6）＝12．故答案为：12．（2）过点B作BE⊥x轴，如图1所示．设BE＝m，则CE＝＝m，AE＝＝m．∵AE+CE＝12，∴m+m＝12，∴m＝8，∴OE＝OC﹣CE＝6﹣×8＝2．∴点B的坐标为（2，8）．（3）∵点B的坐标为（2，8），BD⊥y于点D，∴点D的坐标为（0，8），∴BD＝2．∵点A的坐标为（﹣6，0），∴OA＝6．设点P的坐标为（0，n）（0＜n＜8），则OP＝n，DP＝8﹣n．∵∠AOP＝∠BDP＝90°，以P，B，D为顶点的三角形与以P，O，A为顶点的三角形相似，∴＝或＝，即＝或＝，解得：n＝2或n＝6，∴在线段OD上存在点P（0，2）或（0，6），使以P，B，D为顶点的三角形与以P，O，A为顶点的三角形相似．8．解：（1）∵A（1，6），B（n，2）在反比例函数的图象上，∴m＝6，∴反比例函数的解析式是y＝，∴2n＝6，解得n＝3，∴B（3，2），∵一次函数y＝kx+b与反比例函数y＝的图象交于A、B两点．∴，解得，∴一次函数解析式为y＝﹣2x+8；设直线y＝﹣2x+8与x轴相交于点C，C的坐标是（4，0）．S△AOB ＝S△AOC﹣S△BOC＝OC|y A|﹣OC|y B）＝8；（2）分两种情况讨论：①当m＜n＜﹣，即m、n在对称轴的左侧时，二次函数y的值随x增大而减小，∵，∴方程组中的第一个方程×n得，n3+3n2﹣4n＝12∴（n+2）（n﹣2）（n+3）＝0解得n＝﹣2或2或﹣3，同理由方程组中的第二个方程×m得m＝﹣2或2或3，∵m＜n＜﹣，∴m＝﹣3，n＝﹣2；②当﹣＜m＜n，即m、n在对称轴的右侧时，二次函数y的值随x增大而增大，∵，，方程①×n﹣2×m，得m2n﹣n2m+4（m﹣n）＝0，∴（mn+4）（m﹣n）＝0，∵m﹣n≠0，∴mn+4＝0，m＝﹣，将m＝﹣代入方程②得，n2+3n﹣4＝﹣3n，∴n＝﹣3±∵n＞﹣n＝﹣3+∴m＝﹣3﹣＜﹣，与上述﹣＜m＜n矛盾，∴没有满足的m、n．综上，在对称轴的左侧存在实数m、n，当m≤x≤n时，y的取值范围为，此时m＝﹣3，n＝﹣2；（3）设点A（x1，y1）、B（x2，y2），则x1、x2是方程2tx﹣2＝（t2﹣1）x2﹣1即（t2﹣1）x2﹣2tx+1＝0，解得x1＝，x2＝，∴x1+x2＝，y1+y2＝2tx1﹣2+2tx2﹣2＝2t（x1+x2）﹣4＝．∵点C是AB的中点，∴点C的坐标为（，）即（，）．设直线DC的解析式为y＝mx+n，则有，解得．∴直线与y轴的交点纵坐标h＝n＝．∵点A、B在y轴的左侧，∴x1＝＜0且x2＝＜0，解得t＜﹣1．设k＝2t2+t﹣1，则有h＝，k＝2（t+）2﹣，∵2＞0，∴当t＜﹣1时k随着t的增大而减小，∴k＞2（﹣1+）2﹣即k＞﹣1，对于h＝，①当﹣1＜k＜0时，h＜﹣4；②当k＞0时，h＞0，∴直线与y轴的交点纵坐标h的取值范围是h＜﹣4或h＞0．9．解：（1）将A（，1）代入y＝，得：1＝，解得：k＝，∴反比例函数的表达式为y＝．（2）∵点A的坐标为（，1），AB⊥x轴于点C，∴OC＝，AC＝1，∴OA＝＝2＝2AC，∴∠AOC＝30°．∵OA⊥OB，∴∠AOB＝90°，∴∠B＝∠AOC＝30°，∴AB＝2OA＝4，＝AB•OC＝×4×＝2．∴S△AOB（3）在Rt△AOB中，OA＝2，∠AOB＝90°，∠ABO＝30°，∴OB＝＝2．分三种情况考虑：①当OP＝OB时，如图2所示，∵OB＝2，∴OP＝2，∴点P的坐标为（﹣2，0），（2，0），（0，﹣2），（0，2）；②当BP＝BO时，如图3，过点B做BD⊥y轴于点D，则OD＝BC＝AB﹣AC＝3，∵BP＝BO，∴OP＝2OC＝2或OP＝2OD＝6，∴点P的坐标为（2，0），（0，﹣6）；③当PO＝PB时，如图4所示．若点P在x轴上，∵PO＝PB，∠BOP＝60°，∴△BOP为等边三角形，∴OP＝OB＝2，∴点P的坐标为（2，0）；若点P在y轴上，设OP＝a，则PD＝3﹣a，∵PO＝PB，∴PB2＝PD2+BD2，即a2＝（3﹣a）2+12，解得：a＝2，∴点P的坐标为（0，﹣2）．综上所述：在坐标轴上存在一点P，使得以O、B、P三点为顶点的三角形是等腰三角形，点P的坐标为（﹣2，0），（2，0），（0，﹣2），（0，2），（0，﹣6），（0，﹣2）．10．解：（1）∵点A（a，b）是双曲线y＝（x＞0）上，∴ab＝8，∵AC⊥y轴于C点，AD⊥x轴于D点，∴AC＝a，AD＝b，∴△P AC的面积＝AD•AC＝ab＝4；故答案为：4；（2）∵a＝2，∴b＝4，∴AC＝2，AD＝4，A（2，4），设直线AP的解析式为y＝kx+b，∴，∴，∴直线AP的解析式为y＝x+2，∴B（0，2），∴S＝AC•BC＝＝2；△ABC（3）同理直线AP的解析式为y＝﹣，∴B（0，﹣），∴BC＝4+＝∴S＝×2×＝．11．解：（1）∵点A（m，4）和点B（8，n）在y＝图象上，∴m＝＝2，n＝＝1，即A（2，4），B（8，1）把A（2，4），B（8，1）两点代入y＝kx+b中得解得：，所以直线AB的解析式为：y＝﹣x+5；（2）由图象可得，当x＞0时，kx+b＞的解集为2＜x＜8．（3）由（1）得直线AB的解析式为y＝﹣x+5，当x＝0时，y＝5，∴C（0，5），∴OC＝5，当y＝0时，x＝10，∴D点坐标为（10，0）∴OD＝10，∴CD＝＝5∵A（2，4），∴AD＝＝4设P点坐标为（a，0），由题可以，点P在点D左侧，则PD＝10﹣a 由∠CDO＝∠ADP可得①当△COD∽△APD时，，∴，解得a＝2，故点P坐标为（2，0）②当△COD∽△P AD时，，∴，解得a＝0，即点P的坐标为（0，0）因此，点P的坐标为（2，0）或（0，0）时，△COD与△ADP相似．12．解：（1）如图1，过点A作AD⊥x轴于D，∵B（5，0），∴OB＝5，∵S＝，△OAB∴×5×AD＝，∴AD＝3，∵OB＝AB，∴AB＝5，在Rt△ADB中，BD＝＝4，∴OD＝OB+BD＝9，∴A（9，3），将点A坐标代入反比例函数y＝中得，m＝9×3＝27，∴反比例函数的解析式为y＝，将点A（9，3），B（5，0）代入直线y＝kx+b中，，∴，∴直线AB的解析式为y＝x﹣；（2）由（1）知，AB＝5，∵△ABP是等腰三角形，∴①当AB＝PB时，∴PB＝5，∴P（0，0）或（10，0），②当AB＝AP时，如图2，由（1）知，BD＝4，易知，点P与点B关于AD对称，∴DP＝BD＝4，∴OP＝5+4+4＝13，∴P（13，0），③当PB＝AP时，设P（a，0），∵A（9，3），B（5，0），∴AP2＝（9﹣a）2+9，BP2＝（5﹣a）2，∴（9﹣a）2+9＝（5﹣a）2∴a＝，∴P（，0），即：满足条件的点P的坐标为（0，0）或（10，0）或（13，0）或（，0）．13．解：（1）把A （2，3）代入y ＝得：k ＝2×3＝6， 答：k 的值为：6．（2）过点A 、C 、B 分别作AF ⊥x 轴，CD ⊥x 轴，BE ⊥x 轴，垂足为F 、D 、E ， ∵A （2，3） ∴OF ＝2，AF ＝3， 由△OCD ∽△OBE 得：，∴CD ＝1，把y ＝1代入y ＝得：x ＝6， ∴C （6，1）， ∴OE ＝18，∴S △OAB ＝S 梯形OABE ﹣S △OBE ＝（18+16）×3﹣×18×3＝24， ∵OB ＝3OC ， ∴S △ABC ＝S △AOB ＝＝16．答：点C 的坐标为（6，1），△ABC 的面积为16．14．（1）解：将点P（﹣1，2）代入y＝mx，得：2＝﹣m，解得：m＝﹣2，∴正比例函数解析式为y＝﹣2x；将点P（﹣1，2）代入y＝，得：2＝﹣（n﹣3），解得：n＝1，∴反比例函数解析式为y＝﹣．联立正、反比例函数解析式成方程组，得：，解得：，，∴点A的坐标为（1，﹣2）．（2）证明：∵四边形ABCD是菱形，∴AC⊥BD，AB∥CD，∴∠DCP＝∠BAP，即∠DCP＝∠OAE．∵AB⊥x轴，∴∠AEO＝∠CPD＝90°，∴△CPD∽△AEO．（3）解：∵点A的坐标为（1，﹣2），∴AE＝2，OE＝1，AO＝＝．∵△CPD∽△AEO，∴∠CDP＝∠AOE，∴sin∠CDB＝sin∠AOE＝＝＝．15．解：（1）∵点A是一次函数y＝mx﹣4的图象上，∴﹣4m﹣4＝0，∴m＝﹣1，∴一次函数的解析式为y＝﹣x﹣4，∵点C（﹣5，n）是直线y＝﹣x﹣4上，∴n＝﹣（﹣5）﹣4＝1，∴C（﹣5，1），∵点C（﹣5，1）是反比例函数y＝（k≠0）的图象上，∴k＝﹣5×1＝﹣5，∴反比例函数的解析式为y＝﹣；（2）由（1）知，C（﹣5，1），直线AB的解析式为y＝﹣x﹣4，∴B（0，﹣4），设点Q（q，0），P（p，﹣），∵以B，C，P，Q为顶点的四边形是平行四边形，且P，Q两点在直线AB的同侧，∴①当BP与CQ是对角线时，∴BP与CQ互相平分，∴，∴，∴P（﹣1，5），Q（4，0）②当BQ与CP是对角线时，∴BQ与CP互相平分，∴，∴，∴P（﹣1，5），Q（﹣4，0），此时，点C，Q，B，P在同一条线上，不符合题意，舍去，即以B，C，P，Q为顶点的四边形是平行四边形，点P（﹣1，5），点Q（4，0）．。
北师大版九年级数学上学期期末压轴题培优第六章：反比例函数(含答案)
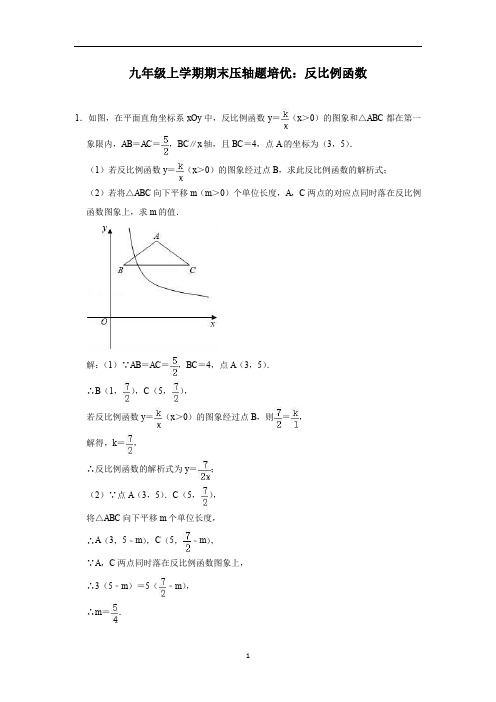
九年级上学期期末压轴题培优：反比例函数1．如图，在平面直角坐标系xOy中，反比例函数y＝（x＞0）的图象和△ABC都在第一象限内，AB＝AC＝，BC∥x轴，且BC＝4，点A的坐标为（3，5）．（1）若反比例函数y＝（x＞0）的图象经过点B，求此反比例函数的解析式；（2）若将△ABC向下平移m（m＞0）个单位长度，A，C两点的对应点同时落在反比例函数图象上，求m的值．解：（1）∵AB＝AC＝，BC＝4，点A（3，5）．∴B（1，），C（5，），若反比例函数y＝（x＞0）的图象经过点B，则＝，解得，k＝，∴反比例函数的解析式为y＝；（2）∵点A（3，5）．C（5，），将△ABC向下平移m个单位长度，∴A（3，5﹣m），C（5，﹣m），∵A，C两点同时落在反比例函数图象上，∴3（5﹣m）＝5（﹣m），∴m＝．2．一次函数y ＝kx +b 的图象与反比例函数y ＝的图象相交于A （﹣1，m ），B （n ，1）两点．（1）求出这个一次函数的表达式； （2）求△OAB 的面积．解：（1）把A （﹣1，m ），B （n ，﹣1）分别代入y ＝得﹣m ＝﹣2，﹣n ＝﹣2，解得m＝2，n ＝2，所以A 点坐标为（﹣1，2），B 点坐标为（2，﹣1），把A （﹣1，2），B （2，﹣1）代入y ＝kx +b 得，解得，所以这个一次函数的表达式为y ＝﹣x +1； （2）设直线AB 交y 轴于P 点，如图， 当x ＝0时，y ＝1，所以P 点坐标为（0，1），所以S △OAB ＝S △AOP +S △BOP ＝×1×1+×1×2＝．3．如图所示，已知双曲线y＝（k＞0，x＞0）的图象上有两点P1（x1，y1），P2（x2，y2），且x1＜x2，分别过P1，P2向x轴作垂线，垂足为B，D，过P1，P2向y轴作垂线，垂足分别为A，C．（1）若记四边形AP1BO和四边形CP2DO的面积分别为S1，S2，试比较S1和S2的大小．（2）若记四边形AP1BO和四边形CP2DO的周长分别为C1和C2，试比较C1，C2的大小．（3）若P是双曲线y＝（k＞0，x＞0）上一点，分别过P向x轴、y轴作垂线，垂足分别为M，N．试问当P在何处时四边形PMON的周长最小，最小值为多少？解：（1）根据反比例函数系数k的几何意义可知S1＝S2＝k；（2）∵C1＝2OB+2AO＝2BO+2CO+2AC，C2＝2CO+2OD＝2CO+2OB+2BD，∴当y1﹣y2＝x2﹣x1，即AC＝BD时，C1＝C2；当y1﹣y2＜x2﹣x1，即AC＜BD时，C1＜C2；当y1﹣y2＞x2﹣x1，即AC＞BD时，C1＞C2．（3）设P（x，y），即（x，），四边形PMON的周长＝2（x+y）＝2（x+），因为面积相等的四边形中正方形的周长最小，所以x＝，即x2＝k，解得x＝，故P点坐标为（，）．∴最小值为4．4．如图，在平面直角坐标系中，过点M （0，2）的直线l 与x 轴平行，且直线l 分别与反比例函数y ＝（x ＞0）和y ＝（x ＜0）的图象分别交于点P ，Q ． （1）求P 点的坐标；（2）若△POQ 的面积为9，求k 的值．解：（1）∵PQ ∥x 轴， ∴点P 的纵坐标为2，把y ＝2代入y ＝得x ＝3， ∴P 点坐标为（3，2）；（2）∵S △POQ ＝S △OMQ +S △OMP ，∴|k |+×|6|＝9， ∴|k |＝12， 而k ＜0， ∴k ＝﹣12．5．如图，四边形OABC是矩形，A、C分别在y轴、x轴上，且OA＝6cm，OC＝8cm，点P 从点A开始以2cm/s的速度向B运动，点Q从点B开始以1cm/s的速度向C运动，设运动时间为t．（1）如图（1），当t为何值时，△BPQ的面积为4cm2？（2）当t为何值时，以B、P、Q为顶点的三角形与△ABC相似？（3）如图（2），在运动过程中的某一时刻，反比例函数y＝的图象恰好同时经过P、Q 两点，求这个反比例函数的解析式．解：（1）由题意AB＝OC＝8cm，AO＝BC＝6cm，∠B＝90°，∵P A＝2t，BQ＝t，∴PB＝8﹣2t，∵△BPQ的面积为4cm2，∴•（8﹣2t）•t＝4，解得t＝2，∴t＝2s时，△PBQ的面积为4．（2）①当△BPQ∽△BAC时，＝，∴＝，解得t＝．②当△BPQ∽△BCA时，＝，∴＝，解得t＝，∴t为s或s时，以B、P、Q为顶点的三角形与△ABC相似．（3）由题意P（2t，6），Q（8，6﹣t），∵反比例函数y＝的图象恰好同时经过P、Q两点，∴12t＝8（6﹣t），解得t＝，∴P（，6），∴m＝，∴反比例函数的解析式为y＝．6．如图1，在平面直角坐标系中，点A（0，4），B（1，m）都在直线y＝﹣2x+b上，反比例函数y＝（x＞0）的图象经过点B．（1）直接写出m和k的值；（2）如图2，将线段AB向右平移n个单位长度（n≥0），得到对应线段CD，连接AC，BD．①在平移过程中，若反比例函数图象与线段AB有交点，求n的取值范围；②在平移过程中，连接BC，若△BCD是直角三角形，请直接写出所有满足条件n的值．解：（1）∵点A（0，4）在直线y＝﹣2x+b上，∴﹣2×0+b＝4，∴b＝4，∴直线AB的解析式为y＝﹣2x+4，将点B（1，m）代入直线AB的解析式y＝﹣2x+4中，得﹣2×1+4＝m，∴b＝2，∴B（1，2），将B（1，2）在反比例函数解析式y＝（x＞0）中，得k＝xy＝1×2＝2；（2）①∵将线段AB向右平移n个单位长度，∴A（n，4），把A（n，4）代入y＝中，得，4＝，∴n＝，∴在平移过程中，若反比例函数图象与线段AB有交点，n的取值范围为0≤n≤；②∵将线段AB向右平移n个单位长度（n≥0），得到对应线段CD，∴AB∥CD，∴∠CDB≠90°，当∠CBD＝90°时，△BCD是直角三角形，∴CB⊥BC，∴C（1，4），∴n＝1；当∠BCD＝90°，△BCD是直角三角形，则C（n，4），D（n+1，2），∵BC2+CD2＝BD2，∴（n﹣1）2+（4﹣2）2+12+（4﹣2）2＝n2，解得：n＝5，综上所述，若△BCD是直角三角形，n的值为1或5．7．如图，在平面直角坐标系xOy中，直线y＝﹣x+1与图数y＝的限象交于A（﹣2，a），B两点．（1）求a，k的值；（2）已知点P（0，n），过点P作平行于x轴的直线l，交函数y＝的图象于点C（x1，y1），交直线y＝﹣x+1的图象于点D（x2，y2），若|x1|≤|x2|，结合函数图象，请求出m的取值范围．解：（1）∵直线y＝﹣x+1与函数y＝的图象交于A（﹣2，a），把A（﹣2，a）代入y＝﹣x+1解得a＝3，∴A（﹣2，3）．把A（﹣2，3）代入y＝，解得k＝﹣6；（2）画出函数图象如图解得或，∵A （﹣2，3）， ∴B （3，﹣2），根据图象可得：若|x 1|≤|x 2|，则m ≥3或﹣2≤m ＜0．8．如图，在直角坐标系xOy 中，矩形ABCD 的DC 边在x 轴上，D 点坐标为（﹣6，0）边AB 、AD 的长分别为3、8，E 是BC 的中点，反比例函数y ＝的图象经过点E ，与AD 边交于点F ．（1）求k 的值及经过A 、E 两点的一次函数的表达式；（2）若x 轴上有一点P ，使PE +PF 的值最小，试求出点P 的坐标；（3）在（2）的条件下，连接EF 、PE 、PF ，在直线AE 上找一点Q ，使得S △QEF ＝S △PEF 直接写出符合条件的Q 点坐标．解：（1）在矩形ABCD 中，AB ＝3，AD ＝8， ∴CD ＝AB ＝3，BC ＝AD ＝8， ∵D （﹣6，0），∴A （﹣6，8），C （﹣3，0），B （﹣3，8）， ∵E 是BC 的中点， ∴E （﹣3，4），∵点D 在反比例函数y ＝的图象上， ∴k ＝﹣3×4＝﹣12，设经过A 、E 两点的一次函数的表达式为y ＝k 'x +b ，∴，∴，∴经过A 、E 两点的一次函数的表达式为y ＝﹣x ；（2）如图1，由（1）知，k ＝﹣12，∴反比例函数的解析式为y ＝﹣，∵点F 的横坐标为﹣6， ∴点F 的纵坐标为2， ∴F （﹣6，2），作点F 关于x 轴的对称点F '，则F '（﹣6，﹣2）， 连接EF '交x 轴于P ，此时，PE +PF 的值最小， ∵E （﹣3，4），∴直线EF '的解析式为y ＝2x +10， 令y ＝0，则2x +10＝0， ∴x ＝﹣5， ∴P （﹣5，0）；（3）如图2，由（2）知，F '（﹣6，﹣2）， ∵E （﹣3，4），F （﹣6，2），∴S △PEF ＝S △EFF '﹣S △PFF '＝×（2+2）×（﹣3+6）﹣（2+2）×（﹣5+6）＝4， ∵E （﹣3，4），F （﹣6，2），∴直线EF 的解析式为y ＝x +6，由（1）知，经过A 、E 两点的一次函数的表达式为y ＝﹣x ，设点Q （m ，﹣m ），过点Q 作y 轴的平行线交EF 于G ，∴G （m ， m +6），∴QG ＝|﹣m ﹣m ﹣6|＝|2m +6|， ∵S △QEF ＝S △PEF ，∴S △QEF ＝|2m +6|×（﹣3+6）＝4，∴m ＝﹣或m ＝﹣，∴Q （﹣，）或（﹣，）．9．如图，直线y ＝2x +6与反比例数y ＝（x ＞0）的图象交于点A （1，m ），与x 轴交于点B ，与y 轴交于点D ．（1）求m 的值和反比例函数的表达式；（2）在y 轴上有一动点P （0，n ）（n ＜6），过点P 作平行于x 轴的直线，交反比例函数的图象于点M ，交直线AB 于点N ，连接OM ，MN①当n ＝4时，判断四边形BOMN 的形状，并简要写出证明思路； ②若S △BDM ＞S △BOD ，直接写出点P 的纵坐标n 的取值范围．解：（1）当x＝1时，m＝2x+6＝8，∴点A的坐标为（1，8）．∵点A（1，8）在反比例数y＝的图象上，∴k＝1×8＝8，∴反比例函数的解析式为y＝．（2）①四边形BOMN为平行四边形．证明：当y＝0时，2x+6＝0，解得：x＝﹣3，∴点A的坐标为（﹣3，0），OB＝3；当y＝4时，2x+6＝4，＝4，解得：x＝﹣1，x＝2，∴点M的坐标为（2，4），点N的坐标为（﹣1，4），∴MN＝2﹣（﹣1）＝3，∴MN＝OB．∵MN∥x轴，OB在x轴上，∴MN∥OB，∴四边形BOMN为平行四边形．②过点O作直线l∥AB，交反比例数y＝（x＞0）的图象于点M．∵直线AB的解析式为y＝2x+6，∴直线l的解析式为y＝2x．联立直线l 和反比例函数解析式成方程组，得：，解得：，（舍去），∴点M 的坐标为（2，4）；同理，可求出直线y ＝2x +12与反比例函数y ＝的图象交点M 3（﹣3﹣，6﹣2）（舍去），M 4（﹣3+，6+2）（舍去）．∵S △BDM ＞S △BOD ， ∴0＜n ＜4．10．小明家饮水机中原有水的温度为20℃，通电开机后，饮水机自动开始加热（此过程中水温y （℃）与开机时间x （分）满足一次函数关系），当加热到100℃时自动停止加热，随后水温开始下降（此过程中水温y （℃）与开机时间x （分）成反比例关系），当水温降至20℃时，饮水机又自动开始加热…，重复上述程序（如图所示），根据图中提供的信息，解答下列问题：（1）当0≤x≤10时，求水温y（℃）与开机时间x（分）的函数关系式；（2）求图中t的值；（3）若小明在通电开机后即外出散步，请你预测小明散步57分钟回到家时，饮水机内的温度约为多少℃？解：（1）当0≤x≤10时，设水温y（℃）与开机时间x（分）的函数关系为：y＝kx+b，依据题意，得，解得：，故此函数解析式为：y＝8x+20；（2）在水温下降过程中，设水温y（℃）与开机时间x（分）的函数关系式为：y＝，依据题意，得：100＝，即m＝1000，故y＝，当y＝20时，20＝，解得：t＝50；（3）∵57﹣50＝7≤10，∴当x＝7时，y＝8×7+20＝76，答：小明散步57分钟回到家时，饮水机内的温度约为76℃．11．如图，平面直角坐标系中，一次函数y＝kx﹣2的图象与反比例函数y＝（x＜0）的图象交于点B，与x轴，y轴交于点D，E，BC⊥x轴于C，BA⊥y轴于A，＝，△ABE 的面积为24．（1）点E的坐标是（0，﹣2）；（2）求一次函数和反比例函数的表达式；（3）以BC为边作菱形CBMN，顶点M在点B左侧的一次函数y＝kx﹣2的图象上，判断边MN与反比例函数y＝（x＜0）的图象是否有公共点．解：（1）∵一次函数y＝kx﹣2的图象与y轴交于点E，令x＝0，得到y＝﹣2，∴E（0，﹣2），故答案为（0，﹣2）．（2）∵BC⊥x轴于C，BA⊥y轴于A，∴∠BCO＝∠BAO＝∠AOD＝90°，∴四边形ACOB是矩形，∴OC∥AB，OC＝AB，∵＝，∴＝＝＝，∵OE＝2，∴EA＝6，∴OA＝4，＝×AB×6＝24，∵S△ABE∴AB＝8，∴B（﹣8，4），∵点B在y＝上，∴m＝﹣32，把B（﹣8，4）代入y＝kx﹣2得到k＝﹣，∴一次函数的解析式为y ＝﹣x ﹣2，反比例函数的解析式为y ＝﹣．（3）设M （m ，﹣m ﹣2），延长MN 交x 轴于H ．由题意D （﹣，0），∵BC ＝BM ＝4，BD ＝＝，∵BC ∥MH ，∴＝，∴＝，解得m ＝﹣，∴M （﹣，），N （﹣，），对于反比例函数y ＝﹣，当x ＝﹣时，y ＝，∵＜，∴线段MN 与反比例函数的图象有交点．12．如图，已知一次函数y 1＝ax +b 的图象与x 轴、y 轴分别交于点D ，C ，与反比例函数y 2＝的图象交于A ，B 两点，且点A 的坐标是（1，3）、点B 的坐标是（3，m ）． （1）求一次函数与反比例函数的解析式； （2）求C 、D 两点的坐标，并求△AOB 的面积；（3）根据图象直接写出：当x 在什么取值范围时，y 1＞y 2？解：（1）把点A （1，3）代入y 2＝， ∴3＝，即k ＝3，故反比例函数的解析式为：y 2＝．把点B 的坐标是（3，m ）代入y 2＝，得：m ＝＝1， ∴点B 的坐标是（3，1）．把A （1，3），B （3，1）代入y 1＝ax +b ，得，解得，故一次函数的解析式为：y 1＝﹣x +4；（2）令x ＝0，则y 1＝4； 令y 1＝0，则x ＝4， ∴C （0，4），D （4，0），∴S △AOB ＝S △AOD ﹣S △BOD ＝×4×3﹣×4×1＝4；（3）当x 满足1＜x ＜3时，则y 1＞y 2．13．如图，正比例函数y ＝2x 的图象与反比例函数的图象交于A 、B 两点，过点A 作AC 垂直x 轴于点C ，连结BC ．若△ABC 的面积为2． （1）求k 的值；（2）直接写出：①点A 坐标 （1，2） ；点B 坐标 （﹣1，﹣2） ；②当时，x 的取值范围 x ≥1或0＞x ≥﹣1 ；（3）x 轴上是否存在一点D ，使△ABD 为直角三角形？若存在，求出点D 的坐标；若不存在，请说明理由．解：（1）∵反比例函数与正比例函数的图象相交于A、B两点，∴A、B两点关于原点对称，∴OA＝OB，∴△BOC的面积＝△AOC的面积＝2÷2＝1，又∵A是反比例函数y＝图象上的点，且AC⊥x轴于点C，∴△AOC的面积＝|k|，∴|k|＝1，∵k＞0，∴k＝2；（2）①解得，或，∴点A坐标（1，2），点B坐标（﹣1，﹣2），②当时，x的取值范围为x≥1或0＞x≥﹣1；故答案为：（1，2），（﹣1，﹣2），x≥1或0＞x≥﹣1；（3）x轴上存在一点D，使△ABD为直角三角形．∵A（1，2），B（﹣1，﹣2），①当AD⊥AB时，如图1，设直线AD的关系式为y＝﹣x+b，将A（1，2）代入上式得：b＝，∴直线AD的关系式为y＝﹣x+，令y＝0得：x＝5，∴D（5，0）；②当BD⊥AB时，如图2，设直线BD的关系式为y＝﹣x+b，将B（﹣1，﹣2）代入上式得：b＝﹣，∴直线BD的关系式为y＝﹣x﹣，令y＝0得：x＝﹣5，∴D（﹣5，0）；③当AD⊥BD时，如图3，∵O为线段A的中点，∴OD＝AB＝OA，∵A（1，2），∴OC＝1，AC＝2，由勾股定理得：OA＝＝＝，∴OD＝，∴D（，0）．根据对称性，当D为直角顶点，且D在x轴负半轴时，D（﹣，0）．故x轴上存在一点D，使△ABD为直角三角形，点D的坐标为（5，0）或（﹣5，0）或（，0）或（﹣，0）．14．如图，平面直角坐标系xOy中，函数y＝（x＜0）的图象经过点A（﹣1，6），直线y ＝mx﹣2与x轴交于点B（﹣1，0）．（1）求k，m的值．（2）点P是直线y＝﹣2x位于第二象限上的一个动点，过点P作平行于x轴的直线，交直线y＝mx﹣2于点C，交函数y＝（x＜0）的图象于点D，设P（n，﹣2n）．①当n＝﹣1时，判断线段PD与PC的数量关系，并说明理由②当PD≥2PC时，结合函数的图象，直接写出n的取值范围．解：（1）∵函数y＝（x＜0）的图象经过点A（﹣1，6），∴k＝﹣1×6＝﹣6；将B（﹣1，0）代入y＝mx﹣2，得：0＝﹣m﹣2，解得：m＝﹣2．（2）①PD＝2PC，理由如下：当n＝﹣1时，点P的坐标为（﹣1，2）．当y＝2时，﹣2x﹣2＝2，＝2，解得：x＝﹣2，x＝﹣3，∴点C 的坐标为（﹣2，2），点D 的坐标为（﹣3，2）， ∴PC ＝1，PD ＝2， ∴PD ＝2PC ．②当n ＝﹣3时，点P 的坐标为（﹣3，6）．当y ＝6时，﹣2x ﹣2＝6，＝6，解得：x ＝﹣4，x ＝﹣1，∴点C 的坐标为（﹣4，6），点D 的坐标为（﹣1，6）， ∴PC ＝1，PD ＝2， ∴PD ＝2PC ．∵点P 是直线y ＝﹣2x 位于第二象限上的一个动点， ∴当PD ≥2PC 时，﹣1≤n ＜0或n ≤﹣3．15．如图，在平面直角坐标系xOy 中，矩形OABC 的顶点A 在x 轴的正半轴上，顶点C 在y 轴的正半轴上，D 是BC 边上的一点，OC ：CD ＝5：3，DB ＝6．反比例函数y ＝（k ≠0）在第一象限内的图象经过点D ，交AB 于点E ，AE ：BE ＝1：2． （1）求这个反比例函数的表达式；（2）动点P 在矩形OABC 内，且满足S △P AO ＝S 四边形OABC ． ①若点P 在这个反比例函数的图象上，求点P 的坐标；②若点Q 是平面内一点使得以A 、B 、P 、Q 为顶点的四边形是菱形求点Q 的坐标．解：（1）设点B 的坐标为（m ，n ），则点E 的坐标为（m ， n ），点D 的坐标为（m ﹣6，n ）．∵点D ，E 在反比例函数y ＝（k ≠0）的图象上， ∴k ＝mn ＝（m ﹣6）n ， ∴m ＝9．∵OC ：CD ＝5：3， ∴n ：（m ﹣6）＝5：3， ∴n ＝5，∴k ＝mn ＝×9×5＝15，∴反比例函数的表达式为y ＝．（2）∵S △P AO ＝S 四边形OABC ，∴OA •y P ＝OA •OC ，∴y P ＝OC ＝4．①当y ＝4时，＝4，解得：x ＝，∴若点P 在这个反比例函数的图象上，点P 的坐标为（，4）．②由（1）可知：点A 的坐标为（9，0），点B 的坐标为（9，5）， ∵y P ＝4，y A +y B ＝5，∴y P ≠，∴AP ≠BP ，∴AB不能为对角线．设点P的坐标为（t，4）．分AP＝AB和BP＝AB两种情况考虑（如图所示）：（i）当AB＝AP时，（9﹣t）2+（4﹣0）2＝52，解得：t1＝6，t2＝12（舍去），∴点P1的坐标为（6，4）．又∵P1Q1＝AB＝5，∴点Q1的坐标为（6，9）；（ii）当BP＝AB时，（9﹣t）2+（5﹣4）2＝52，解得：t3＝9﹣2，t4＝9+2（舍去），∴点P2的坐标为（9﹣2，4）．又∵P2Q2＝AB＝5，∴点Q2的坐标为（9﹣2，﹣1）．综上所述：点Q的坐标为（6，9）或（9﹣2，﹣1）．16．（1）如图1，已知△ABC与△ABD的面积相等，证明AB∥CD；（2）①如图2，点M，N在反比例函数y＝（k＞0）的图象上，过点M作ME⊥y轴，过点N作NF⊥x轴，垂足分别为E，E，请利用（1）的结果，证明：MN∥EF；②若①中的其他条件不变，只改变点M，N的位置如图3所示，请判断MN与EF是否平行（不用写理由）．（1）证明：在图1中，过点C 作CP ⊥AB 于点P ，过点D 作DQ ⊥AB 于点Q ，则∠CP A ＝∠DQB ＝90°， ∴CP ∥DQ ．∵△ABC 与△ABD 的面积相等， ∴CP ＝DQ ，∴四边形CPQD 为平行四边形， ∴AB ∥CD ．（2）①证明：在图2中，连接FM ，EN ．设点M 的坐标为（x 1，y 1），点N 的坐标为（x 2，y 2）．∵点M ，N 在反比例函数y ＝（k ＞0）的图象上， ∴k ＝x 1y 1＝x 2y 2． ∵ME ⊥y 轴，NF ⊥x 轴，∴OE ＝y 1，OF ＝x 2，ME ＝x 1，NF ＝y 2．∵S △EFM ＝ME •OE ＝x 1y 1＝k ，S △EFN ＝NF •OF ＝x 2y 2＝k ， ∴S △EFM ＝S △EFN ， ∴MN ∥EF ；②解：MN ∥EF ，理由如下： 在图3中，连接MN ，FM ，EN ．设点M 的坐标为（x 1，y 1），点N 的坐标为（x 2，y 2）．∵点M ，N 在反比例函数y ＝（k ＞0）的图象上， ∴k ＝x 1y 1＝x 2y 2．∵ME ⊥y 轴，NF ⊥x 轴，∴OE ＝y 1，OF ＝x 2，ME ＝x 1，NF ＝y 2．∵S △EFM ＝ME •OE ＝x 1y 1＝k ，S △EFN ＝NF •OF ＝x 2y 2＝k ， ∴S △EFM ＝S △EFN ， ∴MN ∥EF ；17．如图，正比例函数y 1＝kx 与反比例函数y ＝（x ＞0）交于点A （2，3），AB ⊥x 轴于点B ，平移直线y 1＝kx 使其经过点B ，得到直线y 2，y 2与y 轴交于点C ，与y ＝交于点D ．（1）求正比例函数y 1＝kx 及反比例函数y ＝的解析式；（2）求点D 的坐标； （3）求△ACD 的面积．解：（1）将点A （2，3）分别代入y 1＝kx 、得3＝2k 、，解得k ＝，m ＝6，∴正比例函数及反比例函数的解析式分别为y 1＝x 、；（2）∵y 2由y 1平移得到，所以设y 2＝x +b ，∵AB ⊥x 轴，∴B （2，0），将其代入y 2＝x +b 得b ＝﹣3，∴y 2＝x ﹣3，由题意得：解得：，（舍去），∴点D 坐标为（，）；（3）连接OD ，过点D 作DE ⊥y 轴，垂足为E ，则DE ＝1+，把x ＝0代入y 2＝x ﹣3得，y ＝﹣3， ∴C （0，﹣3） ∵直线y 1∥y 2，∴S △ACD ＝S △OCD ＝OC •DE ＝×3×（）＝．答：△ACD 的面积为．18．已知，矩形OABC在平面直角坐标系内的位置如图所示，点O为坐标原点，点A的坐标为（10，0），点B的坐标为（10，8），已知直线AC与双曲线y＝（m≠0）在第一象限内有一交点Q（5，n）．（1）求直线AC和双曲线的解析式；（2）若动点P从A点出发，沿折线AO→OC的路径以每秒2个单位长度的速度运动，到达C处停止．求△OPQ的面积S与的运动时间t秒的函数关系式，并求当t取何值时S＝10．解：设直线AC的解析式为y＝kx+b（k≠0），过A（10，0）、C（0，8），，解得：，∴直线AC的解析式为y＝﹣x+8，又∵Q（5，n）在直线AC上，∴n＝﹣×5+8＝4，又∵双曲线y＝过Q（5，4），∴m＝5×4＝20，∴双曲线的解析式为：y＝；②当0≤t≤5时，OP＝10﹣2t，过Q作QD⊥OA，垂足为D，如图1，∵Q（5，4），∴QD＝4，∴S＝（10﹣2t）×4＝20﹣4t，当S＝10时，20﹣4t＝10解得t＝2.5，当5＜t≤9时，OP＝2t﹣10，过Q作QE⊥OC，垂足为E，如图2∵Q（5，4），∴QE＝5，∴S＝（2t﹣10）×5＝5t﹣25，当S＝10时，5t﹣25＝10，解得t＝7，综上，S＝，当t＝5秒时，△OPQ的面积不存在，∴当t＝2.5秒或t＝7秒时，S＝10．19．如图，一次函数y1＝k1x+2与反比例函数y2＝的图象交于点A（4，m）和B（﹣8，﹣2），与y轴交于点C．（1）k1＝，k2＝16；（2）根据函数图象可知，当y1＞y2时，x的取值范围是﹣8＜x＜0或x＞4；（3）过点A作AD⊥x轴于点D，点P是反比例函数在第一象限的图象上一点．设直线OP与线段AD交于点E，当S四边形ODAC ：S△ODE＝3：1时，求直线OP的解析式．解：（1）把B（﹣8，﹣2）代入y1＝k1x+2得﹣8k1+2＝﹣2，解得k1＝，∴一次函数解析式为y1＝x+2；把B（﹣8，﹣2）代入y2＝得k2＝﹣8×（﹣2）＝16，∴反比例函数解析式为y2＝，故答案为：，16；（2）∵当y1＞y2时即直线在反比例函数图象的上方时对应的x的取值范围，∴﹣8＜x＜0或x＞4；故答案为：﹣8＜x＜0或x＞4；（3）把A（4，m）代入y2＝得4m＝16，解得m＝4，∴点A的坐标是（4，4），而点C的坐标是（0，2），∴CO＝2，AD＝OD＝4．∴S梯形ODAC＝×（2+4）×4＝12，∵S梯形ODAC ：S△ODE＝3：1，∴S△ODE＝×12＝4，∴OD•DE＝4，∴DE＝2，∴点E的坐标为（4，2）．设直线OP的解析式为y＝kx，把E（4，2）代入得4k＝2，解得k＝，∴直线OP的解析式为y＝x．20．如图，在平面直角坐标系中，边长为4的等边△OAB的边OB在x轴的负半轴上，反比例函数y＝（x＜0）的图象经过AB边的中点C，且与OA边交于点D．（1）求k的值；（2）连接OC，CD，求△OCD的面积；（3）若直线y＝mx+n与直线CD平行，且与△OAB的边有交点，直接写出n的取值范围．解：（1）∵等边△OAB，∴AB＝BO＝AO＝4，∠ABO＝∠BOA＝∠OAB＝60°，∵点C是AB的中点，∴BC＝AC＝2，过点C作CM⊥OB，垂足为M，在Rt△BCM中，∠BCM＝90°﹣60°＝30°，BC＝2，∴BM＝1，CM＝，∴OM＝4﹣1＝3，∴点C的坐标为（﹣3，），代入y＝得：k＝﹣3答：k的值为﹣3．（2）过点A作AN⊥OB，垂足为N，由题意得：AN＝2CM＝2，ON＝OB＝2，∴A（﹣2，2），设直线OA的关系式为y＝kx，将A的坐标代入得：k＝﹣，∴直线OA的关系式为：y＝﹣x，31由题意得：，解得：舍去，，∴D（﹣，3） 过D 作DE ⊥OB ，垂足为E ，S △OCD ＝S CMED +S △DOE ﹣S △COM ＝S CMED＝（+3）×（3﹣）＝3， 答：△OCD 的面积为3．（3）①当与直线CD 平行的直线y ＝mx +n 过点O 时，此时y ＝mx +n 的n ＝0， ②当与直线CD 平行的直线y ＝mx +n 经过点A 时，设直线CD 的关系式为y ＝ax +b ，把C 、D 坐标代入得：，解得：a ＝1，b ＝3+∴直线CD 的关系式为y ＝x+3+， ∵y ＝mx +n 过与直线y ＝x+3+平行， ∴m ＝1，把A （﹣2，2）代入y ＝x +n 得：n ＝2+2因此：0≤n ≤2+2．答：n 的取值范围为：0≤n ≤2+2．。
最新1、北师大版初三数学几何压轴题专项训练(探究题)资料
压轴题几何专项训练（一）——几何探究题渗透思想方法：特殊到一般、类比、化归解题策略：运用特殊情况解答中所积累的经验和知识，进一步完成一般情况。
1、课外兴趣小组活动时，许老师出示了如下问题：如图1，己知四边形ABCD 中，AC平分∠DAB, ∠DAB＝60°, ∠B与∠D互补，求证：AB＋AD＝ 3 AC．小敏反复探索，不得其解．她想，若将四边形ABCD特殊化，看如何解决该问题．（1）特殊情况入手添加条件：“∠B＝∠D”, 如图2，可证AB＋AD＝ 3 AC．（请你完成此证明）（2）解决原来问题受到（1）的启发，在原问题中，添加辅助线：如图3，过Ｃ点分别作AB、AD的垂线，垂足分别为E、F．（请你补全证明）2、如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF＝BE．⑴求证：CE＝CF；⑵在图1中，若G在AD上，且∠GCE＝45°，则GE＝BE＋GD成立吗？为什么？⑶运用⑴⑵解答中所积累的经验和知识，完成下题：如图2，在直角梯形ABCD中，AD∥BC（BC＞AD），∠B＝90°，AB＝BC＝12，E是AB上一点，且∠DCE＝45°，BE＝4，求DE的长．图1A DEB C图23、（1）问题发现如图1，△ACB和△DCE均为等边三角形，点A，D，E在同一直线上，连接BE．填空：①∠AEB的度数为；②线段AD，BE之间的数量关系为．（2）拓展探究如图2，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A，D，E在同一直线上，CM为△DCE中DE边上的高，连接BE，请判断∠AEB 的度数及线段CM、AE、BE之间的数量关系，并说明理由．（3）解决问题如图3，在正方形ABCD中，CD=，若点P满足PD=1，且∠BPD=90°，请直接写出点A到BP的距离．4、（1）如图1，在正方形ABCD中，点E，H分别在BC，AB上，若AE⊥DH 于点O，求证：AE=DH；类比探究：（2）如图2，在正方形ABCD中，点H，E，G，F分别在AB，BC，CD，DA上，若EF⊥HG于点O，探究线段EF与HG的数量关系，并说明理由；综合运用：（3）在（2）问条件下，HF∥GE，如图3所示，已知BE=EC=2，EO=2FO，求图中阴影部分的面积。
北师大版九年级数学上学期期末备考压轴题专项习题：特殊的平行四边形(含答案)
期末备考压轴题专项习题：特殊的平行四边形1．已知四边形ABCD是正方形，点E是边BC上的任意一点，AE⊥EF，且直线EF交正方形外角的平分线CF于点F．（1）如图1，求证：AE＝EF；（2）如图2，当AB＝2，点E是边BC的中点时，请直接写出FC的长．2．如图，矩形ABCD中，E是AD的中点，延长CE，BA交于点F，连接AC，DF．（1）判断四边形ACDF的形状；（2）当BC＝2CD时，求证：CF平分∠BCD．3．在菱形A BCD中，∠ABC＝60°，延长BA至点F，延长CB至点E，使BE＝AF，连结CF，EA，AC，延长EA交CF于点G．（1）求证：△ACE≌△CBF；（2）求∠CGE的度数．4．如图，△ABC中，AD是角平分线，DE∥AC交AB于点E，DF∥AB交AC于点F．（1）试判断四边形AEDF的形状．（2）当△ABC满足条件时，EF∥BC；当△ABC满足条件时，EF＝AD．5．如图正方形ABCD，E、F分别为BC、CD边上一点．（1）若∠EAF＝45°，求证：EF＝BE+DF；（2）若该正方形ABCD的边长为1，如果△CEF的周长为2．求∠EAF的度数．6．一个六边形的花坛被分割成7个部分，其中四边形PRBA，RQDC，QPFE为正方形．记正方形PRBA，RQDC，QPFE的面积分别为S1，S2，S3，RH⊥PQ，垂足为H．（友情提示：正方形的四个内角都等于90度，四边都相等）（1）若PR⊥QR，S1＝16，S2＝9，则S3＝，RH＝；（2）若四边形PRBA，RQDC，QPFE的面积分别为25m2、13m2、36m2①求△PRQ的面积；②请判断△PRQ和△DEQ的面积的数量关系，并证明你的结论；③六边形花坛ABCDEF的面积是m2．7．已知，如图所示，正方形ABCD的边长为1，G为CD边上的一个动点（点G与C、D 不重合），以CG为一边向正方形ABCD外作正方形GCEF，连接DE交BG的延长线于点H．（1）求证：①△BCG≌△DCE．②BH⊥DE．（2）当BH平分DE时，求GC的长．8．如图，过矩形ABCD的对角线AC的中点O做EF⊥AC，交BC边于点E，交AD边于点F，分别连接AE、CF．（1）求证：四边形AECF是菱形；（2）若AB＝，∠DCF＝30°，求EF的长．9．已知：如图，在平行四边形ABCD中，G、H分别是AD、BC的中点，E、O、F分别是对角线BD上的四等分点，顺次连接G、E、H、F．（1）求证：四边形GEHF是平行四边形；（2）当平行四边形ABCD满足条件时，四边形GEHF是菱形；（3）若BD＝2AB，探究四边形GEHF的形状，并说明理由．10．如图，平行四边形ABCD中，G是CD的中点，E是边AD上的动点，EG的延长线与BC的延长线交于点F，连结C E，DF．（1）求证：四边形CEDF为平行四边形；（2）若AB＝6cm，BC＝10cm，∠B＝60°，①当AE＝cm时，四边形CEDF是矩形；②当AE＝cm时，四边形CEDF是菱形．11．如图，在四边形ABCD中，AD∥BC，AB＝8，AD＝16，BC＝22，∠ABC＝90°，点P 从点A出发，以每秒1单位的速度向点D运动，点Q从点C同时出发，以每秒v单位的速度向点B运动，其中一个动点到达终点时，另一个动点也随之停止运动，设运动时间为t秒．（1）当v＝3时，若以点P，Q和点A，B，C，D中的两个点为顶点的四边形为平行四边形，且线段PQ为平行四边形的一边，求t的值；（2）若以点P，Q和点A，B，C，D中的两个点为顶点的四边形为菱形，且线段PQ为菱形的一条对角线，请直接写出t的值．12．如图，在四边形ABCD中，AB∥CD，AC垂直平分BD，交BD于点F，延长DC到点E，使得CE＝DC，连接BE．（1）求证：四边形ABCD是菱形．（2）填空：①当∠ADC＝°时，四边形ACEB为菱形；②当∠ADC＝90°，BE＝4时，则DE＝．13．如图，在矩形ABCD中，M是BC上一点，EF垂直平分AM，分别交BC，AM，AD于点E，O，F，连接AE，MF．（1）求证：四边形AEMF是菱形；（2）若AB＝6，H为AB的中点，连接OH交AE于点P，OH+OA＝9，求△OPE的周长．14．在菱形ABCD中，P、Q分别是边BC、CD的中点，连接AP、AQ．（1）如图（1），求证：AP＝AQ；（2）如图（2），连接PQ、AC，在不添加任何辅助线的情况下，请直接写出图中所有的等腰三角形．15．如图，四边形ABCD为菱形，∠BCD＝60°，E为对角线AC上一点，且AE＝AB，F 为CE的中点，接DF、BF，BG⊥BF与AC交于点G；（1）若AB＝2，求EF的长；（2）求证：CG﹣EF＝BG．参考答案1．（1）证明：如图1，在AB上截取BM＝BE，连接ME，∵∠B＝90°，∴∠BME＝∠BEM＝45°，∴∠AME＝135°＝∠ECF，∵AB＝BC，BM＝BE，∴AM＝EC，在△AME和△ECF中，∴△AME≌△ECF（ASA），∴AE＝EF；（2）解：取AB中点M，连接EM，∵AB＝BC，E为BC中点，M为AB中点，∴AM＝CE＝BE，∴∠BME＝∠BME＝45°，∴∠AME＝135°＝∠ECF，∵∠B＝90°，∴∠BAE+∠AEB＝90°，∵∠AEF＝90°，∴∠AEB+∠FEC＝90°，∴∠BAE＝∠FEC，在△AME和△ECF中，∴△AME≌△ECF（ASA），∴EM＝CF，∵AB＝2，点E是边BC的中点，∴BM＝BE＝1，∴CF＝ME＝．2．（1）解：四边形ACDF是平行四边形，理由如下：∵四边形ABCD是矩形，∴AB∥CD，∠BCD＝∠B＝90°，∴∠F AE＝∠CDE，∵E是AD的中点，∴AE＝DE，在△F AE和△CDE中，，∴△F AE≌△CDE（ASA），∴CD＝F A，又∵CD∥AF，∴四边形ACDF是平行四边形；（2）证明：∵BC＝2CD，AB＝CD，四边形ACDF是平行四边形，∴AF＝CD，BF＝BC，∴△BCF是等腰直角三角形，∴∠BCF＝45°，∴∠DCF＝45°，∴CF平分∠BCD．3．（1）证明：∵AB＝AC，∠ABC＝60°，∴△ABC是等边三角形，∴BC＝AC，∠ACB＝∠ABC，∵BE＝AF，∴BE+BC＝AF+AB，即CE＝BF，在△ACE和△CBF中，，∴△ACE≌△CBF（SAS）；（2）解：由（1）可知：△ABC是等边三角形，△ACE≌△CBF，∴∠E＝∠F，∵∠BAE＝∠F AG，∴∠E+∠BAE＝∠F+∠F AG，∴∠CGE＝∠ABC，∵∠ABC＝60°，∴∠CGE＝60°．4．解：（1）四边形AEDF是菱形；理由如下：∵DE∥AC交AB于点E，DF∥AB交AC于点F，∴四边形AEDF是平行四边形，∠EAD＝∠ADF，∵AD是△ABC的角平分线，∴∠EAD＝∠F AD，∴∠ADF＝∠F AD，∴F A＝FD，∴四边形AEDF是菱形；（2）当△ABC满足AB＝AC条件时，EF∥BC；当△ABC满足∠BAC＝90°条件时，EF ＝AD．理由如下：由（1）得：四边形AEDF是菱形，∴AD⊥EF，∵AB＝AC，AD是角平分线，∴AD⊥BC，∴EF∥BC；当∠ABC＝90°时，四边形AEDF是正方形，∴EF＝AD；故答案为：AB＝AC，∠BAC＝90°．5．（1）证明：如图，延长CD至E'，使DE'＝BE，连接AE'，∵四边形ABCD为正方形，∴AB＝AD＝CB＝CD，∠BAD＝∠B＝90°，∴∠ADE'＝90°＝∠ABE，在△ADE'和△ABE中，，∴△ADE'≌△ABE（SAS），∴AE'＝AE，∠DAE'＝∠BAE，∵∠EAF＝45°，∴∠DAF+∠B AE＝45°，∴∠DAF+∠DAE'＝∠E'AF＝45°＝∠EAF，在△E′AF和△EAF中，，∴△E′AF≌△EAF（SAS），∴E′F＝EF，∵E′F＝DE′+DF＝BE+DF，∴EF＝BE+DF；（2）延长CD至E'使DE'＝BE，连接AE'，由（1）知，△ADE'≌△ABE（SAS），∴AE'＝AE，∠DAE'＝BAE，设BE＝x，DF＝y，∵正方形ABCD的边长为1，∴CE＝1﹣x，CF＝1﹣y，∵△CEF的周长为2，∴CE+CF+EF＝2，∴1﹣x+1﹣y+EF＝2，∴EF＝x+y＝BE+DF＝DE'+DF＝E'F，在△E'AF和△EAF中，，∴△E'AF≌△EAF（SSS），∴∠E'AF＝∠EAF，∴∠DAE'+∠DAF＝∠BAE+∠DAF＝∠EAF，∵∠DAF+∠EAF+∠BAE＝90°，∴∠EAF＝45°．6．解：（1）∵PR⊥QR，∴∠PRQ＝90°，∴PR2+RQ2＝PQ2，∵S1＝16，S2＝9，∴S3＝16+9＝25，∴PR＝4，RQ＝3，PQ＝5，∵RH⊥PQ，∴PR•RQ＝PQ•RH，∴RH＝＝，故答案为：25，2.4；（2）①设PH＝a，则QH＝6﹣a，∵RH2＝PR2﹣PH2＝RQ2﹣HQ2，∴25﹣a2＝13﹣（6﹣a）2，解得：a＝4，∴RH2＝PR2﹣PH2＝25﹣16＝9，∴RH ＝3，∴S △PQR ＝×6×3＝9；②S △PRQ ＝S △DQE ，证明：延长RQ 到点M ，使QM ＝RQ ，连结PM ，∵QD ＝QM ，∠DQE ＝∠MQP ，QE ＝QP∴△DQE ≌△MQP （SAS ），∴S △DQE ＝S △MQP ，∵RQ ＝QM ，∴S △PRQ ＝S △MQP ，∴S △PRQ ＝S △DQE ；③六边形花坛ABCDEF 的面积＝25+13+36+4×9＝74+36＝110m 2． 故答案为：110．7．（1）证明：∵正方形ABCD ，∴∠BCD ＝90°，BC ＝CD ，同理：CG ＝CE ，∠GCE ＝90°，∴∠BCD ＝∠GCE ＝90°，，∴△BCG ≌△DCE （SAS ），∴∠GBC＝∠CDE，在Rt△DCE中∠CDE+∠CED＝90°，∴∠GBC+∠BEH＝90°，∴∠BHE＝180°﹣（∠GBC+∠BHE）＝90°，∴BH⊥DE；（2）若BH垂直平分DE，连接BD，∴BD＝BE，∵BD＝，∴CG＝CE＝BE﹣BC＝﹣1．8．解：（1）证明：∵O是AC的中点，且EF⊥AC，∴AF＝CF，AE＝CE，OA＝OC，∵四边形ABCD是矩形，∴AD∥BC，∴∠AFO＝∠CEO，在△AOF和△COE中，，∴△AOF≌△COE（AAS），∴AF＝CE，∴AF＝CF＝CE＝AE，∴四边形AECF是菱形；（2）∵四边形ABCD是矩形，∴CD＝AB＝，在Rt△CDF中，cos∠DCF＝，∠DCF＝30°，∴CF＝＝2，∵四边形AECF是菱形，∴CE＝CF＝2．9．（1）证明：连接AC，如图1所示：∵四边形ABCD是平行四边形，∴OA＝OC，OB＝OD，∴BD的中点在AC上，∵E、O、F分别是对角线BD上的四等分点，∴E、F分别为OB、OD的中点，∵G是AD的中点，∴GF为△AOD的中位线，∴GF∥OA，GF＝OA，同理：EH∥OC，EH＝OC，∴EH＝GF，EH∥GF，∴四边形GEHF是平行四边形；（2）解：当▱ABCD满足AB⊥BD条件时，四边形GEHF是菱形；理由如下：连接GH，如图2所示：则AG＝BH，AG∥BH，∴四边形ABHG是平行四边形，∴AB∥GH，∵AB⊥BD，∴GH⊥BD，∴GH⊥EF，∴四边形GEHF是菱形；故答案为：AB⊥BD；（3）解：四边形GEHF是矩形；理由如下：由（2）得：四边形GEHF是平行四边形，∴GH＝AB，∵BD＝2AB，∴AB＝BD＝EF，∴GH＝EF，∴四边形GEHF是矩形．10．（1）证明：∵四边形ABCD是平行四边形，∴CF∥ED，∴∠FCD＝∠GCD，∵G是CD的中点，∴CG＝DG，在△FCG和△EDG中，∴△CFG≌△EDG（ASA），∴FG＝EG，∴四边形CEDF是平行四边形；（2）①解：当AE＝7时，平行四边形CEDF是矩形，理由是：过A作AM⊥BC于M，∵∠B＝60°，AB＝6，∴BM＝3，∵四边形ABCD是平行四边形，∴∠CDA＝∠B＝60°，DC＝AB＝6，BC＝AD＝10，∵AE＝7，∴DE＝3＝BM，在△MBA和△EDC中，，∴△MBA≌△EDC（SAS），∴∠CED＝∠AMB＝90°，∵四边形CEDF是平行四边形，∴四边形CEDF是矩形，故答案为：7；②当AE＝4时，四边形CEDF是菱形，理由是：∵AD＝10，AE＝4，∴DE＝6，∵CD＝6，∠CDE＝60°，∴△CDE是等边三角形，∴CE＝DE，∵四边形CEDF是平行四边形，∴四边形CEDF是菱形，故答案为：4．11．解：（1）∵当P、Q两点与A、B两点构成的四边形是平行四边形时，∵AP∥BQ，∴当AP＝BQ时，四边形APQB为平行四边形．此时，t＝22﹣3t，t＝．当P、Q两点与C、D两点构成的四边形是平行四边形时，∵PD∥QC，∴当PD＝QC时，四边形PQCD为平行四边形．此时，16﹣t＝3t，t＝4，∵线段PQ为平行四边形的一边，故当t＝或4时，线段PQ为平行四边形的一边．（2）当PD＝BQ＝BP时，四边形PBQD能成为菱形．由PD＝BQ，得16﹣t＝22﹣3t，解得t＝3，当t＝3时，PD＝BQ＝13，AP＝AD﹣PD＝16﹣13＝3．在Rt△ABP中，AB＝8，根据勾股定理得，BP═≠13∴四边形PBQD不能成为菱形；如果Q点的速度改变为vcm/s时，能够使四边形PBQD在时刻ts为菱形，由题意得，，解得，．故点Q的速度为2cm/s时，能够使四边形PBQD在t＝6时为菱形．12．（1）证明：∵AC垂直平分BD，∴AB＝AD，BF＝DF，∵AB∥CD，∴∠ABD＝∠CD B．∵∠AFB＝∠CFD，∴△AFB≌△CFD（ASA），∴AB＝CD．又∵AB∥CD，∴四边形ABCD是平行四边形，∵AB＝AD，∴平行四边形ABCD是菱形；（2）①当∠ADC＝60°，四边形ACEB为菱形，∵∠ADC＝60°，∴∠BCE＝60°，∴△BCE是等边三角形，∴CE＝BE，∴四边形ACEB为菱形，故答案为：60；②当∠ADC＝90°，BE＝4时，DE＝4，故答案为：4．13．（1）证明：∵EF垂直平分AM，∴AE＝EM，OA＝OM．∵四边形ABCD是矩形，∴AD∥BC．∴∠AFO＝∠MEO，在△OF和△MOE中，，∴△AOF≌△MOE（AAS）．∴OF＝OE．∴四边形AEMF是平行四边形．∵AE＝EM．∴四边形AEMF是菱形；（2）解：∵O、H分别为AM、AB的中点，∴BM＝2OH，AM＝2OA，∴AM+BM＝2OA+2OH＝18．设BM＝x，则AM＝18﹣x，在Rt△ABM中，由勾股定理得：62+x2＝（18﹣x）2，解得：x＝8，∴BM＝8，AM＝10．∴OA＝AM＝5，设EM＝m，则BE＝8﹣m，AE＝EM＝m，在Rt△ABE中，由勾股定理得：62+（8﹣m）2＝m2，解得：m＝，∴AE＝EM＝在Rt△AOE中，EO＝＝＝．∵OP∥EM，∴＝＝1，∴AP＝PE，∴OP＝EM＝，∵PE＝AE＝，∴△OPE的周长＝EO+PE+OP＝++＝10．14．证明：（1）∵四边形ABCD是菱形，∴AB＝BC＝CD＝AD，∠B＝∠D，∵P、Q分别是边BC、CD的中点，∴BP＝CQ，在△ABP和△ADQ中，，∴△ABP≌△ADQ（SAS），∴AP＝AQ，（2）∵AP＝AQ，∴△APQ是等腰三角形，∵BC＝CD，∵P、Q分别是边BC、CD的中点，∴PC＝CQ，∴△PQC是等腰三角形，∵AB＝BC，AD＝CD，∴△ABC，△ACD是等腰三角形，∴图中所有的等腰三角形有△ABC，△APQ，△ACD，△CPQ．15．（1）解：连接BD交AC于O，如图所示：∵四边形ABCD是菱形，∴∠BAD＝∠BCD＝60°，AC⊥BD，OB＝OD，OA＝OC，∠OAB＝∠BAD＝30°，∴OB＝AB＝1，OA＝OB＝，∴AC＝2OA＝2，∵AE＝AB＝2，∴CE＝AC﹣AE＝2﹣2，∵F为CE的中点，∴EF＝CE＝﹣1；（2）证明：设AB＝2a，同（1）得：OB＝AB＝a，OA＝OB＝a，∴AC＝2OA＝2a，∵AE＝AB＝2a，∴CE＝AC﹣AE＝（2﹣2）a，OE＝AE﹣OA＝（2﹣）a，∵F为CE的中点，∴EF＝CE＝（﹣1）a，∴OF＝OE+EF＝（2﹣）a+（﹣1）a＝a，∴OB＝OF，∵AC⊥BD，∴△BOF是等腰直角三角形，∴∠BFG＝45°，∵BG⊥BF，∴△BFG是等腰直角三角形，∴GF＝BG，∵GF＝CG﹣CF＝CG﹣EF，∴CG﹣EF＝BG．。
1、北师大版初三数学几何压轴题专项训练(探究题)
压轴题几何专项训练（一）——几何探究题渗透思想方法：特殊到一般、类比、化归解题策略：运用特殊情况解答中所积累的经验和知识，进一步完成一般情况。
1、课外兴趣小组活动时，许老师出示了如下问题：如图1，己知四边形ABCD 中，AC平分∠DAB, ∠DAB＝60°, ∠B与∠D互补，求证：AB＋AD＝ 3 AC．小敏反复探索，不得其解．她想，若将四边形ABCD特殊化，看如何解决该问题．（1）特殊情况入手添加条件：“∠B＝∠D”, 如图2，可证AB＋AD＝ 3 AC．（请你完成此证明）（2）解决原来问题受到（1）的启发，在原问题中，添加辅助线：如图3，过Ｃ点分别作AB、AD的垂线，垂足分别为E、F．（请你补全证明）2、如图1，在正方形ABCD 中，E 是AB 上一点，F 是AD 延长线上一点，且DF ＝BE ．⑴求证：CE ＝CF ；⑵在图1中，若G 在AD 上，且∠GCE ＝45°，则GE ＝BE ＋GD 成立吗？为什么？⑶运用⑴⑵解答中所积累的经验和知识，完成下题： 如图2，在直角梯形ABCD 中，AD ∥BC （BC ＞AD ），∠B ＝90°，AB ＝BC ＝12，E 是AB 上一点，且∠DCE ＝45°，BE ＝4，求DE 的长．B C A G D FE图1 图2B CA DE3、（1）问题发现如图1，△ACB和△DCE均为等边三角形，点A，D，E在同一直线上，连接BE．填空：△△AEB的度数为；△线段AD，BE之间的数量关系为．（2）拓展探究如图2，△ACB和△DCE均为等腰直角三角形，△ACB=△DCE=90°，点A，D，E在同一直线上，CM为△DCE中DE边上的高，连接BE，请判断△AEB的度数及线段CM、AE、BE之间的数量关系，并说明理由．（3）解决问题如图3，在正方形ABCD中，CD=，若点P满足PD=1，且△BPD=90°，请直接写出点A到BP的距离．4、（1）如图1，在正方形ABCD中，点E，H分别在BC，AB上，若AE⊥DH 于点O，求证：AE=DH；类比探究：（2）如图2，在正方形ABCD中，点H，E，G，F分别在AB，BC，CD，DA上，若EF⊥HG于点O，探究线段EF与HG的数量关系，并说明理由；综合运用：（3）在（2）问条件下，HF∥GE，如图3所示，已知BE=EC=2，EO=2FO，求图中阴影部分的面积。
2023学年北师大版九年级数学上学期专项讲练1-29 《特殊平行四边形》全章复习与巩固(培优篇)
专题1.29 《特殊平行四边形》全章复习与巩固（培优篇）（专项练习）一、单选题1．如图，菱形OABC 的顶点O 与原点重合，点C 在x 轴上，点A 的坐标为（3，4）．将菱形OABC 绕点O 逆时针旋转，每次旋转90°，则第2022次旋转结束时，点B 的坐标为（ ）A ．（-8，-4）B ．（-9，-4）C ．（-9，-3）D ．（-8，-3） 2．如图，在边长为4的菱形ABCD 中，∠ABC ＝60°，将△ABD 沿射线BD 方向平移，得到△EFG ，连接EC 、GC ．则EC +GC 的最小值为（ ）A ．B ．C ．D ．3．如图，在平面直角坐标系中，点A 的坐标为（1，0），四边形OABC 是菱形，60AOC ∠=︒，以OB 为边作菱形11OBB C ，使顶点1B 在OC 的延长线上，再以1OB 为边作菱形122OB B C ，使顶点2B 在1OC 的延长线上，再以2OB 为边作菱形233OB B C ，使顶点3B 在2OC 的延长线上，按照此规律继续下去，则2021B 的坐标是（ ）A ．101130-（，）B ．101132（，）C ．20210-（，）D ．202310113322（-，）4．如图，点H ，F 分别在菱形ABCD 的边AD ，BC 上，点E ，G 分别在BA ，DC 的延长线上，且AE AH CG CF ===．连结EH ，EF ，GF ，GH ，若菱形ABCD 和四边形EFGH 的面积相等，则AH AD的值为（ ）A ．12 B C D ．15．如图，矩形ABCD 中，AB ＝8，AD ＝4，E 为AB 的中点，F 为EC 上一动点，P 为DF 中点，连接PB ，则PB 的最小值是（ ）A．4 B ．8 C ．D ．6．如图，在矩形ABCD 中，1AB =，AD =O 是对角线的交点，过C 作CE BD ⊥于点E ，EC 的延长线与BAD ∠的平分线相交于点H ，AH 与BC 交于点F .给出下列四个结论：∠AF FH =；∠BF BO =；∠AC CH =；∠3BE DE =.其中正确结论有( ).A ．1个B ．2个C ．3个D ．4个7．如图，四边形ABCD 是矩形纸片，6AB =，对折矩形纸片ABCD ，使AD 与BC 重合，折痕为EF ．展平后再过点B 折叠矩形纸片，使点A 落在EF 上的点N ，折痕为BM ，再次展平，连接BN ，MN ，延长MN 交BC 于点G ．有如下结论：∠60ABN ∠=︒；∠3AM =；∠∠BMG是等边三角形；∠EN =∠P 为线段BM 上一动点，H 是线段BN 上的动点，则PN PH+的最小值是 ）A ．∠∠∠∠B ．∠∠∠∠C ．∠∠∠∠D ．∠∠∠∠∠8．如图，将四边形纸片ABCD 沿过点A 的直线折叠，使得点B 落在CD 上的点M 处，折痕为AP ；再将PCM △，ADM △分别沿PM ，AM 折叠，此时点C ，D 落在AP 上的同一点N 处．下列结论不．正确的是（ ）A ．M 是CD 的中点B ．MN AP ⊥C ．当四边形APCD 是平行四边形时，AB =D ．AD BC ∥ 9．如图，在∠ABC 中，∠ACB ＝90°， 分别以AC ， BC 为边向外作正方形ACDE 与正方形BCFG ， H 为EG 的中点，连接DH ，FH ．记∠FGH 的面积为S 1，∠CDH 的面积为S 2，若S 1－S 2＝6，则AB 的长为（ ）A ．B ．C ．D ．10．如图，正方形ABCD 边长为4，点E 是CD 边上一点，且75ABE ∠=︒．P 是对角线BD 上一动点，则12AP BP +的最小值为（ ）A．4 B ．C D 11．如图，在平面直角坐标系中，正方形纸片ABCD 的顶点A 的坐标为（-1，3），在纸的正方形1111D C B A ，将该纸片以O 为旋转中心进行逆时针旋转，每次旋转45°，则第298次旋转后，点C 和点1B 的坐标分别为（ ）A ．（-3，-1），（1，0）B ．（-3，-1），（0，-1）C ．（3，1），（0，-1）D ．（3，1），（1，0） 12．如图，将正方形纸片ABCD 沿EF 折叠，使点B 落在AD 边的点P 处（不与点A ，点D 重合），点C 落在G 点处，PG 交DC 于点H ，连接BP ，BH ．BH 交EF 于点M ，连接PM ．下列结论：∠PB 平分∠APG ；∠PH =AP +CH ；∠BM ，∠若BE =53，AP =1，则S 四边形BEPM =113，其中正确结论的序号是（ ）A ．∠∠∠∠B ．∠∠∠C ．∠∠∠D ．∠∠∠二、填空题 13．如在菱形ABCD 中，2BC =，120C ∠=︒，E 为AB 的中点，P 为对角线BD 上的任意一点，则PA PE +的最小值为__________．14．如图，已知ABC 中，5AB AC ==，8BC =，将ABC 沿射线BC 方向平移m 个单位得到DEF ，顶点A ，B ，C 分别与D ，E ，F 对应，若以A ，D ，E 为顶点的三角形是等腰三角形，则m 的值是___________．15．如图，在菱形ABCD 中，∠ABC ＝120°，对角线AC 、BD 交于点O ，BD ＝4，点E 为OD 的中点，点F 为AB 上一点，且AF ＝3BF ，点P 为AC 上一动点，连接PE 、PF ，则PF ﹣PE 的最大值为 ___．16．如图，在菱形ABCD 中，∠BAD ＝60°，点E 在边BC 上，将∠ABE 沿直线AE 翻折180°，得到∠AB ′E ，点B 的对应点是点B ′．若AB ′∠BD ，BE ＝2，则BB ′的长是___．17．如图，在矩形ABCD 中，E 是BC 上一动点，将ABE △沿AE 折叠后得到AFE △，点F 在矩形ABCD 内部，延长AF 交CD 于点G ，3AB =，4=AD ．当点E 是BC 的中点时，线段GC 的长为______；点E 在运动过程中，当∠CFE 的周长最小时，BE 的长为______．18．如图，在等腰Rt ABC 中，CA BA =，90CAB ∠=︒，点M 是AB 上一点，点P 为射线CA （除点C 外）上一个动点，直线PM 交射线CB 于点D ，若1AM =，3BM =，CPD ∆的面积的最小值为________．19．如图，在四边形ABCD 中，AB ∠BC ，AD ∠AC ，AD ＝AC ，∠BAD ＝105°，点E 和点F 分别是AC 和CD 的中点，连接BE ，EF ，BF ，若CD ＝8，则BEF 的面积是_____．20．如图，点E 是矩形ABCD 的边AB 的中点，点P 是边AD 上的动点，沿直线PE 将△APE 对折，点A 落在点F 处. 已知AB =6，AD =4，连结CF 、CE ，当△CEF 恰为直角三角形时，AP 的长度等于___________.21．如图，在正方形ABCD 中，E 、F 分别是边BC 、CD 上的点，∠EAF ＝45°，∠ECF 的周长为8，则正方形ABCD 的边长为_____．22．如图，Rt ABC 中，90ABC ∠=︒，30C ∠=︒，1AB =，点D 为AC 边上任意一点，将BCD 沿BD 折叠，点C 的对应点为点E ，当30ADE ∠=︒时，CD 的长为______．23．如图，正方形ABCD 的边长为4，E ，F ，H 分别是边BC ，CD ，AB 上的一点，将正方形ABCD 沿FH 折叠，使点D 恰好落在BC 边的中点E 处，点A 的对应点为点P ，则折痕FH 的长为______．24．图，正方形ABCD 的边长为6，点E ，F 分别在边AB ，BC 上，若F 是BC 的中点，45EDF ∠=︒，则DE 的长为 _____．三、解答题25．直线443y x =-+与x 轴交于点A ，与y 轴交于点B ，菱形ABCD 如图放置在平面直角坐标系中，其中点D 在x 轴负半轴上，直线y x m =+经过点C ，交x 轴于点E ．(1)请直接写出点C ，点D 的坐标，并求出m 的值；(2)点()0,P t 是线段OB 上的一个动点（点P 不与O 、B 重合），经过点P 且平行于x 轴的直线交AB 于M ，交CE 于.N 当四边形NEDM 是平行四边形时，求点P 的坐标；(3)点()0,P t 是y 轴正半轴上的一个动点，Q 是平面内任意一点，t 为何值时，以点C 、D 、P 、Q 为顶点的四边形是菱形？26．综合与实践：如图，在平面直角坐标系中，A ，B 两点的坐标分别为(0,)A a ，点(,0)B b ，且a ．b 满足：4b +=C 与点B 关于y 轴对称，点P ，点E 分别是x 轴，直线AB 上的两个动点．(1)求点C 的坐标；(2)连接PA ，PE ．∠如图1，当点P 在线段BO （不包括B ，O 两个端点）上运动，若APE 为直角三角形，F 为PA 的中点，连接EF ，OF ，试判断EF 与OF 的关系，并说明理由；∠如图2，当点P 在线段OC （不包括O ，C 两个端点）上运动，若APE 为等腰三角形，M 为底边AE 的中点，连接MO ，请直接写出PA 与OM 的数量关系．27．操作与证明：如图1，把一个含45°角的直角三角板ECF 和一个正方形ABCD 摆放在一起，使三角板的直角顶点和正方形的顶点C 重合，点E 、F 分别在正方形的边CB 、CD 上，连接AF ；取AF 中点M ，EF 的中点N ，连接MD ，MN ．(1)连接AE ，求证：△AEF 是等腰三角形；猜想与发现：(2)在（1）的条件下，请判断MD 、MN 的数量关系和位置关系，得出结论．结论1：DM、MN的数量关系是___________________________；结论2：DM、MN的位置关系是___________________________；拓展与探究：(3)如图2，将图1中的直角三角板ECF绕点C顺时针旋转180°，其他条件不变，则（2）中的两个结论还成立吗？若成立，请加以证明；若不成立，请说明理由．28．正方形ABCD的边长为6，点E是BC边上一动点，点F是CD边上一动点，过点E作AF的平行线，过点F作AE的平行线，两条线交于点G．(1)如图1，若BE＝DF，求证：四边形AEGF是菱形；(2)如图2，在（1）小题条件下，若∠EAF＝45°，求线段DF的长；(3)如图3，若点F运动到DF＝2的位置，且∠EAF依然保持为45°，求四边形AEGF的面积．参考答案1．A【分析】过点A作AE∠OC于E，设第一次旋转点B的对应点为B1，作B1F∠y轴于F，利用全等三角形的性质求出的坐标，根据循环性规律，得出第2022次旋转结束时，点B的坐标即可．解：过点A作AE∠OC于E，设第一次旋转点B的对应点为B1，作B1F∠y轴于F，∠点A的坐标为（3，4），∠5OA，∠菱形OABC的顶点O与原点重合，∠5AB OA==，AB∠OC，∠点B的坐标为（8，4），延长BA交y轴于H，∠BH∠OF，∠∠BHO=∠B1FO=90°，∠∠BOB1=90°，∠∠BOH+∠FOB1=90°，∠BOH+∠OBH=90°，∠∠FOB1=∠OBH，∠OB1=OB，∠∠OBH∠∠OB1F，∠FB1=OH=4，FO1=BH=8，B1的坐标为（-4，8）；同理可求，第二次旋转点B的坐标为（-8，-4）,第三次旋转点B的坐标为（4，-8）,第四次旋转点B的坐标为（8，4）,四次一循环，∠2022÷4=505……2，故第2022次旋转结束时，点B的坐标（-8，-4）,故选：A．【点拨】本题考查了菱形的性质、勾股定理、点的坐标变换，解题关键是熟练运用相关性质求出变换后点的坐标，发现规律求解．2．B【分析】连接AE ，作点D 关于直线AE 的对称点H ，连接DE ，DH ，EH ，AH ，CH ．由平移和菱形的性质可证明四边形CDEG 为平行四边形，即得出HE CG =，从而可得出EC GC EC HE CH +=+≥，即CH 的长为EC GC +的最小值．最后根据等边三角形的判定和性质，含30度角的直角三角形的性质与勾股定理求出CH 的长即可．解：如图，连接AE ，作点D 关于直线AE 的对称点H ，连接DE ，DH ，EH ，AH ，CH ．由平移的性质可知AB EG =，AB EG ．∠四边形ABCD 为菱形，∠AB CD =，AB CD ，1302ADB ABD ABC ∠=∠=∠=︒， ∠CD EG =，∥EG CD ，∠四边形CDEG 为平行四边形，∠GC DE =．由轴对称的性质可知HE DE =，DAE HAE ∠=∠，AH AD =，∠HE CG =，∠EC GC EC HE CH +=+≥，即CH 的长为EC GC +的最小值．∠AB EG =，AB EG ，∠四边形ABGE 为平行四边形，∠AE BG ∥，∠30EAD ADB ∠=∠=︒，∠260HAD EAD ∠=∠=︒，∠ADH 为等边三角形，∠4DH AD CD ===，60ADH ∠=︒，∠2120CDH ADH ∠=∠=︒，∠30HCD ∠=︒，即CDH △为顶角是120°，底角为30°的等腰三角形，结合含30°角的直角三角形和勾股定理即可求224CH === 故选B ．【点拨】本题考查平移的性质，菱形的性质，平行四边形的判定和性质，等边三角形的判定和性质，轴对称变换，含30°角的直角三角形的性质以及勾股定理等知识，综合性强，为选择题中的压轴题．正确的作出辅助线是解题关键．3．A【分析】连接AC 、BC 1，分别交OB 、OB 1于点D 、D 1，利用菱形的性质及勾股定理即可得OB 的长，进一步在菱形OBB 1C 1计算出OB 1，过点B 1作B 1M ∠x 轴于M ，利用勾股定理计算出B 1M ，OM ，从而得B 1的坐标，同理可得B 2，B 3，B 4，B 5，B 6，B 7，B 8，B 9，B 10，B 11，B 12，根据循环规律可得B 2021的坐标．解：如图所示，连接AC ，1BC 分别交OB ，1OB 与D 、1D ，∠点A 的坐标为（1，0），∠OA =1，∠四边形OABC 是菱形，∠AOC =60°，∠OC =OA =1，OB =2OD ，∠COD =30°，∠CDO =90°， ∠1122CD OC ==，∠OD ==∠OB =∠∠AOC =60°，∠∠B 1OC 1=90°-60°=30°，∠四边形OBB 1C 1是菱形，11111902C DO OC OB OB OD ∴∠=︒===，，在Rt ∠OC 1D 1中11112C D OC ==，∠132OD ==， ∠OB 1=2OD 1=3，过点B 1作B 1M ∠x 轴于点M ，在Rt ∠OMB 1中，11322OM OB ==∠1B M ==∠13(2B ，同理可得2345927(((27,0)22B B B B ---，，，6788181(,(,(0,22B B B ---，，，91011243729(,(,(729,0)22B B B ，，，12729)2B ， 由此可以发现规律“每经过12次作图后点的坐标符号与第一次坐标符号相同，每次1n n OB +=，∠2021÷12=168……5，∠B 2021的纵坐标符号与B 5的相同，则B 2021在y 轴的负半轴上，又2022101120213OB ==∠B 2021的坐标为1011(3,0)-，故选A【点拨】本题考查平面直角坐标系找规律，利用菱形的性质处理条件，掌握循环规律的处理方法是解题的关键．4．D【分析】根据题意先证四边形EFGH 是平行四边形，由平行四边形的性质求出EH ∠AC ，进而由面积关系进行分析即可求解．解：连接HC 、AF 、HF 、AC ，HF 交AC 于O ，连接EG ．∠四边形ABCD 是菱形，∠D =∠B ，AB =CD =AD =BC ，∠AE =AH =CG =CF ，∠DH =BF ，BE =DG ，在∠DHG 和∠BFE 中，DH BF D B BE DG =⎧⎪∠=∠⎨⎪=⎩，∠∠DHG ∠∠BFE ，∠HG =EF ，∠DHG =∠BFE，∠BC ∠AD ，∠∠BFE =∠DKF ，∠∠DHG =∠DKG ，∠HG ∠EF ，∠四边形EFGH 是平行四边形．∠AH =CF ，AH ∠CF ，∠四边形AHCF 是平行四边形，∠AC 与HF 互相平分，∠四边形EFGH 是平行四边形，∠HF 与EG 互相平分，∠HF 、AC 、EG 互相平分，相交于点O ，∠AE =AH ，DA =DC ，BE ∠DC ，∠∠EAH =∠D ，∠∠AEH =∠AHE =∠DAC =∠DCA ，∠EH ∠AC ，∠S △AEH =S △EHO =S △AHO =12S △AHC =14S 四边形EFGH =14S 四边形ABCD ， ∠S △AHC =12S 四边形ABCD =S △ADC ，∠AD =AH ， ∠AH AD =1. 故选：D ．【点拨】本题考查菱形的性质，平行四边形的判定和性质，全等三角形的判定和性质，平行线的判定和性质等知识，解题的关键是正确寻找全等三角形解决问题，学会添加常用辅助线，证明EH ∠AC 是解题的关键．5．C【分析】取CD 中点H ，连接AH ，BH ，根据矩形的性质题意得出四边形AECH 是平行四边形，可知AC CE ∥，然后根据三角形中位线的性质得PH CE ∥，得出点P 在AH 上，然后判断BP 的最小值，再求出值即可.解：如图，取CD 中点H ，连接AH ，BH ，设AH 与DE 的交点为O ，∠四边形ABCD 是矩形，∠AB ＝CD ＝8，AD ＝BC ＝4，CD AB ∥，∠点E 是AB 中点，点H 是CD 中点，∠CH ＝AE ＝DH ＝BE ＝4，∠四边形AECH 是平行四边形，∠AH CE ∥，∠点P 是DF 的中点，点H 是CD 的中点，∠PH 是∠CDF 的中位线，∠PH CE ∥，∠点P 在AH 上，∠当BP ∠AH 时，此时点P 与H 重合，BP 有最小值，∠AD ＝DH ＝CH ＝BC ＝4，∠∠DHA＝∠DAH ＝∠CBH ＝∠CHB ＝45°，AH BH ==∠∠AHB ＝90°，∠BP 的最小值为故选：C ．【点拨】本题主要考查了矩形的性质，平行四边形的判定，中位线的性质和定义等，确定点P 的位置是解题的关键．6．C【分析】利用矩形性质及勾股定理，30所对的直角边等于斜边的一半，可知60ABO ∠=︒，进一步可得AOB 为等边三角形，得到1BO BA ==，再利用角平分线的性质可证明1BF BA ==，故∠正确；证明15CHA OAH ∠=∠=︒，即可知∠正确；求出1122DE CD ==，13222BE =-=，即可知∠正确；无法证明F 是AH 中点，故∠错误．解：∠ABCD 为矩形，1AB =，AD =，∠90DAB ∠=︒，30ADB ∠=︒，2BD =，∠AF 平分DAB ∠，∠45FAB AFB ∠=∠=︒，即1BF BA ==，∠30ADB ∠=︒，∠60ABO ∠=︒，∠OA OB =，∠AOB 为等边三角形，∠1BO BA ==，∠BF BO =，故∠正确；∠AOB 为等边三角形，且45FAB ∠=︒，∠15OAH ∠=︒，同理：COD △为等边三角形，∠CE BD ⊥，∠30ECO ∠=︒，∠15CHA ∠=︒，∠15CHA OAH ∠=∠=︒，即AC CH =，故∠正确；∠30ECO ∠=︒，∠30DCE ∠=︒，∠1CD AB ==， ∠1122DE CD ==， ∠2DB =， ∠13222BE =-=， ∠3BE DE =，故∠正确；∠AC CH =，但是无法证明F 是AH 中点，故∠错误；综上所述：正确的有∠∠∠．故选：C ．【点拨】本题考查矩形性质及勾股定理，30所对的直角边等于斜边的一半，等边三角形，角平分线，三角形外角的定义及性质．解题的关键是熟练掌握以上知识点，证明1BO BA ==， 1BF BA ==；证明15CHA OAH ∠=∠=︒；求出1122DE CD ==，13222BE =-=． 7．C【分析】∠首先根据EF 垂直平分AB ，可得AN =BN ，然后根据折叠的性质，可得AB =BN ，据此判断出∠ABN 为等边三角形，即可判断出∠ABN =60°；∠首先根据∠ABN =60°，∠ABM = ∠NBM ，求出∠ABM =∠NBM =30°，然后在Rt ∠ABM 中，根据AB =6，求出AM 的大小即可；∠求出∠AMB =60°，得到∠BMG =60°，根据AD ∠BC ，求出∠BGM =60°即可；∠根据勾股定理求出EN 即可；∠根据轴对称图形的性质得到AP =PN ，PN +PH =AH ，且当AH ∠BN 时，PN +PH 最小，应用勾股定理，求出AH 的值即可．解：如图，连接AN ，∠EF 垂直平分AB ，∠AN =BN ，根据折叠的性质，可得AB =BN ，∠AN =AB =BN ，∠△ABN 为等边三角形，∠∠ABN =60°，∠PBN =12⨯60°=30°，即结论∠正确； ∠∠ABN =60°，∠ABM =∠NBM ，∠∠ABM =∠NBM =12⨯60°=30°， ∠BM =2AM ，∠AB =6，222AB AM BM +=，∠62+AM 2=（2AM ）2，解得AM =∠不正确；∠∠AMB =90°-∠ABM =60°，∠∠BMG=∠AMB=60°，∠ AD∠BC，∠∠MBG=∠AMB=60°，∠∠BGM=60°，∠BMG是等边三角形；即结论∠正确；∠BN=AB=6，BN=3，∠EN=∠正确；连接AN，∠△ABM与∠NBM关于BM轴对称，∠AP=NP，∠PN+PH=AP+PH，∠当点A、P、H三点共线时，AP+PH=AH，且当AH∠BN时AH有最小值，∠AB=6，∠ABH=60°，∠∠BAH=30°，∠BH=3，∠AH=∠PN＋PH的最小值是∠正确；【点拨】此题考查了矩形的性质，轴对称的性质，全等三角形的判定及性质，等边三角形的判定及性质，直角三角形30度角的性质，熟记等边三角形的判定及性质是解题的关键．8．B【分析】由折叠的性质可得DM＝MN，CM＝MN，即M是CD的中点；故∠正确；∠B＝∠AMP，∠DAM＝∠MAP＝∠P AB，∠DMA＝∠AMN，∠CMP＝∠PMN，∠D＝∠ANM，∠C＝∠MNP，由平角的性质可得∠D+∠C＝180°，∠AMP＝90°，可证AD∠BC，由平行线的性质可得∠DAB＝90°，由平行四边形和折叠的性质可得AN＝PN，由直角三角形的性质可得ABMN．解：由折叠的性质可得：DM＝MN，CM＝MN，∠DM＝CM，即M是CD的中点；故A正确；由折叠的性质可得：∠B＝∠AMP，∠DAM＝∠MAP＝∠P AB，∠DMA＝∠AMN，∠CMP ＝∠PMN，∠D＝∠ANM，∠C＝∠MNP，∠∠MNA+∠MNP＝180°，∠∠D+∠C＝180°，∠AD∥BC，故D正确；∠∠B+∠DAB＝180°，∠∠DMN+∠CMN＝180°，∠∠DMA+∠CMP＝90°，∠∠AMP＝90°，∠∠B＝∠AMP＝90°，∠∠DAB＝90°，若MN∠AP，则∠ADM＝∠MNA＝∠C＝90°，则四边形ABCD为矩形及AB∥CD，而题目中无条件证明此结论，故B不正确；∠∠DAB＝90°，∠∠DAM＝∠MAP＝∠P AB＝30°，由折叠的性质可得：AD＝AN，CP＝PN，∠四边形APCD是平行四边形，∠AD＝PC，∠AN＝PN，又∠∠AMP＝90°，AP，∠MN＝12∠∠P AB＝30°，∠B＝90°，AP，∠PB＝12∠PB＝MN∠AB，故C正确；故选：B ．【点拨】本题考查了翻折变换，平行四边形的性质及直角三角形的性质等知识，熟练掌握相关知识点并灵活运用这些性质是解题的关键．9．A【分析】连接AD 交EC 于点M ，连接BF 交CG 于点N ，设,AC a BC b ==，分别求出EC ，AD =，DM =，,CG FN ==，)EG a b =+，)HG EH a b ==+，)CH b a =-，分别求得1S ，2S ，由126S S -=得，2224a b +=，由勾股定理可得结论． 解：连接AD 交EC 于点M ，连接BF 交CG 于点N ，∠四边形ACDE ，BCFG 是正方形，∠,,,AD EC BF CG AD EC BF CG ⊥⊥==，1122DM AD FN BF ==，， 设,AC a BC b ==，∠∠90,=EAC AE AC a =︒=，∠EC ∠AD =，∠1122DM AD ===，同理可证：,CG FN ==， ∠EG EC CG =+，∠)EG a b =+，∠H 为EG 的中点，∠1))2HG EH a b a b ==+=+，∠)CH EH EC b a =-=-， ∠121124FG H ab b S S HG FN ∆+==⋅⋅=，22(124DH ab a S S CH DM ∆-=== 又∠126S S -=，∠22644ab b ab a +--=， 整理得，2224a b +=，∠∠90ACB =︒，∠AB ，故选：A ．【点拨】本题主要考查了正方形的性质，勾股定理等知识，正确作出辅助线是解答本题的关键．10．D【分析】连接AC ，作PG BE ⊥，证明当12AP BP +取最小值时，A ，P ，G 三点共线，且AG BE ⊥，此时最小值为AG ，再利用勾股定理，30所对的直角边等于斜边的一半即可求出结果．解：连接AC ，作PG BE ⊥∠ABCD 是正方形且边长为4，∠45ABO ∠=︒，AC BD ⊥，AO =∠75ABE ∠=︒，∠30PBG ∠=︒，∠12PG BP =， ∠当12AP BP +取最小值时，A ，P ，G 三点共线，且AG BE ⊥，此时最小值为AG ，∠75ABE ∠=︒，AG BE ⊥，∠15BAG ∠=︒，∠45BAO ∠=︒，∠30PAO ∠=︒，设OP b =，则2AP b =，∠(()222=2b b +，解得：b 设PG a =，则2BP a =，∠BO =∠2a b +=a∠2AG AP PG b a =+=+=故选：D【点拨】本题考查正方形的性质，动点问题，勾股定理，30所对的直角边等于斜边的一半，解题的关键是证明当12AP BP +取最小值时，A ，P ，G 三点共线，且AG BE ⊥，此时最小值为AG ．11．C【分析】由该纸片以О为旋转中心进行逆时针旋转，每次旋转45°，可得旋转一周360458︒÷︒=次，由2988372÷=⋅⋅⋅，可得第298次旋转后，实际是将纸片逆时针旋转37周后再转90°，由正方形纸片ABCD 对角线中点位于原点，可求点C （1，-3）由11A B =根据勾股定理，2221111+2OA OB A B ==求出B 1（-1，0），连结OD 与OC ，过D 作ED ∠x 轴于E ，CF ∠y 轴于F ，可证△FOC ∠△EOD （AAS ），可求点D （3，1），与点C 1（0，-1）即可．解：∠该纸片以О为旋转中心进行逆时针旋转，每次旋转45°，∠旋转一周360458︒÷︒=次，∠2988372÷=⋅⋅⋅，∠第298次旋转后，实际是将纸片逆时针旋转37周后再转90°，∠正方形纸片ABCD 对角线中点位于原点，∠点A 与点C 关于点O 成中心对称，∠点A （-1，3），∠点C （1，-3），∠11A B又∠11OA OB =，根据勾股定理，2221111+2OA OB A B ==，∠111OA OB ==，∠B 1（-1，0），连结OD 与OC ，过D 作ED ∠x 轴于E ，CF ∠y 轴于F ，绕点O 逆时针旋转90°后点C 位置转到点D 位置，∠四边形ABCD 为正方形，OD OC =，90FOE COD ∠==︒，∠∠FOC +∠COE =∠COE +∠EOD =90°，∠∠FOC =∠EOD ，在△FOC 和△EOD 中，90FOC EOD CFO DEO OC OD ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩，∠∠FOC ∠∠EOD （AAS ），∠CF =DE =1，OF =OE =3，∠点D （3，1），∠点B 1转到C 1位置，点C 1（0，-1），∠第298次旋转后，点C 和点1B 的坐标分别为（3，1）与（0，-1）．故选：C ．【点拨】本题主要考查坐标与旋转规律问题，涉及了正方形性质、中心对称性质、勾股定理应用、三角形全等判定与性质等知识，熟练掌握正方形旋转性质、中心对称性质、勾股定理应用、三角形全等判定与性质，根据旋转一周8次，确定旋转37周再转90°是解题关键．12．B【分析】根据折叠的性质，90EPG EBC ∠∠==，EB EP =，从而得到EPB EBP ∠=∠，根据直角三角形两锐角互余，得到APB BPG ∠=∠，即可判定∠；过点B 作BQ ∠PH ，利用全等三角形的判定与性质，得到CH QH =，AP PQ =，即可判定∠；通过证明BMP 为等腰直角三角形，即可判定∠；根据BEP BMP BEPM S S S =+△△四边形求得对应三角形的面积，即可判定∠．解：由题意可得：90EPG EBC ∠∠==，EB EP =，∠90EPG EPB BPG ∠∠∠=+=，EPB EBP ∠=∠，∠90EBP BPG ∠∠+=，由题意可得：1801809090EBP APB A ∠∠∠+=-=-=，∠APB BPG ∠=∠，∠PB 平分∠APG ；∠正确；过点B 作BQ ∠PH ，如下图：∠90BQP A ∠∠==在APB 和QPB 中，A BQP APB QPB BP BP ∠=∠⎧⎪∠=∠⎨⎪=⎩∠(AAS)APB QPB ≌∠AP PQ AB BQ ==，∠四边形ABCD 为正方形∠AB BC BQ ==，又∠BH BH=∠Rt Rt (HL)BCH BQH ≌，∠CH QH =∠PH PQ QH AP CH =+=+，∠正确；由折叠的性质可得：EF 是PB 的中垂线，∠PM BM =由题意可得：BAP BQP ≌，BCH BQH △≌△，∠,ABP PBQ CBH QBH ∠∠∠∠==， ∠1452PBQ QBH ABP CBH ABC ∠∠∠∠∠+=+==， ∠45PBM ∠=，∠45BPM PBM ∠∠==，∠BMP 为等腰直角三角形，∠222BM PM BP +=，即222BM BP =，∠BM ，∠正确； 若BE =53，AP =1，则53PE BE ==， 在Rt APE 中，222AE AP PE +=∠43AE ==，3AB AE BE ，∠PB =∠BM BP == 21110223BEP BMP BEPM S S S BE AP BM =+=⨯⨯+⨯=△△四边形，∠错误， 故选B ，【点拨】此题考查了正方形与折叠问题，涉及了折叠的性质，正方形的性质，直角三角形的性质，垂直平分线的性质，全等三角形的判定与性质，等腰三角形的判定与性质，勾股定理等知识，综合性比较性，解题的关键是灵活运用相关性质进行求解．13【分析】连接AC ，CE ，则CE 的长即为AP +PE 的最小值，再根据菱形ABCD 中，120BCD ∠=︒得出∠ABC 的度数，进而判断出∠ABC 是等边三角形，故∠BCE是直角三角形，根据勾股定理即可得出CE 的长．解：连接AC ，CE ，∠四边形ABCD 是菱形，∠A 、C 关于直线BD 对称，∠CE 的长即为AP +PE 的最小值，∠120BCD ∠=︒，∠60ABC ∠=︒，∠∠ABC 是等边三角形，∠E 是AB 的中点，∠CE AB ⊥，112122BE BC ==⨯=∠CE ==【点拨】本题考查了轴对称-最短路线问题，熟知菱形的性质及两点之间线段最短是解答此题的关键．14．258或5或8 【分析】∠ADE 是等腰三角形，所以可以分3种情况讨论：∠当AD ＝AE 时，∠ADE 是等腰三角形．作AM ∠BC ，垂足为M ，利用勾股定理列方程可得结论；∠当AD ＝DE 时，四边形ABED 是菱形，可得m ＝5；∠当AE ＝DE 时，此时C 与E 重合，m ＝8．解：分3种情况讨论：∠当AD ＝AE 时，如图1，过A作AM∠BC于M，∠AB＝AC＝5，BM＝12BC＝4，∠AM＝3，由平移性质可得AD＝BE＝m，∠AE＝m，EM＝4−m，在Rt∠AEM中，由勾股定理得：AE2＝AM2＋EM2，∠m2＝32＋（4−m）2，m＝258，∠当DE＝AD时，如图2，由平移的性质得AB DE∥，AB DE，∠四边形ABED是菱形，∠AD＝BE＝ED＝AB＝5，即m＝5；∠当AC＝DE时，如图3，此时C与E重合，m＝8；综上所述：当m＝258或5或8时，∠ADE是等腰三角形．故答案为：258或5或8．【点拨】本题考查了等腰三角形的性质、勾股定理、平移的性质，解题的关键是分三种情况求出BE的长；本题属于基础题，难度不大，但在解决该题时，部分同学会落掉两种情况，故在解决该题型题目时，全面考虑等腰三角形的三种情况是关键．15．1【分析】取OB中点E'，连接PE'，作射线FE'交AC于点P'．则PE＝PE'，当P与P'重合，P'、E'、F三点在同一直线上时，PF﹣PE'有最大值，即为FE'的长．解：如图，取OB中点E'，连接PE'，作射线FE'交AC于点P'．则PE＝PE'，∠PF﹣PE＝PF﹣PE'≤FE'，当P与P'重合，P'、E'、F三点在同一直线上时，PF﹣PE'有最大值，即为FE'的长，∠在菱形ABCD中，∠ABC＝120°，∠∠ABD＝60°，∠DAB＝60°，∠∠ABD为等边三角形．∠AB＝BD＝AD＝4．∠OD＝OB＝2．∠点E'为OB的中点，E'B＝1，AF＝3BF，∠BF1AB＝1，4∠∠ABD＝60°，∠∠BE'F为等边三角形，∠E'F＝FB＝1．故PF﹣PE的最大值为1．故答案为：1．【点拨】本题考查了轴对称﹣最大值问题、菱形的性质、等边三角形的判定与性质，熟练运用轴对称的性质和三角形三边关系是解题的关键．16．【分析】根据菱形ABCD 中，∠BAD ＝60°可知∠ABD 是等边三角形，结合三线合一可得∠BAB '＝30°，求出∠ABB '＝75°，可得∠EB 'B ＝∠EBB '＝45°，则∠BEB '是直角三角形，借助勾股定理求出BB '的长即可．解：∠菱形ABCD ，∠AB ＝AD ，AD //BC ，∠∠BAD ＝60°，∠∠ABC ＝120°，∠AB ′∠BD ，∠∠BAB '1302BAD =∠=︒， ∠将∠ABE 沿直线AE 翻折180°，得到∠AB ′E ，∠BE ＝B 'E ，AB ＝AB '，∠∠ABB '()118030752=⨯︒-︒=︒， ∠∠EBB '＝∠ABE ﹣∠ABB '＝120°﹣75°＝45°，∠∠EB 'B ＝∠EBB '＝45°，∠∠BEB '＝90°，在Rt∠BEB '中，由勾股定理得：BB '==故答案为：．【点拨】本题考查了翻折的性质、菱形的性质、等腰三角形的性质、以及勾股定理等知识，明确翻折前后对应线段相等是解题的关键．17． 43##113 32 【分析】连接GE ，根据点E 是BC 的中点以及翻折的性质可以求出BE ＝EF ＝EC ，然后利用“HL ”证明GFE 和GCE 全等，根据全等三角形对应边相等即可得证FG ＝CG ，设GC ＝x ，表示出AG 、DG ，然后在Rt ADG 中，利用勾股定理列式进行计算即可得解；先判断出EF AC ⊥时，GEF △的周长最小，最后用勾股定理即可得出结论．解：∠如图，连接GE ，∠E 是BC 的中点，∠BE ＝EC ，∠ABE △沿AE 折叠后得到AFE △，∠BE ＝EF ，∠EF ＝EC ，∠在矩形ABCD 中，∠∠C ＝90°，∠∠EFG ＝90°，∠在Rt GFE 和Rt GCE 中，EG EG EF EC =⎧⎨=⎩∠()GFE GCE HL ≌△△， ∠GF ＝GC ；设GC x =，则3AG x =+，3DG x =-，在Rt ADG 中，2224(3)(3)x x +-=+，解得x ＝43，即43GC =； ∠如图：由折叠知，∠AFE ＝∠B ＝90°，EF ＝BE ，∠4EF CE BE CE BC AD +=+===，∠当CF 最小时，CEF △的周长最小，∠CF AC AF ≥-，∠当点A ，F ，C 在同一条直线上时，CF 最小，由折叠知，AF ＝AB ＝3，在Rt ABC 中，AB ＝3，BC ＝AD ＝4，∠AC ＝5，∠2CF AC AF =-=，在Rt CEF 中，222EF CF CE +=，∠222(4)BE CF BE +=-，∠2222(4)BE BE +=-， ∠3=2BE ． 【点拨】此题是四边形综合题，主要考查了矩形的性质，折叠的性质，全等三角形的判定和性质，勾股定理，解题的关键是构造出直角三角形，利用勾股定理解决问题．18．6【分析】设点M 是PD 的中点，过点M 作直线P D ''与射线CA 、CB 分别交于点,P D ''，得到当点M 是PD 的中点时，CPD △的面积最小，再根据直角三角形的性质及三角形的面积公式求解即可．解：设点M 是PD 的中点，过点M 作直线P D ''与射线CA 、CB 分别交于点,P D ''，则点M 不是P D ''的中点当MD MP ''>时，在MD '上截取ME MP '=，连接DEPMP DME'∠=∠()PMP DME SAS '∴≅=P CD PCD P CDE S S S '''∴>四边形当MD MP ''<时，同理可得P CD PCD S S ''>∴当点M 是PD 的中点时，CPD △的面积最小如图，作DH AB ⊥于H则DHM PAM ≌,90,AM MH DHM PAM AP DH ∴=∠=∠=︒=90BHD =∴∠︒1AM =，3BM =1AM MH ∴==2BH ∴=在等腰Rt ABC △中，314CA BA ==+=45B C ∴∠=︒=∠45B BDH ∴∠=∠=︒2BH DH AP ∴===426CP AC AP ∴=+=+=过点D 作DK PC ⊥交于K∴四边形AKDH 是矩形2DK AH AM HM ∴==+=1162622CDP S CP DK ∴=⋅=⨯⨯= 故答案为：6 【点拨】本题考查了全等三角形的判定和性质、矩形的判定和性质、直角三角形的性质，熟练掌握知识点是解题的关键．19．【分析】过点E作EH∠BF于H，利用三角形的中位线定理以及直角三角形斜边中线定理证明∠BFE是顶角为120°的等腰三角形即可解决问题．解：过点E作EH∠BF于H．∠AD=AC，∠DAC=90°，CD=8，∠AD=AC∠DF=FC，AE=EC，∠EF=1AD，EF//AD，2∠∠FEC=∠DAC=90°，∠∠ABC=90°，AE=EC，∠BE=AE=EC∠EF=BE∠∠BAD=105°，∠DAC=90°，∠∠BAE=105°-90°=15°，∠∠EAB=∠EBA=15° ，∠∠CEB=∠EAB+∠EBA=30°，∠∠FEB=90°+30°=120°，∠∠EFB=∠EBF=30°，∠EH∠BF，EF，FH∠EH=1∠ BF=2FH，S △EFB =11··22BF EH =⨯=故答案为【点拨】本题考查三角形中位线定理，直角三角形斜边中线的性质，等腰三角形的判定和性质，三角形的面积等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．20．94或1 【分析】分∠CFE =90°和∠CEF =90°两种情况根据矩形的性质、勾股定理、全等三角形的判定及性质求解．解：∠如图，当∠CFE =90°时，∠四边形ABCD 是矩形，点E 是矩形ABCD 的边AB 的中点，AB =6，AD =4，∠∠P AE =∠PFE =∠EBC = 90°，AE =EF =BE =3，∠∠PFE +∠CFE =180°，∠P 、F 、C 三点一线，∠△EFC ∠△EBC ，∠FC =BC =4，EC ，∠FEC =∠BEC ，∠∠PEF +∠FEC =90°，设AP =x ，则PC =x +4，∠2222(4)35x x +=++,解得x =94； ∠如图，当∠CEF =90°∠∠CEB+2∠PEA =90°，∠∠CEB+∠PEA =90°-∠PEA，延长PE、CB，二线交于点G，∠AE=BE，∠P AE=∠GBE =90°，∠AEP=∠BEG，∠△P AE∠△GBE，∠P A=BG，∠AEP=∠BEG，∠∠G =90°-∠GEB= 90°-∠PEA，∠CEB+∠PEA =90°-∠PEA，∠∠G =∠CEB+∠PEA=∠CEB+∠GEB=∠CEG，∠CE=CBC+BG=BC+AP，∠5=4+AP，解得P A=1，故答案为：94或1．【点拨】本题考查了矩形的性质，折叠的性质，勾股定理，三角形全等的判定和性质，等腰三角形的判定和性质，熟练掌握矩形的性质，勾股定理是解题的关键．21．4【分析】将△DAF绕点A顺时针旋转90度到△BAF′位置，根据旋转的性质得出∠EAF′=45°，进而得出∠F AE∠∠EAF′，即可得出EF+EC+FC=FC+CE+EF′=FC+BC+BF′=DF+FC+BC=2BC=8，求出BC即可．解：将△DAF绕点A顺时针旋转90度到△BAF′位置，由题意可得出：△DAF ∠∠BAF ′，∠DF =BF ′，∠DAF =∠BAF ′，∠∠EAF ′=45°，在△F AE 和△EAF ′中,AF AF FAE EAF AE AE ''=⎧⎪∠=∠⎨⎪=⎩， ∠∠F AE ∠∠EAF ′（SAS ），∠EF =EF ′，∠∠ECF 的周长为8，∠EF +EC +FC =FC +CE +EF ′=FC +BC +BF ′=DF +FC +BC =2BC =8，∠BC =4，即正方形的边长为4．故答案为：4．【点拨】此题主要考查了旋转的性质以及全等三角形的判定与性质等知识，得出△F AE ∠∠EAF ′是解题关键．22．3【分析】根据翻折的性质和已知条件可得点F 和点A 重合，过点D 作DH BC ⊥，DG AB ⊥，垂足分别为H ，G ，得四边形BHDG 是正方形，设DG DH x ==，1x x +=，求出x 的值，进而可以解决问题．解：如图，由折叠可知：30E C ∠=∠=︒，FE FD ∴=，当30ADE ∠=︒时，260BFD E ∠=∠=︒，在Rt ABC 中，90ABC ∠=︒，30C ∠=︒，60A ∴∠=︒，∴点F 和点A 重合，如图，过点D 作DH BC ⊥，DG AB ⊥，垂足分别为H ，G ，由折叠可知：45CBD EBD ∠=∠=︒，DG DH ∴=，∴四边形BHDG 是正方形，设DG DH x ==，AG DG ∴==，AB AG BG AG GD x ∴=+=++，1x x +=，解得x =DG ∴=， 30C ∠=︒，CD DH∴==．23故答案为：3．【点拨】本题考查翻折变换，正方形的判定与性质、勾股定理等知识，解题的关键是学会利用参数构建方程解决问题，属于中考常考题型．23．【分析】过点H作HG∠CD于点G，连接DE，DE交FH于点Q，得到∠HGF=∠HGD=90°，推出∠HFG+∠FHG=90°，根据正方形ABCD中，AD=CD=BC=4，∠A=∠ADC=∠C=90°，得到四边形DAHG中，∠AHG=90°，推出四边形DAHG是矩形，得到GH=AD，GH=CD，根据折叠知，FH∠DE，得到∠DQF=90°，推出∠QFD+∠QDF=90°，得到∠GHF=∠CDE，根据∠HGF=∠C=90°，推出△DCE∠∠HGF(ASA)，得到FH=DE，根据E是BC中点，得到CE=12BC=2，推出DE FH=解：过点H作HG∠CD于点G，连接DE，DE交FH于点Q，则∠HGF=∠HGD=90°，∠∠HFG+∠FHG=90°，∠正方形ABCD中，AD=CD=BC=4，∠A=∠ADC=∠C=90°，∠四边形DAHG中，∠AHG=90°，∠四边形DAHG是矩形，∠GH=AD，∠GH=CD，由折叠知，FH∠DE，∠∠DQF=90°，∠∠QFD+∠QDF=90°，∠∠GHF=∠CDE，∠∠HGF=∠C=90°，∠∠DCE∠∠HGF(ASA)，∠FH=DE，∠E是BC中点，∠CE =12BC=2，∠DE ==，∠FH=故答案为【点拨】本题主要考查了正方形，折叠，矩形，全等三角形，勾股定理．解决问题的关键是熟练掌握正方形的性质，折叠的性质，矩形的判定和性质，全等三角形的判定和性质，勾股定理解直角三角形．24．【分析】延长BA 到点G ，使AG CF =，连接DG ，EF ，利用SAS 证明ADG CDF ≌，得ADG CDF ∠=∠，DG DF =，再证明()GDE FDE SAS △≌△，得=GE FE ，设AE x =，则6BE x =-，3EF x =+，再利用勾股定理即可解决问题．解：：如图，延长BA 到点G ，使AG CF =，连接DG ，EF ，∠ 四边形ABCD 是正方形，∠AD CD =，90DAG DCF ∠=∠=︒，90ADC BAD ABC ∠=∠=∠=︒，在ADG 和CDF 中，AD CD DAG DCF AG CF =⎧⎪∠=∠⎨⎪=⎩∠()ADG CDF SAS △≌△，∠ADG CDF ∠=∠，DG DF =，∠45EDF ∠=︒，。
北师大版数学九年级上学期期末备考压轴题培优：反比例函数(含答案)
期末备考压轴题培优：反比例函数1．如图，在直角坐标系xOy中，直线y＝mx与双曲线y＝相交于A（﹣1，a）、B两点，BC⊥x轴，垂足为C，△AOC的面积是1．（1）求m、n的值；（2）求直线AC的解析式．（3）点P在双曲线上，且△POC的面积等于△ABC面积的，求点P的坐标．2．如图，一次函数y＝﹣x+的图象与反比例函数y＝（k＞0）的图象交于A，B两点，过点A做x轴的垂线，垂足为M，△AOM面积为1．（1）求反比例函数的解析式；并直接写出不等式≤﹣+的解集．（2）在x轴上求一点P，使|P A﹣PB|的值最大，并求出其最大值和P点坐标．（3）连接OB，求三角形AOB的面积．3．如图，一次函数y＝﹣x+3的图象与反比例函数y＝（k≠0）在第一象限的图象交于A （1，a）和B两点，与x轴交于点C．（1）求反比例函数的解析式；（2）若点P在x轴上，且△APC的面积为5，求点P的坐标；（3）直接写出不等式﹣x+3＜的解集．4．已知A（a，﹣2a）、B（﹣2，a）两点是反比例函数y＝与一次函数y＝kx+b图象的两个交点．（1）求一次函数和反比例函数的解析式；（2）求△ABO的面积；（3）观察图象，直接写出不等式kx+b﹣＞0的解集．5．如图，在平面直角坐标系中，直线l1：y＝﹣x与反比例函数y＝的图象交于A，B两点（点A在点B左侧），已知A点的纵坐标是2；（1）求反比例函数的表达式；（2）根据图象直接写出﹣x＞的解集；（3）将直线l1：y＝x沿y向上平移后的直线l2与反比例函数y＝在第二象限内交于点C，如果△ABC的面积为30，求平移后的直线l2的函数表达式．6．如图所示，双曲线y＝（x＞0，k＞0）与直线y＝ax+b（a≠0，b为常数）交于A（2，4），B（m，2）两点．（1）求m的值；（2）若C点坐标为（n，0），当AC+BC的值最小时，求出n的值；（3）求△AOB的面积．7．如图，在平面直角坐标系xOy内，点P在直线y＝x上（点P在第一象限），过点P作P A⊥x轴，垂足为点A，且OP＝2．（1）求点P的坐标；＝6，求点Q的坐标；（2）如果点Q在直线OP上，且S△APQ（3）如果点M和点P都在反比例函数y＝（k≠0）图象上，过点M作MN⊥x轴，垂足为点N，如果△MNA和△OAP全等（点M、N、A分别和点O、A、P对应），求点M 的坐标．8．如图，在平面直角坐标系xOy中，反比例函数y＝（k≠0）的图象经过等边三角形BOC 的顶点B，OC＝2，点A在反比例函数图象上，连接AC，OA．（1）求反比例函数y＝（k≠0）的表达式；（2）若四边形ACBO的面积是3，求点A的坐标．9．如图，反比例函数y1＝的图象与一次函数y2＝ax+b的图象相交于点A（1，4）和B（﹣2，n）．（1）求反比例函数与一次函数的解析式；（2）请根据图象直接写出y1＜y2时，x的取值范围．10．如图，在平面直角坐标系中，已知点A（8，1），B（0，﹣3），反比例函数（x＞0）的图象经过点A，动直线x＝t（0＜t＜8）与反比例函数的图象交于点M，与直线AB交于点N．（1）求k的值；（2）当t＝4时，求△BMA面积；（3）若MA⊥AB，求t的值．12（1）求A、B两点的坐标和反比例函数的解析式；（2）求△AOB的面积．12．如图1，点A（0，8）、点B（2，a）在直线y＝﹣2x+b上，反比例函数y＝（x＞0）的图象经过点B．（1）求a和k的值；（2）将线段AB向右平移m个单位长度（m＞0），得到对应线段CD，连接AC、BD．①如图2，当m＝3时，过D作DF⊥x轴于点F，交反比例函数图象于点E，求E点的坐标；②在线段AB运动过程中，连接BC，若△BCD是等腰三形，求所有满足条件的m的值．12两点．（1）求反比例函数的解析式；（2）观察图象，直接写出使一次函数值不大于反比例函数值的x的取值范围；（3）求△AOB的面积．14．如图，一次函数y＝k1x﹣3（k1＞0）的图象与x轴、y轴分别交于A，B两点，与反比例函y＝（k2＞0）的图象交于C，D两点，作CE⊥y轴，垂足为点E，作DF⊥y轴，垂足为点F，已知CE＝1．（1）①直接写出点C的坐标（用k1来表示）②k2﹣k1＝；（2）若B为AC的中点，求反比例函数的表达式；（3）在（2）的条件下，设点M是x轴负半轴上一点，将线段MF绕点M旋转90°，得到线段MN，当点M滑动时，点N能否在反比例函数的图象上？如果能，求出点N的坐标；如果不能，请说明理由．15．对于一个函数给出如下定义：对于函数y，当a≤x≤b，函数值y满足c≤y≤d，且满足k（b﹣a）＝d﹣c，则称此函数为“k属函数”．例如：正比例函数y＝﹣3x，当1≤x≤3，﹣9≤y≤﹣3，则k（3﹣1）＝﹣3﹣（﹣9），求得：k＝3，所以函数y＝﹣3x为“3属函数”．（1）反比例函数y＝（1≤x≤5）为“k属函数”，求k的值；（2）若一次函数y＝ax﹣1（1≤x≤5）为“2属函数”，求a的值．16．如图，已知一次函数y＝kx+b的图象交反比例函数的图象于点A（2，﹣4）和点B（n，﹣2），交x轴于点C．（1）求这两个函数的表达式；（2）求△AOB的面积；（3）请直接写出使一次函数值大于反比例函数值的x的范围．17．如图，在平面直角坐标系中，直线y＝k1x（x≥0）与双曲线y＝（x＞0）相交于P （2，4），已知点A、B的坐标分别为（4，0）、（0，3），连结AB．将Rt△AOB沿OP方向平移，得到△A′PB′，点O与点P是对应点．过点A′作A′C∥y轴交双曲线于点C．（1）求k1、k2的值；（2）求点C的坐标；（3）判断四边形PCA′B′是否为平行四边形，请说明理由．18．探索函数y＝x+（x＞0）的图象和性质．已知正比例函数y＝x与反比例函数y＝在第一象限内的图象如图所示．若P为函数y＝x+（其中x＞0）图象上任意一点，过P作PC垂直于x轴且与已知函数的图象、x轴分别交于点A、B、C，则PC＝x+＝AC+BC，从而发现下述结论：“点P可以看作点A沿竖直方向向上平移BC个长度单位（P A＝BC）而得到”．（1）根据该结论，在图中作出函数y＝x+（x＞0）图象上的一些点，并画出该函数的图象；（2）观察图象，写出函数y＝x+（x＞0）两条不同类型的性质．19．如图，在平面直角坐标系xOy中，函数的图象经过点A（﹣1，6），直线y ＝mx﹣2与x轴交于点B（﹣1，0）．（1）求k，m的值；（2）过第二象限的点P（n，﹣2n）作平行于x轴的直线，交直线y＝mx﹣2于点C，交函数的图象于点D．①当n＝﹣1时，判断线段PD与PC的数量关系，并说明理由；②若PD≥2PC，结合函数的图象，直接写出n的取值范围．参考答案1．解：（1）∵直线y＝mx与双曲线y＝相交于A（﹣1，a）、B两点，∴B点横坐标为1，即C（1，0），∵△AOC的面积为1，∴A（﹣1，2），将A（﹣1，2）代入y＝mx，y＝可得m＝﹣2，n＝﹣2；（2）设直线AC的解析式为y＝kx+b，∵y＝kx+b经过点A（﹣1，2）、C（1，0）∴，解得k＝﹣1，b＝1，∴直线AC的解析式为y＝﹣x+1；（3）∵A（﹣1，2），C（1，0），∴B（1，﹣2），∴S＝×2×2＝2，△ABC∵△POC的面积等于△ABC面积的，＝，∴S△POC＝OC•|y P|，∵S△POC∴＝•|y P|，解得y P＝±1，∴P（﹣2，1）或（2，﹣1）．2．解：（1）∵反比例函数y＝（k＞0）的图象过点A，过A点作x轴的垂线，垂足为M，△AOM面积为1，∴|k|＝1，∵k＞0，∴k＝2，故反比例函数的解析式为：y＝，由，解得或，∴A（1，2），B（4，），∴不等式≤﹣+的解集为1≤x≤4或x≤0；（2）一次函数y＝﹣x+的图象与x轴的交点即为P点，此时|P A﹣PB|的值最大，最大值为AB的长．∵A（1，2），B（4，），∴AB＝＝，∴|P A﹣PB|的最大值为；∵一次函数y＝﹣x+，令y＝0，则﹣x+＝0，解得x＝5，∴P点坐标为（5，0）；（3）∵P （5，0），∴OP ＝5，∴S △AOB ＝S △AOP ﹣S △BOP ＝×5×2﹣＝．3．解：（1）把点A （1，a ）代入y ＝﹣x +3，得a ＝2，∴A （1，2）把A （1，2）代入反比例函数y ＝，∴k ＝1×2＝2；∴反比例函数的表达式为y ＝；（2）∵一次函数y ＝﹣x +3的图象与x 轴交于点C ，∴C （3，0），设P （x ，0），∴PC ＝|3﹣x |，∴S △APC ＝|3﹣x |×2＝5，∴x ＝﹣2或x ＝8，∴P 的坐标为（﹣2，0）或（8，0）；（3）解得或，∴B （2，1），由图象可知：不等式﹣x +3＜的解集是0＜x ＜1或x ＞2．4．解：（1）∵A （a ，﹣2a ）、B （﹣2，a ）两点在反比例函数y ＝的图象上， ∴m ＝﹣2a •a ＝﹣2a ，解得a ＝1，m ＝﹣2，∴A （1，﹣2），B （﹣2，1），反比例函数的解析式为y ＝﹣．将点A （1，﹣2）、点B （﹣2，1）代入到y ＝kx +b 中， 得：，解得：，∴一次函数的解析式为y ＝﹣x ﹣1．（2）在直线y ＝﹣x ﹣1中，令y ＝0，则﹣x ﹣1＝0，解得x ＝﹣1，∴C （﹣1，0），∴S △AOB ＝S △AOC +S △BOC ＝×1×2+×1＝；（3）观察函数图象，发现：当x ＜﹣2或0＜x ＜1时，反比例函数图象在一次函数图象的上方，∴不等式kx +b ﹣＞0的解集为x ＜﹣2或0＜x ＜1．5．解：（1）∵直线l 1：y ＝﹣x 经过点A ，A 点的纵坐标是2，∴当y ＝2时，x ＝﹣4，∴A （﹣4，2），∵反比例函数y ＝的图象经过点A ，∴k ＝﹣4×2＝﹣8，∴反比例函数的表达式为y ＝﹣；（2）∵直线l 1：y ＝﹣x 与反比例函数y ＝的图象交于A ，B 两点， ∴B （4，﹣2），∴不等式﹣x ＞的解集为x ＜﹣4或0＜x ＜4；（3）如图，设平移后的直线l 2与x 轴交于点D ，连接AD ，BD ，∵CD ∥AB ，∴△ABC 的面积与△ABD 的面积相等，∵△ABC 的面积为30，∴S △AOD +S △BOD ＝30，即OD （|y A |+|y B |）＝30，∴×OD ×4＝30，∴OD ＝15，∴D（15，0），设平移后的直线l2的函数表达式为y＝﹣x+b，把D（15，0）代入，可得0＝﹣×15+b，解得b＝，∴平移后的直线l2的函数表达式为y＝﹣x+．6．解：（1）把A（2，4）代入y＝（x＞0，k＞0），∴k＝2×4＝8，∴反比例函数的解析式为y＝，把B（m，2）代入y＝得，2＝，解得m＝4；（2）由（1）可知：A（2，4），B（4，2），∴B点关于x轴的对称点B′（4，﹣2），连接AB′，交x轴与C，此时AC+BC＝AB′，AC+BC的值最小，设直线AB′的解析式为y＝mx+t，把A（2，4），B′（4，﹣2）代入得，解得：，∴直线AB′的解析式为y＝﹣3x+10，把（n，0）代入得y＝﹣3n+10，∴n＝；（3）把A（2，4），B（4，2）代入y＝ax+b得，解得，∴直线AB的解析式为y＝﹣x+6，∴直线AB 与x 轴的交点C （6，0），∴S △AOB ＝S △AOC ﹣S △BOC ＝×6×4﹣×6×2＝6．7．解：（1）设AP ＝h ，则OA ＝2h ，由勾股定理得，OP 2＝AP 2+OA 2，即（2）2＝h 2+（2h ）2， 解得，h ＝2，∴AP ＝h ＝2，则OA ＝2h ＝4，∴点P 的坐标为（4，2）；（2）设点Q 到AP 的距离为a ，由题意得，×2×a ＝6，解得，a ＝6，∴点Q 的横坐标为4﹣6或4+6，当x ＝4﹣6时，y ＝2﹣3，当x ＝4+6，y ＝2+3，综上所述，点Q 的坐标为（4﹣6，2﹣3）或（4+6，2+3）；（3））∵点P （4，2）在反比例函数y ＝的图象上，∴2＝，解得，k ＝8，∴y ＝，在Rt △P AO 中，∠P AO ＝90°，P A ＝2，AO ＝4，∵∠MNA ＝90°，∴当△MNA 和△APO 全等时，分以下两种情况：①点N 在点A 的左侧时，MN ＝AO ＝4，AN ＝AP ＝2，∴ON ＝OA ﹣AN ＝4﹣2＝2，∴M（2，4），且点M在反比例函数y＝的图象上．②点N在点A的右侧时，AO＝MN＝4，AN＝AP＝2，∴ON＝AN+AO＝4+2＝6．∴M（6，4），但点M不在反比例函数y＝的图象上，综合①②，满足条件的点M的坐标为（2，4）．8．解：（1）作BD⊥OC于D，∵△BOC是等边三角形，∴OB＝OC＝2，OD＝OC＝1，∴BD＝＝，＝OD×BD＝，∴S△OBDS＝|k|，△OBD∴|k|＝，∵反比例函数y＝（k≠0）的图象在一三象限，∴k＝，∴反比例函数的表达式为y＝；＝OC•BD＝＝，（2）∵S△OBC∴S＝3﹣＝2，△AOC＝OC•y A＝2，∵S△AOC∴y A＝2，把y＝2代入y＝，求得x＝，∴点A的坐标为（，2）．9．解：（1）∵反比例函数y1＝的图过点A（1，4），∴4＝，即k＝4，∴反比例函数的解析式为：y1＝，∵反比例函数y1＝的图象过点B（﹣2，n），∴n＝＝﹣2，∴B（﹣2，﹣2），∵一次函数y2＝ax+b的图象过点A（1，4）和点B（﹣2，﹣2），∴，解得：∴一次函数的解析式为：y2＝2x+2；（2）由图象可知：当﹣2＜x＜0或x＞1．10．解：（1）∵反比例函数（x＞0）的图象经过点A，∴1＝，解得k＝8；（2）设直线AB 的解析式为y ＝kx +b ，把点A （8，1），B （0，﹣3）代入得， 解得，∴直线AB 的解析式为y ＝x ﹣3，当t ＝4时，则M （4，2），N （4，﹣1），∴MN ＝2﹣（﹣1）＝3，∴S △BMA ＝×3×8＝12；（3）由题意可知M （t ，），∵A （8，1），B （0，﹣3），∴MA 2＝（t ﹣8）2+（﹣1）2，MB 2＝t 2+（+3）2，AB 2＝82+（1+3）2＝80， ∵MA ⊥AB ，∴MB 2＝MA 2+AB 2，即t 2+（+3）2＝（t ﹣8）2+（﹣1）2+80，整理得：2t +＝17，解得t ＝或t ＝8（舍去），故若MA ⊥AB ，t 的值为．11．解：（1）分别把A （1，m ）、B （4，n ）代入y 1＝﹣x +5，得m ＝﹣1+5＝4，n ＝﹣4+5＝1，所以A 点坐标为（1，4），B 点坐标为（4，1），把A （1，4）代入y 2＝，得k ＝1×4＝4，所以反比例函数解析式为y 2＝；（2）如图，设一次函数图象与x 轴交于点C ，当y ＝0时，﹣x +5＝0，解得x ＝5，则C 点坐标为（5，0），所以S △AOB ＝S △AOC ﹣S △BOC＝×5×4﹣×5×1＝7.5．12．解：（1）∵点A（0，8）在直线y＝﹣2x+b上，∴﹣2×0+b＝8，∴b＝8，∴直线AB的解析式为y＝﹣2x+8，将点B（2，a）代入直线AB的解析式y＝﹣2x+8中，得﹣2×2+8＝a，∴a＝4，∴B（2，4），将B（2，4）代入反比例函数解析式y＝（x＞0）中，得k＝xy＝2×4＝8；（2）①由（1）知，B（2，4），k＝8，∴反比例函数解析式为y＝，当m＝3时，将线段AB向右平移3个单位长度，得到对应线段CD，∴D（2+3，4），即D（5，4），∵DF⊥x轴于点F，交反比例函数y＝的图象于点E，∴E（5，）；②如图，∵将线段AB向右平移m个单位长度（m＞0），得到对应线段CD，∴CD＝AB，AC＝BD＝m，∵A（0，8），B（2，4），∴C（m，8），D（（m+2，4），∵△BCD是以BC为腰的等腰三形，当BC＝CD时，BC＝AB，∴点B在线段AC的垂直平分线上，∴m＝2×2＝4，当BC＝BD时，B（2，4），C（m，8），∴BC＝，∴＝m，∴m＝5，当BD＝AB时，m＝AB＝＝2，综上所述，△BCD是以BC为腰的等腰三角形，满足条件的m的值为4或5或2．13．解：（1）∵点A（2，4）在反比例函数y2＝的图象上，∴k＝2×4＝8，∴反比例函数的解析式为y2＝．（2）∵点B（﹣4，n）在反比例函数y2＝的图象上，∴n＝＝﹣2，∴点B的坐标为（﹣4，﹣2）．观察函数图象，发现：使一次函数值不大于反比例函数值的x的取值范围为x≤﹣4或0＜x≤2．（3）将点A（2，4）、B（﹣4，﹣2）代入到y1＝ax+b中，得：解得：，∴一次函数的解析式为y＝x+2，令y＝0，求得x＝﹣2，∴S△AOB＝S△AOC+S△BOC＝×2×2+2×4＝6．14．解：（1）如图1，∵CE⊥y轴于点E且CE＝1，∴C的横坐标为1，当x＝﹣1时，y＝﹣k1﹣3∴C（﹣1，﹣k1﹣3），∵C在反比例函数的图象上，∴﹣1×（﹣k1﹣3）＝k2，∴k2﹣k1＝3；故答案为（﹣1，﹣k1﹣3），3；（2）如图1，∵CE⊥y轴，DF⊥y轴，∴CE∥DF，∵B为AC的中点，∴AB＝BC，∵∠AOB＝∠BEC＝90°，∠ABO＝∠CBE，∴△ABO≌△CBE（AAS），∴AO＝CE＝1，∴A（1，0），当x＝1时，y＝k1+3＝0，∴k1＝3，由（1）得：k2﹣k1＝3，∴k2＝6；∴反比例函数的解析式：y＝；（3）当点M滑动时，点N能在反比例函数的图象上如图2，MF＝MN，∠FMN＝90°过N作NH⊥x轴于H，易得：△MNH≌△FMO，∴FO＝MH，OM＝NH，由（2）知：反比例函数的解析式：y＝；设D（m，），∵tan∠ABO＝＝＝，∴＝，解得：m＝2，m＝﹣1（舍去），∴N（2，3），∴OF＝MH＝3，设M（x，0），∴N（x+3，x），当点N落在反比例函数的图象上时，x（x+3）＝6，x2+3x﹣6＝0，解得x＝（舍去），x＝，∴点N的坐标为（，）．15．解：（1）∵反比例函数y＝中，k＝5＞0，∴y随x的增大而减小，当1≤x≤5时，1≤y≤5，∴k（5﹣1）＝5﹣1，∴k＝1；（2）①a＞0时，对于一次函数y＝ax﹣1，y随x增大而增大，当1≤x≤5时，a﹣1≤y≤5a﹣1，∴k（5﹣1）＝4a，∵k＝2，∴a＝2；②当a＜0时，y随x增大而减小，当1≤x≤5时，a﹣1≤y≤5a﹣1，∴k（5﹣1）＝﹣4a，∵k＝2，∴a＝﹣2．16．解：（1）把A（2，﹣4）的坐标代入得：，∴4﹣2m＝﹣8，反比例函数的表达式是；把B（n，﹣2）的坐标代入得，解得：n＝4，∴B点坐标为（4，﹣2），把A（2，﹣4）、B（4，﹣2）的坐标代入y＝kx+b得，解得，∴一次函数表达式为y＝x﹣6；（2）当y＝0时，x＝0+6＝6，∴OC＝6，∴△AOB的面积＝×6×4﹣×6×2＝6；（3）由图象知，一次函数值大于反比例函数值的x的范围为0＜x＜2或x＞4．17．解：（1）∵直线y＝k1x过点P（2，4），∴4＝2k1，∴k1＝2，∵双曲线y＝（x＞0）过点P（2，4），∴k2＝2×4＝8；（2）由平移知，点O（0，2）向右平移2个单位，再向上平移4个单位得到点P（2，4），∴点A（4，0）也向右平移2个单位，再向上平移4个单位得到点A'（6，4），∵A'C∥y轴，∴点C的横坐标为6，由（1）知，k2＝8，双曲线的解析式为y＝，∵点C在双曲线y＝上，∴y＝＝，∴C（6，）；（3）四边形PCA′B′不是平行四边形，理由：∵B（0，3），∴OB＝3，由平移知，PB'＝OB＝3，PB'∥y轴，∵A'C∥y轴，∴PB'∥A'C，由（2）知，A'（6，4），C（6，），∴A'C＝4﹣＝≠PB'，∴四边形PCA′B′不是平行四边形．18．解：（1）如图所示：（2）函数两条不同类型的性质是：①图象是轴对称图形：②当0＜x＜1时，y随x的增大而减小，当x＞1时，y随x的增大而增大；③当x＝1时，函数y＝x+（x＞0）的最小值是2；19．解：（1）∵函数的图象经过点A（﹣1，6），∴k＝﹣6．∵直线y＝mx﹣2与x轴交于点B（﹣1，0），∴m＝﹣2．（2）①判断：PD＝2PC．理由如下：当n＝﹣1时，点P的坐标为（﹣1，2），∵y＝﹣2x﹣2交于于点C，且点P（﹣1，2）作平行于x轴的直线，∴点C的坐标为（﹣2，2），∵函数的图象于点D，且点P（﹣1，2）作平行于x轴的直线，点D的坐标为（﹣3，2）．∴PC＝1，PD＝2．∴PD＝2PC．②当PD＝2PC时，有两种情况，分别为：y＝2，或者y＝6．若PD≥2PC，0＜y≤2，或y≥6即0＜﹣2n≤2，或﹣2n≤6解得﹣1≤n＜0．或n≤﹣3。
北师大版九年级(上)期末数学试卷(含答案)
北师大版九年级（上）期末数学试卷及答案一、选择题（本大题共6小题，每小题3分，共18分，每小题只有一个正确选项） 1．（3分）下列既是轴对称图形又是中心对称图形的是( ) A ．菱形B ．平行四边形C ．等边三角形D ．等腰梯形2．（3分）若一元二次方程220x x --=的两根为1x ，2x ，则121(1)(1)x x x ++-的值是( ) A ．4B ．2C ．1D ．2-3．（3分）在如图所示的电路中，随机闭合开关1S ，2S ，3S 中的两个，能让灯泡1L 发光的概率是( )A ．12B ．13C ．14D ．254．（3分）如图，小李打网球时，球恰好打过网，且落在离网4m 的位置上，则球拍击球的高度h 为( )A ．0.6mB ．1.2mC ．1.3mD ．1.4m5．（3分）如图，把抛物线2y x =沿直线y x =平移2个单位后，其顶点在直线上的A 处，则平移后的抛物线解析式是( )A ．2(1)1y x =+-B ．2(1)1y x =++C ．2(1)1y x =-+D ．2(1)1y x =--6．（3分）如图，等边三角形ABC 的边长为4，点O 是ABC ∆的中心，120FOG ∠=︒，绕点O 旋转FOG ∠，分别交线段AB 、BC 于D 、E 两点，连接DE ，给出下列四个结论：①OD OE =；②ODE BDE S S ∆∆=；③四边形ODBE 的面积始终等于433；④BDE ∆周长的最小值为6．上述结论中正确的个数是( )A ．1B ．2C ．3D ．4二、填空题（本大题共6小题，每小题3分，共18分）7．（3分）已知α，β均为锐角，且满足21|sin |(tan 1)02αβ-+-=，则αβ+= ．8．（3分）已知一个正比例函数的图象与一个反比例函数的图象的一个交点为(1,3)，则另一个交点坐标是 ． 9．（3分）某校九（1）班的学生互赠新年贺卡，共用去1560张贺卡，则九（1）班有 名学生．10．（3分）如图，菱形ABCD 中，60DAB ∠=︒，DF AB ⊥于点E ，且DF DC =，连接FC ，则ACF ∠的度数为 度．11．（3分）如图是由一些大小相同的小正方体组成的简单几何体的主视图和俯视图，若组成这个几何体的小正方体的块数为n ，则n 的所有可能的值之和为 ．12．（3分）如图，矩形ABCD 中，6AB =，43AD =，点E 是BC 的中点，点F 在AB 上，2FB =，P 是矩形上一动点．若点P 从点F 出发，沿F A D C →→→的路线运动，当30FPE ∠=︒时，FP 的长为 ．三、解答题（本大题共5小题，每小题6分，共30分） 13．（6分）解方程： （1）2(21)9x +=； （2）2(4)3(4)x x +=+．14．（6分）如图，在ABCD 中，AE BC ⊥，CF AD ⊥，E ，F 分别为垂足． （1）求证：BE DF =；（2）求证：四边形AECF 是矩形．15．（6分）如图，反比例函数(0)k y k x=≠的图象与正比例函数2y x =的图象相交于点(1,)A a ，B 两点，点C 在第四象限，//CA y 轴，90ABC ∠=︒． （1）求k 的值及B 点坐标； （2）求ABC ∆的面积．16．（6分）如图，在矩形ABCD 中，点E 为AD 的中点，请只用无刻度的直尺作图 （1）如图1，在BC 上找点F ，使点F 是BC 的中点；（2）如图2，在AC 上取两点P ，Q ，使P ，Q 是AC 的三等分点．17．（6分）我国于2019年6月5日首次完成运载火箭海上发射，这标志着我国火箭发射技术达到了一个崭新的高度．如图，运载火箭从海面发射站点M 处垂直海面发射，当火箭到达点A 处时，海岸边N 处的雷达站测得点N 到点A 的距离为8千米，仰角为30︒．火箭继续直线上升到达点B 处，此时海岸边N 处的雷达测得B 处的仰角增加15︒，求此时火箭所在点B 处与发射站点M 处的距离．（结果精确到0.1千米）（参考数据：2 1.41≈，3 1.73)≈四、（本大题共3小题，每小题8分，共24分）18．（8分）已知如图，在ABC ∆中，BD 平分ABC ∠交AC 于点D ，点E 在AB 上，且2BD BE BC =； （1）求证：BDE C ∠=∠； （2）求证：2AD AE AB =．19．（8分）如图，//AB CD ，点E ，F 分别在AB ，CD 上，连接EF ，AEF ∠、CFE ∠的平分线交于点G ，BEF ∠、DFE ∠的平分线交于点H ．（1）求证：四边形EGFH 是矩形；（2）小明在完成（1）的证明后继续进行了探索，过G 作//MN EF ，分别交AB ，CD 于点M ，N ，过H 作//PQ EF ，分别交AB ，CD 于点P ，Q ，得到四边形MNQP ，此时，他猜想四边形MNQP 是菱形，他的猜想是否正确，请予以说明．20．（8分）小聪同学周六到某欢乐谷玩迷宫游戏，从迷宫口A到达迷宫口D有多个路口，如图所示（迷宫的一部分），规定从迷宫口A到达D处不能重复走同一路线，且小聪走每一条路线的可能性相同．（1）请用画树状图的方法，求小聪同学从迷宫口A到达D处所走的所有可能路线；（2）求小聪同学从迷宫口A到达D处经过路口B的概率．五、（本大题共2小题，每小题9分，共18分）21．（9分）某商店购进一批成本为每件30元的商品，经调查发现，该商品每天的销售量y（件)与销售单价x（元)之间满足一次函数关系，其图象如图所示．（1）求该商品每天的销售量y与销售单价x之间的函数关系式；（2）若商店按单价不低于成本价，且不高于50元销售，则销售单价定为多少，才能使销售该商品每天获得的利润w（元)最大？最大利润是多少？（3）若商店要使销售该商品每天获得的利润不低于800元，则每天的销售量最少应为多少件？22．（9分）对于两个不相等的有理数a，b，我们规定符号{max a，}b表示a，b中的较大值，如{2max，3}2-=，{1max-，0}0=．请解答下列问题：（1）2{1,1}5max--=；（2）如果{max x，2}x x-=，求x的取值范围；（3）如果{max x ，2}2|1|5x x -=--，求x 的值． 六、（本大题共12分）23．（12分）如图，抛物线2(0)y ax bx a =+≠经过点(2,0)A ，点(3,3)B ，BC x ⊥轴于点C ，连接OB ，等腰直角三角形DEF 的斜边EF 在x 轴上，点E 的坐标为(4,0)-，点F 与原点重合 （1）求抛物线的解析式并直接写出它的对称轴；（2）DEF ∆以每秒1个单位长度的速度沿x 轴正方向移动，运动时间为t 秒，当点D 落在BC 边上时停止运动，设DEF ∆与OBC ∆的重叠部分的面积为S ，求出S 关于t 的函数关系式；（3）点P 是抛物线对称轴上一点，当ABP ∆是直角三角形时，请直接写出所有符合条件的点P 坐标．参考答案与试题解析一、选择题（本大题共6小题，每小题3分，共18分，每小题只有一个正确选项） 1．（3分）下列既是轴对称图形又是中心对称图形的是( ) A ．菱形B ．平行四边形C ．等边三角形D ．等腰梯形【分析】根据轴对称图形和中心对称图形的概念，对各选项分析判断即可得解．把一个图形绕某一点旋转180︒，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形；如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形．【解答】解：A ．菱形既是轴对称图形又是中心对称图形，故此选项符合题意；B ．平行四边形是中心对称图形，不是轴对称图形，故此选项不合题意；C ．等边三角形不是中心对称图形，是轴对称图形，故此选项不合题意；D ．等腰梯形是轴对称图形不是中心对称图形，故此选项不合题意．故选：A ．【点评】本题考查了中心对称图形和轴对称图形的定义，能熟记中心对称图形和轴对称图形的定义是解此题的关键． 2．（3分）若一元二次方程220x x --=的两根为1x ，2x ，则121(1)(1)x x x ++-的值是( ) A ．4B ．2C ．1D ．2-【分析】根据根与系数的关系得到121x x +=，122x x =-，然后利用整体代入的方法计算121(1)(1)x x x ++-的值． 【解答】解：根据题意得121x x +=，122x x =-， 所以1211212(1)(1)111(2)4x x x x x x x ++-=++-=+--=． 故选：A ．【点评】本题考查了根与系数的关系：若1x ，2x 是一元二次方程20(0)ax bx c a ++=≠的两根时，12b x x a+=-，12cx x a=． 3．（3分）在如图所示的电路中，随机闭合开关1S ，2S ，3S 中的两个，能让灯泡1L 发光的概率是( )A ．12 B ．13C ．14D ．25【分析】首先根据题意画出树状图，然后由树状图求得所有等可能的结果与能让灯泡1L 发光的情况，再利用概率公式求解即可求得答案． 【解答】解：画树状图得：共有6种等可能的结果，能让灯泡1L 发光的有2种情况，∴能让灯泡1L 发光的概率为2163=， 故选：B ．【点评】本题考查了列表法、树状图法求概率，画出树状图得出所有可能出现的结果情况是正确解答的关键． 4．（3分）如图，小李打网球时，球恰好打过网，且落在离网4m 的位置上，则球拍击球的高度h 为( )A ．0.6mB ．1.2mC ．1.3mD ．1.4m【分析】利用平行得出三角形相似，运用相似比即可解答． 【解答】解：//AB DE ，∴AB CBDE CD =， ∴40.87h=， 1.4h m ∴=，经检验： 1.4h =是原方程的根． 故选：D ．【点评】此题主要考查了相似三角形的判定，根据已知得出AB CBDE CE=是解决问题的关键． 5．（3分）如图，把抛物线2y x =沿直线y x =平移2个单位后，其顶点在直线上的A 处，则平移后的抛物线解析式是( )A ．2(1)1y x =+-B ．2(1)1y x =++C ．2(1)1y x =-+D ．2(1)1y x =--【分析】首先根据A 点所在位置设出A 点坐标为(,)m m 再根据2AO =，利用勾股定理求出m 的值，然后根据抛物线平移的性质：左加右减，上加下减可得解析式． 【解答】解：A 在直线y x =上，∴设(,)A m m ，2OA =222(2)m m ∴+=，解得：1(1m m =±=-舍去）， 1m ∴=，(1,1)A ∴，∴平移后的抛物线解析式为：2(1)1y x =-+，故选：C ．【点评】此题主要考查了二次函数图象的几何变换，关键是求出A 点坐标，掌握抛物线平移的性质：左加右减，上加下减．6．（3分）如图，等边三角形ABC 的边长为4，点O 是ABC ∆的中心，120FOG ∠=︒，绕点O 旋转FOG ∠，分别交线段AB 、BC 于D 、E 两点，连接DE ，给出下列四个结论：①OD OE =；②ODE BDE S S ∆∆=；③四边形ODBE 的433④BDE ∆周长的最小值为6．上述结论中正确的个数是( )A ．1B ．2C ．3D ．4【分析】连接OB 、OC ，如图，利用等边三角形的性质得30ABO OBC OCB ∠=∠=∠=︒，再证明BOD COE ∠=∠，于是可判断BOD COE ∆≅∆，所以BD CE =，OD OE =，则可对①进行判断；利用BOD COE S S ∆∆=得到四边形ODBE 的面积14333ABC S ∆==则可对③进行判断；作OH DE ⊥，如图，则DH EH =，计算出23ODE S ∆=，利用ODE S ∆随OE 的变化而变化和四边形ODBE 的面积为定值可对②进行判断；由于BDE ∆的周长443BC DE DE OE =+=+=，根据垂线段最短，当OE BC ⊥时，OE 最小，BDE ∆的周长最小，计算出此时OE的长则可对④进行判断．【解答】解：连接OB 、OC ，如图， ABC ∆为等边三角形， 60ABC ACB ∴∠=∠=︒，点O 是ABC ∆的中心，OB OC ∴=，OB 、OC 分别平分ABC ∠和ACB ∠，30ABO OBC OCB ∴∠=∠=∠=︒120BOC ∴∠=︒，即120BOE COE ∠+∠=︒，而120DOE ∠=︒，即120BOE BOD ∠+∠=︒， BOD COE ∴∠=∠，在BOD ∆和COE ∆中 BOD COEBO COOBD OCE ∠=∠⎧⎪=⎨⎪∠=∠⎩， BOD COE ∴∆≅∆，BD CE ∴=，OD OE =，所以①正确； BOD COE S S ∆∆∴=，∴四边形ODBE 的面积21134433343OBC ABC S S ∆∆===⨯⨯=，所以③正确； 作OH DE ⊥，如图，则DH EH =，120DOE ∠=︒，30ODE OEH ∴∠=∠=︒，12OH OE ∴=，332HE OH OE ==， 3DE OE ∴=，21133224ODE S OE OE OE ∆∴=⋅⋅=， 即ODE S ∆随OE 的变化而变化，而四边形ODBE 的面积为定值，ODE BDE S S ∆∆∴≠；所以②错误；BD CE =，BDE ∴∆的周长443BD BE DE CE BE DE BC DE DE OE =++=++=+=+=+，当OE BC ⊥时，OE 最小，BDE ∆的周长最小，此时233OE =， BDE ∴∆周长的最小值426=+=，所以④正确．故选：C ．【点评】本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了等边三角形的性质和全等三角形的判定与性质．二、填空题（本大题共6小题，每小题3分，共18分）7．（3分）已知α，β均为锐角，且满足21|sin |(tan 1)02αβ-+-=，则αβ+= 75︒ ． 【分析】直接利用绝对值的非负性和偶次方的非负性得出1sin 02α-=，tan 10β-=，再结合特殊角的三角函数值得出答案．【解答】解：21|sin |(tan 1)02αβ-+-=， 1sin 02α∴-=，tan 10β-=， 1sin 2α∴=，tan 1β=， 30α∴=︒，45β=︒，则304575αβ+=︒+︒=︒．故答案为：75︒．【点评】此题主要考查了特殊角的三角函数值以及非负数的性质，正确记忆特殊角的三角函数值是解题关键．8．（3分）已知一个正比例函数的图象与一个反比例函数的图象的一个交点为(1,3)，则另一个交点坐标是(1,3)-- ．【分析】反比例函数的图象是中心对称图形，则经过原点的直线的两个交点一定关于原点对称．【解答】解：反比例函数的图象与经过原点的直线的两个交点一定关于原点对称，∴另一个交点的坐标与点(1,3)关于原点对称，∴该点的坐标为(1,3)--．故答案为：(1,3)--．【点评】本题主要考查了反比例函数图象的中心对称性，要求同学们要熟练掌握关于原点对称的两个点的坐标的横、纵坐标都互为相反数．9．（3分）某校九（1）班的学生互赠新年贺卡，共用去1560张贺卡，则九（1）班有 40 名学生．【分析】设九（1）班有x 名学生，则每名学生需送出(1)x -张新年贺卡，利用九（1）班共用去贺卡的数量=人数⨯每人送出新年贺卡的数量，即可得出关于x 的一元二次方程，解之取其正值即可得出结论．【解答】解：设九（1）班有x 名学生，则每名学生需送出(1)x -张新年贺卡，依题意得：(1)1560x x -=，整理得：215600x x --=，解得：140x =，239x =-（不合题意，舍去），∴九（1）班有40名学生．故答案为：40．【点评】本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键．10．（3分）如图，菱形ABCD 中，60DAB ∠=︒，DF AB ⊥于点E ，且DF DC =，连接FC ，则ACF ∠的度数为 15度．【分析】利用菱形的性质得出DCB∠的度数，进而得出答案．∠的度数，再利用等腰三角形的性质得出DCF【解答】解：菱形ABCD中，60∠=︒，DF DC=，DAB∠=∠，AB CD，DFC DCF∴∠=︒，//60BCD⊥于点E，DF AB90∴∠=︒，FDCDFC DCF∴∠=∠=︒，45菱形ABCD中，DCA ACB∠=∠，∴∠=∠=︒，30DCA ACB︒-︒=︒．ACF∴∠的度数为：453015故答案为：15︒．【点评】此题主要考查了菱形的性质以及等腰三角形的性质等知识，得出45∠=∠=︒是解题关键．DFC DCF11．（3分）如图是由一些大小相同的小正方体组成的简单几何体的主视图和俯视图，若组成这个几何体的小正方体的块数为n，则n的所有可能的值之和为38．【分析】从俯视图中可以看出最底层小正方体的个数及形状，从主视图可以看出每一层小正方体的层数和个数，从而算出总的个数．【解答】解：主视图最右边可能有4或5或6个小正方体；由主视图最左边看到只有一列，俯视图也只有一列，则左边有一个小正方体；主视图中间有两列，俯视图亦有两列，则中间可以有3或4个小正方形．n∴的值可能为：1438++=，16411++=，++=，15410++=，1539++=，16310++=，1449则n的所有可能的值之和89101138=+++=．故本题答案为：38．【点评】本题考查对三视图的理解应用及空间想象能力．可从主视图上分清物体的上下和左右的层数，从俯视图上分清物体的左右和前后位置，综合上述分析数出小立方块的个数．12．（3分）如图，矩形ABCD 中，6AB =，43AD =，点E 是BC 的中点，点F 在AB 上，2FB =，P 是矩形上一动点．若点P 从点F 出发，沿F A D C →→→的路线运动，当30FPE ∠=︒时，FP 的长为 4或8或43 ．【分析】如图，连接DF ，AE ，DE ，取DF 的中点O ，连接OA 、OE ．以O 为圆心画O 交CD 于3P ．只要证明12330EPF FP F FP E ∠=∠=∠=︒，即可推出14FP =，28FP =，343FP=解决问题． 【解答】解：如图，连接DF ，AE ，DE ，取DF 的中点O ，连接OA 、OE ．以O 为圆心OE 的长度为半径，画O 交CD 于3P ．四边形ABCD 是矩形，90BAD B ∴∠=∠=︒，2BF =，23BE =4AF =，43AD =3tan tan FEB ADF ∴∠=∠=， 30ADF FEB ∴∠=∠=︒， 易知4EF OF OD ===，OEF ∴∆是等边三角形，12330EPF FP F FP E ∴∠=∠=∠=︒， 14FP ∴=，28FP=，343FP =， 故答案为4或8或3【点评】本题考查矩形的性质、锐角三角函数、圆的有关知识、等边三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造特殊三角形解决问题，属于中考填空题中的压轴题．三、解答题（本大题共5小题，每小题6分，共30分）13．（6分）解方程：（1）2(21)9x +=；（2）2(4)3(4)x x +=+．【分析】（1）两边直接开平方，继而得到两个关于x 的一元一次方程，解之即可；（2）先移项，再利用提公因式法将方程的左边因式分解，继而得出两个关于x 的一元一次方程，再进一步求解即可．【解答】解：（1）2(21)9x +=，213x ∴+=或213x +=-，解得11x =，22x =-；（2）2(4)3(4)x x +=+，2(4)3(4)0x x ∴+-+=，则(4)(1)0x x ++=，40x ∴+=或10x +=，解得14x =-，21x =-．【点评】本题主要考查解一元二次方程，解一元二次方程常用的方法有：直接开平方法、因式分解法、公式法及配方法，解题的关键是根据方程的特点选择简便的方法．14．（6分）如图，在ABCD 中，AE BC ⊥，CF AD ⊥，E ，F 分别为垂足．（1）求证：BE DF =；（2）求证：四边形AECF 是矩形．【分析】（1）由平行四边形的性质得出B D ∠=∠，AB CD =，//AD BC ，由已知得出90AEB AEC CFD AFC ∠=∠=∠=∠=︒，由AAS 证明ABE CDF ∆≅∆即可；（2）证出90EAF AEC AFC ∠=∠=∠=︒，即可得出结论．【解答】（1）证明：四边形ABCD 是平行四边形，B D ∴∠=∠，AB CD =，//AD BC ，AE BC ⊥，CF AD ⊥，90AEB AEC CFD AFC ∴∠=∠=∠=∠=︒，在ABE ∆和CDF ∆中，B D AEB CFD AB CD ∠=∠⎧⎪∠=∠⎨⎪=⎩，()ABE CDF AAS ∴∆≅∆，BE DF ∴=；（2）证明：//AD BC ，90EAF AEB ∴∠=∠=︒，90EAF AEC AFC ∴∠=∠=∠=︒，∴四边形AECF 是矩形．【点评】本题考查了矩形的判定、平行四边形的性质、全等三角形的判定与性质；熟练掌握平行四边形的性质和矩形的判定是解题的关键．15．（6分）如图，反比例函数(0)k y k x=≠的图象与正比例函数2y x =的图象相交于点(1,)A a ，B 两点，点C 在第四象限，//CA y 轴，90ABC ∠=︒．（1）求k 的值及B 点坐标；（2）求ABC ∆的面积．【分析】（1）先把(1,)A a 代入2y x =中求出a 得到(1,2)A ；再把A 点坐标代入k y x=中可确定k 的值，然后利用反比例函数和正比例函数图象的性质确定B 点坐标；（2）设(1,)C t ，根据两点间的距离公式和勾股定理得到22222(11)(2)(11)(22)(2)t t +++++++=-，求出t 得到(1,3)C -，从而得到AC 的长，然后关键三角形面积公式求得即可．【解答】解：（1）把(1,)A a 代入2y x =得2a =，则(1,2)A ；把(1,2)A 代入k y x =得122k =⨯=， 点A 与点B 关于原点对称，(1,2)B ∴--；（2）//CA y 轴，C ∴点的横坐标为1，设(1,)C t ，90ABC ∠=︒．222BC AC AB ∴+=，即22222(11)(2)(11)(22)(2)t t +++++++=-，解得3t =-，(1,3)C ∴-，5AC ∴=，11()5(11)522ABC A B S AC x x ∆∴=-=⨯⨯+=． 【点评】本题考查了反比例函数与一次函数的交点问题：求反比例函数与一次函数的交点坐标，把两个函数关系式联立成方程组求解，若方程组有解则两者有交点，方程组无解，则两者无交点．也考查了待定系数法求函数解析式．16．（6分）如图，在矩形ABCD 中，点E 为AD 的中点，请只用无刻度的直尺作图（1）如图1，在BC 上找点F ，使点F 是BC 的中点；（2）如图2，在AC 上取两点P ，Q ，使P ，Q 是AC 的三等分点．【分析】（1）根据矩形的对角线相等且互相平分作出图形即可；（2）根据矩形的性质和三角形中位线定理作出图形即可．【解答】解：（1）如图1，连接AC 、BD 交于点O ，延长EO 交BC 于F ，则点F 即为所求；（2）如图2，BD 交AC 于O ，延长EO 交BC 于F ，连接EB 交AC 于P ，连接DF 交AC 于Q ，则P 、Q 即为所求．【点评】本题考查的是作图的应用，掌握矩形的性质和三角形中位线定理、正确作出图形是解题的关键．17．（6分）我国于2019年6月5日首次完成运载火箭海上发射，这标志着我国火箭发射技术达到了一个崭新的高度．如图，运载火箭从海面发射站点M 处垂直海面发射，当火箭到达点A 处时，海岸边N 处的雷达站测得点N 到点A 的距离为8千米，仰角为30︒．火箭继续直线上升到达点B 处，此时海岸边N 处的雷达测得B 处的仰角增加15︒，求此时火箭所在点B 处与发射站点M 处的距离．（结果精确到0.1千米）（参考数据：2 1.41≈，3 1.73)≈【分析】利用已知结合锐角三角函数关系得出BM 的长．【解答】解：如图所示：连接MN ，由题意可得：90AMN ∠=︒，30ANM ∠=︒，45BNM ∠=︒，8AN km =， 在直角AMN ∆中，3cos30843()MN AN km =︒==． 在直角BMN ∆中，tan 4543 6.9BM MN km km =︒=≈．答：此时火箭所在点B 处与发射站点M 处的距离约为6.9km ．【点评】本题考查解直角三角形的应用-仰角俯角问题，要求学生能借助仰角构造直角三角形并解直角三角形．四、（本大题共3小题，每小题8分，共24分）18．（8分）已知如图，在ABC ∆中，BD 平分ABC ∠交AC 于点D ，点E 在AB 上，且2BD BE BC =；（1）求证：BDE C ∠=∠；（2）求证：2AD AE AB =．【分析】（1）根据角平分线的定义得到ABD CBD ∠=∠，由2BD BE BC =，得到BD BC BE BD=，推出EBD DBC ∆∆∽，根据相似三角形的性质即可得到结论；（2）由BDE C ∠=∠，推出DBC ADE ∠=∠，等量代换得到ABD ADE ∠=∠，证得ADE ABD ∆∆∽，根据相似三角形的性质即可得到结论．【解答】证明：（1）BD 平分ABC ∠，ABD CBD ∴∠=∠， 2BD BE BC =， ∴BD BC BE BD=， EBD DBC ∴∆∆∽，BDE C ∴∠=∠；（2）BDE C ∠=∠，DBC C BDE ADE ∠+∠=∠+∠，DBC ADE ∴∠=∠，ABD CBD ∠=∠，ABD ADE ∴∠=∠，ADE ABD ∴∆∆∽， ∴AD AE AB AD=， 即2AD AE AB =．【点评】本题考查了相似三角形的判定和性质，角平分线的性质，熟练掌握相似三角形的性质即可得到结论．19．（8分）如图，//AB CD ，点E ，F 分别在AB ，CD 上，连接EF ，AEF ∠、CFE ∠的平分线交于点G ，BEF ∠、DFE ∠的平分线交于点H ．（1）求证：四边形EGFH 是矩形；（2）小明在完成（1）的证明后继续进行了探索，过G 作//MN EF ，分别交AB ，CD 于点M ，N ，过H 作//PQ EF ，分别交AB ，CD 于点P ，Q ，得到四边形MNQP ，此时，他猜想四边形MNQP 是菱形，他的猜想是否正确，请予以说明．【分析】（1）根据角平分线的性质进行导角，可求得四边形EGFH 的四个内角均为90︒，进而可说明其为矩形．（2）根据题目条件可得四边形MNQP 为平行四边形，要证菱形只需邻边相等，连接GH ，由于MN EF GH ==，要证MN MP =，只需证GH MP =，只需证四边形MFHP 为平行四边形，可证G 、H 点分别为MN 、PQ 中点，即可得出结果．【解答】（1）证明：EH 平分BEF ∠，FH 平分DFE ∠，12FEH BEF ∴∠=∠，12EFH DFE ∠=∠， //AB CD ，180BEF DFE ∴∠+∠=︒，11()1809022FEH EFH BEF DFE ∴∠+∠=∠+∠=⨯︒=︒， 180FEH EFH EHF ∠+∠+∠=︒，180()1809090EHF FEH EFH ∴∠=︒-∠+∠=︒-︒=︒，同理可得：90EGF ∠=︒，EG 平分AEF ∠，EH 平分BEF ∠，12GEF AEF ∴∠=∠，12FEH BEF ∠=∠， 点A 、E 、B 在同一条直线上，180AEB ∴∠=︒，即180AEF BEF ∠+∠=︒，11()1809022FEG FEH AEF BEF ∴∠+∠=∠+∠=⨯︒=︒， 即90GEH ∠=︒，∴四边形EGFH 是矩形（2）解：他的猜想正确，理由是：////MN EF PQ ，//MP NQ ，∴四边形MNQP 为平行四边形．如图，延长EH 交CD 于点O ，PEO FEO ∠=∠，PEO FOE ∠=∠，FOE FEO ∴∠=∠，EF FD ∴=，FH EO ⊥，HE HO ∴=，EHP OHQ ∠=∠，EPH OQH ∠=∠，EHP OHQ ∴∆≅∆，HP HQ ∴=，同理可得GM GN =，MN PQ =，MG HP ∴=，∴四边形MGHP 为平行四边形，GH MP ∴=，//MN EF ，//ME NF ，∴四边形MEFN 为平行四边形，MN EF ∴=，四边形EGFH 是矩形，GH EF ∴=，MN MP∴=，∴平行四边形MNQP为菱形．【点评】本题考查矩形、菱形的性质与判定，属于综合题，熟练掌握菱形和矩形的性质及判定方法是解题关键．20．（8分）小聪同学周六到某欢乐谷玩迷宫游戏，从迷宫口A到达迷宫口D有多个路口，如图所示（迷宫的一部分），规定从迷宫口A到达D处不能重复走同一路线，且小聪走每一条路线的可能性相同．（1）请用画树状图的方法，求小聪同学从迷宫口A到达D处所走的所有可能路线；（2）求小聪同学从迷宫口A到达D处经过路口B的概率．【分析】（1）根据题意得出小聪同学从迷宫口A到达D处所走的所有可能路线共有4种；（2）根据概率公式进行求解即可．【解答】解：（1）根据题意画图如下：小聪同学从迷宫口A到达D处所走的所有可能路线共有4种；（2）一共有4种情况，而过B的有3种，故小聪同学从迷宫口A到达D处经过路口B的概率为34．【点评】此题考查的是用列表法或树状图法求概率．列表法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件；树状图法适合两步或两步以上完成的事件．用到的知识点为：概率=所求情况数与总情况数之比．五、（本大题共2小题，每小题9分，共18分）21．（9分）某商店购进一批成本为每件30元的商品，经调查发现，该商品每天的销售量y （件)与销售单价x （元)之间满足一次函数关系，其图象如图所示．（1）求该商品每天的销售量y 与销售单价x 之间的函数关系式；（2）若商店按单价不低于成本价，且不高于50元销售，则销售单价定为多少，才能使销售该商品每天获得的利润w （元)最大？最大利润是多少？（3）若商店要使销售该商品每天获得的利润不低于800元，则每天的销售量最少应为多少件？【分析】（1）将点(30,100)、(45,70)代入一次函数表达式，即可求解；（2）由题意得2(30)(2160)2(55)1250w x x x =--+=--+，即可求解；（3）由题意得(30)(2160)800x x --+，解不等式即可得到结论．【解答】解：（1）设y 与销售单价x 之间的函数关系式为：y kx b =+，将点(30,100)、(45,70)代入一次函数表达式得：100307045k b k b =+⎧⎨=+⎩， 解得：2160k b =-⎧⎨=⎩， 故函数的表达式为：2160y x =-+；（2）由题意得：2(30)(2160)2(55)1250w x x x =--+=--+，20-<，故当55x <时，w 随x 的增大而增大，而3050x ，∴当50x =时，w 有最大值，此时，1200w =，故销售单价定为50元时，该商店每天的利润最大，最大利润1200元；（3）由题意得：(30)(2160)800x x --+，解得：4070x ，又216020y x =-+，则y 的最小值为27016020-⨯+=，每天的销售量最少应为20件．【点评】此题主要考查了二次函数的应用以及一元二次不等式的应用、待定系数法求一次函数解析式等知识，正确利用销量⨯每件的利润w =得出函数关系式是解题关键．22．（9分）对于两个不相等的有理数a ，b ，我们规定符号{max a ，}b 表示a ，b 中的较大值，如{2max ，3}2-=，{1max -，0}0=．请解答下列问题：（1）2{1,1}5max --= 1- ； （2）如果{max x ，2}x x -=，求x 的取值范围；（3）如果{max x ，2}2|1|5x x -=--，求x 的值．【分析】（1）根据定义即可得；（2）由已知等式知2x x >-，解之可得；（3）分2x x >-和2x x <-两种情况分别求解可得．【解答】解：（1）2115->-， ∴2{1,1}15max --=-． 故答案为：1-；（2）{max x ，2}x x -=，2x x ∴>-．1x ∴>．x ∴的取值范围是1x >．（3）由题意，得：2x x ≠-．①若2x x >-，即1x >时，{max x ，2}x x -=，|1|1x x -=-．{max x ，2}2|1|5x x -=--，2(1)5x x ∴=--．解得7x =符合题意；)②若2x x <-，即1x <时，{max x ，2}2x x -=-，|1|(1)1x x x -=--=-．{max x ，2}2|1|5x x -=--，22(1)5x x ∴-=--．解得5x =-符合题意．综上所述，7x =或5x =-．【点评】本题主要考查解一元一次不等式，解题的关键是理解新定义，并根据新定义列出关于x 的不等式及分类讨论思想的运用．六、（本大题共12分）23．（12分）如图，抛物线2(0)y ax bx a =+≠经过点(2,0)A ，点(3,3)B ，BC x ⊥轴于点C ，连接OB ，等腰直角三角形DEF 的斜边EF 在x 轴上，点E 的坐标为(4,0)-，点F 与原点重合（1）求抛物线的解析式并直接写出它的对称轴；（2）DEF ∆以每秒1个单位长度的速度沿x 轴正方向移动，运动时间为t 秒，当点D 落在BC 边上时停止运动，设DEF ∆与OBC ∆的重叠部分的面积为S ，求出S 关于t 的函数关系式；（3）点P 是抛物线对称轴上一点，当ABP ∆是直角三角形时，请直接写出所有符合条件的点P 坐标．【分析】（1）根据待定系数法解出解析式和对称轴即可；（2）从三种情况分析①当03t 时，DEF ∆与OBC ∆重叠部分为等腰直角三角形；②当34t <时，DEF ∆与OBC ∆重叠部分是四边形；③当45t <时，DEF ∆与OBC ∆重叠部分是四边形得出S 关于t 的函数关系式即可；（3）直接写出当ABP ∆是直角三角形时符合条件的点P 坐标．【解答】解：（1）根据题意得042393a b a b=+⎧⎨=+⎩， 解得1a =，2b =-，∴抛物线解析式是22y x x =-，对称轴是直线1x =；（2）有3种情况：①当03t 时，DEF ∆与OBC ∆重叠部分为等腰直角三角形，如图1:214S t =； ②当34t <时，DEF ∆与OBC ∆重叠部分是四边形，如图2:219342S t t =-+-； ③当45t <时，DEF ∆与OBC ∆重叠部分是四边形，如图3:211322S t t =-+-； （3）当ABP ∆是直角三角形时，可得符合条件的点P 坐标为(1,1)或(1,2)或1(1,)3或11(1,)3． 【点评】此题考查了难度较大的函数与几何的综合题，关键是根据03t ，34t <，45t <三种情况进行分析．。
2021-2022学年北师大版九年级数学中考复习压轴题专题提升训练(附答案)
2021-2022学年北师大版九年级数学中考复习压轴题专题提升训练（附答案）1．如图，在平面直角坐标系中，菱形ABCD的顶点D在第二象限，其余顶点都在第一象限，AB∥x轴，AO⊥AD，AO＝AD．过点A作AE⊥CD，垂足为E，DE＝4CE．反比例函数y＝（x＞0）的图象经过点E，与边AB交于点F，连接OE，OF，EF．若S△EOF＝，则k的值为（）A．B．C．7D．2．在△ABC中，AB＝AC，D是边BC上一动点，连接AD，将AD绕点A逆时针旋转至AE 的位置，使得∠DAE+∠BAC＝180°．（1）如图1，当∠BAC＝90°时，连接BE，交AC于点F．若BE平分∠ABC，BD＝2，求AF的长；（2）如图2，连接BE，取BE的中点G，连接AG．猜想AG与CD存在的数量关系，并证明你的猜想；（3）如图3，在（2）的条件下，连接DG，CE．若∠BAC＝120°，当BD＞CD，∠AEC ＝150°时，请直接写出的值．3．有公共顶点A的正方形ABCD与正方形AEGF按如图1所示放置，点E，F分别在边AB 和AD上，连接BF，DE，M是BF的中点，连接AM交DE于点N．【观察猜想】（1）线段DE与AM之间的数量关系是，位置关系是；【探究证明】（2）将图1中的正方形AEGF绕点A顺时针旋转45°，点G恰好落在边AB上，如图2，其他条件不变，线段DE与AM之间的关系是否仍然成立？并说明理由．4．在▱ABCD中，∠BAD＝α，DE平分∠ADC，交对角线AC于点G，交射线AB于点E，将线段EB绕点E顺时针旋转α得线段EP．（1）如图1，当α＝120°时，连接AP，请直接写出线段AP和线段AC的数量关系；（2）如图2，当α＝90°时，过点B作BF⊥EP于点F，连接AF，请写出线段AF，AB，AD之间的数量关系，并说明理由；（3）当α＝120°时，连接AP，若BE＝AB，请直接写出△APE与△CDG面积的比值．5．已知点O是线段AB的中点，点P是直线l上的任意一点，分别过点A和点B作直线l 的垂线，垂足分别为点C和点D．我们定义垂足与中点之间的距离为“足中距”．（1）[猜想验证]如图1，当点P与点O重合时，请你猜想、验证后直接写出“足中距”OC和OD的数量关系是．（2）[探究证明]如图2，当点P是线段AB上的任意一点时，“足中距”OC和OD的数量关系是否依然成立，若成立，请给出证明；若不成立，请说明理由．（3）[拓展延伸]如图3，①当点P是线段BA延长线上的任意一点时，“足中距”OC和OD的数量关系是否依然成立，若成立，请给出证明；若不成立，请说明理由；②若∠COD＝60°，请直接写出线段AC、BD、OC之间的数量关系．6．如图，在矩形ABCD中，AB＝3cm，AD＝cm．动点P从点A出发沿折线AB﹣BC向终点C运动，在边AB上以1cm/s的速度运动；在边BC上以cm/s的速度运动，过点P作线段PQ与射线DC相交于点Q，且∠PQD＝60°，连接PD，BD．设点P的运动时间为x（s），△DPQ与△DBC重合部分图形的面积为y（cm2）．（1）当点P与点A重合时，直接写出DQ的长；（2）当点P在边BC上运动时，直接写出BP的长（用含x的代数式表示）；（3）求y关于x的函数解析式，并写出自变量x的取值范围．7．在等腰△ADE中，AE＝DE，△ABC是直角三角形，∠CAB＝90°，∠ABC＝∠AED，连接CD、BD，点F是BD的中点，连接EF．（1）当∠EAD＝45°，点B在边AE上时，如图①所示，求证：EF＝CD；（2）当∠EAD＝45°，把△ABC绕点A逆时针旋转，顶点B落在边AD上时，如图②所示，当∠EAD＝60°，点B在边AE上时，如图③所示，猜想图②、图③中线段EF和CD又有怎样的数量关系？请直接写出你的猜想，不需证明．8．如图，已知△ABC是等边三角形，P是△ABC内部的一点，连接BP，CP．（1）如图1，以BC为直径的半圆O交AB于点Q，交AC于点R，当点P在上时，连接AP，在BC边的下方作∠BCD＝∠BAP，CD＝AP，连接DP，求∠CPD的度数；（2）如图2，E是BC边上一点，且EC＝3BE，当BP＝CP时，连接EP并延长，交AC 于点F，若AB＝4BP，求证：4EF＝3AB；（3）如图3，M是AC边上一点，当AM＝2MC时，连接MP．若∠CMP＝150°，AB ＝6a，MP＝a，△ABC的面积为S1，△BCP的面积为S2，求S1﹣S2的值（用含a的代数式表示）．9．（1）已知△ABC，△ADE如图①摆放，点B，C，D在同一条直线上，∠BAC＝∠DAE ＝90°，∠ABC＝∠ADE＝45°．连接BE，过点A作AF⊥BD，垂足为点F，直线AF 交BE于点G．求证：BG＝EG．（2）已知△ABC，△ADE如图②摆放，∠BAC＝∠DAE＝90°，∠ACB＝∠ADE＝30°．连接BE，CD，过点A作AF⊥BE，垂足为点F，直线AF交CD于点G．求的值．10．已知△ABC和△DEC都为等腰三角形，AB＝AC，DE＝DC，∠BAC＝∠EDC＝n°．（1）当n＝60时，①如图1，当点D在AC上时，请直接写出BE与AD的数量关系：；②如图2，当点D不在AC上时，判断线段BE与AD的数量关系，并说明理由；（2）当n＝90时，①如图3，探究线段BE与AD的数量关系，并说明理由；②当BE∥AC，AB＝3，AD＝1时，请直接写出DC的长．11．如图1，对角线互相垂直的四边形叫做垂美四边形．（1）概念理解：如图2，在四边形ABCD中，AB＝AD，CB＝CD，问四边形ABCD是垂美四边形吗？请说明理由；（2）性质探究：如图1，垂美四边形ABCD的对角线AC，BD交于点O．猜想：AB2+CD2与AD2+BC2有什么关系？并证明你的猜想．（3）解决问题：如图3，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG 和正方形ABDE，连结CE，BG，GE．已知AC＝4，AB＝5，求GE的长．12．如图1，在正方形ABCD中，点E是边BC上一点，且点E不与点B、C重合，点F是BA的延长线上一点，且AF＝CE．（1）求证：△DCE≌△DAF；（2）如图2，连接EF，交AD于点K，过点D作DH⊥EF，垂足为H，延长DH交BF 于点G，连接HB，HC．①求证：HD＝HB；②若DK•HC＝，求HE的长．13．综合与实践数学实践活动，是一种非常有效的学习方式，通过活动可以激发我们的学习兴趣，提高动手动脑能力，拓展思维空间，丰富数学体验，让我们一起动手来折一折、转一转、剪一剪，体会活动带给我们的乐趣．折一折：将正方形纸片ABCD折叠，使边AB、AD都落在对角线AC上，展开得折痕AE、AF，连接EF，如图1．（1）∠EAF＝°，写出图中两个等腰三角形：（不需要添加字母）；转一转：将图1中的∠EAF绕点A旋转，使它的两边分别交边BC、CD于点P、Q，连接PQ，如图2．（2）线段BP、PQ、DQ之间的数量关系为；（3）连接正方形对角线BD，若图2中的∠P AQ的边AP、AQ分别交对角线BD于点M、点N，如图3，则＝；剪一剪：将图3中的正方形纸片沿对角线BD剪开，如图4．（4）求证：BM2+DN2＝MN2．14．实践与探究操作一：如图①，已知正方形纸片ABCD，将正方形纸片沿过点A的直线折叠，使点B 落在正方形ABCD的内部，点B的对应点为点M，折痕为AE，再将纸片沿过点A的直线折叠，使AD与AM重合，折痕为AF，则∠EAF＝度．操作二：如图②，将正方形纸片沿EF继续折叠，点C的对应点为点N．我们发现，当点E的位置不同时，点N的位置也不同．当点E在BC边的某一位置时，点N恰好落在折痕AE上，则∠AEF＝度．在图②中，运用以上操作所得结论，解答下列问题：（1）设AM与NF的交点为点P．求证：△ANP≌△FNE；（2）若AB＝，则线段AP的长为．15．【阅读理解】如图①，l1∥l2，△ABC的面积与△DBC的面积相等吗？为什么？解：相等．在△ABC和△DBC中，分别作AE⊥l2，DF⊥l2，垂足分别为E，F．∴∠AEF＝∠DFC＝90°，∴AE∥DF．∵l1∥l2，∴四边形AEFD是平行四边形，∴AE＝DF．又S△ABC＝BC•AE，S△DBC＝BC•DF．∴S△ABC＝S△DBC．【类比探究】如图②，在正方形ABCD的右侧作等腰△CDE，CE＝DE，AD＝4，连接AE，求△ADE的面积．解：过点E作EF⊥CD于点F，连接AF．请将余下的求解步骤补充完整．【拓展应用】如图③，在正方形ABCD的右侧作正方形CEFG，点B，C，E在同一直线上，AD＝4，连接BD，BF，DF，直接写出△BDF的面积．16．如图①，在△ABC中，AD⊥BC于点D，BC＝14，AD＝8，BD＝6，点E是AD上一动点（不与点A，D重合），在△ADC内作矩形EFGH，点F在DC上，点G，H在AC上，设DE＝x，连接BE．（1）当矩形EFGH是正方形时，直接写出EF的长；（2）设△ABE的面积为S1，矩形EFGH的面积为S2，令y＝，求y关于x的函数解析式（不要求写出自变量x的取值范围）；（3）如图②，点P（a，b）是（2）中得到的函数图象上的任意一点，过点P的直线l 分别与x轴正半轴，y轴正半轴交于M，N两点，求△OMN面积的最小值，并说明理由．17．下面是某数学兴趣小组探究用不同方法作一个角的平分线的讨论片段，请仔细阅读，并完成相应的任务．小明：如图1，（1）分别在射线OA，OB上截取OC＝OD，OE＝OF（点C，E不重合）；（2）分别作线段CE，DF的垂直平分线l1，l2，交点为P，垂足分别为点G，H；（3）作射线OP，射线OP即为∠AOB的平分线．简述理由如下：由作图知，∠PGO＝∠PHO＝90°，OG＝OH，OP＝OP，所以Rt△PGO≌Rt△PHO，则∠POG＝∠POH，即射线OP是∠AOB的平分线．小军：我认为小明的作图方法很有创意，但是太麻烦了，可以改进如下，如图2，（1）分别在射线OA，OB上截取OC＝OD，OE＝OF（点C，E不重合）；（2）连接DE，CF，交点为P；（3）作射线OP．射线OP即为∠AOB的平分线．……任务：（1）小明得出Rt△PGO≌Rt△PHO的依据是（填序号）．①SSS②SAS③AAS④ASA⑤HL（2）小军作图得到的射线OP是∠AOB的平分线吗？请判断并说明理由．（3）如图3，已知∠AOB＝60°，点E，F分别在射线OA，OB上，且OE＝OF＝+1．点C，D分别为射线OA，OB上的动点，且OC＝OD，连接DE，CF，交点为P，当∠CPE ＝30°时，直接写出线段OC的长．18．如图，在四边形ABCD中，AB∥CD，AB≠CD，∠ABC＝90°，点E、F分别在线段BC、AD上，且EF∥CD，AB＝AF，CD＝DF．（1）求证：CF⊥FB；（2）求证：以AD为直径的圆与BC相切；（3）若EF＝2，∠DFE＝120°，求△ADE的面积．19．已知四边形ABCD是边长为1的正方形，点E是射线BC上的动点，以AE为直角边在直线BC的上方作等腰直角三角形AEF，∠AEF＝90°，设BE＝m．（1）如图，若点E在线段BC上运动，EF交CD于点P，AF交CD于点Q，连接CF，①当m＝时，求线段CF的长；②在△PQE中，设边QE上的高为h，请用含m的代数式表示h，并求h的最大值；（2）设过BC的中点且垂直于BC的直线被等腰直角三角形AEF截得的线段长为y，请直接写出y与m的关系式．20．【推理】如图1，在正方形ABCD中，点E是CD上一动点，将正方形沿着BE折叠，点C落在点F处，连结BE，CF，延长CF交AD于点G．（1）求证：△BCE≌△CDG．【运用】（2）如图2，在【推理】条件下，延长BF交AD于点H．若，CE＝9，求线段DE的长．【拓展】（3）将正方形改成矩形，同样沿着BE折叠，连结CF，延长CF，BF交直线AD于G，H两点，若＝k，＝，求的值（用含k的代数式表示）．21．如图，在△ABC中，AB＝AC，∠BAC＝α，M为BC的中点，点D在MC上，以点A 为中心，将线段AD顺时针旋转α得到线段AE，连接BE，DE．（1）比较∠BAE与∠CAD的大小；用等式表示线段BE，BM，MD之间的数量关系，并证明；（2）过点M作AB的垂线，交DE于点N，用等式表示线段NE与ND的数量关系，并证明．22．如图1，在△ABC中，∠ACB＝90°，AC＝BC，点D是AB边上一点（含端点A、B），过点B作BE垂直于射线CD，垂足为E，点F在射线CD上，且EF＝BE，连接AF、BF．（1）求证：△ABF∽△CBE；（2）如图2，连接AE，点P、M、N分别为线段AC、AE、EF的中点，连接PM、MN、PN．求∠PMN的度数及的值；（3）在（2）的条件下，若BC＝，直接写出△PMN面积的最大值．23．某数学兴趣小组在数学课外活动中，对多边形内两条互相垂直的线段做了如下探究：【观察与猜想】（1）如图1，在正方形ABCD中，点E，F分别是AB，AD上的两点，连接DE，CF，DE⊥CF，则的值为；（2）如图2，在矩形ABCD中，AD＝7，CD＝4，点E是AD上的一点，连接CE，BD，且CE⊥BD，则的值为；【类比探究】（3）如图3，在四边形ABCD中，∠A＝∠B＝90°，点E为AB上一点，连接DE，过点C作DE的垂线交ED的延长线于点G，交AD的延长线于点F，求证：DE•AB＝CF•AD；【拓展延伸】（4）如图4，在Rt△ABD中，∠BAD＝90°，AD＝9，tan∠ADB＝，将△ABD沿BD 翻折，点A落在点C处得△CBD，点E，F分别在边AB，AD上，连接DE，CF，DE⊥CF．①求的值；②连接BF，若AE＝1，直接写出BF的长度．24．在平面直角坐标系中，O为原点，△OAB是等腰直角三角形，∠OBA＝90°，BO＝BA，顶点A（4，0），点B在第一象限，矩形OCDE的顶点E（﹣，0），点C在y轴的正半轴上，点D在第二象限，射线DC经过点B．（Ⅰ）如图①，求点B的坐标；（Ⅱ）将矩形OCDE沿x轴向右平移，得到矩形O′C′D′E′，点O，C，D，E的对应点分别为O′，C′，D′，E′．设OO′＝t，矩形O′C′D′E′与△OAB重叠部分的面积为S．①如图②，当点E′在x轴正半轴上，且矩形O′C′D′E′与△OAB重叠部分为四边形时，D′E′与OB相交于点F，试用含有t的式子表示S，并直接写出t的取值范围；②当≤t≤时，求S的取值范围（直接写出结果即可）25．如图1，在△ABC中，AB＝AC，N是BC边上的一点，D为AN的中点，过点A作BC 的平行线交CD的延长线于T，且AT＝BN，连接BT．（1）求证：BN＝CN；（2）在图1中AN上取一点O，使AO＝OC，作N关于边AC的对称点M，连接MT、MO、OC、OT、CM得图2．①求证：△TOM∽△AOC；②设TM与AC相交于点P，连接PD，求证：PD∥CM，PD＝CM．26．问题提出如图（1），在△ABC和△DEC中，∠ACB＝∠DCE＝90°，BC＝AC，EC＝DC，点E在△ABC内部，直线AD与BE交于点F．线段AF，BF，CF之间存在怎样的数量关系？问题探究（1）先将问题特殊化如图（2），当点D，F重合时，直接写出一个等式，表示AF，BF，CF之间的数量关系；（2）再探究一般情形如图（1），当点D，F不重合时，证明（1）中的结论仍然成立．问题拓展如图（3），在△ABC和△DEC中，∠ACB＝∠DCE＝90°，BC＝kAC，EC＝kDC（k是常数），点E在△ABC内部，直线AD与BE交于点F．直接写出一个等式，表示线段AF，BF，CF之间的数量关系．27．【证明体验】（1）如图1，AD为△ABC的角平分线，∠ADC＝60°，点E在AB上，AE＝AC．求证：DE平分∠ADB．【思考探究】（2）如图2，在（1）的条件下，F为AB上一点，连结FC交AD于点G．若FB＝FC，DG＝2，CD＝3，求BD的长．【拓展延伸】（3）如图3，在四边形ABCD中，对角线AC平分∠BAD，∠BCA＝2∠DCA，点E在AC上，∠EDC＝∠ABC．若BC＝5，CD＝2，AD＝2AE，求AC的长．28．已知，在△ABC中，∠BAC＝90°，AB＝AC．（1）如图1，已知点D在BC边上，∠DAE＝90°，AD＝AE，连结CE．试探究BD与CE的关系；（2）如图2，已知点D在BC下方，∠DAE＝90°，AD＝AE，连结CE．若BD⊥AD，AB＝2，CE＝2，AD交BC于点F，求AF的长；（3）如图3，已知点D在BC下方，连结AD、BD、CD．若∠CBD＝30°，∠BAD＞15°，AB2＝6，AD2＝4+，求sin∠BCD的值．29．在平面直角坐标系中，点A的坐标为（﹣，0），点B在直线l：y＝x上，过点B 作AB的垂线，过原点O作直线l的垂线，两垂线相交于点C．（1）如图，点B，C分别在第三、二象限内，BC与AO相交于点D．①若BA＝BO，求证：CD＝CO．②若∠CBO＝45°，求四边形ABOC的面积．（2）是否存在点B，使得以A，B，C为顶点的三角形与△BCO相似？若存在，求OB 的长；若不存在，请说明理由．30．如图，△OAB的顶点坐标分别为O（0，0），A（3，4），B（6，0），动点P、Q同时从点O出发，分别沿x轴正方向和y轴正方向运动，速度分别为每秒3个单位和每秒2个单位，点P到达点B时点P、Q同时停止运动．过点Q作MN∥OB分别交AO、AB于点M、N，连接PM、PN．设运动时间为t（秒）．（1）求点M的坐标（用含t的式子表示）；（2）求四边形MNBP面积的最大值或最小值；（3）是否存在这样的直线l，总能平分四边形MNBP的面积？如果存在，请求出直线l 的解析式；如果不存在，请说明理由；（4）连接AP，当∠OAP＝∠BPN时，求点N到OA的距离．参考答案1．解：延长EA交x轴于点G，过点F作FH⊥x轴于点H，如图，∵AB∥x轴，AE⊥CD，AB∥CD，∴AG⊥x轴．∵AO⊥AD，∴∠DAE+∠OAG＝90°．∵AE⊥CD，∴∠DAE+∠D＝90°．∴∠D＝∠OAG．在△DAE和△AOG中，．∴△DAE≌△AOG（AAS）．∴DE＝AG，AE＝OG．∵四边形ABCD是菱形，DE＝4CE，∴AD＝CD＝DE．设DE＝4a，则AD＝OA＝5a．∴OG＝AE＝．∴EG＝AE+AG＝7a．∴E（3a，7a）．∵反比例函数y＝（x＞0）的图象经过点E，∴k＝21a2．∵AG⊥GH，FH⊥GH，AF⊥AG，∴四边形AGHF为矩形．∴HF＝AG＝4a．∵点F在反比例函数y＝（x＞0）的图象上，∴x＝．∴F（）．∴OH＝a，FH＝4a．∴GH＝OH﹣OG＝．∵S△OEF＝S△OEG+S梯形EGHF﹣S△OFH，S△EOF＝，∴．××﹣＝．解得：a2＝．∴k＝21a2＝21×＝．故选：A．2．解：（1）连接CE，过点F作FQ⊥BC于Q，∵BE平分∠ABC，∠BAC＝90°，∴F A＝FQ，∵AB＝AC，∴∠ABC＝∠ACB＝45°，∴FQ＝CF，∵∠BAC+∠DAE＝180°，∴∠DAE＝∠BAC＝90°，∴∠BAD＝∠CAE，由旋转知，AD＝AE，∴△ABD≌△ACE（SAS），∴BD＝CE＝2，∠ABD＝∠ACE＝45°，∴∠BCE＝90°，∴∠CBF+∠BEC＝90°，∵BE平分∠ABC，∴∠ABF＝∠CBF，∴∠ABF+∠BEC＝90°，∵∠BAC＝90°，∴∠ABF+∠AFB＝90°，∴∠AFB＝∠BEC，∵∠AFB＝∠CFE，∴∠BEC＝∠CFE，∴CF＝CE＝2，∴AF＝FQ＝CF＝；（2）AG＝CD，理由：延长BA至点M，使AM＝AB，连接EM，∵G是BE的中点，∴AG＝ME，∵∠BAC+∠DAE＝∠BAC+∠CAM＝180°，∴∠DAE＝∠CAM，∴∠DAC＝∠EAM，∵AB＝AM，AB＝AC，∴AC＝AM，∵AD＝AE，∴△ADC≌△AEM（SAS），∴CD＝EM，∴AG＝CD；（3）如图3，连接DE，AD与BE的交点记作点N，∵∠BAC+∠DAE＝180°，∠BAC＝120°，∴∠DAE＝60°，∵AD＝AE，∴△ADE是等边三角形，∴AE＝DE，∠ADE＝∠AED＝60°，∵∠AEC＝150°，∴∠DEC＝∠AEC﹣∠AED＝90°，在△ABC中，AB＝AC，∠BAC＝120°，∴∠ACB＝∠ABC＝30°，∵∠AEC＝150°，∴∠ABC+∠AEC＝180°，∴点A，B，C，E四点共圆，∴∠BEC＝∠BAC＝120°，∴∠BED＝∠BEC﹣∠DEC＝30°，∴∠DNE＝180°﹣∠BED﹣∠ADE＝90°，∵AE＝DE，∴AN＝DN，∴BE是AD的垂直平分线，∴AG＝DG，BA＝BD＝AC，∴∠ABE＝∠DBE＝∠ABC＝15°，∴∠ACE＝∠ABE＝15°，∴∠DCE＝45°，∵∠DEC＝90°，∴∠EDC＝45°＝∠DCE，∴DE＝CE，∴AD＝DE，设AG＝a，则DG＝a，由（2）知，AG＝CD，∴CD＝2AG＝2a，∴CE＝DE＝CD＝a，∴AD＝a，∴DN＝AD＝a，过点D作DH⊥AC于H，在Rt△DHC中，∠ACB＝30°，CD＝2a，∴DH＝a，根据勾股定理得，CH＝a，在Rt△AHD中，根据勾股定理得，AH＝＝a，∴AC＝AH+CH＝a+a，∴BD＝a+a，∴＝＝．3．解：（1）∵四边形ABCD和四边形AEGF都是正方形，∴AD＝AB，AF＝AE，∠DAE＝∠BAF＝90°，∴△DAE≌△BAF（SAS），∴DE＝BF，∠ADE＝∠ABF，∵∠ABF+∠AFB＝90°，∴∠ADE+∠AFB＝90°，在Rt△BAF中，M是BF的中点，∴AM＝FM＝BM＝BF，∴DE＝2AM．∵AM＝FM，∴∠AFB＝∠MAF，又∵∠ADE+∠AFB＝90°，∴∠ADE+∠MAF＝90°，∴∠AND＝180°﹣（∠ADE+∠MAF）＝90°，即AN⊥DN；故答案为DE＝2AM，DE⊥AM．（2）仍然成立，证明如下：延长AM至点H，使得AM＝MH，连接FH，∵M是BF的中点，∴BM＝FM，又∵∠AMB＝∠HMF，∴△AMB≌△HMF（SAS），∴AB＝HF，∠ABM＝∠HFM，∴AB∥HF，∴∠HFG＝∠AGF，∵四边形ABCD和四边形AEGF是正方形，∴∠DAB＝∠AFG＝90°，AE＝AF，AD＝AB＝FH，∠EAG＝∠AGF，∴∠EAD＝∠EAG+∠DAB＝∠AFG+∠AGF＝∠AFG+∠HFG＝∠AFH，∴△EAD≌△AFH（SAS），∴DE＝AH，又∵AM＝MH，∴DE＝AM+MH＝2AM，∵△EAD≌△AFH，∴∠ADE＝∠FHA，∵△AMB≌△HMF，∴∠FHA＝∠BAM，∴∠ADE＝∠BAM，又∵∠BAM+∠DAM＝∠DAB＝90°，∴∠ADE+∠DAM＝90°，∴∠AND＝180°﹣（∠ADE+∠DAM）＝90°，即AN⊥DN．故线段DE与AM之间的数量关系是DE＝2AM．线段DE与AM之间的位置关系是DE ⊥AM．4．解：（1）方法一：如图1，连接PB，PC，∵四边形ABCD是平行四边形，∴AD∥BC，AB∥CD，AD＝BC，∵α＝120°，即∠BAD＝120°，∴∠B＝∠ADC＝60°，∴∠BEP＝60°＝∠B，由旋转知：EP＝EB，∴△BPE是等边三角形，∴BP＝EP，∠EBP＝∠BPE＝60°，∴∠CBP＝∠ABC+∠EBP＝120°，∵∠AEP＝180°﹣∠BEP＝120°，∴∠AEP＝∠CBP，∵DE平分∠ADC，∴∠ADE＝∠CDE＝30°，∴∠AED＝∠CDE＝30°＝∠ADE，∴AD＝AE，∴AE＝BC，∴△APE≌△CPB（SAS），∴AP＝CP，∠APE＝∠CPB，∴∠APE+∠CPE＝∠CPB+∠CPE，即∠APC＝∠BPE＝60°，∴△APC是等边三角形，方法二：如图1，延长PE交CD于点Q，连接AQ，∵四边形ABCD是平行四边形，∴AD∥BC，AB∥CD，∵α＝120°，即∠BAD＝120°，∴∠B＝∠ADC＝60°，∴∠BEP＝60°＝∠B，∴PE∥BC∥AD，∴四边形ADQE和四边形BCQE是平行四边形，∵DE平分∠ADC，∴∠ADE＝∠CDE＝30°，∴∠AED＝∠CDE＝30°＝∠ADE，∴AD＝AE，∴四边形ADQE是菱形，∴∠EAQ＝∠AEQ＝60°，∴△AEQ是等边三角形，∴AE＝AQ，∠AQE＝60°，∵四边形BCQE是平行四边形，∴PE＝BE＝CQ，∠B＝∠CQE＝60°，∵∠AEP＝120°，∠AQC＝∠AQE+∠CQE＝120°，∴∠AEP＝∠AQC，∴△AEP≌△AQC（SAS），∴AP＝AC；（2）AB2+AD2＝2AF2，理由：如图2，连接CF，在▱ABCD中，∠BAD＝90°，∴∠ADC＝∠ABC＝∠BAD＝90°，AD＝BC，∵DE平分∠ADC，∴∠ADE＝∠CDE＝45°，∴∠AED＝∠ADE＝45°，∴AE＝BC，∵BF⊥EP，∴∠BFE＝90°，∵∠BEF＝α＝∠BAD＝×90°＝45°，∴∠EBF＝∠BEF＝45°，∴BF＝EF，∵∠FBC＝∠FBE+∠ABC＝45°+90°＝135°，∠AEF＝180°﹣∠FEB＝135°，∴∠CBF＝∠AEF，∴△BCF≌△EAF（SAS），∴CF＝AF，∠CFB＝∠AFE，∴∠AFC＝∠AFE+∠CFE＝∠CFB+∠CFE＝∠BFE＝90°，∴∠ACF＝∠CAF＝45°，∵sin∠ACF＝，∴AC＝＝＝＝AF，在Rt△ABC中，AB2+BC2＝AC2，∴AB2+AD2＝2AF2；（3）方法一：由（1）知，BC＝AD＝AE＝AB﹣BE，∵BE＝AB，AB＝CD，∴AB＝CD＝2BE，设BE＝a，则PE＝AD＝AE＝a，AB＝CD＝2a，①当点E在AB上时，如图3，过点G作GM⊥AD于点M，作GN⊥CD于点N，过点C作CK⊥AD于点K，过点A作AH⊥PE的延长线于点H，当α＝120°时，∠B＝∠ADC＝60°，∵DE平分∠ADC，GM⊥AD，GN⊥CD，∴GM＝GN，∵S△ACD＝AD•CK＝a•2a•sin60°＝a2，＝＝＝＝2，∴S△CDG＝2S△ADG，∴S△CDG＝S△ACD＝a2，由（1）知PE∥BC，∴∠AEH＝∠B＝60°，∵∠H＝90°，∴AH＝AE•sin60°＝a，∴S△APE＝PE•AH＝a•a＝a2，∴＝＝．②如图4，当点E在AB延长线上时，由①同理可得：S△CDG＝S△ACD＝××2a××3a＝a2，S△APE＝PH•AE＝×a×3a＝a2，∴＝＝，综上所述，△APE与△CDG面积的比值为或．方法二：如图3，∵四边形ABCD是平行四边形，∴AD∥BC，AB∥CD，AB＝CD，∴△AEG∽△CDG，∴＝（）2，＝，①当点E在AB上时，∵BE＝AB，∴AE＝BE＝AB＝CD，∴＝（）2＝，又∵＝＝，∴＝，即＝3，∴＝＝3，当α＝120°时，∠B＝∠ADC＝60°，∵DE平分∠ADC，∴∠ADE＝30°，∴∠AED＝180°﹣∠BAD﹣∠ADE＝30°＝∠ADE，∴AE＝AD，∵EP＝EB＝AE，EP∥AD，∴EP＝AD＝AE，∠AEP＝∠DAE＝120°，∴△AED≌△EAP（SAS），∴S△AED＝S△EAP，∴＝•＝•＝3×＝；②如图4，当点E在AB延长线上时，∵BE＝AB，∴AE＝AB＝CD，由①知，AD＝AE＝CD，∵EP＝BE＝AE＝AD，EP∥AD，∴＝＝，∵＝＝，∴＝，∴＝＝，∵＝（）2＝（）2＝，∴＝••＝××＝；综上所述，△APE与△CDG面积的比值为或．5．解：（1）猜想：OC＝OD．理由：如图1中，∵AC⊥CD，BD⊥CD，∴∠ACO＝∠BDO＝90°在△AOC与△BOD中，，∴△AOC≌△BOD（AAS），∴OC＝OD，故答案为：OC＝OD；（2）数量关系依然成立．理由：过点O作直线EF∥CD，交AC的延长线于点E，∵EF∥CD，∴∠DCE＝∠E＝∠CDF＝90°，∴四边形CEFD为矩形，∴∠OFD＝90°，CE＝DF，由（1）知，OE＝OF，在△COE与△DOF中，，∴△COE≌DOF（SAS），∴OC＝OD；（3）①结论成立．理由：如图3中，延长CO交BD的延长线于点E，∵AC⊥CD，BD⊥CD，∴AC∥BD，∴∠ACO＝∠E，∵点O为AB的中点，∴AO＝BO，又∵∠AOC＝∠BOE，∴△AOC≌△BOE（AAS），∴CO＝OE，∵∠CDE＝90°，∴OD＝OC＝OE，∴OC＝OD．②结论：AC+BD＝OC．理由：如图3中，∵∠COD＝60°，OD＝OC，∴△COD是等边三角形，∴CD＝OC，∠OCD＝60°，∵∠CDE＝90°，∴tan60°＝，∴DE＝CD，∵△AOC≌△BOE，∴AC＝BE，∴AC+BD＝BD+BE＝DE＝CD，∴AC+BD＝OC．6．解：（1）如图，在Rt△PDQ中，AD＝cm，∠PQD＝60°，∴tan60°＝＝，∴DQ＝AD＝1cm．（2）点P在AB上运动时间为3÷1＝3（s），∴点P在BC上时PB＝（x﹣3）．（3）当0≤x≤3时，点P在AB上，作PM⊥CD于点M，PQ交AB于点E，作EN⊥CD 于点N，同（1）可得MQ＝AD＝1cm．∴DQ＝DM+MQ＝AP+MQ＝（x+1）cm，当x+1＝3时x＝2，∴0≤x≤2时，点Q在DC上，∵tan∠BDC＝＝，∴∠DBC＝30°，∵∠PQD＝60°，∴∠DEQ＝90°．∵sin30°＝＝，∴EQ＝DQ＝，∵sin60°＝＝，∴EN＝EQ＝（x+1）cm，∴y＝DQ•EN＝（x+1）×（x+1）＝（x+1）2＝x2+x+（0≤x≤2）．当2＜x≤3时，点Q在DC延长线上，PQ交BC于点F，如图，∵CQ＝DQ﹣DC＝x+1﹣3＝x﹣2，tan60°＝，∴CF＝CQ•tan60°＝（x﹣2）cm，∴S△CQF＝CQ•CF＝（x﹣2）×（x﹣2）＝（x2﹣2x+2）cm2，∴y＝S△DEQ﹣S△CQF＝x2+x+﹣（x2﹣2x+2）＝（﹣x2+x﹣）cm2（2＜x≤3）．当3＜x≤4时，点P在BC上，如图，∵CP＝CB﹣BP＝﹣（x﹣3）＝（4﹣x）cm，∴y＝DC•CP＝×3（4﹣x）＝6﹣x（3＜x≤4）．综上所述，y＝7．（1）证明：如图①中，∵EA＝ED，∠EAD＝45°，∴∠EAD＝∠EDA＝45°，∴∠AED＝90°，∵BF＝FD，∴EF＝DB，∵∠CAB＝90°，∴∠CAD＝∠BAD＝45°，∵∠ABC＝∠AED＝45°，∴∠ACB＝∠ABC＝45°，∴AD垂直平分线段BC，∴DC＝DB，∴EF＝CD．（2）解：如图②中，结论：EF＝CD．理由：取CD的中点T，连接AT，TF，ET，TE交AD于点O．∵∠CAD＝90°，CT＝DT，∴AT＝CT＝DT，∵EA＝ED，∴ET垂直平分线段AD，∴AO＝OD，∵∠AED＝90°，∴OE＝OA＝OD，∵CT＝TD，BF＝DF，∴BC∥FT，∴∠ABC＝∠OFT＝45°，∵∠TOF＝90°，∴∠OTF＝∠OFT＝45°，∴OT＝OF，∴AF＝ET，∵FT＝TF，∠AFT＝∠ETF，F A＝TE，∴△AFT≌△ETF（SAS），∴EF＝CD．如图③中，结论：EF＝CD．理由：取AD的中点O，连接OF，OE．∵EA＝ED，∠AED＝60°，∴△ADE是等边三角形，∵AO＝OD，∴OE⊥AD，∠AEO＝∠OED＝30°，∴tan∠AEO＝＝，∴＝，∵∠ABC＝∠AED＝30°，∠BAC＝90°，∴AB＝AC，∵AO＝OD，BF＝FD，∴OF＝AB，∴＝，∴＝，∵OF∥AB，∴∠DOF＝∠DAB，∵∠DOF+∠EOF＝90°，∠DAB+∠DAC＝90°，∴∠EOF＝∠DAC，∴△EOF∽△DAC，∴＝＝，∴EF＝CD．8．解：（1）如图1，连接BD，∵△ABC是等边三角形，∴AB＝BC，∠ABC＝60°，在△BAP和△BCD中，，∴△BAP≌△BCD（SAS），∴BP＝BD，∠ABP＝∠CBD，∵∠ABP+∠PBC＝60°，∴∠CBD+∠PBC＝60°，即∠PBD＝60°，∴△BDP是等边三角形，∴∠BPD＝60°，∵BC是⊙O的直径，∴∠BPC＝90°，∴∠CPD＝∠BPC﹣∠BPD＝90°﹣60°＝30°；（2）如图2，连接AP交BC于D，∵△ABC是等边三角形，∴AB＝AC＝BC，∠ABC＝∠ACB＝60°，∵BP＝CP，∴AD⊥BC，BD＝CD＝BC＝AB，∴AD＝AB•sin∠ABC＝AB•sin60°＝AB，∵AB＝4BP，∴BP＝AB，∴PD＝＝＝AB，∴PD＝AD，即点P是AD的中点，∵EC＝3BE，∴BE＝BC，BC＝4BE，∵BD＝BC，∴BE＝BD，即点E是BD的中点，∴EP是△ABD的中位线，∴EF∥AB，∴△CEF∽△CBA，∴＝＝＝，∴4EF＝3AB；（3）如图3，过点A作AD⊥BC于点D，过点P作PE⊥BC于点E，交AC于点F，作PH⊥AC于点H，由（2）得：AD＝AB＝3a，∠ACB＝60°，BC＝AC＝AB＝6a，∵∠CMP＝150°，∴∠PMF＝180°﹣∠CMP＝180°﹣150°＝30°，∵∠CHP＝90°，∴PH＝PM•sin∠PMF＝a•sin30°＝a，MH＝PM•cos∠PMF＝a•cos30°＝a，∵EF⊥BC，∴∠CEF＝90°，∴∠CFE＝90°﹣∠ACB＝90°﹣60°＝30°，∴∠CFE＝∠PMF，∴PF＝PM＝a，∴FH＝PF•cos∠PFH＝a•cos30°＝a，∵AM＝2MC，∴CM＝AC＝×6a＝2a，∴CF＝CM++MH+HF＝5a，∴EF＝CF•sin∠ACB＝5a•sin60°＝a，∴PE＝EF﹣PF＝a﹣a＝a，∴S1﹣S2＝S△ABC﹣S△BCP＝BC•AD﹣BC•PE＝BC•（AD﹣PE）＝×6a×（3a ﹣a）＝a2．9．（1）证明：如图，连接EC，∵∠BAC＝∠DAE＝90°，∠ABC＝∠ADE＝45°，∴△ABC和△ADE为等腰直角三角形，∴AB＝AC，AD＝AE，∠BAC+∠CAD＝∠DAE+∠CAD，即∠BAD＝∠CAE，在△BAD与△CAE中，，∴△BAD≌△CAE（SAS），∴∠ABD＝∠ACE＝45°，∴∠ACB+∠ACE＝90°，则CE⊥BD，∵AF⊥BD，∴AF∥CE，BF＝FC，∴＝＝1，∴BG＝EG．（2）解：如图，过点D作DM⊥AG，垂足为点M，过点C作CN⊥AG，交AG的延长线于点N，在△ABC和△AED中，∠BAC＝∠DAE＝90°，∠ACB＝∠ADE＝30°，设AE＝a，AB＝b，则AD＝a，AC＝b，∵∠1+∠EAF＝90°，∠2+∠EAF＝90°，∴∠1＝∠2，∴sin∠1＝sin∠2，∴＝，即＝＝＝，同理可证∠3＝∠4，＝＝，∴＝，∴DM＝CN，在△DGM和△CGN中，有：，∴△DGM≌△CGN（AAS），∴DG＝CG，∴＝1．10．解：（1）①当n＝60时，△ABC和△DEC均为等边三角形，∴BC＝AC，EC＝DC，又∵BE＝BC﹣EC，AD＝AC﹣DC，∴BE＝AD，故答案为：BE＝AD；②BE＝AD，理由如下：当点D不在AC上时，∵∠ACB＝∠ACD+∠DCB＝60°，∠DCE＝∠BCE+∠DCB＝60°，∴∠ACD＝∠BCE，在△ACD和△BCE中，，∴△ACD≌△BCE（SAS），∴AD＝BE；（2）①BE＝AD，理由如下：当n＝90时，在等腰直角三角形DEC中：＝sin45，在等腰直角三角形ABC中：＝，∵∠ACB＝∠ACE+∠ECB＝45°，∠DCE＝∠ACE+∠DCA＝45°，∴∠ECB＝∠DCA在△DCA和△ECB中，，∴△DCA∽△ECB，∴，∴BE＝，②DC＝5或，理由如下：当点D在△ABC外部时，设EC与AB交于点F，如图所示：∵AB＝3，AD＝1由上可知：AC＝AB＝3，BE＝＝，又∵BE∥AC，∴∠EBF＝∠CAF＝90°，而∠EFB＝∠CF A，∴△EFB∽△CF A，∴＝＝，∴AF＝3BF，而AB＝BF+AF＝3，∴BF＝＝，在Rt△EBF中：EF＝＝＝，又∵CF＝3EF＝3×＝，∴EC＝EF+CF＝＝5（或EC＝4EF＝5），在等腰直角三角形DEC中，DC＝EC•cos45°＝5×＝5．当点D在△ABC内部时，过点D作DH⊥AC于H∵AC＝3，AD＝1，∠DAC＝45°∴AH＝DH＝，CH＝AC﹣AH＝，∴CD＝＝＝，综上所述，满足条件的CD的值为5或．11．解：（1）四边形ABCD是垂美四边形．理由如下：如图2，连接AC、BD，∵AB＝AD，∴点A在线段BD的垂直平分线上，∵CB＝CD，∴点C在线段BD的垂直平分线上，∴直线AC是线段BD的垂直平分线，∴AC⊥BD，即四边形ABCD是垂美四边形；（2）AB2+CD2＝AD2+BC2，理由如下：如图1中，∵AC⊥BD，∴∠AOD＝∠AOB＝∠BOC＝∠COD＝90°，由勾股定理得，AD2+BC2＝AO2+DO2+BO2+CO2，AB2+CD2＝AO2+BO2+CO2+DO2，∴AD2+BC2＝AB2+CD2；（3）如图3，连接CG、BE，∵正方形ACFG和正方形ABDE，∴AG＝AC，AB＝AE，∠CAG＝∠BAE＝90°，∴∠CAG+∠BAC＝∠BAE+∠BAC，即∠GAB＝∠CAE，在△GAB和△CAE中，，∴△GAB≌△CAE（SAS），∴∠ABG＝∠AEC，∵∠AEC+∠AME＝90°，∴∠ABG+∠AME＝90°，∵∠AME＝∠BMN，∴∠ABG+∠BMN＝90°，即CE⊥BG，∴四边形CGEB是垂美四边形，由（2）得，CG2+BE2＝CB2+GE2，∵AC＝4，AB＝5，∴BC＝＝＝3，∵CG＝＝＝4，BE＝＝＝5，∴GE2＝CG2+BE2﹣CB2＝（4）2+（5）2﹣32＝73，∴GE＝．12．解：（1）∵四边形ABCD为正方形，∴CD＝AD，∠DCE＝∠DAF＝90°，∵CE＝AF，∴△DCE≌△DAF（SAS）；（2）①∵△DCE≌△DAF，∴DE＝DF，∠CDE＝∠ADF，∴∠FDE＝∠ADF+∠ADE＝∠CDE+∠ADE＝∠ADC＝90°，∴△DFE为等腰直角三角形，∵DH⊥EF，∴点H是EF的中点，∴DH＝EF，同理，由HB是Rt△EBF的中线得：HB＝EF，∴HD＝HB；②∵四边形ABCD为正方形，故CD＝CB，∵HD＝HB，CH＝CH，∴△DCH≌△BCH（SSS），∴∠DCH＝∠BCH＝45°，∵△DEF为等腰直角三角形，∴∠DFE＝45°，∴∠HCE＝∠DFK，∵四边形ABCD为正方形，∴AD∥BC，∴∠DKF＝∠HEC，∴△DKF∽△HEC，∴，∴DK•HC＝DF•HE，在等腰直角三角形DFH中，DF＝HF＝HE，∴DK•HC＝DF•HE＝HE2＝，∴HE＝1．13．（1）解：如图1中，∵四边形ABCD是正方形，∴AB＝AD＝BC＝CD，∠BAD＝90°，∴ABC，△ADC都是等腰三角形，∵∠BAE＝∠CAE，∠DAF＝∠CAF，∴∠EAF＝（∠BAC+∠DAC）＝45°，∵∠BAE＝∠DAF＝22.5°，∠B＝∠D＝90°，AB＝AD，∴△BAE≌△DAF（ASA），∴BE＝DF，AE＝AF，∵CB＝CD，∴CE＝CF，∴△AEF，△CEF都是等腰三角形，故答案为：45，△AEF，△EFC，△ABC，△ADC．（2）解：结论：PQ＝BP+DQ．理由：如图2中，延长CB到T，使得BT＝DQ．∵AD＝AB，∠ADQ＝∠ABT＝90°，DQ＝BT，∴△ADQ≌△ABT（SAS），∴AT＝AQ，∠DAQ＝∠BAT，∵∠P AQ＝45°，∴∠P AT＝∠BAP+∠BAT＝∠BAP+∠DAQ＝45°，∴∠P AT＝∠P AQ＝45°，∵AP＝AP，∴△P AT≌△P AQ（SAS），∴PQ＝PT，∵PT＝PB+BT＝PB+DQ，∴PQ＝BP+DQ．故答案为：PQ＝BP+DQ．（3）解：如图3中，∵四边形ABCD是正方形，∴∠ABM＝∠ACQ＝∠BAC＝45°，AC＝AB，∵∠BAC＝∠P AQ＝45°，∴∠BAM＝∠CAQ，∴△CAQ∽△BAM，∴＝＝，故答案为：．（4）证明：如图4中，将△ADN绕点A顺时针旋转90°得到△ABR，连接RM．∵∠BAD＝90°，∠MAN＝45°，∴∠DAN+∠BAM＝45°，∵∠DAN＝∠BAR，∴∠BAM+∠BAR＝45°，∴∠MAR＝∠MAN＝45°，∵AR＝AN，AM＝AM，∴△AMR≌△AMN（SAS），∴RM＝MN，∵∠D＝∠ABR＝∠ABD＝45°，∴∠RBM＝90°，∴RM2＝BR2+BM2，∵DN＝BR，MN＝RM，∴BM2+DN2＝MN2．14．操作一：解：∵四边形ABCD是正方形，∴∠C＝∠BAD＝90°，由折叠的性质得：∠BAE＝∠MAE，∠DAF＝∠MAF，∴∠MAE+∠MAF＝∠BAE+∠DAF＝∠BAD＝45°，即∠EAF＝45°，故答案为：45；操作二：解：∵四边形ABCD是正方形，∴∠B＝∠C＝90°，由折叠的性质得：∠NFE＝∠CFE，∠ENF＝∠C＝90°，∠AFD＝∠AFM，∴∠ANF＝180°﹣90°＝90°，由操作一得：∠EAF＝45°，∴△ANF是等腰直角三角形，∴∠AFN＝45°，∴∠AFD＝∠AFM＝45°+∠NFE，∴2（45°+∠NFE）+∠CFE＝180°，∴∠NFE＝∠CFE＝30°，∴∠AEF＝90°﹣30°＝60°，故答案为：60；（1）证明：∵△ANF是等腰直角三角形，∴AN＝FN，∵∠AMF＝∠ANF＝90°，∠APN＝∠FPM，∴∠NAP＝∠NFE＝30°，在△ANP和△FNE中，，∴△ANP≌△FNE（ASA）；（2）由（1）得：△ANP≌△FNE，∴AP＝FE，PN＝EN，∵∠NFE＝∠CFE＝30°，∠ENF＝∠C＝90°，∴∠NEF＝∠CEF＝60°，∴∠AEB＝60°，∵∠B＝90°，∴∠BAE＝30°，∴BE＝AB＝1，∴AE＝2BE＝2，设PN＝EN＝a，∵∠ANP＝90°，∠NAP＝30°，∴AN＝PN＝a，AP＝2PN＝2a，∵AN+EN＝AE，∴a+a＝2，解得：a＝﹣1，∴AP＝2a＝2﹣2，故答案为：2﹣2．15．解：【类比探究】过点E作EF⊥CD于点F，连接AF，∵四边形ABCD是正方形，∴AD＝CD＝4，∠ADC＝90°，∵DE＝CE，EF⊥CD，∴DF＝CF＝CD＝2，∠ADC＝∠EFD＝90°，∴AD∥EF，∴S△ADE＝S△ADF，∴S△ADE＝×AD×DF＝×4×2＝4；【拓展应用】如图③，连接CF，∵四边形ABCD和四边形CGFE都是正方形，∴∠BDC＝45°，∠GCF＝45°，∴∠BDC＝∠GCF，∴BD∥CF，∴S△BDF＝S△BCD，∴S△BDF＝BC×BC＝8．16．解：（1）设EF＝m．∵BC＝14，BD＝6，∴CD＝BC﹣BD＝14﹣6＝8，∵AD＝8，∴AD＝DC＝8，∵AD⊥BC，∴∠ADC＝90°，∴AC＝AD＝8，∵四边形EFGH是正方形，∴EH＝FG＝GH＝EF＝m，∠EHG＝∠FGH＝90°，∴∠AHE＝∠FGC＝90°，∵∠DAC＝∠C＝45°，∴∠AEH＝∠EAH＝45°，∠GFC＝∠C＝45°，∴AH＝EH＝m，CG＝FG＝m，∴3m＝8，∴m＝，∴EF＝．（2）∵四边形EFGH是矩形，∴EF∥AC，∴∠DEF＝∠DAC，∠DFE＝∠C，∵∠DAC＝∠C，∴∠DEF＝∠DFE，∴DE＝DF＝x，DA＝DC＝8，∴AE＝CF＝8﹣x，∴EH＝AE＝（8﹣x），EF＝DE＝x，∴y＝＝＝，∴y＝（0＜x＜8）．（3）如图②中，由（2）可知点P在y＝上，设直线MN的解析式为y＝kx+b，把P（a，）代入得到，＝ka+b，∴b＝﹣ka，∴y＝kx+﹣ka，∴N（0，﹣ka），M（a﹣，0），∴ON＝﹣ka，OM＝a﹣∴△MON的面积＝•ON•OM＝×（6﹣a2k﹣）≥×（6+2）•＝6，∴△MON的面积的最小值＝6．解法二：过点P作PR⊥OM于M，PQ⊥ON于Q．设P（a，b），由△NQP∽△NOM，∴＝，设＝＝k，∴MO＝，NQ＝kON，ON＝，∴S△MON＝•OM•ON＝•＝•，∴k＝时，△OMN的面积的最小值为×＝6．17．解：（1）如图1，由作图得，OC＝OD，OE＝OF，PG垂直平分CE，PH垂直平分DF，∴∠PGO＝∠PHO＝90°，∵OE﹣OC＝OF﹣OD，。
北师大版九年级数学上册第一章 特殊平行四边形 压轴题复习练习题
北师大版九年级数学上册第一章特殊平行四边形压轴题复习练习题1、在矩形ABCD中，4AB=，6AD=，M是AD边的中点，P是AB边上的一个动点（不与A、B重合），PM的延长线交射线CD于Q点，MN PQ⊥交射线BC于N点．（1）若点N在BC边上时，如图1．①求证：PN QN=；②请问PMPN是否为定值？若是定值，求出该定值；若不是，请举反例说明；（2）当PBN∆与NCQ∆的面积相等时，求AP的值．2、折纸是一项有趣的活动，在折纸过程中，我们可以通过研究图形的性质和运动，确定图形位置等，进一步发展空间观念．今天，就让我们带着数学的眼光来玩一玩折纸．实践操作如图1，将矩形纸片ABCD沿对角线AC翻折，使点B'落在矩形ABCD所在平面内，B C'和AD相交于点E，连接B D'．解决问题（1）在图1中，①B D'和AC的位置关系是；②将AEC∆剪下后展开，得到的图形是；（2）若图1中的矩形变为平行四边形时()AB BC≠，如图2所示，结论①和结论②是否成立，若成立，请挑选其中的一个结论加以证明；若不成立，请说明理由；拓展应用（3）在图2中，若30oB∠=，AB=AB AD'⊥时，BC的长度为．3、如图1，将三角板放在正方形ABCD上，使三角板的直角顶点E与正方形ABCD的顶点A重合．三角板的一边交CD于点F，另一边交CB的延长线于点G．（1）求证：EF EG=；（2）如图2，移动三角板，使顶点E始终在正方形ABCD的对角线AC上，其他条件不变，（1）中的结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由；（3）如图3，将（2）中的“正方形ABCD”改为“矩形ABCD”，且使三角板的一边经过点B，其他条件不变，若AB a=，BC b=，请直接写出EFEG的值．4、如图，在矩形ABCD中，6AB=，4BC=，动点Q在边AB上，连接CQ，将BQC∆沿CQ 所在的直线对折得到CQN∆，延长QN交直线CD于点M．（1）求证：MC MQ=（2）当1BQ=时，求DM的长；（3）过点D作DE CQ⊥，垂足为点E，直线QN与直线DE交于点F，且13DFDE=，求BQ的长．5、如图，在平面直角坐标系中，四边形ABCD是平行四边形，6AD=，若OA、OB的长是关于x的一元二次方程27120x x-+=的两个根，且OA OB>．（1）求A、B的坐标．（2）求证：射线AO是BAC∠的平分线．（3）若点M在平面直角坐标系内，则在直线AB上是否存在点F，使以A、C、F、M为顶点的四边形为菱形？若存在，直接写出F 点的坐标，若不存在，请说明理由．6、如图1，点M 放在正方形ABCD 的对角线AC （不与点A 重合）上滑动，连结DM ，做MN DM ⊥交直线AB 于N ．（1）求证：DM MN =；（2）若将（1）中的正方形变为矩形，其余条件不变（如图2)，且2DC AD =，求:MD MN ； （3）在（2）中，若CD nAD =，当M 滑动到CA 的延长线上时（如图3)，请你直接写出:MD MN 的比值．7、阅读下面内容：我们已经学习了《二次根式》和《乘法公式》，聪明的你可以发 现：当0a >，0b >时，2(0a b a b -=-2a b ab ∴+，当且仅当a b =时取等号 请利用上述结论解决以下问题： （1）请直接写出答案：当0x >时，1x x +的最小值为 ．当0x <时，1x x+的最大值为 ； （2）若27101x x y x ++=+，(1)x >-，求y 的最小值；（3）如图，四边形ABCD 的对角线AC 、BD 相交于点O ，AOB ∆、COD ∆的面积分别为4和9，求四边形ABCD 面积的最小值．8、如图（1），已知点G 在正方形ABCD 的对角线AC 上，GE BC ⊥，垂足为点E ，GF CD ⊥，垂足为点F ． （1）证明与推断：①求证：四边形CEGF 是正方形； ②推断：AGBE的值为 : （2）探究与证明：将正方形CEGF 绕点C 顺时针方向旋转α角(045)α︒<<︒，如图（2）所示，试探究线段AG 与BE 之间的数量关系，并说明理由； （3）拓展与运用：正方形CEGF 在旋转过程中，当B ，E ，F 三点在一条直线上时，如图（3）所示，延长CG交AD 于点H ．若6AG =，GH =BC = ．9、（1）如图1，将直角的顶点E 放在正方形ABCD 的对角线AC 上，使角的一边交CD 于点F ，另一边交CB 或其延长线于点G ，求证：EF EG =；（2）如图2，将（1）中的“正方形ABCD ”改成“矩形ABCD ”，其他条件不变．若AB m =，BC n =，试求EFEG的值； （3）如图3，将直角顶点E 放在矩形ABCD 的对角线交点，EF 、EG 分别交CD 与CB 于点F 、G ，且EC 平分FEG ∠．若2AB =，4BC =，求EG 、EF 的长．10、在矩形ABCD中，AB＝4，BC＝3，点M，N分别在边AB，CD上，直线MN交矩形对角线AC于点E，将△AME沿直线MN翻折，点A落在点P处，且点P在射线CB上.（1）如图1，当EP⊥BC时，求CN的长；（2）如图2，当EP⊥AC时，求AM的长；（3）请写出线段CP的长的取值范围，并求出当CP的长最大时MN的长.11、【阅读】如图1，四边形OABC中，OA＝a，OC＝3，BC＝2，∠AOC＝∠BCO＝90°，经过点O的直线l将四边形分成两部分，直线l与OC所成的角设为θ，将四边形OABC的直角∠OCB沿直线l折叠，点C落在点D处，我们把这个操作过程记为FZ[θ，a]．【理解】若点D与点A重合，则这个操作过程为FZ[45°，3]；【尝试】（1）若点D恰为AB的中点（如图2），求θ；（2）经过FZ[45°，a]操作，点B落在点E处，若点E在四边形OABC的边AB上，求出a的值；若点E落在四边形OABC的外部，直接写出a的取值范围．12、如图1，在△ABC中，矩形EFGH的一边EF在AB上，顶点G、H分别在BC、AC上，CD是边AB上的高，CD交GH于点I．若CI=4，HI=3，AD=．矩形DFGI 恰好为正方形．（1）求正方形DFGI的边长；（2）如图2，延长AB至P．使得AC=CP，将矩形EFGH沿BP的方向向右平移，当点G刚好落在CP上时，试判断移动后的矩形与△CBP重叠部分的形状是三角形还是四边形，为什么？（3）如图3，连接DG，将正方形DFGI绕点D顺时针旋转一定的角度得到正方形DF′G′I′，正方形DF′G′I′分别与线段DG、DB相交于点M，N，求△MNG′的周长．13、操作探究：数学研究课上，老师带领大家探究《折纸中的数学问题》时，出示如图1所示的长方形纸条ABCD，其中AD＝BC＝1，AB＝CD＝5．然后在纸条上任意画一条截线段MN，将纸片沿MN折叠，MB与DN交于点K，得到△MNK．如图2所示：探究：（1）若∠1＝70°，∠MKN ＝ °；（2）改变折痕MN 位置，△MNK 始终是 三角形，请说明理由； 应用：（3）爱动脑筋的小明在研究△MNK 的面积时，发现KN 边上的高始终是个不变的值．根据这一发现，他很快研究出△KMN 的面积最小值为，此时∠1的大小可以为 °（4）小明继续动手操作，发现了△MNK 面积的最大值．请你求出这个最大值．14、问题背景：如图（1），在四边形ABCD 中．若BC ＝CD ，∠BAD ＝∠BCD ＝90°，则AC 平分∠BAD ．小明为了证明这个结论，将△ABC 绕点C 顺时针旋转90°，请帮助小明完成他的作图．迁移应用：如图（2），在五边形ABCDE 中，∠A ＝∠C ＝90°，AB ＝BC ，BD 平分∠CDE ，求证AE +CD ＝DE ．联系拓展：如图（3），在Rt △ABC 中，AC ＝BC ，若点D 满足AD ＝1716AB ，BD ＝AB ，点P 是AD 的中点，直接写出的值．15、如图，正方形OABC的边OA，OC在坐标轴上，点B的坐标为（﹣4，4）．点P从点A出发，以每秒1个单位长度的速度沿x轴向点O运动；点Q从点O同时出发，以相同的速度沿x轴的正方向运动，规定点P到达点O时，点Q也停止运动．连接BP，过P点作BP的垂线，与过点Q平行于y轴的直线l相交于点D．BD与y轴交于点E，连接PE．设点P运动的时间为t（s）．（1）∠PBD的度数为，点D的坐标为（用t表示）；（2）当t为何值时，△PBE为等腰三角形？（3）探索△POE周长是否随时间t的变化而变化？若变化，说明理由；若不变，试求这个定值．。
【压轴专练】专题07_探索三角形相似的条件(解析版)-2021-2022学年九上压轴题
2021-2022学年北师大版数学九年级上册压轴题专题精选汇编专题07 探索三角形相似的条件一．选择题1．（2021春•沂源县期末）如图，△ABC中，CE⊥AB，垂足为E，BD⊥AC，垂足为点D，CE与BD交于点F，则图中相似三角形有几对（）A．6对B．5对C．4对D．3对【思路引导】根据相似三角形的判定一一证明即可．【完整解答】解：∵BD⊥AC，CE⊥AB，∴∠AEC＝∠ADB＝90°，∠BEF＝∠CDF＝90°，∵∠A＝∠A，∠EFB＝∠DFC，∴△AEC∽△ADB，△BEF∽△CDF，∵∠EBF＝∠ABD，∠BEF＝∠ADB＝90°，∴△BEF∽△BDA∽△CEA∽△CDF，∴共有6对相似三角形，故选：A．2．（2021春•芝罘区期末）如图，小正方形的边长均为1，则A、B、C、D四个选项中的三角形（阴影部分）与△ABC相似的是（）A．B．C．D．【思路引导】应用两三角形相似判定定理，三边对应成比例，分别对各选项进行分析即可得出答案．【完整解答】解：已知给出的三角形的各边分别为、2、、只有选项A的各边为1、、与它的各边对应成比例．故选：A．3．（2021春•周村区期末）平面直角坐标系中，直线y＝﹣x+2和x轴，y轴分别交于A，B两点，在第二象限内有一点P，使△P AO和△AOB相似，则符合要求的点P的个数为（）A．2B．3C．4D．5【思路引导】根据相似三角形的相似条件，画出图形即可解决问题．【完整解答】解：如图，①分别过点O、点A作AB、OB的平行线交于点P1，则△OAP1与△AOB相似（全等），②作AP2⊥OP1，垂足为P2则△AOP2与△AOB相似．③作∠AOP3＝∠ABO交AP1于P3，则△AOP3与△AOB相似．④作AP4⊥OP3垂足为P4，则△AOP4与△AOB相似．故选：C．4．（2021春•雁塔区校级期末）如图，D是△ABC边AB上一点，添加一个条件后，仍不能使△ACD∽△ABC的是（）A．∠ACD＝∠B B．∠ADC＝∠ACB C．AC2＝AD•AB D．【思路引导】直接利用相似三角形的判定方法分别分析得出答案．【完整解答】解：A、当∠ACD＝∠B时，再由∠A＝∠A，可得出△ACD∽△ABC，故此选项不合题意；B、当∠ADC＝∠ACB时，再由∠A＝∠A，可得出△ACD∽△ABC，故此选项不合题意；C、当AC2＝AD•AB时，即＝，再由∠A＝∠A，可得出△ACD∽△ABC，故此选项不合题意；D、当＝时，无法得出△ACD∽△ABC，故此选项符合题意．故选：D．5．（2021•龙湾区模拟）如图，△ABC中，P为边AB上一点，下列选项中的条件，不能说明△ACP与△ACB相似的是（）A．∠ACP＝∠B B．∠APC＝∠ACBC．AC2＝AP×AB D．AB×CP＝AP×AC【思路引导】本题主要应用两三角形相似的判定定理，做题即可．【完整解答】解：A、当∠ACP＝∠B，∠A＝∠A时，△APC∽△ACB，故本选项不符合题意；B、当∠APC＝∠ACB，∠A＝∠A时，△APC∽△ACB，故本选项不符合题意；C、当AC2＝AP•AB，即AC：AB＝AP：AC时，结合∠A＝∠A可以判定△APC∽△ACB，故本选项不符合题意；D、当AB×CP＝AP×AC时，不能判断△APC和△ACB相似．故选：D．6．（2020•黄埔区模拟）如图，在四边形ABCD中，∠BAC＝90°，AB＝6，AC＝8，E是BC 的中点，AD∥BC，AE∥DC，EF⊥CD于点F．下列结论错误的是（）A．四边形AECD的周长是20B．△ABC∽△FECC．∠B+∠ACD＝90°D．EF的长为【思路引导】根据平行四边形和菱形的判定即可证明A选项；根据菱形的性质和三角形的面积公式即可证明C选项和D选项；根据△ABC与△FEC的三边长即可证明B选项．【完整解答】解：∵∠BAC＝90°，AB＝6，AC＝8，∴BC＝＝10，∵AD∥BC，AE∥DC，∴四边形AECD是平行四边形，∵∠BAC＝90°，E是BC的中点，∴AE＝CE＝BC＝5，∴四边形AECD是菱形，∴菱形AECD的周长是20，故A选项正确，不符合题意；∵四边形AECD是菱形，∴∠ACB＝∠ACD，∵∠B+∠ACB＝90°，∴∠B+∠ACD＝90°，故C选项正确，不符合题意；如图，过A作AH⊥BC于点H，∵S△ABC＝BC•AH＝AB•AC，∴AH＝＝，∵点E是BC的中点，BC＝10，四边形AECD是菱形，∴CD＝CE＝5，∵S▱AECD＝CE•AH＝CD•EF，∴EF＝AH＝．故D选项正确，不符合题意；在Rt△EFC中，EF＝，EC＝5，∴FC＝＝，在Rt△CAB中，AB＝6，AC＝8，BC＝10，∵＝，＝，＝，∴△ABC与△FEC不相似，故B选项错误，符合题意．故选：B．7．（2020秋•叶县期中）如图，在△ABC中，点D、E分别在边AB、AC上，则在下列四个条件中：①∠AED＝∠B；②DE∥BC；③；④AD•BC＝DE•AC，能满足△ADE∽△ACB的条件有（）A．1个B．2个C．3个D．4个【思路引导】根据相似三角形的判定定理对各条件进行逐一判断即可．【完整解答】解：①∠B＝∠AED，∠A＝∠A，则可判断△ADE∽△ACB，故①符合题意；②DE∥BC，则△ADE∽△ABC，故②不符合题意，③，且夹角∠A＝∠A，能确定△ADE∽△ACB，故③符合题意；④由AD•BC＝DE•AC可得＝，此时不确定∠ADE＝∠ACB，故不能确定△ADE∽△ACB，故④不符合题意，故选：B．8．（2020•浙江自主招生）已知点A，C在直线BD的同侧，且AB⊥BD于B，CD⊥BD于D，AB＝6，CD＝4，BD＝14，现有点P在直线BD上，并且满足△ABP与△CDP相似，则这样的点P的个数为（）A．3B．5C．6D．7【思路引导】设DP＝x，根据已知可以分三种情况：①当点P在线段BD上时；②当点P在线段BD的右侧时；③当点P在线段BD的左侧时；分别得出比例式得出方程，解方程求出x的值，即可得出结果．【完整解答】解：∵AB⊥DB，CD⊥DB，∴∠D＝∠B＝90°，设DP＝x，分三种情况：①当点P在线段BD上时，当PD：AB＝CD：PB时，△PDC∽△ABP，∴＝，解得：DP＝2或12，当PD：PB＝CD：AB时，△PCD∽△P AB，∴，解得：DP＝5.6；②当点P在线段BD的右侧，如图1所示：当时，△PCD∽△P AB，即，解得：x＝28；当时，△PCD∽△APB，即，解得：x＝﹣7±（负值舍去），∴PD＝﹣7+；③当点P在线段BD的左侧时，如图2所示：当时，△PCD∽△APB，即，解得：x＝7±（负值舍去），∴PD＝7+；综上所述：当DP＝5.6或2或12或28或﹣7+或7+时，△ABP与△CDP相似，即这样的点P的个数有6个；故选：C．9．（2019春•宝安区校级月考）如图，正方形ABCD中，AB＝2，点N为AD为边上一点，连接BN，作AP⊥BN于点P，点M为AB边上一点，且∠PMA＝∠PCB，连接CM．下列结论正确的个数有（）（1）△P AM∽△PBC（2）PM⊥PC；（3）∠MPB＝∠MCB；（4）若点N为AD中点，则S△PCN＝6（5）AN＝AMA．5个B．4个C．3个D．2个【思路引导】根据互余角性质得∠P AM＝∠PBC，进而得△P AM∽△PBC，可以判断（1）；由相似三角形得∠APM＝∠BPC，进而得∠CPM＝∠APB，从而判断（2）；由B、C、P、M四点共圆得∠MPB＝∠MCB，进而判断（3）；过P点作EF⊥BC，分别志AD、BC相交于点EF，由相似三角形得PF，进而由△BCN与△BCP的面积之差求得△PCN的面积便可判断（4）；由△APB∽△NAB得，再结合△P AM∽△PBC便可判断（5）．【完整解答】解：（1）∵AP⊥BN，∴∠P AM+∠PBA＝90°，∵∠PBA+∠PBC＝90°，∴∠P AM＝∠PBC，∵∠PMA＝∠PCB，∴△P AM∽△PBC，故（1）正确；（2）∵△P AM∽△PBC，∴∠APM＝∠BPC，∴∠CPM＝∠APB＝90°，即PM⊥PC，故（2）正确；（3）∵∠MPC+∠MBC＝90°+90°＝180°，∴B、C、P、M四点共圆，∴∠MPB＝∠MCB，故（3）正确；（4）过点P作EF⊥BC，分别交AD、BC于E、F点，∵N为AD的中点，AB＝2∴AN＝DN＝，BC＝EF＝2，∴BN＝，易证△ANP∽△NBA，得，即，∴PN＝1，∴PB＝5﹣1＝4，∵AD∥BC，∴△PEN∽△PFB，∴，∴PF＝，∴，故（4）错误；（5）易证△P AN∽△P AB，∴，∵△P AM∽△PBC，∴，∴，∵AB＝BC，∴AM＝AN，故（5）正确；故选：B．二．填空题10．（2021春•濮阳期末）在△ABC中，AB＝6cm，AC＝9cm，动点D从点B开始沿BA边运动，速度为1cm/s；动点E从点A开始沿AC边运动，速度为2cm/s．如果D，E两动点同时运动，那么当它们运动或s时，由D，A，E三点连成的三角形与△ABC 相似．【思路引导】分两种情形①当＝时，②当＝时，分别构建方程求解即可．【完整解答】解：根据题意得：AE＝2t，BD＝t，∴AD＝6﹣t，∵∠A＝∠A，∴分两种情况：①当＝时，即＝，解得：t＝；②当＝时，即＝，解得：t＝；综上所述：当t＝或时，△ADE与△ABC相似．11．（2021•葫芦岛二模）如图，在△ABC中，AB＝15，AC＝18，D为AB上一点，且AD＝AB，在AC边上取一点E，便以A，D，E为顶点的三角形与△ABC相似，则AE等于12或．【思路引导】根据相似三角形对应边成比例得出＝或＝，再代值计算即可．【完整解答】解：∵△ABC∽△ADE或△ABC∽△AED，∴＝或＝，∵AD＝AB，AB＝15，∴AD＝10，∵AC＝18，∴＝或＝，解得：AE＝12或．故答案为：12或．12．（2020秋•北海期末）如图，在△ABC中，AB＝8，BC＝16，点P是AB边的中点，点Q 是BC边上一个动点，当BQ＝2或8 时，△BPQ与△BAC相似．【思路引导】直接利用△BPQ∽△BAC或△BPQ∽△BCA，分别得出答案．【完整解答】解：∵AB＝8，BC＝16，点P是AB边的中点，∴BP＝4．当△BPQ∽△BAC时，则＝，故＝，解得：BQ＝8；当△BPQ∽△BCA时，则＝，故＝，解得：BQ＝2，综上所述：当BQ＝2或8时，△BPQ与△BAC相似．故答案为：2或8．13．（2021•抚顺县模拟）如图，在正方形网格中有3个斜三角形：①△ABC；②△CDB；③△DEB；其中能与△ABC相似的是③△DEB．（△ABC除外）【思路引导】分别求出三个三角形的三边的比，符合这个结果就是与△ABC相似的．【完整解答】解：∵△ABC的三边之比是AB：AC：BC＝1：：，②△CDB的三边之比是CD：BC：BD＝1：：；③△DEB中DE：BD：BE＝2：2：＝1：：．∴③（△DEB）与△ABC相似，故答案为：③△DEB．14．（2021•河北模拟）如图，在Rt△ABC的直角边AC上有一任意点P（不与点A、C重合），过点P作一条直线，将△ABC分成一个三角形和一个四边形，则所得到的三角形与原三角形相似的直线最多有 4 条．【思路引导】过点P作直线与另一边相交，使所得的三角形与原三角形已经有一个公共角，只要再作一个等于△ABC的另一个角即可．【完整解答】解：如图所示，①过点P作AB的垂线段PD，则△ADP∽△ACB；②过点P作BC的平行线PE，交AB于E，则△APE∽△ACB；③过点P作AB的平行线PF，交BC于F，则△PCF∽△ACB；④作∠PGC＝∠A，则△GCP∽△ACB．故答案为：4．15．（2020秋•松江区月考）如图，△ABC中，∠C＝90°，∠B＝30°，AC＝2，点P是边AB上一点，将△ABC沿经过点P的直线折叠，使得点A落在边BC上的A′处，若△PBA′恰好和△ABC相似，则此时AP的长为或2﹣2 ．【思路引导】分两种情形：①如图1中，当∠P A′B＝∠C＝90°时，△BP A′∽△BAC，②如图2中，当∠PBC＝90°时，△BP A′∽△BCA，分别利用相似三角形的性质构建方程求解即可．【完整解答】解：①如图1中，当∠P A′B＝∠C＝90°时，设P A＝P A′＝x．在Rt△ABC中，∵∠C＝90°，AC＝2，∠B＝30°，∴AB＝2AC＝4，BC＝AC＝2，∵∠B＝∠B，∠BA′P＝∠C＝90°，∴△BP A′∽△BAC，∴＝，∴＝，∴x＝．②如图2中，当∠BP A′＝90°时，△BP A′∽△BCA，∴＝，∴＝，∴x＝2﹣2，综上所述，满足条件的AP的值为或2﹣2．16．（2020秋•江阴市月考）如图，在△ABC纸板中，AC＝8，BC＝4，AB＝10，P是AC上一点，过点P沿直线剪下一个与△ABC相似的小三角形纸板，如果有4种不同的剪法，那么AP长的取值范围是6≤AP＜8 ．【思路引导】分四种情况讨论，依据相似三角形的对应边成比例，即可得到AP的长的取值范围．【完整解答】解：如图所示，过P作PD∥AB交BC于D或PE∥BC交AB于E，则△PCD∽△ACB或△APE∽△ACB，此时0＜AP＜8；如图所示，过P作∠APF＝∠B交AB于F，则△APF∽△ABC，此时0＜AP≤8；如图所示，过P作∠CPG＝∠CBA交BC于G，则△CPG∽△CBA，此时，△CPG∽△CBA，当点G与点B重合时，CB2＝CP×CA，即42＝CP×8，∴CP＝2，AP＝6，∴此时，6≤AP＜8；综上所述，要有4种不同的剪法，使得过点P沿直线剪下一个与△ABC相似，则AP长的取值范围是6≤AP＜8．故答案为：6≤AP＜8．17．（2019•东平县二模）如图，△ABC是边长为6cm等边三角形，动点P、Q同时从A、B 出发，分别沿AB、BC方向匀速运动，其中点P运动的速度是1cm/s，点Q运动的速度是2cm/s，当点Q到达点C时，P、Q两点停止运动，在运动过程中作QR∥BA交AC于点R，连接PR，设运动的时间为t（s），当t＝1.2 s时△APR∽△PRQ．【思路引导】先证△CRQ为等边三角形，并用含t的式子表示图中的相关线段，由QR∥BA推得∠QRP＝∠APR，从而△PRQ中再有一个角等于∠A，即等于60°，即可得△APR ∽△PRQ．根据相似三角形的性质列比例式求解即可．【完整解答】解：∵△ABC是边长为6cm等边三角形，∴∠A＝∠B＝∠C＝60°∵QR∥BA∴∠CRQ＝∠A＝60°，∠CQR＝∠B＝60°∴△CRQ为等边三角形∵点P运动的速度是1cm/s，点Q运动的速度是2cm/s∴AP＝t，PB＝6﹣t，BQ＝2t，CQ＝CR＝RQ＝6﹣2t，AR＝2t∵QR∥BA∴∠QRP＝∠APR若要△APR∽△PQR，则需满足∠RPQ＝60°∴∠BPQ+∠APR＝120°，∠ARP+∠APR＝120°∴∠BPQ＝∠ARP又∵∠A＝∠B∴△APR∽△BQP∴＝∴＝解得t＝1.2故答案为1.2．18．（2011春•成华区期末）如图，正方形ABCD的边长为4，AE＝EB，MN＝2，线段MN 的两端在CB、CD上滑动，当CM＝或时，△ADE与△CMN相似．【思路引导】根据AE＝EB，△AED中AD＝2AE，所以在△MNC中，分CM与AE和AD 是对应边两种情况利用相似三角形对应边成比例求出CM与CN的关系，然后利用勾股定理列式计算即可．【完整解答】解：∵AE＝EB，∴AD＝2AE，又∵△AED与以M、N、C为顶点的三角形相似，∴分两种情况：①CM与AD是对应边时，CM＝2CN，∴CM2+CN2＝MN2＝4，即CM2+CM2＝4，解得：CM＝；②CM与AE是对应边时，CM＝CN，∴CM2+CN2＝MN2＝4，即CM2+4CM2＝4，解得：CM＝．综上所述：当CM为或时，△AED与△CMN相似．故答案是：或．19．（2003•武汉）△ABC中，以AB为直径的▱O交BC边于点D，连接AD，要使△ABD与△ACD相似，则△ABC的边AB与AC之间，应满足的条件为AB⊥AC．（填入一个即可）【思路引导】本题主要应用两三角形相似的判定定理，做题即可．【完整解答】解：∵AB为▱O的直径∴∠ADC＝∠BDA＝90°∴当∠CAD＝∠B时，△ABD∽△CAD∵∠CAD+∠C＝90°∴∠B+∠C＝90°∴AB⊥AC答案不唯一，如AB⊥AC．三．解答题20．（2021春•朝阳区校级期末）如图所示，在四边形ABCD中，CA是∠BCD的角平分线，且AC2＝CD•BC，求证：△ABC∽△DAC．【思路引导】根据两边成比例夹角相等两三角形相似证明即可．【完整解答】证明：∵AC平分∠BCD，∴∠ACB＝∠ACD，∵AC2＝CD•BC，∴＝，∴△ABC∽△DAC．21．（2021春•龙口市期末）如图，在Rt△ABC中，∠C＝90°，AC＝10cm，BC＝8cm．点M从点C出发，以2cm/s的速度沿CA向点A匀速运动，点N从点B出发，以1cm/s的速度沿BC向点C匀速运动，当一个点到达终点时，另一点也随即停止运动．（1）经过几秒后，△MCN的面积等于△ABC面积的？（2）经过几秒，△MCN与△ABC相似？【思路引导】（1）设经过x秒，△MCN的面积等于△ABC面积的，根据三角形的面积和已知列出方程，求出方程的解即可；（2）根据相似三角形的判定得出两种情况，再求出t即可．【完整解答】解：（1）设经过x秒，△MCN的面积等于△ABC面积的．×2x（8﹣x）＝×8×10×．解得x1＝x2＝4．答：经过4秒后，△MCN的面积等于△ABC面积的；（2）设经过t秒，△MCN与△ABC相似．∵∠C＝∠C，∴可分为两种情况：①＝，即＝，解得t＝；②＝，即＝．解得t＝．答：经过或秒，△MCN与△ABC相似．22．（2021•越秀区校级二模）如图，在△P AB中，点C、D在AB上，PC＝PD＝CD，∠A＝∠BPD，求证：△APC∽△PBD．【思路引导】根据等腰三角形的性质得出∠PCD＝∠PDC，根据三角形的外角性质得出∠A+∠APC＝∠PCD，∠B+∠BPD＝∠PDC，求出∠B＝∠APC，再根据相似三角形的判定推出即可．【完整解答】证明：∵PC＝PD，∴∠PCD＝∠PDC，∵∠A+∠APC＝∠PCD，∠B+∠BPD＝∠PDC，又∵∠A＝∠BPD，∴∠B＝∠APC，∴△APC∽△PBD．23．（2020秋•崇川区期末）如图，已知BD⊥AB于点B，AC⊥AB于点A，且BD＝4，AC＝3，AB＝a，在线段AB上是否存在一点E，使△BDE∽△ACE？【思路引导】当∠ACE＝∠BDE时，△ACE∽△BDE，利用相似三角形的性质解答．【完整解答】解：存在，理由如下：∵BD⊥AB于点B，AC⊥AB，∴∠A＝∠B＝90°，当∠ACE＝∠BDE时，△ACE∽△BDE，∴＝＝，∴AE＝BE，∴AE＝AB＝a．∴点E在线段AB上，距离点A的距离是a．24．（2020秋•宁德期末）如图，在矩形ABCD中，点E是BC边上的点，AC⊥DE，垂足为F．求证：△ABC∽△ECD．【思路引导】利用“两角法”证得结论．【完整解答】证明：∵四边形ABCD是矩形，∴∠B＝∠BCD＝90°．∴∠ACB+∠ACD＝90°．又∵AC⊥DE，∴∠CDE+∠ACD＝90°．∴∠ACB＝∠CDE．∴△ABC∽△ECD．25．（2021•拱墅区二模）如图，在△ABC中，D、E分别是边AC、BC的中点，F是BC延长线上一点，∠F＝∠B．（1）若AB＝10，求FD的长；（2）若AC＝BC，求证：△CDE∽△DFE．【思路引导】（1）首先利用中位线定理得到DE∥AB以及DE的长，再证明∠DEC＝∠F 即可；（2）根据等腰三角形的性质得到∠A＝∠B，进而求出∠CDE＝∠F并结合∠CED＝∠DEF即可证明△CDE∽△DFE．【完整解答】解：（1）∵D、E分别是AC、BC的中点，∴DE∥AB，DE＝AB＝5，∵DE∥AB，∴∠DEC＝∠B，而∠F＝∠B，∴∠DEC＝∠F，∴DF＝DE＝5；（2）∵AC＝BC，∴∠A＝∠B，∵∠CDE＝∠A，∠CED＝∠B，∴∠CDE＝∠B，∵∠B＝∠F，∴∠CDE＝∠F，∵∠CED＝∠DEF，∴△CDE∽△DFE．26．（2020秋•肇源县期末）已知：如图，在Rt△ACB中，∠C＝90°，AC＝4cm，BC＝3cm，点P由B出发沿BA方向向点A匀速运动，速度为1cm/s；点Q由A出发沿AC方向向点C匀速运动，速度为2cm/s；连接PQ．若设运动的时间为t（s）（0＜t＜2），当t为何值时，以A、P、Q为顶点的三角形与△ABC相似？【思路引导】先利用勾股定理计算出AB＝5，由于∠P AQ＝∠BAC，根据两组对应边的比相等且夹角对应相等的两个三角形相似，当＝时，△APQ∽△ABC，即＝；当＝时，△APQ∽△ACB，即＝，然后分别解方程求出t即可．【完整解答】解：∵∠C＝90°，AC＝4cm，BC＝3cm，∴AB＝＝5，则BP＝t，AQ＝2t，AP＝5﹣t，∵∠P AQ＝∠BAC，当＝时，△APQ∽△ABC，即＝，解得t＝；当＝时，△APQ∽△ACB，即＝，解得t＝；答：t为s或s时，以A、P、Q为顶点的三角形与△ABC相似．27．（2019秋•临安区期末）如图，点B、D、E在一条直线上，BE交AC于点F，＝，且∠BAD＝∠CAE．（1）求证：△ABC∽△ADE；（2）求证：△AEF∽△BCF．【思路引导】（1）根据相似三角形的判定定理证明；（2）根据相似三角形的性质定理得到∠C＝∠E，结合图形，证明即可．【完整解答】（1）∵∠BAD＝∠CAE∴∠BAD+∠CAD＝∠CAE+∠CAD即∠BAC＝∠DAE在△ABC和△ADE中＝，∠BAC＝∠DAE，∴△ABC∽△ADE；（2）∵△ABC∽△ADE，∴∠C＝∠E、在△AEF和△BFC中，∠C＝∠E，∠AFE＝∠BFC，∴△AEF∽△BCF．28．（2020春•肇源县期末）如图，在△ABC中，∠B＝90°，AB＝6cm，BC＝12cm，点P从点A开始，沿AB边以1cm/s的速度向点B运动：点Q从点B开始，沿BC边以2cm/s的速度向点C运动，当点P运动到点B时，运动停止，如果P、Q分别从A、B两点同时出发．（1）几秒后△PBQ的面积等于8cm2？（2）几秒后以P、B、Q为顶点的三角形与△ABC相似？【思路引导】（1）设t秒后△PBQ的面积等于8cm，此时，AP＝t，BP＝6﹣t，BQ＝2t，再由三角形的面积公式即可得出结论；（2）设x秒后以P、B、Q为顶点的三角形与△ABC相似，此时，AP＝x，BP＝6﹣x，BQ＝2x，再分△BPQ∽△BAC与△BPQ∽△BCA两种情况进行讨论即可．【完整解答】解：（1）设t秒后△PBQ的面积等于8cm，此时，AP＝t，BP＝6﹣t，BQ＝2t，∵S△PBQ＝BP•BQ，即（6﹣t）×2t＝8，即t2﹣6t+8＝0，解得t1＝2，t2＝4．∴2秒或4秒后，△PBQ的面积等于8cm2；（2）设x秒后以P、B、Q为顶点的三角形与△ABC相似，此时，AP＝x，BP＝6﹣x，BQ＝2x，①若△BPQ∽△BAC，则＝，即＝，解得x＝3；②若△BPQ∽△BCA，则＝，即＝，解得x＝1.2．综上所述，1.2秒或3秒后，以P、B、Q为顶点的三角形与△ABC相似．。
北师大版九年级数学上册期末压轴题综合复习题(含答案)
2021-2022年北师大版九年级数学上册期末压轴题综合复习题1、如图，矩形ABCD中，AD＝3，AB＝4，点P是对角线AC上一动点（不与A，C重合），连结BP，作PE⊥PB，交射线DC于点E，以线段PE，PB为邻边作矩形BPEF．过点P 作GH⊥CD，分别交AB、CD于点G、H．（1）求证：△PGB∽△EHP；（2）求的值；（3）求矩形BPEF的面积的最小值．2、已知：如图，菱形ABCD中，点E，F，G，H分别在边AB，BC，CD，DA上，且BE＝BF＝DH＝DG．（1）求证：四边形EFGH是矩形；（2）已知∠B＝60°，AB＝6．请从A，B两题中任选一题作答，我选择题．A题：当点E是AB的中点时，矩形EFGH的面积是．B题：当BE＝时，矩形EFGH的面积是8．3、在△ABC中，∠ABC＝90°，ABnBC，M是BC上一点，连接AM．（1）如图1，若n＝1，N是AB延长线上一点，CN与AM垂直，求证：BM＝BN．（2）过点B作BP⊥AM，P为垂足，连接CP并延长交AB于点Q．①如图2，若n＝1，求证：CP BM．PQ BQ②如图3，若M是BC的中点，求证：∠BPQ ＝∠BAC．4、已知：矩形OABC的顶点O在平面直角坐标系的原点，边OA、OC分别在x、y轴的正半轴上，且OA＝3cm，OC＝4cm，点M从点A出发沿AB向终点B运动，点N从点C 出发沿CA向终点A运动，点M、N同时出发，且运动的速度均为1cm/秒，当其中一个点到达终点时，另一点即停止运动．设运动的时间为t秒．（1）当点N运动1秒时，求点N的坐标；（2）试求出多边形OAMN的面积S与t的函数关系式；（3）t为何值时，以△OAN的一边所在直线为对称轴翻折△OAN，翻折前后的两个三角形所组成的四边形为菱形？5、已知：如图，在Rt△ACB中，∠C＝90°，AC＝3cm，BC＝3cm，点P由B点出发沿BA方向向点A匀速运动，速度为2cm/s；点Q由A点出发沿AC方向向点C匀速运动，速度为cm/s；若设运动的时间为t（s）（0＜t＜3），解答下列问题：（1）如图①，连接PC，当t为何值时△APC∽△ACB，并说明理由；（2）如图②，当点P，Q运动时，是否存在某一时刻t，使得点P在线段QC的垂直平分线上，请说明理由；（3）如图③，当点P，Q运动时，线段BC上是否存在一点G，使得四边形PQGB为菱形？若存在，试求出BG长；若不存在请说明理由．6、如图，已知菱形ABCD中，AB＝5，点E是BC边上一点（不与B，C重合），以BE为边构造菱形BEFG，使点G落在AB的延长线上，连接BD，GE，射线FE交BD于点H．（1）求证：四边形BGEH是平行四边形；（2）请从下面A，B两题中任选一题作答．我选择题．A．若四边形BGEH为菱形，则BD的长为．B．连接HC，CF，BF，若BD＝6，且四边形BHCF为矩形，则CF的长为3．7、如图，在平面直角坐标系中，点A（﹣4，2），点B在第一象限，AB平行于x轴且AB＝5．（1）点B的坐标为．（2）如图1，过点A作AC⊥x轴于C，在x轴上是否存在点D，使得△AOC与△BOD 相似？（3）如图2，将△AOB折叠，使得点A刚好落在O处，此时折痕交AB于点D，交AO 于点E，在直线AO上有两个动点P，Q（点P在点Q的左侧），且线段PQ＝，求四边形BDPQ的周长最小值．8、如图1，已知四边形ABCD的对角线AC，BD相交于点O，点M是BC边的中点，过点M作ME∥AC交BD于点E，作MF∥BD交AC于点F．（1）如图2，若四边形ABCD是菱形，求证：四边形OEMF是矩形；（2）如图3，若四边形ABCD是矩形，则四边形OEMF是（在横线上填一个特殊平行四边形的名称）（3）如图4，若四边形ABCD是矩形，点M是BC延长线上的一个动点，点F落在AC的延长线上，点E落在线段OD上，其余条件不变，写出OB，ME，MF三条线段之间存在的数量关系，并说明理由．9、如图1，一张矩形纸片ABCD，其中AD＝8cm，AB＝6cm，先沿对角线BD折叠，点C落在点C′的位置，BC′交AD于点G．（1）求证：BG＝DG；（2）求C′G的长；（3）如图2，再折叠一次，使点D与A重合，折痕EN交AD于M，求EM的长．10、如图（1）是矩形纸片ABCD连续两次对折展开平铺后的图形，折痕分别为EF，MN，GH．（1）如图（2），连接BD，与折痕GH，EF，MN分别交于点S，O，T，求证：OE=OF；（2）如图（3），连接ET并延长交CD于点Q，连接FS并延长交AB于点P，连接EP，FQ．求证：四边形EPFQ是菱形；（3）若四边形EPFQ是正方形，则矩形ABCD需满足的条件是．12、如图1，在正方形ABCD的外部，分别以AB，CD为边作菱形ABEF和菱形CDGH，连接EH，FG（1）求证：FG=EH（2）请从A，B两个题目中任选一题作答A 如图2，若AB=4，∠BAF=60°，∠CDG=30°，求四边形AFGD的面积B 如图3，若∠BAF=∠CDG，求证；四边形EFGH是矩形13、问题情境：如图1，在菱形ABCD中，点E、F分别为AB，BC边上的点，连接AF，DE相交于点O，且∠AOE=∠ADC，试探究：AF与DE的数量关系．特例探究：如图2，当菱形ABCD是正方形时，AF与DE有怎样的数量关系呢？请你直接写出结论，不必证明；类比解答：类比特例探究的结论，猜想问题情境中AF与DE的数量关系，并说明理由；拓展延伸：将图1中的菱形ABCD改为▱ABCD（如图3）其中AB=a，AD=b，点E、F、G、H 分别为AB、BC、CD、DA边上的动点，连接EG、HF相交于点O，且∠HOE=∠ADC，试探究：EG与FH的数量关系，用含a、b的式子直接写出的值，不必说明理由．14、问题情境：已知，菱形ABCD，点B关于直线AD的对称点为点E，连接AE、CE，线段CE交直线AD于点F，连接BF．（1）特例研究：如图1，当∠ABC=90°时，点A、B、E在同一条直线上，求证：BF=CE．（2）类比思考：请从下列A、B两题中任选一题作答：我选择A或B题．当90°＜∠ABC＜180°时，小彬提出如下问题：A、若点E、D、C三点在同一直线上，请在下面画出符合条件的图形，并直接写出∠ABC的度数；B、如图2，若点E、D、C三点不在同一直线上，判断（1）中的结论是否仍然成立，若成立，请证明；若不成立，说明理由．（3）拓展分析：请从下列A、B两题中任选一题作答，我选择A或B题．A：如图3，当∠ABC=135°时，CD的延长线交AE于点G，直接写出的值；B：当∠ABC=45°时，直线AE与CD相交于点G，请在下面画出符合条件的图形，并直接写出的值．15、阅读下列材料，完成任务：自相似图形定义：若某个图形可分割为若干个都与它相似的图形，则称这个图形是自相似图形．例如：正方形ABCD中，点E、F、G、H分别是AB、BC、CD、DA边的中点，连接EG，HF交于点O，易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形，且与原正方形相似，故正方形是自相似图形．任务：（1）图1中正方形ABCD分割成的四个小正方形中，每个正方形与原正方形的相似比为；（2）如图2，已知△ABC中，∠ACB=90°，AC=4，BC=3，小明发现△ABC也是“自相似图形”，他的思路是：过点C作CD⊥AB于点D，则CD将△ABC分割成2个与它自己相似的小直角三角形．已知△ACD∽△ABC，则△ACD与△ABC的相似比为；（3）现有一个矩形ABCD是自相似图形，其中长AD=a，宽AB=b（a＞b）．请从下列A、B两题中任选一条作答：我选择题．A：①如图3﹣1，若将矩形ABCD纵向分割成两个全等矩形，且与原矩形都相似，则a=（用含b的式子表示）；②如图3﹣2若将矩形ABCD纵向分割成n个全等矩形，且与原矩形都相似，则a=（用含n，b的式子表示）；B：①如图4﹣1，若将矩形ABCD先纵向分割出2个全等矩形，再将剩余的部分横向分割成3个全等矩形，且分割得到的矩形与原矩形都相似，则a=或（用含b的式子表示）；②如图4﹣2，若将矩形ABCD先纵向分割出m个全等矩形，再将剩余的部分横向分割成n个全等矩形，且分割得到的矩形与原矩形都相似，则a=（用含m，n，b的式子表示）．16、综合与实践问题情境：正方形折叠中的数学已知正方形纸片ABCD中，AB＝4，点E是AB边上的一点，点G是CE的中点，将正方形纸片沿CE所在直线折叠，点B的对应点为点B′．（1）如图1，当∠BCE＝30°时，连接BG，B′G，求证：四边形BEB′G是菱形；深入探究：（2）在CD边上取点F，使DF＝BE，点H是AF的中点，再将正方形纸片ABCD沿AF 所在直线折叠，点D的对应点为D′，顺次连接B′，G，D′，H，B'，得到四边形B′GD′H．请你从A，B两题中任选一题作答，我选择题．A题：如图2，当点B'，D′均落在对角线AC上时，①判断B′G与D′H的数量关系与位置关系，并说明理由；②直写出此时点H，G之间的距离．B题：如图3，点M是AB的中点，MN∥BC交CD于点N，当点B'，D′均落在MN上时，①判断B′G与D′H的数量关系与位置关系，并说明理由；②直接写出此时点H，G之间的距离．17、如图，直线y＝x+n交x轴于点A（﹣8，0），直线y＝﹣x﹣4经过点A，交y轴于点B，点P是直线y＝﹣x﹣4上的一个动点，过点P作x轴的垂线，过点B作y轴的垂线，两条垂线交于点D，连接PB，设点P的横坐标为m．（1）若点P的横坐标为m，则PD的长度为（用含m的式子表示）；（2）如图1，已知点Q是直线y＝x+n上的一个动点，点E是x轴上的一个动点，是否存在以A，B，E，Q为顶点的平行四边形，若存在，求出E的坐标；若不存在，说明理由；（3）如图2，将△BPD绕点B旋转，得到△BD′P′，且旋转角∠PBP′＝∠OCA，当点P的对应点P′落在坐标轴上时，请直接写出点P的坐标．18、如图，在平面直角坐标系中，过原点O及A（8，0）、C（0，6）作矩形OABC，连接AC，一块直角三角形PDE的直角顶点P始终在对角线AC上运动（不与A、C重合），且保持一边PD始终经过矩形点B，PE交x轴于点Q（1）＝；（2）在点P从点C运动到点A的过程中，的值是否发生变化？如果变化，请求出其变化范围，如果不变，请说明理由，并求出其值；（3）若将△QAB沿直线BQ折叠后，点A与点P重合，则PC的长为．19、在直角坐标系中，过原点O及点A（8，0），C（0，6）作矩形OABC，连接OB，点D为OB的中点，点E是线段AB上的动点，连接DE，作DF⊥DE，交OA于点F，连接EF．已知点E从A点出发，以每秒1个单位长度的速度在线段AB上移动，设移动时间为t秒．（1）如图1，当t＝3时，求DF的长．（2）如图2，当点E在线段AB上移动的过程中，的大小是否发生变化？如果变化，请说明理由；如果不变，请求出的值．（3）连接AD，当AD将△DEF分成的两部分的面积之比为1：2时，求相应的t的值．20、如图①，已知点A（﹣1，0），B（0，﹣2），▱ABCD的边AD与y轴交于点E，且E为AD的中点，双曲线y＝经过C、D两点．（1）求k的值；（2）点P在双曲线y＝上，点Q在y轴上，若以点A、B、P、Q为顶点的四边形是平行四边形，直接写出满足要求的所有点Q的坐标；（3）以线段AB为对角线作正方形AFBH（如图③），点T是边AF上一动点，M是HT 的中点，MN⊥HT，交AB于N，当点T在AF上运动时，的值是否发生改变？若改变，求出其变化范围：若不改变，请求出其值，并给出你的证明．参考答案1、如图，矩形ABCD中，AD＝3，AB＝4，点P是对角线AC上一动点（不与A，C重合），连结BP，作PE⊥PB，交射线DC于点E，以线段PE，PB为邻边作矩形BPEF．过点P 作GH⊥CD，分别交AB、CD于点G、H．（1）求证：△PGB∽△EHP；（2）求的值；（3）求矩形BPEF的面积的最小值．1、【解答】（1）证明：∵∠PGB＝∠EHP＝∠BPE＝90°，∴∠PBG＝∠EPH（同角的余角相等），∴△PGB∽△EHP；（2）解：连接BE，∵PE⊥PB，∴∠BPE＝90°，∵∠BCE＝90°，∴∠BCE+∠BPE＝180°，∴P，B，E，C四点共圆，∴∠PBE＝∠PCE，在Rt△BPE与Rt△ADC中，∠D＝∠BP E＝90°，∠ACD＝∠PBE，∴Rt△BPE∽Rt△ADC，∴＝，即＝＝；（3）设AP的长为x．∵AD＝3，AB＝4，∴由勾股定理得到：AC＝＝＝5∵cos∠GAP＝＝＝，∴AG＝AP＝x．同理，sin∠GAP＝＝＝．则GP＝x．在Rt△PBG中，PB2＝BG2+PG2＝（4﹣x）2+（x）2＝x2﹣x+16，∵＝＝．∴PE＝PB，∴S矩形BPEF＝PB•PE＝PB2＝（x2﹣x+16）＝（x﹣）2+，∵0＜x＜5，∴x＝时，S有最小值．2、已知：如图，菱形ABCD中，点E，F，G，H分别在边AB，BC，CD，DA上，且BE＝BF＝DH＝DG．（1）求证：四边形EFGH是矩形；（2）已知∠B＝60°，AB＝6．请从A，B两题中任选一题作答，我选择A或B题．A题：当点E是AB的中点时，矩形EFGH的面积是9．B题：当BE＝2或4时，矩形EFGH的面积是8．2、【解答】（1）证明：∵四边形ABCD是菱形，∴AD∥BC，AB＝BC＝CD＝AD，∴∠A+∠B＝180°，∵BE＝BF＝DH＝DG，∴AE＝AH＝CF＝CG，∴∠AEH＝∠AHE＝（180°﹣∠A），∠BEF＝∠BFE＝（180°﹣∠B），∴∠AEH+∠BEF＝（180°﹣∠A）+（180°﹣∠B）＝90°，同法可证：∠EFG＝∠EHG＝90°，∴四边形EFGH是矩形．（2）解：A题：连接AC，BD交于点O．∵AE＝BE，∴AH＝DH，BF＝CF，CG＝GD，∴EF＝AC，EH＝BD，∵AB＝BC＝6，∠ABC＝60°，∴△ABC是等边三角形，∴AC＝AB＝6，∵OB⊥AC，∴OB＝3，BD＝2OB＝6，∴EF＝3，EH＝3，∴S矩形EFGH＝EF•EH＝9．故答案为9．B题：设BE＝x，则AE＝6﹣x，EF＝x，EH＝（6﹣x），由题意：x•（6﹣x）＝8，解得x＝4或2，∴BE＝2或4．故答案为A或B，9，2或4．3、在△ABC中，∠ABC＝90°，ABnBC=，M是BC上一点，连接AM．（1）如图1，若n＝1，N是AB延长线上一点，CN与AM垂直，求证：BM＝BN．（2）过点B作BP⊥AM，P为垂足，连接CP并延长交AB于点Q．①如图2，若n＝1，求证：CP BMPQ BQ=．②如图3，若M是BC的中点，求证：∠BPQ ＝∠BAC．3、【解答】（1）证明：如图1中，延长AM交CN于点H．∵AM⊥CN，∴∠AHC＝90°，∵∠ABC＝90°，∴∠BAM+∠AMB＝90°，∠BCN+∠CMH＝90°，∵∠AMB＝∠CMH，∴∠BAM＝∠BCN，∵BA＝BC，∠ABM＝∠CBN＝90°，∴△ABM≌△CBN（ASA），∴BM＝BN．（2）①证明：如图2中，作CH∥AB交BP的延长线于H．∵BP⊥AM，∴∠BPM＝∠ABM＝90°，∵∠BAM+∠AMB＝90°，∠CBH+∠BMP＝90°，∴∠BAM＝∠CBH，∵CH∥AB，∴∠HCB+∠ABC＝90°，∵∠ABC＝90°，∴∠ABM＝∠BCH＝90°，∵AB＝BC，∴△ABM≌△BCH（ASA），∴BM＝CH，∵CH ∥BQ ， ∴＝＝．②简解：(射影定理)证2BM PM AM = 由BM =CM 得2CM PM AM = 则△PMC ∽△CMA 可得∠BPQ ＝∠BAC4、已知：矩形OABC 的顶点O 在平面直角坐标系的原点，边OA 、OC 分别在x 、y 轴的正半轴 上，且OA ＝3cm ，OC ＝4cm ，点M 从点A 出发沿AB 向终点B 运动，点N 从点C 出发沿CA 向终点A 运动，点M 、N 同时出发，且运动的速度均为1cm /秒，当其中一个点到达终点时，另一点即停止运动．设运动的时间为t 秒． （1）当点N 运动1秒时，求点N 的坐标；（2）试求出多边形OAMN 的面积S 与t 的函数关系式；（3）t 为何值时，以△OAN 的一边所在直线为对称轴翻折△OAN ，翻折前后的两个三角形所组成的四边形为菱形？4、【解答】解：（1）∵t ＝1∴CN ＝1，AM ＝1 过N 作NE ⊥y 轴，作NF ⊥x 轴 ∴△CEN ∽△COA ，∴，即，∴EN ＝．（1分） 由勾股定理得：，，∴．（2分）（2）由（1）得，∴∴N 点坐标为． ∵多边形OAMN 由△ONA 和△AMN 组成 ∴＝（3分） ＝（4分） ∴多边形OAMN 的面积S ＝．（0≤t≤4）（5分）（3）①直线ON为对称轴时，翻折△OAN得到△OA′N，此时组成的四边形为OANA′，当AN＝A′N＝A′O＝OA，四边形OANA’是菱形．即AN＝OA，∴5﹣t＝3∴t＝2．（6分）②直线OA为对称轴时，翻折△OAN得到△OAN′，此时组成的四边形为ONAN′，连接NN′，交OA于点G．当NN′与OA互相垂直平分时，四边形ONAN′是菱形．即OA⊥NN′，OG＝AG＝，∴NG∥CO，∴点N是AC的中点，∴CN＝，∴（7分）③直线AN为对称轴时，翻折△OAN得到△O′AN，此时组成的四边形为ONO′A，连接OO’，交AN于点H．当OO′与AN互相垂直平分时，四边形ONO’A是菱形．即OH⊥AC，AH＝NH＝，由面积法可求得OH＝，在Rt△OAH中，由勾股定理得，AH＝．∴，∴．（8分）综上所述，t的值为．5、已知：如图，在Rt△ACB中，∠C＝90°，AC＝3cm，BC＝3cm，点P由B点出发沿BA方向向点A匀速运动，速度为2cm/s；点Q由A点出发沿AC方向向点C匀速运动，速度为cm/s；若设运动的时间为t（s）（0＜t＜3），解答下列问题：（1）如图①，连接PC，当t为何值时△APC∽△ACB，并说明理由；（2）如图②，当点P，Q运动时，是否存在某一时刻t，使得点P在线段QC的垂直平分线上，请说明理由；（3）如图③，当点P，Q运动时，线段BC上是否存在一点G，使得四边形PQGB为菱形？若存在，试求出BG长；若不存在请说明理由．5、【解答】解：（1）在Rt△ACB中，∠C＝90°，AC＝3cm，BC＝3cm，∴AB＝6，由运动知，BP＝2t，AQ＝t，∴AP＝6﹣2t，∵△APC∽△ACB，∴，∴，∴t＝；（2）存在，理由：如图②，由运动知，BP＝2t，AQ＝t，∴AP＝6﹣2t，CQ＝3﹣t，∵点P是CQ的垂直平分线上，∴QM＝CM＝CQ＝（3﹣t）＝（3﹣t），∴AM＝AQ+QM＝t+（3﹣t）＝（t+3）过点P作PM⊥AC，∵∠ACB＝90°，∴PM∥BC，∴，∴∴t＝1（3）不存在，理由：由运动知，BP＝2t，AQ＝t，∴AP＝6﹣2t，假设线段BC上是存在一点G，使得四边形PQGB为平行四边形，∴PQ∥BG，PQ＝BG，∴△APQ∽△ABC，∴，∴，∴t＝，PQ＝，∴BP＝2t＝3，∴PQ≠BP，∴平行四边形PQGB不可能是菱形．即：线段BC上不存在一点G，使得四边形PQGB为菱形．6、如图，已知菱形ABCD中，AB＝5，点E是BC边上一点（不与B，C重合），以BE为边构造菱形BEFG，使点G落在AB的延长线上，连接BD，GE，射线FE交BD于点H．（1）求证：四边形BGEH是平行四边形；（2）请从下面A，B两题中任选一题作答．我选择A题．A．若四边形BGEH为菱形，则BD的长为5．B．连接HC，CF，BF，若BD＝6，且四边形BHCF为矩形，则CF的长为3．6、【解答】（1）证明：∵四边形ABCD和四边形BEFG是菱形，∴CD∥AG∥FH，BC∥GF，∠ABD＝∠ABC，∠BGE＝∠BGF，∴∠ABC＝∠BGF，∴∠ABD＝∠BGE，∴BH∥GE，∵EH∥BG，∴四边形BGEH是平行四边形；（2）解：A、∵四边形ABCD和四边形BGEH为菱形，∴AB＝AD，∠ABD＝∠CBD＝∠GBE＝60°，∴△ABD是等边三角形，∴BD＝AB＝5；故答案为：A，5；B、如图所示：∵四边形BHCF为矩形，∴CE＝BE，∵EH∥BG，∴EH∥CD，∴EH是△BCD的中位线，∴BH＝BD＝3，∴CF＝3；故答案为：3；8、如图，在平面直角坐标系中，点A（﹣4，2），点B在第一象限，AB平行于x轴且AB＝5．（1）点B的坐标为（1，2）．（2）如图1，过点A作AC⊥x轴于C，在x轴上是否存在点D，使得△AOC与△BOD 相似？（3）如图2，将△AOB折叠，使得点A刚好落在O处，此时折痕交AB于点D，交AO 于点E，在直线AO上有两个动点P，Q（点P在点Q的左侧），且线段PQ＝，求四边形BDPQ的周长最小值．7、【解答】解：（1）∵点A（﹣4，2），点B在第一象限，AB平行于x轴且AB＝5，∴点B（1，2），故答案为：B（1，2）；（2）如图1，过点B作BD⊥CO，则点D（1，0），∴OD＝1，BD＝2，∵AC⊥x轴，点A（﹣4，2），∴AC＝2，CO＝4，∴，且∠ACO＝∠ODB＝90°，∴△ACO∽△ODB，∴当点D为（1，0）时，△AOC与△BOD相似；∵△ACO∽△ODB，∴∠AOC＝∠OBD，∠CAO＝∠BOD，∵∠AOC+∠CAO＝90°，∴∠AOC+∠BOD＝90°，∴AO⊥BO，∵AC＝2，CO＝4，∴AO＝＝＝2，∵OD＝1，BD＝2，∴OB＝＝＝，过点B作BD'⊥OB，交x轴于D'，∵∠ACO＝∠OBD'，∠BOD＝∠CAO，∴△ACO∽△OCD'，∴，∴OD'＝＝5，∴D'（5，0）综上所述：当点D为（1，0）或（5，0）时，△AOC与△BOD相似；（3）连接DO，∵将△AOB折叠，使得点A刚好落在O处，∴AD＝DO，∵DN2+ON2＝DO2，∴DN2+4＝（4﹣DN）2，∴DN＝，∴点D坐标（﹣，2），∴BD＝2+＝，∵四边形BDPQ的周长＝BD+PQ+PD+BQ＝++PD+BQ，∴当PD+BQ最小时，四边形BDPQ的周长有最小值，作点B关于AO的对称点B'（﹣1，﹣2），过点D作DH∥AO，且DH＝，∴H（，1），∴B'H为PD+BQ的最小值，∴B'H＝＝，∴四边形BDPQ的周长最小值＝++＝．8、如图1，已知四边形ABCD的对角线AC，BD相交于点O，点M是BC边的中点，过点M作ME∥AC交BD于点E，作MF∥BD交AC于点F．（1）如图2，若四边形ABCD是菱形，求证：四边形OEMF是矩形；（2）如图3，若四边形ABCD是矩形，则四边形OEMF是菱形（在横线上填一个特殊平行四边形的名称）（3）如图4，若四边形ABCD是矩形，点M是BC延长线上的一个动点，点F落在AC的延长线上，点E落在线段OD上，其余条件不变，写出OB，ME，MF三条线段之间存在的数量关系，并说明理由．8、【解答】证明：（1）如图2，∵ME∥AC，MF∥BD，∴四边形OEMF是平行四边形，∵四边形ABCD是菱形，∴AC⊥BD，∴∠BOC=90°，∴▱OEMF是矩形；（2）如图3，若四边形ABCD是矩形，则四边形OEMF是菱形，理由是：由（1）得：四边形OEMF是平行四边形，∵四边形ABCD是矩形，∴OB=BD，OC=AC，AC=BD，∴OB=OC，∴∠OBC=∠OCB，∵EM∥OC，∴∠EMB=∠OCB，∴∠EMB=∠OBC，∴BE=EM，∵BM=MC，EM∥OC，∴BE=OE，∴OE=EM，∴▱OEMF是菱形；故答案为：菱形；（3）如图4，ME=OB+MF，理由是：由（2）得：OB=OC，∴∠OBC=∠OCB，∵MF∥BE，∴∠OBC=∠BMF，∴∠OCB=∠BMF，∵∠OCB=∠FCM，∴∠FCM=∠BMF，∴FC═FM，由（1）得四边形OEMF是平行四边形，∴OF=EM，∵OF=OC+FC=OB+FM，∴ME=OB+MF．9、如图1，一张矩形纸片ABCD，其中AD＝8cm，AB＝6cm，先沿对角线BD折叠，点C落在点C′的位置，BC′交AD于点G．（1）求证：BG＝DG；（2）求C′G的长；（3）如图2，再折叠一次，使点D与A重合，折痕EN交AD于M，求EM的长．9、【解答】解：（1）∵沿对角线BD对折，点C落在点C′的位置，∴∠A＝∠C′，AB＝C′D，∴在△GAB和△GC′D中，，∴△GAB≌△GC′D（AAS），∴BG＝DG；（2）∵△GAB≌△GC′D，∴AG＝C′G，设C′G＝x，则GD＝BG＝8﹣x，∴x2+62＝（8﹣x）2，解得：，∴；（3）∵点D与点A重合，得折痕EN，∴DM＝4cm，∵AD＝8cm，AB＝6cm，∴在Rt△ABD中，BD＝10cm，∵EN⊥AD，AB⊥AD，∴EN∥AB，∴MN是△ABD的中位线，∴DN＝BD＝5cm，在Rt△MND中，MN＝＝3（cm），由折叠的性质可知∠NDE＝∠NDC，∵EN∥CD，∴∠END＝∠NDC，∴∠END＝∠NDE，∴EN＝ED，设EM＝x，则ED＝EN＝x+3，由勾股定理得ED2＝EM2+DM2，即（x+3）2＝x2+42，解得x＝，即EM＝cm．10、如图（1）是矩形纸片ABCD连续两次对折展开平铺后的图形，折痕分别为EF，MN，GH．（1）如图（2），连接BD，与折痕GH，EF，MN分别交于点S，O，T，求证：OE=OF；（2）如图（3），连接ET并延长交CD于点Q，连接FS并延长交AB于点P，连接EP，FQ．求证：四边形EPFQ是菱形；（3）若四边形EPFQ是正方形，则矩形ABCD需满足的条件是AB=AD．11、【解答】证明：（1）如图（2），∵四边形ABCD是矩形，∴AD=BC，AD∥BC，∴∠ADB=∠CBD，由折叠得：G、E、M将AD四等分，∴ED=BF，∵∠EOD=∠FOB，∴△EOD≌△FOB，∴OE=OF；（2）由（1）得：△EOD≌△FOB，∴OD=OB，连接AC，∴A、O、C共线，∵GT∥EO，∴=1，∴DT=OT，∵AE=ED，OT=DT，∴ET∥AC，ET=AO，即EQ∥AC，同理得：TQ=OC，∴EQ=AC，同理得：PF=AC，PF∥AC，∴PF=EQ，PF=EQ，∴四边形EPFQ是平行四边形，∵PF∥AC，F是BC的中点，∴P为AB的中点，同理得：Q为DC的中点，∴AP=QD=AB，∵AE=AD，∠BAD=∠ADC=90°，∴△APE≌△DQE，∴PE=EQ，∴▱EPFQ是菱形．（3）当AB=AD时，四边形EPFQ是正方形，理由是：∵E是AD的中点，P是AB的中点，∴AE=AD，AP=AB，∵AB=AD，∴AP=AE，∴△APE是等腰直角三角形，∴∠AEP=45°，同理∠QED=45°，∴∠PEQ=90°，由（2）得：四边形EPFQ是菱形，∴四边形EPFQ是正方形；故答案为：AB=AD．12、如图1，在正方形ABCD的外部，分别以AB，CD为边作菱形ABEF和菱形CDGH，连接EH，FG（1）求证：FG=EH（2）请从A，B两个题目中任选一题作答A 如图2，若AB=4，∠BAF=60°，∠CDG=30°，求四边形AFGD的面积B 如图3，若∠BAF=∠CDG，求证；四边形EFGH是矩形12、【解答】解：（1）∵AB，CD为边作菱形ABEF和菱形CDGH，∴EF∥AB，EF=AB，HG∥CD，HG=CD，∵四边形ABCD是正方形，∴AB∥CD，AB=CD，∴EF∥HG，EF=HG，∴四边形EFGH是平行四边形，∴FG=EH；（2）A、如图2，延长FA，GD交于M，∵四边形ABCD是正方形，∴∠BAD=∠ADC=90°，∴∠BAF+∠DAM=90°，∠CDG+∠ADM=90°，∵∠BAF=60°，∠CDG=30°，∴∠DAM=30°，∠ADM=60°，∴∠ADM=180°﹣∠DAM﹣∠ADM=90°在Rt△ADM中，∠DAM=30°，AD=4，∴DM=AD=2，AM=2，∵AF=DG=4，∴FM=AF +AM=4+2，MG=MD +DG=6，∴S 四边形AFGD =S △FMG ﹣S △MAD=×FM ×GM ﹣×AM ×DM=×（4+2）×6﹣×2×2=12+4，B 、方法1、如图3．连接FD ，AG （简化图），∵∠BAF=∠CDG ，∴∠DAF=∠ADG在△ADF 和△ADG 中，，∴△ADF ≌△ADG ，∴∠ADF=∠DAG ，DF=AG ，∴∠ADF=（180°﹣∠AOD ）在△AFG 和△DGF 中，， ∴△AFG ≌△DGF ，∠AGF=∠DFG ，∴∠DFG=（180°﹣∠FOG ）∵∠FOG=∠AOD ，∴∠ADF=∠DFG ，∴AD ∥FG ，∵AB ⊥AD ，∴AB ⊥FG ，∵AB ∥EF ，∴EF ⊥FG ，∴∠EFG=90°，由（1）知，四边形EFGH 为平行四边形，∴平行四边形EFGH 是矩形，即：四边形EFGH是矩形．方法2、延长FA，GD交于M，∵四边形ABCD是正方形，∴∠BAD=∠ADC=90°，∵∠BAF=∠CDG，∴∠MAD=∠MDA，∴MA=MD，∵四边形ABCD是正方形，∴AB=CD，∵四边形ABEF，CDGH是菱形，∴MF=MG，∠AFE=∠DGH，∴∠EFG=∠HGF，由（1）知，四边形EFGH是平行四边形，∴∠AFE+∠HGF=180°，∴∠EFG=90°，∴平行四边形EFGH是矩形．13、问题情境：如图1，在菱形ABCD中，点E、F分别为AB，BC边上的点，连接AF，DE相交于点O，且∠AOE=∠ADC，试探究：AF与DE的数量关系．特例探究：如图2，当菱形ABCD是正方形时，AF与DE有怎样的数量关系呢？请你直接写出结论，不必证明；类比解答：类比特例探究的结论，猜想问题情境中AF与DE的数量关系，并说明理由；拓展延伸：将图1中的菱形ABCD改为▱ABCD（如图3）其中AB=a，AD=b，点E、F、G、H 分别为AB、BC、CD、DA边上的动点，连接EG、HF相交于点O，且∠HOE=∠ADC，试探究：EG与FH的数量关系，用含a、b的式子直接写出的值，不必说明理由．13、【解答】解：（1）特例探究：AF=DE．理由：如图2，∵四边形ABCD是正方形，∴AD=BA，∠DAE=∠B=90°，∵∠AOE=∠ADC=90°，∴∠ADE+∠DAO=∠BAF+∠DAO=90°，∴∠ADE=∠BAF，∴在ADE和△BAF中，，∴△ADE≌△BAF（ASA），∴AF=DE；（2）类比解答：AF与DE的数量关系为AF=DE．理由：如图1，在AB上取点M使得DM=DA，连接DM，交AF于N，则∠DAM=∠DMA，DM=AD=AB，∵∠DAB+∠B=180°，∠DMA+∠DME=180°，∴∠DME=∠B，∵∠AOE=∠ADC，∴∠ADO+∠DAO=∠ADO+∠CDO，∴∠DAO=∠CDO，又∵CD∥AB，AD∥BC，∴∠CDO=∠MED，∠DAO=∠BFA，∴∠MED=∠BFA，在△MED和△BFA中，，∴△MED≌△BFA（AAS），∴AF=DE；（3）拓展延伸：=．如图3，过G作GM⊥AB于M，过H作HN⊥BC于N，∵四边形ABCD是平行四边形，∴AD∥BC，DC∥AB，∵平行四边形ABCD的面积=AB×GM=BC×HN，∵AB=a，AD=b，∴=，∵GM⊥AB，HN⊥BC，∴∠GME=∠HNF=90°，∵∠ADC=∠HOE，∴∠ADC+∠HOG=∠EOH+∠HOG=180°，∴∠DHO+∠DGE=360°﹣180°=180°，∵AD∥BC，DC∥AB，∴∠NFH=∠DHF，∠DGE+∠GEM=180°，∴∠HFN=∠GEM，∴△GME∽△HNF，∴==．14、问题情境：已知，菱形ABCD，点B关于直线AD的对称点为点E，连接AE、CE，线段CE交直线AD于点F，连接BF．（1）特例研究：如图1，当∠ABC=90°时，点A、B、E在同一条直线上，求证：BF=CE．（2）类比思考：请从下列A、B两题中任选一题作答：我选择A或B题．当90°＜∠ABC＜180°时，小彬提出如下问题：A、若点E、D、C三点在同一直线上，请在下面画出符合条件的图形，并直接写出∠ABC的度数；B、如图2，若点E、D、C三点不在同一直线上，判断（1）中的结论是否仍然成立，若成立，请证明；若不成立，说明理由．（3）拓展分析：请从下列A、B两题中任选一题作答，我选择A或B题．A：如图3，当∠ABC=135°时，CD的延长线交AE于点G，直接写出的值；B：当∠ABC=45°时，直线AE与CD相交于点G，请在下面画出符合条件的图形，并直接写出的值．14、【解答】解：（1）如图1中，∵∠ABC=90°，四边形ABCD是菱形，∴四边形ABCD是正方形，根据对称性可知，AE=AB，BE⊥AD，∴B、A、E共线，∵AF∥BC，∴EF=FC，∴BF=EC．（2）A、如图2中，当E、D、C共线时，由（1）可知：DE=DC，∵EB⊥AD，AD∥BC，∴EB⊥BC，∴∠EBC=90°，∴BD=DC=DE=CB，∴△BDC是等边三角形，∴∠C=60°，∵AB∥CD，∴∠ABC=180°﹣60°=120°．B、（1）中结论成立．理由如下：如图3中，设BE交AD于H．∵B、E关于AD对称，∴BE⊥AD，EH=BH，∵AD∥BC，∴BE⊥BC，∴∠EBC=90°，∵EH=HB，HF∥BC，∴EF=FC，∴BF=EC．故答案为A或B．（3）A、如图4中，作FH⊥CD于H．∵∠ABC=135°，AD∥BC，∴∠EAF=∠BAF=45°，∠ADC=135°，∠ADG=45°，∴∠AGD=90°，∵∠FHC=90°，∴∠FHC=∠EGC=90°，∴FH∥FG，∵FE=FC，∴HC=HG，∴FH=EG，∵△DFH是等腰直角三角形，∴DF=FH，∴EG=DF，∴=．B、如图5中，作FH⊥CD于H．同法可证：EG=2FH，DF=FH，∴=．故答案为A或B．15、阅读下列材料，完成任务：自相似图形定义：若某个图形可分割为若干个都与它相似的图形，则称这个图形是自相似图形．例如：正方形ABCD中，点E、F、G、H分别是AB、BC、CD、DA边的中点，连接EG，HF交于点O，易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形，且与原正方形相似，故正方形是自相似图形．任务：（1）图1中正方形ABCD分割成的四个小正方形中，每个正方形与原正方形的相似比为；（2）如图2，已知△ABC中，∠ACB=90°，AC=4，BC=3，小明发现△ABC也是“自相似图形”，他的思路是：过点C作CD⊥AB于点D，则CD将△ABC分割成2个与它自己相似的小直角三角形．已知△ACD∽△ABC，则△ACD与△ABC的相似比为；（3）现有一个矩形ABCD是自相似图形，其中长AD=a，宽AB=b（a＞b）．请从下列A、B两题中任选一条作答：我选择A或B题．A：①如图3﹣1，若将矩形ABCD纵向分割成两个全等矩形，且与原矩形都相似，则a=（用含b的式子表示）；②如图3﹣2若将矩形ABCD纵向分割成n个全等矩形，且与原矩形都相似，则a=（用含n，b的式子表示）；B：①如图4﹣1，若将矩形ABCD先纵向分割出2个全等矩形，再将剩余的部分横向分割成3个全等矩形，且分割得到的矩形与原矩形都相似，则a=或（用含b的式子表示）；②如图4﹣2，若将矩形ABCD先纵向分割出m个全等矩形，再将剩余的部分横向分割成n个全等矩形，且分割得到的矩形与原矩形都相似，则a=b 或b（用含m，n，b的式子表示）．15、【解答】解：（1）∵点H是AD的中点，∴AH=AD，∵正方形AEOH∽正方形ABCD，∴相似比为：==；故答案为：；（2）在Rt△ABC中，AC=4，BC=3，根据勾股定理得，AB=5，∴△ACD与△ABC相似的相似比为：=，故答案为：；（3）A、①∵矩形ABEF∽矩形FECD，∴AF：AB=AB：AD，即a：b=b：a，∴a=b；故答案为：②每个小矩形都是全等的，则其边长为b和a，则b：a=a：b，∴a=b；故答案为：B、①如图2，由①②可知纵向2块矩形全等，横向3块矩形也全等，∴DN=b，Ⅰ、当FM是矩形DFMN的长时，∵矩形FMND∽矩形ABCD，∴FD：DN=AD：AB，即FD：b=a：b，解得FD=a，∴AF=a﹣a=a，∴AG===a，∵矩形GABH∽矩形ABCD，∴AG：AB=AB：AD即a：b=b：a得：a=b；Ⅱ、当DF是矩形DFMN的长时，∵矩形DFMN∽矩形ABCD，∴FD：DN=AB：AD即FD：b=b：a解得FD=，∴AF=a﹣=，∴AG==，∵矩形GABH∽矩形ABCD，∴AG：AB=AB：AD即：b=b：a，得：a=b；故答案为：或；②如图3，由①②可知纵向m块矩形全等，横向n块矩形也全等，∴DN=b，Ⅰ、当FM是矩形DFMN的长时，∵矩形FMND∽矩形ABCD，∴FD：DN=AD：AB，即FD：b=a：b，解得FD=a，∴AF=a﹣a，∴AG===a，∵矩形GABH∽矩形ABCD，∴AG：AB=AB：AD即a：b=b：a得：a=b；Ⅱ、当DF是矩形DFMN的长时，∵矩形DFMN∽矩形ABCD，∴FD：DN=AB：AD即FD：b=b：a解得FD=，∴AF=a﹣，∴AG==，∵矩形GABH∽矩形ABCD，∴AG：AB=AB：AD即：b=b：a，得：a=b；故答案为：b或b．16、综合与实践问题情境：正方形折叠中的数学已知正方形纸片ABCD中，AB＝4，点E是AB边上的一点，点G是CE的中点，将正方形纸片沿CE所在直线折叠，点B的对应点为点B′．（1）如图1，当∠BCE＝30°时，连接BG，B′G，求证：四边形BEB′G是菱形；深入探究：（2）在CD边上取点F，使DF＝BE，点H是AF的中点，再将正方形纸片ABCD沿AF 所在直线折叠，点D的对应点为D′，顺次连接B′，G，D′，H，B'，得到四边形B′GD′H．请你从A，B两题中任选一题作答，我选择A或B题．A题：如图2，当点B'，D′均落在对角线AC上时，①判断B′G与D′H的数量关系与位置关系，并说明理由；②直写出此时点H，G之间的距离．B题：如图3，点M是AB的中点，MN∥BC交CD于点N，当点B'，D′均落在MN上时，①判断B′G与D′H的数量关系与位置关系，并说明理由；②直接写出此时点H，G之间的距离．16、【解答】（1）证明：如图1中，∵四边形ABCD是正方形，∴∠ABC＝90°，由折叠可知：BE＝BE′，∠CB′E＝∠ABC＝90°，在Rt△BCE和Rt△ECB′中，∵EG＝GC，∴BG＝EC，GB′＝EC，∴BG＝GB′，在Rt△BCE中，∵∠BCE＝30°，∴BE＝CE，∴BE＝EB′＝B′G＝BG，∴四边形BEB′G是菱形．（2）选A或B．故答案为A或B．A题：①结论：B′G＝D′H，B′G∥D′H．理由：如图2中，由（1）得到：B′G＝CE，∵点G是CE的中点，∴CG＝CE，∴B′G＝CG，∴∠1＝∠2，∵四边形ABCD是正方形，∴∠B＝∠D＝90°，AD＝BC，∵BE＝DF，∴△BCE≌△ADF（SAS），∴CE＝CF，∠3＝∠4，由折叠可知：∠D＝∠AD′F＝90°，∠2＝∠3，∠4＝∠5，∴∠2＝∠5＝∠1，在Rt△AD′F中，∵H是AF的中点，∴D′H＝AH＝AF，∴B′G＝D′H，∠5＝∠6，∴∠1＝∠6，∴B′G∥D′H．②连接GH，则四边形AEGH是平行四边形，∴AE＝GH，设BE＝EB′＝m，则AE＝m，∴m+m＝4，∴m＝4﹣4，∴GH＝AE＝8﹣4B题：①结论：B′G＝D′H，B′G∥D′H．理由：由（1）得到：B′G＝CE，∵点G是CE的中点，∴CG＝CE，∴B′G＝CG，∴∠1＝∠2，∵四边形ABCD是正方形，∴∠B＝∠D＝90°，AD＝BC，AD∥BC，∵BE＝DF，∴△BCE≌△ADF（SAS），∴CE＝CF，∠3＝∠4，由折叠可知：∠D＝∠AD′F＝90°，∠2＝∠3，∠4＝∠5，∴∠2＝∠5＝∠1，在Rt△AD′F中，∵H是AF的中点，∴D′H＝AH＝AF，∴B′G＝D′H，∠5＝∠6，∴∠1＝∠6，∵MN∥BC，∴MN∥BC∥AD，∴∠AD′M＝∠DAD′＝2∠4，∠CB′N＝∠BCB′＝2∠3，∴∠AD′M＝∠CB′N，。
北师大版九年级数学上期末备考压轴题专项培优：特殊的平行四边形(解析版)
期末备考压轴题专项培优：特殊的平行四边形1．如图，四边形ABCD是正方形，△ABE是等边三角形，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM．设点N的坐标为（m，n）．（1）若建立平面直角坐标系，满足原点在线段BD上，点B（﹣1，0），A（0，1）．且BM＝t（0＜t≤2），则点D的坐标为（1，0），点C的坐标为（0，﹣1）；请直接写出点N纵坐标n的取值范围是0＜n≤；（2）若正方形的边长为2，求EC的长，以及AM+BM+CM的最小值．（提示：连结MN：＝+1，＝﹣1）解：（1）如图1，以直线BD为x轴，直线AC为y轴，建立平面直角坐标系，∵四边形ABCD是正方形，∴OA＝OB＝OC＝OD，∵点B（﹣1，0），A（0，1），∴D（1，0），C（0，﹣1）；过N作NH⊥BD于h，∴∠NHB＝90°，∵将BM绕点B逆时针旋转60°得到BN，∴∠NBH＝60°，BM＝BN，∴NH＝BN＝t，∵0＜t≤2，∴点N纵坐标n的取值范围是0＜n≤；故答案为：（1，0），（0，﹣1）；0＜n≤；（2）如图所示，连接MN，过E作EH⊥BC，交CB的延长线于H，由旋转可得，BM＝BN，∠NBM＝60°，∴△BMN是等边三角形，∴MN＝BM，∵△ABE是等边三角形，∴BE＝BA，∠ABE＝60°，∴∠ABM＝∠EBN，∴△ABM≌△EBN（SAS），∴AM＝EN，∴AM+BM+CM＝EN+MN+CM，∴当E，N，M，C在同一直线上时，AM+BM+CN的最小值是CE的长，又∵∠ABE＝60°，∠ABH＝90°，∴∠EBH＝30°，∴Rt△EBH中，EH＝EB＝×2＝1，∴BH＝＝＝，∴CH＝2+，∴Rt△CEH中，CE＝＝＝＝；∴AM+BM+CM的最小值为+．2．如图，在▱ABCD中，∠BAD的平分线交BC于点E，交DC的延长线于F，以EC、CF 为邻边作▱ECFG．（1）证明▱ECFG是菱形；（2）若∠ABC＝120°，连结BD、CG，求∠BDG的度数；（3）若∠ABC＝90°，AB＝6，AD＝8，M是EF的中点，求DM的长．解：（1）证明：，∵AF平分∠BAD，∴∠BAF＝∠DAF，∵四边形ABCD是平行四边形，∴AD∥BC，AB∥CD，∴∠DAF＝∠CEF，∠BAF＝∠CFE，∴∠CEF＝∠CFE，∴CE＝CF，又∵四边形ECFG是平行四边形，∴四边形ECFG为菱形；（2）∵四边形ABCD是平行四边形，∴AB∥DC，AB＝DC，AD∥BC，∵∠ABC＝120°，∴∠BCD＝60°，∠BCF＝120°由（1）知，四边形CEGF是菱形，∴CE＝GE，∠BCG＝∠BCF＝60°，∴CG＝GE＝CE，∠DCG＝120°，∵EG∥DF，∴∠BEG＝120°＝∠DCG，∵AE是∠BAD的平分线，∴∠DAE＝∠BAE，∵AD∥BC，∴∠DAE＝∠AEB，∴∠BAE＝∠AEB，∴AB＝BE，∴BE＝CD，∴△BEG≌△DCG（SAS），∴BG＝DG，∠BGE＝∠DGC，∴∠BGD＝∠CGE，∵CG＝GE＝CE，∴△CEG是等边三角形，∴∠CGE＝60°，∴∠BGD＝60°，∵BG＝DG，∴△BDG是等边三角形，∴∠BDG＝60°；（3）如图2中，连接BM，MC，∵∠ABC＝90°，四边形ABCD是平行四边形，∴四边形ABCD是矩形，又由（1）可知四边形ECFG为菱形，∠ECF＝90°，∴四边形ECFG为正方形．∵∠BAF＝∠DAF，∴BE＝AB＝DC，∵M为EF中点，∴∠CEM＝∠ECM＝45°，∴∠BEM＝∠DCM＝135°，在△BME和△DMC中，∵，∴△BME≌△DMC（SAS），∴MB＝MD，∠DMC＝∠BME．∴∠BMD＝∠BME+∠EMD＝∠DMC+∠EMD＝90°，∴△BMD是等腰直角三角形．∵AB＝6，AD＝8，∴BD＝10，∴DM＝BD＝5．3．如图，在正方形ABCD中，对角线AC、BD相交于点O，以AD为边向外作等边△ADE，连接CE，交BD于F．（1）如图1，若AE＝，求DF的长；（2）如图2，点M为AB的延长线上一点，连接CM，连接FM且FM平分∠AMC，求证：CM＝MF﹣AM．解：（1）如图1，连接OE，∵四边形ABCD是正方形，∴AD＝CD，∠ADC＝90°，OA＝OD＝OB＝OC∵△ADE是等边三角形∴AD＝DE＝AE＝，∠ADE＝60°∴CD＝AD＝，OD＝OB＝∵AE＝DE，OD＝OA∴OE垂直平分AD即OE⊥AD，DH＝AH∴OE＝OH+EH＝+＝，∵∠ADC＝∠DHE＝90°∴CD∥OE∴△CDF∽△EOF∴＝，即DF＝OF∵DF+OF＝OD＝∴OF＝﹣DF∴DF＝（﹣DF），解得：DF＝﹣1．（2）如图2，连接EO，过点F作PQ⊥CD交EO于N，在MA上截取MT＝MC，连接FT，设正方形边长为a，∵四边形ABCD是正方形，△ADE是等边三角形∴AD＝AB＝CD＝DE＝a，∠ADC＝∠DAB＝90°∠ADE＝60°易证OE⊥AD∴OE＝a，OD＝a，由（1）知△CDF∽△EOF∴＝，即a•DF＝a•OF∵DF+OF＝a∴OF＝a﹣DF∴a•DF＝a（a﹣DF）∴DF＝a，∵△DPF是等腰直角三角形∴DP＝PF＝DF＝a，∴FQ＝a﹣a＝a＝CP，∵FM平分∠AMC，∴∠CMF＝∠AMF在△MCF和△MTF中∴△MCF≌△MTF（SAS）∴CF＝FT∴Rt△CFP≌Rt△FTQ（HL）∴QT＝PF＝a，∵AQ＝DP∴AQ＝QT∵BM+AB﹣AT＝MT＝CM∴CM﹣BM＝AB﹣AT＝a﹣2×a＝a，CM+BM＝MT+BM＝BT+2BM＝a﹣2×a+2BM＝a+2BM∴CM2﹣BM2＝（CM﹣BM）（CM+BM）＝a（a+2BM）∵CM2﹣BM2＝BC2＝a2，∴a（a+2BM）＝a2，∴BM＝a在Rt△BCM中，tan∠BMC＝＝＝，∴∠BMC＝60°∴∠AMF＝30°∴＝cos∠AMF＝cos30°＝∴2MQ＝MF∵2MQ＝2BM+2BQ＝2BM+2BT+2QT＝（BM+BT）+（BM+BT+AT）＝CM+AM∴CM+AM＝MF即CM＝MF﹣AM．4．在菱形ABCD中，∠ABC＝60°，BD为菱形的一条对角线．（1）如图1，过A作AE⊥BC于点E，交BD于点F，若EF＝2，求菱形ABCD的面积；（2）如图2，M为菱形ABCD外一点，过A作AN⊥BM交BM的延长线于点N，连接AM，DM，AG⊥DM于点G，且∠AMN＝∠AMD，求证：DM＝BM+AM．（1）解：如图1中，∵四边形ABC都是菱形，∠ABC＝60°，∴∠ABD＝∠DBC＝30°，∵AE⊥BC，∴∠BEF＝90°，∵EF＝2，∴BF＝2EF＝4，∠BFE＝60°，∵∠BFE＝∠ABF+∠F AB，∴∠ABF＝∠F AB＝30°，∴BF＝AF＝4，∴AE＝AF+EF＝6，∴AB＝＝4，∴BC＝AB＝4，＝BC•AE＝24．∴S菱形ABCD（2）证明：如图2中，∵∠AMN＝∠AMG，AN⊥MN，AG⊥DM，∴AN＝AG，∵∠MNA＝∠MGA＝90°，AM＝AM，AN＝AG，∴Rt△MAN≌Rt△MAG（HL），∴NM＝MG，∵∠ANB＝∠AGD＝90°，AN＝AG，AB＝AD，∴Rt△ANB≌Rt△AGD（HL），∴∠ABN＝∠ADG，BN＝DG，∴∠BMD＝△BAD＝120°，∴∠NMG＝60°，∴∠AMN＝∠AMG＝30°，∴DM﹣BM＝MG+DG﹣（BN﹣MN）＝2MN＝AM，∴DM＝BM+AM．5．如图，点A、B、C、D在同一条直线上，点E、F分别在直线AD的两侧，且AE＝DF，∠A＝∠D，AB＝DC．（1）求证：四边形BFCE是平行四边形；（2）若AD＝12，DC＝3，∠EBD＝60°，则BE＝6时，四边形BFCE是菱形．（只需完成填空，不需写出具体过程．）（1）证明：∵在△ABE和△DCF中，∴△ABE≌△DCF（SAS），∴BE＝FC，∠ABE＝∠DCF，∴∠EBC＝∠FCB，∴BE∥FC，∴四边形BFCE是平行四边形；（2）解：当四边形BFCE是菱形，则BE＝EC，∵AD＝12，DC＝3，AB＝DC，∴BC＝6，∵∠EBD＝60°，EB＝EC，∴△EBC是等边三角形，∴BE＝6．故答案为：6．6．已知：如图，在▱ABCD中，G、H分别是AD、BC的中点，E、O、F分别是对角线BD 上的四等分点，顺次连接G、E、H、F．（1）求证：四边形GEHF是平行四边形；（2）当▱ABCD满足AB⊥BD条件时，四边形GEHF是菱形；（3）若BD＝2AB，①探究四边形GEHF的形状，并说明理由；②当AB＝2，∠ABD＝120°时，直接写出四边形GEHF的面积．（1）证明：连接AC，如图1所示：∵四边形ABCD是平行四边形，∴OA＝OC，OB＝OD，∴BD的中点在AC上，∵E、O、F分别是对角线BD上的四等分点，∴E、F分别为OB、OD的中点，∵G是AD的中点，∴GF为△AOD的中位线，∴GF∥OA，GF＝OA，同理：EH∥OC，EH＝OC，∴EH＝GF，EH∥GF，∴四边形GEHF是平行四边形；（2）解：当▱ABCD满足AB⊥BD条件时，四边形GEHF是菱形；理由如下：连接GH，如图2所示：则AG＝BH，AG∥BH，∴四边形ABHG是平行四边形，∴AB∥GH，∵AB⊥BD，∴GH⊥BD，∴GH⊥EF，∴四边形GEHF是菱形；故答案为：AB⊥BD；（3）解：①四边形GEHF是矩形；理由如下：由（2）得：四边形GEHF是平行四边形，∴GH＝AB，∵BD＝2AB，∴AB＝BD＝EF，∴GH＝EF，∴四边形GEHF是矩形；②作AM⊥BD于M，GN⊥BD于N，如图3所示：则AM∥GN，∵G是AD的中点，∴GN是△ADM的中位线，∴GN＝AM，∵∠ABD＝120°，∴∠ABM＝60°，∴∠BAM＝30°，∴BM＝AB＝1，AM＝BM＝，∴GN＝，∵BD＝2AB＝4，∴EF＝BD＝2，∴△EFG的面积＝EF×GN＝×2×＝，∴四边形GEHF的面积＝2△EFG的面积＝．7．如图，边长为6的正方形ABCD中，E，F分别是AD，AB上的点，AP⊥BE，P为垂足．（1）如图1，AF＝BF，AE＝2，点T是射线PF上的一个动点，当△ABT为直角三角形时，求AT的长；（2）如图2，若AE＝AF，连接CP，求证：CP⊥FP．（1）解：在正方形ABCD中，可得∠DAB＝90°．∵在Rt△BAE中，tan∠ABE＝＝＝，∴∠ABE＝30°．点T是射线PF上的一个动点，当△ABT为直角三角形时，分三种情况：①当点T在AB的上方，∠ATB＝90°，显然此时点T和点P重合，即AT＝AP＝AB＝3；②当点T在AB的下方，∠ATB＝90°，如图①所示．在Rt△APB中，由AF＝BF，可得：AF＝BF＝PF＝3，∴∠BPF＝∠FBP＝30°，∴∠BFT＝60°．在Rt△ATB中，TF＝BF＝AF＝3，∴△FTB是等边三角形，∴TB＝3，AT＝＝3；③当点T在AB的下方，∠ABT＝90°时，如图②所示．在Rt△FBT中，∠BFT＝60°，BF＝3，BT＝BF•tan60°＝3．在Rt△ATB中：AT＝＝3．综上所述：当△ABT为直角三角形时，AT的长为3或3或3；（2）证明：如图③所示，∵四边形ABCD是正方形，∴AB＝AD＝BC，AD∥BC，∠DAB＝90°，∴∠3＝∠4．∵在Rt△EAB中，AP⊥BE，∴∠1+∠2＝90°，∠3+∠2＝90°，∴∠1＝∠3，∴∠1＝∠3＝∠4，∵tan∠1＝，tan∠3＝，∴＝，∵AE＝AF，AB＝BC，∴＝，∴△PBC∽△P AF，∴∠5＝∠6．∵∠6+∠7＝90°，∴∠5+∠7＝90°，即∠CPF＝90°，∴CP⊥FP．8．已知：如图，在▱ABCD中，G、H分别是AD、BC的中点，AE⊥BD，CF⊥BD，垂足分别为E、F．（1）求证：四边形GEHF是平行四边形；（2）已知AB＝5，AD＝8．求四边形GEHF是矩形时BD的长．（1）证明：∵四边形ABCD是平行四边形，∴AD∥BC，AD＝BC，∴∠GDE＝∠FBH，∵G、H分别是AD、BC的中点，AE⊥BD，CF⊥BD，∴在Rt△AED和Rt△CFB中，EG＝AD＝GD，FH＝BC＝HB，∴EG＝FH，∠GED＝∠GDE，∠FBH＝∠BFH，∴∠GED＝∠BFH，∴EG∥FH，∴四边形GEHF是平行四边形；（2）解：连接GH，当四边形GEHF是矩形时，∠EHF＝∠BFC＝90°，∵∠FBH＝∠BFH，∴△EFH∽△CBF，∴＝，由（1）可得：GA∥HB，GA＝HB，∴四边形GABH是平行四边形，∴GH＝AB＝5，∵在矩形GEHF中，EF＝GH，且AB＝5，AD＝8，∴＝，解得：BF＝，∴BE＝BF﹣EF＝﹣5＝，在△ABE和△CDF中∴△ABE≌△CDF（AAS），∴BE＝DF＝，∴BD＝BF+DF＝+＝．9．如图，点M是正方形ABCD的边BC上一点，连接AM，点E是线段AM上一点，∠CDE 的平分线交AM延长线于点F．（1）如图1，若点E为线段AM的中点，BM：CM＝1：2，BE＝，求AB的长；（2）如图2，若DA＝DE，求证：BF+DF＝AF．解：（1）设BM＝x，则CM＝2x，BC＝3x，∵BA＝BC，∴BA＝3x．在Rt△ABM中，E为斜边AM中点，∴AM＝2BE＝2．由勾股定理可得AM2＝MB2+AB2，即40＝x2+9x2，解得x＝2．∴AB＝3x＝6．（2）延长FD交过点A作垂直于AF的直线于H点，过点D作DP⊥AF于P点．∵DF平分∠CDE，∴∠1＝∠2．∵DE＝DA，DP⊥AF∴∠3＝∠4．∵∠1+∠2+∠3+∠4＝90°，∴∠2+∠3＝45°．∴∠DFP＝90°﹣45°＝45°．∴AH＝AF．∵∠BAF+∠DAF＝90°，∠HAD+∠DAF＝90°，∴∠BAF＝∠DAH．又AB＝AD，∴△ABF ≌△ADH （SAS ）．∴AF ＝AH ，BF ＝DH ．∵Rt △F AH 是等腰直角三角形，∴HF ＝AF ．∵HF ＝DH +DF ＝BF +DF ，∴BF +DF ＝AF ．10．在四边形ABCD 中，对角线AC 、BD 相交于点O ，过点O 的两条直线分别交边AB 、CD 、AD 、BC 于点E 、F 、G 、H ．【感知】如图①，若四边形ABCD 是正方形，且AG ＝BE ＝CH ＝DF ，则S四边形AEOG ＝ S 正方形ABCD ；【拓展】如图②，若四边形ABCD 是矩形，且S 四边形AEOG ＝S 矩形ABCD ，设AB ＝a ，AD ＝b ，BE ＝m ，求AG 的长（用含a 、b 、m 的代数式表示）；【探究】如图③，若四边形ABCD 是平行四边形，且AB ＝3，AD ＝5，BE ＝1，试确定F 、G 、H 的位置，使直线EF 、GH 把四边形ABCD 的面积四等分．解：【感知】如图①，∵四边形ABCD 是正方形，∴∠OAG ＝∠OBE ＝45°，OA ＝OB ，在△AOG 与△BOE 中，，∴△AOG ≌△BOE ，∴S 四边形AEOG ＝S △AOB ＝S 正方形ABCD ； 故答案为：；【拓展】如图②，过O 作ON ⊥AD 于N ，OM ⊥AB 于M ，∵S △AOB ＝S 矩形ABCD ，S 四边形AEOG ＝S 矩形ABCD ，∴S △AOB ＝S 四边形AEOG ，∵S △AOB ＝S △BOE +S △AOE ，S 四边形AEOG ＝S △AOG +S △AOE ，∴S △BOE ＝S △AOG ，∵S △BOE ＝BE •OM ＝mb ＝mb ，S △AOG ＝AG •ON ＝AG •a ＝AG •a ， ∴mb ＝AG •a ，∴AG ＝； 【探究】如图③，过O 作KL ⊥AB ，PQ ⊥AD ，则KL ＝2OK ，PQ ＝2OQ ，∵S 平行四边形ABCD ＝AB •KL ＝AD •PQ ，∴3×2OK ＝5×2OQ ， ∴＝，∵S △AOB ＝S 平行四边形ABCD ，S 四边形AEOG ＝S 平行四边形ABCD ，∴S △AOB ＝S 四边形AEOG ，∴S △BOE ＝S △AOG ，∵S △BOE ＝BE •OK ＝×1×OK ，S △AOG ＝AG •OQ ， ∴×1×OK ＝AG •OQ ，∴＝AG ＝，∴当AG＝CH＝，BE＝DF＝1时，直线EF、GH把四边形ABCD的面积四等分．11．如图，在矩形ABCD中，AB＝8cm，BC＝16cm，点P从点D出发向点A运动，运动到点A停止，同时，点Q从点B出发向点C运动，运动到点C即停止，点P、Q的速度都是1cm/s．连接PQ、AQ、CP．设点P、Q运动的时间为ts．（1）当t为何值时，四边形ABQP是矩形；（2）当t为何值时，四边形AQCP是菱形；（3）分别求出（2）中菱形AQCP的周长和面积．解：（1）∵在矩形ABCD中，AB＝8cm，BC＝16cm，∴BC＝AD＝16cm，AB＝CD＝8cm，由已知可得，BQ＝DP＝tcm，AP＝CQ＝（16﹣t）cm，在矩形ABCD中，∠B＝90°，AD∥BC，当BQ＝AP时，四边形ABQP为矩形，∴t＝16﹣t，得t＝8，故当t＝8s时，四边形ABQP为矩形；（2）∵AP＝CQ，AP∥CQ，∴四边形AQCP为平行四边形，∴当AQ＝CQ时，四边形AQCP为菱形即＝16﹣t时，四边形AQCP为菱形，解得t＝6，故当t＝6s时，四边形AQCP为菱形；（3）当t＝6s时，AQ＝CQ＝CP＝AP＝16﹣6＝10cm，则周长为4×10cm＝40cm；面积为10cm×8cm＝80cm2．12．如图，在四边形ABCD中，AB＝AD，CB＝CD，E是CD上的点，BE交AC于点F，连接DF．（1）求证：∠BAF＝∠DAF，∠AFD＝∠CFE；（2）若AB∥CD，试证明：四边形ABCD是菱形；（3）在（2）的条件下，试确定点E的位置，使得∠EFD＝∠BCD，并说理由．证明：（1）在△ABC和△ADC中，，∴△ABC≌△ADC，∴∠BAC＝∠DAC，在△ABF和△ADF中，∴△ABF≌△ADF，∴∠AFB＝∠AFD，∵∠CFE＝∠AFB，∴∠AFD＝∠CFE，∴∠BAF＝∠DAC，∠AFD＝∠CFE；（2）∵AB∥CD，∴∠BAC＝∠ACD，∵∠BAC＝∠DAC，∴∠BAC＝∠ACD，∴∠DAC＝∠ACD，∴AD＝CD，∵AB＝AD，CB＝CD，∴AB＝CB＝CD＝AD，∴四边形ABCD是菱形；（3）∵四边形ABCD是菱形，∴BC＝CD，∠BCF＝∠DCF，∵CF＝CF，∴△BCF≌△DCF，∴∠CBF＝∠CDF，∵BE⊥CD，∴∠BEC＝∠DEF＝90°，∴∠EFD＝∠BCD．13．如图，在△ABC中，点O是边AC上一个点，过点O作直线MN∥BC分别交∠ACB、外角∠ACD的平分线于点E、F．（1）若CE＝8，CF＝6，求OC的长；（2）连接AE、AF．问：当点O在边AC上运动到什么位置时，四边形AECF是矩形？证明你的结论．（1）证明：∵EF交∠ACB的平分线于点E，交∠ACB的外角平分线于点F，∴∠OCE＝∠BCE，∠OCF＝∠DCF，∵EF∥BC，∴∠OEC＝∠BCE，∠OFC＝∠DCF，∴∠OEC＝∠OCE，∠OFC＝∠OCF，∴OE＝OC，OF＝OC，∴OE＝OF；∵∠OCE+∠BCE+∠OCF+∠DCF＝180°，∴∠ECF＝90°，在Rt△CEF中，由勾股定理得：EF＝＝10，∴OC＝OE＝EF＝5；（2）当点O在边AC上运动到AC中点时，四边形AECF是矩形．理由如下：当O为AC的中点时，AO＝CO，∵EO＝FO，∴四边形AECF是平行四边形，∵∠ECF＝90°，∴平行四边形AECF是矩形．14．如图，菱形ABCD的对角线AC、BD相交于点O，过点D作DE∥AC且DE＝AC，连接CE、OE，连接AE交OD于点F．（1）求证：OE＝CD；（2）若菱形ABCD的边长为2，∠ABC＝60°．求AE的长．（1）证明：在菱形ABCD中，OC＝AC．∴DE＝OC．∵DE∥AC，∴四边形OCED是平行四边形．∵AC⊥BD，∴平行四边形OCED是矩形．∴OE＝CD．（2）在菱形ABCD中，∠ABC＝60°，∴AC＝AB＝2．∴在矩形OCED中，CE＝OD＝．在Rt△ACE中，AE＝．15．如图，以△ABC的各边，在边BC的同侧分别作三个正方形ABDI，BCFE，ACHG．（1）求证：△BDE≌△BAC；（2）求证：四边形ADEG是平行四边形．（3）直接回答下面两个问题，不必证明：①当△ABC满足什么条件时，四边形ADEG是矩形？②当△ABC满足什么条件时，四边形ADEG是正方形？（1）证明：∵四边形ABDI、四边形BCFE、四边形ACHG都是正方形，∴AC＝AG，AB＝BD，BC＝BE，∠GAC＝∠EBC＝∠DBA＝90°．∴∠ABC＝∠EBD（同为∠EBA的余角）．在△BDE和△BAC中，，∴△BDE≌△BAC（SAS），（2）∵△BDE≌△BAC，∴DE＝AC＝AG，∠BAC＝∠BDE．∵AD是正方形ABDI的对角线，∴∠BDA＝∠BAD＝45°．∵∠EDA＝∠BDE﹣∠BDA＝∠BDE﹣45°，∠DAG＝360°﹣∠GAC﹣∠BAC﹣∠BAD＝360°﹣90°﹣∠BAC﹣45°＝225°﹣∠BAC∴∠EDA+∠DAG＝∠BDE﹣45°+225°﹣∠BAC＝180°∴DE∥AG，∴四边形ADEG是平行四边形（一组对边平行且相等）．（3）①当四边形ADEG是矩形时，∠DAG＝90°．则∠BAC＝360°﹣∠BAD﹣∠DAG﹣∠GAC＝360°﹣45°﹣90°﹣90°＝135°，即当∠BAC＝135°时，平行四边形ADEG是矩形；②当四边形ADEG是正方形时，∠DAG＝90°，且AG＝AD．由①知，当∠DAG＝90°时，∠BAC＝135°．∵四边形ABDI是正方形，∴AD＝AB．又∵四边形ACHG是正方形，∴AC＝AG，∴AC＝AB．∴当∠BAC＝135°且AC＝AB时，四边形ADEG是正方形．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
下学期九年级数学上册期末复习压轴题专题训练试题
1.如图，在△ABC 中，∠ACB =90°，D 、E 分别是BC 、BA 的中点，连接DE 并延长至F ，使AF =AE ．(1)证明：四边形ACEF 是平行四边形；(2)若四边形ACEF 是菱形，求∠B 的度数．
2.已知:如图，在矩形ABCD 中，对角线AC ，BD 相交于点O ，E 是CD 中点，连接OE.过点C 作CF ∥BD 交线段OE 的延长线于点F ，连接DF.求证: (1)△ODE ≌△FCE;(2)四边形ODFC 是菱形.
3.已知关于x 的方程2(3)(2)0x x p ---=．
（1）求证：无论p 取何值时，方程总有两个不相等的实数根．
（2）设方程两实数根分别为1x ，2x ，且满足22
12
123x x x x +=，求实数p 的值．
4.如图，高高的路灯挂在学校操场旁边上方．王刚同学拿起一根2 m 长的竹竿去
测量路灯的高度，他走到路灯旁的一个地方点A 竖起竹竿(AE)，这时他量了一下竹竿的影长AC 正好是1 m ，他沿着影子的方向走，向远处走出两个竹竿的长度(即4 m )到点B ，他又竖起竹竿(BF 表示)，这时竹竿的影长BD 正好是一根竹竿的长度(即2 m )，此时，王刚同学抬头若有所思地说道：“噢，原来路灯有10 m 高
呀．”你觉得王刚同学的判断对吗？若对，请给出解答，若不对，请说明理由．
5.如图，已知点A(1,a)是反比例函数y=−3
x
的图象上一点，直线y=
−1
2x+1
2
与反比例函数y=−3
x
的图象在第四象限的交点为B．
（1）求直线AB的表达式；
（2）动点P(x,0)在x轴的正半轴上运动，当线段PA与线段PB之差达到最大时，求点P的坐标．
6.如图，一次函数y
1＝kx＋b(k≠0)的图象与反比例函数y
2
＝
m
x
(m≠0，x＜0)的图
象交于点A(－3，1)和点C，与y轴交于点B，△AOB的面积是6；
(1)求一次函数与反比例函数的表达式；(2)当x＜0时，比较y
1与y
2
的大小．
7.如图，一次函数y
1=kx+b(k≠0)和反比例函数y
2
＝
m
x
(m≠0)的图象交
点A(-1，6)，B(a，-2)
(1)求一次函数和反比例函数的表达式;
(2)根据图象直接写出y
1>y
2
时x的取值范围.
8.如图，已知直线y=1
2
x与双曲线y＝
k
x
(k＞0)交于A，B两点，且点A的横坐
标为4.
(1)求k的值及B点的坐标;
(2)若双曲线y＝k
x
(k＞0)上一点C的横坐标为8，求△AOC的面积.
9.如图，在矩形ABCD中，对角线AC，BD相交于点0，B是CD的中点，连接OE 过点C作CF∥BD交线段OE的延长线于点F，连接DF.
(1)求证:CF＝OD
(2)求证:四边形OCFD是菱形.
10.如图，在平行四边形ABCD中，EF垂直平分AC交BC于E，交AD于F．
（1）求证：四边形AECF 菱形．
（2）若AC CD ⊥．6AB =，10BC =，求四边形AECF 的面积．
11.如图，一次函数y ＝kx+b 与反比例函数y ＝
m
x
的图象交于点A(1，4)，B(4，n)两点.
(1)求反比例函数的表达式;(2)求一次函数的表达式;
(3)点P 是x 轴上的一动点，试确定点P 并求出它的坐标，使PA+PB 最小.
12.如图，四边形 ABCD 中，AD ∥BC ，∠A =90∘，AD =1 cm ，AB =3 cm ，BC =5 cm ，动点 P 从点 B 出发以 1 cm/s 的速度沿 BC 的方向运动，动点 Q 从点 C 出发以 2 cm/s 的速度沿 CD 方向运动，P ，Q 两点同时出发，当 Q 到达点 D 时停止运动，点 P 也随之停止，设运动的时间为 t s (t >0)．
（1）求线段 CD 的长；
（2）t 为何值时，线段 PQ 将四边形 ABCD 的面积分为 1:2 两部分? 13.如图，AB ⊥BC ，DC ⊥BC ，E 是BC 上一点，使得AE ⊥DE ；
D
A B
C
E
F
（1）求证：△ABE∽△ECD；
（2）若AB=4，AE=BC=5，求CD的长；
（3）当△AED∽△ECD时，请写出线段AD、AB、CD之间数量关系，并说明理由．
14.如图，在四边形ABCD中，∠ACB＝∠ADB，BC，AD的延长线相交于点E.求证:
(1)△ACE∽△BDE;
(2) BE.DC=AB.DE
15.如图，一次函数y＝－x＋4的图象与反比例函数y＝k
x
(k为常数，且k≠0)的
图象交于A(1，a)，B两点．
(1)求反比例函数的表达式及点B的坐标；
(2)在x轴上找一点P，使PA＋PB的值最小，求满足条件的点P的坐标及△PAB 的面积．
16.如图，正方形ABCD的对角线交于点O，点E，F分别在AB，BC上(AE<BE)，且∠EOF＝90°，OE，DA的延长线交于点M，OF，AB的延长线交于点N，连接MN.
(1)求证：OM＝ON；
(2)若正方形ABCD的边长为4，E为OM的中点，求MN的长．
17.如图，四边形ABCD的四个顶点分别在反比例函数y＝m
x
与y＝
n
x
(x>0，0<m<n)
的图象上，对角线BD∥y轴，且BD⊥AC于点P.已知点B的横坐标为4.
(1)当m＝4，n＝20时．
①若点P的纵坐标为2，求直线AB的函数表达式；
②若点P是BD的中点，试判断四边形ABCD的形状，并说明理由；
(2)四边形ABCD能否成为正方形？若能，求此时m，n之间的数量关系；若不能，试说明理由．
18.已知函数y=6
x
−1与函数y=kx交于点A(2,b)、B(−3,m)两点（点A在第一象限），
（1）求b，m，k的值；
（2）函数 y =6
x −1 与 x 轴交于点 C ，求 △ABC 的面积．
19.如图，在同一直角坐标系中，正比例函数的图象可以看作是：将x 轴所在的直线绕着原点O 逆时针旋转α
度角后的图形．若它与反比例函数y 的图象分别交于第一、三象限的点B 、D ，已知点(,0)A m -、 (,0)C m ．
（1）直接判断并填写：不论α取何值，四边形ABCD 的形状一定是__________．
（2）①当点B 为(,1)p 时，四边形ABCD 是矩形，试求p 和m 的值． ②观察猜想：对①中的m 值，直接写出能使四边形ABCD 为矩形的点B 坐标． （3）试探究四边形ABCD 能不能是菱形？若能，直接写出B 点的坐标，若不能，说明理由．
20.如图，在口ABCD 中，AE 是BC 边上的高，将△ABE 沿BC 方向平移，使点E 与点C 重合，得△CFC (1)求证:BE ＝DG
(2)若∠B ＝60°当AB 与BC 满足什么数量关系时，四边形 ABFC 是菱形?证明你的结论.
21.已知AC ，EC 分别为四边形ABCD 和EFCG 的对角线，点E 在△ABC 内，∠CAE+∠CBE ＝90°.
(1)如图1，当四边形ABCD和EFCG均为正方形时，连接BF
①求证:△CAEC∽△CBF;
②若BE＝1，AE＝2，求CE的长;
(2)如图2，当四边形ABCD和EFCG均为矩形，且AB
BC
=
EF
FC
=k时，若BE＝1,AE
＝2，CE＝3，求K的值.
(3)如图3，当四边形ABCD和EFCG均为菱形，且∠DAB＝∠GEF＝45°时，设BE ＝m，AE＝n，CE＝p，试探究m,n,p三者之间满足的等量关系.(直接写出结果，不必写出解答过程).
22.如图①，在四边形ABCD中，AC⊥BD于点E，AB＝AC＝BD，点M为BC中点，N 为线段AM上的点，且MB＝MN.
(1)求证：BN平分∠ABE；
(2)若BD＝1，连接DN，当四边形DNBC为平行四边形时，求线段BC的长；
(3)如图②，若点F为AB的中点，连接FN，FM，求证：△MFN∽△BDC.
23.如图，在平面直角坐标系中，正方形OABC的顶点O与坐标原点重合，点C的坐标为(0,3)，点A在x轴的负半轴上，点D，M分别在边AB，OA上，且AD=2DB，AM=2MO，一次函数y=kx+b的图象过点D和M，反比例函数y=m
x
的图象经过点D，与BC的交点为N．
（1）求反比例函数和一次函数的表达式；
（2）若点P在直线DM上，且使△OPM的面积与四边形OMNC的面积相等，求点P的坐标．
24.如图，BD是△ABC的角平分线，它的垂直平分线分别交AB，BD，BC于点E，F，G，连接ED，DG.
(1)请判断四边形EBGD的形状，并说明理由;
(2)若∠ABC＝30°，∠C＝45°，ED＝点P是BD上的一个动点，求PG+PC 的最小值.
25．如图， ABCD在平面直角坐标系中，AD＝6，若OA，OB的长是关于x的一元二次方程x2－7x＋12＝0的两个根，且OA>OB.
(1)由已知，AB＝_______；(直接写出结果)
(2)若点E为x轴上的点，且S
△AOE ＝
16
3
.
①E点坐标为_____________；(直接写出结果)
②证明：△AOE∽△DAO；
(3)若点M在平面直角坐标系内，则在直线AB上是否存在点F，使以A，C，F，M
为顶点的四边形为菱形？若存在，请直接写出F点的坐标；若不存在，请说明理由．。