光泵磁共振实验
实验光泵磁共振实验
实验 光泵磁共振实验在五十年代初期，法国物理学家卡斯特勒（A ·H ·Kastler ）提出了光抽运（optical pumping ，又称光泵）技术，并发现和发展了研究原子核磁共振的光学方法，因此于1966年荣获诺贝尔物理学奖。
光抽运（即光泵）是用圆偏振光束激发气态原子的方法，以打破原子在所研究的能级间的玻耳兹曼热平衡分布，造成所需的布居数差，从而在低浓度的条件下提高了核磁共振强度，这时再用相应频率的射频场激励原子的磁共振。
在探测核磁共振方面，不是直接探测原子对射频量子发射或吸收，而是采用光电探测的方法，探测原子对光量子的发射或吸收。
由于光量子的能量比射频量子高八个数量级，所以探测信号的灵敏度比一般磁共振探测技术高八个数量级。
三十多年来，用光抽运——磁共振——光电探测技术对许多原子、离子和分子进行了大量研究，增进了对微观粒子结构的了解。
如对原子的磁矩、朗德因子g ，能级结构、塞曼分裂等，尤以对碱金属原子（铷等）激发态精细与超精细结构的研究方面起了很大推动作用。
此外光抽运技术在激光、原子频标和精测弱磁场等方面也都有广泛的应用。
本实验以碱金属——铷（Rb ）原子做为研究对象，所涉及的物理内容丰富，应用到原子物理学，光学，电磁学及无线电电子学等方面的知识，并定性或定量地了解到原子内部的很多信息。
它是典型的波谱学教学实验之一。
实验原理1、 铷（Rb ）原子的精细结构与超精细结构能级本实验研究气态的自由原子——铷（Rb ）,它和所有碱金属原子Li 、Na 、K 一样，在紧紧束缚的满壳层外只有一个电子。
铷的价电子处于第五壳层，主量子数n = 5。
n 为5的电子，其轨道量子数L = 0，1，2，3，4，(n -1)。
基态L = 0，最低激发态L = 1，电子自旋量子数s = 1/2。
由于电子的轨道运动与自旋的相互作用（即L-S 耦含）而发生的能级分裂，称为原子的精细结构（见图1）。
轨道角动量L P 与自旋角动量S P 合成为总角动量S L J P P P+=。
光泵磁共振实验报告结论
一、实验概述光泵磁共振实验是一种重要的物理实验，通过观察原子在特定磁场和光场作用下的能级跃迁，研究原子能级结构、磁共振现象以及光抽运效应等。
本次实验采用DH807型光泵磁共振实验装置，通过观察铷原子的光抽运信号和光泵磁共振信号，加深对原子超精细结构和塞曼子能级的理解，并测定铷原子超精细结构塞曼子能级的朗德因子。
二、实验目的1. 观察铷原子光抽运信号，加深对原子超精细结构的理解。
2. 观察铷原子的磁共振信号，测定铷原子超精细结构塞曼子能级的朗德因子。
3. 学会利用光磁共振的原理和实验方法，提高实验技能。
三、实验原理光泵磁共振实验基于以下原理：1. 光抽运效应：当原子处于激发态时，吸收特定频率的光子，原子会跃迁到更高能级。
通过调节光场强度，可以使原子处于高能级状态的粒子数增加。
2. 磁共振：当原子处于特定磁场中，能级发生塞曼分裂。
通过调节磁场强度，可以使原子能级发生跃迁，产生磁共振现象。
3. 光泵磁共振：光泵磁共振实验中，利用光抽运效应和磁共振原理，观察原子能级跃迁和磁共振信号。
四、实验结果与分析1. 光抽运信号观察在实验中，我们观察到了铷原子的光抽运信号。
通过调节光场强度和频率，可以观察到不同能级跃迁的光抽运信号。
这表明光抽运效应在实验中得到了充分体现。
2. 磁共振信号观察在实验中，我们观察到了铷原子的磁共振信号。
通过调节磁场强度，可以观察到不同能级跃迁的磁共振信号。
这表明磁共振现象在实验中得到了充分体现。
3. 塞曼子能级朗德因子测定根据实验数据，我们计算了铷原子超精细结构塞曼子能级的朗德因子。
实验结果显示，铷原子超精细结构塞曼子能级的朗德因子与理论值基本吻合。
五、实验结论1. 通过本次实验，我们成功地观察到了铷原子的光抽运信号和磁共振信号，验证了光泵磁共振实验的原理。
2. 实验结果表明，铷原子超精细结构塞曼子能级的朗德因子与理论值基本吻合，表明实验具有较高的准确性。
3. 通过本次实验，我们加深了对原子超精细结构和塞曼子能级的理解，提高了实验技能。
实验 光泵磁共振实验
实验 光泵磁共振实验在五十年代初期，法国物理学家卡斯特勒（A ·H ·Kastler ）提出了光抽运（optical pumping ，又称光泵）技术，并发现和发展了研究原子核磁共振的光学方法，因此于1966年荣获诺贝尔物理学奖。
光抽运（即光泵）是用圆偏振光束激发气态原子的方法，以打破原子在所研究的能级间的玻耳兹曼热平衡分布，造成所需的布居数差，从而在低浓度的条件下提高了核磁共振强度，这时再用相应频率的射频场激励原子的磁共振。
在探测核磁共振方面，不是直接探测原子对射频量子发射或吸收，而是采用光电探测的方法，探测原子对光量子的发射或吸收。
由于光量子的能量比射频量子高八个数量级，所以探测信号的灵敏度比一般磁共振探测技术高八个数量级。
三十多年来，用光抽运——磁共振——光电探测技术对许多原子、离子和分子进行了大量研究，增进了对微观粒子结构的了解。
如对原子的磁矩、朗德因子g ，能级结构、塞曼分裂等，尤以对碱金属原子（铷等）激发态精细与超精细结构的研究方面起了很大推动作用。
此外光抽运技术在激光、原子频标和精测弱磁场等方面也都有广泛的应用。
本实验以碱金属——铷（Rb ）原子做为研究对象，所涉及的物理内容丰富，应用到原子物理学，光学，电磁学及无线电电子学等方面的知识，并定性或定量地了解到原子内部的很多信息。
它是典型的波谱学教学实验之一。
实验原理1、 铷（Rb ）原子的精细结构与超精细结构能级本实验研究气态的自由原子——铷（Rb ）,它和所有碱金属原子Li 、Na 、K 一样，在紧紧束缚的满壳层外只有一个电子。
铷的价电子处于第五壳层，主量子数n = 5。
n 为5的电子，其轨道量子数L = 0，1，2，3，4，(n -1)。
基态L = 0，最低激发态L = 1，电子自旋量子数s = 1/2。
由于电子的轨道运动与自旋的相互作用（即L-S 耦含）而发生的能级分裂，称为原子的精细结构（见图1）。
轨道角动量L P 与自旋角动量S P 合成为总角动量S L J P P P+=。
光泵磁共振实验
光泵磁共振实验探讨无锡高等师范学校毛宏伟摘要光泵磁共振实验是利用光抽运效应来研究原子超精细结构塞曼能级间的磁共振。
它是近代物理实验中一个基本而重要的实验。
本文主要从光抽运信号观察、磁共振信号观察、测量gF因子、测量扬州地区地磁场等几个方面展开探讨。
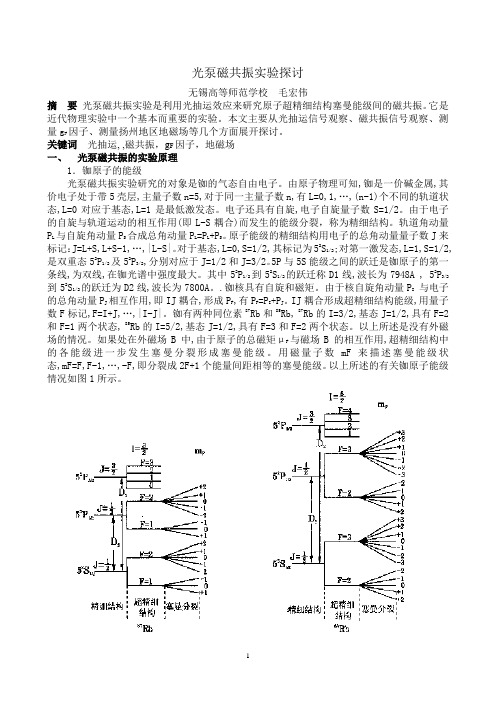
关键词光抽运, ,磁共振，g F因子，地磁场一、光泵磁共振的实验原理1．铷原子的能级光泵磁共振实验研究的对象是铷的气态自由电子。
由原子物理可知,铷是一价碱金属,其价电子处于带5壳层,主量子数n=5,对于同一主量子数n,有L=0,1,…,(n-1)个不同的轨道状态,L=0对应于基态,L=1是最低激发态。
电子还具有自旋,电子自旋量子数S=1/2。
由于电子的自旋与轨道运动的相互作用(即L-S耦合)而发生的能级分裂，称为精细结构。
轨道角动量P L 与自旋角动量PS合成总角动量PL=PL+PS。
原子能级的精细结构用电子的总角动量量子数J来标记：J=L+S,L+S-1,…,|L-S|。
对于基态,L=0,S=1/2,其标记为52S1/2;对第一激发态,L=1,S=1/2,是双重态52P1/2及52P3/2,分别对应于J=1/2和J=3/2。
5P与5S能级之间的跃迁是铷原子的第一条线,为双线,在铷光谱中强度最大。
其中52P1/2到52S1/2的跃迁称D1线,波长为7948A , 52P3/2到52S1/2的跃迁为D2线,波长为7800A。
.铷核具有自旋和磁矩。
由于核自旋角动量PI与电子的总角动量PJ 相互作用,即IJ耦合,形成PF,有PF=PI+PJ。
IJ耦合形成超精细结构能级,用量子数F标记,F=I+J,…,|I-J|。
铷有两种同位素87Rb和85Rb, 87Rb的I=3/2,基态J=1/2,具有F=2和F=1两个状态, 85Rb的I=5/2,基态J=1/2,具有F=3和F=2两个状态。
以上所述是没有外磁场的情况。
如果处在外磁场B 中,由于原子的总磁矩μF与磁场B 的相互作用,超精细结构中的各能级进一步发生塞曼分裂形成塞曼能级。
光泵磁共振_3
中国石油大学 近代物理实验 实验报告 成 绩：实验B4 光泵磁共振【实验目的】1．观察铷原子光抽运信号，加深对原子超精细结构的理解。
2．观察铷原子的磁共振信号，测定铷原子超精细结构塞曼子能级的朗德因子。
3．学会利用光磁共振的方法测量地磁场。
【实验原理】一．铷原子基态和最低激发态的能级铷（Z =37）是一价金属元素，基态轨道量子数L =0，自旋量子数S =1/2，总角动量量子数J =1/2，因而它们的基态都是52S 1/2。
通过L —S 耦合形成了电子的总角动量P J ，与此相联系的核外电子的总磁矩J μ为 2J JJ eeg P m μ=- （B4-1） 式中)1(2)1()1()1(1++++-++=J J S S L L J J g J （B4-2）是著名的朗德因子，m e 是电子质量，e 是电子电量。
原子核也有自旋和磁矩，核自旋量子数用I 表示。
核角动量I P 和核外电子的角动量J P 耦合成一个更大的角动量，用符号 F P 表示，其量子数用F 表示，则I J F P P P+= （B4-3）与此角动量相关的原子总磁矩为2F FF eeg P m μ=- （B4-4） 式中图B4-1 Rb 原子精细结构的形成)1(2)1()1()1(++-+++=F F I I J J F F g g JF （B4-5）F g 是对应于F μ与F P 关系的朗德因子。
在有外静磁场B 的情况下，总磁矩将与外场相互作用，使原子产生附加的能量22F FF F F F F B e ee e E B g P B g M B g M B m m μμ=-⋅=⋅== （B4-6） 其中2B eem μ=124102741.9--⨯=JT 称为玻尔磁子，F M 是F P 在外场方向上分量的量子数，F M ＝－F ，－F ＋１，…F －１，F ，共有2F ＋1个值。
可以看到，原子在磁场中的附加能量E 随F M 变化，原来对F M 简并的能级发生分裂，称为超精细结构，一个F 能级分裂成2F ＋1个子能级，相邻的子能级的能量差为B g E B F μ=∆ （B4-7） 再来看一下具体的分裂情况。
近代物理实验6-3光泵磁共振
2.弛豫过程 光抽运造成大的粒子数差，使系统处于非热平衡状态。使 系统趋向于热平衡分布的过程即弛豫。实验中主要有以下过程：
a.铷原子与器壁碰撞导致子能级间的跃迁 b.铷原子之间碰撞导致自旋—自旋交换弛豫 c.铷原子与缓冲气体间的碰撞 a、b过程会使系统失去偏极化，且铷原子与器壁碰撞是失 去偏极化的主要原因，而c过程对偏极化基本无影响，故在样 品泡中冲入缓冲气体，大大减少了铷原子与器壁碰撞的机会， 可以保持高度偏极化。
近代物理实验
6-3光泵磁共振
光泵磁共振是光抽运和磁共振结合在一起的物
理过程，与传统的光谱技术相比具有更高的分辨率
和灵敏度，且克服了核磁共振中的一些限制因素， 在研究原子结构、磁场精确测量、激光技术等领域
有着广泛应用。
本实验通过光抽运下的磁共振测量过程，学习
观察原子与辐射场相互作用过程中的量子跃迁。
高立模，《近代物理实验》 [M]，南开大学出版社 杨福家，《原子物理学》 [M]，高等教育出版社
光泵磁共振实验装置
全套实验装置方框图
1.观察光抽运信号
使扫场线圈的方形波磁场与H地垂直相反，调节H水平及 H垂直为零，旋转起偏镜，观察到部分光被吸收的信 号。调节起偏镜透振方向和H垂直的大小，使吸收信 号达到最强，此时H垂直与H地垂直刚好抵消。
2.测量87Rb的gF值 h ν =gF μ BB
3.磁共振原理 塞曼能级差： Δ E=gF μ BB 在垂直于B的方向加一射频线偏振场，左 旋圆偏振场与原子磁矩进动方向一致， 调节射频场频率与拉莫尔角频率相等， 发生吸收或感应跃迁： ω=ΔE=gFμBB
4.光磁共振 通过光抽运造成能级间显著的粒子数差，满足磁共振条件时， 发生感应跃迁。测量D1 σ +光强的变化可得磁共振信号。
光泵磁共振-物理试验
实验 4.5 光泵磁共振20世纪50年代初期，法国科学家卡斯特莱（A.Kastler）提出采用光抽运技术（光泵），即用圆偏振光来激发原子，打破原子在能级间的热平衡，造成能级上粒子集聚差数，使得在低浓度下有较高的共振强度。
这时再以相应频率的射频场激励原子磁共振，并采用光探测法，使探测信号灵敏度有很大提高。
这个方法的出现不仅使微观粒子结构的研究前进了一步，而且在激光、量子标频和精测弱磁场等方面也有重要突破。
1966年, A.Kastler由于发现和发展了研究原子中核磁共振的光学方法（既光泵磁共振）而获诺贝尔物理奖。
一、实验目的1.加深对原子超精细结构、光跃迁及磁共振的理解；2.掌握以光抽运为基础的光检测磁共振方法；3.测定铷原子超精细结构塞曼子能级的朗德因子。
二、仪器与用具光泵磁共振实验装置、射频信号发生器、示波器、频率计等三、实验原理1．铷（Rb）原子基态及最低激发态的能级铷是一价的碱金属，它的价电子处于第5壳层，主量子数n=5，轨道量子数L=0,1,…,n-1，电子自旋量子数S=1/2。
由电子的自旋与轨道运动相互作用（L-S耦合）发生能级分裂，形成原子的精细结构(如图1)。
电子总角动量的量子数J=L+S，L+S-1，…，|L-S|。
对于铷原子的基态，L=0，S=1/2，故J=1/2；其最低激发态，L=1，S=1/2，故J=1/2和2/3。
在5P与5S 能级之间产生的跃迁是铷原子光谱主线系第一条线，为双线，在铷灯的光谱中强度特变大。
52P1/2到52S1/2的跃迁产生的谱线为D1线，波长是7947A；52P3/2到52S1/2的跃迁产生的谱线为D2线，波长是7800A。
互作用造成能级的附加分裂，称为超精细结构(如图2)。
铷元素在自然界主要有两种同位素Rb 87和Rb 85。
两种同位素Rb 87和Rb 85核的自旋量子数I 是不同的。
核自旋角动量P I 与电子总角动量P J 耦合成P F （P F =P I +P J ），耦合后的总量子数F=I+J ，…，︱I -J ︱, Rb 87的I = 3/2，Rb 85的I = 5/2，故Rb 87基态的F=1和2； Rb 85的基态的F=2和3。
光泵磁共振教案 实验原理
光泵磁共振实验 实验原理、数据记录及数据处理【引言】气体原子中的磁共振信号十分微弱，观测十分困难。
1950年，法国物理学家卡斯特勒（Ａ．Kastler ）提出了光抽运的方法（即Optical Pumping ，故又译作光泵），可使原子能级的粒子数分布产生重大改变（偏极化），并可利用抽运光对磁共振信号作光检测，从而大大的提高了信号强度和检测灵敏度。
卡斯特勒因此而荣获1966年诺贝尔物理学奖。
【实验目的】1、加深对原子超精细结构的理解；2、掌握以光抽运为基础的光检测共振方法。
【实验仪器】光磁共振实验仪、示波器、频率计、射频信号发生器。
【实验原理】 ●铷原子基态和激发态能级（1）L S 耦合，,1,||J L S L S L S =++-- 。
铷原子基态0L =，12S =，故12J =；其最低激发态1L =，12S =，故12J =和32；为精细结构。
（2）IJ 耦合，,1,||F I J I J I J =++-- 。
铷原子核自旋不为零，两个同位素核自旋量子数I 也不相同。
87Rb 的3/2I =，85Rb 的5/2I =，故87Rb 的基态的1F =和2，85Rb 的基态的2F =和3。
由F 定标的能级称为超精细结构。
在磁场中铷原子的超精细结构能级产生塞曼分裂。
定标这些磁量子数,1,F m F F F =-- ，因而一个超精细结构能级分裂为21F +。
设原子总角动量对应的原子总磁矩为F μ，F μ与外磁场0B 的相互作用能为： 00F F F B E B g m B μμ=-⋅=（其中：2419.2741102B ee J Tm μ--==⨯⋅ ，(1)(1)(1)2(1)F J F F J J I I g g F F +++-+=⋅+（其中： (1)(1)(1)12(1)J J J S S L L g J J +++-+=++）相邻塞曼子能级能量差为： 0F B E g B μ∆= ●光抽运效应由于超精细塞曼子能级间的能量差E ∆很小，这些能级上的粒子数近似相等，不利于观察这些子能级间的共振现象，为此卡斯特勒提出光抽运的方法，即用圆偏振光激发原子，使原子能级的粒子数分布产生重大改变。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
7-7 光泵磁共振实验光磁共振，是把光频跃迁和射频磁共振跃迁结合起来的一种物理过程, 是利用光抽运效应来研究原子超精细结构塞曼子能级间的磁共振。
所研究的对象是碱金属原子铷Rb 。
天然铷中含量大的同位素有两种：87Rb 占27.85 %，85Rb 占72．15%。
气体原子塞曼子能级间的磁共振信号非常弱，用磁共振的方法难于观察。
本实验中应用了光探测的方法，既保持了磁共振分辨率高的优点，同时将探测灵敏度提高了几个以至十几个数量级。
此方法一方面可用于基础物理研究，另一方面在量子频标、精确测定磁场等问题上也都有很大的实际应用价值。
通过实验可加深对原子超精细结构、光跃迁及磁共振的理解。
一．实验目的：1、了解光泵磁共振的原理，观察光磁共振现象。
2、测量铷（Rb ）原子的F g 因子及地磁场的大小。
二．实验原理：1、铷原子基态和最低激发态的能级铷（Z =37）是一价金属元素，天然铷有两种稳定的同位素: 85Rb 和87Rb,二者的比例接近2比1。
它们的激态都是52S 1/2， 即电子的主量子数n =5，轨道量子数L =0，自旋量子数S =1/2，总角动量量子数J =1/2（L —S 耦合）。
在L —S 耦合下，铷原子的最低激发态仅由价电子的激发所形成，其轨道量子数L =1，自旋量子数S =1/2，电子的总角动量J =L +S 和L -S ，即J =3/2和1/2，形成双重态：52P 1/2和52P 3/2，这两个状态的能量不相等，产生精细分裂。
因此，从5P 到5S 的跃迁产生双线，分别称为D 1和D 2线，它们的波长分别是794.8nm 和780.0nm （见图7-7-1）。
通过L —S 耦合形成了电子的总角动量P J ，与此相联系的核外电子的总磁矩μJ 为： J J J P m e g ρρ2-=μ 其中)1(2)1()1()1(1++++-++=J J S S L L J J g J 就是著名的Longde 因子，m 是电子质量，e 是电子电量。
原子核也有自旋和磁矩，核自旋量子数用I 表示。
核角动量P I 和核外电子的角动量P J 耦合成一个更大的角动量，用符号 P F 表示，其量子数用F 表示，则 I J F P P P ρρρ+=与此角动量相关的原子总磁矩为F F F P m e g ρρ2-=μ 其中)1(2)1()1()1(++-+++=F F I I J J F F g g J F 在有外静磁场B 的情况下，总磁矩将与外场相互作用，使原子产生附加的能量B M g B M me g B P m e g B E B F F F F F F F μμ==•=•-=ηρρρρ22 其中m e B 2η=μ124102741.9--⨯=JT 称为玻尔磁子，ＭＦ是ＰＦ的第三分量的量子数，ＭＦ＝－Ｆ，－Ｆ＋１，…Ｆ－１，Ｆ，共有２Ｆ＋１个值。
我们看到，原子在磁场中的附加能量Ｅ随ＭＦ变化，原来对ＭＦ简并的能级发生分裂，称为超精细结构，一个Ｆ能级分裂成２Ｆ＋１个子能级，相邻的子能级的能量差为B g E B F μ=∆我们来看一下具体的分裂情况。
87Rb 的核自旋2/3=I ，85Rb 的核自璇2/5=I ，因此，两种原子的超精细分裂将不同。
我们以87Rb 为例，介绍超精细分裂的情况，可以对照理解85Rb 的分裂（如图7-7-1所示）。
图7-7-1 87Rb 原子能级超精细分裂对于电子态52S 1/2，角动量P J 与角动量P I 耦合成的角动量P F 有两个量子数：F =I +J 和I -J ，即F =2和1。
同样，对于电子态52P 1/2，耦合成的角动量P Ｆ也有两个量子数：Ｆ＝２和１。
对于电子态５２P 3/2，耦合后的角动量P Ｆ有四个量子数：Ｆ=3，2，1，0。
我们可以画出原子在磁场中的超精细分裂情况，如图7-7-1所示。
由于实验中D 2线被滤掉，所涉及的52P 3/2态的耦合分裂也就不用考虑。
实验中，我们要对铷光源进行滤光和变换，只让D 1σ+(左旋圆偏振光)光通过并照射到铷原子蒸气上，观察铷蒸气D 1σ+对光的吸收情况。
我们要指出的是：１）从常温对应的能量k B T 来衡量，超精细分裂和之后的塞曼分裂的裂距都是很小的，根据玻尔兹曼分布：T k E totalB e N N 11-= 由52S 1/2分列出的8条子能级上的原子数应接近均匀分布；同样，由52P 1/2分裂出的8条子能级上的原子数也接近均匀分布。
２）如果考虑到热运动造成的多普勒效应，铷光源发出的D 1σ+光实际包含了连续频率的光，这些光使得D 1线有一定的宽度，同时也为铷蒸气可能进行的各种吸收提供了丰富的谱线。
2、光磁共振跃迁处于磁场环境中的铷原子对D 1σ+光的吸收遵守如下的选择定则1±=∆L 0,1±=∆F ； 1+=∆F M根据这一选择定则可以画出吸收跃迁图，如图7-7-2所示。
图7-7-2 87Rb 原子对D 1σ+光的吸收和退激跃迁我们看到，5S 能级中的8条子能级除了M F =+2的子能级外，都可以吸收D 1σ+光而跃迁到5P 的有关子能级，M F =+2的子能级上的原子既不能往高能级跃迁也没有条件往低能级跃迁，所以这些原子数是不变的；另一方面，跃迁到高能级的原子通过自发辐射等途径很快又跃迁回5S 低能级，发出自然光，跃迁选择定则是：0,1±=∆F ； 0,1±=∆F M相应的跃迁见图7-7-2的右半部分。
我们注意到，退激跃迁中有一部分的状态变成了5S 能级中的M F =+2的状态，而这一部分原子是不会吸收光再跃迁到5P 去的，那些回到其它7个子能级的原子都可以再吸收光重新跃迁到5P 能级。
当光连续照着，跃迁5S →5P →5S →5P →…这样的过程就会持续下去。
这样，5S 态中2+=F M 子能级上的原子数就会越积越多，而其余７个子能级上的原子数越来越少，相应地，对D 1σ+光的吸收越来越弱，最后，差不多所有的原子都跃迁到了5S 态的M F =+2的子能级上，其余7个子能级上的原子数少到如此程度，以至于没有几率吸收光，光强测量值不再发生变化。
通过以上的考察可以得出这样的结论：在没有D 1σ+光照射时，5S 态上的8个子能级几乎均匀分布着原子，而当D 1σ+光持续照着时，较低的7个子能级上的原子逐步被“抽运”到M F =+2的子能级上，出现了“粒子数反转”的现象。
在“粒子数反转”后，如果在垂直于静磁场B 和垂直于光传播方向上加一射频振荡的磁场，并且调整射频频率ν，使之满足B g h B F μν= （1）这时将出现“射频受激辐射”，在射频场的扰动下，处于M F =+2子能级上的原子会放出一个频率为ν、方向和偏振态与入射量子完全一样的量子而跃迁到M F =+1的子能级，M F =+2上的原子数就会减少；同样，M F =+1子能级上的原子也会通过“射频受激辐射”跃迁到M F =0的子能级上……如此下去，5S 态的上面5个子能级很快就都有了原子，于是光吸收过程重又开始，光强测量值又降低；跃迁到5P 态的原子在退激过程中可以跃迁到5S 态的最下面的3个子能级上，所以，用不了多久，5S 态的8个子能级上全有了原子。
由于此时M F =+2子能级上的原子不再能久留，所以，光跃迁不会造成新的“粒子数反转”。
通过以上的分析得到了如下的结论：处于静磁场中的铷原子对偏振光D 1σ+的吸收过程能够受到一个射频信号的控制，当没有射频信号时，铷原子对D 1σ+光的吸收很快趋于零，而当加上一个能量等于相邻子能级的能量差的射频信号（即公式（1）成立）时又引起强烈吸收。
根据这一事实，如果能让公式（1）周期性成立，则可以观察到铷原子对D 1σ+光的周期性吸收的现象。
实验中是固定频率ν而采用周期性的磁场B 来实现这一要求的，称为“扫场法”。
3、光磁共振的观察“扫场法”采用的周期性信号一般有两种：方波信号和三角波信号。
方波信号用于观察“光抽运”过程，三角波信号用于测量有关参数。
在加入了周期性的“扫描场”以后，总磁场为：B total =B DC +B S +B e∕∕其中B DC 是一个由通有稳定的直流电流的线圈所产生的磁场，方向在水平方向，B e∕∕是地球磁场的水平分量，这两部分在实验中不变；B S 是周期性的扫描场，也是水平方向的。
地球磁场的垂直分量被一对线圈的磁场所抵消。
1）用方波观察“光抽运”将直流磁场B DC调到零，加上方波扫场信号，其波形见图7-7-3，它是关于零点对称的。
图7-7-3 “光抽运”的形成和波形在方波刚加上的瞬间，样品泡内铷原子5S态的8个子能级上的原子数近似相等，即每个子能级上的原子数各占总原子数的1/8，因此，将有7/8的原子能够吸收D1σ+光，此时对光的吸收最强，探测器上接受的光信号最弱。
随着原子逐步被“抽运”到M F=+2的子能级上，能够吸收D1σ+光的原子数逐渐减少，透过样品泡的光逐渐增强。
当“抽运”到M F=+2子能级上的原子数达到饱和，透过样品泡的光强达到最大而不再发生变化。
当“扫场”过零并反向时，各子能级简并，原来是M F=+2的原子，通过碰撞，自旋方向混杂而使各个自旋方向上的原子数又接近相等，当“扫场”反向、铷原子各子能级重新分裂以后，对D1σ+光的吸收又达到了最大。
2、三角波观察光磁共振调节直流磁场B DC至某个值，加上三角波“扫场”信号和射频信号，通过调节“扫场”幅度和射频信号的频率，可以观察到如图7-7-4所示的光磁共振信号。
图7-7-4 光磁共振的信号图像Ⅰ在光磁共振实验中，一个重要的任务是测量g F 因子，为此提出如下方法：在某个射频ν1下调出光磁共振信号（类似于图7-7-4），通过交替调节B DC 和“扫场”信号，使共振信号的谷点对应“扫场”信号的峰点或谷点 ，如图7-7-5所示。
图7-7-5 光磁共振的信号图像Ⅱ当光磁共振发生时，满足量子条件：B B B g h S DC B F ++=(1μνe∕∕) (2) 通过仪器上的换向开关将直流磁场的方向倒转，此时可能观察不到共振信号。
调节射频的频率，又可以看到共振信号，并调到如图7-7-6所示的状态，记下射频的频率ν2，则有如下的量子条件成立：B B B g h S DC B F ++-=-(2μνe∕∕) (3)图7-7-6 光磁共振信号图像Ⅲ由（２）、（3）式得： DCB F B h g μνν2)(21+= （4） 直流磁场B DC 可以通过读出两个并联线圈的电流之和I 来计算（亥姆霍兹线圈公式）72/310516-⨯=rNI B DC π （T ） 式中N 和ｒ是两个水平线圈的匝数和有效半径，因为两个线圈是并联的，数字表显示的Ｉ值是流过两个线圈的电流之和。