高中数学立体几何讲义一
立体几何 讲义
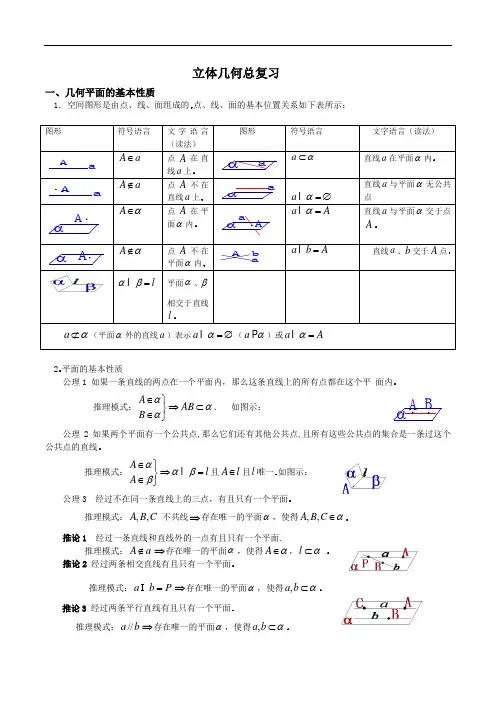
立体几何总复习一、几何平面的基本性质1α=∅ A α=b A =l αβ= a α=∅(α)或a A α=公理1 如果一条直线的两点在一个平面内,那么这条直线上的所有点都在这个平 推理模式:A AB B ααα∈⎫⇒⊂⎬∈⎭. 如图示: 公理2如果两个平面有一个公共点,那么它们还有其他公共点,且所有这些公共点的集合是一条过这个 推理模式:A l A ααββ∈⎫⇒=⎬∈⎭且A l ∈且l公理3 推理模式:,, A B C 不共线⇒存在唯一的平面α,使得,,A B C α∈ 推论1 经过一条直线和直线外的一点有且只有一个平面.推理模式:A a ∉⇒存在唯一的平面α,使得A α∈,l α⊂ 推论2 推理模式:P b a = ⇒存在唯一的平面α,使得,a b α⊂推论3 推理模式://a b ⇒存在唯一的平面α,使得,a b α⊂动手练习:1 下面是一些命题的叙述语,其中命题和叙述方法都正确的是( ) A .∵αα∈∈B A ,,∴α∈AB . B .∵βα∈∈a a ,,∴a =βα . C .∵α⊂∈a a A ,,∴A α∈. D .∵α⊂∉a a A ,,∴α∉A . 2.下列推断中,错误的是( )A .ααα⊂⇒∈∈∈∈lB l B A l A ,,,C .βα∈∈C B A C B A ,,,,,,且A,B,C 不共线βα,⇒B .B B A A =⇒∈∈∈∈βαβαβα ,,, D .αα∉⇒∈⊄A l A l ,3.两个平面把空间最多分成___ 部分,三个平面把空间最多分成__部分. 4.判断下列命题的真假,真的打“√”,假的打“×” (1)空间三点可以确定一个平面 ( )(2)两个平面若有不同的三个公共点,则两个平面重合( ) (3)两条直线可以确定一个平面( )(4)若四点不共面,那么每三个点一定不共线( ) (5)两条相交直线可以确定一个平面( ) (6)三条平行直线可以确定三个平面( ) (7)一条直线和一个点可以确定一个平面( ) (8)两两相交的三条直线确定一个平面( ) 5.看图填空(1)AC ∩BD = (4)平面A 1C 1CA ∩平面D 1B 1BD = (2)平面AB 1∩平面A 1C 1= (5)平面A 1C 1∩平面AB 1∩平面B 1C = (3)平面A 1C 1CA ∩平面AC = (6)A 1B 1∩B 1B ∩B 1C 1= 6 6.选择题(1)下列图形中不一定是平面图形的是 ( )A 三角形B 菱形C 梯形D 四边相等的四边形(2)空间四条直线每两条都相交,最多可以确定平面的个数是( )A 1个B 4个C 6个D 8个(3)空间四点中,无三点共线是四点共面的 ( )A 充分不必要条件B 必要不充分条件C 充分必要条件D 既不充分也不必要1二、立体几何线面关系(一)、判定两线平行的方法1、平行于同一直线的两条直线互相平行2、垂直于同一平面的两条直线互相平行3、如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行4、如果两个平行平面同时和第三个平面相交,那么它们的交线平行5、在同一平面内的两条直线,可依据平面几何的定理证明(二)、判定线面平行的方法6、据定义:如果一条直线和一个平面没有公共点7、如果平面外的一条直线和这个平面内的一条直线平行,则这条直线和这个平面平行8、两面平行,则其中一个平面内的直线必平行于另一个平面9、平面外的两条平行直线中的一条平行于平面,则另一条也平行于该平面10、平面外的一条直线和两个平行平面中的一个平面平行,则也平行于另一个平面(三)、判定面面平行的方法1、定义:没有公共点2、如果一个平面内有两条相交直线都平行于另一个平面,则两面平行3 垂直于同一直线的两个平面平行4、平行于同一平面的两个平面平行(四)、面面平行的性质1、两平行平面没有公共点2、两平面平行,则一个平面上的任一直线平行于另一平面3、两平行平面被第三个平面所截,则两交线平行4、垂直于两平行平面中一个平面的直线,必垂直于另一个平面(五)、判定线面垂直的方法1、定义:如果一条直线和平面内的任何一条直线都垂直,则线面垂直2、如果一条直线和一个平面内的两条相交线垂直,则线面垂直3、如果两条平行直线中的一条垂直于一个平面,则另一条也垂直于该平面4、一条直线垂直于两个平行平面中的一个平面,它也垂直于另一个平面5、如果两个平面垂直,那么在一个平面内垂直它们交线的直线垂直于另一个平面6、如果两个相交平面都垂直于另一个平面,那么它们的交线垂直于另一个平面(六)、判定两线垂直的方法1、 定义:成︒90角2、 直线和平面垂直,则该线与平面内任一直线垂直3、 在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直4、 在平面内的一条直线,如果和这个平面的一条斜线垂直,那么它也和这条斜线的射影垂直5、 一条直线如果和两条平行直线中的一条垂直,它也和另一条垂直 (七)、判定面面垂直的方法1、 定义:两面成直二面角,则两面垂直2、 一个平面经过另一个平面的一条垂线,则这个平面垂直于另一平面 (八)、面面垂直的性质 1、 二面角的平面角为︒902、 在一个平面内垂直于交线的直线必垂直于另一个平面3、 相交平面同垂直于第三个平面,则交线垂直于第三个平面(九)、各种角的范围 1、异面直线所成的角的取值范围是:︒≤<︒900θ (]︒︒90,0 2、直线与平面所成的角的取值范围是:︒≤≤︒900θ []︒︒90,0 3、斜线与平面所成的角的取值范围是:︒≤<︒900θ (]︒︒90,04、二面角的大小用它的平面角来度量;取值范围是:︒≤<︒1800θ (]︒︒180,0动手练习1.判断题(对的打“√”,错的打“×”)(1)垂直于两条异面直线的直线有且只有一条 ( )(2)两线段AB 、CD 不在同一平面内,如果AC =BD ,AD =BC ,则AB ⊥CD ( ) (3)在正方体中,相邻两侧面的一对异面的对角线所成的角为60º ( ) (4)四边形的一边不可能既和它的邻边垂直,又和它的对边垂直 ( ) 2.右图是正方体平面展开图,在这个正方体中①BM 与ED 平行;②CN 与BE 是异面直线; ③CN 与BM 成60º角;④DM 与BN 垂直.以上四个命题中,正确命题的序号是( )(A )①②③ (B )②④ (C )③④ (D 3 ,,,E F G H 分别是空间四边形四条边,,,AB BC CD DA 的中点,EA FB CMN D(1)求证四边形EFGH(2)若AC ⊥BD 时,求证:EFGH 为矩形; (3)若BD =2,AC =6,求22HF EG +;(4)若AC 、BD 成30º角,AC =6,BD =4,求四边形EFGH 的面积;(5)若AB =BC =CD =DA =AC =BD =2,求AC 与BD 间的距离.4 ABCD 中,2AD BC ==,,E F 分别是,AB CD 的中点,EF = 求异面直线,AD BC5. 在正方体ABCD -A 1B 1C 1D 1中,求(1)A 1B 与B 1D 1所成角; (2)AC 与BD 1所成角.6.在长方体D C B A ABCD '''-中,已知AB=a ,BC=b ,A A '=c(a >b),求异面直线B D '与AC7.如图,已知P 是平行四边形ABCD 所在平面外一点,M 、N 分别是AB 、PC (1)求证://MN 平面PAD ;(2)若4MN BC ==,PA = 求异面直线PA 与MN8.如图,正方形ABCD 与ABEF 不在同一平面内,M 、N 分别在AC 、BF 上,且AM FN =求证://MN 平面CBE三、空间图形一、面积:1、ch s =直棱柱侧 ()为直截面周长斜棱柱侧``c l c s = rh cl s π2==圆柱侧 2、中截面面积:2`0ss s += 3、`21ch s =正棱锥侧 rl cl s π==21圆锥侧 4、()``21h c c s +=正棱台侧()()l r r l c c s ``21+=+=π圆台 5、预备定理ph s π2=锥球内接圆台,圆柱,圆①24r s π=球 ②rh s π2=球带 ③)(222h r rh s +==ππ球冠 6、面积比是相似比的平方,体积比是相似比的立方7、圆锥轴截面的顶角α和侧面展开图的圆心角θ的关系为:2sin 22αππθ⋅=⋅=l r 8、圆台上、下底面半径为r`、r ,母线为l,圆台侧面展开后所得的扇环圆心角为θ,则:lc c l r r l r r `2`360`-=⋅-=︒⋅-=πθ 9、圆锥中,过两母线的截面面积为s当轴截面顶角(]︒︒∈90,0α时,αsin 212l s s ==轴截面截面最大 当轴截面顶角[)︒︒∈180,90α时,轴截面截面最大s l l s ≠=︒=222190sin 21 10、球面距离θ⋅=R l (θ用弧度表示,Rl =θ) 二、体积 1、l s sh V `==棱柱(s`为直截面面积) sh h r V =⋅=2π圆柱2、sh V 31=棱锥sh h r V 31312=⋅=π圆锥3、`)`(31s s s s h V +⋅+=棱台 =++=)``(3122r rr r h V π圆台`)`(31s s s s h +⋅+ 4、334R V π=球5、)3(31)3(61222h R h h r h V -=+=ππ球缺6、)(31体适用于有内切球的多面内切球半径表体r S V ⋅=1 n 面体共有8条棱,5个顶点,求n 2.一个正n 面体共有8个顶点,每个顶点处共有三条棱,求n 3.一个简单多面体的各面都是三角形,证明它的顶点数V 和面数F 有下面的关系:F =2V -4 4.有没有棱数是75.①过球面上任意两点,作球的大圆的个数是 .②球半径为25cm ,球心到截面距离为24cm ,则截面面积为 .③已知球的两个平行截面的面积分别是5π和8π,它们位于球心同一侧,且相距1,则球半径是 .④球O 直径为4,,A B 为球面上的两点且AB =,A B 两点的球面距离为 . ⑤北纬60圈上,M N 两地,它们在纬度圈上的弧长是2Rπ(R 为地球半径),则这两地间的球面距离为 .7.北纬45圈上有,A B 两地,A 在东径120,B 在西径150,设地球半径为R ,,A B 两地球面距离为 ;8.一个球夹在120二面角内,两切点在球面上最短距离为cm π,则球半径为 ;9.设地球的半径为R ,在北纬45°圈上有A 、B 两点,它们的经度相差90°,那么这两点间的纬线的长为_________,两点间的球面距离是_________. 球的大圆面积增大为原来的4倍,则体积增大为原来的 倍;11.三个球的半径之比为1:2:3,那么最大的球的体积是其余两个球的体积和的 倍; 12.若球的大圆面积扩大为原来的4倍,则球的体积比原来增加 倍; 13.把半径分别为3,4,5的三个铁球,熔成一个大球,则大球半径是 ; 14.正方体全面积是24,它的外接球的体积是 ,内切球的体积是 . 球O 1、O 2分别与正方体的各面、各条棱相切,正方体的各顶点都在球O 3的表面上,求三个球的表面积之比.16.表面积为324π的球,其内接正四棱柱的高是1417. 正四面体ABCD 的棱长为a ,球O 是内切球,球O 1是与正四面体的三个面和球O 都相切的一个小球,求球O 1的体积.D'C'B'A'D CBAH OA'D'C'B'DCBA判断下列结论是否正确,为什么?(1)有一个面是多边形,其余各面是三角形的几何体是棱锥; (2)正四面体是四棱锥;(3)侧棱与底面所成的角相等的棱锥是正棱锥;(4)侧棱长相等,各侧面与底面所成的角相等的棱锥是正棱锥.2 ABCD A B C D ''''-中,,3A AB A AD BAD π''∠=∠∠=,,AB AD a AA b '===,求对角面BB D D ''3.已知:正四棱柱ABCD A B C D ''''-的底面边长为2 (1)求二面角B AC B '--的大小;(2)求点B 到平面AB C '4.棱长为a 的正方体OABC O A B C ''''-中,,E F 分别为棱,AB BC 上的动点,且(0)AE BF x x a ==≤≤,(1)求证:A F C E ''⊥;(2)当BEF ∆的面积取得最大值时,求二面角B EF B '--的大小.5. 如图,M 、N 分别是棱长为1的正方体''''D C B A ABCD -的棱'BB 、''C B 的中点.求异面直线MN 与CBOCBA A GEP D CBA'CD 所成的角.6.在三棱锥P ABC -中,ABC ∆为正三角形,90PCA ∠=,D 为PA 中点,二面角P AC B --为120,2,PC AB ==(1)求证:AC BD ⊥;(2)求BD 与底面ABC 所成的角,(3)求三棱锥P ABC -的体积.7. 斜三棱柱的底面的边长是4cm 的正三角形,侧棱长为3cm,侧棱1AA 与底面相邻两边都成060角. (1)求证:侧面11CC B B 是矩形; (2)求这个棱柱的侧面积; (3)求棱柱的体积.。
高一数学立体几何讲义

I. 基础知识要点一、 平面.1. 经过不在同一条直线上的三点确定一个面.注:两两相交且不过同一点的四条直线必在同一平面内.2. 两个平面可将空间分成3或4部分.(①两个平面平行,②两个平面相交)3. 过三条互相平行的直线可以确定1或3个平面.(①三条直线在一个平面内平行,②三条直线不在一个平面内平行)[注]:三条直线可以确定三个平面,三条直线的公共点有0或1个.4. 三个平面最多可把空间分成 8 部分.(X 、Y 、Z 三个方向)二、 空间直线.1. 空间直线位置分三种:相交、平行、异面. 相交直线——共面有且仅有一个公共点;平行直线——共面没有公共点;异面直线——不同在任一平面内[注]:①两条异面直线在同一平面内射影一定是相交的两条直线.(×)(可能两条直线平行,也可能是点和直线等)②直线在平面外,指的位置关系:平行或相交③若直线a 、b 异面,a 平行于平面α,b 与α的关系是相交、平行、在平面α内. ④两条平行线在同一平面内的射影图形是一条直线或两条平行线或两点.⑤在平面内射影是直线的图形一定是直线.(×)(射影不一定只有直线,也可以是其他图形) ⑥在同一平面内的射影长相等,则斜线长相等.(×)(并非是从平面外一点..向这个平面所引的垂线段和斜线段)⑦b a ,是夹在两平行平面间的线段,若b a =,则b a ,的位置关系为相交或平行或异面.2. 异面直线判定定理:过平面外一点与平面内一点的直线和平面内不经过该点的直线是异面直线.(不在任何一个平面内的两条直线)3. 平行公理:平行于同一条直线的两条直线互相平行.4. 等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等(如下图).(二面角的取值范围[) 180,0∈θ) (直线与直线所成角(] 90,0∈θ)(斜线与平面成角() 90,0∈θ)(直线与平面所成角[] 90,0∈θ) 推论:如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成锐角(或直角)相等.5. 两异面直线的距离:公垂线的长度.空间两条直线垂直的情况:相交(共面)垂直和异面垂直.21,l l 是异面直线,则过21,l l 外一点P ,过点P 且与21,l l 都平行平面有一个或没有,但与21,l l 距离相等的点在同一平面内. (1L 或2L 在这个做出的平面内不能叫1L 与2L 平行的平面)三、 直线与平面平行、直线与平面垂直.1. 空间直线与平面位置分三种:相交、平行、在平面内.2. 直线与平面平行判定定理:如果平面外一条直线和这个平面内一条直线平行,那么这条直线和这个平面平行.(“线线平行,线面平行”)[注]:①直线a 与平面α内一条直线平行,则a ∥α. (×)(平面外一条直线)②直线a 与平面α内一条直线相交,则a 与平面α相交. (×)(平面外一条直线) 12方向相同12方向不相同③若直线a 与平面α平行,则α内必存在无数条直线与a 平行. (√)(不是任意一条直线,可利用平行的传递性证之)④两条平行线中一条平行于一个平面,那么另一条也平行于这个平面. (×)(可能在此平面内)⑤平行于同一直线的两个平面平行.(×)(两个平面可能相交)⑥平行于同一个平面的两直线平行.(×)(两直线可能相交或者异面)⑦直线l 与平面α、β所成角相等,则α∥β.(×)(α、β可能相交)3. 直线和平面平行性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.(“线面平行,线线平行”)4. 直线与平面垂直是指直线与平面任何一条直线垂直,过一点有且只有一条直线和一个平面垂直,过一点有且只有一个平面和一条直线垂直.● 若PA ⊥α,a ⊥AO ,得a ⊥PO (三垂线定理), 得不出α⊥PO . 因为a ⊥PO ,但PO 不垂直OA .● 三垂线定理的逆定理亦成立.直线与平面垂直的判定定理一:如果一条直线和一个平面内的两条相交直线都垂直,那么这两条直线垂直于这个平面.(“线线垂直,线面垂直”)直线与平面垂直的判定定理二:如果平行线中一条直线垂直于一个平面,那么另一条也垂直于这个平面.推论:如果两条直线同垂直于一个平面,那么这两条直线平行.[注]:①垂直于同一平面....的两个平面平行.(×)(可能相交,垂直于同一条直线.....的两个平面平行)②垂直于同一直线的两个平面平行.(√)(一条直线垂直于平行的一个平面,必垂直于另一个平面)③垂直于同一平面的两条直线平行.(√)5. ⑴垂线段和斜线段长定理:从平面外一点..向这个平面所引的垂线段和斜线段中,①射影相等的两条斜线段相等,射影较长的斜线段较长;②相等的斜线段的射影相等,较长的斜线段射影较长;③垂线段比任何一条斜线段短.[注]:垂线在平面的射影为一个点. [一条直线在平面内的射影是一条直线.(×)]⑵射影定理推论:如果一个角所在平面外一点到角的两边的距离相等,那么这点在平面内的射影在这个角的平分线上四、 平面平行与平面垂直.1. 空间两个平面的位置关系:相交、平行.2. 平面平行判定定理:如果一个平面内有两条相交直线都平行于另一个平面,哪么这两个平面平行.(“线面平行,面面平行”)推论:垂直于同一条直线的两个平面互相平行;平行于同一平面的两个平面平行.[注]:一平面间的任一直线平行于另一平面.3. 两个平面平行的性质定理:如果两个平面平行同时和第三个平面相交,那么它们交线平行.(“面面平行,线线平行”)4. 两个平面垂直性质判定一:两个平面所成的二面角是直二面角,则两个平面垂直.两个平面垂直性质判定二:如果一个平面与一条直线垂直,那么经过这条直线的平面垂直于这个平面.(“线面垂直,面面垂直”)注:如果两个二面角的平面对应平面互相垂直,则两个二面角没有什么关系.5. 两个平面垂直性质定理:如果两个平面垂直,那么在一个平面内垂直于它们交线的直线也垂直于另一个平面.P OA a P αβ推论:如果两个相交平面都垂直于第三平面,则它们交线垂直于第三平面.证明:如图,找O 作OA 、OB 分别垂直于21,l l ,因为ααββ⊥⊂⊥⊂OB PM OA PM ,,,则OB PM OA PM ⊥⊥,.五、 棱锥、棱柱.1. 棱柱.⑴①直棱柱侧面积:Ch S =(C 为底面周长,h 是高)该公式是利用直棱柱的侧面展开图为矩形得出的.②斜棱住侧面积:l C S 1=(1C 是斜棱柱直截面周长,l 是斜棱柱的侧棱长)该公式是利用斜棱柱的侧面展开图为平行四边形得出的.⑶棱柱具有的性质:①棱柱的各个侧面都是平行四边形,所有的侧棱都相等;直棱柱的各个侧面都是矩形........;正棱柱的各个侧面都是全等的矩形......②棱柱的两个底面与平行于底面的截面是对应边互相平行的全等..多边形. ③过棱柱不相邻的两条侧棱的截面都是平行四边形.注:①棱柱有一个侧面和底面的一条边垂直可推测是直棱柱. (×)(直棱柱不能保证底面是钜形可如图)②(直棱柱定义)棱柱有一条侧棱和底面垂直.[注]:①有两个侧面是矩形的棱柱是直棱柱.(×)(斜四面体的两个平行的平面可以为矩形) ②各侧面都是正方形的棱柱一定是正棱柱.(×)(应是各侧面都是正方形的直.棱柱才行) ③对角面都是全等的矩形的直四棱柱一定是长方体.(×)(只能推出对角线相等,推不出底面为矩形) ④棱柱成为直棱柱的一个必要不充分条件是棱柱有一条侧棱与底面的两条边垂直. (两条边可能相交,可能不相交,若两条边相交,则应是充要条件)2. 棱锥: [注]:①一个棱锥可以四各面都为直角三角形.②一个棱柱可以分成等体积的三个三棱锥;所以棱柱棱柱3V Sh V ==.⑴①正棱锥定义:底面是正多边形;顶点在底面的射影为底面的中心.[注]:i. 正四棱锥的各个侧面都是全等的等腰三角形.(不是等边三角形)ii. 正四面体是各棱相等,而正三棱锥是底面为正△侧棱与底棱不一定相等iii. 正棱锥定义的推论:若一个棱锥的各个侧面都是全等的等腰三角形(即侧棱相等);底面为正多边形. ②正棱锥的侧面积:'Ch 21S =(底面周长为C ,斜高为'h ) ⑵棱锥具有的性质:①正棱锥各侧棱相等,各侧面都是全等的等腰三角形,各等腰三角形底边上的高相等(它叫做正棱锥的斜高).②正棱锥的高、斜高和斜高在底面内的射影组成一个直角三角形,正棱锥的高、侧棱、侧棱在底面内的射影也组成一个直角三角形.⑶特殊棱锥的顶点在底面的射影位置:①棱锥的侧棱长均相等,则顶点在底面上的射影为底面多边形的外心.②棱锥的侧棱与底面所成的角均相等,则顶点在底面上的射影为底面多边形的外心. ③棱锥的各侧面与底面所成角均相等,则顶点在底面上的射影为底面多边形内心. ④棱锥的顶点到底面各边距离相等,则顶点在底面上的射影为底面多边形内心.⑤三棱锥有两组对棱垂直,则顶点在底面的射影为三角形垂心.⑥三棱锥的三条侧棱两两垂直,则顶点在底面上的射影为三角形的垂心.⑦每个四面体都有外接球,球心0是各条棱的中垂面的交点,此点到各顶点的距离等于球半径;⑧每个四面体都有内切球,球心I 是四面体各个二面角的平分面的交点,到各面的距离等于半径.[注]:i. 各个侧面都是等腰三角形,且底面是正方形的棱锥是正四棱锥.(×)(各个侧面的等腰三角形不知是否全等)3. 球:⑴球的截面是一个圆面.①球的表面积公式:24R S π=. ②球的体积公式:334R V π=. 附:①圆柱体积:h r V 2π=(r 为半径,h 为高) ②圆锥体积:h r V 231π=(r 为半径,h 为高) ③锥形体积:Sh V 31=(S 为底面积,h 为高) 侧面积公式S 直棱柱侧=ch ( c -底面周长,h -高 )S 正棱锥侧=1/2 ch ( c -底面周长,h -斜高 )S 正棱台侧=1/2 (c +c')h (c ,c'-上、下底面周长,h -斜高)S 圆柱侧=cl =2πrl (c -底面周长,l -母线长 ,r -底面半径) S 圆锥侧=1/2cl =πrl (c -底面周长,l -母线长 ,r -底面半径) S 圆台侧=1/2(c +c')l =π(r +r')l(c ,c' -上、下底面周长,r ,r -上、下底面半径)体积公式V 柱体=Sh ( S -底面积,h -高 )V 椎体=1/3Sh ( S -底面积,h -高 )()h ss s s V '31'++=台体 (S ,S -上下底面积,h -高 ) 3R 34π=球V (R 为球的半径) 24R S π=球。
立体几何—建系讲义

立体几何(向量法)一建系引入空间向量坐标运算,使解立体几何问题避免了传统方法进行繁琐的空间分析,只需建立空间直角坐标系进行向量运算,而如何建立恰当的坐标系,成为用向量解题的关键步骤之一•所谓“建立适当的坐标系”,一般应使尽量多的点在数轴上或便于计算。
一、利用共顶点的互相垂直的三条线构建直角坐标系例1 (2012高考真题重庆理19)(本小题满分12分如图,在直三棱柱ABC AB iG中,AB=4, AC=BC=3 D为AB 的中点(I)求点C到平面A1ABB1的距离;(n)若AB1 AC求二面角的平面角的余弦值.【答案】解:(1)由AC= BC, D为AB的中点,得CD丄AB.又CD丄AA1,故CD丄面A1ABB1,所以点C到平面A1ABB1的距离为CD = BC2—BD2= 5.(2)解法一:如图,取D1为A1B1的中点,连结DD1,贝U DD1// AA1 //CC1.又由(1)知CD丄面A i ABB i,故CD丄A i D, CD丄DD i,所以/ A i DD i为所求的二面角A i —CD —C i的平面角.因A i D为A i C在面A i ABB i上的射影,又已知AB i丄A i C,由三垂线定理的逆定理得AB i丄A i D,从而/ A i AB i、/ A i DA都与/ B i AB互余,因此/ A i AB i =AA i ^\i B i/ A i DA,所以Rt A A i AD s Rt A B i A i A.因此応=云石,即卩AA i = ADA i B i = 8,得AA i = 22.从而A i D = ,AA i + AD2= 2 3.所以,在Rt△ A i DD i中,/ DD i AA i V6cos/A iDDi= A i D = A i D =亍解法二:如图,过D作DD i// AA i交A i B i于点D i,在直三棱柱中,易知DB,DC,DD i两两垂直.以D为原点,射线DB,DC,DD i分别为x轴、y轴、z轴的正半轴建立空间直角坐标系D —xyz.设直三棱柱的高为h,则A( —2,0,0), A i( —2,0,h),B i(2,0, h),C(0,5, 0),C i(0, 5, h),从而A B i= (4,0, h), A i C= (2, 5,—h).由晶i丄A i C,有8—h2= 0, h = 2 2.故D X i= ( —2,0,2 2), CC i = (0,0,2 2), DC =(0, 5, 0).设平面A i CD的法向量为m= (x i, y i, z i),贝U m丄DC, m丄DA i,即卩cos BD, EFBD ?FE|BD||FE|0 18 64 82 100 ^82 10设异面直线BD 与EF 所成角为,则cos| cosBD, EF-82直线BD 与 EF 所成的cos〈 m ,m-n _ 2|m||n 厂;2+ 1 1 J6 3 .所以二面角A 1 — CD — C 1的平面角的余弦值为_36.、利用线面垂直关系构建直角坐标系例2.如图所示, AF 、DE 分别是圆O 、圆O 1的直径,AD 8. BC 是圆 O 的直径,AB AC 6 , OE // AD .(I) 求二面角B AD F 的大小;(II) 求直线BD 与EF 所成的角的余弦值. 19.解:(I ) •/ AD 与两圆所在的平面均垂直,••• ADLAB, AD 丄AF,故/ BAD 是二面角 B — AD — F 的平面角, 依题意可知,ABCD 是正方形,所以/ BAD= 450. 即二面角B — AD — F 的大小为45°;(II)以O 为原点,BC AF 、OE 所在直线为坐标轴,建立空间直角坐标系(如图所示) ,贝U O (0, 0, 0) , A (0, 3/2 ,0), B ( ^' 2 , 0 , 0) ,D (0 , 3/2, 8) , E (0 , 0 , 8) , F(0 , 3 2 , 0)所以,BD ( 3、2, 3.2,8),FE (0,3 2,8) 、■‘5y= 0, —2x i + 2 2z i = 0,取乙=1,得 m = ( :2, 0,1),设平面C i CD 的法向量为n = (X 2, y 2, Z 2),贝U n 丄DC, n 丄CC i ,即:5y2= 0,2 :2z 2 = 0,取 X 2= 1,得 n = (1,0,0),所以AD 与两圆所在的平面均垂直,角为余弦值为竺•10三、利用图形中的对称关系建立坐标系例3(2013年重庆数学(理))如图,四棱锥P ABCD中,PA 底面ABCD , BC CD 2,A C 4, ACB ACD 3,F为P C 的中点,AF P B.B【答案】(1)求PA的长;(2) 求二面角B AF D的正弦值•題(13)0z- 2解: (1)如图,联结BD 交AC 于O,因为BC = CD ,即△ BCD 为等腰三角形,又AC 平分/ BCD , 故AC 丄BD.以O 为坐标原点,OB , OC , AP 的方向分别为x 轴,y 轴,z 轴的正方向,建立 n n空间直角坐标系 O — xyz,则 0C = CDcosT = 1,而 AC = 4,得 AO = AC — OC = 3•又 OD = CDsin3 3 3=3,故 A(0, — 3, 0), B( 3, 0, 0), C(0, 1, 0), D( — . 3 , 0 , 0) •因PA 丄底面ABCD ,可设P(0 , — 3 , z),由F 为PC 边中点,得F 0 , — 1, 2 ,又A F =—z),因 AF 丄 PB ,故AF PB = 0,即 6 — - = 0, z = 2,3(舍去一2.3),所以 |PA|= 2 .3(2)由⑴知 AD = (— 3, 3, 0), AB = ( 3 3, 0), AF = (0, 2, '3) •设平面 FAD 的法 向量为1=(x i , y i , z i ),平面FAB 的法向量为2= (X 2, y 2, Z 2).由 i AD = 0, i AF = 0,得 —3xi+ 3yi =0,因此可取 i =(3, 3 — 2).2y i + . 3z i = 0,由2 AB = 0, 2 AF = 0,得 3x 2+ 3y 2= 0, _故可取2= (3,—衍,2).2y 2 + .3Z 2= 0,从而向量i , 2的夹角的余弦值为 n i n 2 icos 〈 i , 2>= =-.|n i | |n 2| 8故二面角B — AF — D 的正弦值为 斗78四、利用正棱锥的中心与高所在直线,投影构建直角坐标系 例4-i (20i3大纲版数学(理))如图,四棱锥P ABCD中,ABC BAD 90o , BC 2AD, PAB 与 PAD 都是等边三角形(I)证明:PB CD; (II)求二面角 A PD C 的余弦值•【答案】 解:⑴取BC 的中点E ,联结DE ,则四边形 ABED 为正方形. 过P 作PO 丄平面 ABCD ,垂足为 O.联结 OA , OB , OD , OE.由厶FAB 和厶FAD 都是等边三角形知 PA = PB = PD,所以OA = OB= OD,即点0为正方形ABED对角线的交点,故OE丄BD,从而PB丄OE.因为O是BD的中点,E是BC的中点,所以OE // CD.因此PB丄CD.所以 cos / AFG = FG 2+ AF 2— AG 2 _2 F G AF —63 .解法由⑴知,OE , OB , OP 两两垂直. O —xyz.(2)解法一:由(1)知 CD 丄 PB , CD 丄 PO , PB A PO = P , 故CD 丄平面PBD. 又PD?平面PBD ,所以CD 丄PD. 取PD 的中点F , PC 的中点G ,连FG. 则 FG // CD , FG 丄 PD.联结AF ,由△ APD 为等边三角形可得 AF 丄PD. 所以/ AFG 为二面角A — PD — C 的平面角. 联结 AG , EG ,贝U EG // PB. 又PB 丄AE ,所以EG 丄AE.1设 AB = 2,贝U AE = 2 .2, EG = ?PB = 1, 故 AG = AE 2 + EG 2= 3,1在厶 AFG 中,FG = ^CD = .2, AF = .3, AG = 3.以O 为坐标原点,OE 的方向为x 轴的正方向建立如图所示的空间直角坐标系设|AB|= 2,则A( —2, 0, 0), D(0,- ,2, 0),C(2 2,—2, 0), P(0, 0, .2),PC= (2 .2,—. 2 , —2), PD = (0 , —2 , —2),AP= ( 2 , 0 , 2) , AD = ( 2 , —2 , 0).设平面PCD的法向量为1= (x , y , z),贝V1 PC = (x , y , z) (2 2 , — 2 , —2) = 0 ,1 PD = (x , y , z) (0 , —2 , —2) = 0 ,可得2x—y —z= 0 , y+ z= 0.取y =—1,得x= 0 , z= 1,故i= (0 , —1 , 1). 设平面PAD的法向量为2= (m , p , q),贝U2 AP = (m , p , q) (- 2 , 0 , 2) = 0 ,2 AD = (m , p , q) (• 2 , — 2 , 0) = 0 ,可得m + q = 0 , m—p= 0.取m= 1,得p = 1 , q=—1,故2= (1, 1, —1).于是COS〈, 2> = n1n2 .6「|n 1||n2| 3 .例4-2如图1--5 ,在三棱柱ABC—A1B1C1 中,已知AB = AC = AA1 = 5 , BC =4,点A1在底面ABC的投影是线段BC的中点O.(1) 证明在侧棱AA1上存在一点E ,使得0E丄平面BB1C1C ,并求出AE的长;(2) 求平面A1B1C与平面BB1C1C夹角的余弦值.【答案】解:⑴证明:连接人0,在厶AOA i 中,作 0E 丄AA i 于点E ,因为0B = 0C ,所以 A0丄BC ,所以BC 丄平面 AA i O. 所以0E 丄平面 AA i = . 5,AA i // BB i ,所以 0E 丄BB i .因为A i 0丄平面ABC ,所以A i 0丄BC. 因为AB = AC ,所以BC 丄0E , BB i C i C ,又 A0= AB 2— B02= i ,得AE =疇、违(2)如图,分别以0A , 0B , 0A i 所在直线为x , y , z 轴,建立空间直角坐标系,贝U A(i,0,0), B(0,2,0), C(0,— 2,0), A i (0,0,2),cos 〈 OE ,〉OE n V 30 |0E| |n| 10A A Q由AE = 5AA 1得点E 的坐标是5, 0, 2 ,— 4 2由⑴得平面BB i C i C 的法向量是0E = 5,0,5,设平面A I B I C 的法向量=(x , y , z),AB = 0,— x + 2y = 0,由得nAC = 0 y +z = 0,令 y = 1,得 x = 2, z =— 1,即二(2,1,— 1),所以即平面BB 1C 1C 与平面A 1B 1C 的夹角的余弦值是三、利用面面垂直关系构建直角坐标系例5 (2012高考真题安徽理18)(本小题满分12分)平面图形ABB 1A 1C 1C 如图1— 4(1)所示,其中BB 1C 1C 是矩形,BC = 2, BB 110=4, AB=AC= 2, A i B i= A i C i= 5.图1-4现将该平面图形分别沿BC和B i C i折叠,使△ ABC与厶A i B i C i所在平面都与平面BB i C i C垂直,再分别连接A i A, A i B, A i C,得到如图i-4(2)所示的空间图形.对此空间图形解答下列问题.(i)证明:AA i 丄BC;⑵求AA i的长;(3)求二面角A-BC-A i的余弦值.【答案】解:(向量法):(i)证明:取BC,B iC i的中点分别为D和D i,连接A i D i, DD i, AD. 由BB i C i C为矩形知,DD i丄B i C i,因为平面BB i C i C丄平面A1B1C1,所以DD i丄平面A i B i C i,又由A i B i = A i C i 知,A i D i 丄B iC i.故以D i为坐标原点,可建立如图所示的空间直角坐标系D i—xyz.由题设,可得A i D i = 2, AD = i.由以上可知AD丄平面BB i C i C, A i D i丄平面BB i C i C,于是AD// A i D i.所以A(0,—i,4), B(i,0,4), A i(0,2,0), C( —i,0,4), D(0,0,4). 故A A i= (0,3,—4), BC= ( —2,0,0), AA i BC = 0, 因此A X i丄BC, 即卩AA i丄BC.(2) 因为AA i = (0,3,—4),所以| AA i卜5,即AA匸5.(3) 连接A i D,由BC丄AD, BC丄AA i,可知BC丄平面A i AD, BC丄A i D,所以/ ADA i为二面角A—BC—A i的平面角.cos〈IDA, DA i>因为D A = (0,—i,0), DA i = (0,2,—4),所以2即二面角A—BC—A i的余弦值为—电5(综合法)(1)证明:取BC, B i C i的中点分别为D和D i,连接A i D i, DD i, AD, A i D.由条件可知,BC丄AD, B i C i丄A i D i,由上可得AD丄面BB i C i C, A i D i丄面BB i CC因此AD // A i D i,即AD, A i D i 确定平面AD i A i D.又因为DD i / BB i, BB i丄BC,所以DD i丄BC.又考虑到AD丄BC,所以BC丄平面AD i A i D,故BC丄AA i.⑵延长A i D i到G点,使GD i= AD,连接AG.因为AD綊GD i,所以AG綊DD i綊BB i.由于BB i丄平面A i B i C i,所以AG丄A i G. 由条件可知,A i G = A i D i + D i G= 3, AG = 4, 所以AA i = 5.⑶因为BC丄平面AD i A i D,所以/ ADA i为二面角A-BC- A i的平面角. 在Rt A A i DD i 中,DD i = 4, A i D i = 2,解得sin/ D i DA i =5冗 / ^[5cos/ ADA i = cos 2+/ D i DA i = —g.即二面角A- BC- A i的余弦值为—f.。
【精】高中数学:立体几何优质讲义.docx

高中数学:立体几何优质讲义姓名:指导:日期:立体几何证平行(一)甄蟻平有<■图丄E)--------------- K如果两条蛾切平行于第三条最,那么这两条蛾相互平行.2.如果一条蛛平行于另一个平面,那么这条蟻就平行于这这条地的平面与已知平而的交蟻. 图丄】3 .血果商个平面平行,那玄另一个平血虹诳两个平血的交妹互制平行.4如果两喪直蟻都制另一•个平而垂直.那么这两条直蟻平有.5一在同T面内,如果两条直或垂直于同一条直墟,那么这两条直慟'成.,程茜师中学亞建化L.如果平而外一条直絞平行于平面内的一条直銭,那衣宜城与平而干径 :!.如果两个平部平行,一个平薊内的任何一条直域平行于另一个平面. 3 .州果平血*了平而如一条如果干时垂直于另--条直邑, 4 一如果平面与平面外一条直理同时垂直于另一个平面,I. 如果一个平而内有两果闵全平f li 平有于另一个平而,丄如果两个平面揺平行于第三个平潮,那互这两个平面平有. 3.如果两个平面问畦垂直于同一条面雄,那么这两个平ffii 平行.证塔直大部分毎是通过隼直证垂直:下能ii 史旳时榛.平移到另i 一个位置证垂直. (一) 或蟻垂西如果一案直蛾垂直于一个平St 那佥谊条宜戒垂直于这个平ifi 内的任何一条直銭一 (二) 蜷海垂苴【一如果一条直蜷垂直于平而内两条招交的部,那么这条直坡就垂直于两条相交直域所在的平面. 丄如果睥个平而常有,在其中一个 平血內,垂森于公芯検的il 注垂立于yi-t-Tni!. t 三)而而垂直(■囲At )【.辻一个平而垂洼旳平而垂辻于巳辻平而. 土二部南为直请的两个平面垂直.〈理科)(四〉不能祝匿征垂直的情况L 把已知蟻成ffii 平秽到容駐证照垂直的位置 2.询和已知蟻或面平行的蟻凍海证垂直一那么场面平有. 图卩二.求相疔,求距离,成求体根〈一)求術》〈理我丄技线爾.絞血曲•和二而跆歩L建系,崖可能il.薮将计算的点落在抽我和軸而L坐株系可以任意拆向*凡是角度渉成的面都要至少已如(SU出)3个点,肅度演及的絞都要至少巳知《成求出)£个点.歩,标期段坐标,不能表廚的可以持定字毋系数,当盧坐岳中只舍有一个未知字毋时可以直接代入下一歩求解:当点坐标中含有£个以上未知字毋盹需要握据以下三点列式求字母取住.①前量垂成a ijj =>^15 +y L k'i + -^i = u囲向量其蟻,"Jj2n W =虹2.乂 =加.=切崖向0模,何|=巧了「了歩丄表航向量,终点跋起点歩4:朮法曲丽1也(歩I上(如丄"I'""(歩3丄不姉妨X."中一一个字辱为。
立体几何第1讲
立体几何
立体几何
第一节 空间几何体的结构特征、三视图和直观图
一、基础知识
1.简单几何体 1多面体的结构特征
名称
棱柱
棱锥
棱台
图形
底面 侧棱 侧面形状
互相平行且相等 互相平行且相等
平行四边形
多边形 相交于一点,但不一定
相等 三角形
互相平行且相似 延长线交于一点
梯形
①特殊的四棱柱
平行
直平行
四棱柱
底面为
――――→
平行四边形
六面体
侧棱垂直
――――→
于底面
六面体
底面为
――→
矩形
长方体
底面
――――→
正四棱柱
侧棱与底面
――――→
正方体
边长相等
边长相等
上 述 四 棱 柱 有 以 下 集 合 关 系 : { 正 方 体 }{ 正 四 棱 柱 }{ 长 方 体 }{ 直 平 行 六 面
体}{平行六面体}{四棱柱}.
2.一个几何体的三视图形状都相同、大小均相等,那么这个几何体不可以是( )
A.球
B.三棱锥
C.正方体
D.圆柱
3.(2019·福州模拟)一水平放置的平面图形,用斜二测画法画出它的直
观图如图所示,此直观图恰好是一个边长为 2 的正方形,则原平面图形的面
立体几何
[题组训练] 1.下列结论中错误的是( ) A.由五个面围成的多面体只能是三棱柱 B.正棱台的对角面一定是等腰梯形 C.圆柱侧面上的直线段都是圆柱的母线 D.各个面都是正方形的四棱柱一定是正方体
2.下列命题正确的是( ) A.两个面平行,其余各面都是梯形的多面体是棱台 B.两个面平行且相似,其余各面都是梯形的多面体是棱台 C.直角梯形以一条直角腰所在的直线为旋转轴,其余三边旋转形成的面所围成的旋转 体是圆台 D.用平面截圆柱得到的截面只能是圆和矩形
立体几何讲义

一、知识结构1.空间多边形不在同一平面内的若干线段首尾相接所成的图形叫做空间折线.若空间折线的最后一条线段的尾端与最初一条线段的首端重合,则叫做封闭的空间折线.若封闭的空间折线各线段彼此不相交,则叫做这空间多边形平面,平面是一个不定义的概念,几何里的平面是无限伸展的.平面通常用一个平行四边形来表示.平面常用希腊字母α、β、γ…或拉丁字母M 、N 、P 来表示,也可用表示平行四边形的两个相对顶点字母表示,如平面AC.在立体几何中,大写字母A ,B ,C ,…表示点,小写字母,a,b,c,…l,m,n,…表示直线,且把直线和平面看成点的集合,因而能借用集合论中的符号表示它们之间的关系,例如:A∈l—点A 在直线l 上;A ∉α—点A 不在平面α内;l ⊂α—直线l 在平面α内;a ⊄α—直线a 不在平面α内;l∩m=A—直线l 与直线m 相交于A 点;α∩l=A—平面α与直线l 交于A 点;α∩β=l —平面α与平面β相交于直线l.2.平面的基本性质公理1 如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内.公理2 如果两个平面有一个公共点,那么它们有且只有一条通过这个点的公共直线. 公理3 经过不在同一直线上的三个点,有且只有一个平面.根据上面的公理,可得以下推论.推论1 经过一条直线和这条直线外一点,有且只有一个平面.推论2 经过两条相交直线,有且只有一个平面.推论3 经过两条平行直线,有且只有一个平面.3.证题方法4.空间线面的位置关系 平行—没有公共点 共面(1)直线与直线 相交—有且只有一个公共点异面(既不平行,又不相交)直线在平面内—有无数个公共点(2)直线和平面 直线不在平面内 平行—没有公共点(直线在平面外) 相交—有且只有一个公共点相交—有一条公共直线(无数个公共点)(3)平面与平面证题方法 间接证法直接证法反证法 同一法平行—没有公共点5.异面直线的判定证明两条直线是异面直线通常采用反证法.有时也可用定理“平面内一点与平面外一点的连线,与平面内不经过该点的直线是异面直线”.6.线面平行与垂直的判定(1)两直线平行的判定①定义:在同一个平面内,且没有公共点的两条直线平行.②如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行,即若a∥α,a β,α∩β=b,则a∥b.③平行于同一直线的两直线平行,即若a∥b,b∥c,则a∥c.④垂直于同一平面的两直线平行,即若a⊥α,b⊥α,则a∥b⑤两平行平面与同一个平面相交,那么两条交线平行,即若α∥β,α∩γ,β∩γ=b,则a∥b⑥如果一条直线和两个相交平面都平行,那么这条直线与这两个平面的交线平行,即若α∩β=b,a∥α,a∥β,则a∥b.(2)两直线垂直的判定①定义:若两直线成90°角,则这两直线互相垂直.②一条直线与两条平行直线中的一条垂直,也必与另一条垂直.即若b∥c,a⊥b,则a⊥c③一条直线垂直于一个平面,则垂直于这个平面内的任意一条直线.即若a⊥α,b⊂α,a⊥b.④三垂线定理和它的逆定理:在平面内的一条直线,若和这个平面的一条斜线的射影垂直,则它也和这条斜线垂直.⑤如果一条直线与一个平面平行,那么这条直线与这个平面的垂线垂直.即若a∥α,b⊥α,则a⊥b.⑥三个两两垂直的平面的交线两两垂直,即若α⊥β,β⊥γ,γ⊥α,且α∩β=a,β∩γ=b,γ∩α=c,则a⊥b,b⊥c,c⊥a.(3)直线与平面平行的判定①定义:若一条直线和平面没有公共点,则这直线与这个平面平行.②如果平面外一条直线和这个平面内的一条直线平行,则这条直线与这个平面平行.即若a⊄α,b⊂α,a∥b,则a∥α.③两个平面平行,其中一个平面内的直线平行于另一个平面,即若α∥β,l⊂α,则l∥β.④如果一个平面和平面外的一条直线都垂直于同一平面,那么这条直线和这个平面平行.即若α⊥β,l⊥β,l⊄α,则l∥α.⑤在一个平面同侧的两个点,如果它们与这个平面的距离相等,那么过这两个点的直线与这个平面平行,即若A∉α,B∉α,A、B在α同侧,且A、B到α等距,则AB∥α.⑥两个平行平面外的一条直线与其中一个平面平行,也与另一个平面平行,即若α∥β,a⊄α,a⊄β,a∥α,则α∥β.⑦如果一条直线与一个平面垂直,则平面外与这条直线垂直的直线与该平面平行,即若a⊥α,b⊄α,b⊥a,则b∥α.⑧如果两条平行直线中的一条平行于一个平面,那么另一条也平行于这个平面(或在这个平面内),即若a∥b,a∥α,b∥α(或b⊂α)(4)直线与平面垂直的判定①定义:若一条直线和一个平面内的任何一条直线垂直,则这条直线和这个平面垂直.②如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面.即若m⊂α,n⊂α,m∩n=B,l⊥m,l⊥n,则l⊥α.③如果两条平行线中的一条垂直于一个平面,那么另一条也垂直于同一平面.即若l∥a,a⊥α,则l⊥α.④一条直线垂直于两个平行平面中的一个平面,它也垂直于另一个平面,即若α∥β,l⊥β,则l⊥α.⑤如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面,即若α⊥β,a∩β=α,l⊂β,l⊥a,则l⊥α.⑥如果两个相交平面都垂直于第三个平面,则它们的交线也垂直于第三个平面,即若α⊥γ,β⊥γ,且a∩β=α,则a⊥γ.(5)两平面平行的判定①定义:如果两个平面没有公共点,那么这两个平面平行,即无公共点⇔α∥β.②如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行,即若a,b⊂α,a∩b=P,a∥β,b∥β,则α∥β.③垂直于同一直线的两平面平行.即若α⊥a,β⊥a,则α∥β.④平行于同一平面的两平面平行.即若α∥β,β∥γ,则α∥γ.⑤一个平面内的两条直线分别平行于另一平面内的两条相交直线,则这两个平面平行,即若a,b⊂α,c,d⊂β,a∩b=P,a∥c,b∥d,则α∥β.(6)两平面垂直的判定①定义:两个平面相交,如果所成的二面角是直二面角,那么这两个平面互相垂直,即二面角α-a-β=90°⇔α⊥β.②如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直,即若l⊥β,l⊂α,则α⊥β.③一个平面垂直于两个平行平面中的一个,也垂直于另一个.即若α∥β,α⊥γ,则β⊥γ.7.直线在平面内的判定(1)利用公理1:一直线上不重合的两点在平面内,则这条直线在平面内.(2)若两个平面互相垂直,则经过第一个平面内的一点垂直于第二个平面的直线在第一个平面内,即若α⊥β,A∈α,AB⊥β,则AB⊂α.(3)过一点和一条已知直线垂直的所有直线,都在过此点而垂直于已知直线的平面内,即若A∈a,a⊥b,A∈α,b⊥α,则a⊂α.(4)过平面外一点和该平面平行的直线,都在过此点而与该平面平行的平面内,即若P∉α,P∈β,β∥α,P∈a,a∥α,则a⊂β.(5)如果一条直线与一个平面平行,那么过这个平面内一点与这条直线平行的直线必在这个平面内,即若a∥α,A∈α,A∈b,b∥a,则b⊂α.8.存在性和唯一性定理(1)过直线外一点与这条直线平行的直线有且只有一条;(2)过一点与已知平面垂直的直线有且只有一条;(3)过平面外一点与这个平面平行的平面有且只有一个;(4)与两条异面直线都垂直相交的直线有且只有一条;(5)过一点与已知直线垂直的平面有且只有一个;(6)过平面的一条斜线且与该平面垂直的平面有且只有一个;(7)过两条异面直线中的一条而与另一条平行的平面有且只有一个;(8)过两条互相垂直的异面直线中的一条而与另一条垂直的平面有且只有一个.9.射影及有关性质(1)点在平面上的射影自一点向平面引垂线,垂足叫做这点在这个平面上的射影,点的射影还是点.(2)直线在平面上的射影自直线上的两个点向平面引垂线,过两垂足的直线叫做直线在这平面上的射影.和射影面垂直的直线的射影是一个点;不与射影面垂直的直线的射影是一条直线.(3)图形在平面上的射影一个平面图形上所有的点在一个平面上的射影的集合叫做这个平面图形在该平面上的射影.当图形所在平面与射影面垂直时,射影是一条线段;当图形所在平面不与射影面垂直时,射影仍是一个图形.(4)射影的有关性质从平面外一点向这个平面所引的垂线段和斜线段中:(i)射影相等的两条斜线段相等,射影较长的斜线段也较长;(ii)相等的斜线段的射影相等,较长的斜线段的射影也较长;(iii)垂线段比任何一条斜线段都短.10.空间中的各种角等角定理及其推论定理若一个角的两边和另一个角的两边分别平行,并且方向相同,则这两个角相等.推论若两条相交直线和另两条相交直线分别平行,则这两组直线所成的锐角(或直角)相等.异面直线所成的角(1)定义:a、b是两条异面直线,经过空间任意一点O,分别引直线a′∥a,b′∥b,则a′和b′所成的锐角(或直角)叫做异面直线a和b所成的角.(2)取值范围:0°<θ≤90°.(3)求解方法①根据定义,通过平移,找到异面直线所成的角θ;②解含有θ的三角形,求出角θ的大小.11.直线和平面所成的角(1)定义和平面所成的角有三种:(i)垂线面所成的角的一条斜线和它在平面上的射影所成的锐角,叫做这条直线和这个平面所成的角.(ii)垂线与平面所成的角直线垂直于平面,则它们所成的角是直角.(iii)一条直线和平面平行,或在平面内,则它们所成的角是0°的角.(2)取值范围0°≤θ≤90°(3)求解方法①作出斜线在平面上的射影,找到斜线与平面所成的角θ.②解含θ的三角形,求出其大小.③最小角定理斜线和平面所成的角,是这条斜线和平面内经过斜足的直线所成的一切角中最小的角,亦可说,斜线和平面所成的角不大于斜线与平面内任何直线所成的角.12.二面角及二面角的平面角(1)半平面直线把平面分成两个部分,每一部分都叫做半平面.(2)二面角条直线出发的两个半平面所组成的图形叫做二面角.这条直线叫做二面角的棱,这两个平面叫做二面角的面,即二面角由半平面一棱一半平面组成.若两个平面相交,则以两个平面的交线为棱形成四个二面角.二面角的大小用它的平面角来度量,通常认为二面角的平面角θ的取值范围是0°<θ≤180°(3)二面角的平面角①以二面角棱上任意一点为端点,分别在两个面内作垂直于棱的射线,这两条射线所组成的角叫做二面角的平面角.如图,∠PCD 是二面角α-AB-β的平面角.平面角∠PCD 的大小与顶点C 在棱AB 上的位置无关.②二面角的平面角具有下列性质:(i)二面角的棱垂直于它的平面角所在的平面,即AB⊥平面PCD.(ii)从二面角的平面角的一边上任意一点(异于角的顶点)作另一面的垂线,垂足必在平面角的另一边(或其反向延长线)上.(iii)二面角的平面角所在的平面与二面角的两个面都垂直,即平面PCD⊥α,平面PCD⊥β.③找(或作)二面角的平面角的主要方法.(i)定义法(ii)垂面法(iii)三垂线法(Ⅳ)根据特殊图形的性质(4)求二面角大小的常见方法①先找(或作)出二面角的平面角θ,再通过解三角形求得θ的值.②利用面积射影定理S′=S·cos α其中S 为二面角一个面内平面图形的面积,S′是这个平面图形在另一个面上的射影图形的面积,α为二面角的大小.③利用异面直线上两点间的距离公式求二面角的大小.13.空间的各种距离点到平面的距离(1)定义 面外一点引一个平面的垂线,这个点和垂足间的距离叫做这个点到这个平面的距离.(2)求点面距离常用的方法:1)直接利用定义求①找到(或作出)表示距离的线段;②抓住线段(所求距离)所在三角形解之.2)利用两平面互相垂直的性质.即如果已知点在已知平面的垂面上,则已知点到两平面交线的距离就是所求的点面距离.3)体积法其步骤是:①在平面内选取适当三点,和已知点构成三棱锥;②求出此三棱锥的体积V 和所取三点构成三角形的面积S ;③由V=31S·h,求出h 即为所求.这种方法的优点是不必作出垂线即可求点面距离.难点在于如何构造合适的三棱锥以便于计算.4)转化法将点到平面的距离转化为(平行)直线与平面的距离来求.14.直线和平面的距离(1)定义一条直线和一个平面平行,这条直线上任意一点到平面的距离,叫做这条直线和平面的距离.(2)求线面距离常用的方法①直接利用定义求证(或连或作)某线段为距离,然后通过解三角形计算之.②将线面距离转化为点面距离,然后运用解三角形或体积法求解之.③作辅助垂直平面,把求线面距离转化为求点线距离.15.平行平面的距离(1)定义个平行平面同时垂直的直线,叫做这两个平行平面的公垂线.公垂线夹在两个平行平面间的部分,叫做这两个平行平面的公垂线段.两个平行平面的公垂线段的长度叫做这两个平行平面的距离.(2)求平行平面距离常用的方法①直接利用定义求证(或连或作)某线段为距离,然后通过解三角形计算之.②把面面平行距离转化为线面平行距离,再转化为线线平行距离,最后转化为点线(面)距离,通过解三角形或体积法求解之.16.异面直线的距离(1)定义条异面直线都垂直相交的直线叫做两条异面直线的公垂线.两条异面直线的公垂线在这两条异面直线间的线段的长度,叫做两条异面直线的距离.任何两条确定的异面直线都存在唯一的公垂线段.(2)求两条异面直线的距离常用的方法①定义法题目所给的条件,找出(或作出)两条异面直线的公垂线段,再根据有关定理、性质求出公垂线段的长.此法一般多用于两异面直线互相垂直的情形.②转化法为以下两种形式:线面距离面面距离③等体积法④最值法⑤射影法⑥公式法。
高二立体几何数学讲义1.doc
高二立体几何数学讲义(一)一、空间几何体的结构特征及三视图和直观图知识点回顾1.空间几何体的结构特征2.空间几何体的三视图三视图:用得到,这种投影下与投影面的平面图形留下的影子与平面图形的形状和大小是的.三视图包括、、.3.空间几何体的直观图空间几何体的直观图常用画法来画,基本规则是:(1)原图形中x轴、y轴、z轴两两垂直,直观图中,x′轴、y′轴的夹角为,z′轴与x′轴和y′轴所在平面.(2)原图形中平行于坐标轴的线段,直观图中. 平行于x轴和z轴的线段长度在直观图中,平行于y轴的线段长度在直观图中.巩固练习1.下列有关棱柱的命题中正确的是()A.有两个面平行,其余各面都是四边形的几何体叫棱柱B.有两个面平行,其余各面都是平行四边形的几何体叫棱柱C.一个棱柱至少有五个面、六个顶点、九条棱D.棱柱的侧棱长有的都相等,有的不都相等2.用任意一个平面截一个几何体,各个截面都是圆,则这个几何体一定是()A.圆柱B.圆锥C.球体D.圆柱,圆锥,球体的组合体3.如图所示,下列几何体各自的三视图中,有且仅有两个视图相同的是() A.①② B.①③ C.①④ D.②④4.如图所示,图①、②、③是图④表示的几何体的三视图,其中图①是,图②是,图③是(说出视图名称).5.下面有四个命题:(1)各个侧面都是等腰三角形的棱锥是正棱锥;(2)三条侧棱都相等的棱锥是正三棱锥;(3)底面是正三角形的棱锥是正三棱锥;(4)顶点在底面上的射影是底面多边形的内心,又是外心的棱锥必是正棱锥.其中正确命题的个数是()A.1B.2C.3D.4二、平面的基本性质1.下列命题:①两两相交的三条直线共面;②两条相交直线上的三个点可以确定一个平面;③梯形是平面图形;④一条直线和一个点可以确定一个平面;⑤两条相交直线可以确定一个平面;⑥若点P不在平面α内,A,B,C三点都在平面α内,则P、A、B、C四点不在同一平面内.其中正确的有.2.下列命题中不正确的是.①若一条直线上有一点在平面外,则直线上有无穷多点在平面外;②若点,,A B C ABαα∈∈∈,则Cα∈;③若,,,a b l a A l b Bαα⊂⊂==,则lα⊂;④若一条直线上有两点在已知平面外,则直线上所有点在平面外。
高三立体几何讲义
立体几何讲义一、空间几何体 球与正方体的组合体问题(1)正方体的内切球: 球与正方体的每个面都相切,切点为每个面的中心,显然球心为正方体的中心。
设正方体的棱长为a ,球半径为R 。
如图3,截面图为正方形EFGH 的内切圆,得2aR =; (2)与正方体各棱相切的球:球与正方体的各棱相切,切点为各棱的中点,如图4作截面图,圆O 为正方形EFGH 的外接圆,易得a R 22=。
(3)正方体的外接球:正方体的八个顶点都在球面上,如图5,以对角面1AA 作截面图得,圆O 为矩形C C AA 11的外接圆,易得a O A R 231==。
例1.某三棱锥的三视图如图所示,该三棱锥的表面积是().ABCD例2.(1) 在球面上有四个点P 、A 、B 、C .如果PA 、PB 、PC 两两互相垂直,且a PC PB PA ===,那么这个球的表面积是______.(2)正四棱锥S ABCD -,点S 、A 、B 、C 、D 都在同一个球面上,则该球的体积为_________。
二、平行关系例3. 如图,直三棱柱ABC-A'B'C',∠BA点M,N 分别为A'B 和B'C'的中点.图3图4图5证明:MN ∥平面A'ACC';三、垂直关系例4.如图,三棱柱ABC -A 1B 1C 1中,侧棱垂直底面,∠ACB=90°,AC=BC=12AA 1,D 是棱AA 1的中点证明:平面BDC 1⊥平面BDC(2). 如图,三棱柱ABC-A 1B 1C 1中,CA=CB,AB=A A 1,∠BA A 1=60°.证明AB ⊥A 1C; 如图,三棱柱ABC-A 1B 1C 1中,CA=CB,AB=A A 1,∠BA A 1=60°.(Ⅰ)证明AB ⊥A 1C;(Ⅱ)若平面ABC⊥平面AA 1B 1B,AB=CB=2,求直线A 1C 与平面BB 1C 1C 所成角的正弦值.B 1CB A DC 1A 1(3)如图,AB 是圆的直径,PA 垂直圆所在的平面,C 是圆上的点.(I)求证:PAC PBC ⊥平面平面;(II)2.AB AC PA C PB A ===--若,1,1,求证:二面角的余弦值练习题1. 一个长方体全面积是20cm 2,所有棱长的和是24cm ,求长方体的对角线长.2.如图所示是一个几何体的三视图,根据图中标出的尺寸(单位:cm),可得该几何体的表面积为________cm 2.3. 如图,某三棱锥的三视图都是直角边为2的等腰直角三角形,则该三棱锥的体积是(A)43 (B) 83(C) 4 (D) 8 4.一个长方体共一顶点的三个面的面积分别是6,3,2,这个长方体对角线的长是( ) A .23B .32C .6D .65. 如图,已知四棱锥P -ABCD 的底面为等腰梯形,AB ∥CD ,AC ⊥BD ,垂足为H ,PH 是四棱锥的高.(1)证明:平面PAC ⊥平面PBD ;(2) )若AB =6,∠APB =∠ADB =60°,求面APD 与面BPC 所成二面角的余弦值。
高中数学空间立体几何讲义
第1讲 空间几何体高考《考试大纲》的要求:① 认识柱、锥、台、球及其简单组合体的结构特征,并能运用这些特征描述现实生活中简单物体的结构.② 能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的三视图,能识别上述的三视图所表示的立体模型,会用斜二测法画出它们的直观图.③ 会用平行投影与中心投影两种方法,画出简单空间图形的三视图与直观图,了解空间图形的不同表示形式.④ 会画某些建筑物的视图与直观图(在不影响图形特征的基础上,尺寸、线条等不作严格要求). ⑤ 了解球、棱柱、棱锥、台的表面积和体积的计算公式(不要求记忆公式). (一)例题选讲:例1.四面体ABCD 的外接球球心在CD 上,且CD =2,AB =3,在外接球面上两点A 、B 间的球面距离是( )A .6π B .3πC .32πD .65π例2.如果圆台的母线与底面成60°角,那么这个圆台的侧面积与轴截面面积的比为( )A .π2B .π23C .π332D .π21例3.在正三棱柱ABC —A 1B 1C 1中,侧棱长为2,底面三角形的边长为1,则BC 1与侧面ACC 1A 1所成的角是 .例4.如图所示,等腰△ABC 的底边AB =66,高CD =3,点B 是线段BD 上异于点B 、D 的动点.点F 在BC 边上,且EF ⊥AB .现沿EF 将△BEF 折起到△PEF 的位置,使PE ⊥AE .记BE =x ,V (x )表示四棱锥P-ACFE 的体积.(1)求V (x )的表达式;(2)当x 为何值时,V (x )取得最大值?(3)当V (x )取得最大值时,求异面直线AC 与PF 所成角的余弦值。
(二)基础训练:1.下列几何体各自的三视图中,有且仅有两个视图相同的是( )A .①②B .①③C .①④D .②④2.设地球半径为R ,若甲地位于北纬045东经0120,乙地位于南纬度075东经0120,则甲、乙两地球面距离为( )(A )3R (B) 6R π(C)56R π(D) 23R π①正方形 ②圆锥 ③三棱台 ④正四棱锥C3.若一个底面边长为2的正六棱柱的所有顶点都在一个球的面上,则此球的体积为 .4. 已知,,A B C 三点在球心为O ,半径为R 的球面上,AC BC ⊥,且AB R =,那么,A B 两点的球面距离为___________,球心到平面ABC 的距离为________ 5.如图,四棱锥P —ABCD 中,底面ABCD 为矩形,AB=8,AD=43,侧面PAD 为等边三角形,并且与底面所成二面角为60°. (Ⅰ)求四棱锥P —ABCD 的体积; (Ⅱ)证明PA ⊥BD.(三)巩固练习:1.若一个圆锥的轴截面是等边三角形,其面积为3,则这个圆锥的全面积是( )(A )π3 (B )π33 (C )π6 (D )π92、已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是( )A .16πB .20πC .24πD .32π3.一个圆锥和一个半球有公共底面,如果圆锥的体积恰好与半球的体积相等,那么,这个圆锥轴截面顶角的余弦值是( ) A.34 B.45 C.35 D.-35 4.已知球O 的半径为1,A 、B 、C 三点都在球面上,且每两点间的球面距离为2π,则球心O 到平面ABC 的距离为( )(A )31 (B )33 (C )32 (D)36 5.表面积为的正八面体的各个顶点都在同一个球面上,则此球的体积为()A .3 B .13π C.23π D .36.已知正四棱锥的体积为12,底面对角线的长为,则侧面与底面所成的二面角等于________7.请您设计一个帐篷。
立体几何讲义
立体几何讲义一、三种平行关系的相互转化:判定定理 判定定理线线平行 线面平行 面面平行 定义 性质定理例1、如图,在正方体1111ABCD A B C D -中,(1)若P 为11B D 的中点,证明:1||AP BC D 面 (2) 若P 为11B D 的动点,证明:1||AP BC D 面 (3)若面11111BC D A B C D l =面证明:11||l B D2.如图,在棱长为1的正方体ABCD ﹣A1B1C1D1中,点E ,F 分别是棱BC ,CC1的中点,P 是侧面BCC1B1内一点,若A1P ∥平面AEF ,则线段A1P 长度的取值范围是( ) A .[1,] B .[,] C .[,] D .[,]3、如图,若Ω是长方体1111ABCD-A B C D 被平面EFGH 截去几何体11EFGH B C 后得到的几何体,其中E 为线段11A B 上异于1B 的点,F 为线段1B B 上异于1B 的点,且EH ∥11A D ,则下列结论中不正确的是( ) A. EH ∥FG B.四边形EFGH 是矩形 C. Ω是棱柱 D. Ω是棱台4、如图,E 是以AB 为直径的半圆上异于A 、B 的点,矩形ABCD 所在的平面垂直于该半圆所在的平面 (Ⅱ)设平面ECD 与半圆弧的另一个交点为F . 试证://EF AB ;思考:平面α过正方体ABCD —A1B1C1D1的顶点A ,11//CB D α平面,ABCD m α=平面,11ABB A n α=平面,则m ,n 所成角的正弦值为( )(A )32 (B )22(C )33 (D )13二、垂直关系:(1)垂直要集中,然后由旧垂推出新垂判定定理 判定定理线线垂直 线面垂直 面面垂直 定义 性质定理注:(1)线面垂直的性质又揭示了平行与垂直之间的转化 (2)转化的思想:⊥⊥⇒⊥⇒⇒线线或利用面面的性质(后者较多)证明(或做出)线面体积高体积例1、如图,在斜三棱柱111ABC A B C -中,90BAC ∠=,1BC AC ⊥,则1C 在底面ABC 上的射影必在( )A.直线AB 上B.直线BC 上C.直线AC 上D.△ABC 内部回顾:如图,棱长为1的正方体1111D C B A ABCD -中,P 为线段B A 1上的动点,则下列结论正确的有__________ ①P D DC 11⊥ ②平面⊥P A D 11平面AP A 1C 1B 1A 1CBA D 1C 1B 1A 1③三棱锥11_C PDD 的体积与P 点位置无关④若动点Q 在正方体的表面上运动,且总保持1AQ BD ⊥。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平面与空间直线(Ⅰ)、平面的基本性质及其推论1、空间图形是由点、线、面组成的。
点、线、面的基本位置关系如下表所示:图形符号语言文字语言(读法) AaA a ∈ 点A 在直线a 上。
AaA a ∉ 点A 不在直线a 上。
AαA α∈点A 在平面α。
AαA α∉ 点A 不在平面α。
b a Aa b A = 直线a 、b 交于A 点。
aαaα直线a 在平面α。
aαa α=∅直线a 与平面α无公共点。
aAαa A α= 直线a 与平面α交于点A 。
l αβ= 平面α、β相交于直线l 。
α⊄a αa a α=∅a A α=。
2、平面的基本性质公理1: 如果一条直线的两点在一个平面,那么这条直线上的所有点都在这个平面推理模式:A AB B ααα∈⎫⇒⎬∈⎭。
如图示:应用:是判定直线是否在平面的依据,也是检验平面的方法。
公理2:如果两个平面有一个公共点,那么它们还有其他公共点,且所有这些公共点的集BA α合是一条过这个公共点的直线。
推理模式:A l A ααββ∈⎫⇒=⎬∈⎭且A l ∈且l 唯一如图示:应用:①确定两相交平面的交线位置;②判定点在直线上。
例1.如图,在四边形ABCD 中,已知AB ∥CD ,直线AB ,BC ,AD ,DC 分别与平面α相交于点E ,G ,H ,F .求证:E ,F ,G ,H 四点必定共线.解:∵AB ∥CD ,∴AB ,CD 确定一个平面β.又∵AB α=E ,AB ⊂β,∴E ∈α,E ∈β, 即E 为平面α与β的一个公共点.同理可证F ,G ,H 均为平面α与β的公共点.∵两个平面有公共点,它们有且只有一条通过公共点的公共直线, ∴E ,F ,G ,H 四点必定共线.说明:在立体几何的问题中,证明若干点共线时,常运用公理2,即先证明这些点都是某二平面的公共点,而后得出这些点都在二平面的交线上的结论.例2.如图,已知平面α,β,且α β=l .设梯形ABCD 中,AD ∥BC ,且AB ⊂α,CD ⊂β,求证:AB ,CD ,l 共点(相交于一点). 证明 ∵梯形ABCD 中,AD ∥BC , ∴AB ,CD 是梯形ABCD 的两条腰. ∴ AB ,CD 必定相交于一点, 设AB CD =M .α D C BA EF HGα DCBAl 例2βM又∵AB ⊂α,CD ⊂β,∴M ∈α,且M ∈β.∴M ∈α β. 又∵α β=l ,∴M ∈l , 即AB ,CD ,l 共点.说明:证明多条直线共点时,一般要应用公理2,这与证明多点共线是一样的.公理3: 经过不在同一条直线上的三点,有且只有一个平面。
推理模式:,, A B C 不共线⇒存在唯一的平面α,使得,,A B C α∈。
应用:①确定平面;②证明两个平面重合 。
例3.已知:a ,b ,c ,d 是不共点且两两相交的四条直线,求证:a ,b ,c ,d 共面.证明 1o 若当四条直线中有三条相交于一点,不妨设a ,b ,c 相交于一点A , 但A ∉d ,如图1.∴直线d 和A 确定一个平面α.又设直线d 与a ,b ,c 分别相交于E ,F ,G , 则A ,E ,F ,G ∈α.∵A ,E ∈α,A ,E ∈a ,∴a ⊂α. 同理可证b ⊂α,c ⊂α. ∴a ,b ,c ,d 在同一平面α.2o 当四条直线中任何三条都不共点时,如图2.∵这四条直线两两相交,则设相交直线a ,b 确定一个平面α.设直线c 与a ,b 分别交于点H ,K ,则H ,K ∈α. 又 H ,K ∈c ,∴c ⊂α.αb adcG F EA 图1a bcd αH K图2同理可证d ⊂α.∴a ,b ,c ,d 四条直线在同一平面α.说明:证明若干条线(或若干个点)共面的一般步骤是:首先根据公理3或推论,由题给条件中的部分线(或点)确定一个平面,然后再根据公理1证明其余的线(或点)均在这个平面.本题最容易忽视“三线共点”这一种情况.因此,在分析题意时,应仔细推敲问题中每一句话的含义.“有且只有一个”的含义分两部分理解,“有”说明图形存在,但不唯一,“只有一个”说明图形如果有顶多只有一个,但不保证符合条件的图形存在,“有且只有一个”既保证了图形的存在性,又保证了图形的唯一性.在数学语言的叙述中,“确定一个”,“可以作且只能作一个”与“有且只有一个”是同义词,因此,在证明有关这类语句的命题时,要从“存在性”和“唯一性”两方面来论证。
推论1: 经过一条直线和直线外的一点有且只有一个平面。
推理模式:A a ∉⇒存在唯一的平面α,使得A α∈,lα 。
推论2: 经过两条相交直线有且只有一个平面。
推理模式:P b a = ⇒存在唯一的平面α,使得,a bα。
推论3: 经过两条平行直线有且只有一个平面。
推理模式://a b ⇒存在唯一的平面α,使得,a b α。
练习:1.如图,在平行六面体ABCD -A 1B 1C 1D 1的中,A 1C 1 B 1D 1=O 1,B 1D 平面A 1BC 1=P .求证:P ∈BO 1.证明 在平行六面体ABCD -A 1B 1C 1D 1中,∵B 1D 平面A 1BC 1=P ,∴P ∈平面A 1BC 1,P ∈B 1D .∵B 1D ⊂平面BB 1D 1D .∴P ∈平面A 1BC 1,且P ∈平面BB 1D 1D .∴P ∈平面A 1BC 1 平面BB 1D 1D ,∵A 1C 1 B 1D 1=O 1,A 1C 1⊂平面A 1BC 1,B 1D 1⊂平面BB 1D 1D , ∴O 1∈平面A 1BC 1,且O 1∈平面BB 1D 1D . 又B ∈平面A 1BC 1,且B ∈平面BB 1D 1D , ∴平面A 1BC 1 平面BB 1D 1D =BO 1.∴P ∈BO 1说明一般地,要证明一个点在某条直线上,只要证明这个点在过这条直线的两个平面上。
(Ⅱ)、空间两条直线1、空间两直线的位置关系:(1)相交——有且只有一个公共点;(2)平行——在同一平面,没有公共点;(3)异面——不在任何..一个平面,没有公共点;2、公理4 :平行于同一条直线的两条直线互相平行。
推理模式://,////a b b c a c ⇒。
3、等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等。
4、等角定理的推论:如果两条相交直线和另两条相交直线分别平行,那么这两条直线所成的锐角(或直角)相等。
5、异面直线判定定理:连结平面一点与平面外一点的直线,和这个平面不经过此点的直线是异面直线。
推理模式:,,,A B l B l ααα∉∈⊂∉⇒AB 与l 是异面直线。
异面直线的判定方法:①判定定理;②定义法;③反证法是证明两直线异面的有效方法。
A 1ABB 1 D D 1 CC 1O 1PPBCD b ca例1.已知不共面的三条直线a 、b 、c 相交于点P ,a A ∈,a B ∈,b C ∈,c D ∈,求证:AD 与BC 是异面直线.证一:(反证法)假设AD 和BC 共面,所确定的平面为α,那么点P 、A 、B 、C 、D 都在平面α,∴直线a 、b 、c 都在平面α,与已知条件a 、b 、c 不共面矛盾,假设不成立,∴AD 和BC 是异面直线。
证二:(直接证法)∵a ∩c=P ,∴它们确定一个平面,设为α,由已知C ∉平面α,B ∈平面α,AD ⊂平面α,B ∉AD ,∴AD 和BC 是异面直线。
6、异面直线所成的角:已知两条异面直线,a b ,经过空间任一点O 作直线//,//a a b b '',,a b ''所成的角的大小与点O 的选择无关,把,a b ''所成的锐角(或直角)叫异面直线,a b 所成的角(或夹角).为了简便,点O 通常取在异面直线的一条上。
异面直线所成的角的围:]2,0(π。
7、异面直线垂直:如果两条异面直线所成的角是直角,则叫两条异面直线垂直.两条异面直线,a b 垂直,记作a b ⊥。
8、求异面直线所成的角的方法:几何法:(1)通过平移,在一条直线上找一点,过该点做另一直线的平行线;(2)找出与一条直线平行且与另一条相交的直线,那么这两条相交直线所成的角即为所求。
向量法:用向量的夹角公式。
例2.在正方体-ABCD ''''D C B A 中,M 、N 分别是棱'AA 和AB 的中点,P 为上底面ABCD 的中心,则直线PB 与MN 所成的角为( A )()A 300 ()B 450 ()C 600 ()D例3. 一条长为cm 2的线段AB 夹在互相垂直的两个平面α、β之间,AB 与α所成角为045,与β所成角AE GF DB α为030,且l =βα ,l AC ⊥,l BD ⊥,C 、D 是垂足,求(1)CD 的长;(2)AB 与CD 所成的角解:(1)连BC 、AD ,可证AC ⊥β,BD ⊥α,∴ABC=300, ∠BAD=450 ,Rt △ACB 中,BC=AB ·cos300=3 , 在Rt △ADB 中,BD=AB ·sin450=2在Rt △BCD 中,可求出CD=1cm (也可由AB 2=AC 2+BD 2+CD 2-2AC ·BD ·cos900求得)(2)作BE//l ,CE//BD ,BE ∩CE ,则∠ABE 就是AB 与CD 所成的角,连AE ,由三垂线定理可证BE ⊥AE ,先求出AE=3,再在Rt △ABE 中,求得∠ABE=600。
说明:在(3)中也可作CH ⊥AB 于H ,DF ⊥AB 于F ,HF 即为异面直线CH 、DF 的公垂线,利用公式CD 2=CH 2+DF 2+HF 2-2·CH ·DFcos α,求出cos α=33。
9、两条异面直线的公垂线、距离:和两条异面直线都垂直相交....的直线,我们称之为异面直线的公垂线。
理解:因为两条异面直线互相垂直时,它们不一定相交,所以公垂线的定义要注意“相交”的含义。
两条异面直线的公垂线在这两条异面直线间的线段(公垂线段)的长度,叫做两条异面直线间的距离。
两条异面直线的公垂线有且只有一条。
计算方法:①几何法;②向量法。
例4.在棱长为a 的正四面体中,相对两条棱间的距离为__ _.(答案:a 22) 例5.两条异面直线a 、b 间的距离是1cm ,它们所成的角为600,a 、b 上各有一点A 、B ,距公垂线的垂足都是10cm ,则A 、B 两点间的距离为_______. 答案:cm cm 301101或练习:1.如图,在正方体ABCD -A 1B 1C 1D 1的中,求证:B 1D 被平面A 1BC 1分成1∶2的两段.A 1B 1 D D 1C C 1O证明:如图1,在正方体ABCD -A 1B 1C 1D 1中, 连结B 1D 1,A 1C 1,BD ,AC . 设B 1D 1 A 1C 1=M ,BD AC =N . ∴ M ,N 分别是B 1D 1,AC 的中点. 连结BM ,D 1N .∵ BB 1∥DD 1,且BB 1=DD 1, ∴ 四边形BDD 1B 1是平行四边形.在平面BDD 1B 1中,设B 1D BM =O ,B 1D D 1N =O 1, 在平行四边形BDD 1B 1中,∵ D 1M ∥NB ,且D 1M =NB , ∴ 四边形BND 1M 是平行四边形. ∴ BM ∥ND 1,即 OM ∥O 1D 1, ∴ O 是BO 1的中点,即 O 1O =OB 1. 同理,OO 1=O 1D . ∴ O 1O =OB 1=O 1D . 综上,OB 1∶OD 1=1∶2.2.如图,已知平面α、β交于直线l ,AB 、CD 分别在平面α,β,且与l 分别交于B ,D 两点.若∠ABD =∠CDB ,试问AB ,CD 能否平行?并说明理由. 证明:直线AB ,CD 不能平行.否则,若AB ∥CD ,则AB ∥CD 共面,记这个平面为γ.∴ AB ,CD γ.AαA 1AB B 1D D 1C C 1图1MO N O 1∴ AB ⊂α,D ∈γ.由题知,AB ⊂α,D ∈α,且D ∉AB ,根据过一条直线及这条直线外一点,有且仅有一个平面,α与γ重合. 同理,β与γ重合.∴ α与β重合,这与题设矛盾. ∴ AB ,CD 不能平行.3.平行六面体ABCD -A 1B 1C 1D 1中,求证:CD 1所在的直线与BC 1所在的直线是异面直线.证明:假设CD 1所在的直线与BC 1所在的直线不是异面直线.设直线CD 1与BC 1共面α.∵C ,D 1∈CD 1,B ,C 1∈BC 1,∴C ,D 1,B ,C 1∈α.∵CC 1∥BB 1,∴CC 1,BB 1确定平面BB 1C 1C , ∴C ,B ,C 1∈平面BB 1C 1C .∵不共线的三点C ,B ,C 1只有一个平面, ∴平面α与平面BB 1C 1C 重合. ∴D 1∈平面BB 1C 1C ,矛盾.因此,假设错误,即CD 1所在的直线与BC 1所在的直线是异面直线.基础巩固训练1、 下列推断中,错误的是( )。
