高中数学立体几何专项练习

高三立体几何专题练习(含答案)

立体几何专题练习卷一、填空题（本大题满分56分，每小题4分） 1．正方体DC B A ABCD 111-的棱长为a ，则异面直线1AB 与1BC 所成的角的大小是__________．2．已知某铅球的表面积是2484cm π，则该铅球的体积是___________2cm ．3．若圆锥的侧面积为20π，且母线与底面所成的角为4arccos5，则该圆锥的体积为___________．4．在长方体1111ABCD A B C D -中，若12,1,3AB BC AA ===，则1BC 与平面11BB D D 所成的角θ可用反三角函数值表示为θ=____________．5．若取地球的半径为6371米，球面上两点A 位于东经O12127'，北纬O 318'，B 位于东经O12127'，北纬O 255'，则A B 、两点的球面距离为_____________千米(结果精确到1千米)．6．已知圆锥的母线长为5cm ，侧面积为π15 2cm ，则此圆锥的体积为__________3cm ．7．若圆锥的底面半径和高都是2，则圆锥的侧面积是_____________． 8．如图，是一个无盖正方体盒子的表面展开图，A B C 、、为其上的三个点，则在正方体盒子中，ABC ∠=____________.9．一个圆柱形容器的轴截面尺寸如右图所示，容器内有一个实心的球，球的直径恰等于圆柱的高.现用水将该容器注满，然后取出该球（假设球的密度大于水且操作过程中水量损失不计），则球取出后，容器中水面的高度为__________cm. （精确到0.1cm ）10．如图，用铁皮制作一个无盖的圆锥形容器，已知该圆锥的母线与底面所在平面的夹角为45︒，容器的高为10cm ．制作该容器需要铁皮面积为__________cm2．（衔接部分忽略不计，结果保留整第9题数）11．如图，圆锥的侧面展开图恰好是一个半圆，则该圆锥的母线与底面所成的角的大小是__________ .12．如右下图，ABC ∆中， 90=∠C ，30=∠A ，1=BC ．在三角形内挖去半圆（圆心O 在边AC 上，半圆与BC 、AB 相切于点C 、M ，与AC 交于N ），则图中阴影部分绕直线AC 旋转一周所得旋转体的体积为__________ ．13．如图所示，以圆柱的下底面为底面，并以圆柱的上底面圆心为顶点作圆锥，则该圆锥与圆柱等底等高。

高三数学立体几何专项练习题及答案

高三数学立体几何专项练习题及答案一、选择题1. 下列哪个几何体的所有面都是三角形？A. 正方体B. 圆柱体C. 正六面体D. 球体答案：C2. 一个有8个面的多面体，其中6个面是正方形，另外2个面是等边三角形，它的名字是？A. 正八面体B. 正十二面体C. 正二十面体D. 正二十四面体答案：C3. 空间中任意一点到四个角落连线的垂直距离相等的四棱锥称为？A. 正四棱锥B. 圆锥台C. 四棱锥D. 无法确定答案：C4. 任意多面体的面数与顶点数、棱数的关系是？A. 面数 + 顶点数 = 棱数 + 2B. 面数 + 棱数 = 顶点数 + 2C. 顶点数 + 棱数 = 面数 + 2D. 顶点数 + 面数 = 棱数 + 2答案：A5. 求下列多面体的棱数：（1）正六面体（2）正八面体（3）正十二面体答案：（1）正六面体的棱数为 12（2）正八面体的棱数为 24（3）正十二面体的棱数为 30二、填空题1. 下列说法正确的是：一棱锥没有底面时，它的底面是一个______。

答案：点2. 铅垂线是指从一个多面体的一个顶点到与它相对的棱上所作的垂线，它与该棱垂足的连线相交于该多面体的______上。

答案：中点3. 对正八面体，下列说法不正确的是：_____条对角线与_____两两垂直。

答案：六，相邻面三、计算题1. 一个棱锥的底面是一个边长为6cm的正三角形，其高为8cm。

求棱锥体积。

解答：底面积 S = (1/2) ×底边长 ×高 = (1/2) × 6 × 8 = 24 cm²棱锥体积 V = (1/3) × S ×高 = (1/3) × 24 × 8 = 64 cm³所以，棱锥的体积为64 cm³。

2. 一个正四棱锥的底面是一个边长为10cm的正方形，其高为12cm。

求四棱锥的体积。

解答：底面积 S = 边长² = 10² = 100 cm²四棱锥体积 V = (1/3) × S ×高 = (1/3) × 100 × 12 = 400 cm³所以，四棱锥的体积为400 cm³。

高中数学立体几何经典题型练习题集(附有答案)

高中数学立体几何经典题型练习题集学校：______姓名：_____班级：______考号：______一．单选题1．正三棱锥的底边长和高都是2，则此正三棱锥的斜高长度为（）A．B．C．D．2.在棱长为1的正方体ABCD-A1B1C1D1中，若E，F，G分别为C1D1，AA1，BB1的中点，则空间四边形EFBG在正方体下底面ABCD上的射影面积为（）A．1B．C．D．3．一个棱柱是正四棱柱的条件是（）A．底面是正方形，有两个侧面是矩形B．底面是正方形，有两个侧面垂直于底面C．底面是菱形，且有一个顶点处的三条棱两两垂直D．每个侧面都是全等矩形的四棱柱4、如图，P是正方体ABCD-A1B1C1D1对角线AC1上一动点，设AP的长度为x，若△PBD的面积为f（x），则f（x）的图象大致是（）A．B．C．D．5、如图所示，AB是圆O的直径，C是异于A，B两点的圆周上的任意一点，PA垂直于圆O 所在的平面，则△PAB，△PAC，△ABC，△PBC中，直角三角形的个数是（）A．1B．2C．3D．46、如图，在正方体ABCD-A1B1C1D1中，E、F、G分别是棱A1B1、BB1、B1C1的中点，则下列结论中：①FG⊥BD；②B1D⊥面EFG；③面EFG∥面ACC1A1；④EF∥面CDD1C1．正确结论的序号是（）A．①和②B．③和④C．①和③D．②和④7、三棱锥P-ABC，PC⊥面ABC，△PAC是等腰三角形，PA=4，AB⊥BC，CH⊥PB，垂足为H，D是PA的中点，则△CDH的面积最大时，CB的长是（）A．B．C．D．8、正方体的直观图如图所示，则其展开图是（）A．B．C．D．二．填空题（共__小题）9、如图所示，ABCD是空间四边形，E、F、G、H分别是四边上的中点，并且AC⊥BD，AC=m，BD=n，则四边形EFGH的面积为______．10、如图，已知六棱锥P-ABCDEF的底面是正六边形，PA⊥平面ABC，PA=2AB，给出下列结论：①PB⊥AE；②平面ABC⊥平面PBC；③直线BC∥平面PAE；④∠PDA=45°；⑤直线PD 与平面PAB所成角的余弦值为．其中正确的有______（把所有正确的序号都填上）．11．如图所示，三棱锥M，PA⊥底面ABC，∠ABC=90°，则此三棱锥P-ABC中直角三角形有______个．12、如图，正三棱柱ABC-A1B1C1的各棱长都等于2，D在AC1上，F为BB1中点，且FD⊥AC1，有下述结论（1）AC1⊥BC；（2）=1；（3）二面角F-AC1-C的大小为90°；（4）三棱锥D-ACF的体积为．正确的有______．13．各棱长为a的正三棱柱的六个顶点都在同一个球面上，则此球的表面积为______．14．一四棱锥被平行于底面的平面所截，若截面面积与底面面积之比为1：4，则此截面把一条侧棱分成的两段之比为______．15、如图所示正方体ABCD-A1B1C1D1的棱长为2，线段B1D1上有两个动点E，F且EF=，给出下列五个结论①AC⊥BE②EF∥平面ABCD③异面直线AE，BF所成的角为60°④A1点到面BEF的距离为定值⑤三棱柱A-BEF的体积为定值其中正确的结论有：______（写出所有正确结论的编号）三．简答题（共__小题）16、如图，立体图形A-BCD的四个面分别为△ABC、△ACD、△ADB和△BCD，E、F、G分别是线段AB、AC、AD上的点，且满足AE：AB=AF：AC=AG：AD，求证：△EFG∽△BCD．17、如图，在三棱锥D-ABC中，已知△BCD是正三角形，AB⊥平面BCD，AB=BC=a，E为BC 的中点，F在棱AC上，且AF=3FC．（1）求三棱锥D-ABC的表面积；（2）求证AC⊥平面DEF；（3）若M为BD的中点，问AC上是否存在一点N，使MN∥平面DEF？若存在，说明点N 的位置；若不存在，试说明理由．参考答案一．单选题（共__小题）1．正三棱锥的底边长和高都是2，则此正三棱锥的斜高长度为（）A．B．C．D．答案：D解析：解：在正三棱锥中，顶点P在底面的射影为底面正三角形的中心O，延长A0到E，则E为BC的中点，连结PE，则PE为正三棱锥的斜高．∵正三棱锥的底边长和高都是2，∴AB=PO=2，即AE=，OE=，∴斜高PE==，故选：D．2、在棱长为1的正方体ABCD-A1B1C1D1中，若E，F，G分别为C1D1，AA1，BB1的中点，则空间四边形EFBG在正方体下底面ABCD上的射影面积为（）A．1B．C．D．答案：B解析：解：过E点做EH垂直CD于H，连接EH，易得H即为E在平面ABCD上的射影，连接AH，BH，如下图所示则AH，BH，AB分别为FE，EG，FB在平面ABCD上的射影，又由G在平面ABCD上的射影为B，故△ABH即为空间四边形EFBG在正方体下底面ABCD上的射影∵S△ABH=S ABCD=故选B3．一个棱柱是正四棱柱的条件是（）A．底面是正方形，有两个侧面是矩形B．底面是正方形，有两个侧面垂直于底面C．底面是菱形，且有一个顶点处的三条棱两两垂直D．每个侧面都是全等矩形的四棱柱答案：C解析：解：上、下底面都是正方形，且侧棱垂直于底面的棱柱叫做正四棱柱．故A和B错在有可能是斜棱柱，D错在上下底面有可能不是正方形，底面是菱形，且有一个顶点处的三条棱两两垂直能保证上、下底面都是正方形，且侧棱垂直于底面．故选C．4、如图，P是正方体ABCD-A1B1C1D1对角线AC1上一动点，设AP的长度为x，若△PBD的面积为f（x），则f（x）的图象大致是（）A．B．C．D．答案：A解析：解：设正方体的棱长为1，连接AC交BD于O，连PO，则PO是等腰△PBD的高，故△PBD的面积为f（x）=BD×PO，在三角形PAO中，PO==，∴f（x）=××=，画出其图象，如图所示，对照选项，A正确．故选A．5、如图所示，AB是圆O的直径，C是异于A，B两点的圆周上的任意一点，PA垂直于圆O所在的平面，则△PAB，△PAC，△ABC，△PBC中，直角三角形的个数是（）A．1B．2C．3D．4答案：D解析：证明：∵AB是圆O的直径∴∠ACB=90°即BC⊥AC，三角形ABC是直角三角形又∵PA⊥圆O所在平面，∴△PAC，△PAB是直角三角形．且BC在这个平面内∴PA⊥BC 因此BC垂直于平面PAC中两条相交直线，∴BC⊥平面PAC，∴△PBC是直角三角形．从而△PAB，△PAC，△ABC，△PBC中，直角三角形的个数是，4．故选D．6、如图，在正方体ABCD-A1B1C1D1中，E、F、G分别是棱A1B1、BB1、B1C1的中点，则下列结论中：①FG⊥BD；②B1D⊥面EFG；③面EFG∥面ACC1A1；④EF∥面CDD1C1．正确结论的序号是（）A．①和②B．③和④C．①和③D．②和④答案：D解析：解：如图连接A1C1、A1B、BC1、BD、B1D，因为E、F、G分别是棱A1B1、BB1、B1C1的中点对于①因为FG∥BC1，△BDC1是正三角形，FG⊥BD，不正确．对于②因为平面A1C1B∥平面EFG，并且B1D⊥平面A1C1B，所以B1D⊥面EFG，正确．③面EFG∥面ACC1A1；显然不正确．④EF∥平面CDD1C1内的D1C，所以EF∥面CDD1C1．正确．故选D7、三棱锥P-ABC，PC⊥面ABC，△PAC是等腰三角形，PA=4，AB⊥BC，CH⊥PB，垂足为H，D是PA的中点，则△CDH的面积最大时，CB的长是（）A．B．C．D．答案：D解析：解：三棱锥P-ABC中，PC⊥面ABC，AB⊂平面ABC，∴PC⊥AB；又AB⊥BC，BC∩PC=C，∴AB⊥平面PBC；又CH⊂平面PBC，∴AB⊥CH，又CH⊥PB，PB∩AB=B，∴CH⊥平面PAB，又DH⊂平面PAB，∴CH⊥DH；又△PAC是等腰直角三角形，且PA=4，D是PA的中点，∴CD=PA=2，设CH=a，DH=b，则a2+b2=CD2=4，∴4=a2+b2≥2ab，即ab≤1，当且仅当a=b=时，“=”成立，此时△CDH的面积最大；在Rt△PBC，设BC=x，则PB===，∴PC•BC=PB•CH，即2•x=•；解得x=，∴CB的长是．故选：D．8、正方体的直观图如图所示，则其展开图是（）A．B．C．D．答案：D解析：解：根据题意，可得对于A，展开图中的上下两边的正方形的对边中点连线应该呈左右方向显现，故A的图形不符合题意；对于B，展开图中最右边的“日”字形正方形的对边中点连线应该是上下方向呈现，且应该在含有圆形的正方形的左边放置，故B的图形不符合题意；对于C，展开图中最右边的正方形应该与含有圆形的正方形相邻，故C的图形不符合题意；对于D，沿如图的红线将正方体的侧面剪裁，展开可得如D项图的形状，故D的图形符合题意故选：D二．填空题（共__小题）9、如图所示，ABCD是空间四边形，E、F、G、H分别是四边上的中点，并且AC⊥BD，AC=m，BD=n，则四边形EFGH的面积为______．答案：解析：解：由ABCD是空间四边形，E、F、G、H分别是四边上的中点，并且AC⊥BD，可得四边形EFGH为矩形，且此矩形的长和宽分别为和，故四边形EFGH的面积为=，故答案为：．10、如图，已知六棱锥P-ABCDEF的底面是正六边形，PA⊥平面ABC，PA=2AB，给出下列结论：①PB⊥AE；②平面ABC⊥平面PBC；③直线BC∥平面PAE；④∠PDA=45°；⑤直线PD与平面PAB所成角的余弦值为．其中正确的有______（把所有正确的序号都填上）．答案：①④⑤解析：解：对于①、由PA⊥平面ABC，AE⊂平面ABC，得PA⊥AE，又由正六边形的性质得AE⊥AB，PA∩AB=A，得AE⊥平面PAB，又PB⊂平面PAB，∴AE⊥PB，①正确；对于②、又平面PAB⊥平面ABC，所以平面ABC⊥平面PBC不成立，②错；对于③、由正六边形的性质得BC∥AD，又AD⊂平面PAD，∴BC∥平面PAD，∴直线BC∥平面PAE也不成立，③错；对于④、在Rt△PAD中，PA=AD=2AB，∴∠PDA=45°，∴④正确；对于⑤、由于DE∥AB，∴D到平面PAB的距离即为E到平面PAB的距离，即E到直线PA的距离，即EA，EA=AB，在Rt△PAD中，PA=AD=2AB，∴PD=2AB，∴直线PD与平面PAB所成角的正弦值为=，∴直线PD与平面PAB所成角的余弦值为=，∴⑤正确．故答案为：①④⑤．11．如图所示，三棱锥M，PA⊥底面ABC，∠ABC=90°，则此三棱锥P-ABC中直角三角形有______个．答案：4解析：解：由已知PA⊥底面ABC，∠ABC=90°，所以CB⊥PA，CB⊥AB，又PA∩AB=A，所以CB⊥平面PAB，所以CB⊥PB，所以此三棱锥P-ABC中直角三角形有△ABC，△ABP，△ACP，△PBC共有4个．故答案为：4．12、如图，正三棱柱ABC-A1B1C1的各棱长都等于2，D在AC1上，F为BB1中点，且FD⊥AC1，有下述结论（1）AC1⊥BC；（2）=1；（3）二面角F-AC1-C的大小为90°；（4）三棱锥D-ACF的体积为．正确的有______．答案：（2）（3）（4）解析：解：（1）连接AB1，则∠B1C1A即为BC和AC1所成的角，在三角形AB1C1中，B1C1=2，AB1=2，AC1=2，cos∠B1C1A==，故（1）错；（2）连接AF，C1F，则易得AF=FC1=，又FD⊥AC1，则AD=DC1，故（2）正确；（3）连接CD，则CD⊥AC1，且FD⊥AC1，则∠CDF为二面角F-AC1-C的平面角，CD=，CF=，DF===，即CD2+DF2=CF2，故二面角F-AC1-C的大小为90°，故（3）正确；（4）由于CD⊥AC1，且FD⊥AC1，则AD⊥平面CDF，则V D-ACF=V A-DCF=•AD•S△DCF=×××=．故（4）正确．故答案为：（2）（3）（4）13．各棱长为a的正三棱柱的六个顶点都在同一个球面上，则此球的表面积为______．答案：解析：解：∵正三棱柱的六个顶点都在同一个球面上，所以球心在上下底面中心的连线的中点上，AB=a，OA=R，在△OEA中，OE=，AE=，∵AO2=OE2+AE2，∴，∴球的表面积为4πR2=，故答案为．14．一四棱锥被平行于底面的平面所截，若截面面积与底面面积之比为1：4，则此截面把一条侧棱分成的两段之比为______．答案：1：1解析：解：根据题意，设截得小棱锥的侧棱长为l，原棱锥的侧棱长为L，∵截面与底面相似，且截面面积与底面面积之比为1：4，∴相似比为：==，∴截面把棱锥的一条侧棱分成的两段之比是l：（L-l）=1：1．故答案为：1：1．15、如图所示正方体ABCD-A1B1C1D1的棱长为2，线段B1D1上有两个动点E，F且EF=，给出下列五个结论①AC⊥BE②EF∥平面ABCD③异面直线AE，BF所成的角为60°④A1点到面BEF的距离为定值⑤三棱柱A-BEF的体积为定值其中正确的结论有：______（写出所有正确结论的编号）答案：①②④⑤解析：解：①AC⊥BE，由题意及图形知，AC⊥面DD1B1B，故可得出AC⊥BE，此命题正确；②EF∥平面ABCD，由正方体ABCD-A1B1C1D1的两个底面平行，EF在其一面上，故EF与平面ABCD无公共点，故有EF∥平面ABCD，此命题正确；③由图知，当F与B1重合时，令上底面顶点为O，则此时两异面直线所成的角是∠A1AO，当E与D1重合时，此时点F与O重合，则两异面直线所成的角是∠OBC1，此二角不相等，故异面直线AE、BF所成的角不为定值，故不正确．④A1点到面DD1B1B距离是定值，所以A1点到面BEF的距离为定值，正确；⑤三棱锥A-BEF的体积为定值，由几何体的性质及图形知，三角形BEF的面积是定值，A点到面DD1B1B距离是定值，故可得三棱锥A-BEF的体积为定值，此命题正确．故答案为：①②④⑤．三．简答题（共__小题）16、如图，立体图形A-BCD的四个面分别为△ABC、△ACD、△ADB和△BCD，E、F、G分别是线段AB、AC、AD上的点，且满足AE：AB=AF：AC=AG：AD，求证：△EFG∽△BCD．答案：证明：在△ABD中，∵AE：AB=AG：AD，∴EG∥BD．同理，GF∥DC，EF∥BC．又∠GEF与∠DBC方向相同．∴∠GEF=∠DBC．同理，∠EGF=∠BDC．∴△EFG∽△BCD．17、如图，在三棱锥D-ABC中，已知△BCD是正三角形，AB⊥平面BCD，AB=BC=a，E为BC的中点，F在棱AC上，且AF=3FC．（1）求三棱锥D-ABC的表面积；（2）求证AC⊥平面DEF；（3）若M为BD的中点，问AC上是否存在一点N，使MN∥平面DEF？若存在，说明点N 的位置；若不存在，试说明理由．答案：解：（1）∵AB⊥平面BCD，∴AB⊥BC，AB⊥BD．∵△BCD是正三角形，且AB=BC=a，∴AD=AC=．设G为CD的中点，则CG=，AG=．∴，，．三棱锥D-ABC的表面积为．（2）取AC的中点H，∵AB=BC，∴BH⊥AC．∵AF=3FC，∴F为CH的中点．∵E为BC的中点，∴EF∥BH．则EF⊥AC．∵△BCD是正三角形，∴DE⊥BC．∵AB⊥平面BCD，∴AB⊥DE．∵AB∩BC=B，∴DE⊥平面ABC．∴DE⊥AC．∵DE∩EF=E，∴AC⊥平面DEF．（3）存在这样的点N，当CN=时，MN∥平面DEF．连CM，设CM∩DE=O，连OF．由条件知，O为△BCD的重心，CO=CM．∴当CF=CN时，MN∥OF．∴CN=．。

新教材高二数学立体几何专项训练

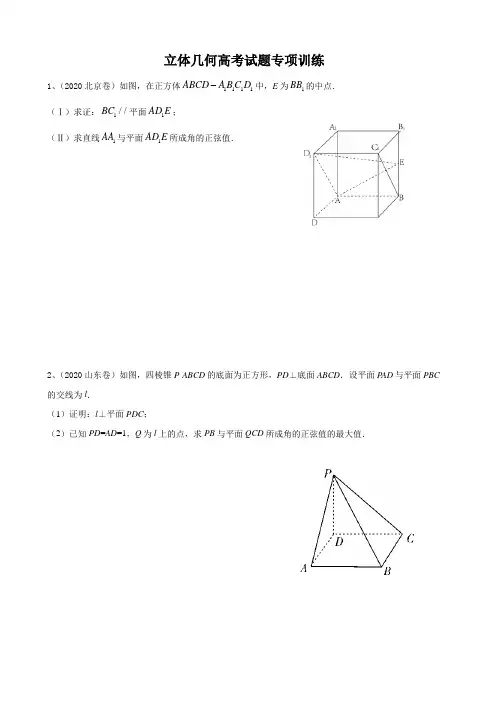
立体几何高考试题专项训练1、（2020北京卷）如图，在正方体1111ABCD A B C D 中，E 为1BB 的中点．（Ⅰ）求证：1//BC 平面1AD E ；（Ⅱ）求直线1AA 与平面1AD E 所成角的正弦值．2、（2020山东卷）如图，四棱锥P -ABCD 的底面为正方形，PD ⊥底面ABCD ．设平面P AD 与平面PBC 的交线为l ．（1）证明：l ⊥平面PDC ；（2）已知PD =AD =1，Q 为l 上的点，求PB 与平面QCD 所成角的正弦值的最大值．3、（2019全国理Ⅰ）如图，直四棱柱ABCD–A1B1C1D1的底面是菱形，AA1=4，AB=2，∠BAD=60°，E，M，N分别是BC，BB1，A1D的中点．（1）证明：MN∥平面C1DE；（2）求二面角A-MA1-N的正弦值．4、（2020全国理Ⅰ）如图，D为圆锥的顶点，O是圆锥底面的圆心，AE为底面直径，AE AD=．ABC是底面的内接正三角形，P为DO上一点，66PO DO=．（1）证明：PA⊥平面PBC；（2）求二面角B PC E--的余弦值．5、（2020全国Ⅲ）如图，在长方体1111ABCD A B C D -中，点,E F 分别在棱11,DD BB 上，且12DE ED =，12BF FB =．（1）证明：点1C 在平面AEF 内；（2）若2AB =，1AD =，13AA =，求二面角1A EF A --的正弦值．6、（2020浙江卷）如图，三棱台DEF —ABC 中，面ADFC ⊥面ABC ，∠ACB =∠ACD =45°，DC =2BC ．（I ）证明：EF ⊥DB ；（II ）求DF 与面DBC 所成角的正弦值．7、（2020天津卷）如图，在三棱柱111ABC A B C -中，1CC ⊥平面,,2ABC AC BC AC BC ⊥==，13CC =，点,D E 分别在棱1AA 和棱1CC 上，且12,AD CE M ==为棱11A B 的中点．（Ⅰ）求证：11C M B D ⊥；（Ⅱ）求二面角1B B E D --的正弦值；（Ⅲ）求直线AB 与平面1DB E 所成角的正弦值．（2020全国Ⅱ）如图，已知三棱柱ABC -A 1B 1C 1的底面是正三角形，侧面BB 1C 1C 是矩形，M ，N 分别为BC ，B 1C 1的中点，P 为AM 上一点，过B 1C 1和P 的平面交AB 于E ，交AC 于F . （1）证明：AA 1∥MN ，且平面A 1AMN ⊥EB 1C 1F ；（2）设O 为△A 1B 1C 1的中心，若AO ∥平面EB 1C 1F ，且AO =AB ，求直线B 1E 与平面A 1AMN 所成角的正弦值.。

高中数学立体几何测试题(10套)

∴ BD ∥平面 PMN ，
位置关系为
平行
。
∴ O 到平面 PMN 的距离即为 BD 到平面 PMN 的距离。
11 、a,b 为异面直线，且 a,b 所成角为 40 °，直线 c 与 a,b 均异面，且所成角均为
∵ BD ⊥ AC ， MN ∥ BD
∵ PA⊥面 ABCD
θ，若这样的 c 共有四条，则 θ的范围为 (70 °， 90° ) 。
D
C
A
B
D1 A1
C1 B1
17 、已知异面直线 a， b 的公垂线段 AB 的中点为 O，平面满足 a∥ ， b∥ ，且 O ， M 、 N 是 a， b 上的任意两点， MN ∩ ＝ P，求证： P 是 MN 的中
点
A aM
O
P
BN b
.
立几面测试 001
参考答案
一、 1- 8 ACDDBDBA
2、已知 m， n 为异面直线， m∥平面， n∥平面， ∩ =l ，则 l（）（ A）与 m， n 都相交（ B）与 m，n 中至少一条相交（ C）与 m， n 都不相交（ D ）与 m， n 中一条相交
3、已知 a， b 是两条相交直线， a∥ ，则 b 与的位置关系是（）
A 、 b∥
PAM
∵ AB=2 ， BM=1 ， CM=1
∴ AM= 5 ，
P
A H
O
.
B
F M
B
D N C
立几面测试 003
一、选择题
1．异面直线是指
(A) 在空间内不能相交的两条直线
(B) 分别位于两个不同平面的两条直线
(C) 某一个平面内的一条直线和这个平面外的一条直线

高中数学立体几何专项练习题及答案

高中数学立体几何专项练习题及答案一、选择题1. 下面哪个选项不是描述柱体的特点？A. 体积恒定B. 底面形状不限C. 侧面是矩形D. 顶面和底面平行答案：A2. 如果一个四面体的一个顶点的对边垂直于底面，那么这个四面体是什么类型？A. 正方形四面体B. 倒立四面体C. 锥体D. 正方锥体答案：C3. 以下哪个选项正确描述了一个正方体的特点？A. 全部面都是正方形B. 12 条棱长度相同C. 8 个顶点D. 6 个面都是正方形答案：D4. 若长方体的高度是 6cm，底面积是 5cm²，底面对角线长为 a cm，那么 a 的值为多少？A. √11B. √29C. √31D. √41答案：C二、填空题1. 一个正方体的棱长为 4cm，它的体积是多少？答案：64cm³2. 一个球的表面积是100π cm²，那么它的半径是多少？答案：5cm3. 一个圆柱体的底面半径为 3cm，高度为 8cm，它的体积是多少？答案：72π cm³4. 一个圆锥的底面半径为 6cm，高度为 10cm，它的体积是多少？答案：120π cm³三、计算题1. 一个四棱锥的底面是边长为 5cm 的正方形，高度为 8cm，它的体积是多少？答案：单位为 cm³，计算过程如下：首先计算底面积：5cm * 5cm = 25cm²再计算体积：25cm² * 8cm / 3 = 200cm³2. 一个圆柱体的底面直径为 12cm，高度为 15cm，它的体积是多少？答案：单位为 cm³，计算过程如下：首先计算底面半径：12cm / 2 = 6cm再计算底面积：π * 6cm * 6cm = 36π cm²最后计算体积：36π cm² * 15cm = 540π cm³3. 一个球的直径为 8cm，它的体积是多少？答案：单位为 cm³，计算过程如下：首先计算半径：8cm / 2 = 4cm再计算体积：4/3 * π * 4cm * 4cm * 4cm = 268.08π cm³4. 一个圆锥的底面半径为 10cm，高度为 20cm，它的体积是多少？答案：单位为 cm³，计算过程如下：首先计算底面积：π * 10cm * 10cm = 100π cm²最后计算体积：100π cm² * 20cm / 3 = 2000π cm³四、解答题1. 若一个长方体的长度、宽度、高度分别为 a、b、c，它的表面积为多少？答案：单位为 cm²，计算过程如下：首先计算侧面积：2 * (a * b + a * c + b * c)再计算底面积：a * b最后计算表面积：2 * (a * b + a * c + b * c) + a * b2. 一个四棱锥的底面为边长为 a 的正三角形，高度为 h，求这个四棱锥的体积。

高中立体几何专题训练

2023届高考数学一轮复习立体几何专练1.如图,ABC △和BCD △都是边长为2的正三角形,且它们所在平面互相垂直.DE ⊥平面BCD ,且AE =.(1)设P 是DE 的中点,求证://AP 平面BCD .(2)求二面角B AE C --的正弦值.2.如图，直三棱柱111ABC A B C -的体积为4，1A BC △的面积为（1）求A 到平面1A BC 的距离；（2）设D 为1A C 的中点，1AA AB =，平面1A BC ⊥平面11ABB A ，求二面角A BD C --的正弦值.3.如图，在三棱台111ABC A B C -中，底面ABC △是边长为2的正三角形，侧面11ACC A 为等腰梯形，且1111A C AA ==，D 为11A C 的中点.（1）证明：AC BD ⊥；（2）记二面角1A AC B --的大小为θ，π2π,33θ⎡⎤∈⎢⎥⎣⎦时，求直线1AA 与平面11BB C C 所成角的正弦值的取值范围.4.如图，在棱柱1111ABCD A B C D -中，1AA ⊥平面ABCD ，四边形ABCD 是菱形，60ABC ∠=︒，点N 为AD 的中点，且14,2AA AB ==.(1)设M 是线段1BD 上一点，且1BMMD λ=.试问：是否存在点M ，使得直线1//AA 平面MNC ？若存在，请证明1//AA 平面MNC ，并求出λ的值；若不存在，请说明理由；(2)求二面角1N CD D --的余弦值.5.已知四棱柱1111ABCD A B C D -的底面为菱形,1π2,,,3AB AA BAD AC BD O AO ==∠=⋂=⊥平面111,A BD A B A D =.(1)证明:1B C P 平面1A BD ;(2)求二面角1B AA D --的余弦值.6.如图，在四棱锥P ABCD -中，AP ⊥平面ABCD ，底面ABCD 是边长为2的正方形，AP AB =，M 为线段PC 上一点.(1)若平面MAB⋂平面PCD l=，证明：//l CD；(2)若二面角D AM B--的平面角为2π3，求三棱锥P AMD-的体积.7.如图，在多面体ABCDEF中，四边形BCEF是矩形，//,AD BC BC CD⊥，1,2,2BC CD AD FA FB CM ME======.(1)证明：FA CD⊥；(2)求直线AF与平面MBD所成角的正弦值.8.如图，在四棱锥P ABCD-中，底面ABCD是边长为1的菱形，60BCD∠=︒，E为AD的中点，PE⊥平面ABCD，F为PC上的一点，且12PF FC=uu u r uu u r.(1)证明：//PA平面BEF；(2)若二面角P BE F--的平面角为30°，求四棱锥P ABCD-的体积.9.如图，在平面五边形ABCDE中ADE△是边长为2的等边三角形，四边形ABCD是直角梯形，其中//,,1,⊥==.将ADEAD BC AD DC BC CD△沿AD折起，使得点E到达点M的位置，且使BM=.(1)求证：平面MAD⊥平面ABCD；(2)设点P为棱CM上靠近点C的三等分点，求平面PBD与平面MAD所成的二面角的正弦值.10.如图,四棱锥P ABCD△是边长为2的等边-的底面为矩形,平面PCD⊥平面ABCD,PCD三角形,BC=,点E为CD的中点,点M为PE上一点(与点,P E不重合).(1)证明:AM BD⊥.(2)当AM为何值时,直线AM与平面BDM所成的角最大?答案以及解析1.答案：(1)见解析解析：(1)证明：取BC 的中点O ,连接,,AO DO AD .ABC ∴△是正三角形,OA BC ∴⊥.∵平面ABC ⊥平面BCD ,平面ABC I 平面BCD BC =,OA ∴⊥平面BCD .OD ⊂Q 平面BCD ,AO OD ∴⊥.在Rt AOD △中,2sin 60AO DO ===o ,AD ∴==.又AE =,ADE ∴△为等腰三角形.P Q 是DE 的中点,AP DE ∴⊥.DE ⊥Q 平面BCD ,//,//,AO DE AP AO AP OD ∴∴⊥∴.OD ⊂Q 平面,BCD AP ⊄平面BCD ,//AP ∴平面BCD .(2)由(1)知,,////OA DP AP OD ,∴四边形APDO 为平行四边形,PD OA ∴==,DE ∴=.以点O 为坐标原点,以,,OD OC OA uuu r uuu r uu r的方向分别为x 轴、y 轴、z 轴的正方向,建立如图的空间直角坐标系O xyz -,则(0,1,0)A B-,(0,1,0), C E,(0,1,BA AE AC∴===-uu r uu u r uuu r.设平面ABE的法向量为(,,)x y z=m,则0,0,BAAE⎧⋅=⎪⎨⋅=⎪⎩uu ruu u rmm即0,0.y⎧=⎪+=令y=,则1,1x z==-,1)∴=-m.设平面ACE的法向量为(,,)a b c=n,则0,0,AEAC⎧⋅=⎪⎨⋅=⎪⎩uu u ruuu rnn即0,0.b+==⎪⎩令1a=-,则1b c==,(∴=-n.1cos,||||5⋅∴==m nm nm n.sin,∴=m n∴二面角B AE C--的正弦值为265.2.答案：（1（2解析：（1）设点A到平面1A BC的距离为h，因为直三棱柱111ABC A B C-的体积为4，所以11111114333A A BC ABC ABC ABC V S AA V --=⨯==△，又1A BC △的面积为11114333A A BC A BC V S h -==⨯=△，所以h =，即点A 到平面1A BC.（2）取1A B 的中点E ，连接AE ，则1AE A B ⊥，因为平面1A BC ⊥平面11ABB A ，平面1A BC 平面111ABB A A B =，所以AE ⊥平面1A BC ，所以AE BC ⊥，又1AA ⊥平面ABC ，所以1AA BC ⊥，因为1AA AE A = ，所以BC ⊥平面11ABB A ，所以BC AB ⊥.以B 为坐标原点，分别以BC，BA，1BB的方向为x ，y ，z 轴的正方向，建立如图所示的空间直角坐标系B xyz -，由（1）知，AE =12AA AB ==，1A B =，因为1A BC △的面积为112A B BC =⨯⨯，所以2BC =，所以(0,2,0)A ，(0,0,0)B ，(2,0,0)C ，1(0,2,2)A ，(1,1,1)D ，(0,1,1)E ，则(1,1,1)BD = ，(0,2,0)BA =，设平面ABD 的法向量为(,,)x y z =n ，则0,0,BD BA ⎧⋅=⎪⎨⋅=⎪⎩n n 即0,20,x y z y ++=⎧⎨=⎩令1x =，得(1,0,1)=-n ，又平面BDC 的一个法向量为(0,1,1)AE =-，所以1cos ,2||||AE AE AE ⋅〈〉==-⋅nn n ，设二面角A BD C --的平面角为θ，则sin θ==，所以二面角A BD C --的正弦值为32.3.答案：（1）见解析（2）7⎣⎦解析：（1）如图，取AC 的中点M ，连接DM ，BM ，在等腰梯形11ACC A 中，D ，M 分别为11A C ，AC 的中点，AC DM ∴⊥.在正三角形ABC 中，M 为AC 的中点，AC BM ∴⊥.DM BM M ⋂= ，DM ，BM ⊂平面BDM ，AC ∴⊥平面BDM .又BD ⊂平面BDM ，AC BD ∴⊥.（2）DM AC ⊥ ，BM AC ⊥，DMB ∴∠为二面角1A AC B --的平面角，即DMB θ∠=.AC ⊥ 平面BDM ，∴在平面BDM 内作Mz BM ⊥，以M 为坐标原点，以MA ，MB ，Mz的方向分别为x ，y ，z 轴正方向，建立如图所示空间直角坐标系，则(1,0,0)A，B，(1,0,0)C-，22Dθθ⎛⎫⎪⎪⎝⎭，11222Cθθ⎛⎫- ⎪⎪⎝⎭，112Aθθ⎛⎫⎪⎪⎝⎭，则CB=，1133222CCθθ⎛⎫= ⎪⎪⎝⎭.设平面11BB C C的法向量为(,,)x y z=n，则有10,0,CBCC⎧⋅=⎪⎨⋅=⎪⎩nn即0,1cos0,222xx y zθθ⎧+=⎪⎨+⋅+⋅=⎪⎩令x=1y=，1cossinzθθ-=，则1cossinθθ-⎛⎫= ⎪⎝⎭n.设直线1AA与平面11BB C C所成角为α，又1133222AAθθ⎛⎫=-⎪⎪⎝⎭，1sin cos,AAα∴===n.π2π,33θ⎡⎤∈⎢⎥⎣⎦，11cos,22θ⎡⎤∴∈-⎢⎥⎣⎦，sin713α∴∈⎣⎦.4.答案：(1)存在，2λ=.(2)余弦值为17.解析：(1)取11A D的中点P，连接CP交1BD于点M，点M即为所求.证明：连接PN，因为N是AD的中点，P是11A D的中点，所以1//PN AA，又PN⊂平面MNC，1AA⊂/平面MNC，所以直线1//AA平面MNC.因为11//,//A D AD AD BC ，所以1// PD BC .所以112BM CBMD PD λ===.(2)连接AC .由(1)知1//AA PN .又1AA ⊥平面ABCD ，所以PN ⊥平面ABCD .因为60ADC ABC ∠=∠=︒，四边形ABCD 是菱形，所以ADC △为正三角形，所以NC AD ⊥.以N 为坐标原点，NC ，ND ，NP 所在的直线分别为x ，y ，z 轴，建立空间直角坐标系N xyz -.又14,2AA AB ==，所以1NC ND ==，所以点1(0,0,0),(0,1,0),(0,1,4)N C D D ，则111(0,1,4),1,4),(0,0,4)ND D C DD ==--=uuur uuu r uuu u r.设平面1ND C 的法向量()111,,x y z =m ，则110,0,ND D C ⎧⋅=⎪⎨⋅=⎪⎩m m uuur uuu r即1111140,40,y z y z +=⎧⎪--=令11z =，得(0,4,1)=-m .设平面1CDD 的法向量()222,,x y z =n ，则110,0,DD D C ⎧⋅=⎪⎨⋅=⎪⎩n n uuu u ruuu r即222240,40,z y z =⎧⎪--=令21x =，得=n ，所以cos ,||||17⋅〈〉===⋅m n m n m n ，由图易得二面角1N CD D --为锐角，所以二面角1N CD D --的余弦值为25117.5.答案：(1)见解析(2)17-解析：(1)连接1AB 交1A B 于点 Q ,连接OQ ,易知 Q 为1AB 的中点,O 为AC 的中点,∴在1AB C V 中,112OQ B C P,OQ ⊂Q 平面11,A BD B C ⊂/平面1A BD ,1B C ∴P 平面1A BD .(2)连接1,A O AO ⊥Q 平面11,A BD AO A O ∴⊥,11A B A D =Q 且O 为BD 的中点,1A O BD ∴⊥,,AO BD ⊂Q 平面ABCD 且AO BD O ⋂=,1A O ∴⊥平面ABCD .如图,以O 为坐标原点,1,,OA OB OA 所在直线分别为,,x y z 轴,建立空间直角坐标系O xyz -.易得1(0,1,0),(0,1,0),(0,0,1)A B D A -,1((AA AB ∴==uuu r uu u r,设平面1A AB 的法向量为(,,)x y z =n ,则10,0,AA AB ⎧⋅=⎪⎨⋅=⎪⎩n n uuu r uu ur 0,0,z y ⎧+=⎪∴⎨+=⎪⎩令1x =,得y z ==,∴=n .同理可得平面1A AD的一个法向量为(1,=m ,1cos ,||||7⋅∴〈〉==m n m n m n ,结合图形知,二面角1B AA D --为钝二面角,∴二面角1B AA D --的余弦值为17-.6.答案：(1)见解析.(2)见解析.解析：(1)因为底面ABCD 是正方形，所以//CD AB .又因为AB ⊂/平面,PCD CD ⊂平面PCD ，所以//AB 平面PCD .又平面PCD ⋂平面MAB l =，所以//AB l .又因为//CD AB ，所以//CD l .(2)由题易知AD ，AB ，AP 两两垂直.以A 为坐标原点，AD 为x 轴，AB 为y 轴，AP 为z 轴建立如图所示的空间直角坐标系，则(0,0,0),(0,2,0),(2,2,0),(2,0,0),(0,0,2)A B C D P ，设(01)PM PC λλ=≤≤uuu ruu u r，则(2,2,22)M λλλ-+，则(2,2,22),(0,2,0),(2,0,0)AM AB AD λλλ=-+==uuu r uu u r uuu r.设平面AMB 的法向量为()111,,x y z =m ，则00AM AB ⎧⋅=⎪⎨⋅=⎪⎩m m uuu ruu u r，即111122(22)020x y z y λλλ++-+=⎧⎨=⎩，令11x =，则1,0,1λλ⎛⎫= ⎪-⎝⎭m .设平面AMD 的法向量为()222,,x y z =n ，则00AM AD ⎧⋅=⎪⎨⋅=⎪⎩n n uuu ruuu r，即222222(22)020x y z x λλλ++-+=⎧⎨=⎩，令21y =，则0,1,1λλ⎛⎫= ⎪-⎝⎭n ，因为二面角D AM B --的平面角为2π3，是钝角，所以222||111|cos ,|||||211λλλλλ⎛⎫⎛⎫ ⎪ ⎪⋅-⎝⎭〈〉==⎛⎫+ ⎪-⎝⎭m n m n m n ，解得12λ=，则(1,1,1)M ，所以M 为线段PC 的中点，点M 到平面PAD 的距离为1，所以112221323P AMD M APD V V --==⨯⨯⨯⨯=.7.答案：(1)证明过程见解析.(2)解析：(1)如图，取AD 的中点O ，连接OB ，OF ，则1OA OD BC CD ====.因为//,BC AD BC CD ⊥，所以CD AD ⊥，所以四边形OBCD 是正方形，OB BC ⊥.因为四边形BCEF 是矩形，所以BC BF ⊥.因为OB BF B ⋂=，所以BC ⊥平面OBF ，又OF ⊂平面OBF ，所以BC OF ⊥，所以AD OF ⊥.因为,,FA FB OA OB OF OF ===，所以OAF OBF ≅△△.因为OA OF ⊥，所以OB OF ⊥，所以CD OF ⊥.又,CD AD OF AD O ⊥⋂=，所以CD ⊥平面ADEF ，又AF ⊂平面ADEF ，所以CD AF ⊥.(2)以O 为坐标原点，OA ，OB ，OF 所在直线分别为x 轴、y 轴、z 轴，建立如图所示的空间直角坐标系，则(1,0,0),(0,1,0),(1,1,0),(1,0,0),(1,0,A B C D E F ---.所以(1,1,0),(1,0,(0,1,BD FA EC =--==uu u r uu r uu u r，由2CM ME =，得1130,,333EM EC ⎛⎫==- ⎪ ⎪⎝⎭uuu r uu u r ，所以1231,,33M ⎛- ⎝⎭，所以21,,33BM ⎛⎫=-- ⎪ ⎪⎝⎭uuu r .设平面MBD 的法向量(,,)x y z =m ，则00BD BM ⎧⋅=⎪⎨⋅=⎪⎩m m uu u r uuu r ，所以0223033x y x y z --=⎧⎪⎨--+=⎪⎩，令3x =，则3332x y z =⎧⎪=-⎪⎨⎪=⎪⎩，所以3,⎛=- ⎝⎭m .设直线AF 与平面MBD 所成的角为θ，则3||2sin |cos ,|53||||2FA FA FA θ⋅=〈〉==m m m uu r uu r uu r.直线AF 与平面MBD所成角的正弦值为10.8.答案：(1)见解析.(2)体积为14.解析：(1)证明：如图，连接AC 交BE 于G ，连接FG .因为底面ABCD 是菱形，所以//,AD BC AD BC =.又E 为AD 的中点，所以12AE BC =，所以12AG AE GC BC ==.因为12PF FC =uu u r uu u r ，即12PF FC =，所以AG PF GC FC=，所以//PA FG .又FG ⊂平面BEF ，PA ⊂/平面BEF ，所以//PA 平面BEF .(2)在ABE △中，1||1,||,602AB AE BAE ==∠=︒，所以由余弦定理得2221113||||||2||||cos 601214224BE AE AB AE AB =+-⋅⋅-⨯⨯︒=+⨯=，即2BE =，所以222||||||AB AE BE =+，所以AE BE ⊥.如图，以E 为坐标原点，EA 所在直线为x 轴，EB 所在直线为y 轴，EP 所在直线为z 轴，建立空间直角坐标系.令||(0)PE a a =>，则13(0,0,0),,0,0,,(0,,)22E A B P a ⎛⎫⎛⎫⎪ ⎪ ⎪⎝⎭⎝⎭，所以10,,0,,0,22EB PA a ⎛⎫⎛⎫==- ⎪ ⎪ ⎪⎝⎭⎝⎭uu r uu r .因为,,AE PE AE BE PE BE E ⊥⊥⋂=，所以AE ⊥平面PBE ，所以平面PBE 的一个法向量为(1,0,0)=m .设平面BEF 的法向量为(,,)x y z =n ，由EB ⊥n uur，可得0y =.因为,//FG PA FG ⊥n uu u r ，所以PA ⊥n uu r，即有1002x y az +⨯-=，令1z =，则2x a =，所以(2,0,1)a =n .由二面角P BE F --的平面角为30°，得||cos30||||⋅=︒=m n m n=，解得a 负值舍去)，所以||PE =，所以1111||||||||13334P ABCD ABCD V S PE AD BE PE -=⨯=⨯⨯=⨯⨯四棱锥菱形.9.答案：(1)见解析.(2)正弦值为5.解析：如图，取AD 的中点N ，连接MN ，BN .因为MAD △是等边三角形，所以MN AD ⊥，且sin 60MN AM =︒=，在直角梯形ABCD 中，因为1,//,DN BC DN BC AD DC ==⊥，所以四边形BCDN 是矩形，所以BN AD ⊥，且BN CD ==所以2226BN MN BM +==，即BN MN ⊥，又AD MN N ⋂=，所以BN ⊥平面MAD .因为BN ⊂平面ABCD ，所以平面MAD ⊥平面ABCD .(2)由(1)知NA ，NB ，NM 两两互相垂直，以N 为坐标原点，直线NA 为x 轴、NB 为y 轴、NM 为z 轴建立如图所示的空间直角坐标系，根据题意，(0,0,0),(1,0,0),(1,(0,0,(1,0,0),N A B C M D DB --=uu u r，由P 是棱CM 的靠近点C的三等分点得，11233(1,0,0)(1,,33333BP BC CM ⎛⎫=+=-+=- ⎪ ⎪⎝⎭uu r uu u r uuu r ，设平面PBD 的一个法向量为(,,)x y z =n ，则0,0,BP DB ⎧⋅=⎪⎨⋅=⎪⎩n n uu r uu u r即2330,3330,x y x ⎧--+=⎪⎨⎪+=⎩令1y =，则1x z ==-，故平面BDP的一个法向量为(1)=-n .而平面MAD的一个法向量为NB =uu u r，设平面PBD 与平面MAD 所成的二面角的平面角为θ，则|||cos ||cos ,|5||||NB NB NB θ⋅=〈〉===n n n uu u ruu u r uu u r ，所以sin θ=，所以平面PBD 与平面MAD.10.答案：(1)见解析(2)30°解析：(1)证明：如图,连接AE ,交BD 于点F 因为四边形ABCD 为矩形,2,CD BC ==,点E 为CD 的中点,所以tan 2DE DAE AD ∠==,tan 2BC BDC CD ∠==,所以tan tan DAE BDC ∠=∠,则DAE BDC ∠=∠.因为90DAE AED ∠+∠=o ,所以90BDC AED ∠+∠=︒,所以90DFE ∠=︒,则BD AE ⊥.因为PCD V 是边长为2的等边三角形,点E 为CD 的中点,所以PE CD ⊥.因为平面PCD ⊥平面ABCD ,平面PCD I 平面ABCD CD =,所以PE ⊥平面ABCD .又BD ⊂平面ABCD ,所以PE BD ⊥.因为PE AE E =I ,所以BD ⊥平面APE .因为AM ⊂平面APE ,所以BD AM ⊥.(2)取AB 的中点H ,连接EH ,则EH CD ⊥.以E 为坐标原点,,,EH EC EP 所在的直线分别为x 轴、y 轴、z 轴建立如图的空间直角坐标系,由已知条件可知,1,0),(0,1,0),A D B --,PE =设(0,0,)(0M m m <<,则(),(2,0),(0,1,)AM m BD DM m ==-=uuu r uu u r uuu u r.设平面BDM 的一个法向量为(,,)x y z =n ,则0,0,BD DM ⎧⋅=⎪⎨⋅=⎪⎩uu u r uuu u r n n即20,0.y y mz ⎧-=⎪⎨+=⎪⎩令1z =,则,y m x =-=,所以,,1)m =-n .设直线AM 与平面BDM 所成的角为θ，则||sin |cos ,|||||AM AM AM θ⋅====uuur uuur uuur n nn 12≤=,当且仅当2233m m=,即1m =时,等号成立.uuu r.所以直线AM与平面BDM所成的角的最大值为30°,此时||2==AM AM。

高中数学立体几何小题100题(含答案与解析)

立体几何小题100例一、选择题1．如图，已知正方体1111ABCD A B C D -的棱长为4，点E ，F 分别是线段AB ，11C D 上的动点，点P 是上底面1111A B C D 内一动点，且满足点P 到点F 的距离等于点P 到平面11ABB A 的距离，则当点P 运动时，PE 的最小值是（）A ．5B ．4C ．42．5【答案】D 【解析】试题分析：因为点P 是上底面1111A B C D 内一动点，且点P 到点F 的距离等于点P 到平面11ABB A 的距离，所以，点P 在连接1111,A D B C 中点的连线上．为使当点P 运动时，PE 最小，须PE 所在平面平行于平面11AA D D ,2244()52PE =+=选D考点：1．平行关系；2．垂直关系；3．几何体的特征．2．如图在一个二面角的棱上有两个点A ，B ，线段,AC BD 分别在这个二面角的两个面内，并且都垂直于棱AB ，=46,AB cm AC cm =， 8,217BD cm CD cm ==，则这个二面角的度数为（）A ．30︒B ．60︒C ．90︒D ．120︒ 【答案】B 【解析】试题分析：设所求二面角的大小为θ，则,BD AC θ<>=，因为CD DB BA AC =++，所以22222()222CD DB BA AC DB BA AC DB BA DB AC BA AC =++=+++⋅+⋅+⋅CA DB而依题意可知,BD AB AC AB ⊥⊥，所以20,20DB BA BA AC ⋅=⋅=所以2222||||||||2CD DB BA AC BD AC =++-⋅即222417468286cos θ⨯=++-⨯⨯所以1cos 2θ=，而[0,]θπ∈，所以60θ=︒，故选B. 考点：1.二面角的平面角；2.空间向量在解决空间角中的应用.3．已知某个几何体的三视图如图所示，根据图中标出的尺寸（单位：cm ）可得这个几何体的体积是（）112222侧视图俯视图主视图A ．343cmB ．383cmC ．33cmD ．34cm【答案】B ．【解析】试题分析：分析题意可知，该几何体为一四棱锥，∴体积382231312=⨯⨯==Sh V ．考点：空间几何体的体积计算．4．如图，P 是正方体1111ABCD A B C D -对角线1AC 上一动点，设AP 的长度为x ，若PBD ∆的面积为(x)f ，则(x)f 的图象大致是（）【答案】A 【解析】试题分析：设AC 与BD 交于点O ,连接OP .易证得BD ⊥面11ACC A ,从而可得BD OP ⊥.设正方体边长为1,在1Rt ACC ∆中126cos 33C AC ∠==.在AOP ∆中 22OA =,设(),03AP x x =≤≤,由余弦定理可得2222226231222362OP x x x x ⎛⎫=+-⋅⨯=-+ ⎪ ⎪⎝⎭,所以223162OP x x =-+.所以()22231262f x x x =-+.故选A. 考点：1线面垂直,线线垂直;2函数图象.5．如图所示，正方体ABCD A B C D ''''-的棱长为1， ,E F 分别是棱AA '，CC '的中点，过直线,E F 的平面分别与棱BB '、DD '交于,M N ，设 BM x =，[0,1]x ∈，给出以下四个命题：（1）平面MENF ⊥平面BDD B ''；（2）当且仅当x=12时，四边形MENF 的面积最小；（3）四边形MENF 周长()L f x =，[0,1]x ∈是单调函数；（4）四棱锥C MENF '-的体积()V h x =为常函数；以上命题中假命题．．．的序号为（） A ．（1）（4） B ．（2） C ．（3） D ．（3）（4）【答案】C 【解析】试题分析：（1）由于AC EF //，B B AC BD AC '⊥⊥,，则D D B B ''⊥平面AC ，则D D B B EF ''⊥平面，又因为EMFN EF 平面⊂，则平面MENF ⊥平面BDD B ''；（2）由于四边形MENF 为菱形，MN EF S MENF ⋅=21，2=EF ，要使四边形MENF 的面积最小，只需MN 最小，则当且仅当21=x 时，四边形MENF 的面积最小；（3）因为1)21(2+-=x MF ，1)21(4)(2+-=x x f ，)(x f 在]1,0[上不是单调函数；（4）NE C F EC M F MENF C V V V '-'--'+=，ME C S '∆=41121=⋅'E C ，F 到平面ME C '的距离为1，1214131=⋅='-ME C F V ，又41121=⋅'⋅='∆E C S NE C ，1214131=⋅='-NE C F V ，61)(=x h 为常函数.故选（3）考点：1.面面垂直的判定定理；2.建立函数模型.6．已知三棱柱111ABC A B C -的侧棱与底面边长都相等，1A 在底面ABC 上的射影为BC 的中点，则异面直线AB 与1CC 所成的角的余弦值为（）（A）4 （B ）4 （C ）4 （D ）34【答案】D. 【解析】试题分析：连接B A 1；11//CC AA ,AB A 1∠∴是异面直线AB 与1CC 所成的角或其补角；在1ADA Rt ∆中，设11=AA ，则21,231==D A AD ；在1BDA Rt ∆中，2121=B A ；在1ABA ∆中，431122111cos 1=⨯⨯-+=∠AB A ；即面直线AB 与1CC 所成的角的余弦值为34. 考点：异面直线所成的角.7．一个几何体的三视图如图所示，其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形，则该几何体的外接球的表面积为A ．π312B ．π12C ．π34D ．π3 【答案】D 【解析】试题分析：由三视图可知，该几何体为四棱锥，侧棱垂直底面，底面是正方形，将此四棱锥还原为正方体，则正方体的体对角线即外接球的直径，32=r ，23=∴r ，因此ππ342==r S 表面积，故答案为D. 考点：由三视图求外接球的表面积.8．如图，棱长为1的正方体ABCD-A 1B 1C 1D 1中，P 为线段A 1B 上的动点，则下列结论错误的是（）A ．11DC D P ⊥B ．平面11D A P ⊥平面1A APC ．1APD ∠的最大值为90 D ．1AP PD +22+ 【答案】C 【解析】试题分析：111DC D A ⊥ ，11DC B A ⊥，1111A B A D A = ，⊥∴1DC 平面11BCD A ，⊂P D 1平面11BCD A 因此P D DC 11⊥，A 正确；由于⊥11A D 平面11ABB A ，⊂11A D 平面P A D 11，故平面⊥P A D 11平面AP A 1 故B 正确，当2201<<P A 时，1APD ∠为钝角，C 错；将面B AA 1与面11BCD A 沿B A 1展成平面图形，正视图侧视图俯视图线段1AD 即为1PD AP +的最小值，利用余弦定理解221+=AD ，故D 正确，故答案为C ．考点：棱柱的结构特征． 9．下列命题中，错误的是（）A ．一条直线与两个平行平面中的一个相交，则必与另一个平面相交B ．平行于同一平面的两条直线不一定平行C ．如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面βD ．若直线l 不平行于平面α，则在平面α内不存在与l 平行的直线【答案】B 【解析】试题分析: 由直线与平面的位置关系右知A 正确;平行于同一个平面的两条直线可以相交、平行或异面，故B 错，所以选B.考点:直线、平面平行与垂直的判定与性质.10．已知如图所示的正方体ABCD ﹣A 1B 1C 1D 1，点P 、Q 分别在棱BB 1、DD 1上，且=，过点A 、P 、Q作截面截去该正方体的含点A 1的部分，则下列图形中不可能是截去后剩下几何体的主视图的是（）【答案】A【解析】试题分析：当P 、B 1重合时，主视图为选项B ；当P 到B 点的距离比B 1近时，主视图为选项C ；当P 到B 点的距离比B 1远时，主视图为选项D ，因此答案为A. 考点：组合体的三视图11．一个几何体的三视图及尺寸如图所示，则该几何体的外接球半径为（）A. B. C. D.【答案】C 【解析】试题分析：由三视图可知：该几何体是一个如图所示的三棱锥P-ABC ，它是一个正四棱锥P-ABCD 的一半，其中底面是一个两直角边都为6的直角三角形，高PE=4．设其外接球的球心为O ，O 点必在高线PE 上，外接球半径为R ，则在直角三角形BOE 中，BO 2=OE 2+BE 2=（PE-EO ）2+BE 2，即R 2=（4-R ）2+（32）2，解得：R=174，故选C.考点：三视图，球与多面体的切接问题，空间想象能力12．如右图，在长方体1111ABCD A B C D -中，AB =11，AD =7，1AA =12，一质点从顶点A 射向点()4312E ，，，遇长方体的面反射（反射服从光的反射原理），将1i -次到第i 次反射点之间的线段记为()2,3,4i L i =，1L AE =，将线段1234,,,L L L L 竖直放置在同一水平线上，则大致的图形是（）【答案】C 【解析】试题分析：因为37411>，所以1A E 延长交11D C 于F ，过F 作FM 垂直DC 于.M 在矩形1AA FM 中分析反射情况：由于35105AM =>，第二次反射点为1E 在线段AM 上，此时153E M =,第三次反射点为2E 在线段FM 上，此时24E M =,第四次反射点为3E 在线段1AF 上,由图可知，选C.考点：空间想象能力13．一块石材表示的几何体的三视图如图所示，将该石材切削、打磨、加工成球，则能得到的最大球的半径等于（）A.1B.2C.3D.4【答案】B【解析】试题分析：由图可得该几何体为三棱柱,因为正视图,侧视图,俯视图的内切圆半径最小的是正视图(直角三角形)所对应的内切圆,所以最大球的半径为正视图直角三角形内切圆的半径r , 则2286862r r r -+-+⇒=,故选B. 考点：三视图内切圆球三棱柱14．已知二面角l αβ--为60︒，AB α⊂，AB l ⊥，A 为垂足，CD β⊂，C l ∈，135ACD ∠=︒，则异面直线AB 与CD 所成角的余弦值为 A ．14 B ．24 C ．34 D ．12【答案】B. 【解析】试题分析：如图作BE β⊥于E ，连结AE ，过A 作AG ∥CD ，作EG AG ⊥于G ，连结BG ，则.BG AG ⊥设2AB a =．在ABE ∆中，60,90,2,.BAE AEB AB a AE a ∠=︒∠=︒=∴=在Rt AEG ∆中，29045,90,cos 45.2GAE CAG AGE AG a a ∠=︒-∠=︒∠=︒∴=︒=在Rt ABG∆中，222cos 24AG BAG AB a ∠===∴异面直线AB 与CD 所成角的余弦值为24，故选B ．βαElBDACG考点：1.三垂线定理及其逆定理；2. 空间角（异面直线所成角）的计算．15．在空间直角坐标系Oxyz 中,已知(2,0,0)(2,2,0),(0,2,0),(1,1,2)A B C D .若123,,S S S 分别是三棱锥D ABC -在,,xOy yOz zOx 坐标平面上的正投影图形的面积，则（）A ．123S S S ==B ．21S S =且23S S ≠C ．31S S =且32S S ≠D ．32S S =且31S S ≠ 【答案】D 【解析】试题分析：三棱锥ABC D -在平面xoy 上的投影为ABC ∆，所以21=S ，设D 在平面yoz 、zox 平面上的投影分别为2D 、1D ，则ABC D -在平面yoz 、zox 上的投影分别为2OCD ∆、1OAD ∆，因为)2,1,0(1D ，)2,0,1(2D ，所以212=-S S ，故选D.考点：三棱锥的性质，空间中的投影，难度中等.16．正方形ABCD 的边长为2，点E 、F 分别在边AB 、BC 上，且1AE =，12BF =，将此正方形沿DE 、DF 折起，使点A 、C 重合于点P ，则三棱锥P DEF -的体积是（） A ．13B 523 D ．23【答案】B【解析】试题分析：解：因为90,DPE DPF ∠=∠=所以,DP PE DP PF ⊥⊥又因为PE ⊂平面PEF ,PF ⊂平面PEF ,且PE PF P =,所以DP ⊥平面PEF在PEF ∆中，22223151,,1222PE PF EF EB BF ⎛⎫===+=+= ⎪⎝⎭所以222351222cos 33212EPF ⎛⎫⎛⎫+- ⎪ ⎪⎝⎭⎝⎭∠==⨯⨯,225sin 133EPF ⎛⎫∠=-= ⎪⎝⎭ 所以11355sin 122234PEF S PE PF EPF ∆=⋅⋅∠=⨯⨯⨯= 115523346PEF P DEF D PEF V V DP S ∆--==⋅⋅=⨯⨯=三棱锥三棱锥所以应选B.考点：1、直线与平面垂直的判定；2、正弦定理与余弦定理；3、棱锥的体积.17．高为的四棱锥S ﹣ABCD 的底面是边长为1的正方形，点S ，A ，B ，C ，D 均在半径为1的同一球面上，则底面ABCD 的中心与顶点S 之间的距离为（）A. B. C. D.【答案】A【解析】试题分析：由题意可知ABCD 是小圆，对角线长为，四棱锥的高为，推出高就是四棱锥的一条侧棱，最长的侧棱就是球的直径，然后利用勾股定理求出底面ABCD 的中心与顶点S 之间的距离．解：由题意可知ABCD 是小圆，对角线长为，四棱锥的高为，点S ，A ，B ，C ，D 均在半径为1的同一球面上，球的直径为2，所以四棱锥的一条侧棱垂直底面的一个顶点，最长的侧棱就是直径，所以底面ABCD 的中心与顶点S 之间的距离为：=故选A点评：本题是基础题，考查球的内接多面体的知识，能够正确推出四棱锥的一条侧棱垂直底面的一个顶点，最长的侧棱就是直径是本题的关键，考查逻辑推理能力，计算能力．18．二面角l αβ--为60°，A 、B 是棱l 上的两点，AC 、BD 分别在半平面,αβ内，AC l ⊥，BD l ⊥，且AB ＝AC ＝a ，BD ＝2a ，则CD 的长为( )A ．2aB ．5aC ．aD ．3a【答案】A【解析】试题分析：根据异面直线上两点间的距离公式2222cos EF d m n mn θ=++± ，对于本题中，d a =，m a =，2n =，60θ=，故()222222cos 602CD a a a a a a =++-⋅⋅⋅=．考点：异面直线上两点间距离,空间想象能力．19．长方体的表面积是24，所有棱长的和是24，则对角线的长是（）．Ａ．14 B ．4 C ．32 D ．23【答案】B【解析】试题分析：设出长方体的长、宽、高，表示出长方体的全面积，十二条棱长度之和，然后可得对角线的长度．考点：长方体的结构特征，面积和棱长的关系.20．已知棱长为l 的正方体1111ABCD A B C D -中，E ，F ，M 分别是AB 、AD 、1AA 的中点，又P 、Q 分别在线段11A B 11、A D 上,且11A P=A Q=x,0<x<1，设面MEF 面MPQ=l ，则下列结论中不成立的是( )A ．//l 面ABCDB ．l ⊥ACC ．面MEF 与面MPQ 不垂直D ．当x 变化时，l 不是定直线【答案】D【解析】试题分析：解：连结1111,,,AC BD AC B D ,,AC BD 交于点O 1111,AC B D 交于点1O由正方体的性质知，11111111////,,BD B D AC AC AC BD AC B D ⊥⊥，因为,E F 是,AD AB 的中点，所以//EF BD因为11A P A Q =,所以11//PQ B D所以//PQ EF ,所以//PQ 平面MEF ,//EF 平面MPQ , 由MEF 面MPQ=l ，EF ⊂ 平面MEF ，所以//EF l ，而EF ⊂平面ABCD ,l ⊂/平面ABCD , 所以，//l 面ABCD ，所以选项A 正确；由AC BD ⊥，//EF BD 得EF AC ⊥而//EF l ，所以l ⊥AC ，所以选项B 正确；连111,,MB MD O M ,则11//,O M AC 而1111,//,//AC A B AC BD BD EF A B MF ⊥⊥，所以，11,O M EF O M MF ⊥⊥,所以1O M ⊥平面MEF ，过直线l 与平面MEF 垂直的平面只能有一个，所以面MEF 与面MPQ 不垂直，所以选项C 是正确的；因为//EF l ，M 是定点，过直线外一点有且只有一条直线与已知直线平行，所以直线l 是唯一的，故选项D 不正确．考点：1、直线平面的位置关系；2、直线与直线，直线与平面，平面与平面的平行与垂直的判定及性质．21．如图，等边三角形ABC 的中线AF 与中位线DE 相交于G ，已知ED A '∆是△ADE 绕DE 旋转过程中的一个图形，下列命题中，错误的是( )A ．动点A '在平面ABC 上的射影在线段AF 上B ．恒有平面GF A '⊥平面BCDEC ．三棱锥EFD A -'的体积有最大值D ．异面直线E A '与BD 不可能垂直【答案】D【解析】试题分析：由于',A G DE FG DE ⊥⊥．所以DE ⊥平面'A FG ．经过点'A 作平面ABC 的垂线垂足在AF上．所以A 选项正确．由A 可知B 选项正确．当平面'A DE 垂直于平面BCDE 时，三棱锥EFD A -'的体积最大，所以C 正确．因为BD EF ，设2AC a =．所以'EF A E a ==，当'2A F a =时，32'(')2a A G GF A G GF a <+==．所以异面直线E A '与BD 可能垂直．所以D 选项不正确．考点：1．线面位置关系．2．面面的位置关系．3．体积公式．4．异面直线所成的角．5．空间想象力．22．已知棱长为l 的正方体1111ABCD A B C D -中，E ，F ，M 分别是AB 、AD 、1AA 的中点，又P 、Q 分别在线段11A B 11、A D 上,且11A P=A Q=x,0<x<1，设面MEF 面MPQ=l ，则下列结论中不成立的是( )A ．//l 面ABCDB ．l ⊥ACC ．面MEF 与面MPQ 不垂直D ．当x 变化时，l 不是定直线【答案】D【解析】试题分析：解：连结1111,,,AC BD AC B D ,,AC BD 交于点O 1111,AC B D 交于点1O由正方体的性质知，11111111////,,BD B D AC AC AC BD AC B D ⊥⊥，因为,E F 是,AD AB 的中点，所以//EF BD因为11A P A Q =,所以11//PQ B D所以//PQ EF ,所以//PQ 平面MEF ,//EF 平面MPQ ,由MEF 面MPQ=l ，EF ⊂ 平面MEF ，所以//EF l ，而EF ⊂平面ABCD ,l ⊂/平面ABCD , 所以，//l 面ABCD ，所以选项A 正确；由AC BD ⊥，//EF BD 得EF AC ⊥而//EF l ，所以l ⊥AC ，所以选项B 正确；连111,,MB MD O M ,则11//,O M AC 而1111,//,//AC A B AC BD BD EF A B MF ⊥⊥，所以，11,O M EF O M MF ⊥⊥,所以1O M ⊥平面MEF ，过直线l 与平面MEF 垂直的平面只能有一个，所以面MEF与面MPQ不垂直，所以选项C是正确的；EF l，M是定点，过直线外一点有且只有一条直线与已知直线平行，所以直线l是唯一的，故选因为//项D不正确．考点：1、直线平面的位置关系；2、直线与直线，直线与平面，平面与平面的平行与垂直的判定及性质．23．把四个半径都是1的球中的三个放在桌面上，使它两两外切，然后在它们上面放上第四个球，使它与前三个都相切，求第四个球的最高点与桌面的距离（）A．B．C．D．3【答案】A【解析】由题意，四球心组成棱长为2的正四面体的四个顶点，则正四面体的高．而第四个球的最高点到第四个球的球心距离为求的半径1，且三个球心到桌面的距离都为1，故第四个球的最高点与桌面的距离为，选A．24．如图所示，四边形ABCD为正方形，QA⊥平面ABCD，PD∥QA，QA＝AB＝PD.则棱锥Q－ABCD的体积与棱锥P－DCQ的体积的比值是（）A. 2:1B. 1:1C. 1:2D. 1:3【答案】C。

(完整word版)高中数学立体几何专项练习

立体几何简答题练习1、正方形ABCD与正方形ABEF所在平面相交于AB,在AE、BD上各有一点P、Q,且AP=DQ。

求证:PQ∥平面BCE.（用两种方法证明）2、如图所示,P是平行四边形ABCD所在平面外一点,E、F分别在PA、BD上,且PE:EA=BF:FD,求证:EF∥平面PBC.3、如图，E，F，G，H分别是正方体ABCD-A1B1C1D1的棱BC，CC1，C1D1，AA1的中点。

求证：（1）EG∥平面BB1D1 D；（2）平面BDF∥平面B1D1 H．4、如图所示，已知P 是平行四边形ABCD 所在平面外一点，M 、N 分别为AB 、PC 的中点，平面PAD ∩平面PBC ＝l. (1)求证：l ∥BC ；(2)MN 与平面PAD 是否平行？试证明你的结论。

5、如图，在四棱锥S-ABCD 中，底面ABCD 是正方形，SA ⊥底面ABCD ，SA=SB ，点M 是SD 的中点，AN ⊥SC ，且交SC 于点N 。

（1）求证：SB ∥平面ACM ；（2）求证：平面SAC ⊥平面AMN ；（3）求二面角D-AC-M 的余弦值。

6、如图,在四棱锥P-ABCD 中,底面ABCD 是边长为2的正方形,侧面PAD ⊥底面ABCD,且PA=PD=22AD,E 、F 分别为PC 、BD 的中点. 求证:(1) 求证:EF ∥平面PAD; (2) 求证:平面PAB ⊥平面PDC;(3) 在线段AB 上是否存在点G,使得二面角C-PD-G 的余弦值为31?说明理由.7、如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,∠DAB=60°,AB=2CD=2,M是线段AB的中点。

(1)求证:C1M∥平面A1ADD1;(2)若CD1垂直于平面ABCD且CD1=3,求平面C1D1M和平面ABCD所成的角(锐角)的余弦值。

8、如图，在四棱锥P﹣ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，E是PC的中点．（1）证明：PA∥平面EDB；（2）证明：BC⊥DE．9、三棱柱ABC﹣A1B1C1中，侧棱与底面垂直，∠ABC=90°，AB=BC=BB1=2，M，N分别是AB，A1C的中点．（Ⅰ）求证：MN||平面BCC1B1；（Ⅰ）求证：平面AMN⊥平面A1B1C．10、如图，在三棱锥P﹣ABC中，PA⊥PC，AB=PB，E，F分别是PA，AC的中点．求证：（1）EF∥平面PBC；（2）平面BEF⊥平面PAB．11、如图所示，四棱锥P﹣ABCD中，底面ABCD是矩形，PA⊥平面ABCD，点M，N分别是AB，PC的中点，且PA=AD（1）求证：MN∥平面PAD（2）求证：平面PMC⊥平面PCD．12、如图，在直三棱柱ABC﹣A1B1C1中，BC⊥AC，D，E分别是AB，AC的中点．（1）求证：B1C1∥平面A1DE；（2）求证：平面A1DE⊥平面ACC1A1．8、如图所示，P是四边形ABCD所在平面外的一点，四边形ABCD是∠DAB=60°且边长为a的菱形.△PAD为正三角形，其所在平面垂直于底面ABCD.若G为AD 边的中点，求证：平面PBG⊥平面PAD；9、如图所示,在四棱柱P-ABCD中,底面ABCD是边长为a菱形,且∠DAB=60°,侧面PAD为正三角形,其所在平面垂直于底面ABCD。

大题立体几何(精选30题)(学生版)

大题立体几何1(2024·黑龙江·二模)如图，已知正三棱柱ABC-A1B1C1的侧棱长和底面边长均为2，M是BC的中点，N是AB1的中点，P是B1C1的中点．(1)证明：MN⎳平面A1CP；(2)求点P到直线MN的距离．2(2024·安徽合肥·二模)如图，在四棱锥P-ABCD中，底面ABCD是边长为2的菱形，∠BAD= 60°,M是侧棱PC的中点，侧面PAD为正三角形，侧面PAD⊥底面ABCD．(1)求三棱锥M-ABC的体积；(2)求AM与平面PBC所成角的正弦值．3(2023·福建福州·模拟预测)如图，在三棱柱ABC-A1B1C1中，平面AA1C1C⊥平面ABC,AB= AC=BC=AA1=2，A1B=6．(1)设D为AC中点，证明：AC⊥平面A1DB；(2)求平面A1AB1与平面ACC1A1夹角的余弦值．4(2024·山西晋中·三模)如图，在六面体ABCDE中，BC=BD=6，EC⊥ED，且EC=ED= 2，AB平行于平面CDE，AE平行于平面BCD，AE⊥CD.(1)证明：平面ABE⊥平面CDE；(2)若点A到直线CD的距离为22，F为棱AE的中点，求平面BDF与平面BCD夹角的余弦值．5(2024·辽宁·二模)棱长均为2的斜三棱柱ABC-A1B1C1中，A1在平面ABC内的射影O在棱AC的中点处，P为棱A1B1(包含端点)上的动点．(1)求点P到平面ABC1的距离；(2)若AP⊥平面α，求直线BC1与平面α所成角的正弦值的取值范围．6(2024·重庆·模拟预测)在如图所示的四棱锥P-ABCD中，已知AB∥CD，∠BAD=90°，CD= 2AB，△PAB是正三角形，点M在侧棱PB上且使得PD⎳平面AMC．(1)证明：PM=2BM；(2)若侧面PAB⊥底面ABCD，CM与底面ABCD所成角的正切值为311，求二面角P-AC-B的余弦值．7(2024·安徽·模拟预测)2023年12月19日至20日，中央农村工作会议在北京召开，习近平主席对“三农”工作作出指示．某地区为响应习近平主席的号召，积极发展特色农业，建设蔬菜大棚．如图所示的七面体ABG-CDEHF是一个放置在地面上的蔬菜大棚钢架，四边形ABCD是矩形，AB=8m，AD=4m，ED=CF=1m，且ED，CF都垂直于平面ABCD，GA=GB=5m，HE=HF，平面ABG⊥平面ABCD．(1)求点H到平面ABCD的距离；(2)求平面BFHG与平面AGHE所成锐二面角的余弦值．8(2024·重庆·模拟预测)如图，ACDE为菱形，AC=BC=2，∠ACB=120°，平面ACDE⊥平面ABC，点F在AB上，且AF=2FB，M，N分别在直线CD，AB上．(1)求证：CF⊥平面ACDE；(2)把与两条异面直线都垂直且相交的直线叫做这两条异面直线的公垂线，若∠EAC=60°，MN为直线CD，AB的公垂线，求ANAF的值；(3)记直线BE与平面ABC所成角为α，若tanα>217，求平面BCD与平面CFD所成角余弦值的范围．9(2024·安徽·二模)将正方形ABCD 绕直线AB 逆时针旋转90°，使得CD 到EF 的位置，得到如图所示的几何体．(1)求证：平面ACF ⊥平面BDE ；(2)点M 为DF 上一点，若二面角C -AM -E 的余弦值为13，求∠MAD ．10(2024·安徽黄山·二模)如图，已知AB 为圆台下底面圆O 1的直径，C 是圆O 1上异于A ,B 的点，D 是圆台上底面圆O 2上的点，且平面DAC ⊥平面ABC ，DA =DC =AC =2，BC =4，E 是CD 的中点，BF =2FD ．(1)证明：DO 2⎳BC ；(2)求直线DB 与平面AEF 所成角的正弦值.11(2024·黑龙江哈尔滨·一模)正四棱台ABCD -A 1B 1C 1D 1的下底面边长为22，A 1B 1=12AB ，M 为BC 中点，已知点P 满足AP =1-λ AB +12λ⋅AD +λAA 1 ，其中λ∈0,1 ．(1)求证D 1P ⊥AC ；(2)已知平面AMC 1与平面ABCD 所成角的余弦值为37，当λ=23时，求直线DP 与平面AMC 1所成角的正弦值．12(2024·辽宁·三模)如图，在三棱柱ABC -A 1B 1C 1中，侧面ACC 1A 1⊥底面ABC ,AC =AA 1=2，AB =1,BC =3，点E 为线段AC 的中点.(1)求证：AB 1∥平面BEC 1；(2)若∠A 1AC =π3，求二面角A -BE -C 1的余弦值.13(2024·广东广州·一模)如图，在四棱锥P-ABCD中，底面ABCD是边长为2的菱形，△DCP是等边三角形，∠DCB=∠PCB=π4，点M，N分别为DP和AB的中点.(1)求证：MN⎳平面PBC；(2)求证：平面PBC⊥平面ABCD；(3)求CM与平面PAD所成角的正弦值.14(2024·广东梅州·二模)如图，在四棱锥P-ABCD中，平面PAD⊥平面ABCD，底面ABCD 为直角梯形，△PAD为等边三角形，AD⎳BC，AD⊥AB，AD=AB=2BC=2．(1)求证：AD⊥PC；(2)点N在棱PC上运动，求△ADN面积的最小值；(3)点M为PB的中点，在棱PC上找一点Q，使得AM⎳平面BDQ，求PQQC的值．15(2024·广东广州·模拟预测)如图所示，圆台O1O2的轴截面A1ACC1为等腰梯形，AC=2AA1= 2A1C1=4,B为底面圆周上异于A,C的点，且AB=BC,P是线段BC的中点.(1)求证：C1P⎳平面A1AB.(2)求平面A1AB与平面C1CB夹角的余弦值.16(2024·广东深圳·二模)如图，三棱柱ABC-A1B1C1中，侧面BB1C1C⊥底面ABC，且AB= AC，A1B=A1C．(1)证明：AA1⊥平面ABC；(2)若AA1=BC=2，∠BAC=90°，求平面A1BC与平面A1BC1夹角的余弦值．17(2024·河北保定·二模)如图，在四棱锥P -ABCD 中，平面PCD 内存在一条直线EF 与AB 平行，PA ⊥平面ABCD ，直线PC 与平面ABCD 所成的角的正切值为32，PA =BC =23，CD =2AB =4.(1)证明：四边形ABCD 是直角梯形.(2)若点E 满足PE =2ED ，求二面角P -EF -B 的正弦值.18(2024·湖南衡阳·模拟预测)如图，在圆锥PO 中，P 是圆锥的顶点，O 是圆锥底面圆的圆心，AC 是圆锥底面圆的直径，等边三角形ABD 是圆锥底面圆O 的内接三角形，E 是圆锥母线PC 的中点，PO =6,AC =4.(1)求证：平面BED ⊥平面ABD ；(2)设点M 在线段PO 上，且OM =2，求直线DM 与平面ABE 所成角的正弦值.19(2024·湖南岳阳·三模)已知四棱锥P -ABCD 的底面ABCD 是边长为4的菱形，∠DAB =60°，PA =PC ，PB =PD =210，M 是线段PC 上的点，且PC =4MC ．(1)证明：PC ⊥平面BDM ；(2)点E 在直线DM 上，求BE 与平面ABCD 所成角的最大值．20(2024·湖南·二模)如图，直四棱柱ABCD -A 1B 1C 1D 1的底面是边长为2的菱形，∠ABC =60°,BD 1⊥平面A 1C 1D .(1)求四棱柱ABCD -A 1B 1C 1D 1的体积；(2)设点D 1关于平面A 1C 1D 的对称点为E ，点E 和点C 1关于平面α对称(E 和α未在图中标出)，求平面A 1C 1D 与平面α所成锐二面角的大小.21(2024·山东济南·二模)如图，在四棱锥P-ABCD中，四边形ABCD为直角梯形，AB∥CD，∠DAB=∠PCB=60°,CD=1,AB=3,PC=23，平面PCB⊥平面ABCD，F为线段BC的中点，E为线段PF上一点.(1)证明：PF⊥AD；(2)当EF为何值时，直线BE与平面PAD夹角的正弦值为74.22(2024·山东潍坊·二模)如图1，在平行四边形ABCD中，AB=2BC=4，∠ABC=60°，E为CD 的中点，将△ADE沿AE折起，连结BD，CD，且BD=4，如图2．(1)求证：图2中的平面ADE⊥平面ABCE；(2)在图2中，若点F在棱BD上，直线AF与平面ABCE所成的角的正弦值为3010，求点F到平面DEC 的距离．23(2024·福建·模拟预测)如图，在三棱锥P-ABC中，PA⊥PB,AB⊥BC,AB=3,BC=6，已知二面角P-AB-C的大小为θ，∠PAB=θ.(1)求点P到平面ABC的距离；(2)当三棱锥P-ABC的体积取得最大值时，求：(Ⅰ)二面角P-AB-C的余弦值；(Ⅱ)直线PC与平面PAB所成角.24(2024·浙江杭州·二模)如图，在多面体ABCDPQ中，底面ABCD是平行四边形，∠DAB=60°, BC=2PQ=4AB=4,M为BC的中点，PQ∥BC,PD⊥DC,QB⊥MD．(1)证明：∠ABQ=90°；(2)若多面体ABCDPQ的体积为152，求平面PCD与平面QAB夹角的余弦值．25(2024·浙江嘉兴·二模)在如图所示的几何体中，四边形ABCD为平行四边形，PA⊥平面ABCD,PA∥QD，BC=2AB=2PA=2,∠ABC=60°.(1)证明：平面PCD⊥平面PAC；(2)若PQ=22，求平面PCQ与平面DCQ夹角的余弦值.26(2024·浙江绍兴·二模)如图，在三棱锥P-ABC中，AB=4，AC=2，∠CAB=60°，BC⊥AP.(1)证明：平面ACP⊥平面ABC；(2)若PA=2，PB=4，求二面角P-AB-C的平面角的正切值.27(2024·河北沧州·一模)如图，在正三棱锥A -BCD 中，BC =CD =BD =4，点P 满足AP =λAC ，λ∈(0,1)，过点P 作平面α分别与棱AB ，BD ，CD 交于Q ，S ，T 三点，且AD ⎳α，BC ⎳α.(1)证明：∀λ∈(0,1)，四边形PQST 总是矩形；(2)若AC =4，求四棱锥C -PQST 体积的最大值.28(2024·湖北·二模)如图1．在菱形ABCD 中，∠ABC =120°，AB =4，AE =λAD ，AF =λAB (0<λ<1)，沿EF 将△AEF 向上折起得到棱锥P -BCDEP ．如图2所示，设二面角P -EF -B 的平面角为θ．(1)当λ为何值时，三棱锥P -BCD 和四棱锥P -BDEF 的体积之比为95(2)当θ为何值时，∀λ∈0,1 ，平面PEF 与平面PFB 的夹角φ的余弦值为5529(2024·湖北·模拟预测)空间中有一个平面α和两条直线m ，n ，其中m ，n 与α的交点分别为A ，B ，AB =1，设直线m 与n 之间的夹角为π3，(1)如图1，若直线m ，n 交于点C ，求点C 到平面α距离的最大值；(2)如图2，若直线m ，n 互为异面直线，直线m 上一点P 和直线n 上一点Q 满足PQ ⎳α，PQ ⊥n 且PQ ⊥m ，(i )求直线m ，n 与平面α的夹角之和；(ii )设PQ =d 0<d <1 ，求点P 到平面α距离的最大值关于d 的函数f d ．30(2024·浙江绍兴·模拟预测)如图所示，四棱台ABCD -A 1B 1C 1D 1，底面ABCD 为一个菱形，且∠BAD =120°. 底面与顶面的对角线交点分别为O ，O 1. AB =2A 1B 1=2，BB 1=DD 1=392，AA 1与底面夹角余弦值为3737.(1)证明：OO 1⊥平面ABCD ；(2)现将顶面绕OO 1旋转θ角，旋转方向为自上而下看的逆时针方向. 此时使得底面与DC 1的夹角正弦值为64343，此时求θ的值(θ<90°)；(3)求旋转后AA 1与BB 1的夹角余弦值.。

高三精选立体几何大题30题(含详细解答)

A BC第1题图ABCD第1题图立体几何大题1．如下图，一个等腰直角三角形的硬纸片ABC中，∠ACB＝90°，AC＝4cm，CD是斜边上的高沿CD 把△ABC折成直二面角．（1）如果你手中只有一把能度量长度的直尺，应该如何确定A，B的位置，使二面角A－CD－B是直二面角？证明你的结论．（2）试在平面ABC上确定一个P，使DP与平面ABC内任意一条直线都垂直，证明你的结论．（3）如果在折成的三棱锥内有一个小球，求出小球半径的最大值．2．如图，已知正四棱柱ABCD—A1B1C1D1的底面边长为3，侧棱长为4，连结A1B过A作AF⊥A1B垂足为F，且AF的延长线交B1B于E。

（Ⅰ）求证：D1B⊥平面AEC；（Ⅱ）求三棱锥B—AEC的体积；（Ⅲ）求二面角B—AE—C的大小的正弦值.3．如图，正三棱柱ABC—A1B1C1的底面边长为1，点M在BC上，△AMC1是以M为直角顶点的等腰直角三角形.（I）求证：点M为BC的中点；（Ⅱ）求点B到平面AMC1的距离；（Ⅲ）求二面角M—AC1—B 的正切值. 4．如图，已知多面体ABCDE中，AB⊥平面ACD，DE⊥平面ACD，三角形ACD是正三角形，且AD=DE=2，AB=1，F是CD的中点．（Ⅰ）求证：AF∥平面BCE；（Ⅱ）求多面体ABCDE的体积；（Ⅲ）求二面角C-BE-D 的正切值．5．已知：ABCD是矩形，设PA=a，PA⊥平面ABCD.M、N分别是AB、PC的中点.（Ⅰ）求证：MN⊥AB；（Ⅱ）若PD=AB，且平面MND⊥平面PCD，求二面角P—CD—A的大小；（Ⅲ）在（Ⅱ）的条件下，求三棱锥D—AMN的体积.6．在正方体ABCD—A1B1C1D1中，P、M、N分别为棱DD1、AB、BC的中点。

（I）求二面角B1—MN—B的正切值；（II）证明：PB⊥平面MNB1；（III）画出一个正方体表面展开图，使其满足“有4个正方形面相连成一个长方形”的条件，并求出展开图中P、B两点间的距离。

高中数学立体几何经典题型专题训练试题(含答案)

高中数学立体几何经典题型专题训练试题姓名班级学号得分说明：１、本试卷包括第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

满分100分。

考试时间120分钟。

２、考生请将第Ⅰ卷选择题的正确选项填在答题框内，第Ⅱ卷直接答在试卷上。

考试结束后，只收第Ⅱ卷第Ⅰ卷（选择题）评卷人得　分一．单选题（共10小题，每题3分，共30分）1、如图，在正方体中ABCD-A1B1C1D1，M为BC的中点，点N在四边形CDD1C1及其内部运动．⊥1C1，则N点的轨迹为（）若MN AA．线段B．圆的一部分C．椭圆的一部分D．双曲线的一部分2、如图，正方体ABCD-A1B1C1D1的棱长为1，过点A作平面A1BD的垂线，垂足为H，则以下命题中，错误的是（）A．点H是△A1BD的垂心B．直线AH与CD1的成角为900C．AH的延长线经过点C1D．直线AH与BB1的成角为4503、如图，正方体ABCD-A1B1C1D1中，点P为线段AD1上一动点，点Q为底面ABCD内（含边界）一动点，M为PQ的中点，点M构成的点集是一个空间几何体，则该几何体为（　）A．棱柱B．棱锥C．棱台D．球4．下列说法中正确的是（）A．棱柱的面中，至少有两个面互相平行B．棱柱中两个互相平行的平面一定是棱柱的底面C．棱柱中一条侧棱就是棱柱的高D．棱柱的侧面一定是平行四边形，但它的底面一定不是平行四边形5．用一个平面去截一个正方体，所得截面不可能是（1）钝角三角形；（2）直角三角形；（3）菱形；（4）正五边形；（5）正六边形．下述选项正确的是（）A．（1）（2）（5）B．（1）（2）（4）C．（2）（3）（4）D．（3）（4）（5）6、如图，正方体ABCD-A1B1C1D1的棱长为1，线段B1D1上有两个动点E、F，且EF=，则下列结论中错误的是（）⊥A．AC BEB．A1C⊥平面AEFC．三棱锥A-BEF的体积为定值D．异面直线AE、BF所成的角为定值7．已知一个正六棱锥的体积为12，底面边长为2，则它的侧棱长为（）A．4B．C．D．28．一正四棱锥的高为2，侧棱与底面所成的角为45°，则这一正四棱锥的斜高等于（）A．2B．C．2D．29、如图，正方体ABCD-A1B1C1D1中，O为底面ABCD的中心，M为棱BB1的中点，则下列结论中错误的是（）A．D1O∥平面A1BC1B．D1O⊥平面AMCC．异面直线BC1与AC所成的角等于60°D．点B到平面AMC的距离为10．如图，E为正方体的棱AA1的中点，F为棱AB上的一点，且∠C1EF=90°，则AF：FB=（）A．1：1B．1：2C．1：3D．1：4第Ⅱ卷（非选择题）评卷人得　分二．填空题（共14小题，每题3分，共42分）11、正方体ABCD-A1B1C1D1中，M，N分别是AA1和BB1的中点，G是BC上一点，使⊥，则∠D1NG=______．C1N MG12、已知如图，正方体ABCD-A1B1C1D1的棱长为1，E，F分别为棱DD1，AB上的点（不含顶点）．则下列说法正确的是______．①A1C⊥平面B1EF；②△B1EF在侧面上的正投影是面积为定值的三角形；③在平面A1B1C1D1内总存在与平面B1EF平行的直线；④平面B1EF与平面ABCD所成的二面角（锐角）的大小与点E位置有关，与点F位置无关；⑤当E，F分别为中点时，平面B1EF与棱AD交于点P，则三棱锥P-DEF的体积为．⊥，∠BAC=θ（0＜θ≤），且13、如图，三棱锥A-BCD中，AB AD⊥，AC ADAB=AC=AD=2，E、F分别为AC、BD的中点，则EF的最大值为______．14、如图，在正方体的一角上截取三棱锥P-ABC，PO为棱锥的高，记，，那么M，N的大小关系是______．15．若空间四边形ABCD的两条对角线AC，BD的长分别为4，6，过AB的中点E且平行BD，AC的截面四边形的周长为______．⊥1D则EF和BD1的关系是______．16、正方体ABCD-A1B1C1D1中，EF AC⊥，EF A17、已知正方体AC1的棱长为1，点P是面AA1D1D的中心，点Q是面A1B1C1D1的对角线B1D1上一点，且PQ∥平面AA1B1B，则线段PQ的长为______．18、如图，正方体ABCD-A1B1C1D1中，E，F分别为棱DD1，AB上的点．已知下列判断：①A1C⊥平面B1EF；②△B1EF在侧面BCC1B1上的正投影是面积为定值的三角形；③在平面A1B1C1D1内总存在与平面B1EF平行的直线；④平面B1EF与平面ABCD所成的二面角（锐角）的大小与点E的位置有关，与点F的位置无关．其中正确结论的序号为______（写出所有正确结论的序号）．19、如图，正方体ABCD-A1B1C1D1的棱长为4，E，F分别是棱CD、C1D1的中点，长为2的线段MN的一个端点M在线段EF上运动，另一个端点N在底面A1B1C1D1上运动，则线段MN 的中点P的轨迹（曲面）与二面角D-C1D1-B1所围成的几何体的体积为______．∈1，且AM=BN，有以下四个结论：20、如图，正方体ABCD-A1B1C1D1中，点M AB∈1，N BC⊥；①AA1MN∥；②A1C1MN③MN与面A1B1C1D1成0°角；④MN与A1C1是异面直线．其中正确结论的序号是______．21、在正方体ABCD-A1B1C1D1中，过对角线BD1的一个平面交AA1于点E，交CC1于F，①四边形BFD1E一定是平行四边形②四边形BFD1E有可能是正方形③四边形BFD1E在底面ABCD内的投影一定是正方形④四边形BFD1E点有可能垂直于平面BB1D以上结论正确的为______（写出所有正确结论的编号）22、如图，正方体ABCD-A1B1C1D1中，对角线BD1与过A1、D、C1的平面交于点M，则=______．23．设A是自然数集的一个非空子集，如果k2A∉，且A，那么k是A的一个“酷元”，⊆，且集合M中的两个元素都是“酷元”那么这样的结给定S={0，1，2，3，4，5}，设M S合M有______个．24、如图，AC为圆O的直径，B为圆周上不与A、C重合的点，SA⊥圆O所在的平面，连接SB、SC、AB、BC，则图中直角三角形的个数是______．评卷人得　分三．简答题（共28分）25、四棱锥P-ABCD中，底面ABCD为菱形，且∠DAB=60°，点P为平面ABCD所在平面外的⊥．一点，若△PAD为等边三角形，求证：PB AD26、如图，设三棱锥S-ABC的三个侧棱与底面ABC所成的角都是60°，又∠BAC=60°，且⊥．SA BC（1）求证：S-ABC为正三棱锥；（2）已知SA=a，求S-ABC的全面积．27、如图，E、F、G、H分别是空间四边形ABCD四边上的中点．（1）若BD=2，AC=6，则EG2+HF2等于多少？（2）若AC与BD成30°的角，且AC=6，BD=4，则四边形EFGH的面积等于多少？28、已知三棱锥S-ABC的三条侧棱SA、SB、SC两两互相垂直且长度分别为a、b、c，设O 为S在底面ABC上的射影．求证：（1）O为△ABC的垂心；（2）O在△ABC内；（3）设SO=h，则++=．29．已知正三棱锥的高为1，底面边长为2，其内有一个球和该三棱锥的四个面都相切，求：（1）棱锥的全面积；（2）球的半径R．30、如图，在三棱锥D-ABC中，已知△BCD是正三角形，AB⊥平面BCD，AB=BC=a，E为BC 的中点，F在棱AC上，且AF=3FC．（1）求三棱锥D-ABC的表面积；（2）求证AC⊥平面DEF；（3）若M为BD的中点，问AC上是否存在一点N，使MN∥平面DEF？若存在，说明点N 的位置；若不存在，试说明理由．参考答案评卷人得　分一．单选题（共__小题）1、如图，在正方体中ABCD-A1B1C1D1，M为BC的中点，点N在四边形CDD1C1及其内部运动．⊥1C1，则N点的轨迹为（）若MN AA．线段B．圆的一部分C．椭圆的一部分D．双曲线的一部分答案：A解析：解：正方体中ABCD-A1B1C1D1中，M为BC的中点，点N在四边形CDD1C1及其内部运动；如图所示，取CD、C1D1的中点Q、P，连接PQ，⊥1C1；当点N在线段PQ上时，MN A因为正方体ABCD-A1B1C1D1中，⊥1D1，连接B1D1，交A1C1于点O，∴B1D1A取B1C1的中点E，连接PE，则PE B∥1D1，⊥1C1；∴PE A∥1，又CC1⊥平面A1B1C1D1，PQ CC∴PQ⊥平面A1B1C1D1，∵A1C1⊂平面A1B1C1D1，⊥1C1；∴PQ A且PQ∩PE=P，∴A1C1⊥平面PQME，PQ⊂平面PQME，⊥；∴A1C1PQ∴N点的轨迹为线段PQ．故选：A．2、如图，正方体ABCD-A1B1C1D1的棱长为1，过点A作平面A1BD的垂线，垂足为H，则以下命题中，错误的是（）A．点H是△A1BD的垂心B．直线AH与CD1的成角为900C．AH的延长线经过点C1D．直线AH与BB1的成角为450答案：D解析：解：由ABCD-A1B1C1D1是正方体，得A-A1BD是一个正三棱锥，因此A点在平面A1BD上的射影H是三角形A1BD的中心，故A正确；⊥1B，又CD1A∥1B，可得直线AH与CD1的成角为90°，故B正确；∵AH⊥面A1BD，∴AH A连接AC1，由三垂线定理及线面垂直的判定可得AC1⊥面A1DB，再由过一点与已知平面垂直的直线有且只有一条可得AH与AC1重合，可得C正确；直线AH与BB1所成的角，即为AH与AA1所成的角，设为θ，由正方体棱长为1，可得正三棱锥的底面边长为，从而求得AH=，则cos，∴D错误．故选：D．3、如图，正方体ABCD-A1B1C1D1中，点P为线段AD1上一动点，点Q为底面ABCD内（含边界）一动点，M为PQ的中点，点M构成的点集是一个空间几何体，则该几何体为（　）A．棱柱B．棱锥C．棱台D．球答案：A解析：解：∵Q点不能超过边界，若P点与A点重合，设AB中点E、AD中点F，移动Q点，则此时M点的轨迹为：以AE、AF为邻边的正方形；下面把P点从A点向上沿线段AD1移动，在移动过程中可得M点轨迹为正方形，…，最后当P点与D1点重合时，得到最后一个正方形，故所得几何体为棱柱，故选：A4．下列说法中正确的是（）A．棱柱的面中，至少有两个面互相平行B．棱柱中两个互相平行的平面一定是棱柱的底面C．棱柱中一条侧棱就是棱柱的高D．棱柱的侧面一定是平行四边形，但它的底面一定不是平行四边形答案：A解析：解：棱柱的定义是，有两个面互相平行，其余各面都是四边形，相邻的公共边互相平行，有这些面围成的几何体是棱柱；可以判断A正确；B不正确，例如正六棱柱的相对侧面；C 不正确，只有直棱柱满足C的条件；D不正确，例如长方体．故选A5．用一个平面去截一个正方体，所得截面不可能是（1）钝角三角形；（2）直角三角形；（3）菱形；（4）正五边形；（5）正六边形．下述选项正确的是（）A．（1）（2）（5）B．（1）（2）（4）C．（2）（3）（4）D．（3）（4）（5）答案：B解析：解：如图所示截面为三角形ABC，OA=a，OB=b，OC=c，AC2=a2+c2，AB2=a2+b2，BC2=b2+c2∠=＞0，∴cos CAB=∴∠CAB为锐角，同理∠ACB与∠ABC也为锐角，即△ABC为锐角三角形；如右图，取相对棱的中点，得到的四边形是菱形；正方体有六个面，用平面去截正方体时最多与六个面相交得六边形，如图为正六边形；经过正方体的一个顶点去切就可得到5边形．但此时不可能是正五边形．故不可能是（1）（2）（4）．故选：B．6、如图，正方体ABCD-A1B1C1D1的棱长为1，线段B1D1上有两个动点E、F，且EF=，则下列结论中错误的是（）⊥A．AC BEB．A1C⊥平面AEFC．三棱锥A-BEF的体积为定值D．异面直线AE、BF所成的角为定值答案：D解析：解：∵AC⊥平面BB1D1D，又BE⊂平面BB1D1D，⊥．故A正确．∴AC BE∵EF垂直于直线AB1，AD1，∴A1C⊥平面AEF．故B正确．C中由于点B到直线B1D1的距离不变，故△BEF的面积为定值．又点A到平面BEF的距离为，故V A-BEF为定值．C正确当点E在D1处，F为D1B1的中点时，异面直线AE，BF所成的角是∠FBC1，当E在上底面的中心时，F在C1的位置，异面直线AE，BF所成的角是∠EAA1显然两个角不相等，D不正确．故选D．7．已知一个正六棱锥的体积为12，底面边长为2，则它的侧棱长为（）A．4B．C．D．2答案：A解析：解：由于正六棱锥可知底面是六个正三角形组成，∴底面积S=6×=6，∴体积V==12，∴h=，夺直角三角形SOB中，侧棱长为SB=．故选A．8．一正四棱锥的高为2，侧棱与底面所成的角为45°，则这一正四棱锥的斜高等于（）A．2B．C．2D．2答案：C解析：解：如图PO⊥底面ABCD，连接OA，取AD的中点E，连接OE，PE，则PE为斜高．∠PAO为侧棱与底面所成的角，且为45°，在直角△PAO中，PO=2，AO=2，PA=4，在直角△AEO中，AE=2，故在直角△PEA中，PE==2．故选C．9、如图，正方体ABCD-A1B1C1D1中，O为底面ABCD的中心，M为棱BB1的中点，则下列结论中错误的是（）A．D1O∥平面A1BC1B．D1O⊥平面AMCC．异面直线BC1与AC所成的角等于60°D．点B到平面AMC的距离为答案：D解析：解：如图，∥，连接B1D1，交A1C1于N，则可证明OD1BN由OD1⊄面A1BC1，BN⊂面A1BC1，可得D1O∥面A1BC1，A正确；⊥，由三垂线定理的逆定理可得OD1AC设正方体棱长为2，可求得OM2=3，，，⊥，由线面垂直的判定可得D1O⊥平面AMC，B正确；则，有OD1OM由正方体的面对角线相等得到△A1BC1为正三角形，即∠A1C1B=60°，∴异面直线BC1与AC所成的角等于60°，C正确；设点B到平面AMC的距离为d，正方体的棱长为2a，则，，由V B-AMC=V A-BCM，得，即，解得：d=，D错误．故选：D．10．如图，E为正方体的棱AA1的中点，F为棱AB上的一点，且∠C1EF=90°，则AF：FB=（）A．1：1B．1：2C．1：3D．1：4答案：C解析：解：解：设正方体的棱长为：2，由题意可知C1E==3，∠C1EF=90°，所以设AF=x，12+x2+C1E2=22+22+（2-x）2，解得：x=，所以AF：FB=：=1：3；故选：C．评卷人得　分二．填空题（共__小题）11、正方体ABCD-A1B1C1D1中，M，N分别是AA1和BB1的中点，G是BC上一点，使⊥，则∠D1NG=______．C1N MG答案：90°解析：解：连接MN，∵M，N分别是AA1和BB1的中点，∥1D1，由正方体的几何特征可得MN C在正方体ABCD-A1B1C1D1中，D1C1⊥平面B1C1CB∵C1N⊂平面B1C1CB⊥1N∴D1C1C⊥1N∴MN C⊥，MN∩MG=M，MD1，MG⊂平面MNG又∵C1N MG∴C1N⊥平面MNG又∵NG⊂平面MNG⊥∴C1N NG故∠D1NG=90°故答案为：90°12、已知如图，正方体ABCD-A1B1C1D1的棱长为1，E，F分别为棱DD1，AB上的点（不含顶点）．则下列说法正确的是______．①A1C⊥平面B1EF；②△B1EF在侧面上的正投影是面积为定值的三角形；③在平面A1B1C1D1内总存在与平面B1EF平行的直线；④平面B1EF与平面ABCD所成的二面角（锐角）的大小与点E位置有关，与点F位置无关；⑤当E，F分别为中点时，平面B1EF与棱AD交于点P，则三棱锥P-DEF的体积为．答案：②③⑤解析：解：对于①A1C⊥平面B1EF，不一定成立，因为A1C⊥平面AC1D，而两个平面面B1EF与面AC1D不一定平行．对于②△B 1EF 在侧面BCC 1B 1上的正投影是面积为定值的三角形，此是一个正确的结论，因为其投影三角形的一边是棱BB 1，而E 点在面上的投影到此棱BB 1的距离是定值，故正确；对于③在平面A 1B 1C 1D 1内总存在与平面B 1EF 平行的直线，此两平面相交，一个面内平行于两个平面的交线一定平行于另一个平面，此结论正确；对于④平面B 1EF 在平面ABCD 中的射影为△DFB ，面积为定值，但△B 1EF 的面积不定，故不正确；对于⑤由面面平行的性质定理可得EQ B ∥1F ，故D 1Q=，B 1Q PF ∥，故AP=，所以三棱锥P-DEF 的体积为，故正确故答案为：②③⑤．13、如图，三棱锥A-BCD 中，AB AD ⊥，AC AD ⊥，∠BAC=θ（0＜θ≤），且AB=AC=AD=2，E 、F 分别为AC 、BD 的中点，则EF 的最大值为______．答案：解析：⊥，垂足为G，连接GE，解：过F作FG AB⊥，∵AD AB∥，∴G为AB的中点，∴AD FG∴FG=1，AG=1，∵E为AC的中点，∴AE=1，∠BAC=θ，∴EG=∵AD⊥平面ABC，∴FG⊥平面ABC，△中，EF===，在Rt FGE∵0，∴EF≤．故答案是．14、如图，在正方体的一角上截取三棱锥P-ABC，PO为棱锥的高，记，，那么M，N的大小关系是______．答案：M=N解析：解：根据平面中直角三角形的勾股定理类比得，S ABC△2=S PAB△2+S PBC△2+S PAC△2①，由等体积法得，∴②，①÷②整理得M=N．故答案为：M=N．15．若空间四边形ABCD的两条对角线AC，BD的长分别为4，6，过AB的中点E且平行BD，AC的截面四边形的周长为______．答案：10解析：解：设截面四边形为EFGH，F、G、H分别是BC、CD、DA的中点，∴EF=GH=2，FG=HE=3，∴周长为2×（2+3）=10．故答案为：10．16、正方体ABCD-A1B1C1D1中，EF AC⊥，EF A⊥1D则EF和BD1的关系是______．答案：平行解析：解：法一：根据图象可知：⊥，AC∩B1C=C，⊥1D，A1D B∥1C，B1C EFEF AC⊥，EF A∥．∴EF⊥面AB1C，而BD1⊥面AB1C，即BD1EF法二：建立以D1为原点的空间直角坐标系D1-xyz，且设正方形的边长为1所以就有D1（0，0，0），B（1，1，0），A1（1，0，0），D（0，0，1），A（1，0，1），C（0，1，1）所以=（-1，0，1），=（-1，1，0），=（-1，-1，1）⊥1，所以•=-1+1=0 所以A1D BD⊥1，•=1-1=0 所以AC BD所以BD1与A1D和AC都垂直又∵EF是AC、A1D的公共垂线，∥．∴BD1EF故答案为：平行．17、已知正方体AC1的棱长为1，点P是面AA1D1D的中心，点Q是面A1B1C1D1的对角线B1D1上一点，且PQ∥平面AA1B1B，则线段PQ的长为______．答案：解析：解：∵正方体AC1的棱长为1，点P是面AA1D1D的中心，点Q是面A1B1C1D1的对角线B1D1上一点，且PQ∥平面AA1B1B，连结AD1，AB1，∴由正方体的性质，得：AD1∩A1D=P，P是AD1的中点，∥1，PQ AB∴PQ=AB1==．故答案为：．18、如图，正方体ABCD-A1B1C1D1中，E，F分别为棱DD1，AB上的点．已知下列判断：①A 1C ⊥平面B 1EF ；②△B 1EF 在侧面BCC 1B 1上的正投影是面积为定值的三角形；③在平面A 1B 1C 1D 1内总存在与平面B 1EF 平行的直线；④平面B 1EF 与平面ABCD 所成的二面角（锐角）的大小与点E 的位置有关，与点F 的位置无关．其中正确结论的序号为______（写出所有正确结论的序号）．答案：②③解析：解：若A 1C ⊥平面B 1EF ，则A 1C B ⊥1F ，由三垂线逆定理知：B 1F A ⊥1B ，又当F 与A 不重合时，B 1F 与A 1B 不垂直，∴①错误；∵E 在侧面BCC 1B 1上的投影在CC 1上，F 在侧面BCC 1B 1上的投影是B ，∴△B 1EF 在侧面BCC 1B 1上的正投影是三角形，三角形的面积S=×棱长×棱长为定值．∴②正确；设平面A 1B 1C 1D 1∩平面B 1EF=l ，∵平面A 1B 1C 1D 1内总存在与l 平行的直线，由线面平行的判定定理得与l 平行的直线，与平面B 1EF 平行，∴③正确；设E 与D 重合，F 位置变化，平面B 1EF 与平面ABCD 所成的二面角（锐角）的大小也在变化，∴④错误．故答案为：②③．19、如图，正方体ABCD-A 1B 1C 1D 1的棱长为4，E ，F 分别是棱CD 、C 1D 1的中点，长为2的线段MN 的一个端点M 在线段EF 上运动，另一个端点N 在底面A 1B 1C 1D 1上运动，则线段MN 的中点P 的轨迹（曲面）与二面角D-C 1D 1-B 1所围成的几何体的体积为______．答案：解析：解：依题意知|FP|=|MN|=1，因此点P的轨迹是以点F为球心、1为半径的球的．∴所求几何体的体积是×π×13=．故答案为：．∈1，且AM=BN，有以下四个结论：∈1，N BC20、如图，正方体ABCD-A1B1C1D1中，点M AB⊥；①AA1MN∥；②A1C1MN③MN与面A1B1C1D1成0°角；④MN与A1C1是异面直线．其中正确结论的序号是______．答案：①③解析：解：当M 为A ，N 为B ，排除②；当M 为B 1，N 为C 1，排除④．作MM′A ⊥1B 1于M′，作NN′B ⊥1C 1于N′，易证|MM′|=|NN′|，MM′NN′∥∴MN M′N′∥，由此知①③正确．故答案为：①③21、在正方体ABCD-A 1B 1C 1D 1中，过对角线BD 1的一个平面交AA 1于点E ，交CC 1于F ，①四边形BFD 1E 一定是平行四边形②四边形BFD 1E 有可能是正方形③四边形BFD 1E 在底面ABCD 内的投影一定是正方形④四边形BFD 1E 点有可能垂直于平面BB 1D以上结论正确的为______（写出所有正确结论的编号）答案：①③④解析：解：如图：①由平面BCB 1C 1∥平面ADA 1D 1，并且B 、E 、F 、D 1四点共面，∴ED 1BF ∥，同理可证，FD 1EB ∥，故四边形BFD 1E 一定是平行四边形，故①正确；②若BFD 1E 是正方形，有ED 1BE ⊥，这个与A 1D 1BE ⊥矛盾，故②错误；③由图得，BFD 1E 在底面ABCD 内的投影一定是正方形ABCD ，故③正确；④当点E 和F 分别是对应边的中点时，平面BFD 1E ⊥平面BB 1D 1，故④正确．故答案为：①③④．22、如图，正方体ABCD-A 1B 1C 1D 1中，对角线BD 1与过A 1、D 、C 1的平面交于点M ，则=______．答案：2解析：解：由正方体的性质可得：D 1B ⊥平面DA 1C 1，∴D 1M 是三棱锥D 1-A 1DC 1的高．不妨设正方体的棱长为1．∵=，∴=，解得D 1M==．∴=2．故答案为：2．∉，且A，那么k是A的一个“酷元”，23．设A是自然数集的一个非空子集，如果k2A⊆，且集合M中的两个元素都是“酷元”那么这样的结给定S={0，1，2，3，4，5}，设M S合M有______个．答案：5解析：解：∵S={0，1，2，3，4，5}，由题意可知：集合M不能含有0，1，也不能同时含有2，4故集合M可以是{2，3}、{2，5}、{3，5}、{3，4}、{4，5}，共5个故答案为：524、如图，AC为圆O的直径，B为圆周上不与A、C重合的点，SA⊥圆O所在的平面，连接SB、SC、AB、BC，则图中直角三角形的个数是______．答案：4解析：解：题题意SA⊥圆O所在的平面，AC为圆O的直径，B为圆周上不与A、C重合的点，可得出AB，BC垂直由此两个关系可以证明出CB垂直于面SAB，由此可得△ADB，△SAC，△ABC，△SBC都是直角三角形故图中直角三角形的个数是4个故答案为：4．评卷人得　分三．简答题（共__小题）25、四棱锥P-ABCD中，底面ABCD为菱形，且∠DAB=60°，点P为平面ABCD所在平面外的⊥．一点，若△PAD为等边三角形，求证：PB AD答案：证明：如图，连结BD ，取AD 的中点E ，连结PE ，BE ；从而易知△ABD 也是等边三角形，又∵△PAD 为等边三角形，∴AD PE ⊥，AD BE ⊥，又∵PE∩BE=E ；故AD ⊥平面PBE ；故AD PB ⊥．解析：证明：如图，连结BD ，取AD 的中点E ，连结PE ，BE ；从而易知△ABD 也是等边三角形，又∵△PAD 为等边三角形，∴AD PE ⊥，AD BE ⊥，又∵PE∩BE=E ；故AD ⊥平面PBE ；故AD PB ⊥．26、如图，设三棱锥S-ABC 的三个侧棱与底面ABC 所成的角都是60°，又∠BAC=60°，且SA BC ⊥．（1）求证：S-ABC 为正三棱锥；（2）已知SA=a ，求S-ABC 的全面积．答案：（1）证明：正棱锥的定义中，底面是正多边形；顶点在底面上的射影是底面的中心，两个条件缺一不可．作三棱锥S-ABC 的高SO ，O 为垂足，连接AO 并延长交BC 于D ．因为SA BC ⊥，所以AD BC ⊥．又侧棱与底面所成的角都相等，从而O 为△ABC 的外心，OD 为BC 的垂直平分线，所以AB=AC ．又∠BAC=60°，故△ABC 为正三角形，且O 为其中心．所以S-ABC 为正三棱锥．（2）解：在Rt SAO △中，由于SA=a ，∠SAO=60°，所以SO=a ，AO=a ．因O 为重心，所以AD=AO=a ，BC=2BD=2ADcot60°=a ，OD=AD=a ．在Rt SOD △中，SD 2=SO 2+OD 2=（a ）2+（a ）2=，则SD=a ．于是，（S S-ABC ）全=•（a ）2sin60°+3••a•a=a 2．解析：（1）证明：正棱锥的定义中，底面是正多边形；顶点在底面上的射影是底面的中心，两个条件缺一不可．作三棱锥S-ABC 的高SO ，O 为垂足，连接AO 并延长交BC 于D ．因为SA BC ⊥，所以AD BC ⊥．又侧棱与底面所成的角都相等，从而O 为△ABC 的外心，OD 为BC 的垂直平分线，所以AB=AC ．又∠BAC=60°，故△ABC 为正三角形，且O 为其中心．所以S-ABC 为正三棱锥．（2）解：在Rt SAO △中，由于SA=a ，∠SAO=60°，所以SO=a ，AO=a ．因O 为重心，所以AD=AO=a ，BC=2BD=2ADcot60°=a ，OD=AD=a ．在Rt SOD △中，SD 2=SO 2+OD 2=（a ）2+（a ）2=，则SD=a ．于是，（S S-ABC ）全=•（a ）2sin60°+3••a•a=a 2．27、如图，E 、F 、G 、H 分别是空间四边形ABCD 四边上的中点．（1）若BD=2，AC=6，则EG 2+HF 2等于多少？（2）若AC 与BD 成30°的角，且AC=6，BD=4，则四边形EFGH 的面积等于多少？答案：解：（1）∵E 、F 、G 、H 分别是空间四边形ABCD 四边上的中点，∴EH BD ∥，且EH=BD ；FG BD ∥，且FG=BD ；∴EH FG ∥，且EH=FG ，∴四边形EFGH 是平行四边形；又BD=2，AC=6，∴EH=BD=1，EF=AC=3，在△EFG 和△HFG 中，由余弦定理得，EG 2=EF 2+FG 2-2EF•FG•cos EFG∠=32+12-2×3×1×cos EFG∠=10-6cos EFG ∠，HF 2=HG 2+FG 2-2HG•FG•cos FGH∠=32+12-2×3×1×cos （π-EFG ∠）=10+6cos EFG ∠，∴EG 2+HF 2=20；（2）∵AC 与BD 成30°的角，且EF AC ∥，FG BD ∥，∴∠EFG=30°，又AC=6，BD=4，∴EF=AC=3，FG=BD=2；∠．∴四边形EFGH的面积为S=EF•FG•sin EFG=3×2×sin30°=3解析：解：（1）∵E、F、G、H分别是空间四边形ABCD四边上的中点，∥，且EH=BD；∴EH BDFG BD∥，且FG=BD；∥，且EH=FG，∴EH FG∴四边形EFGH是平行四边形；又BD=2，AC=6，∴EH=BD=1，EF=AC=3，在△EFG和△HFG中，由余弦定理得，∠EG2=EF2+FG2-2EF•FG•cos EFG∠=32+12-2×3×1×cos EFG∠，=10-6cos EFG∠HF2=HG2+FG2-2HG•FG•cos FGH∠）=32+12-2×3×1×cos（π-EFG=10+6cos EFG∠，∴EG2+HF2=20；（2）∵AC 与BD 成30°的角，且EF AC ∥，FG BD ∥，∴∠EFG=30°，又AC=6，BD=4，∴EF=AC=3，FG=BD=2；∴四边形EFGH 的面积为S=EF•FG•sin EFG=3×2×sin30°=3∠．28、已知三棱锥S-ABC 的三条侧棱SA 、SB 、SC 两两互相垂直且长度分别为a 、b 、c ，设O 为S 在底面ABC 上的射影．求证：（1）O 为△ABC 的垂心；（2）O 在△ABC 内；（3）设SO=h ，则++=．答案：证明：（1）∵SA SB ⊥，SA SC ⊥，∴SA ⊥平面SBC ，BC ⊂平面SBC ．∴SA BC ⊥．而AD 是SA 在平面ABC 上的射影，∴AD BC ⊥．同理可证AB CF ⊥，AC BE ⊥，故O 为△ABC 的垂心．（2）证明△ABC 为锐角三角形即可．不妨设a≥b≥c ，则底面三角形ABC 中，AB=为最大，从而∠ACB 为最大角．用余弦定理求得cos ACB=∠＞0，∴∠ACB 为锐角，△ABC 为锐角三角形．故O 在△ABC 内．（3）SB•SC=BC•SD ，故SD=，=+，又SA•SD=AD•SO ，∴===+=++=．解析：证明：（1）∵SA SB ⊥，SA SC ⊥，∴SA ⊥平面SBC ，BC ⊂平面SBC ．∴SA BC ⊥．而AD 是SA 在平面ABC 上的射影，∴AD BC ⊥．同理可证AB CF ⊥，AC BE ⊥，故O 为△ABC 的垂心．（2）证明△ABC 为锐角三角形即可．不妨设a≥b≥c ，则底面三角形ABC 中，AB=为最大，从而∠ACB 为最大角．用余弦定理求得cos ACB=∠＞0，∴∠ACB 为锐角，△ABC 为锐角三角形．故O 在△ABC 内．（3）SB•SC=BC•SD ，故SD=，=+，又SA•SD=AD•SO ，∴===+=++=．29．已知正三棱锥的高为1，底面边长为2，其内有一个球和该三棱锥的四个面都相切，求：（1）棱锥的全面积；（2）球的半径R．答案：解：（1）设正三棱锥的底面中心为H，由题意知PH=1，边长BC=2，取BC中点E，连接HE、PE，则HE=S全=3×=9⊥于点G，（2）过O作OG PE∽△，且OG=OH=R，则△POG PEH∴，∴R=解析：解：（1）设正三棱锥的底面中心为H，由题意知PH=1，边长BC=2，取BC中点E，连接HE、PE，则HE=S全=3×=9⊥于点G，（2）过O作OG PE∽△，且OG=OH=R，则△POG PEH∴，∴R=30、如图，在三棱锥D-ABC中，已知△BCD是正三角形，AB⊥平面BCD，AB=BC=a，E为BC 的中点，F在棱AC上，且AF=3FC．（1）求三棱锥D-ABC 的表面积；（2）求证AC ⊥平面DEF ；（3）若M 为BD 的中点，问AC 上是否存在一点N ，使MN ∥平面DEF ？若存在，说明点N 的位置；若不存在，试说明理由．答案：解：（1）∵AB ⊥平面BCD ，∴AB BC ⊥，AB BD ⊥．∵△BCD 是正三角形，且AB=BC=a ，∴AD=AC=．设G 为CD 的中点，则CG=，AG=．∴，，．三棱锥D-ABC 的表面积为．（2）取AC 的中点H ，∵AB=BC ，∴BH AC ⊥．∵AF=3FC ，∴F 为CH 的中点．∵E 为BC 的中点，∴EF BH ∥．则EF AC ⊥．∵△BCD 是正三角形，∴DE BC ⊥．∵AB ⊥平面BCD ，∴AB DE ⊥．∵AB∩BC=B ，∴DE ⊥平面ABC ．∴DE AC ⊥．∵DE∩EF=E ，∴AC ⊥平面DEF ．（3）存在这样的点N ，当CN=时，MN ∥平面DEF ．连CM ，设CM∩DE=O ，连OF ．由条件知，O 为△BCD 的重心，CO=CM ．∴当CF=CN 时，MN OF ∥．∴CN=．解析：解：（1）∵AB ⊥平面BCD ，∴AB BC ⊥，AB BD ⊥．∵△BCD 是正三角形，且AB=BC=a ，∴AD=AC=．设G 为CD 的中点，则CG=，AG=．∴，，．三棱锥D-ABC 的表面积为．（2）取AC 的中点H ，∵AB=BC ，∴BH AC ⊥．∵AF=3FC ，∴F 为CH 的中点．∵E 为BC 的中点，∴EF BH ∥．则EF AC ⊥．∵△BCD 是正三角形，∴DE BC ⊥．∵AB ⊥平面BCD ，∴AB DE ⊥．∵AB∩BC=B ，∴DE ⊥平面ABC ．∴DE AC ⊥．∵DE∩EF=E ，∴AC ⊥平面DEF ．（3）存在这样的点N ，当CN=时，MN ∥平面DEF ．连CM ，设CM∩DE=O ，连OF ．由条件知，O 为△BCD 的重心，CO=CM ．∴当CF=CN 时，MN OF ∥．∴CN=．。

高中数学立体几何小题100题(含答案与解析)

立体几何小题100例一、选择题1．如图，已知正方体1111ABCD A B C D -的棱长为4，点E ，F 分别是线段AB ，11C D 上的动点，点P 是上底面1111A B C D 内一动点，且满足点P 到点F 的距离等于点P 到平面11ABB A 的距离，则当点P 运动时，PE 的最小值是（）A ．5B ．4C ．42．5【答案】D 【解析】试题分析：因为点P 是上底面1111A B C D 内一动点，且点P 到点F 的距离等于点P 到平面11ABB A 的距离，所以，点P 在连接1111,A D B C 中点的连线上．为使当点P 运动时，PE 最小，须PE 所在平面平行于平面11AA D D ,2244()52PE =+=选D考点：1．平行关系；2．垂直关系；3．几何体的特征．2．如图在一个二面角的棱上有两个点A ，B ，线段,AC BD 分别在这个二面角的两个面内，并且都垂直于棱AB ，=46,AB cm AC cm =， 8,217BD cm CD cm ==，则这个二面角的度数为（）A ．30︒B ．60︒C ．90︒D ．120︒ 【答案】B 【解析】试题分析：设所求二面角的大小为θ，则,BD AC θ<>=，因为CD DB BA AC =++，所以22222()222CD DB BA AC DB BA AC DB BA DB AC BA AC =++=+++⋅+⋅+⋅CA DB而依题意可知,BD AB AC AB ⊥⊥，所以20,20DB BA BA AC ⋅=⋅=所以2222||||||||2CD DB BA AC BD AC =++-⋅即222417468286cos θ⨯=++-⨯⨯所以1cos 2θ=，而[0,]θπ∈，所以60θ=︒，故选B. 考点：1.二面角的平面角；2.空间向量在解决空间角中的应用.3．已知某个几何体的三视图如图所示，根据图中标出的尺寸（单位：cm ）可得这个几何体的体积是（）112222侧视图俯视图主视图A ．343cmB ．383cmC ．33cmD ．34cm【答案】B ．【解析】试题分析：分析题意可知，该几何体为一四棱锥，∴体积382231312=⨯⨯==Sh V ．考点：空间几何体的体积计算．4．如图，P 是正方体1111ABCD A B C D -对角线1AC 上一动点，设AP 的长度为x ，若PBD ∆的面积为(x)f ，则(x)f 的图象大致是（）【答案】A 【解析】试题分析：设AC 与BD 交于点O ,连接OP .易证得BD ⊥面11ACC A ,从而可得BD OP ⊥.设正方体边长为1,在1Rt ACC ∆中126cos 33C AC ∠==.在AOP ∆中 22OA =,设(),03AP x x =≤≤,由余弦定理可得2222226231222362OP x x x x ⎛⎫=+-⋅⨯=-+ ⎪ ⎪⎝⎭,所以223162OP x x =-+.所以()22231262f x x x =-+.故选A. 考点：1线面垂直,线线垂直;2函数图象.5．如图所示，正方体ABCD A B C D ''''-的棱长为1， ,E F 分别是棱AA '，CC '的中点，过直线,E F 的平面分别与棱BB '、DD '交于,M N ，设 BM x =，[0,1]x ∈，给出以下四个命题：（1）平面MENF ⊥平面BDD B ''；（2）当且仅当x=12时，四边形MENF 的面积最小；（3）四边形MENF 周长()L f x =，[0,1]x ∈是单调函数；（4）四棱锥C MENF '-的体积()V h x =为常函数；以上命题中假命题．．．的序号为（） A ．（1）（4） B ．（2） C ．（3） D ．（3）（4）【答案】C 【解析】试题分析：（1）由于AC EF //，B B AC BD AC '⊥⊥,，则D D B B ''⊥平面AC ，则D D B B EF ''⊥平面，又因为EMFN EF 平面⊂，则平面MENF ⊥平面BDD B ''；（2）由于四边形MENF 为菱形，MN EF S MENF ⋅=21，2=EF ，要使四边形MENF 的面积最小，只需MN 最小，则当且仅当21=x 时，四边形MENF 的面积最小；（3）因为1)21(2+-=x MF ，1)21(4)(2+-=x x f ，)(x f 在]1,0[上不是单调函数；（4）NE C F EC M F MENF C V V V '-'--'+=，ME C S '∆=41121=⋅'E C ，F 到平面ME C '的距离为1，1214131=⋅='-ME C F V ，又41121=⋅'⋅='∆E C S NE C ，1214131=⋅='-NE C F V ，61)(=x h 为常函数.故选（3）考点：1.面面垂直的判定定理；2.建立函数模型.6．已知三棱柱111ABC A B C -的侧棱与底面边长都相等，1A 在底面ABC 上的射影为BC 的中点，则异面直线AB 与1CC 所成的角的余弦值为（）（A）4 （B ）4 （C ）4 （D ）34【答案】D. 【解析】试题分析：连接B A 1；11//CC AA ,AB A 1∠∴是异面直线AB 与1CC 所成的角或其补角；在1ADA Rt ∆中，设11=AA ，则21,231==D A AD ；在1BDA Rt ∆中，2121=B A ；在1ABA ∆中，431122111cos 1=⨯⨯-+=∠AB A ；即面直线AB 与1CC 所成的角的余弦值为34. 考点：异面直线所成的角.7．一个几何体的三视图如图所示，其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形，则该几何体的外接球的表面积为A ．π312B ．π12C ．π34D ．π3 【答案】D 【解析】试题分析：由三视图可知，该几何体为四棱锥，侧棱垂直底面，底面是正方形，将此四棱锥还原为正方体，则正方体的体对角线即外接球的直径，32=r ，23=∴r ，因此ππ342==r S 表面积，故答案为D. 考点：由三视图求外接球的表面积.8．如图，棱长为1的正方体ABCD-A 1B 1C 1D 1中，P 为线段A 1B 上的动点，则下列结论错误的是（）A ．11DC D P ⊥B ．平面11D A P ⊥平面1A APC ．1APD ∠的最大值为90 D ．1AP PD +22+ 【答案】C 【解析】试题分析：111DC D A ⊥ ，11DC B A ⊥，1111A B A D A = ，⊥∴1DC 平面11BCD A ，⊂P D 1平面11BCD A 因此P D DC 11⊥，A 正确；由于⊥11A D 平面11ABB A ，⊂11A D 平面P A D 11，故平面⊥P A D 11平面AP A 1 故B 正确，当2201<<P A 时，1APD ∠为钝角，C 错；将面B AA 1与面11BCD A 沿B A 1展成平面图形，正视图侧视图俯视图线段1AD 即为1PD AP +的最小值，利用余弦定理解221+=AD ，故D 正确，故答案为C ．考点：棱柱的结构特征． 9．下列命题中，错误的是（）A ．一条直线与两个平行平面中的一个相交，则必与另一个平面相交B ．平行于同一平面的两条直线不一定平行C ．如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面βD ．若直线l 不平行于平面α，则在平面α内不存在与l 平行的直线【答案】B 【解析】试题分析: 由直线与平面的位置关系右知A 正确;平行于同一个平面的两条直线可以相交、平行或异面，故B 错，所以选B.考点:直线、平面平行与垂直的判定与性质.10．已知如图所示的正方体ABCD ﹣A 1B 1C 1D 1，点P 、Q 分别在棱BB 1、DD 1上，且=，过点A 、P 、Q作截面截去该正方体的含点A 1的部分，则下列图形中不可能是截去后剩下几何体的主视图的是（）【答案】A【解析】试题分析：当P 、B 1重合时，主视图为选项B ；当P 到B 点的距离比B 1近时，主视图为选项C ；当P 到B 点的距离比B 1远时，主视图为选项D ，因此答案为A. 考点：组合体的三视图11．一个几何体的三视图及尺寸如图所示，则该几何体的外接球半径为（）A. B. C. D.【答案】C 【解析】试题分析：由三视图可知：该几何体是一个如图所示的三棱锥P-ABC ，它是一个正四棱锥P-ABCD 的一半，其中底面是一个两直角边都为6的直角三角形，高PE=4．设其外接球的球心为O ，O 点必在高线PE 上，外接球半径为R ，则在直角三角形BOE 中，BO 2=OE 2+BE 2=（PE-EO ）2+BE 2，即R 2=（4-R ）2+（32）2，解得：R=174，故选C.考点：三视图，球与多面体的切接问题，空间想象能力12．如右图，在长方体1111ABCD A B C D -中，AB =11，AD =7，1AA =12，一质点从顶点A 射向点()4312E ，，，遇长方体的面反射（反射服从光的反射原理），将1i -次到第i 次反射点之间的线段记为()2,3,4i L i =，1L AE =，将线段1234,,,L L L L 竖直放置在同一水平线上，则大致的图形是（）【答案】C 【解析】试题分析：因为37411>，所以1A E 延长交11D C 于F ，过F 作FM 垂直DC 于.M 在矩形1AA FM 中分析反射情况：由于35105AM =>，第二次反射点为1E 在线段AM 上，此时153E M =,第三次反射点为2E 在线段FM 上，此时24E M =,第四次反射点为3E 在线段1AF 上,由图可知，选C.考点：空间想象能力13．一块石材表示的几何体的三视图如图所示，将该石材切削、打磨、加工成球，则能得到的最大球的半径等于（）A.1B.2C.3D.4【答案】B【解析】试题分析：由图可得该几何体为三棱柱,因为正视图,侧视图,俯视图的内切圆半径最小的是正视图(直角三角形)所对应的内切圆,所以最大球的半径为正视图直角三角形内切圆的半径r , 则2286862r r r -+-+⇒=,故选B. 考点：三视图内切圆球三棱柱14．已知二面角l αβ--为60︒，AB α⊂，AB l ⊥，A 为垂足，CD β⊂，C l ∈，135ACD ∠=︒，则异面直线AB 与CD 所成角的余弦值为 A ．14 B ．24 C ．34 D ．12【答案】B. 【解析】试题分析：如图作BE β⊥于E ，连结AE ，过A 作AG ∥CD ，作EG AG ⊥于G ，连结BG ，则.BG AG ⊥设2AB a =．在ABE ∆中，60,90,2,.BAE AEB AB a AE a ∠=︒∠=︒=∴=在Rt AEG ∆中，29045,90,cos 45.2GAE CAG AGE AG a a ∠=︒-∠=︒∠=︒∴=︒=在Rt ABG∆中，222cos 24AG BAG AB a ∠===∴异面直线AB 与CD 所成角的余弦值为24，故选B ．βαElBDACG考点：1.三垂线定理及其逆定理；2. 空间角（异面直线所成角）的计算．15．在空间直角坐标系Oxyz 中,已知(2,0,0)(2,2,0),(0,2,0),(1,1,2)A B C D .若123,,S S S 分别是三棱锥D ABC -在,,xOy yOz zOx 坐标平面上的正投影图形的面积，则（）A ．123S S S ==B ．21S S =且23S S ≠C ．31S S =且32S S ≠D ．32S S =且31S S ≠ 【答案】D 【解析】试题分析：三棱锥ABC D -在平面xoy 上的投影为ABC ∆，所以21=S ，设D 在平面yoz 、zox 平面上的投影分别为2D 、1D ，则ABC D -在平面yoz 、zox 上的投影分别为2OCD ∆、1OAD ∆，因为)2,1,0(1D ，)2,0,1(2D ，所以212=-S S ，故选D.考点：三棱锥的性质，空间中的投影，难度中等.16．正方形ABCD 的边长为2，点E 、F 分别在边AB 、BC 上，且1AE =，12BF =，将此正方形沿DE 、DF 折起，使点A 、C 重合于点P ，则三棱锥P DEF -的体积是（） A ．13B 523 D ．23【答案】B【解析】试题分析：解：因为90,DPE DPF ∠=∠=所以,DP PE DP PF ⊥⊥又因为PE ⊂平面PEF ,PF ⊂平面PEF ,且PE PF P =,所以DP ⊥平面PEF在PEF ∆中，22223151,,1222PE PF EF EB BF ⎛⎫===+=+= ⎪⎝⎭所以222351222cos 33212EPF ⎛⎫⎛⎫+- ⎪ ⎪⎝⎭⎝⎭∠==⨯⨯,225sin 133EPF ⎛⎫∠=-= ⎪⎝⎭ 所以11355sin 122234PEF S PE PF EPF ∆=⋅⋅∠=⨯⨯⨯= 115523346PEF P DEF D PEF V V DP S ∆--==⋅⋅=⨯⨯=三棱锥三棱锥所以应选B.考点：1、直线与平面垂直的判定；2、正弦定理与余弦定理；3、棱锥的体积.17．高为的四棱锥S ﹣ABCD 的底面是边长为1的正方形，点S ，A ，B ，C ，D 均在半径为1的同一球面上，则底面ABCD 的中心与顶点S 之间的距离为（）A. B. C. D.【答案】A【解析】试题分析：由题意可知ABCD 是小圆，对角线长为，四棱锥的高为，推出高就是四棱锥的一条侧棱，最长的侧棱就是球的直径，然后利用勾股定理求出底面ABCD 的中心与顶点S 之间的距离．解：由题意可知ABCD 是小圆，对角线长为，四棱锥的高为，点S ，A ，B ，C ，D 均在半径为1的同一球面上，球的直径为2，所以四棱锥的一条侧棱垂直底面的一个顶点，最长的侧棱就是直径，所以底面ABCD 的中心与顶点S 之间的距离为：=故选A点评：本题是基础题，考查球的内接多面体的知识，能够正确推出四棱锥的一条侧棱垂直底面的一个顶点，最长的侧棱就是直径是本题的关键，考查逻辑推理能力，计算能力．18．二面角l αβ--为60°，A 、B 是棱l 上的两点，AC 、BD 分别在半平面,αβ内，AC l ⊥，BD l ⊥，且AB ＝AC ＝a ，BD ＝2a ，则CD 的长为( )A ．2aB ．5aC ．aD ．3a【答案】A【解析】试题分析：根据异面直线上两点间的距离公式2222cos EF d m n mn θ=++± ，对于本题中，d a =，m a =，2n =，60θ=，故()222222cos 602CD a a a a a a =++-⋅⋅⋅=．考点：异面直线上两点间距离,空间想象能力．19．长方体的表面积是24，所有棱长的和是24，则对角线的长是（）．Ａ．14 B ．4 C ．32 D ．23【答案】B【解析】试题分析：设出长方体的长、宽、高，表示出长方体的全面积，十二条棱长度之和，然后可得对角线的长度．考点：长方体的结构特征，面积和棱长的关系.20．已知棱长为l 的正方体1111ABCD A B C D -中，E ，F ，M 分别是AB 、AD 、1AA 的中点，又P 、Q 分别在线段11A B 11、A D 上,且11A P=A Q=x,0<x<1，设面MEF 面MPQ=l ，则下列结论中不成立的是( )A ．//l 面ABCDB ．l ⊥ACC ．面MEF 与面MPQ 不垂直D ．当x 变化时，l 不是定直线【答案】D【解析】试题分析：解：连结1111,,,AC BD AC B D ,,AC BD 交于点O 1111,AC B D 交于点1O由正方体的性质知，11111111////,,BD B D AC AC AC BD AC B D ⊥⊥，因为,E F 是,AD AB 的中点，所以//EF BD因为11A P A Q =,所以11//PQ B D所以//PQ EF ,所以//PQ 平面MEF ,//EF 平面MPQ , 由MEF 面MPQ=l ，EF ⊂ 平面MEF ，所以//EF l ，而EF ⊂平面ABCD ,l ⊂/平面ABCD , 所以，//l 面ABCD ，所以选项A 正确；由AC BD ⊥，//EF BD 得EF AC ⊥而//EF l ，所以l ⊥AC ，所以选项B 正确；连111,,MB MD O M ,则11//,O M AC 而1111,//,//AC A B AC BD BD EF A B MF ⊥⊥，所以，11,O M EF O M MF ⊥⊥,所以1O M ⊥平面MEF ，过直线l 与平面MEF 垂直的平面只能有一个，所以面MEF 与面MPQ 不垂直，所以选项C 是正确的；因为//EF l ，M 是定点，过直线外一点有且只有一条直线与已知直线平行，所以直线l 是唯一的，故选项D 不正确．考点：1、直线平面的位置关系；2、直线与直线，直线与平面，平面与平面的平行与垂直的判定及性质．21．如图，等边三角形ABC 的中线AF 与中位线DE 相交于G ，已知ED A '∆是△ADE 绕DE 旋转过程中的一个图形，下列命题中，错误的是( )A ．动点A '在平面ABC 上的射影在线段AF 上B ．恒有平面GF A '⊥平面BCDEC ．三棱锥EFD A -'的体积有最大值D ．异面直线E A '与BD 不可能垂直【答案】D【解析】试题分析：由于',A G DE FG DE ⊥⊥．所以DE ⊥平面'A FG ．经过点'A 作平面ABC 的垂线垂足在AF上．所以A 选项正确．由A 可知B 选项正确．当平面'A DE 垂直于平面BCDE 时，三棱锥EFD A -'的体积最大，所以C 正确．因为BD EF ，设2AC a =．所以'EF A E a ==，当'2A F a =时，32'(')2a A G GF A G GF a <+==．所以异面直线E A '与BD 可能垂直．所以D 选项不正确．考点：1．线面位置关系．2．面面的位置关系．3．体积公式．4．异面直线所成的角．5．空间想象力．22．已知棱长为l 的正方体1111ABCD A B C D -中，E ，F ，M 分别是AB 、AD 、1AA 的中点，又P 、Q 分别在线段11A B 11、A D 上,且11A P=A Q=x,0<x<1，设面MEF 面MPQ=l ，则下列结论中不成立的是( )A ．//l 面ABCDB ．l ⊥ACC ．面MEF 与面MPQ 不垂直D ．当x 变化时，l 不是定直线【答案】D【解析】试题分析：解：连结1111,,,AC BD AC B D ,,AC BD 交于点O 1111,AC B D 交于点1O由正方体的性质知，11111111////,,BD B D AC AC AC BD AC B D ⊥⊥，因为,E F 是,AD AB 的中点，所以//EF BD因为11A P A Q =,所以11//PQ B D所以//PQ EF ,所以//PQ 平面MEF ,//EF 平面MPQ ,由MEF 面MPQ=l ，EF ⊂ 平面MEF ，所以//EF l ，而EF ⊂平面ABCD ,l ⊂/平面ABCD , 所以，//l 面ABCD ，所以选项A 正确；由AC BD ⊥，//EF BD 得EF AC ⊥而//EF l ，所以l ⊥AC ，所以选项B 正确；连111,,MB MD O M ,则11//,O M AC 而1111,//,//AC A B AC BD BD EF A B MF ⊥⊥，所以，11,O M EF O M MF ⊥⊥,所以1O M ⊥平面MEF ，过直线l 与平面MEF 垂直的平面只能有一个，所以面MEF与面MPQ不垂直，所以选项C是正确的；EF l，M是定点，过直线外一点有且只有一条直线与已知直线平行，所以直线l是唯一的，故选因为//项D不正确．考点：1、直线平面的位置关系；2、直线与直线，直线与平面，平面与平面的平行与垂直的判定及性质．23．把四个半径都是1的球中的三个放在桌面上，使它两两外切，然后在它们上面放上第四个球，使它与前三个都相切，求第四个球的最高点与桌面的距离（）A．B．C．D．3【答案】A【解析】由题意，四球心组成棱长为2的正四面体的四个顶点，则正四面体的高．而第四个球的最高点到第四个球的球心距离为求的半径1，且三个球心到桌面的距离都为1，故第四个球的最高点与桌面的距离为，选A．24．如图所示，四边形ABCD为正方形，QA⊥平面ABCD，PD∥QA，QA＝AB＝PD.则棱锥Q－ABCD的体积与棱锥P－DCQ的体积的比值是（）A. 2:1B. 1:1C. 1:2D. 1:3【答案】C【解析】设AB ＝a.由题设知AQ 为棱锥Q －ABCD 的高，所以棱锥Q －ABCD 的体积V 1＝.易证PQ ⊥面DCQ ，而PQ ＝，△DCQ 的面积为，所以棱锥P －DCQ 的体积V 2＝.故棱锥Q －ABCD 的体积与棱锥P －DCQ 的体积的比值为1:1，选C.25．正四面体ABCD ，线段AB //平面α，E ，F 分别是线段AD 和BC 的中点，当正四面体绕以AB 为轴旋转时，则线段AB 与EF 在平面α上的射影所成角余弦值的范围是（）A ． [0，22]B ．[22，1]C ．[21，1] D ．[21，22] 【答案】B【解析】试题分析：如图，取AC 中点为G ，结合已知得GF //AB ，则线段AB 、EF 在平面α上的射影所成角等于GF 与EF 在平面α上的射影所成角，在正四面体中，AB ⊥CD ，又GE //CD ，所以GE ⊥GF,所以222GF GE EF +=，当四面体绕AB 转动时，因为GF //平面α，GE 与GF 的垂直性保持不变，显然，当CD 与平面α垂直时，GE 在平面上的射影长最短为0，此时EF 在平面α上的射影11F E 的长取得最小值21，当CD 与平面α平行时，GE 在平面上的射影长最长为21，11F E 取得最大值22，所以射影11F E 长的取值范围是 [21，22]，而GF 在平面α上的射影长为定值21，所以AB 与EF 在平面α上的射影所成角余弦值的范围是[22，1].故选B 考点：1线面平行；2线面垂直。

(完整word版)高中立体几何大量习题及答案

立体几何一、选择题1. 给出下列四个命题①垂直于同一直线的两条直线互相平行；②垂直于同一平面的两个平面互相平行；③若直线4与同一平面所成的角相等，则4互相平行；④若直线 /|仏是异面直线，则与都相交的两条直线是异面直线。

其中假命题的个数是（）A. 1B. 2 C ・ 3 D. 42. 将正方形ABCD 沿对角线〃£）折成一个120。

的二面角，点C 到达点G ，这时异面直线AD 与BCi 所成角的余弦值是（）A. —B. -C.逅D.- 2 2 4 43. —个长方体一顶点的三个面的面积分别是血、巧、后，这个长方体对角线的长为（）6. 正方体A ,B ,C ,D ,—ABCD 的棱长为a, EF 在AB 上滑动，且|EF|=b （b<a=9 Q 点在DC 上滑动，则四面体N —EFQ 的体积（）A ・与E 、尸位置有关 B.与Q 位置有关C.与E 、F 、0位置都有关D.与E 、F 、0位買均无关，是定值 7. 三个两两垂直的平面，它们的三条交线交于一点O,点P 到三个平面的距离比为1 ：2 ： 3, PO=2V14 ,则P 到这三个平面的距离分别是（）4. A. 2^3 B. 3^2 C. 6 如图，在正三角形ABC 中，D 、E 、尸分别为各边的中点，G 、H 、I 、丿分别为AF 、AD. BE 、DE 的中点.将△ ABC 沿QE 、EF 、Q 尸折成三棱锥以后，与〃所成角的度数为（A. 90° B ・ 60° C. 45。

5.两相同的正四棱锥组成如图所示的几何体，可放棱长为1的正方体内，使正四棱锥的底面ABCD 与正方体的某一个平面平行，且各顶点均在正方体的面上，则这样的几何体体积的可能值有（）A ・I 个B. 2个C. 3个 D0°D.A. 1, 2, 3 B・ 2, 4, 6 C・ 1, 4, 6 D・ 3, 6, 98. 如图，在四而体ABCD 中，截rfij AEF 经过四面体的内切球（与四个面都相切的球）球心O,且与BC, DC 分别截于E 、F,如果截面将四面体分成体积相等的两部分，设四棱锥A —BEFD 与三棱锥A-EFC 的表面积分别是Si ，52,则必有（）A. S\<S2B. Si>S2C. S I =52D. 5I ，S2的大小关系不能确定 9. 条件甲：四棱锥的所有侧面都是全等三角形，条件乙：这个四棱锥是正四棱锥，则条件甲是条件乙的（）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件10. 已知棱锥的顶点为P, P 在底面上的射影为O, PO=a,现用平行于底面的平面去截这个棱锥，截面交PO 于点M,并使截得的两部分侧面积相等，设OM=b ，则a 与b 的关系是（） B ・ h= （ V2 +1） aD.后土色 2 —♦ f11. 已知向量d=（2, 4, x ）, 〃=（2, y, 2）,若f |=6, “ 丄〃，则 x+y 的值是（）12. 一个长方体共一顶点的三个面的面积分别是迈,JI 亦，这个长方体它的八个顶点都在同一个球面上，这个球的表面积是（）A.1271B. 1871C.3671D. 6兀 13. 己知某个几何体的三视图如下，图中标出的尺寸（单位:cm ）,则这个几何体的体积是（）已知圆锥的全面积是底面积的3倍，那么该圆锥的侧tfri 展开图扇形的圆心角为（ A.12O 0 B.15O 0 C.180° D.24O 0A ・ b= ( 5/2 —l)a A. 4000 14. A8000 正视图俯视图20. 15.在一个倒置的正三棱锥容器内，放入一个钢球，钢球恰好与棱锥的四个而都接触，经过棱锥的一条侧棱和高作截面，正确的截面图形是（）“（-1,0,2）,且几+》与必―》互相垂直，贝IJR 值是（）厂3 “7 C. — D.— 5516. 正四棱柱 ABCD-AiBiCiDi 中，AB=3, BBi=4.长为 1 的线段PQ 在棱AAi 上移动，长为3的线段MN 在棱 CCi±移动，点R 在棱BBi 上移动，则四棱锥R- PQMN 的体积是（）A. 6B. 10 C ・12 D ・不确定17. 已知三棱锥0—ABC 中，OA 、OB 、OC 两两互相垂直，若x+y=4,则已知三棱锥O —ABC 体积的最大值是（）1 2 >/3 B. — C. — D. 3 3 3 A.l18. 如图，在正四面体A-BCD 中，E 、F 、G 分别是三角形ADC 、ABD 、BCD 的中心, 则AEFG 在该正四面体各个面上的射影所有可能的序号是（）A.①③B.②®® c.③④D.②④ A/ \ /◎、L ________ \ ① MB — — —②19. 如來底而直径和高相等的圆柱的侧面积是s •那么圆柱的体积等于A.-VSB.-J-C.-VSD.- 2 2V K 44 vn 已知直线AB. CD 是异面直线，AC 丄AB, AC 丄CD, BD 丄CD, 则异面直线AB 与CD 所成角的大小为（）A. 30°B. 45° 且 AB=2, CD=1,C. 60°D. 75°已知向量”m°）,B.- 5 A. 1 OC=1, OA=x, OB=y,22. 在四棱锥的四个侧面中，直角三角形最参可有（）A.4个B.2个C.3个D.1个23. 三棱锥A-BCD 中，AC 丄BD, E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点，则四边形EFGH 是（）A.菱形B.矩形C.梯形D.正方形24. 在正四面体P —ABC 中，D 、E 、F 分别是AB 、BC 、CA 的中点，下面四个结论中不成立的是（）25. 一棱锥被平行于底面的平面所截，若截面1何积与底面面积的比为1： 3,则此截面把一条侧棱分成的两线段之比为（）A.1： 3B.1： 2C.1：羽D.1：羽一 1 26. 正四面体P —ABC 中，M 为棱AB 的中点，则PA 与CM 所成角的余弦值为（）A 並B 並C 返D 迴 A. 2 B. § C. 4 D. 327. —个三棱锥S —ABC 的三条侧棱SA 、SB 、SC 两两互相垂直，且长度分别为1, & ,3 已知该三棱锥的四个顶点都在一个球而上，则这个球的表面积为（）A.16nB.32 兀C.36 兀D.64 兀28. 在棱长为。

高中数学立体几何习题(含答案与解析)

立体几何试卷五一、选择题1、线段AB 在平面α内，则直线AB 与平面α的位置关系是A 、AB α⊂ B 、AB α⊄C 、由线段AB 的长短而定D 、以上都不对 2、下列说法正确的是A 、三点确定一个平面B 、四边形一定是平面图形C 、梯形一定是平面图形D 、平面α和平面β有不同在一条直线上的三个交点 3、垂直于同一条直线的两条直线一定A 、平行B 、相交C 、异面D 、以上都有可能 4、在正方体1111ABCD A B C D -中，下列几种说法正确的是A 、11AC AD ⊥B 、11DC AB ⊥ C 、1AC 与DC 成45角D 、11AC 与1B C 成60角 5、若直线l 平面α，直线a α⊂，则l 与a 的位置关系是A 、l aB 、l 与a 异面C 、l 与a 相交D 、l 与a 没有公共点6、下列命题中：（1）、平行于同一直线的两个平面平行；（2）、平行于同一平面的两个平面平行；（3）、垂直于同一直线的两直线平行；（4）、垂直于同一平面的两直线平行.其中正确的个数有 A 、1 B 、2 C 、3 D 、4 二、填空题1、等体积的球和正方体,它们的表面积的大小关系是S 球_____S 正方体(填”大于、小于或等于”).2、正方体1111ABCD A B C D -中，平面11AB D 和平面1BC D 的位置关系为3、已知PA 垂直平行四边形ABCD 所在平面，若PC BD ⊥，平行则四边形ABCD 一定是 .4、如图，在直四棱柱A 1B 1C 1 D 1－ABCD 中，当底面四边形ABCD 满足条件_________时，有A 1 B ⊥B 1 D 1． 5．正三棱锥P －ABC 中，三条侧棱两两垂直，且侧棱长为a ，则P 点到面ABC 的距离是6．三个平面两两垂直，它们的三条交线交于一点O ，P 到三个面的距离分别是6，8，10，则OP 的长为。

（理科）已长方体的全面积是8，则其对角线长的最小值是认为正确的一种条件即可，不必考虑所有可能的情形.) 三、解答题1、已知圆台的上下底面半径分别是2、5,且侧面面积等于两底面面积之和,求该圆台的母线长.(10分) 2、已知E 、F 、G 、H 为空间四边形ABCD 的边AB 、BC 、CD 、DA 上的点，且ＥＨ∥ＦＧ．求证：EH ∥BD . (12分)3、已知ABC ∆中90ACB ∠=，SA ⊥面ABC ，AD SC ⊥，求证：AD ⊥面SBC ．(12分)4、一块边长为10cm 的正方形铁片按如图所示的阴影部分裁下,H G FE DB A CSD CB A四棱锥形容器,试建立容器的容积V 与x 的函数关系式,并求出函数的定义域. (12分)5、已知正方体1111ABCD A B C D -，O 是底ABCD 对角线的交点. 求证：（１）1C O 面11AB D ；（2 ）1AC ⊥面11AB D ． (14分)6、已知△BCD 中，∠BCD =90°，BC =CD =1，AB ⊥平面BCD ，∠ADB =60°，E 、F 分别是AC 、AD 上的动点，且(01).AE AFAC AD λλ==<< （Ⅰ）求证：不论λ为何值，总有平面BEF ⊥平面ABC ；（Ⅱ）当λ为何值时，平面BEF ⊥平面ACD ？ (14分)7、如图3所示，一个圆锥形的空杯子上面放着一个半球形冰淇淋，如果冰淇淋融化了，会溢出杯子吗？8、矩形ABCD 中，1,(0)AB BC a a ==>，PA ⊥平面AC ，BC 边上存在点Q ，使得PQ QD ⊥，求a 的取值范围．参考答案选择ACDDDB填空1、小于2、平行3、菱形4、1111AC B D 对角线与互相垂直5、设P 点到面ABC 的距离为h ，由体积公式可得：()3261231a h a =⋅，故a h 332=。

立体几何经典大题(各个类型的典型题目)

1．如图，已知△ABC 是正三角形，EA ，CD 都垂直于平面ABC ，且EA ＝AB ＝2a ，DC ＝a ，F 是BE 的中点．（1）FD ∥平面ABC ；（2）AF ⊥平面EDB ．2．已知线段PA ⊥矩形ABCD 所在平面，M 、N 分别是AB 、PC 的中点。

（1）求证：MN //平面PAD ；（2）当∠PDA ＝45°时，求证：MN ⊥平面PCD ；F CBAEDA B C D EF 3．如图，在四面体ABCD 中，CB=CD,BD AD ⊥，点E ，F 分别是AB,BD 的中点．求证：（1）直线EF// 面ACD ；（2）平面⊥EFC 面BCD ．4．在斜三棱柱A 1B 1C 1—ABC 中，底面是等腰三角形，AB =AC ，侧面BB 1C 1C ⊥底面ABC （1）若D 是BC 的中点，求证 AD ⊥CC 1；（2）过侧面BB 1C 1C 的对角线BC 1的平面交侧棱于M ，若AM =MA 1，求证截面MBC 1⊥侧面BB 1C 1C ；（3）AM =MA 1是截面MBC 1⊥平面BB 1C 1C 的充要条件吗？请你叙述判断理由]立体几何大题训练(3)C15. 如图，在正方体ABCD —A 1B 1C 1D 1中，M 、N 、G 分别是A 1A ，D 1C ，AD 的中点．求证：（1）MN//平面ABCD ；（2）MN ⊥平面B 1BG ．6. 如图，在正方体ABCD －A 1B 1C 1D 1中，E 、F 为棱AD 、AB 的中点．（1）求证：EF ∥平面CB 1D 1；（2）求证：平面CAA 1C 1⊥平面CB 1D 1．立体几何大题训练(4)7、如图，在直四棱柱ABCD-A 1B 1C 1D 1中，底面ABCD 为等腰梯形，AB ∥CD ，AB=4，BC=CD=2，AA 1=2，_ G_ M _ D_1_ C_1_ B_1_ A_1_ N_ D _ C_ B _ ABA 1FE、E1分别是棱AD、AA1的中点(1)设F是棱AB的中点，证明：直线EE1∥面FCC1；(2)证明：平面D1AC⊥面BB1C1C。

高中立体几何专题练习附答案

高中立体几何专题练习附答案一、单项选择题1.平面α与平面β,γ都相交,则这三个平面的交线可能有（）A.1条或2条B.2条或3条C.仅2条D.1条或2条或3条2.如图是正方体的平面展开图,在这个正方体中,下列正确的是（）①BM与ED平行;②CN与BE是异面直线;③CN与BM成60°的角;④DM与BN垂直A.①②B.②③C.③④D.①④3.设O是矩形ABCD的边CD上一点,以直线CD为轴旋转这个矩形所得圆柱的体积为V,其中以OA 为母线的圆锥的体积为,则以OB为母线为圆锥的体积等于（）A.B.C.D.4.已知m ,n 表示两条不同直线,α表示平面,下列说法正确的是（）A.若m ∥α,n ∥α,则m ∥nB.若m ⊥α,m ⊥n ,则n ∥αC.若m ⊥α,n α,则m ⊥nD.若m ∥α,m ⊥n ,则n ⊥α5.已知圆柱底面周长为8πcm ，高为3cm ，则轴截面的面积是（）A .12cm 2B .24cm 2C .36cm 2D .48cm 26.圆锥的侧面展开图是一个直径为8的半圆，则圆锥的体积为________. （）A.2π3B .4π3C .3πD.83π37.正方体的棱长为233，则它的外接球的表面积为（）A.8π3B.2πC.16πD.4π38.在正方体ABCD-A1B1C1D1中，P是AA1的中点，则二面角P-BD-C1的大小为（）A.45°B.60°C.75°D.90°9.若α，β是两个不重合的平面，在下列条件中可判断两平面平行的条件是________.（）A.平面α，β都垂直于平面γB.α内不共线的三点到β的距离相等C.l，m是平面α内的直线，且l∥β，m∥βD.l，m是两条异面直线，l⊂α，m⊂β，且l∥β，m∥α10.各棱长相等的正三棱锥，侧棱与底面所成的角的余弦值为（）A.32B.33C.36D.1211.如图，AB是⊙O的直径，C是圆周上不同于A，B的任意一点，PA⊥平面ABC，则四面体P －ABC的四个面中，直角三角形的个数有________. （）A.4个B.3个C.2个D.1个12.a，b是两条不同的直线，α、β是两个不同的平面，则下列命题中正确命题的个数是（）①若a⊥b，a⊥α，b α，b∥α；②若a∥α，α⊥β，则a⊥β；③a⊥β，α⊥β，则a∥α，或a（α；④a⊥b，a⊥α，b⊥β，则α⊥β.A.0个B.1个C.2个D.3个13.空间不共面的4个点最多可以确定的平面个数为________.（）A.0个B.3个C.4个D.5个14.已知α∥β，a⊥α，则a与β的位置关系为（）A.a∥βB.a⊥βC.不相交D.a⊂β15.在长方体ABCD-A1B1C1D1中，与平面B1BCC1垂直的平面的个数为（）A.2B.3C.4D.5二、填空题16.在棱长为2的正方体AC1中,对角线AC1,在六个面的射影长总和是.17.正方体ABCD-A1B1C1D1的棱长为1，P是AA1的中点，E是BB1上的一点，则PE＋EC1的最小值为________.18.一个平面截得球的小圆半径为4，球心到截面的距离为3，则该球的表面积是________.19.二面角α-l-β的棱l上有两点A，B，过点A，B分别在二面角的两个面所在的平面内作棱的垂线a，b，则异面直线a，b所成的角与二面角的平面角的关系是________.20.△ABC的边BC在平面α内，顶点A在平面α外，已知∠ABC＝π3，△ABC所在平面与平面α所成二面角的大小为π6，则直线AB与平面α所成角的正弦值为______.21.设m，n是两条不同的直线，α，β是两个不同的平面，有下列四个命题：①若m⊥n，n∥α，则m⊥α；②若m⊥α，m⊥β，n⊥α则n⊥β；③若mγα，nγα，m∥β，n∥β，m∩n＝P，则α∥β；④若m∥β，β⊥α则m⊥α.写出所有正确结论的序号.22.若平面外的一条斜线长4cm，它在这个平面上的射影长为23cm，则这条斜线和这个平面所成的角的大小为.23.已知PA垂直平行四边形ABCD所在平面，若PC⊥BD，则平行四边形ABCD一定是.24.两两平行的三条直线可以确定______个平面.25.若平面α∥平面β，平面γ与平面α，β分别相交于直线a，b，则a与b的位置关系是________.三、解答题解答题应写出文字说明及演算步骤26.如图,在四棱锥P-ABCD中,已知ABCD是正方形,PA⊥面ABCDPA=AB=4.求:（1）二面角P-BD-A的正切值的大小;（2）三棱锥P-ABD的体积.27.如图所示，已知M是边长为2的正方形ABCD的边CD的中点，沿AM，BM折起，使C，D两点重合于点P，得到三棱锥P-ABM，求三棱锥P-ABM的体积.28.已知圆锥的底面半径为14 cm，母线与底面所成的角为45°，平行于底面的截面的半径为8 cm，求圆锥的截面和底面之间的那部分体积.29.如图所示，在棱长为3的正方体ABCD-A1B1C1D1中，求：（1）直线BC1与平面AA1C1C所成的角；（2）三棱锥C1-ABC的体积.30.如图所示，圆柱的轴截面是边长为5 cm的正方形ABCD，求圆锥侧面上从A到C的最短距离.31.如图，将直角三角形绕直线l旋转一周，求围成的几何体的表面积.32.如图所示，平面α∥平面β，PD ⊥β交α于C ，交β于D ，斜线PB 交α于A ，交β于B .已知PC =3，AC =2，BD =4.求平面α与平面β的距离.33.如图，已知正三棱柱ABC －A 1B 1C 1的侧棱与底面边长都是a ，M 是侧棱CC 1的中点，求：（1）正三棱柱ABC －A 1B 1C 1的全面积；（2）二面角M －AB －C 的大小.34.平面四边形ABCD 中，AB ＝BC ＝2，AD ＝CD ＝，∠B ＝120°，将△ABC 沿四边形ABCD 的对角线AC 折起来，使DB 的距离为，求△ABC 所在平面与△ADC 所在平面所成二面角的平面角度数.35.如图所示，已知正方体ABCD-A 1B 1C 1D 1. （1）写出与平面AA 1B1B 垂直的平面；（2）写出与平面AA 1B 1B 平行的平面.答案一、单项选择题1.D 【提示】当β、γ相交,且a 过它们的交线时,有一条交线；当β、γ平行时,α与其都相交,有两条交线；当α、β、γ两两相交时,有三条交线.2.C3.A4.C5.B6.D 【提示】设圆锥底面半径为r .由题知母线长为4.得πr ·4＝π·42×12⇒r ＝2，则圆锥的高为h ＝2242-＝23.圆锥的体积为V ＝13×π×22×23＝83π3.7.C8.D 【提示】如图所示，连结AC 交BD 于O ，连结OP ，A 1C 1，OC 1，PC 1，则AC ⊥BD . ∵AA 1⊥平面ABCD ，∴AA 1⊥BD .∵AA 1∩AC ＝A ，∴BD ⊥平面A 1ACC 1.∵OP ⊂平面A 1ACC 1，OC 1⊂平面A 1ACC 1，∴BD ⊥OP ，BD ⊥OC 1，∴∠POC 1为二面角P -BD -C 1的平面角.设正方体边长为2，则AP ＝1，OA ＝OC ＝2，CC 1＝2，A 1C 1＝22，∴OP ＝＝3，OC 1＝＝6，PC 1＝＝3.∵OP 2＋OC 21＝PC 21，∴OP ⊥OC 1，∴∠POC 1＝90°.9.D 【分析】由两个平面平行的判断方法知A 、B 、C 均错，只有D 正确. 10.B11.A 【提示】∵AB 是圆O 的直径，∴∠ACB ＝90°即BC ⊥AC ，三角形ABC 是直角三角形.又∵PA ⊥圆O 所在平面，∴△PAC ，△PAB 是直角三角形，且BC 在这个平面内，∴PA ⊥BC ，因此BC 垂直于平面PAC 中两条相交直线，∴BC ⊥平面PAC ，△PBC 是直角三角形.从而△PAB ，△PAC ，△ABC ，△PBC 中，直角三角形的个数是4，故选A . 12.D13.C 【提示】由平面的定义知不共面的四个点在空间里可以最多确定四个平面.14.B15.C二、填空题16.122【提示】对角线AC1在每个面内的射影均为222222+=,所以对角线在六个面内的射影长总和为622122⨯=.17.172【提示】将平面AA1B1B与平面BB1C1C展开形成一个平面，如图所示，则PE＋EC1的最小值，即点P到点C1的最小距离，∴PC1＝＝172.18.100π【提示】R=5.19.相等或互补【提示】当a，b分别在平面α和β中时，a，b所成的角等于二面角的平面角；当a，b中有一条不在二面角的两个半平面中时，a，b所成的角与二面角的平面角互补.20.【提示】过A作AO⊥α，垂足为O，过O作OD⊥BC于D，连接AD，OB，OC，设AO=a.∵AD在平面α射影为OD，∴∠ADO是二面角A-BC-O的平面角，∴∠ADO＝30°，则AD=2a.在Rt△ADB中，∠ABD=60°，AD=2a，∴AB=a.在Rt△AOB中，sin∠ABO==.21.②③【分析】①、④中可能有m⊂α，④错误；③符合直线与平面的位置关系，正确.22.30°【提示】cosθ＝32.22d R r=-23.菱形24.1或325.平行三、解答题26.(1)2(2)24 327.解：∵C，D两点重合于点P，∴AB＝AP＝PB＝2，∴S△ABP＝1 2PA·PB·sin60°＝ 3.∵MP⊥AP，MP⊥BP，AP∩BP＝P，∴MP⊥平面PAB，∴MP为三棱锥M-PAB的高，∴V P-ABM ＝V M-PAB＝13S△ABP·MP＝13×3×1＝33.28.解：∵母线与底面所成角为45°，∴底面半径R与高h相等，即R＝h＝14 cm.∵小圆锥的半径r＝8 cm.∴小圆锥的高h1＝r＝8 cm.∴V＝V大圆锥－V小圆锥＝13πR2·h－13πr2·h1＝13π·142×14－13·π·82×8＝744π cm3.29.解：（1）连接BD交AC于点O，连接C1O.在正方体ABCD-A1B1C1D1中，∵BD⊥AC，BD ⊥CC1，∴BD⊥平面ACC1A1，∴∠BC1O为直线BC1与平面ACC1A1所成的角.又∵CC1＝3，∴BC1＝32，BO＝32 2.又∵△BOC1为直角三角形，∴∠BC1O＝30°，∴直线BC1与平面ACC1A1所成的角为30°.（2）1C ABCV＝13S△ABC·|CC1|＝13×12×3×3×3＝92.30.解如图所示.底面周长＝2πr=5π，∴BC=π，AB=5，∴AC=.31.336π532.解∵α∥β，α∩平面PBD=AC，β∩平面PBD=BD，∴AC∥BD，∴PC ACPD BD=，∴PD=6，∴CD=PD-PC=3，∴平面α与平面β的距离为3.33.（1）（3a2（2）30°34.【解】取AC中点O，连DO，BO，则DO⊥AC，BO⊥AC，∴∠DOB为二面角的平面角，AB＝BC＝2，∠B＝120°，∴BO＝1，AODO＝cos∠DOB=，∴cos∠DOB＝30°.35.解：（1）平面A1ADD1，平面A1B1C1D1，平面ABCD，平面B1BCC1. （2）平面DCC1D1.11。

(完整版)高中立体几何经典练习试题[最新版]

1.如图，在四棱锥P﹣ABCD中，CB⊥平面PAB，AD∥BC，且PA=PB=AB=BC=2AD=2．（Ⅰ）求证：平面DPC⊥平面BPC；（Ⅱ）求二面角C﹣PD﹣B的余弦值．2.如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，底面ABCD为菱形，且PA=AD=2，，E、F分别为AD、PC中点．（1）求点F到平面PAB的距离；（2）求证：平面PCE⊥平面PBC；（3）求二面角E﹣PC﹣D的大小．3.《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.如图,在阳马P ABCD中,侧棱PD⊥底面ABCD,且PD=CD,过棱PC的中点E,作EF⊥PB交PB于点F,连接DE,DF,BD,BE.(1)证明:PB⊥平面DEF.试判断四面体DBEF是否为鳖臑;(2)若面DEF与面ABCD所成二面角的大小为,求的值.4.如图所示三棱柱111C B A ABC -中，⊥1AA 平面ABC ，四边形ABCD 为平行四边形，CD AD 2=，CD AC ⊥.（Ⅰ）若AC AA =1,求证：⊥1AC 平面CD B A 11；（Ⅱ）若D A 1与1BB 所成角的余弦值为721，求二面角11C D A C --的余弦值.5.在直角梯形ABCD 中，//,,3,2,AB CD AD AB DC AB ⊥== 1,AD =,1AE EB DF ==,现把EF 它沿折起，得到如图所示的几何体，连接,,DB AB DC ，使 5.DC =（1）求证：平面DBC ⊥平面DFB ；（2）判断在线段DC 上是否存在一点H ，使得二面角E BH C --的余弦值为306-，若存在，确定H 的位置，若不存在，说明理由.6.如图，四棱锥P ABCD -中，底面ABCD 为平行四边形，24AB AD ==，23BD =，PD ⊥底面ABCD ．（1）证明：平面PBC ⊥平面PBD ；（2）若二面角P BC D --的大小为6π，求AP 与平面PBC 所成角的正弦值．7.在三棱锥A BCD -中，4,22AB BC AD BD CD =====,在底面BCD 内作CE CD ⊥，且 2.CE =（1）求证：//CE 平面ABD ；（2）如果二面角A BD C --的大小为90，求二面角B AC E --的余弦值.8.如图，在四棱锥P ABCD -中，底面ABCD 为正方形， PA ⊥底面ABCD ，AD AP =，E 为棱PD 中点.（1）求证：PD ⊥平面ABE ；（2）若F 为AB 中点，(01)PM PC λλ=<<，试确定λ的值，使二面角P FM B --的余弦值为33-.9.如图，在三棱柱111ABC A B C -中，点C 在平面111A B C 内的射影点为11A B 的中点 1,,90O AC BC AA ACB ==∠=.（1）求证:AB ⊥ 平面1OCC ；（2）求二面角1A CC B --的正弦值.F PM A CD EB10.已知多面体ABCDEF 如图所示.其中ABCD 为矩形，DAE △为等腰直角三角形，DA AE ⊥，四边形AEFB 为梯形，且AE BF ∥，90ABF =︒∠，22AB BF AE ===.（1）若G 为线段DF 的中点，求证：EG ∥平面ABCD .（2）线段DF 上是否存在一点N ，使得直线BN 与平面FCD 所成角的余弦值等于215若存在，请指出点N 的位置；若不存在，请说明理由.11.在如图所示的几何体中，平面ADNM ⊥平面ABCD ，四边形ABCD 是菱形，四边形ADNM 是矩形，π3DAB ∠=，2AB =，1AM =，E 是AB 的中点．(Ⅰ)求证：DE ⊥平面ABM ； (II)在线段AM 上是否存在点P ，使二面角P EC D --的大小为π4？若存在，求出AP 的长；若不存在，请说明理由．12.如图，已知梯形CDEF 与△ADE 所在平面垂直，AD ⊥DE ，CD ⊥DE ，AB ∥CD ∥EF ，AE=2DE=8，AB=3，EF=9．CD=12，连接BC ，BF ．（Ⅰ）若G 为AD 边上一点，DG=DA ，求证：EG ∥平面BCF ；（Ⅱ）求二面角E ﹣BF ﹣C 的余弦值．N M D CE B A13.如图三棱柱中，侧面为菱形，.(1)证明：；(2)若，，，求二面角的余弦值.14.如图，在三棱柱ABC﹣A1B1C1中，∠BAC=90°，AB=AC=2，A1A=4，A1在底面ABC的射影为BC的中点，D是B1C1的中点．（1）证明：A1D⊥平面A1BC；（2）求二面角A1﹣BD﹣B1的平面角的余弦值．15.如图,在四棱锥中,底面为菱形,为的中点.(Ⅰ)若,求证:平面平面;(Ⅱ)若平面平面,且,点在线段上,试确定点的位置,使二面角大小为,并求出的值.16.已知在边长为4的等边△ABC （如图1所示）中，MN ∥BC ，E 为BC 的中点，连接AE 交MN 于点F ，现将△AMN 沿MN 折起，使得平面AMN ⊥平面MNCB （如图2所示）．（1）求证：平面ABC ⊥平面AEF ；（2）若S BCNM =3S △AMN ，求直线AB 与平面ANC 所成角的正弦值．17.如图（1），在五边形BCDAE 中，AB CD //，90=∠BCD ，1==BC CD ，2=AB ，ABE ∆是以AB 为斜边的等腰直角三角形.现将ABE ∆沿AB 折起，使平面⊥ABE 平面ABCD ，如图（2），记线段AB 的中点为O . （1）求证：平面⊥ABE 平面EOD ；（2）求平面ECD 与平面ABE 所成的锐二面角的大小.18.如图，在等腰梯形ABCD 中，//AB CD ，1AD DC CB ===，60ABC ∠=，四边形ACFE 为矩形，平面ACFE ⊥平面ABCD ，2CF =.（1）求证：BC ⊥平面ACFE ；（2）点M 在线段EF 上运动，设平面MAB 与平面FCB 二面角的平面角为(90)θθ≤，试求cos θ的取值范围.。

2024届高考数学专项立体几何大题含答案

立体几何大题1.空间中的平行关系（1）线线平行（2）线面平行的判定定理：平面外一直线与平面内一直线平行，则线面平行（3）线面平行的性质定理若线面平行，经过直线的平面与该平面相交，则直线与交线平行（4）面面平行的判定定理判定定理1：一个平面内有两条相交直线分别平行于另一个平面，则面面平行判定定理2：一个平面内有两条相交直线分别于另一个平面内两条相交直线平行，则面面平行（5）面面平行的性质定理性质定理1：两平面互相平行，一个平面内任意一条直线平行于另一个平面性质定理2：两平面互相平行，一平面与两平面相交，则交线互相平行6.空间中的垂直关系（1）线线垂直（2）线面垂直的判定定理一直线与平面内两条相交直线垂直，则线面垂直（3）线面垂直的性质定理性质定理1：一直线与平面垂直，则这条直线垂直于平面内的任意一条直线性质定理2：垂直于同一个平面的两条直线平行（4）面面垂直的判定定理一个平面内有一条直线垂直于另一个平面，则两个平面垂直(或：一个平面经过另一个平面的垂线，则面面垂直)（5）面面垂直的性质定理两平面垂直，其中一个平面内有一条直线与交线垂直，则这条直线垂直于另一个平面6.异面直线所成角cos θ=cos a ,b =|a ⋅b ||a |⋅|b |=|x 1x 2+y 1y 2+z 1z 2|x 12+y 12+z 12⋅x 22+y 22+z 22(其中θ(0°<θ≤90°)为异面直线a ,b 所成角，a ,b 分别表示异面直线a ,b 的方向向量)7.直线AB 与平面所成角，sin β=AB ⋅m |AB ||m |(m 为平面α的法向量).8.二面角α-l -β的平面角cos θ=m ⋅n |m ||n |(m ，n 为平面α，β的法向量).9.点B 到平面α的距离d =|AB ⋅n | (n 为平面α的法向量，AB 是经过面α的一条斜线，A ∈α).2024届高考数学专项立体几何大题含答案模拟训练一、解答题1(22·23下·湖南·二模)如图，在直三棱柱ABC -A B C 中，∠ABC =120°,AB =BC =2,AC =BB ，点D 为棱BB 的中点，AE =13AC ．(1)求DE 的长度；(2)求平面CDE 与平面BDE 夹角的余弦值．2(22·23下·绍兴·二模)如图，在多面体ABCDE 中，DE ⊥平面BCD ,△ABC 为正三角形，△BCD 为等腰Rt △,∠BDC =90°,AB =2,DE =2.(1)求证：AE ⊥BC ；(2)若AE ⎳平面BCD ，求直线BE 与平面ABC 所成的线面角的正弦值.3(22·23·张家口·三模)如图，在三棱柱ABC-A1B1C1中，侧面BB1C1C为菱形，∠CBB1=60°，AB= BC=2，AC=AB1=2.(1)证明：平面ACB1⊥平面BB1C1C；(2)求平面ACC1A1与平面A1B1C1夹角的余弦值.4(22·23·湛江·二模)如图1，在五边形ABCDE中，四边形ABCE为正方形，CD⊥DE，CD=DE，如图2，将△ABE沿BE折起，使得A至A1处，且A1B⊥A1D．(1)证明：DE⊥平面A1BE；(2)求二面角C-A1E-D的余弦值．5(22·23下·长沙·三模)如图，在多面体ABCDE 中，平面ACD ⊥平面ABC ，BE ⊥平面ABC ，△ABC 和△ACD 均为正三角形，AC =4，BE =3，点F 在AC 上.(1)若BF ⎳平面CDE ，求CF ；(2)若F 是AC 的中点，求二面角F -DE -C 的正弦值.6(22·23下·湖北·二模)如图，S 为圆锥的顶点，O 是圆锥底面的圆心，△ABC 内接于⊙O ,AC ⊥BC ,AC =BC =322，AM =2MS ,AS =3,PQ 为⊙O 的一条弦，且SB ⎳平面PMQ .(1)求PQ 的最小值；(2)若SA ⊥PQ ，求直线PQ 与平面BCM 所成角的正弦值.7(22·23·深圳·二模)如图，在四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD,PA= AD=2AB，点M是PD的中点.(1)证明：AM⊥PC；(2)设AC的中点为O，点N在棱PC上(异于点P，C)，且ON=OA，求直线AN与平面ACM所成角的正弦值.8(22·23下·温州·二模)已知三棱锥D-ABC中，△BCD是边长为3的正三角形，AB=AC=AD, AD与平面BCD所成角的余弦值为33．(1)求证：AD⊥BC；(2)求二面角D-AC-B的平面角的正弦值．9(22·23下·浙江·二模)如图，四面体ABCD,AD⊥CD,AD=CD,AC=2,AB=3,∠CAB=60°，E为AB上的点，且AC⊥DE,DE与平面ABC所成角为30°，(1)求三棱锥D-BCE的体积；(2)求二面角B-CD-E的余弦值.10(22·23下·襄阳·三模)如图，在三棱柱ABC-A1B1C1中，侧面BB1C1C为矩形，∠BAC=90°，AB= AC=2，AA1=4，A1在底面ABC的射影为BC的中点N，M为B1C1的中点.(1)求证：平面A1MNA⊥平面A1BC；(2)求平面A1B1BA与平面BB1C1C夹角的余弦值.11(22·23·唐山·二模)如图，在三棱柱ABC-A1B1C1中，△ABC是等边三角形，侧面ACC1A1⊥底面ABC，且AA1=AC，∠AA1C1=120°，M是CC1的中点．(1)证明：A1C⊥BM．(2)求二面角A1-BC-M的正弦值．12(22·23下·盐城·三模)如图，该几何体是由等高的半个圆柱和14个圆柱拼接而成，点G为弧CD的中点，且C，E，D，G四点共面.(1)证明：平面BDF⊥平面BCG；(2)若平面BDF与平面ABG所成二面角的余弦值为155，且线段AB长度为2，求点G到直线DF的距离.13(22·23下·江苏·三模)如图，圆锥DO中，AE为底面圆O的直径，AE=AD，△ABC为底面圆O的内接正三角形，圆锥的高DO=18，点P为线段DO上一个动点.(1)当PO=36时，证明：PA⊥平面PBC；(2)当P点在什么位置时，直线PE和平面PBC所成角的正弦值最大.14(22·23下·镇江·三模)如图，四边形ABCD是边长为2的菱形，∠ABC=60°，四边形PACQ为矩形，PA=1，从下列三个条件中任选一个作为已知条件，并解答问题(如果选择多个条件分别解答，按第一个解答计分).①BP,DP与平面ABCD所成角相等；②三棱锥P-ABD体积为33；③cos∠BPA=55(1)平面PACQ⊥平面ABCD；(2)求二面角B-PQ-D的大小；(3)求点C到平面BPQ的距离.15(22·23下·江苏·一模)在三棱柱ABC -A 1B 1C 1中，平面A 1B 1BA ⊥平面ABC ，侧面A 1B 1BA 为菱形，∠ABB 1=π3，AB 1⊥AC ，AB =AC =2，E 是AC 的中点.(1)求证：A 1B ⊥平面AB 1C ；(2)点P 在线段A 1E 上(异于点A 1，E )，AP 与平面A 1BE 所成角为π4，求EP EA 1的值.16(22·23下·河北·三模)如图，四棱锥P -ABCD 的底面ABCD 是菱形，其对角线AC ,BD 交于点O ，且PO ⊥平面ABCD ,OC =1,OD =OP =2,M 是PD 的中点，N 是线段CD 上一动点．(1)当平面OMN ⎳平面PBC 时，试确定点N 的位置，并说明理由；(2)在(1)的前提下，点Q 在直线MN 上，以PQ 为直径的球的表面积为214π．以O 为原点，OC ,OD ,OP 的方向分别为x 轴、y 轴、z 轴的正方向建立空间直角坐标系O -xyz ，求点Q 的坐标．17(22·23·汕头·三模)如图，圆台O1O2的轴截面为等腰梯形A1ACC1，AC=2AA1=2A1C1=4,B为底面圆周上异于A,C的点.(1)在平面BCC1内，过C1作一条直线与平面A1AB平行，并说明理由；(2)若四棱锥B-A1ACC1的体积为23，设平面A1AB∩平面C1CB=l,Q∈l，求CQ的最小值.18(19·20下·临沂·二模)如图①，在Rt△ABC中，B为直角，AB=BC=6，EF∥BC，AE=2，沿EF将△AEF折起，使∠AEB=π3，得到如图②的几何体，点D在线段AC上．(1)求证：平面AEF⊥平面ABC；(2)若AE⎳平面BDF，求直线AF与平面BDF所成角的正弦值．19(22·23下·广州·三模)如图，四棱锥P-ABCD的底面为正方形，AB=AP=2，PA⊥平面ABCD，E,F分别是线段PB,PD的中点，G是线段PC上的一点.(1)求证：平面EFG⊥平面PAC；(2)若直线AG与平面AEF所成角的正弦值为13，且G点不是线段PC的中点，求三棱锥E-ABG体积.20(22·23下·长沙·一模)斜三棱柱ABC-A1B1C1的各棱长都为2，∠A1AB=60°，点A1在下底面ABC 的投影为AB的中点O．(1)在棱BB1(含端点)上是否存在一点D使A1D⊥AC1若存在，求出BD的长；若不存在，请说明理由；(2)求点A1到平面BCC1B1的距离．21(22·23下·长沙·三模)如图，三棱台ABC -A 1B 1C 1，AB ⊥BC ，AC ⊥BB 1，平面ABB 1A 1⊥平面ABC ，AB =6,BC =4，BB 1=2，AC 1与A 1C 相交于点D ，AE =2EB，且DE ∥平面BCC 1B 1.(1)求三棱锥C -A 1B 1C 1的体积；(2)平面A 1B 1C 与平面ABC 所成角为α，CC 1与平面A 1B 1C 所成角为β，求证：α+β=π4.22(22·23·衡水·一模)如图所示，A ,B ,C ,D 四点共面，其中∠BAD =∠ADC =90°，AB =12AD ，点P ,Q 在平面ABCD 的同侧，且PA ⊥平面ABCD ，CQ ⊥平面ABCD .(1)若直线l ⊂平面PAB ，求证：l ⎳平面CDQ ；(2)若PQ ⎳AC ，∠ABP =∠DAC =45°，平面BPQ ∩平面CDQ =m ，求锐二面角B -m -C 的余弦值.23(22·23下·湖北·三模)已知平行六面体(底面是平行四边形的四棱柱)ABCD-A1B1C1D1的各条棱长均为2，且有∠AA1D1=∠AA1B1=∠D1A1B1=60°．(1)求证：平面AA1C1C⊥平面A1B1C1D1；(2)求直线B1D与平面AA1C1C所成角的正弦值．24(22·23下·武汉·三模)如图，在四棱锥P-ABCD中，底面ABCD为正方形，PA⊥平面ABCD，PA=AB=2，E为线段PB的中点，F为线段BC上的动点.(1)求证：平面AEF⊥平面PBC；(2)求平面AEF与平面PDC夹角的最小值.25(22·23下·黄冈·三模)如图1，在四边形ABCD中，BC⊥CD，AE∥CD,AE=BE=2CD=2,CE =3．将四边形AECD沿AE折起，使得BC=3，得到如图2所示的几何体．(1)若G为AB的中点，证明：DG⊥平面ABE；(2)若F为BE上一动点，且二面角B-AD-F的余弦值为63，求EFEB的值．26(22·23·德州·三模)图1是直角梯形ABCD，AB⎳CD，∠D=90°，AD=3，AB=2，CD=3，四边形ABCE为平行四边形，以BE为折痕将△BCE折起，使点C到达C1的位置，且AC1=6，如图2．(1)求证：平面BC1E⊥平面ABED；(2)在线段BE上存在点P使得PA与平面ABC1的正弦值为365，求平面BAC1与PAC1所成角的余弦值．27(22·23·山东·二模)如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AB⎳CD，AB⊥BC，PA =AB=BC=2，CD=4．(1)证明：AD⊥PC；(2)若M为线段PB的靠近B点的四等分点，判断直线AM与平面PDC是否相交？如果相交，求出P到交点H的距离，如果不相交，说明理由．28(22·23·黄山·三模)如图，在直角梯形ABCD中，AD⎳BC，AD⊥CD，四边形CDEF为平行四边形，对角线CE和DF相交于点H，平面CDEF⊥平面ABCD，BC=2AD，∠DCF=60°，G是线段BE上一动点(不含端点)．(1)当点G为线段BE的中点时，证明：AG⎳平面CDEF；(2)若AD=1,CD=DE=2，且直线DG与平面CDEF成45°角，求二面角E-DG-F的正弦值．29(22·23·菏泽·三模)已知在直三棱柱ABC-A1B1C1中，其中AA1=2AC=4,AB=BC,F为BB1的中点，点E是CC1上靠近C1的四等分点，A1F与底面ABC所成角的余弦值为2 2．(1)求证：平面AFC⊥平面A1EF；(2)在线段A1F上是否存在一点N，使得平面AFC与平面NB1C1所成的锐二面角的余弦值为277，若存在，确定点N的位置，若不存在，请说明理由．30(22·23·福州·三模)如图，在三棱锥P-ABC中，PA⊥底面ABC，PA=2，AB=AC=1，将△PAB绕着PA逆时针旋转π3到△PAD的位置，得到如图所示的组合体，M为PD的中点.(1)当∠BAC为何值时，该组合体的体积最大，并求出最大值；(2)当PC⎳平面MAB时，求直线PC与平面PBD所成角的正弦值.31(22·23·福州·二模)如图1，在△ABC 中，AB =AC =2,∠BAC =2π3,E 为BC 的中点，F 为AB 上一点，且EF ⊥AB .将△BEF 沿EF 翻折到△B EF 的位置，如图2.(1)当AB =2时，证明：平面B AE ⊥平面ABC ；(2)已知二面角B -EF -A 的大小为π4，棱AC 上是否存在点M ，使得直线B E 与平面B MF 所成角的正弦值为1010？若存在，确定M 的位置；若不存在，请说明理由.32(22·23·三明·三模)如图，平面五边形ABCDE 由等边三角形ADE 与直角梯形ABCD 组成，其中AD ∥BC ，AD ⊥DC ，AD =2BC =2，CD =3，将△ADE 沿AD 折起，使点E 到达点M 的位置，且BM =a .(1)当a =6时，证明AD ⊥BM 并求四棱锥M -ABCD 的体积；(2)已知点P 为棱CM 上靠近点C 的三等分点，当a =3时，求平面PBD 与平面ABCD 夹角的余弦值.33(22·23·宁德·一模)如图①在平行四边形ABCD 中，AE ⊥DC ，AD =4，AB =3，∠ADE =60°，将△ADE 沿AE 折起，使平面ADE ⊥平面ABCE ，得到图②所示几何体．(1)若M 为BD 的中点，求四棱锥M -ABCE 的体积V M -ABCE ；(2)在线段DB 上，是否存在一点M ，使得平面MAC 与平面ABCE 所成锐二面角的余弦值为235，如果存在，求出DMDB的值，如果不存在，说明理由．34(22·23·龙岩·二模)三棱柱ABC -A 1B 1C 1中，AB ⊥AC ，AB =AC =2，侧面A 1ACC 1为矩形，∠A 1AB =2π3，三棱锥C 1-ABC 的体积为233．(1)求侧棱AA 1的长；(2)侧棱CC 1上是否存在点E ，使得直线AE 与平面A 1BC 所成角的正弦值为55？若存在，求出线段C 1E 的长；若不存在，请说明理由．35(22·23下·浙江·二模)如图，在多面体ABC-A1B1C1中，AA1⎳BB1⎳CC1，AA1⊥平面A1B1C1，△A1B1C1为等边三角形，A1B1=BB1=2，AA1=3，CC1=1，点M是AC的中点．(1)若点G是△A1B1C1的重心，证明；点G在平面BB1M内；(2)求二面角B1-BM-C1的正弦值．36(22·23下·浙江·三模)如图，三棱台ABC-A1B1C1中，A1C1=4，AC=6，D为线段AC上靠近C的三等分点.(1)线段BC上是否存在点E，使得A1B⎳平面C1DE，若不存在，请说明理由；若存在，请求出BEBC的值；(2)若A1A=AB=4，∠A1AC=∠BAC=π3，点A1到平面ABC的距离为3，且点A1在底面ABC的射影落在△ABC内部，求直线B1D与平面ACC1A1所成角的正弦值.37(22·23下·苏州·三模)如图，在三棱锥P-ABC中，△ABC是边长为62的等边三角形，且PA= PB=PC=6，PD⊥平面ABC，垂足为D,DE⊥平面PAB，垂足为E，连接PE并延长交AB于点G.(1)求二面角P-AB-C的余弦值；(2)在平面PAC内找一点F，使得EF⊥平面PAC，说明作法及理由，并求四面体PDEF的体积.38(22·23·沧州·三模)如图，该几何体是由等高的半个圆柱和14个圆柱拼接而成.C,E,D,G在同一平面内，且CG=DG.(1)证明：平面BFD⊥平面BCG；(2)若直线GC与平面ABG所成角的正弦值为105，求平面BFD与平面ABG所成角的余弦值.39(23·24上·永州·一模)如图所示，在四棱锥P-ABCD中，底面ABCD为矩形，侧面PAD为正三角形，且AD=2AB=4,M、N分别为PD、BC的中点，H在线段PC上，且PC=3PH．(1)求证：MN⎳平面PAB；(2)当AM⊥PC时，求平面AMN与平面HMN的夹角的余弦值．40(22·23·潍坊·三模)如图，P为圆锥的顶点，O是圆锥底面的圆心，AC为底面直径，△ABD为底面圆O的内接正三角形，且边长为3，点E在母线PC上，且AE=3，CE=1．(1)求证：PO∥平面BDE；(2)求证：平面BED⊥平面ABD(3)若点M为线段PO上的动点．当直线DM与平面ABE所成角的正弦值最大时，求此时点M到平面ABE的距离．立体几何大题1.空间中的平行关系（1）线线平行（2）线面平行的判定定理：平面外一直线与平面内一直线平行，则线面平行（3）线面平行的性质定理若线面平行，经过直线的平面与该平面相交，则直线与交线平行（4）面面平行的判定定理判定定理1：一个平面内有两条相交直线分别平行于另一个平面，则面面平行判定定理2：一个平面内有两条相交直线分别于另一个平面内两条相交直线平行，则面面平行（5）面面平行的性质定理性质定理1：两平面互相平行，一个平面内任意一条直线平行于另一个平面性质定理2：两平面互相平行，一平面与两平面相交，则交线互相平行6.空间中的垂直关系（1）线线垂直（2）线面垂直的判定定理一直线与平面内两条相交直线垂直，则线面垂直（3）线面垂直的性质定理性质定理1：一直线与平面垂直，则这条直线垂直于平面内的任意一条直线性质定理2：垂直于同一个平面的两条直线平行（4）面面垂直的判定定理一个平面内有一条直线垂直于另一个平面，则两个平面垂直(或：一个平面经过另一个平面的垂线，则面面垂直)（5）面面垂直的性质定理两平面垂直，其中一个平面内有一条直线与交线垂直，则这条直线垂直于另一个平面6.异面直线所成角cos θ=cos a ,b =|a ⋅b ||a |⋅|b |=|x 1x 2+y 1y 2+z 1z 2|x 12+y 12+z 12⋅x 22+y 22+z 22(其中θ(0°<θ≤90°)为异面直线a ,b 所成角，a ,b 分别表示异面直线a ,b 的方向向量)7.直线AB 与平面所成角，sin β=AB ⋅m |AB ||m |(m 为平面α的法向量).8.二面角α-l -β的平面角cos θ=m ⋅n |m ||n |(m ，n 为平面α，β的法向量).9.点B 到平面α的距离d =|AB ⋅n | (n 为平面α的法向量，AB 是经过面α的一条斜线，A ∈α).模拟训练一、解答题1(22·23下·湖南·二模)如图，在直三棱柱ABC -A B C 中，∠ABC =120°,AB =BC =2,AC =BB ，点D 为棱BB 的中点，AE =13AC ．(1)求DE 的长度；(2)求平面CDE 与平面BDE 夹角的余弦值．【答案】(1)393(2)34【分析】(1)在△ABC 中，用余弦定理可得到AC =23，在△ABE 中，用余弦定理可得BE =233，即可求得DE =DB 2+BE 2=393；(2)以B 为原点，分别以BE ,BC ,BB 所在的直线为x ,y ,z 轴建立空间直角坐标系，求出平面CDE 与平面BDE 的法向量，即可求解【详解】(1)因为在直三棱柱ABC -A B C 中，∠ABC =120°,AB =BC =2，在△ABC 中，由余弦定理得cos ∠ABC =AB 2+BC 2-AC 22AB ⋅BC=22+22-AC 22×2×2=-12，解得AC =23，则AE =13AC =233，在△ABE 中，由余弦定理得cos ∠BAE =AB 2+AE 2-BE 22AB ⋅AE =22+233 2-BE 22×2×233=32，解得BE =233，又AC =BB =23，所以BD =12BB =3，因为BB ⊥平面ABC ，BE ⊂平面ABC ，所以BB ⊥BE ，在直角三角形DBE 中，DE =DB 2+BE 2=(3)2+233 2=393；(2)因为AE =BE =233，所以∠ABE =∠BAE =30°，则∠CBE =∠ABC -∠ABE =120°-30°=90°，则BE ,BC ,BB 两两互相垂直，以B 为原点，分别以BE ,BC ,BB 所在的直线为x ,y ,z 轴建立如下图所示的空间直角坐标系：设平面CDE 的法向量为n =x ,y ,z ，由n ⋅CD =x ,y ,z ⋅0,-2,3 =-2y +3z =0n ⋅CE =x ,y ,z ⋅233,-2,0 =233x -2y =0 ，得z =233y x =3y，令y =3，得平面CDE 的一个法向量为n =3,3,2 ；平面BDE 的一个法向量为m =0,1,0 ．设平面CDE 与平面BDE 夹角的大小为θ，则cos θ=m ⋅n m n =0,1,0 ⋅3,3,2 1×4=34，故平面CDE 与平面BDE 夹角的余弦值为34．2(22·23下·绍兴·二模)如图，在多面体ABCDE 中，DE ⊥平面BCD ,△ABC 为正三角形，△BCD 为等腰Rt △,∠BDC =90°,AB =2,DE =2.(1)求证：AE ⊥BC ；(2)若AE ⎳平面BCD ，求直线BE 与平面ABC 所成的线面角的正弦值.【答案】(1)证明见解析(2)63【分析】(1)由线面垂直的性质定理和判定定理即可证明；(2)法一：由分析可知，∠EBH 就是直线BE 与平面ABC 所成的线面角，设∠AFD =α，当α<90°时，O 与D 重合，可得A ,E 两点重合，不符合题意，当α>90°时，求出EH ,BE ，即可得出答案；法二：建立空间直角坐标系，求出直线BE 的方向向量与平面ABC 的法向量，由线面角的向量公式代入即可得出答案.【详解】(1)设F 为BC 中点，连接AF ,EF ，则由△ABC 为正三角形，得AF ⊥BC ；DE ⊥平面BCD ，且△BCD 为等腰直角三角形，计算可得：BE =CE =2,∴EF ⊥BC .EF ∩AF =F ,EF ,AF ⊂面AEF ，于是BC ⊥面AEF ，AE ⊂面AEF ，从而BC ⊥AE .(2)法一：由(1)可知，过点E 作EH ⊥AF ，垂足为H ，则∠EBH 就是直线BE 与平面ABC 所成的线面角.当AE ⎳平面BCD 时，可得A 到平面BCD 的距离为 2.设∠AFD =α，所以AF ⋅sin α=2，可得sin α=63，当α<90°时，cos α=33，不妨设A 在底面BCD 射影为O ，则FO =1，此时O 与D 重合，可得A ,E 两点重合，不符合题意，舍去；当α>90°时，FO =1，此时O 在DF 的延长线上，作EH ⊥AF ，由于AODE 为矩形，可得AE =DO =2,AE ∥OD ，可得sin ∠EAH =63，可得EH =263.于是sin ∠EBH =EH BE=63.法二：建立如图坐标系，可得F 0,0,0 ,B 1,0,0 ，C -1,0,0 ,D 0,1,0 ,E 0,1,2 ,A 0,a ,b由AF =3，解得a 2+b 2=3，又∵AE ⎳平面BCD ，令n =0,0,1 ，可得AB ⋅n =0，解得b =2,a =±1.当a =1时A ,E 重合，所以a =-1，此时A 0,-1,2 .不妨设平面ABC 的法向量为m =x ,y ,z ，则CB ⋅m =0CA ⋅m =0代入得x -y +2z =02x =0 ，令z =1，则y =2，所以m =0,2,1 .由于BE =-1,1,2 ，不妨设所成角为θ，则sin θ=∣cos BE ,m |=63.3(22·23·张家口·三模)如图，在三棱柱ABC -A 1B 1C 1中，侧面BB 1C 1C 为菱形，∠CBB 1=60°，AB =BC =2，AC =AB 1=2.(1)证明：平面ACB 1⊥平面BB 1C 1C ；(2)求平面ACC 1A 1与平面A 1B 1C 1夹角的余弦值.【答案】(1)证明见解析；(2)57.【分析】(1)利用面面垂直的判定定理进行证明；(2)利用垂直关系建立空间直角坐标系，用向量法进行求解.【详解】(1)如图，连接BC 1，交B 1C 于O ，连接AO .因为侧面BB 1C 1C 为菱形，所以B 1C ⊥BC 1，且O 为BC 1的中点.又AC =AB 1=2，故AO ⊥B 1C .又AB =BC =2，且∠CBB 1=60°，所以CO =1,BO =3，所以AO =AC 2-CO 2=1.又AB =2，所以AB 2=BO 2+AO 2，所以AO ⊥BO .因为BO ,CB 1⊂平面BB 1C 1C ，BO ∩CB 1=O ，所以AO ⊥平面BB 1C 1C .又AO ⊂平面ACB 1，所以平面ACB 1⊥平面BB 1C 1C .(2)由(1)知，OA ,OB ,OB 1两两互相垂直，因此以O 为坐标原点，OB ,OB 1,OA 所在直线分别为x 轴，y 轴，z 轴，建立如图所示的空间直角坐标系O -xyz ，则A (0,0,1)，B (3,0,0)，C (0,-1,0)，C 1(-3,0,0).故CC 1 =(-3,1,0)，CA =(0,1,1)，CB =(3,1,0).设n =(x 1,y 1,z 1)为平面ACC 1A 1的一个法向量，则有n ⋅CC 1 =0n ⋅CA =0 ，即-3x 1+y 1=0y 1+z 1=0 ，令x 1=1，则n =(1,3,-3).设m =(x 2,y 2,z 2)为平面ABC 的一个法向量，则有m ⋅CA =0m ⋅CB =0，即y 2+z 2=03x 2+y 2=0 ，令x 2=1，则m =(1,-3,3).因为平面A 1B 1C 1∥平面ABC ，所以m =(1,-3,3)也是平面A 1B 1C 1的一个法向量.所以cos <n ,m > =n ⋅m n m=1-3-3 7×7=57.所以平面ACC 1A 1与平面A 1B 1C 1夹角的余弦值57. 4(22·23·湛江·二模)如图1，在五边形ABCDE 中，四边形ABCE 为正方形，CD ⊥DE ，CD =DE ，如图2，将△ABE 沿BE 折起，使得A 至A 1处，且A 1B ⊥A 1D ．(1)证明：DE ⊥平面A 1BE ；(2)求二面角C -A 1E -D 的余弦值．【答案】(1)证明见解析(2)63【分析】(1)由已知易得DE ⊥BE ，即可证明线面垂直；(2)建立空间直角坐标系，用坐标公式法求解即可．【详解】(1)由题意得∠BEC =∠CED =π4，∠BED =π2，DE ⊥BE ，又A 1B ⊥A 1D ，A 1E ∩A 1D =A 1,A 1E ,A 1D ⊂面A 1ED ，所以A 1B ⊥面A 1ED ，又DE ⊂面A 1ED ，则DE ⊥A 1B ，又DE ⊥BE ，A 1B ∩BE =B ，A 1B ⊂平面A 1BE ，BE ⊂平面A 1BE ，所以DE ⊥平面A 1BE ．(2)取BE 的中点O ，可知BE =2CD ,OE =CD ，由DE ⊥BE ，且CD ⊥DE 可得OE ⎳CD ，所以四边形OCDE 是平行四边形，所以CO ∥DE ，则CO ⊥平面A 1BE ，设BE =2，以点O 为坐标原点，OB ,OC ,OA 1所在直线为坐标轴建立空间直角坐标系，如图，则A 1(0,0,1),E (-1,0,0),B (1,0,0),C (0,1,0),D (-1,1,0)，EA 1 =(1,0,1),EC =(1,1,0),ED =(0,1,0)，设平面A 1EC 的一个法向量为n 1 =(x 1,y 1,z 1)，则n 1 ⋅EA 1 =0n 1 ⋅EC =0 ，即x 1+z 1=0x 1+y 1=0 ，取x 1=1，则n 1 =(1,-1,-1)，设平面A 1ED 的一个法向量为n 2 =(x 2,y 2,z 2)，则n 2 ⋅E 1A =0n 2 ⋅ED =0 ，即x 2+z 2=0y 2=0 ，取x 2=1，则n 2 =(1,0,-1)，所以cos n 1 ,n 2 =n 1 ⋅n 2 n 1 n 2=63，由图可知，二面角C -A 1E -D 为锐角，所以面角C -A 1E -D 的余弦值为63．5(22·23下·长沙·三模)如图，在多面体ABCDE 中，平面ACD ⊥平面ABC ，BE ⊥平面ABC ，△ABC 和△ACD 均为正三角形，AC =4，BE =3，点F 在AC 上.(1)若BF ⎳平面CDE ，求CF ；(2)若F 是AC 的中点，求二面角F -DE -C 的正弦值.【答案】(1)CF =1(2)8517【分析】(1)记AC 中点为M ，连接DM 、BM ，依题意可得DM ⊥AC ，根据面面垂直的性质得到DM ⊥平面ABC ，如图建立空间直角坐标系，求出平面CDE 的法向量，设F a ,0,0 ，a ∈2,-2 ，依题意可得BF ⋅n =0求出a 的值，即可得解；(2)依题意点F 与点M 重合，利用空间向量法计算可得.【详解】(1)记AC 中点为M ，连接DM 、BM ，△ACD 为正三角形，AC =4，则DM ⊥AC ，且DM =2 3.所以DM ⊥平面ABC ，又△ABC 为正三角形，所以BM ⊥AC ，所以BM =23，如图建立空间直角坐标系，则B 0,23,0 ，C -2,0,0 ，D 0,0,23 ，E 0,23,3 ，所以CD =2,0,23 ，CE =2,23,3 ，设平面CDE 的法向量为n =x ,y ,z ，则n ⋅CD =2x +23z =0n ⋅CE =2x +23y +3z =0，令x =3，则z =-3，y =-32，则n =3,-32,-3 ，设F a ,0,0 ，a ∈-2,2 ，则BF =a ,-23,0 ，因为BF ⎳平面CDE ，所以BF ⋅n =3a +-23 ×-32+0×-3 =0，解得a =-1，所以F 为CM 的中点，此时CF =1.(2)若F 是AC 的中点，则点F 与点M 重合，则平面FDE 的一个法向量可以为m =1,0,0 ，设二面角F -DE -C 为θ，显然二面角为锐角，则cos θ=m ⋅n m ⋅n=332+-32 2+-3 2=651，所以sin θ=1-cos 2θ=1-651 2=8517，所以二面角F -DE -C 的正弦值为8517.6(22·23下·湖北·二模)如图，S 为圆锥的顶点，O 是圆锥底面的圆心，△ABC 内接于⊙O ,AC ⊥BC ,AC =BC =322，AM =2MS ,AS =3,PQ 为⊙O 的一条弦，且SB ⎳平面PMQ .(1)求PQ 的最小值；(2)若SA ⊥PQ ，求直线PQ 与平面BCM 所成角的正弦值.【答案】(1)22(2)3010【分析】(1)作出辅助线，找到符合要求的PQ ，并利用垂径定理得到最小值；(2)在第一问基础上，得到当PQ 取得最小值时，SA ⊥PQ ，并建立空间直角坐标系，利用空间向量求解线面角.【详解】(1)过点M 作MH ⎳SB 交AB 于点H ，过点H 作PQ ⊥AB ，此时满足SB ⎳平面PMQ ，由平面几何知识易知，PQ =2r 2-d 2，当弦心距d 最大时，d =OH ，弦长最短，即PQ 取得最小值，因为AM =2MS ,AS =3，所以AH =2HB ，因为AC ⊥BC ,AC =BC =322，由勾股定理得AB =322⋅2=3，故AH =2,HB =1，连接OQ ，则OQ =32，由勾股定理得HQ =OQ 2-OH 2=94-14=2，所以PQ =2HQ =22；(2)连接OS ，则OS ⊥平面ACB ，因为PQ ⊂平面ACB ，故OS ⊥PQ ，而SA ⊥PQ ，OS ∩SA =S ，所以PQ ⊥平面AOS ，即有PQ ⊥AB .以O 为坐标原点，过点O 且平行PQ 的直线为x 轴，OB 所在直线为y 轴，OS 所在直线为z 轴，建立空间直角坐标系，则P -2,12,0 ,Q 2,12,0 ,B 0,32,0 ,C 32,0,0 ,M 0,-12,3 ，设平面BCM 的法向量为m =x ,y ,z ，则m ⋅CB =x ,y ,z ⋅-32,32,0 =-32x +32y =0m ⋅MB =x ,y ,z ⋅0,2,-3 =2y -3z =0，令x =1，则y =1,z =233，故m =1,1,233，设直线PQ 与平面BCM 所成角的大小为θ，则sin θ=cos PQ ,m =PQ ⋅m PQ ⋅m =22,0,0 ⋅1,1,233 22×1+1+43=3010.故直线PQ与平面BCM所成角的正弦值为30 10.7(22·23·深圳·二模)如图，在四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD,PA= AD=2AB，点M是PD的中点.(1)证明：AM⊥PC；(2)设AC的中点为O，点N在棱PC上(异于点P，C)，且ON=OA，求直线AN与平面ACM所成角的正弦值.【答案】(1)证明见解析(2)1510【分析】(1)由等腰三角形的性质可得AM⊥PD，由面面垂直的性质可得CD⊥平面PAD，则CD⊥AM，所以由线面垂直的判定可得AM⊥平面PCD，从而可得结论；(2)以AB,AD,AP所在直线分别为x,y,z轴建立空间直角坐标系，利用空间向量求解即可.【详解】(1)证明：因为PA=AD，点M是PD的中点，所以AM⊥PD.因为PA⊥平面ABCD,PA⊂平面PAD，所以平面PAD⊥平面ABCD，因为四边形ABCD为矩形，所以CD⊥AD，因为平面PAD∩平面ABCD=AD，CD⊂平面ABCD，所以CD⊥平面PAD，所以CD⊥AM，因为PD∩CD=D，PD,CD⊂平面PCD，所以AM⊥平面PCD，因为PC⊂平面PCD，所以AM⊥PC.(2)解：由题意可得AB,AD,AP两两垂直，设AB=1，如图，以AB,AD,AP所在直线分别为x,y,z轴建立空间直角坐标系，则A(0,0,0),B(1,0,0),C(1,2,0),D(0,2,0),P(0,0,2)，22所以AM =0,22,22 ,AC =1,2,0 ，设平面ACM 的法向量为n =x ,y ,z ，则AM ⋅n =22y +22z =0AC ⋅n =x +2y =0，令y =-1可得x =2,z =1，所以平面ACM 的一个法向量n =2,-1,1 .PC =1,2,-2 ，设N x N ,y N ,z N ,PN =λPC =λ,2λ,-2λ (0<λ<1)，即x N ,y N ,z N -2 =λ,2λ,-2λ ，所以N λ,2λ,2-2λ .又O 12,22,0 ,ON =OA =32，所以λ-12 2+2λ-22 2+(2-2λ)2=34，化简得5λ2-7λ+2=0，解得λ=25或λ=1(舍去).所以AN =25,225,325，设直线AN 与平面ACM 所成的角为θ，则sin θ=n ⋅AN n ⋅AN=3252+1+1×425+825+1825=1510，所以直线AN 与平面ACM 所成角的正弦值为1510.8(22·23下·温州·二模)已知三棱锥D -ABC 中，△BCD 是边长为3的正三角形，AB =AC =AD ,AD 与平面BCD 所成角的余弦值为33．(1)求证：AD ⊥BC ；(2)求二面角D -AC -B 的平面角的正弦值．【答案】(1)证明见解析(2)223【分析】(1)取BC 的中点E ，连接AE ,DE ，证明BC ⊥平面ADE ，即可得证；(2)取正三角形BCD 的中心O ，连接OA ，从而可得OA ⊥平面BCD ，则∠ODA 即为AD 与平面BCD 所成角的平面角，进而可得AB =AC =AD =3，取AC 中点为H ，连接DH ,BH ，则DH ⊥AC ,BH ⊥AC ，故∠BHD 即为二面角D -AC -B 的平面角，解△BDH 即可得解.【详解】(1)取BC 的中点E ，连接AE ,DE ，因为△BCD 是边长为3的正三角形，所以DE ⊥BC ，又AE ∩DE =E ,AE ,DE ⊂平面ADE ，所以BC ⊥平面ADE ，因为AD ⊂平面ADE ，所以AD ⊥BC ；(2)取正三角形BCD 的中心O ，连接OA ，则点O 在DE 上，且OD =23DE ，由AB =AC =AD ，△BCD 是正三角形，得三棱锥A -BCD 为正三棱锥，则OA ⊥平面BCD ，故∠ODA 即为AD 与平面BCD 所成角的平面角，又AD 与平面BCD 所成角的余弦值为33，所以OD AD =3×32×23AD=33，即AB =AC =AD =3，即三棱锥A -BCD 是正四面体，取AC 中点为H ，连接DH ,BH ，则DH ⊥AC ,BH ⊥AC ，故∠BHD 即为二面角D -AC -B 的平面角，在△BDH 中，BH =DH =332,BD =3，则cos ∠BHD =BH 2+DH 2-BD 22⋅BH ⋅DH =274+274-92×332×332=13，所以sin ∠BHD =1-cos 2∠BHD =223，所以二面角D -AC -B 的平面角的正弦值223．9(22·23下·浙江·二模)如图，四面体ABCD ,AD ⊥CD ,AD =CD ,AC =2,AB =3,∠CAB =60°，E 为AB 上的点，且AC ⊥DE ,DE 与平面ABC 所成角为30°，(1)求三棱锥D -BCE 的体积；(2)求二面角B -CD -E 的余弦值.【答案】(1)答案见解析；(2)答案见解析．【分析】(1)取AC 中点F ，可证明AC ⊥平面DEF ，得平面ABC ⊥平面DEF ，DE 在平面ABC 内的射影就是直线EF ，∠DEF 是DE 与平面ABC 所成的角，即∠DEF =30°，由正弦定理求得∠FDE ，有两个解，在∠FDE =60°时可证DF ⊥平面ABC ，在∠FDE =120°时，取FE 中点H 证明DH ⊥平面ABC ，然后由棱锥体积公式计算体积；(2)建立如图所示的空间直角坐标系，用空间向量法求二面角．【详解】(1)取AC 中点F ，连接FE ,FD ，因为AD =CD ，所以DF ⊥AC ，又AC ⊥DE ，DE ∩DF =D ，DE ,DF ⊂平面DEF ，所以AC ⊥平面DEF ，而FE ⊂平面DEF ，所以AC ⊥FE ，由AC ⊥平面DEF ，AC ⊂平面ABC 得平面ABC ⊥平面DEF ，因此DE 在平面ABC 内的射影就是直线EF ，所以∠DEF 是DE 与平面ABC 所成的角，即∠DEF =30°，AD =CD ,AC =2，因此DF =12AC =1，在△DEF 中，由正弦定理EF sin ∠FDE =DF sin ∠DEF 得1sin30°=3sin ∠FDE ，sin ∠FDE =32，∠FDE 为△DEF 内角，所以∠FDE =60°或120°，S △ABC =12AB ×AC ×sin ∠BAC =12×3×2×sin60°=333，S △CBE =BE BAS △ABC =3-23×332=32，若∠FDE =60°，则∠DFE =90°，即DF ⊥FE ，AC ∩FE =F ，AC ,FE ⊂平面ABC ，所以DF ⊥平面ABC ，V D -BCE =13S △BCE ⋅DF =13×32×1=36；若∠FDE =120°，则∠DFE =30°，DF =DE =1，取EF 中点H ，连接DH ，则DH ⊥EF ，因为平面ABC ⊥平面DEF ，平面ABC ∩平面DEF =EF ，而DH ⊂平面DEF ，所以DH ⊥平面ABC ，DH =DF sin ∠DFE =1×sin30°=12，所以V D -BCE =13S △BCE ⋅DF =13×32×12=312；(2)若∠FDE =60°，以FA ,FE ,FD 为x ,y ,z 轴建立如图所示的空间直角坐标系F -xyz ，则D (0,0,1)，C (-1,0,0)，A (1,0,0)，E (0,3,0)，AE =(-1,3,0)，EB =12AE =-12,32,0 ，所以B 点坐标为-12,332,0 ，CD =(1,0,1)，CB =12,332,0 ，CE =(1,3,0)，设平面DBC 的一个法向量是m =(x 1,y 1,z 1)，则m ⋅CD =x 1+z 1=0m ⋅CB =12x 1+332y 1=0，取y 1=-1，则x 1=33，z 1=-33，即m =(33,-1,-33)，设平面DEC 的一个法向量是n =(x 2,y 2,z 2)，则n ⋅CD =x 2+z 2=0n ⋅CE =x 2+3y 2=0，取y 2=-1，则x 2=3，z 2=-3，即m =(3,-1,-3)，cos m ,n =m ⋅n m n =9+1+955×7=19385385，所以二面角B -CD -E 的余弦值是19385；若∠FDE =120°，以FA 为x 轴，FE 为y 轴，过F 且平行于HD 的直线为z 轴建立如图所示的空间直角坐标系F -xyz ，FH =12FE =32，则D 0,32,12 ，C (-1,0,0)，A (1,0,0)，E (0,3,0)，AE =(-1,3,0)，EB =12AE =-12,32,0 ，所以B 点坐标为-12,332,0 ，CD =1,32,12 ，CB =12,332,0 ，CE =(1,3,0)，设平面DBC 的一个法向量是m =(x 1,y 1,z 1)，则m ⋅CD =x 1+32y 1+12z 1=0m ⋅CB =12x 1+332y 1=0，取y 1=-1，则x 1=33，z 1=-53，即m =(33,-1,-53)，设平面DEC 的一个法向量是n =(x 2,y 2,z 2)，则n ⋅CD =x 2+32y 2+12z 2=0n ⋅CE =x 2+3y 2=0，取y 2=-1，则x 2=3，z 2=-3，即m =(3,-1,-3)，cos m ,n =m ⋅n m n =9+1+15103×7=25721721，所以二面角B -CD -E 的余弦值是25721721．10(22·23下·襄阳·三模)如图，在三棱柱ABC -A 1B 1C 1中，侧面BB 1C 1C 为矩形，∠BAC =90°，AB =AC =2，AA 1=4，A 1在底面ABC 的射影为BC 的中点N ，M 为B 1C 1的中点.(1)求证：平面A 1MNA ⊥平面A 1BC ；(2)求平面A 1B 1BA 与平面BB 1C 1C 夹角的余弦值.【答案】(1)证明见解析(2)23015【分析】(1)利用线面垂直和面面垂直的判定定理证明；(2)利用空间向量的坐标运算求面面夹角的余弦值.【详解】(1)如图，∵A 1N ⊥面ABC ，连AN ，则AN ⊥A 1N ，又AB =AC =2，∴AN ⊥BC ，又AN ∩BC =N ，A 1N ⊂面A 1BC ，BC ⊂面A 1BC ，于是AN ⊥面A 1BC ，又AN ⊂面A 1MN ，，所以面A 1BC ⊥面A 1MNA .(2)由(1)可得，以NA ,NB ,NA 1 为x ,y ,z 轴，建系如图，∠BAC =90°，AB =AC =2，BC =22则A (2,0,0),B (0,2,0),C (0,-2,0),因为AA 1=4,AN =2,所以A 1N =14,则A 1(0,0,14),因为NB 1 =NB +BB 1 =NB +AA 1 =0,2,0 +-2,0,14 =-2,2,14 ,所以B 1-2,2,14 ,设平面A 1BB 1的一个法向量为m =(x ,y ,z )，因为A 1B =(0,2,-14),B 1B =(2,0,-14),所以A 1B ⋅m =2y -14z =0B 1B ⋅m =2x -14z =0 ，令y =7，则x =7,z =1，所以m =(7,7,1)，设平面BCC 1B 1的一个法向量为n =(a ,b ,c )，因为BC =(0,-22,0),BB 1 =(-2,0,14),所以BC ⋅n =-22b =0BB 1 ⋅n =-2a +14c =0，令a =7，则b =0,c =1，所以n =(7,0,1)，设平面A 1BB 1与平面BCC 1B 1夹角为θ，则cos θ=cos <m ,n >=m ⋅n m n=7+0+17+7+1×7+0+1=23015，所以平面A 1BB 1与平面BCC 1B 1夹角的余弦值为23015.11(22·23·唐山·二模)如图，在三棱柱ABC -A 1B 1C 1中，△ABC 是等边三角形，侧面ACC 1A 1⊥底面ABC ，且AA 1=AC ，∠AA 1C 1=120°，M 是CC 1的中点．(1)证明：A 1C ⊥BM ．(2)求二面角A 1-BC -M 的正弦值．【答案】(1)证明见解析(2)45【分析】(1)根据菱形的性质、结合面面垂直的性质，线面垂直的判定定理进行证明即可；(2)建立空间直角坐标系，运用空间向量夹角公式进行求解即sk .【详解】(1)取AC 的中点O ，连接OM ，OB ，AC 1．在三棱柱ABC -A 1B 1C 1中，由AA 1=AC ，得四边形ACC 1A 1为菱形，所以A 1C ⊥AC 1，易知OM ∥AC 1，则A 1C ⊥OM ．由△ABC 是等边三角形，知OB ⊥AC ，又平面ACC 1A 1⊥平面ABC ，平面ACC 1A 1∩平面ABC =AC ，OB ⊂平面ABC ，知OB ⊥平面ACC 1A 1，则OB ⊥A 1C ，又OB ∩OM =O ,OB ,OM ⊂平面OBM ，得A 1C ⊥平面OBM ，又BM ⊂平面OBM ，故A 1C ⊥BM ．.(2)连接OA 1，因为侧面ACC 1A 1为菱形，∠AA 1C 1=120°，则∠A 1AC =60°，则△A 1AC 为等边三角形，所以A 1O ⊥AC ，又由(1)易知OA 1，OB ，AC 两两垂直，故以O 为坐标原点，分别以OB ，OC ，OA 1 的方向为x 轴、y 轴、z 轴的正方向，建立空间直角坐标系．不妨设AB =2，则O 0,0,0 ，B 3,0,0 ，C 0,1,0 ，A 10,0,3 ，C 10,2,3 ，BA 1 =-3,0,3 ，BC =-3,1,0 ，CC 1 =0,1,3 ，。

高考数学立体几何练习题及答案

高考数学立体几何练习题及答案一、选择题1. 已知正方体的体积为216cm³，求正方体一个面上的对角线长度。

（选项）A. 12cmB. 9cmC. 6cmD. 3cm2. 锥体的侧面积为15√3cm²，求锥体的体积。

（选项）A. 45cm³B. 30cm³C. 15cm³D. 10cm³3. 平面α与平面β相交于直线l，直线l与平面γ相交于点O，若平面α与平面β的夹角为60°，直线l与平面γ的夹角为45°，则平面α与平面γ的夹角为（选项）A. 45°B. 30°C. 60°D. 75°二、填空题1. 一个正方体的棱长为a，其对角线的长度为____。

2. 若棱长为3的正方体的一个面上有一点P，离该面的距离为2，则线段OP的长度为_____。

3. 一个正方体的一个顶点到另一个顶点的距离为a，其体对角线的长度为____。

三、解答题1. 已知一个正方体的棱长为a，求：a) 正方体的体积；b) 正方体一个面的面积；c) 正方体的对角线长度。

解答：a) 正方体的体积为a³。

b) 正方体一个面的面积为a²。

c) 正方体的对角线长度为a√3。

2. 一个圆柱的高为10cm，直径为6cm，求：a) 圆柱的底面积；b) 圆柱的侧面积；c) 圆柱的体积。

解答：a) 圆柱的底面积为π(3cm)²=9πcm²。

b) 圆柱的侧面积为2π(3cm)(10cm)=60πcm²。

c) 圆柱的体积为π(3cm)²(10cm)=90πcm³。

3. 已知一个球的表面积为100πcm²，求球的体积。

解答：设球的半径为r，则球的表面积为4πr²。

根据题意，4πr²=100π，解得r=5cm。

球的体积为4/3πr³=(4/3π)(5cm)³=500/3πcm³。

高中数学立体几何专项练习

高三立体几何专题练习(含答案)

高三数学立体几何专项练习题及答案

高中数学立体几何经典题型练习题集(附有答案)

新教材高二数学立体几何专项训练

高中数学立体几何测试题(10套)

高中数学立体几何专项练习题及答案

高中立体几何专题训练

高中数学立体几何小题100题(含答案与解析)

(完整word版)高中数学立体几何专项练习

大题 立体几何(精选30题)(学生版)

高三精选立体几何大题30题(含详细解答)

高中数学立体几何经典题型专题训练试题(含答案)

高中数学立体几何小题100题(含答案与解析)

(完整word版)高中立体几何大量习题及答案

高中数学立体几何习题(含答案与解析)

立体几何经典大题(各个类型的典型题目)

高中立体几何专题练习附答案

(完整版)高中立体几何经典练习试题[最新版]

2024届高考数学专项立体几何大题含答案

高考数学立体几何练习题及答案

大题立体几何(精选30题)(学生版)