基本逻辑关系和常用逻辑门电路.doc
基本逻辑门电路

基本逻辑门电路————————————————————————————————作者:————————————————————————————————日期:第一节基本逻辑门电路1.1 门电路的概念:实现基本和常用逻辑运算的电子电路,叫逻辑门电路。
实现与运算的叫与门,实现或运算的叫或门,实现非运算的叫非门,也叫做反相器,等等(用逻辑1表示高电平;用逻辑0表示低电平)11.2 与门:逻辑表达式F=A B即只有当输入端A和B均为1时,输出端Y才为1,不然Y为0.与门的常用芯片型号有:74LS08,74LS09等.11.3 或门:逻辑表达式F=A+ B即当输入端A和B有一个为1时,输出端Y即为1,所以输入端A和B均为0时,Y才会为O.或门的常用芯片型号有:74LS32等.11.4.非门逻辑表达式F=A即输出端总是与输入端相反.非门的常用芯片型号有:74LS04,74LS05,74LS06,74LS14等.11.5.与非门 逻辑表达式 F=AB即只有当所有输入端A 和B 均为1时,输出端Y 才为0,不然Y 为1.与非门的常用芯片型号有:74LS00,74LS03,74S31,74LS132等.11.6.或非门: 逻辑表达式 F=A+B即只要输入端A 和B 中有一个为1时,输出端Y 即为0.所以输入端A 和B 均为0时,Y 才会为1.或非门常见的芯片型号有:74LS02等.11.7.同或门: 逻辑表达式F=A B+A BA F B11.8.异或门:逻辑表达式F=A B+A B=AF B11.9.与或非门:逻辑表逻辑表达式F=AB+CD AB C F D11.10.RS 触发器:电路结构把两个与非门G1、G2的输入、输出端交叉连接,即可构成基本RS 触发器,其逻辑电路如图7.2.1.(a)所示。
它有两个输入端R 、S 和两个输出端Q 、Q 。
工作原理 :基本RS 触发器的逻辑方程为:根据上述两个式子得到它的四种输入与输出的关系:1.当R=1、S=0时,则Q=0,Q=1,触发器置1。
逻辑门电路基础知识讲解

+VCC RP
& L1
L
&
L2
+5V 270Ω
&
OC门进行线与时,外接上拉电阻RP的选择: (1)当输出高电平时,
RP不能太大。RP为最大值时要保证输出电压为VOH(min), 由
得:
+VCC RP
&
VOH
II H &
…… ……
II H
n
m
&
II H
&
(2)当输出低电平时, RP不能太小。RP为最小值时要保证输出电压为VOL(max), 由
1 1
33
D
A
31
T1A
T22A T22B
13
T1B
B
L
3
1
2T3
A
≥1
R3
B
(a)
(b)
L=A+B
3.与或非门
R1A
R2
R1B
1
+V CC R4
3
T2 4
1 1
33
D
A1
31
T1A
T22A T22B
13
T1B
B1LA2源自B2312T3 R3
4.集电极开路门( OC门)
在工程实践中,有时需要将几个门的输出端并联使用,以实现与逻辑, 称为线与。普通的TTL门电路不能进行线与。 为此,专门生产了一种可以进行线与的门电路——集电极开路门。
低电平噪声容限 VNL=VOFF-VOL(max)=0.8V-0.4V=0.4V 高电平噪声容限 VNH=VOH(min)-VON=2.4V-2.0V=0.4V
四、TTL与非门的带负载能力
数字电路第2章逻辑代数基础及基本逻辑门电路

(5)AB+A B = A (6)(A+B)(A+B )=A 证明: (A+B)(A+B )=A+A B+AB+0 A( +B+B) = 1 JHR A =
二、本章教学大纲基本要求 熟练掌握: 1.逻辑函数的基本定律和定理; 门、 2.“与”逻辑及“与”门、“或”逻辑及“或”
“非”逻辑及“非”门和“与”、“或”、“非” 的基本运算。 理解:逻辑、逻辑状态等基本概念。 三、重点与难点 重点:逻辑代数中的基本公式、常用公式、 基本定理和基本定律。
JHR
难点:
JHR
1.具有逻辑“与”关系的电路图
2.与逻辑状态表和真值表
JHR
我们作如下定义: 灯“亮”为逻辑“1”,灯“灭”为逻辑“0” 开关“通”为逻辑“1”,开关“断”为逻辑 “0” 则可得与逻辑的真值表。 JHR
3.与运算的函数表达式 L=A·B 多变量时 或 读作 或 L=AB L=A·B·C·D… L=ABCD… 1.逻辑表达式 2.逻辑符号
与非逻辑真值表
Z = A• B
3.逻辑真值表
逻辑规律:有0出1 全1 出0
JHR
A 0 0 1 1
B 0 1 0 1
Z 1 1 1 0
二、或非逻辑 1.逻辑表达式 2.逻辑符号
Z = A+ B
先或后非
3.逻辑真值表
JHR
三、与或非逻辑 1.逻辑表达式 2.逻辑符号
1.代入规则 在任一逻辑等式中,若将等式两边出现的同 一变量同时用另一函数式取代,则等式仍然成立。
JHR
代入规则扩大了逻辑代数公式的应用范围。例如摩 根定理 A+B = A ⋅ B 若将此等式两边的B用B+C 取代,则有
5-1 逻辑代数及门电路

Y 0 1 1 1
(3)非门电路(晶体管反相器)
晶体管构成的反相器电路如图所示。
在线开放课程
反相器 从图中可以看出,输出电平与输入电平反相,输出 电平和输入电平之间是非逻辑关系,所以该电路称为反
相器,又称为非门。
图b为非门的逻辑符号,也是非逻辑的逻辑符号。
5、复合逻辑门电路
复合门,就是把与门,或门和非门结合起来作为一个门 电路来使用。常用的复合门及其逻辑符号、代数式如下图所示。
2)或逻辑和或运算
在线开放课程
当决定某一结果的几个条件中,只要有一个或一个以 上的条件具备,结果就发生,这种逻辑关系,就称为或逻 辑关系,简称或逻辑。 例如,把两只开关并联再和一只灯泡串联接到电源上,
这样只要有一个开关接通,灯泡就亮。因此灯亮和开关接
通是或逻辑关系,可以用逻辑代数中的或运算来表示(灯泡 的状态用Y表示,开关的状态分别用A、B表示): Y=A+B
在线开放课程
复合门电路 a) 与非门
L A BC
b) 或非门 d) 异或门
L A BC
c) 与或非门 L A B C D
L AB AB
=
AB
根据函数的不同表达式,可得函数L的逻辑图如图
所示,同一逻辑函数可以用不同的逻辑门来实现。
在线开放课程
函数的逻辑图 a) L AB BC b) L AB BC e) c)
(2)二极管或门电路 如图a所为二极管 或门电路及逻辑符号,
在线开放课程
图b也是或逻辑的逻
辑符号。或门电路的 真值表见表2。
表7-2 与门真值表
或门的逻辑功能为:
“有1出1,全0出0”。 A 0 0 1 1
电工电子技术基础知识点详解1-2-基本逻辑门电路

基本逻辑门电路1.基本概念在数字电路中,门电路是最基本的逻辑元件,它的应用极为广泛。
所谓门就是一种开关,它能按照一定的条件去控制数字信号通过或不通过。
门电路的输入信号和输出信号之间存在一定的逻辑关系,所以门电路又称为逻辑门电路。
基本逻辑门电路有与门、或门和非门,逻辑门电路可以用二极管、三极管等分立元件组成,更常用的是集成门电路。
2. 基本逻辑关系逻辑电路的基本逻辑关系有“与逻辑”、“或逻辑”和“非逻辑”。
(1) 与逻辑“与”逻辑是指当决定某件事的几个条件全部具备时,该件事才会发生,这种因果关系称为“与”逻辑关系,实现“与”逻辑关系的电路称为“与”门电路。
例如在图1所示的照明电路中,开关A和B串联,只有当A“与”B同时接通时(条件),电灯才亮(结果),电路具有“与”逻辑功能。
“与”逻辑可用下式表示B=F⋅A图1 “与”门电路举例式中小圆点“.”表示A、B的“与”运算,又称逻辑乘,应用时往往省略“.”。
(2)“或”逻辑“或”逻辑是指当决定某件事的几个条件中,只要有一个条件具备,该件事就会发生,这种因果关系称为“或”逻辑关系,实现“或”逻辑关系的电路称为“或”门电路。
例如在图2所示的照明电路中,开关A和B关联,只要开关A “或”B有一闭合,灯就会亮,所以图2电路具有“或”逻辑功能。
“或”逻辑可用下式表示B=AF+图2 “或”门电路举例式中符号“+”表示A 、B “或”运算,又称逻辑加。
3.“非”逻辑在逻辑关系中,“非”就是否定或相反的意思。
实现“非”逻辑关系的电路称为“非”门电路。
图3所示照明电路中,当开关A 断开(“0”)时,灯亮(“1”);开关A 合上(“1”)时,灯不亮(“0”)。
这表示条件和结果是相反的逻辑关系,这种关系称为“非”逻辑关系,所以图3电路具有“非”逻辑功能。
可写为A F =图3 “非”门电路式中A 上的短横线表示“非”的意思,读作“A 非”或“非A ”。
能够实现逻辑运算的电路称为逻辑门电路。
基本逻辑门电路
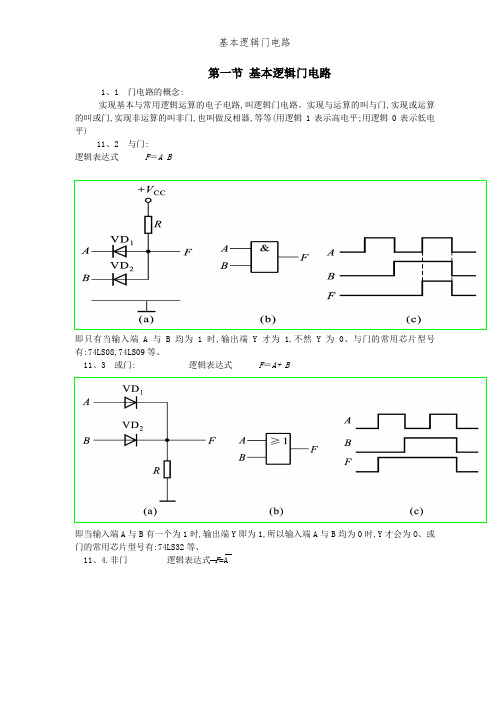
第一节基本逻辑门电路1、1 门电路的概念:实现基本与常用逻辑运算的电子电路,叫逻辑门电路。
实现与运算的叫与门,实现或运算的叫或门,实现非运算的叫非门,也叫做反相器,等等(用逻辑1表示高电平;用逻辑0表示低电平)11、2 与门:逻辑表达式F=A B即只有当输入端A与B均为1时,输出端Y才为1,不然Y为0、与门的常用芯片型号有:74LS08,74LS09等、11、3 或门: 逻辑表达式F=A+ B即当输入端A与B有一个为1时,输出端Y即为1,所以输入端A与B均为0时,Y才会为O、或门的常用芯片型号有:74LS32等、11、4.非门逻辑表达式F=A即输出端总就是与输入端相反、非门的常用芯片型号有:74LS04,74LS05,74LS06,74LS14等、11、5.与非门逻辑表达式 F=AB即只有当所有输入端A与B均为1时,输出端Y才为0,不然Y为1、与非门的常用芯片型号有:74LS00,74LS03,74S31,74LS132等、11、6.或非门: 逻辑表达式 F=A+B即只要输入端A与B中有一个为1时,输出端Y即为0、所以输入端A与B均为0时,Y才会为1、或非门常见的芯片型号有:74LS02等、11、7.同或门: 逻辑表达式F=A B+A BAFB11、8、异或门:逻辑表达式F=A B+A B=1FB11、9、与或非门:逻辑表逻辑表达式F=AB+CDABC F11、10、RS触发器:电路结构把两个与非门G1、G2的输入、输出端交叉连接,即可构成基本RS触发器,其逻辑电路如图7.2.1、(a)所示。
它有两个输入端R、S与两个输出端Q、Q。
工作原理 :基本RS触发器的逻辑方程为:根据上述两个式子得到它的四种输入与输出的关系:1、当R=1、S=0时,则Q=0,Q=1,触发器置1。
2、当R=0、S=1时,则Q=1,Q=0,触发器置0。
=1&≥1如上所述,当触发器的两个输入端加入不同逻辑电平时,它的两个输出端Q与Q有两种互补的稳定状态。
知识单元-基本逻辑关系和常用逻辑门
第二章逻辑门电路S10101B为实现图逻辑表达式的功能,请将多余输入端C进行处理(只需一种处理方法),其中图Y1、Y2为TTL 电路,图Y3、Y4为CMOS电路。
Y1的C端应接,Y2的C端应接,Y3的C端应接,Y4的C端应接。
解:接地、悬空、接地、接地S10101G下图是TTL电气特性曲线,请按表中给定的已知条件将表填写完整。
解:S10101ITTL反相器电气特性如图所示,该门电路输入短路电流I IS=(),高电平输入电流I IH=()若带同类门,其带负载能力N≤( )。
解:I IS=(-1.2mA),I IH=(25μA),N≤(20)S10101N有一两端输入的TTL与非门带同类负载门的个数为N,已知门电路的|I IS|=1.5mA,I IH=10μA,|I OL|=15mA,|I OH|=400μA。
试问电路带负载门个数N= 。
解:5S10102B三态门具有、、三种状态,因此常用于结构中。
解:断开、导通、高阻、数据总线S10102G常用的可直接用于线与的门电路有与非门和与非门。
解:集电极开路、三状态S10102I正与门和门等效。
解:负或S10102N电路中的二极管均为理想二极管,各二极管的状态(导通或截止)和输出电压V o 的大小分别为:D 1 ;D 2 ;D 3 ;V O 。
解:截止、截止、导通、1VS10103B在图中所示电路中,当电路其他参数不变:仅R b 减小时,三极管的饱和程度 ;仅R b 增大时,三极管的饱和程度 ,它的饱和压降V CES 。
解:加深、减轻、增大S10103GTTL 与非门电路中,为了提高工作速度可采取以下措施:(1) ,(2) ,(3) 。
解:(1)采用抗饱和三极管(2)输出选用复合管(3)加大电阻阻值S10103I双极性三极管饱和工作状态的条件是 。
解:i B <βCSIS10104BTTL 或非门多余输入端的处理是 。
解:接地或接固定低电平S10201BNMOS 管的开启电压V GS(th)=2V ,外加漏源电压V DD =10V ,为使管子截止,则要求V GS(th)A. >2VB. =2VC. <2V 解:CS10201G 在图中,选择能实现给定逻辑功能A Y =的电路是( )。
2.1基本逻辑运算和基本门电路
第二章逻辑代数与逻辑门电路基本要求:理解“与”逻辑及“与”门、“或”逻辑及“或”门、“非”逻辑及“非”门;理解正、负逻辑的概念,掌握逻辑代数的基本定律、基本规则和常用公式;理解复合逻辑的概念;了解集成门电路的分类;理解TTL、MOS门电路;理解逻辑函数的表示方法;掌握逻辑函数的代数化简法和卡诺图化简法。
本章主要内容:介绍逻辑代数、集成逻辑门电路和逻辑函数化简。
逻辑代数是数字电路的理论基础,是组合逻辑和时序逻辑电路分析、设计中要用到的基本工具;集成逻辑门电路是组成数字逻辑电路的基本单元电路;逻辑函数化简是逻辑电路分析的基础。
本章重点:基本逻辑门电路和功能逻辑代数的基本定律及常用公式逻辑函数的代数化简法本章难点:基本定律、公式及化简法的正确与准确一、逻辑变量与逻辑函数:在逻辑代数中的变量称逻辑变量,用字母A、B、C……来表示。
逻辑变量只能有两种取值:真和假。
常把真记作“1”,假记作“0”。
这里的“1”和“0”并不表示数量的大小,而是表示完全对立的两种状态。
在逻辑问题的研究中,涉及到问题产生的条件和结果。
表示条件的逻辑变量称输入变量,表示结果的逻辑变量称输出变量。
将输入变量和输出变量通过逻辑运算符连接起来的式子称逻辑函数,常用F、L表示。
基本的逻辑运算有“与”运算、“或”运算、“非”运算。
二、逻辑运算:逻辑运算的值要通过对逻辑变量进行逻辑运算来确定。
1.与运算及与门逻辑运算F与逻辑变量A、B的逻辑与运算表达式是:F=A·B, 式中“·”为与运算符。
在逻辑电路中,把能实现与运算的基本单元叫与门,它是逻辑电路中最基本的一种门电路。
二极管构成的与门电路及逻辑符号如下:2.或运算及或门逻辑函数F与逻辑变量A、B的逻辑运算表达式是:F=A+B,式中“+”为或运算符。
在逻辑电路中,把能实现或运算的基本单元叫或门。
二极管构成的或门电路及逻辑符号如下:3.非逻辑及非门对逻辑变量A进行逻辑非运算的表达式是:F=,这里的“-”是非运算符。
基本逻辑门电路
第三节基本逻辑门电路基本逻辑运算有与、或、非运算,对应的基本逻辑门有与、或、非门。
本节介绍简单的二极管门电路和BJT反相器(非门),作为逻辑门电路的基础。
用电子电路来实现逻辑运算时,它的输入、输出量均为电压(以V为单位)或电平(用1或0表示)。
通常将门电路的输入量作为条件,输出量作为结果。
一、二极管与门及或门电路1.与门电路当门电路的输入与输出量之间能满足与逻辑关系时,则称这样的门电路为与门电路。
下图表示由半导体二极管组成的与门电路,右边为它的代表符号。
图中A、B、C为输入端,L为输出端。
输入信号为+5V或0V。
下面分析当电路的输入信号不同时的情况:(1)若输入端中有任意一个为0时,例如V A=0V,而V A=V B=+5V时,D1导通,从而导致L点的电压V L被钳制在0V。
此时不管D2、D3的状态如何都会有V L≈0V (事实上D2、D3受反向电压作用而截止)。
由此可见,与门几个输入端中,只有加低电压输入的二极管才导通,并把L钳制在低电压(接近0V),而加高电压输入的二极管都截止。
(2)输入端A、B、C都处于高电压+5V ,这时,D1、D2、D3都截止,所以输出端L点电压V L=+V CC,即V L=+5V。
如果考虑输入端的各种取值情况,可以得到下表输入(V)输出(V)V A V B V C V L0 0 +5 +5 +5 +5+5+5+5+5+5+5+5+5+5将表中的+5V用1代替,则可得到真值表:A B C L0 0 1 1 1 10111111111由表中可见该门电路满足与逻辑关系,所以这是一种与门。
输入变量A、B、C与输出变量L只间的关系满足逻辑表达式。
2.或门电路对上图所示电路可做如下分析:(1)输入端A、B、C都为0V时,D1、D2、D3两端的电压值均为0V,因此都处于截止状态,从而V L=0V;(2)若A、B、C中有任意一个为+5V,则D1、D2、D3中有一个必定导通。
我们注意到电路中L点与接地点之间有一个电阻,正是该电阻的分压作用,使得V L处于接近+5V的高电压(扣除掉二极管的导通电压),D2、D3受反向电压作用而截止,这时 V L≈+5V。
理论三 逻辑门电路
1
课前预备
熟练数制间的转换
重、难点
基本逻辑运算及基本逻辑门电路
1.基本逻辑运算及基本逻辑门电路
概念
在数字电路中往往用输入信号表示“条件”,用输出信号表示“结果”,而
条件与结果之间的因果关系称为逻辑关系,能实现某种逻辑关系的数字电
子电路称为逻辑门电路。
基本的逻辑关系有:与逻辑、或逻辑、非逻辑;
能实现非逻辑功能的电路称为非门电路,又称 反相器 ,简称非
门
非门电路的电路图形符号
非逻辑函数表达式: =
ഥ
非逻辑功能为:“有0出1,有1出0”
2.复合逻辑运算
几种常用的复合逻辑运算
• 与非
或非
与或非
几种常用的复合逻辑运算
• 异或
• Y= A B
A
B
Y
0
0
0
0
1
1
1
0
1
1
1
0
几种常用的复合逻辑运算
与之相应的基本逻辑门电路有:与门、或门、非门。来自逻辑代数中的三种基本运算
与(AND)
或(OR)
非(NOT)
以A=1表示开关A合上,A=0表示开关A断开;
以Y=1表示灯亮,Y=0表示灯不亮;
三种电路的因果关系不同:
一、与逻辑和与门电路
1.与逻辑关系
当一件事情的几个条件全部具备之后,这件事情才能发生,否则不
三极管、MOS管和电阻等分立元件组成,也可以由集成电路组成。
与逻辑的真值表
与逻辑功能为:
“有0出0,全1出1”
与门电路的电路图形符号
逻辑表达式Y=A·B或
Y=AB
二、或逻辑和或门电路
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
通常,把反映“条件”和“结果”之间的关系称为逻辑关系。
如果以电路的输入信号反映“条件”,以输出信号反映“结果”,此时电路输入、输出之间也就存在确定的逻辑关系。
数字电路就是实现特定逻辑关系的电路,因此,又称为逻辑电路。
逻辑电路的基本单元是逻辑门,它们反映了基本的逻辑关系。
基本逻辑关系和逻辑门2.1.1基本逻辑关系和逻辑门逻辑电路中用到的基本逻辑关系有与逻辑、或逻辑和非逻辑,相应的逻辑门为与门、或门及非门。
一、与逻辑及与门与逻辑指的是:只有当决定某一事件的全部条件都具备之后,该事件才发生,否则就不发生的一种因果关系。
如图 2.1.1所示电路,只有当开关 A 与 B 全部闭合时,灯泡Y 才亮;若开关 A 或 B 其中有一个不闭合,灯泡Y就不亮。
这种因果关系就是与逻辑关系,可表示为Y= AB,读作“A 与 B”。
在逻辑运算中,与( a)常用符号(b)国标符号图 2.1.1与逻辑举例图 2.1.2与逻辑符号逻辑称为逻辑乘。
与门是指能够实现与逻辑关系的门电路。
与门具有两个或多个输入端,一个输出端。
其逻辑符号如图 2.1.2所示,为简便计,输入端只用 A 和 B 两个变量来表示。
与门的输出和输入之间的逻辑关系用逻辑表达式表示为:Y= AB= AB两输入端与门的真值表如表 2.1.1所示。
波形图如图所示。
表 2.1.1与门真值表A B Y0 0 00 1 01 0 01 1 1图 2.1.3与门的波形图由此可见,与门的逻辑功能是,输入全部为高电平时,输出才是高电平,否则为低电平。
二、或逻辑及或门或逻辑指的是:在决定某事件的诸条件中,只要有一个或一个以上的条件具备,该事件就会发生;当所有条件都不具备时,该事件才不发生的一种因果关系。
如图 2.1.4 所示电路,只要开关 A 或 B 其中任一个闭合,灯泡 Y 就亮; A、B 都不闭合,灯泡Y 才不亮。
这种因果关系就是或逻辑关系。
可表示为:Y=A+B读作“A 或 B”。
在逻辑运算中或逻辑称为逻辑加。
图 2.1.4或逻辑举例(a)常用符号(b)国标符号图 2.1.5 或逻辑符号或门是指能够实现或逻辑关系的门电路。
或门具有两个或多个输入端,一个输出端。
其逻辑符号如图 2.1.5所示。
或门的输出与输入之间的逻辑关系用逻辑表达式表示为:Y=A+ B两输入端或门电路的真值表和波形图分别如表 2.1.2和图所示。
表 2.1.2A B Y0 0 00 1 11 0 11 1 1图 2.1.6或门的波形图由此可见,或门的逻辑功能是,输入有一个或一个以上为高电平时,输出就是高电平;输入全为低电平时,输出才是低电平。
三、非逻辑及非门非逻辑是指:决定某事件的唯一条件不满足时,该事件就发生;而条件满足时,该事件反而不发生的一种因果关系。
(a)常用符号( b)国标符号图 2.1.7非逻辑举例如图 2.1.7所示电路,当开关 A 闭合时,灯泡Y 不亮;当开关这种因果关系就是非逻辑关系。
可表示为Y=,读作“A 非”或“非非逻辑称为“求反”。
图 2.1.8非逻辑符号A 断开时,灯泡Y 才亮。
A”。
在逻辑代数中,非门是指能够实现非逻辑关系的门电路。
它有一个输入端,一个输出端。
其逻辑符号如图 2.1.8所示。
表 2.1.3 非门的输出与输入之间的逻辑关系用逻辑表达式表示为:Y =A Y0 110图 2.1.9非门的波形图其真值表和波形图分别如表 2.1.3和图所示。
由此可见,非门的逻辑功能为,输出状态与输入状态相反,通常又称作反相器。
2.1.2复合逻辑门由与门、或门和非门可以组合成其他逻辑门。
把与门、或门、非门组成的逻辑门叫复合门。
常用的复合门有与非门、或非门、异或门、与或非门等。
一、与非门将一个与门和一个非门按图 2.1.10连接,就构成了一个与非门。
与非门有多个输入端,一个输出端。
三端输入与非门的逻辑符号如图所示,它的逻辑表达式为:Y==( a)常用符号(b)国标符号图 2.1.10与非逻辑图 2.1.11与非逻辑符号真值表和波形图分别如表 2.1.4和图所示。
表 2.1.4A B C Y0 0 0 10 0 1 10 1 0 10 1 1 11 0 0 11 0 1 11 1 0 11 1 1 0图 2.1.12 与非门的波形由此可知,与非门的逻辑功能为:当输入全为高电平时,输出为低电平;当输入有低电平时,输出为高电平。
二、或非门把一个或门和一个非门连接起来就可以构成一个或非门,如图 2.1.13所示。
或非门也可有多个输入端和一个输出端。
三端输入或非门的逻辑符号如图 2.1.14所示,它的逻辑表达式为:Y=真值表和波形图分别如表 2.1.5和图所示。
( a)常用符号( b)国标符号图 2.1.13 或非逻辑图 2.1.14 或非逻辑符号由此可知,或非门的逻辑功能为:当输入全为低电平时,输出为高电平;当输入有高电平时,输出为低电平。
表 2.1.5A B C Y0 0 0 10 0 1 00 1 0 00 1 1 01 0 0 01 0 1 01 1 0 0图 2.1.15或非门的波形图1 1 10三、异或门当两个输入变量的取值相同时,输出变量取值为 0;当两个输入变量的取值相异时,输出变量取值为 1。
这种逻辑关系称为异或逻辑。
能够实现异或逻辑关系的逻辑门叫异或门。
异或门只有两个输入端和一个输出端,其逻辑符号如图 2.1.16 ( a)所示。
异或门的逻辑表达式为:Y=A·+·B= A⊕ B(a) 逻辑符号(b)波形图图 2.1.16异或门的逻辑符号和波形图式中,符号⊕表示异或逻辑。
异或门真值表如表 2.1.6所示。
波形图如图(b)所示。
异或门的逻辑功能可简述为:输入相异,输出为高电平。
输入相同,输出为低电平。
表 2.1.6异或门真值表A B Y0 0 00 1 11 0 11 1 0图 2.1.17与或非门的逻辑符号和波形图四、与或非门把两个与门、一个或门和一个非门联结起来,就构成了与或非门。
它有多个输入端、一个输出端,逻辑符号如图 2.1.17 ( a)所示。
其逻辑表达式为:Y =真值表如表 2.1.7所示,波形图见图(b)。
与或非门的逻辑功能是:当任一组与门输入端全为高电平或所有输入端全为高电平时,输出为低电平;当任一组与门输入端有低平或所有输入端全为低电平时,输出为高电平。
表 2.1.7与或非门真值表输入输出ABCD Y0 0 0 0 10 0 0 1 10 0 1 0 10 0 1 1 00 1 0 0 10 1 0 1 10 1 1 0 10 1 1 1 01 0 0 0 11 0 0 1 11 0 1 0 11 0 1 1 01 1 0 0 01 1 0 1 01 1 1 0 01 1 1 1 0逻辑代数基础逻辑代数是讨论逻辑关系的一门学科,它是分析和设计逻辑电路的数学基础。
逻辑代数是由英国科学家乔治·布尔(George·Boole )创立的,故又称布尔代数。
逻辑代数也是用字母表示变量,但是逻辑代数和普通代数有着根本的区别。
逻辑代数中的逻辑变量只有两种可能取值——0 和1,而且这里的0 和 1 不同于普通代数中的0和1。
它只表示两种对立的逻辑状态,并不表示数量的大小。
2.2.1逻辑代数的基本定理与规则在逻辑运算中,基本的逻辑关系有与、或、非三种。
在逻辑代数中,相应地也有三种基本运算,即与运算、或运算和非(求反)运算。
1.与运算(逻辑乘)图 T1101 所示与门电路的逻辑关系为Y= AB,由此可得与运算的规则为:0·0=0 0 ·1=0 1 ·0=0 1 ·1= 1A·0=0 A·1=A A·A=A2.或运算(逻辑和)图T1104 所示或门电路的逻辑关系为0+0=00+1=1 Y= A+ B,由此可得或运算的规则为:1+0=11+1=1A+0 = A A+1 =1 A+A = A3.非运算(求反运算)图 T1107 所示非门电路的逻辑关系为Y=,由此可得非运算的规则为:=1 = 0A+ =1 A·=0= A2.2.2逻辑代数的基本定律逻辑代数不但有与普通代数相似的交换律、结合律和分配律,其本身还有一些特殊定律。
常用的定律如下:(1)交换律A·B=B·A A + B= B+ A(2)结合律(A·B)· C=A·(B·C)(A+B)+ C = A+( B+ C)(3)分配律A·( B+ C)=A· B+A·CA 十 BC=( A+B)( A+C)(4)重迭律A·A= A A +A= A(5) 0-1 律0·A= 00 +A=A1·A=A1+A= 1( 6)互补律A·= 0A+= 1( 7)摩根定律=+=·( 8)吸收律A·( A+ B)= A A +AB=A1)与门 (AND Gate)[ 学生活动 ]通过演示实验,学习与门电路的逻辑关系。
观察实验结果,填写真值表。
输入输出A B Z0 0 00 1 01 0 01 1 1我们把输入 A 与输入 B 均是高电势时,输出Z 才是高电势的逻辑电路叫做与门。
[ 讨论 ] 与逻辑为:当决定某一事件的所有条件全部具备时,这一事件才会发生。
与门用来实现与逻辑关系的电路。
A&ZB与门的符号(2)或门 (OR Gate)[ 学生活动 ]分组实验,填写真值表。
输入输出A B Z00001 110 111 1我们把输入 A 与输入 B 任一个或者两个都为高电势时,输出Z就为高电势的逻辑电路叫做或门。
[ 讨论 ] 或逻辑为:当决定某一事件的各个条件中,只要一个或一个以上条件成立,这一事件就会发生。
与门的符号A≥ 1ZB(2)非门 (NOT Gate)观察演示实验,填写真值表。
输入输出A Z0 110我们把输入 A 为高电势时输出Z 为低电势输入 A 为低电势时输出Z 为高电势的逻辑电路叫做非门。
事件不发生;条件不非逻辑为:当某一事件的发生总是和条件相反,即条件成立,成立,事件发生。
A1Z非门的符号。
