材力 第五章
材料力学 第五章扭转变形.强度、刚度条件(6,7,8)汇总
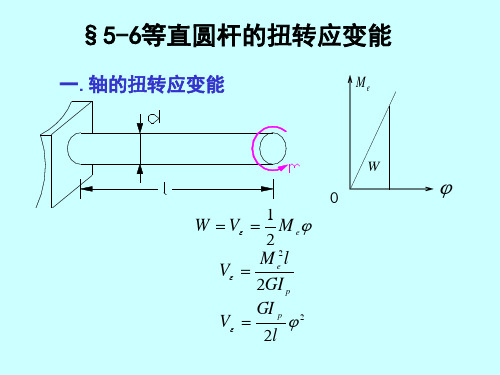
( 4)
例题 6-6
5. 实心铜杆横截面上任意点的切应力为 Ta Ga M e 0 ra ρa I pa Ga I pa Gb I pb 空心钢杆横截面上任意 点的切应力为
b
Tb Gb M e I pb Ga I pa Gb I pb
2
1 dV (dxdydz ) 2 dV dW v dV dxdydz 1 v 2
一、密圈螺旋弹簧
——螺旋角
F
O
d
d ——簧丝横截面的直径 D ——弹簧圈的平均直径
O D
密圈螺旋弹簧 ——螺旋角<5°时的圆柱形弹簧
§4.5
密圈螺旋弹簧的计算
O F
例题 6-6
Me Tb Ta
解: 1. 实心铜杆和空心钢杆横截面上的扭矩分别为Ta 和Tb(图b),但只有一个独立平衡方程 Ta+Tb= Me (1) 故为一次超静定问题。
例题 6-6
Me Tb Ta
2. 位移相容条件为实心杆和空心杆的B截面相对 于A截面的扭转角相等。在图b中都用表示(设 A端固定)。 Ba Bb ( 2)
a
b
ra
ra
a rb
切应力沿半径的变化 情况如图c所示。
ra
rb
(c)
§5-8非圆截面等直杆扭转的概念
圆截面杆扭转时的应力和变形公式,均建立在平 面假设 的基础上。对于非圆截面杆,受扭时横截面不 再保持为平面,杆的横截面已由原来的平面变成了曲 面。这一现象称为截面翘曲。因此,圆轴扭转时的应 力、变形公式对非圆截面杆均不适用。
(2)
材料力学课件第5章

M
zM
x
等截面梁
y
注意 当梁为变截面梁时, max 并不一定
发生在|M|max 所在面上.
22
5.3 横力弯曲时梁横截面上的正应力 弯曲正应力强度条件
h
常用图y形Wz
c b
Wz =Iz /ymax
z
Wz
Iz h
bh3 2 12 h
bh2 6
2
h2
h1
y
c
z
Wz
Iz h1
1 ( b1h13 h1 6
z
于是
M
E
Iz
M
得
1 M
EIz
y
x
代入
E
y得
My
Iz
15
5.2 纯弯曲时梁横截面上的正应力
常用图形y、Iz
h
y
1.矩形
dy
c
y z
Iz
Ay2 d A
h 2
y2b d y bh3
h 2
12
b
y
同理:
Iy
hb3 12
z
Iz
b1h13 12
b2h23 12
c
b2 b1
同理: I y
h1b13 12
y
12 rp
mn
x2
x
x1
12
dx
'=
x2 FN1
FN2
'=
38
5.4 横力弯曲时梁横截面上的切应力 弯曲切应力强度条件
F
Fx 0
FN 2 FN1 dx b
x1
y
12 rp mn
x2
x
12
dx
材料力学第五章 弯曲应力分析

B
D
1m
1m
1m
y2
20
120
FRA
F1=9kN FRB F2=4kN
A C
BD
1m
1m
1m
2.5 Fs
+
+
4 kN
-
6.5 2.5
M
kNm
-
+
4
解: FRA 2.5kN FRB 10.5kN
88
52
-
+
C 2.5
4 B 80
z
20
120
20
B截面
σ t max
M B y1 Iz
4 • 52 763
20
+
-
+
10
Fs
kN
10
20
30
30
25
25
M
kNm
max
M max W
[ ]
W Mmax 30 187.5cm3
[ ] 160
1)圆 W d 3 187.5
32
d 12.4cm
A d 2 121cm2
4
2)正方形
a3 W 187.5
6
3)矩形
a 10.4cm
A a2 108cm2
压,只受单向拉压. (c)同一层纤维的变形相同。 (d)不同层纤维的变形不相同。
推论:必有一层变形前后长度不变的纤维—中性层
中性轴
中性轴⊥横截面对称轴
中性层
横截面对称轴
二、变形几何关系
dx
dx
图(a)
O
O
zb
O yx b
y
图(b)
《材料力学》 第五章 弯曲内力与弯曲应力

第五章 弯曲内力与应力 §5—1 工程实例、基本概念一、实例工厂厂房的天车大梁,火车的轮轴,楼房的横梁,阳台的挑梁等。
二、弯曲的概念:受力特点——作用于杆件上的外力都垂直于杆的轴线。
变形特点——杆轴线由直线变为一条平面的曲线。
三、梁的概念:主要产生弯曲变形的杆。
四、平面弯曲的概念:受力特点——作用于杆件上的外力都垂直于杆的轴线,且都在梁的纵向对称平面内(通过或平行形心主轴且过弯曲中心)。
变形特点——杆的轴线在梁的纵向对称面内由直线变为一条平面曲线。
五、弯曲的分类:1、按杆的形状分——直杆的弯曲;曲杆的弯曲。
2、按杆的长短分——细长杆的弯曲;短粗杆的弯曲。
3、按杆的横截面有无对称轴分——有对称轴的弯曲;无对称轴的弯曲。
4、按杆的变形分——平面弯曲;斜弯曲;弹性弯曲;塑性弯曲。
5、按杆的横截面上的应力分——纯弯曲;横力弯曲。
六、梁、荷载及支座的简化(一)、简化的原则:便于计算,且符合实际要求。
(二)、梁的简化:以梁的轴线代替梁本身。
(三)、荷载的简化:1、集中力——荷载作用的范围与整个杆的长度相比非常小时。
2、分布力——荷载作用的范围与整个杆的长度相比不很小时。
3、集中力偶(分布力偶)——作用于杆的纵向对称面内的力偶。
(四)、支座的简化:1、固定端——有三个约束反力。
2、固定铰支座——有二个约束反力。
3、可动铰支座——有一个约束反力。
(五)、梁的三种基本形式:1、悬臂梁:2、简支梁:3、外伸梁:(L 称为梁的跨长) (六)、静定梁与超静定梁静定梁:由静力学方程可求出支反力,如上述三种基本形式的静定梁。
超静定梁:由静力学方程不可求出支反力或不能求出全部支反力。
§5—2 弯曲内力与内力图一、内力的确定(截面法):[举例]已知:如图,F ,a ,l 。
求:距A 端x 处截面上内力。
解:①求外力la l F Y l FaF m F X AYBY A AX)(F, 0 , 00 , 0-=∴==∴==∴=∑∑∑ F AX =0 以后可省略不求 ②求内力xF M m l a l F F F Y AY C AY s ⋅=∴=-==∴=∑∑ , 0)( , 0∴ 弯曲构件内力:剪力和弯矩1. 弯矩:M ;构件受弯时,横截面上存在垂直于截面的内力偶矩。
材料力学第5章-剪力图与弯矩图

第5章 梁的强度问题
剪力方程与弯矩方程
建立剪力方程和弯矩方程的方法与过程,实际上与前面所 介绍的确定指定横截面上的剪力和弯矩的方法和过程是相似的 ,所不同的,现在的指定横截面是坐标为x的横截面。
需要特别注意的是,在剪力方程和弯矩方程中,x是变量, 而FQ(x)和M(x)则是x的函数。
第5章 梁的强度问题
剪力方程与弯矩方程
例题2
MO=2FPl
FP
B
A
C
l
l
悬臂梁在B、C两处分别承受集中力FP和集中力偶M=2FPl
的作用。梁的全长为2l。 试写出:梁的剪力方程和弯矩方程。
第5章 梁的强度问题
剪力方程与弯矩方程
y
MO=2FPl
O
A
C
l
FP
B l
解:1.确定控制面和分段
本例将通过考察截开截面的右
边部分平衡建立剪力方程和弯矩方 程,因此可以不必确定左端的约束 力。
本章首先介绍如何建立剪力方程和弯矩方程;讨论载荷、 剪力、弯矩之间的微分关系;怎样根据载荷、剪力、弯矩之间 的微分关系绘制剪力图与弯矩图;然后应用平衡、变形协调以 及物性关系,建立确定弯曲的应力和变形公式;最后介绍弯曲 强度设计方法。
第5章 梁的强度问题
工程中的弯曲构件 梁的内力及其与外力的相互关系 剪力方程与弯矩方程 载荷集度、剪力、弯矩之间的微分关系 剪力图与弯矩图 刚架的内力与内力图 结论与讨论(1)
根据以上分析,不难得到结论: 杆件各截面上内力变化规律随着外力的 变化而改变。
第5章 梁的强度问题
梁的内力及其与外力的相互关系
所谓剪力和弯矩变化规律是指表示剪力和弯矩变 化的函数或变化的图线。这表明,如果在两个外力 作用点之间的梁上没有其他外力作用,则这一段梁 所有横截面上的剪力和弯矩可以用同一个数学方程 或者同一图线描述。
材料力学第五章

F l a x
l
材料力学
第五章 梁的剪力图与弯矩图
梁的横截面上位于横截面 内的内力FS是与横截面左右两 侧的两段梁在与梁轴相垂直方 向的错动(剪切)相对应,故称 为剪力;梁的横截面上作用在 纵向平面内的内力偶矩是与梁 的弯曲相对应,故称为弯矩。
材料力学
第五章 梁的剪力图与弯矩图
为使无论取横截面左边或右边为分离体,求得同一横
截面上的剪力和弯矩其正负号相同,剪力和弯矩的正负号
要以其所在横截面处梁的微段的变形情况确定,如下图。
材料力学
第五章 梁的剪力图与弯矩图
综上所述可知: (1) 横截面上的剪力——使截开部分梁产生顺时针方向
转动为正;产生逆时针方向转动为负。
(2) 横截面上的弯矩——作用在左侧面上使截开部分 逆时针方向转动,或者作用在右侧截面上使截开部分顺时 针方向转动者为正;反之为负。
图d,e所示梁及其约束力不能单独利用平衡方程确定, 称为超静定梁。
材料力学
第五章 梁的剪力图与弯矩图
§5.2 梁的内力及其与外力的相互关系
Ⅰ. 梁的剪力和弯矩(梁的横截面上的两种内力)
图a所示跨度为l的简支梁其
约束力为:
FA
Fl
l
a,
FB
Fa l
梁的左段内任一横截面m-
m上的内力,由m-m左边分离
杆件:某一方向尺寸远大于其它方向尺寸的构件。 直杆:杆件的轴线为直线。 杆的可能变形为:
轴向拉压—内力为轴力。如拉、撑、活塞杆、钢缆、柱。
扭转 —内力为扭矩。如各种传动轴等。
(轴)
弯曲 —内力为弯矩。如桥梁、房梁、地板等。(梁)
材料力学
梁的分类
F
q
第五章 梁的剪力图与弯矩图
材料力学第五章

y
= ∫ y dA
2 A
1 1 π ⋅ d4 π ⋅ d4 I y = Iz = I ρ = ⋅ = z 2 2 32 64
1 π ⋅ (D4 − d 4 ) 对空心圆截面: 对空心圆截面: I = I = I = y z ρ 2 64
第五章 弯曲应力
§5-2 对称弯曲正应力 对称弯曲正应力
M⋅ y 二、弯曲正应力一般公式: 弯曲正应力一般公式: σ= Iz
Ip
弯曲 剪力Q 剪力
?
第五章 弯曲应力
§5-1 引言 y
梁段
M τ Q
z
σ
横截面上剪应力 横截面上正应力
横截面上内力
Q = ∫τdA
剪应力造成剪力
M = ∫σydA
正应力造成弯矩
剪应力和正应力的分布规律是什么? 剪应力和正应力的分布规律是什么?
超静定问题
第五章 弯曲应力
§5-1 引言
§5-2 对称弯曲正应力 对称弯曲正应力 §5-3 对称弯曲切应力 对称弯曲切应力 弯曲 §5-4 梁的强度条件与合理强度设计 梁的强度条件与合理强度设计 §5-5 双对称截面梁的非对称弯曲 双对称截面梁的非对称弯曲 §5-6 弯拉(压)组合 弯拉( 对称弯曲(平面弯曲): 对称弯曲(平面弯曲): 外力作用在纵向对称面内, 外力作用在纵向对称面内,梁轴线变形 后为一平面曲线,也在此纵向对称面内。 后为一平面曲线,也在此纵向对称面内。
(3)
Mz = ∫ σ ⋅ y ⋅ dA = M (5) A E 2 E 2 E (5) M z = ∫ ρ y dA = ∫ y dA = ρ I z = M
A
ρ
A
1 M = ρ EIz
第五章 弯曲应力
材料力学第5章弯曲应力

M
M
中性轴
z
m
n
y
o
o
dA
z
mn
y
dx
Mzy
Iz
max
Mz Wz
M
MZ:横截面上的弯矩
y:到中性轴的距离
IZ:截面对中性轴的惯性矩
M
中性轴
§5-2 惯性矩的计算
一、静矩 P319
y
Sz ydA
A
z dA
zc
c y
S y zdA
yc
A
o
z
分别为平面图形对z 轴和 y 轴的静矩。
ySc Az ydA
F M
F
a
B
F
Fa
5.3 梁弯曲时的正应力
若梁在某段内各横截
面上的弯矩为常量, F
F
a
a
剪力为零, 则该段梁 A 的弯曲就称为纯弯曲。
B
Fs
在 AC 和 DB 段 内 横 截 面上既有弯矩又有剪 M 力, 这种情况称为横 力弯曲或剪切弯曲。
F F
Fa
平面假设
变形前原为平面的梁的横截面变形后仍保持为 平面, 并绕垂直于纵对称面的某一轴旋转, 且仍 然垂直于变形后的梁轴线。这就是弯曲变形的 平面假设。
C y'
a
x'
xc
b
注意!C点必须为截面形心。
六、组合截面的惯性矩
Iy Iyi
Iz Izi
例2:求对倒T字型形心 轴yC和zC的惯性矩。
解:1. 取参考轴yOz 2. 求形心
2cm y(yc)
1 c1
6 cm
yc
Ai yi A
y
c 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5—3 图示悬臂梁,横截面为矩形,承受载荷F 1与F 2作用,且F 1=2F 2=5 kN,试计算梁内的最
大弯曲正应力,及该应力所在截面上K 点处的弯曲正应力。
解:(1) 画梁的弯矩图:
(2) 最大弯矩(位于固定端):
max 7.5 M kN =
(3) 计算应力: 最大应力:
K 点的应力:
5—4 图示梁,由No22槽钢制成,弯矩M =80 N 、m,并位于纵向对称面(即x-y 平面)内。
试求
梁内的最大弯曲拉应力与最大弯曲压应力。
6max max max
227.510176 408066
Z
M M MPa
bh W σ⨯====⨯6max max 33
7.51030
132 ********
K Z
M y M y MPa bh I σ⋅⋅⨯⨯====⨯40
1m F 1
C y 1m F 2 80 K
z
30 M M y
z
y 0 b C
s F ()-
kN
5.2 kN 5
(+)
7、5kNm
x
M
5kN
kNm 5.7
kNm 5
解:(1) 查表得截面的几何性质:
4020.3 79 176 z y mm b mm I cm ===
(2) 最大弯曲拉应力(发生在下边缘点处):
()30max
8
80(7920.3)10 2.67 17610x M b y MPa I σ
-+-⋅-⨯-⨯===⨯ (3) 最大弯曲压应力(发生在上边缘点处):
30max
8
8020.3100.92 17610x M y MPa I σ
---⋅⨯⨯===⨯
5—5图示简支梁,由No18工字钢制成,在集度为q 的均布载荷作用下,测得横截面C 底边的纵
向正应变ε=3、0×10-4,试计算梁内的最大弯曲正应力,已知钢的弹性模量E =200 Gpa,a =1 m 。
解:(1) 求支反力:
31 44
A B R qa R qa ==
(2) 画内力图:
(3) 由胡克定律求得截面C 下边缘点的拉应力为:
q
x
x
F S
M
49
max
3.010*******
C
E MPa
σε
+-
=⋅=⨯⨯⨯=也可以表达为:
2
max
4
C
C
z z
qa
M
W W
σ+==
(4) 梁内的最大弯曲正应力:
2
max
max max
9
9
3267.5
8C
z z
qa
M
MPa
W W
σσ+
====
5—12图示矩形截面木梁,许用应力[σ+]=10MPa。
(1)试根据强度要求确定截面尺寸b;
(2)若在截面A处钻一直径d=60mm的圆孔,试问就是否安全。
(1)解:如图所示为剪力弯矩图,由图可知:
x
kN
3
kN
5
s
F
M
kNm
13
kNm
3x
()-
kNm M 13max -=
26
h b W z =
z
W M max
max =
σ []+≤σσmax
解得:mm
b 125.0≥
(2)
6
125.0125.02⨯=总
z W
34-m 1026.3⨯=
6
03.0125.02
1⨯=z I
35m 10875.1-⨯=
z I =1-z z I I 总
33-z m 1007.3⨯=I
[]+≤==
σσMPa W M A
79.7z
所以安全
5—13 图示槽形截面悬臂梁,F =10 kN,M e =70 kNm,许用拉应力[σ+]=35 MPa,许用压应力
[σ-]=120 MPa,试校核梁的强度。
解:(1) 截面形心位置及惯性矩:
z C
112212(150250)125(100200)150
96 (150250)(100200)
C A y A y y mm A A ⋅+⋅⨯⋅+-⨯⋅=
==+⨯+-⨯
332
284
1505025200(15050)(25)2(25200)(150)12121.0210 zC
C C I y y mm ⎡⎤⨯⨯=+⨯⋅-++⨯⋅-⎢⎥
⎣⎦=⨯ (2) 画出梁的弯矩图:
(3) 计算应力
A +截面下边缘点处的拉应力及上边缘点处的压应力分别为:
68(250)
4010(25096)60.4 1.0210C A A zC M y MPa I σ
++
+⋅-⨯-=
==⨯
68
40109637.61.0210
C
A A zC
M y MPa I σ-
++
⋅⨯⨯=
==⨯ A -截面下边缘点处的压应力为:
68
(250)
3010(25096)45.3 1.0210C A A zC
M y MPa I σ
--
-⋅-⨯-=
==⨯
可见梁内最大拉应力超过许用拉应力,梁不安全。
5—14图示铸铁梁,载荷F 可沿梁AC 水平移动,其活动范围为0<η<3l/2,试确定载荷F 的许用值。
已知许用拉应力[σt ]=35MPa,许用压应力[σc ] =140MPa,l=1m 、
M x
40kNm
30kNm
(+)
(-)
10kNm
s F
kN 10
()+
解:y c =(
020
.0080.0020.0010.0060
.0020.0080.0010.0020.0100.0⨯+⨯⨯⨯+⨯⨯)m=0、03222m
]m )03222.0060.0(080.0020.012080.0020.002222.0020.0100.012020.0100.0[4232
3-⨯⨯+⨯+⨯⨯+⨯=z I 46-m 10142.3⨯=z I
分析可知可能的危险面有两个:当F 作用在AB 段时,危险位置就是:
η=
2l ,4
max Fl M =+ 此时剪力弯矩图如图所示:
2
F ()+
s F
4
Fl M
()+
20
100
20
80
100
c y
20
20
80
y
当F 作用在BC 段时,危险位置就是:
η=23l ,|-m ax M |=2
Fl 此时剪力弯矩图如图所示:
确定载荷F 的许用值:
由危险面B 的压力强度要求:
[]c c z
c c y I Fl
y M σσ≤-=-⨯=)100.0(2)100.0(I | |z -max max ,
得:
F ≤)(c y -000.1l ]
2Iz[c σ=)(03222.0-100.01.00010140103.14226-6⨯
⨯⨯⨯⨯N =N N k 98.1210298.14=⨯
由截面B 的拉应力强度要求:
][2|M |-max max t t C Z
c z y I fl
y I σσ≤==,
得:
kN N N
ly I F c t z 83.61083.6)
03222.0100.0(000.11014010142.32][2366=⨯=-⨯⨯⨯⨯⨯=≤-σ
由+
m ax M 作用面的拉应力强度要求:
][-100.04-100.0|M |max max t t C Z
c z y I Fl y I σσ≤==+)()(, 得
()+
()-
()-
F
2
F s F
M
2
Fl
kN N N
y l I F c t z 49.61049.6)
03222.0100.0(000.1103510142.34-100.0][4366=⨯=-⨯⨯⨯⨯⨯=≤-)(σ
比较以上结果,最后确定取载荷的许用值为:
F=6、49kN。
