点集拓扑学-拓扑空间和连续映射1
《点集拓扑》课件

点集拓扑的基本性质
01
02
03
04
性质1
任意两个不同的点不能是等价 的。
性质2
有限多个开集的并集仍然是开 集。
性质3
闭集的补集是开集。
性质4
连续映射下的开集和闭集保持 不变。
点集拓扑的重要性
应用广泛
点集拓扑在数学、物理学、工程 学等领域都有广泛应用,如微分 几何、代数几何、微分方程等领
域。
基础学科
点集拓扑是数学的一门基础学科, 为其他学科提供了数学工具和语言 ,促进了数学的发展。
理论意义
点集拓扑的研究有助于深入探讨数 学中的一些基本问题,如连续性、 连通性、紧致性等,推动了数学理 论的发展。
02
拓扑空间与基
拓扑空间的定义
总结词
抽象的空间
详细描述
拓扑空间是一个由点集构成的空间,这些点集通过集合的并、交、补等运算形 成。它是一个抽象的概念,不依赖于度量或连续性的具体性质。
连通性与道路连通性
连通性的定义与分类
总结词
连通性是描述点集拓扑空间中点之间的相互关系的重要概念,它分为三种类型:强连通 、弱连通和道路连通。
详细描述
连通性定义为一个点集拓扑空间中任意两点可以通过一系列连续变换(如移动、旋转、 缩放等)相互到达。根据连通性的不同性质,可以分为强连通、弱连通和道路连通三种 类型。强连通是指任意两点都相互可达;弱连通是指任意两点至少有一个可达;道路连
基的定义与性质
总结词
定义与性质
详细描述
基是拓扑空间中一个特殊的子集系统,它具有一些重要的性质,如基的任意并仍 属于基,基的有限交仍属于基等。基是定义拓扑空间的重要工具。
基在拓扑空间中的应用
点集拓扑学(第一章1.1)

1736年欧拉 解决七桥问题
哥尼斯堡 七桥问题 四色问题 Euler示性数
1976年9月四
Mö bius带
色问题得到解决
Department of Mathematics
哥尼斯堡七桥问题
哥尼斯堡是东普鲁士的首都,普莱格尔河横贯其中。 十八世纪在这条河上建有七座桥,将河中间的两个岛和河
岸联结起来。人们闲暇时经常在这上边散步
一天有人提出:能不能每座桥 都只走一遍,最后又回到原来的
位置。
这个问题看起来很简单, 有很有趣的问题吸引了大家. 很多人在尝试各种各样的走法,但谁也没有做到。看
来要得到一个明确理想的答案还不那么容易
Department of Mathematics
1736年,有人带着这个问题找到了当时的大数学家 欧拉,欧拉经过一番思考,很快就用一种独特的方法给出
了解答。
他把两座小岛和河的两岸分别看作四个点, 而把七座桥看 作这四个点之间的连线。那么这个问题就简化成,能不能用一 笔就把这个图形画出来。 经过进一步的分析,欧拉得出结论——不可能每座桥都走一 遍,最后回到原来的位置。并且给出了所有能够一笔画出来的 图形所应具有的条件。这是拓扑学的“先声”。
Department of Mathematics
和数学知识,能对实际问题进行分析、归纳、
提炼和解决,提高他们的数学素养。
Department of Mathematics
教学目标
掌握拓扑空间、度量空间和连续映射的定义、例子、
性质。掌握连通性,可数性,分离性,紧性等拓扑性质。 掌握几个重要的拓扑性质的可积性、可商性和遗传性。
教学要点
拓扑空间、度量空间和连续映射的定义、例子、性 质。连通性,可数性,分离性,紧性等拓扑性质。几个重
数学中的拓扑学分支

数学中的拓扑学分支数学是一门广泛而深奥的学科,涵盖了许多分支和领域。
其中,拓扑学作为数学的一个重要分支,主要研究集合和空间的性质及其之间的映射关系。
在本文中,我们将深入探讨数学中拓扑学的几个分支,包括点集拓扑学、代数拓扑学和微分拓扑学。
一、点集拓扑学点集拓扑学是拓扑学的最基础、最基本的分支,它研究的是点集及其子集的性质。
在点集拓扑学中,我们关注的是集合中的点及其之间的关系,而不考虑度量和距离。
通过引入开集、闭集、连通性等概念,点集拓扑学研究了集合的性质,如连通性、紧致性、分离性等。
例如,欧几里得空间中的开集是指任意一点存在一个足够小的邻域,使得该邻域中的所有点仍然属于该集合。
闭集则是指集合包含了所有其极限点。
通过对开集和闭集的研究,我们可以推导出许多重要的性质,如集合的交、并、差运算、闭包、内部等。
二、代数拓扑学代数拓扑学是拓扑学中的另一个重要分支,它结合了拓扑学和代数学的方法和思想,研究了在拓扑空间上定义的代数结构。
代数拓扑学的研究内容主要包括群论、环论、域论等代数结构与拓扑空间之间的关系。
代数拓扑学的一个重要应用是同伦论,它是研究拓扑空间中连续变形的方法。
同伦论通过引入同伦等价的概念,研究了拓扑空间之间的变形和形状不变性。
例如,同伦论可以用来研究环面和球面是否同胚,即它们是否具有相同的形状。
三、微分拓扑学微分拓扑学是拓扑学中应用最广泛的分支之一,它结合了微积分和拓扑学的知识,研究了光滑流形和向量场等对象的性质。
微分拓扑学主要关注的是流形及其上的微分结构和微分同胚。
光滑流形是一个具有光滑结构的拓扑空间,它可以用来描述现实世界中的各种物理现象。
微分拓扑学通过引入切空间、切丛和微分同胚等概念,研究了流形的性质,如维度、切空间的结构、流形的切向量场等。
微分拓扑学的一个重要结果是斯托克斯定理,它建立了微分形式在流形上的积分与边界的关系,是微分几何和微分拓扑学的基础。
总结起来,数学中的拓扑学分支涵盖了点集拓扑学、代数拓扑学和微分拓扑学三个重要方向。
拓扑学的基础原理

拓扑学的基础原理拓扑学是数学的一个分支,研究的是空间中点、线、面等基本要素的性质以及它们之间的关系。
在现代数学中,拓扑学已经成为一个独立且重要的学科,应用于各个领域,如物理学、化学、计算机科学等。
本文将介绍拓扑学的基础原理,涵盖了点集、邻域、开集、闭包、连通性等概念。
一、点集与邻域拓扑学研究的基本单位是点与集合。
在拓扑学中,我们将点集视为一个整体,而不关心点之间的距离或顺序。
任何集合中的元素都被称为点。
一个点集的邻域是指包含该点并且可以通过某种方式完全包含该点的开集。
二、开集与闭包在拓扑学中,开集是一个重要的概念。
一个集合中的每个点都有一个邻域,那么我们可以将所有点的邻域的并集称为该集合的开集。
开集具有如下性质:空集和全集都是开集,开集的有限交集仍然是开集,任意多个开集的并集仍然是开集。
与开集相对应的是闭集。
闭集是指其补集为开集的集合。
闭包是一个集合与其相邻的点的闭集的并集。
闭包的性质与开集类似:全集和空集的闭包分别为全集和空集,闭集的有限并集仍然是闭集,闭包的任意多个交集仍然是闭集。
三、连通性在拓扑学中,连通性是一个重要的概念,用于描述一个集合内部的连续性。
一个集合被称为是连通的,当且仅当在该集合中的任意两点之间都存在一条连续的路径。
除了连通性,拓扑学还研究了可分性、紧性、同胚等概念。
可分性指的是一个集合中存在可数的稠密子集,稠密子集的定义为该集合中的点在其邻域内都有该稠密子集的点。
紧性是指一个集合中的任意开覆盖都可以从中选取有限个作为覆盖,而仍然可以覆盖该集合。
同胚是指两个集合通过一种特殊的映射关系相互对应,并且映射关系是双射、连续且具有连续逆映射的。
同胚也可以理解为两个具有相同结构的空间。
结论拓扑学作为数学领域中的一个重要分支,研究了空间中点、线、面等基本要素的性质及其相互关系。
通过引入点集、邻域、开集、闭包、连通性等概念,我们能够描述和分析空间的特征及其变化。
拓扑学的基础原理为其他领域的研究提供了重要的工具和方法,对理解和解决实际问题具有重要的理论意义和应用价值。
点集拓扑学教案
点集拓扑学教案为聊城大学数学科学学院数学与应用数学专业三年级本科生开设《点集拓扑》课程。
按熊金城《点集拓扑讲义》(第三版,北京:高等教育出版社, 2003)第一至七章编写的教案。
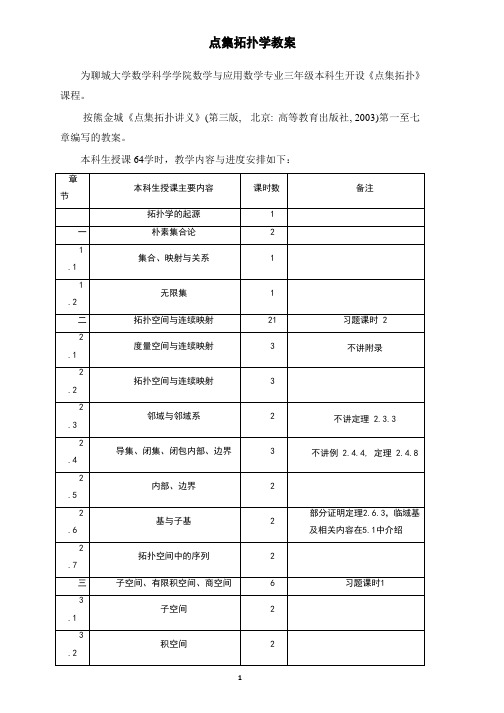
本科生授课 64学时,教学内容与进度安排如下:第一章 朴素集合论点集拓扑学(Point-set Topology)现称一般拓扑学(General Topology), 它的起源与出发点都是 集合论. 作为基本的点集拓扑学知识, 所需的只是一些朴素集合论的预备知识. 本章介绍本书中 要用到的一些集合论内容, 主要涉及集合及集族的运算、等价关系、映射、可数集、选择公理等. 作为一教材, 讲义对各部分内容均有较系统的论述 , 作为授课, 我们只强调一些基本内容, 而对 已有过了解的知识不提或少提.记号: Z, Z +, R, Q 分别表示整数集, 正整数集, 实数集和有理数集.教学重点:集合的基本概念、运算,映射的概念;教学难点:选择公理一. 集合的运算幂集 P )(X , 交∩ 、并∪、差-(补, 余/,A A c ).运算律: De Morgan 律: (1) C)-(A B)-(A C)(B -A ⋂=⋃. (2) C)-(A B)-(A C) (B -A ⋃=⋂A-(B∩ C)=(A -B)∪(A-C) 利用集合的包含关系证明(1).类似可定义任意有限个集的交或并, 如记n i ni i i n n n A A A A A A A A ≤=-==⋃⋃⋃=⋃⋃⋃11121)...(...A i . 规定 0 个集之并是φ, 不用 0 个集之交.二. 关系R 是集合X 的一个关系, 即R y x X X R ∈⨯⊂),(,记为 xRy , 称 x 与 y 是 R 相关的. R 称为自反的, 若X x ∈∀, xRx; R 称为对称的, 若 xRy, 则 yRx; R 称为传递的, 若 xRy, yRz, 则 xRz. 等价关系: 自反、对称、传递的关系.如, Δ(X)={(x, x )|x ∈X}, 恒同关系, 它是等价关系; y} x R,y x,|y) {(x,<∈,小于关系, 它是传递 的, 但不是对称的、不是自反的.设 R 是 X 上等价关系,X x ∈∀, x 的 R 等价类或等价类R [x]或[x]为 xRy}| X {y ∈,R [x] 的元称为R [x] 的代表元; 商集 X} x | {[x]R X/R ∈=.定理 1.4.1 设 R 是非空集合 X 的等价关系, 则R [x] x X,x ∈∈∀;(2)X y x, ∈∀,或者[x]R =[y]R , 或者φ=⋂R R [y] [x]证(2). 设R R [y] [x]z ⋂∈, 则zRy ZRx ,, 于是R R [y] [x]⊂且R R [y] [x]⊃, 于是R R [y] [x]=.三. 映射函数:Y X f →:.像:}|)({)(,A x x f A f X A ∈=⊂∀; 原像:})(|{)(,1B x f X x B f Y B ∈∈=⊂∀-满射、单射、一一映射(双射)、可逆映射、常值映射、恒同映射X i 、限制A f |、扩张、内射X A i A X →:|集合n i X i ≤,, 笛卡儿积∏∏=≤≤≤∈===⨯⨯⨯ni i i n i n i i n n i X x x x x X X X X X 121121},)...,{(...到第i 个坐标集iX 的投射i i X X p →: 定义为i x x p =)(, 其中),..,(1n x x x =.对等价关系,R 集合X 到商集R X /的自然投射R X X p /:→定义为 R x x p ][)(=. 四. 集族数列+∈=Z n n n }{x }{x , 有标集族τγγ∈}{A , 指标集 Γ, 与}{τγγ∈A 不同, 可记有标集族A A A ∈=γγ}{; 类似地, 定义其并 τγλ∈A (或∪A )、交 τγλ∈A (或∩ A ), 不定义 0 个集的交. 与有限集族有相同的运 算律, 如 De Morgan 律τγγτγγτγγτγγ∈∈∈∈=--=-A A A A A A A ,)(,映射对应的集族性质: τγγτγτγγγτγγ∈∈∈∈==)()(),()(A f A f A f A f ,τγγτγτγγγτγγ∈-∈∈--∈-==)()(),()(1111B fB fB fB f五. 无限集通过一一映射来确定两集合的个数的多少.有限集(φ或与某{1, 2, … , n}有一一映射), 无限集, 可数集(φ或存在X 到 Z +的单射),不可数集.易验证: 有限集是可数集, 可数集的子集是可数集, 可数集的映像是可数集. 定理 1.7.3X 是可数集X ⇔是 Z +的映像.由此, Q 是可数集, 两可数集的笛卡儿积集是可数集, 可数个可数集之并集是可数集.定理 1.7.8 R 是不可数集.利用 Cantor 对角线法证明开区间(0, 1)中的实数不可数 .直观上, 集合 A 中元素的个数称为该集合的基数, 记为card A, 或|A|. |Z +|=a , |R |=c . 若存在 从集合 A 到集合 B 的单射, 则定义|A|≤ |B|.连续统假设: 不存在基数α, 使得c a <<α选择公理: 若 A 是由非空集构成的集族, 则∈∀A A , 可取定.)(A A ∈ε.由选择公理可证明, 若βα,是基数, 则下述三式中有且仅有一成立: βαβαβα>=<,,第二章 拓扑空间与连续映射本章是点集拓扑学基础中之基础, 从度量空间及其连续映射导入一般拓扑学中最基本的两 个概念: 拓扑空间、连续映射, 分析了拓扑空间中的开集、邻域、聚点、闭集、闭包、内部、边 界、基与子基的性质,各几种不同的角度生成拓扑空间,及刻画拓扑空间上的连续性.教学重点:拓扑空间与连续映射,邻域与邻域系; 教学难点:基与子基;可度量化空间2.1 度量空间与连续映射在 R 上, |x-y|表示点 x 与 y 之间的距离. 绝对值是一非负函数, 具有三条重要性质. 定义 2.1.1 设 X 是一集合R X X →⨯:ρ. 如果满足正定性、对称性和三角不等式, 则称ρ是X 的一个度量.),(ρX 称为度量空间, y) (x,ρ表示两点 x, y 之间的距离.例 2.1.1 实数空间 R .-y|, R 的通常度量.例 2.1.2 n 维欧氏空间 R R R R n⨯⨯⨯=.... 对于nR x ∈, 记 n i i x x ≤≤=1)( 定义∑=-=ni i iy xy x 12)(),(ρ 为 R n 的通常度量, n 维欧氏空间. R 2 称为欧氏平面或平面.例 2.1.3 Hilbert 空间 H .},...),..,({1221∑∞=∞<==i i n x x x x x H∑∞=-=→→⨯12)(),(),(:i i iy xy x y x R H H ρρ定义, 易证ρ为度量 则度量空间 ),(ρH 称为 Hilbert 空间.例 2.1.4 离散度量空间.度量空间),(ρX 称为离散的, 若0,>∃∈x X x δ, 使得不存在X 中的点x y ≠, 满足xy x δρ<),(如对集合X , 按如下方式定义R X X →⨯:ρ 是X 上的离散度量:⎩⎨⎧≠==y x y x y x ,1,0),(ρ定义2.1.2 设),(ρX 是度量空间}),({),(ερε<∈=y x X y x B 称为以x 为心,ε为半径的球形邻域或ε邻域, 或球形邻域. 对(R, |.|), )+x ,-(x =) B(x, εεε.定理 2.1.1 度量空间),(ρX 的球形邻域具有性质: (1)).(,0,εεx B x X x ∈>∈∀(2))2,.(),.(),.(,0,0,,313321εεεεεεx B x B x B x X x ⋂⊂∈>∃>∈∀满足则;(3) 若 0),,(>∃∈δεx B y 使),(),(εδx B y B ⊂ ;证 (2)},min{0213εεε<<;(3)),(),(),,(εδρεδx B y B y x ⊂-=则 定义 2.1.3X 的子集A 称为),(ρX 的开集, 若A x B A a ⊂>∃∈),(,0,εε使. 每一球形邻域是开集.例 2.1.5 R 中的开区间是开集.),(b a x ∈让},min{x b a x --=ε 则 ),(),(b a x B ⊆ε 同样可证, 无限开区也是开集. 闭区间[a, b] 不是开集.定理 2.1.2 度量空间的开集具有以下性质:(1)φ,X 是开集; (2)两开集的交是开集; (3)任意开集族之并是开集. 证 (1)由定理 2.1.1(1); (2), (3)由定理 2.1.1(2).定义 2.1.4 设X 是度量空间, U X U X x ,,⊆∈ 称为x 的邻域, 若有开集V , 使U V x ⊆∈.定理 2.1.3U 是X 中点x 的邻域存在ε>0, 使 B(x, ε) ⊂U.定义 2.1.5 设Y X ,是两度量空间.Y X f →:, X x ∈0 称f 在0x 连续, 若)(0x f 的球形邻域)0(),),((0>εεx f B存在0x 的球形邻域 B(x 0, δ), 使).),(()),((00εδx f B x B f ⊂ 称f 在X 连续, 若f 在X 的每一点连续.定理 2.1.4 设Y X ,是两度量空间. Y X f →:, X x ∈0, 那么 (1)f 在0x 连续若U 是)(0x f 的邻域, 则)(1U f -是0x 的邻域;(2) f 在X 连续若U 是Y 的开集, 则)(1U f-是X 的开集.证 (1)利用定义 2.1.5, 2.1.4.-1 (U)是每一点的邻域证每一点连续,利用(1).由此可见,度量空间的连续只与邻域或开集有关.它导入建立比度量空间更一般的拓扑空间的概念及其连续性.2.2 拓扑空间与连续映射定义 2.2.1 设 τ是集合 X 的子集族, 若τ 满足:τττττττφ∈⊂∀∈⋂⇒∈∀∈ 11,)3(;,)2(;,)1(B A B A X称τ是X 的一个拓扑),(τX 是拓扑空间, τ的元称为X 的开集.空间 X 的拓扑是 X 的全体开集的族.定义 2.2.2),(ρX 度量空间.ρτ由 X 的所有开集构成的族 . (X, ρτ)称为由度量ρ诱导出的拓扑空间. ρτ简称为度量拓扑.度量空间一定是拓扑空间.例 2.2.1 平庸拓扑},{φτX =平庸空间.例 2.2.2 离散拓扑)(X P =τ. 离散空间. X 的每一子集是开集. 由离散度量空间导出的拓扑是 离散拓扑.例 2.2.4 有限补拓扑}{}{/φτ⋃⊂=的有限子集是X U X U .验证 τ是 X 上的拓扑. (1)显然 X B A,⊂, 讨论 A ∩B 时分两种情形, 一是 A, B中有一是φ, 二是 A, B 都不是φ ;(3)ττ⊂1,不妨设10τφ∈≠∃A 利用 De Morgan 律.有限补空间.例 2.2.5 可数补拓扑}{}{/φτ⋃⊂=的可数子集是X U X U定义 2.2.3 可度量化空间.离散空间是可度量化空间. 多于一点的平庸空间不是可度量化空间. 度量化问题是点集拓扑学研究的中心问题之一. 本书将在6.6中给出该问题的一个经典的解 .定义 2.2.4 Y X , 是两拓扑空间. Y X f →:称f 连续, 若 Y 中每一开集 U 的原象 f -1(U)是 X 中的开集.定理 2.2.1 恒同映射连续. 连续函数的复合是连续的.定义 2.2.5 Y X f →:称为同胚或同胚映射, 若f f 是一一映射且f f 及 1-f均连续.定义 2.2.6 称两空间 X 与 Y 同胚, 或 X 同胚于 Y, 若存在从 X 到 Y 的同胚. 定理 2.2.2(2.2.3) 恒同映射同胚(X 与 X 同胚); f 同胚 ⇒1-f同胚 (若 X 与 Y 同胚, 则 Y与 X 同 胚); 同胚的复合是同胚(若 X 与 Y 同胚, 且 Y 与 Z 同胚, 则 X 与 Z 同胚).空间的同胚关系是等价关系.拓扑学的中心任务 :研究拓扑不变性质.抽象化过程:欧氏空间→度量空间→拓扑空间;点距离→度量→开集.2.3 邻域定义 2.3.1 设),(τX 是拓扑空间. X U X x ⊂∈,称为 x 的邻域, 如果存在τ∈V 使U V x ⊆∈; 若 U 是开的, U 称为 x 的开邻域.定理 2.3.1 设U X U .⊂是 X 的开集⇔U 是它的每一点的邻域 .证 由定义得“⇒”; 利用开集之并为开得“⇐”.x 在 X 的所有邻域构成的族称为 x 的邻域系, 记为 U x .定理 2.3.2 U x 的性质:(1) X ∈U x∈U x , x ∈U; (2) U, V ∈U x ∈U x ;(3) U ∈U x 且 U ⊂V ⇒V ∈U x ; (4) U ∈U x ∃⇒∈U x 使 V ⊂U 且 V y ∈∀, V ∈U y . 证 由定义 2.3.1 得(1); 由开集的交是开集得 (2); 由定义 2.3.1 得(3); 取V 为满足U v x ⊂∈的开集.由邻域系出发可建立拓扑空间的理论, 显得自然 , 但不流行. 利用邻域与开集的关系 (定理2.3.1)导出开集, 从 U x )(X x ∈∀具有定理 2.3.2 的性质的(1)-(4)出发, 定义∈∈∀⊂=U U x X U ,{τU x }, 则),(τX 是拓扑空间, 且这空间中每一点 x 的邻域系恰是 U x . 详见定理 2.3.3.定义 2.3.2(点连续) 映射Y X f →:称为在点 x ∈X 连续, 如果 U 是 f(x)在 Y 中的邻域, 则 f -1(U)是 x 在 X 中的邻域.定理 2.1.4 保证了在度量空间中点的连续性与由度量导出的拓扑空间中的点的连续性的一致 . 另一方面 , 关于点的连续性 , 易验证(定理 2.3.4), 恒等映射在每一点连续, 两点连续的函数之复 合仍是点连续的. 定义 2.2.4 与定义 2.3.2 所定义的“整体”连续与每一“点”连续是一致的.定理 2.3.5 设 Y X f →: 则 f 连续⇔f 在每一 x ∈X 连续.证 “⇒”若 U 是 f(x)的邻域∃开集 V 使U V x f ⊂∈)()()(11U f V f x --⊂∈ “⇐”若 U 是 Y 的开集)(1U f x -∈, U 是 f(x)的邻域, f -1 (U)是 x 的邻域, 所以 f -1 (U)在 X 中开.2.4 导集、闭集 、闭包定义 2.4.1 设x X A ,⊂称为 A 的聚点(凝聚点, 极限点), 如果 x 的每一邻域 U 中有 A 中异于 x 的点, 即 U∩ (A -{x})φ≠. A 的全体聚点之集称为 A 的导集, 记为 d(A). x 称为 A 的孤立点, 若 x 不 是 A 的聚点, 即存在 x 的邻域 U 使 U∩ (A -{x})=φ, 即 U∩ A ⊂{x}.例 2.4.1 X 是离散空间. 若X A ⊂, 则.φ=)(A d,X x ∈∀取 U={x}, 则 U∩ A ⊆{x}, 所以)(A d x ∉.例 2.4.2 X 是平庸空间, X A ⊂若 A=φ 则φ=)(A d ; 若|A|=1, 则 d(A)=X-A; 若|A|>1, 则X A d =)(.对于,X x ∈∀, 若 U 是 x 的邻域, 则 U=X, 于是 U ∩(A-{x})}{}{}){(x A x A x A U ⊄⇔≠-⇔≠-⋂φφ由此, 易计算 d(A).定理 2.4.1X B A ⊂,, 则(1)φφ=)(d ;(2))()(B d A d B A ⊂⇒⊂;(3) )()()(B d A d B A d ⋃=⋃;(4) )())((A d A A d d ⋃⊆证 由定义 2.4.1 得(1)和(2).关于(3). 由(2)得)()()(B A d B d A d ⋃⊂⋃. 设)()(B d A d x ⋃∉, 分别存在x 的邻域 V U ,使得}{},{x B V x A U ⊂⋂⊂⋂, 令V U D ⋂=, 则}{)(x B A D ⊂⋃⋂.关于(4). 设)(A d A x ⋃∉, 存在x 的邻域U , 使得},{x A U ⊂⋂取x 的开邻域U V ⊂, 则)).((,)(),(,}){(,,A d d x A d V A d y y A V V y A V ∉=⋂∉=-⋂∈∀=⋂φφφ.定义 2.4.2 X A ⊂称为 X 的闭集 , 如果 A d(A)⊂.定理 2.4.2 A 闭⇔/A 开 .证 “⇒A x ∈∀ 由于A A d ⊂)(, 存在x 的邻域U 使φ=⋂A U , 于是/A U ⊂⇐),(,,//A d x A A A x ∉=⋂∈∀φ所以 A A d ⊂)(’例 2.4.3 R 的闭区间是闭集.),(),(],[/+∞⋃-∞=b a b a 开集.),(b a 不是闭集, 因为a 是聚点.定理 2.4.3 记 F 是空间X 的全部闭集族, 则(1) ∈φ,X F ;(2) ∈B A ,F ∈⇒B A F ;(3) F 对任意交封闭.证 利用 De Morgan 定律及拓扑的定义. F }{/τ∈=U U 直接验证可得(1)、(2)、(3) Cantor 集(例 2.4.4)是集合论、点集拓扑或实变函数论中是具有特别意义的例子 , 它说明 R 中 的闭集可以是很复杂的, 在此不介绍.定义 2.4.3 A ∪ d(A)称为 A 的闭包, 记为-A A ,_.定理 2.4.5 对X B A ⊂,, 有 φφ=-;(2) -⊂A A ;(3)---⋃=⋃B A B A )( ;(4)---=A A )( .证 (3) ---⋃=⋃⋃⋃=⋃⋃⋃=⋃B A B d B A d A B A d B A B A )()()()(.(4) .))(()()())(()(------=⋃=⋃=⋃=A A d d A d A A d A A d A A .上述 4 条确定了闭包运算, 称为 Kuratowski 闭包公理, 由此可建立拓扑空间的概念. 事实上阿记此运算为)(A c , 定义 }U )c(U | X {U //=⊂=τ , 则),(τX 是拓扑空间, 且这空间中每一-=A A c )( , 详见定理 2.4.8.关于闭包的几个相关结果:(1) ⇔∈-A x 对 x 的任一邻域有φ≠⋂A U . (定义 2.4.3 后)(2) --=}){()(x A A d ;(3) A 闭 -=⇔⊂⇔A A A A d )( . (定理 2.4.4)(4 )-A 是闭集. (定理 2.4.6)(5 ) -A 是包含A 的所有闭集之交, 是包含A 的最小闭集. (定理 2.4.7: 设 F 是包含A 的所有闭 集之交, 则F A A F A ⊂⊂⊂--,, 所以-=A F .)定义2.4.5),(ρX 是度量空间.对非空的X x X A ∈⊂,定义}),(inf{),(A y y x A x ∈=ρρ. 定理 2.4.9 对度量空间),(ρX 的非空子集 A(1)0),(=⇔∈-A x A x ρ;(2) 0}){,()(=-⇔∈x A x A d x ρ.证明:⇔≠⋂⇔<∈∃>∀⇔=φεερερA x B y x A y A x ),(),(,,00),(-∈⇔≠⋂∈∀A x A U U U x φ,定理 2.4.10 设 Y X f →:, 则下述等价(1)f 连续;(2) 若B 闭于Y , 则)(1B f-闭于X ; (3) --⊂⊂∀)()(,A f A f X A证明;B )2()1(⇒是Y 的闭集,/B 是Y 的开集,/1/1)()(B f B f--=是 X的开集, f -1(B)是 X 的闭集. )3()2(⇒ --------⊂⊂⊂⊂)()(),)((),)((,)()(1A f A f A f f A A f f A A f A f)1()3(⇒设U 是Y 的开集,/U 是Y 的闭集且/1/1/1/1//1/1)()(),()(,))(())((U f U f U f U f U U f f U f f ----------=⊂⊂⊂是闭,)(1U f -是开2.5 内部、边界定义 2.5.1 若A 是x 的邻域, 则称x 是A 的内点. A 的所有内点的集合称为A 的内部, 记为0A .定理2.5.1对/0///0,,A A A A X A ==⊂--证明:,0A x ∈由于,/φ=⋂A A 于是,/-∉A x 从而.//-∈A x反之x A x A x ∃∉∈--,,.///的邻域0/,,A x A V A V ∈⊆=⋂φ,因此,//0-=A A .从而---===A A A A A /0/////0/,.定理 2.5.3 对X B A ⊂,, 有(1)0X X =; A A ⊂0)2(;000)()3(B A B A ⋂=⋂000)4(A A =.证明:(1),(2)是显然的.00///////0)()(B A B A B A B A ⋂=⋂=⋃=⋂---而0//////00A A A A ===---关于内部的几个结果:(1)A 是x 的邻域0A x ∈⇔;(2)0A 是开集;(3)A 是开集;(4)0A 是A 所包含的所有开集之并,是含于A 内的最大开集.证明://0)2(-=AA 是开集 (3)A 开/A ⇔闭0////A A A A A ==⇔=⇔--(4)设O 是含于A 内的所有开集之并,O A A O A o o ⊃⊂⊂,所以O A o =定义 2.5.2 x 称为A 的边界点, 若x 的每一邻域, 既含有A 中的点又有 /A 中 的点. A 的边界点 之集称为边界, 记为A ∂.定理2.5.6 对X A ⊂,有A A A A A A A A A A o o ∂-=∂⋃=∂=⋂=∂----)3(;)2();()1(// 证明:;)()()()2(/-----=⋃⋂⋃=⋂⋃=∂⋃A A A A A A A A A A o o o o o(3)o A A A A A A A A A A =⋂=-=⋂-=∂---------///)(2.6 基与子基度量空间→球形邻域→ 开集→ 拓扑 . 在度量空间中球形邻域的作用就是拓扑空间中基的作用.定义 2.6.1 设 τ是空间 X 的拓扑, B τ⊂, 如果τ中每一元是B 中某子集族之并, 称B 是 X 的基.所有单点集的族是离散空间的基.定理 2.6.2 设B τ⊂ ,B 为 X 的基X x ∈∀⇔ 及x 的邻域 U xx V ∃ 使x x U V x ⊂∈. 证 “⇒存在开集 W x 使得 Ux Wx x ⊂∈, ∃B 1⊂B 使得 =x W B 1 ∈∃x V B 1 ⊂B 1使x x U V x ⊂∈;“⇐ 设τ∈U ,∈∃∈∀x V U x ,B 使x x U V x ⊂∈, 从而⊂∈}|{U x V x B 且U x xV U ∈= 在度量空间中, 所有球形邻域的族是度量拓扑的基(定理 2.6.1). 所有开区间的族是 R 的基. 定理 2.6.3 拓扑空间X 的基B 满足:(i) ⋃B X =; (ii) ∈∀21,B B B ,∈∃⋂∈∀321,B B B x B , ,213B B B x ⋂⊂∈∀. 反之, 若集合 X 的子集族 B 满足(1)、(2), 定义}B {11B B ⊂⋃=τ, 则τ是X 的以 B 作为基的唯一拓扑.证 验证 τ是X 的拓扑. (1) φφ⋃= 先设∈21,B B B , 21B B x ⋂∈ , ∈∃x w B使21B B W x x ⋂⊂∈,于是τ∈⋂∈=⋂}|{2121B B x W B B x . 如果τ∈21,A A , 设⋃=1A B 1 , ⋃=2A B 2,则∈⋂⋃=⋂12121|{B B B A A B 1, ∈1B B 2}τ∈..(3) 设∃∈∀⊂,,11τττA B A ⊂B , 使得⋃=A B A , 那么{(1⋃⋃=⋃τB A | })1τ∈A .较强于(ii)且易于验证的条件是 (ii∈∀21,B B B , ∈⋂21B B B . 例 2.6.1 实数下限拓扑空间.令 B b}a R,b a,|b) {[a,<∈=,则B 为 R 上一拓扑的基. 这空间称为实数下限拓扑空间, 记为 R l . 开区间是 R l 中的开集, 因为 +∈+=Z i b ia b a ),1[),(. 定义 2.6.2 设),(τX 是拓扑空间, S τ⊂. 若 S 的元之所有有限交构成的族是τ的基, 则称 S 是τ的子基.S 的元之有限交构成的族∈⋂⋂⋂i n S S S S |...{21S ,}+∈≤Z n i . 显然, 空间X 的基是子基.例 2.6.2 S }|),{(}|),{(R b b R a a ∈-∞⋃∈+∞=是R 的子基.对照定理 2.6.3, 集合 X 的子集族 S 要作为子基生成X 上的拓扑的充要条件是∪S X =. (定理2.6.4)映射的连续性可用基、子基来刻画或验证.定理 2.6.5 设Y X ,是两拓扑空间, Y X f →:, 下述等价:(1)f 连续;(2) Y 基 B , 使得 B 中每一元的原像在X 中开;(3) Y 有子基 S , 使得 S 中每一元的原像在X 中开.证 (3)⇒ (2) 设 B 是 S 的元之所有有限交构成的族 , 则 B 满足(2).(2)⇒ (1) 设U 在Y 中开,则⋃=U B 1 , 于是∈=--B B f U f |)({)(11B 1 }在X 中开. 类似地, 可定义点的邻域基与邻域子基的概念, 同时用它们来验证映射的连续性等. 在第五章中定义第一可数性时再介绍这些概念.2.7 拓扑空间中的序列可以与R 中一样地定义序列、常值序列、子序列, 见定义 2.7.1, 2.7.3..定义 2.7.2 X 中序列x x i →极限 , 收敛序列 .平庸空间中任意序列收敛于空间中的任一点. 数学分析中的一些收敛性质还是保留的, 如常 值序列收敛, 收敛序列的子序列也收敛 . (定理 2.7.1)定理 2.7.2 {x}-A 中序列)(A d x x x i ∈⇒→证x ∀的邻域,}){(,φ≡-x A U U 所以.)(A d x ∈定理 2.7.3f 在 x 0 连续且)()(00x f x f x x i i →⇒→证 设 U 是)(0x f 的邻域, 则)(1U f -是0x 的邻域+∈∃Z n , 当n i >时有)(1U f x i -∈, 从而U x f i ∈)(.上述两定理的逆命题均不成立.例 2.7.1 设 X 是不可数集赋予可数补拓扑, 则(1)在X 中+∈∃⇔→Z n x x i , 当n i > 时有.x x i =;(2)若A 是X 的不可数子集, 则X A d =)(.证(1)的必要性,令},|{+∈≠=Z i x x x D i i ,则/D 是x 的邻域,n i Z n >∀∈∃+,时有/D x i ∈,即x x i =证x ∀)2(的邻域/}{,U x A U ⊄-(可数集),所以).(,}){(A d x x A U ∈≠-⋂φ 定理 2.7.2 的逆命题不真. 如例 2.7.1, 取定X x ∈0, 让}{0x X A -=, 则)(0A d x ∈, 但A 中没有序列收敛于0x .定理 2.7.3 的逆命题不真. 取X 是实数集赋予可数补拓扑, 让R X i →:是恒等映射, 若在X 中x x i → , 则在R 中)()(x f x f i →, 但 i 在 x 不连续, 因为x x 在R R 的开邻域)1,1(+-x x 的原像)1,1())1,1((1+-=+--x x x x i 在X 中不是开的.定理 2.7.4 设{x i }是度量空间),(τX 中的序列, 则0),(→⇔→x x x x i i ρ. 证 x x x i ∀⇔→的邻域+∈∃Z n U ,, 当 i>n 时有+∈∃>∀⇔∈Z n U x i ,0ε当 i>n 时有+∈∃>∀⇔∈Z n x B x i .0),(εε当n i >时有0),(→x x i ρ.第三章 子空间、积空间、商空间介绍三种从原有的拓扑空间或拓扑空间族构造新空间的经典方法, 引入遗传性、可积性、可 商性等概念, 这些是研究拓扑性质的基本构架.教学重点:子空间与积空间;教学难点:子空间、(有限)积空间和商空间3.1 子空间对于空间 X 的子集族 A 及X Y ⊂, A 在 Y 上的限制 A |Y ∈⋂=A Y A |{A }.(定义 3.1.2) 引理 3.1.2 设Y 是空间),(τX 的子集, 则是Y 上的拓扑.证 按拓扑的三个条件逐一验证. 如, 设ττττ∈∃∈∀⊂A Y B A ,,1|1, 使得Y B A A ⋂=, 于是Y A A Y A B A Y B |111})|{(}|{ττττ∈⋂∈⋃=∈⋂⋃=⋃定义 3.1.3 对),(,|Y Y X Y τ⊂称为),(τX 的子空间, Y |τ称为相对拓扑.“子空间”= “子集”+ “相对拓扑”.易验证, 若Z 是Y 的子空间, 且 Y 是X 的子空间, 则Z 是X 的子空间. (定理 3.1.4), 定理 3.1.5(3.1.7) 设 Y 是X 的子空间, Y y ∈, 则(1)若*,ττ分别为Y X ,的拓扑, 则Y |*ττ=; (2)若 F , F *分别为Y X ,的全体闭集族, 则 F *=F |Y ;(3)若 U y , U y *分别为y 在 Y X , 中的邻域系, 则 U y *=U Y y |;(4)若 B 是X 的基, 则 B |Y 是Y 的基.证 (2) ∈*F F *,**Y U F Y F Y Y ⋂=-⇔∈-⇔τ Y F U Y U X F U |**,)(τττ∈⇔∈⋂-=⇔∈.U 开于Y 存在X 的开集V , 使得Y V U ⋂=B 1 ⊂B , 满足⋃=V B 1, 则 ⋃=U (B 1 |Y ).在 R 的子空间),0(+∞中]1.0(是闭集.定理 3.1.6 设Y 是X 的子空间,Y A ⊂, 则Y A c A c Y A d A d X Y X Y ⋂=⋂=)()()2(;)()()1(证 (1) )(A d y X ∈在X 中的邻域φ≠-⋂⋂⊃-⋂}){()(}){(,y A Y U y A U U , 所以 Y A d y X ⋂∈)(. 反 之 , 设Y A d y X ⋂∈)(y 在Y 中 的 邻 域y V ∃,在 X 中 的 邻 域 U 使Y U V ⋂=, 于 是φ≠-⋂=⋂-=-}){(})){((}){(y A U Y y A U y A V , 所以).(A d y ∈.(2)Y A c Y A A d A Y A d A A d A A c X X X Y Y ⋂=⋃⋂⋃=⋂⋃=⋃=)()())(())(()()(.3.2 有限积空间就平面的球形邻域),(εx B d 而言, 我们知道球形邻域内含有方形邻域 , 方形邻域内含有球形邻域 . 从基的角度而言,形如),(),(222111εεx B x B ⨯的集合就是平面拓扑的基了. 对于两个拓扑空间Y X ,, 在笛卡儿积集Y X ⨯中可考虑形如V U ⨯的集合之全体, 其中 U, V 分别是 X, Y 的开集. 对于有限个空间n X X X ,...,,21, 可考虑形如n U U U ⨯⨯⨯...21的集合. 定理 3.2.2 设),(i i X τ是 n 个拓扑空间, 则n X X X X ⨯⨯⨯=...21 有唯一的拓扑, 以 X 的子集族 B n i U U U U i i n ≤∈⨯⨯⨯=,|...{21τ为它的一个基 .证 验证 B 满足定理 2.6.3 的条件(i), (ii). (1) ∈⨯⨯⨯=n X X X X ...21B ,∪B =X; (2) 若 ∈⨯⨯⨯⨯⨯⨯n n V V V U U U ...,...2121B , 则∈⋂⨯⨯⋂⨯⋂=⨯⨯⨯⋂⨯⨯⨯)(...)()()...()...(22112121n n n n V U V U V U V V V U U U B . 定义 3.2.2 以定理 3.2.2 中 B 为基生成n X X X X ⨯⨯⨯=...21 上的唯一拓扑, 称为拓扑n τττ,...,21的积拓扑.),(τX 称为),,),...(,(),,(2211n n X X X τττ的(有限 )积空间. 定理 3.2.4设n X X X X ⨯⨯⨯=...21是积空间, B i 是i X 的基, 则 B ∈⨯⨯⨯=i n B B B B |...{21Bi,}n i ≤是 积拓扑τ的基.证 利用定理 2.6.2. 设i i U U x ττ∈∃∈∈,使∈∃⊂⨯⨯⨯∈i n B U U U U x ,...21B i 使 i i i U B x ⊂∈, 那么.......2121U U U U B B B x n n ⊂⨯⨯⨯⊂⨯⨯⨯∈.例 3.2.1 形如),(...),(),(2211n n b a b a b a ⨯⨯⨯的集合构成n R 的基.设),(),,(2211ρρX X 是两个度量空间.令22222111),(),(),(y x y x y x ρρρ+=,则ρ是21X X ⨯上的度量, 导出X 上的度量拓扑τ. 对于n 个度量空间之积可类似地定义. (定义3.2.1)定理 3.2.1 度量空间的有限积: 积拓扑与度量拓扑一致.验证2=n 的情形. 易验证),(),(),()2/,()2/,(22112211εεεεεx B x B x B x B x B ⨯⊂⊂⨯于是每一),(εx B 是积拓扑的开集, 且每一),(),(2211εεx B x B ⨯是度量拓扑的开集, 所以导出相同的拓扑. 定理 3.2.5 有限积空间n X X X X ⨯⨯⨯=...21以 S },)({1n i U U p i i i i ≤∈=-τ为子基, 其中i τ是i X 的拓扑, i i X X p →:是投射.仅证2=n 的情形.2121221111)(,)(U X U p X U U p ⨯=⨯=--, 所以∈⨯=⋂--21212111)()(U U U p U p B .定义 3.2.3 Y X f →:称为开(闭)映射, 若U 开(闭)于X , 则)(U f 开(闭)于Y . 定理 3.2.6 i i X X p →:是满、连续、开映射, 未必是闭映射.由于n i i i X U X X U p ⨯⨯⨯⨯⨯=-......)(211, 所以i p 连续. 由于i n i i U U U U U p =⨯⨯⨯⨯⨯)......(21, 所以是i p 开的. 但是R R p →21:不是闭的.定理 3.2.7 设映射X Y f →:其中X 是积空间n X X X ⨯⨯⨯..21. 则f 连续i i X Y f p n i →≤∀⇔:, 连续.证 充分性. 对X 的子基 S )()())((},,)({1111i i i i i i i i U f p U p fn i U U p ----=≤∈= τ开于Y .多元函数连续当且仅当它的每一分量连续.定理 3.2.8 积拓扑是使每一投射都连续的最小拓扑 . 即设τ是积空间n X X X X ⨯⨯⨯=...21的积拓扑, 若集合 X 的拓扑*τ满足: 每一投射i i X X p →),(:*τ连续, 则*ττ⊂.证 由于*1},)({ττ⊆≤∈-n i U U p i i i i , 所以*ττ⊂.3.3 商空间回忆, 商集R X /, 及自然投射R X X p /:→定义为R x x p ][)(=. 问题: 设X 是拓扑空间, 要在R X /上定义拓扑, 使p 连续的最大的拓扑.讨论更一般的情形, 设),(τX 是拓扑空间且YX f →:是满射. 赋予集合Y 什么拓扑, 使f 连续的最大的拓扑. 若f 连续, 且U 是Y 的开集, 则)(1U f -是X 的开集. 让})(|{11ττ⋃⊂=-U f Y U , 易验 证1τ是Y 上的拓扑.定义 3.3.1(3.3.2) 称1τ 是 Y 的相对于f 满射而言的商拓扑, ),(),(:1ττY X f →称为商映射. 这时, U 在 Y 中开)(1U f -⇔在X 中开;F 在Y 中闭)(1F f -⇔在X 中闭. 定理 3.3.1 商拓扑是使f 连续的最大拓扑.证 设),(),(:1ττY X f →是商映射. 显然, f 是连续的. 如果2τ是Y 的拓扑使),(),(:1ττY X f →连续, 则ττ∈∈∀-)(,12U f U , 于是,1τ∈U 即,12ττ⊂, 所以1τ 是使 f 连续的最大拓扑.定理 3.3.2 设Y X f →:是商映射. 对于空间Z , 映射Z Y g →:连续⇔映射Z X f g →: 连续.证 设Z X f g →: 连续,W ∀开于))(()()(,111W g fW f g Z ---= 开于,X 由于f 是商映射, 所以)(1W g -开于Y , 故g 连续.定理 3.3.3 连续, 满开(闭)映射⇒商映射.证 设),(),(:Y X Y X f ττ→是连续的满开(闭)映射, 1τ是Y 的相对于f 而言的商拓扑, 要证Y ττ=1. 由定理 3.3.1, Y ττ⊃1 . 反之,X V f V ττ∈∈∀-)(,11. 对于开映射的情形Y V f f V τ∈=-))((1,; 对于闭映 射的情形, Y V f X f Y V τ∈--=-))((1, 所以总有Y ττ⊂1.定义 3.3.3 设R 是空间),(τX 的等价关系, 由自然投射R X X p i /:→确定了 X/R 的商拓扑, 称),/(R R X τ为商空间, 这时R X X p i /:→是商映射.例 3.3.1 在R 中定义等价关系⇔∈∀y x R y x ~,,或者Q y x ∈,, 或者Q y x ∉,商空间 R /~是由两点组成的平庸空间. 由于 Q 在 R 中既是开集, 也不是闭集, 所以单点集[Q ]在 R /~中既不是开集,也不是闭集. 习惯上, 把 R /~说成是在 R 中将所有有理点和所有无理点分别粘合为一点所得到的商空间.例 3.3.2 在1] [0,上定义等价关系⇔∈∀y x y x ~],1,0[,~:或者y x =, 或者~/]1,0}.[1,0{},{=y x 是 在1] [0,中粘合 0, 1 两点所得到的商空间, 这商空间同胚于单位圆周1S .第四章 连通性本章起的四章介绍 4 类重要的拓扑不变性质. 本章讨论连通性、道路连通性、局部连通性及 其在实分析中的一些简单的应用.教学重点:连通空间、局部连通空间;教学难点:连通分支.4.1 连通空间在拓扑中怎样定义连通, 分隔区间(0, 1), (1, 2)的关系与(0, 1), [1, 2)的关系不同, 虽然他们都 不相交, 但相连的程度不一样.定义 4.1.1 设,,X B A ⊂ 若φ=⋂=⋂--B A B A , 则称B A ,是隔离的.区间(0, 1)与(1, 2)隔离, 但区间(0, 1)与[1, 2)不隔离.几个基本事实: (1)两不交的开集是隔离 的; (2)两不交的闭集是隔离的; (3)隔离子集的子集是隔离的 .定义 4.1.2X 称为不连通的, 若X 中有非空的隔离子集B A ,使B A X ⋃=, 即X 可表为两非空 隔离集之并. 否则X 称为连通的.包含多于一个点的离散空间不连通, 平庸空间是连通的.定理 4.1.1 对空间X , 下述等价:(1) X 是不连通的;(2) X 可表为两非空不交闭集之并;(3) X 可表为两非空不交开集之并;(4) X 存在既开又闭的非空真子集.证 (1)⇒(2)设隔离集B A ,之并是B B B A B B A B B X =⋂⋃⋂=⋃⋂=----)()()(,. 同理, A 也是闭的.(2)⇒(3)设X 是两非空不交闭集B A ,之并, 则X 是两非空不交开集B A ,之 并.(3)⇒(4)设X 是两非空不交开集B A , 之并, 则B A , 都是X 的既开又闭的非空真子集.(4)⇒ (1)若A 是X 的开闭集, 则A X A -,隔离.例 4.1.1 Q 不是R 的连通子空间, 因为)),())(,((+∞⋂-∞⋂=ππQ Q Q .定理 4.1.2 R 是连通的.证 若R 不连通, 则R 是两非空不交闭集B A , 之并 . 取定,,B b A a ∈∈ 不妨设b a <. 令B b a B A b a A ⋂=⋂=],[,],[**则**,B A 是R 两非空不交闭集且**],[B A b a ⋃=.让 *sup A c =. 因*A 是闭的, **],(,,B b c b c A c ⊂<∈, 因*B 是闭的, *B c ∈, 从而φ≠⋂**B A , 矛盾.定义 4.1.3 若X 的子空间Y 是连通的, 则称Y 为连通子集, 否则, 称为不连通子集. 定理 4.1.3 设,,X Y B A ⊂⊂, 则B A ,是Y 的隔离集B A ,⇔ 是X 的隔离集.证 B A c Y B A c B A c X X Y ⋂=⋂⋂=⋂)()()(; 同理, A B c A B c X Y ⋂=⋂)()(.定理 4.1.4 设Y 是X 的连通子集. 如果X 有隔离子集B A ,使B A Y ⋃⊂, 则A Y ⊂ 或B Y ⊂.证Y B Y A ⋂⋂,是Y 的隔离集, 所以φ=⋂Y A , 或 φ=⋂Y B , 于是A Y ⊂ 或B Y ⊂.定理 4.1.5 若Y 是X 的连通子集且-⊂⊂Y Z Y , 则Z 是连通的.证 若Z 不连通, X 的非空隔离集B A , 使Y B A Z ⊃⋃=, 于是A Y ⊂ 或B Y ⊂, 不妨设A Y ⊂, 那 么--⊂⊂A Y Z , 于是 φ=⋂=B Z B , 矛盾.定理 4.1.6 设τγλ∈}{Y 是空间X 的连通子集族. 如果φτγλ≠∈ Y 则X 连通. 证 若 τγλ∈Y 是 X 中隔离集B A ,之并, 取定φτγλ≠∈∈ Y x , 不妨设A x ∈, 则A Y ⊂∈∀γτγ,, 所以A Y ⊂∈ τγλ,于是φ=B .定理 4.1.7 设X Y ⊂. 若X Y y x ∃∈∀,,的连通子集 Y xy 使 Y Y y x xy ⊂∈,, 则Y 连通. 证 设φ≠Y ,取定Y a ∈, 则A Y ay ⊂∈ τγ且 τγ∈∈ay Y a , 所以Y 连通.定理 4.1.8(连续映射保持) 设Y X f →:连续. 若X 连通, 则)(X f 连通.证 若)(X f 不连通, 则)(X f 含有非空的开闭真子集A . 由于)(:X f X f →连续, 于是)(1A f -是X 的 非空开闭真子集. 连续映射保持性可商性拓扑不变性.有限可积性. 对于拓扑性质 P, 要证有限可积性, 因为n X X X ⨯⨯⨯...21同胚于n n X X X ⨯⨯⨯-11..., 所以只须证: 若Y X ,具性质 P, 则Y X ⨯具有性质 P.定理 4.1.9 (有限可积性) 设n X X X ,...,,21 连通, 则n X X X ⨯⨯⨯...21连通.证 仅证若Y X , 连通, 则 Y X ⨯连通. 取定Y X y x Y X b a ⨯∈∀⨯∈),(.),( 令 )}})({{(Y a y X S xy ⨯⨯=由于}{y X ⨯同胚于Y a X ⨯}{, 同胚于Y , 所以}{y X ⨯,Y a ⨯}{, 都 连通且)}({}){(),(Y a y X y a ⨯⋂⨯∈, 由定理41.6, xy S 连 通 且xy S y x ∈),(, 再 由 定 理 4.1.7}),(|{Y X y x S Y X xy ⨯∈=⨯连通.4.2 连通性的应用利用 R 连通性的证明(定理 4.1.2)知, 区间都是连通的. 区间有 9 类:无限区间 5 类:],,(),,(),,[),,(),,(b b a a -∞-∞+∞+∞+∞-∞有限区间 4 类:(a, b), [a, b), (a, b], [a, b].定理 4.2.1 设R E ⊂, 则E 连通⇔E 是区间.证 若 E 不是区间,b c a <<∃ , 使E b a ∈,但E c ∉令),(,),(+∞=⋂-∞=c B E c A 则 E 是不交的 非空开集B A , 之并.定理 4.2.2 设X 连通, R X f →:连续, 则)(X f 是 R 的一个区间.注X y x ∈,, 如果 t 介于)(x f 与)(y f 之间, 则X z ∈∃, 使t z f =)(. 事实上, 不妨设)()(y f t x f ≤≤则)()](),([X f y f x f t ⊂∈所以Xz ∈∃, 使t z f =)(. 定理 4.2.3(介值定理) 设R b a f →],[:连续, 若r 介于)(a f 与)(b f 之间, 则],[b a z ∈∃使r z f =)(.定理 4.2.4(不动点定理) 设]1,0[]1,0[:→f 连续, 则]1,0[∈z 使z z f =)(.证 不妨设 1)1(),0(0<<f f .定义R F →]1,0[:使)()(x f x x F -=, 则F 连续且 ]1,0[),1(0)0(∈<<z F F 使得0)(=z F , 即z z f =)(.定义2:R R f →为)2sin ,2(cos )(t t t f ππ=, 则f 连续且1)(S R f =, 于是1S 是连通的. 对121121),(,),(S x x x S x x x ∈--=-∈=称为x 的对径点, 映射11:S S r →定义为x x r -=)(称为对径映射, 则 r 连续.定理 4.2.5(Borsuk-Ulam 定理) 设R S f →1:连续, 则1S x ∈, 使)()(x f x f -=.证 定义R S F →1:为)()()(x f x f x F --=, 则F 连续. 若1S a ∈ , 使得)()(a f a f -≠ 则0)()(<-⋅a F a F , 由定理 4.1S z ∈∃, 使得0)(=z F , 即)()(z f z f -=. 定理 4.2.6}0{-n R 连通, 其中.)0,...,0,0(0,1nR n ∈=>证 只证 n=2 的情形. 令})0{(]0,(}),0{(),0[-⨯-∞-⨯+∞=R B R A , 则}0{-=⋃n R B A . 由于})0{(),0[})0{(),0(-⨯+∞⊂⊂-⨯+∞R A R , 所以A 连通. 同理B 连通, 从而B A ,连通.定理 4.2.7 2R 与 R 不同胚.证 若存在同胚R R f →2:, 令R R f g R →-=-}0{:2}0{2, 则g 连续, 从而}0{})0{(22-=-R R g 连通, 矛盾.4.3 连通分支将不连通集分解为一些“最大”连通子集(“连通分支”)之并.定义 4.3.1 X y x ∈,称为连通的, 若X 的连通子集同时含y x ,, 记为y x ~. 点的连通关系~是等 价关系: z x z y y x x y y x x x ~~,~)3(;~~)2(;~)1(⇒⇔.定义 4.3.2 空间X 关于点的连通关系的每一等价类称为X 的一个连通分支.x~y ⇔x, y 属于X 的同一连通分支. X 是X 的全体连通分支的互不相交并. 定理 4.3.1 设 C 是空间X 的连通分支, 则(1)若Y 是X 的连通子集且φ≠⋂C Y , 则C Y ⊂;(2)C 是连通的闭集.证 (1)取定Y y C Y x ∈∀⋂∈, 则y x ~所以 .C y ∈(2)取定X C x C c ∃∈∀∈,,的连通集),(x x Y x c Y ∈,由于C Y C Y x x ⊂≠⋂,φ,于是}|{C x Y C x ∈⋃=且}|{C x Y c x ∈⋂∈, 所以 C 是连通的. 从而 -C 连通且φ≠⋂-C C , 于是C C ⊂-, 故 C 闭.以上说明:连通分支是最大的连通子集.连通分支可以不是开集. Q 的连通分支都是单点集, 不是Q 的开子集Q y x ∈∀,, 由定理4.2.1, 不存在Q 的连通子集同时含有y x ,,所以Q 的连通分支都是单点集 .4.4 局部连通空间例 4.4.1 (拓扑学家的正弦曲线 ) 令T S S T x x x S ⋃=-⨯=∈=1],1,1[}0{]},1,0(|)/1sin(,{(,则1S S =-, 于是 S, S 1 连通. 在 S 1 中, S 中点与 T 中点的“较小的”邻域表现出不同的连通性 .S S 1=S ∪T=ST定义 4.4.1 设X x ∈若x 的每一邻域U 中都含有x 的某一连通的邻域V , 称X 在x 是局部连 通的. 空间X 称为局部连通的, 若X 在每一点是局部连通的.S 1 是连通, 非局部连通的. 多于一点的离散空间是局部连通, 非连通的.定理 4.4.1 对空间X , 下述等价:(1) X 是局部连通;(2) X 的任一开集的任一连通分支是开集;(3) X 有一个基, 每一元是连通的.证 (1)⇒(2)设 C 是X 的开集U 的连通分支. x C x ∃∈∀,的连通的邻域 U V ⊂, 于是 C V C V ⊂≠⋂,φ, 所以 C 是x 的邻域, 故 C 开.(2)⇒ (3)令 B C X C |{⊂= 是X 的开集U 的连通分支}, 则 B 是X 的基.(3)⇒ (1)设U 是x 的邻域存在开集V 使U V x ⊂∈连通开集 C 使U V C x ⊂⊂∈, 所以X 局部连通.定理 4.4.2 设Y X f →:是连续开映射. 若X 局部连通, 则)(X f 局部连通. 证 )(X f y ∈∀, 及 y 在)(X f 中的邻域U , 取)(1y f x -∈, 则 0(1U f -是x 的邻域X 的连通开集V 使)(1U f V x -⊂∈, 于是 U V f x f y ⊂∈=)()(.定理 4.4.3 局部连通性是有限可积性, 即设n X X X ,...,,21局部连通, 则n X X X ⨯⨯⨯...21局部连通.证 仅证若21,X X 局部连通, 则21X X ⨯局部连通. 设 B 1, B 2 分别是21,X X 的由连通开集组成的基, 则{ 121|B B B ⨯ ∈B 1, ∈2B B 2}是21X X ⨯的由连通开集组成的基(定理3.2.4).证1, y21, x 2使 f(x1)=y1, f(x2)=y24.5 道路连通空间定义 4.5.1 设X 是拓扑空间, 连续映射 X f →]1,0[:称为X 中的一条道路,)1(),0(f f 分别称为f 的起点和终点, f 称为从)0(f 到)1(f 的一条道路,])1,0([f 称为X 中的一条曲线. 若)1()0(f f =, f 称为闭路.定义 4.5.2 对空间X , 如果X X y x ∃∈∀,, 中从x 到y 的道路, 则称X 是道路连通的.类似可定义道路连通子集.R 是道路连通的, R y x ∈∀,, 定义R f →]1,0[:为ty x t t f +-=)1()(.定理 4.5.1 道路连通⇒连通.证 设 X 道路连通X X y x ∃∈∀,,中从x 到y 的道路X f →]1,0[:, 这时])1,0([f 是X 中含y x ,的连通子集, 所以X 连通.拓扑学家正弦曲线 S 1 是连通, 非道路连通的空间.定理 4.5.2 设Y X f →:连续. 若X 道路连通, 则)(X f 道路连通.证X x x X f y y ∈∃∈∀2121,),(,使)(),(2211x f y x f y ==,存在道路X g →]1,0[: 使21)1(,)0(x g x g ==, 则 f◦g: [0, 1]→ Y 是 f(X)中从1y 到2y 的道路.定理 4.5.3 道路连通性是有限可积性.证 仅证若21,X X 是道路连通, 则21X X ⨯道路连通.212121),(),,(X X y y y x x x ⨯∈==∀, 则存在道路21]1,0[:X X f i ⨯→使i i i i y f x f ==)1(,)0(,定义21]1,0[:X X f ⨯→为))(),(()(21t f t f t f =, 则 f 是从 x 到 y 的道路.可引进局部道路连通空间的概念. 同时, 与连通分支类似 , 可建立道路连通分支: 空间中最大的道路连通子集.第五章 可数性公理本章主要介绍 4 种与可数性相关的拓扑性质, 它们与度量空间性质、下章要讨论的分离性公 理都是密切相关的. 本章的要点是给出它们之间的基本关系.教学重点:第一与第二可数性公理;教学难点:分离性公理.5.1 第一与第二可数性定理第二章介绍的空间的基, 在生成拓扑空间, 描述局部连通性, 刻画连续性等方面都发挥了积 极的作用. 较少的基元对于进一步讨论空间的属性是重要的.定义 5.1.1 若X 有可数基, 称X 满足第二可数(性)公理, 或是第二可数空间, 简称2A 空间.定理 5.1.1 . 2A R ⇒证 令 B },|),{(Q b a b a ∈=, 定理 2.6.2, B 是 R 的可数基. 离散空间X 具有可数基X 是可数集.下面讨论“局部基”性质. (定义 2.6.3)对X x ∈, 设 U x 是x 的邻域系, 若 V x ⊂U x 满足: ∈∀U U x ∈∃V V x 使U V ⊂, 则称 V x 是 x 的邻域基, 若更设 V x 中每一元都是开的, 则称 V x 是 x 的开邻域基或 局部基. 易验证, (1) 若 V x 是x 在X 的邻域基, 则∈V V o |{V x }是x 在 X 的局部基; (2)(定理 2.6.7) 若 B 是空间X 的基, X x ∈则 B x ∈=B {B }B x ∈是x 的局部基.定义 5.1.2 若X 的每一点有可数邻域基, 称X 满足第一可数(性)公理, 或是第一可数空间, 简 称1A 空间.定理 5.1.2 度量空间1A ⇒.证}|)/1,({+∈=Z n n x B B x 是x 的可数邻域基.例 5.1.1 不可数多个点的可数补空间X , 非1A证X x ∈有可数局部基V ,∈∃-∈∀y V x X y },{V 使//}{,}{y y V y y V ⊂⊂从而不可数集}{}{//y V x ⋃⊂可数集, 矛盾.定理 5.1.3 12A A ⇒.证 若 B 是X 的可数基, 则 B x ∈=B {B }|B x ∈是X x ∈的可数邻域基.逆命题不成立, 不可数的离散空间是反例.。
第二章 拓扑空间与连续映射

-1
2.3 邻域
定义2 定义2.3.1 设(X, T)是拓扑空间. x∈X, UX称为x 的邻域, 如果存在V∈T使x∈VU; 若U是开的, U称 为x的开邻域. 定理2.3.1 设UX. U是X的开集U是它的每一 定理2 点的邻域. 证 由定义得“”; 利用开集之并为开得 “” . x在X的所有邻域构成的族称为x的邻域系, 记为 Ux.
2010-8-31
宁德师范高等专科学校
9
2.2 拓扑空间与连续映射(3)
定义2 定义2.2.3 可度量化空间. 离散空间是可度量化空间. 多于一点的平庸空间不是可 度量化空间. 度量化问题是点集拓扑学研究的中心问题之 一. 本书将在§6.6中给出该问题的一个经典的解. 定义2 定义2.2.4 X, Y是两拓扑空间. f: X→Y. 称f连续, 若Y中每 -1 一开集U的原象f (U)是X中的开集. 定理2 定理2.2.1 恒同映射连续. 连续函数的复合是连续的. 定义2.2.5 f: X→Y称为同胚或同胚映射, 若f是一一映射且 定义2 -1 f及f 均连续.
设f是包含a的所有闭集之交20121027宁德师范高等专科学校2224定理249对度量空间x20121027宁德师范高等专科学校232420121027宁德师范高等专科学校2425定义251a的所有内点的集合称为a的内部记为a20121027宁德师范高等专科学校2525是a所包含的所有开集之并是含于a内的最大开集
2010-8-31 宁德师范高等专科学校 13
2.3 邻域(3)
利用邻域与开集的关系(定理2.3.1)导出开集, 从Ux(x∈X) 具有定理2.3.2的性质的(1)-(4)出发, 定义 T={UX|x∈U, U∈Ux}, 则(X, T)是拓扑空间, 且这空间中每一点x的邻域系 恰是Ux. 详见定理2.3.3. 定义2.3.2(点连续) 映射f: X→Y称为在点x∈X连续, 如果U 定义2 -1 是f(x)在Y中的邻域, 则f (U)是x在X中的邻域. 定理2.1.4保证了在度量空间中点的连续性与由度量导出 的拓扑空间中的点的连续性的一致. 另一方面, 关于点的连 续性, 易验证(定理2.3.4), 恒等映射在每一点连续, 两点连续 的函数之复合仍是点连续的.
河北师大点集拓扑课件1
2.1拓扑空间的定义及性质。
2.2开集、闭集的定义及性质,例题讲解。
2.3连续映射的概念及判断方法,例题讲解。
3.随堂练习:针对每个知识点,设计相应的练习题,让学生及时巩固所学内容。
4.课堂小结:总结本节课所学知识点,强调重点和难点。
5.课后作业布置:布置相关习题,巩固所学知识。
六、板书设计
2.知识讲解(25分钟):详细讲解拓扑空间、开集、闭集、连续映射等概念和性质。
3.例题讲解(15分钟):结合具体例题,引导学生运用所学知识解决问题。
4.随堂练习(10分钟):设计针对性的练习题,让学生及时巩固所学知识。
5.课堂小结(5分钟):总结本节课的重点和难点,强调注意事项。
三、课堂提问
1.在讲解过程中,适时提问,了解学生对知识点的掌握情况。
2.课堂时间分配是否合理?是否需要调整讲解和练习的时间比例?
3.课堂提问的效果如何?是否需要增加提问的频次和深度?
4.情景导入是否吸引学生的兴趣?是否需要寻找更多有趣的例子?
5.学生对连续映射的判断方法是否熟练?是否需要增加相关例题和练习题?
6.整体教学效果如何?是否存在需要改进的地方?如何调整教学策略以提高教学效果?
3.习题3:判断给定映射是否连续。
答案:根据连续映射的定义,分析映射在开集上的性质。
八、课后反思及拓展延伸
1.反思:本节课的教学效果,学生的掌握程度,对重难点的理解。
2.拓展延伸:
2.1研究更一般的拓扑空间,如度量空间、赋范线性空间等。
2.2探讨不同拓扑空间的性质,如紧性、可分性等。
2.3学习高级拓扑学概念,如同伦、同调等。
2.闭集:集合的补集是开集。
关于开集和闭集的性质,有以下几点需要重点关注:
拓扑学的基本概念与拓扑空间
拓扑学的基本概念与拓扑空间拓扑学是数学的一个分支,研究的对象是空间的性质与结构,而不关注其度量或形状。
拓扑学的基本概念包括拓扑空间、连续映射、开集、闭集等,它们构成了拓扑学的基础。
一、拓扑空间的定义与基本性质拓扑空间是拓扑学中最基本的概念之一。
一个集合X,若其满足以下三个条件,则称X是一个拓扑空间:1. X本身与空集∅是开集;2. 任意多个开集的交集仍是开集;3. 有限多个开集的并集仍是开集。
在拓扑空间中,我们可以定义许多重要的概念和性质。
例如,连续映射是拓扑空间之间的一种映射,它在保持点与点之间的接近程度方面具有重要作用。
连续映射的定义是:若拓扑空间X和Y上的一个映射f满足对于任意开集V,其原像f^(-1)(V)是X上的开集,则称f是一个连续映射。
二、开集与闭集在拓扑学中,开集和闭集是两个基本的概念。
开集是指拓扑空间中的一个子集,满足其包含的每个点都是该空间中的一个内点。
闭集是指拓扑空间中的一个子集,满足其包含了该空间中的所有边界点。
开集和闭集具有一些基本的性质:1. 空集∅和整个拓扑空间X既是开集又是闭集;2. 有限个开集的并集是开集,有限个闭集的交集是闭集;3. 任意多个开集的交集是开集,任意多个闭集的并集是闭集。
三、拓扑基与拓扑生成拓扑基和拓扑生成是拓扑学中用于描述拓扑空间性质的重要工具。
拓扑基是指拓扑空间中的一个子集合,满足以下两个条件:1. 拓扑基中的每个元素都是开集;2. 对于任意开集U和任意元素x∈U,存在一个拓扑基中的元素B,使得x∈B且B⊆U。
通过拓扑基,我们可以用更简洁的方式描述拓扑空间中的开集。
拓扑基的定义有助于我们研究拓扑空间的性质和结构。
拓扑生成是指通过给定的拓扑生成集合,来定义拓扑空间中的开集。
拓扑生成集合是一个集合,满足以下两个条件:1. 拓扑生成集合中的每个元素都是开集;2. 对于任意开集U,其包含的点都属于拓扑生成集合中的某个元素。
拓扑基和拓扑生成的引入,使得我们可以根据拓扑空间的结构特点和需要,选择不同的刻画方式,方便地研究和构造拓扑空间。
拓扑学第2章拓扑空间连续映射
第二章 拓扑空间与连续映射本章是点集拓扑学基础中之基础, 从度量空间及其连续映射导入一般拓扑学中最基本的两个概念: 拓扑空间、连续映射, 分析了拓扑空间中的开集、邻域、聚点、闭集、闭包、内部、边界、基与子基的性质,各几种不同的角度生成拓扑空间,及刻画拓扑空间上的连续性.教材中先介绍度量空间概念,由于刚刚结束泛函分析课程,所以此节不讲,而补充如下内容。
§ 2-1 数学分析中对连续性的刻画由于映射的连续性是刻画拓扑变换的重要概念,所以,我们先回顾一下数学分析中函数的连续性是如何刻画的。
设11:f E E →是一个函数,10x E ∈,则f 在0x 处连续的定义有如下几种描述方法:(1)序列语言若序列1,2,{}n n x = 收敛于0x ,则序列1,2,{()}n n f x = 收敛于0()f x ;(2)εδ-语言对于0ε∀>,总可以找到0δ>,使当0x x δ-<时,有0()()f x f x ε-<(3)邻域语言若V 是包含0()f x 的邻域(开集),则存在包含0x 的邻域U ,使得()f U V ⊂。
解释:(1)和(2)中用到距离的概念,可用于度量空间映射连续性的描述; 对于没有度量的场合,可以用(3)来描述;所谓拓扑空间就是具有邻域(开集)结构的空间。
§ 2-2 拓扑空间的定义一、 拓扑的定义注:这是关于拓扑结构性的定义定义1 设X 是一非空集,X 的一个子集族2Xτ⊆称为X 的一个拓扑,若它满足(1),X τ∅∈;(2)τ中任意多个元素(即X 的子集)的并仍属于τ;(3) τ中有限多个元素的交仍属于τ。
集合X 和它的一个拓扑τ一起称为一个拓扑空间,记(,)X τ。
τ中的元素称为这个拓扑空间的一个开集。
下面我们解释三个问题:(1)拓扑公理定义的理由; (2) 为什么τ中的元素称为开集;(3) 开集定义的完备性。
● 先解释拓扑定义的理由:① 从εδ-语言看:0x x δ-<和0()()f x f x ε-<分别为1E 上的开区间;② 从邻域语言看:,U V 是邻域,而()f U 是0()f x 的邻域,连续的条件是()f U V ⊂,即一个邻域包含了另一个邻域,也就是说,0()f x 是V 的内点,有内点构成的集合为开集。
河北师大点集拓扑第二章教案
一、教学目的与要求
本章是点集拓扑学的基础知识,在本章中建立了点集拓扑学许多最基本的概念,为学习点集拓扑 学的核心内容打下基础。本章应掌握的概念有:度量空间、开集、邻域、拓扑空间、映射在一点连续、 连续映射、度量诱导的拓扑、可度量化空间、同胚、拓扑不变性质、邻域系、聚点、孤立点、闭集、 闭包、内点、内部、边界点、边界、基、子基、邻域基、邻域子基、序列、序列的极限点、收敛、子 序列。 学生还应该掌握:典型的拓扑和度量空间的例子、开集和邻域的性质、连续映射和同胚映射 的性质、(集合的)内部的性质内部和边界和闭包之间关系、连续映射的等价条件(分别用开集、闭 集、邻域来描述)、邻域系的性质和判定方法、基的判定法和子集族成为基(或子基)的条件、映射 在一点连续的性质和判定法则、拓扑空间和度量空间中序列的性质。
2.1 度量空间与连续映射
首先,我们从在数学分析中学过的连续函数出发, 抽象出度量和度量空间的概念.
定义 2.1.1 设 X 是一个集合, ρ : X × X → R .如果对于任何 x, y, z ∈ X ,有 (1) (正定性) ρ(x, y) ≥ 0, 并且 ρ(x, y) = 0当且仅当 x = y ; (2) (对称性) ρ(x, y) = ρ( y, x) ;
(2) 对于点 x∈ X 的任意两个球形邻域,存在 x ; 的一个球形邻域同时包含于两者
(3) 如果 y∈ X 属于 x∈ X 的某一个球形邻域,则 y 有一个球形邻域包含于 x 的
那个球形邻域. 定义 2.1.3 设 A 是度量空间 X 的一个子集. 如果 A 中的每一个点有一个球形邻域包
含于 A (即对于每一个 a∈ A, ε 存在实数 > 0 使得 B(a,ε ) ⊂ A),则称 A 是度量空间
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
定义2.3. 设A是度量空间X的一个子集.如果A中 的每一个点都有一个球形邻域包含于A(即对于每 一个a∈A,存在实数ε>0使得B(a,ε)
),则称A A
是度量空间X中的一个开集.
例2.4 实数空间R中的开区间 (a,b)为开集. 例2.5 度量空间 X 中的开球为开集. 例2.6 [a,b]={x∈R|a≤x≤b} (a.b]={x∈R|a<x≤b},[a,b)={x∈R|a≤x<b} 都不是R中的开集.
称为一个以x为中心以 为半径的球形邻域.
定理2.1. 度量空间(X,ρ)的球形邻域具有性质: 1) 对任意x∈X,至少有一个 B ( x ) .且 x B ( x ) 2) 对x∈X的任意两个B1 ( x), B 2 ( x) ,
B ( x), s.t x B ( x) B1 ( x) B 2 ( x)
现 代 工 程 数 学
第二章 拓扑空间与连续映射
本章教学基本要求
掌握度量空间及度量空间的连续映射的概念掌握拓 扑与拓扑空间的概念,并在此空间上建立起来的连续映
射,同胚的概念,熟悉几个拓扑空间的例子掌握邻域与
邻域系的概念及性质;掌握连续映射的两种定义;掌 握证明开集与邻域的证明方法 掌握闭集和闭包等相关
空间 ( X , ) 诱导的拓扑空间.
常见的拓扑 例2.1 平庸空间.
设X是一个集合.令 ( X , ) ,则 ( X , ) 是拓扑 空间,称为平庸拓扑空间.
例2.2 离散空间. 集构成的族.容易验证, 是X的一个拓扑,称之 为X的离散拓扑;可知,在离散空间(X,)中, X的每一个子集都是开集.
三. 拓扑空间中的连续映射和同胚映射 定义2.7 设X和Y是两个拓扑空间,f : X→Y,以及 x0 X 如果对于 f ( x0 ) 的任意一个邻域 U U f ( x0 ) , 有: f 1 (U ) U x ,则称 f 在点 x0 处是连续的.
0
如果映射f 在X的每一个点x∈X处连续,则 称f 是拓扑空间X上的一个连续映射. 定理2.6 f 是连续的 充分必要条件是Y中开集的 原象是X中的开集
定理2.7
设X,Y和Z都是拓扑空间.则
(1)恒同映射: X : X→X是一个连续映射; i (2)如果f : X→Y和g:Y→Z都是连续映射, 则 gof : X→Z也是连续映射. (3)常值映射: : X y0 Y 是一个连续映射; C (4)从离散空间到任何空间的映射都是连续的 (5)从X到平凡空间的任何映射都是连续的
则 gof : X→Z也是同胚映射.
定义2.9
设X和Y是两个拓扑空间.如果存在一个
同胚f :X→Y,则称拓扑空间X与拓扑空间Y是同胚的,
或称X与Y同胚,或称X同胚于Y.
定理2.9 设X,Y和Z都是拓扑空间.则
(1)X与X同胚;
(2)如来X与Y同胚,则Y与X同胚;
(3)如果X与Y同胚,Y与Z同胚,
则X与Z同胚.
二. 邻域与邻域系 定义2.6
U是X的一个子集,满足条件:存在一个开集V∈
使得 x V U , 则称U是点x的一个邻域. 说明 点x的所有邻域构成的x的子集族称为 点x的邻域系,记为U x 如果U是包含着点x的一个开集,那么 它一定是x的一个邻域,于是我们称U 是点x的一个开邻域.
设(X, )是一个拓扑空间,x∈X.如果
四. 子空间的概念
设(X, )是一个拓扑空间, X A 令 A {V AV } ,则 A 是A上的拓扑,拓扑空间 定义2.10
( A, A )称为 ( X , ) 的子空间.
说明
拓扑空间 ( X , ) 的任何子集都可以看作拓扑
空间,即子空间 ( X , A )
间所具有,则必为与其同胚的任何一个拓扑空间 所具有,则称此性质P是一个拓扑不变性质.换 言之,拓扑不变性质即为同胚的拓扑空间所共有 的性质. 拓扑学的中心任务便是研究拓扑不变性质.
定理2.10 设X,Y,Z都是拓扑空间.如果Y是X的 一个子空间,Z是Y的一个子空间,则Z是X的一个 子空间.
定理2.11 设 ( X , ) 是拓扑空间, B A X
(1) 若B是X中的开集,则B也是A中的开集. (2) 若A是X的开集,B是A的开集,则B也是X中的开集 关于拓扑性质
拓扑空间的某种性质P,如果为某一个拓扑空
0, x y ; ( x, y ) 是一个离散度量 1, x y.
离散的度量空间或许是我们以前未曾接触过
的一类空间,但今后会发现它的性质是简单的.
2. 度量空间的其他概念
定义2.2. 设(X,ρ)是一个度量空间,x∈X.
对于任意给定的实数 >0,集合:
B( x, ) { y X | ( x, y) }
设X是一个集合.令 =P (X),即由X的所有子
练习2.1 设X={a,b,c}. 1 {, (a ),(a, b),(a, b, c)}
1是否X的拓扑
例2.3 有限补空间.可数补空间.
{U X U 是X的一个有限子集 } { }
C
{U X U C 是X的一个可数子集 } { }
定义2.8 设X和Y是两个拓扑空间.如果 f :X→Y 是一个一一映射,并且 f 和 f 1 :Y→X都是连续的, 则称 f 是一个同胚映射或同胚. 定理2.8 设X,Y和Z都是拓扑空间.则
i (1)恒同映射: X : X→X是一个同胚映射;
(2)如果f :X→Y是一个同胚,则 f 1: Y→X 也是一个同胚; (3)如果f : X→Y和g:Y→Z都是同胚映射,
定理2.4
拓扑空间X的一个子集U是开集的充分必
要条件是U是它的每一点的邻域,即只要x∈U,U便
是x的一个邻域. 定理2.5 设X是一个拓扑空间.x∈X, U x 为x的
邻域系,则:
U (1) 对于任何x∈X, x ,如果 U U x ,则x∈U
(2) 如果U ,V U x ,则U∩V∈ U x . (3) 如果 U U x ,并且 U V , 则: V U x . (4) 如果 U U x ,则存在 V U x .满足: (a) V U , (b) 对于任何y∈V,有V U y
1 . 则
称 中的元素为拓扑空间(X, ) 中的开集.
是X的一个拓扑 ,称(X, )为拓扑空间.
A 1
A ∈
说明 拓扑空间的开集和度量空间的开集有区别 设 ( X , ) 是一个度量空间, {V X V是( X , )} 则称 为由度量 诱导的拓扑,( X , )是由度量
概念. 重点:拓扑空间,同胚映射,拓扑的建立和证明. 难点:拓扑空间,同胚映射
§2.1 度量空间与连续映射 一. 度量空间 1. 度量空间的定义 定义2.1. 设 X 为集合, : X X R 为一映射,如果 对于任何x,y,z∈X,有:
1) ( x, y ) 0, ( x, y ) 0 x y
ρ是R的一个度量,因此偶对(R,ρ)是一个度
量空间,通常称为实数空间. 例2.2 n维欧氏空间,对于实数集合R的n重笛卡儿积, 定义ρ: R n R n R ,对于任意的
x ( x1 , x2 ,, xn ), y ( y1 , y2 ,, yn ) Rn
定义: ( x , y )
定理2.2. 度量空间(X,ρ)的开集具有以下性质: (1)集合X本身和空集 都是开集. (2) 有限个开集的交是一个开集 . (3)任意一个开集族(即由开集构成的族) 的并是一个开集 定义2.4. 设x是度量空间X中的一个点,U是度量 空间X的一个子集.如果存在一个开集V满足:
x V U ,则称U是点x的一个邻域.
二. 度量空间中的连续映射 定义2.4. 设X和Y是两个度量空间,f : X→Y,以及 x0 X 如果对于 f ( x0 )的任意一个球形邻域 B( f ( x0 ), ) , 存在 x0 的某一球形邻域 B( x0 , ) ,使得:
f ( B( x0 , ) B( f ( x0 ), )
n ( xi yi )2 则ρ是 R上的一个度量
n
i 1
例2.3 离散的度量空间. 设(X,ρ)是一个度量空间.如果对于每一个x∈X, 存在一个实数 , 使得 0 x
( x, y ) x ,对
任意的 x , y X , x y 都成立, 称(X,ρ)是离散的, 或者称ρ是X的一个离散度量. 例如:
则称映射f 在点 x0处是连续的. 如果映射f 在X的每一个点x∈X处连续,则 称f 是一个连续映射.
定理2.3 设X和Y是两个度量空间,f : X→Y,以及 x0 X
则下述条件(1)和(2)分别等价于条件 (1 )和 (2 ) : (1) f 在点 x0 处是连续的.
(1 ) f ( x0 ) 的每一个邻域的原象是 x0的一个邻域.
2) ( x, y ) ( y, x )
对于任意两点x,y∈X,实数 3) ( x, z ) ( x, y ) ( y, z ) ρ(x,y)称
为从点x到点y的距离. 则称ρ是集合X的一个度量. 并称 ( X , ) 为度量空间.
例2.1 对于实数集合R ,定义ρ:R×R→R如下: 对于任意x,y∈R,令ρ(x,y)=|x-y|.
(2) f 是连续的
(2 ) Y中每一个开集的原象是X中的一个 映射是否是连续的,或者在某一点处是否是连续
的,本质上只与度量空间中的开集有关
§2.2 拓 扑 空 间 与 连 续 映 射 一. 拓扑空间的定义 如果 满足: 定义2.5 设X是一个集合 是X的幂集P(X)的子集 (1) X , (2) 若A, B∈ . 则A∩B∈ (3) 若 则称
