天然气物性参数及管线压降与温降的计算
天然气管存量的两种计算公式

天然气管存量的两种计算公式天然气管存量的两种计算公式Prepared on 22 November 2020天然气管存量计算公式1、第一种计算公式Q=*V*P 均/(T 均**Z) 其中V 是该管段内容积(即管段管容),Z 是压缩因子,Z=1/(1+*1000000*P 均*10^^C 2/T 均^,P 均=2/3[P 1++(P 2+)2/(P 1+P 2+2*]T 均=(T 1+T 2)/2+P 1、P 2、T 1、T 2分别为管段起、终点压力和温度;C 2是天然气相对密度(注:一定周期内会有小调整)。
总管存Q n 为各分段管存的求和。
2、第二种计算公式(1)管段管存计算公式:100001pj pj V P T Z V P T Z =??式中:0V ——管段在标准状态下的管存量,单位为立方米(m 3) ; 1V ——管段的设计管容量,单位为立方米(m 3) ,计算公式为:4V 21L d ??=π 式中:π=;d ——管段的内直径,单位为米(m );L ——管段的长度,单位为米(m );pj P ——管段内气体平均压力(绝对压力),单位为兆帕(MPa );0T ——标准参比条件的温度,数值为;0Z ——标准参比条件下的压缩因子,数值为;P——标准参比条件的压力,数值为;T——管段内气体平均温度,单位为开尔文(K);pjZ——工况条件下的压缩因子,根据GB/T 《天然气压缩因子的计1算第2部分:用摩尔组成进行计算》计算求得。
(2)平均压力计算公式:式中:P——管段起点气体压力,单位为兆帕(MPa);1P——管段终点气体压力,单位为兆帕(MPa)。
2(3)平均温度计算公式:式中:T——管段起点气体温度,单位为开尔文(K);1T——管段终点气体温度,单位为开尔文(K)。
2注:气体体积的标准参比条件是p0=,T0=。
天然气物性参数及管线压降与温降的计算

整个计算过程的公式包括三部分:一. 天然气物性参数及管线压降与温降的计算 二. 天然气水合物的形成预测模型 三. 注醇量计算方法.天然气物性参数及管线压降与温降的计算 20 C 标准状态1y i M i24.055任意温度与压力下Y i M i式中厂混合气体的密度,P —任意温度、压力下i 组分的密度,kg/m 3; y i — i 组分的摩尔分数; M i —i组分的分子量, V i —i 组分摩尔容积, 天然气密度计算公式pMW gZRT天然气相对密度天然气相对密度△的定义为:在相同温度,压力下,天然气的密度与空气密 度之比。
天然气分子量标准状态下,Ikmol 天然气的质量定义为天然气的平均分子量,Y i M iM式中 M —气体的平均分子量,kg/kmol ; y i —气体第i 组分的摩尔分数;M —气体第i 组分的分子量,kg/kmol天然气密度混合气体密度指单位体积混合气体的质量。
0 °C 标准状态按下面公式计算:1 22.414y i M i简称分子量。
(1)kg/m 3;kg/kmol;⑹式中 △—气体相对密度;厂气体密度,kg/m 3;p —空气密度,kg/m 3,在 P o =1O1.325kPa, T o =273.15K 时,p =1.293kg/m 3;在 P o =1O1.325kPa T O =273.15K 时,p =1.293kg/m 3。
因为空气的分子量为28.96,固有28.96假设,混合气和空气的性质都可用理想气体状态方程描述,则可用下列关系 式表示天然气的相对密度天然气的虚拟临界参数任何气体在温度低于某一数值时都可以等温压缩成液体,但当高于该温度时, 无论压力增加到多大,都不能使气体液化。
可以使气体压缩成液态的这个极限温 度称为该气体的临界温度。
当温度等于临界温度时,使气体压缩成液体所需压力 称为临界压力,此时状态称为临界状态。
混合气体的虚拟临界温度、虚拟临界压 力和虚拟临界密度可按混合气体中各组分的摩尔分数以及临界温度、临界压力和 临界密度求得,按下式计算。
天然气基本物理量计算公式

天然气基本物理量计算公式天然气是一种重要的能源资源,其基本物理量的计算是天然气开发和利用过程中的重要环节。
天然气的基本物理量包括压力、温度、体积、质量等,针对不同的物理量,有相应的计算公式。
本文将分别介绍天然气压力、温度、体积和质量的计算公式及其应用。
一、天然气压力的计算公式。
天然气的压力是指天然气分子对容器壁的撞击力,通常用帕斯卡(Pa)或千帕(kPa)来表示。
天然气压力的计算公式为:P = nRT/V。
其中,P表示天然气的压力,n表示天然气的摩尔数,R为气体常数,T表示天然气的绝对温度,V表示天然气的体积。
在实际应用中,可以根据天然气的摩尔数、温度和体积来计算天然气的压力,从而为天然气的输送和储存提供参考数据。
二、天然气温度的计算公式。
天然气的温度是指天然气分子的平均动能,通常用摄氏度(℃)或开尔文(K)来表示。
天然气温度的计算公式为:T = PV/nR。
其中,T表示天然气的温度,P表示天然气的压力,V表示天然气的体积,n表示天然气的摩尔数,R为气体常数。
通过这个计算公式,可以根据天然气的压力、体积和摩尔数来计算天然气的温度,为天然气的加工和利用提供重要参数。
三、天然气体积的计算公式。
天然气的体积是指天然气所占据的空间大小,通常用立方米(m³)或升(L)来表示。
天然气体积的计算公式为:V = nRT/P。
其中,V表示天然气的体积,n表示天然气的摩尔数,R为气体常数,T表示天然气的绝对温度,P表示天然气的压力。
通过这个计算公式,可以根据天然气的摩尔数、温度和压力来计算天然气的体积,为天然气的储存和运输提供重要数据。
四、天然气质量的计算公式。
天然气的质量是指天然气中所含的化学元素的质量总和,通常用千克(kg)或吨(t)来表示。
天然气质量的计算公式为:m = nM。
其中,m表示天然气的质量,n表示天然气的摩尔数,M表示天然气的摩尔质量。
通过这个计算公式,可以根据天然气的摩尔数和摩尔质量来计算天然气的质量,为天然气的生产和利用提供重要数据。
燃气管道 压降计算

燃气管道压降计算
燃气管道的压降计算是工程设计中非常重要的一部分,它涉及到管道内流体的流动特性、管道材料、管道尺寸、流体性质等多个因素。
压降是指流体在管道中由于管道摩擦、弯头、阀门等元件的阻力而产生的压力损失。
在进行压降计算时,需要考虑以下几个方面:
首先,需要确定流体的流量、流速和流体的性质,包括密度、粘度等参数。
这些参数将直接影响到压降的计算。
其次,需要考虑管道的材质和尺寸,包括管道的直径、长度、壁厚等参数。
这些参数将影响到管道内的摩擦阻力。
另外,管道中的附件,如弯头、阀门、管道变径等也会对压降产生影响,需要对这些附件进行适当的修正计算。
在进行压降计算时,可以采用Darcy-Weisbach公式或者其他流体力学公式进行计算。
同时,也可以借助计算机辅助工具进行精确的压降计算。
此外,还需要考虑流体在管道中的流动状态,如层流或湍流状态,这将影响到压降的计算方法和结果。
最后,需要根据实际工程要求和安全标准,对计算得到的压降结果进行合理的评估和校核,以确保管道系统的安全稳定运行。
综上所述,燃气管道的压降计算涉及到多个因素,需要综合考虑流体性质、管道参数、流动状态等多个方面的因素,以确保计算结果的准确性和可靠性。
天然气高位发热量和低位发热量计算说明
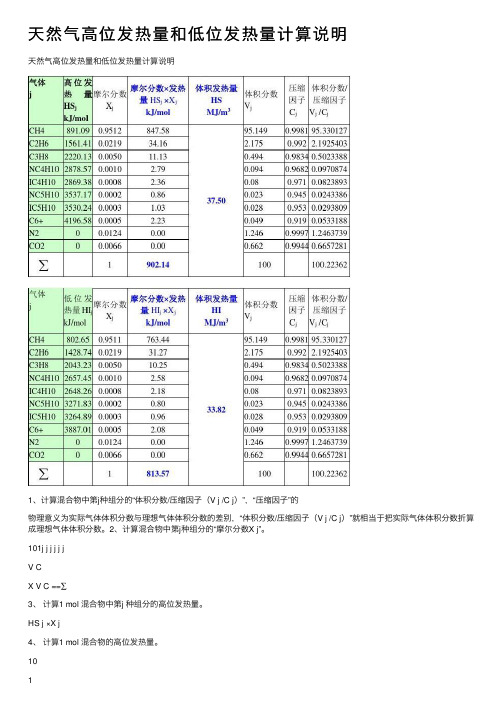
天然⽓⾼位发热量和低位发热量计算说明天然⽓⾼位发热量和低位发热量计算说明1、计算混合物中第j种组分的“体积分数/压缩因⼦(V j /C j)”,“压缩因⼦”的物理意义为实际⽓体体积分数与理想⽓体体积分数的差别,“体积分数/压缩因⼦(V j /C j)”就相当于把实际⽓体体积分数折算成理想⽓体体积分数。
2、计算混合物中第j种组分的“摩尔分数X j”。
101j j j j j jV CX V C ==∑3、计算1 mol 混合物中第j 种组分的⾼位发热量。
HS j ×X j4、计算1 mol 混合物的⾼位发热量。
101()jj j HSX =?∑5、计算在P 压⼒、T 温度下的⾼位体积发热量,计算公式:101()8.31451j j j PHS HS X T ==∑ MJ/m 3式中:8.31451为天然⽓混合物的⽓体常数R 。
6、计算在P 压⼒、T 温度下的低位体积发热量,与⾼位体积发热量相似,从步骤1到步骤5,只不过把步骤3、4、5中的⾼位发热量换成低位发热量。
性能计算中⽤到的是天然⽓的低位发热量,燃烧室的能量平衡关系公式为:(3.9)式中:— 燃烧室的空⽓摩尔流量— 压⽓机出⼝空⽓焓— 燃烧室的燃料摩尔流量— 燃料的低位发热量— 燃烧室的燃烧效率— 燃⽓透平进⼝燃⽓焓上式中燃料的低位发热量Q l 单位为MJ/kMol ,所以3122.4/36.37/22.4/814.688/Q HI L Mol MJ m L Mol MJ kMol=?=?=,其中22.4L/Mol 为天然⽓在标准状态下的摩尔体积。
由于Q 1单位为MJ/kMol ,所以在计算天然⽓的低位发热量时,统⼀使⽤标准状态下的压⼒P 和温度T 计算HI ,其⽬的是能够使⽤标准状态下天然⽓的摩尔体积22.4L/Mol 。
天然气管道计算

一、天然气计量原理及计算方法测量原理:天然气流经节流装置时,流速在孔板处形成局部收缩,从而使流速增加,静压力降低,在孔板前后产生静压压差,气流的流速越大,孔板前后产生的差压越大,从而可通过测量差压来衡量天然气流经节流装置的流量大小。
(注:这种测量流量的方法是以能量守恒定律和流动连续性方程为基础的。
)1、天然气流量的计算方法1)公式引用SY/T6143—1996 标准Q n= A s CEd2F G∑F z F T√p1△p其中:Q n——体积流量Nm3/h 标准状态:0.101325MpaA s——计量系数 1.145X10-2C——流出系数0.6E——渐进速度系数 1d——孔板开孔直径F z——超压缩因子 1.1F G——相对密度系数 1.1∑——可膨胀性系数 1F T——流动温度系数 1经过推导和实践中运用,找出各个系数与本站输气计量中的关系。
推导出了经验公式,简便了运算,便于掌握。
输气站流量计算经验公式:Q n = 8.4×10-3d2√p1△p注意:(1)上述公式系数取值要精确,计算误差在5%左右。
(2)天然气计量中对孔板上端面,锐角等要求较严格,孔板必须经检验合格方可使用。
(3)上述公式是对于确定的孔板可推出孔板的测量范围。
如反过来,知道了一定的流量,也可算出需要多大的孔板。
2、输气管线储气量的计算输气管线储气量的计算(引用《输气管道设计与管理》)Q储= VT0/P0T(P1m/Z1-P2m/Z2)式中:Q储——管道的储气量m3V——管道的容积m3V=53275.56 m3(轮库输气管线长192.4km、管径610mm、壁厚7—8mm)T0——293.15kP0——0.101325MpaP1m P2m——分别为计算管内气体的最高、最低平均压力(绝压)MPa,一般P2m为0。
Z1Z2——对P1m P2m气体压力下的压缩系数。
(Z1=Z2)T——气体的平均温度k注:上式可作为压力P1降到P2可有多少m3的天然气计算式。
台南气田参考2
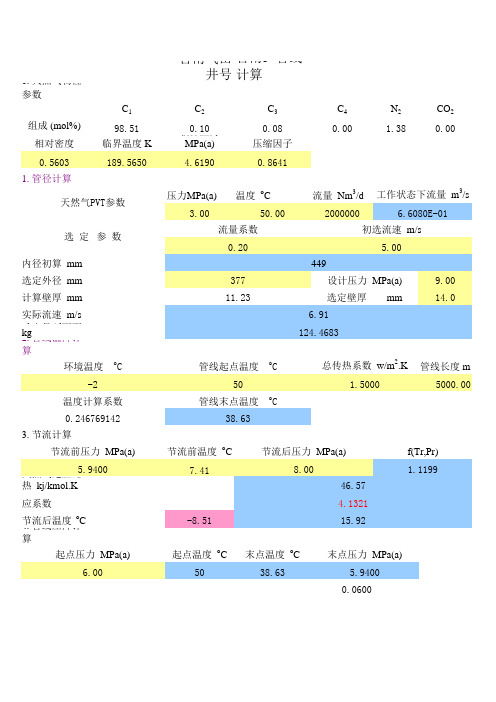
台南气田井号台南5 管线计算0. 天然气物性参数C 1C 2C 3C 4N 2CO 298.510.100.080.001.380.00相对密度临界温度 K 临界压力 MPa(a)压缩因子0.5603189.56504.61900.86411. 管径计算压力MPa(a)温度 o C流量 Nm 3/d 3.0050.002000000内径初算 mm 选定外径 mm 9.00计算壁厚 mm 14.0实际流速 m/s 每米管线重量 kg 2. 管线温降计算管线长度 m 5000.003. 节流计算节流前温度 o C7.41天然气定压比热 kj/kmol.K 焦耳-汤姆逊效应系数 o C/MPa 节流后温度 o C -8.514. 管线压降计算起点温度 oC末点温度 oC 5038.630.060015.92f(Tr,Pr)节流后压力 MPa(a)4.132146.57-2508.0038.63管线末点温度 o C温度计算系数组成 (mol%)11.236.91选定壁厚 mm449初选流速 m/s5.00天然气PVT参数工作状态下流量 m 3/s6.6080E-01流量系数末点压力 MPa(a)377设计压力 MPa(a)1.5000124.4683总传热系数 w/m 2.K管线起点温度 o C5.9400选 定 参 数0.20起点压力 MPa(a)6.000.246769142节流前压力 MPa(a)5.94001.1199环境温度 o C。
天然气温压补偿公式

天然气温压补偿公式天然气温压补偿公式是一个在物理学和工程学中较为重要的概念。
这玩意儿听着挺复杂,其实跟咱的日常生活也有点关系。
咱就说有一次我去爬山,那山可高了。
爬着爬着,我就感觉呼吸越来越急促,身体也越来越累。
一开始我还以为是自己体力不行,后来才发现,这是因为随着海拔的升高,气温下降,气压也降低了。
在物理学中,天然气温压补偿公式就能够帮助我们理解和计算这种变化。
这个公式考虑了温度和压力对气体状态的影响。
比如说,在一个封闭的容器里,如果温度升高,气体分子的运动就会更剧烈,压力也就会相应增大;反过来,如果温度降低,压力就会减小。
咱们再回到爬山的例子。
随着高度增加,气温降低,空气变得稀薄,气压下降。
这就好比是容器的体积变大了,但是里面的气体分子数量没有变,所以每个分子所产生的压力就变小了。
在实际的工程应用中,这个公式也非常重要。
比如在汽车发动机的设计中,要考虑到不同的环境温度和气压对燃烧效率的影响。
如果不进行温压补偿,发动机可能就不能正常工作,要么动力不足,要么油耗过高。
还有在气象学中,通过天然气温压补偿公式,能够更准确地预测天气变化。
比如说,知道了当前的气温和气压,结合这个公式,就能推测出未来的天气趋势。
在工业生产中,像是化工流程、气体储存和输送等方面,天然气温压补偿公式也发挥着重要作用。
比如在储存天然气的时候,就得根据温度和压力的变化,调整储存设备的参数,以确保安全和高效。
总之,天然气温压补偿公式虽然看起来复杂,但在我们的生活和各种科学技术领域中都有着不可或缺的作用。
它就像一个默默无闻的幕后英雄,悄悄地为我们的生活提供着保障和便利。
不管是爬山时的呼吸变化,还是汽车发动机的高效运行,亦或是准确的天气预报和安全的工业生产,都离不开这个神奇的公式。
所以,可别小看了这个看似深奥的天然气温压补偿公式,它其实就在我们身边,影响着我们生活的方方面面。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
整个计算过程的公式包括三部分:一.天然气物性参数及管线压降与温降的计算 二.天然气水合物的形成预测模型 三.注醇量计算方法一.天然气物性参数及管线压降与温降的计算 天然气分子量标准状态下,1kmol 天然气的质量定义为天然气的平均分子量,简称分子量。
∑=ii M y M(1) 式中 M —气体的平均分子量,kg/kmol ;y i —气体第i 组分的摩尔分数;M i —气体第i 组分的分子量,kg/kmol 。
天然气密度混合气体密度指单位体积混合气体的质量。
按下面公式计算: 0℃标准状态∑=i i M y 14.4221ρ (2) 20℃标准状态∑=i i M y 055241.ρ (3) 任意温度与压力下∑∑=ii ii V y M y ρ(4)式中 ρ—混合气体的密度,kg/m 3;ρi —任意温度、压力下i 组分的密度,kg/m 3; y i —i 组分的摩尔分数;M i —i 组分的分子量,kg/kmol ; V i —i 组分摩尔容积,m 3 /kmol 。
天然气密度计算公式gpMW ZRTρ= (5)天然气相对密度天然气相对密度Δ的定义为:在相同温度,压力下,天然气的密度与空气密度之比。
aρρ∆=(6) 式中 Δ—气体相对密度;ρ—气体密度,kg/m 3; ρa —空气密度,kg/m 3,在P 0=101.325kPa ,T 0=273.15K 时,ρa =1.293kg/m 3;在P 0=101.325kPa ,T 0=273.15K 时,ρa =1.293kg/m 3。
因为空气的分子量为28.96,固有28.96M∆=(7) 假设,混合气和空气的性质都可用理想气体状态方程描述,则可用下列关系式表示天然气的相对密度28.96gg ga a pMW MW MW RT pMW MW RT∆===(8) 式中 MW a —空气视相对分子质量;MW g —天然气视相对分子质量。
天然气的虚拟临界参数任何气体在温度低于某一数值时都可以等温压缩成液体,但当高于该温度时,无论压力增加到多大,都不能使气体液化。
可以使气体压缩成液态的这个极限温度称为该气体的临界温度。
当温度等于临界温度时,使气体压缩成液体所需压力称为临界压力,此时状态称为临界状态。
混合气体的虚拟临界温度、虚拟临界压力和虚拟临界密度可按混合气体中各组分的摩尔分数以及临界温度、临界压力和临界密度求得,按下式计算。
∑=icii c T y T(9)∑=icii c P y P(10)∑=icii c y ρρ(11)式中 T c —混合气体虚拟临界温度,K ;P c —混合气体虚拟临界压力(绝),Pa ; ρc —混合气体虚拟临界密度,kg/m 3; T ci —i 组分的临界温度,K ; P ci —i 组分的临界压力(绝),Pa ; ρci —i 组分的临界密度,kg/m 3;y i —i 组分的摩尔分数。
天然气的对比参数天然气的压力、温度、密度与其临界压力、临界温度和临界密度之比称为天然气对比压力、对比温度和对比密度。
c r P PP =(12)c r T TT =(13)c r ρρρ=(14)式中 P r —气体对比压力;T r —气体对比温度; ρr —气体对比密度。
天然气压缩系数对于理想气体,在所有状态下都有RT P ρ=。
对于实际气体,引入一个修正系数以使得RT Z P ρ= (15)式中Z 叫做压缩系数,它表示实际气体与理想气体的偏离程度。
对于理想气体,在所有状态下Z 的值都为l 。
对于实际气体,Z 是状态函数。
关于天然气压缩因子的计算,主要采用Pong-Robinson 方程:()()()RT a T p V b V V b b V b =--++- (16) 式中0.511()()(1)n ni j i j i j ij i j a T x x a a K αα===-∑∑ (17)1ni i j b x b ==∑ (18)220.45724cri crR T a p = (19) 0.0788cri crRT b p = (20) ()20.5ri 11i i m T α⎡⎤=+-⎣⎦ (21)20.37464 1.54220.26992i i i m ωω=+- (22)式中 K ij —天然气的交互作用参数;p cr —组分i 的气体临界压力; T cr —组分i 的气体临界温度; T r —组分i 的对比温度; ωi —组分i 的偏心因子。
由方程(16)可得到关于Z 的方程()()023)1(32223=-----+--B B AB Z B B A Z B Z (23)22T R aPA =(24) RTbPB = (25)天然气质量定压比热容混合物质量定压热容0Piii P C y C ∑= (26) 式中 C p 0—理想气体混合物质量定压热容,kJ/(kg·K); y i —组分i 的摩尔分数。
天然气的粘度计算公式根据天然气所处压力、温度条件下的密度和标准状态下的相对密度Δ,可按下式计算天然气粘度exp 1000y C x ρμ⎡⎤⎛⎫=⎢⎥ ⎪⎝⎭⎢⎥⎣⎦ (27)1063.62.570.2781x T=+∆+(28) 1.110.04y x =+ (29)() 1.542.4157.770.184410122.4377.58 1.8T C T-+∆=⨯+∆+ (30)天然气的导热系数计算公式气体碳氢化合物的导热系数随温度或压力的升高而增大,确定气体导热系数可按查图法和计算法确定。
若压力较低时,混合气体的导热系数按下式计算∑∑=iii iiii My M y 3131λλ(31)式中 λ—混合气体的导热系数,W/(m·K); λi —混合气体i 组分的导热系数,W/(m·K);y i —混合气体i 组分摩尔分数;M i —混合气体i 组分的分子量,kg/kmol 。
低压单组分气体的导热系数在低压下,对于甲烷、环烷烃、芳香烃r P T ΓMC 51004746.2-⨯=λ 1<r T (32) 对于其它碳氢化合物及其它的对比温度范围()ΓMC T P r 32614.552.141060104.4-⨯=-λ (33) 32211c c P M T Γ= (34)式中 λ—气体的导热系数,W/(m·K);T r —气体对比温度;C P —气体质量定压热容,J/(kg·K); T c —气体临界温度,K ; P c —气体临界压力,MPa ; M —气体分子量,kg/kmol 。
温度对导热系数的影响20273273⎪⎭⎫⎝⎛++=T C T C λλ (35)式中 λ—气体在T 时的导热系数,W/(m·K);λ0—气体在273K 时的导热温度,W/(m·K); C —与气体性质有关的无因次实验系数,见表4-1。
对混合气体,还可按下式计算()()()()∑=ii i iT T y T T 1212λλλλ (36) 式中 λ(T 1)—温度为T 1时混合气体导热系数,W/(m·K); λ(T 2)—温度为T 2时混合气体导热系数,W/(m·K);y i —混合气体i 组分摩尔分数;λi (T 1)—温度为T 1时i 组分气体导热系数,W/(m·K); λi (T 2)—温度为T 2时i 组分气体导热系数,W/(m·K)。
压力对气体导热系数的影响在高压下,单组分气体导热系数可根据对比密度ρr 进行计算ρr <0.5时()()()1e 106965425350450-⨯=--r c ΓZ ρλλ.. (37)0.5<ρr <2.0 时()()()0691e 10519722670450...-⨯=--r c ΓZ ρλλ (38)2.0<ρr <2.8 时()()()0162e 107467351551550...+⨯=--r c ΓZ ρλλ (39)式中 ρr —气体对比密度;λ0—低压气体导热系数,W/(m·K); ρ—高压下气体密度,kg/m 3; λ—高压下气体导热系数,W/(m·K); Z c —临界压缩系数。
公式(36)~(39)也适应高压混合气体导热系数的计算。
此时,公式中各量为混合气体对应参数。
计算气体导热系数步骤如下:(1)由公式(32)或(33)计算低压气体各组分在273K 时的导热系数。
(2)由公式(34)或(35)计算低压气体各组分在给定温度下的导热系数。
(3)由公式(31)计算低压混合气体在给定温度下的导热系数。
(4)按公式(37)~(39)计算混合气体在所需温度和压力下的导热系数。
天然气管流的温降根据能量守恒定律和气体动力学理论,可建立一元气流的能量方程,即2222qv v v u gz v h gz x t x δρρρ⎡⎤⎡⎤⎛⎫⎛⎫∂∂-=+++++⎢⎥⎢⎥ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎣⎦⎣⎦(40)若忽略高程并设流动为稳定流,则式(7-5)可改写为p Th dT h dpq T dx p dx dx δ⎛⎫∂∂⎛⎫+=- ⎪ ⎪∂∂⎝⎭⎝⎭ (41) 式中 h —气流的焓,J/kg 。
引入定压比热c p 和焦耳—汤姆逊系数D i 后上式可表示为p p i c dT c D dp q δ-=- (42)由热量平衡关系可得dx 管段上的热量损失为0()K D T T q dx Mπδ-= (43)式中 K —管道的总传热系数,W/(m 2·K)。
联立式(42)和(43)0()p i p K D T T dx c G dp c dT Mπ-=- (44)对上式积分可得管道x 处的温度为000()()xaxaxaxQ i dp T x T T T eG ee dx dx --=+-+⎰ (45) 式中 a =K πD /(Mc p )。
关于焦耳—汤姆逊系数G i 的计算,有热力学关系式可知起计算式为12T p P T T 1D i c ρP ρρρ⎡∂⎤⎛⎫ ⎪⎢⎥∂⎝⎭⎢⎥=-⎢⎥⎛⎫∂⎢⎥ ⎪∂⎝⎭⎢⎥⎣⎦(46)式中 D i —焦耳—汤姆逊系数,K/Pa ; ;C p —质量定压热熔,J/(Kg ·K); P —压力,Pa ; T —温度,K ; ρ—密度,kg/m 3V —比容,m 3/ kg 。
总传热系数K 指当的温差为1︒C 时,单位时间内通过单位传热面积所传递的热量。
对于埋地管道,管道散热的传热过程由三部分组成,即气流至管壁的放热,钢管壁、沥青绝缘层或保温层的热传导和管外壁至周围土壤的传热。
在稳定传热的情况下,已在管内外建立了稳定的温度场时,热平衡关系可表示为:011(1)2(1)012()()()()ln /iy y b bi b i w b i i iD T T D T T T T D T T D D πλKπαπαπ+++-=-=-=-(47)式中 D —计算直径,m ,对于保温管道,可取保温层内外直径的平均值;D i 、D i +1—钢管、绝缘层及保温层的内外径,m ; λi —与上述的层相应的导热系数,W/(m·K); T b 1—钢管内壁的温度,℃;T bi 、(1)b i T +—钢管、绝缘层及保温层的内外壁的温度,℃; α1—油流至管内壁的放热系数,W/(m 2·K); α2—油流至管内壁的放热系数,W/(m 2·K)。
