高中导数经典知识点及例题讲解.
高中数学导数知识点归纳总结材料与例题
导数考试内容:导数的背影.导数的看法.多项式函数的导数.利用导数研究函数的单调性和极值.函数的最大值和最小值.考试要求:(1)认识导数看法的某些本质背景.(2)理解导数的几何意义.( 3)掌握函数, y=c(c 为常数 )、y=xn(n ∈ N+)的导数公式,会求多项式函数的导数.( 4)理解极大值、极小值、最大值、最小值的看法,并会用导数求多项式函数的单调区间、极大值、极小值及闭区间上的最大值和最小值.( 5)会利用导数求某些简单实诘责题的最大值和最小值.§14. 导数知识要点导数的看法导数的几何意义、物理意义常有函数的导数导数导数的运算导数的运算法规函数的单调性导数的应用函数的极值函数的最值1.导数(导函数的简称)的定义:设 x0是函数y f (x) 定义域的一点,若是自变量 x 在 x0处有增量x,则函数值 y也引起相应的增量y f (x0x) f (x0 ) ;比值y f ( x0x) f ( x0 ) 称为函数y f (x) 在点x0到 x0x 之间的平均变化率;若是极限x xlim y lim f ( x0x) f ( x0 ) 存在,则称函数y f (x) 在点x0处可导,并把这个极限叫做x0x x0xy f (x) 在x0处的导数,记作f'''(x0 ) = limy f ( x0x) f ( x0 ) ( x0 ) 或y|x x0,即f lim.x 0x x0x注:①x 是增量,我们也称为“改变量”,因为 x 可正,可负,但不为零 .②以知函数 y f (x) 定义域为 A ,y f'( x)的定义域为 B ,则 A 与 B 关系为 A B .2.函数 y f (x) 在点x0处连续与点x0处可导的关系:⑴函数 y f ( x) 在点x0处连续是y f (x) 在点x0处可导的必要不充分条件.可以证明,若是y f (x) 在点x0处可导,那么y f (x) 点x0处连续 .事实上,令x x0x ,则 x x0相当于x0 .于是 lim f (x) lim f ( x0x) lim [ f ( x x0 ) f (x0 ) f ( x0 )]x x0x 0x 0lim [ f (x 0 x) f ( x 0 )x f (x 0 )]lim f ( x 0x)f ( x 0 ) limlim f ( x 0 ) f '(x 0 ) 0 f ( x 0 ) f ( x 0 ).x 0xx 0xx0 x 0⑵若是 y f ( x) 点 x 0 处连续,那么 y f ( x) 在点 x 0 处可导,是不成立的 .例: f (x) | x |在点 x 00 处连续,但在点 x 0 0 处不可以导,因为 y| x | ,当 x > 0 时,x xy 1 ;当 x <0 时, y 1 ,故 lim y不存在 .x x x 0 x注:①可导的奇函数函数其导函数为偶函数 .②可导的偶函数函数其导函数为奇函数 .3. 导数的几何意义:函数 yf ( x) 在点 x 0 处的导数的几何意义就是曲线y f ( x) 在点 ( x 0 , f (x)) 处的切线的斜率,也 就 是 说 , 曲 线 y f ( x) 在 点 P ( x ,( ))f '( x ) , 切 线 方 程 为f x 处 的 切 线 的 斜 率 是y y 0f ' (x)( x x 0 ).4. 求导数的四则运算法规:(u v)'u ' v 'y f 1 (x)f 2 (x) ... f n (x)y 'f 1 ' (x) f 2' (x)... f n ' (x)( uv) 'vu ' v 'u( cv) 'c 'v cv ' cv ' ( c 为常数)'vu 'v ' uu0 )vv2( v注:① u, v 必定是可导函数 .②若两个函数可导, 则它们和、 差、积、商必可导; 若两个函数均不可以导, 则它们的和、 差、积、商不用然不可以导 .比方:设 f ( x)2sin x 2 , g (x) cos x 2,则 f (x), g( x) 在 x0 处均不可以导,但它们和x xf ( x)g( x) sin x cos x 在 x 0 处均可导 .5. 复合函数的求导法规:f x ' ( (x))f ' (u)'( x) 或 y ' xy ' u u ' x复合函数的求导法规可实行到多此中间变量的状况 .6. 函数单调性:⑴函数单调性的判断方法: 设函数 y f (x) 在某个区间内可导, 若是 f ' ( x) > 0,则 y f (x) 为增函数;若是f ' (x) <0,则 y f (x) 为减函数 .⑵常数的判断方法;若是函数 y f (x) 在区间 I 内恒有 f ' ( x) =0,则 yf ( x) 为常数 .注:① f (x)0 是 f ( x )递加的充分条件,但不是必要条件,如y2x 3 在 ( , ) 上其实不是都有 f (x) 0 ,有一个点例外即 x=0 时 f ( x ) = 0,同样 f (x)0 是 f ( x )递减的充分非必要条件 .②一般地, 若是 f (x )在某区间内有限个点处为零,在其余各点均为正(或负),那么 f ( x )在该区间上仍旧是单调增加(或单调减少)的.7. 极值的鉴识方法:(极值是在x0周边所有的点,都有f (x)<f ( x0),则f (x0)是函数f ( x)的极大值,极小值同理)当函数 f (x) 在点x0处连续时,①若是在x 0周边的左侧 f ' ( x) >0,右侧f②若是在x 0周边的左侧 f ' ( x) <0,右侧f ''(x) <0,那么 f ( x0 ) 是极大值;(x) >0,那么 f ( x0 ) 是极小值 .也就是说 x 0是极值点的充分条件是x0点两侧导数异号,而不是 f '①( x) =0 .其余,函数不可导的点也可能是函数的极值点②. 自然,极值是一个局部看法,极值点的大小关系是不确定的,即有可能极大值比极小值小(函数在某一点周边的点不同样样).注①:若点 x 0是可导函数 f (x) 的极值点,则f'(x) =0. 但反过来不用然成立. 对于可导函数,其一点 x0是极值点的必要条件是若函数在该点可导,则导数值为零.比方:函数 y f (x)x 3,x 0使 f ' ( x) =0,但x 0不是极值点.②比方:函数 y f (x)| x | ,在点 x 0 处不可以导,但点 x 0 是函数的极小值点 .8.极值与最值的差异:极值是在局部对函数值进行比较,最值是在整体区间上对函数值进行比较 .注:函数的极值点必定有意义 .9.几种常有的函数导数:I. C '0 ( C 为常数)(sin x) 'cos x(arcsin x) '1x 21(x n )'nx n 1(n R )(cos x) 'sin x(arccos x) '1x21 II. (ln x) '1(log a x)'1log a e(arctan x) '11 x x x2( e x) ' e x(a x ) ' a x ln a(arc cot x) '11x 2 III.求导的常有方法:①常用结论:(ln | x |)'1.②形如 y(x a)(x a)...(x a) 或 y( x a1 )( x a2 )...(x a n )两x12n( x b1 )( x b2 )...( x b n )边同取自然对数,可转变求代数和形式.③无理函数或形如 y x x这类函数,如y x x取自然对数此后可变形为ln y xln x ,对两边求导可得 y 'ln x x 1y 'y ln x y y 'x x ln x x x.y x导数中的切线问题例题 1:已知切点,求曲线的切线方程32曲线 y x3x 1在点 (1, 1) 处的切线方程为()例题 2:已知斜率,求曲线的切线方程与直线 2 x y 4 0 的平行的抛物线y x2的切线方程是()注意:此题所给的曲线是抛物线,故也可利用法加以解决,即设切线方程为y 2 x b ,代入 y x2,得 x2 2 x b 0 ,又因为0 ,得 b 1 ,应选D.例题 3:已知过曲线上一点,求切线方程过曲线上一点的切线,该点未必是切点,故应先设切点,再求切点,即用待定切点法.求过曲线 y x3 2 x 上的点 (1, 1) 的切线方程.例题 4:已知过曲线外一点,求切线方程1 相切的直线方程.求过点 (2,0) 且与曲线 yx练习题:已知函数y x33x ,过点 A(0,16) 作曲线 y f (x) 的切线,求此切线方程.看看几个高考题1.( 2009全国卷Ⅱ)曲线yx在点1,1 处的切线方程为2x12.( 2010江西卷)设函数 f ( x)g( x)x2,曲线 y g(x) 在点 (1,g (1)) 处的切线方程为y 2x1,则曲线 y f ( x) 在点 (1, f (1))处切线的斜率为3.( 2009宁夏海南卷)曲线 y xe x2x 1 在点(0,1)处的切线方程为。
(完整版)导数知识点总结及应用

《导数及其应用》知识点总结一、导数的概念和几何意义1. 函数的平均变化率:函数()f x 在区间12[,]x x 上的平均变化率为:2121()()f x f x x x --。
2. 导数的定义:设函数()y f x =在区间(,)a b 上有定义,0(,)x a b ∈,若x ∆无限趋近于0时,比值00()()f x x f x y x x+∆-∆=∆∆无限趋近于一个常数A ,则称函数()f x 在0x x =处可导,并称该常数A 为函数()f x 在0x x =处的导数,记作0()f x '。
函数()f x 在0x x =处的导数的实质是在该点的瞬时变化率。
3. 求函数导数的基本步骤:(1)求函数的增量00()()y f x x f x ∆=+∆-;(2)求平均变化率:00()()f x x f x x +∆-∆;(3)取极限,当x ∆无限趋近与0时,00()()f x x f x x+∆-∆无限趋近与一个常数A ,则0()f x A '=.4. 导数的几何意义:函数()f x 在0x x =处的导数就是曲线()y f x =在点00(,())x f x 处的切线的斜率。
由此,可以利用导数求曲线的切线方程,具体求法分两步:(1)求出()y f x =在x 0处的导数,即为曲线()y f x =在点00(,())x f x 处的切线的斜率; (2)在已知切点坐标和切线斜率的条件下,求得切线方程为000()()y y f x x x '-=-。
当点00(,)P x y 不在()y f x =上时,求经过点P 的()y f x =的切线方程,可设切点坐标,由切点坐标得到切线方程,再将P 点的坐标代入确定切点。
特别地,如果曲线()y f x =在点00(,())x f x 处的切线平行与y 轴,这时导数不存在,根据切线定义,可得切线方程为0x x =。
5. 导数的物理意义:质点做直线运动的位移S 是时间t 的函数()S t ,则()V S t '=表示瞬时速度,()a v t '=表示瞬时加速度。
高中数学导数知识点归纳总结及例题

高中数学导数知识点归纳总结及例题导数考试知识要点1. 导数(导函数的简称)的定义:设x0是函数y f(x)定义域的一点,如果自变量x在x0处有增量x,则函数值y也引起相应的增量y f(x0x)f(x0);比值yf(x0x)f(x0)称为函数y f(x)在点x0到x0x之间的平均变化率;如果极限x xf(x0x)f(x0)y存在,则称函数y f(x)在点x0处可导,并把这个极限叫做lim x0x x0xlim记作f’(x0)或y’|x x0,即f’(x0)=limy f(x)在x0处的导数,f(x0x)f(x0)y. lim x0x x0x注:①x是增量,我们也称为“改变量”,因为x可正,可负,但不为零.②以知函数y f(x)定义域为A,y f’(x)的定义域为B,则A与B关系为A B.2. 函数y f(x)在点x0处连续与点x0处可导的关系:⑴函数y f(x)在点x0处连续是y f(x)在点x0处可导的必要不充分条件.可以证明,如果y f(x)在点x0处可导,那么y f(x)点x0处连续.事实上,令x x0x,则x x0相当于x0.1于是limf(x)limf(x0x)lim[f(x x0)f(x0)f(x0)] x x0x0x0 lim[x0f(x0x)f(x0)f(x0x)f(x0)x f(x0)]lim lim limf( x0)f’(x0)0f(x0)f(x0).x0x0x0x xy|x|,当x>0时,x x⑵如果y f(x)点x0处连续,那么y f(x)在点x0处可导,是不成立的. 例:f(x)|x|在点x00处连续,但在点x00处不可导,因为y y y不存在. 1;当x<0时,1,故lim x0x x x注:①可导的奇函数函数其导函数为偶函数.②可导的偶函数函数其导函数为奇函数.3. 导数的几何意义:函数y f(x)在点x0处的导数的几何意义就是曲线y f(x)在点(x0,f(x))处的切线的斜率,也就是说,曲线y f(x)在点P(x0,f(x))处的切线的斜率是f’(x0),切线方程为y y0f’(x)(x x0).4. 求导数的四则运算法则:(u v)’u’v’y f1(x)f2(x)...fn(x)y’f1’(x)f2’(x)...fn’(x) (uv)’vu’v’u(cv)’c’v cv’cv’(c为常数)vu’v’u u(v0) 2v v’注:①u,v必须是可导函数.②若两个函数可导,则它们和、差、积、商必可导;若两个函数均不可导,则它们的和、差、积、商不一定不可导. 例如:设f(x)2sinx22,g(x)cosx,则f(x),g(x)在x0处均不可导,但它们和xx f(x)g(x)sinx cosx在x0处均可导.5. 复合函数的求导法则:fx’((x))f’(u)’(x)或y’x y’u u’x复合函数的求导法则可推广到多个中间变量的情形.6. 函数单调性:⑴函数单调性的判定方法:设函数y f(x)在某个区间内可导,如果f’(x)>0,则y f(x)为增函数;如果f’(x)<0,则y f(x)为减函数.⑵常数的判定方法;如果函数y f(x)在区间I内恒有f’(x)=0,则y f(x)为常数.注:①f(x)0是f(x)递增的充分条件,但不是必要条件,如y2x3在(,)上并不是都有f(x)0,有一个点例外即x=0时f(x)= 0,同样f(x)0是f(x)递减的充分非必2要条件.②一般地,如果f(x)在某区间(sinx)cosx (arcsinx)’1 x2(xn)’nxn1(n R)(cosx)’sinx (arccosx)’ 1x2 1’11’(arctanx)II. (lnx)(logax)logae xxx21’(ex)’ex (ax)’axlna (arccotx)’III. 求导的常见方法:①常用结论:(ln|x|)’1x2 1 (x a1)(x a2)...(x an)1.②形如y(x a1)(x a2)...(x an)或y两(x b1)(x b2)...(x bn)x边同取自然对数,可转化求代数和形式.③无理函数或形如y xx这类函数,如y xx取自然对数之后可变形为lny xlnx,对两边y’1lnx x y’ylnx y y’xxlnx xx. 求导可得yx 3导数中的切线问题例题1:已知切点,求曲线的切线方程曲线y x33x21在点(1,1)处的切线方程为()例题2:已知斜率,求曲线的切线方程与直线2x y40的平行的抛物线y x2的切线方程是()注意:此题所给的曲线是抛物线,故也可利用法加以解决,即设切线方程为y2x b,代入y x2,得x22x b0,又因为0,得b1,故选D.例题3:已知过曲线上一点,求切线方程过曲线上一点的切线,该点未必是切点,故应先设切点,再求切点,即用待定切点法.求过曲线y x32x上的点(1,1)的切线方程.例题4:已知过曲线外一点,求切线方程1求过点(2,0)且与曲线y相切的直线方程.x4练习题:已知函数y x33x,过点A(016) ,作曲线y f(x)的切线,求此切线方程.看看几个高考题1.(2009全国卷Ⅱ)曲线y x在点1,1处的切线方程为2x 122.(2010江西卷)设函数f(x)g(x)x,曲线y g(x)在点(1,g(1))处的切线方程为y2x1,则曲线y f(x)在点(1,f(1))处切线的斜率为3.(2009宁夏海南卷)曲线y xe2x1在点(0,1)处的切线方程为。
导数知识点总结及例题

导数知识点总结及例题一、导数的定义1.1 函数的变化率在生活中,我们经常会遇到函数随着自变量的变化而发生变化的情况,比如一辆汽车的速度随着时间的变化而变化、货物的销售量随着价格的变化而变化等。
这种情况下,我们就需要考虑函数在某一点处的变化率,也就是导数。
对于函数y=f(x),在点x处的变化率可以用函数的增量Δy和自变量的增量Δx的比值来表示:f'(x) = lim(Δx→0) (Δy/Δx)其中f'(x)表示函数f(x)在点x处的导数。
利用导数的定义,我们可以计算得到函数在某一点处的变化率。
1.2 导数的几何意义导数还有一个重要的几何意义,它表示了函数曲线在某一点处的切线的斜率。
例如,对于函数y=x^2,在点(1,1)处的导数就代表了曲线在这一点处的切线斜率。
这也意味着,导数可以帮助我们理解函数曲线在不同点处的形状和走向。
1.3 导数存在的条件对于一个函数f(x),它在某一点处的导数存在的条件是:在这一点处函数曲线的切线存在且唯一。
也就是说,如果函数在某一点处导数存在,那么这个点就是函数的可导点。
二、导数的性质2.1 导数与函数的关系导数是函数的一个重要属性,它可以帮助我们理解函数的性质。
例如,导数可以表示函数在某一点处的斜率,可以告诉我们函数曲线的凹凸性,还可以帮助我们找到函数的极值点等。
2.2 导数与导函数当一个函数在某一点处的导数存在时,我们可以使用导数的定义来求出函数在该点处的导数。
我们把这个过程称为求导,求出的导数称为导函数。
导函数的值就是原函数在对应点处的导数值。
2.3 导数的性质导数具有一些重要的性质,比如导数存在的条件、可导函数的和、差、积、商的导数求法则等。
这些性质是我们求解导数的问题时的重要依据,也是我们理解函数性质的基础。
三、求导法则3.1 基本求导法则基本求导法则是求解导数问题的基础,它包括常数函数、幂函数、指数函数、对数函数、三角函数、反三角函数等函数的导数求法。
高中数学典型例题解析导数及其应用

高中数学典型例题分析第十章 导数及其应用§10.1导数及其运算一、知识导学1.瞬时变化率:设函数)(x f y =在0x 附近有定义,当自变量在0x x =附近改变量为x ∆时,函数值相应地改变)()(0x f x x f y -∆+=∆,如果当x ∆趋近于0时,平均变化率xx f x x f x y ∆-∆+=∆∆)()(00趋近于一个常数c (也就是说平均变化率与某个常数c 的差的绝对值越来越小,可以小于任意小的正数),那么常数c 称为函数)(x f 在点0x 的瞬时变化率。
2.导数:当x ∆趋近于零时,xx f x x f ∆-∆+)()(00趋近于常数c 。
可用符号“→”记作:当0→∆x 时,x x f x x f ∆-∆+)()(00c →或记作c xx f x x f x =∆-∆+→∆)()(lim 000,符号“→”读作“趋近于”。
函数在0x 的瞬时变化率,通常称作)(x f 在0x x =处的导数,并记作)(0x f '。
3.导函数:如果)(x f 在开区间),(b a 内每一点x 都是可导的,则称)(x f 在区间),(b a 可导。
这样,对开区间),(b a 内每个值x ,都对应一个确定的导数)(x f '。
于是,在区间),(b a 内,)(x f '构成一个新的函数,我们把这个函数称为函数)(x f y =的导函数。
记为)(x f '或y '(或x y ')。
4.导数的四则运算法则:1)函数和(或差)的求导法则:设)(x f ,)(x g 是可导的,则)()())()((x g x f x g x f '±'='±即,两个函数的和(或差)的导数,等于这两个函数的导数的和(或差)。
2)函数积的求导法则:设)(x f ,)(x g 是可导的,则)()()()(])()([x g x f x g x f x g x f '+'='即,两个函数的积的导数,等于第一个函数的导数乘上第二个函数,加上第一个函数乘第二个函数的导数。
导数知识点总结经典例题及解析近年高考题带答案
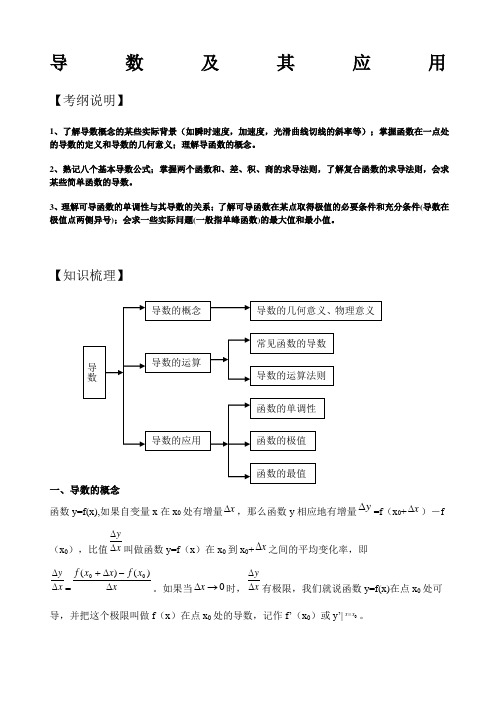
导数及其应用【考纲说明】1、了解导数概念的某些实际背景(如瞬时速度,加速度,光滑曲线切线的斜率等);掌握函数在一点处的导数的定义和导数的几何意义;理解导函数的概念。
2、熟记八个基本导数公式;掌握两个函数和、差、积、商的求导法则,了解复合函数的求导法则,会求某些简单函数的导数。
3、理解可导函数的单调性与其导数的关系;了解可导函数在某点取得极值的必要条件和充分条件(导数在极值点两侧异号);会求一些实际问题(一般指单峰函数)的最大值和最小值。
【知识梳理】函数y=f(x),如果自变量x 在x 0处有增量x ∆,那么函数y 相应地有增量y ∆=f (x 0+x ∆)-f(x 0),比值x y∆∆叫做函数y=f (x )在x 0到x 0+x ∆之间的平均变化率,即x y ∆∆=x x f x x f ∆-∆+)()(00。
如果当0→∆x 时,x y ∆∆有极限,我们就说函数y=f(x)在点x 0处可导,并把这个极限叫做f (x )在点x 0处的导数,记作f’(x 0)或y’|0x x =。
即f (x 0)=0lim →∆x x y∆∆=0lim →∆x x x f x x f ∆-∆+)()(00。
说明:(1)函数f (x )在点x 0处可导,是指0→∆x 时,x y ∆∆有极限。
如果x y∆∆不存在极限,就说函数在点x 0处不可导,或说无导数。
(2)x ∆是自变量x 在x 0处的改变量,0≠∆x 时,而y ∆是函数值的改变量,可以是零。
由导数的定义可知,求函数y=f (x )在点x 0处的导数的步骤: (1)求函数的增量y ∆=f (x 0+x ∆)-f (x 0);(2)求平均变化率x y ∆∆=x x f x x f ∆-∆+)()(00;(3)取极限,得导数f’(x 0)=x yx ∆∆→∆0lim。
二、导数的几何意义函数y=f (x )在点x 0处的导数的几何意义是曲线y=f (x )在点p (x 0,f (x 0))处的切线的斜率。
导数基础知识点汇总及经典习题解答

导数导数基础:1. 导数(导函数的简称)的定义:设是函数定义域的一点,如果自变量在处有增量,则函数值也引起相应的增量;比值称为函数在点到之间的平均变化率;如果极限存在,则称函数在点处可导,并把这个极限叫做在处的导数,记作或,即=. ②以知函数定义域为,的定义域为,则与关系为.2. 函数在点处连续与点处可导的关系:函数在点处连续是在点处可导的必要不充分条件.常用性质:①可导的奇函数函数其导函数为偶函数. ②可导的偶函数函数其导函数为奇函数.3. 导数的几何意义:函数在点处的导数的几何意义就是曲线在点处的切线的斜率,也就是说,曲线在点P 处的切线的斜率是,切线方程为0x )(x f y =x 0x x ∆y )()(00x f x x f y -∆+=∆x x f x x f x y ∆-∆+=∆∆)()(00)(x f y =0x x x ∆+0x x f x x f x yx x ∆-∆+=∆∆→∆→∆)()(limlim0000)(x f y =0x )(x f y =0x )(0'x f 0|'x x y =)(0'x f x x f x x f x yx x ∆-∆+=∆∆→∆→∆)()(limlim0000)(x f y =A )('x f y =BA BB A ⊇)(x f y =0x 0x )(x f y =0x )(x f y =0x )(x f y =0x )(x f y =))(,(0x f x )(x f y =))(,(0x f x )(0'x f ).)((0'0x x x fy y -=-4. 求导数的四则运算法则:(为常数)②若两个函数可导,则它们和、差、积、商必可导;若两个函数均不可导,则它们的和、差、积、商不一定不可导.I.(为常数)().5. 复合函数的求导法则:或6. 函数单调性:⑴函数单调性的判定方法:设函数在某个区间内可导,如果>0,则为增函数;如果<0,则为减函数''')(v u v u ±=±)(...)()()(...)()(''2'1'21x f x f x f y x f x f x f y n n +++=⇒+++=⇒''''''')()(cv cv v c cv u v vu uv =+=⇒+=c )0(2'''≠-=⎪⎭⎫⎝⎛v v u v vu v u 0'=C Cxx cos )(sin '=2'11)(arcsin x x -=1')(-=n n nx x Rn ∈xx sin )(cos '-=2'11)(arccos x x --=xx 1)(ln '=e x x a a log 1)(log '=11)(arctan 2'+=x x xx e e =')(aa a x x ln )('=11)cot (2'+-=x x arc )()())(('''x u f x f x ϕϕ=xu x u y y '''⋅=)(x f y =)('x f )(x f y =)('x f )(x f y =注:①是f (x )递增的充分条件,但不是必要条件,如在上并不是都有,有一个点例外即0时f (x ) = 0,同样是f (x )7. 极值的判别方法:(极值是在附近所有的点,都有<,则是函数的极大值,极小值同理)当函数在点处连续时,②如果在附近的左侧<0,右侧>0,那么是极小值.①如果在附近的左侧>0,右侧<0,那么是极大值;例1. 8.函数313y x x =+- 有 ( )A.极小值-1,极大值1B. 极小值-2,极大值3C.极小值-1,极大值3D. 极小值-2,极大值26.函数344+-=x x y 在区间[]2,3-上的最小值为( ) A .72 B .36 C .12 D .00)( x f 32x y =),(+∞-∞0)( x f 0)( x f 0x )(x f )(0x f )(0x f )(x f )(x f 0x 0x )('x f )('x f )(0x f 0x )('x f )('x f )(0x f6.函数x xy ln =的最大值为( )A .1-eB .eC .2e D .3102.函数x e x x f -⋅=)(的一个单调递增区间是( )(A)[]0,1- (B) []8,2 (C) []2,1 (D) []2,03.已知对任意实数x ,有()()()()f x f xg x g x -=--=,,且0x >时,()0()0f x g x ''>>,,则0x <时( )A .()0()0f x g x ''>>,B .()0()0f x g x ''><,C .()0()0f x g x ''<>,D .()0()0f x g x ''<<,4.若函数b bx x x f 33)(3+-=在()1,0内有极小值,则( )(A ) 10<<b (B ) 1<b (C ) 0>b (D )21<b5.若曲线4y x =的一条切线l 与直线480x y +-=垂直,则l 的方程为( )A .430x y --= B .450x y +-= C .430x y -+=D .430x y ++=6.曲线x y e =在点2(2)e ,处的切线与坐标轴所围三角形的面积为( )A.294eB.22e C.2e D.22e2.若'0()3fx =-,则000()(3)limh f x h f x h h →+--=( )A .3-B .6-C .9-D .12- 1.(2005全国卷Ⅰ文)函数93)(23-++=x ax x x f ,已知)(x f 在3-=x 时取得极值,则a =( )(A )2 (B )3 (C )4 (D )52.(2008海南、宁夏文)设()ln f x x x =,若0'()2f x =,则0x =( )A. 2e B. e C. ln 22D. ln 23.(2005广东)函数13)(23+-=x x x f 是减函数的区间为( )A .),2(+∞B .)2,(-∞C .)0,(-∞D .(0,2)4.(2008安徽文)设函数1()21(0),f x x x x =+-< 则()f x ( )A .有最大值B .有最小值C .是增函数D .是减函数5.(2007福建文、理)已知对任意实数x 有f(-x)=-f(x),g()(x),且x>0时,f’(x)>0,g’(x)>0,则x<0时( )A f’(x)>0,g’(x)>0B f’(x)>0,g’(x)<0C f’(x)<0,g’(x)>0D f’(x)<0,g’(x)<0 6.(2008全国Ⅱ卷文)设曲线2ax y =在点(1,a )处的切线与直线062=--y x 平行,则=a ( )A .1B .12C .12-D .1-导数答案。
第01讲 导数的概念及运算 (精讲+精练)(学生版)

第01讲导数的概念及运算 (精讲+精练)目录第一部分:知识点精准记忆第二部分:课前自我评估测试第三部分:典型例题剖析高频考点一:导数的概念高频考点二:导数的运算高频考点三:导数的几何意义①求切线方程(在型)②求切线方程(过型)③已知切线方程(或斜率)求参数④导数与函数图象⑤共切点的公切线问题⑥不同切点的公切线问题⑦与切线有关的转化问题第四部分:高考真题感悟第五部分:第01讲导数的概念及运算(精练)1、平均变化率(1)变化率事物的变化率是相关的两个量的“增量的比值”。
如气球的平均膨胀率是半径的增量与体积增量的比值. (2)平均变化率一般地,函数()f x 在区间[]21,x x 上的平均变化率为:2121()()f x f x x x --.(3)如何求函数的平均变化率求函数的平均变化率通常用“两步”法:①作差:求出21()()y f x f x ∆=-和21x x x ∆=-②作商:对所求得的差作商,即2121()()f x f x y x x x -∆=∆-. 2、导数的概念(1)定义:函数()f x 在0x x =处瞬时变化率是()()xx f x x f x yx x ∆-∆+=∆∆→∆→∆0000limlim,我们称它为函数()x f y =在0x x =处的导数,记作() 或0x f '即 0x x y ='()()()xx f x x f x yx f x x ∆-∆+=∆∆'→∆→∆00000limlim =. (2)定义法求导数步骤:① 求函数的增量:00()()y f x x f x ∆=+∆-; ② 求平均变化率:00()()f x x f x y x x+∆-∆=∆∆; ③ 求极限,得导数:00000()()'()limlim x x f x x f x yf x x x∆→∆→+∆-∆==∆∆.3、导数的几何意义函数()y f x =在点0x x =处的导数的几何意义,就是曲线()y f x =在点00(,)P x y 处的切线的斜率k ,即0()k f x '=.4、基本初等函数的导数公式5若()f x ',()g x '存在,则有 (1)[()()]()()f x g x f x g x '''±=±(2)[()()]()()()()f x g x f x g x f x g x '''⋅=⋅+⋅ (3)2()()()()()[]()()f x f xg x f x g x g x g x ''⋅-⋅'= 6、复合函数求导复合函数(())y f g x =的导数和函数()y f u =,()u g x =的导数间的关系为x u x y y u '''=,即y 对x 的导数等于y 对u 的导数与u 对x 的导数的乘积.7、曲线的切线问题(1)在型求切线方程已知:函数)(x f 的解析式.计算:函数)(x f 在0x x =或者))(,(00x f x 处的切线方程.步骤:第一步:计算切点的纵坐标)(0x f (方法:把0x x =代入原函数)(x f 中),切点))(,(00x f x . 第二步:计算切线斜率'()k f x =.第三步:计算切线方程.切线过切点))(,(00x f x ,切线斜率)('0x f k =。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§ 1.1 变化率与导数 1.1.1 变化率问题自学引导1.通过实例分析,了解平均变化率的实际意义.2.会求给定函数在某个区间上的平均变化率. 课前热身1.函数f (x )在区间[x 1,x 2]上的平均变化率为ΔyΔx=________. 2.平均变化率另一种表示形式:设Δx =x -x 0,则ΔyΔx=________,表示函数y =f (x )从x 0到x 的平均变化率.1.f (x 2)-f (x 1)x 2-x 1答 案2.f (x 0+Δx )-f (x 0)Δx名师讲解1.如何理解Δx ,Δy 的含义Δx 表示自变量x 的改变量,即Δx =x 2-x 1;Δy 表示函数值的改变量,即Δy =f (x 2)-f (x 1).2.求平均变化率的步骤求函数y =f (x )在[x 1,x 2]内的平均变化率. (1)先计算函数的增量Δy =f (x 2)-f (x 1). (2)计算自变量的增量Δx =x 2-x 1.(3)得平均变化率Δy Δx =f x 2-f x 1x 2-x 1.对平均变化率的认识函数的平均变化率可以表现出函数在某段区间上的变化趋势,且区间长度越小,表现得越精确.如函数y =sin x 在区间[0,π]上的平均变化率为0,而在[0,π2]上的平均变化率为sin π2-sin0π2-0=2π.在平均变化率的意义中,f (x 2)-f (x 1)的值可正、可负,也可以为零.但Δx =x 2-x 1≠0.典例剖析题型一求函数的平均变化率例1 一物体做直线运动,其路程与时间t的关系是S=3t-t2.(1)求此物体的初速度;(2)求t=0到t=1的平均速度.分析t=0时的速度即为初速度,求平均速度先求路程的改变量ΔS=S(1)-S(0),再求时间改变量Δt=1-0=1.求商ΔSΔt就可以得到平均速度.解(1)由于v=St=3t-t2t=3-t.∴当t=0时,v0=3,即为初速度.(2)ΔS=S(1)-S(0)=3×1-12-0=2 Δt=1-0=1∴v=ΔSΔt=21=2.∴从t=0到t=1的平均速度为2.误区警示本题1不要认为t=0时,S=0.所以初速度是零.变式训练1 已知函数f(x)=-x2+x的图像上一点(-1,-2)及邻近一点(-1+Δx,-2+Δy),则ΔyΔx=( )A.3 B.3Δx-(Δx)2 C.3-(Δx)2D.3-Δx 解析Δy=f(-1+Δx)-f(-1)=-(-1+Δx)2+(-1+Δx)-(-2)=-(Δx)2+3Δx.∴ΔyΔx=-Δx2+3ΔxΔx=-Δx+3答案D题型二平均变化率的快慢比较例2 求正弦函数y=sin x在0到π6之间及π3到π2之间的平均变化率.并比较大小.分析用平均变化率的定义求出两个区间上的平均变化率,再比较大小.解设y=sin x在0到π6之间的变化率为k1,则k 1=sinπ6-sin0π6-0=3π.y =sin x 在π3到π2之间的平均变化率为k 2,则k 2=sin π2-sin π3π2-π3=1-32π6=32-3π.∵k 1-k 2=3π-32-3π=33-1π>0,∴k 1>k 2.答:函数y =sin x 在0到π6之间的平均变化率为3π,在π3到π2之间的平均变化率为32-3π,且3π>32-3π.变式训练2 试比较余弦函数y =cos x 在0到π3之间和π3到π2之间的平均变化率的大小.解 设函数y =cos x 在0到π3之间的平均变化率是k 1,则k 1=cos π3-cos0π3-0=-32π.函数y =cos x 在π3到π2之间的平均变化率是k 2,则k 2=cosπ2-cos π3π2-π3=-3π.∵k 1-k 2=-32π-(-3π)=32π>0,∴k 1>k 2.∴函数y =cos x 在0到π3之间的平均变化率大于在π3到π2之间的平均变化率.题型三 平均变化率的应用例3 已知一物体的运动方程为s (t )=t 2+2t +3,求物体在t =1到t =1+Δt 这段时间内的平均速度.分析 由物体运动方程―→写出位移变化量Δs ―→ΔsΔt解 物体在t =1到t =1+Δt 这段时间内的位移增量 Δs =s (1+Δt )-s (1)=[(1+Δt )2+2(1+Δt )+3]-(12+2×1+3) =(Δt )2+4Δt .物体在t =1到t =1+Δt 这段时间内的平均速度为Δs Δt =(Δt )2+4ΔtΔt=4+Δt .变式训练3 一质点作匀速直线运动,其位移s 与时间t 的关系为s (t )=t 2+1,该质点在[2,2+Δt ](Δt >0)上的平均速度不大于5,求Δt 的取值范围.解 质点在[2,2+Δt ]上的平均速度为v -=s 2+Δt -s 2Δt=[2+Δt 2+1]-22+1Δt=4Δt +Δt2Δt=4+Δt .又v -≤5,∴4+Δt ≤5. ∴Δt ≤1,又Δt >0,∴Δt 的取值范围为(0,1]. § 1.1 函数的单调性与极值 1.1.2 导数的概念自学引导1.经历由平均变化率过渡到瞬时变化率的过程,了解导数概念建立的一些实际背景.2.了解瞬时变化率的含义,知道瞬时变化率就是导数.3.掌握函数f (x )在某一点x 0处的导数定义,并且会用导数的定义求一些简单函数在某一点x 0处的导数.课前热身1.瞬时速度.设物体的运动方程为S =S (t ),如果一个物体在时刻t 0时位于S (t 0),在时刻t 0+Δt 这段时间内,物体的位置增量是ΔS =S (t 0+Δt )-S (t 0).那么位置增量ΔS 与时间增量Δt 的比,就是这段时间内物体的________,即v =S t 0+Δt -S t 0Δt.当这段时间很短,即Δt 很小时,这个平均速度就接近时刻t 0的速度.Δt 越小,v 就越接近于时刻t 0的速度,当Δt →0时,这个平均速度的极限v =lim Δt →0ΔS Δt =lim Δt →0S t 0+Δt -S t 0Δt就是物体在时刻t 0的速度即为________. 2.导数的概念.设函数y =f (x )在区间(a ,b )上有定义,x 0∈(a ,b ),当Δx 无限趋近0时,比值Δy Δx =f x 0+Δx -f x 0Δx无限趋近于一个常数A ,这个常数A 就是函数f (x )在点x =x 0处的导数,记作f ′(x 0)或y ′|x =x 0.用符号语言表达为f ′(x 0)=lim Δx →0Δy Δx=________1.平均速度 瞬时速度 答 案2.lim Δx →0f (x 0+Δx )-f (x 0)Δx名师讲解1.求瞬时速度的步骤(1)求位移增量ΔS =S (t +Δt )-S (t );(2)求平均速度v =ΔS Δt;(3)求极限limΔt→0ΔSΔt=limΔt→0S t +Δt-S tΔt;(4)若极限存在,则瞬时速度v=limΔt→0ΔS Δt.2.导数还可以如下定义一般地,函数y=f(x)在x=x0处的瞬时变化率是limΔx→0f x+Δx-f x0Δx=limΔx→0ΔyΔx.我们称它为函数y=f(x)在x=x0处的导数.记作f′(x0)或y′|x=x,即f′(x0)=limΔx→0ΔyΔx=limΔx→0f x+Δx-f x0Δx.3.对导数概念的理解(1)“导数”是从现实生活中大量类似问题里,撇开一些量的具体意义,单纯地抓住它们数量上的共性而提取出来的一个概念,所以我们应很自然的理解这个概念的提出与其实际意义.(2)某点导数即为函数在这点的变化率.某点导数概念包含着两层含义:①limΔx→0ΔyΔx存在,则称f(x)在x=x0处可导并且导数即为极限值;②limΔx→0ΔyΔx不存在,则称f(x)在x=x0处不可导.(3)Δx称为自变量x的增量,Δx可取正值也可取负值,但不可以为0.(4)令x=x0+Δx,得Δx=x-x0,于是f′(x)=limx→x0f x-f xx-x与定义中的f′(x0)=limΔx→0f x+Δx-f x0Δx意义相同.4.求函数y=f(x)在点x0处的导数的步骤(1)求函数的增量:Δy=f(x0+Δx)-f(x0);(2)求平均变化率:ΔyΔx=f x+Δx-f x0Δx;(3)取极限,得导数:f′(x0)=limΔx→0Δy Δx.典例剖析题型一物体运动的瞬时速度例1 以初速度v0(v0>0)竖直上抛的物体,t秒时高度为s(t)=v0t-12gt2,求物体在时刻t0处的瞬时速度.分析先求出Δs,再用定义求ΔsΔt,当Δt→0时的极限值.解∵Δs=v0(t0+Δt)-12g(t+Δt)2-(v0t0-12gt2)=(v0-gt0)Δt-12g(Δt)2,∴ΔsΔt=v0-gt0-12g·Δt.∴当Δt→0时,ΔsΔt→v0-gt0.故物体在时刻t0处的瞬时速度为v0-gt0.规律技巧瞬时速度v是平均速度v在Δt→0时的极限.因此,v=limΔt→0v=limΔt→0ΔsΔt.变式训练1 一作直线运动的物体,其位移s与时间t的关系是s=5t-t2,求此物体在t=2时的瞬时速度。
解∵Δs=5(2+Δt)-(2+Δt)2-(5×2-22)=Δt-(Δt)2,∴ΔsΔt=1-Δt.∴v=limΔt→0ΔsΔt=limΔt→0(1-Δt)=1.∴物体在t=2时的瞬时速度为1.题型二求函数在某点处的导数例2 求函数y=x在x=1处的导数.分析根据导数的定义求导数是求函数的导数的基本方法.解法1∵Δy=1+Δx-1,∴ΔyΔx=1+Δx-1Δx=ΔxΔx1+Δx+1=11+Δx+1.∴limΔx→0ΔyΔx=limΔx→011+Δx+1=12.∴y′|x=1=1 2 .解法2(先求导数,再求导数值) ∵Δy=x+Δx-x,∴Δy Δx =x +Δx -xΔx=1x +Δx +x.∴y ′=lim Δx →01x +Δx +x=12x.∴y ′|x =1=12.规律技巧 求函数y =f x 在x =x 0处的导数有两种方法:一是应用导数定义;二是先求导数再求导数值.变式训练2 利用定义求函数y =x +1x的导数,并据此求函数在x =1处的导数.解∵Δy =(x +Δx )+1x +Δx -(x +1x)Δy Δx =1-1x x +Δx, ∴y ′=lim Δx →0ΔyΔx=lim Δx →0[1-1xx +Δx]=1-1x2.∴y ′|x =1=1-112=0.=Δx -Δxx x +Δx ,题型三 导数的应用例3 某物体按照s (t )=3t 2+2t +4的规律作直线运动,求自运动开始到4s 时,物体运动的平均速度和4s 时的瞬时速度.分析 解答本题,可先求自运动开始到t s 时的平均速度v (t )及函数值的增量Δs ,自变量的增量Δt ,再利用公式求解即可.解 自运动开始到t s 时,物体运动的平均速度v -(t )=s t t =3t +2+4t,故前4秒物体的平均速度为v -(t )=3×4+2+44=15.由于Δs=3(t+Δt)2+2(t+Δt)+4-(3t2+2t+4) =(2+6t)Δt+3(Δt)2,∴ΔsΔt=2+6t+3Δt .∴limΔt→0ΔsΔt=2+6t .∴4s时物体的瞬时速度为2+6×4=26.规律技巧导数的物理意义:1若已知位移s 与时间t的函数关系s=s t,则在t0时刻的瞬时速度v=s′t0;2若已知速度v与时间t的函数关系v=v t,则在t0时刻的瞬时加速度a=v′t0.变式训练3 竖直上抛一小球,其位移与时间的关系为h(t)=100t-12gt2,试求小球何时瞬时速度为0(g≈9.8).解小球的运动方程为h(t)=100t-12gt2,∴Δh=[100(t+Δt)-12g(t+Δt)2]-(100t-12gt2)=∴limΔt→0ΔhΔt=100-gt,令100-gt=0,得t=100g=1009.8≈10.2(s).因此,小球被上抛10.2s时速度变为0.100Δt-gtΔt-12g(Δt)2.例4 已知质点M按规律s=at2+3(单位:cm)做直线运动,且质点M在t =2s时的瞬时速度为8cm/s,求a的值.分析这是一道逆向思维的题目,知导数s′|t=2=8,求系数a,先对s求导,可得含a的方程.解出a即可.解Δs=a(2+Δt)2+3-(a·22+3)=4a·Δt+a(Δt)2∴limΔt→0ΔsΔt=limΔt→0(4a+a·Δt)=4a.依题意有4a=8,∴a=2.变式训练4 已知f(x)=ax+b,且f′(1)=2,求实数a的值.解Δy=f(1+Δx)-f(1) =a(1+Δx)+b-(a+b)=aΔx.∴f′(1)=limΔx→0ΔyΔx=limΔx→0a=a.又f′(1)=2,∴a=2.§ 1.1函数的单调性与极值1.1.3导数的几何意义自学引导1.通过函数的图像直观地理解导数的几何意义.2.会求函数在点(x0,y0)处的切线方程.课前热身1.几何意义:f(x)在x=x0处的导数f′(x0)即为f(x)所表示的曲线在x=x处的切线的斜率,即k=f′(x0)=limΔx→0f x+Δx-f x0Δx.过点(x0,f(x0))的切线方程为________.2.物理意义:如果把函数y=f(x)看作是物体的运动方程(或叫位移公式),那么导数f′(x0)表示运动物体在时刻t0的速度,即在x0的________.即vx0=f′(x0)=limΔx→0Δy Δx.3.如果f(x)在开区间(a,b)内每一点x的导数都存在,那么称f(x)在区间(a,b)内可导.这样对开区间(a,b)内每一个值x,都对应一个确定的导数f′(x),于是在区间(a,b)内f′(x)构成一个新的函数,我们把这个函数称为函数y=f(x)的________,记为________,简称为________.今后,如不特别指明某一点的导数,求导数就是指求导函数.答案1.y-f(x0)=f′(x0)(x-x0)2.瞬时速度3.导函数f′(x)(或y′x 、y′) 导数名师讲解1.“函数f(x)在点x0处的导数”、“导函数”、“导数”三者之间的区别与联系:“函数f(x)在点x0处的导数”是一个数值;“导函数”简称“导数”,是一个函数.所以求函数在某点处的导数时,一般是先求出函数的导函数,再计算这点的导函数值.2.可以利用导数求曲线的切线方程.由于函数y=f(x)在x=x0处的导数,表示曲线在点P(x0,f(x0))处的切线的斜率.因此,曲线y=f(x)在点P(x0,f(x0))处的切线方程可如下求得:(1)求出f′(x0),则f′(x0)就是点P(x0,f(x0))处的切线的斜率.(2)代入直线的点斜式方程可得切线方程为y-f(x)=f′(x0)(x-x0).如果曲线y=f(x)在点P(x0,f(x0))处的切线平行于y轴时(此时导数不存在),切线方程为x=x0.典例剖析题型一求曲线上某点处的切线方程例1 已知曲线C:y=x3.(1)求曲线C上横坐标为1的点处的切线方程;(2)第(1)小题中的切线与曲线C是否还有其他的公共点.分析先求出函数y=x3在x=1处的导数,即切线的斜率,然后写出切线方程,最后列方程看交点个数.解(1)将x=1代入曲线C的方程得y=1,∴切点P(1,1).∵y′=limΔx→0Δy Δx=limΔx→0x+Δx3-x3Δx=limΔx→03x2Δx+3xΔx2+Δx3Δx=limΔx→0[3x2+3xΔx+(Δx)2]=3x2,∴y′|x=1=3.∴过P点的切线方程为y-1=3(x-1),即3x-y-2=0.(2)由⎩⎨⎧y =3x -1+1y =x3可得(x -1)(x 2+x -2)=0,解得x 1=1,x 2=-2,从而求得公共点为P (1,1)或P (-2,-8).说明切线与曲线C 的公共点除了切点外,还有另外的公共点.规律技巧 先求出函数y =f x 在x =x 0处的导数,即曲线在该点处的切线斜率,再由直线方程的点斜式便可求出切线方程.变式训练1 求双曲线y =1x 在点(12,2)处的切线的斜率,并写出切线方程.解 ∵y =1x,∴k =lim Δx →0ΔyΔx=lim Δx →01x +Δx -1xΔx=lim Δx →0-1x 2+x Δx =-1x 2.∴当x =12时,k =-4,∴切线斜率为k =-4.切线方程为y -2=-4(x -12),即4x +y -4=0.题型二 求过某点的切线方程例2 求抛物线y =x 2过点(52,6)的切线方程.分析 点(52,6)不在抛物线上,先设出切点坐标,求出切线的斜率,利用等量关系,求出切点坐标,最后写出切线方程.解 设此切线在抛物线上的切点为(x 0,x 20),则y ′|x =x 0=lim Δx →0 x 0+Δx 2-x 20Δx=lim Δx →0(2x 0+Δx )=2x 0,∴x 20-6x 0-52=2x 0,即x 20-5x 0+6=0,解得x=2,或x0=3.即切线经过抛物线y=x2上的点(2,4),(3,9).故切线方程分别为y-4=4(x-2),y-9=6(x-3),即4x-y-4=0,或6x-y-9=0为所求的切线方程.规律技巧求切线方程时,注意两种说法:一是在某点处的切线方程,此时点在曲线上,且以此点为切点;二是过某点的切线方程,如本例,此时求解时,首先要设出切点坐标,然后求解.变式训练2 求抛物线y=14x2过点(4,74)的切线方程.解设切线在抛物线上的切点为(x0,14x2),∴y′|x=x0=limΔx→014x+Δx2-14x2Δx=limΔx→0 (12x+14Δx)=12x.∴14x2-74x-4=12x.即x20-8x0+7=0,解得x0=7,或x0=1,即切线过抛物线y=14x2上的点(7,494),(1,14),故切线方程分别为y-494=72(x-7),或y-14=12(x-1),化简得14x-4y-49=0,或2x-4y-1=0,此即所求的切线方程.题型三导数几何意义的综合应用例3 求曲线y=x2在点(3,9)处的切线与两坐标轴所围成的三角形的面积.分析由题设知切线与两坐标轴围成的三角形为直角三角形,故需求出切线方程及其在两坐标轴上的截距,代入三角形面积公式计算.解Δy=(3+Δx)2-32=6Δx+(Δx)2,∴f′(3)=limΔx→0ΔyΔx=limΔx→0(6+Δx)=6.∴点(3,9)处的切线方程为y-9=6(x-3),即y=6x-9.切线与两坐标轴的交点分别为(32,0),(0,-9).∴切线与两坐标轴围成的三角形面积为S=12×32×9=274.变式训练3 在曲线y=x2上求一点P,使过点P的切线与直线y=4x-5平行.解设P(x0,x20),则f′(x0)=limΔx→0Δy Δx=limΔx→0x+Δx2-x20Δx=limΔx→0(2x0+Δx)=2x0.由题意可得2x0=4,∴x0=2.故点P的坐标为(2,4).§ 1.2导数的计算1.2.1几种常用函数的导数及导数的运算法则自学引导1.能根据导数的定义,会求函数y=c,y=x,y=x2,y=x3,y=1x,y=x的导数.2.能利用给出的基本初等函数的导数公式及导数的运算法则求简单函数的导数.课前热身原函数导函数(1)f(x)=c f′(x)=________(2)f(x)=x n(n∈Q)f′(x)=________(3)f(x)=sin x f′(x)=________(4)f(x)=cos x f′(x)=________(5)f(x)=a x f′(x)=________原函数导函数(6)f(x)=e x f′(x)=________(7)f(x)=log a x f′(x)=________(8)f(x)=ln x f′(x)=________ 2.(1)[f(x)±g(x)]′=________;(2)[f(x)·g(x)]′=________;(3)[f xg x]′=________.答案1.(1)0(2)nx n-1(3)cos x(4)-sin x(5)a x ln a(a>0)(6)e x(7)1x ln a(a>0,且a≠1)(8)1x答案2.(1)f′(x )±g′(x)(2)f′(x)g(x)+f(x)g′(x)(3)f′(x)g(x)-f(x)g′(x)[g(x)]2(g(x)≠0)名师讲解(3)公式中n∈Q,但对于n∈R公式也成立.(4)特别注意n为负数或分数时,求导不要搞错.如2.两函数和差的求导法则的推广(1)[f(x)±g(x)]′=f′(x)±g′(x)此法则可以推广到有限个可导函数的情形.[f1(x)±f2(x)±…±f n(x)]′=f1′(x)±f2′(x)±…±f n′(x).(2)[af(x)±bg(x)]′=af′(x)±bg′(x)(a,b为常数).3.两函数商的求导法则⎣⎢⎡⎦⎥⎤f xg x′=f′x g x-f x g′xg2x(g(x)≠0),当f(x)=1时,则有⎣⎢⎡⎦⎥⎤1g x′=-g′xg2x(g(x)≠0).这是一个函数倒数的求导法则.4.求导运算的技巧在求导数中,有些函数表示形式很复杂,直接求导比较困难,但经过化简整理,有可能很简单,这时再求导可能很简便,也就是说,先把复杂式子化简后再求导,减少运算量.题型一求导函数例1 求下列函数的导数.(1)y=x12;(2)y=1x3;(3)y=3x2.分析这三个小题都可归为x n类,用公式(x n)′=nx n-1完成.典例剖析解(1)y′=(x12)′=12x12-1=12x11.(2)y′=(1x3)′=(x-3)′=-3x-3-1=-3x-4.变式训练1 求下列函数的导数.(1)f(x)=10x;(2)f(x)=log2x;(3)g(t)=e t.解(1)f′(x)=(10x)′=10x ln10.(2)f′(x)=(log2x)′=1x ln2.(3)g′(t)=(e t)′=e t.题型二求函数在某点处的导数例2 (1)求函数y=a x,在点P(3,f(3))处的导数;(2)求函数y=ln x在点Q(5,ln5)处的导数.分析先按求导公式求出导函数,再求导函数在相应点的函数值.解(1)∵y=a x,∴y′=(a x)′=a x ln a.则y′|x=3=a3ln a.(2)∵y=ln x,∴y′=(ln x)′=1 x .则y′|x=5=15 .规律技巧求函数在某定点点在函数曲线上的导数,一般过程是:①先求导函数;②把定点的横坐标代入导函数求出导数值.变式训练2 求下列函数在某点处的导数.(1)y=log a x,x=2;(2)y=cos x,x=π4;(3)y=2x3+3x,x=1;(4)y=sin x,x=π3.解(1)∵y=log a x,∴y′=1x ln a.则y′|x=2=12ln a.(2)∵y=cos x,∴y′=-sin x.则y′|x=π4=-sinπ4=-22.则y′|x=1=6+13=193.(4)∵y=sin x,∴y′=cos x.则y′|x=π3=cosπ3=12.题型三利用运算法则求导数例3 求下列函数的导数.(1)y=x2·sin x+cos x;(2)y=ln xx+1;(3)f(x)=(x3+1)(2x2+8x-5);(4)f(x)=1+x1-x+1-x1+x.分析对于(1)、(2)可以利用公式直接求导,(3)、(4)先化简再求导.解(1)y′=(x2sin x+cos x)′=(x2sin x)′+(cos x)′=2x sin x+x2cos x-sin x=(2x-1)sin x+x2cos x.(2)y′=(ln xx+1)′=1xx+1-ln xx+12=1-ln x+1xx+12=x-x ln x+1x x+12.(3)∵f(x)=(x3+1)(2x2+8x-5)=2x5+8x4-5x3+2x2+8x-5f′(x)=(2x5+8x4-5x3+2x2+8x-5)′=10x4+32x3-15x2+4x+8.(4)∵f(x)=1+x1-x+1-x1+x=1+x21-x+1-x21-x=21+x1-x=41-x-2,∴f′(x)=(41-x-2)′=4′1-x-41-x′1-x2=41-x2.规律技巧运用求导法则和导数公式求可导函数的导数,一定要先分析函数y =f(x)的结构特征,对于直接求导很繁琐的,一定要先化简,再求导.变式训练3 求下列函数的导数.(1)y=tan x;(2)y=11-x+11+x;(3)y=1+sin x2cosx2;(4)y=xx+1-2x.解(1)y=tan x=sin x cos x,∴y′=(sin xcos x)′=sin x′cos x-sin x cos x′cos2x=cos2x+sin2xcos2x=1cos2x.(2)∵y=11-x+11+x=21-x,∴y′=(21-x)′=-21-x′1-x2=21-x2.(3)∵y=1+sin x2cosx2=1+12sin x,∴y′=(1+12sin x)′=12cos x.(4)y′=(xx+1)′-(2x)′=x+1-xx+12-2x ln2=1x+12-2x ln2.题型四求切线方程例4 求过点(1,-1)的曲线y=x3-2x的切线方程.分析点(1,-1)虽然在曲线上,但它不一定是切点,故应先求切点.解设P(x0,y0)为切点,则切线的斜率为f′(x0)=3x20-2,故切线方程为y-y=(3x20-2)(x-x0),即y-(x30-2x0)=(3x20-2)(x-x0),又知切线过点(1,-1)代入上述方程,得-1-(x30-2x0)=(3x20-2)(1-x0),解得x0=1,或x0=-1 2,∴切点为(1,-1)或(-12,78).故所求的切线方程为y+1=x-1,或y-78=-54(x+12),即x-y-2=0,或5x+4y-1=0.规律技巧1在求曲线的切线方程时,注意两个“说法”:求曲线在点P处的切线方程和求曲线过点P的切线方程.在点P处的切线,一定是以点P为切点,过点P的切线,不论点P在不在曲线上,点P不一定是切点.2求过点P的曲线的切线方程的步骤为:先设出切点坐标为x0,y0,然后写出切线方程y-y0=f′x0x-x0,代入点P的坐标,求出x,y0,再写出切线方程.变式训练4 已知曲线y=x3-3x,过点(0,16)作曲线的切线,求曲线的切线方程.解设切点为(x1,y1),则切线的斜率k=y′ |x=x1=3x21-3,∴切线方程为y=(3x21-3)x+16.又切点在切线上,∴y1=(3x21-3)x1+16.∴x31-3x1=(3x21-3)x1+16,解得x1=-2.∴切线方程为y=9x+16,即9x-y+16=0§ 1.2导数的计算1.2.2复合函数的导数自学引导能利用出的基本初等函数的导数公式和导数的四则运算法则求简单的复合函数(仅限于形如f(ax+b))的导数.课前热身1.复合函数的概念.一般地,对于两个函数y=f(u)和u=g(x),如果通过变量u,y可以表示成x的函数,那么称这个函数为函数________和________的复合函数,记作________.2.复合函数y=f(g(x))的导数和函数y=f(u),u=g(x)的导数间的关系为________.即y对x的导数等于y对u的导数与u对x的导数的乘积.名师讲解1.求复合函数的导数的关键是处理好以下几个环节(1)中间变量的选择应是基本函数结构;(2)关键是正确分析出复合过程;(3)一般从最外层开始,由外及里,一层层地求导;(4)善于把一部分表达式作为一个整体;(5)最后结果要把中间变量换成自变量的函数.典例剖析2.求复合函数导数的方法步骤(1)分解复合函数为基本初等函数,适当选择中间变量;(2)求每一层基本初等函数的导数;(3)每层函数求导后,需把中间变量转化为自变量的函数.题型一复合函数的求导方法例1求下列函数的导数.(1)y=1(1-3x)4;(2)y=cos x2;(3)y=sin(2x-π3);(4)y=1+x2.分析注意中间变量的选取,分层求导.解(1)令u=1-3x,则y=1u4=u-4,∴y′u=-4u-5,u′x=-3.∴y′x=y′u·u′x=12u-5=12(1-3x)5.(2)令u=x2,则y=cos u,∴y′x=y′u·u′x=-sin u·2x=-2x sin x2.(3)令u=2x-π3,则y=sin u,∴y′x=y′u·u′x=cos u·2=2cos(2x-π3).(4)令u=1+x2,则y=u 12,∴y′x=y′u·u′x=12u -12·2x=x·u -12=x1+x2.规律技巧求复合函数的导数,要分清函数的复合关系,对于分式型的可化为幂的形式求导,关键选好中间变量.最后将中间变量代回到原自变量的函数.变式训练1 求下列函数的导数.(1)y=11+3x5;(2)y=sin(x2-π6 );(3)y=ln(ln x);(4)y=e2x 2+1.解(1)令u=1+3x,则y=1u5=u-5,∴y′x=y′u·u′x=-5u-6·3=-15u-6=-151+3x6.(2)令u=x2-π6,则y=sin u,∴y′x=y′u·u′x=cos u·(x2-π6)′=2x cos u=2x cos(x2-π6).(3)令u=ln x,则y=ln u,∴y′x=y′u·u′x=1u·1x=1x ln x.(4)令u=2x2+1,则y=e u,∴y′x=y′u·u′x=e u·4x=4x·e2x 2+1.例2 求下列函数的导数.(1)y=(x2-4)2;(2)y=log2(2x2+3x+1);(3)y=e sin(ax+b)分析先将复合函数分解,找出中间变量,然后按复合函数求导公式y′=y′u·u′x进行求导.解(1)方法1:y=(x2-4)2=x4-8x2+16∴y′=(x4-8x2+16)′=4x3-16x.方法2:y′=2(x2-4)(x2-4)′=2(x2-4)·2x=4x3-16x.(2)y′=[log2(2x2+3x+1)]′=12x2+3x +1ln2·(2x2+3x+1)′=4x+32x2+3x+1ln2.(3)y′=[e sin(ax+b)]′=e sin(ax+b)[sin(ax+b)]′=e sin(ax+b)·cos(ax+b)·(ax+b)′=a cos(ax+b)·e sin(ax+b).规律技巧求复合函数的导数,当复合步骤熟练后,可以直接求导.变式训练2 求下列函数的导数.(1)y=33x2+1;(2)y=sin3x+sin x3.解(1)y=33x2+1=(3x2+1)13,∴y′=13(3x2+1)-23(3x2+1)′=13(3x2+1)-23·6x=2x33x2+12.(2)y′=(sin3x+sin x3)′=3sin2x·(sin x)′+cos x3·(x3)′=3sin2x·cos x+3x2cos x3.题型二求导法则的综合应用例3 已知函数f(x)是关于x的二次函数,其导函数为f′(x),且∀x∈R,x2f′(x)-(2x-1)f(x)=1恒成立,求函数f(x)的解析式.分析可设f(x)=ax2+bx+c=0(a≠0),利用待定系数法求出a,b,c的值.解设f(x)=ax2+bx+c(a≠0),则f′(x)=2ax+b.又x2f′(x)-(2x-1)f(x)=x2(2ax+b)-(2x-1)(ax2+bx+c)=(a-b)x2+(b-2c)x+c=1恒成立,∴⎩⎨⎧ a -b =0,b -2c =0,c =1,∴⎩⎨⎧ a =2,b =2,c =1. ∴f (x )=2x 2+2x +1.变式训练3 已知函数f (x )是关于x 的三次函数,且f (0)=3,f ′(0)=0,f ′(1)=-3,f ′(2)=0,求f (x )的解析式.解 设f (x )=ax 3+bx 2+cx +d (a ≠0),则f ′(x )=3ax 2+2bx +c .由f (0)=3,得d =3,由f ′(0)=0,得c =0,由f ′(1)=-3,f ′(2)=0,得⎩⎨⎧ 3a +2b =-3,12a +4b =0,解得⎩⎨⎧a =1,b =-3. ∴f (x )=x 3-3x 2+3.。
