2015届高考数学集合、常用逻辑用语专题汇编及详细答案

合集下载

专题01 集合与常用逻辑用语(学生卷)- 十年(2015-2024)高考真题数学分项汇编(全国通用)

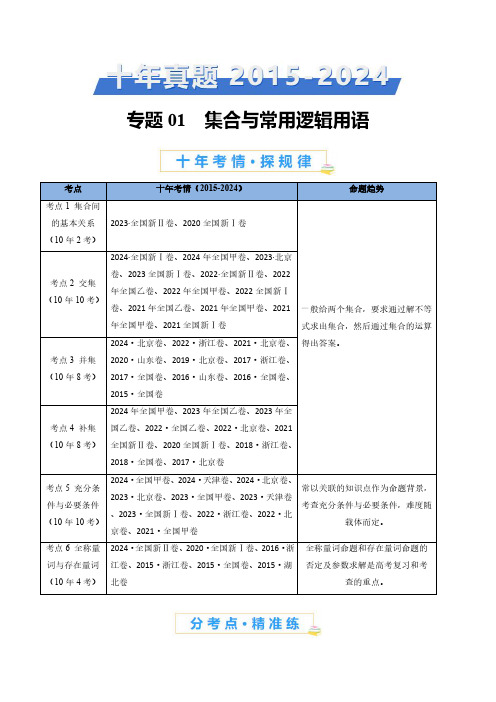
专题01集合与常用逻辑用语考点十年考情（2015-2024）命题趋势考点1集合间的基本关系（10年2考）2023·全国新Ⅱ卷、2020全国新Ⅰ卷一般给两个集合，要求通过解不等式求出集合，然后通过集合的运算得出答案。

考点2交集（10年10考）2024·全国新Ⅰ卷、2024年全国甲卷、2023·北京卷、2023全国新Ⅰ卷、2022·全国新Ⅱ卷、2022年全国乙卷、2022年全国甲卷、2022全国新Ⅰ卷、2021年全国乙卷、2021年全国甲卷、2021年全国甲卷、2021全国新Ⅰ卷考点3并集（10年8考）2024·北京卷、2022·浙江卷、2021·北京卷、2020·山东卷、2019·北京卷、2017·浙江卷、2017·全国卷、2016·山东卷、2016·全国卷、2015·全国卷考点4补集（10年8考）2024年全国甲卷、2023年全国乙卷、2023年全国乙卷、2022·全国乙卷、2022·北京卷、2021全国新Ⅱ卷、2020全国新Ⅰ卷、2018·浙江卷、2018·全国卷、2017·北京卷考点5充分条件与必要条件（10年10考）2024·全国甲卷、2024·天津卷、2024·北京卷、2023·北京卷、2023·全国甲卷、2023·天津卷、2023·全国新Ⅰ卷、2022·浙江卷、2022·北京卷、2021·全国甲卷常以关联的知识点作为命题背景，考查充分条件与必要条件，难度随载体而定。

考点6全称量词与存在量词（10年4考）2024·全国新Ⅱ卷、2020·全国新Ⅰ卷、2016·浙江卷、2015·浙江卷、2015·全国卷、2015·湖北卷全称量词命题和存在量词命题的否定及参数求解是高考复习和考查的重点。

2015高考理科数学集合与常用逻辑用语总复习题(含答案)

2015高考理科数学集合与常用逻辑用语总复习题(含答案)A组基础演练•能力提升]一、选择题1．(2013年高考浙江卷)设集合S＝{x|x>－2}，T＝{x|x2＋3x－4≤0}，则(∁RS)∪T＝()A．(－2,1]B．(－∞，－4]C．(－∞，1]D．1，＋∞)解析：T＝{x|－4≤x≤1}，根据补集定义，∁RS＝{x|x≤－2}，所以(∁RS)∪T ＝{x|x≤1}，选C.答案：C2．(2013年高考辽宁卷)已知集合A＝{x|0A．(0,1)B．(0,2]C．(1,2)D．(1,2] 解析：0∴集合A＝{x|1答案：D3．已知集合A＝xx－2x≤0，x∈N，B＝{x|x≤2，x∈Z}，则满足条件A⊆C⊆B 的集合C的个数为()A．1B．2C．4D．8解析：由x－2x≤0得0答案：D4．若集合A＝{x∈Z|20}，则A∩(∁RB)所含的元素个数为()A．0B．1C．2D．3解析：∵A＝{0,1}，B＝{x|x>2或x答案：C5．已知集合A＝{－1,1}，B＝{x|ax＋1＝0}，若B⊆A，则实数a的所有可能取值的集合为()A．{－1}B．{1}C．{－1,1}D．{－1,0,1}解析：由题意知集合B的元素为1或－1或者B为空集，故a＝0或1或－1.故选D.答案：D6．(2013年高考广东卷)设整数n≥4，集合X＝{1,2,3，…n}．令集合S＝{(x，y，z)|x，y，z∈X，且三条件xA．(y，z，w)∈S，(x，y，w)∉S B．(y，z，w)∈S，(x，y，w)∈SC．(y，z，w)∉S，(x，y，w)∈SD．(y，z，w)∉S，(x，y，w)∉S解析：题目中x答案：B二、填空题7．(2014年武汉模拟)已知A，B均为集合U＝{1,2,3,4,5,6}的子集，且A∩B ＝{3}，(∁UB)∩A＝{1}，(∁UA)∩(∁UB)＝{2,4}，则B∩(∁UA)＝________.解析：依题意及韦恩图得，B∩(∁UA)＝{5,6}．答案：{5,6}8．已知集合A＝{x∈R||x＋2|解析：A＝{x∈R||x＋2|由A∩B＝(－1，n)可知m则B＝{x|m答案：－119．设集合M＝，＝＋－1＋y＋3，－52≤y≤3，若(a，b)∈M，且对M中的其他元素(c，d)，总有c≥a，则a＝________.解析：依题可知，本题等价于求函数x＝f(y)＝(y＋3)•|y－1|＋y＋3在－52≤y≤3时的最小值．当－52≤y≤1时，x＝(y＋3)(1－y)＋y＋3＝－y2－y＋6＝－y＋122＋254，所以当y＝－52时，xmin＝94.当1≤y≤3时，x＝(y＋3)(y－1)＋y＋3＝y2＋3y＝y＋322－94，所以当y＝1时，xmin＝4.又4>94，因为当y＝－52时，x有最小值94，即a＝94.答案：94三、解答题10．设集合A＝{x2,2x－1，－4}，B＝{x－5,1－x,9}，若A∩B＝{9}，求A∪B. 解析：由9∈A，可得x2＝9，或2x－1＝9，解得x＝±3，或x＝5.当x＝3时，A＝{9,5，－4}，B＝{－2，－2,9}，B中元素重复，故舍去；当x＝－3时，A＝{9，－7，－4}，B＝{－8,4,9}，A∩B＝{9}满足题意，故A∪B＝{－8，－7，－4,4,9}；当x＝5时，A＝{25,9，－4}，B＝{0，－4,9}，此时A∩B＝{－4,9}与A∩B ＝{9}矛盾，故舍去．综上所述，A∪B＝{－8，－7，－4,4,9}11．已知集合A＝{x|x2－2x－3≤0，x∈R}，B＝{x|m－2≤x≤m＋2}．(1)若A∩B＝1,3]，求实数m的值；(2)若A⊆∁RB，求实数m的取值范围．解析：A＝{x|－1≤x≤3}，B＝{x|m－2≤x≤m＋2}．(1)∵A∩B＝1,3]，∴m－2＝1，m＋2≥3.得m＝3.(2)∁RB＝{x|xm＋2}，∵A⊆∁RB，∴m－2>3或m＋2∴m>5或m12．(能力提升)设集合A＝{x|－1≤x≤2}，B＝{x|x2－(2m＋1)x＋2m(1)当m(2)若A∪B＝A，求实数m的取值范围．解析：∵不等式x2－(2m＋1)x＋2m(1)当m∴集合B＝{x|2m(2)若A∪B ＝A，则B⊆A，∵A＝{x|－1≤x≤2}，①当m此时－1≤2m②当m＝12时，B＝∅，有B⊆A成立；③当m>12时，B＝{x|1此时1综上所述，m的取值范围是－12≤m≤1. B组因材施教•备选练习]1．已知集合P＝{y＝x2＋1}，Q＝{y|y＝x2＋1，x∈R}，S＝{x|y＝x2＋1，x∈R}，T＝{(x，y)|y＝x2＋1，x∈R}，M＝{x|x≥1}，则()A．P＝MB．Q＝SC．S＝TD．Q＝M解析：集合P是用列举法表示，只含有一个元素，集合Q是函数y＝x2＋1的值域，Q＝{y|y≥1}，集合S是函数y＝x2＋1中x的取值范围R，集合M是不等式的解集{x|x≥1}，而集合T的元素是平面上的点，此集合是函数y＝x2＋1的图象上所有的点组成的集合，故选D.答案：D2．已知集合A＝{x|log2x≤2}，B＝(－∞，a)，若A⊆B，则实数a的取值范围是(c，＋∞)，其中c＝________.解析：A＝{x|log2x≤2}＝{x|0答案：43．(2014年合肥模拟)对于任意的两个正数m，n，定义运算⊙：当m，n都为偶数或都为奇数时，m⊙n＝m＋n2，当m，n为一奇一偶时，m⊙n ＝mn，设集合A＝{(a，b)|a⊙b＝6，a，b∈N*}，则集合A中的元素个数为________．解析：(1)当a，b都为偶数或都为奇数时，a＋b2＝6⇒a＋b＝12，即2＋10＝4＋8＝6＋6＝1＋11＝3＋9＝5＋7＝12，故符合题意的点(a，b)有2×5＋1＝11个．(2)当a，b为一奇一偶时，ab＝6⇒ab＝36，即1×36＝3×12＝4×9＝36，故符合题意的点(a，b)有2×3＝6个．综上可知，集合A中的元素共有17个．答案：174．已知A＝{(x，y)|y＝|x2－1|}，B＝{(x，y)|y＝1－x2}，则A∩B的真子集个数为________．解析：由题意，知集合A表示函数y＝|x2－1|的图象，由y＝1－x2，得x2＋y2＝1(y≥0)，该方程表示以原点为圆心，1为半径的半圆，所以集合B表示半圆，所以A∩B中的元素就是函数y＝|x2－1|与y＝1－x2的图象的交点．因为y＝|x2－1|＝x2－1，x∈－∞，－1]∪1，＋∞，1－x2，x∈－1，，如图所示，作出y＝|x2－1|与y＝1－x2的图象，可知y＝|x2－1|与y＝1－x2的图象有三个交点，分别为D(－1，0)，E(1,0)，C(0,1)，即A∩B中有3个元素，故A∩B的子集有23＝8(个)，真子集个数为8－1＝7.答案：7。

【解密高考】2015届高考数学大一轮总复习集合与常用逻辑用语、基本初等函数、导数及其应用阶段性综合

集合与常用逻辑用语、基本初等函数、导数及其应用时间120分钟满分150分第Ⅰ卷(选择题，共60分)一、选择题(本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．(2014·某某河西质量调查)设集合A ＝{4,5,7,9}，B ＝{3,4,7,8,9}，全集U ＝A ∪B ，则集合∁U (A ∩B )中的元素共有( )A ．3个B ．4个C ．5个D ．6个解析：由题意得A ∩B ＝{4,7,9}，U ＝A ∪B ＝{3,4,5,7,8,9}，所以∁U (A ∩B )＝{3,5,8}．答案：A2．(2014·某某质检)若集合A ＝{x ||x ＋1|＝x ＋1}，B ＝{x |x 2＋x ＜0}，则A ∩B ＝( ) A ．(－1,0) B ．[－1,0) C ．(－1,0]D ．[－1,0]解析：因为A ＝{x |x ≥－1}，B ＝{x |－1＜x ＜0}，所以A ∩B ＝{x |－1＜x ＜0}．答案：A3．(2014·某某某某十校期末)满足M ⊆{a 1，a 2，a 3，a 4}，且M ∩{a 1，a 2，a 3}＝{a 1，a 2}的集合M 的个数是( )A ．1B ．2C ．3D ．4解析：由题意得{a 1，a 2}⊆M ⊆{a 1，a 2，a 4}，所以M ＝{a 1，a 2}或M ＝{a 1，a 2，a 4}．答案：B4．(2014·某某调研)设集合P ＝{x |x 2－x －2≥0}，Q ＝{y |y ＝12x 2－1，x ∈P }，则P ∩Q＝( )A ．{m |－1≤m ＜2}B ．{m |－1＜m ＜2}C ．{m |m ≥2}D ．{－1}解析：P ＝{x |x ≥2或x ≤－1}，又x ∈P 时，y ＝12x 2－1∈[－12，＋∞)，故Q ＝{y |y ≥－12}，故P ∩Q ＝{m |m ≥2}．答案：C5．(2013·某某)已知函数f (x )为奇函数，且当x ＞0时，f (x )＝x 2＋1x，则f (－1)＝( )A ．2B ．1C ．0D ．－2解析：因f (x )为奇函数，故f (－1)＝－f (1)＝－(1＋1)＝－2. 答案：D6．(2014·某某综合测试)设全集I 是实数集R ，M ＝{x |x 2＞4}与N ＝{x |2x －1≥1}都是I 的子集(如图所示)，则阴影部分所表示的集合为( )A ．{x |x ＜2}B ．{x |－2≤x ＜1}C ．{x |1＜x ≤2}D ．{x |－2≤x ≤2}解析：M ＝{x |x ＞2或x ＜－2}，N ＝{x |3－xx －1≥0}＝{x |1＜x ≤3}，阴影部分所表示的集合为(∁R M )∩N ＝{x |－2≤x ≤2}∩{x |1＜x ≤3}＝{x |1＜x ≤2}．答案：C7.(2013·某某)“(2x－1)x ＝0”是“x＝0”的( )A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件解析：由(2x －1)x ＝0可得x ＝12或0，因为“x＝12或0”是“x＝0”的必要不充分条件，故答案选B .答案：B8．(2014·东城期末)有下列四个命题： ①“若xy ＝1，则x ，y 互为倒数”的逆命题； ②“面积相等的三角形全等”的否命题；③“若m≤1，则x 2－2x ＋m ＝0有实数解”的逆否命题； ④“若A∩B＝B ，则A B”的逆否命题．其中真命题为( )A ．①②B ．②③C ．④D ．①②③解析：①中逆命题为“若x ，y 互为倒数，则xy ＝1”，为真命题． ②中否命题为“若两三角形面积不相等，则两三角形不全等”，为真命题． ③中x 2－2x ＋m ＝0有实数解⇔Δ＝4－4m≥0⇔m≤1，故原命题正确，其逆否命题为真命题．④若A∩B＝B ，则B ⊆A ，为假命题，故其逆否命题为假命题．答案：D9．(2014·某某某某期末)已知命题p ：∃x ∈R ，使sin x －cos x ＝3，命题q ：集合{x |x2－2x ＋1＝0，x ∈R }有2个子集，下列结论：①命题“p ∧q ”是真命题；②命题“p ∧(綈q )”是假命题；③命题“(綈p )∨(綈q )”是真命题，正确的个数是( )A ．0B ．1C ．2D ．3解析：sin x －cos x ＝2sin(x －π4)∈[－2，2]，而3∉[－2，2]，故命题p 是假命题；集合{x |x 2－2x ＋1＝0，x ∈R }＝{1}，故其子集有Ø与{1}两个，故命题q 是真命题，所以命题“p ∧q ”是假命题，命题“p ∧(綈q )”是假命题，命题“(綈p )∨(綈q )”是真命题，②③正确．答案：C10．(2014·某某某某第二次测试)已知函数f (x ＋1)是偶函数，当x 2＞x 1＞1时，[f (x 2)－f (x 1)]·(x 2－x 1)＞0恒成立，设a ＝f (－12)，b ＝f (2)，c ＝f (3)，则a ，b ，c 的大小关系为( )A ．b ＜a ＜cB ．c ＜b ＜aC ．b ＜c ＜aD ．a ＜b ＜c解析：本题主要考查抽象函数的性质．由函数f (x ＋1)为偶函数知f (x )的对称轴为x ＝1.当x 2＞x 1＞1时，[f (x 2)－f (x 1)]·(x 2－x 1)＞0得到f (x )在(1，＋∞)上是递增的，所以f (－12)＝f (52)，所以f (2)＜f (52)＜f (3)．即b ＜a ＜c .答案：A11．(2014·某某苏北四市第一次调研)若函数y ＝f (x )在R 上可导且满足不等式xf ′(x )＋f (x )＞0恒成立，且常数a ，b 满足a ＞b ，则下列不等式一定成立的是( )A ．af (a )＞bf (b )B ．af (b )＞bf (a )C ．af (a )＜bf (b )D ．af (b )＜bf (a )解析：由题意设F (x )＝xf (x )，则F ′(x )＝xf ′(x )＋f (x )，则F ′(x )＞0，∴F (x )为单调增函数，又a＞b，∴F(a)＞F(b)．∴af(a)＞bf(b)．答案：A12．(2014·某某调研)定义在R上的函数f(x)满足f(－x)＝－f(x＋4)，当x≥2时，f(x)单调递增，如果x1＋x2＞4，且(x1－2)(x2－2)＜0，则f(x1)＋f(x2)的值为( ) A．恒小于0 B．恒大于0C．可能为0 D．可正可负解析：可以由f(x)＝－f(4－x)得函数图象关于点(2,0)成中心对称直观解答；也可直接推理，由(x1－2)(x2－2)＜0不妨设x1＞2，x2＜2，由条件得f(x2)＝－f(4－x2)，故f(x1)＋f(x2)＝f(x1)－f(4－x2)，由x2＜2且x1＋x2＞4⇒x1＞4－x2＞2，由于函数在[2，＋∞)上为增函数，可得f(x1)＞f(4－x2)，故选B.答案：B第Ⅱ卷(非选择题，共90分)本卷包括必考题和选考题两部分，第13题～第21题为必考题，每个试题考生都必须做答，第22题～第24题为选考题，考生根据要求做答。

2015年高考数学(新课标Ⅱ版)分项汇编专题01集合与常用逻辑用语(含解析)理

专题01 集合与常用逻辑用语一．基础题组1. 【2013课标全国Ⅱ，理1】已知集合M＝{x|(x－1)2＜4，x∈R}，N＝{－1,0,1,2,3}，则M∩N ＝( )．A．{0,1,2} B．{－1,0,1,2}C．{－1,0,2,3} D．{0,1,2,3}【答案】：A2. 【2012全国，理2】已知集合A＝{1,3，}，B＝{1， m}，A∪B＝A，则m＝( )A．0或 B．0或3 C．1或 D．1或3【答案】 B3. 【2015高考新课标2，理1】已知集合，,则（）A．B．C．D．【答案】A二．能力题组1.【2014新课标，理1】设集合M=｛0,1,2｝，N=，则=( )A. ｛1｝B. ｛2｝C. ｛0，1｝D. ｛1，2｝【答案】D【解析】因为N=，所以，故选D.2. 【2006全国2，理1】已知集合M={x|x<3},N={x|log2x>1},则M∩N等于（A. B.{x|0<x<3} C.{x|1<x<3} D.{x|2<x<3}【答案】:D3. 【2005全国2，理9】已知集合，，则为（）(A) 或(B) 或(C) 或(D) 或【答案】A三．拔高题组1. 【2011新课标，理10】已知a与b均为单位向量，其夹角为θ，有下列四个命题：p1： |a＋b|＞1θ∈[0，)p2：|a＋b|＞1θ∈(，π]p3：|a－b|＞1θ∈[0，)p4：|a－b|＞1θ∈(，π]其中的真命题是( )A．p1，p4B．p1，p3C．p2，p3D．p2， p4【答案】A【解析】2. 【2005全国2，理16】下面是关于三棱锥的四个命题：①底面是等边三角形，侧面与底面所成的二面角都相等的三棱锥是正三棱锥．②底面是等边三角形，侧面都是等腰三角形的三棱锥是正三棱锥．③底面是等边三角形，侧面的面积都相等的三棱锥是正三棱锥．④侧棱与底面所成的角都相等，且侧面与底面所成的二面角都相等的三棱锥是正三棱锥.其中，真命题的编号是______________．(写出所有真命题的编号）【答案】①④。

2015届高考数学文科一轮总复习集合与常用逻辑用语.docx

2015 届高考数学（文科）一轮总复习集合与常用逻辑用语第一篇集合与常用逻辑用语第 1 讲集合及其运算基础巩固题组( 建议用时： 40 分钟 )一、填空题1 ．(2013 ?安徽卷改编 ) 已知 A＝ {x|x ＋ 1＞ 0} ，B＝ { － 2，－1,0,1} ．则 ( ?RA)∩ B＝ ________.解析因为 A＝ {x|x ＞－ 1} ，则 ?RA＝ {x|x ≤－ 1} ，所以( ?RA)∩B＝ { － 2，－ 1} ．答案{ －2，－ 1}2．已知集合＝ {1,2,3} ，N＝ {2,3,4} ，则下列各式不正确的是 ________．①? N；② N? ；③∩ N＝{2,3} ；④∪ N＝ {1,4} ．解析由已知得∩ N＝{2,3}，故选①②④ .答案①②④3．已知集合＝{0,1,2,3,4}，N＝ {1,3,5}，P＝∩N，则P 的子集个数有________．解析P＝∩ N＝ {1,3}，故P 的子集共有 4 个．答案44．已知集合 A＝ {x|x2 －x－ 2＜ 0} ，B＝ {x| － 1＜x＜ 1} ，则 A 与 B 的关系是 ________．解析集合 A＝ {x| － 1＜ x＜2} ，B＝ {x| －1＜ x＜ 1} ，则BA.答案BA5．设集合 A＝ {x|x2 ＋ 2x－ 8＜ 0} ， B＝ {x|x ＜ 1} ，则图中阴影部分表示的集合为 ________．解析阴影部分是A∩ ?RB.集合 A＝ {x| － 4＜ x＜2} ，?RB＝{x|x ≥1} ，所以 A∩?RB＝ {x|1 ≤ x＜2} ．答案 {x|1 ≤ x＜ 2}6 ．(2013 ?湖南卷 ) 已知集合 U＝ {2,3,6,8}，A＝{2,3}，B＝ {2,6,8}，则( ?UA)∩ B＝________.解析由集合的运算，可得 ( ?UA)∩ B＝{6,8}∩{2,6,8}＝{6,8} ．答案 {6,8}7 ．集合A＝ {0,2 ， a} ， B＝ {1 ， a2} ，若A∪ B＝{0,1,2,4,16}，则 a 的值为________．解析根据并集的概念，可知{a， a2}＝ {4,16}，故只能是a＝ 4.答案48．集合 A＝ {x ∈ R||x － 2| ≤ 5} 中的最小整数为________．解析由 |x－ 2|≤ 5，得－5≤ x－ 2≤ 5，即－3≤ x≤ 7，所以集合 A 中的最小整数为－ 3.答案－ 3二、解答题9．已知集合 A＝ {a2 ， a＋ 1，－ 3} ， B＝{a － 3，a－ 2，a2＋ 1} ，若 A∩ B＝{ －3} ，求 A∪ B.解由 A∩B＝{ －3} 知，－ 3∈B.又 a2＋ 1≥ 1，故只有 a－ 3， a－ 2 可能等于－ 3.①当 a－3＝－ 3 时，a＝ 0，此时 A＝ {0,1 ，－ 3} ，B＝ { －3，－ 2，1} ， A∩B＝ {1 ，－ 3} ．故 a＝ 0 舍去．②当 a－2＝－ 3 时， a＝－ 1，此时 A＝{1,0 ，－ 3} ， B＝ { － 4，－ 3,2} ，满足 A∩B＝ { － 3} ，从而 A∪ B＝ { － 4，－ 3,0,1,2}．10．设 A＝ {x|x2 ＋ 4x＝ 0} ， B＝ {x|x2＋ 2(a ＋1)x ＋ a2－1＝0} ，(1)若 B? A，求 a 的值；(2)若 A? B，求 a 的值．解(1)A ＝ {0 ，－ 4} ，①当 B＝?时，＝4(a＋1)2－4(a2－1)＝8(a＋1)＜0，解得 a＜－ 1；②当 B 为单元素集时，a＝－ 1，此时 B＝ {0} 符合题意；③当 B＝A 时，由根与系数的关系得：－2 a＋ 14， a2－1＝ 0，解得 a＝1.综上可知： a≤－ 1 或 a＝ 1.(2)若 A? B，必有 A＝ B，由 (1) 知 a＝ 1.能力提升题组( 建议用时： 25 分钟 )一、填空题1 ．若集合 A＝ { － 1,1} ，B＝ {0,2} ，则集合 {z|z ＝ x＋ y，x∈ A， y∈ B} 中的元素的个数为 ________．解析当 x＝－ 1，y＝ 0 时， z＝－ 1；当 x＝－ 1， y＝ 2时， z＝1；当 x＝ 1，y＝ 0 时， z＝ 1；当 x＝ 1，y＝ 2 时， z＝ 3. 故z 的值为－ 1,1,3 ，故所求集合为 { － 1,1,3} ，共含有 3 个元素．答案32．已知集合A＝ {x∈ R||x＋ 2|解析A＝ {x|－ 5答案－113．设g(x) ＝ (axa， b， c＋ 1)(cx2为实数，＋ bx＋1)f(x)＝(x．记集合＋ a) ?(x2S＝ {x|f(x)＋ bx＋ c) ，＝0， x∈R}， T＝ {x|g(x)＝0，x∈ R}．若|S|，|T|分别为集合S， T 的元素个数，则下列结论：①|S| ＝ 1 且|T| ＝ 0；② |S| ＝ 1且 |T| ＝1，③ |S| ＝2 且 |T| ＝ 2；④ |S| ＝ 2 且 |T| ＝3，其中不可能成立的是________．解析取 a＝ 0，b＝ 0，c＝ 0，则 S＝ {x|f(x)＝x3＝0}，|S| ＝ 1，T＝ {x|g(x)＝1≠0}，|T|＝0.因此①可能成立．取a＝ 1， b＝ 0， c＝1，则 S＝ {x|f(x)＝ (x ＋ 1)(x2 ＋ 1) ＝ 0} ，|S| ＝ 1， T＝ {x|g(x) ＝ (x ＋ 1)(x2＋ 1) ＝0} ， |T| ＝1，因此②可能成立．取 a＝－ 1， b＝ 0， c＝－ 1，则 S＝ {x|f(x)＝(x － 1)(x2 － 1) ＝ 0} ， |S| ＝ 2， T＝ {x|g(x) ＝ ( － x＋1)?( －x2＋ 1) ＝0} ，|T| ＝ 2. 因此③可能成立．对于④，若 |T|＝ 3，则＝ b2－ 4c＞ 0，从而导致 f(x)＝ (x ＋ a)(x2 ＋ bx＋c)也有3 解，因此 |S| ＝ 2 且 |T| ＝3 不可能成立．故④不可能成立．答案④二、解答题4．已知集合A＝ {y|y＝ 2x－ 1,0＜ x≤ 1}， B＝ {x|(x－a)[x－ (a ＋ 3)]＜ 0} ．分别根据下列条件，求实数 a 的取值范围．(1)A∩ B＝A；(2)A∩ B≠ ?.解因为集合 A 是函数 y＝ 2x－ 1(0 ＜ x≤ 1) 的值域，所以 A＝ ( － 1,1] ， B＝ (a ， a＋ 3) ．(1)A∩ B＝A? A? B? a≤－1，a＋3＞1，即－ 2＜ a≤－ 1，故当 A∩ B＝A 时，a 的取值范围是 ( － 2，－1] ．(2)当 A∩B＝ ?时，结合数轴知， a≥ 1 或 a＋ 3≤－ 1，即a≥ 1 或 a≤－ 4.故当 A∩B≠ ?时， a 的取值范围是 ( － 4,1).。

2015年高考数学试题分类汇编A单元集合与常用逻辑用语

数学A单元集合与常用逻辑用语A1 集合及其运算2．A1[2015·安徽卷] 设全集U＝{1,2,3,4,5,6},A＝{1,2},B＝{2,3,4},则A∩(∁U B)＝() A．{1,2,5,6} B．{1}C．{2} D．{1,2,3,4}2．B[解析] 由∁U B＝{1,5,6}得A∩(∁U B)＝{1}．1．A1[2015·广东卷] 若集合M＝{－1,1},N＝{－2,1,0},则M∩N＝()A．{0,－1} B．{0}C．{1} D．{－1,1}1．C[解析] M∩N＝{1},故选C.10.A1[2015·湖北卷] 已知集合A＝{(x,y)|x2＋y2≤1,x,y∈Z},B＝{(x,y)||x|≤2,|y|≤2,x,y∈Z},定义集合A B＝{(x1＋x2,y1＋y2)|(x1,y1)∈A,(x2,y2)∈B},则A B中元素的个数为() A．77 B．49C．45 D．3010．C[解析] 集合A,集合B”点,集合A B显然是集合{(x,y)||x|≤3,|y|≤3,x,y∈Z}中除去四个点(－3,－3),(－3,3),(3,－3),(3,3)之外的所有整点(即横坐标与纵坐标都为整数的点),即集合A B表示如图所示的所有“”点＋所有“,共45个．故A B中元素的个数为45.故选C.1．A1[2015·全国卷Ⅰ] 已知集合A＝{x|x＝3n＋2,n∈N},B＝{6,8,10,12,14},则集合A∩B 中元素的个数为()A．5 B．4C．3 D．21．D[解析] 集合A＝{2,5,8,11,14,17,…},所以A∩B＝{8,14},所以A∩B中有2个元素．1．A1[2015·全国卷Ⅱ] 已知集合A＝{x|－1<x<2},B＝{x|0<x<3},则A∪B＝()A．(－1,3) B．(－1,0)C．(0,2) D．(2,3)1．A[解析] 根据并集的概念可知A∪B＝{x|－1<x<2}∪{x|0<x<3}＝{x|－1<x<3}＝(－1,3),选A.1．A12015·北京卷若集合A＝{x|－5<x<2},B＝{x|－3<x<3},则A∩B＝()A．{x|－3<x<2} B．{x|－5<x<2}C．{x|－3<x<3} D．{x|－5<x<3}1．A[解析] A∩B＝{x|－5<x<2}∩{x|－3<x<3}＝{x|－3<x<2},故选A.2．A1[2015·福建卷] 若集合M＝{x|－2≤x<2},N＝{0,1,2},则M∩N等于()A．{0} B．{1}C．{0,1,2} D．{0,1}2．D[解析] 根据交集的概念得M∩N＝{0,1}．11．A1[2015·湖南卷] 已知集合U＝{1,2,3,4},A＝{1,3},B＝{1,3,4},则A∪(∁U B)＝________．11．{1,2,3} [解析] ∁U B＝{2},故A∪(∁U B)＝{1,3}∪{2}＝{1,2,3}．1．A1[2015·山东卷] 已知集合A＝{x|2<x<4},B＝{x|(x－1)(x－3)<0},则A∩B＝()A．(1,3) B．(1,4)C．(2,3) D．(2,4)1．C[解析] ∵B＝{x|1<x<3},∴A∩B＝(2,3)．1．A1[2015·陕西卷] 设集合M＝{x|x2＝x},N＝{x|lg x≤0},则M∪N＝()A．[0,1] B．(0,1]C．[0,1) D．(－∞,1]1．A[解析] 由题得集合M＝{0,1},N＝(0,1],所以M∪N＝[0,1]．1．A12015·四川卷设集合A＝{x|－1<x<2},集合B＝{x|1<x<3},则A∪B＝()A．{x|－1<x<3}B．{x|－1<x<1}C．{x|1<x<2}D．{x|2<x<3}1．A[解析] 集合A＝(－1,2),B＝(1,3),故A∪B＝(－1,3)．1．A1[2015·天津卷] 已知全集U＝{1,2,3,4,5,6},集合A＝{2,3,5},集合B＝{1,3,4,6},则集合A∩(∁U B)＝()A．{3}B．{2,5}C．{1,4,6}D．{2,3,5}1．B[解析] ∁U B＝{2,5},A∩(∁U B)＝{2,3,5}∩{2,5}＝{2,5},故选B.1．A12015·浙江卷已知集合P＝{x|x2－2x≥3},Q＝{x|2<x<4},则P∩Q＝()A．[3,4) B．(2,3]C．(－1,2) D．(－1,3]1．A[解析] 不等式x2－2x≥3,即x2－2x－3≥0,即(x＋1)(x－3)≥0,解得x≤－1或x≥3,即P＝(－∞,－1]∪[3,＋∞),所以P∩Q＝[3,4)．1．A1[2015·重庆卷] 已知集合A＝{1,2,3},B＝{1,3},则A∩B＝()A．{2} B．{1,2}C．{1,3} D．{1,2,3}1．C[解析] 由集合交集的定义,得A∩B＝{1,3}．1．A1[2015·江苏卷] 已知集合A＝{1,2,3},B＝{2,4,5},则集合A∪B中元素的个数为________．1．5[解析] 因为A∪B＝{1,2,3,4,5},所以A∪B中元素的个数为5.A2 命题及其关系、充分条件、必要条件 3．A2[2015·安徽卷] 设p ：x <3,q ：－1<x <3,则p 是q 成立的( ) A ．充分必要条件 B ．充分不必要条件 C ．必要不充分条件D ．既不充分也不必要条件3．C [解析] 因为(－1,3)是(－∞,3)的真子集,所以q ⇒p ,但p ⇒/ q ,因此p 是q 的必要不充分条件．5．A2、G3[2015·湖北卷] l 1,l 2表示空间中的两条直线,若p ：l 1,l 2是异面直线；q ：l 1,l 2不相交,则( )A ．p 是q 的充分条件,但不是q 的必要条件B ．p 是q 的必要条件,但不是q 的充分条件C ．p 是q 的充分必要条件D ．p 既不是q 的充分条件,也不是q 的必要条件5．A [解析] 由l 1,l 2是异面直线,可得l 1,l 2不相交,所以p ⇒q ；由l 1,l 2不相交,可得l 1,l 2是异面直线或l 1∥l 2,所以q ⇒/ p ．所以p 是q 的充分条件,但不是q 的必要条件．故选A.6．A2,F3[2015·北京卷] 设a ,b 是非零向量．“a·b ＝|a||b|”是“a ∥b ”的( ) A ．充分而不必要条件 B ．必要而不充分条件 C ．充分必要条件 D ．既不充分也不必要条件 6．A [解析] 根据数量积的定义,a ·b ＝||a ·||b cos θ,由a ·b ＝||a ·||b 可得cos θ＝1,根据向量所成角的范围得到θ＝0,所以a ∥b ；若a ∥b ,可得向量a 与向量b 共线,即所成的角为0或π,所以a ·b ＝±||a ·||b ,故选A. 12．A2、E1[2015·福建卷] “对任意x ∈0,π2,k sin x cos x <x ”是“k <1”的( )A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件12．B [解析] 当x ∈0,π2时,k sin x cos x <x ⇔k <x sin x cos x ＝2xsin 2x ,令t ＝2x ∈(0,π),则y ＝2x sin 2x ＝tsin t>1,所以k ≤1,故选B. 3．A2[2015·湖南卷] 设x ∈R ,则“x >1”是“x 3>1”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件3．C [解析] ∵x >1,∴x 3>1,由x 3－1>0得(x －1)(x 2＋x ＋1)>0,解得x >1,∴“x >1”是“x 3>1”的充要条件,选C.5．A2[2015·山东卷] 设m ∈R ,命题“若m >0,则方程x 2＋x －m ＝0有实根”的逆否命题是( )A ．若方程x 2＋x －m ＝0有实根,则m >0B ．若方程x 2＋x －m ＝0有实根,则m ≤0C ．若方程x 2＋x －m ＝0没有实根,则m >0D ．若方程x 2＋x －m ＝0没有实根,则m ≤05．D[解析] ∵逆否命题是将原命题的条件与结论互换并分别否定,∴命题“若m>0,则方程x2＋x－m＝0有实根”的逆否命题是“若方程x2＋x－m＝0没有实根,则m≤0”．图1-16．A2[2015·陕西卷] “sin α＝cos α”是“cos 2α＝0”的()A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件6．A[解析] sin α＝cos α时,cos 2α＝cos2α－sin2α＝0,反之,sin α＝±cos α,即“sin α＝cos α”是“cos 2α＝0”的充分不必要条件．4．A2、B7[2015·四川卷] 设a,b为正实数,则“a>b>1”是“log2a>log2b>0”的()A．充要条件B．充分不必要条件C．必要不充分条件D．既不充分也不必要条件4．A[解析] 当a＞b＞1时,log2a＞log2b＞0成立；反之也正确．故选A.4．A2、E2[2015·天津卷] 设x∈R,则“1<x<2”是“|x－2|<1”的()A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件4．A[解析] 由|x－2|<1,解得1<x<3.若1<x<2,则1<x<3,反之不成立,所以“1<x<2”是“|x －2|<1”成立的充分不必要条件．3．A2[2015·浙江卷] 设a,b是实数,则“a＋b>0”是“ab>0”的()A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件3．D[解析] 当a＝－2,b＝3时,a＋b>0,而ab<0；当a＝－2,b＝－3时,ab>0,而a＋b<0.故“a＋b>0”是“ab>0”的既不充分也不必要条件．2．A2[2015·重庆卷] “x＝1”是“x2－2x＋1＝0”的()A．充要条件B．充分而不必要条件C．必要而不充分条件D．既不充分也不必要条件2．A[解析] 由x2－2x＋1＝0,解得x＝1,所以“x＝1”是“x2－2x＋1＝0”的充要条件,故选A.A3 基本逻辑联结词及量词3．A3[2015·湖北卷] 命题“∃x0∈(0,＋∞),ln x0＝x0－1”的否定是()A．∃x0∈(0,＋∞),ln x0≠x0－1B．∃x0∉(0,＋∞),ln x0＝x0－1C ．∀x ∈(0,＋∞),ln x ≠x －1D ．∀x ∉(0,＋∞),ln x ＝x －13．C [解析] 特称命题的否定是全称命题,且注意否定结论,故原命题的否定是“∀x ∈(0,＋∞),ln x ≠x －1”．故选C.A4 单元综合 4．[2015·沈阳二中模拟] 下列说法正确的是( )A ．命题“若x 2＝1,则x ＝1”的否命题为“若x 2＝1,则x ≠1”B ．“x ＝－1”是“x 2－5x －6＝0”的必要不充分条件C ．命题“若x ＝y ,则sin x ＝sin y ”的逆否命题为真命题D ．命题“∃x 0∈R ,x 20＋x 0＋1<0”的否定是“∀x ∈R ,x 2＋x ＋1<0”4．C [解析] 命题“若x 2＝1,则x ＝1”的否命题为“若x 2≠1,则x ≠1”,所以选项A 不正确．由x ＝－1,能够得到x 2－5x －6＝0,反之,由x 2－5x －6＝0,得到x ＝－1或x ＝6,所以“x ＝－1”是“x 2－5x －6＝0”的充分不必要条件,所以选项B 不正确．命题“若x ＝y ,则sin x ＝sin y ”为真命题,所以其逆否命题也为真命题,所以选项C 正确．命题“∃x 0∈R ,x 20＋x 0＋1＜0”的否定是“∀x ∈R ,x 2＋x ＋1≥0”,所以选项D 不正确．6．[2015·重庆一中模拟] “x <0”是“ln(x ＋1)<0”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件D ．既不充分也不必要条件6．B [解析] ∵x ＜0,∴x ＋1＜1,∴当x ＋1＞0时,ln(x ＋1)＜0；∵ln(x ＋1)＜0,∴0＜x ＋1＜1,∴－1＜x ＜0,∴x ＜0,∴“x ＜0”是“ln(x ＋1)＜0”的必要不充分条件．9．[2015·佛山一中模拟] 若a ＝2x ,b ＝log 12x ,则“a >b ”是“x >1”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件9．B [解析] 如图所示,当x ＝x 0时,a ＝b .若a ＞b ,则得到x 00b 不一定得到x ＞1,∴“a ＞b ”不是“x ＞1”的充分条件；若x ＞1,则由图像得到a ＞b ,∴“a ＞b ”是“x ＞1”的必要条件．故“a ＞b ”是“x ＞1”的必要不充分条件． 13．[2015·杭州二中模拟] 给出下列说法： ①“若p ,则q ”的否命题是“若綈 p ,则綈 q ”； ②“∀x >2,x 2－2x >0”的否定是“∃x 0≤2,x 20－2x 0≤0”； ③“p ∧q 是真命题”是“p ∨q 是真命题”的充分不必要条件；④若“b ＝0,则函数f (x )＝ax 2＋bx ＋c 是偶函数”的逆命题是真命题．其中,错误说法的序号是________．13．② [解析] 根据命题与否命题的关系知①正确；“∀x >2,x 2－2x >0”的否定是“∃x 0>2,x 20－2x 0≤0”,②错误；若“p ∧q ”是真命题,则p ,q 均为真命题,所以“p ∨q ”是真命题,反之,若“p ∨q ”是真命题,则p ,q 可能是一真一假或都为真,则“p ∧q ”不一定是真命题,所以③正确；若f(x)＝ax2＋bx＋c为偶函数,则f(x)＝f(－x),解得b＝0,所以④正确．。

全国名校高考数学试题分类汇编(12月第四期)A单元集合

【备考2015】2015届全国名校数学试题分类汇编（12月第四期）A单元集合与常用逻辑用语（含解析）目录A1 集合及其运算 ........................................................ - 1 - A2 命题及其关系、充分条件、必要条件 ..................................... - 4 - A3 基本逻辑联结词及量词 ............................................... - 12 - A4 单元综合 ........................................................... - 13 -A1 集合及其运算【数学理卷·2015届黑龙江省大庆市铁人中学高三12月月考（期中）（201412）】1.设集合A ＝{x |y ＝3x －x 2}，B ＝{y |y ＝2x，x >1}，则A ∩B 为( )A ．[0,3]B ．(2,3]C ．[3，＋∞) D．[1,3] 【知识点】集合及其运算A1 【答案】B【解析】A ＝{x |0≤x 3≤},B={y |y >2}则A ∩B=(2,3] 【思路点拨】先分别求出A ，B 再求交集。

【数学理卷·2015届重庆市巴蜀中学高三12月月考（201412）】5．已知()(){}3,3,,202y M x y N x y ax y a x ⎧-⎫===++=⎨⎬-⎩⎭且∅=⋂N M ，则a =（）A.-6或-2B.-6C.2或-6D.2【知识点】两个集合交集是空集的条件. A1【答案】【解析】A 解析：若∅=⋂N M ，则3232aa ⎧-=⎪⎪⎨⎪-≠-⎪⎩或32260a a a ⎧-≠⎪⎨⎪++=⎩，解得a= -6或a= -2,故选A.【思路点拨】要使∅=⋂N M ，需使：缺少点（2，3）的直线y-3=3(x-2)与直线ax+2y+a=0平行，或者直线ax+2y+a=0过点（2，3），但不与直线y-3=3(x-2)重合即可.【数学理卷·2015届重庆市巴蜀中学高三12月月考（201412）】1．已知集合A={1,3,4,6,7,8}，B=｛1,2,4,5,6｝则集合A ∩B 有（）个子集 A.3 B.4 C.7 D.8【知识点】集合运算；子集的概念. A1【答案】【解析】D 解析：∵A ∩B={1,4,6}，∴A ∩B 有328=个子集，故选D. 【思路点拨】求得A ∩B ，再用公式求其子集个数.【数学理卷·2015届河北省唐山一中高三12月调研考试（201412）】1．设集合1122M x x ⎧⎫=-<<⎨⎬⎩⎭，{}2N x x x =≤，则M N =I ( )A ．1[0,)2B ．C ．1[1,)2-D ．1(,0]2-【知识点】集合及其运算A1 【答案】A【思路点拨】解一元二次不等式求得N ，再根据两个集合的交集的定义求得M∩N．【数学理卷·2015届江苏省扬州中学高三上学期质量检测（12月）（201412）】1.已知集合},2|{},1|{≤=->=x x B x x A 那么=⋃B A _________.【知识点】并集及其运算.A1【答案】【解析】R 解析：由并集的运算律可得=⋃B A R ，故答案为R 。

(2021年整理)2015年高考数学试题分类汇编常用逻辑用语

2015年高考数学试题分类汇编常用逻辑用语编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2015年高考数学试题分类汇编常用逻辑用语）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2015年高考数学试题分类汇编常用逻辑用语的全部内容。

题十一常用逻辑用语1.(15北京理科）设α,β是两个不同的平面,m 是直线且m α⊂．“m β∥"是“αβ∥”的A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件【答案】B【解析】试题分析:因为α，β是两个不同的平面，m 是直线且m α⊂．若“m β∥”，则平面、αβ可能相交也可能平行,不能推出//αβ,反过来若//αβ，m α⊂,则有m β∥，则“m β∥”是“αβ∥”的必要而不充分条件。

考点：1.空间直线与平面的位置关系；2。

充要条件。

2。

(15年安徽文科）设p ：x 〈3，q ：-1〈x 〈3,则p 是q 成立的( ）（A ）充分必要条件 (B)充分不必要条件（C ）必要不充分条件（D ）既不充分也不必要条件【答案】C【解析】试题分析：∵3: x p ，31: x q -∴p q ⇒，但p ⇒/q ，∴p 是q 成立的必要不充分条件，故选C.考点：充分必要条件的判断.3.（15年新课标1理科）设命题P ：∃n ∈N ，2n >2n ,则⌝P 为(A ）∀n ∈N ， 2n 〉2n （B ）∃ n ∈N ， 2n ≤2n（C)∀n ∈N ， 2n ≤2n （D ）∃ n ∈N ， 2n =2n【答案】C【解析】p ⌝：2,2n n N n ∀∈≤，故选C 。

十年(2015-2024)高考真题分项汇编数学专题01集合与常用逻辑用语

广东省2015届高三数学(理)一轮复习参考试题集合与常用逻辑用语Word版含答案

集合与常用逻辑用语1.【2014广东（理）高考1】已知集合{}1,0,1M =-，{}0,1,2N =，则MN =( )A .{}1,0,1-B .{}1,0,1,2-C .{}1,0,2-D .{}0,1 【答案】B2.【2013广东（理）高考1】设集合M ＝{x |x 2＋2x ＝0,x ∈R },N ＝{x |x 2－2x ＝0,x ∈R },则M ∪N ＝( ).A .{0}B .{0,2}C .{－2,0}D .{－2,0,2} 【答案】D3.【2012广东（理）高考2】设集合{1,2,3,4,5,6},{1,2,4}U M ==；则U C M =( ) A .U B .{1,3,5} C . {,,}356 D .{,,}246【答案】C4．（广东省佛山市南海区2014届普通高中高三8月质量检测理科数学试题）设集合{}{}>1,|(2)0A x x B x x x ==-<,则B A 等于（）A ．{|01}x x <<B ．{}21<<x xC ．{}20<<x x D ．{|2}x x >【答案】B 错误！未指定书签。

5错误！未指定书签。

．（广东省湛江市第二中学2014届高三理科数学8月考试题）已知集合{}9|7|＜-=x x M ,{|N x y =,且N M 、都是全集U 的子集,则下图韦恩图中阴影部分表示的集合（）A ．{}23-≤-＜x xB ．}{23-≤≤-x xC ．}{16≥x xD ．}{16＞x x【答案】B6错误！未指定书签。

．（广东省佛山市南海区2014届普通高中高三8月质量检测理科数学试题）给出下列命题:①在区间(0,)+∞上,函数1y x -=,12y x =,2(1)y x =-,3y x =中有三个是增函数;②若log 3log 30m n <<,则01n m <<<;③若函数()f x 是奇函数,则(1)f x -的图象关于点(1,0)A 对称;④已知函数233,2,()log (1),2,x x f x x x -⎧≤=⎨->⎩则方程 1()2f x =有2个实数根,其中正确命题的个数为（）A ．1B ．2C ．3D ．4【答案】C7错误！未指定书签。

2015年高考数学《新高考创新题型》之1：集合与常用逻辑用语(含精析)

之1。

集合与常用逻辑用语（含精析）一、选择题。

1．用C （A ）表示非空集合A 中的元素个数，定义A ＊B=⎩⎨⎧<-≥-)()(),()()()(),()(B C A C A C B C B C A C B C A C 。

若A ={1，2｝,B=}0)2()(|{22=++⋅+ax x ax x x ，且A ＊B=1,设实数a 的所有可能取值集合是S ，则C （S ）=（ ) A.4 B.3 C 。

2 D 。

12．下列命题:①△ABC 的三边分别为c b a ,,则该三角形是等边三角形的充要条件为bc ac ab c b a ++=++222；②数列{}n a 的前n 项和为n S ，则Bn An S n +=2是数列{}n a 为等差数列的必要不充分条件；③在△ABC 中,A ＝B 是sin A ＝sin B 的充分必要条件;④已知222111,,,,,c b a c b a 都是不等于零的实数，关于x 的不等式01121>++c x b x a 和02222>++c x b x a 的解集分别为P ，Q ，则212121c c b b a a ==是Q P =的充分必要条件，其中正确的命题是（）A ．①④B ．①②③C ．②③④D ．①③3．若存在实常数k 和b ,使得函数()F x 和()G x 对其公共定义域上的任意实数x 都满足:≥+()F x kx b 和≤+()G x kx b 恒成立，则称此直线=+y kx b 为()F x 和()G x 的“隔离直线"．已知函数=∈=<=21()(),()(0),()2ln f x x x R g x x h x e x x．有下列命题：①=-()()()F x f x g x 在∈-31(,0)2x 内单调递增;②()f x 和()g x 之间存在“隔离直线”，且b 的最小值为—4； ③()f x 和()g x 之间存在“隔离直线”，且k 的取值范围是-(4,0]; ④()f x 和()h x 之间存在唯一的“隔离直线”=-2y ex e ．其中真命题的个数有( ）A ．1个B ．2个C ．3个D ．4个4．定义一个集合A 的所有子集组成的集合叫做集合A 的幂集，记为()P A ,用()n A 表示有限集A 的元素个数，给出下列命题：①对于任意集合A ，都有()A P A ∈;②存在集合A ,使得()3n P A =⎡⎤⎣⎦; ③用∅表示空集，若AB =∅，则()()P A P B =∅；④若A B ⊆,则()()P A P B ⊆;⑤若()n A -()1n B =，则()()2n P A n P B =⨯⎡⎤⎡⎤⎣⎦⎣⎦其中正确的命题个数为（ )A 。

2015高考理科数学试题分类解析之专题一集合与常用逻辑用语.doc

专题一集合与常用逻辑用语试题部分1.【2015高考四川，理1】设集合{|(1)(2)0}A x x x =+-<，集合{|13}B x x =<<，则A B =(){|13}A x x -<< (){|11}B x x -<< (){|12}C x x <<(){|23}D x x <<2.【2015高考广东，理1】若集合{|(4)(1)0}M x x x =++=，{|(4)(1)0}N x x x =--=，则M N = A ．∅ B ．{}1,4-- C ．{}0D ．{}1,43.【2015高考新课标1，理3】设命题p ：2,2n n N n ∃∈>，则p ⌝为( )（A ）2,2n n N n ∀∈> （B ）2,2n n N n ∃∈≤ （C ）2,2n n N n ∀∈≤ （D ）2,=2n n N n ∃∈4.【2015高考陕西，理1】设集合2{|}M x x x ==，{|lg 0}N x x =≤，则M N =（）A ．[0,1]B ．(0,1]C ．[0,1)D ．(,1]-∞5.【2015高考湖北，理5】设12,,,n a a a ∈R ，3n ≥. 若p ：12,,,n a a a 成等比数列；q ：22222221212312231()()()n n n n a a a a a a a a a a a a --++++++=+++，则（）A ．p 是q 的充分条件，但不是q 的必要条件B ．p 是q 的必要条件，但不是q 的充分条件C ．p 是q 的充分必要条件D ．p 既不是q 的充分条件，也不是q 的必要条件6.【2015高考天津，理4】设x R ∈ ，则“21x -< ”是“220x x +-> ”的( )（A ）充分而不必要条件（B ）必要而不充分条件（C ）充要条件（D ）既不充分也不必要条件7.【2015高考重庆，理1】已知集合A ={}1,2,3,B ={}2,3，则（）A 、A =B B 、A ⋂B =∅C 、A ØBD 、B ØA8.【2015高考福建，理1】若集合{}234,,,A i i i i = （i 是虚数单位），{}1,1B =- ，则A B 等于 ( )A ．{}1-B ．{}1C ．{}1,1-D ．φ9.【2015高考重庆，理4】“1x >”是“12log (2)0x +<”的（）A 、充要条件B 、充分不必要条件C 、必要不充分条件D 、既不充分也不必要条件10.【2015高考新课标2，理1】已知集合21,01,2A =--｛，，｝，{}(1)(20B x x x =-+<,则A B =（）A ．{}1,0A =-B ．{}0,1C ．{}1,0,1-D ．{}0,1,211.【2015高考天津，理1】已知全集{}1,2,3,4,5,6,7,8U = ，集合{}2,3,5,6A = ，集合{}1,3,4,6,7B = ，则集合U A B =ð( )（A ）{}2,5 （B ）{}3,6 （C ）{}2,5,6 （D ）{}2,3,5,6,812.【2015高考安徽，理3】设:12,:21x p x q <<>，则p 是q 成立的（）（A ）充分不必要条件（B ）必要不充分条件（C ）充分必要条件（D ）既不充分也不必要条件13.【2015高考山东，理1】已知集合{}2430A x x x =-+<，{}24B x x =<<,则A B =（）（A ）（1，3）（B ）（1，4）（C ）（2，3）（D ）（2，4）14.【2015高考浙江，理4】命题“**,()n N f n N ∀∈∈且()f n n ≤的否定形式是（）A. **,()n N f n N ∀∈∈且()f n n >B. **,()n N f n N ∀∈∈或()f n n >C. **00,()n N f n N ∃∈∈且00()f n n >D. **00,()n N f n N ∃∈∈或00()f n n >15.【2015高考浙江，理1】已知集合2{20}P x x x =-≥，{12}Q x x =<≤，则()R P Q =ðA.[0,1)B. (0,2]C. (1,2)D. [1,2]16.【2015高考山东，理12】若“0,,tan 4x x m π⎡⎤∀∈≤⎢⎥⎣⎦”是真命题，则实数m 的最小值为 .17.【2015高考江苏，1】已知集合{}3,2,1=A ，{}5,4,2=B ，则集合B A 中元素的个数为_______.18.【2015高考湖南，理2】.设A ，B 是两个集合，则“A B A =”是“A B ⊆”的（）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件19.【2015高考上海，理1】设全集U R =．若集合{}1,2,3,4A =，{}23x x B =≤≤，则U A B =ð ．参考答案1.【解析】{|12},{|13},{|13}A x x B x x A B x x =-<<=<<∴=-<<，选A.2.【解析】因为()(){}{}|4104,1M x x x =++==--，()(){}{}|4101,4N x x x =--==，所以MN =∅，故选A ．3.【解析】p ⌝:2,2n n N n ∀∈≤，故选C.4.【解析】{}{}20,1x x x M ===，{}{}lg 001x x x x N =≤=<≤，所以[]0,1MN =，故选A ．5.6.【解析】2112113x x x -<⇔-<-<⇔<<,2202x x x +->⇔<-或1x >，所以 “21x -< ”是“220x x +-> ”的充分不必要条件，故选A.7.【解析】由于2,2,3,3,1,1A B A B A B ∈∈∈∈∈∉，故A 、B 、C 均错，D 是正确的，选D .8.【解析】由已知得{},1,,1A i i =--，故A B ={}1,1-，故选C ．9.【解析】12log (2)0211x x x +<⇔+>⇔>-，因此选B .10.【解析】由已知得{}21B x x =-<<，故{}1,0A B =-，故选A ．11.【解析】{2,5,8}U B =ð,所以{2,5}U A B =ð，故选A. 12.13.【解析】因为{}{}243013A x x x x x =-+<=<<，所以{}{}{}132423A B x x x x x x =<<<<=<<.故选：C.14.【解析】根据全称命题的否定是特称命题，可知选D.15.【解析】由题意得，)2,0(=P C R ，∴()(1,2)R P Q =ð，故选C. 16.17.【解析】{123}{245}{12345}A B ==，，，，，，，，，,，则集合B A 中元素的个数为5个.18.【解析】由题意得，A B A A B =⇒⊆，反之，A B A B A =⇒⊆ ，故为充要条件，选C.19.【答案】{}1,4【解析】因为{|32}U C B x x x =><或，所以{4,1}U A C B =。

2015高考数学(文)真题分类汇编：专题01+集合与常用逻辑用语

(A) {2}
【答案】C
(B) {1, 2}
(C) {1, 3}
(D) {1, 2,3}
【解析】由已知及交集的定义得 A B {1, 3} ，故选 C.
【考点定位】集合的运算.
【名师点睛】本题考查集合的概念和运算，本题属于基础题，注意观察的仔细.
3.【2015 高考浙江，文 3】设 a ， b 是实数，则“ a b 0 ”是“ ab 0 ”的（）
【答案】 A 【解析】由 M {x | x2 x} M {0,1}， N {x | lg x 0} N {x | 0 x 1}，
所以 M N [0,1] ，故答案选 A .
【考点定位】集合间的运算. 【名师点睛】1.本题考查以不等式为基础的集合间的运算，解不等式时注意原式意义的范
A、充分不必要条件 C、充要条件【答案】C
B、必要不充分条件 D、既不充分也不必要条件
【解析】由题易知“ x >1”可以推得“ x2 >1”， “ x2 >1”不一定得到“ x >1”，所以“ x
>1”是“ x2 >1”的充分不必要条件，故选 A.
【考点定位】充要关系【名师点睛】判断充分条件和必要条件的方法
(A) 充要条件 (C)必要不充分条件
【答案】A
(B) 充分不必要条件 (D)既不充分也不必要条件
【解析】由“ x =1 ”显然能推出“ x2 - 2x +1 = 0 ”，故条件是充分的，又由“ x2 - 2x +1 = 0 ”
可得 (x 1)2 0 x 1，所以条件也是必要的，故选 A.
【考点定位】充要条件. 【名师点睛】本题考查充要条件的概念和判断，采用推出法进行判断，本题属于基础题，注意推理的正确性.

2015年高考数学真题分类汇编：专题(01)集合与常用逻辑用语(理科)及答案

专题一集合与常用逻辑用语1.【2015高考四川，理1】设集合{|(1)(2)0}A x x x =+-<，集合{|13}B x x =<<，则A B =（）(){|13}A x x -<< (){|11}B x x -<< (){|12}C x x <<(){|23}D x x <<【答案】A【解析】{|12},{|13},{|13}A x x B x x A B x x =-<<=<<∴=-<<，选A.【考点定位】集合的基本运算.【名师点睛】集合的概念及运算一直是高考的热点，几乎是每年必考内容，属于容易题.一般是结合不等式，函数的定义域值域考查，解题的关键是结合韦恩图或数轴解答.2.【2015高考广东，理1】若集合{|(4)(1)0}M x x x =++=，{|(4)(1)0}N x x x =--=，则M N =（）A ．∅B ．{}1,4--C ．{}0D ．{}1,4【答案】A ．【解析】因为()(){}{}|4104,1M x x x =++==--，()(){}{}|4101,4N x x x =--==，所以M N =∅，故选A ．【考点定位】一元二次方程的解集，集合的基本运算.【名师点睛】本题主要考查一元二次方程的解集，有限集合的交集运算和运算求解能力，属于容易题．3.【2015高考新课标1，理3】设命题p ：2,2n n N n ∃∈>，则p ⌝为( )（A ）2,2n n N n ∀∈> （B ）2,2n n N n ∃∈≤（C ）2,2n n N n ∀∈≤ （D ）2,=2n n N n ∃∈【答案】C【解析】p ⌝:2,2n n N n ∀∈≤，故选C.【考点定位】本题主要考查特称命题的否定【名师点睛】全称命题的否定与特称命题的否定是高考考查的重点，对特称命题的否定，将存在换成任意，后边变为其否定形式，注意全称命题与特称命题否定的书写，是常规题，很好考查了学生对双基的掌握程度.4.【2015高考陕西，理1】设集合2{|}M x x x ==，{|lg 0}N x x =≤，则M N =（）A ．[0,1]B ．(0,1]C ．[0,1)D ．(,1]-∞【答案】A 【解析】{}{}20,1x x x M ===，{}{}lg 001x x x x N =≤=<≤，所以[]0,1M N =，故选A ．【考点定位】1、一元二次方程；2、对数不等式；3、集合的并集运算．【名师点晴】本题主要考查的是一元二次方程、对数不等式和集合的并集运算，属于容易题．解题时要看清楚是求“”还是求“”和要注意对数的真数大于0，否则很容易出现错误．5.【2015高考湖北，理5】设12,,,n a a a ∈R ，3n ≥. 若p ：12,,,n a a a 成等比数列； q ：22222221212312231()()()n n n n a a a a a a a a a a a a --++++++=+++，则（）A ．p 是q 的充分条件，但不是q 的必要条件B ．p 是q 的必要条件，但不是q 的充分条件C ．p 是q 的充分必要条件D ．p 既不是q 的充分条件，也不是q 的必要条件【答案】A【考点定位】等比数列的判定，柯西不等式，充分条件与必要条件.【名师点睛】判断p 是q 的什么条件，需要从两方面分析：一是由条件p 能否推得条件q ，二是由条件q 能否推得条件p .对于带有否定性的命题或比较难判断的命题，除借助集合思想把抽象、复杂问题形象化、直观化外，还可利用原命题和逆否命题、逆命题和否命题的等价性，转化为判断它的等价命题．6.【2015高考天津，理4】设x R ∈ ，则“21x -< ”是“220x x +-> ”的( )（A ）充分而不必要条件（B ）必要而不充分条件（C ）充要条件（D ）既不充分也不必要条件【答案】A 【解析】2112113x x x -<⇔-<-<⇔<<,2202x x x +->⇔<-或1x >，所以 “21x -< ”是“220x x +-> ”的充分不必要条件，故选A.【考点定位】不等式解法与充分条件、必要条件.【名师点睛】本题主要考查不等式的解法、充分条件与必要条件相关问题，将含绝对值不等式与一元二次不等式和解法、充分条件、必要条件、充要条件相关的问题联系在起来，体现综合应用数学知识解决问题的能力，是基础题7.【2015高考重庆，理1】已知集合A ={}1,2,3,B ={}2,3，则（）A 、A =B B 、A ⋂B =∅C 、A ØBD 、B ØA 【答案】D【解析】由于2,2,3,3,1,1A B A B A B ∈∈∈∈∈∉，故A 、B 、C 均错，D 是正确的，选D .【考点定位】本题考查子集的概念，考查学生对基础知识的掌握程度.【名师点晴】考查集合的关系，涉及集合的相等.集合的交集运算，子集等概念，是送分题.8.【2015高考福建，理1】若集合{}234,,,A i i i i = （i 是虚数单位），{}1,1B =- ，则A B 等于 ( )A ．{}1-B ．{}1C ．{}1,1-D ．φ【答案】C【解析】由已知得{},1,,1A i i =--，故A B ={}1,1-，故选C ．【考点定位】1、复数的概念；2、集合的运算．【名师点睛】本题考查复数的概念和集合的运算，利用21i =-和交集的定义求解，属于基础题，要注意运算准确度．9.【2015高考重庆，理4】“1x >”是“12log (2)0x +<”的（）A 、充要条件B 、充分不必要条件C 、必要不充分条件D 、既不充分也不必要条件【答案】B 【解析】12log (2)0211x x x +<⇔+>⇔>-，因此选B .【考点定位】充分必要条件.【名师点晴】本题把充分必要条件与对数不等式结合在一起，既考查了对数函数的性质，又考查了充分必要条件的判断，从本题可知我们可能用集合的观点看充分条件、必要条件：A ＝{x |x 满足条件p }，B ＝{x |x 满足条件q }，(1)如果A ⊆B ，那么p 是q 的充分不必要条件；(2)如果B ⊆A ，那么p 是q 的必要不充分条件；(3)如果A ＝B ，那么p 是q 的充要条件；(4)如果A B ⊂≠，且B A ⊂≠，那么p 是q 的既不充分也不必要条件．本题易错点在于解对数不等式时没有考虑对数的定义域.10.【2015高考新课标2，理1】已知集合21,01,2A =--｛，，｝，{}(1)(20B x x x =-+<,则A B =（）A ．{}1,0A =-B ．{}0,1C ．{}1,0,1-D ．{}0,1,2【答案】A 【解析】由已知得{}21B x x =-<<，故{}1,0AB =-，故选A ．【考点定位】集合的运算．【名师点睛】本题考查一元二次不等式解法和集合运算，要求运算准确，属于基础题．11.【2015高考天津，理1】已知全集{}1,2,3,4,5,6,7,8U = ，集合{}2,3,5,6A = ，集合{}1,3,4,6,7B = ，则集合U A B =ð( )（A ）{}2,5 （B ）{}3,6 （C ）{}2,5,6 （D ）{}2,3,5,6,8【答案】A【解析】{2,5,8}U B =ð,所以{2,5}U AB =ð，故选A.【考点定位】集合的运算.【名师点睛】本题主要考查集合的运算，涉及全集、补集、交集相关概念和求补集、交集的运算,是基础题.12.【2015高考安徽，理3】设:12,:21x p x q <<>，则p 是q 成立的（）（A ）充分不必要条件（B ）必要不充分条件（C ）充分必要条件（D ）既不充分也不必要条件【答案】A【考点定位】1.指数运算；2.充要条件的概念.【名师点睛】对于指对数运算问题，需要记住常见的等式关系，如0112,22,1log ,0log 1a a a ====，进而转化成同底的问题进行计算；充要关系的判断问题，可以分为由“:12p x <<”推证“:0q x >”以及由“:0q x >”推证“:12p x <<”.13.【2015高考山东，理1】已知集合{}2430A x x x =-+<，{}24B x x =<<,则A B =（）（A ）（1，3）（B ）（1，4）（C ）（2，3）（D ）（2，4）【答案】C 【解析】因为{}{}243013A x x x x x =-+<=<<，所以{}{}{}132423A B x x x x x x =<<<<=<<.故选：C.【考点定位】1、一元二次不等式；2、集合的运算.【名师点睛】本题考查集合的概念与运算，利用解一元二次不等式的解法化简集合并求两集合的交集，本题属基础题，要求学生最基本的算运求解能力.14.【2015高考浙江，理4】命题“**,()n N f n N ∀∈∈且()f n n ≤的否定形式是（）A. **,()n N f n N ∀∈∈且()f n n >B. **,()n N f n N ∀∈∈或()f n n >C. **00,()n N f n N ∃∈∈且00()f n n >D. **00,()n N f n N ∃∈∈或00()f n n >【答案】D.【解析】根据全称命题的否定是特称命题，可知选D.【考点定位】命题的否定【名师点睛】本题主要考查了全称命题的否定等知识点，属于容易题，全称(存在性)命题的否定与一般命题的否定有着一定的区别，全称(存在性)命题的否定是将其全称量词改为存在量词(或把存在量词改为全称量词)，并把结论否定；而一般命题的否定则是直接否定结论即可，全称量词与特称量词的意义，是今年考试说明中新增的内容，在后续的复习时应予以关注.15.【2015高考浙江，理1】已知集合2{20}P x x x =-≥，{12}Q x x =<≤，则()R P Q =ð（）A.[0,1)B. (0,2]C. (1,2)D. [1,2]【答案】C.【解析】由题意得，)2,0(=P C R ，∴()(1,2)R P Q =ð，故选C.【考点定位】1.解一元二次不等式；2.集合的运算.【名师点睛】本题主要考查了解一元二次不等式，求集合的补集与交集，属于容易题，在解题过程中要注意在求补集与交集时要考虑端点是否可以取到，这是一个易错点，同时将不等式与集合融合，体现了知识点之间的交汇.16.【2015高考山东，理12】若“0,,tan 4x x m π⎡⎤∀∈≤⎢⎥⎣⎦”是真命题，则实数m 的最小值为 .【答案】1【考点定位】1、命题；2、正切函数的性质.【名师点睛】本题涉及到全称命题、正切函数的性质、不等式恒成立问题等多个知识点，意在考查学生综合利用所学知识解决问题的能力，注意等价转化的思想的应用，此题属中档题.17.【2015高考江苏，1】已知集合{}3,2,1=A ，{}5,4,2=B ，则集合B A 中元素的个数为_______.【答案】5【解析】{123}{245}{12345}A B ==，，，，，，，，，,，则集合B A 中元素的个数为5个.【考点定位】集合运算【名师点晴】研究集合问题，一定要抓住元素，看元素应满足的属性.研究两集合的关系时，关键是将两集合的关系转化为元素间的关系，本题实质求满足属于集合A 或属于集合B 的元素的个数. 本题需注意检验集合的元素是否满足互异性，否则容易出错．18.【2015高考湖南，理2】.设A ，B 是两个集合，则“A B A =”是“A B ⊆”的（）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】C.【解析】试题分析：由题意得，AB A A B =⇒⊆，反之，A B A B A =⇒⊆ ，故为充要条件，选C.【考点定位】1.集合的关系；2.充分必要条件.【名师点睛】本题主要考查了集合的关系与充分必要条件，属于容易题，高考强调集合作为工具与其他知识点的结合，解题的关键是利用韦恩图或者数轴求解，充分，必要条件的判断性问题首要分清条件和结论，然后找出条件和结论之间的推出或包含关系.19.【2015高考上海，理1】设全集U R =．若集合{}1,2,3,4A =，{}23x x B =≤≤，则U A B =ð ．【答案】{}1,4【解析】因为{|32}U C B x x x =><或，所以{4,1}U A C B =【考点定位】集合运算【名师点睛】研究集合问题，一定要抓住元素，看元素应满足的属性.研究两集合的关系时，关键是将两集合的关系转化为元素间的关系，本题实质求满足属于集合A 或不属于集合B 的元素的集合. 本题需注意两集合一个是有限集，一个是无限集，按有限集逐一验证为妥。

2015年高考试题分类汇编(常用逻辑用语)

2015年高考试题分类汇编（常用逻辑用语）考点1 简单的命题1.（2015·山东卷·理科）若m R ∈, 如题“0m >,则方程20x x m +-=有实根”的逆否命题是A.若方程20x x m +-=有实根，则0m >B.若方程20x x m +-=有实根，则0m ≤C.若方程20x x m +-=没有实根，则0m >D.若方程20x x m +-=没有实根，则0m ≤2.（2015·广东卷·文科）若直线1l 和2l 是异面直线，1l 在平面α内，2l 在平面β内，l 是平面α与平面β的交线，则下列命题正确的是A ．l 至少与1l ，2l 中的一条相交B ．l 与1l ，2l 都相交C ．l 至多与1l ，2l 中的一条相交D ．l 与1l ，2l 都不相交3.（2015·山东卷·理科）若“[0,]4x π∀∈，tan x m ≤”是真命题，则实数m 的最小值为 .考点2 充分、必要条件1.（2015·北京卷·理科）设,A B 是两个集合，则“A B A =”是“A B ⊆”的A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件2.（2015·北京卷·理科）设,αβ是两个不同的平面，m 是直线且m α⊂. “m β∥”是“αβ∥” 的A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件3.（2015·北京卷·理科）若,l m 是两条不同的直线，m 垂直于平面α，则“l m ⊥”是“//l α”的A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件 4.（2015·北京卷·文科）设a r ，b r 是非零向量，“a b a b ⋅=r r r r ”是“a r //b r ”的A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件5.（2015·陕西卷·文理科）sin cos αα=“”是cos 20α=“”的A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件6.（2015·福建卷·文科）“对任意(0,)2x π∈，sin cos k x x x <”是“1k <”的 A.充分而不必要条件 B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件7.（2015·重庆卷·文科）“1x =”是“2210x x -+=”的A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件8.（2015·天津卷·理科）设x R ∈，则“21x -<”是“220x x +->”的A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件9.（2015·天津卷·文科）设R x ∈，则“12x <<”是“|2|1x -<”的A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件10.（2015·重庆卷·理科）“0x >”是“12(2)0x log +<”的A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件11.（2015·四川卷·理科）设,a b 都是不等于1的正数，则“333a b >>”是 “log 3log 3a b <”的A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件12.（2015·四川卷·文科）设,a b 为正实数，则“1a b >>”是“22log log 0a b >>”的A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件13.（2015·安徽卷·理科）设p ：12x <<，q ：21x >，则p 是q 成立的A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件14.（2015·安徽卷·文科）设p ：3x <，q ：13x -<<，则p 是q 成立的A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件15.（2015·湖南卷·文科）设x R ∈，则“1x >”是“31x >”的A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件16.（2015·浙江卷·文科）设a ，b 是实数，则“0a b +>”是“0ab >”的A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件考点3 全称命题、特称命题1.（2015·全国卷Ⅰ·理科）设命题P ：n N ∃∈，22n n >，则p ⌝为A.n N ∀∈, 22n n >B.n N ∃∈，22n n ≤C.n N ∀∈，22n n ≤D.n N ∀∈，22n n =2.（2015·浙江卷·理科）命题“任意*n N ∈，*()f n N ∈且()f n n ≤的否定形式是A.任意*n N ∈，*()f n N ∉且()f n n >B.任意*n N ∈，*()f n N ∉或()f n n >C.存在*0n N ∈，*()f n N ∉且00()f n n >D.存在*0n N ∈，*()f n N ∉或00()f n n >3.（2015·湖北卷·文科）命题“存在0(0,)x ∈+∞，00ln 1x x =-”的否定是A ．任意(0,)x ∈+∞，ln 1x x ≠-B ．任意(0,)x ∉+∞，ln 1x x =-C ．存在0(0,)x ∈+∞，00ln 1x x ≠-D ．存在0(0,)x ∉+∞，00ln 1x x =-。

【名师伴你行】2015届高考数学二轮复习集合与常用逻辑用语提能专训

提能专训(五) 集合与常用逻辑用语A 组一、选择题1．(2014·某某第二次诊断)已知集合S ＝{1,2}，集合T ＝{x |(x －1)(x －3)＝0}，那么S ∪T ＝( )A ．∅B ．{1}C ．{1,2}D ．{1,2,3} [答案] D[解析] 依题意得，T ＝{1,3}，S ∪T ＝{1,2,3}，故选D.2．(2014·西城区期末)设集合A ＝{x |0＜x ＜2}，B ＝{x ||x |≤1}，则集合A ∩B ＝( ) A ．(0,1) B ．(0,1] C ．(1,2) D ．[1,2) [答案] B[解析] 由|x |≤1，得－1≤x ≤1，即B ＝{x |－1≤x ≤1}，所以A ∩B ＝{x |0＜x ≤1}．3．(2014·某某十校联考)已知全集U ＝R ，集合A ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ＋2x ≤0，则集合∁U A 等于( ) A ．{x |x ＜－2或x ＞0} B ．{x |x ≤－2或x ＞0} C ．{x |x ＜－2或x ≥0} D．{x |x ≤－2或x ≥0} [答案] C [解析]∵A ＝⎩⎨⎧x ⎪⎪⎪⎭⎬⎫x ＋2x ≤0＝{x |－2≤x ＜0}，∴∁U A ＝{x |x ＜－2或x ≥0}，故选C.4．(2014·某某中学二调)已知R 是实数集，M ＝⎩⎨⎧x ⎪⎪⎪⎭⎬⎫2x ＜1，N ＝{y |y ＝x －1＋1}，则N ∩(∁R M )＝( )A ．(1,2)B ．[0,2]C ．∅D ．[1,2] [答案] D[解析]∵2x ＜1，∴x －2x＞0，∴x ＜0或x ＞2，∴M ＝{x |x ＜0或x ＞2}，∴∁R M ＝{x |0≤x ≤2}．∵y ＝x －1＋1，∴y ≥1，∴N ＝{y |y ≥1}，∴N ∩∁R M ＝[1,2]，故选D.5．(2014·某某质检一)已知集合A ＝{x |x ＞2}，B ＝{x |x ＜2m }且A ⊆∁R B ，那么m 的值可以是( )A ．1B ．2C ．3D ．4 [答案] A[解析] 由B ＝{x |x ＜2m }，得∁R B ＝{x |x ≥2m }，∵A ⊆∁R B ，∴2m ≤2，∴m ≤1，故选A. 6．(2014·某某模拟)已知集合A ＝{x ||x －1|＜2}，B ＝{x |y ＝lg(x 2＋x )}，设U ＝R ，则A ∩(∁UB )等于( )A ．[3，＋∞) B．(－1,0] C ．(3，＋∞) D．[－1,0] [答案] B[解析] 因为x 2＋x ＞0，所以x ＞0或x ＜－1，所以∁U B ＝[－1,0]，又A ＝(－1,3)，所以A ∩(∁U B )＝(－1,0]．7．(2014·某某八校联考)设全集U ＝R ，A ＝{x |2x (x －2)＜1}，B ＝{x |y ＝ln(1－x )}，则图中阴影部分表示的集合为( )A ．{x |x ≥1} B．{x |x ≤1} C ．{x |0＜x ≤1} D．{x |1≤x ＜2} [答案] D[解析] 令x (x －2)＜0得0＜x ＜2，即A ＝(0,2)；令1－x ＞0得x ＜1，即B ＝(－∞，1)，因此图中阴影部分表示的集合为A ∩(∁U B )＝[1,2)，故选D.8．(2014·某某模拟三)已知集合M ＝(x ，y )⎪⎪⎪x29＋y 24＝1，N ＝{(x ，y )|y ＝k (x －b )}，若∃k ∈R ，使得M ∩N ＝∅成立，则实数b 的取值X 围是( )A ．[－3,3]B ．(－∞，－3)∪(3，＋∞)C ．[－2,2]D ．(－∞，－2)∪(2，＋∞) [答案] B[解析] 集合M 表示椭圆上的点集，集合N 表示过点(b,0)的直线的点集，∃k ∈R ，使得M ∩N ＝∅成立，即表示存在过定点(b,0)的直线与椭圆没有交点，即定点(b,0)在椭圆外面，故b 29＋0＞1，解得b ＞3或b ＜－3，故选B. 9．(2014·某某一模)给出如下四个叙述： ①若“p 且q ”为假命题，则p ，q 均为假命题；②命题“若a >b ，则2a >2b －1”的否命题为“若a ≤b ，则2a ≤2b－1”； ③“∀x ∈R ，x 2＋1≥1”的否定是“∃x ∈R ，x 2＋1≤1”； ④在△ABC 中，“A >B ”是“sin A >sin B ”的充要条件．其中叙述不正确的个数是( ) A ．4 B ．3 C ．2 D ．1 [答案] C[解析]①错，因为p ，q 只要有一假即可；③错，因为其否定是“∃x ∈R ，x 2＋1<1”．故选C.10．(2014·某某十三校调研)集合S ＝{(x ，y ，z )|x ，y ，z ∈N *，且x ＜y ＜z ，y ＜z ＜x ，z ＜x ＜y 恰有一个成立}，若(x ，y ，z )∈S ，且(z ，w ，x )∈S ，则下列选项正确的是( )A ．(y ，z ，w )∈S ，(x ，y ，w )∉SB ．(y ，z ，w )∈S ，(x ，y ，w )∈SC ．(y ，z ，w )∉S ，(x ，y ，w )∈SD ．(y ，z ，w )∉S ，(x ，y ，w )∉S [答案] B[解析] 因为(x ，y ，z )∈S ，所以x ＜y ＜z 或y ＜z ＜x 或z ＜x ＜y ；又因为(z ，w ，x )∈S ，所以z ＜w ＜x 或w ＜x ＜z 或x ＜z ＜w ；两者结合有w ＜x ＜y ＜z 或x ＜y ＜z ＜w 或y ＜z ＜w＜x 或z ＜w ＜x ＜y .同理，若(y ，z ，w )∈S ，则有y ＜z ＜w 或z ＜w ＜y 或w ＜y ＜z ；若(x ，y ，w )∈S ，则有x ＜y ＜w 或y ＜w ＜x 或w ＜x ＜y ；两者结合有x ＜y ＜z ＜w 或y ＜z ＜w ＜x 或z ＜w＜x ＜y 或w ＜x ＜y ＜z .故选B.二、填空题11．(2014·西城区期末)设M ＝{(x ，y )|F (x ，y )＝0}为平面直角坐标系xOy 内的点集，若对于任意(x 1，y 1)∈M ，存在(x 2，y 2)∈M ，使得x 1x 2＋y 1y 2<0，则称点集M 满足性质P .给出下列三个点集：①R ＝{(x ，y )|cos x －y ＝0}； ②S ＝{(x ，y )|ln x －y ＝0}； ③T ＝{(x ，y )|x 2－y 2＝1}．其中所有满足性质P 的点集的序号是________． [答案]①③[解析] 对于任意(x 1，y 1)∈M ，存在(x 2，y 2)∈M ，使得x 1x 2＋y 1y 2<0，也就是图象上任意一点(x 1，y 1)，都会在图象上存在另一点(x 2，y 2)，使这两个点与原点形成的夹角大于90°.在y ＝ln x 的图象上取点(1,0)，则不存在另一点使这两个点与原点形成的夹角大于90°，所以②不满足性质P ；画出①③的图象观察可知，①③都满足性质P ，故选①③.12．(2014·某某四校联考)已知集合U ＝{2,3，a 2＋2a －3}，A ＝{|2a －1|,2}，∁U A ＝{5}，则实数a 的值为________．[答案] 2[解析] 根据已知得⎩⎪⎨⎪⎧a 2＋2a －3＝5，|2a －1|＝3，解得a ＝2.13．(2014·某某模拟)如图所示的韦恩图中，A ，B 是非空集合，定义A *B 表示阴影部分集合，若x ，y ∈R ，A ＝{x |y ＝2x －x 2}，B ＝{y |y ＝3x，x ＞0}，则A *B ＝________.[答案] [0,1]∪(2，＋∞)[解析]∵A ＝{x |y ＝2x －x 2}＝[0,2]，B ＝{y |y ＝3x，x ＞0}＝(1，＋∞)， ∴A ∪B ＝[0，＋∞)，A ∩B ＝(1,2]， ∴A *B ＝[0,1]∪(2，＋∞)．14．(2014·某某嘉定一模)设集合A ＝{(x ，y )|(x －4)2＋y 2＝1}，B ＝{(x ，y )|(x －t )2＋(y －at ＋2)2＝1}，若存在实数t ，使得A ∩B ≠∅，则实数a 的取值X 围是________．[答案]⎣⎢⎡⎦⎥⎤0，43 [解析] 集合A 表示的是以(4,0)为圆心，以1为半径的圆，集合B 表示的是以(t ，at －2)为圆心，以1为半径的圆．A ∩B ≠∅说明这两个圆至少有一个交点，故t －42＋at －22≤1＋1＝2，即(a 2＋1)t 2－4(a ＋2)t ＋16≤0，据题意此不等式有实数解，故判别式Δ＝16(a ＋2)2－4(a 2＋1)×16≥0，即3a 2－4a ≤0，解得0≤a ≤43.15．(2014·某某徐汇、金山、松江二模)对于集合A ＝{a 1，a 2，…，a n }(n ∈N *，n ≥3)，定义集合S ＝{x |x ＝a i ＋a j,1≤i ＜j ≤n }，记集合S 中的元素个数为S (A )．若a 1，a 2，…，a n 是公差大于零的等差数列，则S (A )＝________.[答案] 2n －3[解析] 由题意，集合S 中最小项为a 1＋a 2＝2a 1＋d ，最大项为a n －1＋a n ＝2a 1＋(2n －3)d ，对任意的i (1≤i ≤2n －3)，如果i ≤n －1，则可取2a 1＋id ＝a 1＋(a 1＋id )＝a 1＋a i ＋1∈S ，若n ≤i ≤2n －3，可取2a 1＋id ＝a 1＋(n －1)d ＋a 1＋(i －n ＋1)d ＝a n ＋a i －n ＋2，显然由于n ≤i ≤2n－3，有2≤i －n ＋2≤n －1，即2a 1＋id ∈S ，所以S (A )＝2n －3.16．(2014·昌平区期末质量抽测)将含有3n 个正整数的集合M 分成元素个数相等且两两没有公共元素的三个集合A ，B ，C ，其中A ＝{a 1，a 2，…，a n }，B ＝{b 1，b 2，…，b n }，C ＝{c 1，c 2，…，}，若A ，B ，C 中的元素满足条件：c 1＜c 2＜…＜，a k ＋b k ＝c k (k ＝1,2,3，…，n )，则称M 为“完并集合”．(1)若M＝{1，x,3,4,5,6}为“完并集合”，则x的一个可能值为________．(写出一个即可)(2)对于“完并集合”M＝{1,2,3,4,5,6,7,8,9,10,11,12}，在所有符合条件的集合C中，其元素乘积最小的集合是________．[答案](1)7(或9或11)(写出一个即可)(2){6,10,11,12}[解析](1)M＝{1，x,3,4,5,6}共有6个元素，所以3个集合A，B，C中各有2个元素，因为a k＋b k＝c k，所以集合C中必含有6个元素中最大的一个．当x＜6时，由集合元素的互异性可知x＝2，此时不能满足a k＋b k＝c k，故舍去．当x＞6时，C＝{6，x}，当1＋5＝6时，3＋4＝x，此时x＝7.当C＝{5，x}时，1＋4＝5,3＋6＝x，此时x＝9.当C＝{4，x}时，1＋3＝4,5＋6＝x，此时x＝11.当集合C中另一个元素小于等于3时，不能满足a k＋b k＝c k，故舍去．所以x的可能取值为7,9,11.(2)M＝{1,2,3,4,5,6,7,8,9,10,11，12}共含有12个元素，所以集合C中含有元素4个．其中包含最大的元素12.集合C的所有可能有{8,9,10,12}，{7,9,11,12}，{6,10,11,12}．经计算可知元素乘积最小的集合是{6,10,11,12}．B组一、选择题1．(2014·某某)设a，b∈R，则“a＋b>4”是“a>2且b>2”的( )A．充分非必要条件 B．必要非充分条件C．充要条件 D．既非充分也非必要条件[答案] B[解析]若a>2且b>2，则a＋b>4，但当a＝4，b＝1时也有a＋b>4，故选B.2．(2014·某某综合检测)命题“对任意x∈R，都有x3＞x2”的否定是( )A．存在x0∈R，使得x30＞x20B．不存在x0∈R，使得x30＞x20C．存在x0∈R，使得x30≤x20D．对任意x∈R，都有x3≤x2[答案] C[解析]全称命题的否定是特称命题，易得命题“对任意x∈R，都有x3＞x2”的否定是“存在x0∈R，使得x30≤x20”，故选C.3．(2014·某某七市联考)下列说法错误的是( )A．命题“若x2－5x＋6＝0，则x＝2”的逆否命题是“若x≠2，则x2－5x＋6≠0”B．已知命题p和q，若p∨q为假命题，则命题p与q中必一真一假C ．若x ，y ∈R ，则“x ＝y ”是“xy ≥⎝⎛⎭⎪⎫x ＋y 22”的充要条件D ．若命题p ：∃x 0∈R ，x 20＋x 0＋1＜0，则綈p ：∀x ∈R ，x 2＋x ＋1≥0 [答案] B[解析] 对于B 选项，若p ∨q 为假命题，则p ，q 均为假命题，所以B 错误，故选B. 4．(2014·某某二诊)设命题p ：∃α0，β0∈R ，cos(α0＋β0)＝cos α0＋cos β0；命题q ：∀x ，y ∈R ，且x ≠π2＋k π，y ≠π2＋k π，k ∈Z ，若x ＞y ，则tan x ＞tan y ．则下列命题中真命题是( )A ．p ∧qB ．p ∧(綈q )C ．(綈p )∧qD ．(綈p )∧(綈q ) [答案] B[解析] 当α0＝3π4，β0＝－π4时，命题p 成立，所以命题p 为真命题；当x ，y 不在同一个单调区间内时命题q 不成立，命题q 为假命题．故p ∧(綈q )为真命题．5．(2014·海淀区统考)在数列{a n }中，“a n ＝2a n －1，n ＝2,3,4，…”是“{a n }是公比为2的等比数列”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件 [答案] B[解析] 当a n ＝0时，也有a n ＝2a n －1，n ＝2,3,4，…，但{a n }是等差数列，不是等比数列，因此充分性不成立．当{a n }是公比为2的等比数列时，有a na n －1＝2，n ＝2,3,4，…，即a n ＝2a n －1，n ＝2,3,4，…，所以必要性成立．故选B.6．(2014·某某二模)命题p 为：抛物线x 2＝4y 的焦点坐标为(0,1)；命题q 为：“a ＝3”是“直线ax ＋2y ＝0与直线2x －3y ＝3垂直”的充要条件．则以下结论正确的是( )A ．p 或q 为真命题B ．p 且q 为假命题C ．p 且綈q 为真命题D ．綈p 或q 为假命题 [答案] A[解析]p 为真；2a －6＝0，a ＝3，∴q 为真，则p 或q 为真．7．(2014·某某重点中学联考)给出下列命题，其中真命题的个数是( ) ①存在x 0∈R ，使得sin x 0＋cos x 0＝2sin 7π24成立；②对于任意的三个平面向量a ，b ，c ，总有(a·b )·c ＝a·(b·c )成立； ③相关系数r (|r |≤1)，|r |值越大，变量之间的线性相关程度越高．A ．0B ．1C ．2D ．3 [答案] B[解析]∵π4＜7π24＜π3，∴2＜2sin 7π24＜ 3.而sin x 0＋cos x 0＝2sin ⎝⎛⎭⎪⎫x 0＋π4≤2， ∴①是假命题，向量的数量积不满足结合律，∴②是假命题，③是真命题．8．(2014·某某中学二调)给定命题p ：函数y ＝ln[(1－x )(1＋x )]为偶函数；命题q ：函数y ＝e x－1e x ＋1为偶函数，下列说法正确的是( )A ．p ∨q 是假命题B ．(綈p )∧q 是假命题C ．p ∧q 是真命题D ．(綈p )∨q 是真命题 [答案] B[解析] 对于命题p ：y ＝f (x )＝ln[(1－x )(1＋x )]，令(1－x )(1＋x )＞0，得－1＜x ＜1，∴函数f (x )的定义域为(－1,1)，关于原点对称，∵f (－x )＝ln[(1＋x )(1－x )]＝f (x )，∴函数f (x )为偶函数，∴命题p 为真命题；对于命题q ：y ＝f (x )＝e x－1e x ＋1，函数f (x )的定义域为R ，关于原点对称，∵f (－x )＝e －x －1e －x ＋1＝1e x －11ex ＋1＝1－ex1＋ex ＝－f (x )，∴函数f (x )为奇函数，∴命题q 为假命题，∴(綈p )∧q 是假命题，故选B. 9．(2014·东北三省二模)已知p ：x ≥k ，q ：3x ＋1＜1，如果p 是q 的充分不必要条件，则k 的取值X 围是( )A ．[2，＋∞) B．(2，＋∞) C．[1，＋∞) D ．(－∞，－1] [答案] A [解析]q ：3x ＋1＜1⇒3x ＋1－1＜0⇒2－x x ＋1＜0⇒(x －2)·(x ＋1)＞0⇒x ＜－1或x ＞2.因为p 是q 的充分不必要条件，所以k ≥2，故选A.10．(2014·某某二模)下列说法正确的是( )A ．命题“存在x 0∈R ，x 20＋x 0＋2 013＞0”的否定是“任意x ∈R ，x 2＋x ＋2 013＜0” B ．两个三角形全等是这两个三角形面积相等的必要条件 C ．函数f (x )＝1x在其定义域上是减函数D ．给定命题p ，q ，若“p 且q ”是真命题，则綈p 是假命题 [答案] D[解析] 对于A ，特称命题的否定为全称命题，所以命题“存在x 0∈R ，x 20＋x 0＋2 013＞0”的否定是“任意x ∈R ，x 2＋x ＋2 013≤0”，故A 不正确．对于B ，两个三角形全等，则这两个三角形面积相等；反之，不然．即两个三角形全等是这两个三角形面积相等的充分不必要条件，故B 不正确．对于C ，函数f (x )＝1x在(－∞，0)，(0，＋∞)上分别是减函数，但在定义域(－∞，0)∪(0，＋∞)内既不是增函数，也不是减函数，如取x 1＝－1，x 2＝1，有x 1＜x 2，且f (x 1)＝－1，f (x 2)＝1，则f (x 1)＜f (x 2)，所以函数f (x )＝1x在其定义域上不是减函数，故C 不正确．对于D ，因为“p 且q ”是真命题，则p ，q 都是真命题，所以綈p 是假命题，故D 正确．二、填空题11．(2014·某某重点中学统一考试)已知r (x )：sin x ＋cos x ＞m ；s (x )：x 2＋mx ＋1＞0.如果∀x ∈R ，r (x )与s (x )有且仅有一个是真命题，则实数m 的取值X 围是________．[答案] (－∞，－2]∪[－2，2)[解析] 由sin x ＋cos x ＝2sin ⎝⎛⎭⎪⎫x ＋π4，故sin x ＋cos x 的最小值为－2，若∀x∈R 时，命题r (x )为真命题，则m ＜－ 2.若命题s (x )为真命题，即∀x ∈R ，不等式x 2＋mx ＋1＞0恒成立，则Δ＝m 2－4＜0，解得－2＜m ＜2.若命题r (x )为真命题，命题s (x )为假命题，则m ≤－2；若命题r (x )为假命题，命题s (x )为真命题，则－2≤m ＜2.综上所述，实数m 的取值X 围是(－∞，－2]∪[－2，2)．12．(2014·某某大学附属中学一模)设a 为实常数，y ＝f (x )是定义在R 上的奇函数，当x ＜0时，f (x )＝9x ＋a 2x＋7.若“∃x ∈[0，＋∞)，f (x )＜a ＋1”是假命题，则a 的取值X围为________．[答案]⎝⎛⎦⎥⎤－∞，－87 [解析]y ＝f (x )是定义在R 上的奇函数，故可求解析式为f (x )＝⎩⎪⎨⎪⎧9x ＋a 2x－7，x ＞0，0，x ＝0，9x ＋a 2x ＋7，x ＜0.又“∃x ≥0，f (x )＜a ＋1”是假命题，则∀x ≥0，f (x )≥a ＋1是真命题．①当x ＝0时，0≥a ＋1，解得a ≤－1；②当x ＞0时，9x ＋a 2x －7≥a ＋1，结合基本不等式有6|a |－7≥a ＋1，解得a ≥85或a ≤－87. ①②取交集，得a 的取值X 围是a ≤－87.13．(2014·某某一模)已知下列命题：①设m 为直线，α，β为平面，且m ⊥β，则“m ∥α”是“α⊥β”的充要条件；②⎝⎛⎭⎪⎫x 3＋1x 5的展开式中含x 3的项的系数为60； ③设随机变量ξ～N (0,1)，若P (ξ≥2)＝p ，则P (－2＜ξ＜0)＝12－p;④若不等式|x ＋3|＋|x －2|≥2m ＋1恒成立，则m 的取值X 围是(－∞，2)．其中真命题的序号是________．(写出所有真命题的序号) [答案]③[解析]①因为m ⊥β，m ∥α⇒α⊥β成立，但由α⊥β，m ⊥β，可得到m ∥α或m ⊂α，故该命题为假命题；②⎝⎛⎭⎪⎫x 3＋1x 5的展开式中第r ＋1项T r ＋1＝C r 5x 15－4r，令15－4r ＝3，解得r ＝3，含x 3的项的系数为10，故该命题是假命题；③由随机变量ξ～N (0,1)，若P (ξ≥2)＝p ，则P (ξ≤－2)＝P (ξ≥2)＝p ，所以，P (－2＜ξ＜2)＝1－2p ，P (－2＜ξ＜0)＝P (0＜ξ＜2)＝12－p ，该命题是真命题；④因|x ＋3|＋|x －2|≥|x ＋3－(x －2)|＝5，故2m ＋1≤5，解得m ≤2，④是假命题．14．(2014·某某质检二)△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，下列命题正确的是________．(写出所有正确命题的编号)①总存在某内角α，使cos α≥12；②若A sin B ＞B sin A ，则B ＞A ；③存在某钝角△ABC ，有tan A ＋tan B ＋tan C ＞0; ④若2aBC →＋bCA →＋cAB →＝0，则△ABC 的最小角小于π6；⑤若a ＜tb (0＜t ≤1)，则A ＜tB . [答案]①④⑤ [解析]①对；②设f (x )＝sin x x ，0<x <π，f ′(x )＝x cos x －sin xx2，故②错；③tan A ＋tan B ＋tan C ＝tan A ·tan B ·tan C <0，③错； ④2aBC →＋bCA →＋cAB → ＝2a (BA →＋AC →)＋bCA →＋cAB → ＝(2a －b )AC →＋(c －2a )AB →＝0，∴⎩⎪⎨⎪⎧2a －b ＝0，c －2a ＝0，∴b ＝c ＝2a ，cos A ＝78>32，故④对；⑤对．15．(2014·某某质检)给出以下命题： ①双曲线y 22－x 2＝1的渐近线方程为y ＝±2x ；②命题p ：“∀x ∈R ，sin x ＋1sin x≥2”是真命题； ③已知线性回归方程为y ^＝3＋2x ，当变量x 增加2个单位，其预报值平均增加4个单位； ④设随机变量ξ服从正态分布N (0，σ2)，若P (ξ＞1)＝0.2，则P (－1＜ξ＜0)＝0.6； ⑤已知22－4＋66－4＝2，55－4＋33－4＝2，77－4＋11－4＝2，1010－4＋－2－2－4＝2，依照以上各式的规律，得到一般性的等式为nn －4＋8－n8－n －4＝2(n ≠4)．则正确命题的序号为________．(写出所有正确命题的序号) [答案]①③⑤[解析]①正确，注意双曲线焦点在y 轴上；②错误，不符合均值不等式的使用条件；③正确；④错误，因为P (ξ＞1)＝P (ξ＜－1)＝0.2，所以P (－1＜ξ＜0)＝1－P ξ＞1－P ξ＜－12＝0.62＝0.3；⑤正确，由特殊到一般可得等式为nn －4＋8－n8－n －4＝2(n ≠4)，综上，可得命题①③⑤为真命题．16．(2014·某某调研)已知命题p ：“∀x ∈[1,2]，12x 2－ln x －a ≥0”与命题q ：“∃x∈R ，x 2＋2ax －8－6a ＝0”都是真命题，则实数a 的取值X 围是________．[答案] (－∞，－4]∪⎣⎢⎡⎦⎥⎤－2，12 [解析] 命题p ：a ≤12x 2－ln x 在x ∈[1,2]上恒成立，令f (x )＝12x 2－ln x ，f ′(x )＝x －1x＝x －1x ＋1x，当1＜x ＜2时，f ′(x )＞0，word11 / 11 ∴f (x )min ＝f (1)＝12.∴a ≤12. 命题q ：Δ＝4a 2－4(－8－6a )≥0，∴a ≥－2或a ≤－4. 综上，两个命题都是真命题，则有a ∈(－∞，－4]∪ ⎣⎢⎡⎦⎥⎤－2，12.。