材料力学-扭转1ppt课件
合集下载
材料力学-扭转

扭转角( 扭转角(ϕ):任意两截面绕轴线相对转动的角度。又称为角 位移。通常用ϕ表示。ϕB − A表示B截面相对A截面转过的角度。 剪应变( 剪应变(γ): 剪应变又叫角应变或切应变,它是两个相互垂直方 向上的微小线段在变形后夹角的改变量(以弧度表示, 角度减小时为正) O ϕ B m
A m
γ
第二节 杆受扭时的内力计算
四、圆截面的极惯性矩 Ip 和抗扭截面系数Wp
实心圆截面: 实心圆截面:
2
I p = ∫ ρ d A = ∫ ρ (2 πρ d ρ )
2
ρ
d O
dρ
A
d 2 0
= 2 π(
ρ
4
d /2
4
)
0
πd = 32
4
d A = 2 πρ d ρ
πd 3 Wp = = d / 2 16 Ip
空心圆截面: 空心圆截面:
T T = ρ max = IP IP T = WP
ρ max
Ip—截面的极惯性矩, 截面的极惯性矩,单位: 单位:m 4 , mm 4 Ip 3 3 WP —抗扭截面模量, WP = 抗扭截面模量,单位:m , mm .
ρ max
整个圆轴上——等直杆: 等直杆: τ max
Tmax = WP
三、公式的使用条件: 公式的使用条件: 1、等直的圆轴, 等直的圆轴, 2、弹性范围内工作。 弹性范围内工作。
Tmax Wp
πD 3 实心, 16 T max W = 2)设计截面尺寸: 设计截面尺寸:WP ≥ 3 P [τ ] πD (1 − α 4 ) 空心. 16 ≤ ⇒ m 3)确定外荷载: 确定外荷载: Tmax WP ⋅ [τ ]
≤
材料力学-扭转

8
从圆轴中取一微小的正六面体(单元体), 其对称两面上的剪应力构成一个力偶,因此 另两个对称面上也必存在转向相反的、由 剪应力构成的力偶。由此得出, 剪应力互等定理: 两个相互垂直的截面上,在其相交处的 剪应力成对存在,且其数值相等而符号相反, 指向或背离交线。 剪应力符号规定: 使单元体产生顺时针方向转动趋势时的剪应力为正 使单元体产生反时针方向转动趋势时的剪应力为负
§7-4 圆轴扭转时的强度计算
要使圆轴杆件扭转时不致产生破坏,应满足各横截面上的最 大剪应力小于材料的许用剪应力,而最大剪应力发生在扭矩最大 的横截面上的边缘处。设圆周半径为R,则圆轴扭转的强度条件 为:
τmax
T = R ≤ [τ ] Ip
Wp =
Ip R
把与截面尺寸和形状有关的参量归到一个参量,令 T 则有:
T ρ ρ 由此,圆轴扭转时横截面上半径为 处的剪应力为:τ ρ = Ip 4、极惯性矩 I 的计算 p πD 4
dϕ T = dX GI p
I p = ∫ ρ dA
2 A
直径为D的实心轴圆截面: I p = 空心轴圆环截面:I p =
π (D 4 − d 4 )
32
32
例:一轴AB传递的功率为Nk=7.5kw, 转速n=360r/min,轴的AC段为实心圆截面, CB段为空心圆截面,如图。已知D=3cm, d=2cm.试计算AC段横截面边缘处的剪应力 以及CB段横截面上外边缘和内边缘处的剪应力。计算扭矩、惯性矩、应力
Wp
≤ [τ ]
Wp
, 称为抗扭截面系数
Wp = 0.2D3
实心圆:
许用剪应力的确定:料 [τ ] = (0.5 ~ 0.6)[σ] 塑 材 : 性 一般取 脆 材 :τ ] = (0.8 ~1.0)[σ] 性 料 [
从圆轴中取一微小的正六面体(单元体), 其对称两面上的剪应力构成一个力偶,因此 另两个对称面上也必存在转向相反的、由 剪应力构成的力偶。由此得出, 剪应力互等定理: 两个相互垂直的截面上,在其相交处的 剪应力成对存在,且其数值相等而符号相反, 指向或背离交线。 剪应力符号规定: 使单元体产生顺时针方向转动趋势时的剪应力为正 使单元体产生反时针方向转动趋势时的剪应力为负
§7-4 圆轴扭转时的强度计算
要使圆轴杆件扭转时不致产生破坏,应满足各横截面上的最 大剪应力小于材料的许用剪应力,而最大剪应力发生在扭矩最大 的横截面上的边缘处。设圆周半径为R,则圆轴扭转的强度条件 为:
τmax
T = R ≤ [τ ] Ip
Wp =
Ip R
把与截面尺寸和形状有关的参量归到一个参量,令 T 则有:
T ρ ρ 由此,圆轴扭转时横截面上半径为 处的剪应力为:τ ρ = Ip 4、极惯性矩 I 的计算 p πD 4
dϕ T = dX GI p
I p = ∫ ρ dA
2 A
直径为D的实心轴圆截面: I p = 空心轴圆环截面:I p =
π (D 4 − d 4 )
32
32
例:一轴AB传递的功率为Nk=7.5kw, 转速n=360r/min,轴的AC段为实心圆截面, CB段为空心圆截面,如图。已知D=3cm, d=2cm.试计算AC段横截面边缘处的剪应力 以及CB段横截面上外边缘和内边缘处的剪应力。计算扭矩、惯性矩、应力
Wp
≤ [τ ]
Wp
, 称为抗扭截面系数
Wp = 0.2D3
实心圆:
许用剪应力的确定:料 [τ ] = (0.5 ~ 0.6)[σ] 塑 材 : 性 一般取 脆 材 :τ ] = (0.8 ~1.0)[σ] 性 料 [
材料力学课件 扭转

x = y
2020/3/22
17
5.3 纯剪切
剪应力互等定理:
单元体两个相互垂直的平面 上,垂至于两平面交线的剪 应力总是同时存在,且大小 相等,都指相(或都背离) 两平面的交线。
纯剪应力状态:
y
τy
d
a
τx
τx
x
dy
b
τy
z
dx
c
单元体平面上只有剪应力而无正应力,则称该单元
体为纯剪应力状态。
2020/3/22
4、扭矩图——扭转变形的内力图
➢扭矩图的作图步骤:
①先画基线(横坐标x轴),基线‖轴线; ②画纵坐标, “正在上,负在下”; ③标注正负号、值的大小及图形名称。
➢扭矩图的注意事项:
①多力偶作用时要分段求解,一律先假定为正方向;
②基线‖轴线,“正在上,负在下”,比例一致,封闭图形
③正负号标注在图形内,图形上下方相应的地方只标注轴力
19
思考题
指出下面图形的剪应变
剪应变为 α
2020/3/22
剪应变为 0
20
5.4 圆轴扭转时的应力和变形
前面推导得到:薄壁圆筒横截面 剪应力与扭矩之间的关系:
T 2R 2t
t——壁厚 R ——平均半径
τ
T
τ
剪应力沿壁厚均匀分布
2020/3/22
21
5.4 圆轴扭转时的应力和变形
一、圆截面杆受扭时横截面上的应力
值的大小,不带正负号;
④202阴0/3/2影2 线一定垂直于基线,阴影线可画可不画。
8
例题:
例5-1: 已知A轮输入功率为50kW,B、C、D轮输出功率分别 为15、15、20kW,轴的转速为300r/min,画出该轴扭矩图。
材料力学课件:扭转

B
D
C
12 3
A P
Page4
§3-6 热应力与预应力
扭转
§4-1 引言 §4-2 圆轴扭转应力
Page5
§3-6 热应力与预应力
lT=ll T
B
C
A A’
变形不受限制(静定结构),杆内未引起应力
Page6
B lT=ll T
CB
C
A’
A
A
变形受到限制(静不定结构),杆内引起应力
热应力:因温度的变化在杆件内部引起的应力 预应力:由于实际尺寸的误差在杆件内部引起的应力
各
截面的扭矩。
Page20
扭矩图:外扭力矩随杆轴线变化的情况。
M 3ml
m
x
A
B
C
D
l
l/2 l/2
T1 ( x)
x
T ml
x
2ml
例:(m:单位长度的扭力偶矩)
AB段: T1 x mx
BC段: T2 ml CD段: T3 2ml
Page21
思考:
M
M’
M’
M
(1)
M’
(2)
M’
(3)
FN3
FN1
FN2
Page9
3
1
2
3
1
2
协调方程:
l3+ l1/cos()=
l3
FN3
FN1
FN2
Page10
➢ 装配应力在工程结构中的应用
1 23
P
在准确加工、装配的情况下,2杆 的应力最大。
如果能使3根杆同时达到许用应力, 将对结构更有利。
FN1 [1 ]A FN 2 [ 2 ]A FN 3 [ 3 ]A
材料力学课件——扭转的强度与刚度计算
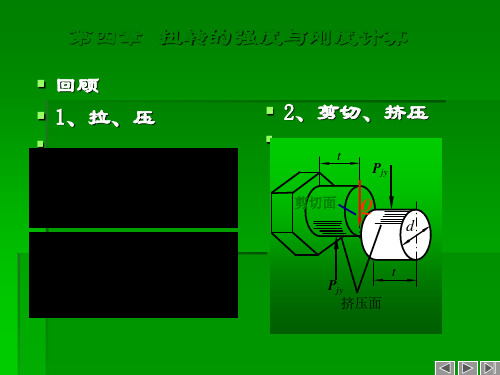
MMnMnⅢⅢMnMⅢMnDMⅢD DMD
351N· m
468N·
(+)m (-)
702N· m
解 (1)计算外力偶矩:
MA
9550 NA n
9550 36.75 300
1170N m
MB
MC
9550 NB n
9550 11 300
351N m
MD
9550 ND n
9550 14.7 300
P B mB
B
mB (a)
P
mB
B
(b)
本章主要内容
▪ 第一节 概述 ▪ 第二节 扭转时的内力 ▪ 第三节 纯剪切、剪应力互等定理、剪切胡
克定律 ▪ 第四节 圆轴扭转时的应力与变形 ▪ 第五节 圆轴扭转时的强度和刚度计算 ▪ 第六节 密圈螺旋弹簧应力及变形的计算 ▪ 第七节 非圆截面等直杆的纯扭转
扭矩
N(kW ) Me 9550 n(r / min ) (Nm)
•当N为马力 扭矩
N(Ps)
Me 7024 n(r / min )(N m)
二、扭矩 扭矩图
扭矩mn符号规定如下:按右手螺旋法则把mn 表示为矢量,当矢量方向与截面的外法线方向一
致时, mn为正;反之为负。
内力—扭矩
mn
j mn
t dy
nm
x 定理。(rocal
theorem of shear stresses )
dx
z
▪ 剪应力互等定理(Reciprocal theorem of shear stresses )
▪ 单元体上两个互垂面上剪应力的大小相等、方
向相反(共同指向交线或背离交线)
▪ 类似可证明 —— 每两个邻近边剪应力值相 等
材料力学(孙训方)PPT课件

[例3-2-1]已知:一传动轴, n =300r/min,主动轮输P1=500kW,
从动轮输出 P2=150kW,P3=150kW,P4=200kW,试绘制扭矩图。
m2
m3
m1
m4
解:①计算外力偶矩
m1
9.55P1 n
9.55500 300
A
15.9(kN m)
B
C
D
m 2 m 3 9 .5P n 5 2 9. 5 1 35 5 0 4 .0 0 7(8 k m N) m 49 .5P n 5 49. 5 3 25 0 0 6 0 0 .3(7km N)
单元体的四个侧面上只有剪应力而无正应力作用,这 种应力状态称为纯剪切应力状态。
四、剪切虎克定律:
其中:P n
— —
功率,马力(PS) 转速,转/分(rpm)
1PS=735.5N·m/s , 1kW=1.36PS
二、扭矩及扭矩图 1 扭矩:构件受扭时,横截面上的内力偶矩,记作“T”。 2 截面法求扭矩
mx 0 T m 0
m
m
T m
3 扭矩的符号规定:
x
m
T
“T”的转向与截面外法线方向满足右手螺旋法则为正, 反之为负。
m2
m3
m1
m4
A
B
C
T
– –
4.78 kNm
9.56 kNm
D
6.37 kNm
x
例 32-2已知 :m12kN m,m2 4kN m,m3
1kN m,m4 1kN m,求:各段扭矩及画扭
解:1——1:
m4 3 m3 2 m2 1 m1
M0 m1T10
T1 m1 2kNm
材料力学-第4章 扭转 ppt课件

dA
T
O
dA
23
材料力学-第4章 扭转
圆轴扭转横截面上的应力
A dA T
代入:
G
G
d dx
得到:
G d 2dA T dx A
记: IP -2dA称为圆截面的极惯性矩
A
则:圆轴扭转角的变化率 d T
dx GIP
圆截面切应力
采用右手螺旋法则,如果用四指表示扭矩的转向, 拇指的指向与截面的外法线n的方向相同时,该扭矩为 正;反之,规定扭矩为负
正扭矩
负扭矩
——保证了无论从哪一段计算,扭矩的大小和符号 都相同
12
材料力学-第4章 扭转
扭力偶矩计算与扭矩
讨论:如图受扭圆轴,m-m截面上扭矩为多少?
Me
m
2M e
m m
T Me
17
材料力学-第4章 扭转
圆轴扭转横截面上的应力
几何变形:
1. 横截面绕圆轴的轴线转动
?
主要
2. 圆轴中段的横截面缩小 几何变形特征
有剪切应变 rz 次要
3. 圆轴的长度略有增长
有轴向应变 z 次要
– 变形后,横截面仍保持为平面,其形状和大小均不
改变,半径仍为直线
– 变形后,相邻横截面的间距保持不变,相邻横截面 绕圆轴轴线转动一定的角度
外力偶矩的计算
• 工程中的传动轴,通常给出传动轴所传递的功率和转 速,而不直接给出外力偶矩的数值
• 设外力偶矩为Me,传动轴的功率为P,角速度为w,则
有(理论力学)
Me
P
w
外力偶矩Me 单位:N·m (牛顿·米) 功率为P 单位:J (焦耳)
材料力学扭转

Wt
Ip R
max
抗扭截面系数
T Wt
公式适用 条件
1.等直圆杆—只有横截面不变的圆轴,才满足 平面假设的要求。
2.最大切应力低于剪切比例极限—满足胡克定 律的要求。
如何计算截面极 惯性矩和抗扭截 面系数?
§3.4 圆轴扭转时的应力
计算截面极惯性矩和 抗扭截面系数
T
实 心 轴
D/2 ρ O
M eB M eC 4.78kN.m
M eA 15.9kN.m
2.利用截面法计算各段内的扭转
MeB MeC 2 MeA MeD
CA段:
假设T2为正,由平衡方程
T2 M eB M eC 0
B C
2
A
D
MeB
MeC
T2 M eB M eC 9.56kN.m
结果为负,说明T2为负值扭矩。
同理,可以求得距圆心为ρ处的切应变为
d dx
2.物理关系
横截面上任意点的切应变与该点到圆 心的距离ρ成正比。
由剪切胡克定律求得横截面上距圆心 为ρ处的切应力为
G
d G dx
横截面上任意点的切 应力与该点到圆心的 距离ρ成正比。
图 3.10
由切应力互等定理可知,在纵向截面和横截面上,沿半径方向的 切应力分布情况如图3.10所示。
扭转图—当作用于轴上的外力偶多于两个时,为了表示各横截
面上扭矩沿轴线变化的情况,在图中以横轴表示横截面的位置 ,纵轴表示相应截面上的扭矩,这种图线称为扭矩图。
实例:一传动轴如图所示,其转速 n = 300 r/min ,主动轮A
输入的功率为PA = 500 kW 。若不计轴承摩擦所耗的功率,三 个从动轮输出的功率分别为PB = PC = 150 kW及PD = 200 kW。 试做扭矩图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
横截面上 —
max
T IP
max
IP
T
max
T WP
Ip—截面的极惯性矩,单位:m4 , mm 4
WP
Ip
max
WP —抗扭截面模量,单位:m3, mm3.
整个圆轴上——等直杆:
max
Tm a x WP
三、公式的使用条件: 1、等直的圆轴, 2、弹性范围内工作。
30
四、圆截面的极惯性矩 Ip 和抗扭截面系数Wp
d
dx
d / dx-扭转角变化率
二)物理关系:
弹性范围内 max P
G → G
G
d
dx
方向垂直于半径。
28
三)静力关系:
T A dA
T A dA
G d 2dA dx A
I p
2dA
A
Ip
横截面对形心的极惯性矩
T
GI p
d
dxp
29
二、圆轴中τmax的确定
结论:
横截面上 0, 0 0 0
根据对称性可知剪应力沿圆周均匀分布;
t D, 可认为剪应力沿壁厚均匀分布,
且方向垂直于其半径方向。
t
D
20
3、剪应力的计算公式:
T
AdA.r0
2 0
r0
2td
r02t2
d
T
2r0 2t
薄壁圆筒横截面上的剪应力计算式
21
二、关于剪应力的若干重要性质
例题: 1、一传动轴作200r/min的匀速转动,轴上装有五个轮子。 主动轮2输入的功率为60kW,从动轮1、3、4、5依次输出的 功率为18kW、12kW、22kW和8kW。试作出该轴的扭矩图。
15
解: (一)外力偶矩 (二)求解各段内力
16
由平衡条件可解得各段内力为 :
Mn1 m1 0.86KN m Mn2 m1 m2 2.01KN m Mn3 m1 m2 m3 1.435KN m Mn4 m5 0.385KN m
负号说明与假设方向相反。
17
(三)绘扭矩图。
扭矩图
18
§5-3 纯剪切
薄壁圆筒轴的扭转
一、薄壁圆筒横截面上的应力
(壁厚
t
1 10
r0
, r0:平均半径)
1、实验:
19
2、变形规律:
'
圆周线——形状、大小、间距不变,各圆周线只是绕轴线转动了一个角度。
纵向线——倾斜了同一个角度,小方格变成了平行四边形。
11
二、扭转杆件的内力——扭矩及扭矩图
圆轴受扭时其横截面上的内力偶矩称为扭矩,用符号T 表示。
1、扭转杆件的内力(截面法)
m
m
左段:
m x
0,
T m0
T m
右段:
m x
0,
mT 0
T m
m
Tx
T
m
x
内力偶矩——扭矩 T
12
2、扭矩的符号规定:按右手螺旋法则判断。
+
T
-
13
14
3、内力图(扭矩图) 扭矩图作法:同轴力图:
阻抗力偶
Me
主动力偶
2
2、汽车方向盘的转动轴工作时受扭。
3
2、汽车方向盘的转动轴工作时受扭。
4
3、机器中的传动轴工作时受扭。
汽车传动轴
5
4、汽车离合器连接时受扭。
6
5、扳手卸轮胎
7
二、扭转的概念
受力特点:杆两端作用着大小相等、转向相反的力偶,且力 偶作用面垂直于杆的轴线。
阻抗力偶
Me
主动力偶
d
实心圆截面:
O
d
Ip
2dA
A
2 2 (2π d )
0
2π( 4
)
d/2
πd
4
4 0 32
d A 2π d
Wp
Ip d /2
πd 3 16
31
空心圆截面:
D
Ip
2 d
2π
3
d
2
d
π D4 d 4
D
32
πD4 1 4
32
D d
O
d A 2π d
Wp
Ip D/2
π
D4 d 16D
4
πD3 1 4
16
32
§5-5 扭转变形 扭转强度和刚度计算
一、 扭转强度计算
1、强度条件: max [ ]
交线。
纯剪切
23
2、剪切虎克定律
在剪应力的作用下,单 元体的直角将发生微小的
G
τ
改变,这个改变量 称为
剪应变。
当剪应力不超过材料 的剪切比例极限时,剪应
变 与剪应力τ成正比,
这个关系称为剪切胡克定 律。
G — 剪切弹性模量(GN/m2)
各向同性材料, 三个弹性常数之间的 关系:
G E
2(1 )
以及间距不变,半径仍为直线。
定性分析横截面上的应力
(1) 0 0
(2) 0 0
因为同一圆周上剪应变相同,所以同 一圆周上剪应力大小相等,并且方向 垂直于其半径方向。
26
取楔形体 O1O2ABCD 为
研究对象
tg BB' Rd
dx dx
微段扭转
变形 d
tg
bb dx
d
dx 27
mA
me
8
变形特点:杆任意两个横截面将绕杆轴线作相对转动而产生 相对角位移。这种相对角位移称为扭转角,用表示。
轴:以扭转变形为主的杆件。
9
§5-2外力偶矩的计算 扭矩和扭矩图 一、外力偶矩计算
按输入功率和转速计算
已知 轴转速-n 转/分钟 输出功率-P 千瓦 求:力偶矩Me
电机每秒输入功: W P 1000(N m s )1(s)
1、剪应力互等定理
单元体—— 从受扭的薄壁圆筒表面处截取一微小的正六面体
m
mt
φ r
L
Mz 0
d y d zd x d x d zd y 得
22
剪应力互等定理:
纯剪切
在相互垂直的
两个平面上,剪
应力必然成对存
在,且数值相等;
两者都垂直于两
个平面的交线,
方向则共同指向
各个截面上只有剪应
或共同背离这一 力没有正应力的情况称为
外力偶所做的功:
W
Me
1
Me
2
n 60
P
P
10
已知轴所传递的功率和轴的转速,则外力偶矩(N•m)
m 9549 P n
m 7024 P n
P——功率,单位为千瓦(KW) n——转速,单位为rod/min
P——功率 ,单位为马力(PS) n——转速,单位为rod/min
1PS=735.5N·m/s , 1kW=1.36PS
第五章 扭 转
§5-1 扭转概念和工程实例 §5-2 外力偶矩的计算 扭矩和扭矩图 §5-3 纯剪切 §5-4 圆轴扭转时横截面上的应力 §5-5 扭转变形 扭转强度和刚度计算 §5-6 扭转静不定问题 §5-7 矩形截面杆的自由扭转
1
§5-1 扭转概念和工程实例
一、扭转的工程实例 1、螺丝刀杆工作时受扭。
24
§5-4 圆轴扭转时横截面上的应力
一、圆轴扭转时横截面上的应力 一)、几何关系: 1、实验:
25
观察变形规律:
圆周线——形状、大小、间距不变,各圆周线只是绕轴线转动 了一个不同的角度。
纵向线——倾斜了同一个角度,小方格变成了平行四边形。
扭转平面假设:变形前的横截面,变形后仍为平面,且形状 、大小
