【精品】PPT课件 杭州绿城育华学校 初二(3)班 张林文君 制作
2015-2家长会课件模板
4、（3）加大了学校教研力度。积极参加、 杭州市、西湖区等上级部门的教研会议，定 期召开睿励项目教师会议、理科创新班教师 会议，带领骨干教师参加全国培训等。学校 教师多次在各级各类教研活动中做主题报告， 并多次在各级各类比赛中获奖……(教务处添 加）
4、（4）每学期多次举办“班主任心理成长工 作坊”，关注了班主任心理健康和内心成长， 指导了班主任关注学生的心理健康，提升了班 主任整体管理水平。本学期请了杭州会森教育 集团的“正面管教”团队，他们利用自己的心 理学专业知识在初一（5）班指导了班会课的 开展，并在全校公开，以利于全校所有教师的 成长。
平等交流，精诚合作，
共同创造孩子美好的明天！
感谢您的光临！
本班情况：
班级任课教师情况介绍
语文、数学、英语、科学等。
（老师的荣誉、成绩、联系方式等，切忌过 高评价，但也要为后面任课教师的出场做好 铺垫）
班级管理情况：
班干部名单 班级管理思路及在此思路下班级目前的状 态，同学们在各类活动中的出色表现、取 得的成绩等
期中考试情况分析：
对本班总分及各科考的好的同学进行表扬； 对进步大的同学进行表扬； 表扬时请结合学生在校的学习表现，将优秀学生的学 习特点进行归纳； 力争多表扬，少批评。
考得不好的学生在平时表现的共性分析（如自觉性欠 缺，需要老师盯；兴奋点不在学习上；紧迫感不强、 自信心不足；心理负担重，考试焦虑过度等） 对考的不好的学生不要在大会上批评，可以会后留下 来和家长单独交流。
班主任针对以上情况将要采取的措施：
需要家长配合的方面：
1、学生的心理调适与辅导
切实解决学生心理问题，树立信心，轻装上阵；
正确分析孩子目前现状， 找到孩子身上的闪光点，
寻找教育的突破口，
浙教版初中数学八年级上册 1.6 尺规作图 课件 _2优秀课件PPT
B D
B` D`
O
A C
O`
C`
A`
（1）以O为圆心，适当长为半径画弧，交OA于C点，交OB于D点。
（2）画射线O′A′
（3）以O′为圆心，OC长为半径画弧，交O′A′于C′点 。
（4）以C′为圆心，DC长为半径画弧，交弧于D′点 。
（5）过D′做射线O′A′
则∠A′O′B′为所求作的角
请选择一种你喜欢的方法画一画. A
B
5厘米
C
本节课你学到了什么?
画一个角等于已知角，画一条线段垂直 平分线。
画一个三角形等于另一个三角形。
一定要记住！！！
还要注意： 1. 过点x、点x作直线；或作直线
xx，射线xx。 2. 连接两点x、x；或连接xx。 3. 在xx上截取xx=xx。 4. 以点x为圆心，xx为半径作圆
四、拓展园1
有 A, B ,C 三农户准备一起挖一口井， 使它到三农户家的距离相等.这口井应挖在 何处？请在图中标出井的位置，并说明理由.
A
C
B
四、拓展园2
在ABC中,BC＝5厘米,AC＝3厘米, AB＝3．5厘米,∠B ＝35°,∠C＝45°,请你选择适当数据,画与△ABC全等的 三角形，说一说你有几种办法呢？
数 学 八年级（上 册） 义务教育教科书 1.6学科网 尺规作图
一、知识园
据说，为了显示谁的逻辑能力更强，古 希腊人限制了几何作图的工具，结果一些普 通的画图题让数学家思索了2000多年。尺 规作图特有的魅力，使无数人沉湎其中。
尺规作图：在几何作图中，我们把用没 有刻度的直尺和圆规作图。
尺：只用来画线 规：只用来画弧
作△ABC，使∠A ＝ ，∠B = AB = a.
【精品】2016年浙江省杭州市上城区绿城育华中学八年级上学期期中物理试卷与答案
2015-2016学年浙江省杭州市上城区绿城育华中学八年级（上）期中物理试卷一、选择题（每小题只有一个答案，每小题2分，共44分）1．（2.00分）小勇准备用吸管制作一个密度计，完成后他发现密度计相邻两刻度线之间的距离太小，导致用此密度计测量液体密度时误差较大，为此他同组的其他同学提出了如下改进方案，其中可行的是（）A．换大的容器做实验B．换细的吸管制作密度计C．换稍长的吸管制作密度计D．适当减小密度计的配重2．（2.00分）甲、乙二物体都浸没在同种液体中，关于它们所受浮力大小的下面各种说法中正确的是（）A．如果甲物体比乙物体重，则甲物体受到的浮力比乙物体受到的浮力大B．如果甲物体的密度比乙物体大，则甲物体受到的浮力比乙物体受到的浮力小C．如果甲物体的体积比乙物体小，则甲物体受到的浮力比乙物体受到的浮力小D．如果甲物体空心，乙物体实心，则甲物体受到的浮力比乙物体受到的浮力大3．（2.00分）下列现象中没有利用大气压强的是（）A．把药液注射进肌肉里B．用吸管吸瓶中的饮料C．茶壶上留有小孔 D．利用离心水泵抽水4．（2.00分）某外型确定的潜水艇从长江潜行（在水面下航行）到东海某地执行任务。
若它悬浮在江水中所受的重力和浮力分别为G1、F1，悬浮在海水中所受的重力和浮力分别为G2、F2，则（）A．F1＞F，G1＞G2B．F1=F，G1=G2 C．F1＜F，G1＜G2D．无法确定5．（2.00分）为改善地铁地下车站的通风状况，小明设计了抽气管道，利用地面横风实现自动抽气。
为提高抽气效果，管道上方遮雨盖的形状应设计成下列图中的（）A．B．C．D．6．（2.00分）有一空心球，它的空心部分是整个球体的一半，将此球放入水里，稳定后恰有3/4的体积浸入水中。
如果此球是实心的（与空心球是同种物质），放入水中将会（）A．下沉到水底B．漂浮于水面C．悬浮在水中D．无法判断浮沉情况7．（2.00分）如图所示是高压锅的结构示意图，锅盖紧扣在锅体上，盖上装有一金属管做排气孔，金属管上方倒扣着一个像大砝码模样的重锤，起限压阀作用。
2021-2022学年浙江省杭州市西湖区绿城育华学校八年级(上)期中化学试卷(附答案详解)
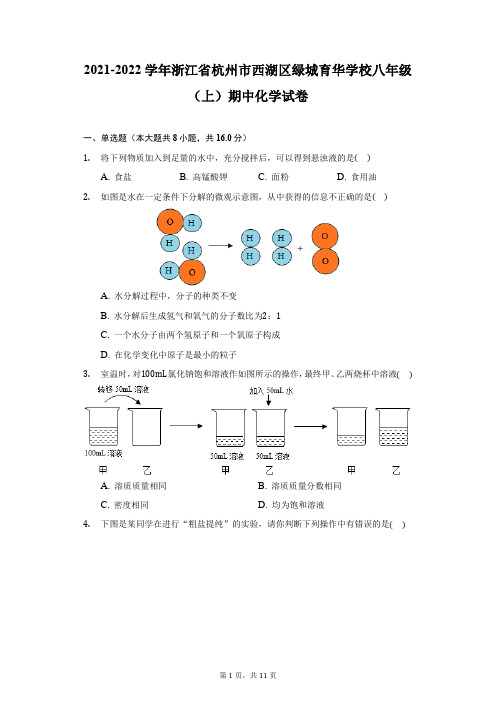
2021-2022学年浙江省杭州市西湖区绿城育华学校八年级（上）期中化学试卷一、单选题（本大题共8小题，共16.0分）1.将下列物质加入到足量的水中，充分搅拌后，可以得到悬浊液的是()A. 食盐B. 高锰酸钾C. 面粉D. 食用油2.如图是水在一定条件下分解的微观示意图，从中获得的信息不正确的是()A. 水分解过程中，分子的种类不变B. 水分解后生成氢气和氧气的分子数比为2：1C. 一个水分子由两个氢原子和一个氧原子构成D. 在化学变化中原子是最小的粒子3.室温时，对100mL氯化钠饱和溶液作如图所示的操作，最终甲、乙两烧杯中溶液()A. 溶质质量相同B. 溶质质量分数相同C. 密度相同D. 均为饱和溶液4.下图是某同学在进行“粗盐提纯”的实验，请你判断下列操作中有错误的是()A. 取样B. 溶解C. 过滤D. 蒸发5.一定温度下，向盛有100克蔗糖溶液的烧杯中再加入10克蔗糖，充分搅拌后，一定保持不变的是()A. 溶质的质量B. 溶液的质量C. 溶质的质量分数D. 蔗糖的溶解度6.晓燕在实验室过滤浑浊的天然水的过程中，她一直使液面的高度高于滤纸的边缘，则该操作最可能导致的后果是()A. 滤纸被弄破B. 过滤后的水仍有许多杂质C. 过滤后的水变为纯水D. 过滤后的水十分清澈7.20℃时，有甲、乙两瓶质量相等的KNO3饱和溶液，若将甲溶液降温至10℃；将乙溶液蒸发掉10g水后，使之成为30℃时的不饱和溶液，则此时甲、乙两瓶溶液的溶质质量分数的数值关系是()A. 甲<乙B. 甲=乙C. 甲>乙D. 不能确定8.25℃时，探究某固体物质的溶解性，实验记录如下表。
下列实验结论正确的是()编号①②③④水的质量/g5*******加入固体质量/g5101520现象固体完全溶解固体完全溶解剩余少量固体剩余较多固体A. 实验①所得溶液质量分数为10%B. 实验②说明25℃时该物质的溶解度是20gC. 实验③④所得溶液质量分数相同D. 实验④所得溶液中含溶质20g二、探究题（本大题共2小题，共20.0分）9.某温度时，蒸干35g硝酸钾饱和溶液，得到10g硝酸钾，该温度时硝酸钾的溶解度为______克，一木块漂浮于50℃时的硝酸钾饱和溶液中(见图甲)，温度改变时(不考虑由此引起的木块和溶液体积的变化)，木块排开液体的体积(V排)随时间(t)发生了如图乙所示的变化．由此推测出温度的改变方式是______(填“升温”“降温”)，同时观察到烧杯底部硝酸钾晶体______(填“增多”“减少”)10.某同学配制50g6%氯化钠溶液，整个操作过程如图所示，回答下列问题：(1)配制溶液的正确操作顺序为②①______(填序号，下同)，其中操作错误的是______。
杭州绿城育华学校数学全等三角形(培优篇)(Word版 含解析)
杭州绿城育华学校数学全等三角形（培优篇）（Word 版 含解析）一、八年级数学轴对称三角形填空题（难）1．如图，在四边形ABCD 中，BC CD = ，对角线BD 平分ADC ∠，连接AC ，2ACB DBC ∠=∠，若4AB =，10BD =，则ABC S =_________________．【答案】10【解析】【分析】由等腰三角形的性质和角平分线的性质可推出AD ∥BC ，然后根据平行线的性质和已知条件可推出CA=CD ，可得CB=CA=CD ，过点C 作CE ⊥BD 于点E ，CF ⊥AB 于点F ，如图，根据等腰三角形的性质和已知条件可得DE 的长和BCF CDE ∠=∠，然后即可根据AAS 证明△BCF ≌△CDE ，可得CF=DE ，再根据三角形的面积公式计算即得结果．【详解】解：∵BC CD =，∴∠CBD =∠CDB ，∵BD 平分ADC ∠，∴∠ADB =∠CDB ，∴∠CBD =∠ADB ，∴AD ∥BC ，∴∠CAD =∠ACB ，∵2ACB DBC ∠=∠，2ADC BDC ∠=∠，∠CBD =∠CDB ，∴ACB ADC ∠=∠，∴CAD ADC ∠=∠，∴CA=CD ，∴CB=CA=CD ，过点C 作CE ⊥BD 于点E ，CF ⊥AB 于点F ，如图，则152DE BD ==，12BCF ACB ∠=∠， ∵12BDC ADC ∠=∠，ACB ADC ∠=∠，∴BCF CDE ∠=∠， 在△BCF 和△CDE 中，∵BCF CDE ∠=∠，∠BFC =∠CED =90°，CB=CD ，∴△BCF ≌△CDE （AAS ），∴CF=DE =5，∴11451022ABC S AB CF =⋅=⨯⨯=． 故答案为：10．【点睛】本题考查了等腰三角形的判定和性质、平行线的判定和性质、角平分线的定义以及全等三角形的判定和性质等知识，涉及的知识点多、综合性强、具有一定的难度，正确添加辅助线、熟练掌握上述知识是解题的关键．2．在平面直角坐标系xOy中，已知点A（2，3），在x轴上找一点P，使得△AOP是等腰三角形，则这样的点P共有_____个．【答案】4【解析】【分析】以O为圆心，OA为半径画弧交x轴于点P1、P3，以A为圆心，AO为半径画弧交x轴于点P4，作OA的垂直平分线交x轴于P2．【详解】解：如图，使△AOP是等腰三角形的点P有4个．故答案为4．【点睛】本题考查了在平面直角坐标系中寻找等腰三角形，掌握两圆一线找等腰三角形是解题的关键．3．如图，在01A BA △中，20B ∠=︒，01A B A B =，在1A B 上取点C ，延长01A A 到2A ，使得121A A AC =；在2A C 上取一点D ，延长12A A 到3A ，使得232A A A D =；…，按此做法进行下去，第n 个等腰三角形的底角n A ∠的度数为__________．【答案】11()802n -︒⋅.【解析】【分析】先根据等腰三角形的性质求出∠BA 1 A 0的度数，再根据三角形外角的性质及等腰三角形的性质分别求出∠CA 2A 1，∠DA 3A 2及∠EA 4A 3的度数，找出规律即可得出第n 个等腰三角形的底角∠A n 的度数．【详解】解：∵在△A 0BA 1中，∠B=20°，A 0B=A 1B ， ∴∠BA 1 A 0= 1801802022B ︒︒︒-∠-= =80°， ∵A 1A 2=A 1C ，∠BA 1 A 0是△A 1A 2C 的外角，∴∠CA 2A 1= 108022BA A ︒∠= =40°； 同理可得，∠DA 3A 2=20°，∠EA 4A 3=10°，∴第n 个等腰三角形的底角∠A n = 11()802n -︒⋅.【点睛】本题考查的是等腰三角形的性质及三角形外角的性质，根据题意得出∠CA 2A 1，∠DA 3A 2及∠EA 4A 3的度数，找出规律是解答此题的关键．4．如图，在ABC ∆中，ABC ∠和ACB ∠的平分线相交于点O ，过点O 作//EF BC 交AB 于E ，交AC 于F ，过点O 作OD AC ⊥于D 下列结论：①EF BE CF =+；②点O 到ABC ∆各边的距离相等；③1902BOC A ∠=+∠；④设OD m =，AE AF n +=，则AEF S mn ∆=；⑤1()2AD AB AC BC =+-.其中正确的结论是.__________．【答案】①②③⑤【解析】【分析】由在△ABC 中，∠ABC 和∠ACB 的平分线相交于点O ，根据角平分线的定义与三角形内角和定理，即可求得③∠BOC =90°+12∠A 正确；由平行线的性质和角平分线的定义得出△BEO 和△CFO 是等腰三角形得出EF =BE +CF 故①正确；由角平分线的性质得出点O 到△ABC 各边的距离相等，故②正确；由角平分线定理与三角形面积的求解方法，即可求得④设OD =m ，AE +AF =n ，则S △AEF =12mn ，故④错误，根据HL 证明△AMO ≌△ADO 得到AM =AD ，同理可证BM =BN ，CD =CN ，变形即可得到⑤正确．【详解】 ∵在△ABC 中，∠ABC 和∠ACB 的平分线相交于点O ，∴∠OBC =12∠ABC ，∠OCB =12∠ACB ，∠A +∠ABC +∠ACB =180°，∴∠OBC +∠OCB =90°﹣12∠A ，∴∠BOC =180°﹣（∠OBC +∠OCB ）=90°+12∠A ；故③正确； ∵在△ABC 中，∠ABC 和∠ACB 的平分线相交于点O ，∴∠OBC =∠OBE ，∠OCB =∠OCF ． ∵EF ∥BC ，∴∠OBC =∠EOB ，∠OCB =∠FOC ，∴∠EOB =∠OBE ，∠FOC =∠OCF ，∴BE =OE ，CF =OF ，∴EF =OE +OF =BE +CF ，故①正确；过点O 作OM ⊥AB 于M ，作ON ⊥BC 于N ，连接OA ．∵在△ABC 中，∠ABC 和∠ACB 的平分线相交于点O ，∴ON =OD =OM =m ，∴S △AEF =S △AOE +S △AOF =12AE •OM +12AF •OD =12OD •（AE +AF ）=12mn ；故④错误； ∵在△ABC 中，∠ABC 和∠ACB 的平分线相交于点O ，∴点O 到△ABC 各边的距离相等，故②正确；∵AO =AO ，MO =DO ，∴△AMO ≌△ADO （HL ），∴AM =AD ；同理可证：BM =BN ，CD =CN ．∵AM+BM=AB，AD+CD=AC，BN+CN=BC，∴AD=12（AB+AC﹣BC）故⑤正确．故答案为：①②③⑤．【点睛】本题考查了角平分线的定义与性质，等腰三角形的判定与性质．此题难度适中，解题的关键是注意数形结合思想的应用．5．如图，在△ABC中，∠C＝90°，∠B＝30°，以点A为圆心，任意长为半径画弧分别交AB，AC于点M和N，再分别以点M，N为圆心，大于12MN的长为半径画弧，两弧交于点P，连接AP并延长交BC于点D，则下列说法：①AD是∠BAC的平分线；②∠ADC＝60°；③点D在AB的垂直平分线上；④S△DAC：S△ABC＝1：3.其中正确的是__________________．(填所有正确说法的序号)【答案】4【解析】【分析】①连接NP，MP，根据SSS定理可得△ANP≌△AMP，故可得出结论；②先根据三角形内角和定理求出∠CAB的度数，再由AD是∠BAC的平分线得出∠1=∠2=30°，根据直角三角形的性质可知∠ADC=60°；③根据∠1=∠B可知AD=BD，故可得出结论；④先根据直角三角形的性质得出∠2=30°，CD=12AD，再由三角形的面积公式即可得出结论．【详解】①连接NP ，MP ．在△ANP 与△AMP 中，∵AN AM NP MP AP AP =⎧⎪=⎨⎪=⎩，∴△ANP ≌△AMP ，则∠CAD =∠BAD ，故AD 是∠BAC 的平分线，故此选项正确；②∵在△ABC 中，∠C =90°，∠B =30°，∴∠CAB =60°．∵AD 是∠BAC 的平分线，∴∠1=∠2=12∠CAB =30°，∴∠3=90°﹣∠2=60°，∴∠ADC =60°，故此选项正确；③∵∠1=∠B =30°，∴AD =BD ，∴点D 在AB 的中垂线上，故此选项正确；④∵在Rt △ACD中，∠2=30°，∴CD =12AD ，∴BC =BD +CD =AD +12AD =32AD ，S △DAC =12AC •CD =14AC •AD ，∴S △ABC=12AC •BC =12AC •32AD =34AC •AD ，∴S △DAC ：S △ABC =1：3，故此选项正确． 故答案为①②③④．【点睛】本题考查的是作图﹣基本作图，熟知角平分线的作法是解答此题的关键．6．如图，在直角坐标系中，点()8,8B -，点()2,0C -，若动点P 从坐标原点出发，沿y 轴正方向匀速运动，运动速度为1/cm s ，设点P 运动时间为t 秒，当BCP ∆是以BC 为腰的等腰三角形时，直接写出t 的所有值__________________．【答案】2秒或6秒或14秒【解析】【分析】分两种情况：PC 为腰或BP 为腰.分别作出符合条件的图形，计算出OP 的长度，即可求出t的值．【详解】解：如图所示，过点B作BD⊥x轴于点D，作BE⊥y轴于点E，分别以点B和点C为圆心，以BC长为半径画弧交y轴正半轴于点F，点H和点G∵点B（-8，8），点C（-2，0），∴DC=6cm，BD=8cm，由勾股定理得：BC=10cm∴在直角三角形COG中，OC=2cm，CG=BC=10cm，∴OP=OG= 2210246(cm)-=，当点P运动到点F或点H时，BE=8cm，BH=BF=10cm，∴EF=EH=6cm∴OP=OF=8-6=2（cm）或OP=OH=8+6=14（cm），故答案为：2秒，46秒或14秒．【点睛】本题综合考查了勾股定理和等腰三角形在平面直角坐标系中的应用，通过作图找出要求的点的位置，利用勾股定理来求解是本题的关键．7．如图，在四边形ABCD中，∠A+∠C＝180°，E、F分别在BC、CD上，且AB＝BE，AD ＝DF，M为EF的中点，DM＝3，BM＝4，则五边形ABEFD的面积是_____．【答案】12【解析】【分析】延长BM至G，使MG＝BM，连接FG、DG，证明△BME≌△GMF（SAS），得出FG＝BE，∠MBE＝∠MGF，证出AB＝FG，证明△DAB≌△DFG（SAS），得出DB＝DG，由等腰三角形的性质即可得DM⊥BM，由五边形ABEFD的面积＝△DBG的面积，可求解．【详解】延长BM至G，使MG＝BM＝4，连接FG、DG，如图所示：∵M为EF中点，∴ME＝MF，在△BME和△GMF中，BM MGBME GMFME MF=⎧⎪∠=∠⎨⎪=⎩，∴△BME≌△GMF（SAS），∴FG＝BE，∠MBE＝∠MGF，S△BEM＝S△GFM，∴FG∥BE，∴∠C＝∠GFC，∵∠A+∠C＝180°，∠DFG+∠GFC＝180°，∴∠A＝∠DFG，∵AB＝BE，∴AB＝FG，在△DAB和△DFG中，AB FGA DFGAD DF=⎧⎪∠=∠⎨⎪=⎩，∴△DAB≌△DFG（SAS），∴DB＝DG，S△DAB＝S△DFG，∵MG＝BM，∴DM⊥BM，∴五边形ABEFD的面积＝△DBG的面积＝12×BG×DM＝12×8×3＝12，故答案为：12．【点睛】本题考查了全等三角形的判定与性质、平行线的性质、等腰三角形的判定与性质等知识；熟练掌握等腰三角形的判定由性质，证明三角形全等是解题的关键．8．如图，∠AOB＝45°，点M、点C在射线OA上，点P、点D在射线OB上，且OD＝32，则CP+PM+DM的最小值是_____．34【解析】【分析】如图，作点C关于OB的对称点C′，作点D关于OA的对称点D′，连接OC′，PC′，D′M，OD′，C′D′，根据轴对称的性质得到OC′＝OC＝2，OD′＝OD＝2，CP＝C′P，DM＝D′M，∠C′OD＝′COD＝∠COD′＝45°，于是得到CP+PM+MD＝C′+PM+D′M≥C′D′，当仅当C′，P，M，D′三点共线时，CP+PM+MD最小为C′D′，作C′T⊥D′O于点T，于是得到结论．【详解】解：如图，作点C关于OB的对称点C′，作点D关于OA的对称点D′，连接OC′，PC′，D′M，OD′，C′D′，则OC′＝OC＝2，OD′＝OD＝2，CP＝C′P，DM＝D′M，∠C′OD＝′COD＝∠COD′＝45°，∴CP+PM+MD＝C′+PM+D′M≥C′D′，当仅当C′，P，M，D′三点共线时，CP+PM+MD最小为C′D′，作C′T⊥D′O于点T，则C′T＝OT2，∴D′T＝2，∴C′D34∴CP+PM+DM3434【点睛】本题考查了最短路径问题，掌握作轴对称点是解题的关键.9．如图，过边长为1的等边三角形ABC的边AB上一点P，作PE⊥AC于点E，Q为BC延长线上一点，当AP＝CQ时，PQ交AC于D，则DE的长为______．【答案】1 2【解析】过点Q作AD的延长线的垂线于点F.因为△ABC是等边三角形，所以∠A=∠ACB=60°.因为∠ACB=∠QCF，所以∠QCF=60°.因为PE⊥AC，QF⊥AC，所以∠AEP=∠CFQ=90°，又因为AP=CQ，所以△AEP≌△CFQ，所以AE=CF，PE=QC.同理可证，△DEP≌△DFQ，所以DE=DF.所以AC=AE+DE+CD=DE+CD+CF=DE+DF=2DE，所以DE=12AC=12.故答案为1 2 .10．如图，在△ABC 中，AD 是高，DE 是 AC 的垂直平分线，AE=4cm ，△ABD 的周长为 15cm ， 则△ABC 的周长为______【答案】23cm ．【解析】【分析】根据线段垂直平分线的性质得到AC=2AE=8，DA=DC ，根据三角形的周长公式计算即可．【详解】解：∵DE 是AC 的垂直平分线，∴AC=2AE=8，DA=DC ，∵△ABD 的周长=AB+BD+AD=AB+BD+DC=AB+BC=15，∴△ABC 的周长=AB+BC+AC=15+8=23cm ，故答案是：23cm ．【点睛】本题考查的是线段垂直平分线的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．二、八年级数学轴对称三角形选择题（难）11．如图所示，OP 平分AOB ∠，PA OA ⊥，PB OB ⊥，垂足分别为A 、B ．下列结论中不一定成立的是（ ）．A ．PA PB =B ．PO 平分APB ∠C ．OA OB =D ．AB 垂直平分OP【答案】D【解析】【分析】 根据角平分线上的点到角的两边距离相等可得出PA=PB ，再利用“HL ”证明△AOP 和△BOP 全等，可得出APO BPO ∠=∠，OA=OB ，即可得出答案．【详解】解：∵OP 平分AOB ∠，PA OA ⊥，PB OB ⊥∴PA PB =，选项A 正确；在△AOP 和△BOP 中，PO PO PA PB =⎧⎨=⎩， ∴AOP BOP ≅∴APO BPO ∠=∠，OA=OB ，选项B ，C 正确；由等腰三角形三线合一的性质，OP 垂直平分AB ，AB 不一定垂直平分OP ，选项D 错误． 故选：D ．【点睛】本题考查的知识点是角平分线的性质以及垂直平分线的性质，熟记性质定理是解此题的关键．12．边长为a 的等边三角形，记为第1个等边三角形，取其各边的三等分点，顺次连接得到一个正六边形，记为第1个正六边形，取这个正六边形不相邻的三边中点，顺次连接又得到一个等边三角形，记为第2个等边三角形，取其各边的三等分点，顺次连接又得到一个正六边形，记为第2个正六边形（如图），…，按此方式依次操作，则第6个正六边形的边长为（ ）A ．511a 32⨯（）B ．511a 23⨯（）C ．611a 32⨯（）D ．611a 23⨯（） 【答案】A【解析】 连接AD 、DB 、DF ，求出∠AFD=∠ABD=90°，根据HL 证两三角形全等得出∠FAD=60°，求出AD ∥EF ∥GI ，过F 作FZ ⊥GI ，过E 作EN ⊥GI 于N ，得出平行四边形FZNE 得出EF=ZN=13a ，求出GI 的长，求出第一个正六边形的边长是13a ，是等边三角形QKM 的边长的13；同理第二个正六边形的边长是等边三角形GHI 的边长的13；求出第五个等边三角形的边长，乘以13即可得出第六个正六边形的边长． 连接AD 、DF 、DB ．∵六边形ABCDEF 是正六边形， ∴∠ABC=∠BAF=∠AFE ，AB=AF ，∠E=∠C=120°，EF=DE=BC=CD ，∴∠EFD=∠EDF=∠CBD=∠BDC=30°，∵∠AFE=∠ABC=120°，∴∠AFD=∠ABD=90°，在Rt △ABD 和RtAFD 中AF=AB {AD=AD∴Rt △ABD ≌Rt △AFD （HL ），∴∠BAD=∠FAD=12×120°=60°， ∴∠FAD+∠AFE=60°+120°=180°，∴AD ∥EF ，∵G 、I 分别为AF 、DE 中点，∴GI ∥EF ∥AD ，∴∠FGI=∠FAD=60°，∵六边形ABCDEF 是正六边形，△QKM 是等边三角形，∴∠EDM=60°=∠M ，∴ED=EM ，同理AF=QF，即AF=QF=EF=EM，∵等边三角形QKM的边长是a，∴第一个正六边形ABCDEF的边长是13a，即等边三角形QKM的边长的13，过F作FZ⊥GI于Z，过E作EN⊥GI于N，则FZ∥EN，∵EF∥GI，∴四边形FZNE是平行四边形，∴EF=ZN=13a，∵GF=12AF=12×13a=16a，∠FGI=60°（已证），∴∠GFZ=30°，∴GZ=12GF=112a，同理IN=112a，∴GI=112a+13a+112a=12a，即第二个等边三角形的边长是12a，与上面求出的第一个正六边形的边长的方法类似，可求出第二个正六边形的边长是13×12a；同理第第三个等边三角形的边长是12×12a，与上面求出的第一个正六边形的边长的方法类似，可求出第三个正六边形的边长是13×12×12a；同理第四个等边三角形的边长是12×12×12a，第四个正六边形的边长是13×12×12×12a；第五个等边三角形的边长是12×12×12×12a，第五个正六边形的边长是1 3×12×12×12×12a；第六个等边三角形的边长是12×12×12×12×12a，第六个正六边形的边长是1 3×12×12×12×12×12a，即第六个正六边形的边长是13×512（）a，故选A．13．如图，ABC ∆中，AB 的垂直平分线DG 交ACB ∠的平分线CD 于点D ，过D 作DE AC ⊥于点E ，若10AC =，4CB =，则AE =（ ）A ．7B ．6C ．3D ．2【答案】C【解析】【分析】 连接BD 、AD,过点D 作DF ⊥CB 于点F ，利用角平分线及线段垂直平分线的性质可求出BD=AD ，DE=DF ，依据HL 定理可判断出Rt △AED ≌Rt △BFD ，根据全等三角形的性质即可得出BF=AE ，再运用AAS 定理可证得Rt △CED ≌Rt △CFD ，证出CE=CF ，设AE 的长度为x ，根据CE=CF 列方程求解即可．【详解】如图, 连接BD 、AD,过点D 作DF⊥CB 于点F.∵AB 的垂直平分线DG 交ACB ∠的平分线CD 于点D ，DE⊥AC ，DF⊥BC，∴BD=AD，DE=DF ．∴Rt△AED≌Rt△BFD．∴BF=AE．又∵∠ECD=∠FCD，∠CED=∠CFD，CA=CA ，∴Rt△CED≌Rt△CFD，∴CE=CF，设AE 的长度为x ，则CE=10-x ，CF=CB ＋BF= CB ＋AE= 4＋x,∴可列方程10-x=4＋x ，x=3，∴AE=3；故选C.【点睛】本题涉及到线段垂直平分线及角平分线的性质，直角三角形全等的判定定理及性质，解答此题的关键是作出辅助线，构造出直角三角形解答．14．如图，四边形ABCD中，∠C=，∠B=∠D=，E，F分别是BC，DC上的点，当△AEF的周长最小时，∠EAF的度数为（）．A．B．C．D．【答案】D【解析】【分析】【详解】作点A关于直线BC和直线CD的对称点G和H，连接GH，交BC、CD于点E、F，连接AE、AF，则此时△AEF的周长最小，由四边形的内角和为360°可知，∠BAD=360°-90°-90°-50°=130°，即∠1+∠2+∠3=130°①，由作图可知，∠1=∠G，∠3=∠H，△AGH的内角和为180°，则2（∠1+∠3）+ ∠2=180°②，又①②联立方程组，解得∠2=80°．故选D．考点：轴对称的应用；路径最短问题．15．如图，C为线段AE上一动点（不与点A、E重合），在AE同侧分别作等边三角形ABC 和等边三角形CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连接PQ．以下五个结论：①AD＝BE；②AP＝BQ；③PQ∥AE；④DE＝DP；⑤∠AOE＝120°；其中正确结论的个数为（）A．2个B．3个C．4个D．5个【答案】C【解析】【分析】①由于△ABC和△CDE是等边三角形，可知AC=BC，CD=CE，∠ACB=∠DCE=60°，从而证出△ACD≌△BCE，可推知AD=BE，故①正确；②由△ACD≌△BCE得∠CBE=∠DAC，加之∠ACB=∠DCE=60°，AC=BC，得到△ACP≌△BCQ （ASA），所以AP=BQ；故②正确；③根据②△CQB≌△CPA（ASA），再根据∠PCQ=60°推出△PCQ为等边三角形，又由∠PQC=∠DCE，根据内错角相等，两直线平行，可知③正确；④根据∠QCP=60°，∠DPC=∠BCA+∠PAC＞60°，可知PD≠CD，可知④错误；⑤利用等边三角形的性质，BC∥DE，再根据平行线的性质得到∠CBE=∠DEO，于是∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°，由平角的性质可得∠AOE=120°，可知⑤正确；【详解】①∵△ABC和△CDE为等边三角形∴AC＝BC，CD＝CE，∠BCA＝∠DCB＝60°∴∠ACD＝∠BCE∴△ACD≌△BCE（SAS）∴AD＝BE，故①正确；由（1）中的全等得∠CBE＝∠DAC，且BC＝AC，∠ACB＝∠BCQ＝60°∴△CQB≌△CPA（ASA），∴AP＝BQ，故②正确；∵△CQB≌△CPA，∴PC＝PQ，且∠PCQ＝60°∴△PCQ为等边三角形，∴∠PQC＝∠DCE＝60°，∴PQ∥AE，故③正确，∵∠QCP＝60°，∠DPC＝∠BCA+∠PAC＞60°，∴PD≠CD，∴DE≠DP，故④DE＝DP错误；∵BC∥DE，∴∠CBE＝∠BED，∵∠CBE＝∠DAE，∴∠AOB＝∠OAE+∠AEO＝60°，∴∠AOE ＝120°，故⑤正确，故选C ．【点睛】本题考查了全等三角形的判定与性质，利用了等边三角形的判定与性质，全等三角形的判定与性质，平行线的判定与性质，综合性较强，题目难度较大．16．已知：如图，ABC ∆、CDE ∆都是等腰三角形，且CA CB =，CD CE =，ACB DCE α∠=∠=，AD 、BE 相交于点O ，点M 、N 分别是线段AD 、BE 的中点.以下4个结论：①AD BE =；②180DOB α∠=-；③CMN ∆是等边三角形；④连OC ，则OC 平分AOE ∠.正确的是( )A ．①②③B ．①②④C ．①③④D ．①②③④【答案】B【解析】【分析】 ①根据∠ACB=∠DCE 求出∠ACD=∠BCE,证出ACD BCE ≅△△即可得出结论，故可判断； ②根据全等求出∠CAD=∠CBE,根据三角形外角定理得∠DOB=∠OBA+∠BAO,通过等角代换能够得到∠DOB=∠CBA+∠BAC,根据三角形内角和定理即可求出∠CBA+∠BAC,即可求出∠DOB ，故可判断；③根据已知条件可求出AM=BN,根据SAS 可求出CAM CBN ≅,推出CM=CN ，∠ACM=∠BCN,然后可求出∠MCN=∠ACB=α,故可判断CMN ∆的形状；④在AD 上取一点P 使得DP=EO,连接CP ，根据ACD BCE ≅△△，可求出∠CEO=∠CDP ,根据SAS 可求出 CEO CDP ≅,可得∠COE=∠CPD,CP=CO,进而得到 ∠COP=∠COE ，故可判断.【详解】①正确，理由如下：∵ACB DCE α∠=∠=,∴∠ACB+∠BCD=∠DCE+∠BCD,即∠ACD=∠BCE,又∵CA=CB,CD=CE,∴ACD BCE ≅△△(SAS),∴AD=BE,故①正确；②正确，理由如下：由①知，ACD BCE ≅△△，∴∠CAD=∠CBE,∵∠DOB 为ABO 的外角,∴∠DOB=∠OBA+∠BAO=∠EBC+∠CBA+∠BAO=∠DAC+∠BAO+∠CBA=∠CBA+∠BAC, ∵∠CBA+∠BAC+∠ACB=180°,∠ACB=α,∴∠CBA+∠BAC=180°-α,即∠DOB=180°-α,故②正确；③错误，理由如下：∵点M 、N 分别是线段AD 、BE 的中点,∴AM=12AD,BN= 12BE, 又∵由①知，AD=BE,∴AM=BN,又∵∠CAD=∠CBE,CA=CB,∴CAM CBN ≅(SAS), ∴CM=CN ，∠ACM=∠BCN,∴∠MCN=∠MCB+∠CBN=∠MCB+∠ACM=∠ACB=α,∴MCN △为等腰三角形且∠MCN=α,∴MCN △不是等边三角形，故③错误；④正确，理由如下：如图所示，在AD 上取一点P 使得DP=EO,连接CP ，由①知，ACD BCE ≅△△，∴∠CEO=∠CDP ,又∵CE=CD,EO=DP ,∴CEO CDP ≅(SAS),∴∠COE=∠CPD,CP=CO,∴∠CPO=∠COP ,∴∠COP=∠COE,即OC平分∠AOE,故④正确；故答案为：B.【点睛】本题考查了三角形全等的判定和性质，三角形内角和定理和外角定理，等边三角形的判定，根据已知条件作出正确的辅助线，找出全等三角形是解题的关键.17．如图，在△ABC中，BI，CI分别平分∠ABC，∠ACB，过I点作DE∥BC，交AB于D，交AC于E，给出下列结论：①△DBI是等腰三角形；②△ACI是等腰三角形；③AI平分∠BAC；④△ADE周长等于AB＋AC．其中正确的是( )A．①②③B．②③④C．①③④D．①②④【答案】C【解析】【分析】根据角平分线的性质、平行线的性质、等腰三角形的判定与性质分别对各选项分析判断后利用排除法求解．【详解】①∵IB平分∠ABC，∴∠DBI=∠CBI．∵DE∥BC，∴∠DIB=∠CBI，∴∠DBI=∠DIB，∴BD=DI，∴△DBI是等腰三角形．故本选项正确；②∵∠BAC不一定等于∠ACB，∴∠IAC不一定等于∠ICA，∴△ACI不一定是等腰三角形．故本选项错误；③∵三角形角平分线相交于一点，BI，CI分别是∠ABC和∠ACB的平分线，∴AI平分∠BAC．故本选项正确；④∵BD=DI，同理可得EI=EC，∴△ADE的周长=AD+DI+EI+AE=AD+BD+EC+AE=AB+AC．故本选项正确；其中正确的是①③④．故选C．【点睛】本题考查了等腰三角形的判定与性质，熟记三角形的角平分线相交于一点是解题的关键．18．如图，已知等边△ABC的面积为3 P、Q、R分别为边AB、BC、AC上的动点，则PR＋QR的最小值是（）A．3B．23C．15D．4【答案】B【解析】如图，作△ABC关于AC对称的△ACD，点E与点Q关于AC对称，连接ER，则QR=ER，当点E，R，P在同一直线上，且PE⊥AB时，PE的长就是PR+QR的最小值，设等边△ABC的边长为x，则高为3 x，∵等边△ABC的面积为43，∴12x×3x=43，解得x=4，∴等边△ABC的高为3x=23，即PE=23，所以PR+QR的最小值是23，故选B.【点睛】本题考查了轴对称的性质，最短路径问题等，解题的关键是正确添加辅助线构造出最短路径.19．如图，在△ABC中，∠A=36°，AB=AC，AB的垂直平分线OD交AB于点O，交AC于点D，连接BD．有下列结论：①∠C=2∠A；②BD平分∠ABC；③S△BCD=S△BOD．其中正确的选项是（）A．①③B．②③C．①②③D．①②【答案】D【解析】①、∵∠A=36°，AB=AC，∴∠C=∠ABC=72°，∴∠C=2∠A，正确；②、∵DO是AB垂直平分线，∴AD=BD．∴∠A=∠ABD=36°．∴∠DBC=72°﹣36°=36°=∠ABD．∴BD是∠ABC的角平分线，正确；③，根据已知不能推出△BCD的面积和△BOD面积相等，错误；故选：D.20．如图所示，把腰长为1的等腰直角三角形折叠两次后，得到的一个小三角形的周长是（）A．2B．1+22C．2D2-1【答案】B 【解析】第一次折叠后，等腰三角形的底边长为12；第一次折叠后，等腰三角形的底边长为22，腰长为12，所以周长为11221 2222 ++=+.故答案为B.。
综合性学习 献给母亲的歌 (4)
献给母亲的歌
下一页
上一页
退出
首页
古今中外，多少文人墨客都歌颂着伟大的母爱， 同学们知道哪些与母爱有关的诗句或格言吗？
谁言寸草心，报得三春晖。（孟郊） 世界上的一切光荣和骄傲，都来自母亲。（高尔基） 母爱是一种巨大的火焰。（罗曼罗兰） 世界上有一种最美丽的声音，那便是母亲的呼唤（但丁） 成功的时候，谁都是朋友。但只有母亲-----她是失败时的伴侣。 （郑振铎） 慈母的胳膊是慈爱构成的，孩子睡在里面怎能不甜？（雨果） ……
献给母亲的歌
下一页
上一页
退出
首页
慈 母 颂
襁褓时，母亲的甘甜乳汁，是滋润肌肤的甘露， 襁褓时，母亲的甘甜乳汁，是滋润肌肤的甘露， 孩提时，母亲的苦涩汗水，是浇灌心田的清泉。 孩提时，母亲的苦涩汗水，是浇灌心田的清泉。 求学时，母亲的耐心诱导，是启动灵感的马达， 求学时，母亲的耐心诱导，是启动灵感的马达， 困惑时，母亲的殷切教诲，是拨正航向的罗盘。 困惑时，母亲的殷切教诲，是拨正航向的罗盘。 失足时，母亲的善意规劝，是迷途识返的路标， 失足时，母亲的善意规劝，是迷途识返的路标， 成功时，母亲的热情鼓励，是乘胜前进的风帆。 成功时，母亲的热情鼓励，是乘胜前进的风帆。 攻关时，母亲的积极鞭策，是攀登要隘的阶梯， 攻关时，母亲的积极鞭策，是攀登要隘的阶梯， 拼搏时，母亲的大力支持，是冲越激流的航船。 拼搏时，母亲的大力支持，是冲越激流的航船。 挫折时，母亲的亲切关怀，是闯出困境的号角， 挫折时，母亲的亲切关怀，是闯出困境的号角， 患病时，母亲的精心护理，是战胜苦痛的灵丹。 患病时，母亲的精心护理，是战胜苦痛的灵丹。 困倦时，母亲的爱心，是安然入梦的摇篮， 困倦时，母亲的爱心，是安然入梦的摇篮， 疲惫时，母亲的怀抱，是停泊小憩的港湾。 疲惫时，母亲的怀抱，是停泊小憩的港湾。 远行时，缝进衣物的细密针线，是母亲数不清的嘱咐和挂牵； 远行时，缝进衣物的细密针线，是母亲数不清的嘱咐和挂牵； 归来时，摸遍全身的颤抖双手，是母亲述不尽的爱抚和思念。 归来时，摸遍全身的颤抖双手，是母亲述不尽的爱抚和思念。 母爱之专，心系一身。 母爱之专，心系一身。 母爱之大，情牵万里。 母爱之大，情牵万里。 母爱之久，如江河行地，同日月经天。 母爱之久，如江河行地，同日月经天。 母爱似古老的车辙，伴随岁月的运转，越碾越深， 母爱似古老的车辙，伴随岁月的运转，越碾越深， 母爱如陈年的老酒，偕同时间的推移，越酿越甜。 母爱如陈年的老酒，偕同时间的推移，越酿越甜。 母亲的伟大形象，将与天地共存，与日月同辉，为历代尊祟，受世人敬仰。 母亲的伟大形象，将与天地共存，与日月同辉，为历代尊祟， 受世人敬仰。
POWERPOINT 演示文稿 - 杭州第二中学
杭州第二中学继承“高标准、严要求”的办学传统，为了实现把 杭州第二中学办成 一所高水平、现代化的一流中华名校，成为教 改科研的实验性学校、 教育教学的示范性学校、对外开放的窗口 学校的目标，学校抓了“课程结构改革”、“教学方法改革”、 “学校管理改革 ”，积极推 进 “自主发展教育”，形成了良性 的动势。 学校探索建立以“学科课程”、“活动课程”、“环境课程” 为内 容的，每类课程均配以必修、选修、自修三种修业方式的课 程体系，结合不同评价方式和相应的教师制、导师制，实行制度 化的课程管 理。在此同时，还研究建立了以“目标达成度”、 “学生参与度” 、“时间利用率”为必要条件的“理想化课堂教 学模型”，并以 “模型”为指导，探索趋近“理想化效果”的最 优化教学方式和教 学方法，提高教学质量。在学校管理方面，学 校重视“过程管理”， 强调具体工作的指导与长远目标的引导相 结合、对教师的管理与对 学生的管理相结合、严格制度下的外部 约束与基于职业责任意识的 自我约束相结合、物质激励与思想教 育相结合，形成了自己的特色。 学校坚持办了十余年的“学生业余党校”，培养了一批全面 发展的 尖子学生入党，这些学生党员或党校学员在进入高校后又 都成为优 秀学生，有的还被评为“清华十杰”、“上海市三好学 生十大标兵”。 “学生业余党校”的办学经验获得了省、市领导
蕙兰中学最后一届毕业生
1950年
杭州第二中学第一届毕业生 1951年
蕙 兰 校 训 ： 诚 、 勤 、 爱
立 志 、 努 力 、 为 公
竺 可 桢 的 训 词 ：
二 中 校 明 今 训 日 日 ： 二 我 中 以 以 二 我 中 为 为 荣 荣
1901（光绪二十七年） 主要课程设置为：国文、英语、算学、史地、理 科、道学。第一级高班课本，国文以《孟子》为 蓝本。学生可以跨年级选课，实行学分制。学校 标明的办学宗旨为“授诸生以圣道”，因此规定 宗教课程为必修课。毕业生可保送美国腾纳逊、 许耳立、非佛兰、格林格拉、麦苏等大学。 1912（民国元年） 1月 19日，南京临时政府教育部公布《普通教育 暂行办法》，规定学堂改称“学校”，监督、堂 长改称“校长”。蕙兰中学堂更名为“蕙兰中学 校”，改学制为4年。各年级每周主课安排均为： 国文6课时，英文9课时，算学5课时，科学5课时， 历史3 课时，圣经2课时。
浙江省杭州绿城育华学校八年级科学上册《溶液》练习.doc
A.溶液变浑浊C.溶液质量变小 《溶液》练习班级 姓名1、 把少量下列物质分别放到水中，充分搅拌，可以得到溶液是的（ ）A. 蔗糖B.面粉C.植物油 DM 贝餐2、 下列物质中，属于溶液的是（）A. 糖水B.牛奶C.米粥D.豆浆3、 根据图4信息判断，下列叙述不正确的是（） • • ♦A. 硝酸钾的溶解度随温度升高而增大B. t.°C 时，氯化钠和硝酸钾的溶解度相同C. 将t2°C 时的硝酸钾饱和溶液降温到t 「C,有晶体析出D. t 2 °C 时，80g 硝酸钾溶于100g 水中可制得饱和溶液4、 A 、B 、C 三种不含结品水的固体物质的溶解度曲线如图，下列说法中不正确的是（） • • • A. tl°C 时，A 的饱和溶液65 g 中含有溶剂50 gB. 将t2°C A 、B 、C 三种物质的饱和溶液降温至tl°C 时，C 溶液中溶质的质量分 数保持不变C. 在t2°C, A 、B 两种溶液中溶质的质量分数相同D. 要从A 溶液中得到A ,通常可采用蒸发溶剂使其结晶的方法 5、下列有关粗盐提纯的实验操作不正确的是（）6、下图是氢氧化钙的溶解度曲线。
在冬天气温为5"C 时配制的氢氧化钙饱和溶液，在夏天气温为38"C 时（水的 蒸发忽略不计），不可能出现的情况是B.溶液变为不饱和 D.溶质质量分数变小B.溶解c.过滤 D.蒸发a11化图437、（1）汽油与酒精分别加入蒸儒水中，能形成溶液的是▲°（2）白糖固体放入口中有清凉感觉。
请从溶解现象推测其可能原因是▲。
（3）右图是a、b两种同体物质的溶解度曲线。
%1当温度低于20°C时，溶解度：a A b（选填">” 或"二”）；%1t°C时，将a、b两物质的饱和溶液均加热至40°C（a、b不分解，水分未蒸发），两种溶液中溶质的质量分数：a ▲b （选填">” 或“二”）°8、右图是甲、乙两种固体物质的溶解度曲线。
绿城育华2014学年第一学期八年级期中考英语
杭州绿城育华学校2014学年第一学期八年级期中考笔试部分四单项填空16which of the following underlined parts is different in pronunciation from the others?A showerB borrowC growD below17 Baseball is not so fast—paced(快节奏的) a game _____ basketball. But it’s relaxing to see a baseball gameA likeB soC asD with18 The players spends 3 hours_____ tennis in the tennis court every dayA to practice playingB practicing playingC practice to playD to practice to play19 ---_____ your math teacher_______?--she is friendly and helpfulA How is, likeB What is, likeC How does, likeD What does, like20 My mother and I____ at home ______that snowy nightA were, atB was, atC were, onD was, on21We can hardly hear_____, could you please turn the radio offA anythingB somethingC nothingD everything22---what do you think of Li Yang’s crazy English?I think it’s______, but someone thinks it’s much too_______A creative enough, boredB enough creative, boringC creative enough, boringD enough creative, bored23 Kate does her homework_____ than her classmatesA much carefulB much more carefulC much carefullyD much more carefully24—Can you tell me_____? == With Lucy’s helpA when you did it so wellB when did you do it so wellC how you did it so wellD how did you do it so well25 –Haven’t I told you that you should be home earlier-- Yes, but I _____ home earlier than I usually doA getB will getC gotD am getting26—I wonder_____ you water this kind of tree---Once a weekA how oftenB how longC how soonD how much27 It’s nice _____ Andy me with my English studyA at, to helpB of, to helpC with, helpD of, help28 –Who broke the mirror? –I don’t know, in fact, I plan to_____ who didA come outB find outC go outD put out29 – Would you mind watching the children, just for a second? --_________A Sure, go aheadB Of course not, dearC Oh , don’t you like childrenD yeah, I hope so30—I think you should phone Jenny and say sorry to her=______ It was her fault(错误)A Not at allB Not possibleC No chanceD No way五完形填空Once I went shopping on my first visit to Macao. Coming 31 cold and cloudy England, I enjoyed the sun and dressed in a T-shirt and a 32 skirt. Not having much 33 to enjoy the sun in England, my legs were very 34 . In England this is not a fashionable colour at all. Most women spend every 35 day out trying to get darker skin. The darker the skin, the better they look. I have tried to get darker but 36 works for me!As I 37 around one shop, the two shop assistants kept looking at my legs all the 38 , talking quietly to each other in Chinese. I began to feel 39 and asked my friend if we could leave. After we left the shop, she asked me what was40 . I complained about the shop assistants being very impolite. They must be41 at my white skin. My friend laughed. “They weren’t laughing at you. They were saying 42 nice your legs were. Many Chinese women want to have white skin like yours. As a result , there are many beauty products (美容产品) in the shops to make skin whiter and a lot of money is spent 43 them.‖It just shows that we are never happy with what we have. The grass is much 44 on the other side. If the women of the West and East thought the same way, Western women wouldn’t spend so much money on beauty products 45 makes skin darker and women from the East wouldn’t need to use cream that makes skin whiter.31. A. from B. for C. to D. with32. A. long B. short C. cheap D. expensive33. A. money B. exercise C. space D. chance34 A black B beautiful C ugly D white35. A. cloudy B. rainy C. sunny D. windy36. A. anything B. everything C. nothing D. something37. A. jumped B. ran C. rode D. walked38 A time B day C hour D minte39. A. uncomfortable B. unhealthy C. uninterested D. unlucky40. A. unusual B. wrong C. serious D. terrible41. A. laughing B. talking C. smiling D. singing42. A. how a B. what a C. what D. how43 A in B on C by D with44. A. green B. greenest C. more green D. greener45. A. that B. who C. when D. what六阅读理解第一节；阅读下列短文，从每题所给选项选出最佳选项AOn a small farm in Mexico，there are no schools．A bus is the school．The driver of the bus is the teacher．It’s a school bus，but it doesn’t take the children to school．It just goes round from place to place，and sometimes it comes to this farm．The bus will stay here for three months．The farmers call it a school onwheels．Every time when the bus comes，the farmers will come，running to it，shouting and laughing．They warmly welcome the school bus．When the bus is on the farm，in the morning，the teacher teaches the small children．In the afternoon．the bigger children come to have their lessons because they must work in the morning．At night．the fathers and mothers come to school．They want to learn．too．How the farmers hope that some day they can have a real school on their farm!( )46．The driver of the bus is ________．A．the teacher B．the student C．the farmer D．the school( )47．The bus school will ________．A．take the children to school B．stay here for a long time C．take the fathers and mothers to school D．go round from place to place( )48．When the bus school comes the farmers will ________．A．stop working B．warmly welcome it C．be happy D．both B and C ( )49．The bigger children have their lessons in the afternoon because ________ in the morning．A．they can’t get up early B．the teacher wants to teach the small children first C．they have a lot of work to do D．they have to do their homework( )50．Which is true?A．A school bus is a real school for farmers’childrenB．The bus school has no teacher at all．C．The bus school has no students．D．The children and their parents on the farm all come to the bus school to learn．BWelcome to Share Ideas! I’m Tony Brown. This is Professor (教授)Lin. He is a scientist. He has many exciting ideas about life in the future. Let’s listen to what he has to say.“I think in the future, traveling will be much cleaner and safer. Most cars will run on solar energy( 太阳能). That way, there will be less pollution . that cars will be driven by computers and there will be an accidents ( 事故) . All of the computers will work together with radio signals(信号).“I also think that people will be able to go back to the past through a time tunnel(隧道), If they do something wrong, they will be able to go back and do it again and try not to make the same mistakes.“Housework will become much easier because you’ll just tell a robot to do it.“in the future, people will be able to talk with each other on the phone more easily, and you’ll be able to see the person you’re talking to on the screen of the cellphone . The telephones that we have today will seem out of date.‖What do you think life in the future will be like? Send us a letter.Our e-mail address: shareideas @ see you next time!( )51. What are professor Lin’s ideas about?A. Travel in the futureB. TV programsC. Life in the futureD. Future telephone( )52. Professor Lin thinks that cars might be driven by_________.A．radio signals B. computers C. solar energy D. policeman( )53. Which of the following is NOT possible according to Professor Lin?A. There will be fewer car accidents.B. People won’t get sick B. robots willhelp people do housework D. People will not use telephone.( )54. What does the underlined word”mistake”mean in Chinese?A．破损B。
浙江省杭州市绿城育华中学八年级历史与社会《得天独厚的大河文明》课件 人教版
前3000年，苏美尔人 建立了很多小国。
前18世纪汉谟拉比统一
前16世纪被外族灭亡
前 4000
前 2000
公元 元年
灿烂的古巴比伦文明
巴别塔和空中花园
楔形文字
《汉谟拉比法典》 是世界上现存的古代第一部比较完备的成文法典
• 古巴比伦王国的消失。原因？
印度河和恒 河流域有哪些孕 育文明的优越自 然条件？
古代两河流域所在地主要在今天的哪一个国家？ 这一地区与当今世界上哪些热点地区与焦点问题有关？
• 根据两河流域的自然条件怎样？你认为那里的居民要发展 农业,最需要做的是什么?
自然条件：干旱少雨，河水水量不稳定。 需要：修建灌溉系统。
两河流域兴衰史
前3500年 出现城镇、 神庙、宫 殿和文字, 成为最早 的文明发 祥地之一
四大文明古国
文明古国 地理位置 发源河流 文明孕育年代
古代埃及 古巴比伦 古代印度 古代中国
非洲东北部 尼罗河
你能画出古代埃及的历 史发展的时间轴吗？
前3500年出 现小国
前3000统一 国家建立
前15世纪 地跨亚非
前6世纪灭 亡
灿烂的古埃及文明
• 古埃及人除以建筑金字塔、狮身人面像及制造木乃伊而闻名 天下外，还发明了许多对后世影响深远的东西。
• 古埃及的文化非常丰富。创造的象形文字对后来腓尼基 字母的影响很大，而希腊字母是在腓尼基字母的基础上创建 的。此外，金字塔、亚历山大灯塔、阿蒙神庙等建筑体现了 埃及人高超的建筑技术和数学知识，在几何学、历法等方面 也有很大的成就。
7月--- 10月 尼罗河的泛滥期
10月底 大水开始撤退
11月—2月 下种季节
3月—6月 收获季节
初中班主任培训plt课件
个性化辅导计划
制定针对性的辅导计划，帮助学 生解决学习困难。
激励与鼓励
通过正面激励和鼓励，增强学生 的自信心和学习动力。
青春期教育问题应对
1 2
青春期生理变化应对
引导学生正确面对青春期的生理变化，养成良好 的卫生习惯。
青春期心理问题疏导
关注学生的心理健康，及时进行心理疏导和干预 。
3
青春期性教育引导
开展适当的性教育，引导学生正确对待性和情感 问题。
CHAPTER 05
班级突发事件处理与预防
安全事故应急处理方案制定
制定应急预案
针对可能发生的安全事故，制定相应的应急处理 预案，明确处理流程、责任人和联系方式。
开展应急演练
定期组织学生进行应急演练，熟悉应急处理流程 ，提高应对能力。
建立安全档案
记录学生的健康状况、家庭背景等信息，以便在 发生安全事故时迅速了解学生的基本情况。
职业发展规划建议
自我认知与定位
深入了解自己的兴趣、特长和优势，明确职业发展方向。
目标设定与分解
根据职业发展目标，制定长期、中期和短期计划，明确各阶段的任 务和目标。
行动计划与执行
制定具体的行动计划，包括学习时间规划、任务分配、优先级等， 确保计划的执行。
THANKS
[ 感谢观看 ]
师生冲突化解方法论述
倾听与理解
认真倾听学生的诉求和意见，理解学生的立场和情感，避免情绪 激化。
沟通与协商
与学生进行平等、开放的沟通，协商解决问题，达成共识。
引导与教育
引导学生树立正确的价值观和人生观，教育学生尊重他人、遵守 纪律，预防冲突发生。
家长投诉处理流程介绍
01
02
03
杭州绿城育华学校初三八年级物理第五章 透镜及其应用汇编
杭州绿城育华学校初三八年级物理第五章透镜及其应用汇编一、选择题1．学习了透镜知识后，李华同学回家认真研究爷爷的老花镜，并得出以下结论。
你认为他的这些结论中不正确的是A．老花镜能在阳光下点燃白纸 B．老花镜可以用来做放大镜C．老花镜是一种凹透镜 D．爷爷是个远视眼2．如图所示，有一圆柱体PQ，放在凸透镜前图示的位置，它所成像P′Q′的形状应该是下列图中的（）A．B．C．D．3．如图所示是一个魔术箱，魔术箱的顶部的中央有一条窄缝，使激光笔产生的激光束从左侧的小孔射入，从右侧小孔射出．将一块遮光板从顶部的窄缝插入箱中，发现遮光板并没有挡住激光束的传播．下面几种设计方案中错误的是A．B．C．D．4．如图所示，早期照相馆里摄影师取景时看到的像是倒立的，有几位同学对此现象展开了讨论，下述观点正确的是（）A．将照相机靠近两位照相的人，可以看到两位照相人的全身像B．调整相机和两位照相人之间的距离，人像变小时，应增大相机镜头和胶片之间的距离C．要使人像更亮，必须在两位照相的人身后进行“补光”D．现在的相机利用光学或电子技术，把倒立的像转变成正立的，便于观察5．我们出入医院要手持绿色健康通行码，用手机扫描通行码，相当于给通行码拍了一张照片，手机摄像头相当于凸透镜，影像传感器相当于光屏，下列说法正确的是（）A．纸质的绿色健康通行码是光源B．扫码时绿色健康通行码要位于摄像头一倍焦距和二倍焦距之间C．要使屏幕上通行码的像变小，只需将通行码靠近凸透镜D．当通行码超岀手机上设定的方框时，通行码不动，应把手机远离通行码6．如图所示，下列关于光学现象的描述正确的是（）A．图甲中，小孔成倒立的虚像B．图乙中，配戴凹透镜可以矫正近视眼C．图丙中，光的三原色是红、黄、蓝D．图丁中，漫反射不遵循光的反射定律7．如图所示，给凸透镜“戴”上远视眼镜，此时光屏上能成一清晰的像，若“取”下远视眼镜，光屏上的像变模糊。
为使光屏上的像清晰，某小组提出的做法如下：①将光屏远离透镜；②将光屏靠近透镜；③将蜡烛远离透镜；④将蜡烛靠近透镜，你认为可行的是（）A．①和④B．②和④C．①和③D．②和③8．在探究凸透镜成像规律时，小明在光具座上将蜡烛沿主光轴由90cm处移至120cm处时(蜡烛图上未画出)，发现烛焰在图示位置的光屏上恰好成一清晰的像.若他再将蜡烛在光具座上沿主光轴移至135cm处，移动光屏再现一清晰的像，则屏上的像一定是A．缩小的像 B．等大的像 C．放大的像 D．正立的像9．在光具座上做观察凸透镜成像的实验时，把物体放在距离凸透镜光心60厘米处时，能在光屏上得到一个倒立缩小的清晰的像；若把物体放在距该凸透镜光心30厘米处时，则该凸透镜所成的清晰的像（）A．可能是虚像 B．一定是正立的像C．一定是倒立的 D．一定是缩小的10．如图所示的四幅图，有的能够说明近视眼或远视眼的成像原理，有的给出了近视眼或远视眼的矫正方法．下列判断正确的是( )A．图①能够说明远视眼的成像原理，图④给出了远视眼的矫正方法B．图②能够说明远视眼的成像原理，图④给出了远视眼的矫正方法C．图①能够说明近视眼的成像原理，图③给出了近视眼的矫正方法D．图②能够说明近视眼的成像原理，图④给出了近视眼的矫正方法11．显微镜的物镜和目镜的成像原理分别和下列哪组仪器成像原理类似A．投影仪、照相机B．照相机、放大镜 C．投影仪、放大镜D．放大镜、投影仪12．许多家庭的门上都装有防盗门镜，从室内透过防盗门镜向外看，可以看到来客的正立、缩小的像，由此可以断定，此时防盗门镜的作用相当于一个A．凸透镜 B．凹透镜 C．三棱镜 D．玻璃砖13．在“探究凸透镜成像规律”的实验中，记录像到凸透镜的距离v(像距)跟物体到凸透镜的距离u(物距)之间对应关系，并作出如图所示的u-v，关系图线，下列判断正确的是A．该凸透镜的焦距是20cmB．该凸透镜的焦距是8cmC．当物距u=40cm时，像距v=1 0cmD．把物体从距凸透镜15cm处移动到25cm处的过程中，像一直在变小14．在做“探究凸透镜成像的规律”实验时，某实验小组所描绘的像距随物距变化的关系图线如图所示．图线中 A、B、C 三点分别与蜡烛在光具座上移动过程中的三个位置相对应．则下列说法正确的是A．蜡烛处于 AB 间某一位置时，成倒立、缩小的实像B．蜡烛处于 BC 间某一位置时，成倒立、放大的实像C．将蜡烛从 C 移动到 B 的过程中，所成像逐渐增大D．将蜡烛从 B 移动到 A 的过程中，所成像逐渐减小15．由中国著名演员吴京自导自演的3D电影《战狼2》引发了观众强烈的爱国主义共鸣，3D电影具有三维立体视觉效果，拍摄时，将两个摄像头按照人两眼间的距离放置，同时拍摄，制成胶片；放映时，两个放映机在银幕上呈现两个略有差异的画面，观看者带上特殊眼镜后，就和直接用双眼看到物体的效果一样。
杭州绿城育华学校物理八年级简单机械单元专项训练
杭州绿城育华学校物理八年级简单机械单元专项训练一、选择题1．如图所示，斜面高为1m，长为4m，用沿斜面向上大小为75N的拉力F，将重为200N 的木箱由斜面底端以0.2m/s的速度匀速拉到顶端，下列判断正确的是（）A．重力做功的大小为800J B．斜面对木箱的摩擦力大小为25NC．拉力做功的功率为125W D．斜面的机械效率为75%2．如图所示，A物体受到的重力是 100N，在拉力F 的作用下，能以 0.2m/s 的速度在水平地面上向左匀速直线运动。
已知拉力F＝5N，滑轮组的机械效率为 80%，则下列说法正确的是（）A．拉力F 的功率是 1W B．2s 内绳子自由端移动的距离是 1.2m C．5s 内拉力所做功的大小是 15J D．物体 A受到水平地面的摩擦力大小是 8N 3．如图所示，一块厚度很薄、质量分布均匀的长方体水泥板放在水平地面上，若分别用一竖直向上的动力F1、F2作用在水泥板一端的中间，欲使其一端抬离地面，则（）A．F1>F2，因为甲中的动力臂长B．F1<F2，因为乙中的阻力臂长C．F1>F2，因为乙中的阻力臂短D．F1=F2，因为动力臂都是阻力臂的2倍4．小兰和爸爸、妈妈一起参加了一个家庭游戏活动．活动要求是：家庭成员中的任意两名成员分别站在如图所示的木板上，恰好使木板水平平衡．若小兰和爸爸的体重分别为400N 和800N，小兰站在距离中央支点2米的一侧，爸爸应站在距离支点l米的另一侧，木板水平平衡．现在他们同时开始匀速相向行走，小兰的速度是0.5米/秒，则爸爸的速度是多大才能使木板水平平衡不被破坏？A．1.0米/秒B．0.75米/秒C．0.5米/秒D．0.25米/秒5．如图所示，不计滑轮自重及绳子与滑轮之间的摩擦，三个弹簧测力计拉力F A、F B、F c三者的关系正确的是A ．F A ：FB ：F c ＝3：2：1B ．F A ：F B ：F c ＝1：2：3C ．F A ：F B ：F c ＝6：3：2D ．F A ：F B ：F c ＝2：3：66．某同学自制了一架天平，由于制作粗糙，天平两侧长度不同．当将一物体放在天平的左盘时，右侧砝码的质量为m 1，恰好平衡；当将该物体放在天平的右盘时，左侧砝码的质量为m 2，天平才平衡．则该物体的质量应为：（ ）A ．B ．C ．D ．无法确定7．用F 1的拉力直接将重为G 的物体A 匀速提升h （如图甲）；换用斜面把物体A 匀速提升相同的高度，拉力为F 2 ， 物体沿斜面运动的距离为L （如图乙），利用斜面工作过程中A ．有用功为F 2hB ．额外功为F 2L －F 1hC ．总功为（F 1+F 2）L D．机械效率为12F F 8．如图，小明分别用甲、乙两个滑轮把同一袋沙子从地面提到二楼，用甲滑轮所做的总功为W 1，机械效率为η1；用乙滑轮所做的总功为W 2，机械效率为η2．若不计绳重与摩擦，则（ ）A ．W 1=W 2 η1=η2B ．W 1＜W 2 η1＜η2C ．W 1＞W 2 η1＞η2D ．W 1＜W 2 η1＞η29．如图所示，可绕O 点转动的轻质杠杆，在D 点挂一个重为G 的物体M ，用一把弹簧测力计依次在A ，B ，C 三点沿圆O 相切的方向用力拉，都使杠杆在水平位置平衡，读出三次的示数分别为F 1、F 2、F 3 ， 它们的大小关系是A ．F 1＜F 2＜F 3＜GB ．F 1＞F 2＞F 3＞GC ．F 1=F 2=F 3=GD ．F 1＞F 2=F 3=G10．如图所示的是工人在平台上通过滑轮组向上拉起重物G的情景．已知重物G所受的重力为700 N，当他沿水平方向用400 N的力拉重物G时，重物G恰好做匀速直线运动．不计绳重及摩擦，下列说法正确的是A．该滑轮组的动滑轮所受的重力为100 NB．若工人拉动绳子的速度为0.5 m/s，则4 s后，绳子的拉力所做的功为1 400 JC．当工人用等大的力使绳子以不同速度匀速运动，且绳端运动相同的距离时，工人所做的功大小不同D．若将重物G换为质量更大的物体，则在不改变其他条件的情况下，工人将更省力二、填空题11．如图甲所示为一种搬运建筑材料的机械装置，A B是个杠杆，O为支点，杠杆平衡时，B端受到的向下的拉力________A端受到的向下拉力（选填“大于”、“小于”或“等于”）；用于装载货物的小车自重为500N，若搬运2000N的货物，电动卷扬机拉钢丝绳的力F甲＝1600N，该滑轮组的效率η甲＝________；若用同样的滑轮按乙图组装，匀速提升相同的货物，电动卷扬机拉钢丝绳的力为F乙，乙滑轮组的效率为η乙，考虑实际情况，则F甲________F乙，η甲________η乙（选填“>”、“<”或“＝”）．12．如图所示，小超同学用滑轮组匀速提升重200N的物体，若每个滑轮均重10N，绳重和摩擦忽略不计，则他对绳子的拉力是_____N。
杭州绿城育华学校物理八年级第九章 压强单元专项训练
杭州绿城育华学校物理八年级第九章压强单元专项训练一、选择题1．在两个完全相同的容器中分别倒入甲和乙两种不同的液体，如图所示，下列分析正确的是（）A．若甲和乙的质量相等，则甲的密度小于乙的密度B．若甲和乙对容器底部的压强相等，则甲的密度小于乙的密度C．若甲和乙对容器底部的压强相等，则甲的质量小于乙的质量D．若甲和乙的质量相等，则甲对容器底部的压强小于乙对容器底部的压强2．如图所示，甲、乙是两个形状、大小相同的容器，其中一个正放，另一个倒放，里面装有等质量的同种液体，液体对容器底部的压强p甲和p乙，液体对容器底部压力F甲和F乙则下列说法正确的是（）A．p甲＞p乙，F甲=F乙B．p甲＜p乙，F甲＜F乙C．p甲＜p乙，F甲＞F乙D．p甲=p乙， F甲=F乙3．下列各组连线配对中，完全正确的是（）A．生产运输工具与制造原理：推土机安装履带——增大受力面积减小压力；潜水艇原理——利用“空心法”；飞机能上升——流速大的地方压强小B．物理量及单位：压强——P；速度——m/s；力——NC．物理学家及其主要贡献：汤姆生——发现中子；牛顿——发现万有引力定律；托勒玫——提出“日心说”D．物理量及测量工具：力——测力计；大气压——气压计；液体体积——量筒4．如图所示，质地均匀的实心圆柱体A、B叠放在水平地面上，已知他们的密度之比ρA：ρB=1：3，底面积之比S A：S B=4：3，A对B的压强和B对地面的压强之比P A：P B=1：2，则他们的高度之比h A：h B为（）A．9：4 B．3：2 C．3：1 D．9：25．如图所示，实心正方体物体甲、乙放在水平地面上．沿水平方向切去不同的厚度，使二者剩余部分的体积相同、剩余部分对地面压强相同．则切去部分的质量△m甲、△m乙和切去前甲、乙对地面的压强 p 甲、p 乙的关系是（ ）A ．△m 甲＞△m 乙 p 甲＞p 乙B ．△m 甲＞△m 乙 p 甲＜p 乙C ．△m 甲＜△m 乙 p 甲＞p 乙D ．△m 甲＜△m 乙 p 甲＜p 乙6．如图所示，甲、乙两个实心均匀正方体放在水平地面上，甲对地面的压强小于乙对地面的压强。