27-27 澳门统计年鉴数据处理:按受教育程度统计14岁及以上人口(便于2001-2016多年数据分析对比)
基础教育学校(机构)统计报表(九年一贯制学校、十二年一贯制学校)

基础教育学校(机构)统计报表(九年一贯制学校、十二年一贯制学校)九年一贯制学校、十二年一贯制学校统计报表填报总体说明1.填报范围:九年一贯制学校、十二年一贯制学校填报本表。
2.报送日期:9月20日前报出。
3.学年:是指教育年度,即从本年的9月1日(学年初)至第二年的8月31日(学年末)。
4.统计时点:是指统计数据的调查截止时间,即本学年初9月1日。
如在校生数、教职工数、占地面积、固定资产总值等指标为统计时点数。
5.统计时期:是指统计数据的调查区间时间,即从上学年度的学年初9月1日至学年末8月31日时间区间。
如毕业生数、复学学生数等指标为统计时期数。
6.归档:本表由学校(机构)和县级教育行政部门归档管理。
基础基111学校(机构)基本情况一、指标解释1.学校(机构)学校(机构):是指经县级及以上人民政府按照国家规定设置标准和审批程序批准成立、备案的实施各级各类教育的单位。
学校(机构)名称:是指在教育行政部门备案的学校(机构)全称。
学校(机构)标识码:是指由教育部按照国家标准及编码规则编制,赋予每一个学校(机构)在全国范围内唯一的、始终不变的识别标识码。
2.学校(机构)办学类型九年一贯制学校:是根据国家义务教育法有关实施九年义务教育年限的规定组建起来的,贯穿小学与初中教育的一体化学校。
十二年一贯制学校:是根据国家教育法有关实施教育年限的规定组建起来的,贯穿小学与中学教育的一体化学校。
少数民族学校:是指以少数民族学生为主的实施初等、中等教育的独立设置学校。
3.学校(机构)驻地城乡类型:是指学校(机构)驻地的城乡分类属性,分为城区、镇区、乡村,以国务院关于市镇建制的规定和行政区划为基础,以民政部门确认的居民委员会和村民委员会为最小划分单元。
城区:是指在市辖区和不设区(包括不设区的地级市和县级市)的市中,街道办事处所辖的居民委员会地域;城市公共设施、居住设施等连接到的其他居民委员会地域和村民委员会地域。
镇区:是指在城市以外的镇和其他区域中,镇所辖的居民委员会地域;镇的公共设施、居住设施等连接到的村民委员会地域;常住人口在3000人以上独立的工矿区、开发区、科研单位、大专院校、农场、林场等特殊区域。
澳门青年对学士毕业后持续升学的意向调查撮要

“澳門青年對學士畢業後持續升學的意向調查”撮要歸源社會研究學會近年,隨著本澳人口素質的日漸提升,青年研究成為社會大眾所關注的一項議題,尤其是青年教育方面。
本研究將著重探討20-29歲澳門青年對學士畢業後持續升學的原因及意圖,作出升學決定的因素,升學人士選擇升讀的科目及地區的趨勢和原因,並綜合受訪者對現行狀況的意見。
研究目的:z了解20-29歲澳門青年對持續升學的原因及意圖反映澳門青年對持續升學的原因及意圖,探討各方面所提供的資源是否充足,支援及設施配套是否完善。
z探討影響澳門青年作出升學決定的因素分析澳門青年對持續升學的取向因素,將有利於更清楚地了解各種因素的影響,再採取適合的措施,完善高等教育的持續發展。
z分析升學人士對選修學科的趨勢和原因分析升學人士及意圖升學人士所選修學科的趨勢,作出合適的配合以達致資源合理分配的最佳效果。
z整合受訪者對現行制度的意見向當局反映受訪者的意見,希望藉此能夠集思廣益,完善現存制度及相關法規。
研究方法:本次研究主要以問卷調查形式收集數據,受訪對象必須同時滿足以下三項條件:z擁有澳門特別行政區永久或非永久性居民身份z年齡界乎二十至二十九歲z過往曾經接受大專教育的在職人士、正在就讀澳門或外地大專院校的現職學生數據收集方式以街頭隨機抽樣為主,其次亦以網上問卷收集數據。
本次研究共回收有效問卷815份。
街頭隨機抽樣的總回收問卷有568份,而網上回收問卷共有247份。
98/99年度至07/08年度間的升大人數總計不多於32,773人。
因此,本次研究樣本數量約佔總體研究對象的2.5%。
研究結果:本次研究受訪者總數為815人,當中男性佔376人,女性佔439人;20-23歲佔557人、24-26歲佔175人、27-29歲佔80人。
首次入讀大學年齡為19歲或以下的佔630人、20-23歲佔152人、24-26歲和27-29歲各佔6人。
高學歷情況為正就讀學士的佔446人、學士畢業的佔308人、碩士畢業的佔31人。
社会统计知识学知识题卢淑华
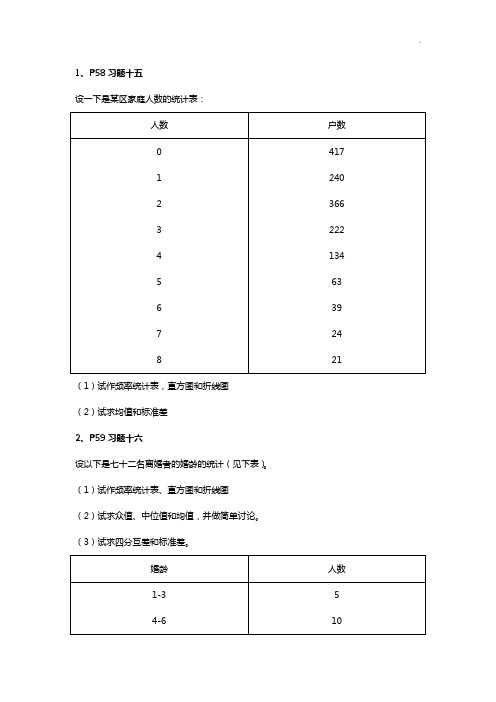
1、P58习题十五设一下是某区家庭人数的统计表:(1)试作频率统计表,直方图和折线图(2)试求均值和标准差2、P59习题十六设以下是七十二名离婚者的婚龄的统计(见下表)。
(1)试作频率统计表、直方图和折线图(2)试求众值、中位值和均值,并做简单讨论。
(3)试求四分互差和标准差。
3、P59习题十七设以下是1209名抽烟者年龄的统计(见下表)(1)试作频率统计表、直方图和折线图(2)试求四分互差。
4、P72例10某年级共有学生一百名,其中来自广东省的有二十五名,来自广西省的有十名,问任抽一名,来自两广的概率是多少?根据某市职业代际流动的统计,服务性行业代际向下流动的概率为0.07,静止不流动的概率为0.85,求服务性行业代际向上流动的概率是多少?6、P75例13为了呀牛父代文化程度对子代文化程度的影响,某大学统计出学生中父亲具有大学文化程度的占30%,母亲具有大学文化程度的占20%,而父母双方都具有大学文化程度的占10%,问学生中任抽一名,父代至少有一名具有大学文化程度的概率是多少?7、P75例14某地对外国旅游者旅游动机进行了调查,发现旅游者处于游览名胜的概率为0.219;处于异族文化的吸引占0.509;而两种动机兼而有之的占0.102.问旅游动机为游览名胜或为异族文化吸引的概率是多少?8、P76例16根据统计结果,在自然生育情况下,男婴出生的概率为22/43;女婴出生的概率为21/43.某单位有两名孕妇,问两名孕妇都生男婴的概率是多少?两名孕妇都生女婴的概率是多少?其中一名孕妇生男婴、一名孕妇生女婴的概率是多少?9、P77例17某居民楼共十二户,其中直系家庭为两户,问访问两户都是直系家庭的概率是多少?10、P78例18某居民楼共二十户,其中直系家庭为两户,问访问第二户才是直系家庭的概率是多少?11、P78例20设居民楼共有住户一千户,其中核心家庭占60%,问访谈中散户都是核心家庭的概率是多少?10人抓阄,其中共有2张球票,问第2个人抓到球票的概率?13、P85例23设出口商标为Made in China的产品,其中有50%为上海厂的产品;30%为北京厂得产品;20%为天津厂的产品。
学生基本信息表
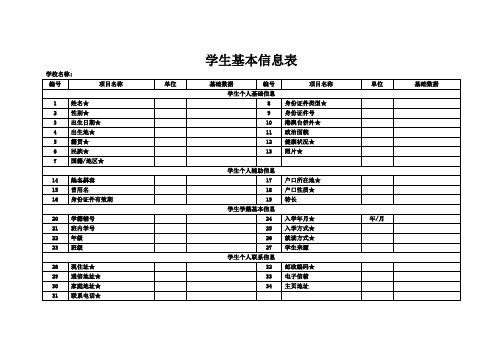
学生基本信息表学校名称:填表人:填表日期:审核人:审核日期:指标解释及填报说明1.姓名:在公安户籍管理部门正式登记注册、人事档案中正式记载的中文姓名(包括外国人正式的汉字姓名)。
2.性别:1-男,2-女。
3.出生日期:在公安户籍部门正式登记注册、人事档案中记载的时间日,年填4位数字、月填2位数字、日期填2位数字。
如:“20110101”。
4.出生地:学生出生所在的行政区划。
5.籍贯:祖居或本人出生的地方,现多用于父辈以上的居住地。
6.民族:学生的民族,用两位数字代码,如:01-汉族,02-蒙古族,参见《中国各民族代码》。
7.国籍/地区:学生所属的国籍/地区。
8.身份证类型:可证明学生身份的证件类型:1-居民身份证,6-香港特区护照/身份证明,7-澳门特区护照/身份证明,8-台湾居民来往大陆通行证,9-境外永久居住证,A-护照,Z-其他。
身份证件类型为Z-其他时,身份证件号可不填,但学校需提供学生在本校就读证明(需学生和家长签字,学校盖章,提交上级教育主管部门备案)。
9.身份证件号:身份证件类型对应的证件号码。
身份证件类型为Z-其他以外的证件类型时,身份证件号必填。
10.港澳台侨外:在大陆上学,持非大陆身份证明的学生的来源类型,分为:‘00-否,01-香港同胞,02-香港同胞亲属,03-澳门同胞,04-澳门同胞亲属,05-台湾同胞,06-台湾同胞亲属,11-华侨,12-侨眷,13-归侨,14-归侨子女,21-归国留学人员,31-非华裔中国人,41-外籍华裔人,51-外国人,99-其他’。
11.政治面貌:分为:“01-中共党员,02-中共预备党员,03-共青团员,13-群众”。
12.健康状况:学生的身体情况,分为:“10-健康或良好、20-一般或较弱、30-有慢性病、40-有生理缺陷、50-残疾”。
13.照片:导入学生的照片。
14.姓名拼音:姓名全称的汉语拼音。
15.曾用名:曾正式使用过的姓名。
16.身份证件有效期:身份证件上显示的有效期限。
(北师大版)北京市选修1-2第一章《统计案例》测试卷(含答案解析)

一、选择题1.2020年初,新型冠状病毒(19COVID -)引起的肺炎疫情爆发以来,各地医疗机构采取了各种针对性的治疗方法,取得了不错的成效,某地开始使用中西医结合方法后,每周治愈的患者人数如下表所示:由表格可得y 关于x 的二次回归方程为2ˆ6yx a =+,则此回归模型第4周的残差(实际值与预报值之差)为( ) A .5B .4C .1D .02.在一个质地均匀的小正方体的六个面中,三个面标0,两个面标1,一个面标2,将这个小正方体连续抛掷两次,若向上的数字的乘积为偶数,则该乘积为非零偶数的概率为( ) A .14 B .89 C .116D .5323.某校高二(1)班甲、乙两同学进行投篮比赛,他们进球的概率分别是34和45,现甲、乙各投篮一次,恰有一人进球的概率是( ) A .120B .320C .15D .7204.为研究某种细菌在特定环境下,随时间变化的繁殖情况,得到如下实验数据:由最小二乘法得与的线性回归方程为,则当时,繁殖个数y 的预测值为( ) A .4.9 B .5.25 C .5.95D .6.155.甲、乙两名同学参加2018年高考,根据高三年级一年来的各种大、中、小型数学模拟考试总结出来的数据显示,甲、乙两人能考140分以上的概率分别为12和45,甲、乙两人是否考140分以上相互独立,则预估这两个人在2018年高考中恰有一人数学考140 分以上的概率为( )A .12B .23C .34D .136.某研究型学习小组调查研究学生使用智能手机对学习的影响,部分统计数据如右表,则下列说法正确的是( )参考公式:22()()()()()n ad bc K a b c d a c b d -=++++,其中n a b c d =+++.参考数据:A .有99.9%的把握认为使用智能手机对学习有影响.B .有99.9%的把握认为使用智能手机对学习无影响.C .在犯错误的概率不超过0.005的前提下认为使用智能手机对学习有影响.D .在犯错误的概率不超过0.005的前提下认为使用智能手机对学习无影响.7.随机变量a 服从正态分布()21,N σ,且()010.3000P a <<=.已知0,1a a >≠,则函数1x y a a =+-图象不经过第二象限的概率为( ) A .0.3750 B .0.3000C .0.2500D .0.20008.抛掷红、黄两颗骰子,当红色骰子的点数为4或6时,两颗骰子的点数之积大于20的概率是( ) A .35B .14C .12D .139.四名同学根据各自的样本数据研究变量,x y 之间的相关关系,并求得回归直线方程,分别得到以下四个结论:①y 与x 负相关且 2.7567.3ˆ25yx =-+. ②y 与x 负相关且 3.47654ˆ.68y x =+ ③y 与x 正相关且 1.226 6.5ˆ78yx =-- ④y 与x 正相关且8.96786ˆ.13y x =+ 其中一定不正确的结论的序号是( ) A .①②B .②③C .③④D .①④10.两个变量y 与x 的回归模型中,分别选择了4个不同模型,它们对应的22121()1(ˆ)nii nii y yR y y ==-=--∑∑的值如下,其中拟合效果最好的模型是( )A .模型1对应的20.48R =B .模型2对应的20.96R =C .模型3对应的20.15R =D .模型4对应的20.30R =11.甲、乙两人同时报考某一所大学,甲被录取的概率为0.6,乙被录取的概率为0.7,两人是否被录取互不影响,则其中至少有一人被录取的概率为( ) A .0.12B .0.42C .0.46D .0.8812.为了研究经常使用手机是否对数学学习成绩有影响,某校高二数学研究性学习小组进行了调查,随机抽取高二年级50名学生的一次数学单元测试成绩,并制成下面的2×2列联表:则有( )的把握认为经常使用手机对数学学习成绩有影响.参考公式:()()()()()22=n ad bc K a b c d a c b d -++++,其中n a b c d =+++A .97.5%B .99%C .99.5%D .99.9%二、填空题13.某校组织甲、乙、丙、丁、戊、己等6名学生参加演讲比赛,采用抽签法决定演讲顺序,在“学生甲和乙都不是第一个出场,且甲不是最后一个出场”的前提下,学生丙第一个出场的概率为__________.14.某人进行射击训练,射击一次命中靶心的概率是0.9,各次射击相互独立,他连续射击3次,则“第一次没有命中靶心后两次命中靶心” 的概率是______.15.某一部件由四个电子元件按如图方式连接而成,元件1或元件2正常工作,且元件3或元件4正常工作,则部件正常工作.设四个电子元件的使用寿命(单位:小时)均服从正态分布2(1000,50)N ,且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为__________.16.甲、乙两队进行排球比赛,已知在一局比赛中甲队获胜的概率是23,没有平局,若采用三局两胜制比赛,即先胜两局者获胜且比赛结束,则甲队获胜的概率等于__________. 17.体育课上定点投篮项目测试规则:每位同学有3次投篮机会,一旦投中,则停止投篮,视为合格,否则一直投3次为止.每次投中与否相互独立,某同学一次投篮投中的概率为p ,若该同学本次测试合格的概率为0.784,则p =_____.18.关于变量,x y 的一组样本数据11()a b ,,22()a b ,,……,(),n n a b (2n ≥,12,,,n a a a ⋅⋅⋅不全相等)的散点图中,若所有样本点(,)i i a b (1,2,,i n =⋅⋅⋅)恰好都在直线21y x =-+上,则根据这组样本数据推断的变量,x y 的相关系数为_____________.19.在10个形状大小均相同的球中有4个红球和6个白球,不放回地依次摸出2个球,在第1次摸出红球的条件下,第2次也摸出红球的概率为_________.20.投到某出版社的稿件,先由两位初审专家进行评审,若能通过两位初审专家的评审,则直接予以录用,若两位初审专家都未予通过,则不予录用,若恰能通过一位初审专家的评审,则再由第三位专家进行复审,若能通过复审专家的评审,则予以录用,否则不予录用.设稿件能通过各初审专家评审的概率均为12,复审的稿件能通过评审的概率为14,各专家独立评审,则投到该出版社的1篇稿件被录用的概率为__________.三、解答题21.随着网络的发展,人们可以在网络上购物、玩游戏、聊天、导航等,所以人们对上网流量的需求越来越大.某电信运营商推出一款新的“流量包”套餐.为了调查不同年龄的人是否愿意选择此款“流量包”套餐,随机抽取50个用户按年龄分组进行访谈,统计结果如下表. 组号 年龄 访谈人数愿意使用1 [20,30) 5 52 [30.40) 10 103 [40.50) 15 124 [50.60) 14 8 5[60,70)62(1)若在第2、3、4组愿意选择此款“流量包”套餐的人中,用分层抽样的方法抽取15人,则各组应分别抽取多少人?(2)若从第5组的被调查者访谈人中随机选取2人进行追踪调查,求2人中至少有1人愿意选择此款“流量包”套餐的概率.(3)按以上统计数据填写下面2×2列联表,并判断以50岁为分界点,能否在犯错误不超过1%的前提下认为是否愿意选择此款“流量包”套餐与人的年龄有关;参考公式:()()()()()22n ad bc K a b c d a c b d -=++++,其中n a b c d =+++.22.高三(1)班班主任李老师为了了解本班学生喜爱中国古典文学是否与性别有关,对全班50人进行了问卷调查,得到如下列联表:已知从全班50人中随机抽取1人,抽到喜欢中国古典文学的学生的概率为35. (1)请将上面的列联表补充完整;(2)是否有99.5%的把握认为喜欢中国古典文学与性别有关?请说明理由;(3)已知在喜欢中国古典文学的10位男生中,1A ,2A ,3A 还喜欢数学,1B ,2B 还喜欢绘画,1C ,2C 还喜欢体育.现从喜欢数学、绘画和体育的男生中各选出1名进行其他方面的调查,求1B 和1C 不全被选中的概率.参考公式及数据:22()()()()()n ad bc K a b c d a c b d -=++++,其中n a b c d =+++.23.随着运动App 和手环的普及和应用,在朋友圈、运动圈中出现了每天1万步的健身打卡现象,“日行一万步,健康一辈子”的观念广泛流传.“健康达人”小王某天统计了他朋友圈中所有好友(共400人)的走路步数,并整理成下表:间中点值作代表);(2)若用A 表示事件“走路步数低于平均步数”,试估计事件A 发生的概率;(3)若称每天走路不少于8千步的人为“健步达人”,小王朋友圈中岁数在40岁以上的中老年人有200人,其中健步达人恰有150人,请填写下面22⨯列联表.根据列联表判断有多大把握认为,健步达人与年龄有关?附:()()()()()2n ad bc K a b c d a c b d -=++++24.某植物学家培养出一种观赏性植物,会开出红花或黄花,已知该植物第一代开红花和黄花的概率都是12,从第二代开始,若上一代开红花,则这一代开红花的概率是13,开黄花的概率是23;若上一代开黄花,则这一代开红花的概率是35,开黄花的概率是25.记第n代开红花的概率为n p ,第n 代开黄花的概率为n q . (1)求2p ;(2)①证明:数列9()19n p n N *⎧⎫-∈⎨⎬⎩⎭为等比数列; ②第*(,2)n n N n ∈≥代开哪种颜色花的概率更大?25.3月底,我国新冠肺炎疫情得到有效防控,但海外确诊病例却持续暴增,防疫物资供不应求,某医疗器械厂开足马力,日夜生产防疫所需物品.已知该厂有两条不同生产线A 和B 生产同一种产品各10万件,为保证质量,现从各自生产的产品中分别随机抽取20件,进行品质鉴定,鉴定成绩的茎叶图如下所示:该产品的质量评价标准规定:鉴定成绩达到[90,100)的产品,质量等级为优秀;鉴定成绩达到[80,90)的产品,质量等级为良好;鉴定成绩达到[60,80)的产品,质量等级为合格.将这组数据的频率视为整批产品的概率.(1)从等级为优秀的样本中随机抽取两件,记X 为来自B 机器生产的产品数量,写出X 的分布列,并求X 的数学期望;(2)请完成下面质量等级与生产线产品列联表,并判断能不能在误差不超过0.05的情况下,认为产品等级是否达到良好以上与生产产品的生产线有关.A 生产线的产品B 生产线的产品 合计良好以上 合格 合计附:22()()()()()n ad bc K a b c d a c b d -=++++()20P K k0.10 0.05 0.01 0.005 0k 2.7063.8416.6357.87926.自然资源部门对某市饮用水厂中的地下水质量进行监测,随机抽查了100眼水井进行监测,得到溶解性总固体浓度(单位:mg L )和硫酸盐浓度(单位:mg L )的分布如下表:(1)估计事件“该市某一水井中溶解性总固体浓度不超过500,且硫酸盐浓度不超过150”的概率;(2)根据所给数据,完成下面的22⨯列联表:(3)根据(2)中的列联表,判断是否有99%的把握认为该市水井中溶解性总固体浓度与硫酸盐浓度有关?附:()()()()()22n ad bcKa b c d a c b d-=++++,n a b c d=+++.【参考答案】***试卷处理标记,请不要删除一、选择题1.A解析:A【分析】设2t x =,求出t ,y 的值,由最小二乘法得出回归方程,代入4x =,即可得出答案. 【详解】 设2t x =,则()11491625115t =++++=,()12173693142585y =++++= 586118a =-⨯=-,所以2ˆ68yx =-.令4x =,得2444936485ˆe y y =-=-⨯+=. 故选:A 【点睛】本题考查回归分析的应用,属于中档题.2.D解析:D 【分析】首先确定是条件概率,在出现数字乘积为偶数的前提下,乘积为非零偶数的概率, 首先求两次数字乘积为偶数的概率, 然后两次为非零偶数的概率,再按照条件概率的公式求解. 【详解】两次数字乘积为偶数,可先考虑其反面——只需两次均出现1向上,概率是22169⎛⎫= ⎪⎝⎭,所以两次数字乘积为偶数的概率P =228169⎛⎫-= ⎪⎝⎭ ; 若乘积非零且为偶数,需连续两次抛掷小正方体的情况为(1,2)或(2,1)或(2,2),P =111152366636⨯⨯+⨯=, .故所求条件概率为55368329P ==.故选:D 【点睛】本题主要考查了条件概率的计算和独立事件,考查了学生的计算能力,属于基础题.3.D解析:D 【分析】利用相互独立事件的概率乘法公式求得 甲投进而乙没有投进的概率,以及乙投进而甲没有投进的概率,相加即得所求. 【详解】甲投进而乙没有投进的概率为343(1)4520⨯-=,乙投进而甲没有投进的概率为341(1)455-⨯=,故甲、乙各投篮一次,恰有一人投进球的概率是 31720520+=,故选:D 【点睛】本题主要考查了相互独立事件的概率乘法公式的应用,体现了分类讨论的数学思想,属于中档题.4.B解析:B 【分析】根据表格中的数据,求得样本中心为97(,)22,代入回归直线方程,求得ˆ0.35a=,得到回归直线的方程为ˆ0.70.35yx =+,即可作出预测,得到答案. 【详解】由题意,根据表格中的数据,可得34569 2.534 4.57,4242x y ++++++====, 即样本中心为97(,)22,代入回归直线方程ˆˆ0.7yx a =+,即79ˆ0.722a=⨯+, 解得ˆ0.35a=,即回归直线的方程为ˆ0.70.35y x =+, 当7x =时,ˆ0.770.35 5.25y=⨯+=,故选B . 【点睛】本题主要考查了回归直线方程的应用,其中解答中熟记回归直线方程的特征,求得回归直线的方程是解答的关键,着重考查了运算与求解能力,属于基础题.5.A解析:A 【解析】分析:根据互斥事件概率加法公式以及独立事件概率乘积公式求概率.详解:因为这两个人在2018年高考中恰有一人数学考140 分以上的概率为甲考140 分以上乙未考到140 分以上事件概率与乙考140 分以上甲未考到140 分以上事件概率的和,而 甲考140 分以上乙未考到140 分以上事件概率为14(1)25⨯-,乙考140 分以上甲未考到140 分以上事件概率为14(1)25-⨯,因此,所求概率为14(1)25⨯-1451(1)25102+-⨯==, 选A.点睛:本题考查互斥事件概率加法公式以及独立事件概率乘积公式,考查基本求解能力.6.C解析:C 【解析】经计算,()2230421681020101218K ⨯-⨯==⨯⨯⨯,27.87910.828K <<,对照数表知,在犯错误的概率不超过0.005的前提下认为使用智能手机对学习有影响,故选C .点睛:本题考查了独立性检验的应用问题,是基础题;其解题步骤为:(1)认真读题,取出相关数据,作出22⨯列联表;(2)根据22⨯列联表中的数据,计算2K 的观测值k ;(3)通过观测值k 与临界值0k 比较,得出事件有关的可能性大小.7.C解析:C 【解析】1x y a a =+-图象不经过第二象限,11,2a a ∴-≤-∴≥,随机变量ξ服从正态分布()21,N σ,且()()()()1010.3000,120.3000,210.60000.20002P a P a P a <<=∴<<=∴>=-=,∴函数1x y a a =+-图象不经过第二象限的概率为0.20.250010.2=-,故选C. 8.D解析:D 【解析】抛掷红、黄两枚骰子,第一个数字代表红色骰子,第二个数字代表黄色骰子,当红色骰子的点数为4或6时有(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)共12种, 两颗骰子的点数之积大于20的种数有(4,6),6,4),(6,5),(6,6)4种, 根据概率公式得,两颗骰子的点数之积大于20的概率41123P ==. 本题选择D 选项.点睛:有关古典概型的概率问题,关键是正确求出基本事件总数和所求事件包含的基本事件数.(1)基本事件总数较少时,用列举法把所有基本事件一一列出时,要做到不重复、不遗漏,可借助“树状图”列举.(2)注意区分排列与组合,以及计数原理的正确使用.9.B解析:B 【解析】根据题意,依次分析4个结论:对于①、y 与x 负相关且ˆy=−2.756x+7.325,此结论正确,线性回归方程符合负相关的特征;对于②、y 与x 负相关且ˆy=3.476x+5.648,此结论误,由线性回归方程知,此两变量的关系是正相关;对于③、y 与x 正相关且ˆy=−1.226x−6.578,此结论误,由线性回归方程知,此两变量的关系是负相关;对于④、y 与x 正相关且ˆy=8.967x+8.163,此结论正确,线性回归方程符合正相关的特征;故②③一定错误; 本题选择B 选项.点睛:在回归直线方程y bx a =+中,b 代表x 每增加一个单位,y 平均增加的单位数,一般来说,当回归系数b >0时,说明两个变量呈正相关关系;当回归系数b <0时,说明两个变量呈负相关关系.10.B解析:B 【解析】回归分析中,相关指数R 2越接近于1,拟合效果越好; 越接近0,拟合效果越差,由模型2对应的R 2最大,其拟合效果最好。
计算机等级考试理论题题库

Page 1
151780912.xls
2306 2304 2299 2305 2255 2311 2279 2310 2309 2308 2307 2301 2271 2262 2263 2264 2265 2266 2267 2268 2253 2270 2259 2272 2273 2274 2275 2276 2277 2278 2269 2251 2242 2243 2244 2245 2246 2247 2248 2261 2250 2260 2252 2293 2254 2285 2256 2257 2258 2241 2249 2234 2478 2287 2292
WINDOWS基础-B WINDOWS基础-B WINDOWS基础-B WINDOWS基础-B WINDOWS基础-B WINDOWS基础-B WINDOWS基础-B WINDOWS基础-B WINDOWS基础-B WINDOWS基础-B WINDOWS基础-B WINDOWS基础-B WINDOWS基础-B WINDOWS基础-B WINDOWS基础-B WINDOWS基础-B WINDOWS基础-B WINDOWS基础-B WINDOWS基础-B WINDOWS基础-B 计算机基础知识A 计算机基础知识A 计算机基础知识A 计算机基础知识A 计算机基础知识A 计算机基础知识A 计算机基础知识A 计算机基础知识A 计算机基础知识A 计算机基础知识A 计算机基础知识A 计算机基础知识A 计算机基础知识B 计算机基础知识B 计算机基础知识B 计算机基础知识B 计算机基础知识B 计算机基础知识B 计算机基础知识B 计算机基础知识B 计算机基础知识B 计算机基础知识B 计算机基础知识B 计算机基础知识B 计算机基础知识B 计算机基础知识B 计算机基础知识B 计算机基础知识B 计算机基础知识B 计算机基础知识B 计算机基础知识B 计算机基础知识B 计算机基础知识B 计算机基础知识B 计算机基础知识B
应用回归分析-第2章课后习题参考答案

第二章 一元线性回归分析思考与练习参考答案2.1 一元线性回归有哪些基本假定?答: 假设1、解释变量X 是确定性变量,Y 是随机变量;假设2、随机误差项ε具有零均值、同方差和不序列相关性: E(εi )=0 i=1,2, …,n Var (εi )=σ2 i=1,2, …,n Cov(εi, εj )=0 i≠j i,j= 1,2, …,n 假设3、随机误差项ε与解释变量X 之间不相关: Cov(X i , εi )=0 i=1,2, …,n假设4、ε服从零均值、同方差、零协方差的正态分布 εi ~N(0, σ2 ) i=1,2, …,n 2.2 考虑过原点的线性回归模型 Y i =β1X i +εi i=1,2, …,n误差εi (i=1,2, …,n )仍满足基本假定。
求β1的最小二乘估计 解: 得:2.3 证明(2.27式),∑e i =0 ,∑e i X i =0 。
证明:∑∑+-=-=nii i ni X Y Y Y Q 121021))ˆˆ(()ˆ(ββ其中: 即: ∑e i =0 ,∑e i X i =02.4回归方程E (Y )=β0+β1X 的参数β0,β1的最小二乘估计与最大似然估计在什么条件下等价?给出证明。
答:由于εi ~N(0, σ2 ) i=1,2, …,n所以Y i =β0 + β1X i + εi ~N (β0+β1X i , σ2 ) 最大似然函数:使得Ln (L )最大的0ˆβ,1ˆβ就是β0,β1的最大似然估计值。
同时发现使得Ln (L )最大就是使得下式最小,上式恰好就是最小二乘估计的目标函数相同。
值得注意的是:最大似然估计是在εi ~N (0, σ2 )21112)ˆ()ˆ(i ni i ni ii e X Y Y Y Q β∑∑==-=-=01ˆˆˆˆi ii i iY X e Y Y ββ=+=-0100ˆˆQQββ∂∂==∂∂的假设下求得,最小二乘估计则不要求分布假设。
广东公务员考试《行测》真题模拟试题及答案解析【2022】795

广东公务员考试《行测》通关模拟试题及答案解析【2022】:791:从所给的四个选项中,选择最合适的一个填入问号处,使之呈现肯定的规律性:()单项选择题A、B、 alt=\C、 border=\D、 />E、2:2, 4, 3, 7, 16, 107,()单项选择题A. 1594B. 1684C. 1707D. 18563:2, 6, 15, 30, 45,()单项选择题A. 63B. 57C. 51D. 454:以下园林建筑中,不属于皇家园林的是()。
单项选择题A、承德避暑山庄B、颐和园C、圆明园D、拙政园5:一头羊用10米长的绳拴在一个长方形小屋外的墙角处,小屋长9米宽7米,小屋四周都是草地,羊能吃到草的草地面积为_______平方米。
单项选择题A.B.C.D.6:两种报纸全年定价分别为168元、216元,全室人员都订阅这两种报纸中的一种,用去2184元;假如他们都换订另一种,需要用2040元。
问该室有多少人()单项选择题A. 12B. 11C. 9D. 87:有些信息是政府没有义务公开甚至有义务不公开的,公民隐私即其中一例。
政府明显不应主动侵害公民隐私,而应尽量避开接触涉及公民隐私的信息,但为了更好地治理社会,政府需要收集大量统计信息,其中难免会涉及个人隐私、商业隐秘等公开后可能对个人或企业产生损害的信息。
这段话主要支持了这样一种论点,即()。
单项选择题A、政府不能够侵害个人隐私,更不能将其公开B、政府工作涉及个人隐私和商业机密在所难免C、政府收集个人隐私目的在于更好地治理社会D、个人隐私和商业机密需要政府下大力度爱护8:在空间中最多能放置多少个正方体,使得任意两个正方体都有一部分表面相接触()单项选择题A. 4B. 5C. 6D. 79:价格竞争是指商品生产者为了增加商品销售量,击败对手,提高赢利水平,利用价格作为竞争手段,通过降低商品的价格或采纳其他价格策略所绽开的竞争。
它是商业经营中频繁使用的竞争手段之一。
