银川一中2018届高三第一次月考文科数学试题(含答案)
2018年银川一中--高三第一次模拟数学(文科)试卷答案 最新

银川一中2018届高三第一次模拟文科数学试题参考答案及评分标准一、选择题:本大题共12小题,每小题5分.二.填空题:13:-1;14.541; 15.4; 16.215+ 三.解答题:17.(本小题满分12分)解:(1)1sin 2S bc A = 分4cos bc A =则1tan 12A S =≥42A ππ∴≤<(2)111()cos sin()2262f A A A A π=+=++ 521263A πππ≤+< 3A π=时()f A 取得最大值为3218.(本小题满分12分)(1)∵PA ⊥底面ABC ,∴PA ⊥BE 。
又∵△ABC 是正三角形,且E 为AC 的中点, ∴BE ⊥CA 。
又PA CA=A ,∴BE ⊥平面PAC 。
∵BE ⊂平面PBE , ∴平面PBE ⊥平面PAC(2)取CD 的中点F ,则F 即为所求。
∵E 、F 分别为CA 、CD 的中点, ∴EF//AD 。
又EF ⊂平面PEF ,AD ⊄平面PEF , ∴AD//平面PEF 。
(3).4423232123131=⋅⋅⋅⋅=⋅==--BEF BEFP PEF B S PA V V 19.(本小题满分12分)20.解:(1)第6小组的频率为1-(0.04+0.10+0.14+0.28+0.30)=0.14,∴此次测试总人数为7500.14=(人). ∴第4、5、6组成绩均合格,人数为(0.28+0.30+0.14)×50=36(人).(2)直方图中中位数两侧的面积相等,即频率相等.前三组的频率和为0.28,前四组的频率和为0.56,∴中位数位于第4组内.(3)设成绩优秀的9人分别为,,,,,,,,,a b c d e f g h k 则选出的2人所有可能的情况为:,,,,,,,;ab ac ad ae af ag ah ak ,,,,,,;bc bd be bf bg bh bk ,,,,,;cd ce cf cg ch ck ,,,,;de df dg dh dk ,,,;ef eg eh ek ,,;fg fh fk ,;gh gk hk .共36种,其中a 、b 到少有1人入选的情况有15种,∴a 、b 两人至少有1人入选的概率为155.3612P == 20.(本小题满分12分) 解:(1)椭圆C 的离心率22=e , 得22=a c ,其中22b ac -=…………1分 椭圆C 的左、右焦点分别为),0,(1c F -、)0,(2c F ,又点2F 在线段1PF 的中垂线上,221PF F F =∴,222)2()3()2(c c -+=∴解得1,2,122===b a c ,∴椭圆C 的方程为1222=+y x .(2)由题意,直线l 的方程为)2(-=x k y ,且0≠k , 联立⎪⎩⎪⎨⎧=+-=12)2(22y x x k y ,得0288)21(2222=-+-+k x k x k ,由0)21(82>-=∆k ,得2222<<-k ,且0≠k设),(),,(2211y x N y x M ,则有2221218k k x x +=+,,21282221k k x x +-= (*) A MF F NF 212∠=∠ ,且由题意 ︒≠∠902A NF ,022=+∴NF MF k k , 又),0,1(2F 0112211=-+-∴x yx y ,即01)2(1)2(2211=--+--x x k x x k , 0)1111(221=-+--∴x x , 整理得04)(322121=++-x x x x , 将(*)代入得,-+-2221416k k 04212422=++kk , 知上式恒成立,故直线l 的斜率k 的取值范围是)22,0()0,22(⋃-. 21.(本小题满分12分)解:(1)由x x f ln )(=(0>x ),可得xx f 1)(/=(0>x ),∴f (x )在点(1,f (1))处的切线方程是)1)(1()1(/-=-x f f y ,即1-=x y ,所求切线方程为1-=x y ; (2)∵又g (x )= bx ax -2可得b ax x g -=2)(/,且g (x )在x =2处取得极值-2.∴⎩⎨⎧-==2)2(0)2(/g g ,可得⎩⎨⎧-=-=-22404b a b a 解得21=a ,2=b .所求g (x )=x x 2212-(x ∈R ) . (3)∵bx x x x g x f x h -+=+=221ln )()()(,x bx x x h 1)(2/+-=(0>x ). 依题存在0>x 使01)(2/<+-=xbx x x h ,∴即存在0>x 使012<+-bx x ,∵不等式012<+-bx x 等价于xx b 1+> (*) 令)0(1)(>+=x x x x λ,∵)0()1)(1(11)(22/>-+=-=x x x x x x λ.∴)(x λ在(0,1)上递减,在[1,∞+)上递增,故2[1)(∈+=xx x λ,∞+)∵存在0>x ,不等式(*)成立,∴2>b .所求b 2(∈,∞+).22.(本小题满分10分) 选修4-4:坐标系与参数方程 解:(1)由)4(24πθρ+=Cos 得:θθρSin Cos 44-=,θρθρρSin Cos 442-=∴即:04422=+-+y x y x ,∴C 的直角坐标方程为:()()82222=++-y x(2)设A,B 两点对应的 参数分别为21,t t ,直线t t y x ⎪⎪⎩⎪⎪⎨⎧=+=22222和圆的 方程联立得:,04222=-+t t 所以,4,222121-=-=+t t t t <0所以,261111212121=-=+=+t t t t t t PB PA 23.选修4-5:不等式(本题满分10分) (1)因为m a x ≤-所以m a x m a +≤≤-3,251==∴⎩⎨⎧=+-=-m a m a m a -------------5分 (2)2=a 时等价于x t x ≥+-2 当20,2,2<≤≥+-≥t x t x x 所以舍去 当,220,2,20+≤≤∴≥+-<≤t x x t x x 成立 当x t x x -≥+-<2,0成立所以,原不等式解集是⎥⎦⎤⎝⎛+∞-22,t -----------10分银川一中2018届高三第一次模拟政治试卷参考答案12-16 ADDCC 17-21 BDDBB 22-23 AA38.(1)(劳动者角度)①劳动者具有享受社会保险和福利的权利,大病保险全面覆盖,有利于维护劳动者的权益,保障劳动者主人翁地位,充分调动和发挥劳动者的积极性、创造性。
2018年银川一中--数学(文科)答案 最新

银川一中2018届高三第二次模拟文科数学试题参考答案二.填空题:13.1 14. 2 15.(3) (4) 16. 2513三、解答题: 17.解:(1)由得,,由得, B B B C B sin 32cos 5cos 32sin 532sin 5sin 5sin 3πππ-=⎪⎭⎫⎝⎛-==B B sin 25cos 235+=……4分,所以B B cos 235sin 21=,(2)设角、、所对边的长分别为、、 由和正弦定理得, 由得解得(负值舍去)由余弦定理得,18.(本小题满分12分)(1)解:取CD 的中点F ,连结BF ,则直角梯形A B C D 中,B F C D ⊥,B F C FD F ==90CBD ∴∠=︒即:BD BC ⊥⊥DE 平面ABCD ,⊂BC 平面ABCD DE BC ⊥∴又B D D E D ⋂= BDE BC 平面⊥∴ (2)解: 1112433233ABCE E ABC ABC V V DE S DE AB AD DE -∆==⨯⨯=⨯⨯⨯⨯== 2DE ∴=2222=+=∴AD DE EA ,3222=+=BD DE BE ,又2=AB 222AE AB BE +=∴ AE AB ⊥∴ ∴四棱锥A B C D E -的侧面积为6222621212121++=⨯⨯+⨯⨯+⨯⨯+⨯⨯CD DE BE BC AB AE AD DE19.(Ⅰ)-x =50×0.0010×100+150×0.0020×100+250×0.0030×100+350×0.0025×100+450×0.0015×100=265.(Ⅱ)当日需求量不低于300公斤时,利润Y =(20-15)×300=1500元; 当日需求量不足300公斤时,利润Y =(20-15)x -(300-x )×3=8x -900元;故Y =⎩⎨⎧8x -900,0≤x <300,1500,300≤x ≤500.由Y ≥700得,200≤x ≤500,所以P (Y ≥700)=P (200≤x ≤500)=0.0030×100+0.0025×100+0.0015×100 =0.7.20.解:(Ⅰ)由题意可得,1b =,c =2a =,, 椭圆C 的标准方程为2214xy +=. (Ⅱ)设000(,)(02)P x y x <≤,(0,1)A -,(0,1)B ,所以001PA y k x +=,直线PA 的方程为0011y y x x +=-,同理得直线PB 的方程为0011y y x x -=+,直线PA 与直线3x =的交点为003(1)(3,1)y M x +-,直线PB 与直线3x =的交点为⎪⎪⎭⎫⎝⎛+-1)1(3300x y N ,,线段MN 的中点003(3,)y x , 所以圆的方程为22200033(3)()(1)y x y x x -+-=-.令0y =,则222020093(3)(1)y x x x -+=-, 因为220014x y +=,所以20136(3)4x x -=-, 因为这个圆与x 轴相交,所以该方程有两个不同的实数解,则013604x ->,又002x <≤,解得024(,2]13x ∈.解法二:直线AP 的方程为111(0)y k x k =->,与椭圆2244x y +=联立得:2211(14)80k x k x +-=,121814P k x k =+,同理设BP 直线的方程为21y k x =+可得222814P k x k -=+,由121814k k +222814k k -=+,可得1241k k =-, 所以1(3,31)M k -,2(3,31)N k +,MN 的中点为123()(3,)2k k +,所以MN 为直径的圆为22212123()3()2(3)()()22k k k k x y +---+-=.0y =时,22212123()3()2(3)()()22k k k k x +---+=,所以212(62)(62)(3)4k k x ----=, 因为MN 为直径的圆与x 轴交于,E F 两点,所以12(62)(62)04k k --->,代入1241k k =-得:111(31)(43)04k k k --<,所以11334k <<,所以12111881144P k x k k k ==++在11(,)32单增,在13(,)24单减,所以24(,2]13px ∈.…12分 21.解:(1)由题意,知()()x x x g x af x e axe e =+=+,∴()()'1x g x ax a e =++. ①若0a =时,()'x g x e =,()'0g x >在R 上恒成立,所以函数()g x 在R 上单调递增; ②若0a >时,当1a x a+>-时,()'0g x >,函数()g x 单调递增, 当1a x a+<-时,()'0g x <,函数()g x 单调递减; ③若0a <时,当1a x a+>-时,()'0g x <,函数()g x 单调递减;当1a x a+<-时,()'0g x >,函数()g x 单调递增.综上,若0a =时,()g x 在R 上单调递增;若0a >时,函数()g x 在1,a a +⎛⎫-∞-⎪⎝⎭内单调递减,在区间1,a a +⎛⎫-+∞ ⎪⎝⎭内单调递增;当0a <时,函数()g x 在区间1,a a +⎛⎫-∞- ⎪⎝⎭内单调递增,在区间1,a a +⎛⎫-+∞ ⎪⎝⎭内单调递减.(2)由题可知,原命题等价于方程2xxe x =+在[],1x m m ∈+上有解,由于0xe >,所以0x =不是方程的解, 所以原方程等价于210xe x--=,令()21x r x e x =--,因为()'220xr x e x =+>对于()(),00,x ∈-∞+∞恒成立, 所以()r x 在(),0-∞和()0,+∞内单调递增.又()130r e =-<,()2220r e =->,()311303r e -=-<,()2120r e -=>,所以直线2y x =+与曲线()y f x =的交点仅有两个,且两交点的横坐标分别在区间[]1,2和[]3,2--内,所以整数m 的所有值为3-,1.22.(1)解:由2sin 2cos (0)a a ρθθ=>得:2(sin )2cos a ρθρθ= ∴曲线C 的直角坐标方程为:22y ax =(a > 0)由24x y ⎧=-⎪⎪⎨⎪=-⎪⎩消去参数t 得直线l 的普通方程为2y x =-(2)解:将直线l的参数方程24x y ⎧=-⎪⎪⎨⎪=-⎪⎩代入22y ax =中得:2(4)8(4)0t a t a -+++= 6分设M 、N 两点对应的参数分别为t 1、t 2,则有1212)8(4)t t a t t a +=+=+, 8分 ∵2||||||PM PN MN ⋅=,∴2212121212()()4=t t t t t t t t -=+- 即28(4)40(4)a a +=+,解得1a =.或4-=a 又因为4-=a 时,0<∆,故舍去,所以1a =.23.(本小题满分10分)选修4—5;不等式选讲.解法一:【命题意图】本题旨在考查绝对值不等式的解法、分析法在证明不等式中的应用,考查考生的推理论证能力与运算求解能力。
推荐-宁夏银川一中2018届高三第一次月考测试数学试卷

宁夏银川一中2018届高三年级第一次月考测试数学试卷本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分.第II 卷第22题为选考题,其他题为必考题.考生作答时,将答案答在答题卡上,在本试卷上答题无效.考试结束后,将本试卷和答题卡一并交回. 注意事项:1.答题前,考生先将自己的姓名、准考证号填写在答题卡上,2.选择题答案使用2B 铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或炭素笔书写,字体工整,笔迹清楚.3.请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效. 4.保持卡面清洁,不折叠,不破损.5.作选考题时,考生按照题目要求作答,并用2B 铅笔在答题卡上把所选题目对应的标号涂黑.第I 卷一、选择题:本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设全集U 是实数集R ,}034|{},22|{2<+-=>-<=x x x N x x x M 或,则图中阴影部分所表示的集合是 ( )A .}12|{<≤-x xB .}22|{≤≤-x xC .}21|{≤<x xD .}2|{<x x2.函数)13lg(13)(2++-=x xx x f 的定义域是( )A .),31(+∞-B . )1,31(-C . )31,31(-D . )31,(--∞3.汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车,若把这一过程中汽车的行驶路程s 看作时间t的函数,其图像可能是 ( )4.已知两个函数)(x f 和)(x g 的定义域和值域都是集合{1,2,3},其定义如下表:)A .{1}B .{2}C .{3}D .φA .B .C .D .5.设函数)(x f 的定义域为R ,有下列三个命题:①若存在常数M ,使得对任意,R x ∈有,)(M x f ≤则M 是函数)(x f 的最大值;②若存在,0R x ∈使得对任意,R x ∈,0x x ≠有),()(0x f x f <则)(0x f 是函数)(x f 的最大值; ③若存在,0R x ∈使得对任意,R x ∈有),()(0x f x f ≤则)(0x f 是函数)(x f 的最大值. 这些命题中,真命题的个数是 ( ) A . 0 B .1 C .2 D .36.设)(x f 是定义在R 上的函数,其图像关于原点对称,且当x >0时,32)(-=x x f ,则=-)2(f( )A .1B .-1C .41D .411-7.函数)1(log )(++=x a x f a x 在区间]1,0[上的最大值与最小值之和为a ,则a = ( )A .41B .21C .2D .48.下列函数中,在其定义域是减函数的 ( )A .1)(2++-=x x x fB .xx f 1)(=C .||)31()(x x f = D .)2ln()(x x f -=9.设函数⎪⎩⎪⎨⎧>≤++=0,20,)(2x x c bx x x f ,若2)2(),0()4(-=-=-f f f ,则关于x 的方程x x f =)( 的解的个数是( )A .1B .2C .3D .4 10.已知实数b a ,满足等式b a 32=,下列五个关系式: ①;0a b << ②;0<<b a ③;0b a <<④;0<<a b⑤.b a =其中可能成立的关系式有( ) A .①②③ B .①②⑤C .①③⑤D .③④⑤ 11.设奇函数)(x f 在(0,+∞)上为增函数,且0)1(=f ,则不等式0)()(<--xx f x f 的解集为( )A .(-1,0)∪(1,+∞)B .(-∞,-1)∪(0,1)C .(-∞,-1)∪(1,+∞)D .(-1,0)∪(0,1)12.函数|1||ln |--=x e y x 的图像大致是 ( )第Ⅱ卷本卷包括必考题和选考题两部分,第13题-第21题为必考题,每个试题考生都必须做答,第22题为选考题,考生根据要求做答.二、填空题:本大题共4小题,每小题5分,满分20分.13.若正整数m 满足m m 102105121<<-,则=m .(3010.02lg ≈)14.函数)(x f 对于任意实数x 满足条件)(1)2(x f x f =+,若5)1(-=f ,则))5((f f =_________.15.对于函数)(x f 定义域中任意的)(,2121x x x x ≠,有如下结论:①)()()(2121x f x f x x f ⋅=+; ②)()()(2121x f x f x x f +=⋅; ③0)()(2121>--x x x f x f ; ④2)()()2(2121x f x f x x f +<+. 当x x f lg )(=时,上述结论中正确结论的序号是 .16.把下面不完整的命题补充完整,并使之成为真命题.若函数x x f 2log 3)(+=的图像与)(x g 的图像关于对称,则函数)(x g = . (注:填上你认为可以成为真命题的一种情形即可,不必考虑所有可能的情形)三、解答题:本大题共6小题,满分70分.解答须写出文字说明,证明过程和演算步骤. 17.(本题满分12分)已知集合}.02|{},,116|{2<--=∈≥+=m x x x B R x x x A (1)当m =3时,求)(B C A R ;(2)若}41|{<<-=x x B A ,求实数m 的值.19.(本题满分12分) 设函数⎪⎩⎪⎨⎧≥<+-+-=.1,log .1,48)14()(2x x x a x a x x f a(1)当21=a 时,求函数)(x f 的值域;(2)若函数)(x f 是(-∞,+∞)上的减函数,求实数a 的取值范围.20.(本题满分12分)设函数b x ax x f ++=1)((a ,b 为常数),且方程x x f 23)(=有两 个实根为2,121=-=x x .(1)求)(x f y =的解析式;(2)证明:曲线)(x f y =的图像是一个中心对称图形,并求其对称中心.DAFEOBC21. (本题满分12分)设0≥a ,函数x x x a x f --++-=111)(2的最大值为)(a g . (1)设x x t --+=11,求t 的取值范围,并把)(x f 表示为t 的函数)(t m ; (2)求)(a g ;(3)试求满足)1()(ag a g =的所有实数a .22.选做题.(本小题满分10分.请考生在A 、B 、C 三题中任选一题作答,如果多做,则按所做的第一题记分.作答时,用2B 铅笔在答题卡上把所选题目对应的标号涂黑.) A .选修4-1:几何证明选讲.如图,AB 是⊙O 的直径,C ,F 是⊙O 上的点,OC 垂直于直径AB ,过F 点作⊙O 的切线交AB 的延长线于D .连结CF 交AB 于E 点.(1)求证:DA DB DE ⋅=2;(2)若⊙O 的半径为32,OB =3OE ,求EF 的长.B .选修4-4:坐标系与参数方程.已知曲线C 的极坐标方程是θρcos 4=.以极点为平面直角坐标系的原点,极轴为x 轴的正半轴,建立平面直角坐标系,直线l 的参数方程是:t t y t x (22122⎪⎪⎩⎪⎪⎨⎧=+=是参数).(1)将曲线C 的极坐标方程转化为普通方程;(2)若直线l 与曲线C 相交于A 、B 两点,试求线段AB 的长.C .选修4-5:不等式选讲.设函数|3||22|)(++-=x x x f . (1)解不等式6)(>x f ;(2)若关于x 的不等式|12|)(-≤a x f 的解集不是空集,试求a 的取值范围.参考答案一、选择题:本大题共12小题,每小题5分,满分60分。
2018年银川一中--高一第一次月考数学试卷答案最新

值域为 y | y 1 ………………………… 12 分
19. (本题满分
10 )已知函数
f(x)=
mx2
2x 1
的定义域为
6mx m 8
解:
若函数定义域为 R,则 mx2 6mx m 8 0
(1)当 m 0时 8 0恒成立
(2)当 m 0时,则 0恒成立
即36m 2 4m(m 8) 0
f ( x)
(x 1)2 在区间
1,t 2 上单调
递增
f ( x) min f ( 1) 0
当 t 1时, f ( x) (x 1)2 在区间 t ,t 2 上单调递增, f ( x)min
f (t ) (t 1)2
高一第一次月考语文试卷答案
1、 C 2、 A 凄婉,惆怅,噩耗 3、D( A. “风华正茂 ”不能用来修饰 “学习和生活 ”。B. “亡羊补牢 ”指已经发生的过失。 C. “年 富力强 ”用来形容中青年) 4、 C 项。 A 项搭配不当, "官兵 " 可以放弃休假,坚守岗位, " 消防车 " 则不能。 B 项属句式 杂糅,应为 " 深受广大消费者欢迎 " 。 D 项介词搭配不当,应将 " 关于 " 改为 " 对于 " 。 5、 C“国别体 ”应为 “编年体 ” 6.D 7.D 8.A 9.A(更:改变)
f ( 3)
f ( 2) 15 、 -3 16 、 (
1 , ) (1,
3
)
三、解答题 : 17. (本题满分 12)已知函数 f ( x)
x3
1 的定义域为集合 A , 7x
B x Z 2 x 10 , C x R x a或x a 1
2018年银川一中--一模数学(文科)答案 最新
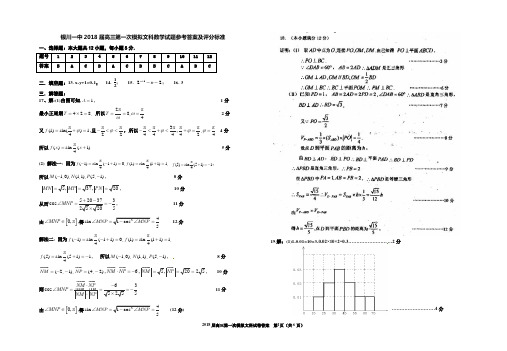
银川一中2018届高三第一次模拟文科数学试题参考答案及评分标准一、选择题:本大题共12小题,每小题5分.二.填空题:13. x-y+1=0-1; 14. 12; 15. 221--+n n ; 16. 3三.解答题:17、解:(1)由图可知,1A =, 1分 最小正周期428,T =⨯= 所以2ππ8,.4T ωω===2分 又π(1)sin()14f ϕ=+=,且ππ22ϕ-<<,所以ππ3π444ϕ-<+<,πππ,.424ϕϕ+== 4分 所以π()sin(1)4f x x =+5分 (2) 解法一: 因为ππ(1)sin (11)0,(1)sin(11)1,44f f -=-+==+= π(5)sin (51)14f =+=-,所以(1,0),(1,1),(5,1)M N P --,8分 , 10分从而3cos 5MNP ∠==-, 11分由[]0,πMNP ∠∈,得4sin5MNP ∠==12分 解法二: 因为ππ(1)sin (11)0,(1)sin (11)1,44f f -=-+==+=π(5)sin (51)14f =+=-, 所以(1,0),(1,1),(5,1)M N P --, 8分(2,1),(4,2)NM NP =--=-,NM NP ⋅=5,20NM NP ===, 10分则3cos 55NM NPMNP NM NP⋅∠===-⋅ 11分由[]0,πMNP ∠∈,得4sin 5MNP ∠==(12分)19.解:(1)1-0.01×10×3-0.02×10×2=0.3………………………2分………………………4分(2)200.1300.2400.3500.2600.1700.143⨯+⨯+⨯+⨯+⨯+⨯=(百元) …5分即这50人的平均月收入估计为4300元。
………………………………6分 (3)[65,75]的人数为5人,其中2人赞成,3人不赞成。
宁夏回族自治区银川一中2018届高三第一次月考数学(文)试卷Word版含答案

银川一中2018届高三年级第一次月考数 学 试 卷(文)命题人:张莉第Ⅰ卷 (选择题 共60分)一、选择题:本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合⎭⎬⎫⎩⎨⎧≥+-=021A x x x,{}13B >=x x 则 A .{}2B A ->=⋃x x B .{}2B A -≥=⋃x x C .{}002-B A ><<=⋃x x x 或 D .{}10B A ≤<=⋃x x2.“x>1”是“)2(log 21<+x ”的A .充要条件B .充分不必要条件C .必要不充分条件D .既不充分也不必要条件3.函数2cos 2y x x =+的一个对称轴为A .x=4π B .x=π2 C .x=2π3 D .x=65π4.设0.6 1.50.60.60.6 1.5a b c ===,,,则a b c ,,的大小关系是 A .a b c <<B .a cb << C .b ac <<D .b c a <<5.函数()cos 6f x x πω⎛⎫=+ ⎪⎝⎭(0ω>)的最小正周期为π,则()f x 满足 A .在0,3π⎛⎫⎪⎝⎭上单调递增B .图象关于直线6x π=对称C .3f π⎛⎫=⎪⎝⎭D .当512x π=时有最小值1- 6.函数()cos2sin 2f x x x π⎛⎫=++ ⎪⎝⎭的最小值是A .2-B .89-C .87-D .07.函数2()ln(28)f x x x =--的单调递减区间是 A .(,2)-∞-B .(,1)-∞-C .(1,)+∞D .(4,)+∞8.在△ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,且满()C b B c a cos cos 2=-,则A 的取值范围⎪⎭⎫ ⎝⎛320.A π, ()π,0.B ⎪⎭⎫ ⎝⎛323.C ππ, ⎪⎭⎫ ⎝⎛ππ,32.D9.已知函数1222,1()log (1),1x x f x x x -⎧-≤=⎨-+>⎩ ,且4)a (-=f ,则=-)14(a fA .74-B .54-C .34-D .14- 10.当210≤<x 时,有x a xlog 4<,则a 的取值范围是 ⎪⎪⎭⎫⎝⎛220A., ⎪⎪⎭⎫⎝⎛1,22B. ()21C., ()22D., 11.已知函数)sin()(ϕω+=x A x f 的图象如图所示,则该函数的解析式可能是)623sin(43)(.A π+=x x f )5154sin(54)(.B +=x x f )665sin(54)(.C π+=x x f )5132sin(54)(.D -=x x f 12. 设函数a ax x e x f x +--=)12()(其中1<a ,若存在唯一的整数0x ,使得0)(0<x f ,则a 的取值范围是⎪⎭⎫⎢⎣⎡1,23-A.e ⎪⎭⎫⎢⎣⎡-43,23B.e ⎪⎭⎫⎢⎣⎡43,23C.e ⎪⎭⎫⎢⎣⎡1,23D.e 第Ⅱ卷(非选择题 共90分)本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须做答.第22题~第23题为选考题,考生根据要求做答. 二、填空题:本大题共4小题,每小题5分.13.对于任意的两个正数m ,n ,定义运算⊙:当m 、n 都为偶数或都为奇数时,m ⊙n =2nm +;当m 、n 为一奇一偶时,m ⊙n =mn ,设集合A ={(a ,b )|a ⊙b =4,a ,b ∈N*},则集合A 的子集个数为________.14.如图,某工程中要将一长为100 m ,倾斜角为75°的斜坡改造成倾斜角为30°的斜坡,并保持坡高不变,则坡底 需加长________m .15.已知命题p :关于x 的不等式)10(1≠>>a a a x 且的解集是{}0>x x ,命题q :函数)lg(2a x ax y +-=的定义域为R ,如果p ∨q 为真命题,p ∧q 为假命题,则实数a 的取值范围为________________.16.设函数))((R x x f ∈满足 x x f x f sin )()(+=+π当π<≤x 0时,0)(=x f 则=)623(πf ________ . 三、解答题:本大题共6小题,共70分。
推荐-宁夏银川一中2018届高三年级第一次月考测试数学(理科) 精品
宁夏银川一中2018届高三年级第一次月考测试数学(理科)一、选择题(本题共10小题,每题6分,共60分) 1.集合},0|{2<-=x x x M , }2|{<=x x N ,则A .φ=⋂N MB .M N M =⋂C .M N M =⋃D .R N M =⋃2.函数x y 3=的反函数是A .3x y =B .3x y =C .x y 3log =D . ) 31(x=y3.已知c b a ,,依次成等比数列,那么函数c bx ax x f ++=2)(的图象与x 轴的交点的个数为A .1或2B .1C .2D .04.下列四个函数中,在区间(0,1)上为增函数的是A .x y 2log -=B .x y sin =C .xy )21(= D .21-=x y5.函数f (x )=a x 与g (x )=xa-的图象A .关于直线y =x 对称B .关于x 轴对称C .关于y 轴对称D .关于原点对称6.已知f (x )是定义域在区间(0,+∞)上增函数,若f (21)=0,三角形的一个锐角A 满足f (cosA)<0, 则A 的取值范围是A .(2,6ππ) B .(2,4ππ) C .(6,3ππ) D .(2,3ππ) 7.若函数)10(log )(<<=a x x f a 在区间]2,[a a 上的最大值是最小值的3倍,则a 的值为A .42 B .22 C .41 D .21 8.已知定义在R 上的奇函数)(x f 满足)()2(x f x f -=+,则)6(f 的值为A .-1B .0C .1D . 29.为了保证信息安全传输,有一种称为秘密密钥密码系统,英才其加密、解密原理如下图:现在加密密钥为)2(log +=x y a ,如上所示,明文“6”通过加密后得到密文“3”,再发送, 接受方通过解密密钥解密得到明文“6”。
问:若接受方接到密文为“4”,则解密后得到明文为A .12B .13C .14D .1510.关于x 的方程|2x -1|=k ,给出下列四个命题:①存在实数k ,使得方程恰有1个零根; ②存在实数k ,使得方程恰有1个正根;③存在实数k ,使得方程恰有1个正根、一个负根; ④存在实数k ,使得方程没有实根。
宁夏银川一中高三数学试卷第一次月考测试(文科)
宁夏银川一中2009届高三数学试卷第一次月考测试(文科)本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分.第II 卷第22题为选考题,其他题为必考题.考生作答时,将答案答在答题卡上,在本试卷上答题无效.考试结束后,将本试卷和答题卡一并交回. 注意事项:1.答题前,考生先将自己的姓名、准考证号填写在答题卡上,2.选择题答案使用2B 铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或炭素笔书写,字体工整,笔迹清楚.3.请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效. 4.保持卡面清洁,不折叠,不破损.5.作选考题时,考生按照题目要求作答,并用2B 铅笔在答题卡上把所选题目对应的标号涂黑.第I 卷一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项符合题目要求.1.集合P={x|x 2=1},Q={x|mx=1},若Q ⊆P ,则m 等于 ( )A .1B .-1C .1或-1D .0,1或-1 2.已知函数f (x )=x-11定义域为M ,g (x )=ln (1+x )定义域N ,则M ∩N 等于( )A .{x|x>-1}B .{x|x<1}C .{x|-1<x<1}D .φ 3.下列函数中,表示同一个函数的一组是( )A .f (x )=|x|与g (x )=2xB .y=x 0与y=1C .y=x=1与y=112--x x D .y=x-1与y=122+-x x4.圆柱的一个底面积为S ,侧面展开图是一个正方形,那么这个圆柱的侧面积是 ( )A .4πSB .2πSC .πSD .332πS5.如图为一个几何体的三视图,其中俯视图为正三角形,AA 1=4,MN=3,则该几何体的表.面积..为( )M AA 1‘主视图 左视图 俯视图 A .6+3 B .24+3 C .24+23 D .326.函数f (x )=|x|和g (x )=x (2-x )的增区间依次是 ( )A .(-∞,0),(-∞,1)B .(-∞,0),[1,+∞]C .[0,+∞],(-∞,1)D .[0,+∞],[1,+∞]7.已知函数f (x )=2x +2-x,若f (a )=3,则f (2a )= ( )A .5B .7C .9D .118.如下正方体或四面体中,P 、Q 、R 、S 分别是所在棱的中点,这四个点不共面...的一个图是( )A B C D9.设直线m 与平面α相交且但不垂直,则下列说法正确的是( )A .在平面α内有且只有一条直线与直线m 垂直B .过直线m 有且只有一个平面与平面α垂直C .与直线m 垂直的直线不可能与平面α平行D .与平面α垂直的平面不可能与直线m 平行 10.函数y=|log |33x 的图象是 ( )11.若正三棱锥的斜高是高的332倍,则棱锥的侧面积是底面积的几倍。
最新-宁夏银川一中2018届高三上学期第一次月考试题(数
宁夏银川一中2018届高三上学期第一次月考试题(数学理科)第Ⅰ卷一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.满足M ⊆{a 1, a 2, a 3, a 4},且M ∩{a 1 ,a 2, a 3}={ a 1,a 2}的集合M 的个数是 ( )A .1B .2C .3D .42.若)12(log 1)(21+=x x f ,则)(x f 定义域为( )A .)0,21(-B .]0,21(- C .),21(+∞-D .),0(+∞3.已知函数f (x )=⎩⎨⎧2x , x >0x +1,x ≤0,若f (a )+f (1)=0,则实数a 的值等于( ) A .-3 B .-1 C .1 D .3 4.以下有关命题的说法错误的是( ) A .命题“若0232=+-x x 则x=1”的逆否命题为“若023,12≠+-≠x x x 则” B .“1=x ”是“0232=+-x x ”的充分不必要条件 C .若q p ∧为假命题,则p 、q 均为假命题D .对于命题01,:,01,:22≥++∈∀⌝<++∈∃x x R x p x x R x p 均有则使得5.函数y =f (x )在定义域(-32,3)内的图像如图所示.记y =f (x )的导函数为y =f '(x ),则不等式f '(x )≤0的解集为( ) A .[-13,1]∪[2,3)B .[-1,12]∪[43,83]C .[-32,12]∪[1,2)D .(-32,-13]∪[12,43]∪[43,3)6.设奇函数)(x f 在(0,+∞)上为增函数,且0)1(=f ,则不等式0)()(<--xx f x f 的解集为( ) A .(-1,0)∪(1,+∞)B .(-∞,-1)∪(0,1)C .(-∞,-1)∪(1,+∞)D .(-1,0)∪(0,1)7.已知函数x x x f 2)(+=,Lnx x x g +=)(,1)(--=x x x h 的零点分别为,,21x x 3x ,则321,,x x x 的大小关系是( )A .123x x x <<B .213x x x <<C .132x x x <<D .321x x x <<8.已知()y f x =的图象是顶点在原点的抛物线,且方程()3x f x -=有一个根2x =,则不等式||)31()(x x f <的解集是( )A .(2,2)-B .(2,0)(0,2)-UC .(0,2)D .∅9.设0<b <a <1,则下列不等式成立的是( )A .ab <b 2<1B .21log b <21log a <0C .2b <2a <2D .a 2<ab <110.已知f (x ),g (x )都是定义在R 上的函数,对任意x 、y 满足f (x-y )=f (x )·g (y )-g (x )·f (y ),且f (-2)=f (1)≠0,则g (1)+g (-1)= ( ) A .-1 B .1 C .2 D .-211.若实数y x ,满足01|1|=--y Ln x ,则y 是x 的函数的图象大致是( )12.用min{a,b,c}表示a,b,c 三个数中的最小值。
2018年宁夏银川一中高考数学一模试卷和答案(文科)
2018年宁夏银川一中高考数学一模试卷(文科)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知集合A={﹣1,1,3},B={1,a2﹣2a},B⊆A,则实数a的不同取值个数为()A.2 B.3 C.4 D.52.(5分)已知z是纯虚数,是实数,那么z等于()A.2i B.i C.﹣i D.﹣2i3.(5分)已知函数,则的值是()A.9 B.C.D.﹣94.(5分)已知x、y满足约束条件则z=x+2y 的最大值为()A.﹣2 B.﹣1 C.1 D.25.(5分)已知直线ax+by+c=0与圆O:x2+y2=1相交于A,B两点,且,则的值是()A.B.C.D.06.(5分)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的表面积为()A.96 B.C.D.7.(5分)已知角ϕ的终边经过点P(﹣4,3),函数f(x)=sin(ωx+ϕ)(ω>0)的图象的相邻两条对称轴之间的距离等于,则f()的值为()A.B.C.﹣ D.﹣8.(5分)已知程序框图如图所示,则该程序框图的功能是()A.求数列的前10项和(n∈N*)B.求数列的前10项和(n∈N*)C.求数列的前11项和(n∈N*)D.求数列的前11项和(n∈N*)9.(5分)某单位安排甲、乙、丙三人在某月1日至12日值班,每人4天.甲说:我在1日和3日都有值班;乙说:我在8日和9日都有值班;丙说:我们三人各自值班的日期之和相等.据此可判断丙必定值班的日期是()A.2日和5日B.5日和6日C.6日和11日 D.2日和11日10.(5分)设函数f(x)=ln(1+|x|)﹣,则使得f(x)>f(2x﹣1)成立的x的取值范围是()A.(﹣∞,)∪(1,+∞)B.(,1)C.()D.(﹣∞,﹣,)11.(5分)设F1,F2是双曲线﹣=1(a>0,b>0)的左、右两个焦点,若双曲线右支上存在一点P,使(+)•=0(O为坐标原点),且|PF1|=|PF2|,则双曲线的离心率为()A.B.C.D.+112.(5分)若函数f(x)=x3﹣3x在(a,6﹣a2)上有最小值,则实数a的取值范围是()A.(﹣,1) B.[﹣,1) C.[﹣2,1)D.(﹣2,1)二、填空题:本大题共4小题,每小题5分.13.(5分)曲线y=x2+在点(1,2)处的切线方程为.14.(5分)已知P是△ABC所在平面内一点,,现将一粒黄豆随机撒在△ABC内,则黄豆落在△PBC内的概率是.15.(5分)对于数列{a n},定义数列{a n+1﹣a n}为数列{a n}的“差数列”,若a1=1,{a n}的“差数列”的通项公式为a n﹣a n=2n,则数列{a n}的前n项和S n=.+116.(5分)已知抛物线C:y2=2px (p>0)的焦点为F,过点F倾斜角为60°的直线l与抛物线C在第一、四象限分别交于A、B两点,则的值等于.三、解答题:解答应写出文字说明,证明过程或演算步骤.17.(12分)已知函数f(x)=Asin(ωx+φ),x∈R,(其中A>0,ω>0,﹣<φ<),其部分图象如图所示.(1)求函数f(x)的解析式;(2)已知横坐标分别为﹣1、1、5的三点M、N、P都在函数f(x)的图象上,求sin∠MNP的值.18.(12分)如图,四棱锥P﹣ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,M为AB的中点,△PAD为等边三角形,且平面PAD⊥平面ABCD.(Ⅰ)证明:PM⊥BC.(Ⅱ)若PD=1,求点D到平面PAB的距离.19.(12分)为了解某市民众对某项公共政策的态度,在该市随机抽取了50名市民进行调查,做出了他们的月收入(单位:百元,范围:[15,75])的频率分布直方图,同时得到他们月收入情况以及对该项政策赞成的人数统计表:(1)求月收入在[35,45)内的频率,并补全这个频率分布直方图,并在图中标出相应纵坐标;(2)根据频率分布直方图估计这50人的平均月收入;(3)若从月收入(单位:百元)在[65,75]的被调查者中随机选取2人,求2人都不赞成的概率.20.(12分)已知椭圆+=1(a>b>0)的离心率e=,连接椭圆的四个顶点得到的菱形的面积为4.(1)求椭圆的方程.(2)设直线l与椭圆相交于不同的两点A,B,已知点A的坐标为(﹣a,0),点Q(0,y0)在线段AB的垂直平分线上,且•=4,求y0的值.21.(12分)已知函数f(x)=ax3﹣x2+bx(a,b∈R,f′(x)为其导函数,且x=3时f(x)有极小值﹣9(Ⅰ)求f(x)的单调递减区间;(Ⅱ)若不等式f′(x)>k(xlnx﹣1)﹣6x﹣4(k为正整数)对任意正实数x恒成立,求k的最大值.(解答过程可参考使用以下数据:ln7≈1.95,ln8≈2.08)请考生在第22-23题中任选一题作答,如果多做,则按所做的第一题计分.选修4-4:坐标系与参数方程22.(10分)在直角坐标系xOy中,曲线C1的参数方程为(α为参数),曲线C2的参数方程为(β为参数),以O为极点,x轴的正半轴为极轴建立极坐标系.(1)求曲线C1和曲线C2的极坐标方程;(2)已知射线l1:θ=α(0<α<),将射线l1顺时针旋转得到射线l2;θ=α﹣,且射线l1与曲线C1交于O,P两点,射线l2与曲线C2交于O,Q两点,求|OP|•|OQ|的最大值.选修4-5;不等式选讲.23.设不等式﹣2<|x﹣1|﹣|x+2|<0的解集为M,且a,b∈M.(1)证明:|a+b|<;(2)比较|1﹣4ab|与2|a﹣b|的大小,并说明理由.2018年宁夏银川一中高考数学一模试卷(文科)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知集合A={﹣1,1,3},B={1,a2﹣2a},B⊆A,则实数a的不同取值个数为()A.2 B.3 C.4 D.5【解答】解:∵B⊆A,∴a2﹣2a=﹣1或a2﹣2a=3.①由a2﹣2a=﹣1得a2﹣2a+1=0,解得a=1.当a=1时,B={1,﹣1},满足B⊆A.②由a2﹣2a=3得a2﹣2a﹣3=0,解得a=﹣1或3,当a=﹣1时,B={1,3},满足B⊆A,当a=3时,B={1,3},满足B⊆A.综上,若B⊆A,则a=±1或a=3.故选:B.2.(5分)已知z是纯虚数,是实数,那么z等于()A.2i B.i C.﹣i D.﹣2i【解答】解:由题意得z=ai.(a∈R且a≠0).∴==,则a+2=0,∴a=﹣2.有z=﹣2i,故选:D.3.(5分)已知函数,则的值是()A.9 B.C.D.﹣9【解答】解:=f(log2)=f(log22﹣2)=f(﹣2)=3﹣2=,故选:B.4.(5分)已知x、y满足约束条件则z=x+2y 的最大值为()A.﹣2 B.﹣1 C.1 D.2【解答】解:作出不等式组对应的平面区域如图:由z=x+2y得y=﹣x+z,平移直线y=﹣x+z由图象可知当直线y=﹣x+z经过点A时,直线y=﹣x+z的截距最大,此时z最大,由,即,即A(0,1),此时z=0+2=2,故选:D.5.(5分)已知直线ax+by+c=0与圆O:x2+y2=1相交于A,B两点,且,则的值是()A.B.C.D.0【解答】解:取AB的中点C,连接OC,,则AC=,OA=1∴sin =sin∠AOC==所以:∠AOB=120°则•=1×1×cos120°=.故选:A.6.(5分)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的表面积为()A.96 B.C.D.【解答】解:由三视图可知几何体为边长为4的正方体挖去一个圆锥得到的,圆锥的底面半径为2,高为2,∴圆锥的母线长为2.∴几何体的平面部分面积为6×42﹣π×22=96﹣4π.圆锥的侧面积为=4.∴几何体的表面积为96﹣4π+4.故选:C.7.(5分)已知角ϕ的终边经过点P(﹣4,3),函数f(x)=sin(ωx+ϕ)(ω>0)的图象的相邻两条对称轴之间的距离等于,则f()的值为()A.B.C.﹣ D.﹣【解答】解:由于角ϕ的终边经过点P(﹣4,3),可得cosϕ=,sinϕ=.再根据函数f(x)=sin(ωx+ϕ)(ω>0)的图象的相邻两条对称轴之间的距离等于,可得周期为=2×,求得ω=2,∴f(x)=sin(2x+ϕ),∴f()=sin(+ϕ)=cosϕ=﹣,故选:D.8.(5分)已知程序框图如图所示,则该程序框图的功能是()A.求数列的前10项和(n∈N*)B.求数列的前10项和(n∈N*)C.求数列的前11项和(n∈N*)D.求数列的前11项和(n∈N*)【解答】解:根据题意,s=s+n=n+2∴数列为又∵K≤10∴计算的是求数列的前10项和(n∈N*)故选:B.9.(5分)某单位安排甲、乙、丙三人在某月1日至12日值班,每人4天.甲说:我在1日和3日都有值班;乙说:我在8日和9日都有值班;丙说:我们三人各自值班的日期之和相等.据此可判断丙必定值班的日期是()A.2日和5日B.5日和6日C.6日和11日 D.2日和11日【解答】解:由题意,1至12的和为78,因为三人各自值班的日期之和相等,所以三人各自值班的日期之和为26,根据甲说:我在1日和3日都有值班;乙说:我在8日和9日都有值班,可得甲在1、3、10、12日值班,乙在8、9、2、7或8、9、4、5,据此可判断丙必定值班的日期是6日和11日,故选:C.10.(5分)设函数f(x)=ln(1+|x|)﹣,则使得f(x)>f(2x﹣1)成立的x的取值范围是()A.(﹣∞,)∪(1,+∞)B.(,1)C.()D.(﹣∞,﹣,)【解答】解:∵函数f(x)=ln(1+|x|)﹣为偶函数,且在x≥0时,f(x)=ln(1+x)﹣,导数为f′(x)=+>0,即有函数f(x)在[0,+∞)单调递增,∴f(x)>f(2x﹣1)等价为f(|x|)>f(|2x﹣1|),即|x|>|2x﹣1|,平方得3x2﹣4x+1<0,解得:<x<1,所求x的取值范围是(,1).故选:B.11.(5分)设F1,F2是双曲线﹣=1(a>0,b>0)的左、右两个焦点,若双曲线右支上存在一点P,使(+)•=0(O为坐标原点),且|PF1|=|PF2|,则双曲线的离心率为()A.B.C.D.+1【解答】解:取PF2的中点A,则=2∵()•=0,∴2•=0∴⊥∵O是F1F2的中点∴OA∥PF1,∴PF1⊥PF2,∵|PF1|=|PF2|,∴2a=|PF1|﹣|PF2|=(﹣1)|PF2|,∵|PF1|2+|PF2|2=4c2,∴c=|PF2|,∴e===故选:D.12.(5分)若函数f(x)=x3﹣3x在(a,6﹣a2)上有最小值,则实数a的取值范围是()A.(﹣,1) B.[﹣,1) C.[﹣2,1)D.(﹣2,1)【解答】解:由题意可得:函数f(x)=x3﹣3x,所以f′(x)=3x2﹣3.令f′(x)=3x2﹣3=0可得,x=±1;因为函数f(x)在区间(a,6﹣a2)上有最小值,其最小值为f(1),所以函数f(x)在区间(a,6﹣a2)内先减再增,即f′(x)先小于0然后再大于0,所以结合二次函数的性质可得:a<1<6﹣a2,且f(a)=a3﹣3a≥f(1)=﹣2,且6﹣a2﹣a>0,联立解得:﹣2≤a<1.故选:C.二、填空题:本大题共4小题,每小题5分.13.(5分)曲线y=x2+在点(1,2)处的切线方程为x﹣y+1=0.【解答】解:曲线y=x2+,可得y′=2x﹣,切线的斜率为:k=2﹣1=1.切线方程为:y﹣2=x﹣1,即:x﹣y+1=0.故答案为:x﹣y+1=0.14.(5分)已知P是△ABC所在平面内一点,,现将一粒黄豆随机撒在△ABC内,则黄豆落在△PBC内的概率是.【解答】解:以PB、PC为邻边作平行四边形PBDC,则,∵,∴,得:,由此可得,P是△ABC边BC上的中线AO的中点,点P到BC的距离等于A到BC的距离的.∴S=S△ABC.△PBC将一粒黄豆随机撒在△ABC内,黄豆落在△PBC内的概率为P==故答案为:15.(5分)对于数列{a n},定义数列{a n+1﹣a n}为数列{a n}的“差数列”,若a1=1,﹣a n=2n,则数列{a n}的前n项和S n=2n+1﹣n {a n}的“差数列”的通项公式为a n+1﹣2.【解答】解:∵a n﹣a n=2n,+1∴a n=(a n﹣a n﹣1)+(a n﹣1﹣a n﹣2)+(a n﹣2﹣a n﹣3)+…+(a2﹣a1)+a1=2n﹣1+2n﹣2+2n﹣3+…+2+1==2n﹣1,∴数列{a n}的前n项和:S n=(2+22+…+2n)﹣n==2n+1﹣n﹣2.故答案为:2n+1﹣n﹣2.16.(5分)已知抛物线C:y2=2px (p>0)的焦点为F,过点F倾斜角为60°的直线l与抛物线C在第一、四象限分别交于A、B两点,则的值等于3.【解答】解:设A(x1,y1),B(x2,y2),则y12=2px1,y22=2px2,|AB|=x1+x2+p==p,即有x1+x2=p,由直线l倾斜角为60°,则直线l的方程为:y﹣0=(x﹣),即y=x﹣p,联立抛物线方程,消去y并整理,得12x2﹣20px+3p2=0,则x1x2=,可得x1=p,x2=p,则==3,故答案为:3.三、解答题:解答应写出文字说明,证明过程或演算步骤.17.(12分)已知函数f(x)=Asin(ωx+φ),x∈R,(其中A>0,ω>0,﹣<φ<),其部分图象如图所示.(1)求函数f(x)的解析式;(2)已知横坐标分别为﹣1、1、5的三点M、N、P都在函数f(x)的图象上,求sin∠MNP的值.【解答】解:(1)由图可知,最小正周期T=(3﹣1)×4=8,所以ω==.又∵当x=1时,f(x)有最大值为1,∴f(1)=sin(+φ)=1,得+φ=+2kπ,k∈Z∵﹣<φ<,∴取k=0,得φ=.所以函数的解析式为f(x)=sin(x+).(2)∵f(﹣1)=0,f(1)=1且f(5)=sin(×5+)=﹣1.∴三点坐标分别为M(﹣1,0),N(1,1),P(5,﹣1),由两点的距离公式,得|MN|=,|PN|=2,|MP|=,∴根据余弦定理,得cos∠MNP==﹣.∵∠MNP∈(0,π)∴sin∠MNP是正数,得sin∠MNP==.18.(12分)如图,四棱锥P﹣ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,M为AB的中点,△PAD为等边三角形,且平面PAD⊥平面ABCD.(Ⅰ)证明:PM⊥BC.(Ⅱ)若PD=1,求点D到平面PAB的距离.【解答】(Ⅰ)证明:取AD中点O,连接PO,OM,DM,由已知得PO⊥平面ABCD,∴PO⊥BC,∵∠DAB=60°,AB=2AD,∴△ADM是正三角形,∴OM⊥AD,OM∥BD,OM=BD,∴OM⊥BC∵PO∩OM=O,∴BC⊥平面POM,∵PM⊂平面POM,∴PM⊥BC.(Ⅱ)解:∵PD=1,∠DAB=60°,AB=2AD=2PD=2,∴△ABD是直角三角形,BD⊥AD,∴BD=,∵PO=,∴V P==﹣ABO设点D到平面P取AB的距离为h,由BD⊥AD,BD⊥PO,∴BD⊥平面ABD,∴BD⊥PD,∴△PBD是直角三角形,∴PB=2,在△PBD中,PA=1,AB=PB=2,∴△PBD是等腰三角形,=,∴S△PAB=V D﹣PAB,可得=,∴由V P﹣ABD∴h=,∴点D到平面PAB的距离为.19.(12分)为了解某市民众对某项公共政策的态度,在该市随机抽取了50名市民进行调查,做出了他们的月收入(单位:百元,范围:[15,75])的频率分布直方图,同时得到他们月收入情况以及对该项政策赞成的人数统计表:(1)求月收入在[35,45)内的频率,并补全这个频率分布直方图,并在图中标出相应纵坐标;(2)根据频率分布直方图估计这50人的平均月收入;(3)若从月收入(单位:百元)在[65,75]的被调查者中随机选取2人,求2人都不赞成的概率.【解答】解:(1)1﹣0.01×10×3﹣0.02×10×2=0.3(2)20×0.1+30×0.2+40×0.3+50×0.2+60×0.1+70×0.1=43(百元)即这50人的平均月收入估计为4300元.(3)[65,75]的人数为5人,其中2人赞成,3人不赞成.记赞成的人为a,b,不赞成的人为x,y,z任取2人的情况分别是:ab,ax,ay,az,bx,by,bz,xy,xz,yz共10种情况.其中2人都不赞成的是:xy,yz,xz共3种情况.∴2人都不赞成的概率是P=20.(12分)已知椭圆+=1(a>b>0)的离心率e=,连接椭圆的四个顶点得到的菱形的面积为4.(1)求椭圆的方程.(2)设直线l与椭圆相交于不同的两点A,B,已知点A的坐标为(﹣a,0),点Q(0,y0)在线段AB的垂直平分线上,且•=4,求y0的值.【解答】解:(1)由e=,得3a2=4c2.再由c2=a2﹣b2,解得a=2b.由题意可知,即ab=2.解方程组得a=2,b=1.所以椭圆的方程为.(2)由(Ⅰ)可知点A的坐标是(﹣2,0).设点B的坐标为(x1,y1),直线l的斜率为k.则直线l的方程为y=k(x+2).于是A、B两点的坐标满足方程组消去y并整理,得(1+4k2)x2+16k2x+(16k2﹣4)=0.由,得.从而.所以.设线段AB的中点为M,则M的坐标为.以下分两种情况:①当k=0时,点B的坐标是(2,0),线段AB的垂直平分线为y轴,于是.由,得.②当k≠0时,线段AB的垂直平分线方程为.令x=0,解得.由,,==,整理得7k2=2.故.所以.综上,或.21.(12分)已知函数f(x)=ax3﹣x2+bx(a,b∈R,f′(x)为其导函数,且x=3时f(x)有极小值﹣9(Ⅰ)求f(x)的单调递减区间;(Ⅱ)若不等式f′(x)>k(xlnx﹣1)﹣6x﹣4(k为正整数)对任意正实数x恒成立,求k的最大值.(解答过程可参考使用以下数据:ln7≈1.95,ln8≈2.08)【解答】解:(Ⅰ)由f′(x)=3ax2﹣2x+b,因为函数在x=3时有极小值﹣9,所以,从而得a=,b=﹣3,所求的f(x)=x3﹣x2﹣3x,所以f′(x)=x2﹣2x﹣3,由f′(x)<0解得﹣1<x<3,所以f(x)的单调递减区间为(﹣1,3).(Ⅱ)因为f′(x)=x2﹣2x﹣3,所以f′(x)>k(xlnx﹣1)﹣6x﹣4等价于x2+4x+1>k(xlnx﹣1),即x++4﹣klnx>0,记g(x)=x++4﹣klnx,则g′(x)=,由g′(x)=0,得x=k+1,所以g(x)在(0,k+1)上单调递减,在(k+1,+∞)上单调递增,所以g(x)≥g(k+1)=k+6﹣kln(k+1),g(x)>0对任意正实数x恒成立,等价于k+6﹣kln(k+1)>0,即1+﹣ln(k+1)>0,记h(x)=1+﹣ln(x+1),则h′(x)=﹣﹣<0,所以h(x)在(0,+∞)上单调递减,又h(6)=2﹣ln7>0,h(7)=﹣ln8<0,所以k的最大值为6.请考生在第22-23题中任选一题作答,如果多做,则按所做的第一题计分.选修4-4:坐标系与参数方程22.(10分)在直角坐标系xOy中,曲线C1的参数方程为(α为参数),曲线C2的参数方程为(β为参数),以O为极点,x轴的正半轴为极轴建立极坐标系.(1)求曲线C1和曲线C2的极坐标方程;(2)已知射线l1:θ=α(0<α<),将射线l1顺时针旋转得到射线l2;θ=α﹣,且射线l1与曲线C1交于O,P两点,射线l2与曲线C2交于O,Q两点,求|OP|•|OQ|的最大值.【解答】解:(1)曲线C1的参数方程为(α为参数),利用平方关系消去参数可得:曲线C1的普通方程为(x﹣2)2+y2=4,展开可得:x2+y2﹣4x=0,利用互化公式可得:ρ2﹣4ρcosθ=0,∴C1极坐标方程为ρ=4cosθ.曲线C2的参数方程为(β为参数),消去参数可得:曲线C2的普通方程为x2+(y﹣2)2=4,展开利用互化公式可得C2极坐标方程为ρ=4sinθ.(2)设点P极点坐标(ρ1,4cosα),即ρ1=4cosα.点Q极坐标为,即.则==.∵,∴,当,即时,|OP|•|OQ|取最大值4.选修4-5;不等式选讲.23.设不等式﹣2<|x﹣1|﹣|x+2|<0的解集为M,且a,b∈M.(1)证明:|a+b|<;(2)比较|1﹣4ab|与2|a﹣b|的大小,并说明理由.【解答】解:(1)证明:﹣2<|x﹣1|﹣|x+2|<0,可得|x﹣1|<|x+2|,即有x2﹣2x+1<x2+4x+4,解得x>﹣,则x+2>0,可得﹣2<|x﹣1|﹣(x+2),即有x<|x﹣1|,可得x﹣1>x或x﹣1<﹣x,解得﹣<x<,则|a|<,|b|<,|a+b|≤|a|+|b|<(+)×=;(2)|1﹣4ab|>2|a﹣b|.理由:|1﹣4ab|2﹣4|a﹣b|2=(1﹣4ab﹣2a+2b)(1﹣4ab+2a﹣2b)=(1﹣2a)(1+2b)(1+2a)(1﹣2b)=(1﹣4a2)(1﹣4b2),由|a|<,|b|<,可得4a2<1,4b2<1,则(1﹣4a2)(1﹣4b2)>0,可得|1﹣4ab|>2|a﹣b|.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 1 页 共 10 页
9.已知函数 f ( x) A.
2 x 1 2, x 1 log 2 ( x 1), x 1
B.
,且 f (a ) 4 ,则 f (14 a ) C.
7 4
5 4
3 4
D.
1 4
10.当 0 x
1 x 时,有 4 log a x ,则 a 的取值范围是 2 2 B. 2 ,1 C. 1,2
2 A. 0 , 2
3 3 sin( x ) 4 2 6 4 5 sin( x ) 5 6 6
D. 2, 2
11.已知函数 f ( x ) A sin(x ) 的图象如图所示,则该函数的解析式可能是
A. f ( x ) C. f ( x ) B. f ( x ) D. f ( x ) 4 4 1 sin( x ) 5 5 5 4 2 1 sin( x ) 5 3 5
5.函数 f x cos x A.在 0, C. f
( 0 )的最小正周期为 ,则 f x 满足 6
B.图象关于直线 x D.当 x
上单调递增 3
对称 6
3 3 2
5 时有最小值 1 12
第 2 页 共 10 页
16 . 设 函 数 f ( x )( x R ) 满 足
f ( x ) f ( x ) sin x 当 0 x 时 , f ( x) 0 则
f(
23 ) ________ . 6
三、解答题:本大题共 6 小题,共 70 分。解答应写出文字说明,证明过程或演算步骤。 17.(本小题满分 12 分) 设函数 f ( x ) 对称轴的距离为
上有两个零点,求 m 的范围。 (2)若方程 g ( x ) f ( x ) m 在 ,Leabharlann 1 2第Ⅱ卷(非选择题
共 90 分)
本卷包括必考题和选考题两部分.第 13 题~第 21 题为必考题,每个试题考生都必须 做答.第 22 题~第 23 题为选考题,考生根据要求做答. 二、填空题:本大题共 4 小题,每小题 5 分. 13. 对于任意的两个正数 m, n, 定义运算⊙: 当 m、 n 都为偶数或都为奇数时, m⊙n=
6.函数 f x cos2 x sin A. - 2
x 的最小值是 2 9 8
C. -
B. -
7 8
D. 0
2 7.函数 f ( x ) ln( x 2 x 8) 的单调递减区间是
A. ( , 2)
B. ( , 1)
C. (1, )
12. 设函数 f ( x ) e x ( 2 x 1) ax a 其中
a 1 ,若存在唯一的整数 x0 ,使得 f ( x0 ) 0 ,
则 a 的取值范围是
3 A.- ,1 2e 3 3 C. , 2e 4
3 3 B. , 2e 4 3 D. ,1 2e
银川一中 2018 届高三年级第一次月考
文 科 数 学
命题人:张莉
第Ⅰ卷
有一项是符合题目要求的. 1.已知集合 A x
(选择题
共 60 分)
一、选择题:本大题共 12 小题,每小题 5 分,满分 60 分.在每小题给出的四个选项中,只
C. A B x - 2 x 0或x 0
D. (4, )
8.在△ABC 中,角 A,B,C 的对边分别是 a,b,c,且满 2a c cos B b cos C ,则 A 的取值范围
2 A. 0, 3
B.0,
2 C. , 3 3
2 D. , 3
3 3 sin 2 x sin x cos x( 0) 且 y f ( x) 的图象的两个相邻 2
. 2
3
(1)求ω的值; (2)求 f ( x ) 在区间 , 上的最大值和最小值. 2
18.(本小题满分 12 分) 已知函数 f ( x ) x 3 ax 2 bx a 2 在 x 1 处有极值 10。 (1)求 a , b 。
A.充要条件 3.函数 y A.x=
B.充分不必要条件
3 sin 2 x cos 2 x 的一个对称轴为
B.x=
4
π 2
C.x=
2π 3
D.x=
5 6
4.设 a 0.60.6,b 0.61.5,c 1.50.6, 则 a,b,c 的大小关系是 A. a<b<c B. a<c<b C. b<a<c D. b<c<a
A. A B x x 2 2. “x>1”是“
log 1 ( x 2) 0
2
1 x 0 , B x 3x 1 则 x2
B. A B x x 2
D. A B x 0 x 1
D.既不充分也不必要条件
”的 C.必要不充分条件
mn ; 2
当 m、n 为一奇一偶时,m⊙n= mn,设集合 A={(a,b)|a⊙b=4,a,b∈N},则集合 A 的子集个数为________.
14.如图,某工程中要将一长为 100 m,倾斜角为 75°的斜坡 改造成倾斜角为 30°的斜坡,并保持坡高不变,则坡底 需加长________m. 15.已知命题 p:关于 x 的不等式 a x 1( a 0且a 1) 的解 集是 x x 0 ,命题 q:函数 y lg(ax 2 x a ) 的定义域为 R,如果 p∨q 为真命题, p∧q 为假命题,则实数 a 的取值范围为________________.
