2011-2012(A)概率论与数理统计期末试卷+答案
2011-2012公共基础《概率论与数理统计》期末考试试卷答案-NEW

1华南农业大学期末考试试卷A 答案2011-2012学年第 1 学期 考试科目: 概率论与数理统计 填空题(本大题共 5 小题,每小题 3 分,共 15分) 1、32;2、0.6;3、1;4、21θθD D ≤;5、(2.68963,2.72037)。
二、选择题(本大题共 6小题,每小题 3 分,共 18 分)1、D ;2、B ;3、C ;4、A ;5、C ;6、B 。
三、解答题(本题8分)解:设A 为事件“产品合格”,B 为事件“机器状态良好”.已知(|)0.98P A B =,(|)0.55P A B =,()0.95P B =,()1()0.05P B P B =-=. …………… 2分由全概率公式可知,9585.055.005.098.095.0)|()()|()()(=⨯+⨯=+=B A P B P B A P B P A P ……… 3分由贝叶斯公式,所求概率为97.09585.098.095.0)()|()()|(≈⨯==A PB A P B P A B P … 3分四、解答题(本题11分)解:(1) 由(2)01d (,)d d e d x y x f x y y x A y +∞+∞+∞+∞-+-∞-∞==⎰⎰⎰⎰20e d e d 2x y AAx y +∞+∞--==⎰⎰.得2A =. … 2分 (2) (,)d (,)d xyF x y x f x y y -∞-∞=⎰⎰2002e d e d ,0,0,0,x y x y x y x y --⎧>>⎪=⎨⎪⎩⎰⎰其它. 2(1e )(1e ),0,0,0,x y x y --⎧-->>=⎨⎩其它. … 4分 (3) X 与Y 的边沿密度分别为(2)02,0,0()()0,00,0x y x X edy x e x f x f x y dy x x +∞-+-+∞-∞⎧⎧>>⎪===⎨⎨≤⎩⎪≤⎩⎰⎰, …… 2分 (2)202,02,0()()0,00,0x y y Y edx y e y f y f x y dx y y +∞-+-+∞-∞⎧⎧>>⎪===⎨⎨≤⎩⎪≤⎩⎰⎰, …… 2分 显然, (,)()()X Y f x y f x f y =成立,故X 与Y 独立. ……………………1分 五、解答题(本题8分)解:由X 服从区间]2,1[上的均匀分布,即⎩⎨⎧≤≤=其他,,0211)(~x x f X 当Xe Y 2=时,)ln 21(}ln 21{}{}{)(2y F y X P y e P y Y P y F X X Y =<=<=<= … 3分其中)(x F X 是X 的分布函数。
概率论与数理统计期终考试试卷A及参考答案

上海应用技术学院2011—2012学年第一学期 《概率论与数理统计》期(末)(A )试卷课程代码: B2220073 学分: 3 考试时间: 100 分钟 课程序号: 112-7244、7246、7248、7249、7251、7254、7255、7257、7258等共9个教学班 班级: 学号: 姓名:我已阅读了有关的考试规定和纪律要求,愿意在考试中遵守《考场规则》,如有违反将愿接受相应的处理。
试卷共6页,请先查看试卷有无缺页,然后答题。
一、填空题(每题3分,共计18分)1、有321,,R R R 三个电子元件,用321,,A A A 分别表示事件“元件i R 正常工作”)3,2,1(=i ,试用321,,A A A 表示事件“至少有一个元件正常工作”:_______________。
2、连续型随机变量X 的分布函数为20,0,(),01,1, 1.x F x x x x ⎧<⎪=≤<⎨⎪≥⎩则(0.5 1.5)P X <<=_____。
3、设随机变量X 服从(3,7)F 分布,则随机变量1~Y X=____________。
4、设()28,10~N X ,()=<<200X P (用()Φ表示)。
5、已知随机变量,X Y ,有cov(,)5X Y =,设31U X =+,24V Y =-,则cov(,)U V =____。
6、设随机变量,X Y 相互独立~(5,0.5)X N ,~(2,0.6)Y N ,则()E XY =___________。
二、选择题(每题3分,共计18分)1、设S 表示样本空间,下述说法中正确的是( )(A )若A 为一事件,且()0P A =,则A =∅(B )若B 为一事件,且()1P B =,则B S = (C )若C S =,则()1P C =(D )若,A B 相互独立,则()()()P AB P A P B =+2、设随机变量X 与Y 均服从正态分布2~(,4)X N μ,2~(,5)Y N μ。
2011-2012学期期末考试《概率论与数理统计》A卷上海海事大学
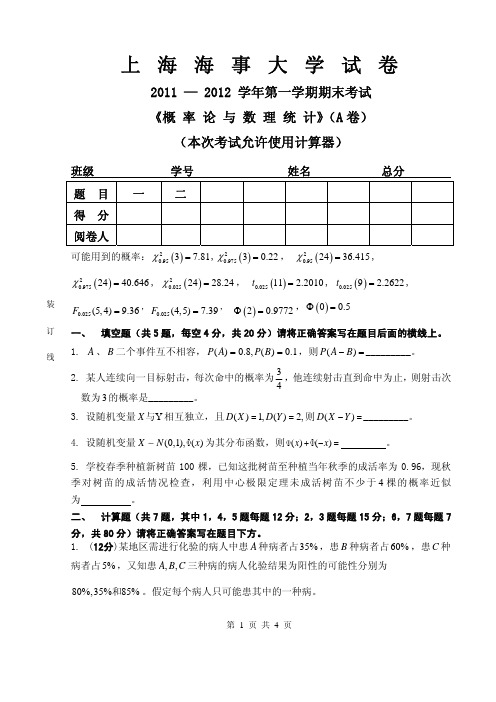
第 1 页 共 4 页上 海 海 事 大 学 试 卷2011 — 2012 学年第一学期期末考试 《概 率 论 与 数 理 统 计》(A 卷)(本次考试允许使用计算器)班级 学号 姓名 总分 可能用到的概率:()20.9537.81χ=,()20.97530.22χ=, ()20.952436.415χ=, ()20.9752440.646χ=, ()20.0252428.24χ=, ()0.02511 2.2010t =, ()0.0259 2.2622t =,0.025(5,4)9.36F =,0.025(4,5)7.39F =, ()20.9772Φ=,()00.5Φ=一、 填空题(共5题,每空4分,共20分)请将正确答案写在题目后面的横线上。
1. A 、B 二个事件互不相容,1.0)(,8.0)(==B P A P ,则=−)(B A P _________。
2. 某人连续向一目标射击,每次命中的概率为34,他连续射击直到命中为止,则射击次数为3的概率是_________。
3. 设随机变量Y X 与相互独立,且()1,()2,D X D Y ==则()D X Y -=_________。
4. 设随机变量(0,1),()X N x ∼F 为其分布函数,则()()x x F +F -= 。
5. 学校春季种植新树苗100棵,已知这批树苗至种植当年秋季的成活率为0.96,现秋季对树苗的成活情况检查,利用中心极限定理未成活树苗不少于4棵的概率近似为 。
二、 计算题(共7题,其中1,4,5题每题12分;2,3题每题15分;6,7题每题7分,共80分)请将正确答案写在题目下方。
1. (12分)某地区需进行化验的病人中患A 种病者占35%,患B 种病者占60%,患C 种病者占5%,又知患,,A B C 三种病的病人化验结果为阳性的可能性分别为80%,35%85%和。
假定每个病人只可能患其中的一种病。
概率统计A解答(1)

湖州师范学院 2010 — 2011 学年第 一 学期 《概率论与数理统计》期末考试试卷(A 卷)适用班级 090126 090127 考试时间 120 分钟学院 班级 学号 姓名 成绩题号 一 二 三 四 五 六 七 八 九 总分 得分一、填空题 (本题共20分,每空格2分)1.设A 、B 、C 表示三个随机事件,则事件“A 、B 、C 中恰有一个发生”可表示为C B A C B A C B A ++,事件“A 、B 、C 中至少发生二个”可表示为AC BC AB ++。
2.把5本书任意地放在书架上,其中指定的3本书放在一起的概率为103。
3.进行独立重复试验,每次试验成功的概率为p ,则在首次试验成功时共进行了m 次试验的概率为()11--m p p 。
4.若随机变量X 服从正态分布)21,1(N ,则X 的密度函数为=)(x ϕ2)1(1--x e π。
5.一批为产品共20个,其中3个次品,从中任取的3个中次品数不多于一个的概率为32013217317C C C C +。
6.设事件A 、B 、A ⋃B 的概率分别为p 、q 、r ,则=)(AB P r q p -+,=)(B A P q r -。
7.若随机变量X 服从泊松分布,)2()1(===X P X P ,则=≤)1(X P 23-e8.进行独立重复试验,每次试验事件A 发生的概率为p ,则在n 次试验中事得分件A 恰好发生()n k k ≤≤0次的概率为()kn kk np p C --1。
9.已知随机变量X 服从标准正态分布)1,0(N ,=≤)96.1(X P 0.975, 则=<)96.1(X P 0.95 。
10.加工在全产品要经过三道工序,第一、二、三道工序不出废品的概率分别为0.9、0.95、0.8,若假定各工序是否出废品是相互独立的,则经过三道工序生产出的产品是废品的概率是 0.316 。
11.设随机变量X 服从参数为p n ,的二项分布,则=EX np ,DX =()p np -1。
天津科技大学2011-2012学年第一学期《概率论与数理统计》(多概)期末考试试题(A卷)参考答案及评分标准

4
2011-2012 学年第一学期《概率论与数理统计》 (多概)期末考试试题(A 卷)参考答案及评分标准
查表得 1 / 2 ( n 1)
2 2 2 02..975 (8) 2.18, / 2 ( n 1) 0.025 (8) 17.53 , 7 分
而 0.975 (8) 2.18
九、某种虾的身长 X (单位:cm)服从正态分布 N ( , 2 ) ,现在随机抽取 9 只,算得平
均身长为 x 6 (cm) ,样本标准差 s 0.5745 (cm),求 的置信水平为 0.95 的置信区间. (本题 8 分) 解:由于 未知,故 的置信区间为 ( x
s t / 2 n
2
2
~(
(B) F ( n,n)
1) (C) F ( n,
(D) F (1,n)
三、某灯泡厂有甲、乙两条生产线,它们各自出产的灯泡中寿命大于 2500 小时的分别占有
80%和 90%,从它们出产的灯泡中各自随机地抽取一个, (1)求两个灯泡寿命都大于 2500 小 时的概率; (2)求两个灯泡中至少有一个寿命大于 2500 小时的概率. (本题 8 分)
8000 0.2 40 . 3 分
P(8100 X n 10000) P( X n np np (1 p )
8100 8000 40
X n np np (1 p )
10000 8000 )5分 40
P(2.5
50) (50) (2.5) 7 分 1 0.9938 0.0062 . 8 分
解:用 A, B 分别表示从甲、乙两个流水线上的产品中抽取的灯泡寿命大于 2500 小时,则 它们相互独立. 2 分 (1) P( AB) 3 分 P( A) P( B) 4 分 0.8 0.9 0.72 ; 5 分 (2) P( A
概率论与数理统计 期末试卷及答案 A

第 1 页 共 5 页班级 姓名 准考证号‥‥‥‥‥‥密‥‥‥‥‥‥封 ‥‥‥‥‥ 线 ‥‥‥‥内 ‥‥‥‥‥不 ‥‥‥‥‥准 ‥‥‥‥‥答 ‥‥‥‥‥题 ‥‥‥‥‥‥期末考试试卷 参考答案学年学期: 课程名称: 《概率论与数理统计》 适用专业:(满分:100分 时间:120分钟)一、单项选择题(本大题共15小题,每小题2分,共30分)在每小题列出的备选项中选择符合题目要求的,请将其代码填涂在答题卡上相应的位置,错涂、多涂或未涂均无分。
1.设二项分布的随机变量,其数学期望与方差之比为4:3,则该分布的参数p =( ).A .0.5B .0.25C .0.75D .不能确定2.设随机变量X 与Y 的关系为21Y X =+,如果()D X =2,则()D Y =( ).A .4B .6C .8D .103.若X 服从区间[]2,6上的均匀分布,则{23}P x <<=( ).A .0.2B .0.75C .0.5D .0.254.若随机变量X 的期望EX 存在,则()E aX b +=( ).A .aEXB .2a EXC .aEX b +D .2a EX b +5.当随机变量X 的可能值充满( )时,则()cos f x x =可以成为随机变量X 的密度函数.A .π[0,]2B .π[,π]2C .[0,π]D .3π7π[,]226.矿砂中铜含量服从正态分布),(~2σμN X ,2μσ,未知,现从总体中抽取样本521,,,X X X ,5115i i X X ==∑,52211()5i i S X X ==-∑,在显著水平α下检验00:μμ=H ,则所取的统计量为( ).A .5/0σμ-X B .5/0S X μ- C .4/0σμ-X D .4/0S X μ-7.事件表达式A B +的表示( ).A .事件A 与事件B 同时发生 B .事件A 发生但事件B 不发生C .事件B 发生但事件A 不发生D .事件A 与事件B 至少有一个发生8.样本空间S 中的事件A 与B 相互独立的充要条件是( ). A .A B S += B .()()()P AB P A P B =C .AB =∅D .()()()P A B P A P B +=+9.设1X 、2X 是总体X 的样本,则下列统计量不是总体X 的期望的无偏估计量的是( ).A .1XB .121233X X + C .121()2X X + D .121()3X X +10.任何一个连续型随机变量X 的密度函数()f x 一定满足( ).A 卷第 2 页 共 5 页‥‥‥‥‥‥‥‥‥‥‥‥‥‥ 密 ‥‥‥‥‥‥‥‥‥‥‥‥‥‥ 封 ‥‥‥‥‥‥‥‥‥‥‥‥‥‥ 线‥‥‥‥‥‥‥‥‥‥‥‥‥A .0()1f x ≤≤B .() d 1f x x +∞-∞=⎰C .在定义域内单调不减D .lim ()1x f x →+∞= 11.袋中有5球,3新2旧,从中任取一球,无返回的取两次,A =第一次取新球,B =第二次取新球.求P (B|A )=( ).A .12B .23C .35D .1312.已知事件A 和B 互不相容,()0,()0P A P B >>,下式成立的是( ). A .()()()P A B P A P B =+ B .()()()P AB P A P B =C .()1P A B =D .()0P AB >13.若随机变量2(,),3,1,X N EX DX μσ==则11}P X ≤≤={-( ).A .2(1)1A Φ-、 B .(4)(2)B Φ-Φ、C .(4)(2)Φ--Φ-C 、 D .(2)(4)Φ-ΦD 、 14.参数为λ的指数分布的方差是( ).A .1λB .2λC .λD .21λ15.设X 为连续型随机变量,则{1}P X ==( ). A .1B .0C .不能确定D .以上都不对二、判断题(本大题共5小题,每小题2分,共10分)判断正误,正确代码为A ,错误代码为B ,请将正确的答案代码涂在答题卡相应的题号下。
概率论与数理统计期末考试试卷答案

《概率论与数理统计》试卷A(考试时间:90分钟; 考试形式:闭卷)(注意:请将答案填写在答题专用纸上,并注明题号。
答案填写在试卷和草稿纸上无效)一、单项选择题(本大题共20小题,每小题2分,共40分) 1、A ,B 为二事件,则AB =()A 、AB B 、A BC 、A BD 、A B2、设A ,B ,C 表示三个事件,则A B C 表示()A 、A ,B ,C 中有一个发生 B 、A ,B ,C 中恰有两个发生C 、A ,B ,C 中不多于一个发生D 、A ,B ,C 都不发生 3、A 、B 为两事件,若()0.8P AB =,()0.2P A =,()0.4P B =,则()成立A 、()0.32P AB = B 、()0.2P A B =C 、()0.4P B A -=D 、()0.48P B A = 4、设A ,B 为任二事件,则()A 、()()()P AB P A P B -=- B 、()()()P AB P A P B =+C 、()()()P AB P A P B =D 、()()()P A P AB P AB =+ 5、设事件A 与B 相互独立,则下列说法错误的是()A 、A 与B 独立 B 、A 与B 独立C 、()()()P AB P A P B =D 、A 与B 一定互斥 6、设离散型随机变量X 的分布列为其分布函数为()F x ,则(3)F =()A 、0B 、0.3C 、0.8D 、17、设离散型随机变量X 的密度函数为4,[0,1]()0,cx x f x ⎧∈=⎨⎩其它 ,则常数c =()A 、15 B 、14C 、4D 、58、设X ~)1,0(N,密度函数22()x x ϕ-=,则()x ϕ的最大值是()A 、0B 、1 C、9、设随机变量X 可取无穷多个值0,1,2,…,其概率分布为33(;3),0,1,2,!k p k e k k -==,则下式成立的是()A 、3EX DX ==B 、13EX DX == C 、13,3EX DX == D 、1,93EX DX ==10、设X 服从二项分布B(n,p),则有()A 、(21)2E X np -=B 、(21)4(1)1D X np p +=-+C 、(21)41E X np +=+D 、(21)4(1)D X np p -=-11、独立随机变量,X Y ,若X ~N(1,4),Y ~N(3,16),下式中不成立的是()A 、()4E X Y +=B 、()3E XY =C 、()12D X Y -= D 、()216E Y += 12、设随机变量X 的分布列为:则常数c=()A 、0B 、1C 、14 D 、14- 13、设X ~)1,0(N ,又常数c 满足{}{}P X c P X c ≥=<,则c 等于()A 、1B 、0C 、12D 、-1 14、已知1,3EX DX =-=,则()232E X ⎡⎤-⎣⎦=()A 、9B 、6C 、30D 、36 15、当X 服从( )分布时,EX DX =。
浙江大学概率论2011-2012秋冬试卷

E X _, P X 2 _。
答案:0.5; 1 1.5e0.5 0.09 3.有甲乙两只袋,甲袋里有 4 个红球,2 个白球;乙袋里有 2 个红球,2 个 白球。 现从甲袋中不放回抽取 2 个球放入乙袋,然后再从乙袋中不放回取出 2 球。以 X 表示从甲袋中取到的红球数,Y 表示从乙袋中取到的红球数,则
五、 某电子监视器的屏幕为单位圆。 设目标出现的位置点 A x, y 服从单位圆 ( x2 y 2 1)上的均匀分布。求(1)点 A 与屏幕中心位置(0,0)的距离 小于 0.5 的概率; (2) f Y X y x ; (3)若在某个时间段陆续观测到了 108 个目标点,求其中至多有 36 个目标点出现在第一象限( x 0 , y 0 )的 概率近似值。 答案: (1) P X 2 Y 2 1 4 0.25
1.6 1.5 答案: (1) P X 1.6 1 1 1 0.16 0.1
15 30 30 0.5 1 (2) P X i X i 0.5 1 6 0.18 i 1 0.1 30 i 16
ˆ 2 2 ,求 的置信度为 95%的单侧置信下限。 (3)若 n
答案: (1)似然函数 L
1 i1 e 2n
X i n
2
n
, xi , i 1, 2,, n 是 的单调增
ˆ min X1,, X n 函数,所以 的极大似然估计量
15 2 S 或 B2 ; 1 16 ; X 0.4375S ; S 2 7.26 16 二、 为比较三个型号的汽车的油耗情况, 随即抽取 A 型汽车 6 辆, B 型汽车 5 辆, C 型汽车 7 辆,记录每辆汽车每公升汽油行驶的公里数,得如下数据: 12.9 11.3 12.6 14.1 13.2 12.1 A型
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2010-2011(1)概率论与数理统计期末试卷专业班级 姓名 得分一、单项选择题(每题2分,共20分)1.设A 、B 是相互独立的事件,且()0.7,()0.4,P A B P A ⋃==则()P B = ( A ) A. 0.5 B. 0.3C. 0.75D. 0.422、设X 是一个离散型随机变量,则下列可以成为X 的分布律的是 ( D )A.101p p ⎛⎫ ⎪-⎝⎭(p 为任意实数) B.123450.10.30.30.20.2x x x x x ⎛⎫ ⎪⎝⎭C. 33()(1,2,...)!ne P X n n n -=== D. 33()(0,1,2,...)!ne P X n n n -===3.下列命题不正确的是 ( D ) (A)设X 的密度为)(x f ,则一定有⎰+∞∞-=1)(dx x f ;(B)设X 为连续型随机变量,则P (X =任一确定值)=0; (C)随机变量X 的分布函数()F x 必有01)(≤≤x F ; (D)随机变量X 的分布函数是事件“X =x ”的概率;4.若()()()E XY E X E Y =,则下列命题不正确的是 ( B ) (A)(,)0Cov X Y =; (B)X 与Y 相互独立 ; (C)0=XY ρ; (D)()()D X Y D X Y -=+;5. 已知两随机变量X 与Y 有关系0.80.7Y X =+,则X 与Y 间的相关系数为 ( B ) (A)-1 ( B)1 (C)-0.8 (D)0.7 6.设X 与Y 相互独立且都服从标准正态分布,则( B ) (A)(0)0.25P X Y -≥= (B)(min(,)0)0.25P X Y ≥= (C)(0)0.25P X Y +≥= (D)(max(,)0)0.25P X Y ≥=7. 设随机变量X 服从正态分布),2(2σN ,其分布函数为()F x ,则对任意实数x ,有( B ) (A)()()1F x F x +-= (B)1)2()2(=-++x F x F (C)1)2()2(=-++x F x F (D)1)2()2(=-+-x F x F8.设(,)X Y 的联合分布律如下,且已知随机事件(0X =)与(1X Y +=)相互独立, 则b a ,的值为 ( A )(A) 1.0,4.0==b a ,(B) 3.0,2.0==b a ,(C) 4.0,1.0==b a ,(D) 2.0,3.0==b a 9.设袋中有编号为1,2,…,n 的n 张卡片,采用有放回地随机抽取k ()n k ≤张卡片, 记X 表示k 张卡片的号码之和,则()E X 为 ( A )(A) (+1)2k n (B) (+1)2n (C)(+1)2n k (D) (-1)2n k10.设X ~12)-1)(X -E(X )(=且λπ,则λ= ( C ) (A)3; (B)4 ; (C)1; (D)2; 二、填充题(每格2分,共32分)1、已知P(A)=P(B)=P(C)=25.0,P(AC)=0,P(AB)=P(BC)=15.0,则A 、B 、C 中至少有一个发生的概率为 0.45 。
2、A 、B 互斥且A=B ,则P(A)= 0 。
3、设A 、B 为二事件,P(A)=0.8,P(B)=0.7,P(A ∣B )=0.6,则P(A ∪B)= 0.88 。
4、设X 、Y 相互独立,X ~)3,0(U ,Y 的概率密度为⎪⎩⎪⎨⎧>=-其它,00,41)(41x e x f x ,则(253)E X Y -+= -14 ,(234)D XY -+=147 。
5、设某试验成功的概率为0.5,现独立地进行该试验3次,则至少有一次成功的概率为 0.8756、已知()3E X =,()D X =2,由切比雪夫不等式估计概率 (34)P X -≥≤ 0.125 。
7、设(100,0.2)X B ,则概率(P 20-X )4≤≈ 0.68 ()84.0)1(=Φ。
8.设X 的分布函数⎪⎩⎪⎨⎧≥-<=1,111,0)(2x x x x F ,则=)(X E 29.已知随机变量X ~),(2σμN ,且)1()5(,5.0)2(-Φ=≥=≥X P X P ,则=μ 2 ,=2σ9 。
10.设Y X 与相互独立,X ~),(2σμN ,Y 在[]4,0上服从均匀分布,则Y X 与的联合概率密度为(,)f x y=22()2,,040,x x y μσ--⎧-∞<<+∞≤≤⎩其它11.把9本书任意地放在书架上,其中指定3本书放在一起的概率为11212. 已知()0.6P A =,()0.8P B =,则()P AB 的最大值为 0.6 ,最小值为 0.4 。
13.已知()0.5,()0.6,()0.2P A P B P A B ===,则()P AB = 0.3 。
三、(4分)一袋中有4个白球,4个红球,2个黑球,现作有放回抽取3次,每次从中取一个,求下列事件的概率。
(1)第三次才取到白球 (2)3个颜色不全相同解:设A为“第三次才取到白球”的事件;B为“3个颜色不全相同”的事件 (1) 664()0.144101010P A =⋅⋅= (2) 333()1(0.40.40.2)0.864P B =-++=四、(6分)设随机变量X 的概率密度为0.2,01()0.4,460,x f x x ≤≤⎧⎪=≤≤⎨⎪⎩其它又知()0.8P X k ≥=,求(1)k 的取值范围,(2)X 的分布函数()F x 解:(1) 显然646414(4)0.40.8,(1)00.40.8P X dx P X dx dx ≥==≥=+=⎰⎰⎰故满足()0.8P X k ≥=的k 的取值范围是[]1,4 (2) X 的分布函数()F x =0,00.2,010.2,140.4 1.4,461,6x x x x x x x <⎧⎪≤<⎪⎪≤<⎨⎪-≤<⎪≥⎪⎩ 五、(9分)设连续型随机变量X 的分布函数为,1()ln ,1,a x F x bx x cx d x e d x e<⎧⎪=++≤≤⎨⎪>⎩求(1)常数,,,a b c d ;(2)密度函数()f x ;(3)()E X解: (1) 由()0()1(10)(10),(0)(0)0,1,1,1F a F d c d F F a d F e F e be ce d a b c d -∞==+∞==+=+=-==+=-=++===-=解得(2) X 的密度函数ln ,1()0,x x ef x <<⎧=⎨⎩其它(3) 22111()()ln ln 24eexe E X xf x dx x xdx xd+∞∞+===⎰⎰⎰-=六、(13分) 设离散型随机变量X 具有分布律X 1- 0 1 2 k p 0.25 2a a a 8.02+ 0.15 (1) 求常数a ;(2)求X 的分布函数)(x F ;(3)计算)23(≤X P ;(4) 求26X Y -=的分布律;(5)计算()D X . 解:(1) 由分布律的性质2220.2520.80.15 2.80.412.80.600.2,3(k kp a a a a a a a a a =++++=++=∴+-=∴==-∑舍去)(2) X 的分布函数010.25,10()0.65,010.85,121,2x x F x x x x <-⎧⎪-≤<⎪⎪=≤<⎨⎪≤<⎪≥⎪⎩,(3) 33()()0.8522P X F ≤== (4) 26X Y -=的分布律为Y 2 5 6 k p 0.15 0.45 0.4 (5)222()0.25,() 1.05,()()[()]0.9875E X E X D X E X E X ===-=七.(10分)设(,)X Y 的联合密度函数(1) 求常数k ; (2)求关于X 及关于Y 的边缘密度函数; (3) X 与Y 是否独立?说明理由。
解:(1) 由联合密度函数的性质12(,)188k f x y dxdy dxdy k +∞+∞-∞-∞===∴=⎰⎰⎰⎰(2) X 的边缘密度函数21728(),018,01()(,)30,0,x X x x x xy dy x f x f x y dy +∞-∞⎧⎧-≤≤≤≤⎪⎪==⎨⎨⎪⎪⎩⎩⎰⎰=其它其它 Y 的边缘密度函数3204,01,01()(,)0,0,Y y y xy dx y f y f x y dx +∞-∞⎧⎧≤≤≤≤⎪==⎨⎨⎩⎪⎩⎰=其它其它(3) 由于(,)()()X Y f x y f x f y ≠,故X 与Y 不相互独立八.(6分)设X 与Y 相互独立,其中X 的分布律如下,而Y 的概率密度)(y f Y 为已知,求XY U =的概率密度)(u g .解:()()(2)(2)(3)(3)0.2()0.8()230.2()0.8()23U Y Y F u P X Y u P X P X Y u X P X P X Y u X u u P Y P Y u uF F =≤==≤=+=≤==≤+≤=+()()110.2().0.8().22330.80.1()()233U Y Y Y Y g u F u u u f f u uf f '==+=+2,01(,)0,kxy x f x y ⎧<<<⎪=⎨⎪⎩其它。
