《由三视图确定几何体》练习题
由三视图判断几何体或几何体组成的小正方体个数

由三视图判断小正方体个数问题通过小正方体组合图形的三视图,确定组合图形中小正方体的个数,在中考或竞赛中经常会遇到。
解决这类问题如果没有掌握正确的方法,仅仅依赖空间想象去解决,不仅思维难度很大,还很容易出错。
通过三视图计算组合图形的小正方体的个数,关键是要弄清楚这个小正方体组合图形共有多少行、多少列、每行每列中各有多少层,理清了这些行、列、层的数量,小正方体的个数就迎刃而解了.在三视图中,通过主视图、俯视图可以确定组合图形的列数;通过俯视图、左视图可以确定组合图形的行数;通过主视图、左视图可以确定行与列中的最高层数.以上方法可简要地概括为:“主俯看列,俯左看行,主左看层,分清行列层,计数不求人.”一、结果唯一的计数例1在一仓库里堆放着若干个相同的正方体货箱,仓库管理员将这堆货箱的三视图画了出来,如图所示,则这堆正方体货箱共有()。
A.9箱B.10箱C.11箱D.12箱分析:由三视图可知,这堆货箱共有从前到后3行,从左到右3列。
由左视图:第一行均为1层,第二行最高2层,第三行最高3层;由主视图:第一列、第三列均为1层,第二列(中间列)最高为3层。
故第二行、第二列为2层,第三行第二列为3层,其余皆为1层。
各行、各列小正方体的个数如俯视图中所表示.这堆货箱共有3+1+1+2+1+1=9(箱)。
二、结果不唯一的计数例2(“希望杯”数学邀请赛试题)如图2,是由若干个(大于8个)大小相同的正方体组成的一个几何体的主视图和俯视图,则这个几何体的左视图不可能是()。
分析:由给出的主视图、俯视图可以看出,该几何体共有2行,3列。
第1列均为1层,第2列最高2层,第3列最高3层。
左视图为A时,第1行、第2行最高均为3层。
几何体中,第1列第1行为1层;第2列第1行、第2行均可为1层或2层,,但不能同时为1层;第3列两行均为3层。
此时,小正方体的个数如俯视图A所示,最少为1+2+1+3+3=10(个),最多为1+2+2+3+3=11个.左视图为B时,第一行均为1层,第二行最高为3层。
人教版九年级下册数学第二十九章第2节《三视图》训练题 (33)(含答案解析)
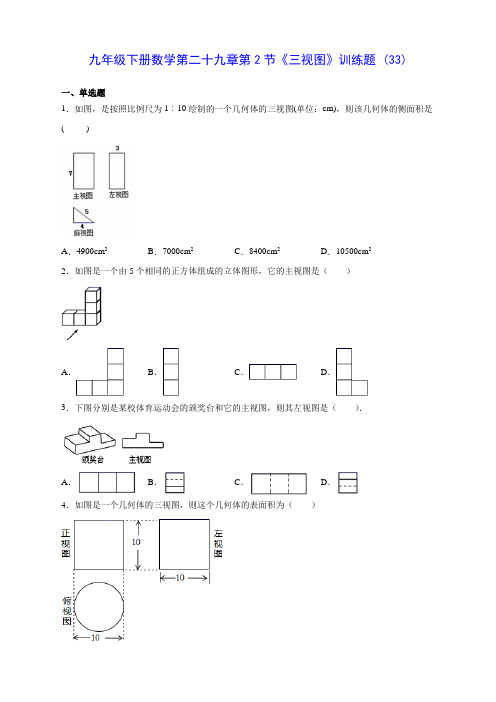
九年级下册数学第二十九章第2节《三视图》训练题 (33)一、单选题1.如图,是按照比例尺为1︰10绘制的一个几何体的三视图(单位:cm),则该几何体的侧面积是( )A.4900cm2B.7000cm2C.8400cm2D.10500cm22.如图是一个由5个相同的正方体组成的立体图形,它的主视图是()A.B.C.D.3.下图分别是某校体育运动会的颁奖台和它的主视图,则其左视图是().A.B.C.D.4.如图是一个几何体的三视图,则这个几何体的表面积为()A.50πB.100πC.150πD.175π5.如图,是由完全相同的5个小立方体组成的4个立体图形,主视图和左视图完全相同的()A.B.C.D.6.如图所示的几何体的主视图是()A.B.C.D.7.由若干块形状相同的小正方块搭成的立体模型的主视图与左视图如图,则搭成这个立体模型所使用的小正方块的最少块数是()A.3 B.4 C.5 D.68.如图所示的几何体的左视图是()A.B.C.D.9.如图是一个空心圆柱体,它的主视图是( )A .B .C .D .10.下列给出的几何体中,主视图和俯视图都是圆的是( )A .球B .正方体C .圆锥D .圆柱11.一透明的敞口正方体容器ABCD A B C D ''''-装有一些液体,棱AB 始终在水平桌面上,容器底部的倾斜角为α(CBE α∠=,如图1所示).如图1,液面刚好过棱CD ,并与棱BB '交于点Q ,此时液体的形状为直三棱柱,其三视图及尺寸如图2所示.则此时BQ 的长为( )A .5dmB .4dmC .1dmD .3dm12.如图所示,几何体是由一些大小相同的小正方体组成,其三视图中面积最小的是( )A .主视图B .左视图C .俯视图D .都一样13.如图是由三个正方体组成的几何体,它的主视图是( )A.B.C.D.14.一个几何体的主视图、左视图、俯视图都是圆形,这个几何体可能是()A.圆柱B.圆锥C.球D.半球15.下列几何体中,主视图不是矩形的几何体是()A.B.C.D.16.如下图是一个几何体的三视图,则这个几何体是()A.B.C.D.17.如图,是由四个相同的小正方体组成的立体图形,它的主视图是()A.B.C.D.18.如图所示的几何体,它的左视图是()A.B.C.D.19.图中所示的几何体的左视图为()A.B.C.D.20.用一些完全一样的小正方体搭成一个几何体,它的主视图、俯视图与左视图都是如图所示的图形,则小正方体的个数可能是()A.9 B.8 C.5 D.421.如图所示为某一物体的主视图,下面是这个物体的是()A.B.C.D.22.如图,下列水平放置的几何体中,左视图不是矩形的是()A.B.C.D.23.在下面的四个几何体中,它们各自的左视图与主视图不相同的是()A.B.C.D.24.如图是一根空心方管,它的俯视图是()A.B.C.D.25.如图是手提水果篮抽象的几何体,它的三视图中既是轴对称图形又是中心对称图形的是()A.B.C.D.26.如图所示的物体组合,它的左视图是()A.B.C.D.27.如图,由4个大小相同的正方体组成的几何体的主视图是()A.B.C.D.二、解答题28.一作图题:下列物体是由六个小正方体搭成的,请在下列网格中分别画出从正面、左面、上面看到的立体图形的形状.三、填空题29.如图是一个由圆柱与圆锥组合而成的几何体的三视图,根据图中所示数据计算这个几何体的侧面积是_____.30.一个长方体的主视图和左视图如图所示(单位:cm),则其俯视图的形状是________,面积cm.等于_________2【答案与解析】1.C【解析】根据三视图可知,该几何体是三棱柱,高为7,两个底面三边长分别为3、4、5,三棱柱的侧面积是三个长方形,用底面周长⨯高即可得出答案.由三视图可知,该几何体是三棱柱,侧面积为:2(345)784cm ++⨯=,∵是按照比例尺为1︰10绘制的一个几何体的三视图,∴原几何体的侧面积2841008400cm =⨯=,故选:C .本题考查了三视图还原几何体,棱柱侧面积的计算等知识,能通过三视图还原成三棱柱以及清楚每边长是解决本题的关键.2.A【解析】根据主视图就是从正面看到的图形即可解答.解:从正面看第一层是三个小正方形,第二层右边一个小正方形,第三层右边一个小正方形, 故答案为A .本题考查了简单组合体的三视图,掌握主视图、俯视图、左视图的概念是解答本题的关键. 3.D【解析】根据左视图是从左边看到的图形解答即可.解:颁奖台从左边看是一个矩形被分为3部分,上面分线是实线,下面的分线是虚线. 故选:D本题考查了由几何体判断三视图,从左边看到的图形是左视图,注意能看到的线用实线画,看不到的线用虚线画.4.C【解析】根据主视图、左视图、俯视图是分别从物体正面、左面和上面看所得到的图形,判断出几何体的形状,再根据三视图的数据,求出几何体的表面积即可.解:根据三视图可得这个几何体是圆柱,底面积=π×52=25π,侧面积为=10π•10=100π,则这个几何体的表面积=25π×2+100π=150π;故选:C.此题考查了由三视图判断几何体,用到的知识点是三视图,几何体的表面积的求法,准确判断几何体的形状是解题的关键.5.C【解析】根据几何体的主视图和左视图即可求解.解:A、主视图有3列,从左往右正方形的个数是2,1,1;左视图有2列,从左往右正方形的个数是1,2;不符合题意;B、主视图有2列,从左往右正方形的个数是2,1;左视图有3列,从左往右正方形的个数是1,2,1;不符合题意;C、主视图有2列,从左往右正方形的个数是2,1;左视图有2列,从左往右正方形的个数是2,1;符合题意;D、主视图有2列,从左往右正方形的个数是2,1;左视图有2列,从左往右正方形的个数是1,2;不符合题意.故选:C.考查简单几何体的三视图,主视图、左视图、俯视图实际上就是从正面、左面、上面对该几何体正投影所得到的图形.画三视图时还要注意“长对正、宽相等、高平齐”.6.A【解析】找到从前面看所得到的图形即可.解:从前面看可得到左边下方有1个正方形,右边有2个正方形,故选A.本题考查了三视图的知识,主视图是指从前面看所得到的图形.7.A【解析】左视图底面有2个小正方体,主视图与左视图相同,则可以判断出该几何体底层最少有2个小正方体,上面这层只有一个小正方体.根据这个思路可判断出该几何体有多少个小立方块.解:左视图与主视图相同,可判断出底层最少有2个小正方体,而第二层则只有1个小正方体.摆放方法是田字格的左上格有两个,右下格有一个小正方体,则这个几何体的小立方块最少为3个.故选:A.本题的难度不大,主要考查了考生的空间想象能力以及三视图的相关知识.8.D【解析】根据左视图是从左边看得到的图形,可得答案.从左边看一个正方形被分成两部分,正方形中间有一条横向的虚线,如图:故选:D.本题考查了几何体的三视图,从左边看得到的是左视图.9.C【解析】找到从前面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中.解:从前面观察物体可以发现:它的主视图应为矩形,又因为该几何体为空心圆柱体,故中间的两条棱在主视图中应为虚线,故选:C.本题考查了三视图的知识,主视图是从物体的正面看得到的视图;注意看得到的棱画实线,看不到的棱画虚线.10.A【解析】主视图是从正面看,俯视图是从上往下看,分别进行判断即可.A.球的主视图和俯视图都是圆,故选项A正确;B.正方体主视图和俯视图都是正方形,故选项B错误;C.圆锥的主视图是三角形,俯视图是圆,故选项C错误;D.圆柱的主视图是长方形,俯视图是圆,故选项D错误;故选:A.本题考查了几何体的三视图,解题关键是明确主视图、俯视图、左视图分别是从物体的正面、上面、左面看所得到的图形.【解析】根据水面与水平面平行可以得到CQ与BE平行,利用勾股定理即可求得BQ的长;解:根据题意,得CQ与BE的位置关系是:CQ∥BE,CQ=5,BC=AB=4,在Rt△BCQ中,(dm).本题考查了四边形的体积计算以及三视图的认识,正确理解棱柱的体积的计算是关键.12.A【解析】根据几何体的三视图进行判断即可.解:如图,该几何体主视图是由4个小正方形组成,左视图是由5个小正方形组成,俯视图是由5个小正方形组成,故三种视图面积最小的是主视图,故选:A.本题考查了三视图,正确识别几何体的三视图是解题关键.13.A【解析】根据主视图的定义,观察图形即可得出结论.解:主视图是从正面看得到图形,由几何体以及正面方向可知,主视图为:故选A.此题考查的是几何体主视图的判断,掌握主视图的定义是解决此题的关键.14.C【解析】在正面内得到的由前向后观察物体的视图,叫做主视图;在水平面内得到的由上向下观察物体的视图,叫做俯视图;在侧面内得到的由左向右观察物体的视图,叫做左视图.由此可判断出正确选项.因为几何体的主视图、左视图、俯视图是圆形,所以该几何体可能是球.故答案为:C.本题主要考查物体的三视图,能根据三视图确定几何体的形状是解题的关键.【解析】根据各几何体从正面看到的图形判断即可.解:A、圆柱的主视图是矩形,故此选项不合题意;B、圆锥的主视图是等腰三角形,故此选项符合题意;C、长方体的主视图是矩形,故此选项不合题意;D、三棱柱的主视图是矩形,故此选项不合题意;故选:B.本题考查了简单几何体的三视图,掌握三视图的知识点是解题关键.16.D【解析】根据三视图的定义逐项分析即可.A.主视图是一个矩形,左视图是一个矩形,俯视图是一个画有圆心的圆,故不符合题意;B.主视图是两个矩形,左视图是一个矩形,俯视图是一个矩形,故不符合题意;C.主视图是两个三角形,左视图是一个三角形,俯视图是一个三角形,且内部有一个点,故不符合题意;D.主视图是两个矩形,左视图是一个矩形,俯视图是一个三角形,故符合题意;故选D.本题考查由物体的三种视图推出原来几何体的形状,考查了学生的思考能力和对几何体三种视图的空间想象能力和综合能力.17.A【解析】找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中.解:从正面看易得第一层有2个正方形,第二层左上有1个正方形.故选:A.本题考查了三视图的知识,主视图是从物体的正面看得到的视图.18.D【解析】根据左视图的定义“平面内,从左往右观察所得到的视图”即可得.依据“长对正、高平齐、宽相等”画如图所示的几何体的三视图如下:故选:D.本题考查了左视图的定义,掌握左视图的定义是解题关键.三视图的另两个概念是:主视图和俯视图.19.B【解析】找到从左面看所得到的图形即可.解:如图,几何体的左视图是:.故选:B.本题考查了几何体的三视图,掌握定义是关键.主视图、左视图、俯视图分别是从物体正面、左面和上面看,所得到的图形.20.B【解析】易得这个几何体共有2层,由俯视图可得第一层立方体的个数,由主视图可得第二层立方体的可能的个数,相加即可.结合主视图、俯视图可知,上层有4个,下层一定有4个,∴组成这个几何体的小正方体的个数可能是8个,故选:B.本题考查由三视图确定几何体的形状,主要考查学生空间想象能力.21.D【解析】从该组合体的主视图看从左至右共有三列,从左到右第一列有两个正方体,第二列有三个正方体,第三列有一个,据此找到答案即可.解:从该组合体的主视图看从左至右共有三列,从左到右第一列有两个正方体,第二列有三个正方体,第三列有一个,可得只有选项D符合题意.故选:D.此题主要考查了画三视图的知识;用到的知识点为:主视图,左视图,俯视图分别是从物体的正面,左面,上面看得到的图形.22.B【解析】根据左视图的定义,逐一作出分析即可.解:A、C、D的左视图都是长方形,而B的主视图是等腰三角形,故选B.本题考查了三视图的知识,做视图是从物体的左面看得到的视图.23.B【解析】根据主视图、左视图的定义,可得答案.A、左视图与主视图都是正方形,故A不符合题意;B、主视图是两个矩形,两个矩形的邻边是虚线,左视图是一个矩形,故B符合题意;C、左视图与主视图都是矩形,故C不符合题意;D、左视图与主视图都是等腰三角形.故D不符合题意.故选:B.本题考查了简单几何体的三视图,从正面看得到的图形是主视图,从左边看得到的图形是左视图.24.B【解析】俯视图是从物体的上面看,所得到的图形:注意看到的用实线表示,看不到的用虚线表示.如图所示:俯视图应该是故选:B.本题考查了作图−三视图,解题的关键是掌握看到的用实线表示,看不到的用虚线表示.25.B【解析】根据从上边看得到的图形是俯视图,再依据轴对称图形与中心对称图形的定义可得答案.解:因为该几何体的俯视图是B,主视图是C,左视图是D,所以既是轴对称图形,又是中心对称图形的是B,故选B.本题考查的是简单几何体的三视图,轴对称图形及中心对称图形,掌握以上知识点是解题的关键.26.D【解析】通过对简单组合体的观察,从左边看圆柱是一个长方形,从左边看正方体是一个正方形,但是两个立体图形是并排放置的,正方体的左视图被圆柱的左视图挡住了,只能看到长方形,邻边用虚线画出即可.从左边看圆柱的左视图是一个长方形,从左边看正方体的左视图是一个正方形,从左边看圆柱与正方体组合体的左视图是一个长方形,两图形的邻边用虚线画出,则如图所示的物体组合的左视图如D选项所示,故选:D.本题考查了简单组合体的三视图.解答此题要注意进行观察和思考,既要丰富的数学知识,又要有一定的生活经验和空间想象力.27.C【解析】找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中.从正面看易得有2列小正方形,左边第一列有1个正方形且在下面,第二列有2个小正方形,故选项C正确.故选:C.本题考查了三视图的知识,主视图是从物体的正面看得到的视图.28.答案见解析【解析】根据主视图,左视图,俯视图定义,首先运用形体分析法把组合体分解为若干个形体,确定它们的组合形式,判断形体间邻接表面是否处于共面、相切和相交的特殊位置;然后逐个画出形体的三视图.本题考查了三视图的作图,三视图是主视图、俯视图、左视图的统称,从物体的前面向后面投射所得的视图称主视图,从物体的上面向下面投射所得的视图称俯视图,从物体的左面向右面投射所得的视图称左视图.29.185π cm2【解析】由三视图得圆锥的地面直径为10cm,圆锥的高为12cm,在轴截面中根据勾股定理求出圆锥母线长,进而求出圆锥侧面积;根据三视图确定圆锥底面直径为10cm,高为12cm,求出圆柱侧面积;相加即可求出几何体侧面积.解:由三视图可知,圆锥的底面直径为10cm,高为12cm,圆柱地面直径为10cm,高为12cm.则OA=5cm,在Rt△POA中,13PA cm=,圆的周长为10πcm,∴几何体的侧面积为110131012=65120=1852πππππ⨯⨯+⨯+cm2.故答案为:185π cm2本题考查了三视图,圆锥的侧面积,圆柱的侧面积等知识点,解题的关键是根据三视图确定圆锥,圆锥的相关数据,牢记圆锥,圆锥的侧面积公式.30.矩形 6【解析】根据主视图和左视图可推断出长方体的俯视图是长为3cm,宽为2cm的矩形,从而可得出答案.根据主视图和左视图可推出长方体的俯视图如下:∴它的俯视图是一个长为3cm,宽为2cm的矩形,∴S=2×3=6cm2,故答案为:矩形;6cm2.本题考查了由三视图判断几何体的知识,解决本题的关键是根据所给视图得到俯视图的矩形的边长.。
三视图 练习题
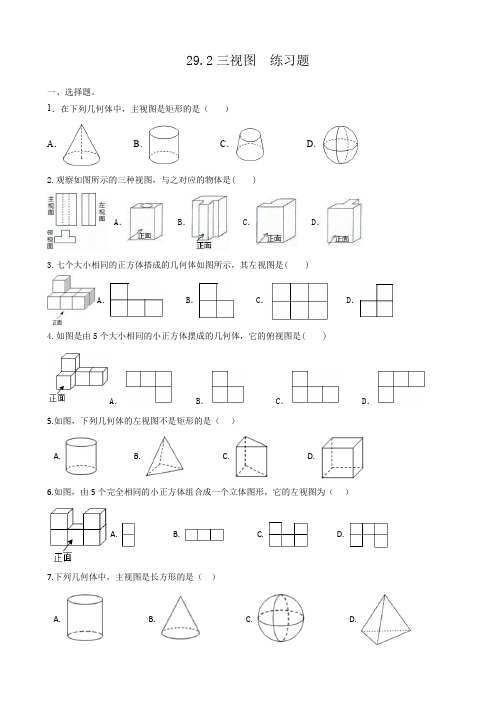
29.2三视图练习题一、选择题。
1.在下列几何体中,主视图是矩形的是()A.B.C.D.2.观察如图所示的三种视图,与之对应的物体是( )A. B. C. D.3.七个大小相同的正方体搭成的几何体如图所示,其左视图是( )A. B. C. D.4.如图是由5个大小相同的小正方体摆成的几何体,它的俯视图是( )A. B. C. D.5.如图,下列几何体的左视图不是矩形的是()A. B. C. D.6.如图,由5个完全相同的小正方体组合成一个立体图形,它的左视图为()A. B. C. D.7.下列几何体中,主视图是长方形的是()A. B. C. D.二、填空题8.如图是将两个棱长为40mm的正方体分别切去一块后剩下的余料,在它们的三视图中,完全相同的是_____.9.长方体的主视图和左视图如图所示(单位:cm),则其俯视图...的面积是.10.某几何体的三视图如图所示,则该几何体是________.11.如图是一个上下底密封纸盒的三视图,请你根据图中数据,计算这个密封纸盒的表面积为_______cm2.(结果可保留根号)13.一个几何体的三视图如图,那么这个几何体是_________.三、解答题14.如图,是一些小正方块所搭几何体从上面看到的图形,小正方块中的数字表示该位置的小正方块的个数,请画出这个几何体从正面、左面看到的形状.15.如图所示是一个正方体积木的三视图,试回答下列问题:(1)该正方体积木有几层高?(2)该正方体积木个数为多少?16.由几个相同的棱长为1的小立方块搭成的几何体的俯视图如图所示,方格中的数字表示该位置的小立方块的个数.(1)请在下图方格纸中分别画出该几何体的主视图和左视图;(2)这个几何体的体积为________个立方单位.。
高三专项训练:三视图练习题(一)
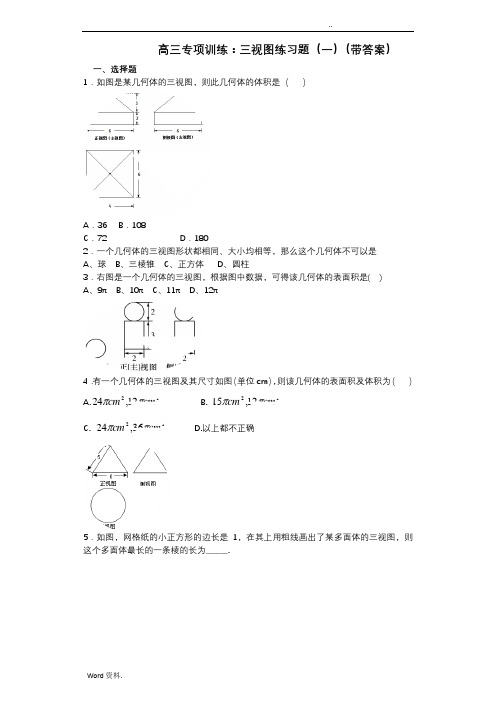
高三专项训练:三视图练习题(一)(带答案)一、选择题1.如图是某几何体的三视图,则此几何体的体积是( )A .36B .108C .72D .1802.一个几何体的三视图形状都相同、大小均相等,那么这个几何体不可以是A 、球B 、三棱锥C 、正方体D 、圆柱3.右图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )A 、9πB 、10πC 、11πD 、12π4.有一个几何体的三视图及其尺寸如图(单位cm ),则该几何体的表面积及体积为( )A.3212,24cm cm ππB. 3212,15cm cm ππC. 3236,24cm cm ππD.以上都不正确5.如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为______.A. B. CD .36.一空间几何体的三视图如图所示,则该几何体的体积为.A. B. C D. [7. 若某空间几何体的三视图如图所示,则该几何体的体积是A .13 B .23C .1D .28.右图是某几何体的三视图,则该几何体的体积为( )A . B.C. D.1362942π+3618π+9122π+9182π+正视图俯视图9.已知一个几何体的三视图如图所示,则该几何体外接球的表面积为( )A .43π B . 163π C .1912π D . 193π 10.某几何体的正视图如图所示,则该几何体的俯视图不可能的是11.已知某个几何体的三视图如图(主视图中的弧线是半圆),根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )cm 3.A .π+8B .328π+C .π+12D .3212π+侧视图主视俯视第8题图俯视图侧视图 正视图12.已知正六棱柱的底面边长和侧棱长均为2cm ,其三视图中的俯视图如图所示,则其左视图的面积是( )(A )243cm (B )223cm (C )28cm (D )24cm13.下图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )A .6πB .7πC .8πD .9π14.如右图所示,一个空间几何体的正视图和侧视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的表面积为 ( )A .π3B .π2C .π23 D .π4 15.如图是一个几何体的三视图,若它的体积是33,则图中正视图所标a=( )A .1B 3C 3D .316.已知某几何体的三视图如图所示(单位:cm ),其中正视图、侧视图都是等腰直角三角形,则这个几何体的体积是( )A .338cmB .3316cm C .33216cm D . 3332cm17.一个几何体的三视图如右图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该几何体的外接球的表面积为A .B .C .D .18.若某空间几何体的三视图如图所示,则该几何体的体积是 ( )A.13 B. 23C. 1D. 2 俯视图侧视图正视图22119.某物体是空心的几何体,其三视图均为右图,则其体积为( )A 、8B 、43π C 、483π+ D 、483π- π12π34π3π312正视图 侧视图俯视图 正视第9题22 4 2侧视图 22俯视20.如图,水平放置的三棱柱ABC-A 1B 1C 1中,侧棱AA 1⊥平面A 1B 1C 1,其正视图是边长为a 的正方形.俯视图是边长为a 的正三角形,则该三棱柱的侧视图的面积为A .a 2B .a 2C a 2D 221.右图是一个几何体的三视图(侧视图中的弧线是半圆),则该几何体的表面积是( )A .20+3π B .24+3π C .20+4π D .24+4π22.一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该几何体的外接球的表面积为A .12πB .π34C .3πD .π312.23.如右图为一个几何体的三视图,其中俯视图为正三角形,A 1B 1=2,AA 1=4,则该几何体的表面积为( )12正视图 侧视图 俯视图 AC A 11正视图 侧视图俯视图24.图1是设某几何体的三视图,则该几何体的体积为()A.942π+B.3618π+C.9122π+D.9182π+、25.已知某几何体的三视图如图所示,根据图中标注的尺寸(单位cm)可得该几何体的体积是()A.313cm B.323cmC.343cm D.383cm26.小红拿着一物体的三视图(如图所示)给小明看,并让小明猜想这个物件的形状是A. 长方形 B. 圆柱 C. 立方体 D. 圆锥27.一个几何体的三视图如图所示,则这个几何体的体积为()正视图侧视图俯视图332正视图俯视图图1AB .12C .32 D1+28.一个空间几何体的三视图如图(1)所示,其中正视图为等腰直角三角形,侧视图与俯视图为正方形,则该几何体的体积和表面积分别为 ( )A 、64,48+B 、32,48+ C 、643,32+D 、332,48+29.若某多面体的三视图(单位: cm )如图所示,则此多面体的体积是( ) A .21cm 3 B .32cm 3 C .65cm 3 D .87cm 3正视图俯视图图(1)侧(左)视图 1111130.一个空间几何体的正视图、侧视图均是长为2、高为3的矩形,俯视图是直径为2的圆(如右图),则这个几何体的表面积为A .12π+B .7πC . π8D .π2031.(一空间几何体的三视图如图所示,则该几何体的体积为( ).A. B.C.D. 32.已知几何体其三视图(如图),若图中圆半径为1,等腰三角形腰为3,则该几何体表面积为 ( ) A .6π B .5π C.4π D.3π2π+4π+2π4π+正视侧视俯视俯视..A .2,23B .22,2D .2,434.如图,有一个几何体的正视图与侧视图都是底为6cm ,腰为5cm 的等腰三角形,俯视图是直径为6cm 的圆,则该几何体的体积为 ( )A .12πcm 3B .24πcm 3C .36πcm 3D .48πcm 335 (A )348cm (B )324cm (C )332cm (D )328cm36. 如图,直三棱柱的侧棱长和底面边长均为2,正视图和俯视图如图所示,则其侧视图的面积为 ( )A .4B .3C .32D .237.某四面体的三视图如下图所示,则该四面体的四个面中,直角三角形的面积和是_______.二、填空题 正视图 左视图俯视图正视图侧视图 俯视图 第6题 ·38.一个几何体的三视图如右图所示,主视图与俯视图都是一边长为3cm 的矩形,左视图是一个边长为2cm 的等边三角形,则这个几何体的体积为________.39.如图所示是一个几何体的三视图(单位:cm ),主视图和左视图是底边长为4cm ,腰长为22的等腰三角形,俯视图是边长为4的正方形,则这个几何体的表面积是-__________40.某几何体的三视图如图所示,则该几何体的体积的最大值为 .41.一正多面体其三视图如图所示,该正多面体的体积为___________.主视图 左视图俯视图3主视图 俯视图 侧视图42.若某几何体的三视图(单位:cm )如右图所示,则该几何体的体积为 cm 2.43.已知某几何体的三视图如图所示,其中侧视图是等腰直角三角形,正视图是直角三角形,俯视图ABCD 是直角梯形,则此几何体的体积为 ;44.某四面体的三视图如上图所示,该四面体四个面的面积中最大的是1正视图俯视图左视图45.一个几何体的三视图如右图所示(单位:),则该几何体的体积为__________46.一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,若该几何体的所有顶点在同一球面上,则球的表面积是_____.47.如图,一个简单空间几何体的三视图其主视图与左视图都是边长为的正三角形,其俯视图轮廓为正方形,则其体积是_________.48. 某几何体的三视图如图所示,则它的体积是___________俯视图m 3m 249.设某几何体的三视图如图所示,则该几何体表面积是50.一个几何体的三视图如右图所示,正视图是一个边长为2的正三角形,侧视图是一个等腰直角三角形,则该几何体的体积为.三视图练习题(一)参考答案1.B【解析】此几何体是一个组合体,下面是一个正四棱柱上面是一个四棱锥.其体积为166********V =⨯⨯+⨯⨯⨯=.2.D【解析】圆的正视图(主视图)、侧视图(左视图)和俯视图均为圆; 三棱锥的正视图(主视图)、侧视图(左视图)和俯视图可以为全等的三角形; 正方体的正视图(主视图)、侧视图(左视图)和俯视图均为正方形; 圆柱的正视图(主视图)、侧视图(左视图)为矩形,俯视图为圆。
通过三视图确定几何体的个数

第一讲:1、通过三视图确定正方体的个数此类题型为中考常考点,主要分为两类:1、给出三类视图,求解组成的几何体的个数;2、只给出部分视图,如只有主、左视图,然后要求组成的几何体的个数最多或者最少的个数例1.由一些大小相同的小正方体组成的几何体的三种视图如图所示,那么组成几何体的小正方体有( )个.(A )4 (B )5 (C )6 (D )7析解:解决这类问题要做到,一看俯视图,从左至右共有三列,从上到下共三行;二看主视图,共有三列两行,第一列和第三列上分别只有一层,第二列上有两层,则俯视图中的一、三列上分别只有一个正方体,分别填1(如图1);三看左视图,共三列两行,第一列和第三列上分别只有一层,第二列上有两层,则俯视图中第一行只有一个正方体,填1,第二行有两个正方体,填2,第三行第二列只有一个正方体,填1,所以该俯视图上每个小正方体的个数如图1所示,搭成这个几何体的小正方体的个数是1+2+1+1+1=6,故本题结果就选 (C). 相应的几何体如图2所示.图121111 图2例2. 如图是由几个相同的小正方体搭成的几何体的三种视图,则搭成这个几何体的小正方体的个数是 个.主视图左视图 俯视图例3.一个几何体是由若干个相同正方体组成的,其主视图和左视图如图5所示,则这个几何体最多可由多少个这样的正方体组成?()(A)12个(B)13个(C)14个(D)18个图6111112222解析:主视图和左视图都为3列,可知几何体的俯视图有三列三行,最多为33 的正方形,由主视图可知在俯视图第1、3列每个正方形内填2,第2列每个正方形内填1;又由左视图可知,在俯视图的1、3行中(观察者需站在俯视图的左侧看)每个小正方形内都填入2,第2行填1,重叠交叉处数字取小,如上图,故最多由13个组成. 故选(B).点评:由三视图到确定几何体,应根据主视图和俯视图情况分析,再结合左视图的情况定出几何体,最后便可得出这个几何体组合的小正方体个数.练习:图52、计算11111(1)(1)(1)(1)(1)20042003200210011000-•-•--•-的值3、1111(1)(1)(1)(1)23410÷-÷-÷-÷÷-计算:1 4、已知 21421842m m x y x y +-++是一个七次多项式,则m=5、4(x 2+y )(x 2-y )-(2x 2-y )2 , 其中 x=2, y=-56、计算 乘积⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛⋯⋯⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-2222220001119991-1411311211 的值7、()()()[]22234322ab x a x a xa -÷⎥⎦⎤⎢⎣⎡---,其中21=a ,x =-4。
人教版九年级下册数学第二十九章第2节《三视图》训练题 (3)(含答案解析)

九年级下册数学第二十九章第2节《三视图》训练题 (3)一、单选题1.如图所示的几何体的左视图是()A.A B.B C.C D.D2.如图所示,从上面看该几何体的形状图为()A.B.C.D.3.如图试一个几何体的三视图,则这个几何体的形状是()A.圆柱B.圆锥C.球D.三棱锥4.如图是一个立体图形从左面和上面看到的形状图,这个立体图形是由相同的小正方体构成,这些相同的小正方体的个数最少是()5.如图,正方形ABCD 的边长为3cm ,以直线AB 为轴,将正方形旋转一周,所得几何体的主视图的面积是( )A .29cmB .29πcmC .218πcmD .218cm6.下列立体图形中,左视图与主视图不同的是( )A .正方体B .圆柱C .圆锥D .球7.一个几何体的三视图如图所示,则这个几何体是( )A .B .C .D .8.如图是一个立方体的三视图,这个立方体由一些相同大小的小正方体组成,这些相同的小正方体的个数是( )A .4B .5C .6D .79.如图所示的几何体的左视图为( )A.B.C.D.10.如图所示的立体图形是一个圆柱被截去四分之一后得到的几何体,它的左视图是()A.B.C.D.11.由若干个相同的小正方体搭建而成的几何体的三视图如图所示,则这个几何体共有小正方体()A.4个B.5个C.6个D.7个12.如图①是由大小相同的小正方体搭成的几何体,将上层的小正方体平移后得到图②.关于平移前后几何体的从三个方向看得图形,下列说法正确的是()A.从正面看到的图相同B.从左面看到的图相同C.从上面看到的图相同D.从三个方向看到的图都不相同二、解答题13.如图,这是一个由小立方块塔成的几何体的俯视图,小正方形中的数字表示该位置的小立方块的个数.请你画出它的主视图与左视图.14.下图的几何题是由8个相同的立方块搭成的,请画出它从正面、左面、上面看到的形状图.15.下图是由几个棱长为1的小立方块搭成的几何体的俯视图,小正方形中的数字表示在该位置小立方块的个数,请画出这个几何体的主视图和左视图;并计算出该几何体的表面积16.如图,这是一个小正方体所搭建的几何体的俯视图,正方形中的数字表示在该位置小正方体的个数,请你画出从正面看和从侧面看的图形.17.如图所示,这是由小立方体搭成的几何体,请画出主视图、左视图、俯视图.18.下面图是几个小方块所搭几何体俯视图,小正方形中的数字表示在该位置的小立方块的个数.请画出这个几何体的主视图、左视图.19.由12个完全相同的棱长为1cm的小正方体搭成的几何体,如图所示.(1)请画出这个几何体的三视图.(2)请计算它的表面积.20.画出如图所示的几何体的主视图、左视图、俯视图:从正面看主视图_____左视图_____俯视图______21.如图是某几何体从正面、左面、上面看到的形状图.(1)这个几何体的名称是.(2)若从正面看到的长方形的宽为4cm,长为9cm,从左面看到的宽为3cm,从上面看到的直角三角形的斜边为5cm,则这个几何体中所有棱长的和是多少?它的表面积是多少?22.用棱长为2cm的若干小正方体按如所示的规律在地面上搭建若干个几何体.图中每个几何体自上而下分别叫第一层、第二层,,第n层(n为正整数)(1)搭建第④个几何体的小立方体的个数为.(2)分别求出第②、③个几何体的所有露出部分(不含底面)的面积.1cm需要油漆0.2克,(3)为了美观,若将几何体的露出部分都涂上油漆(不含底面),已知喷涂2求喷涂第20个几何体,共需要多少克油漆?23.图中几何体由7个边长为1cm的正方体搭成,分别画如图几何体的主视图、左视图、俯视图.并算出此几何体的表面积24.用小立方块搭一个几何体,使它的主视图和俯视图如图所示,俯视图中小正方形中字母表示该位置小立方块的个数,请解答下列问题:(1)a=________,b=_________,c=_________.(2)这个几何体最少由________个小立方块搭成,最多由________个小立方块搭成.(3)当d=e=1,f=2时,画出这个几何体的左视图.25.如图1所示,从大正方体中截去一个小正方体之后,可以得到图2的几何体.(1)设原大正方体的表面积为a,图2中几何体的表面积为b,那么a与b的大小关系是;A.a>b;B.a<b;C.a=b;D.无法判断.(2)小明说“设图1中大正方体的棱长之和为m,图2中几何体的各棱长之和为n,那么n比m正好多出大正方体的3条棱的长度.”你认为小明的说法正确吗?为什么?(3)如果截去的小正方体的棱长为大正方体的棱长的一半,那么图3是图2几何体的表面展开图吗?如有错误,请予修正.26.如图是由9个相同的棱长为2cm小立方体组成的一个几何体(1)请利用下方网格画出这个几何体的从正面看到主视图、从左面看到的左视图和从上面看到的俯视图(一个网格为小立方体的一个面).(2)计算这个堆积几何体的表面积(含底面).三、填空题27.10个棱长为a cm的正方体摆放成如图的形状,这个图形的表面积是____________.28.若干个桶装方便面摆放在桌子上,小明从三个不同方向看到的图形(分别是:主视图,左视图,和俯视图)如图所示,则这一堆方便面共有__________个29.由若干个小正方体搭成的几何体的主视图和俯视图,如图所示,则搭成该几何体所用的小正方体的个数最多是________个,最少是________个.主视图俯视图30.如图,一个几何体是由若干个棱长为3的小正方体搭成的,小正方形中的数字表示在该位置小立方体的个数,则这个几何体的表面积是______.【答案与解析】1.D【解析】利用左视图的定义,从左向右看,看到的图形是一个长方形,由于右侧有一横线没看见,用虚线突出出来即可.从左向右看,看到的图形是一个长方形,右侧有横线看不见,为此用虚线显现出横线,左视图为D.故选:D.本题考查三视图的知识,左视图是从物体的左面看到的视图,掌握定义,会用定义选图是关键.2.C【解析】俯视图是从物体上面所看到的图形,可根据物体的特点作答;解:这是一个中间部分掏空的长方体,根据俯视图是从物体上面所看到的图形,故选:C本题考查了三视图的知识,俯视图是从物体的上面看得到的视图,根据物体的特征回答是解题的关键.3.B【解析】根据主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形,再根据几何体的特点即可得出答案.由于主视图和左视图为三角形可得此几何体为锥体,由俯视图为圆形可得为圆锥.故选:B.本题主要考查了学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.4.C【解析】先根据俯视图和左视图确定底层和第二层正方体的最少个数,最后求和即可.解:根据俯视图可得:底层正方体最少5个正方体,根据左视图可得:第二层最少有1个正方体;则构成这个立体图形的小正方体的个数最少为5+1=6个.故答案为C.本题考查了根据三视图确定立体图形中正方体的个数,具有较好的空间想象能力是解答本题的关键.5.D【解析】先确定几何体的主视图,得到边长分别为3cm 、6cm ,再根据面积公式计算得出答案.如图,所得几何体的主视图是一个长方形,边长分别为3cm 、6cm ,∴所得几何体的主视图的面积是36 =218cm ,故选:D.此题考查几何体的三视图,平面图形的面积计算公式,正确理解几何体的三视图是解题的关键. 6.B【解析】根据三视图的意义可以得到解答.解:∵正方体的左视图与主视图均为以正方体棱长为边长的正方形,∴A 不符合题意; ∵倒放的圆柱体左视图为圆形,主视图为矩形,∴B 符合题意;∵圆锥的左视图与主视图均为以圆锥母线为腰、以底面直径为底的等腰三角形,∴C 不符合题意; ∵球的左视图与主视图均为以球半径为半径的圆,∴D 不符合题意;故选B .本题考查三视图的应用,熟练掌握三视图的意义和性质是解题关键 .7.C【解析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.解:由于主视图和左视图为长方形可得此几何体为柱体,由俯视图为四边形,只有C 符合条件;故选:C .本题考查由三视图想象立体图形.做这类题时要借助三种视图表示物体的特点,从主视图上弄清物体的上下和左右形状;从俯视图上弄清物体的左右和前后形状;从左视图上弄清楚物体的上下和前后形状,综合分析,合理猜想,结合生活经验描绘出草图后,再检验是否符合题意.8.D【解析】根据主视图和左视图小正方形的个数,在俯视图上标记每个位置上正方形的个数即可求解.根据题意,在俯视图上标注各个位置的个数为:所以一共有:1+2+2+1+1=7(个)故选D.本题考查了投影与视图,问题的关键是了解三种视图的关系与区别.9.C【解析】找到从左面看所得到的图形即可,注意所有的看到的棱都应表现在左视图中.从左边看是一个正方形,对面看不到的切割部分是虚线,故选:C.本题考查了简单组合体的三视图,从左边看得到的图形是左视图,注意看不到而且存在的线是虚线.10.C【解析】根据左视图的定义:一般指由物体左边向右做正投影得到的视图,即可得出结论.解:根据左视图的定义,该几何体的左视图是:故选C.此题考查的是几何体左视图的判断,掌握左视图的定义是解题关键.11.B【解析】先由俯视图得出这个几何体的底层共有4个小正方体,再结合主视图和左视图可得第二层应该有1个小正方体,进而可得答案.解:由俯视图可得:这个几何体的底层共有4个小正方体,结合主视图和左视图可得:第二层应该有1个小正方体,因此搭成这个几何体的小正方体的个数为4+1=5个.故选:B.本题考查了几何体的三视图,属于基础题型,掌握解答的方法是解题的关键.12.C【解析】根据从正面看到的是主视图,从上面看到的是俯视图,从左面看到的是左视图画出两个组合图形的三视图,再进行判断即可.解:图①的三视图为:图②的三视图为:故选:C.本题考查了简单组合体的三视图.解题的关键是学生对几何体三视图的空间想象能力.13.见解析【解析】主视图有3列,每列小正方形数目分别为2,3,4;左视图有2列,每列小正方形数目分别为4,3.依此画出图形即可求解.解:如图所示:本题考查了画三视图.在画图时一定要将物体的边缘、棱、顶点都体现出来,看得见的轮廓线都画成实线,看不见的画成虚线,不能漏掉.本题画几何体的三视图时应注意小正方形的数目及位置.14.见解析观察图形可知,从正面看到的图形是3列,从左往右正方形个数依次是3,1,2;从左面看到的图形是2列,从左往右正方形个数依次是3,1;从上面看到的图形是3列,从左往右正方形个数依次是2,2,1;据此即可画图.解:如图所示:本题考查了作图-三视图:确定主视图位置,画出主视图;再在主视图的正下方画出俯视图,注意与主视图“长对正”;然后在主视图的正右方画出左视图,注意与主视图“高平齐”、与俯视图“宽相等”.15.画图见解析;40【解析】先根据题意可得主视图有3列,每列小正方数形数目分别为3,3,2;左视图有2列,每列小正方形数目分别为3,2,然后画出立体图形计算表面积即可.解:主视图和左视图如图所示:此几何体为:∴其几何表面积为:()855222++⨯+⨯=⨯+1824=+364本题主要考查了几何体的三视图画法以及立体图形表面积的求法,正确画出三视图和立体图形是解答本题的关键.16.见详解【解析】由已知条件可知,主视图有3列,每列小正方数形数目分别为2,3,3;左视图有2列,每列小正方形数目分别为3,3.据此可画出图形.解:如图所示:本题考查几何体的三视图画法.由几何体的俯视图及小正方形内的数字,可知主视图的列数与俯视数的列数相同,且每列小正方形数目为俯视图中该列小正方形数字中的最大数字.左视图的列数与俯视图的行数相同,且每列小正方形数目为俯视图中相应行中正方形数字中的最大数字.17.见解析【解析】根据三视图的定义,分别画出几何体的主视图、左视图以及俯视图即可.由图可得几何体的三视图如下:主视图左视图俯视图本题主要考查几何体三视图的画法,熟记三视图的概念以及空间想象力的运用是解题关键.18.见解析【解析】由已知条件可知,主视图有3列,每列小正方数形数目分别为4,2,3,左视图有3列,每列小正方形数目分别为2,4,,3.据此可画出图形.如图,即为所求.本题考查几何体的三视图画法.由几何体的俯视图及小正方形内的数字,可知主视图的列数与俯视数的列数相同,且每列小正方形数目为俯视图中该列小正方形数字中的最大数字.左视图的列数与俯视图的行数相同,且每列小正方形数目为俯视图中相应行中正方形数字中的最大数字.19.(1)画图见解析;(2)242cm.【解析】(1)由已知条件可知,主视图有3列,每列小正方数形数目分别为3,1,2;左视图有3列,每列小正方形数目分别为3,2,2;俯视图有3列,每列小正方数形数目分别为3,3,1.据此可画出图形;(2)利用几何体的形状进而求出其表面积;(1)S=⨯+++(2)2(677)2=⨯+2202()2=42cm答:它的表面积是42cm2.本题考查了三视图的画法以及表面积的求法.主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形,物体的表面积是指露在外部的所有表面积之和.20.见解析【解析】主视图有4列,每列小正方形数目分别为1,3,1,1;左视图有3列,每列小正方形数目分别为3,1,1;俯视图有4列,每列小正方形数目分别为1,3,1,1,从而可得答案.解:主视图左视图俯视图考查了作图-三视图,主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形,掌握以上知识是解题的关键.21.(1)直三棱柱;(2)51cm;2120cm【解析】(1)直接利用三视图可得出几何体的形状;(2)利用已知各棱长分别得出棱长和与表面积.(1)这个几何体是直三棱柱;故答案为:直三棱柱(2)由题意可得:它的所有棱长之和为:(3+4+5)×2+9×3=51(cm);它的表面积为:2×(12×3×4)+(3+4+5)×9=120(cm2)答:所有棱长的和是51cm,它的表面积为120cm2.此题主要考查了由三视图判断几何体的形状,正确得出物体的形状是解题关键.22.(1)30;(2)第②个几何体露出部分(不含底面)面积为264cm,第③个几何体露出部分(不含底面)面积为2132cm;(3)992克.【解析】(1)归纳出前3个几何体的规律即可得;(2)分别画出两个几何体的三视图,再根据四个侧面和向上的面的小正方形的个数即可得;(3)先根据(1)的方法得出第20个几何体每一层小立方体的个数,再根据(2)的方法得出第20个几何体的所有露出部分(不含底面)的面积,然后乘以0.2即可得.(1)搭建第①个几何体的小立方体的个数为1, 搭建第②个几何体的小立方体的个数为21412+=+, 搭建第③个几何体的小立方体的个数为22149123++=++,归纳类推得:搭建第④个几何体的小立方体的个数为22212341491630+++=+++=, 故答案为:30;(2)第②个几何体的三视图如下:由题意,每个小正方形的面积为2224()cm ⨯=,则第②个几何体的所有露出部分(不含底面)面积为()232324464()cm ⨯+⨯+⨯=;第③个几何体的三视图如下:则第③个几何体的所有露出部分(不含底面)面积为()2626294132()cm ⨯+⨯+⨯=;(3)第20个几何体从第1层到第20层小立方体的个数依次为221,2,,20,则第20个几何体的所有露出部分(不含底面)面积为()()2221220212202044960()cm ⎡⎤⨯++++⨯++++⨯=⎣⎦, 因此,共需要油漆的克数为49600.2992⨯=(克), 答:共需要992克油漆.本题考查了三视图、几何体的表面积、图形变化的规律型问题,依据题意,正确归纳类推出规律是解题关键.23.图见解析,228cm . 【解析】根据主视图、左视图、俯视图的定义画出图形即可;有顺序的计算前后面、左右面、上下面的表面积之和即可得.由主视图、左视图、俯视图的定义画出图形如下所示:由题意得:小正方体的每个面的面积为()2111cm⨯=, 则其表面积为()262142142128cm⨯⨯+⨯⨯+⨯⨯=.本题考查了三视图、几何体的表面积,熟练掌握三视图的概念是解题关键. 24.(1)3,1,1a b c ===;(2)9,11;(3)画图见解析. 【解析】(1)由主视图可知,第二列小立方体的个数均为1,第3列小正方体的个数为3,从而可得答案; (2)第一列小立方体的个数最少为2+1+1,最多为2+2+2,那么加上其它两列小立方体的个数即可得到答案;(3)左视图有3列,每列小正方形数目分别为3,1,2,从而可得左视图.解:(1)由主视图可知,第二列小立方体的个数均为1,第3列小正方体的个数为3, 所以:3,1,1a b c ===. 故答案为:3,1,1;(2)由第一列小立方体的个数最少为2+1+1,最多为2+2+2, 所以这个几何体最少由4+2+3=9个小立方块搭成; 这个几何体最多由6+2+3=11个小立方块搭成; 故答案为:9,11.(3)由左视图有3列,每列小正方形数目分别为3,1,2, 如图所示:本题考查了三视图的知识,掌握主视图是从物体的正面看得到的视图,左视图是从物体的左面看得到的视图;注意主视图主要告知组成的几何体的层数和列数.25.(1)C;(2)不正确,理由见解析;(3)图③不是图②几何体的表面展开图,改后的图形见解析【解析】(1)根据“切去三个面”但又“新增三个面”,因此与原来的表面积相等;(2)根据多出来的棱的条数及长度得出答案;(3)根据展开图判断即可.解:(1)根据“切去三个小面”但又“新增三个相同的小面”,因此与原来的表面积相等,即a=b故答案为:a=b;(2)如图④红颜色的棱是多出来的,共6条,当且仅当每一条棱都等于原来正方体的棱长的一半,n比m正好多出大正方体的3条棱的长度,故小明的说法是不正确的;图④图⑤(3)图③不是图②几何体的表面展开图,改后的图形,如图⑤所示.本题考查几何体表面积的意义、棱长之和、几何体的表面展开图,考查学生的观察能力,关键是抓住几何图形变换后边长和棱长的变与不变的量.26.(1)见解析;(2)144cm2【解析】(1)主视图有3列,每列小正方形数目分别为2,3,1;左视图有3列,每列小正方形数目分别为3,1,2;俯视图有3列,每列小正方形数目分别为1,3,2;(2)分别求出各个方向的小正方形的个数,进一步即可求解.解:(1)如图所示:(2)6×6×(2×2)=144(cm 2).故这个堆积几何体的表面积(含底面)是144cm 2.本题考查了简单组合体的三视图及求小立方块堆砌图形的表面积.在画图时一定要将物体的边缘、棱、顶点都体现出来,看得见的轮廓线画成实线,看不见的轮廓画成虚线,不要漏掉. 27.2236a cm 【解析】先画出这个图形的三视图,从而可得上下面、前后面、左右面的小正方形的个数,再根据正方形的面积公式即可得.由题意,画出这个图形的三视图如下:则这个图形的表面积是()()22226262636a acm ⨯+⨯+⨯=,故答案为:2236a cm .本题考查了求几何体的表面积,正确画出图形的三视图是解题关键. 28.5 【解析】利用三视图得到排数及列数,即可得到答案. 由三视图可知,此摆放体有两排, 第一排有一列,第二排有两列,第一排一列有一个,第二排两列分别有两个,∴1+2+2=5个,故答案为:5.此题考查三视图的应用,会看三视图的组成特点及分析得到排数列数是解题的关键.29.17 11【解析】易得这个几何体共有3层,由俯视图可得第一层正方体的个数,由主视图可得第二层和第三层最少或最多的正方体的个数,相加即可.++=(个)由主视图和俯视图可知:几何体的第一层最多有1337++=(个)第二层最多有1337++=(个)第三层最多有1113++=(个)故正方体的个数最多有77317++=(个),几何体的第一层最少有1337++=(个)第二层最少有1113第三层最少有1个,++=(个)故正方体的个数最少有73111故答案为:17;11.本题考查了学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.30.396【解析】首先确定该几何体的裸露的正方形的个数,然后确定面积即可.解:由该位置小立方体的个数可知,主视图为:有9个正方形左视图为:有6个正方形,俯视图为:有5个正方形,另外,该几何体有4个正方形的表面被遮挡,++⨯⨯+⨯=,∴这个几何体的表面积是(965)2949396故答案为:396.本题主要考查了学生对三视图掌握程度和灵活运用能力,同时也考查了空间想象能力.解题的关键是由几何体的俯视图及小正方形内的数字,可知主视图的列数与俯视图的列数相同,且每列小正方形数目为俯视图中该列小正方形数字中的最大数字.左视图的列数与俯视图的行数相同,且每列小正方形数目为俯视图中相应行中正方形数字中的最大数字.。
三视图练习题大全

三视图练习题大全1、若某空间几何体的三视图如图所示,则该几何体的体积是2112、一个几何体的三视图如图,该几何体的表面积是72609803一个长方体去掉一个小长方体,所得几何体的正视图与侧视图则该几何体的俯视图为:4、若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积等于...A.C..65、图2中的三个直角三角形是一个体积为20cm的几何体的三视图,则h= cm、一个几何体的三视图如图所示,则这个几何体的体积为。
、如图,网格纸的小正方形的边长是1,则这个几何体的体积为。
129、一空间几何体的三视图如图所示,则该几何体的体积为.A.2??B.??C.?? 俯视图正视图侧视图D.??3正视图侧视图俯视图10、上图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是A.9πB.10π C.11π D.12π11、已知某个几何体的三视图如下,根据图中标出的尺寸,可得这个几何体的体积是A.4000380003cm B.cm C.2000cm3D.4000cm333B.2π C.3π D.4π12、一个几何体的三视图如上图所示,其中正视图与侧视图都是边长为2的正三角形,则这个几何体的侧面积为A.13、如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积为A.32π B.16π C.12πD.8π14、下图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是A.9πB.10πC.11π D.12π15、右图是一个多面体的三视图,则其全面积为正视图侧视俯视图2ABCD616、如图所示,一个空间几何体的正视图和侧视图都是底为1,高为2的矩形,俯视图是一个圆,那么这个几何体的表面积为A.2? B.5?C.4?D.5?217、一个几何体的三视图及其尺寸如图所示,则该几何体的侧面积为_ ______cm2.18、如果一个几何体的三视图如图所示, 则此几何体的表面积是A. AB?6C6D424. 如图所示,一个空间几何体的正视图和侧视图都是底为1,高为2的矩形,俯视图是一个圆,那么这个几何体的表面积为5?C.4? D.5?A.2? B.25.如果一个几何体的三视图如图所示, 则此几何体的表面积是A. 如图所示,则该几何体的侧面积为_______cm2.22左视侧视图俯视俯视图4三视图练习题1.如图是某几何体的三视图,则此几何体的体积是 A.3B.10C.7D.1802.一个几何体的三视图形状都相同、大小均相等,那么这个几何体不可以是A、球B、三棱锥C、正方体D、圆柱3.如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是A、9πB、10πC、11πD、12π4.有一个几何体的三视图及其尺寸如图,则该几何体的表面积及体积为A.24?cm2,12?cm3B. 15?cm2,12?cm32C.4?cm,36?cm3D.以上都不正确5.如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为______.A. B. CD.6.一空间几何体的三视图如图所示,则该几何体的体积为. A. 1B. CD.7.若某空间几何体的三视图如图所示,则该几何体的体积是 A.??B. C.1D.??8.某几何体的正视图如图所示,则该几何体的俯视图不可能的是9.已知某个几何体的三视图如图,根据图中标出的尺寸,可得这个几何体的体积是cm3.A.8?? C.12??2?32?D.12?3B.8?10.已知正六棱柱的底面边长和侧棱长均为2cm,其三视图中的俯视图如图所示,则其左视图的面积是122238cm cm22侧视图主视图11.右图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是A.6πB.7π C.8πD.9π俯视图12.如图是一个几何体的三视图,若它的体积是a=A.1 B.13.已知某几何体的三视图如图所示,其中正视图、侧视图都是等腰直角三角形,则这个几何体的体积是 A.cm B.14.如图,水平放置的三棱柱ABC-A1B1C1中,侧棱AA1⊥平面A1B1C1,其正视图是边长为a的正方形.俯视图是边长为a的正三角形,则该三棱柱的侧视图的面积为A.a2B.正视图2,则该几何体的表面积是俯视图A.20+3π B.24+3πC.20+4π D.24+4π16.如图为一个几何体的三视图,其中俯视图为正三角形,A1B1=2,AA1=4,则该几何体的表面积为A11A.+B.4+C.4+2D.2AC正视图侧视图俯视图17.图1是设某几何体的三视图,则该几何体的体积为 A.9??42B.36??1C.??1 D.??18929218.已知某几何体的三视图如图所示,根据图中标注的尺寸可得该几何体的体积是正视图123cm3348C.cm3D.cm333A.cmB.俯视图图119.已知几何体其三视图,若图中圆半径为1,等腰三角形腰为3,则该几何体表面积为A.6π B.5π C.4π D.3π20.若一个正三棱柱的三视图如下图所示,则这个正三棱柱的高和底面边长分别为A.2, B.2, C.4,2D.2,4正视图左视图俯视图1.1.5三视图课程学习目标[课程目标]目标重点:正投影与三视图的画法与应用, 目标难点:三视图的画法以及应用学法关键1.画三视图时,可以把垂直投影面的视线想象成平行光线从不同的方向射向几何体,体会可见的轮廓线的投影就是所要画出的视图,画出的三视图要检验是否符合.长对正、高平齐、宽相等.的基本特征.2.由三视图想象几何体时也要根据.长对正、高平齐、宽相等.的基本特征,想象视图中每部分对应的实物的形象,特别注意几何体中与投影面垂直或平行的线及面的位置研习教材重难点研习点1 正投影1.定义:在物体的平行投影中,如果投射线与投射面垂直,则称这样的平行投影为正投影.. 正投影的性质:①直线或线段的平行投影仍是直线或线段;②平行直线的平行投影是平行或重合的直线;③平行于投影面的线段,它的投影与这条线段平行且等长;④与投影面平行的平面图形,它的投影与这个图形全等;⑤在同一直线或平行直线上,两条线段平行投影的比等于这两条线段的比;⑥垂直于投影面的直线或线段的正投影是点;⑦垂直于投影面的平面图形的正投影是直线或直线的一部分.研习点三视图1. 水平投射面:一个投射面水平放置,叫做水平投射面.. 俯视图:投射到水平投射面内的图形叫做俯视图.3. 直立投射面:一个投射面放置在正前方,这个投射面叫做直立投射面.. 主视图:投射到直立投射面内的图形叫做主视图.5. 侧立投射面:和直立、水平两个投射面都垂直的投射面叫做侧立投射面.. 左视图:投射到侧立投射面内的图形叫做左视图.7. 三视图:将空间图形向水平投射面、直立投射面、侧立投射面作正投影,然后把这三个投影按一定的布局放在一个平面内,这样构成的图形叫做空间图形的三视图.研习点3.三视图的画法要求:三视图的主视图、俯视图、左视图分别是人从物体的正前方、正上方、正左方看到的物体轮廓线的正投影组成的平面图形;一个物体的三视图的排列规则是:俯视图放在主视图的下面,长度与主视图一样,左视图放在主视图的右面,高度与主视图一样,宽度与俯视图的宽度一样;记忆口诀:长对正,高平齐,宽相等;主左一样高,主俯一样长,俯、左一样宽。
三视图练习题有答案

三视图练习
1.(三视图→直观图)下面是一些立体图形的三视图(如图),•请在括号内填上立体图形
的名称.
2.(平面展开图与直观图)下列图形都是几何体的平面展开图,你能说出这些几何体的名称?
3.(直观图→三视图)如图,从不同方向看下面左图中的物体,右图中三个平面图形分别是从哪个方向看到的?
4.一天,小明的爸爸送给小明一个礼物,小明打开包装后画出它的主视图和俯视图如图所示.根据小明画的视图,你猜小明的爸爸送给小明的礼物是()
A.钢笔 B.生日蛋糕 C.光盘 D.一套衣服
5.一个几何体的主视图和左视图如图所示,它是什么几何体?请你补画出这个几何体的俯视图.
6.一个物体的三视图如图所示,试举例说明物体的形状.
7.已知一个几何体的三视图如图所示,则该几何体的直观图?
8.已知几何体的主视图和俯视图如图所示.
(1)画出该几何体的左视图;
(2)该几何体是几面体?它有多少条棱?多少个顶点?
(3)该几何体的表面有哪些你熟悉的平面图形?
9.小刚的桌上放着两个物品,它的三视图如图所示,你知道这两个物品是什么吗?
参考答案:
1.圆柱,正三棱锥 2.圆锥圆柱正方体三棱柱
3.上正侧 4.B 5.略
6.如粉笔,灯罩等 7.120
8.(1)略(2)六面体,12条,8个(3)等腰梯形,•正方形。
