第五章气体内的运输过程知识讲解
热学 (4 第四章 气体内的输运过程)

Q
dT
A
傅立叶定律
dz 若设热流密度为JT,则:
JT
dT dz
20
T2 ( T1 )
B
温度梯度 dT
dz
z0
dS dQ
T T(z)
表示流体中温度沿z
轴方向的空间变化率。
o
T1
Ax
在dt时间内,从温度较高的一侧,通过这一平
面向温度较低的一侧所传递的热量,与这一平面所
在处的温度梯度和面积元成正比
热导率
能量流动方 向与温度梯 度方向相反
恒为正值
dQ κ dT dSdt dz z0
21
三、扩散现象的宏观规律 扩散 (diffusion)
在混合气体内部,当某种气体在各处的密度不均匀时, 这种气体将从密度大的地方向密度小的地方散布,这 种现象叫扩散。
输运过程
扩散:密度 不均匀 m的迁移
热传导:温度T不均均 热的迁移
内摩擦(黏性): 分子定向速度u 不均匀 定向运动动量 p的迁移 22
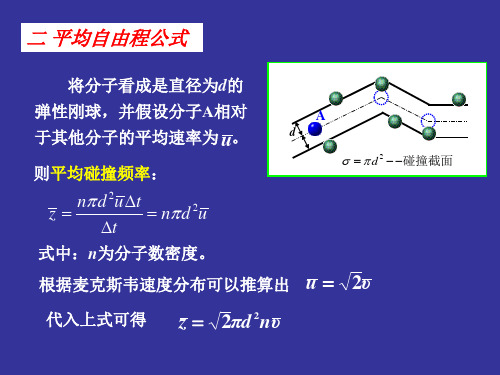
§ 5-1 气体分子的平均自由程
一、分子的平均自由程和碰撞频率
非平衡态平衡态,碰撞起重要作用。
克劳修斯指出:气体分子的速度虽然很大,但前进中要与其 他分子作频繁的碰撞,每碰一次,分子运动方向就发生改变, 所走的路程非常曲折。
若不均
一种气体
n不均
p不均
生宏 气流
22
我们这里研究的是:纯扩散--仅仅是由于分 子的无规则运动和碰撞引起的扩散过程。
实现纯扩散的条件
气体的输运现象知识分享

流速梯度及面积可测定,故黏度
可测。
测定 实验
上页 下页 返回 退出
上页 下页 返回 退出
二、热传导现象
如果气体内各部分的温度不同,从温度较高
处向温度较低处,将有热量的传递,这一现象就 叫热传导现象。
S T1 T2
T1
T2
x
x
设沿 x 方向温度梯度最大,实验指出,单位时 间内,通过垂直于x 轴的某指定面传递的热量与该 处的温度梯度成正比,与该面的面积成正比,即
选择进入下一节 §5-0 教学基本要求 §5-1 热运动的描述 理想气体模型和物态方程 §5-2 分子热运动和统计规律 §5-3 理想气体的压强和温度公式 §5-4 能量均分定理 理想气体的内能 §5-5 麦克斯韦速率分布律 *§5-6 麦克斯韦-玻耳兹曼能量分布律 重力场中粒
子按高度的分布 §5-7 分子碰撞和平均自由程 *§5-8 气体的输运现象 *§5-9 真实气体 范德瓦尔斯方程
介绍三种输运现象的基本规律:
黏滞现象 热传导现象 扩散现象
上页 下页 返回 退出
一、 黏滞现象
流动中的气体 ,如果各气层的流速不相等,那么 相邻的两个气层之间的接触面上,形成一对阻碍两气 层相对运动的等值而反向的摩擦力,这种摩擦力叫黏 性力。气体的这种性质,叫黏性。
例 A盘自由,B盘由电机带动而转
则不同流层之间有黏性力。
dy
实验证明:不同流层之间(CD面处)黏滞力与
流速梯度成正比,与CD面积成正比,
F du S
dy
比例系数称为动力黏度(或黏度),±表示黏性
力成对出现,满足牛顿第三定律。
上页 下页 返回 退出
C
M
测定 实验
B
A,B 为两筒,C 为悬丝,
气体运输的概念(二)

气体运输的概念(二)气体运输的概念概念定义•气体运输是指将气体从一个地点运送到另一个地点的过程。
•气体可以以压缩、液化或气化的形式进行运输。
•气体运输通常需要特殊的容器和设备,如气瓶、储罐和管道。
气体运输的分类1.液化气体运输–液化气体是将气体通过降温或增压使其变为液体状态,以便更方便地进行运输和储存。
–常见的液化气体包括液化石油气(LPG)、液化天然气(LNG)等。
–液化气体通常以罐车、集装箱或船舶的形式进行运输。
2.压缩气体运输–压缩气体是通过增压将气体储存为高压气体,以便更方便地进行运输和储存。
–常见的压缩气体包括工业气体、医用气体等。
–压缩气体通常以气瓶、储气罐或管道的形式进行运输。
3.气化气体运输–气化气体是将液体气体或固体气体通过升温或减压使其恢复为气体状态,以便进行运输和使用。
–常见的气化气体包括液化煤气、液化氧气等。
–气化气体通常以罐车、集装箱或管道的形式进行运输。
气体运输的特点•高能量密度:相比液体和固体,气体具有更高的能量密度,能够在相对较小的体积和重量内储存更多的能量。
•易于压缩和扩展:气体可以被相对容易地压缩为较小的体积,也可以被相对容易地扩展为较大的体积,使其更方便地进行运输。
•可燃性和易爆性:一些气体具有较高的可燃性和易爆性,需要特殊的安全措施来确保运输过程的安全性。
•温度和压力对气体性质的影响较大:气体的性质会随着温度和压力的变化而发生显著的变化,需要在运输过程中进行恰当的控制。
气体运输的应用领域•工业和化工领域:气体用于供应生产过程中的能源、燃料和原料,如燃气、氧气、氢气等。
•医疗领域:气体用于供应医院中的各种医用气体,如氧气、笑气、氩气等。
•家庭和商业领域:液化石油气(LPG)用于供应家庭和商业的燃料,如燃气灶、燃气水热器等。
•航空航天领域:液化天然气(LNG)用作舰船和飞机燃料,具有高能量密度和低污染排放的特点。
通过气体运输,人们能够方便地获取和利用气体资源,满足各种领域的需求,促进经济发展和生活改善。
气体内的输运过程

热传导:温度 T 不均匀 热的迁移; 内摩擦(粘滞):定向速度u不均 输运过程 定向动量的迁移; 扩散:密度 不均匀 m的迁移。
热学
13
一、粘滞现象的宏观规律
1、层流 在流动过程中,相邻质点的轨迹线彼此仅稍有差别, 不同流体质点的轨迹线不相互混杂,这样的流动称 为层流。
由于分子的热运动,从而引起质量从密度大的区域 向密度小的区域迁移的现象。 d 1 2 ( z ) 密度梯度 2 dz
z z0
dM dS
表示气体的密度沿x 轴方向 的空间变化率。
在dt时间内,通过dS传递的质量
o
1
x
d dM D dSdt dz z0
热学
23
§3. 输运过程的微观解释
首先是气体分子的热运动 另一个重要原因就是分子间的碰撞。 一、粘滞现象的微观解释 气体黏性系数的导出
1 1 nmv或 v 3 3
讨论: 注意:*近平衡非平衡过程;
*气体既足够稀薄又不 太稀薄
1)、η 与n无关。 2)、 η仅仅是温度的函数。
热学
21
D 扩散系数
d dM D dSdt dz z0
' ' 表示扩散总沿减小的方向
1自扩散与互扩散 当物质中粒子数密度不均匀时,由于分子的热运动 使粒子从密度高的地方迁移到数密度低的地方的现象 称为扩散。 互扩散:发生在混合气体中,由于各成分的气体空间 分布不均匀,各成分分子均要从高密度区向低密度区 迁移的现象。 自扩散:是互扩散的一种特例
空气的平均分子量为29。
解: 已知 T 273K , p 1.0atm 1.013 105 Pa,
气体内的输运过程
1 du f ( ) z0 dA,其中 nmv 3 dz 称为牛顿黏性定律. η的单位为泊,以P表示
1P 1N s m 0.1kg m s
2
1
1
考虑到相邻两层流体中相对速度较大的流体总是受到阻力, 即速度较大一层流体受到的黏性力的方向总与速度梯度方向相反,故在式中加上负号
1 υ 平均自由程: λ 2 z 2d n 2d 2 n
式中:d为分子的有效直径,n为分子数密度。
由 p nkT n
p kT
kT λ 2 2πd p
思考 在一封闭容器中装有1mol氦气(视作理想气体),这 时分子无规则运动的平均自由程将决定于什么? (A)压强p (B)体积V (C)温度T (D)平均碰撞频率 z
实验发现,流体在流速较小时将作分层平行流动, 流体质点
轨迹是有规则的光滑曲线, 不同质点轨迹线不相互混杂。 这样的流体流动称为层流。 直圆管中流体流速分布如图 流速箭头的包络面为抛物面, 其平均流速箭头的包络面为 平面
稳恒层流中的黏性 牛顿黏性定律
•流 体 作 层 流 时 , 通过任一平行于流 速的截面两侧的相 邻两层流体上作用 有一对阻止它们相 对“滑动”的切向 作用力与反作用力。
二.热传导现象的宏观规律
当系统与外界之间或系统内部各部分之间存在温度 差时就有热量的传输. 热传递有热传导、对流与辐射 三种方式,本节将讨论热传导
1. 傅里叶定律(Fourier law of heat conduction ) •1822法国科学家傅里叶(Fourier)在热质说思想的指导下 发现了傅里叶定律。 该定律认为热流dQ/dt (单位时间内 通过的热量)与温度梯度 dT /dz 及横截面积dA成正比,
气体的输运现象知识分享

我们在前面所讨论的都是气体在平衡状态下的 性质.实际上,系统各部分的物理性质,如流速、温 度或密度不均匀时,系统处于非平衡态。
处于非平衡态系统, 由于气体分子不断地相互 碰撞和相互掺和,分子之间将经常交换质量、动量 和能量,分子速度的大小和方向也不断地改变,最 后气体内各部分的物理性质将趋向均匀,气体状态 趋于平衡. 这种现象叫气体的输运现象。
则不同流层之间有黏性力。
dy
实验证明:不同流层之间(CD面处)黏滞力与
流速梯度成正比,与CD面积成正比,
F du S
dy
比例系数称为动力黏度(或黏度),±表示黏性
力成对出现,满足牛顿第三定律。
上页 下页 返回 退出
C
M
测定 实验
B
A,B 为两筒,C 为悬丝,
M为镜面;A保持恒定转速,B会
跟着转一定角度,大小可通过M A 来测定,从而知道黏性力大小,
流速梯度及面积可测定,故黏度
可测。
测定 实验
上页 下页 返回 退出
上页 下页 返回 退出
二、热传导现象
如果气体内各部分的温度不同,从温度较高
处向温度较低处,将有热量的传递,这一现象就 叫热传导现象。
S T1 T2
T1
T2
x
x
设沿 x 方向温度梯度最大量与该 处的温度梯度成正比,与该面的面积成正比,即
介绍三种输运现象的基本规律:
黏滞现象 热传导现象 扩散现象
上页 下页 返回 退出
一、 黏滞现象
流动中的气体 ,如果各气层的流速不相等,那么 相邻的两个气层之间的接触面上,形成一对阻碍两气 层相对运动的等值而反向的摩擦力,这种摩擦力叫黏 性力。气体的这种性质,叫黏性。
气体的交换和运输.

呼吸生理二、气体的交换气体的交拜分为肺换气和组织换气两部分,肺换气指在呼吸器官血液与外环境间的气体交换,组织换气指在组织器官, 血液与组织细胞间的气体交换。
它们均是通过物理扩散的方式实现的。
气体扩散以物理扩散的方式进行,各种气体的扩散主要取决于各种气体分压差,气体分压差是气体交换的动力。
和交换膜的通透性及交换面积有关。
三、气体在血液中的运输在呼吸的过程中,血液担任气体运输的任务,不断把氧从肺运输到组织,又不断把二氧化碳从组织细胞运输到肺部。
(一)氧的运输氧的运输有以下两种方式,少数氧直接溶解于血液中,随血液运输到组织利用,此种方式仅占运输氧的0.8~1.5%左右。
大部分与血红蛋白结合后运输到组织被利用。
在高氧分压情况下氧进入红细胞与血红蛋白中血红素的亚铁离子结合成氧合血红蛋白,叫氧合作用。
这种结合受氧分压的影响,是可逆的。
(三) CO2的运输二氧化碳在血液中的运输有以下三种方式1、有2.7%的二氧化碳直接溶解于血液中,随血液运输2、20%的二氧化碳与血红蛋白结合成氨基甲酸血红蛋白,这种结合也是可逆的,受二氧化碳分压的影响。
在组织毛细血管处,二氧化碳与血红蛋白结合,在肺毛细血管处,二氧化碳与血红蛋白分离。
3、70%的二氧化碳以碳酸氢盐的形式运输,经组织换气,二氧化碳扩散入血液,先部分溶解于血浆,与水结合成碳酸,血浆中缺乏碳酸酐酶,反应速度慢,二氧化碳增多时,由于分压高,进入红细胞,红细胞内含有碳酸酐酶,可使二氧化碳生成碳酸的速度加快,在红细胞内的碳酸又迅速解离出碳酸氢根离子,与钾和钠离子结合。
当碳酸氢盐到肺部时,由于二氧化碳分压低,碳酸氢根离子和水结合生成碳酸,碳酸再释放出二氧化碳。
气体内的输送过程

第五章 气体内的输送过程教学目的和要求:1、掌握钢球模型下的平均自由程和碰撞频率的概念,深刻理解其物理意义。
2、深刻理解和掌握三种输送过程的微观机制和结果,掌握相应的宏观规律。
3、理解描述三种输送过程的系数的统计含义和统计方法重点和难点:λ 、z 是重点,输送过程的微观机制和统计方法是重点和难点,物理性质不均匀的描述是难点,三个输送系数和宏观规律是重点。
平衡态是一种理想状态,实际有价值的问题,是系统在外界的作用下,出现了不平衡,从而成为从一个平衡态转变成一个平衡态的过程,即输送过程,输送过程的问题是非平衡态的问题,这类问题无非有两种情况,其一,过程进行得非常剧烈和迅速,第二种情况,即过程行进得相对缓慢和微弱,这时每时每刻仍不是平衡态,但可认为大系统内的各局部区域近似为平衡态,从而可以把平衡态中的一些理论加以推广应用,所以称近平衡态问题或近平衡态过程,有时又叫非线性平衡过程,那么解决这类问题就不难了,物理意义明确,定律形式简单,但由于用到了平衡态的一些知识来解决不是平衡态的问题,所以其结果也不是很准确的。
我们用统计的方法来讨论这个问题,现在先来作个准备工作5-1 气体分子的平均自由程1平均自由程定义:两次相邻碰撞之间分子所走过路程的统计平均值称为平均自由程。
自由程λ的统计平均λ称为平均自由程。
自由程的长短是有偶然性的,我们对一个分子的自由程进行长时间的统计,或者同时对大量分子的自由程进行统计,则表现出稳定的统计平均值,这就是统计平均值。
Zv =λ2、碰撞频率和平均自由程有简单的关系:Zv=λ,λ和z 都反映了碰撞的频繁程度。
分子碰撞的越频繁,则意味着Z 越大。
而碰撞机会越多,分子运动的方向改变也越频繁,从而平均自由程λ越小。
可见λ的大小的确也能反映碰撞的频繁程度。
下面我们先来计算z :跟踪一个分子,看它与那些分子相碰,并且在一分秒钟内能碰多少次。
不妨考虑一个分子运动,其他分子相对静止,运动的分子与这些相对静止的分子碰撞。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
气体 氢
氮
氧
空气
( m ) 1.13107 0.599107 0.647107 7.0108
d ( m ) 2.301010 3.101010 2.901010 3.701010
例 计算空气分子在标准状态下的平均自由程和平 均碰撞频率。取分子的有效直径d=3.510-10m。已知 空气的平均分子量为29。
流体的不规则运动。
3、稳恒层流中的粘滞现象
内摩擦现象
z
y
u=u(z)
内摩擦 流体内各部分流动速度不同时,就发生内摩擦现象.
相邻流体层之间由于速度不同引起的相互作用力称为内摩 擦力,也叫粘滞力.
流体沿x方向流速是z的函数
z
L
uv 0
B
流速梯度 d u
v
dz
z0
df v dS df
u u(z)
沿z方向所出现的流速
相应圆柱体体积为 u t
发生碰撞的 平均次数
圆柱体内 分子数
n ut
Z nut nu
t
实际上一切分子都在运动
u 2v
平均自பைடு நூலகம்程
单位时间内分子A经过路程为 v
单位时间内A与其它分子发生碰撞的平均次数 Z
平均自由程 v 1 Z 2d2n
与分子的有效直径的平方和分子数密度成反比
p nkT
二、平均碰撞频率和平均自由程
在相同的t时间内,分子由A到B的
位移大小比它的路程小得多
A• •B
扩散速率
(位移量/时间)
平均速率 (路程/时间)
分子碰撞频率: 在单位时间内一个分子与其他分子碰撞的次数。
分子自由程:
气体分子两次相邻碰撞之间自由通过的路程。
大量分子的分子自由程与每秒碰撞次数服从统计分布规律。 可以求出平均自由程和平均碰撞次数。
z0
df v dS df
u u(z) 从下向上垂直越过dS面.
o
u0
A x n 分子数密度
假定1: 等几率
在dt时间内从下向上垂直越过dS 面的平均气体分子数:
1 nvdSdt 6
这些分子是经过最后一次碰撞越过dS面的,
它们离dS面的平均距离为平均自由程 ,所以
假定2: 一次碰撞 同化
在dt时间内,由于分子热运动从下向上带过dS面的定向
气体内的输运过程
输运过程
系统各部分的物理性质,如流速、温度或密度不均匀时, 系统处于非平衡态。
非平衡态问题是至今没有完全解决的问题, 理论只能处理一部分,另一部分问题还在研究中。
最简单的非平衡态问题:不受外界干扰时,系统自发地从非 平衡态向物理性质均匀的平衡态过渡过程 --- 输运过程
介绍三种输运过程的基本规律:
气体的内摩擦现象在微观上是分子在热运动中的输运定 向动量的过程.也就是分子在热运动中通过dS面交换定 向动量的结果.
z
L
uv 0 B
v
z0
df
dS
v df
u u(z)
o
u0
Ax
u 宏观流速 v 分子热运动平均速率 如果 uv
可认为气体处于平衡态
z
L
uv 0
B
根据分子热运动的各向同性,
v
总分子中平均有1/6 的分子
平均碰撞次数
假 每个分子都是有效直径为d 的弹性小球。
定 只有某一个分子A以平均相对速率 u 运动,
其余分子都静止。
d
u
d
u
A
d
d
u
d
u
A
d
球心在圆柱 体内的分子
运动方向上,以 d 为半径的圆柱体内的分子都将
与分子A 碰撞 d2 被称为碰撞截面
t 时间内: 分子A经过路程为 u t
一秒钟内A 与其它分子
粘滞现象
热传导 扩散
§5-1 平均碰撞频率和平均自由程
一、分子间碰撞与无引力的弹性刚球模型
气体分子 平均速率
矛盾
v 1.60 RT M mol
氮气分子在270C时的平均 速率为476m.s-1.
气体分子热运动平均速率高, 但气体扩散过程进行得相当慢。
要考虑分子 的体积了!
气体分子的速度虽然很大,但前进中 要与其他分子作频繁的碰撞,每碰一 次,分子运动方向就发生改变,所走 的路程非常曲折。
空气分子在标准状态下 v
8RT 448m/s
的平均速率
Mmol
zv6.9 4 4 1 8 0 86.5 109s 1
§5-2 粘滞现象的宏观规律及其微观解释
1、层流 2、湍流
在流动过程中,相邻质点的轨迹线彼此仅稍有差别,
不同流体质点的轨迹线不相互混杂,这样的流动称
为层流。
uur
x ur U1
U2
又uz0 uz0 2dduzz0
故dp13nmvdSdtdduzz0
z
L
z0
uv 0
B
v df v dS df
u u(z)
dp13nmvdSdtdduzz0
dp
o
u0
内摩擦力 d f
Ax
dt
df 13nmvdSdduzz0 13vdSdduzz0
又Qdf dduzz0 dS
1 v
3
解: 已知 T273K ,p1.0atm 1.013105P a, d3.51010m
kT 2 d 2 p
1 .4 1 3 .1 4 1 . 3 8 (3 .5 1 0 1 2 0 3 1 0 2 )7 3 1 .0 1 1 0 5 6 .9 1 0 8m
空气摩尔质量为2910-3kg/mol
kT 2d 2 p
当温度恒定时,平均自由程与气体压强成反比
平均自由程与压强、温度的关系
v 1 z 2d2n
p nkT
kT T
2d 2 p
p
T = 273K:
p(atm)
(m)
1
~7×10-8
10-7
~0.7(灯泡内)
10-11 ~7×103(几百公里高空)
在标准状态下,几种气体分子的平均自由程
§5-3 热传导现象的宏观规律及其微观解释
o
u0
Ax
空间变化率。
4、牛顿粘滞定律:
由于流速不均匀, A部分受到B部分的一 个平行与x 轴的力,方 向沿x轴正方向,大小 与接触面积及速度梯 度有关。
f du dS
dz z0
为粘滞系数
z
L
uv 0
B
v
z0
df
dS
v df
u u(z)
o
u0
Ax
它的单位是N.s.m-2
液体内的粘滞力主要起源于分子间的相互作用力,但气体分子 之间的相互作用力很弱。那么气体的粘滞现象是什么引起的?
动量等于分子处于 z 0 的定向动量
z
L
uv 0
B
z 0 处的定向动量
v
z0 o
df dS
v df
u0
u u(z)
Ax
1 dp1 6nvdSdtmuz0
同理,在dt时间内,由于分子热运动从上向下带过dS
面的定向动量
1 dp2 6nvdSdtmuz0
可得dS面上方气体的定向动量增量
1 d p d p 1 d p 26n v d S d tm (u z0 u z0 )
