押题第37道 椭圆中与面积有关的取值范围问题(原卷版)
高中数学破题致胜微方法(椭圆的进阶性质)椭圆中的面积问题 Word版含答案
先看例题:
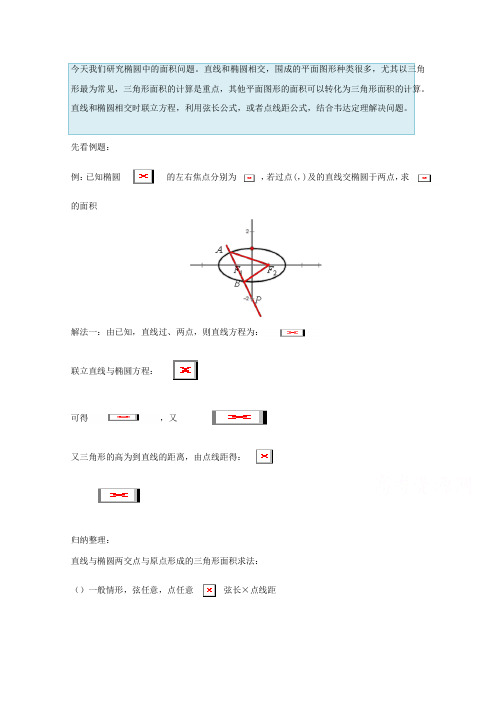
例:已知椭圆的左右焦点分别为,若过点(,)及的直线交椭圆于两点,求的面积
解法一:由已知,直线过、两点,则直线方程为:
联立直线与椭圆方程:
可得,又
又三角形的高为到直线的距离,由点线距得:
归纳整理:
直线与椭圆两交点与原点形成的三角形面积求法:
()一般情形,弦任意,点任意弦长×点线距
()特殊情形,过轴上一定点的直线与椭圆交于、两点,求
()特殊情形,过轴上一定点的直线与椭圆交于、两点,求
再看一个例题,加深印象
例:过椭圆的右焦点作一条斜率为的直线与椭圆交于两点为坐标原点,则△的面积为.
解:由已知椭圆,右焦点坐标为(),故直线(-),与椭圆联立.
设()(),
可得,
利用,求得:.
注意:学会分解三角形面积,有时可以转化问题,回避求弦长等复杂计算。
总结:
.根据直线和椭圆的位置关系,如果弦任意,选择公式弦长×点线距。
.根据直线和椭圆的位置关系,如果直线过轴上一定点,设直线方程,代入椭圆方程计算弦长。
.根据直线和椭圆的位置关系,如果直线过轴上一定点,设直线方程,代入椭圆方程计算弦长。
微专题25 椭圆中与面积有关的定点、定值问题

2-2sinθ-2cosθ+2sinθcosθ =2.所以,四边形 AMNB 的面积为定值. 1-sinθ-cosθ+sinθcosθ
1 说明:将四边形面积转化为2AN· BM,是顺利解题的关键.本例可 以拓展为一般的情形.
x2 2 变式 1 在平面直角坐标系 xOy 中,已知椭圆 C: 4 +y =1,点 A,B 分 别是椭圆的右顶点和上顶点,设 P 是椭圆 C 上一点,直线 PA 与 y 轴交于点 M,直线 PB 与 x 轴交于点 N.求证:AN· BM 为定值.
2 2 1 x0+4y0+4x0y0-4x0-8y0+4 14+4x0y0-4x0-8y0+4 = =2. =2 x0y0-x0-2y0+2 2 x0y0-x0-2y0+2
所以,四边形 AMNB 的面积为定值.
证法 2 设点 P(2cosθ,sinθ),因为 P 在第三象限,所以不妨设 π<θ 3π sinθ sinθ < 2 ,直线 PA:y= (x-2),令 x=0,得 yM= .∴BM= 2cosθ-2 1-cosθ
x2 2 变式 2 如图,已知椭圆 2 +y =1,过椭圆的上顶点 A 作一条与两轴均 不平行的直线 l 交椭圆于另一点 P, 设点 P 关于 x 轴的对称点为 Q, 若直线 AP,AQ 与 x 轴交点的横坐标分别为 m,n,求证:mn 为 常数,并求出此常数.
答案:2.
x2 0 解析:设点 P(x0,y0),则有 2 +y2 0=1. y0-1 x0 所以 AP 方程:y= x x+1,令 y=0,得 m= . 1-y0 0 x0 由题意, 点 Q 与 P 关于 x 轴对称, 所以 Q(x0, -y0), 同理得 n= . 1+y0 x2 0 所以 mn= 2=2.所以 mn=2 为常数. 1-y0
椭圆面积练习题及其完整答案

椭圆面积练习题及其完整答案
本文档包含一系列椭圆面积的练题及其完整答案。
通过这些练题,你可以巩固和提升自己计算椭圆面积的能力。
练题一:求椭圆的面积
已知椭圆的长轴长度为$a$,短轴长度为$b$。
请计算该椭圆的面积$S$。
答案:椭圆的面积可以通过公式$S = \pi \cdot a \cdot b$计算得出。
练题二:已知椭圆的周长,求其面积
已知椭圆的周长为$C$,长轴长度为$a$。
请计算该椭圆的面积$S$。
答案:首先,根据椭圆周长的公式$C = \pi \cdot (a + b)$,可以
求得短轴长度$b = \frac{C}{\pi} - a$。
然后,椭圆的面积可以通过
公式$S = \pi \cdot a \cdot b$计算得出。
练题三:已知椭圆的焦点坐标,求其面积
已知椭圆的焦点坐标为$F_1(x_1, y_1)$和$F_2(x_2, y_2)$,长
轴长度为$a$。
请计算该椭圆的面积$S$。
答案:首先,可以通过焦点坐标和长轴长度计算椭圆的离心率$e$,公式为$e = \frac{F_1F_2}{2a}$,其中$F_1F_2$代表两个焦点
之间的距离。
然后,可以根据离心率和长轴长度计算短轴长度$b$,公式为$b = a \cdot \sqrt{1 - e^2}$。
最后,可以使用公式$S = \pi
\cdot a \cdot b$计算椭圆的面积$S$。
以上就是椭圆面积练习题及其完整答案的内容,希望对你的学
习有所帮助。
如有任何疑问,请随时向我提问。
椭圆中有关的取值范围问题大全(附详解)新高考

椭圆中有关的取值范围问题【目标导航】求解最值,可直接求导. 但是解析几何中的最值,直接求导,暴力求解最值的较少,更多的是化简函数表达式,根据结构采用基本不等式(无法取等的时候就求导来解决)来求解最终的最值(或者值域),必然要有定义域,所以寻找函数的定义域是非常重要的,而解析几何中直线和曲线联立(曲直联立)以后的关于x(或者y)的一元二次方程有解,判别式就是很重要的一个点,也就是定义域的一个重要来源,有些题目甚至是唯一来源.与线段有关的最值问题关键是建立关于线段的目标函数,然后运用基本不等式或者函数有关的问题,运用基本不等式或者函数求解。
线段的长度可以通过两点间的距离或者利用相交弦长公式进行求解。
与向量有关的最值问题关键就是表示出点坐标,通过数量积转化为函数问题,然后运用基本不等式或者求导研究最值。
与面积有关的最值问题通常建立起面积的目标函数,可以通过公式B acC ab sh s sin 21sin 2121===求解。
然后通过基本不等式或者求导研究函数的最值问题。
【例题导读】例1、在平面直角坐标系 xOy 中,已知椭圆 C :x 2a 2+y 2b 2=1(a>b>0)的离心率为32,且过点⎝⎛⎭⎫3,12,点P 在第四象限, A 为左顶点, B 为上顶点, PA 交y 轴于点C ,PB 交x 轴于点D.(1) 求椭圆 C 的标准方程;(2) 求 △PCD 面积的最大值.例2、如图,在平面直角坐标系xOy 中,已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的离心率为22,且右焦点F 到左准线的距离为6 2.(1) 求椭圆C 的标准方程;(2) 设A 为椭圆C 的左顶点,P 为椭圆C 上位于x 轴上方的点,直线P A 交y 轴于点M ,过点F 作MF 的垂线,交y 轴于点N .①当直线P A 的斜率为12时,求△FMN 的外接圆的方程; ②设直线AN 交椭圆C 于另一点Q ,求△APQ 的面积的最大值.例3、如图所示,椭圆M :x 2a 2+y 2b 2=1(a>b>0)的离心率为22,右准线方程为x =4,过点P(0,4)作关于y 轴对称的两条直线l 1,l 2,且l 1与椭圆交于不同两点A ,B ,l 2与椭圆交于不同两点D ,C.(1) 求椭圆M 的方程;(2) 证明:直线AC 与直线BD 交于点Q(0,1);(3) 求线段AC 长的取值范围.例4、在平面直角坐标系 xOy 中,已知椭圆 C :x 2a 2+y 2b 2=1(a>b>0)的离心率为32,且过点⎝⎛⎭⎫3,12,点P 在第四象限, A 为左顶点, B 为上顶点, PA 交y 轴于点C ,PB 交x 轴于点D.(1) 求椭圆 C 的标准方程;(2) 求 △PCD 面积的最大值.。
微专题24 椭圆中与面积有关的取值范围问题

3.已知椭圆 E:x42+y32=1 的焦点在 x 轴上,A 是 E 的左顶点,斜率为
k(k>0)的直线交 E 于 A,M 两点,点 N 在 E 上,AM⊥AN,且 AM 144
=AN,则△AMN 的面积为 49 .
解析:椭圆 E 的方程为x42+y32=1,A 点坐标为(-2,0),则直线 AM 的方 程为 y=k(x+2).联立x42+y32=1, 并整理得(3+4k2)x2+16k2x y=kx+2, +16k2-12=0,解得 x=-2 或 x=-38+k2-4k62,则
过点 P,则有 xx12xx00+ +yy12yy00= =22,.
所以 MN 坐标满足方程 xx0+yy0=2,所以 MN 直线方程为 x0x+y0y =2.
所以 Ax20,0,B0,y20,所以 S△OAB=12·x20·y20=|x02y0|. 又因为1x620 +y420=1≥2 x620y420=|x04y0|,所以|x0y0|≤4,即 S△OAB≥12.
由2x52 +y92=1,
消去 y,得 28x2+200x+325=0,即(14x+65)(2x
y= 3x+4,
+5)=0,
方程组的解为x=-6154, y=-9143,
或x=-25, y=3 2 3.
因为
y>0,所以
yP=3
2
3 .
所以△PF1F2 的面积为 S△PF1F2=12·F1F2·|yP|=12×8×323=6 3.
y=x2+y22=1 ⇒4x2-2 2mx+m2-2=0,由△=0 得 m2=4,又 y=- 2+m
P 在第一象限,∴m=2.
lp:y=-
2x+2.两平行直线的距离为
2.d=2
3- 3
椭圆中的范围问题 专题练习

椭圆中的范围问题 专题练习一、单选题1.若方程2214x y m m+=-表示焦点在y 轴上的椭圆,则实数m 的取值范围是( ).A .2m <B .02m <<C .24m <<D .2m >【答案】B详解:若方程2214x y m m +=-表示焦点在y 轴上的椭圆,则0404m m m m>⎧⎪->⎨⎪->⎩,解得02m <<.故选B .2.设e 是椭圆2214x yk +=的离心率,且1,12e ⎛⎫∈ ⎪⎝⎭,则实数k 的取值范围是( )A .()0,3B .1633,⎛⎫⎪⎝⎭C .()160,3,3⎛⎫+∞ ⎪⎝⎭ D .16,3⎛⎫+∞ ⎪⎝⎭【答案】C【详解】由椭圆方程2214x y k+=,当04k <<时,24a =,2b k =,24c k =-,所以22244c ke a -==,由1,12e ⎛⎫∈ ⎪⎝⎭,解得03k <<,当4k >时,2a k =,24b =,24c k =-,所以2224c k e a k -==,由1,12e ⎛⎫∈ ⎪⎝⎭,解得163k >,故实数k 的取值范围为()160,3,3⎛⎫+∞ ⎪⎝⎭.故选:C.3.若点O 和点F 分别为椭圆2212x y +=的中心和右焦点,P 为椭圆上任意一点,则OP FP ⋅的最小值为( ) A .14B .13C .12D .23【答案】C【详解】设点P 的坐标为(),x y ,则2212x y=-,且有x ≤≤,()1,0F ,()1,FP x y =-,()22222212111211122O x P FP x x y x x x x x ⋅=-+=-+=--+=+-,2x -≤≤1x =时,OP FP ⋅取得最小值12. 故选:C.4.已知F 为椭圆22:162x y C +=的右焦点,过F 的直线l 交椭圆C 于A ,B 两点,M 为AB 的中点,则M到x 轴的最大距离为( ) A .13B .12CD.2【答案】C【详解】因为226,2a b ==,所以椭圆的右焦点坐标为()2,0.设()()1122,,,A x y B x y ,直线l :x =2ty +,(显然当直线斜率为0时,不可能最大),与椭圆方程联立得,()223420ty ty ++-=,所以12243ty y t +=-+, 即弦AB 的中点M 纵坐标为122223y y tt +=-+,所以M 到x 轴的距离为223t t +. 当0t ≠时,22233t t t t=≤=++,故M 到x故选:C .5.设,A B 是椭圆22:14x y C k+=的两个焦点,若C 上存在点P 满足120APB ∠=︒,则k 的取值范围是( ) A .(0,1][16,)⋃+∞ B .10,[8,)2⎛⎤⋃+∞ ⎥⎝⎦C .10,[16,)2⎛⎤⋃+∞ ⎥⎝⎦D .(0,1][8,)⋃+∞【答案】A【详解】①04k <<时,C 上存在点P 满足120APB ∠=︒, 设M 为椭圆短轴端点,当P 位于短轴的端点时,APB ∠取最大值,要使椭圆C 上存在点P 满足120APB ∠=︒则120AMB ∠≥︒,60AMO ∠≥︒,∴1cos cos6022AMO ∠=≤︒=,解得01k <≤; ②当椭圆的焦点在y 轴上时,4k >,同理可得16k ≥;∴k 的取值范围是(0,1][16,)⋃+∞. 故选:A.6.设12F F 、分别是椭圆2212516x y +=的左、右焦点,P 为椭圆上任一点,M 的坐标为(6,4),则1||PM PF +的最大值为( ) A .13 B .14C .15D .16【答案】C【详解】如图所示,由椭圆2212516x y +=可得:5a =,4b =,3c ==,()13,0F ∴-,()23,0F ,由椭圆的定义可得:12210PF PF a +==,()1222210101015PM PF PM a PF PM PF MF ∴+=+-=+-≤+=+=,则1PM PF +的最大值为15, 故选:C7.已知椭圆()222210x y a b a b +=>>的离心率为e ,焦点分别为 12,F F ,P 为椭圆上不同于长轴两端点的动点,x 轴上的点M 满足 1212PF PF PM PF PF λ⎛⎫⎪=+ ⎪⎝⎭.若点M 的横坐标的取值范围是(),e e -,则椭圆的焦距为( ) A .2 B .C 1D .无法确定【答案】A【详解】由题意,P 为椭圆上的动点,x 轴上的点M 满足1212PF PF PM PF PF λ⎛⎫⎪=+ ⎪⎝⎭可得PM 为12F PF ∠的平分线,所以1122MF PF MF PF =,即222M M a PF x c c x PF -+=-,解得()2,M c a PF x a-=又由()2,PF a c a c ∈-+,即22,M c c x a a ⎛⎫∈- ⎪⎝⎭,又因为ce a=,即(),M x ec ec ∈-,因为点M 的横坐标的取值范围是(),e e -,所以1c =,从而椭圆焦距为2. 故选:A .8.已知12,F F 为椭圆()2222:10x y C a b a b+=>>的左右焦点,若椭圆C 上存在点P ,使得线段1PF 的中垂线恰好经过焦点2F ,则椭圆C 离心率的取值范围是( )A .1,13⎡⎫⎪⎢⎣⎭B.1,32⎡⎢⎣⎦C .2,13⎡⎫⎪⎢⎣⎭D .10,3⎛⎤ ⎥⎝⎦【答案】A【详解】解:如图,因为线段1PF 的中垂线经过2F ,2122PF F F c ∴==即在椭圆上存在一点P ,使得22PF c =2min 2PF c ≤,12,3,3c a c c a c a -≤≤≥ 又1ca<, 所以椭圆离心率的取值范围是113ca≤<, 故选:A9.已知点P 是椭圆221169x y +=上任意一点,则点P 到直线70x y +-=的距离最大值为( )A.B.C.D .6【答案】A【解析】:设与70x y +-=平行的直线为0x y m ++=,联立22{1169x y m x y ++=+=,消元得: 22251891440y my m ++-=,令22(18)100(9144)0m m ∆=--=,得:5m =±,当5m =时,d ==5m =-时,d ==P到直线的距离max d =A .10.知12F F ,是椭圆22:18x y C m+=的两个焦点,若椭圆C 上存在点P 满足1290F PF ∠=︒,则m 的取值范围是( )A .(][)0,216,+∞B .(][)0,416,+∞C .(][)0,28,+∞D .(][)0,48,+∞【答案】B【详解】先讨论当点P 在椭圆上时,角12F PF ∠的最大时,点P 的位置.()222221212121212121224cos 22PF PF PF PF c PF PF F F F PF PF PF PF PF +-⋅-+-∠==⋅⋅2222212221212124244422222222a PF PF c b b b PF PF PF PF a PF PF -⋅-==-≥-=-⋅⋅⎛⎫+ ⎪⎝⎭当且仅当12=PF PF 时取得等号,即当点P 在椭圆的短轴的端点上时,12cos F PF ∠最小. 此时12F PF ∠最大.要使得椭圆C 上存在点P 满足1290F PF ∠=︒,则只需12F PF ∠最大时的值大于等于90︒. 如图设椭圆的一个短轴的端点为B ,即只需145F BO∠≥︒. 当椭圆的焦点x 在轴上时,c =由题意可得tan 4508m ≥︒<<⎩, 当椭圆的焦点y 在轴上时,c =或tan 458,m ≥︒>⎩, 解得04m <≤或16.m ≥故选:B.11.已知动点P 在椭圆C :2212516x y +=上,F 为椭圆C 的右焦点,若点M 满足1MF =,且MP MF ⊥,则PM 的最小值为( ) A.3B .2CD .1【答案】C【详解】由已知,(3,0)F ,设(,)P x y ,则22161625x y =-,因P 在椭圆上,所以55x -≤≤,所以32535535PF x x ===-=-, 所以当5x =时,min ||2PF =,又MP MF ⊥,所以PM =minPM ==.故选:C12.椭圆2214y x +=上的动点P 到定点)A距离的最大值为( )A 1B 1C .D .3【答案】C【详解】设椭圆上的点为(),x y ,[]1,1x ∈-,则动点P 到定点)A距离d ==2214y x +=,可得2244y x =-,代入前式可得d ===当x =d 取到最大值,max d =故选:C13.已知椭圆2222:19x y C a a+=+,12F F 、是其左右焦点,若对椭圆C 上的任意一点P ,都有120PF PF ⋅>恒成立,则实数a 的取值范围为( )A .()()3,00,3-B .[)(]3,00,3-C .()(),33,-∞-+∞D .(][),33,-∞⋃+∞【答案】C 【详解】椭圆2222:19x y C a a+=+,12F F 、是其左右焦点,若对椭圆C 上的任意一点P , 画出图象:根据图象可知当点P 移动到y 轴顶点时,12F PF ∠角度最大,此时120PF PF ⋅>,P 移动到椭圆其位置也必有120PF PF ⋅> 根据2222:19x y C a a +=+ ∴()13,0F -,()23,0F ,点P 移动到y 轴顶点时,()0,P a 可得:()13,PF a =--,()23,PF a =由120PF PF ⋅>,可得290a ->,即29<a 解得33a -<<其0a ≠ 故选:C.14.斜率为1的直线l 与椭圆22x y 14+=相交于A 、B 两点,则AB 的最大值为( )A .2B .5C .5D .5【答案】C【详解】解:设直线l 的方程为y =x +t ,代入24x +y 2=1,消去y 得54x 2+2tx +t 2﹣1=0,由题意得△=(2t )2﹣5(t 2﹣1)>0,即t 2<5.弦长|AB |=≤. 故选:C .15.已知椭圆22221x y a b +=(0a b >>)的右焦点为(c,0)F ,上顶点为(0,)A b ,直线2a x c=上存在一点P满足()0FP FA AP +⋅=,则椭圆的离心率取值范围为( )A .1,12⎡⎫⎪⎢⎣⎭B .2⎫⎪⎪⎣⎭C .⎫⎪⎪⎣⎭D .0,2⎛ ⎝⎦【答案】C【详解】取AP 中点Q ,故20FQ AP FQ AP ⋅=∴⊥, 故三角形AFP 为等腰三角形,即FA FP =,且FA a ==由于P 在直线2a x c =上,故2a FP c c ≥-即2222110a a a a c e e c c c≥-∴≥-∴+-≥解得:e ≥e ≤01e <<故1e >≥故选:C16.已知椭圆C :22197x y +=的左焦点为F ,点()A ,P 为椭圆C 上一动点,则PAF △的周长的最小值为( ) A .3 B .4C .7D .10【答案】B【详解】设椭圆的右焦点为F ',3,a b c ===()A 在椭圆内,点()F ,且6PF PF '+=,1AF =,3AF '==,PAF △的周长为()16PA AF FP PA PF '++=++-()77PA PF AF ''=+-≥-,当且仅当P 位于射线F A '与椭圆的交点时,等号成立,所以周长的最小值为4. 故选:B.。
2020届高考数学二轮复习专题《椭圆中与面积有关的取值范围问题》作业评价

θ∈(0,π2).那么△ ACD的面积为ay0,△ BCD的面积为bx0,所以四边形面积SACBD=ay0+bx0
=ab(cosθ+sinθ)=
2absinθ+π4≤
2ab=3b2.当且仅当θ=π4时取“=”,
所以b= a
32,所
以e=ca=
1-ba22=
7 3.
图37-9
过椭圆
1x62 +
y2 4
∴C1-6-k212+33k1,
3-2
3k21-6k1
k12+3
∴kBC=4123kk11= 3
∴直线BC的斜率为kBC= 3.
②设B(x1,y1),C(x2,y2),直线BC的方程为 y= 3x+m,代入方程x22+y62=1得 6x2+2 3mx+m2-6=0, 其中Δ=(2 3m)2-24(m2-6)>0,所以m2<12 ∴x1+x2=- 33m,x1x2=m26-6, ∴|BC|= 1+( 3)2·|x1-x2|= 2· (x1+x2)2-4x1x2=23 3 12-m2,
①kBC= 3,②△ABC面积取得最大值 3.此时,直线BC的方程为y= 3x± 6.
①显然题中等腰三角形腰所在的直线不可能与x轴垂直.因此其斜率必存在,
y- 3=k1(x-1),
且斜率不为0,设两腰的斜率分别为k1,k2,由x22+y62=1,
消去y,得
(3+k21)x2+2k1( 3-k1)x+( 3-k1)2-6=0,
3
|PF1|·|PF|2=20,∴|PF1|·|PF2|= 16 =16(2- 2+ 3
3),可得△ PF1F2的面积为S=
1 2·|PF1
|·|PF2|·sin30°=4(2-
3).
若椭圆
椭圆中与面积有关的取值范围问题专题

椭圆中与面积有关的取值范围问题专题-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN椭圆中与面积有关的取值范围问题范围问题类似于函数的值域,解析几何中几何量的范围问题,需要选择合适的变量例题:如图,已知椭圆C :x 2a2+y 2b2=1(a >b >0)的左焦点为F (-1,0),左准线方程为x =-2.(1)求椭圆C 的标准方程;(2)若A ,B 两点满足OA ⊥OB (O 为坐标原点),求△AOB 面积的取值范围.变式1在平面直角坐标系xOy 中,已知椭圆E :x 22+y 2=1,点A 是椭圆上异于长轴端点的任一点,F 为椭圆的右焦点,直线AF 与椭圆交于B 点,直线AO 与椭圆交于C 点,求△ABC 面积的最大值.变式2设椭圆E :x 216+y 24=1,P 为椭圆C :x 24+y 2=1上任意一点,过点P 的直线y =kx+m 交椭圆E 于A ,B 两点,射线PO 交椭圆E 于点Q.(1)求OQOP 的值;(2)求△ABQ 面积的最大值.串讲1如图,已知椭圆C :x 22+y 2=1,设A 1,A 2分别为椭圆C 的左、右顶点,S 为直线x =22上一动点(不在x 轴上),直线A 1S 交椭圆C 于点M ,直线A 2S 交椭圆于点N ,设S 1,S 2分别为△A 1SA 2,△MSN 的面积,求S 1S 2的最大值.串讲2已知点A(0,-2),椭圆E :x 2a 2+y 2b 2=1(a >b >0)的离心率为32,F 是椭圆E 的右焦点,直线AF 的斜率为233,O 为坐标原点.(1)求E 的方程;(2)设过点A 的直线l 与E 相交于P ,Q 两点,当△OPQ 的面积最大时,求l 的方程.(2018·广西初赛改编)已知椭圆C :x 24+y 2=1,设不过原点O 的直线l 与椭圆C 交于两点P ,Q ,且直线OP ,PQ ,OQ 的斜率成等比数列,求△OPQ 面积的取值范围.(2018·南通泰州一模)如图,在平面直角坐标系xOy 中,已知椭圆x 2a 2+y2b 2=1(a >b >0)的离心率为22,两条准线之间的距离为4 2.(1)求椭圆的标准方程;(2)已知椭圆的左顶点为A ,点M 在圆x 2+y 2=89上,直线AM 与椭圆相交于另一点B ,且△AOB 的面积是△AOM 的面积的2倍,求直线AB 的方程.答案:(1)x 24+y22=1;(2)y =x +2y +2=0,x -2y +2=0.解析:(1)设椭圆的焦距为2c ,由题意得,c a =22,2a2c =42,2分解得a =2,c =2,所以b =2,所以椭圆的标准方程为x 24+y22=分(2)解法1:因为S △AOB =2S △AOM ,所以AB =2AM ,所以点M 为AB 的中点.6分 因为椭圆的方程为x 24+y22=1,所以A(-2,0).设M(x 0,y 0),则B(2x 0+2,2y 0),所以x 02+y 02=89,①(2x 0+2)24+(2y 0)22=1,②10分由①②,得9x 02-18x 0-16=0,解得x 0=-23或x 0=83(舍去).把x 0=-23代入①,得y 0=±23,12分所以k AB =±12,因此,直线AB 的方程为y =±12(x +2),即x +2y +2=0,x -2y +2=分解法2:因为S △AOB =2S △AOM ,所以AB =2AM ,所以点M 为AB 的中点.6分设直线AB 的方程为y =k(x +2),由⎩⎪⎨⎪⎧x 24+y 22=1,y =k (x +2),得(1+2k 2)x 2+8k 2x +8k 2-4=0,所以(x +2)[(1+2k 2)x +4k 2-2]=0,解得x B =2-4k 21+2k2,8分所以x M =x B +(-2)2=-4k21+2k2,10分y M =k(x M +2)=2k 1+2k 2,代入x 2+y 2=89,得⎝ ⎛⎭⎪⎫-4k 21+2k 2+⎝ ⎛⎭⎪⎫2k 1+2k 2=89, 化简得28k 4+k 2-2=0,12分即(7k 2+2)(4k 2-1)=0,解得k =±12,因此,直线AB 的方程为y =±12(x +2),即x +2y +2=0,x -2y +2=分例题答案:(1)x 22+y 2=1;(2)S∈⎣⎢⎡⎦⎥⎤23,22.解析:(1)由题设知e =22,a 2=2c 2=b 2+c 2,即a 2=2b 2,将⎝⎛⎭⎪⎫1,-22代入椭圆C 的方程得到12b 2+12b 2=1,则b 2=1,a 2=2,所以椭圆C :x 22+y 2=1.(2)当直线OA ,OB 分别与坐标轴重合时,易知△AOB 的面积S =22.当直线OA ,OB 的斜率均存在且不为零时,设OA :y =kx ,OB :y =-1k x.设A(x 1,y 1),B(x 2,y 2),将y =kx代入椭圆C 得到x 2+2k 2x 2=2,所以x 12=22k 2+1,y 12=2k 22k 2+1,同理x 22=2k 22+k2,y 22=22+k 2,△AOB 的面积S =OA·OB2= (k 2+1)2(2k 2+1)(k 2+2). 令t =k 2+1∈[1,+∞), S =t2(2t -1)(t +1)=12+1t -1t2,令u =1t ∈(0,1),则S =1-u 2+u +2=1-⎝ ⎛⎭⎪⎫u -12+94∈⎣⎢⎡⎭⎪⎫23,22.综上所述,S ∈⎣⎢⎡⎦⎥⎤23,22. 变式联想变式1 答案: 2.解析:①当直线AB 的斜率不存在时,不妨取A ⎝ ⎛⎭⎪⎫1,22, B ⎝ ⎛⎭⎪⎫1,-22, 则C ⎝⎛⎭⎪⎫-1,-22. 此时S △ABC =12×2×2=2;②当直线AB 的斜率存在时,设直线AB 方程为y =k(x -1),联立⎩⎪⎨⎪⎧y =k (x -1),x 2+2y 2=2. 化简得(2k 2+1)x 2-4k 2x +2k 2-2=0,设A(x 1,y 1),B(x 2,y 2),则有Δ=16k 4-4(2k 2+1)(2k 2-2)=8(1+k 2),x 1,2=4k 2±Δ2(1+2k 2), 所以AB =(1+k 2)·|x 1-x 2|=1+k 2·Δ(1+2k 2)=221+k21+2k2.(弦长公式)另一方面点O 到直线y =k(x -1)的距离d =|k|k 2+1,因为O 是线段AC 的中点,所以点C 到直线AB 的距离为2d =2|k|k 2+1,∴S △ABC =12AB·2d=12·⎝ ⎛⎭⎪⎫22·1+k 21+2k 2·2|k|k 2+1=22k 2(k 2+1)(2k 2+1)2= 2214-14(2k 2+1)2< 2. 综上,△ABC 面积的最大值为 2.说明:O 为AC 中点,所以△ABC 的面积是△OAB 面积的两倍,而△OAB 的面积可以用公式S △OAB =12OF·|y 1-y 2|得出,所以S △ABC =2S △OAB =|y 1-y 2|=|k|·|x 1-x 2|=22k 2(k 2+1)(2k 2+1)2.这样计算可以简洁一些. 变式2答案:(1)2;(2)6 3.解析:(1)设P(x 0,y 0),OQ OP =λ,由题意知Q(-λx 0,-λy 0),因为x 024+y 02=1,又(-λx 0)216+(-λy 0)24=1,即λ24⎝ ⎛⎭⎪⎫x 024+20=1,所以λ=2,即OQ OP =2. (2)设A(x 1,y 1),B(x 2,y 2).将y =kx +m 代入椭圆E 的方程,可得(1+4k 2)x 2+8kmx +4m 2-16=0.由Δ>0,可得m 2<4+16k 2①则有x 1+x 2=-8km 1+4k 2,x 1x 2=4m 2-161+4k2.所以|x 1-x 2|=416k 2+4-m21+4k 2.因为直线y =kx +m 与y 轴交点的坐标为(0,m),所以△OAB 的面积S =12|m|·|x 1-x 2|=216k 2+4-m 2|m|1+4k 2=2(16k 2+4-m 2)·m 21+4k2=2⎝ ⎛⎭⎪⎫4-m 21+4k 2·m 21+4k 2.令m 21+4k 2=t ,将y =kx +m 代入椭圆C 的方程可得(1+4k 2)x 2+8kmx +4m 2-4=0.由Δ≥0,可得m 2≤1+4k 2.②由①②可知0<t≤1.因此S =2(4-t )t =2-t 2+2t ,故S≤2 3.当且仅当t =1,即m 2=1+4k 2时取得最大值2 3.由①知,△ABQ 的面积为3S ,所以△ABQ 面积的最大值为6 3.串讲激活串讲1 答案:43.解析:设S(22,t),则t≠0,直线SA 1:y =t 32(x +2),直线SA 2:y =t 2(x -2).由⎩⎪⎨⎪⎧x 22+y 2=1,y =t32(x +2),得x 2+t 29(x +2)2=2,解得x 1=-2,x 2=-2t 2+92t 2+9,即x M =-2t 2+92t 2+9. 同理,由⎩⎪⎨⎪⎧x 22+y 2=1,y =t2(x -2),可得x N =2t 2-2t 2+1.所以 S 1S 2=12SA 1·SA 2·sin ∠S 12SM ·SN ·sin ∠S =SA 1·SA 2SM ·SN= |22+2|·|22-2|⎪⎪⎪⎪⎪⎪22+2t 2-92t 2+9·⎪⎪⎪⎪⎪⎪22-2t 2-2t 2+1=(t 2+9)(t 2+1)(t 2+3)2=1+4t 2t 4+6t 2+9=1+4t 2+9t2+6≤1+412=43,等号当且仅当t 2=3,即t =±3时成立. 所以,当S(22,±3)时,S 1S 2的最大值为43.说明:本题用三角形面积公式S 1=12SA 1·SA 2·sin ∠S ,最后得到S 1S 2=|x S -xA 1||x S -xA 2||x S -x M ||x S -x N |,这样运算就简单了.还有,用直线SA 1的方程求点M 坐标时,要注意方程组一定有一个解x A1,所以,也可以用韦达定理求出x M .串讲2答案:(1)x 24+y2=1;(2)y =72x -2或y =-72x -2.解析:(1)设F(c ,0),由条件知2c =233,得c =3,又c a =32,所以a =2,b 2=a 2-c 2=1,故E 的方程为x 24+y 2=1.(2)解法1:依题意,当l⊥x 轴不合题意,故设直线l :y =kx -2,设P(x 1,y 1),Q(x 2,y 2),将y =kx -2代入x 24+y 2=1,得(1+4k 2)x 2-16kx +12=0,当Δ=16(4k 2-3)>0,即k 2>34时,x 1,2=8k±24k 2-31+4k 2,从而PQ =k 2+1|x 1-x 2|=4k 2+1·4k 2-31+4k 2,又点O 到直线PQ 的距离d =2k 2+1,所以△OPQ 的面积S △OPQ =12d·PQ=44k 2-31+4k 2,设4k 2-3=t ,则t >0,S △OPQ =4t t 2+4=4t +4t≤1,当且仅当t =2,k =±72时等号成立,且满足Δ>0,所以当△OPQ 的面积最大时,l 的方程为y =72x -2或y =-72x -2. 解法2由题意知直线l 的斜率必存在.则S △OPQ = 12OP 2·OQ 2-(OP →·OQ →)2,设P(2cos α,sin α),Q(2cos β,sin β).所以S △OPQ =12·2·|sin (α-β)|≤1,当sin (α-β)=±1时,等号成立.此时α-β=2k π+π2或α-β=2k π-π2(k∈Z).又P (2cos α,sin α),Q (2cos β,sin β)与A (0,-2)共线,则sin β+22cos β=sin α+22cos αsin(α-β)=2(cosα-cos β)=±1cos α-cos β=±12.又k PQ =sin α-sin β2(cos α-cos β)=±(sin α-sinβ).①若α-β=2k π+π2(k ∈Z),则sin α=sin ⎝⎛⎭⎪⎫2k π+π2+β=cos β,同理cos α=-sin β.所以sin α-sin β=sin α+cos α.因为cos α-cos β=12得到cos α-sin α=12.且(sin α+cos α)2+(sin α-cos α)2=2,所以sin α-sin β=sin α+cos α=±72.②同理,当α-β=2k π-π2(k ∈Z)时,sin α-sin β=±72,所以k PQ =11 ±72.(以下同解法1) 新题在线答案:(0,1).解析:由题意,直线l 的斜率存在且不为0,故设l :y =kx +m (m ≠0).设P (x 1,y 1),Q (x 2,y 2),则x 1≠x 2,且x 1·x 2≠0.联立⎩⎪⎨⎪⎧y =kx +m ,x 2+4y 2=4.消去y 得(1+4k 2)x 2+8kmx +4(m 2-1)=0. 则Δ=64k 2m 2-16(1+4k 2)(m 2-1)=16(4k 2-m 2+1)>0,且x 1+x 2=-8km 1+4k2,x 1x 2=4(m 2-1)1+4k2. 因为直线OP ,PQ ,OQ 的斜率成等比数列,所以y 1x 1·y 2x 2=(kx 1+m )(kx 2+m )x 1x 2=k 2,得-8k 2m 21+4k 2+m 2=0. 因为m ≠0,所以k 2=14,所以k =±12. 因为Δ>0,且x 1·x 2≠0,所以0<m 2<2且m 2≠1.设点O 到直线l 的距离为d ,则d =|m |1+k 2, 所以S △OPQ =12·d ·PQ =12d ·1+k 2|x 1-x 2|=m 2(2-m 2)=-(m 2-1)2+1. 所以△OPQ 面积的取值范围是(0,1).说明:命题人用直线OP ,PQ ,OQ 的斜率成等比数列,是为了告知直线PQ 斜率为±12.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【押题背景】取值范围类似于函数的值域,解析几何中几何量的取值范围问题,需要选择合适的变量构建出可解出范围的函数,是高中数学的传统难点.解决椭圆中的面积取值范围问题,关键在于找到构建面积的合理路径,设法简化表达式,将问题转化为常见的函数模型,从而求出取值范围.【押题典例】典例1 已知椭圆C:2222x ya b+=1(a>b>0)的左右焦点分别为F1,F2,点P是椭圆C上一点,以PF1为直径的圆E:x2292y⎛+=⎝⎭过点F2.(1)求椭圆C的方程;(2)过点P且斜率大于0的直线l1与C的另一个交点为A,与直线x=4的交点为B,过点(3)且与l1垂直的直线l2与直线x=4交于点D,求△ABD面积的最小值.【答案】(1)22184x y+=;(2).【解析】(1)在圆E的方程中,令y=0,得到:x2=4,所以F1(﹣2,0),F2(2,0),又因为212OE F P=,所以P点坐标为(2,所以122a PF PF=+=则a=b=2,因此椭圆的方程为22184x y+=;(2)设直线l1:y=k(x﹣2)(k>0),所以点B的坐标为()42k,设A(x A,y A),D(x D,y D),将直线l1代入椭圆方程得(1+2k2)x2+(﹣8k2)x+8k2﹣k﹣4=0,所以x P x A228412kk--=+,所以x A224212kk--=+,直线l2的方程为y1k=-(x﹣3),所以点D坐标为14k⎛⎫⎪⎝⎭,押题第37道椭圆中与面积有关的取值范围问题所以S △ABD 12=(4﹣x A )|y B ﹣y D |12=•12k k +=2k 3k ++≥,当且仅当2k 3k =,即k =时取等号,综上,△ABD 面积的最小值. 典例2如图所示,已知椭圆C :x 2a 2+y 2b2=1(a >b >0)的左焦点为F (-1,0),左准线方程为x =-2.(1)求椭圆C 的标准方程;(2)若A ,B 两点满足OA ⊥OB (O 为坐标原点),求△AOB 面积的取值范围. 【答案】 (1)x 22+y 2=1;(2)S ∈⎣⎡⎦⎤23,22.【解析】 (1)由题设知,c =1,a 2c =2,又∵a 2=b 2+c 2,∴b 2=a 2-c 2=1, 所以椭圆的标准方程为x 22+y 2=1.(2)解法一:当直线OA ,OB 分别与坐标轴重合时,易知△AOB 的面积S =22; 当直线OA ,OB 的斜率均存在且不为零时,设OA :y =kx ,OB :y =-1k x .设A (x 1,y 1),B (x 2,y 2),将y =kx 代入椭圆C 得到x 2+2k 2x 2=2,所以x 21=22k 2+1,y 21=2k 22k 2+1, 同理x 22=2k 22+k 2,y 22=22+k 2,△AOB 的面积S =OA ·OB 2=(k 2+1)2(2k 2+1)(k 2+2).令t =k 2+1∈(1,+∞),S =t 2(2t -1)(t +1)=12+1t -1t2, 令u =1t∈(0,1),则S =1-u 2+u +2=1-⎝⎛⎭⎫u -122+94∈⎣⎡⎭⎫23,22.综上所述,S ∈⎣⎡⎦⎤23,22. 解法二:设A (x 1,y 1),B (x 2,y 2),因为OAOB ,所以x 1x 2+y 1y 2=0.①当直线AB 的斜率不存在时,△AOB 是等腰直角三角形.所以, 可设A (t ,t ),B (t ,-t ),则t 22+t 2=1,得t 2=23.此时△AOB 面积S =t 2=23;②当直线AB 的斜率存在时,设AB 方程为y =kx +m .由⎩⎪⎨⎪⎧y =kx +m ,x 22+y 2=1.得1+2k 2x 2+4kmx +2m 2-2=0.所以Δ=8(1+2k 2-m 2)>0,且⎩⎪⎨⎪⎧x 1+x 2=-4km1+2k 2,x 1x 2=2m 2-21+2k2,所以x 1x 2+y 1y 2=(1+k 2)x 1x 2+km (x 1+x 2)+m 2=3m 2-2-2k 21+2k2,所以m 2=23(1+k 2). 又AB =(x 1-x 2)2+(y 1-y 2)2=1+k 2|x 1-x 2|,O 到AB 的距离h =|m |1+k 2,所以△AOB 面积S =12AB ·h =12|m ||x 1-x 2|=2|m |·1+2k 2-m 21+2k 2= 2 3· 1+5k 2+4k 4 1+2k 2= 23· 1+k 21+4k 2 +4k 4,当k =0时,S = 2 3,当k≠0时,S =231+ 14k 2+1 k2+4,∵4k 2+1k 2≥4,当且仅当k 2=12取“=”,∴0< 1 4k 2+1k 2+4≤18∴S ∈(23,22],综上,△AOB 面积的取值范围是⎣⎡⎦⎤23,22.【押题匹配】(2020·无锡模拟)在平面直角坐标系xOy 中,已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的离心率为32,且过点(3,12),点P 在第四象限,A 为左顶点,B 为上顶点,P A 交y 轴于点C ,PB 交x 轴于点D .如图所示.(1)求椭圆C 的标准方程;(2)求△PCD 面积的最大值. 【答案】 (1)x 24+y 2=1;(2)2-1.【解析】(1)设c 2=a 2-b 2,则c a = 32,所以a 2=4b 2.又点⎝ ⎛⎭⎪⎫ 3,12在椭圆上,所以3a 2+14b 2=1.解得a 2=4,b 2=1,所以椭圆方程为x 24+y 2=1. (2)由题意,AP 直线斜率存在,所以设直线AP :y =k(x +2),P 在第四象限,所以-12<k <0.令x =0得y C =2k ,所以C (0,2k ).由⎩⎪⎨⎪⎧y =k (x +2),x 24+y 2=1,消去y ,得(1+4k 2)x 2+16k 2x +16k 2-4=0.所以x A x P =16k 2-41+4k 2.又x A =-2,所以x P =-8k 2-21+4k 2,y P =k (x P+2)=4k 1+4k 2.即P ⎝ ⎛⎭⎪⎫-8k 2-21+4k 2,4k 1+4k 2. 设D(m,0),因为B(0,1),P ,B ,D 三点共线,所以m -00-1=-8k 2-21+4k 24k 1+4k 2-1,解得m =2(1+2k )1-2k .即D ⎝ ⎛⎭⎪⎫2(1+2k )1-2k ,0.所以S △PCD =S △P AD -S △CAD =12·AD ·||y P -y C =12·⎝ ⎛⎭⎪⎫2(1+2k )1-2k +2⎪⎪⎪⎪4k 1+4k 2-2k =4||k (1+2k )1+4k 2. 因为-12<k <0,所以S △PCD =-8k 2-4k 1+4k 2=-2+2(1-2k )1+4k 2.令t =1-2k ,则1<t <2,所以2k =1-t ,所以S △PCD =-2+2t t 2-2t +2=-2+2t +2t-2≤-2+22 2-2=2-1.当且仅当t =2时取等号,此时k =1-22,所以△PCD 面积的最大值为2-1.【押题变式】1、(2020江苏无锡高三)若椭圆x 24+y 2b 2=1(0<b <2)的左、右焦点分别为F 1,F 2,B 是短轴的一个端点,则△F 1BF 2的面积的最大值是________.2、(2020江苏盐城高三)椭圆x 2a 2+y 2b 2=1()a >b >0的长轴端点为A ,B ,短轴端点为C ,D ,动点P 满足P APB =2,△P AB 面积的最大值为163,△PCD 面积的最小值为23,则此椭圆的离心率为_________.3、(2020江苏镇江高三)已知A ,B 分别为椭圆x 2a 2+y 2b 2=1(a >b >0)的右顶点和上顶点,直线y =kx (k >0)与椭圆交于C ,D 两点,若四边形ACBD 的面积最大值为3b 2,则椭圆的离心率为________.4、(2020江苏连云港高三)过椭圆x 216+y 24=1上一点P 作圆x 2+y 2=2的两条切线,切点分别为M ,N ,若直线MN 与x 轴、y 轴分别交于点A ,B ,则△OAB 面积的最小值为________.5、(2020江苏泰州高三)椭圆两焦点分别为F 1(-4,0),F 2(4,0),P 为椭圆上的动点,直线PF 2与椭圆的交点为Q ,若△PF 1Q 面积的最大值为15,则该椭圆的标准方程为________.6、(2020江苏通州高三)如图所示,点A (1,3)为椭圆x 22+y 2n =1上一定点,过点A 引两直线与椭圆分别交于B ,C 两点. (1)求椭圆的标准方程;(2)若直线AB ,AC 与x 轴围成的是以点A 为顶点的等腰三角形. ①求直线BC 的斜率;②求△ABC 的面积的最大值,并求出此时直线BC 的方程.7、(2020江苏扬州高三)如图所示,在平面直角坐标系xOy 中,椭圆E :x 2a 2+y 2b 2=1(a >b >0)的左顶点为A ,与x 轴平行的直线与椭圆E 交于B ,C 两点,过B ,C 两点且分别与直线AB ,AC 垂直的直线相交于点D .已知椭圆E 的离心率为53,右焦点到右准线的距离为455. (1)求椭圆E 的标准方程;(2)证明点D 在一条定直线上运动,并求出该直线的方程; (3)求△BCD 面积的最大值.8、(2020江苏徐州高三)已知点A (0,-2),椭圆E :x 2a 2+y 2b 2=1(a >b >0)的离心率为32,F 是椭圆E 的右焦点,直线AF 的斜率为233,O 为坐标原点.如图376所示.(1)求E 的方程;(2)设过点A 的直线l 与E 相交于P ,Q 两点,当△OPQ 的面积最大时, 求l 的方程.9、(2020江苏南京高三)如图所示,已知椭圆C :x 22+y 2=1,设A 1,A 2分别为椭圆C 的左、右顶点,S 为直线x =22上一动点(不在x 轴上),直线A 1S 交椭圆C 于点M ,直线A 2S 交椭圆于点N ,设S 1,S 2分别为△A 1SA 2,△MSN 的面积,求S 1S 2的最大值.10、(2020江苏苏州高三)设椭圆E :x 216+y 24=1,P 为椭圆C :x 24+y 2=1上任意一点,过点P 的直线y =kx+m 交椭圆E 于A ,B 两点,射线PO 交椭圆E 于点Q .如图所示.(1)求OQOP的值;(2)求△ABQ 面积的最大值.。
