数学建模实例-双层玻璃的功效教学提纲

双层玻璃功效问题

双层玻璃功效问题（模型建立）
【模型建立】
根据热传导定律，对于双层玻璃的情况，单位时间内通过单位面积的热量：
Tb − T2 Ta − Tb T1 − Ta = k2 = k1 Q = k1 d L d
双层玻璃功效问题（模型求解）
由上面等式，消去Ta、Tb, 可得
k1 (T1 − T2 ) Q= , d ( s + 2)
Q 2 2 1 k L = = = (因为，s = 1 h = 16h ，h = ） Q' s + 2 16h + 2 8h + 1 k2 d
双层玻璃功效问题（模型求解）
如果假设玻璃的厚度d=1, 则h=L/d=L.
Q 1 1 = = Q ' 8h + 1 8 L + 1
故热量损失比为：
当0<L<6时，热量损失比
双层玻璃功效问题
【问题提出】使房子加热是日常预算中较为昂贵的部分。
如煤、煤气、电等用来加热的燃料成本近些年明显的增加。将尽可能多的热量保持在居室内是非常重要的。据分析，热量的损失主要是通过墙、窗、屋顶和地面发出去，将窗户安装成双层玻璃是控制热量损失的有效方法之一（如图）。试建立一个模型来描述热量通过窗户的流失过程，并将双层玻璃与用同样多材料做成的单层玻璃的热量流失进行对比，对双层玻璃窗能够减少多少热量损失给出定量分析结果。
k 2 = 2.5 × 10 −4 ~ 8 × 10 −4 (焦尔 / 厘米 ⋅ 秒 ⋅ 度）
而这空气是干燥的、不流通的. 作为模型假设的这个条件在实际环境下是不可能完全满足的. 所以, 实际上双层窗户的功效要比上述结果要差一些. 双层玻璃窗户出奇的保热功效是房屋设计和房屋装修的重要参考依据.

数学建模案例分析报告报告材料2.双层玻璃地功效

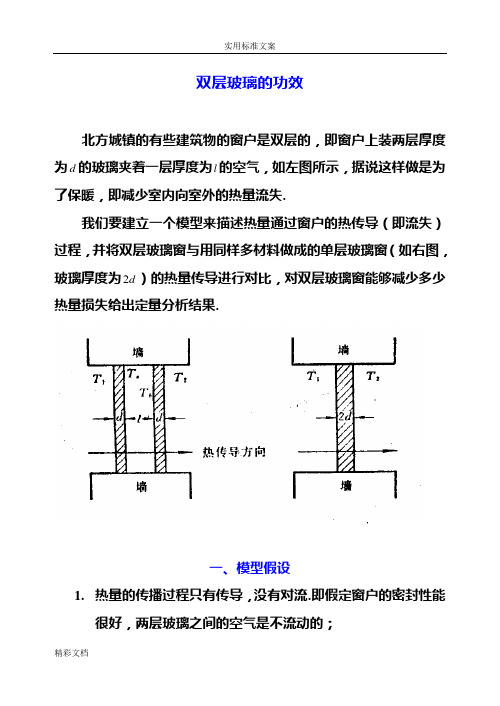
双层玻璃的功效北方城镇的有些建筑物的窗户是双层的，即窗户上装两层厚度为d的玻璃夹着一层厚度为l的空气，如左图所示，据说这样做是为了保暖，即减少室内向室外的热量流失.我们要建立一个模型来描述热量通过窗户的热传导（即流失）过程，并将双层玻璃窗与用同样多材料做成的单层玻璃窗（如右图，玻璃厚度为d2）的热量传导进行对比，对双层玻璃窗能够减少多少热量损失给出定量分析结果.一、模型假设1.热量的传播过程只有传导，没有对流.即假定窗户的密封性能很好，两层玻璃之间的空气是不流动的；2.室内温度T和室外温度2T保持不变，热传导过程已处于稳定1状态，即沿热传导方向，单位时间通过单位面积的热量是常数；3.玻璃材料均匀，热传导系数是常数.二、符号说明T——室内温度1T——室外温度2d——单层玻璃厚度l——两层玻璃之间的空气厚度T——内层玻璃的外侧温度aT——外层玻璃的内侧温度bk——热传导系数Q——热量损失三、模型建立与求解由物理学知道，在上述假设下，热传导过程遵从下面的物理规律：厚度为d的均匀介质，两侧温度差为T∆，则单位时间由温度高的一侧向温度低的一侧通过单位面积的热量为Q，与T∆成正比，与d成反比，即dT k Q ∆= （1）其中k 为热传导系数.1. 双层玻璃的热量流失记双层窗内窗玻璃的外侧温度为a T ，外层玻璃的内侧温度为b T ，玻璃的热传导系数为1k ，空气的热传导系数为2k ，由（1）式单位时间单位面积的热量传导（热量流失）为：d T T k d T T k d T T k Q b b a a 21211-=-=-= （2）由d T T k Q a -=11及dT T k Q b 21-=可得1212)(k Qd T T T T b a --=- 再代入d T T k Q b a -=2就将（2）中a T 、b T 消去，变形可得： ()dl h k k h s s d T T k Q ==+-=, , 2)(21211 （3） 2. 单层玻璃的热量流失对于厚度为d 2的单层玻璃窗户，容易写出热量流失为： d T T k Q 2211-=' （4）3. 单层玻璃窗和双层玻璃窗热量流失比较比较（3）（4）有：22+='s Q Q （5）显然，Q Q '<.为了获得更具体的结果，我们需要21,k k 的数据，从有关资料可知，不流通、干燥空气的热传导系数42105.2-⨯=k （J/cm.s.ºC ），常用玻璃的热传导系数331108~104--⨯⨯=k （J/cm.s.ºC ），于是32~1621=k k 在分析双层玻璃窗比单层玻璃窗可减少多少热量损失时，我们作最保守的估计，即取1621=k k ，由（3）（5）可得：d l h h Q Q =+=' 181 （6） 4. 模型讨论比值Q Q '反映了双层玻璃窗在减少热量损失上的功效，它只与d l h =有关，下图给出了h Q Q ~'的曲线，当h 由0增加时，Q Q '迅速下降，而当h 超过一定值（比如4>h ）后Q Q '下降缓慢，可见h 不宜选得过大.四、模型的应用这个模型具有一定的应用价值.制作双层玻璃窗虽然工艺复杂会增加一些费用，但它减少的热量损失却是相当可观的.通常，建筑规范要求4≈h.按照这个模型，%3≈'QQ，即双层玻璃窗比用同=d l样多的玻璃材料制成的单层窗节约热量97%左右.不难发现，之所以有如此高的功效主要是由于层间空气的极低的热传导系数k，而2这要求空气是干燥、不流通的.作为模型假设的这个条件在实际环境下当然不可能完全满足，所以实际上双层玻璃窗的功效会比上述结果差一些.。

双层玻璃窗的功效

数学模型之初等模型
双层玻璃窗的功效
2012-9-18
初等模型：如果研究对象的机理比较简单，一般用静态、线性、确定性模型描述就能达到建模目的时，我们基本上使用初等数学的方法来构造和求解模型。另外需要指出，衡量一个模型的优劣全在于它的应用，而不是采用了多么高深的数学方法。
问题归纳：两层厚度为d的玻璃夹着一层厚度为l的空气。试描述热量通过窗户的传导过程，并与厚度为2d的单层玻璃窗相比较。
模型构成
热传导定律：设厚度为d的均匀介质，两侧温度差为，则单位时间内从温度高的一侧向温度低的一侧通过单位面积的热量Q与成正比，与d成反比，即 T Q k , (1) d 其中k为热传导系数。
设双层窗内层玻璃外侧温度为 Ta ，外层玻璃内侧温度为Tb，玻璃的热传导系数为k1，空气的热传导系数为k2。由 (1)，单位时间内通过单位面积的热量为
1 2
得：
Q Q
1 8h 1 ,
h
l d
.
(6)
Q
由图知，当h增加时， Q/ Q' 迅速下降，而当h>4后，下降变缓。所以h不宜过大。
Q
0.06 0.03 0应用：
通常建筑要求 h = l / d 4 , 于是， Q/ Q ' 3%。因此，双层玻璃窗比用同样多的玻璃材料制成的单层玻璃窗节约热量97% 左右。当然，由于其他因素的存在，实际情况没这么好。
1 1 2
(4)
Q
Q s 2

2
.
(5)
显然， Q Q .
由数据资料知道，常用玻璃的热传导系数 k1=410-3~ 810-3(焦耳/厘米· 度) ，干燥秒· 不流通的空气的热传导系数k2=2.510-4(焦耳/厘米· 度)。秒· 所以，

数学模型数学论文指导双层玻璃的功效

l
知识引入热传导原理：厚度为 d ，的均匀介质，两侧温
度差为 ∆T ，则单位时间由温度高的一侧向温度低的一侧通过单位面积的热量为：∆T Leabharlann =k dk为热传导系数
模型的建立
由假设知：由假设知：
T1 − Ta Ta − Tb Tb − T2 Q = k1 = k2 = k1 d l d
消去 T , T a b
−3
−3
k 2 = 2.5 × 10 −4
于是：
做保守的估计，取最小的16，得
k1 = 16 ~ 32 k2
Q 1 = Q1 8 ⋅ l + 1 d
可见
Q Q1 仅与
Q1
l 有关， d
Q 小，若取
则
l =4 d
l 越大， d
越
Q ≈ 3% Q1
模型评价：模型具有一定的实用性，但是在实际中效果没有这么好。
模型假设 1、设室内温度为室外温度为，内层玻璃外侧 T1 T2 的温度为，外层玻璃内测的温度为 Ta Tb 2、设双层玻璃在单位时间内通过单位面积的热量为 Q 3、设窗户的密封效果很好，两层玻璃之间的空气不流动。 4、室内、室外温度保持不变，热传导处于稳定状态，即单位时间通过单位面积的热量是常数。玻璃的热传导系数为常数 k1 空气的热传导系数为常数 k2 5、设玻璃的厚度为 d 两层玻璃之间的间隔为
得
k 1 ( T1 − T 2 ) Q = k l d ( 1 + 2) k2d
对于厚度为 2d 的单层玻璃，其传导的热量为： k (T − T 2 ) Q = 1 1
1
从而
Q 2 = k1l Q1 +2 k2d
2d

双层玻璃的功效

2d k2 L1 L2 Ln k1
验
由此可以发现，当 d 一定时，决定保温性能的其实是 L1 至 Ln 之和。也就是说，与
内玻璃层数无关。玻璃厚一点（ d 大一些），间隙大一些（ L 大一些）即可。
容
由以上分析可知，当T1 20C ，T2 10C ， d 1cm ， L 2d 时，
容
二、模型假设
○1 室内的热量传播只有传导形式（不考虑对流、辐射）；
及
○2 室内温度与室外温度保持不变（即单位时间通过窗户单位面积的热量是常数）；
○3 玻璃厚度均匀，玻璃材料均匀（即热传导系数是常数）。
数
三、符号说明
据
T1
处
T2
理
Ta
Tb
d
室内温度室外温度内层玻璃的外侧温度外层玻璃的内侧温度单层玻璃厚度

k2
Ta
Tb d
,
可得：
内
外
Q2

k1k2 (T1 T2 ) 2dk2 Lk1
.墙图 2 双层玻 Nhomakorabea示意图2
实验编号： 01
组别：10
设 s h k1 , h 1 ,
k2
d
则：
Q2

k1 (T1 d(S
T2 ) . 2)
所以 Q1 2 1, 显然双层玻璃减少了热量散失。 Q2 S 2
1
实验编号： 01
L k Q
两层玻璃之间的空气厚度热传导系数
热量损失
组别：10
根据热传导物理定律，即厚度为 d 的均匀介质，两侧的温度差为 T T1 T2 ，则
单位时间内温度高的一侧向温度低的一侧通过单位面积的热量与 T 成正比，与成 d 反比，即：

数学建模基础 12.10双层玻璃的功效

厚度为d的均匀介质,两侧温度差为T,则单位时间由温度高的一侧向温度低的一侧通过单位面积的热量Q,与T成正比,与d成反比,即:Q=k T/d
k为热传导系数.物理定律
模型假设:(根据上定律做假设)
1.室内的热量传播只有传导(不考虑对流,辐射)
2.室内温度与室外温度保持不变(即单位时间通过窗户单位面积的热量是常数)
3.玻璃厚度一定,玻璃材料均匀(热传导系数是常数)
符号说明: d:玻璃厚度 T1:室内温度, T2:室外温度 Ta:靠近内层玻璃温度, T2:靠近外层玻璃的温度 L:玻璃之间的距离 k1:玻璃热传导系数 k2:空气热传导系数
Ta
T1
T2
L
Tb
模型构成:
由热量守恒定律: 过内层玻璃的热量=过中间空气层的热量=过外层玻璃的热量
说明双层玻璃比单层玻璃保温,为得定量结果, 考虑的s的值,查资料有
常用玻璃:k1=410-3 ~ 810-3 (焦耳/厘米.秒.度) 静止的干燥空气:k2=2.510 - 4 (焦耳/厘米.秒.度)
若取最保守的估计,有
k1 16, Q 1 , h L
k2
Q 8h 1 d
显然Q/Q’可以反映双层玻璃在减少热量损失的功效,它是h的函数现方式做保护处理对用户上传分享的文档内容本身不做任何修改或编辑并不能对任何下载内容负责
问题:北方城镇的窗户玻璃是双层的,这样做主要是为室内
保温目的,试用数学建模的方法给出双层玻璃能减少热量损失的定量分析结果
模型准备:热量的传播形式,温度,与热量传播的有关结果:
此函数无极小值,从图中可知: 当h从0变大时,Q/Q’迅速下降,但h超过4后下降变慢, h不易选择过大,以免浪费材料
模型应用:

初等方法建模1双层玻璃窗的功效--数学建模案例分析

第一章初等方法建模如果研究对象的机理比较简单，一般用静态、线性、确定性模型描述就能达到建模目的时，我们基本上可以用初等数学的方法来构造和求解模型。

通过下面介绍的若干例子能够看到，用很简单的数学方法已经可以解决一些饶有兴味的实际问题。

需要强调的是，如果对于某个实际问题可以用初等的方法解决，就不要用更高等的方法。

§1 双层玻璃窗的功效背景将双层玻璃窗与用同样多材料做成的单层窗的热传导进行对比，对双层窗能减少多少热量损失给出定量分析结果。

模型假设1、热量的传播只有传导，没有对流，即假定窗户的密封性能很好，两层玻璃间的空气是不流动的。

2、室内温度1T 和室外温度2T 保持不变，热传导过程已处于稳定状态，即沿热传导方向，单位时间通过单位面积的热量是常数。

3、玻璃材料均匀，热传导系数是常数。

模型构成与求解记 a T —内层玻璃的外侧温度b T —外层玻璃的内侧温度1K —玻璃的热传导系数2K —空气的热传导系数空气Q —单位时间通过双层窗单位面积的热量'Q —单位时间通过单层窗单位面积的热量由热传导过程的物理定律：dT K Q ∆=，得到 dT T K l T T K d T T K Q b b a a 21211-=-=-= （1） d T T K Q 2211'-= （2）从（1）中消去b a T T ,，可得dl h K K h S S d T T K Q ==+-=,,)2()(21211 （3） 22+='S Q Q （4）显然Q Q '<，且S 越大，比例越悬殊，331108~104--⨯⨯=K （焦耳/CM ·秒·度），42105.2-⨯=K （焦耳/CM ·秒·度），于是31~1621=K K ,做最保守的估计，即取1621=K K ，由(3)、(4)即有 dl h h Q Q =+=',181 （5）模型分析比值Q Q '反映了双层玻璃窗在减少热量损失上的功效，它只与d l h =有关，h 不宜选择过大，通常建筑要求是4≈h ，按此模型，%3≈'Q Q ，即使用同样材料制成的双层窗较单层窗节约热量97%左右。

【数学建模实例】双层玻璃的功效

双层玻璃的功效北方城镇的有些建筑物的窗户是双层的，即窗户上装两层厚度为d的玻璃夹着一层厚度为l的空气，如左图所示，据说这样做是为了保暖，即减少室内向室外的热量流失.我们要建立一个模型来描述热量通过窗户的热传导（即流失）过程，并将双层玻璃窗与用同样多材料做成的单层玻璃窗（如右图，玻璃厚度为d2）的热量传导进行对比，对双层玻璃窗能够减少多少热量损失给出定量分析结果.一、模型假设1.热量的传播过程只有传导，没有对流.即假定窗户的密封性能很好，两层玻璃之间的空气是不流动的；2.室内温度T和室外温度2T保持不变，热传导过程已处于稳定1状态，即沿热传导方向，单位时间通过单位面积的热量是常数；3.玻璃材料均匀，热传导系数是常数.二、符号说明1T ——室内温度 2T ——室外温度 d ——单层玻璃厚度l ——两层玻璃之间的空气厚度 a T ——内层玻璃的外侧温度 b T ——外层玻璃的内侧温度 k ——热传导系数 Q ——热量损失三、模型建立与求解由物理学知道，在上述假设下，热传导过程遵从下面的物理规律：厚度为d 的均匀介质，两侧温度差为T ∆，则单位时间由温度高的一侧向温度低的一侧通过单位面积的热量为Q ，与T ∆成正比，与d 成反比，即dTkQ ∆= （1）其中k 为热传导系数. 1. 双层玻璃的热量流失记双层窗内窗玻璃的外侧温度为a T ，外层玻璃的内侧温度为b T ，玻璃的热传导系数为1k ，空气的热传导系数为2k ，由（1）式单位时间单位面积的热量传导（热量流失）为：dT T k d T T k d T T k Q b b a a 21211-=-=-= （2）由d T T k Q a -=11及dT T k Q b 21-=可得1212)(k Qd T T T T b a --=-再代入dT T k Q ba -=2就将（2）中a T 、b T 消去，变形可得： ()dlh k k h s s d T T k Q ==+-=, , 2)(21211 （3）2. 单层玻璃的热量流失对于厚度为d 2的单层玻璃窗户，容易写出热量流失为： dT T k Q 2211-=' （4）3. 单层玻璃窗和双层玻璃窗热量流失比较比较（3）（4）有： 22+='s Q Q （5）显然，Q Q '<.为了获得更具体的结果，我们需要21,k k 的数据，从有关资料可知，不流通、干燥空气的热传导系数42105.2-⨯=k （J/cm.s .ºC ），常用玻璃的热传导系数331108~104--⨯⨯=k （J/cm.s .ºC ），于是32~1621=k k 在分析双层玻璃窗比单层玻璃窗可减少多少热量损失时，我们作最保守的估计，即取1621=k k ，由（3）（5）可得： dlh h Q Q =+=' 181 （6） 4. 模型讨论比值Q Q '反映了双层玻璃窗在减少热量损失上的功效，它只与d l h =有关，下图给出了h Q Q ~'的曲线，当h 由0增加时，Q Q '迅速下降，而当h 超过一定值（比如4>h ）后Q Q '下降缓慢，可见h 不宜选得过大.四、模型的应用这个模型具有一定的应用价值.制作双层玻璃窗虽然工艺复杂会增加一些费用，但它减少的热量损失却是相当可观的.通常，建筑规范要求4≈=d l h .按照这个模型，%3≈'Q ，即双层玻璃窗比用同样多的玻璃材料制成的单层窗节约热量97%左右.不难发现，之所以有如此高的功效主要是由于层间空气的极低的热传导系数2k ，而这要求空气是干燥、不流通的.作为模型假设的这个条件在实际环境下当然不可能完全满足，所以实际上双层玻璃窗的功效会比上述结果差一些.。

数学建模-双层玻璃窗、隔热效果、隔音效果.

数学建模-双层玻璃窗、隔热效果、隔音效果摘要：中国仍处于工业化初期，节能减排具有较大空间。

通过对问题一的数学模型进行分析后得到：一般情况下，建筑规范要求d l /≈4。

据此模型可得12/Q Q ≈3.03%，即双层玻璃窗比同样多的玻璃材料制成的单层玻璃窗节约热量约为96.97%；双层玻璃的隔声优势为：错误！未找到引用源。

lge ，根据以上推导的结果，当空气的吸收系数与两片玻璃的距离越大时，双层玻璃窗的隔音效果就越好。

游客节能低碳的交通出行工具安排：（1）长途参观者建议直接或间接购买碳信用额度；（2）对中短途参观者，建议优先选择火车、轮船和长途客车等公共交通方式；（3）对于长三角等周边地区自驾车出行的参观者，建议采用停车换乘（P+R ）方式；（4）对上海城区内的参观者，建议优先选择轨交、公共汽车等公共交通，减少私人汽车的使用；（5）对距世博园区较近的参观者，建议步行或自行车出行。

最后，我们计算了各种出行方式的二氧化碳的排放量后，据此代表上海世博会组委会给游客写了一份倡议书。

关键字：双层玻璃窗隔热效果隔音效果碳足迹目录1、问题重述与分析 (3)1.1、问题重述 (4)1.2、问题分析 (4)2、条件假设 (4)3、符号说明 (4)4、模型的建立及求解 (5)4.1双层玻璃隔热效果探究 (5)4.1.1模型建立 (5)4.1.2、模型的应用 (8)4.2、双层玻璃隔音效果探究 (9)4.2.1、模型建立 (9)4.2.2结果讨论 (11)4.3绿色出行建议 (11)4.3.1碳排放与出行安排 (11)4.3.2倡议书 (15)参考文献 (16)1、问题重述与分析1.1问题重述中国仍处于工业化初期，节能减排具有较大空间。

中国现在是工业排放量占大头，交通和建筑类排放较小。

随着生活水平的提高，建筑节能的比重将逐步上升，有很大发展潜力。

据研究报告称，相关交通工具所使用燃料释放的气体是目前造成全球变暖的主要原因之一。

双层玻璃窗的功效

双层玻璃的功效
在寒冷的北方，许多住房的玻璃窗都是双层玻璃的，现在我们来建立一个简单的数学模型，研究一下双层玻璃到底有多大的功效。比较两座其他条件完全相同的房屋，它们的差异仅仅在窗户不同。
双层玻璃窗的功效
识别双层玻璃窗与同样多材料的单层 d l d 问题玻璃窗相比，热量损失的比值是不妨可以提出以下假设：多少. 1、设室内热量的流失是热传导引起的，墙不存在户内外的空气对流。即窗户的符 Q ~单位时间单位面积传导的热量密封性很好，两层玻璃之间的空气不号流动。室
室内 T1
室外 T2
Q1
T~温差, d~材料厚度, k~热传导系数
热传导定律
内 2、室内温度 T1与户外温度 T2 均为常数， T 1 2d 热传导过程已处于稳定状态。 T
室外 T2
d 3、玻璃是均匀的，热传导系数为常数。墙
Qk
Q2
建模记双层玻璃窗传导的热量Q1Ta~内层玻璃的外侧温度Tb~外层玻璃的内侧温度
k1~玻璃的热传导系数
室内 T1
Ta T b d l d
室外 T2
Q1
墙
k2~空气的热传导系数
T1 Ta Ta Tb Tb T2 Q1 k1 k2 k1 d l d
推导
T1 T2 k1 l Q1 k1 , sh , h d ( s 2) k2 d
建模记单层玻璃窗传导的热量Q2 T1 T2 T1 T2 Q1 k1 Q2 k1 d ( s 2) 2d
双层与单层窗传导的热量之比
室内 T1
2d
室外 T2
Q2
墙
Q1 2 k1 l , sh , h Q2 s 2 k2 d

【数学建模学习】双层玻璃的功效

双层玻璃的功效北方城镇的有些建筑物的窗户是双层的，即窗户上装两层厚度为d的玻璃夹着一层厚度为l的空气，如左图所示，据说这样做是为了保暖，即减少室内向室外的热量流失.我们要建立一个模型来描述热量通过窗户的热传导（即流失）过程，并将双层玻璃窗与用同样多材料做成的单层玻璃窗（如右图，玻璃厚度为d2）的热量传导进行对比，对双层玻璃窗能够减少多少热量损失给出定量分析结果.一、模型假设1.热量的传播过程只有传导，没有对流.即假定窗户的密封性能很好，两层玻璃之间的空气是不流动的；2.室内温度T和室外温度2T保持不变，热传导过程已处于稳定1状态，即沿热传导方向，单位时间通过单位面积的热量是常数；3.玻璃材料均匀，热传导系数是常数.二、符号说明1T ——室内温度 2T ——室外温度 d ——单层玻璃厚度l ——两层玻璃之间的空气厚度 a T ——内层玻璃的外侧温度 b T ——外层玻璃的内侧温度 k ——热传导系数 Q ——热量损失三、模型建立与求解由物理学知道，在上述假设下，热传导过程遵从下面的物理规律：厚度为d 的均匀介质，两侧温度差为T ∆，则单位时间由温度高的一侧向温度低的一侧通过单位面积的热量为Q ，与T ∆成正比，与d 成反比，即dTkQ ∆= （1）其中k 为热传导系数. 1. 双层玻璃的热量流失记双层窗内窗玻璃的外侧温度为a T ，外层玻璃的内侧温度为b T ，玻璃的热传导系数为1k ，空气的热传导系数为2k ，由（1）式单位时间单位面积的热量传导（热量流失）为：dT T k d T T k d T T k Q b b a a 21211-=-=-= （2）由d T T k Q a -=11及dT T k Q b 21-=可得1212)(k Qd T T T T b a --=-再代入dT T k Q ba -=2就将（2）中a T 、b T 消去，变形可得： ()dlh k k h s s d T T k Q ==+-=, , 2)(21211 （3）2. 单层玻璃的热量流失对于厚度为d 2的单层玻璃窗户，容易写出热量流失为： dT T k Q 2211-=' （4）3. 单层玻璃窗和双层玻璃窗热量流失比较比较（3）（4）有： 22+='s Q Q （5）显然，Q Q '<.为了获得更具体的结果，我们需要21,k k 的数据，从有关资料可知，不流通、干燥空气的热传导系数42105.2-⨯=k （J/cm.s .ºC ），常用玻璃的热传导系数331108~104--⨯⨯=k （J/cm.s .ºC ），于是32~1621=k k 在分析双层玻璃窗比单层玻璃窗可减少多少热量损失时，我们作最保守的估计，即取1621=k k ，由（3）（5）可得： dlh h Q Q =+=' 181 （6） 4. 模型讨论比值Q Q '反映了双层玻璃窗在减少热量损失上的功效，它只与d l h =有关，下图给出了h Q Q ~'的曲线，当h 由0增加时，Q Q '迅速下降，而当h 超过一定值（比如4>h ）后Q Q '下降缓慢，可见h 不宜选得过大.四、模型的应用这个模型具有一定的应用价值.制作双层玻璃窗虽然工艺复杂会增加一些费用，但它减少的热量损失却是相当可观的.通常，建筑规范要求4≈=d l h .按照这个模型，%3≈'Q ，即双层玻璃窗比用同样多的玻璃材料制成的单层窗节约热量97%左右.不难发现，之所以有如此高的功效主要是由于层间空气的极低的热传导系数2k ，而这要求空气是干燥、不流通的.作为模型假设的这个条件在实际环境下当然不可能完全满足，所以实际上双层玻璃窗的功效会比上述结果差一些.。

第03讲双层玻璃窗的功效及确定性存贮模型

1
一周期总费用
C c1 c 2 QT 1 2 c3 r ( T T1 ) 2
2
一周期缺货费
c 3 T q ( t ) dt c 3 B
1
T
一周期总费用
C c1
1 2
c 2 QT 1
1 2
c 3 r (T T1 )
2
2 2 每天总费用 c 3 ( rT Q ) C c1 c 2 Q C (T , Q ) 平均值 T T 2 rT 2 rT （目标函数）求 T ,Q 使 C ( T , Q ) Min
允许缺货的存贮模型
当贮存量降到零时仍有需求r, 出现缺货，造成损失原模型假设：贮存量降到零时Q件立即生产出来(或立即到货)
q Q
r
A
Q rT 1
T1 B T t
0
现假设：允许缺货, 每天每件缺货损失费 c3 , 缺货需补足
周期T, t=T1贮存量降到零
T 一周期 c 2 0 q ( t ) dt c 2 A 贮存费
•Ｔ和Ｑ：经济批量订货公式（EOQ公式）
用于订货、供应、存贮情形
每天需求量 r，每次订货费 c1,每天每件贮存费 c2 ，
T天订货一次(周期), 每次订货Q件，当贮存量降到零时，Q件立即到货。
T 2 c1 rc 2
Q rT
2 c1 r c2
不允许缺货的存贮模型
• 问：为什么不考虑生产费用？在什么条件下才不考虑？
Tb T2 d
Q1 k1
T1 T 2 d (s 2)
, s h
k1 k2
, h
l d
建模记单层玻璃窗传导的热量Q2
Q 2 k1 T1 T 2 2d

数学建模-双层玻璃窗、隔热效果、隔音效果

数学建模-双层玻璃窗、隔热效果、隔音效果摘要：中国仍处于工业化初期，节能减排具有较大空间。

通过对问题一的数学模型进行分析后得到：一般情况下，建筑规范要求d l /≈4。

据此模型可得12/Q Q ≈3.03%，即双层玻璃窗比同样多的玻璃材料制成的单层玻璃窗节约热量约为96.97%；双层玻璃的隔声优势为：lge ，根据以上推导的结果，当空气的吸收系数与两片玻璃的距离越大时，双层玻璃窗的隔音效果就越好。

游客节能低碳的交通出行工具安排：（1）长途参观者建议直接或间接购买碳信用额度；（2）对中短途参观者，建议优先选择火车、轮船和长途客车等公共交通方式；（3）对于长三角等周边地区自驾车出行的参观者，建议采用停车换乘（P+R ）方式；（4）对上海城区内的参观者，建议优先选择轨交、公共汽车等公共交通，减少私人汽车的使用；（5）对距世博园区较近的参观者，建议步行或自行车出行。

最后，我们计算了各种出行方式的二氧化碳的排放量后，据此代表上海世博会组委会给游客写了一份倡议书。

关键字：双层玻璃窗隔热效果隔音效果碳足迹目录1、问题重述与分析 (3)1.1、问题重述 (4)1.2、问题分析 (4)2、条件假设 (4)3、符号说明 (4)4、模型的建立及求解 (5)4.1双层玻璃隔热效果探究 (5)4.1.1模型建立 (5)4.1.2、模型的应用 (8)4.2、双层玻璃隔音效果探究 (9)4.2.1、模型建立 (9)4.2.2结果讨论 (11)4.3绿色出行建议 (11)4.3.1碳排放与出行安排 (11)4.3.2倡议书 (15)参考文献 (16)1、问题重述与分析1.1问题重述中国仍处于工业化初期，节能减排具有较大空间。

中国现在是工业排放量占大头，交通和建筑类排放较小。

随着生活水平的提高，建筑节能的比重将逐步上升，有很大发展潜力。

据研究报告称，相关交通工具所使用燃料释放的气体是目前造成全球变暖的主要原因之一。

为此请考虑以下几个问题：1、请用数学模型说明双层（中间有密封空气层）玻璃窗户对单层玻璃窗户的优势以及双层玻璃窗户的隔音效果如何？2、请你为参观上海世博会的各种游客分别设计节能低碳的交通出行工具安排，计算相应二氧化碳的排放量，并据此代表上海世博会组委会给游客一份倡议书。

数学建模软件相关

广西工业职业技术学院教案首页顺序号（）2.双层玻璃的功效一、问题提出冬天，北方室外温度低，室内供暖以便生活工作，为了保暖，即减少室内向室外的热量流失，从而节约能源，常将单层玻璃窗改为双层玻璃窗，即窗户上装两层厚度为d 的玻璃夹着一层厚度为l 的空气，如下图2.1所示。

试建立数学模型说明，当建筑物室内外的热传递处于一个热力学平衡状态时，双层玻璃窗比单层玻璃窗更能有效地减少热量的流失，并问两层玻璃之间的距离多少为好？二、问题分析1．热力学的相关知识为了解决这个问题，首先应想到这是一个属于哪个领域里的问题？应涉及哪些数学知识和相关领域里的知识？此属于热力学的问题，涉及到热传导的理论。

由热力学知道，热量的传递主要有三种方式：热传导、热对流和热辐射。

热传导 : 温度高的物体通过接触将热量传递给温度低的物体的热传递方式，例如汽车发动机的散热。

热传导方式局限于固体和液体，气体之间能量的传递称为热扩散。

热传导的基本公式为“/Q K A T L =⨯⨯∆”。

其中Q 是传导的热量；K 为材料的热传导系数，A 是两物体的接触面积，T ∆是两端的温度差，L 是两端的距离。

因此，从公式我们就可以发现，热量传递的大小同热传导系数、热传热面积成正比，同距离成反比。

室外 T 2 室内 T 1 室外 T 2室内 T 1 图2.2图2.1热对流 :流体(气体或液体)与温度高的固体的表面接触，流动的流体从固体表面将热带走的热传递方式。

例如电脑机箱的散热。

热对流的公式为“/Q H A T L =⨯⨯∆”。

其中Q 是热量，也就是热对流所带走的热量；H 为热对流系数，A 则代表热对流的有效接触面积；T ∆代表固体表面与区域流体之间的温度差。

可以看出，在热对流传递中，热量传递的数量同热对流系数、有效接触面积和温度差成正比关系；热对流系数越高、有效接触面积越大、温度差越高，所能带走的热量也就越多。

热辐射 : 热辐射是一种可以在没有任何介质的情况下，不需要接触，就能够发生热交换（将热能从热源向外界发散出去）的传递方式，热辐射是以波的形式进行热交换。

双层玻璃的功效

双层玻璃的功效问题：双层玻璃与同样多材料的单层玻璃窗相比，减少多少热量损失。

概念图：平面化：设计原理：保持室温恒定不变，比较相同时间内通过双侧玻璃的热量Q1和通过单层玻璃的热量Q2。

前提：单层玻璃的厚度要与双层玻璃（不含中空层）厚度要一致。

假设：1.热量传播中只有传导没有对流。

2.T1，T2不变，热传导过程处于稳态。

3.材料均匀，热传导系数为常数。

说明：保持室温不变为T1，室外温度为T2，在物理学中，物体是有它的热传导系数的，及任何物体都有它的热阻，在上图中及热量通过玻璃，由于玻璃的热阻所消耗的能量。

由热传导定律 TQ kd∆=，由这个式子我们就可以列出在两种情况下损失的热量Q1 ,Q2 建模：Q :单位时间单位面积传导的热量T ∆：温度差，d ：材料厚度，K1：玻璃的热传导系数，K2：空气的热传导系数l ：中空层厚度计算1Q ：单位时间单位面积下通过的热量为Q1，那我们就知道单位时间单位面积，在第一层玻璃、中空层、第二层玻璃通过的热量都是Q1，而温度的损失正是因为热阻存在，在热量通过的热量一定时，热传导系数越大，温差变化就越小。

由 121121a a b b T T T T T TQ K K K d l d---=== 我们消去a T 及b T ，然后用1T 、2T 把1Q 表示出来。

（可以通过手算由第一个等式得出a T ，第三个式子得出b T ，然后把a T 及b T 代入第二个式子与1Q 相等，解出1Q ）这里我们用Mathematic ，消去a T 及b T 解出1Q通过化简，我们得到这样的一个式子1211(2)T T Q K d s -=+其中12K s hK = ， l h d= 计算2Q ：12212T T Q K d-=为了方便比较，我们把1Q 2Q 作比值1222Q Q s =+ 由这个式子我们可以看出，只要s 大于0，那么1Q 一定是小于2Q 的那么s 又与什么有关呢？我们可以轻松的看出来12K l s d K =⨯ 我们先不管l 与d 的比值，我们看12K K ，根据调查玻璃的导热系数1K 比2K 要大很多，常用玻璃的热传导系数1K =34~810(/)J cm s k -⨯⋅⋅干燥空气的热传导系数2K =42.510(/)J cm s k -⨯⋅⋅ S=16~32我们取最小的16，代入比值12181Q Q h =+ l h d= 我们画出12181Q Q h =+函数的图像当双层玻璃的散热只有单层玻璃的3%时，及双层玻璃少散失的热量是97%，这个效果已经很好了这时我们计算出h 应该是多少也就是ld（空气层的宽度与单层玻璃层的厚度比值为4）=4，如果我们想进一步提升保温效果，还可以增加l 来增加保温效果。

数学建模-双层玻璃窗、隔热效果、隔音效果

数学建模-双层玻璃窗、隔热效果、隔音效果摘要：中国仍处于工业化初期，节能减排具有较大空间。

通过对问题一的数学模型进行分析后得到：一般情况下，建筑规范要求d l /≈4。

据此模型可得12/Q Q ≈3.03%，即双层玻璃窗比同样多的玻璃材料制成的单层玻璃窗节约热量约为96.97%；双层玻璃的隔声优势为：lge ，根据以上推导的结果，当空气的吸收系数与两片玻璃的距离越大时，双层玻璃窗的隔音效果就越好。

游客节能低碳的交通出行工具安排：（1）长途参观者建议直接或间接购买碳信用额度；（2）对中短途参观者，建议优先选择火车、轮船和长途客车等公共交通方式；（3）对于长三角等周边地区自驾车出行的参观者，建议采用停车换乘（P+R ）方式；（4）对上海城区内的参观者，建议优先选择轨交、公共汽车等公共交通，减少私人汽车的使用；（5）对距世博园区较近的参观者，建议步行或自行车出行。

最后，我们计算了各种出行方式的二氧化碳的排放量后，据此代表上海世博会组委会给游客写了一份倡议书。

关键字：双层玻璃窗隔热效果隔音效果碳足迹目录1、问题重述与分析 (3)1.1、问题重述 (4)1.2、问题分析 (4)2、条件假设 (4)3、符号说明 (4)4、模型的建立及求解 (5)4.1双层玻璃隔热效果探究 (5)4.1.1模型建立 (5)4.1.2、模型的应用 (8)4.2、双层玻璃隔音效果探究 (9)4.2.1、模型建立 (9)4.2.2结果讨论 (11)4.3绿色出行建议 (11)4.3.1碳排放与出行安排 (11)4.3.2倡议书 (15)参考文献 (16)1、问题重述与分析1.1问题重述中国仍处于工业化初期，节能减排具有较大空间。

中国现在是工业排放量占大头，交通和建筑类排放较小。

随着生活水平的提高，建筑节能的比重将逐步上升，有很大发展潜力。

据研究报告称，相关交通工具所使用燃料释放的气体是目前造成全球变暖的主要原因之一。

为此请考虑以下几个问题：1、请用数学模型说明双层（中间有密封空气层）玻璃窗户对单层玻璃窗户的优势以及双层玻璃窗户的隔音效果如何？2、请你为参观上海世博会的各种游客分别设计节能低碳的交通出行工具安排，计算相应二氧化碳的排放量，并据此代表上海世博会组委会给游客一份倡议书。

数学建模实例-双层玻璃的功效教学提纲

双层玻璃功效问题

数学建模案例分析报告报告材料2.双层玻璃地功效

双层玻璃窗的功效

数学模型 数学论文指导 双层玻璃的功效

双层玻璃的功效

最新数学建模案例分析2双层玻璃的功效

数学建模基础 12.10双层玻璃的功效

初等方法建模1双层玻璃窗的功效--数学建模案例分析

【数学建模实例】双层玻璃的功效

数学建模-双层玻璃窗、隔热效果、隔音效果.

双层玻璃窗的功效

【数学建模学习】双层玻璃的功效

第03讲 双层玻璃窗的功效及确定性存贮模型

数学建模-双层玻璃窗、隔热效果、隔音效果

数学建模软件相关

双层玻璃的功效

数学建模-双层玻璃窗、隔热效果、隔音效果

数学模型数学论文指导双层玻璃的功效

第03讲双层玻璃窗的功效及确定性存贮模型