第三章 运输问题习题
运筹学教材编写组《运筹学》课后习题-运输问题(圣才出品)

第3章 运输问题3.1 判断表3-l 和表3-2中给出的调运方案能否作为用表上作业法求解时的初始解?为什么?表3-1 表3-2解:表3-l 中有5个基格,而要作为初始解,应有m+n-l=3+4-1=6个基格,所以表3-l 给出的调运方案不能作为表上作业法的初始解;表3-2中,有10个数基格,而理论上只应有m+n-l=9个,多出了一个,所以表3-2给出的调运方案不能作为表上作业法的初始解。
3.2 表3-3和表3-4中,分别给出两个运输问题的产销平衡表和单位运价表,试用伏格尔(Vogel)法直接给出近似最优解。
表3-3 表3-4解:(1)第一步:在表3-3中分别求各行和各列的最小运价和次小运价的差额,并分别填入该表的最右列和最下行,如表3-5所示。
表3-5第二步:从行差额或列差额中选出最大者,选择它所在行或列中的最小元素。
在表3-5中,第3列是最大差额所在列。
第3列中最小元素为1,可确定产地2的产品优先供应销地3的需要,得表3-6。
同时将运价表中的第3列数字划去,如表3-7所示。
表3-6 表3-7第三步:对表3-7中未划去的元素再分别计算出各行、各列的最小运价和次小运价的差额,并填入该表的最右列和最下行。
重复第一、二步,直到给出初始解为止,初始解如表3-8所示。
表3-8(2)第一步:在表3-4中分别计算各行和各列的最小运价和次小运价的差额,并分别填入该表的最右列和最下行,如表3-9所示。
表3-9第二步:从行或列差额中选出最大者,选择它所在行或列中的最小元素。
在表3-9中第3列是最大差额所在列。
第3列中最小元素为3,可确定产地1的产品优先供应销地3的需要。
同时将运价表中的第1行数字划去,如表3-10所示。
表3-10第三步:对表3-10中未划去的元素再分别计算出各行、各列的最小运价和次小运价的差额,填入该表的最右列和最下行。
重复第一、二步,直到给出初始解为止,初始解见表3-10的单位运价中格子的右上方方格中的数据。
运筹学(胡运权版)第三章运输问题课后习题答案
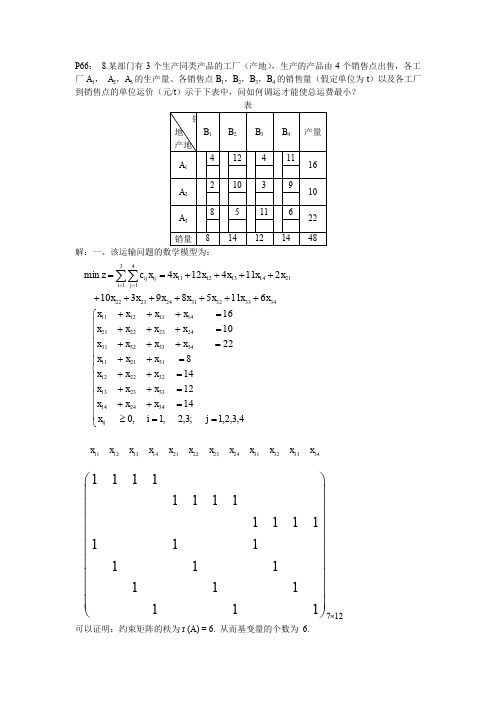
P66: 8.某部门有3个生产同类产品的工厂(产地),生产的产品由4个销售点出售,各工厂A 1, A 2,A 3的生产量、各销售点B 1,B 2,B 3,B 4的销售量(假定单位为t )以及各工厂到销售点的单位运价(元/t )示于下表中,问如何调运才能使总运费最小?表解:一、该运输问题的数学模型为:可以证明:约束矩阵的秩为r (A) = 6. 从而基变量的个数为 6.34333231242322213141141312116115893102114124min x x x x x x x x x x x x x c z i j ij ij +++++++++++==∑∑==⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧==≥=++=++=++=++=+++=+++=+++4,3,2,1;3,2,1,01412148221016342414332313322212312111343332312423222114131211j i x x x x x x x x x x x x x x x x x x x x x x x x x ij 111213142122232431323334x x x x x x x x x x x x 712111111111111111111111111⨯⎛⎫ ⎪⎪⎪ ⎪⎪⎪ ⎪⎪ ⎪⎝⎭二、给出运输问题的初始可行解(初始调运方案)1. 最小元素法思想:优先满足运价(或运距)最小的供销业务。
其余(非基)变量全等于零。
此解满足所有约束条件,且基变量(非零变量)的个数为6(等于m+n-1=3+4-1=6).总运费为(目标函数值) ,1013=x ,821=x ,223=x ,1432=x ,834=x ,614=x ∑∑===3141i j ijij x c Z2. 伏格尔(Vogel)法伏格尔法的基本思想:运输表中各行各列的最小运价与次小运价之差值(罚数)应尽可能地小。
或者说:优先供应罚数最大行(或列)中最小运费的方格,以避免将运量分配到该行(或该列)次小运距的方格中。
第3章运输问题习题3.3表348
3
1 20 7 10 4 0
4
863750
列差
伏格尔法求初始解
销地 甲 乙 丙 丁 戊 巳 行差 产地
1 10 20 5 9 10 0 5
2
2 10 8 30 6 0 2
3
1 20 7 10 4 0 1
4
863750 3
列差 1 4 2 2 1 0
伏格尔法求初始解
销地 甲 乙 丙 丁 戊 巳 行差 产地
1
25
2
4
6
3
2
4
9
销量 4 4 6 2 4 2
伏格尔法求初始解
销地 甲 乙 丙 丁 戊 巳 行差 产地
1 10 20 5 9 10 0 4
2
2 10 8 30 6 0 2
3
1 20 7 10 4 0 3
4
863750 2
列差
4221
伏格尔法求初始解
销地 甲 乙 丙 丁 戊 巳 行差 产地
1 10 20 5 9 10 0 4
3
21 0
0
3
1 20 7 10 4
0 -2
1
14 4
3
0
2
4
8
6
3
7
5
0 -2
8
0
0
0
1
2
vi
2
8
5
9
6
0
结果分析
• 所有检验数都非负,因此已得到最优解。 • 这时,总运费为最少: • 3×5+4×2+2×6+2×4+
4×6+3×3+2×7=90 • 由于存在非基变量检验数为0,故该运输问
(典型例题)《运筹学》运输问题

xj0,yij0,zij0,(i=1,┈,4;j=1,┈,5)
2008/11
--22--
--《Ⅵ 产量
新购 1 第一天 M 第二天 M 第三天 M
第四天 M
1 1 1 1 0 5200
0.2 0.1 0.1 0.1 0 1000
2008/11
--21--
建立模型:
--《运筹学》 运输问题--
设 xj—第j天使用新毛巾的数量;yij—第i天送第j天使用快洗 餐巾的数量;zij—第i天送第j天使用慢洗餐巾的数量;
Min z=∑xj+∑∑0.2yij+∑∑0.1zij
第一天:x1=1000
需 第二天:x2+y12=700
求 约
m1
xij b j (j 1,2,...,n)
i1
x 0 (i 1,...,m,m 1; j 1,...,n) ij
2008/11
--16--
--《运筹学》 运输问题--
销>产问题单位运价表
产地销地 B1 B2 ┈
A1
C11 C12 ┈
A2
C21 C22 ┈
┊ ┆┊┈
Am Cm1 Cm2 ┈
2008/11
--8--
产销平衡表
--《运筹学》 运输问题--
单位运价表
B1 B2 B3 B4 产量
A1 (1) (2) 4 3 7 A2 3 (1) 1 (-1) 4 A3 (10) 6 (12) 3 9 销量 3 6 5 6
B1 B2 B3 B4 A1 3 11 3 10 A2 1 9 2 8 A3 7 4 10 5
Ⅰ Ⅱ
示。又如果生产出来的柴
Ⅲ
第三章 运输问题-转运问题20101029

转运 3
销地 4 5 接收量 40 40
30
10
40 40
40
40 40 60
40
60
运输问题的悖论
在运输问题中,有一种在若干 个产、销地的运价不变的情况下, 当调运量增加,总运费反而会下降 的奇怪现象。这就是运输问题的悖 论
有一位调度员上月做了一个最优调度如 下(检验数全为非正)
B1 A2 A3 bj vj 164 8 -2 4 16 B2 96 5 -6 45 11 9 B3 67 2 2 -1 115 1 8 -2 12 21 B4 138 4 -1 9 -1 8 13 B5 1 6 -1 51 11 15 ai ui 7 18 6 46 -1 5 0 -1 0 -5
1
040
41-M 2-1 1 M
3
2
15-M 040 4 411-M
4
110
M10 40 040 58-M
5
M
320 4 5 040
发送 量
500
70M-1 403 40-1
5
接收量
40M-4
400
401-M 40-3 601
604-M
最优方案
接收 产地 发送 产地 1 2 1 40 40 10 2 转运 销地 3 4 10 20 5 发送 量 50 70
5-10+4=
B4 138 56 105 8 13 11 15 B5
-1
ai 18 6 15 46 ui 0 -1 0 -5
最小调整运量=5,u3+V2=-10+9=-1
7 + 5 -1 5
总运量=56千吨,总运费=409千元
B1 A 1 A 2 A 3 A 4 bj 4 415 11+10 12 8 164 96 B2 B3 612 138 511 10 11 B4 B5 ai 7+5 18 6+5 15 56
运筹学_第3章_运输问题习题
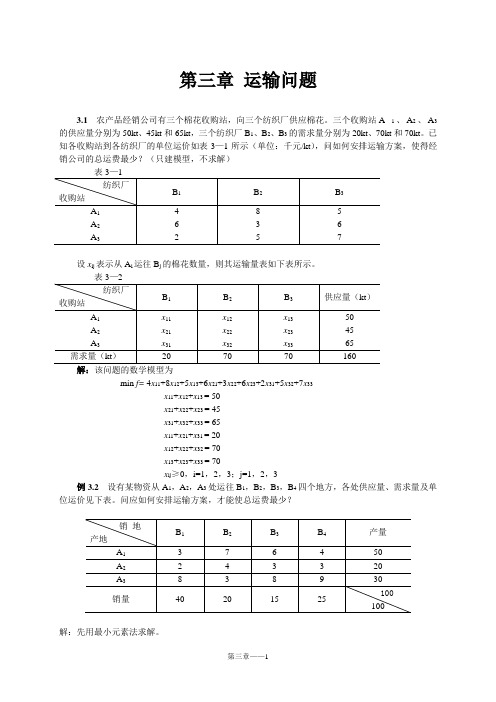
第三章运输问题3.1农产品经销公司有三个棉花收购站,向三个纺织厂供应棉花。
三个收购站A1、A2、A3的供应量分别为50kt、45kt和65kt,三个纺织厂B1、B2、B3的需求量分别为20kt、70kt和70kt。
已知各收购站到各纺织厂的单位运价如表3—1所示(单位:千元/kt),问如何安排运输方案,使得经销公司的总运费最少?(只建模型,不求解)设x ij表示从A i运往B j的棉花数量,则其运输量表如下表所示。
表3—2min f= 4x11+8x12+5x13+6x21+3x22+6x23+2x31+5x32+7x33x11+x12+x13 = 50x21+x22+x23 = 45x31+x32+x33 = 65x11+x21+x31 = 20x12+x22+x32 = 70x13+x23+x33 = 70x ij≥0,i=1,2,3;j=1,2,3例3.2设有某物资从A1,A2,A3处运往B1,B2,B3,B4四个地方,各处供应量、需求量及单位运价见下表。
问应如何安排运输方案,才能使总运费最少?解:先用最小元素法求解。
用位势法对基可行解进行最优性检验。
位势方程组为u1+v1=3 u1+v3=6 u1+v4=4u2+v1=2u3+v2=3u3+v3=8取u1=0,解上述方程组得u1=0u2=-1u3=2v1=3v2=1v3=6v4=4各非基变量的检验数为σ12 =c12-(u1+v2)=7-(0+1)= 4>0σ22 =c22-(u2+v2)=4-(-1+1)= 2>0σ23 =c23-(u2+v3)=3-(-1+6)= -2<0σ24 =c24-(u2+v4)=3-(-1+4)= 0σ31 =c31-(u3+v1)=8-(2+3)= 3>0σ34 =c34-(u3+v4)=9-(2+4)= 3>0由于σ23 =-2<0,故表中基可行解不是最优解。
由于σ该闭回路上,偶数顶点上的基变量最小值为5,以该调整量进行调整得到如表3—11的新的基可行解。
第三章运输问题习题及答案(2012春)

运输问题习题1.甲、乙、丙三个城市每年分别需要煤炭320、250、350吨,由A 、B 两处煤矿负责供应。
已知煤炭年供应量为A ——400万吨,B ——450万吨。
由煤矿至各城市的单位运价(万元/万吨)。
见表1:由于需大于供,经研究平衡决定,甲城市供应量可减少0~30万吨,乙城市需要量应全部满足,丙城市供应量不少于270万吨。
试求将供应量分配完又使总运费为最低的调运方案。
2.已知运输问题的产销平衡表、单位运价表及最优调运方案分别见表2和表3。
(1) 从A 2→B2的单位运价C 22在什么范围内变化时,上述最优调运方案不变?提示: 只需检验数220σ≥(2) A 2→B4的单位运价C 24变为何值时,有无穷多最优调运方案。
提示: 检验数242424()c u v σ=-+=03.试分析分别发生下列情况时,运输问题的最优调运方案及总运价有何变化.(a) 单位运价表第i 行的每个ij c 都加上一个常数λ;对于任意基变量的检验数,在没加常数λ以前,有 ij ij i j c u v σ=--加常数后令**,i i j j u u v v λ==+,那么基变量的检验数等于***()()ij ij i j ij i j ij c u v c u v σλσ=+-+=--=也就是检验数没有变化,因而最优调运方案没有变化 (b) 单位运价表第j 列的每个ij c 都加上一个常数λ; 对于第j 列基变量的检验数,在没加常数λ以前,有 ij ij i j c u v σ=--加常数后令**,i i j j u u v v λ==+,那么基变量的检验数等于***()()ij ij i j ij i j ij c u v c u v σλσ=+-+=--=又由于其它列的位势不改变,因而检验数也不改变 也就是检验数没有变化,因而最优调运方案没有变化 (c) 单位运价表所有ij c 都乘上一个常数λ。
对于第j 列基变量的检验数,在没加常数λ以前,有 ij ij i j c u v σ=--加常数后令**,i i j j u u v v λλ==,那么基变量的检验数等于***()()()ij ij i j ij i j ij c u v c u v σλλλσ=-+=--= 因此,当0λ≥时检验数的符号没有改变,因而最优调运方案没有变化;而0λ<时检验数的符号改变,因而最优调运方案变化。
第三章运输问题习题

第三章 运输问题一、疑问:运输问题中,若出现退化情形,应该在什么地方补0? 答:为了使产销平衡表上有(m + n - 1)个数字格,这时需要添加“0”,它的位置可以对应同时划去的那行或那列的任一空格处。
(这时填数字格不构成闭回路) 二、判断下列说法是否正确 :(a) 运输问题是一种特殊的线性规划模型,因而求解结果也可能出现下列情况之一:有唯一最优解、有无穷多最优解、无界解和无可行解;(b) 在运输问题中,只要给出一组含(m + n –1)个非负的{x ij },且满足axinj ij=∑=1,bxjm i ij=∑=1,就可以作为一个初始基可行解;(c) 表上作业法实质上就是求解运输问题的单纯形法; (d) 按最小元素法(或伏格尔法)给出的初始基可行解,从每一空格出发可以找出而且仅能找出唯一的闭回路; (e) 如果运输问题的单位运价表的某一行(或某一列)元素分别加上一个常数k ,最优调运方案将不会发生变化; (f) 如果运输问题的单位运价表的某一行(或某一列)元素分别乘上一个常数k ,最优调运方案将不会发生变化; 三、选择:1.在产销平衡运输问题中,设产地为m 个,销地为n 个,那么解中非零变量的个数()。
A.不能大于(m+n-1);B.不能小于(m+n-1);C.等于(m+n-1);D.不确定。
2.在运输问题中,每次迭代时,如果有某非基变量的检验数等于零,则该运输问题()。
A.无最优解;B.有无穷多个最优解;C.有唯一最优解;D.出现退化解。
四、判断表(a),(b),(c)中给出的调运方案能否作为作业法求解时的初始解,为什么?表(a)表(b)表(c)解:(a) 可以作为初始方案。
(b) 中非零元素小于9(产地+销地-1),不能作为初始方案。
(c) 中存在以非零元素为顶点的闭回路,不能作为初始方案。
五、已知某运输问题的产销平衡表,单位运价表及给出的一个调运方案分别见下表。
判断所给出的调运方案是否为最优?如是,说明理由,如否,也说明理由。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章 运输问题复习参考试题
1、判断表1到表2中给出的调运方案能否作为用表上作业法求解的初始解?为什么?
表1
表2
解:初始解的个数为 m+n-1
表1 初始解个数 = 5 ; m+n-1 = 6 所以不能。
表2 初始解个数 = 10 ;
m+n-1 = 9 所以不能。
2、 用表上作业法求表3到表5中给出的运输问题的最优解(表中数字M 为任意大正数)。
表3
解:用最大差额法
得初始解,并计算位势和检验数
检验数:
∵不全非负,∴没达到最优解, 用闭回路法: ij r
检验数:
最优解: Z * = 3×3+7×0+4×2+0×4+2×3+3×3 = 32
表4
解:
最小元素法,初始方案,
闭回路法得,
再用闭回路法得, 所有检验数非负
Zmin = 10×3+6×2+7×1+5×3+9×6+6×2= 130
表5
表中供大于求,虚设一销售点
最大差额法:
得:
检验数非负,
Zmin = 5×3+0×2+2×4+6×2+0×0+4×2+6×4+3×3+7×2
3、已知运输问题的产销平衡表及最优调运方案分别见表6。
表6 产销平衡表及最优调运方案
(1) 从A2→B2的单位运价C22在什么范围变化时,上述最优调运方案不变?
(2) A2→B4的单位运价C24变为何值时,有无穷多最优调运方案,除表6中方案外,至少再写出其它两个。
解:
1) 最优调运方案不变,则检验数还非负。
解不等式
220310ij r C ≥⇒≤≤2)非基变量检验数有一个为0,基变量检验数都为0.
11221432112222333140
1611412671932
11
u u v u u v u u v v u v v u v v u v v =⎧+=⎧⎪
=⎪⎪+=⎪⎪=−⎪+=⎪⎪⇒=⎨⎨+=⎪⎪=⎪⎪+=⎪⎪+=⎪⎪⎩=⎩令=
非基变量检验数为:
1113242424323334100642003176111714411716431841111r r r C C r r r =−+==−+==−+=−=−−+==−−+=−−+
=()()()()()=17()
240,17C ∴==24令r 即,2417A B ∴→当的单位运价变为时,有无穷多最优调运方案。
闭回路法进行调整:
○
1以(A 2B 4)点为起点,
○
2以 A 3B 2点为起点,。
