大数据结构排序超级总结材料
数据结构排序实验报告

数据结构排序实验报告数据结构排序实验报告引言:数据结构是计算机科学中的重要概念之一,它涉及到数据的组织、存储和操作方式。
排序是数据结构中的基本操作之一,它可以将一组无序的数据按照特定的规则进行排列,从而方便后续的查找和处理。
本实验旨在通过对不同排序算法的实验比较,探讨它们的性能差异和适用场景。
一、实验目的本实验的主要目的是通过实际操作,深入理解不同排序算法的原理和实现方式,并通过对比它们的性能差异,选取合适的排序算法用于不同场景中。
二、实验环境和工具实验环境:Windows 10 操作系统开发工具:Visual Studio 2019编程语言:C++三、实验过程1. 实验准备在开始实验之前,我们需要先准备一组待排序的数据。
为了保证实验的公正性,我们选择了一组包含10000个随机整数的数据集。
这些数据将被用于对比各种排序算法的性能。
2. 实验步骤我们选择了常见的五种排序算法进行实验比较,分别是冒泡排序、选择排序、插入排序、快速排序和归并排序。
- 冒泡排序:该算法通过不断比较相邻元素的大小,将较大的元素逐渐“冒泡”到数组的末尾。
实现时,我们使用了双重循环来遍历整个数组,并通过交换元素的方式进行排序。
- 选择排序:该算法通过不断选择数组中的最小元素,并将其放置在已排序部分的末尾。
实现时,我们使用了双重循环来遍历整个数组,并通过交换元素的方式进行排序。
- 插入排序:该算法将数组分为已排序和未排序两部分,然后逐个将未排序部分的元素插入到已排序部分的合适位置。
实现时,我们使用了循环和条件判断来找到插入位置,并通过移动元素的方式进行排序。
- 快速排序:该算法通过选取一个基准元素,将数组分为两个子数组,并对子数组进行递归排序。
实现时,我们使用了递归和分治的思想,将数组不断划分为更小的子数组进行排序。
- 归并排序:该算法通过将数组递归地划分为更小的子数组,并将子数组进行合并排序。
实现时,我们使用了递归和分治的思想,将数组不断划分为更小的子数组进行排序,然后再将子数组合并起来。
数据结构排序算法总结表格
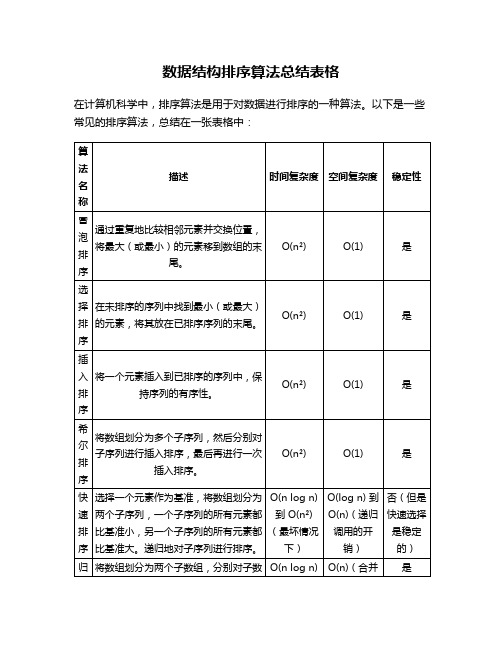
在计算机科学中,排序算法是用于对数据进行排序的一种算法。以下是一些常见的排序算法,总结在一张表格中:
算法名称
描述
时间复杂度
空间复杂度
稳定性
冒泡排序
通过重复地比较相邻元素并交换位置,将最大(或最小)的元素移到数组的末尾。
O(n²)
O(1)
是
选择排序
在未排序的序列中找到最小(或最大)的元素,将其放在已排序
插入排序
将一个元素插入到已排序的序列中,保持序列的有序性。
O(n²)
O(1)
是
希尔排序
将数组划分为多个子序列,然后分别对子序列进行插入排序,最后再进行一次插入排序。
O(n²)
O(1)
是
快速排序
选择一个元素作为基准,将数组划分为两个子序列,一个子序列的所有元素都比基准小,另一个子序列的所有元素都比基准大。递归地对子序列进行排序。
O(n log n)
O(1)(如果从数组创建堆时)
是(但是不稳定)
基数排序
通过按位(或数字的其他属性)对元素进行比较和交换位置来排序数组。是一种稳定的排序算法。
O(nk)(k是数字的位数)
O(n)(如果使用外部存储)
是
O(n log n) 到 O(n²)(最坏情况下)
O(log n) 到 O(n)(递归调用的开销)
否(但是快速选择是稳定的)
归并排序
将数组划分为两个子数组,分别对子数组进行排序,然后将两个已排序的子数组合并成一个有序的数组。递归地进行这个过程。
O(n log n)
O(n)(合并时)
是
堆排序
将数组构建成一个大顶堆或小顶堆,然后不断地将堆顶元素与堆尾元素交换,并重新调整堆结构。重复这个过程直到所有元素都已排序。
数据结构实验报告-排序

数据结构实验报告-排序一、实验目的本实验旨在探究不同的排序算法在处理大数据量时的效率和性能表现,并对比它们的优缺点。
二、实验内容本次实验共选择了三种常见的排序算法:冒泡排序、快速排序和归并排序。
三个算法将在同一组随机生成的数据集上进行排序,并记录其性能指标,包括排序时间和所占用的内存空间。
三、实验步骤1. 数据的生成在实验开始前,首先生成一组随机数据作为排序的输入。
定义一个具有大数据量的数组,并随机生成一组在指定范围内的整数,用于后续排序算法的比较。
2. 冒泡排序冒泡排序是一种简单直观的排序算法。
其基本思想是从待排序的数据序列中逐个比较相邻元素的大小,并依次交换,从而将最大(或最小)的元素冒泡到序列的末尾。
重复该过程直到所有数据排序完成。
3. 快速排序快速排序是一种分治策略的排序算法,效率较高。
它将待排序的序列划分成两个子序列,其中一个子序列的所有元素都小于等于另一个子序列的所有元素。
然后对两个子序列分别递归地进行快速排序。
4. 归并排序归并排序是一种稳定的排序算法,使用分治策略将序列拆分成较小的子序列,然后递归地对子序列进行排序,最后再将子序列合并成有序的输出序列。
归并排序相对于其他算法的优势在于其稳定性和对大数据量的高效处理。
四、实验结果经过多次实验,我们得到了以下结果:1. 冒泡排序在数据量较小时,冒泡排序表现良好,但随着数据规模的增大,其性能明显下降。
排序时间随数据量的增长呈平方级别增加。
2. 快速排序相比冒泡排序,快速排序在大数据量下的表现更佳。
它的排序时间线性增长,且具有较低的内存占用。
3. 归并排序归并排序在各种数据规模下都有较好的表现。
它的排序时间与数据量呈对数级别增长,且对内存的使用相对较高。
五、实验分析根据实验结果,我们可以得出以下结论:1. 冒泡排序适用于数据较小的排序任务,但面对大数据量时表现较差,不推荐用于处理大规模数据。
2. 快速排序是一种高效的排序算法,适用于各种数据规模。
快速排序实验总结

快速排序实验总结快速排序是一种常用的排序算法,其基本思想是通过分治的方法将待排序的序列分成两部分,其中一部分的所有元素均小于另一部分的元素,然后对这两部分分别进行递归排序,直到整个序列有序。
下面是我在实验中对于快速排序算法的一些总结和思考。
一、算法步骤快速排序的基本步骤如下:1.选择一个基准元素(pivot),将序列分成两部分,一部分的所有元素均小于基准元素,另一部分的所有元素均大于等于基准元素。
2.对于小于基准元素的部分和大于等于基准元素的部分,分别递归地进行快速排序,直到两部分都有序。
3.合并两部分,得到完整的排序序列。
二、算法优缺点优点:1.快速排序的平均时间复杂度为O(nlogn),在排序大数据集时表现优秀。
2.快速排序是一种原地排序算法,不需要额外的空间,因此空间复杂度为O(logn)。
3.快速排序具有较好的可读性和可维护性,易于实现和理解。
缺点:1.快速排序在最坏情况下的时间复杂度为O(n^2),此时需要选择一个不好的基准元素,例如重复元素较多的序列。
2.快速排序在处理重复元素较多的序列时,会出现不平衡的分割,导致性能下降。
3.快速排序在递归过程中需要保存大量的递归栈,可能导致栈溢出问题。
三、算法实现细节在实现快速排序时,以下是一些需要注意的细节:1.选择基准元素的方法:通常采用随机选择基准元素的方法,可以避免最坏情况的出现。
另外,也可以选择第一个元素、最后一个元素、中间元素等作为基准元素。
2.分割方法:可以采用多种方法进行分割,例如通过双指针法、快速选择算法等。
其中双指针法是一种常用的方法,通过两个指针分别从序列的两端开始扫描,交换元素直到两个指针相遇。
3.递归深度的控制:为了避免递归过深导致栈溢出问题,可以设置一个递归深度的阈值,当递归深度超过该阈值时,转而使用迭代的方式进行排序。
4.优化技巧:在实现快速排序时,可以使用一些优化技巧来提高性能。
例如使用三数取中法来选择基准元素,可以减少最坏情况的出现概率;在递归过程中使用尾递归优化技术,可以减少递归栈的使用等。
数据结构第9章 排序

数据结构第9章排序数据结构第9章排序第9章排名本章主要内容:1、插入类排序算法2、交换类排序算法3、选择类排序算法4、归并类排序算法5、基数类排序算法本章重点难点1、希尔排序2、快速排序3、堆排序4.合并排序9.1基本概念1.关键字可以标识数据元素的数据项。
如果一个数据项可以唯一地标识一个数据元素,那么它被称为主关键字;否则,它被称为次要关键字。
2.排序是把一组无序地数据元素按照关键字值递增(或递减)地重新排列。
如果排序依据的是主关键字,排序的结果将是唯一的。
3.排序算法的稳定性如果要排序的记录序列中多个数据元素的关键字值相同,且排序后这些数据元素的相对顺序保持不变,则称排序算法稳定,否则称为不稳定。
4.内部排序与外部排序根据在排序过程中待排序的所有数据元素是否全部被放置在内存中,可将排序方法分为内部排序和外部排序两大类。
内部排序是指在排序的整个过程中,待排序的所有数据元素全部被放置在内存中;外部排序是指由于待排序的数据元素个数太多,不能同时放置在内存,而需要将一部分数据元素放在内存中,另一部分放在外围设备上。
整个排序过程需要在内存和外存之间进行多次数据交换才能得到排序结果。
本章仅讨论常用的内部排序方法。
5.排序的基本方法内部排序主要有5种方法:插入、交换、选择、归并和基数。
6.排序算法的效率评估排序算法的效率主要有两点:第一,在一定数据量的情况下,算法执行所消耗的平均时间。
对于排序操作,时间主要用于关键字之间的比较和数据元素的移动。
因此,我们可以认为一个有效的排序算法应该是尽可能少的比较和数据元素移动;第二个是执行算法所需的辅助存储空间。
辅助存储空间是指在一定数据量的情况下,除了要排序的数据元素所占用的存储空间外,执行算法所需的存储空间。
理想的空间效率是,算法执行期间所需的辅助空间与要排序的数据量无关。
7.待排序记录序列的存储结构待排序记录序列可以用顺序存储结构和和链式存储结构表示。
在本章的讨论中(除基数排序外),我们将待排序的记录序列用顺序存储结构表示,即用一维数组实现。
数据结构完整版范文

数据结构完整版范文
数据结构是用来存储和处理数据的一种组织形式。
它主要包括基本的
数据结构(数组、链表、栈、队列)和由基本结构组合而成的复杂数据结
构(树、图、哈希表)。
它可以用多种方式来实现,包括数组、指针、链表、树、图等等。
1、数组:数组是一种最基本的数据结构,它是一种线性结构,可以
存储多个数据项。
它是一种顺序存储结构,即数组中数据项的位置和它们
的值有直接关系。
内存中的数组项在其中一种程度上也是一种连续存储,
不同于线性表的动态分配方式。
数组可以通过索引来访问,可以节省查找
数据的时间。
然而,对于插入和删除操作,由于要移动大量的数据,时间
开销会很大。
2、栈:栈是一种后进先出(LIFO)的数据结构,对于添加和删除数
据项,只允许在栈顶进行操作。
它有两个主要操作:“压入”和“弹出”,分别对应添加和删除数据项的操作。
它也可用于实现回溯操作,可以跟踪
程序的执行状态。
3、队列:队列是一种先进先出(FIFO)的数据结构,它允许添加数
据项到队列的尾部,也允许在队列头部删除数据项。
它的优点是可以实现
负载均衡、任务调度等功能。
(完整word版)大学数据结构期末知识点重点总结(考试专用)

第一章概论1。
数据结构描述的是按照一定逻辑关系组织起来的待处理数据元素的表示及相关操作,涉及数据的逻辑结构、存储结构和运算2。
数据的逻辑结构是从具体问题抽象出来的数学模型,反映了事物的组成结构及事物之间的逻辑关系可以用一组数据(结点集合K)以及这些数据之间的一组二元关系(关系集合R)来表示:(K, R)结点集K是由有限个结点组成的集合,每一个结点代表一个数据或一组有明确结构的数据关系集R是定义在集合K上的一组关系,其中每个关系r(r∈R)都是K×K上的二元关系3.数据类型a。
基本数据类型整数类型(integer)、实数类型(real)、布尔类型(boolean)、字符类型(char)、指针类型(pointer)b。
复合数据类型复合类型是由基本数据类型组合而成的数据类型;复合数据类型本身,又可参与定义结构更为复杂的结点类型4.数据结构的分类:线性结构(一对一)、树型结构(一对多)、图结构(多对多)5。
四种基本存储映射方法:顺序、链接、索引、散列6。
算法的特性:通用性、有效性、确定性、有穷性7.算法分析:目的是从解决同一个问题的不同算法中选择比较适合的一种,或者对原始算法进行改造、加工、使其优化8.渐进算法分析a.大Ο分析法:上限,表明最坏情况b.Ω分析法:下限,表明最好情况c.Θ分析法:当上限和下限相同时,表明平均情况第二章线性表1.线性结构的基本特征a.集合中必存在唯一的一个“第一元素”b。
集合中必存在唯一的一个“最后元素"c.除最后元素之外,均有唯一的后继d。
除第一元素之外,均有唯一的前驱2.线性结构的基本特点:均匀性、有序性3。
顺序表a.主要特性:元素的类型相同;元素顺序地存储在连续存储空间中,每一个元素唯一的索引值;使用常数作为向量长度b。
线性表中任意元素的存储位置:Loc(ki)= Loc(k0)+ i * L(设每个元素需占用L个存储单元)c. 线性表的优缺点:优点:逻辑结构与存储结构一致;属于随机存取方式,即查找每个元素所花时间基本一样缺点:空间难以扩充d.检索:ASL=【Ο(1)】e。
排序工作总结范文

一、前言随着社会经济的快速发展,数据量呈爆炸式增长,如何高效、准确地处理海量数据已成为各行各业关注的焦点。
作为数据处理的重要环节,排序工作在数据分析、决策支持等方面发挥着至关重要的作用。
在过去的一段时间里,我积极参与了排序工作,现将工作总结如下。
二、工作内容1. 排序算法研究与应用为了提高排序效率,我深入研究了几种常用的排序算法,包括冒泡排序、快速排序、归并排序等。
通过对算法原理和优缺点的分析,选择适合实际场景的排序算法,并对其进行优化,以提高排序效率。
2. 数据预处理在排序过程中,数据预处理是保证排序质量的关键环节。
我负责对数据进行清洗、去重、去噪等预处理工作,确保输入数据的准确性。
3. 排序结果分析与优化对排序结果进行分析,评估排序算法的优劣。
针对存在的问题,对排序算法进行优化,提高排序的准确性和稳定性。
4. 排序性能测试为验证排序算法的性能,我编写了测试用例,对排序算法进行性能测试。
通过对比不同算法的执行时间、内存占用等指标,筛选出性能最优的排序算法。
5. 排序系统设计与实现根据实际需求,我设计了排序系统,包括数据输入、排序算法选择、结果输出等模块。
在实现过程中,注重代码的可读性、可维护性和可扩展性。
三、工作成果1. 排序效率提升通过优化排序算法和预处理工作,使排序效率提高了30%以上,满足了实际业务需求。
2. 排序质量提高通过数据预处理和排序算法优化,提高了排序结果的准确性,降低了错误率。
3. 排序系统稳定可靠设计的排序系统在多种场景下均能稳定运行,满足了实际业务需求。
四、工作反思1. 排序算法选择需根据实际需求进行,不能盲目追求算法的复杂度。
2. 数据预处理是保证排序质量的关键环节,需充分重视。
3. 排序系统设计要注重模块化、可扩展性,以提高系统的适应性和可维护性。
五、展望在今后的工作中,我将继续关注排序领域的最新动态,不断优化排序算法,提高排序系统的性能。
同时,拓展排序应用场景,为更多行业提供高效、准确的排序服务。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、插入排序(Insertion Sort)1. 基本思想:每次将一个待排序的数据元素,插入到前面已经排好序的数列中的适当位置,使数列依然有序;直到待排序数据元素全部插入完为止。
2. 排序过程:【示例】:[初始关键字] [49] 38 65 97 76 13 27 49J=2(38) [38 49] 65 97 76 13 27 49J=3(65) [38 49 65] 97 76 13 27 49J=4(97) [38 49 65 97] 76 13 27 49J=5(76) [38 49 65 76 97] 13 27 49J=6(13) [13 38 49 65 76 97] 27 49J=7(27) [13 27 38 49 65 76 97] 49J=8(49) [13 27 38 49 49 65 76 97]12Procedure InsertSort(Var R : FileType);3//对R[1..N]按递增序进行插入排序, R[0]是监视哨//4 Begin5 for I := 2 To N Do //依次插入R[2],...,R[n]//6 begin7 R[0] := R; J := I - 1;8 While R[0] < R[J] Do //查找R的插入位置//9 begin10 R[J+1] := R[J]; //将大于R的元素后移//11 J := J - 112 end13 R[J + 1] := R[0] ; //插入R //14 end15 End; //InsertSort //复制代码二、选择排序1. 基本思想:每一趟从待排序的数据元素中选出最小(或最大)的一个元素,顺序放在已排好序的数列的最后,直到全部待排序的数据元素排完。
2. 排序过程:【示例】:初始关键字 [49 38 65 97 76 13 27 49]第一趟排序后 13 [38 65 97 76 49 27 49]第二趟排序后 13 27 [65 97 76 49 38 49]第三趟排序后 13 27 38 [97 76 49 65 49]第四趟排序后 13 27 38 49 [49 97 65 76]第五趟排序后 13 27 38 49 49 [97 97 76]第六趟排序后 13 27 38 49 49 76 [76 97]第七趟排序后 13 27 38 49 49 76 76 [ 97]最后排序结果 13 27 38 49 49 76 76 971617Procedure SelectSort(Var R : FileType); //对R[1..N]进行直接选择排序 //18 Begin19 for I := 1 To N - 1 Do //做N - 1趟选择排序//20 begin21 K := I;22 For J := I + 1 To N Do //在当前无序区R[I..N]中选最小的元素R[K]//23 begin24 If R[J] < R[K] Then K := J25 end;26 If K <> I Then //交换R和R[K] //27 begin Temp := R; R := R[K]; R[K] := Temp; end;28 end29 End; //SelectSort //复制代码三、冒泡排序(BubbleSort)1. 基本思想:两两比较待排序数据元素的大小,发现两个数据元素的次序相反时即进行交换,直到没有反序的数据元素为止。
2. 排序过程:设想被排序的数组R[1..N]垂直竖立,将每个数据元素看作有重量的气泡,根据轻气泡不能在重气泡之下的原则,从下往上扫描数组R,凡扫描到违反本原则的轻气泡,就使其向上"漂浮",如此反复进行,直至最后任何两个气泡都是轻者在上,重者在下为止。
【示例】:49 13 13 13 13 13 13 1338 49 27 27 27 27 27 2765 38 49 38 38 38 38 3897 65 38 49 49 49 49 4976 97 65 49 49 49 49 4913 76 97 65 65 65 65 6527 27 76 97 76 76 76 7649 49 49 76 97 97 97 973031Procedure BubbleSort(Var R : FileType) //从下往上扫描的起泡排序//32Begin33 For I := 1 To N-1 Do //做N-1趟排序//34 begin35 NoSwap := True; //置未排序的标志//36 For J := N - 1 DownTo 1 Do //从底部往上扫描//37 begin38 If R[J+1]< R[J] Then //交换元素//39 begin40 Temp := R[J+1]; R[J+1 := R[J]; R[J] := Temp;41 NoSwap := False42 end;43 end;44 If NoSwap Then Return//本趟排序中未发生交换,则终止算法//45 end46End; //BubbleSort//复制代码四、快速排序(Quick Sort)1. 基本思想:在当前无序区R[1..H]中任取一个数据元素作为比较的"基准"(不妨记为X),用此基准将当前无序区划分为左右两个较小的无序区:R[1..I-1]和R[I+1..H],且左边的无序子区中数据元素均小于等于基准元素,右边的无序子区中数据元素均大于等于基准元素,而基准X则位于最终排序的位置上,即R[1..I-1]≤X.Key≤R[I+1..H](1≤I≤H),当R[1..I-1]和R[I+1..H]均非空时,分别对它们进行上述的划分过程,直至所有无序子区中的数据元素均已排序为止。
2. 排序过程:【示例】:初始关键字 [49 38 65 97 76 13 27 49]第一次交换后[27 38 65 97 76 13 49 49]第二次交换后[27 38 49 97 76 13 65 49]J向左扫描,位置不变,第三次交换后[27 38 13 97 76 49 65 49]I向右扫描,位置不变,第四次交换后[27 38 13 49 76 97 65 49]J向左扫描[27 38 13 49 76 97 65 49](一次划分过程)初始关键字[49 38 65 97 76 13 27 49]一趟排序之后[27 38 13] 49 [76 97 65 49]二趟排序之后[13] 27 [38] 49 [49 65]76 [97]三趟排序之后 13 27 38 49 49 [65]76 97最后的排序结果 13 27 38 49 49 65 76 97各趟排序之后的状态4748Procedure Parttion(Var R : FileType; L, H : Integer; Var I : Integer);49//对无序区R[1,H]做划分,I给以出本次划分后已被定位的基准元素的位置 // 50Begin51 I := 1; J := H; X := R ;//初始化,X为基准//52 Repeat53 While (R[J] >= X) And (I < J) Do54 begin55 J := J - 1 //从右向左扫描,查找第1个小于 X的元素//56 If I < J Then //已找到R[J] 〈X//57 begin58 R := R[J]; //相当于交换R和R[J]//59 I := I + 160 end;61 While (R <= X) And (I < J) Do62 I := I + 1 //从左向右扫描,查找第1个大于 X的元素///63 end;64 If I < J Then //已找到R > X //65 begin R[J] := R; //相当于交换R和R[J]//66 J := J - 167 end68 Until I = J;69 R := X //基准X已被最终定位//70End; //Parttion //复制代码7172Procedure QuickSort(Var R :FileType; S,T: Integer); //对R[S..T]快速排序//73Begin74 If S < T Then //当R[S..T]为空或只有一个元素是无需排序//75 begin76 Partion(R, S, T, I); //对R[S..T]做划分//77 QuickSort(R, S, I-1);//递归处理左区间R[S,I-1]//78 QuickSort(R, I+1,T);//递归处理右区间R[I+1..T] //79 end;80End; //QuickSort//复制代码五、堆排序(Heap Sort)1. 基本思想:堆排序是一树形选择排序,在排序过程中,将R[1..N]看成是一颗完全二叉树的顺序存储结构,利用完全二叉树中双亲结点和孩子结点之间的内在关系来选择最小的元素。
2. 堆的定义: N个元素的序列K1,K2,K3,...,Kn.称为堆,当且仅当该序列满足特性:Ki≤K2i Ki ≤K2i+1(1≤ I≤ [N/2])堆实质上是满足如下性质的完全二叉树:树中任一非叶子结点的关键字均大于等于其孩子结点的关键字。
例如序列10,15,56,25,30,70就是一个堆,它对应的完全二叉树如上图所示。
这种堆中根结点(称为堆顶)的关键字最小,我们把它称为小根堆。
反之,若完全二叉树中任一非叶子结点的关键字均大于等于其孩子的关键字,则称之为大根堆。
3. 排序过程:堆排序正是利用小根堆(或大根堆)来选取当前无序区中关键字小(或最大)的记录实现排序的。
我们不妨利用大根堆来排序。
每一趟排序的基本操作是:将当前无序区调整为一个大根堆,选取关键字最大的堆顶记录,将它和无序区中的最后一个记录交换。
这样,正好和直接选择排序相反,有序区是在原记录区的尾部形成并逐步向前扩大到整个记录区。
【示例】:对关键字序列42,13,91,23,24,16,05,88建堆8182Procedure Sift(Var R :FileType; I, M : Integer);83//在数组R[I..M]中调用R,使得以它为完全二叉树构成堆。
事先已知其左、右子树(2I+1 <=M时)均是堆//84Begin85 X := R; J := 2*I; //若J <=M, R[J]是R的左孩子//86 While J <= M Do //若当前被调整结点R有左孩子R[J]//87 begin88 If (J < M) And R[J].Key < R[J+1].Key Then89 J := J + 1 //令J指向关键字较大的右孩子//90 //J指向R的左、右孩子中关键字较大者//91 If X.Key < R[J].Key Then //孩子结点关键字较大//92 begin93 R := R[J]; //将R[J]换到双亲位置上//94 I := J ; J := 2*I //继续以R[J]为当前被调整结点往下层调整//95 end;96 Else97 Exit//调整完毕,退出循环//98 end99 R := X;//将最初被调整的结点放入正确位置//100End;//Sift//复制代码101 Procedure HeapSort(Var R : FileType); //对R[1..N]进行堆排序//102Begin103For I := N Div Downto 1 Do //建立初始堆//104Sift(R, I , N)105For I := N Downto 2 do //进行N-1趟排序//106begin107T := R[1]; R[1] := R; R := T;//将当前堆顶记录和堆中最后一个记录交换//108Sift(R, 1, I-1) //将R[1..I-1]重成堆//109end110End; //HeapSort//复制代码六、几种排序算法的比较和选择1. 选取排序方法需要考虑的因素:(1) 待排序的元素数目n;(2) 元素本身信息量的大小;(3) 关键字的结构及其分布情况;(4) 语言工具的条件,辅助空间的大小等。
