同济大学朱慈勉 结构力学 第3章习题答案
最新完整的结构力学答案-同济大学朱慈勉
C 10kN
D
A
40kN·m
6m
精品文档
3m
精品文档
M 30
30 30
Q 10
210
(c)
2kN/m 4kN
B
C
6kN
A
D
6m
M 6
6
3m
3m
10 110
Q
5
4
7
2
2m 2m
(d)
4kN·m 2kN
C
D
E 2kN
A
B
6m
精品文档
精品文档
M 4
4 N
0
Q
4 4 4 4/3
0
0
(e)
C
1kN/m 4m
2
qa 2
q
G
H
qa2 IJ
B
C
a
a
3qa 2 2
qa 2
a
3qa 2 2
qa 2 2
a
对H点求矩：
qa 2
qa 2 2
HC
a
HC
1.5qa()
对F点求矩：
qa 1.5a H A a 0 H A 1.5qa() H D 0, MGF qa2, MGH 1.5qa2
qa 2
qa 2 2
xB
1 EI
M ( )M ( )ds
1
2
qR2(1 cos )R sin Rd
1
qR 4 ()
EI 0
2EI
5-7 试用图乘法计算图示梁和刚架的位移：（a） ΔyC ；（b） ΔyD ；（c） ΔxC ；（d） ΔxE ；（e） D ；（f） ΔyE 。 (a)
同济结构力学3-6章习题共14页文档
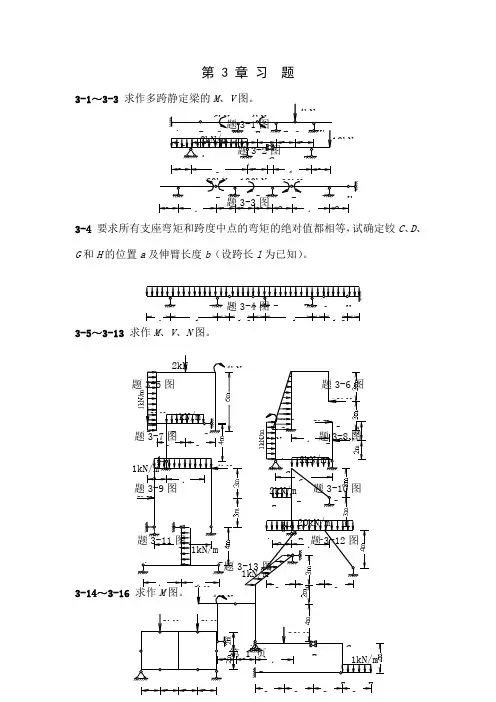
第 3 章 习 题3-1～3-3 3-2题3-3图3-4 要求所有支座弯矩和跨度中点的弯矩的绝对值都相等，试确定铰C 、D 、G 和H 的位置a 及伸臂长度b （设跨长l 为已知）。
3-4图 3-5～3-13 求作M 、V 、N 图。
3-5 3-6图3-8图3-10图图3-14～3-16AE2m6m2m 4m 2m B CD2m4m 2m 2m 2m 4m 2mB D E FG H 2m b B C D EF G Hla l -2a ala l -2aa A 3m10kN40kN 2kN C 2kN4kN A C 4kN D 1kN/m3m 8kN20kN题3-14图题3-15图3-17求图示三铰拱的支座反力。
题3-18图3-18求图示圆弧形三铰拱的支座反力及、剪力F Q D及轴力F N D。
3-19，试求截面D的弯矩M D、剪力F Q D及轴力F N D。
3-19图3-20D、F Q D、F N D及E点左、右截面的剪力3-21～3-22求合理拱轴。
3-23题3-24～3-29用图解法求指定各杆轴力。
)(42xlxlfy-=Q EF3m3m2m2m2m20kN/m4m4m100kN/m4m4mx8mq题3-243-30～试选用两种途径解求指定杆轴力。
题图 3-34～3-37～ 图3-39～试选定求解杆件轴力的合适步骤。
A C 4a A 4×A B C题3-39图题3-40图 题3-41图题3-42图 题3-43图3-44 分别指出桁架各弦杆、各腹杆中受拉、受压的最大值发生在何处。
题3-44图3-45～3-46 求解组合结构中链杆轴力和受弯杆弯矩图。
题3-45图 题3-46图 3-47～3-49 试确定各组合结构的计算步骤并求F N1。
题3-47图 题3-48图题3-49图 3-50～3-51 求作弯矩图及扭矩图。
题3-50图 题3-51图第 4 章 题4-1 试回答：影响线的含义是什么？它在某一位置的竖标代表什么物理意aDqC BAF Pq212d 2d 4×31 2 2 31d2 d 2dd1 235d213a 3a 2 14×10kN/m14a12a a 4aq 1义？4-2 试从图形自变量的含义、竖标的意义、量纲以及图形的范围等方面说出影响线与内力图之间的区别。
《结构力学习题》(含答案解析)
《结构力学习题》(含答案解析)本页仅作为文档封面，使用时可以删除This document is for reference only-rar21year.March20 第三章 静定结构的位移计算一、判断题：1、虚位移原理等价于变形谐调条件，可用于求体系的位移。
2、按虚力原理所建立的虚功方程等价于几何方程。
3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下，静定结构不产生内力，但会有位移且位移只与杆件相对刚度有关。
4、求图示梁铰C 左侧截面的转角时，其虚拟状态应取：A.;; B.D.M C.=1=1=15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。
6、已知M p 、M k 图，用图乘法求位移的结果为：()/()ωω1122y y EI +。
M kM p 21y 1y 2**ωω( a )M =17、图a 、b 两种状态中，粱的转角ϕ与竖向位移δ间的关系为：δ=ϕ 。
8、图示桁架各杆E A 相同，结点A 和结点B 的竖向位移均为零。
Aa a9、图示桁架各杆EA =常数，由于荷载P是反对称性质的，故结点B的竖向位移等于零。
2121二、计算题：10、求图示结构铰A 两侧截面的相对转角ϕA ，EI = 常数。
q l l l /211、求图示静定梁D 端的竖向位移 ∆DV 。
EI = 常数 ，a = 2m 。
a a a 10kN/m12、求图示结构E 点的竖向位移。
EI = 常数 。
l l l /3 2 /3/3q13、图示结构，EI=常数 ，M =⋅90kN m , P = 30kN 。
求D 点的竖向位移。
P 3m 3m 3m14、求图示刚架B 端的竖向位移。
q15、求图示刚架结点C 的转角和水平位移，EI = 常数 。
q16、求图示刚架中Ｄ点的竖向位移。
EI ＝常数。
l ll/217、求图示刚架横梁中Ｄ点的竖向位移。
EI＝常数。
18、求图示刚架中D点的竖向位移。
结构力学课后习题答案
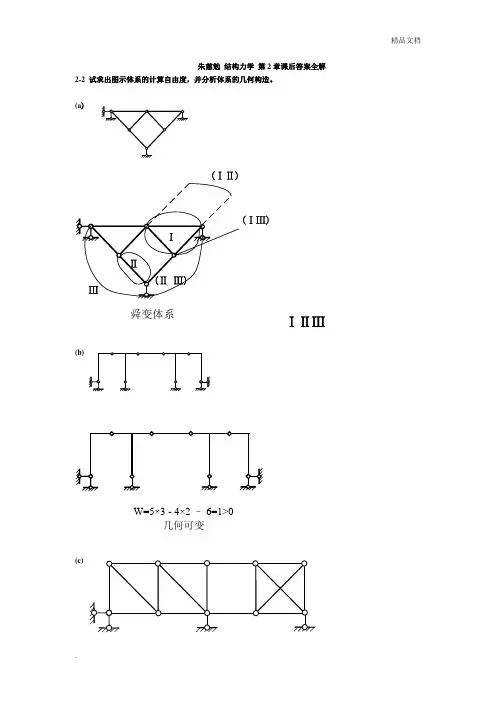
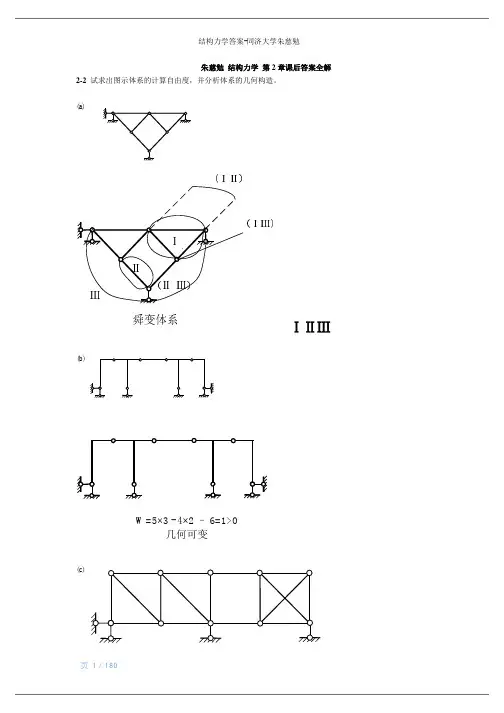
朱慈勉 结构力学 第2章课后答案全解2-2 试求出图示体系的计算自由度，并分析体系的几何构造。
(a)ⅠⅡⅢ(ⅠⅡ)(ⅠⅢ)(Ⅱ Ⅲ)舜变体系`ⅠⅡⅢ(b)W=5×3 - 4×2 – 6=1>0几何可变(c)有一个多余约束的几何不变体系(d)2-3 试分析图示体系的几何构造。
(a)(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(Ⅱ Ⅲ)几何不变W=3×3 - 2×2 – 4=1>0可变体系ⅠⅡⅢ（ⅠⅡ）（ⅠⅢ）（ⅡⅢ）几何不变2-4 试分析图示体系的几何构造。
(a)（ⅠⅢ）（ⅠⅡ）（ⅡⅢ）ⅠⅡⅢ几何不变(b)W=4×3 -3×2 -5=1>0几何可变体系ⅢⅠⅡ（ⅠⅢ）（ⅡⅢ）（ⅠⅡ）几何不变(d)（ⅠⅡ）ⅢⅠⅡ（ⅡⅢ）（ⅠⅢ）二元杆有一个多余约束的几何不变体ⅠⅡⅢ（ⅠⅢ）（ⅡⅢ）（ⅠⅡ）舜变体系(f)ⅠⅡⅢ（ⅠⅢ）（ⅡⅢ）（ⅠⅡ）无多余约束内部几何不变ⅠⅡⅢ（ⅠⅢ）（ⅠⅡ）（ⅡⅢ）二元体(h)ⅠⅡⅢ（ⅠⅢ）（ⅠⅡ）（ⅡⅢ）二元体多余约束W=3×8 - 9×2 – 7= -1, 有1个多余约束2-5 试从两种不同的角度分析图示体系的几何构造。
(a)（ⅠⅢ）ⅠⅡⅢ（ⅠⅡ）（ⅡⅢ）舜变体系(b)ⅠⅡⅢ（ⅠⅡ）（ⅡⅢ）（ⅠⅢ）几何不变同济大学朱慈勉 结构力学 第3章习题答案3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a)4P F a2P F a 2P F a Ｍ4P F Ｑ34P F 2P F(b)ABCaa aaaF P a DEFF P2m6m2m4m2mABCD10kN2kN/m４2020M Q10/326/3４10(c)21018018040M1560704040Q(d)3m2m2mA B CEF15kN 3m3m4m20kN/mD 3m2m2m2mA2m 2m2mABCD E FG H 6kN ·m4kN ·m 4kN2m7.5514482.524MQ3-3 试作图示刚架的内力图。
结构力学答案-同济大学朱慈勉
FP
FP
4
1
FP
4
31
3
2
FP 2
பைடு நூலகம்
2
B
FP
1
3 4
FP
C
1
.1
2
3
.
4
FN1 = −
2 2 FP
∑ . 由 MB = 0,可求得FC = 0.75FP
.
X1
X2
D
FN 3 =
2 2
FP
∑ 由 MD = 0,可求得x1 = −FP → x2 = FP
由节点法,对C分析可求得FN 2
=
FP 4
3-15 试求图示桁架各指定杆件的内力。 (a)
qa 2
qa 2 2
qa 2qa
1.5qa
3-11 试指出图示桁架中的零杆。
1.5qa
FP
FP
页 19 / 180
结构力学答案-同济大学朱慈勉
FP
FP
FP
、
3-12 试求图示桁架各指定杆件的内力。 (b)
3m
3 ×3m
先求出支座反力,如图所示。零杆亦示于图中。 取1-1截面以上部分分析
F3
FBC
然后再依次隔离A, B, D点不难求得 F2 = −7.5KN (−), FBD = 3KN , F1 = −4KN (−)
=
0
→
FB x
=
4 3
P
∑ M C = 0 → FN 4 = −2P
1C
3 2 4D
2P 5 P FP
2
∑
取虚线所示的两个隔离体有：
M B = 0,
2 2
×
FN 2
结构力学下册第三章(部分)
D MB B
Me y1
FBx
AC 段：
FBy
M (x)
=
FA x
−
MA
=
⎜⎛ ⎝
F0
+
Me
+
MA 2a
+
MB
⎟⎞x ⎠
−
MA
∂M (x) = x ∂F0
∂M (x) = x −1 ∂M A 2a
∂M (x) = x ∂M B 2a
BD 段： M ( y1 ) = FBx y1 + M B = F0 y1 + M B
∫ ∫ （b）非线性杆的应变能密度
vε
=
σdε
ε
=
Bε 1 2dε
ε
= 2 Bε 3 2 3
ΔAy
D
G ΔAx
相应的应变能表达式
∫ Vε
=
V vε dV
=
2 Bε 3 2 Al = 3
2BAl ⎜⎛ ε l ⎟⎞3 2 3 ⎝l⎠
=
2BAl ⎜⎛ Δl ⎟⎞3 2 3 ⎝l⎠
杆的变形和节点位移间的关系与（a）情况相同，故结构的应变能
Δ Ay
− Δ Axctg30°
sin 30° =
Δ Ay 2
−
3Δ Ax 2
∑ Vε =
应变能：
EA 2li
(Δli
)2
=
EA 2(2a)
⎜⎜⎝⎛
Δ Ay 2
−
3 2
Δ Ax
⎟⎟⎠⎞ 2
+
EA 2( 3a)
Δ2Ax
[( ) ] = EA 48a
9+6
3 Δ2Ax − 6
结构力学第三章习题参考解答
FAy 6 FAx 2 0
1 ql 2A
1 ql 4
取整体：M A 0
Fy 0
取AC： MC 0
取整体： Fx 0
l
l
0.45ql
FBy
1 2l
ql 3l 2
3 ql 4
FAy
ql
3 4
ql
1 4
ql
FAx
2 ql 2 l4
1 ql 2
FBx
1 ql 2
l 2
1 ql B2 3 ql 4
取左段
FNK
ql cos
3l 4
1 q 3 l 2 2 4
9 ql 2 32
D
C
q
3 ql
4
A
1 ql
l
4
1 ql
4
1 ql 4
3 ql
4
FQ KN
1 ql 2
E
4
1 ql 2 4
9 ql2 32
1 ql
B
4
ql 2 8
M KNm
l
1 ql
4
1 ql
4
1 ql
4
FN KN
1 ql2 4
1 ql 4
3－12解：
q C
q
3 ql
4
A
l
1 ql
B
4
Fy 0
FAy
1 ql 4
1 ql 4
l
l
1 ql
4
取BC：
MC 0
FBx
1 4
ql
取整体：
Fx 0
FAx
ql
1 ql 4
3 ql 4
AD段的最大弯矩 M x 3 qlx 1 qx2 dM 3 ql qx 0
最新完整的结构力学答案-同济大学朱慈勉
对B点求矩
20 9 (4.5 3) RF 6 RF 45() M E 0.5 20 92 45 9 405, RE 135() MCF 45 3 135, MCD 0.5 20 9 90 M BA 0.5 20 9 90
精品文档
精品文档
(b)
1
M
5.75
精品文档
精品文档
5FP
5FP
5FP
5 4
FP
5 4
FP
5FP
2FP
5 4
FP
2FP k
由节点法知：
对A节点 对E节点
FNAD =- 5FP
FNEC
5 4
FP
FNAE 2FP
FNEF
5 4
FP
1
由节点法知：
k
对A节点
FNAD =-
5 2
FNAE 1
yc
F N FNPl EA
1 EA
2
qa 2
q
G
H
qa2 IJ
B
C
a
a
3qa 2 2
qa 2
a
3qa 2 2
qa 2 2
a
对H点求矩：
qa 2
qa 2 2
HC
a
HC
1.5qa()
对F点求矩：
qa 1.5a H A a 0 H A 1.5qa() H D 0, MGF qa2, MGH 1.5qa2
qa 2
qa 2 2
xB
1 EI
M ( )M ( )ds
1
2
qR2(1 cos )R sin Rd
1
qR 4 ()
EI 0
2EI
结构力学课后习题答案(朱慈勉)
朱慈勉 结构力学 第2章课后答案全解2-2 试求出图示体系的计算自由度，并分析体系的几何构造。
(a(ⅠⅡ)(ⅠⅢ)舜变体系ⅠⅡⅢ(b)W=5×3 - 4×2 – 6=1>0几何可变(c)有一个多余约束的几何不变体系(d)W=3×3 - 2×2 – 4=1>0可变体系2-3 试分析图示体系的几何构造。
(a)(ⅡⅢ)Ⅲ几何不变2-4 试分析图示体系的几何构造。
(a)几何不变(b)W=4×3 -3×2 -5=1>0几何可变体系（ⅠⅢ）（ⅡⅢ）几何不变(d)Ⅲ（ⅠⅢ）有一个多余约束的几何不变体（ⅠⅢ）（ⅡⅢ）（ⅠⅡ）舜变体系(f)（ⅠⅢ）（ⅡⅢ）无多余约束内部几何不变(h)二元体W=3×8 - 9×2 – 7= -1, 有1个多余约束2-5 试从两种不同的角度分析图示体系的几何构造。
(a)（ⅠⅢ）ⅠⅡⅢ（ⅠⅡ）（ⅡⅢ）舜变体系(b)Ⅲ（ⅡⅢ）（ⅠⅢ）同济大学朱慈勉 结构力学 第3章习题答案3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a)2P F a 2P F a4P F Ｑ34P F 2P F(b)aa aaa2m6m2m4m2m2020Q10/326/310(c)18060(d)3m2m2m3m3m4m3m2m2m2mA2m 2m2m2m7.5514482.524MQ3-3 试作图示刚架的内力图。
(a)242018616MQ18(b)4kN ·m3m3m6m1k N /m2kN A CBD6m10kN3m3m 40kN ·m ABC D30303011010QM 210(c)45MQ(d)3m3m6m6m2m 2m444444/32MQN(e)4481``(f)4m4m2m3m4m222220M3-4 试找出下列各弯矩图形的错误之处，并加以改正。
(a)F P(b)(c)(d)(e)(f)F3-5 试按图示梁的BC 跨跨中截面的弯矩与截面B 和C 的弯矩绝对值都相等的条件，确定E 、F 两铰的位置。
同济大学朱慈勉结构力学课后习题答案
更多土木工程考研资料见淘宝店铺：征世考研
更多土木工程考研资料见淘宝店铺：征世考研
更多土木工程考研资料见淘宝店铺：征世考研
更多土木工程考研资料见淘宝店铺：征世考研
更多土木工程考研资料见淘宝店铺：征世考研
更多土木工程考研资料见淘宝店铺：征世考研
更多土木工程考研资料见淘宝店铺：征世考研
更多土木工程考研资料见淘宝店铺：征世考研
更多土木工程征世考研
更多土木工程考研资料见淘宝店铺：征世考研
更多土木工程考研资料见淘宝店铺：征世考研
更多土木工程考研资料见淘宝店铺：征世考研
更多土木工程考研资料见淘宝店铺：征世考研
更多土木工程考研资料见淘宝店铺：征世考研
更多土木工程考研资料见淘宝店铺：征世考研
更多土木工程考研资料见淘宝店铺：征世考研
更多土木工程考研资料见淘宝店铺：征世考研
更多土木工程考研资料见淘宝店铺：征世考研
更多土木工程考研资料见淘宝店铺：征世考研
更多土木工程考研资料见淘宝店铺：征世考研
更多土木工程考研资料见淘宝店铺：征世考研
更多土木工程考研资料见淘宝店铺：征世考研
更多土木工程考研资料见淘宝店铺：征世考研
更多土木工程考研资料见淘宝店铺：征世考研
更多土木工程考研资料见淘宝店铺：征世考研
更多土木工程考研资料见淘宝店铺：征世考研
更多土木工程考研资料见淘宝店铺：征世考研
更多土木工程考研资料见淘宝店铺：征世考研
更多土木工程考研资料见淘宝店铺：征世考研
更多土木工程考研资料见淘宝店铺：征世考研
更多土木工程考研资料见淘宝店铺：征世考研
更多土木工程考研资料见淘宝店铺：征世考研
更多土木工程考研资料见淘宝店铺：征世考研
结构力学 第三章 作业参考答案
即可作出全部的弯矩图。
9
华南农业大学 水利与土木工程学院（College of water conservancy and Civil Engineering, SCAU）
3—16 试作出图示刚架的 M 图。
20kN 50kN m D 3m E 10kN/m C FC A FA 4m B FB 4m 2m F
（1）
=＞ FB = 20 kN 首先可得： M DC = 10 × 2 = 40 kNim
D M DB =120 M DC =40 M DA =160
M DB = 30 × 4 = 120 kNim
在 D 结点弯矩平衡： =＞ M DA
M DB + M DC − M DA = 0 = 160 kNim
结构力学 第三章 习题 参考答案
结构力学 第三章习题 参考答案
2005 级 TANG Gui-he（整理）
3—1 试作出图示单跨梁的 M 图和 Fs 图。
40kN
20kN/m
A 2m FAy 4m 4m FB
B 2m
40kN m 80kN m A 20kN m M(kN m) 40kN m B 10kN m
3—19 试作图示刚架的 M 图。
20kN
24 16
C
24
16
B FAx A FBy FAy
FBx
1m
2m
2m
2m
M图(kN m)
（1） （2） （3）
解：对整体：
∑M ∑F
y
A
=0
FBy × 4 + FBx ×1 = 20 × 2 FAy + FBy = 20 FAx − FBx = 0 FBx × 2 − FBy × 2 = 0
结构力学第三章习题及答案
静定结构计算习题3—1 试做图示静定梁的M 、F Q 图。
解：首先分析几何组成:AB 为基本部分，EC 为附属部分。
画出层叠图，如图（b ）所示。
按先属附后基本的原则计算各支反力(c)图。
之後，逐段作出梁的弯矩图和剪力图。
36.67KN15KN •m 20KNM 图（单位：KN/m ）13.323.313.33F Q 图（单位：KN ）3—3 试做图示静定刚架的内力（M 、F Q 、F N ）图，并校核所得结果。
解：（1）计算支反力F AX =48kN （→） M A =60 KN •m (右侧受拉) （2）逐杆绘M 图 （3）绘F Q 图 （4）绘N 图（5）校核: 内力图作出后应进行校核。
(略)3—7 试做图示静定刚架的内力（M 、F Q 、F N ）图，并校核所得结果。
解：（1）计算支反力F AX =20kN （←） F AY =38kN(↑) F BY =62kN(↑) （2）逐杆绘M 图BCM 图（单位：KN/m ） F Q 图（单位：KN ）3030F AX F N图（单位：60）20）（3）绘F Q 图 （4）绘N 图（5）校核: 内力图作出后应进行校核。
(略)3—9 试做图示静定刚架的内力（M 、F Q 、F N ）图，并校核所得结果。
解：（1）计算支反力F AX =0.75qL （←） F AY =-0.25qL( ) F BY =0.25qL(↑) （2）逐杆绘M 图 （3）绘F Q 图 （4）绘N 图（5）校核: 内力图作出后应进行校核。
(略)3—11试做图示静定刚架的内力（M 、F Q 、F N ）图，并校核所得结果。
解：（1）计算支反力F BX =40KN （←） F AY =30KN (↑) F BY =50kN(↑) （2）逐杆绘M 图 （3）绘F Q 图 （4）绘N 图（5）校核: 内力图作出后应进行校核。
(略)C（a ）qBY 23—17 试求图示抛物线三铰拱的支座反力，并求截面D 和E 的内力。
《结构力学习题》(含答案解析)
第三章 静定结构的位移计算一、判断题：1、虚位移原理等价于变形谐调条件，可用于求体系的位移。
2、按虚力原理所建立的虚功方程等价于几何方程。
3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下，静定结构不产生内力，但会有位移且位移只与杆件相对刚度有关。
4、求图示梁铰C 左侧截面的转角时，其虚拟状态应取：A.;; B.D.C.=1=15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。
6、已知M p 、M k 图，用图乘法求位移的结果为：()/()ωω1122y y EI +。
M k M p 21y 1y 2**ωω( a )M =17、图a 、b 两种状态中，粱的转角ϕ与竖向位移δ间的关系为：δ=ϕ 。
8、图示桁架各杆E A 相同，结点A 和结点B 的竖向位移均为零。
a a9、图示桁架各杆EA =常数，由于荷载P 是反对称性质的，故结点B 的竖向位移等于零。
二、计算题：10、求图示结构铰A 两侧截面的相对转角ϕA ，EI = 常数。
q l l l /211、求图示静定梁D 端的竖向位移 ∆DV 。
EI = 常数 ，a = 2m 。
a a a 10kN/m12、求图示结构E 点的竖向位移。
EI = 常数 。
l l l /3 2 /3/3q13、图示结构，EI=常数 ，M =⋅90kN m , P = 30kN 。
求D 点的竖向位移。
P 3m 3m 3m14、求图示刚架B 端的竖向位移。
ql15、求图示刚架结点C 的转角和水平位移，EI = 常数 。
q16、求图示刚架中Ｄ点的竖向位移。
EI ＝常数。
l/217、求图示刚架横梁中Ｄ点的竖向位移。
EI＝常数。
18、求图示刚架中D点的竖向位移。
E I = 常数。
qll l/219、求图示结构Ａ、Ｂ两截面的相对转角，EI＝常数。
l/23l/320、求图示结构A、B两点的相对水平位移，E I = 常数。
ll21、求图示结构B点的竖向位移，EI = 常数。
结构力学第三章习题解析
T
有阻尼时的自振频率小于无阻尼时的自振频率，这说明由于阻尼的存在，将使结构 的自振频率减小，周期增大。 在实际结构中，阻尼比的数值一般都很小，其值大约 0.01 ~ 0.1 在之间。因此有 阻尼频率与无阻尼频率相差不大，在实际计算中可以近似地取
2
1 2
§3.1 概述
二、地震作用
作用
：能引起结构内力、变形等反应的各种因素
直接作用 ——各种荷载：如重力、风载、土压力等
作用分类
间接作用 ——各种非荷载作用：如温度、基础沉降、地震等
等效地震荷载 ：工程上，可将地震作用等效为某种形式的荷载作用
结构的地震作用:地震时，由于地面运动使原来处于静止的结构受到动力作 用，产生受迫振动，由于地面的强迫振动在结构上产生的惯性力
第三章 结构地震反应分析 与抗震计算
3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 3.9 概述 单自由度体系的弹性地震反应分析 单自由度体系的水平地震作用与反应谱 多自由度弹性体系的地震反应分析 多自由度弹性体系最大地震反应与水平地震作用 竖向地震作用 结构平扭耦合地震反应与双向水平地震影响 结构非弹性地震反应分析 结构抗震验算
4.方程的特解III —— 一般强迫振动
求解方法：
(t ) 2x (t ) 分解为很多个脉冲运动
t
0 ( )d x 时刻的地面运动脉冲
引起的体系反应为：
x(t ) e t
dx(t ) e
厂房各跨质量 (b)
单质点体系 (c) 多、高层建筑
(d) 烟囱
集中化描述举例 (a) 水塔 (a) 水塔 c、多、高层建筑
(b) 厂房 厂房 (b) d、烟囱
结构力学 朱慈勉 第3章课后答案全解
结构力学 第3章习题答案3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a)2P F a 2P F a4P F Ｑ34P F 2P F(b)aa aaa2m6m2m4m2m2020Q10/326/310(c)18060(d)3m2m2m3m3m4m3m2m2m2mA2m 2m2m2m7.5514482.524MQ3-3 试作图示刚架的内力图。
(a)242018616MQ18(b)4kN ·m3m3m6m1k N /m2kN A CBD6m10kN3m3m 40kN ·mABC D30303011010QM 210(c)45MQ(d)3m3m6m6m2m 2m444444/32MQN(e)4481``(f)4m4m2m3m4m222220M3-4 试找出下列各弯矩图形的错误之处，并加以改正。
(a)F P(b)(c)(d)(e)(f)F3-5 试按图示梁的BC 跨跨中截面的弯矩与截面B 和C 的弯矩绝对值都相等的条件，确定E 、F 两铰的位置。
lx l lx28ql M2221()222116121618c B C BC C q ql M l x x qx xM M M M ql ql x ql x l=-+===∴=∴=∴=中F D()2ql x -3-6 试作图示刚架的弯矩和剪力图。
(a)9090405M2B 209(4.53)645()0.5209459405,135()453135,0.5209900.520990F F E E CF CD BA R R M R M M M ⨯⨯-=⨯∴=↑=⨯⨯-⨯==↑=⨯==⨯⨯==⨯⨯=对点求矩14.25424213.5 1.50.2525.75A 72425 2.50.5()C 420.524 4.25()3.5(),0.25()5.752.1,24 4.253.752.5E K B B B B A A EF K M M R R H H V H Q Q =⨯-⨯⨯==⨯+⨯=⨯+⨯⨯=⨯→=-↓⨯⨯+⨯=⨯→=→∴=↑=←===⨯-=左对点求矩：对点求矩：2 2.1(c)80/3Q8080380,61603330():(2023304)/2120():61201030420211320()380()3DA ED C C B B A M M H F V A V V V =⨯==⨯==←=⨯⨯+⨯=↑⨯+⨯=⨯+⨯⨯∴=-↓∴=↑对点求矩对点求矩(d)8/34/388414233:41614284()4:441426()38(),03DAB BB BA AMA V VC H HH V=⨯-⨯⨯=⨯⨯+⨯⨯=⨯→=↑⨯-⨯⨯=⨯→=←∴=←=对点求矩对点求矩(e)2FaF2Fa2FaF F F2F----+2Fa2Fa2FaM Q02(),020322222(),2()4(),0C B p E B FB P H P FH P F PD P DM V F M H VM F a a H F a V aH F V FH F V=→=↑=→==→⨯+⨯=⨯+⨯∴=←=↓∴=→=∑∑∑(f)进一步简化BHIH8:4(),4()4(),4(),42810B BI I AH KN V KNH KN V KN M N m=→=↓=-←=-↑=⨯=•可知84 (g)2aqa22221.5()21.50 1.5()0,, 1.5C CA AGF GHHqaqa H a H qaqa a H a H qaH M qa M qa+=⨯→=→⨯+⨯=→=-←===对点求矩：对F点求矩：。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
同济大学朱慈勉 结构力学 第3章习题答案
3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a)
4
P F a
2
P F a 2
P F a Ｍ
4
P F Ｑ
34
P F 2
P F
(b)
A
B
C
a
a a
a
a
F P a D
E
F
F P
2m
6m
2m
4m
2m
A
B
C
D
10kN
2kN/m
４
20
20
M Q
10/3
26/3
４
10
(c)
210
180
180
40
M
15
60
70
40
40
Q
(d)
3m
2m
2m
A B C
E
F
15kN 3m
3m
4m
20kN/m
D 3m
2m
2m
2m
2m 2m
2m
A
B
C
D E F
G H 6kN ·m
4kN ·m 4kN
2m
7.5
5
1
4
4
8
2.5
2
4M
Q
3-3 试作图示刚架的内力图。
(a)
24
20
186
16
M
Q
18
20
(b)
4kN ·m
3m
3m
6m
1k N /m
2kN
A C
B
D
6m
10kN
3m
3m 40kN ·m
A
B
C D
30
30
30
110
10
10
Q
M 210
(c)
6
6
4
2
75
M
Q
(d)
3m
3m
2kN/m
6kN
6m
4kN
A
B
C
D
2kN
6m
2m
2m
2kN
4kN ·m A
C
B
D E
4
4
4
4
4
4/3
2
M
Q
N
(e)
4
4
8
1
4
``
(f)
4m 4m A
B
C
4m
1k N /m
D 4m
4kN
A B
C
2m
3m
4m
2kN/m
22
2220 0.81
5
M Q
N
3-4试找出下列各弯矩图形的错误之处，并加以改正。
(a)
F P
(b)
(c)
F P
(d)
M
(e)
(f)
F P
F P
3-5试按图示梁的BC跨跨中截面的弯矩与截面B和C的弯矩绝对值都相等的条件，确定E、F两铰的位置。
l
B C
E F
x
D
A
q
l l
x
B C E
F
D
A
28
ql M
22
2
1()222116121618c B C BC C q ql M l x x qx x
M M M M ql ql x ql x l
=-+===∴=
∴=∴= 中F D
()2
q
l x -
3-6 试作图示刚架的弯矩和剪力图。
(a)
90
90
45
135
405
M
Q
2B 209(4.53)645()0.5209459405,135()453135,0.5209900.520990
F F E E CF CD BA R R M R M M M ⨯⨯-=⨯∴=↑=⨯⨯-⨯==↑=⨯==⨯⨯==⨯⨯=对点求矩
5.75
1
1
1
M
Q
4.25424213.5 1.50.252
5.75
A 72425 2.50.5()C 420.524 4.25()3.5(),0.25()5.75
2.1,24 4.25
3.752.5
E K B B B B A A E
F K M M R R H H V H Q Q =⨯-⨯⨯==⨯+⨯=⨯+⨯⨯=⨯→=-↓⨯⨯+⨯=⨯→=→∴=↑=←=
==⨯-=左对点求矩：对点求矩：2 2.9
3.75
4.25
2.1
(c)
80
160
160
160
100
60
40
16
80/3
80
30
M
Q
8080
380,6160
33
30()
:(2023304)/2120():61201030420211320
()380()
3DA ED C C B B A M M H F V A V V V =⨯==⨯==←=⨯⨯+⨯=↑⨯+⨯=⨯+⨯⨯∴=-
↓∴=↑对点求矩对点求矩
(d)
8/3
16/3
8/3
4/3
435
435
2035
4/3
M
Q
88414233
:41614284()4
:441426()
3
8
(),0
3
DA B B B B A A M A V V C H H H V =⨯-⨯⨯=
⨯⨯+⨯⨯=⨯→=↑⨯-⨯⨯=⨯→=←∴=←=对点求矩对点求矩
(e)
2Fa
F
2Fa
2Fa F F F
2F
-
---+2Fa
2Fa
2Fa
M
Q
02(),020322222(),2()4(),0
C B p E B F B
P H P F H P F P D P D M V F M H V M
F a a H F a V a
H F V F H F V =→=↑=→==→⨯+⨯=⨯+⨯∴=←=↓∴=→=∑∑∑
(f)
8
8
利用对称性
进一步简化
B
H B
V I
H I
V 8
8
:4(),4()
4(),4(),42810B B I I A H KN V KN H KN V KN M N m
=→=↓=-←=-↑=⨯=∙可知
8
8
8
8
8
8
4
4
4
4
4
4
4
4
-
+
-
--+
+
+
(g)
qa 2
a
a
a
a
a
a a
A B C
G H
F
J
D
E I q
q
22
qa 2
32
qa 2
qa
2
2
qa 2
qa 2
32
qa 2
32
qa 22
qa 2
qa
qa
2qa
1.5qa
1.5qa
2
2
22
1.5()
2
1.50 1.5()
0,, 1.5C C A A D GF GH H qa qa H a H qa qa a H a H qa H M qa M qa +=⨯→=→⨯+⨯=→=-←===对点求矩：
对F 点求矩：。