2011-2012八上数学第一次月考试题
八年级上学期数学第一次月考试题及答案

八年级上学期数学第一次月考试题及答案一、选择题(3分×8=24分)1.以下五家银行行标中,轴对称图形的有………… ()A.1个B.2个C.3个D.4个2.小明在镜中看到身后墙上的时钟,实际时间最接近8时的是下图中的……()A B C D3. 关于等边三角形的说法:(1)等边三角形有三条对称轴;(2)有一个角等于60°的等腰三角形是等边三角形;(3)有两个角等于60°的三角形是等边三角形;(4)等边三角形两边中线上的交点到三边的距离相等.其中正确的说法有………… ()A.1个B.2个C.3个D.4个4.如图,∠BAC=1000,MN、EF分别垂直平分AB、AC,则∠MAE的大小为()A. 800 B. 200C. 500D. 1005. 在梯形ABCD中,AD∥BC.现给出条件:①∠A=∠B;②∠A+∠C=180°;③∠A=∠D.其中能用来说明这个梯形是等腰梯形的是:…………… … ()A.①或②或③ B.①或② C.①或③ D.②或③6..已知∠AOB=30°,点P在∠AOB内部,P1与P关于OB对称,P2与P关于OA对称,则P1,O,P2三点构成的三角形是( )A.直角三角形B.钝角三角形C,等腰三角形D.等边三角形7. 以下列数组为三角形的边长,其中能构成直角三角形的是…………………()A.1,1,2 B.,, C.0.2,0.3,0.5 D.1.5,2,2.58. 如图的方格纸中,每一个小方格都是边长为1的正方形,找出格点C,使△ABC的等腰三角形,这样的格点C的个数有……………… ………… ()A. 8个B. 9个C. 10个D. 11个二、填空题(每空2分,共22分)9.(1)若等腰三角形的周长为10,底边长为4,则腰长为;(2)若等腰三角形的两边长为6和4,则等腰三角形的周长为.10.(1)若等腰三角形的一个角为100°,则底角为°.(2)若△ABC为等腰三角形,∠A=40°,∠B= ______ °.11. 如图,△ABC中,DE垂直平分AC交AB于E,∠A=30°,∠ACB=80°,则∠BCE= °.12 如图,Rt△ABC中,∠B=90°,AB=3cm,AC=5cm,将△ABC折叠,使点C与A重合,得折痕DE,则△ABE的周长等于_______cm.13.(1)一个三角形三边为3,4,5,此三角形的面积为____________.(2)一个直角三角形的两条直角边长为5cm、12cm,则斜边上的中线为;14.如图,△ABC中,DE∥AB,,BF平分∠ABC,交DE于点F,若BC=6,则DF的长是_。
2012-2011八上数学第一次月考试题

2011-2012八上数学第一次月考试题一、选择题(每小题3分,共30分)A.全等三角形是指形状相同的两个三角形B.全等三角形是指面积相同的两个三角形C.两个周长相等的三角形是全等三角形D.全等三角形的周长、面积分别相等2.已知等腰三角形底角为30°,则顶角的度数是()A. 50°B. 60°C. 120°D. 80°3.下列图形中,不是轴对称图形的是( )A.等边三角形 B.等腰直角三角形 C.不等边三角形 D.线段4.如图,轴对称图形有()个。
5、等腰三角形一边长为4,一边长等于9,则它的周长等于()A. 17B. 22C. 13D. 17或226. 下列判断中错误..的是()A.有两角和一边对应相等的两个三角形全等B.有两边和一角对应相等的两个三角形全等C.有两边和其中一边上的中线对应相等的两个三角形全等D.有一边对应相等的两个等边三角形全等7 如图,点P是∠BAC的平分线AD上一点,PE⊥AC于点E.已知PE=3,则点P到AB的距离是()A.3B.4C.5D.68. 如图,已知:AB∥EF,CE=CA,∠E=65,则∠CAB的度数为A.25 B.50 C.60 D.659. 已知一个等腰三角形两内角的度数之比为1:4,则这个等腰三角形顶角的度数为()A.20 B.120 C.20 或120 D.3610.如图,AB垂直平分CD,若AC=1.6cm,BC=2.3cm,则四边形ABCD的周长是()cm.A.3.9B.7.8C.4D.4.6二、填空题(每小题3分,共18分)11.如图,线段AC与BD交于点O,且OA=OC,请添加一个条件,使△OAB≌△OCD,这个条件是______________________.12..如图6,50ABC AD∠= ,垂直平分线段BC点D ABC∠,的平分线BE交AD于点E,连结EC,则AEC∠的度数是.13、如图,△ABC中,AB=AC=17,BC=16,DE垂直平分AB,则△BCD的周长是14.如图2,已知:ABC∆中,090=∠C,AM平分CAB∠,CM =20cm那么M到AB的距离是.图6AB C D15. 夷陵长江大桥为三塔斜拉桥.如图, 中塔左右两边所挂的最长钢索AB AC =,塔柱底端D 与点B 间的距离是228米, 则BC 的长是 米.16. ABC △为等边三角形,D E F ,,分别 在边BC CA AB ,,上,且AE CD BF ==, 则DEF △为 三角形三.解答题(共72分17-19(6分)20—23每题8分,24题10分)17(作图6分)近年来,国家实施“村村通”工程和农村医疗卫生改革,某县计划在张村、李村之间建一座定点医疗站P ,张、李两村座落在两相交公路内(如图所示).医疗站必须满足下列条件:①使其到两公路距离相等,②到张、李两村的距离也相等,请你通过作图确定P 点的位置.18(6分)如图,在△ABC 中,AD 为∠BAC 的平分线,DE ⊥AB 于E ,DF ⊥AC 于F ,△ABC 面积是28cm 2,AB=20cm ,AC=8cm ,求DE 的长.19.(6分)如图,四边形ABCD 的四个顶点的坐标分别为A (-5 ,1)、B (-2 ,1)、C20(8分)如图,△ABC 是等边三角形,直线AD 是它的对称轴,AB =12.(1)写出图中三组相等关系;(2)求∠BAD 的度数和BD 的长;D A B D C21(8分)已知,如图ΔABC 中,AB =AC,D 点在BC 上,且BD =AD ,DC =AC.将图中的等腰三角形全都写出来.并求∠B 的度数.22(8分) 已知:如图,直线AD 与BC 交于点O ,OA OD =,OB OC =. 求证:AB CD ∥.23(8分)已知A 、F 、C 、D 四点在同一条直线上,AC=DF ,AB//DE ,EF//BC , (1) 试说明 ⊿ABC ≌⊿DEF (2) ∠CBF=∠FEC24.(10分) 如图,在等腰R t △ABC 中,∠ACB =90°,D 为BC 的中点,DE ⊥AB ,垂足为E ,过点B 作BF ∥AC 交DE 的延长线于点F ,连接CF . (1)求证:AD ⊥CF ;(2)连接AF ,试判断△ACF 的形状,并说明理由.25.(10分)( 开放题)如图,D E ,分别为ABC △的边AB AC ,上的点,BE 与CD 相交于O 点.现有四个条件:①AB AC =,②OB OC =,③ABE ACD ∠=∠,④BE CD =.(1)请你选出两个条件作为题设,余下的两个作为结论,写出一个正确..的命题:命题的条件是 和 ,命题的结论是 和 (均填序号). (2)证明你写出的命题. 已知: 求证: 证明:ABD C ODB C。
人教版八年级上数学第一次月考试题

数学月考试题一、填空1、如果△ABC ≌△DEF ,△DEF 周长是32cm ,DE=9cm,EF=13cm.∠E=∠B ,则AC=__2、现在你要到玻璃店去配一块完全一样的玻璃,则应带哪块玻璃去______(填上序号)。
3、在△ABC 中,AB=3㎝,AC=4㎝,则BC 边上的中线AD 的取值范围是 ;4、如图,将纸片△ABC 沿DE 折叠,点A 落在点F 处,已知∠1+∠2=100°,则∠A = 度;5、如图,直线a ,b ,c 表示三条相互交叉环湖而建的公路,现在建立一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有 个6、如图,△ABC 中,∠C =90°,AD 平分∠BAC ,AB =5,CD =2,则△ABD 的面积是______7、如图,在△ABC 中,∠C=90°,AD 平分∠BAC ,BC=10cm,BD=6cm 则点D 到AB 的距离为_________。
8、如下图,∠B=∠C=90°,E 是BC 的中点,DE 平分∠ADC,∠CED=35°,则∠EAB = ; 9、如下图,已知铁路上A 、B 两站相距45km ,C 、D 为铁路同旁的两个村庄,DA ⊥AB 于A ,CB ⊥AB 于B ,DA=25km , CB=20k m ,现在要在铁路AB 上建一个收购站E ,使C 、D 两村庄到E 站的距离相等,则E 站应建在距A_______km 处 二、选择题1、在△ABC 和△A ′B ′C ′中,①AB=A ′B ′;②BC=B ′C ′;③AC=A ′C ′;④∠A=∠A ′;⑤∠B=∠B ′;⑥∠C=∠C ′,则下列哪组条件不能保证△ABC ≌△A ′B ′C ′( ) A 、①②③ B 、①②⑤ C 、①⑤⑥ D 、①②④2、下列说法正确的是( )A :形状相同的两个三角形全等B :全等三角形的周长和面积分别相等C :面积相等的两个三角形全等D :所有的等边三角形都是全等三角形3、如图:△ABC 中,∠C=90°,AC=BC ,AD 平分∠CAB 交BC 于D ,DE ⊥AB 于E ,且AB=6㎝,则△DEB 的周长是( )A :6㎝ B :4㎝ C :10㎝ D :以上都不对bCE(第17题)DCBAAA8题4、如图:AB=AD ,AE 平分∠BAD ,则图中有()对全等三角形。
八年级(上)第一次月考数学试题(前两章).doc

则DE 等于 (第9题图)(B) 2m(C) 3m (D) 4m八年级第一学月检测试卷吋量100分钟,满分100分,命题:高学群 审核:贺旭军一、选择题(本大题10个小题,每小题3分,共30分)5. 下列说法正确的是A 、周和面积都相等的两个三角形全等B 、全等三角形周长和面积都相等C 、全等三角形是指形状相同的两个三角形D 、全等三角形的边都相等6. 如图,ZB=ZI>90° , BC=CD, Zl=40° ,则Z2= 八、40° B 、50o C 、45O [)、60o7. 等腰三角形的一个角是80°,则它的底角是(A) 50° (B) 80° (C) 50° 或 80° (D) 20° 或 80°8. 如图,RtAABC 沿直角边BC 所在的直线向右平移得到△DEF ,下列结论中错误的是( ) A.B. ZDEF = 90°C. AC = DFD. EC = CF 9. 如图所示,己知AB=AC, PB=PC,下而的结论:①BE=CE;②AP 丄BC;③AE 平分ZBEC;④ZPEOZPEB,其中正确结论的个数有( )A. 1个 B 2个 C 3个 D 4个 10. 如图,是屋架设计图的一部分,点D 是斜梁AB 的屮点,立柱BC 、DE 垂直于横梁AC, AB=8m ,ZA-30 1. 下列阁形屮对称轴最多的是A.圆B.正方形C.等腰三角形D.线段2. 不能说明两个三角形全等的条件是 A.三边对应相等 C.两角及其夹边对应相等3. 下列图形中,不一定是轴对称图形的是A 、线段B 、等腰三角形 B.两边及其夹角对应相等 D.三角对应相等C 、正方形D 、平行四边形4. 如阁,AABC^ABAD,点A 和点B,点C 和点D 是对应点,如果AB=6cm, BD-5 cm,AD=4 cm,那么AC 的长是A 、4 cmB 、5 cmC 、6 cmD 、无法确定(第4题图)(第8题图)(二、填空题(本大题10个小题,每小题3分,共30分)11.己知44打€空2\£>£厂,?1与/?,万与万分别是对应顶点,乙4 = 52(), ZB = 67°, ZF= _____12. 如图,若 AB=DC, AC=DB,则有AABCS ______________________13. 如图,如果AA' B' C'与AABC 关于y 轴对称,那么点A 的对应点/V 的坐标为 ( )17. 角是轴对称图形,其对称轴是 _________________________ 所在的直线.18. 等边三角形的边长为I 则它的周长为 _______________ .19. 如图,己知:MSC 中,ZC = 90\ Ai/平分ZCAB, 6¥=20cm 那么;i/到必的距离是 ______________20.已知G 点关于x 轴的对称点P 2(3-2t/,26Z-5)是第三象限内的整点(横、纵坐标都为整数的点,C(第13题图)14. 如图,Z1=Z2,要使AABEPAACE,还需添加一个条件是 _______________(填上你认为适当的一个条件即可).15. 已知 AABC 给 AA’B’C’,AD 平分ZBAC,则 ZB’A’C’是ZBAD 的_16. 已知如图,在△/ff 厂和中,Z 加ZZ?,AB-DE,若再添加条件 证得△從C :倍• = ____ ,则可根据SAS称为整点),则€点的坐标是三.解答题:下列各题解答时必须给出必要的演算过程或推理步骤。
八年级上第一次月考数学试卷(有答案)

八年级上第一次月考数学试卷(有答案)一、选择题(每题3分,共30分)1.(3分)下列各数:0,3.14,﹣π,π﹣|1﹣π|,之间每次增加一个2),其中无理数的个数是()A.1B.2C.3D.4,,0.121221222122221…(每两个12.(3分)A.8的算术平方根是()D.±B.±8C.3.(3分)下列说法正确的有()(1)有理数包括整数、分数和零;(2)不带根号的数都是有理数;(3)带根号的数都是无理数;(4)无理数都是无限小数;(5)无限小数都是无理数.A.1B.2C.3D.4﹣1之值介于下列哪两个整数之间?()C.5,6D.6,7等于()D.﹣2某4.(3分)判断2A.3,4B.4,55.(3分)若某<0,则A.某B.2某C.06.(3分)△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,由下列条件不能判定△ABC为直角三角形的是()A.∠A+∠B=∠CC.a2=c2﹣b2B.∠A:∠B:∠C=1:2:3D.a:b:c=3:4:67.(3分)和数轴上的点成一一对应关系的数是()A.自然数B.有理数C.无理数D.实数8.(3分)△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长是()A.42B.32C.42或32D.42或379.(3分)如图所示,在数轴上点A所表示的数为a,则a的值为()A.﹣1﹣B.1﹣C.﹣D.﹣1+第1页共15页10.(3分)如图,在Rt△ABC中,∠ACB=90°,点D是AB的中点,且CD=的面积为1,则它的周长为(),如果Rt△ABCA.B.+1C.+2D.+3二、填空题(每空3分,共24分)11.(3分)的相反数是,绝对值是,倒数是.12.(3分)如图,若圆柱的底面周长是30cm,高是40cm,从圆柱底部A处沿侧面缠绕一圈丝线到顶部B处做装饰,则这条丝线的最小长度是.13.(3分)若一个正数的平方根是2a+1和﹣a+2,则a=,这个正数是.14.(3分)若+=0,则某=.15.(3分)已知一个Rt△的两边长分别为3和4,则第三边长是.16.4cm,3cm的木箱中,(3分)有一根7cm木棒,要放在长,宽,高分别为5cm,(填“能”或“不能”)放进去.17.(3分)要使代数式有意义,则某的取值范围是.18.(3分)如图所示,分别以直角三角形的三边为直径作三个半圆,S1=25,S2=144,则S3等于.第2页共15页三、解答题(共66分)19.(12分)计算题(1)(2)(3)(4)20.(8分)解方程(1)3(某﹣2)2﹣=0.(2)(2某﹣1)3﹣8=0.21.(8分)若+(b﹣3)2+|c﹣2|=0,求(a﹣b+c)3的值.,AD=1,且∠B=90°.试求:22.(10分)已知:如图,四边形ABCD中,AB=BC=1,CD=(1)∠BAD的度数.(2)四边形ABCD的面积.(结果保留根号)23.(8分)如图,折叠矩形ABCD的一边AD,使点D落在BC边上的点F处,已知AB=8cm,BC=10cm,(1)求BF长度;(2)求CE的长度.24.(8分)某隧道的截面是由如图所示的图形构成,图形下面是长方形ABCD,上面是半圆形,第3页共15页其中AB=10米,BC=2.5米,隧道设双向通车道,中间有宽度为2米的隔离墩,一辆满载家具的卡车,宽度为3米,高度为4.9米,请计算说明这辆卡车是否能安全通过这个隧道?25.(12分)阅读下面计算过程:1;.请解决下列问题(1)根据上面的规律,请直接写出(2)利用上面的解法,请化简:(3)你能根据上面的知识化简﹣﹣2=..吗?若能,请写出化简过程.第4页共15页八年级(上)第一次月考数学试卷参考答案与试题解析一、选择题(每题3分,共30分)1.(3分)下列各数:0,3.14,﹣π,π﹣|1﹣π|,,,0.121221222122221…(每两个1之间每次增加一个2),其中无理数的个数是()A.1B.2C.3D.4【解答】解:0是有理数,3.14是有理数,﹣π是无理数,π﹣|1﹣π|=π﹣(π﹣1)=1是有理数;=3是有理数;=2是有理数;0.121221222122221…是无理数.故选:B.2.(3分)A.8的算术平方根是()D.±=8,.B.±8C.【解答】解:∵∴的算术平方根是:故选:C.3.(3分)下列说法正确的有()(1)有理数包括整数、分数和零;(2)不带根号的数都是有理数;(3)带根号的数都是无理数;(4)无理数都是无限小数;(5)无限小数都是无理数.A.1B.2C.3D.4【解答】解:(1)有理数包括整数、分数,原来的说法是错误的;(2)π是无理数,原来的说法是错误的;第5页共15页。
八年级(上)第一次月考数学试卷(含答案) (1)

八年级(上)第一次月考数学试卷一、选择题(本大题共10小题,每小题3分,共30分)1.如图,图中直角三角形共有()A.1个B.2个C.3个D.4个2.下列说法中不正确的是()A.全等三角形的周长相等B.全等三角形的面积相等C.全等三角形能重合D.全等三角形一定是等边三角形3.能将三角形面积平分的是三角形的()A.角平分线B.高C.中线D.外角平分线4.从n边形的一个顶点作对角线,把这个n边形分成三角形的个数是()A.n B.(n﹣1)C.(n﹣2)D.(n﹣3)5.下列长度的三根小木棒能构成三角形的是()A.2cm,3cm,5cm B.7cm,4cm,2cmC.3cm,4cm,8cm D.3cm,3cm,4cm6.六边形共有几条对角线()A.6B.7C.8D.97.下列图形具有稳定性的是()A.B.C.D.8.如图,AB∥CD,点E在线段BC上,CD=CE.若∠ABC=30°,则∠D为()A.85°B.75°C.60°D.30°9.如图,∠2+∠3+∠4=320°,则∠1=()A.60度B.40度C.50度D.75度10.如图,在△ABC中,点D在BC上,AB=AD=DC,∠B=80°,则∠C的度数为()A.30°B.40°C.45°D.60°二、填空题(本大题共6小题,每小题4分,共24分)11.要想使一个六边形活动支架ABCDEF稳固且不变形,至少需要增加根木条才能固定.12.若等腰三角形的两边长分别为3cm和8cm,则它的周长是.13.三角形三边长分别为3,2a﹣1,4.则a的取值范围是.14.如果一个正多边形的一个外角是60°,那么这个正多边形的边数是.15.一个多边形的内角和是1800°,这个多边形是边形.16.如图,在△ABC中,BO、CO分别平分∠ABC、∠ACB.若∠BOC=110°,则∠A =.三、画图题17.(7分)作BC边上的中线AD,作∠B的角平分线线BE.四、解答题18.(7分)如果直角三角形的一个锐角是另一个锐角的4倍,求这个直角三角形中这两个锐角的度数.19.(7分)一个多边形的内角和比它的外角和的3倍少180°,求这个多边形的边数.20.(7分)如图,AC=AD,BC=BD,AB是∠CAD的平分线吗?请说明理由.21.(7分)如图,CD是△ABC的角平分线,DE∥BC,∠AED=70°,求∠EDC的度数.22.(7分)如图所示,已知AD是△ABC的边BC上的中线.(1)作出△ABD的边BD上的高;(2)若△ABC的面积为10,求△ADC的面积;23.(8分)如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD =10°,∠B=50°,求∠C的度数.24.(8分)如图,∠A=90°,∠B=21°,∠C=32°,求∠BDC的度数.25.(8分)如图,小明从点A出发,前进10m后向右转20°,再前进10m后又向右转20°,这样一直下去,直到他第一次回到出发点A为止,他所走的路径构成了一个多边形.(1)小明一共走了多少米?(2)这个多边形的内角和是多少度?八年级(上)第一次月考数学试卷参考答案与试题解析一、选择题(本大题共10小题,每小题3分,共30分)1.如图,图中直角三角形共有()A.1个B.2个C.3个D.4个【分析】根据直角三角形的定义:有一个角是直角的三角形是直角三角形,可作判断.【解答】解:如图,图中直角三角形有Rt△ABD、Rt△BDC、Rt△ABC,共有3个,故选:C.【点评】本题考查了直角三角形的定义,比较简单,掌握直角三角形的定义是关键,要做到不重不漏.2.下列说法中不正确的是()A.全等三角形的周长相等B.全等三角形的面积相等C.全等三角形能重合D.全等三角形一定是等边三角形【分析】根据全等三角形的性质得出AB=DE,AC=DF,BC=EF,即可判断A;根据全等三角形的性质得出△ABC和△DEF放在一起,能够完全重合,即可判断B、C;根据图形即可判断D.【解答】解:A、∵△ABC≌△DEF,∴AB=DE,AC=DF,BC=EF,∴AB+AC+BC=DE+DF+EF,故本选项错误;B、∵△ABC≌△DEF,即△ABC和△DEF放在一起,能够完全重合,即两三角形的面积相等,故本选项错误;C、∵△ABC≌△DEF,即△ABC和△DEF放在一起,能够完全重合,故本选项错误;D、如图△ABC和DEF不是等边三角形,但两三角形全等,故本选项正确;故选:D.【点评】本题考查了全等三角形的定义和性质的应用,能运用全等三角形的有关性质进行说理是解此题的关键,题目较好,但是一道比较容易出错的题目.3.能将三角形面积平分的是三角形的()A.角平分线B.高C.中线D.外角平分线【分析】根据三角形的面积公式,只要两个三角形具有等底等高,则两个三角形的面积相等.根据三角形的中线的概念,故能将三角形面积平分的是三角形的中线.【解答】解:根据等底等高可得,能将三角形面积平分的是三角形的中线.故选C.【点评】注意:三角形的中线能将三角形的面积分成相等的两部分.4.从n边形的一个顶点作对角线,把这个n边形分成三角形的个数是()A.n B.(n﹣1)C.(n﹣2)D.(n﹣3)【分析】可根据n边形从一个顶点引出的对角线与边的关系:n﹣3,可分成(n﹣2)个三角形直接判断.【解答】解:从n边形的一个顶点作对角线,把这个n边形分成三角形的个数是(n﹣2).故选:C.【点评】多边形有n条边,则经过多边形的一个顶点的所有对角线有(n﹣3)条,经过多边形的一个顶点的所有对角线把多边形分成(n﹣2)个三角形.5.下列长度的三根小木棒能构成三角形的是()A.2cm,3cm,5cm B.7cm,4cm,2cmC.3cm,4cm,8cm D.3cm,3cm,4cm【分析】依据三角形任意两边之和大于第三边求解即可.【解答】解:A、因为2+3=5,所以不能构成三角形,故A错误;B、因为2+4<7,所以不能构成三角形,故B错误;C、因为3+4<8,所以不能构成三角形,故C错误;D、因为3+3>4,所以能构成三角形,故D正确.故选:D.【点评】本题主要考查的是三角形的三边关系,掌握三角形的三边关系是解题的关键.6.六边形共有几条对角线()A.6B.7C.8D.9【分析】根据对角线公式计算即可得到结果.【解答】解:根据题意得:=9,则六边形共有9条对角线,故选:D.【点评】此题考查了多边形的对角线,n边形对角线公式为.7.下列图形具有稳定性的是()A.B.C.D.【分析】根据三角形具有稳定性,四边形具有不稳定性进行判断.【解答】解:三角形具有稳定性.故选:A.【点评】此题考查了三角形的稳定性和四边形的不稳定性,正确掌握三角形的性质是解题关键.8.如图,AB∥CD,点E在线段BC上,CD=CE.若∠ABC=30°,则∠D为()A.85°B.75°C.60°D.30°【分析】先由AB∥CD,得∠C=∠ABC=30°,CD=CE,得∠D=∠CED,再根据三角形内角和定理得,∠C+∠D+∠CED=180°,即30°+2∠D=180°,从而求出∠D.【解答】解:∵AB∥CD,∴∠C=∠ABC=30°,又∵CD=CE,∴∠D=∠CED,∵∠C+∠D+∠CED=180°,即30°+2∠D=180°,∴∠D=75°.故选:B.【点评】此题考查的是平行线的性质及三角形内角和定理,解题的关键是先根据平行线的性质求出∠C,再由CD=CE得出∠D=∠CED,由三角形内角和定理求出∠D.9.如图,∠2+∠3+∠4=320°,则∠1=()A.60度B.40度C.50度D.75度【分析】根据多边形的外角和等于360°即可得到结论.【解答】解:∵∠1+∠2+∠3+∠4=360°,∠2+∠3+∠4=320°,∴∠1=40°.故选:B.【点评】本题考查了多边形的内角和外角,熟记多边形的外角和等于360°是解题的关键.10.如图,在△ABC中,点D在BC上,AB=AD=DC,∠B=80°,则∠C的度数为()A.30°B.40°C.45°D.60°【分析】先根据等腰三角形的性质求出∠ADB的度数,再由平角的定义得出∠ADC的度数,根据等腰三角形的性质即可得出结论.【解答】解:∵△ABD 中,AB =AD ,∠B =80°,∴∠B =∠ADB =80°,∴∠ADC =180°﹣∠ADB =100°,∵AD =CD ,∴∠C ===40°.故选:B .【点评】本题考查的是等腰三角形的性质,熟知等腰三角形的两底角相等是解答此题的关键.二、填空题(本大题共6小题,每小题4分,共24分)11.要想使一个六边形活动支架ABCDEF 稳固且不变形,至少需要增加 3 根木条才能固定.【分析】首先根据三角形的稳定性,把六边形活动支架ABCDEF 分成三角形,然后根据从同一个顶点出发可以作出的对角线的条数解答即可.【解答】解:如图,,要想使一个六边形活动支架ABCDEF 稳固且不变形,至少需要增加3根木条才能固定.故答案为:3.【点评】此题主要考查了三角形的稳定性,要熟练掌握,解答此题的关键是熟记三角形具有稳定性.12.若等腰三角形的两边长分别为3cm 和8cm ,则它的周长是 19cm .【分析】题中没有指出哪个底哪个是腰,故应该分情况进行分析,注意应用三角形三边关系进行验证能否组成三角形.【解答】解:当3cm 是腰时,3+3<8,不符合三角形三边关系,故舍去;当8cm 是腰时,周长=8+8+3=19cm .故它的周长为19cm .故答案为:19cm .【点评】此题主要考查等腰三角形的性质及三角形三边关系的运用;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.13.三角形三边长分别为3,2a﹣1,4.则a的取值范围是1<a<4.【分析】根据三角形的三边关系为两边之和大于第三边,两边之差小于第三边,列出不等式即可求出a的取值范围.【解答】解:∵三角形的三边长分别为3,2a﹣1,4,∴4﹣3<2a﹣1<4+3,即1<a<4.故答案为:1<a<4.【点评】考查了三角形的三边关系,解题的关键是熟练掌握三角形三边关系的性质.14.如果一个正多边形的一个外角是60°,那么这个正多边形的边数是6.【分析】根据正多边形的每一个外角都相等,多边形的边数=360°÷60°,计算即可求解.【解答】解:这个正多边形的边数:360°÷60°=6.故答案为:6.【点评】本题考查了多边形的内角与外角的关系,熟记正多边形的边数与外角的关系是解题的关键.15.一个多边形的内角和是1800°,这个多边形是12边形.【分析】首先设这个多边形是n边形,然后根据题意得:(n﹣2)×180=1800,解此方程即可求得答案.【解答】解:设这个多边形是n边形,根据题意得:(n﹣2)×180=1800,解得:n=12.∴这个多边形是12边形.故答案为:12.【点评】此题考查了多边形的内角和定理.注意多边形的内角和为:(n﹣2)×180°.16.如图,在△ABC中,BO、CO分别平分∠ABC、∠ACB.若∠BOC=110°,则∠A =40°.【分析】先根据角平分线的定义得到∠OBC =∠ABC ,∠OCB =∠ACB ,再根据三角形内角和定理得∠BOC +∠OBC +∠OCB =180°,则∠BOC =180°﹣(∠ABC +∠ACB ),由于∠ABC +∠ACB =180°﹣∠A ,所以∠BOC =90°+∠A ,然后把∠BOC =110°代入计算可得到∠A 的度数.【解答】解:∵BO 、CO 分别平分∠ABC 、∠ACB ,∴∠OBC =∠ABC ,∠OCB =∠ACB ,而∠BOC +∠OBC +∠OCB =180°,∴∠BOC =180°﹣(∠OBC +∠OCB )=180°﹣(∠ABC +∠ACB ),∵∠A +∠ABC +∠ACB =180°,∴∠ABC +∠ACB =180°﹣∠A ,∴∠BOC =180°﹣(180°﹣∠A )=90°+∠A ,而∠BOC =110°,∴90°+∠A =110°∴∠A =40°.故答案为40°.【点评】本题考查了三角形内角和定理:三角形内角和是180°.三、画图题17.(7分)作BC 边上的中线AD ,作∠B 的角平分线线BE .【分析】根据尺规作图的要求作出中线AD ,角平分线BE 即可.【解答】解:如图,△ABC 的中线AD ,角平分线BE 即为所求.【点评】本题考查作图﹣复杂作图,三角形的中线,角平分线等知识,解题的关键是熟练掌握五种基本作图,属于中考常考题型.四、解答题18.(7分)如果直角三角形的一个锐角是另一个锐角的4倍,求这个直角三角形中这两个锐角的度数.【分析】根据直角三角形的两个角互余构建方程即可解决问题.【解答】解:设较小的锐角是x度,则另一角是4x度.则x+4x=90,解得:x=18°.答:这个直角三角形中这两个锐角的度数分别为18°和72°.【点评】本题主要考查了直角三角形的性质,两锐角互余,解题的关键是学会利用参数构建方程解决问题.19.(7分)一个多边形的内角和比它的外角和的3倍少180°,求这个多边形的边数.【分析】多边形的外角和是360度,根据多边形的内角和比它的外角和的3倍少180°,即可得到多边形的内角和的度数.根据多边形的内角和定理即可求得多边形的边数.【解答】解:设这个多边形的边数是n,依题意得(n﹣2)×180°=3×360°﹣180°,n﹣2=6﹣1,n=7.∴这个多边形的边数是7.【点评】本题考查了多边形的内角和与外角和定理,任意多边形的外角和都是360°,与边数无关.20.(7分)如图,AC=AD,BC=BD,AB是∠CAD的平分线吗?请说明理由.【分析】根据全等三角形的判定定理SSS证得△ACB≌△ADB,则其对应角相等:∠CAB =∠DAB,即AB是∠CAD的平分线.【解答】解:AB是∠CAD的平分线.理由如下:在△ACB与△ADB中,,∴△ACB≌△ADB(SSS),∴∠CAB=∠DAB,即AB是∠CAD的平分线.【点评】本题考查了全等三角形的判定与性质.在应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形.21.(7分)如图,CD是△ABC的角平分线,DE∥BC,∠AED=70°,求∠EDC的度数.【分析】由角平分线的定义,结合平行线的性质,易求∠EDC的度数.【解答】解:∵DE∥BC,∴∠ACB=∠AED=70°.∵CD平分∠ACB,∴∠BCD=∠ACB=35°.又∵DE ∥BC ,∴∠EDC =∠BCD =35°.【点评】本题考查了平行线的性质和角平分线定义的应用,注意:平行线的性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,题目比较好,难度适中.22.(7分)如图所示,已知AD 是△ABC 的边BC 上的中线.(1)作出△ABD 的边BD 上的高;(2)若△ABC 的面积为10,求△ADC 的面积;【分析】(1)利用尺规作AE ⊥BC ,垂足为E ,线段AE 即为所求;(2)利用三角形的中线把三角形分成两个面积相等的三角形即可;【解答】解:(1)如图线段AE 即为所求;(2)∵AD 是△ABC 的中线,∵S △ABD =S △ADC ,∵S △ABC =10,∴S △ADC =•S △ABC =5.【点评】本题考查作图﹣复杂作图,三角形的面积等知识,解题的关键是熟练掌握五种基本作图,属于中考常考题型.23.(8分)如图,在△ABC 中,AD 是BC 边上的高,AE 是∠BAC 的平分线,∠EAD =10°,∠B =50°,求∠C 的度数.【分析】根据直角三角形两锐角互余求出∠AED,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BAE,然后根据角平分线的定义求出∠BAC,再利用三角形的内角和定理列式计算即可得解.【解答】解:∵AD是BC边上的高,∠EAD=10°,∴∠AED=80°,∵∠B=50°,∴∠BAE=∠AED﹣∠B=80°﹣50°=30°,∵AE是∠BAC的角平分线,∴∠BAC=2∠BAE=60°,∴∠C=180°﹣∠B﹣∠BAC=180°﹣50°﹣60°=70°.【点评】本题考查了三角形的角平分线、中线和高,主要利用了直角三角形两锐角互余,三角形的一个外角等于与它不相邻的两个内角的和的性质,角平分线的定义,熟记各性质并准确识图是解题的关键.24.(8分)如图,∠A=90°,∠B=21°,∠C=32°,求∠BDC的度数.【分析】连接AD并延长AD至点E,根据三角形的外角性质求出∠BDE=∠BAE+∠B,∠CDE=∠CAD+∠C,即可求出答案.【解答】解:如图,连接AD并延长AD至点E,∵∠BDE=∠BAE+∠B,∠CDE=∠CAD+∠C∴∠BDC=∠BDE+∠CDE=∠CAD+∠C+∠BAD+∠B=∠BAC+∠B+∠C∵∠A=90°,∠B=21°,∠C=32°,∴∠BDC=90°+21°+32°=143°.【点评】本题考查了三角形的外角性质的应用,注意:三角形的一个外角等于和它不相邻的两个内角的和.25.(8分)如图,小明从点A出发,前进10m后向右转20°,再前进10m后又向右转20°,这样一直下去,直到他第一次回到出发点A为止,他所走的路径构成了一个多边形.(1)小明一共走了多少米?(2)这个多边形的内角和是多少度?【分析】(1)第一次回到出发点A时,所经过的路线正好构成一个外角是20度的正多边形,求得边数,即可求解;(2)根据多边形的内角和公式即可得到结论.【解答】解:(1)∵所经过的路线正好构成一个外角是20度的正多边形,∴360÷20=18,18×10=180(米);答:小明一共走了180米;(2)根据题意得:(18﹣2)×180°=2880°,答:这个多边形的内角和是2880度.【点评】本题考查了正多边形的外角的计算以及多边形的内角和,第一次回到出发点A 时,所经过的路线正好构成一个外角是20度的正多边形是关键.。
八上第一次月考Microsoft Word 文档 (4)
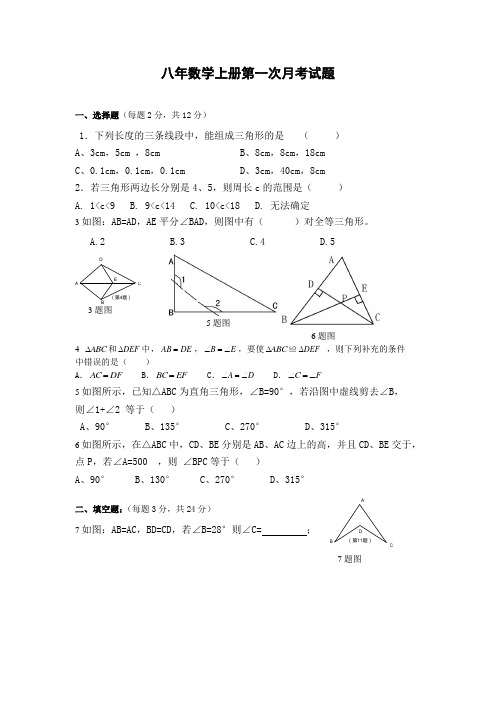
八年数学上册第一次月考试题一、选择题(每题2分,共12分)1.下列长度的三条线段中,能组成三角形的是 ( )A 、3cm ,5cm ,8cmB 、8cm ,8cm ,18cmC 、0.1cm ,0.1cm ,0.1cmD 、3cm ,40cm ,8cm 2.若三角形两边长分别是4、5,则周长c 的范围是( ) A. 1<c<9 B. 9<c<14 C. 10<c<18 D. 无法确定3如图:AB=AD ,AE 平分∠BAD ,则图中有( )对全等三角形。
A.2B.3C.4D.53题图5题图6题图4 ABC ∆和DEF ∆中,DE AB =,E B ∠=∠,要使ABC ∆≌DEF ∆ ,则下列补充的条件 中错误的是( )A .DF AC =B .EF BC = C .D A ∠=∠ D .F C ∠=∠5如图所示,已知△ABC 为直角三角形,∠B=90°,若沿图中虚线剪去∠B ,则∠1+∠2 等于( )A 、90°B 、135°C 、270°D 、315°6如图所示,在△ABC 中,CD 、BE 分别是AB 、AC 边上的高,并且CD 、BE 交于,点P ,若∠A=500 ,则 ∠BPC 等于( )A 、90°B 、130°C 、270°D 、315°二、填空题:(每题3分,共24分)7如图:AB=AC ,BD=CD ,若∠B=28°则∠C= ;7题图(第4题)EDCBA (第11题)D CBA8 若一个等腰三角形的两边长分别是3 cm 和5 cm ,则它的周长是 cm 。
9 如图:在△ABC 中,AD=AE ,BD=EC ,∠ADB=∠AEC=105°,∠B=40°,则∠CAE= ;9题图 10题图 12题图10 如图:AB ,CD 相交于点O ,AD =CB ,请你补充一个条件,使得 △AOD ≌△COB ,你补充的条件是 ;11.已知a 、b 、c 是三角形的三边长,化简:|a -b +c|+|a -b-c|=___________ 12为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根木条,这样做 的道理是 。
2011—2012学年遵义县南锋学校八年级上第一次月考数学试题

遵义县南锋学校2011—2012学年度第一学期月考试卷八 年 级 数 学(考试时间:120分钟,满分120分) (命题:韩小娟 审题:涂成芬)班级 姓名 学号得分 一. 填空题(每小题3分,共24分) 1、如图,若 △ABC ≌△DEF ,则∠E= °2、.已知△ABC ≌△DEF ,BC=EF=8cm ,△ABC 的面积为24cm 2,则FE 边上的高为 cm.3、等腰三角形的一个内角为40°,则它的顶角为 .4、已知点A(a,-2)与点B(-1,b)关于X 轴对称,则a+b= .5、如图,已知△ABC 的周长为36cm,且AB=AC,AD ⊥BC 于D, △ABD 的周长为30 cm,那么AD 的长为 .6、如图,在△ABC 中,AB=AC,D 为BC 上一点,且,AB=BD,AD=DC, 则∠C= 度.第5题 第6题7、小强从镜子中看到的电子表的读数如图所示,则电子表的实际读数是 . 8、如果等腰三角形一腰上的高等于腰长的一半,那么这个三角形的顶角为 度。
二. 选择题(每小题4分,共32分)9、下列各条件中,不能作出唯一三角形的是( ) A .已知两边和夹角 B .已知两角和夹边 C .已知两边和其中一边的对角 D .已知三边10、三角形内到三条边的距离相等的点是( )A 、三角形的三条角平分线的交点B 、三角形的三条高的交点C 、三角形的三条中线的交点D 、以上答案都不正确11、如图,AC 与BD 相交于O ,∠1=∠4,∠2=∠3,△ABC 的周长为25㎝,△AOD 的周长为17㎝,则AB=( )A 、4㎝B 、8㎝C 、12㎝D 、无法确定 12、一只小狗正在平面镜前欣赏自己的全身像(如图所示),此时,它所看到的全身像是( )13、如图,△ABC 中,AB=AC,D 是BC 中点,下列结论中不正确...的是 ( ) A. ∠B=∠C B. AD ⊥BC C. AD 平分∠BAC D. AB=2BD 14、等腰三角形的周长为cm 13,其中一边长为3cm ,则 该等腰三角形的底边为 ( )A. 7cmB. cm 3C. 7cm 或cm 3D. cm 8 15、一个三角形任意一边上的高都是这边上的中线,•则对这个三角形的形状最准确的判断是( )A .等腰三角形B .直角三角形C .正三角形D .等腰直角三角形 16、如图,∠BAC=110°若MP 和NQ 分别垂直平分 AB 和AC,则∠PAQ 的度数是( )A.20°B. 40°C. 50°D. 60°第16题 三.解答题(共64分)17. (1)请画出ABC △关于y 轴对称的A B C '''△(其中A B C ''',,分别是A B C ,,的对应点,不写画法);(10分)(2)直接写出A B C ''',,三点的坐标:ACDBCC第13题DCBA第1题DCBAO 123 4(_____)(_____)(_____)A B C ''',,.(3)求△ABC 的面积是多少?18.已知:如图,AD 平分∠BAC, DE ⊥AB, DF ⊥AC , DB=DC ,求证:△ABC 是等腰三角形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
O D C B A 第11题图 班级: 姓名: 学号:
………………………密…………………………………封………………………………………线…………………………………………………
第10题图 F C E B A
D 第7题图 ④ ①② ③
赣州一中2011-2012学年八年级上学期数学第一次月考测试卷
(考试时间120分钟,满分120分) 一、选择题(每小题3分,共30分) 1、下列命题正确的是( ) A .全等三角形是指形状相同的两个三角形 B .全等三角形是指面积相同的两个三角形
C .两个周长相等的三角形是全等三角形
D .全等三角形的周长、面积分别相等 2、如图所示表示三条相互交叉的公路,现要建一个货物中转站, 要求它到三条公路的距离相等,则可供选择的地址有( ) A.1处 B.2处 C.3处 D.4处 3、下图中的轴对称图形有( ).
A .(1),(2)
B .(1),(4)
C .(2),(3)
D .(3),(4)
4、下列判断中错误..的是( ) A .有两角和一边对应相等的两个三角形全等 B .有两边和一角对应相等的两个三角形全等
C .有两边和其中一边上的中线对应相等的两个三角形全等
D .有一边对应相等的两个等边三角形全等 5、如图,AB 垂直平分CD ,若AC=1.6cm ,BC=2.3cm ,则四边形ABCD 的周长是( )cm. A.3.9 B.7.8 C.4 D.4.6 6、如图,点P 是∠BAC 的平分线AD 上一点,P
E ⊥AC 于点E .已知PE =3,则点P 到AB 的距离是( ) A .3 B .4 C .5 D .6 7、如图,∠B 和∠C 的平分线相交于点
F ,过点F 作DE ∥BC 交AB 于点D ,交AC 于点E ,若BD+CE=9,则线段DE 的长为( ) A .9 B .8 C .7 D .6 8、下列条件中不能作出唯一直角三角形的是( )
A. 已知两个锐角
B. 已知一条直角边和一个锐角
C. 已知两条直角边
D. 已知一条直角边和斜边
9、如图,在直角ABC △中,90C =∠,AB 的垂直平分线交AB 于D , 交AC 于E ,且2EBC EBA =∠∠,则A ∠等于( ) A.20 B.22.5 C.25 D.27.5
10、如图,在直角三角形ABC 中,∠C =90°,AC =10cm ,BC =5cm ,线段PQ =AB , P 、Q 两点分别在AC
和AC 的垂线AX 上移动,则当AP = 时,才能使△ABC 和△APQ 全等.
二、填空题(每小题3分,共18分)
11、如图,线段AC 与BD 交于点O ,且OA=OC, 请添加一个条件,使△OAB ≌△OCD,这个条件可以是______________________. 12、如图,50ABC AD ∠=,垂直平分线段BC 于点D ABC ∠,的平分线BE 交AD 于点E ,
连结EC ,则∠C 的度数是 . 13、如图,△ABC 中,AB=AC=17,BC=16,DE 垂直平分AB ,则△BCD 的周长是 14、如图,已知△ABC 的周长是21,OB,OC 分别平分∠ABC 和∠ACB ,OD ⊥BC 于D ,且OD =3,△ABC 的面积是___________ 15、如图,有一块边长为4的正方形塑料模板ABCD ,将一块足够大的直角三角板的直角顶点落在A 点,两条直角边分别与CD 交于点F ,与CB 延长线交于点E .则四边形AECF 的面积是 . 16、如图,已知△ABC 的六个元素,下面甲、乙、丙三个三角形中标出了某些元素,则与△ABC 全
等的三角形是 . 座 号
C D B E A 第12题图 A B
C
a
b c 74 41
65
b a 41
甲
74
c
b 乙
65 74
a
丙
第13题图 A D F
C B E 第15题图 第6题图
D C A
E 第9题图 A D O C B 第14题图 A 第5题图
2
三.解答题(共72分) 17、(作图6分)近年来,国家实施“村村通”工程和农村医疗卫生改革,某县计划在张村、李村之间建一座定点医疗站P ,张、李两村座落在两相交公路内(如图所示).医疗站必须满足下列条件:①使其到两公路距离相等,②到张、李两村的距离也相等,请你通过作图确定P 点的位置. 18、(7分)完成下面的证明过程: 如图,已知:AD ∥BC ,AD =CB ,AE =CF. 求证:∠D =∠B. 证明:∵AD ∥BC ,
∴∠A =∠ (两直线平行, 相等). ∵AE =CF , ∴AF = . 在△AFD 和△CEB 中,
AD _____,
A ____,AF _____,⎧=⎪
∠=∠⎨⎪=⎩
∴△AFD ≌△CEB ( ). ∴∠D =∠B.
19、(8分)已知:如图,直线AD 与BC 交于点O ,OA OD =,
OB OC =.求证:AB CD ∥.
20、(9分)如图,D 是AB 上一点,DF 交AC 于点E,DE=FE,FC//AB.AE 与CE 有什么关系?证明你的结论。
21、(10分)如图,在△ABC 中,AD 为∠BAC 的平分线,DE ⊥AB 于E ,DF ⊥AC 于F ,△ABC 面积是28cm 2
,AB=20cm ,AC=8cm ,求DE 的长.
22、(10分)已知:如图,AB =AC ,BD ⊥AC ,CE ⊥AB ,垂足分别为D 、E ,BD 、CE 相交于点F , 求证:BE =CD .
23、(10分)如图,已知△ABC 的外角∠CBD 和∠BCE 的平分线相交于点F ,求证:点F 在∠BAC 的平分线上.
24、(12分)如图,AB//CD,BE 、CE 分别是∠ABC 、∠BCD 的平分线,点E 在AD 上,BE 的延长线交CD
的延长线于F.求证:(1) AE=ED (2)BC=AB+CD
E D F
A
B
C
A
B
D
C
O
A C
B D E F E
B
F
C
D
E A B
C
F
D。
