材料力学习题答案_刘文鸿_第四版
材料力学第四版课后习题答案
材料力学第四版课后习题答案1. 引言。
材料力学是材料科学与工程中的重要基础课程，通过学习材料力学，可以帮助我们更好地理解材料的性能和行为。
本文档将针对材料力学第四版的课后习题进行答案解析，帮助学习者更好地掌握课程内容。
2. 第一章。
2.1 课后习题1。
答，根据受力分析，可以得到杆件的受力情况。
然后利用杆件的受力平衡条件，可以得到杆件的应力状态。
最后，根据应力状态计算应变和变形。
2.2 课后习题2。
答，利用受力分析，可以得到杆件的受力情况。
然后利用杆件的受力平衡条件，可以得到杆件的应力状态。
最后，根据应力状态计算应变和变形。
3. 第二章。
3.1 课后习题1。
答，利用受力分析，可以得到梁的受力情况。
然后利用梁的受力平衡条件，可以得到梁的应力状态。
最后，根据应力状态计算应变和变形。
3.2 课后习题2。
答，利用受力分析，可以得到梁的受力情况。
然后利用梁的受力平衡条件，可以得到梁的应力状态。
最后，根据应力状态计算应变和变形。
4. 第三章。
4.1 课后习题1。
答，利用受力分析，可以得到薄壁压力容器的受力情况。
然后利用薄壁压力容器的受力平衡条件，可以得到薄壁压力容器的应力状态。
最后，根据应力状态计算应变和变形。
4.2 课后习题2。
答，利用受力分析，可以得到薄壁压力容器的受力情况。
然后利用薄壁压力容器的受力平衡条件，可以得到薄壁压力容器的应力状态。
最后，根据应力状态计算应变和变形。
5. 结论。
通过对材料力学第四版课后习题的答案解析，我们可以更好地掌握材料力学的基本原理和方法。
希望本文档能够对学习者有所帮助，促进大家对材料力学的深入理解和应用。
刘鸿文材料力学习题册
正确的是（
）
(A) 50 MPa （压应力）； (B) 40 MPa （压应力）；
m
5 kN
4 kN
13 kN
(C) 90 MPa （压应力）； (D) 90 MPa （拉应力）。
m
（2）等截面直杆受轴向拉力 F 作用发生拉伸变形。已知横截面面积为 A，以下给出的横截面上 的正应力和 45 斜截面上的正应力的四种结果，正确的是（ ）
（4）应力是内力分布集度。（ ）
（5）材料力学主要研究构件弹性范围内的小变形问题。（ ）
（6）若物体产生位移，则必定同时产生变形。 （ ）
（7）各向同性假设认为，材料沿各个方向具有相同的变形。（ ）
（8）均匀性假设认为，材料内部各点的力学性质是相同的。
（）
（9）根据连续性假设，杆件截面上的内力是连续分布的，分布内力系的合力必定是一个力。
（D）若物体产生变形，则必定物体内各点均有位移。
（8）关于确定截面内力的截面法的适用范围，有下列说法正确的是（ ） （A）等截面直杆； （B）直杆承受基本变形； （C）不论基本变形还是组合变形，但限于直杆的横截面； （D）不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普遍情
况。
1）同一截面上正应力 与切应力 必相互垂直。
2）同一截面上各点的正应力 必定大小相等，方向相同。
3）同一截面上各点的切应力 必相互平行。
现有四种答案，正确答案是（ ）
（A）1 对；
（B）1、2 对； （C）1、3 对； （D）2、3 对。
（5）材料力学中的内力是指（ ） （A）构件内部的力； （B）构件内部各质点间固有的相互作用力； （C）构件内部一部分与另一部分之间的相互作用力； （D）因外力作用，而引起构件内部一部分对另一部分作用力的改变量
工程力学--材料力学(北京科大、东北大学版)第4版4-6习题答案
第四章习题4-1 求下列各梁指定截面上的剪力Q和弯矩M。
各截面无限趋近于梁上A、B、C等各点。
4-2 试列出下列各梁的剪力方程和弯矩方程，作剪力图和弯矩图，并求和。
4-3 用叠加法作以下各梁的弯矩图。
并求出。
4-4 用剪力、弯矩和分布载荷集度之间的微分关系校核前面已画的剪力图和弯矩图是否正确。
4-5 不列剪力方程和弯矩方程，作以下各梁的剪力图和弯矩图，并求出和。
4-6 用合适的方法作下列各梁的剪力图和弯矩图。
4-7 试根据载荷、剪力图和弯矩图之间的关系，检查下列各梁的剪力图和弯矩图是否正确，并对错误之处加以改正。
4-8 作下列构件的内力图。
4-9 在梁上行走的小车二轮的轮压均为P ，如图所示。
问小车行至何位置时梁内的弯矩最大？最大弯矩值是多少？设小车的轮距为c，大梁的跨度为。
参考答案4-1 解：题（b）（1）求支反力（见图）由，l-P l=0 =由，（2）剪力按计算剪力的规则（3）弯矩按计算弯矩的规则其它各题的答案：（a）（c）（d）（e）（f）4-2 解：题c(1)剪力和弯矩方程以左端A为原点，任一截面距左端的距离为x（图）\剪力方程:弯矩方程:(2 )剪力图与弯矩图按上述剪力方程和弯矩方程绘剪力图和弯矩图（3）与值由及得=200N =950题（f）（1）求支反力（见图）由，600-1004040=0=由，q4020-60=0=校核：+=2667+1333=4000N=q40=10040 所以支反力计算正确（2）剪力和弯矩方程以左端为原点，任一截面距左端的距离为x，则得剪力方程：弯矩方程（2）剪力图和弯矩图按上述剪力及弯矩方程绘出图及所示的剪力图和弯矩图所示剪力图和弯矩图.图中最大弯矩的截面位置可由，即剪力的条件求得Q（x）=3333-100x=0x=33.3cm（4）及由及得=2667N ，=355其他各题的答案：（a）=ql =（b）（d）（e）（g）（h）（i）（j）4-3 解：题c分别作、q单独作用时的弯矩图（图、），然后将此二图叠加得总的弯矩图。
材料力学第四版版答案7.docx
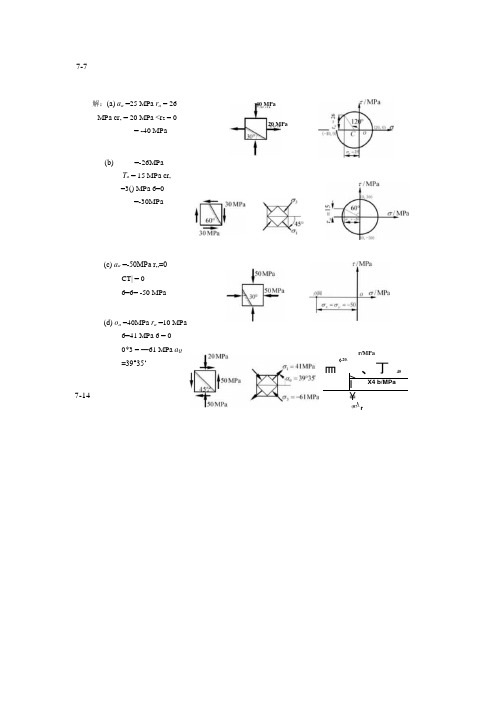
(c) a a =-50MPa r…=0CT| = 0 6=6= -50 MPa(d) o a =40MPa r a =10 MPa6=41 MPa 6 = 0 0*3 = —61 MPa a Q =39°35‘7-7 解：(a) a a =25 MPa r a = 26 MPa cr, = 20 MPa <r 2 = 0= -40 MPa (b) =-26MPa T a = 15 MPa cr, =3() MPa 6=0=-30MPa40 MPa20 MPa7-14(-20.皿、丁40> I X4 b/MPa ¥\ (0?^rr/MPa7-15单元体各面上的应力如图所示。
试用应力圆的儿何关系求主应力及最人切应力。
解：(a)由卩平面内应力值作a, b点,连接"交O•轴得圆心C (5(). 0)应力圆半径心)2+时=44.726 =50+44.7 = 94.7 MPa cr3=50-44.7 = 5.3 MPa (T2 = 50MPa2= 44.7 MPay r/MPa(b)由心平面内应力作g b点,连接血交O•轴丁•(？点，0030.故应力圆半径则: r = >/302 +402 = 506 =30 +50 = 8() MPaa2 =50 MPa a3=-20 MPa= 5() MPa(c)由图7-15 (c)yz平面内应力值作a, b点,圆心为O,半径为50,作应力圆得6 = 5() MPaa2 =-50 MPa6 =-80 MPa50 MPar/MPamax '6 一6 ,二」——=65MPa27-187-19在矩形截面钢拉伸试样的轴向拉力F = 20kN时，测得试样中段B点处与其轴线成30°方向的线应变为a. =3.25x10"。
已知材料的弹性模量£ = 210GPa ,试求泊松比解:F 20X103A " 20x10x10" = 10() MPa CT=a cos2a = —a = 75 MPa4cr|20. = cr cos2a = 25 MPa3.25X10_4 X210X 109 = (75-yx25)x IO6 v = 0.27M c = M n = 690kN- m Fsc 狂=佗 D 右=670 kN7-197-20 D= 120mm,治&hnm 的空心圆轴，两端承受一对扭转力偶矩，如图所示。
材料力学-刘鸿文-第四版-第五章
σmax
M
y max max Iz
σ
1.弯矩最大的截面上
2.离中性轴最远处
3.变截面梁要综合考虑 M与 Iz
4.脆性材料抗拉和抗压性能不同，二方面都要考虑
s t,max s t
s c,max s c
2019年9月22日2时45分
材料力学 第五章 弯曲应力
根据强度条件可进行：
s t,max
2.5103 88103 7.64106
28.8106 Pa 28.8MPa s t
2019年9月22日2时45分
材料力学 第五章 弯曲应力
例5-3-5：图a所示为横截面如图b所示的槽形截面铸铁梁，该 截面对于中性轴z 的惯性矩Iz=5493×104 mm4。已知图a中， b=2 m。铸铁的许用拉应力[st]=30 MPa，许用压应力[s c]=90 MPa 。试求梁的许可荷载[F]。
4
Iz
显然，B截面上的最大拉应力控制了梁的强度。
2019年9月22日2时45分
材料力学 第五章 弯曲应力 第四章 弯曲应力
于是由B截面上最大拉应力不得超过铸铁的许用拉应
力[st]的条件来求该梁的许可荷载[F]：
F 2 m 86103 m
2
5493108 m4
l /2
F
AaCB Nhomakorabeal
z
NO.16
2019年9月22日2时45分
材料力学 第五章 弯曲应力
解： 1)s C EC 210 103 400 10 6 84MPa
M
C
s C
FB (l a) 0.25F
刘鸿文材料力学习题册
材料力学A习题册学院专业学号教师学生姓名练习1 绪论及基本概念1-1 是非题（1）材料力学是研究构件承载能力的一门学科。
（）（2）可变形固体的变形必须满足几何相容条件，即变形后的固体既不可以引起“空隙”，也不产生“挤入”现象。
（）（3）构件在载荷作用下发生的变形，包括构件尺寸的改变和形状的改变。
（）（4）应力是内力分布集度。
（）（5）材料力学主要研究构件弹性范围内的小变形问题。
（）（6）若物体产生位移，则必定同时产生变形。
（）（7）各向同性假设认为，材料沿各个方向具有相同的变形。
（）（8）均匀性假设认为，材料内部各点的力学性质是相同的。
（）（9）根据连续性假设，杆件截面上的内力是连续分布的，分布内力系的合力必定是一个力。
（）（10）因为构件是变形固体，在研究构件的平衡时，应按变形后的尺寸进行计算。
（）1-2 填空题（1）根据材料的主要性质对材料作如下三个基本假设：、、。
（2）工程中的，是指构件抵抗破坏的能力；，是指构件抵抗变形的能力。
（3）保证构件正常或安全工作的基本要求包括，，和三个方面。
（4）图示构件中，杆1发生变形，杆2发生变形，杆3发生变形。
（5）认为固体在其整个几何空间内无间隙地充满了物质，这样的假设称为。
根据这一假设构件的应力，应变和位移就可以用坐标的函数来表示。
（6）图示结构中，杆1发生变形，构件2发生变形，杆件3发生变形。
（7）解除外力后，能完全消失的变形称为，不能消失而残余的的那部分变形称为。
（8）根据条件，可以认为构件的变形远其原始尺寸。
1-3 选择题（1）材料力学中对构件的受力和变形等问题可用连续函数来描述；通过试件所测得的材料的力学性能，可用于构件内部的任何部位。
这是因为对可变形固体采用了（）假设。
（A）连续均匀性；（B）各向同性；（C）小变形；（D）平面。
（2）研究构件或其一部分的平衡问题时，采用构件变形前的原始尺寸进行计算，这是因为采用了（）假设。
（A）平面；（B）连续均匀性；（C）小变形；（D）各向同性。
刘鸿文材料力学习题册
材料力学A习题册学院专业学号教师学生姓名练习1 绪论及基本概念1-1 是非题（1）材料力学是研究构件承载能力的一门学科。
（）（2）可变形固体的变形必须满足几何相容条件，即变形后的固体既不可以引起“空隙”，也不产生“挤入”现象。
（）（3）构件在载荷作用下发生的变形，包括构件尺寸的改变和形状的改变。
（）（4）应力是内力分布集度。
（）（5）材料力学主要研究构件弹性范围内的小变形问题。
（）（6）若物体产生位移，则必定同时产生变形。
（）（7）各向同性假设认为，材料沿各个方向具有相同的变形。
（）（8）均匀性假设认为，材料内部各点的力学性质是相同的。
（）（9）根据连续性假设，杆件截面上的内力是连续分布的，分布内力系的合力必定是一个力。
（）（10）因为构件是变形固体，在研究构件的平衡时，应按变形后的尺寸进行计算。
（）1-2 填空题（1）根据材料的主要性质对材料作如下三个基本假设：、、。
（2）工程中的，是指构件抵抗破坏的能力；，是指构件抵抗变形的能力。
（3）保证构件正常或安全工作的基本要求包括，，和三个方面。
（4）图示构件中，杆1发生变形，杆2发生变形，Array杆3发生变形。
（5）认为固体在其整个几何空间内无间隙地充满了物质，这样的假设称为。
根据这一假设构件的应力，应变和位移就可以用坐标的函数来表示。
（6）图示结构中，杆1发生变形，构件2发生变形，杆件3发生变形。
（7）解除外力后，能完全消失的变形称为，不能消失而残余的的那部分变形称为。
（8）根据条件，可以认为构件的变形远其原始尺寸。
1-3 选择题（1）材料力学中对构件的受力和变形等问题可用连续函数来描述；通过试件所测得的材料的力学性能，可用于构件内部的任何部位。
这是因为对可变形固体采用了（）假设。
（A）连续均匀性；（B）各向同性；（C）小变形；（D）平面。
（2）研究构件或其一部分的平衡问题时，采用构件变形前的原始尺寸进行计算，这是因为采用了（）假设。
（A）平面；（B）连续均匀性；（C）小变形；（D）各向同性。
工程力学--材料力学(北京科大、东北大学版)第4版习题答案
第一章参考答案1-1：解：(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3= -P(d):N1=-2P,N2=P(e):N1= -50N,N2= -90N(f):N1=0.896P,N2=-0.732P注（轴向拉伸为正，压缩为负）1-2：解：σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa ∴σmax=35.3Mpa1-3：解：下端螺孔截面：σ1=19020.065*0.045P S =15.4Mpa上端单螺孔截面：σ2=2PS =8.72MPa上端双螺孔截面：σ3= 3PS =9.15Mpa∴σmax =15.4Mpa1-4：解：受力分析得：F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5 MPa1-5：解:F=6PS1=h*t=40*4.5=180mm2S2=(H-d)*t=(65-30)*4.5=157.5mm2∴σmax=2FS =38.1MPa1-6:解: (1)σAC =-20MPa,σCD =0,σDB =-20MPa;△ l AC =NL EA =AC LEA σ=-0.01mm△ l CD =CD LEA σ=0△ L DB =DB LEA σ=-0.01mm(2) ∴AB l ∆=-0.02mm1-7:解:31.8127AC AC CB CB P MPa S P MPa S σσ==== AC AC AC L NL EA EA σε===1.59*104, CB CB CB L NL EA EA σε===6.36*1041-8:解:Nll EAl l ε∆=∆= ∴NEA ε=62.54*10N EA N ε∴==1-9：解：208,0.317E GPa ν==1-10：解：[][]max 59.5MPa σσ=<1-11：解：（1）当45oα=，[]11.2σσ=>强度不够 （2）当60oα=，[]9.17σσ=< 强度够 1-12：解：[]360,200200200*1013.3100*150*10Y p kNS P kNS MPa A σσ-==∴=====<∑1-13：解：[]max 200213MPa MPa σ=<1-14：解： 1.78, 1.26d cm d cm ==拉杆链环1-15 解：BC F ==70.7 kN70.70.505140F S FS σσ=∴=== 查表得： 45*45*31-16解：(1)[]2401601.5ss n σσ===MPa[][]24P SP dσσπ≤∴≤24.4D mm∴=(2)2119.51602P P MPa MPa S d σπ===≤⎛⎫ ⎪⎝⎭1-17 解：（1） 2*250*6154402D F P A N π⎛⎫=== ⎪⎝⎭78.4AC F MPa S σ== 300 3.8378.4s n σσ∴===[][]''''60*3.14*15*1542390F S F S Nσσ===='61544014.521542390F n F ===≈1-18 解：P=119kN1-19 解：::3:4:535()44AB BC AB BC S P S S P S P =∴==拉，[][][]112841123484AB AB S A kN S P kN P kN σ=====同理所以最大载荷 84kN1-20 解： P=33.3 kN1-21 解：71,,12123A B C P F F P F P ===1-22 解：10MAX MPa σ=-1-23 解：A B X R R R =∴==∑t r l l ∆=∆ t A B l l tα∆= 21211111223533131.3cd R AC DB CD AC CD CD AF CD MAX Rl Rl l l l l EA EA Rl Rl Rl l EA EA EA EA t EA t R l S MPa A ααασ∆=∆+∆+∆=+=+=∴====第二章习题2-1 一螺栓连接如图所示，已知P=200 kN ， =2 cm ，螺栓材料的许用切应力[τ]=80Mpa ，试求螺栓的直径。