球形电容器的电容及场强的讨论
计算电容器电容的一种简易方法

洛 阳师 范 学 院 学 报 2 0 第 5期 02年
・3 ・ 9
计 算 电 容 器 电 容’ 一 种 简 易 方 法 的
陈建新
( 国际关系学 院理工教学 部 , 苏杭州 30 1) 江 105
摘 要 :本 文从 电场 能 量 角度 出发 ,以球 形 电容 器为例 , 导 出 了一 种计 算 电容 的 简 易方 法 , 推 并 结合 实例 说 明 了该 方 法的 具体 应 用 .
求 出 电容 器 内 的 电场 分 布 ,然 后 求 出两极 间 的 电 位 差 , 后 根 据 电容 的定 义 式 求 出 电 容 .这 种方 最 法 具 有求 解 过 程 严 谨 、物 理 思 路 清 晰 的 特 点 ,被 普 遍 采用 .但笔 者 认 为这 种 方 法 在 求 解 某 些具 体
洛 阳 师 范 学 院学 报 20 第 5期 02年
1 直 接 反 映 了 电容 器 电容 只 与 本 身 结 构 有 . 关 的 基本 特 性 ; 2 .在 计 算 对 称 性 电 容 器 电 容 时 更 为 简 捷 、
直观 ;
弯 处 的边 缘效 应 时 ,对 每一 对 平行 板 构 成 的 电容 器 而 言 ,它 的等 位 面仍 可 看 成是 一 个 平 面 ,由 图 可 知 ,距 轴 心 r 的等位 面 面积 的表 达 式 为 处
( ) 的特点 在 于 : 5式
任意形 状 电 容 器 电容 的计 算 公 式 . 中积 分 方 向 式
收 稿 日期 :20 —0 {2 5—1 } 1 作者简介 :陈建新 (90一) 男 、 16 , 湖北 黄石人 ,高级教 师
维普资讯
・
4 ・ 0
法线 方 向为 该 处 的径 向 方 向 ,即场 强 方 向 .根据 式 () 5 ,便 可得 出圆 柱形 电容器 电容 为
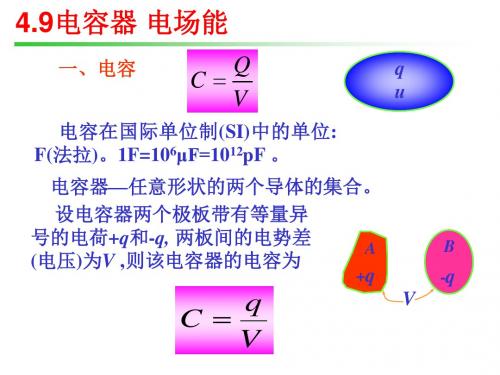
大学物理 4.9 电容器 电场能
L
3. 球型电容器
如图半径不同的两个均匀带电球面, 其带电量为+q、-q,由高斯定理得两球 面间任意点场强为:
RA RB
E
q 4 0 r 2
U A UB q
RB RB RB
所以面间电势差为:
RA
E d r Edr 4
RA RA
q
0
r
2
dr
等效电容 +Q -Q UA C UC
1 1 U A U C Q C C 2 1
一般n 个电容器串 联的等效电容为
Q UA UB C1 Q U B UC +) C2
Q U A UC C 1 1 1 C C1 C 2
n 1 1 C i Ci
C r 1 C0
或
C r C0
平行板电容器 球型电容器
C
o r S
d
有介质时
4 0 r RA RB C RB RA
圆柱形电容器
2 o r L C R2 ln R1
三、电容器的串联与并联
1、串联
+Q -Q UA C1
+Q -Q UB C2 U C
q1+q2 dr -q1 r q1 o
R3 R2 R1
(3) 电介质中的电场能量:
解 (1)由高斯定理有:
q1+q2
R3
0 r R1 : E1 0;
R1 r R2 : E2
4 o r r R2 r R3 : E3 0;
q1
; 2
-q1
q1 o oR1
R2
§12 怎样求电容器的电容和能量

§12 怎样求电容器的电容和能量一、电容的计算电容的计算一般有三种方法: 1、 利用电容的定义式Q Q C U U∆==∆来计算,具体步骤如下: 先计算电场强度,进而计算电势差。
在电势差U ∆的表达式中,已经包含了电量Q 与电势差U 的比值,因此,对电势差表达式进行整理,即可由电容的定义Q Q C U U∆==∆算得电容。
2、 通过电容器的储能公式()221122e Q W C U C=∆=来计算;由U ∆→W e →C ; 或者是Q →W e →C.3、 对于串联、并联、混联,可用前面两种方法,但往往直接用电容的串、并联计算公式更为方便。
即:串联时: 111ni iC C ==∑并联时: 1ni i C C ==∑二、电容器储能的计算 电容器的储能公式为:()222211(1)222111(2)222Q W Q U CU C D W EDV E V Vεε=∆=====式中 U ∆---电容主板间电势差V--------电容器极板间电场所占的空间因为,SC U Ed dε=∆=故式(1)、(2)是一致的。
储能计算时要注意L 是维持电量Q 不变(电容器充电后与电源断开), 还是维持电压U ∆不变(电容器充电后,不与电源断开),否则就会把题做错。
例如:有人问:如增大C ,由()22C W U =∆可知W 应增加;但从22Q W C=看,W 又应减小。
究竟应该是增加还是减小?同一习题之所以出现矛盾的结果 ,是因为问题本身不够明确:没有说明是Q 不变,还是U∆不变。
如在Q 不变下增大C ,则由22Q W C=看,W 应该减小;因Q C U =∆,C 增大时U ∆将减小,故从看,W 也应减小。
[例1]球形电容器由半径为R 1的导体球和与它同心的导体球壳构成,其间有两层同心的均匀介质球壳,介质常数分别为1ε、2ε,两介持的分界面的半径为R 2,导体球壳的内半径为R 3 (图2-12-1) 。
已知球壳不带电,内球带电+Q ,求球形电容器的电容。
专题9 电容器的电容及动态分析-2021年高考物理静电

静电场考点突破微专题9 电容器的电容及动态分析一 知能掌握1.对电容的理解 电容是表示电容器容纳电荷本领的物理量.由电容器本身的介质特性与几何尺寸决定,与电容器是否带电,带电量的多少、板间电势差的大小等均无关.2.平行板电容器电容的决定因素公式C =Q U 和C =εr S 4πkd的比较 (1)定义式:C =Q U,不能理解为电容C 与Q 成正比、与U 成反比,一个电容器电容的大小是由电容器本身的因素决定的,与电容器是否带电及带电多少无关.(2)决定式:C =εr S 4πkd ,εr为介电常数,S 为极板正对面积,d 为板间距离. 平行板的电容与板间距离d 成反比,与两半正对面积S 成正比,与板间介质的介电常数ε成正比,其决定式是:ds kd s C επε∝=4 3.电容器的充放电(1)充电过程:使电容器带电的过程,充电后电容器两极板带上等量的异种电荷,电容器中储存电场能.充电过程中,电容器所带电荷量增加,电容器两极板间电压升高,电容器中电场强度增加。
当电容器充电结束后,电容器所在电路中无电流,电容器两极板间电压与充电电压相等,充电后,电容器从电源中获取的能量称为电场能。
(2)放电过程:使充电后的电容器失去电荷的过程,放电过程中电场能转化为其他形式的能.放电过程中,电容器上电荷量减小,电容器两极板间电压降低,电容器中电场强度减弱,电容器的电场能转化成其他形式的能。
4.电容器的动态分析(1)两种情况:一是电容器两极板的电势差U 保持不变(与电源连接);二是电容器的带电量Q 保持不变(与电源断开)(2)三个公式,C CU Q ∝= dd U E d S kd S C 14∝=∝=,επε (3)一个特情 充电后断开K ,保持电容器带电量Q 恒定,这种情况下sE s d U d s C εεε1,,∝∝∝5.综合分析:(1)电容器始终与恒压电源相连,电容器两极板间的电势差U 保持不变. 电容器的d 、S 、εr 发生变化,将引起电容器的C 、Q 、U 、E 变化.由kd S C πε4r =可知C 随d 、S 、εr 变化而变化.由Q =CU =kdS r πε4可知Q也随着d 、S 、εr 变化而变化.由E=U/d 知,E 随d 的变化而变化.(2)电容器充电后与电源断开,电容器两极所带的电荷量Q 保持不变.平行板电容器充电后,切断与电源的连接,电容器的带电荷量Q 保持不变,电容器的d 、S 、εr 变化,将引起C 、Q 、U 、E 的变化.由kd S C πε4r =可知C 随d 、S 、εr 变化而变化.由SkdQ kd S Q C Q U r r εππε44===可知,U 随d 、S 、εr 变化而变化.由SkQ k S Q Cd Q d U E r r εππε44====可知,E 随S 、εr 变化而变化.二、探索提升题型一 关于电容基本理解【典例1】如图所示为一只“极距变化型电容式传感器”的部分构件示意图.当动极板和定极板之间的距离d 变化时,电容C 便发生变化,通过测量电容C 的变化就可知道两极板之间距离d 的变化情况.在下列图中能正确反映C 与d 之间变化规律的图象是 ( )【答案】A题型二 电容器两类动态问题的分析方法【典例2】 一平行板电容器充电后与电源断开,负极板接地.两板间有一个正试探电荷固定在P 点,如图1所示,以C 表示电容器的电容、E 表示两板间的场强、φ表示P 点的电势,W 表示正电荷在P 点的电势能,若正极板保持不动,将负极板缓慢向右平移一小段距离l 0的过程中,各物理量与负极板移动距离x 的关系图象中正确的是( )图1【答案】C题型三电容器与电流流向、运动分析【典例3】如图2所示是测定液面高度h的电容式传感器示意图,E为电源,G为灵敏电流计,A为固定的导体芯,B为导体芯外面的一层绝缘物质,C为导电液体.已知灵敏电流计指针偏转方向与电流方向的关系为:电流从左边接线柱流进电流计,指针向左偏.如果在导电液体的深度h发生变化时观察到指针正向左偏转,则()图2A.导体芯A所带电荷量在增加,液体的深度h在增大B.导体芯A所带电荷量在减小,液体的深度h在增大C.导体芯A所带电荷量在增加,液体的深度h在减小D.导体芯A所带电荷量在减小,液体的深度h在减小【答案】D【典例4】如图3所示,两块较大的金属板A、B相距为d,平行放置并与一电源相连,S闭合后,两板间恰好有一质量为m、带电荷量为q的油滴处于静止状态,以下说法正确的是()图3A.若将S断开,则油滴将做自由落体运动,G表中无电流B.若将A向左平移一小段距离,则油滴向上加速,G表中有b→a的电流C.若将A向上平移一小段距离,则油滴向下加速运动,G表中有b→a的电流D.若将A向下平移一小段距离,则油滴向上加速运动,G表中有b→a的电流【答案】C【典例5】如图4所示,平行板电容器AB两极板水平放置,A在上方,B在下方,现将其和二极管串联接在电源上,已知A和电源正极相连,二极管具有单向导电性,一带电小球沿AB中心水平射入,打在B极板上的N点,小球的重力不能忽略,现通过上下移动A板来改变两极板AB间距(两极板仍平行),则下列说法正确的是()。
球形电容器的电容及场强的讨论

球形电容器的电容及场强的讨论丁武建安徽省池州市池州学院邮编247000摘要两个同心导体球面的内半径为R ,外半径为R, 球面间充满介电常数为 的各向同性的介质的球形电容器。
利用三种方法求解电容器电容,第一种是电容定义式,第二种是电容能量公式,第三种是电容器串联公式。
利用高斯定理计算同心导体电容器场强,由画出的电场强度大小随r变化的曲线,可以看出球形电容器场强的大小E是不连续的,并且球心内部场强为零,同心球球面之间场强与半径成平方反比关系。
关键词电容器;电容;电场强度;计算Abstract The two concentric spherical conductors within a radius of R, the radius R, between the spherical surface of dielectric constants for isotropic medium spherical e three methods to solve capacitor, the first is a capacitance type defined, the second is capacitance energy formula, and the third is a capacitor in series formula.Gauss theorem is used to calculate the concentric conductor capacitor field intensity, electric field by drawing strength size change with r curve, it can be seen that the size of the spherical capacitor field strength E is discontinuous, and its internal field intensity is zero, concentric spherical ball field intensity between inverse square with radius. Key words capacitor; Capacitance; Electric field intensity; calculate 中图分类号04电容器是一个重要的电器元件,按形状来分有平行板电容器,柱形电容器和球形电容器等,按板间所充的介质来分,有空气电容器,云母电容器,陶瓷电容器和电解电容器等,在电力系统中电容器可以用来储存电荷或电能,电容器也是提高功率因素等的重要元件,在电子电路中,电容器则是获得震荡,滤波,相移,旁路,耦合等的重要元件。
电容器的电容说课稿

电容器的电容说课稿尊敬的各位评委老师:上午好!我是8号考生,我今天说课的内容是《电容器的电容》。
围绕本节内容我将从教材分析、学情分析、教学目标、重点与难点、教法与学法、教学过程及板书设计等几个方面来进行阐述。
一、教材分析首先我来分析一下本节内容在教材中的地位与作用。
《电容器的电容》是人教版高中物理选修3-1第一章第八节的内容,本节内容是本章的重点和难点,在教材中占有非常重要的地位。
这是前面匀强电场的一个重要应用,也是后面学习带电粒子在电场中的运动、交流电路、电磁振荡等知识的基础,起到了承前启后的作用。
二、学情分析为了教师能够好的把握课堂情况,适时加以引导,使教学做到有的放矢,我们还必须切实了解学生的基本情况.本节课的教学对象是高二年级的学生,该阶段的学生好奇、善问,创造意识强烈,并具备较高的逻辑推理能力,对物理实验和多媒体展示的各种物理现象具有浓厚的兴趣,会产生探究其本质的愿望。
三、教学目标根据本教材的结构和内容分析,结合当前学生的心理特点及现有的知识水平,我设定了以下的三维教学目标:知识与技能:1、知道什么是电容器以及常用的电容器;2、理解电容的概念及其定义式,并能用来进行有关的计算;3、知道平行板电容器的电容与哪些因素有关,并掌握平行板电容器电容的决定式。
过程与方法:1、知道利用比值法定义物理量;2、学会利用控制变量法的实验法,提高学生综合运用知识的能力。
情感态度与价值观:结合实际,体会电容器在实际生活中的广泛应用,接近学生与科学的距离,培养学生学习物理的兴趣。
四、教学重、难点透过教学目标不难看出本节课的重点与难点:重点:正确理解电容的概念及决定电容大小的因素难点:电容的计算与应用五、教法、学法为了突出本节课的重点,突破其难点,使学生达到本节内容设定的教学目标,我将主要采用以下的教学方法:情境教学法:创设情境,激发学生的学习兴趣,让学生认识到物理来源于生活;直观教学法:通过插图、实验、多媒体课件等直观教学手段,真实呈现实验现象,使物理情景具体化、形象化,给学生以直观感受,加深学生的影响,促进学生对知识的掌握;实验探究法:用问题引导学生进行实验探究,组织学生进行分组实验、设计实验方案,充分发挥学生的主动性;集体讨论法:针对学生存在的问题,组织学生进行集体和分组讨论,促使学生在讨论中解决问题,培养学生团结协作的精神。
1[1].8电容器的电容(上课用)概论
三、平行板电容器的电容
实验中会 使用静电计测 量平行板电容 器两极板间的 电势差U。
(1)改变两极板的正对面积
保持极板上的电荷 量Q不变,两极板间距 d不变,改变两极板的 正对面积,通过静电计 指针的变化来观测两极 板电势差的变化。
现象:S ,U
结论:电容C随正对 面积S的增大而增大。
电容的定义、单位、表达式。
E
D.断开S,在两极板间插入
一块电介质,则两极板间电势差增大。
2.一空气平行板电容器,极板正对面积为S,两 极板相距d,充以电荷量Q后,两极板间电压 为U,使电容器的电容加倍,可采用办法有 ( CD )。
A.将电压变为U/2 B.将电荷量变为2Q C.将两极板正对面积变为2S D.两极板间充入电介质常数为2的电介质
现象:ε ,U
结论:电容C随电介质 的相对介电常数的增 大而增大。
理论表明:
C rS 4kd
课堂训练
1.有一空气平行板电容器,仅增加两极板的 正对面积,其电容___增__大___;仅缩小极板间距离, 其电容______增__大;仅降低两极板间电压,其电容 ____不__变_;仅在两极板间充以介电常数较大的电介 质,其电容_____增__大__。
(一),电容器的充电
充电:使电容器带 E
上电荷的过程。
电容器的作用: 容纳储存电荷
S
AC
Q
U
Q
充电时两个极板总是带等量的异种电荷。
每个极板带电量的绝对值叫做电容器的 带电量。
充电过程中: (Q增加 E增加 电场能增加)
(二),电容器的放电
放电:使电容器失 去电荷的过程。 E
S
A
C
关于均匀带电球面上电场强度的求解
关于均匀带电球面上电场强度的求解蔡莉莉;张晓燕【摘要】由于均匀带电球面上的电场强度无法用高斯定理求出,现行大部分大学物理基础教材在讨论均匀带电球面产生的场强分布时,只用高斯定理求出了该带电系统内外空间电场的分布,并没有给出球面上场强的计算方法,只是指出在球面上场强值不连续.文章利用叠加原理和电容器能量的变化两种方法分别导出了均匀带电球面上任一点的场强值,验证了均匀带电球面的场强是不连续的,两种方法思路截然不同,但得到的结果完全相同,该结果使得高斯定理求出的均匀带电球面在空间电场分布的结论更加完整.【期刊名称】《物理与工程》【年(卷),期】2015(025)001【总页数】3页(P65-67)【关键词】均匀带电球面;高斯定理;电场强度;叠加原理;电容器能量【作者】蔡莉莉;张晓燕【作者单位】华北科技学院基础部物理教研室,河北廊坊 065201;华北科技学院基础部物理教研室,河北廊坊 065201【正文语种】中文在静电学中求解电荷在空间激发的场强是静电场的基础,当电荷呈对称分布时其所激发的电场也呈对称分布,这时只要选取恰当的高斯面就较容易地求出场强分布[1].例如求半径为R的均匀带电量为q的球面电场强度分布问题,用高斯定理不难求出球面内外的场强为该结论没有给出球面上任一点(即r=R)的电场强度,大部分大学物理教材中只是指出在球面上场强值不连续或有一突变[2,3],但并未给出其具体值,这是由于球面上的场强既不能用两边取极限的办法求出,也无法用高斯定理求解.如果把球面本身作为高斯面就无法确定电荷是在面内还是在面外,由于电荷的面分布是一种理想化的电荷分布模型,实际的带电面总有一定的厚度[4].对于理想化的均匀带电球面上的场强如何求解是初学者经常会提出的疑问,以下我们总结了求均匀带电球面上任一点场强的两种方法.关于球面上场强的求解最直接的方法就是用叠加原理通过积分的方法计算,即把均匀带电球面看作是由无限多个以场点与球心的连线为轴、半径不同的圆环带组成,应用均匀带电圆环轴线上的场强公式结论来计算,该法简单,也容易接受.图1所示为一个半径为R的均匀带电球面,带电量为q,求解球面上任一点P点的场强.可将球面分割成无限多个半径不同的无限窄的环带,在球面上取如图所示的圆环带微元,该环带可近似看成是圆环,其环面垂直于轴线OP.所有带电圆环的场强在P点的叠加形成该点的总场强.其中球面的电荷面密度为所取环带面积环带所带电量为将式(1)、式(2)代入式(3)得根据带电圆环在其轴线上的场强公式的结论[5]可得该圆环带在球面上P点产生的场强大小为P点场强方向沿x轴正向,根据叠加原理,带电球面上P点的场强是所有这些带电环带在该点产生的场强dE的矢量和.因为各个小圆环产生的场强方向都相同,矢量和变为代数和,所以合场强为根据图1中的几何关系可知将式(4)、式(6)、式(7)代入式(5),得通过上述计算可知均匀带电球面上任一点P的场强大小为方向沿着Ox轴正向.利用叠加原理虽然容易理解,但是涉及积分的计算,计算量比较大,以下利用球形电容器能量的变化这一模型来计算球面上的电场强度大小.设想将球形电容器的外壳移动dR,根据能量守恒原理,外力克服静电力所做的功等于球形电容器静电势能的变化,从而求出球形电容器极板所受的静电场力,进而求出极板上的场强.设球形电容器内外球壳的电荷各为+q和-q(如图2所示),球壳的内外半径分别为R1和R2,则球形电容器的电容可表示为[6]由于两球壳之间的距离d=R2-R1很小,因此R1≈R2=R,则上式可化简为电容器中电场储存的能量为[7]式(9)代入式(10)得根据能量守恒定律,当内球壳发生虚位移dR时,外力克服静电力F所做的功Fdr 转化为电容器所储存的静电能,则有由式(12)得到,两球壳之间的静电力F=Eq,因此,其中E表示内外球壳在同一点场强的叠加.设内球壳上的电荷在内壳上某一点产生的场强为E1,外球壳上的电荷在内壳上同一点产生的场强为E2,由对称性分析可知,外极板上任一点产生的场强E2均相等,E2与E1反向.由高斯定理可知E2=0,因内外球壳电荷电性相反,因此合场强E=E1-E2,所以即内壳上的电荷在其上任一点产生的场强为.同理,设外球壳上的电荷在其上任一点产生的场强为E′2,内球壳上的电荷在外壳上同一点产生的场强为E′1,合场强为.由高斯定理可得,故,即外壳上的电荷在其上任一点产生的场强为.由上述分析可得均匀带电球面上任一点的场强大小为通过上述两种方法的计算,给出了半径为R均匀带电量为q的球面上任一点的电场强度的确定值,得出其具体表达式为,其值恰好等于从带电面外无限接近带电面时的电场强度与带电面内电场强度为零之和的一半,这也验证了均匀带电球面的场强是不连续的,场强在球面处确有一间断点.在教学中,可简要引入计算方法,便于加深学生对均匀带电球面产生电场规律的认识,同时启发学生的发散思维,纠正学生认为面上场强为零或为的错误认识,从而形成面内、面上、面外的整体认识.[1]赵凯华,陈熙谋.电磁学[M].北京:高等教育出版社,2003:24-25.[2]梁灿彬,秦光戎,梁竹健.电磁学[M].2版.北京:高等教育出版社,2004:21-22.[3]张三慧.大学基础物理学:下册[M].北京:清华大学出版社,2003:349-350.[4]白俊彪.均匀带电球面上电场强度的计算[J].思茅师范高等专科学校学报,2005,21(3):79-80.[5]吴百诗.大学物理:上册(第三次修订本)[M].西安:西安交通大学出版社,2008:116.[6]程守洙,江之永.普通物理学:第2册[M].4版.北京:高等教育出版社,1995:273.[7]刘景世.“均匀带电球面上的电场强度如何计算”的再讨论[J].河南教育学院学报(自然科学版),2011,20(4):32-33.。
电场与电场强度的关系以及电容器
解(1) C Q 6 10 11 110 12 (F ) U 60
(2)对同一电容器,电容是常数,故 C11012F
(3)由电容的意义,可知 C Q U
故 ΔQC·ΔU21012(C)
2、平行板电容器的电容: (1)构成:两块平行相互绝缘金属板构成的电容器。
(2)电容公式 C Q = Q U U
注意:Q是某一极板所带电量的绝对值。
(3)影响平行板电容器电容的因素 演示实验: 实验说明: 静电计的作用: 显示电容器两极板间电压
; 给电容器充电完毕后,断开极板与起电机连
线,电容器所带电量Q不变。
实验现象 a)改变电容器两极板间距离
板间距增大时,静电计指针偏角变大, 板间距减小时,静电计指针偏角减小。 分析:d增大,Q不变,U增大,根据 CQ/U, 可分析出
C减小。 d减小时,U减小,根据CQ/U ,可分析出C增大。
说明 C 1/d
实验现象 b)改变两板正对面积S,可观察到
S 增大时,指针偏角变小; S减小时,指针偏角变大。 分析: S增大,Q不变,U减小,根据CQ/U,说明C增大,
S减小,Q不变,U增大,根据CQ/U,说明C减小。
•说明 CS
WqU 比较这两个式子,可得 WqEdUq 即 UEd 或 EU/d
即:在匀强电场中,沿场强方向的两点间的电势差等于 场强和这两点间距离的乘积。
注意: (1)公式 UEd 只适用于匀强电场的计算; (2)公式中U为两点间电压,E为场强,d为两点间距 离在场强方向的投影。
3.由 EU/d 可得到场强的另一个单位:V/m
答案:5106,450 分析:根据电势差定义UW/q,可求出ab两点之间
的电势差,Uab Wab /q 200V; 又根据匀强电场电势差与场强的关系式UEd,则: Uab :Ubcdab:dbc 可得: UbcUab (bc·cos60)/ab250V 将此电荷从 b 移到 c 电场力做功 Wbcq Ubc5106J ac 间电势差UacUab + Ubc450V
大学物理13章答案
第13章 静电场中的导体和电介质13.1一带电量为q ,半径为r A 的金属球A ,与一原先不带电、内外半径分别为r B 和r C 的金属球壳B 同心放置,如图所示,则图中P 点的电场强度如何?若用导线将A 和B 连接起来,则A 球的电势为多少?(设无穷远处电势为零)[解答]过P 点作一个同心球面作为高斯面,尽管金属球壳内侧会感应出异种,但是高斯面内只有电荷q .根据高斯定理可得 E 4πr 2 = q /ε0, 可得P 点的电场强度为204q E r πε=.当金属球壳内侧会感应出异种电荷-q 时,外侧将出现同种电荷q .用导线将A 和B 连接起来后,正负电荷将中和.A 球是一个等势体,其电势等于球心的电势.A 球的电势是球壳外侧的电荷产生的,这些电荷到球心的距离都是r c ,所以A 球的电势为04c q U r πε=.13.2 同轴电缆是由半径为R 1的导体圆柱和半径为R 2的同轴薄圆筒构成的,其间充满了相对介电常数为εr 的均匀电介质,设沿轴线单位长度上导线的圆筒的带电量分别为+λ和-λ,则通过介质内长为l ,半径为r 的同轴封闭圆柱面的电位移通量为多少?圆柱面上任一点的场强为多少?[解答]介质中的电场强度和电位移是轴对称分布的.在内外半径之间作一个半径为r 、长为l 的圆柱形高斯面,根据介质中的高斯定理,通过圆柱面的电位移通过等于该面包含的自由电荷,即 Φd = q = λl . 设高斯面的侧面为S 0,上下两底面分别为S 1和S 2.通过高斯面的电位移通量为 ⎰⋅=ΦSdD d 012d d d 2S S S rlDπ=⋅+⋅+⋅=⎰⎰⎰D S D S D S ,可得电位移为 D = λ/2πr , 其方向垂直中心轴向外.电场强度为 E = D/ε0εr = λ/2πε0εr r , 方向也垂直中心轴向外.13.3 金属球壳原来带有电量Q ,壳内外半径分别为a 、b ,壳内距球心为r 处有一点电荷q ,求球心o 的电势为多少? [解答]点电荷q 在内壳上感应出负电荷-q ,不论电荷如何分布,距离球心都为a .外壳上就有电荷q+Q ,距离图13.3球为b .球心的电势是所有电荷产生的电势叠加,大小为000111444o q q Q q U r a b πεπεπε-+=++13.4 三块平行金属板A 、B 和C ,面积都是S = 100cm 2,A 、B 相距d 1 = 2mm ,A 、C 相距d 2 = 4mm ,B 、C 接地,A 板带有正电荷q =3×10-8C ,忽略边缘效应.求(1)B 、C 板上的电荷为多少? (2)A 板电势为多少? [解答](1)设A 的左右两面的电荷面密度分别为σ1和σ2,所带电量分别为σ1S 和q 2 = σ2S ,q 1 = 在B 、C 板上分别感应异号电荷-q 1和-q 2,由电荷守恒得方程q = q 1 + q 2 = σ1S + σ2S . ① A 、B 间的场强为 E 1 = σ1/ε0, A 、C 间的场强为 E 2 = σ2/ε0.设A 板与B 板的电势差和A 板与C 板的的电势差相等,设为ΔU ,则ΔU = E 1d 1 = E 2d 2, ②即 σ1d 1 = σ2d 2. ③解联立方程①和③得σ1 = qd 2/S (d 1 + d 2),所以 q 1 = σ1S = qd 2/(d 1+d 2) = 2×10-8(C);q 2 = q - q 1 = 1×10-8(C).B 、C 板上的电荷分别为q B = -q 1 = -2×10-8(C); q C = -q 2 = -1×10-8(C). (2)两板电势差为ΔU = E 1d 1 = σ1d 1/ε0 = qd 1d 2/ε0S (d 1+d 2), 由于 k = 9×109 = 1/4πε0, 所以 ε0 = 10-9/36π,因此 ΔU = 144π = 452.4(V). 由于B 板和C 板的电势为零,所以U A = ΔU = 452.4(V).13.5 一无限大均匀带电平面A ,带电量为q ,在它的附近放一块与A 平行的金属导体板B ,板B 有一定的厚度,如图所示.则在板B 的两个表面1和2上的感应电荷分别为多少?[解答]由于板B 原来不带电,两边感应出电荷后,由电荷守恒得 0. ①q 1 + q 2 = 虽然两板是无限大的,为了计算的方便,不妨设它们的面积为S ,则面电荷密度分别为σ1 = q 1/S 、σ2 = q 2/S 、σ = q/S ,图13.42 图13.5它们产生的场强大小分别为E 1 = σ1/ε0、E 2 = σ2/ε0、E = σ/ε0.在B 板内部任取一点P ,其场强为零,其中1面产生的场强向右,2面和A 板产生的场强向左,取向右的方向为正,可得E 1 - E 2 – E = 0,即 σ1 - σ2 – σ = 0,或者说 q 1 - q 2 + q = 0. ② 解得电量分别为q 2 = q /2,q 1 = -q 2 = -q /2.13.6 两平行金属板带有等异号电荷,若两板的电势差为120V ,两板间相距为 1.2mm ,忽略边缘效应,求每一个金属板表面的电荷密度各为多少?[解答]由于左板接地,所以σ1 = 0. 由于两板之间的电荷相互吸引,右板右面的电荷会全部吸引到右板左面,所以σ4 = 0. 由于两板带等量异号的电荷,所以 σ2 = -σ3.两板之间的场强为E = σ3/ε0,而 E = U/d , 所以面电荷密度分别为σ3 = ε0E = ε0U/d = 8.84×10-7(C·m -2),σ2 = -σ3 = -8.84×10-7(C·m -2).13.7一球形电容器,内外球壳半径分别为R 1和R 2,球壳与地面及其他物体相距很远.将内球用细导线接地.试证:球面间电容可用公式202214R C R R πε=-表示. (提示:可看作两个球电容器的并联,且地球半径R >>R 2)[一:并联电容法.在外球外面再接一个半径为R 3壳,外壳也接地.内球壳和外球壳之间是容为 104C πε=壳之间也是一个电容器,电容为2023141/1/C R R πε=-.外球壳是一极,由于内球壳和大外球壳都接地,共用一极,所以两个电容并联.当R 3趋于无穷大时,C 2 = 4πε0R 2.并联电容为12120022144R R C C C R R R πεπε=+=+-图13.6202214R R R πε=-.方法二:电容定义法.假设外壳带正电为q ,则内壳将感应电荷q`.内球的电势是两个电荷产生的叠加的结果.由于内球接地,所以其电势为零;由于内球是一个等势体,其球心的电势为0201`044q q R R πεπε+=,因此感应电荷为12`R q q R =-.根据高斯定理可得两球壳之间的场强为122002`44R q q E r R r πεπε==-,负号表示场强方向由外球壳指向内球壳.取外球壳指向内球壳的一条电力线,两球壳之间的电势差为1122d d R R R R U E r=⋅=⎰⎰E l121202()d 4R R R qr R rπε=-⎰1212021202()11()44R q R R q R R R R πεπε-=-=球面间的电容为202214R q C U R R πε==-.13.8球形电容器的内、外半径分别为R 1和R 2,其间一半充满相对介电常量为εr 的均匀电介质,求电容C 为多少?[解答]球形电容器的电容为12012211441/1/R R C R R R R πεπε==--.对于半球来说,由于相对面积减少了一半,所以电容也减少一半:0121212R R C R R πε=-.当电容器中充满介质时,电容为:0122212r R R C R R πεε=-.由于内球是一极,外球是一极,所以两个电容器并联:01212212(1)r R R C C C R R πεε+=+=-.13.9设板面积为S 的平板电容器析板间有两层介质,介电常量分别为ε1和ε2,厚度分别为d 1和d 2,求电容器的电容.[解答]假设在两介质的介面插入一薄导体,可知两个电容器串联,电容分别为 ε1S/d 1和C 2 = ε2S/d 2. C 1 = 总电容的倒数为122112*********d d d d C C C S S S εεεεεε+=+=+=,总电容为122112SC d d εεεε=+.13.10 圆柱形电容器是由半径为R 1的导线和与它同轴的内半径为R 2的导体圆筒构成的,其长为l ,其间充满了介电常量为ε的介质.设沿轴线单位长度导线上的电荷为λ,圆筒的电荷为-λ,略去边缘效应.求:(1)两极的电势差U ;(2)介质中的电场强度E 、电位移D ; (3)电容C ,它是真空时电容的多少倍? [解答]介质中的电场强度和电位移是轴对称分布的.在内外半径之间作一个半径为r 、长为l 的圆柱形高斯面,侧面为S 0,上下两底面分别为S 1和S 2.通过高斯面的电位移通量为 ⎰⋅=ΦS d S D d12d d d 2S S S rlDπ=⋅+⋅+⋅=⎰⎰⎰D S D S D S ,高斯面包围的自由电荷为 q = λl ,根据介质中的高斯定理 Φd = q , 可得电位为 D = λ/2πr , 方向垂直中心轴向外.电场强度为 E = D/ε = λ/2πεr , 方向也垂直中心轴向外.取一条电力线为积分路径,电势差为21d d d 2R LLRU E r r r λπε=⋅==⎰⎰⎰E l21ln 2R R λπε=.电容为212ln(/)q l C U R R πε==.在真空时的电容为00212ln(/)l q C U R R πε==,所以倍数为C/C 0 = ε/ε0.13.11在半径为R 1的金属球外还有一层半径为R 2的均匀介质,相对介电常量为εr .设金属球带电Q 0,求:(1)介质层内、外D 、E 、P 的分布;(2)介质层内、外表面的极化电荷面密度.[解答](1)在介质内,电场强度和电位移以及极化强度是球对称分布的.在内外半径之间作一个半径为r 的球形高斯面,通过高斯面的电位移通量为 Dr S D SSd 24d d π==⋅=Φ⎰⎰S D高斯面包围的自由电荷为q = Q 0, 根据介质中的高斯定理 Φd = q , 可得电位为 D = Q 0/4πr 2, 方向沿着径向.用矢量表示为D = Q 0r /4πr 3.电场强度为E = D /ε0εr = Q 0r /4πε0εr r 3, 方向沿着径向.由于 D = ε0E + P ,所以 P = D - ε0E =031(1)4rQ r επ-r .在介质之外是真空,真空可当作介电常量εr = 1的介质处理,所以 D = Q 0r /4πr 3,E = Q 0r /4πε0r 3,P = 0.(2)在介质层内靠近金属球处,自由电荷Q 0产生的场为E 0 = Q 0r /4πε0r 3;极化电荷q 1`产生的场强为E` = q 1`r /4πε0r 3;总场强为 E = Q 0r /4πε0εr r 3. 由于 E = E 0 + E `,解得极化电荷为`101(1)rq Q ε=-,介质层内表面的极化电荷面密度为``01122111(1)44r Q q R R σπεπ==-. 在介质层外表面,极化电荷为``21q q =-,面密度为``02222221(1)44r Q q R R σπεπ==-.13.12 两个电容器电容之比C 1:C 2 = 1:2,把它们串联后接电源上充电,它们的静电能量之比为多少?如果把它们并联后接到电源上充电,它们的静电能之比又是多少?[解答]两个电容器串联后充电,每个电容器带电量是相同的,根据静电能量公式W = Q 2/2C ,得静电能之比为W 1:W 2 = C 2:C 1 = 2:1.两个电容器并联后充电,每个电容器两端的电压是相同的,根据静电能量公式W = CU 2/2,得静电能之比为W 1:W 2 = C 1:C 2 = 1:2.13.13一平行板电容器板面积为S ,板间距离为d ,接在电源上维持其电压为U .将一块厚度为d 相对介电常量为εr 的均匀介电质板插入电容器的一半空间内,求电容器的静电能为多少?[解答]平行板电容器的电容为C = ε0S/d ,当面积减少一半时,电容为C 1 = ε0S /2d ; 另一半插入电介质时,电容为C 2 = ε0εr S /2d .两个电容器并联,总电容为C = C 1 + C 2 = (1 + εr )ε0S /2d ,静电能为W = CU 2/2 = (1 + εr )ε0SU 2/4d .13.14 一平行板电容器板面积为S ,板间距离为d ,两板竖直放着.若电容器两板充电到电压为U 时,断开电源,使电容器的一半浸在相对介电常量为εr 的液体中.求:(1)电容器的电容C ;(2)浸入液体后电容器的静电能; (3)极板上的自由电荷面密度.[解答](1)如前所述,两电容器并联的电容为C = (1 + εr )ε0S /2d .(2)电容器充电前的电容为C 0 = ε0S/d , 充电后所带电量为 Q = C 0U .当电容器的一半浸在介质中后,电容虽然改变了,但是电量不变,所以静电能为 W = Q 2/2C = C 02U 2/2C = ε0SU 2/(1 + εr )d .(3)电容器的一半浸入介质后,真空的一半的电容为 C 1 = ε0S /2d ; 介质中的一半的电容为 C 2 = ε0εr S /2d . 设两半的所带自由电荷分别为Q 1和Q 2,则Q 1 + Q 2 = Q . ①由于C = Q/U ,所以U = Q 1/C 1 = Q 2/C 2. ②解联立方程得01112211/C U C Q Q C C C C ==++,真空中一半电容器的自由电荷面密度为00112122/2(1/)(1)r C U U Q S C C S d εσε===++.同理,介质中一半电容器的自由电荷面密度为0021222(/1)(1)r r C U UC C S d εεσε==++.13.15平行板电容器极板面积为200cm 2,板间距离为 1.0mm ,电容器内有一块1.0mm 厚的玻璃板(εr = 5).将电容器与300V 的电源相连.求:(1)维持两极板电压不变抽出玻璃板,电容器的能量变化为多少?(2)断开电源维持板上电量不变,抽出玻璃板,电容器能量变化为多少? [解答]平行板电容器的电容为C 0 = ε0εr S/d ,静电能为 W 0 = C 0U 2/2. 玻璃板抽出之后的电容为C = ε0S/d .(1)保持电压不变抽出玻璃板,静电能为 W = CU 2/2, 电能器能量变化为ΔW = W - W 0 = (C - C 0)U 2/2 = (1 - εr )ε0SU 2/2d = -3.18×10-5(J). (2)充电后所带电量为 Q = C 0U , 保持电量不变抽出玻璃板,静电能为W = Q 2/2C ,电能器能量变化为2000(1)2C C U W W W C ∆=-=-20(1)2r r SU dεεε=-= 1.59×10-4(J).13.16设圆柱形电容器的内、外圆筒半径分别为a 、b .试证明电容器能量的一半储存在半径R[解答]设圆柱形电容器电荷线密度为λ,场强为 E = λ/2πε0r , 能量密度为 w = ε0E 2/2, 体积元为 d V = 2πrl d r , 能量元为 d W = w d V .在半径a 到R 的圆柱体储存的能量为20d d 2V V W w V E Vε==⎰⎰2200d ln 44Ral l R r r a λλπεπε==⎰. 当R = b 时,能量为210ln4l b W a λπε=;当R =22200ln48l l b W a λλπεπε==,所以W 2 = W 1/2,即电容器能量的一半储存在半径R13.17 两个同轴的圆柱面,长度均为l ,半径分别为a 、b ,柱面之间充满介电常量为ε的电介质(忽略边缘效应).当这两个导体带有等量异号电荷(±Q )时,求:(1)在半径为r (a < r < b )、厚度为d r 、长度为l 的圆柱薄壳中任一点处,电场能量体密度是多少?整个薄壳层中总能量是多少?(2)电介质中总能量是多少(由积分算出)?(3)由电容器能量公式推算出圆柱形电容器的电容公式?[解答](1)圆柱形内柱面的电荷线密度为 λ = Q/l , 根据介质是高斯定理,可知电位移为D = λ/2πr = Q /2πrl ,场强为 E = D/ε = Q /2πεrl , 能量密度为w = D ·E /2 = DE /2 = Q 2/8π2εr 2l 2.薄壳的体积为d V = 2πrl d r , 能量为 d W = w d V = Q 2d r /4πεlr .(2)电介质中总能量为22d d ln44bV aQ Q bW W r lr l a πεπε===⎰⎰. (3)由公式W = Q 2/2C 得电容为222ln(/)Q l C W b a πε==.13.18 两个电容器,分别标明为200PF/500V 和300PF/900V .把它们串联起来,等效电容多大?如果两端加上1000V 电压,是否会被击穿?[解答]当两个电容串联时,由公式211212111C C C C C C C +=+=,得1212120PFC C C C C ==+.加上U = 1000V 的电压后,带电量为Q = CU ,第一个电容器两端的电压为U 1 = Q/C 1 = CU/C 1 = 600(V); 第二个电容器两端的电压为U 2 = Q/C 2 = CU/C 2 = 400(V).由此可知:第一个电容器上的电压超过它的耐压值,因此会被击穿;当第一个电容器被击穿后,两极连在一起,全部电压就加在第二个电容器上,因此第二个电容器也接着被击穿.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
球形电容器的电容及场强的讨论
丁武建安徽省池州市池州学院邮编247000
摘要两个同心导体球面的内半径为R ,外半径为R, 球面间充满介电常数为 的各向同性的介质的球形电容器。
利用三种方法求解电容器电容,第一种是电容定义式,第二种是电容能量公式,第三种是电容器串联公式。
利用高斯定理计算同心导体电容器场强,由画出的电场强度大小随r变化的曲线,可以看出球形电容器场强的大小E是不连续的,并且球心内部场强为零,同心球球面之间场强与半径成平方反比关系。
关键词电容器;电容;电场强度;计算
Abstract The two concentric spherical conductors within a radius of R, the radius R, between the spherical surface of dielectric constants for isotropic medium spherical e three methods to solve capacitor, the first is a capacitance type defined, the second is capacitance energy formula, and the third is a capacitor in series formula.Gauss theorem is used to calculate the concentric conductor capacitor field intensity, electric field by drawing strength size change with r curve, it can be seen that the size of the spherical capacitor field strength E is discontinuous, and its internal field intensity is zero, concentric spherical ball field intensity between inverse square with radius. Key words capacitor; Capacitance; Electric field intensity; calculate 中图分类号04
电容器是一个重要的电器元件,按形状来分有平行板电容器,柱形电容器和球形电容器等,按板间所充的介质来分,有空气电容器,云母电容器,陶瓷电容器和电解电容器等,在电力系统中电容器可以用来储存电荷或电能,电容器也是提高功率因素等的重要元件,在电子电路中,电容器则是获得震荡,滤波,相移,旁路,耦合等的重要元件。
电容只与组成电容器的极板的大小,形状,两极板的相对位置及其间所充的介质等因素有关,下面来介绍球形电容器的电容和场强计算方法。
方法一:利用电容定义式。
如图1所示,使内球面带电+Q ,外球面带电—Q ,电荷均匀分布在内球的外表面和外球的内表面上。
导体间电场是沿着径向的,取半径为r (R<r<R )的同心面为高斯面,根据高斯定理,场强
大小为E=24r Q πε,两球间的电势差为U=⎰R R ds E 0
.=Edr R R ⎰0=dr r Q R
R ⎰024πε=πε4Q
()11R R - 根据电容的定义可得C=
R R R
R R
R U Q -=
-=πεπε4114
1
方法二:电容能量公式
根据电场强度公式E=2
4r Q
πε,电场的能量密度为ωe=42223221r Q E επε=
如图所示,在电容器中取一个半径为r,厚度为dr 的球壳2,其体积为dV=4dr r 2
π,该体积的
能量为dW=ωedV=2
28r Q πε,由于w=C Q 22
,所以电容器的总能量为:
W=⎰⎰=
R
R V r dr Q dW 0
22
8πε=R R R R Q R R Q -•=-πεπε8)11
(822, C=
R R R
R W Q -=πε422
2 3
方法三:利用电容器串联公式
把球形电容器中划分为许多同心球壳,在球壳之间插入无限薄的导体,每两个导体 之间就形成一个电容器,因此,所有电容器都是串联的。
在球体中取一个半径为r,厚度为
dr 的球壳,其表面积为S=2
4r π,电容的倒数为d(
2
4)1r dr
S d C πεε=
= 总电容的倒数为)11(4141
102R R r
dr C R
R -==
⎰ πεπε
再取倒数得总电容C=
R R R R -πε4
[讨论] R R R
R R
R U Q C -=
-==πεπε4114
①内球半径越大,外径半径越小,导体的电容就越大。
令R →∞,可得孤立导体的电容C=4 R πε,在真空中孤立导体的电容为C=4
R πε②设R-R =d,当d 很小时,可得C d R 24 πε≈=d
s
ε,这是平行板电容器的电容公式。
实际上,孤立导体并不存在,一般来说带电导体的周围总是有这样或那样的物体(导体或者绝缘体),带电导体的电势也会因为外界环境不同而有所变化。
利用高斯定理计算球形电容器场强:真空中的任何静电场中,穿过任一闭合曲面的电
通量,在数值上等于闭合曲面内包围的电量的代数和乘以
ε1
,
即对连续分布的源电荷∑⎰=
•=
Φ内
qi dS E S
ε1
对不连续分布的源电荷: dV dS E S
V
ρε⎰
⎰=
•=Φ 1
由高斯定理可知穿过任何半径的球面的电通量都等于
ε1,设想任意闭合曲面S 包围两个正的点电荷q 1,q 2, q 1发出的电场线条数为11q ε,q2发出的电场线条数为21
q
ε,他
们发出的电场线都穿过了闭合曲面,因此穿过闭合曲面的电通量为
ε1
(q1+q2),如果q1
为正电荷,q2为负电荷,则q 1发出的电场线条数为11
q
ε,终止于q2的电场线条数为
21q
ε,因而净穿入或穿出闭合曲面的电场线条数也为 ε1
(q1+q2)
,显然这时q1+q2是电荷的代数和。
如果高斯面内不包围电荷,电荷在它的外面,此时从高斯面外的电荷发出的每
一条电场
线都穿透了整个曲面,有穿入必有穿出,因此就总的效果来看,穿过高斯面的电通量为零。
高斯定理可以应用到电荷分布具有某些对称的情况中。
通过以上的分析可知,对于球形电容器也可利用高斯定理进行分析计算它的场强。
下面就来具体分析:
如图所示
通过高斯面的电通量为⎰
⎰⎰•==•=•=ΦS
S
S
r E dS E dS E S d E 2
4π
此高斯面内包围的电量∑=内
q qi ,所以E=2
41
r q
πε(R 0<r<R )
考虑到E 的方向,可用矢量式表示为E=
2
41
r q
πεr 0,可以看出,均匀带电球面外的电场
强度分布,好像球面上的电荷都集中在球心时形成的点电荷产生的电场强度分布一样。
对球
面内部一点P*,P*点作一半径为r*的同心球面S*为高斯面,由于它内部没有包围电荷,则
⎰=•=ΦS
dS E 0,故E=0(r<R 0),此结果表明,均匀带电球面内部的场强处处为零.同理,
由上述分析,当r>R 时E=2
42
1r
q q πε+.
结论:球形电容器电容为C =
R R R
R -πε4, 球形电容器产场强为E =0 (r<R 0)
E=
241
r q
πε (R 0<r <R )
E =
2
42
1r q q πε+ (r>R )
注:这里q1=q2=Q
参考文献
【1】胡素芬. 近代物理基础【M 】.杭州.浙江大学出版社.1988
【2】吴百诗. 大学物理【M 】.西安.交通大学出版社.2009.第三次修订本下册。
