流体力学-第三章
合集下载
第三章 流体力学
1、理想流体：
完全不可压缩的无粘滞流体称为理想流体。
液体不易被压缩，而气体的可压缩性大。但当气体可自由流 动时，微小的压强差即可使气体快速流动，从而使气体各部 分的密度差可以忽略不计。
流体内各部分间实际存在着内摩擦力，它阻碍着流体各部分 间的相对运动，称为粘滞性。但对于很“稀”的流体，可近 似看作是无粘滞的。
4l
dQ=vdS
流量
R
Q R4 ( P1 P2 )
8l
泊肃叶定律推导（略）
流速分布： r
r
v P1 P2 ( R2 r 2 )
4l
各流层流速沿径向呈抛 物线分布
v 管轴中心处，流速最大
vmax
P1 P2
4l
R2
管壁处，流速最小 vmin 0
v
平均速度 v P1 P2 R2
由伯努利方程：
p0
gh
p0
1 2
v2
由上式求得：
v 2 gh
p0
A h
B p0 v
习例题题5-1：1 直径为0.10m，高为0.20m的圆筒形容器底部有1cm2的小 孔。水流入容器内的流量为1.4×10-4m3/s 。求：容器内水面能
上升多高？
D
由伯努利方程： v 2 gh
h 当水面升至最高时： QV v S S 2 ghm
若1 < 2 ， 小球(气泡)上浮
1 2
V
v
2 1
gh2V
gh1V
即：
p1
1 2
v
2 1
gh1
完全不可压缩的无粘滞流体称为理想流体。
液体不易被压缩，而气体的可压缩性大。但当气体可自由流 动时，微小的压强差即可使气体快速流动，从而使气体各部 分的密度差可以忽略不计。
流体内各部分间实际存在着内摩擦力，它阻碍着流体各部分 间的相对运动，称为粘滞性。但对于很“稀”的流体，可近 似看作是无粘滞的。
4l
dQ=vdS
流量
R
Q R4 ( P1 P2 )
8l
泊肃叶定律推导（略）
流速分布： r
r
v P1 P2 ( R2 r 2 )
4l
各流层流速沿径向呈抛 物线分布
v 管轴中心处，流速最大
vmax
P1 P2
4l
R2
管壁处，流速最小 vmin 0
v
平均速度 v P1 P2 R2
由伯努利方程：
p0
gh
p0
1 2
v2
由上式求得：
v 2 gh
p0
A h
B p0 v
习例题题5-1：1 直径为0.10m，高为0.20m的圆筒形容器底部有1cm2的小 孔。水流入容器内的流量为1.4×10-4m3/s 。求：容器内水面能
上升多高？
D
由伯努利方程： v 2 gh
h 当水面升至最高时： QV v S S 2 ghm
若1 < 2 ， 小球(气泡)上浮
1 2
V
v
2 1
gh2V
gh1V
即：
p1
1 2
v
2 1
gh1
流体力学第三章
精品课件
11.流体流动时，流场各空间点 的参数不随时间变化，仅随空 间位置而变，这种流动称为 （） A、恒定流； B、非恒定流； C、非均匀流；
D、均匀流；
精品课件
12.一般情况下，流线不能相交，但
在(
)处除外。
A 驻点；
B 奇点；
C相切点；
D 驻点、奇点和相切点
精品课件
13.流线与迹线，在通常情况下
均 可 能 沿 程 有 升 有 降；
（C） 总 压 线 及 位 压 线 总 是 沿 程
下 降 的， 势 压 线 沿 程 可 能 有 升
有 降；
（D） 总 压 线 沿 程 总 是 下 降 的，
势压线与位压线沿程可能有升
有 降。
精品课件
15. 流体在作恒定流动时，过流
场同一固定点的流线和迹线相互
(
)
A 平行；
同一条流线上两点A、B，A点的流速大 于B点的流速，则
（A）A 点 的 测 压 管 水 头>B 点 的 测 压 管 水 头； （B）A 点 的 测 压 管 水 头<B 点 的 测 压 管 水 头； （C）A 点 的 压 强 水 头>B 点 的 压 强 水 头； （D）A 点 的 压 强 水 头<B 点 的 压 强 水 头。 精品课件
D 前三种情况都有可能。
精品课件
18. 水 流 一 定 方 向 应 该
是（ ）
A. 从 高 处 向 低 处 流；
B. 从 压 强 大 处 向 压 强
小 处 流；
C. 从 流 速 大 的 地 方 向
流 速 小 的 地 方 流；
D. 从 单 位 重 量 流 体 机
械能高的地方向低的
地方流
11.流体流动时，流场各空间点 的参数不随时间变化，仅随空 间位置而变，这种流动称为 （） A、恒定流； B、非恒定流； C、非均匀流；
D、均匀流；
精品课件
12.一般情况下，流线不能相交，但
在(
)处除外。
A 驻点；
B 奇点；
C相切点；
D 驻点、奇点和相切点
精品课件
13.流线与迹线，在通常情况下
均 可 能 沿 程 有 升 有 降；
（C） 总 压 线 及 位 压 线 总 是 沿 程
下 降 的， 势 压 线 沿 程 可 能 有 升
有 降；
（D） 总 压 线 沿 程 总 是 下 降 的，
势压线与位压线沿程可能有升
有 降。
精品课件
15. 流体在作恒定流动时，过流
场同一固定点的流线和迹线相互
(
)
A 平行；
同一条流线上两点A、B，A点的流速大 于B点的流速，则
（A）A 点 的 测 压 管 水 头>B 点 的 测 压 管 水 头； （B）A 点 的 测 压 管 水 头<B 点 的 测 压 管 水 头； （C）A 点 的 压 强 水 头>B 点 的 压 强 水 头； （D）A 点 的 压 强 水 头<B 点 的 压 强 水 头。 精品课件
D 前三种情况都有可能。
精品课件
18. 水 流 一 定 方 向 应 该
是（ ）
A. 从 高 处 向 低 处 流；
B. 从 压 强 大 处 向 压 强
小 处 流；
C. 从 流 速 大 的 地 方 向
流 速 小 的 地 方 流；
D. 从 单 位 重 量 流 体 机
械能高的地方向低的
地方流
流体力学课件 第3章流体运动的基本原理
u u (x, y,z, t )
17
二、流场描述
1、迹线：某一质点在某一时段内的运动轨迹曲线。
例： 烟火、火箭、流星、子弹等轨迹线。。。。。
（1）拉格朗日法迹线方程
x x（a，b，c，t） y y（a，b，c，t）
z z（a，b，c，t）
消去参数t并给定（a，b，c）即得相应质点的迹线方 程。
说明：
*（a,b,c）=const, t为变数，可得某个指定质点在任意时刻
所处的位臵，上式即迹线方程； *（a,b,c）为变数,对应时刻 t可以得出某一瞬间不同质点 在空间的分布情况。
3、拉格朗日法的速度与加速度方程
（ 1） 流速方 程
x ux ； t y uy ； t z uz t 均为（a，b，c，t）的函数。
第三章 流体运动的基本原理
静止只是流体的一种特殊的存在形态，运动 或流动是流体更为普遍的存在形态，也更能反映 流体的本质特征。 本章主要讨论流体的运动特征（速度、加速 度等）和流体运动的描述方法，流体连续性方程、 动量守恒及能量守恒方程是研究流体运动的基础。
1
第一节、流体运动的描述方法
一、拉格朗日法（lj）
18
（2）欧拉法迹线方程 若质点P在时间dt内从A点运
Z
A
B
动到B点，则质点移动速度为：
u dr dt
O
Y
得迹线方程:
dx dy dz dt ux uy uz
2、流线
表示某一瞬时流体各点流动 趋势的曲线，其上任一点的切线 方向与该点流速方向重合。即同 一时刻不同质点的速度方向线。
根据行列式的性质，有：
22
流线微分方程
dx dy dz u x u y uz
第三章 流体力学 液体出流
2.非均匀流—流线不是平行直线的流动，us 0
非均匀流中流场中相应点的流速大小或方向或同 时二者沿程改变，即沿流程方向速度分布不均。
例：流体在收缩管、扩散管或弯管中的流动。
（非均匀流又可分为急变流和渐变流）
想一想：何谓均匀流及非均匀流？以上分类与 过流断面上流速分布是否均匀有无关系？
点击这里查看答案
一、拉格朗日法
拉格朗日方法（lagrangian method）是以流场中每 一流体质点作为描述流体运动的方法，它以流体个别 质点随时间的运动为基础，通过综合足够多的质点 （即质点系）运动求得整个流动。——质点系法
研究对象：流体质点
空间坐标
x xa,b, c,t y ya,b, c,t z za,b, c,t
间点上各水力运动要素中, 只要有任何一个随时间的变 化而变化的流动。
即：u ux, y, z
p 0
p px, y,z
t
ux , u y , uz 三者中至少一个 t t t 不等于0
注意
在非恒定流情况下，流线的位置随时间而 变；流线与迹线不重合。在恒定流情况下，流 线的位置不随时间而变，且与迹线重合。
(1) A→A′存在时变加速度,但不存在位变加速度。 (2) B→B′既存在时变加速度,又存在位变加速度。
三、两种方法的比较
拉格朗日法
欧拉法
分别描述有限质点的轨迹 同时描述所有质点的瞬时参数
表达式复杂
表达式简单
不能直接反映参数的空间分布 直接反映参数的空间分布
不适合描述流体微元的 运动变形特性
适合描述流体微元的 运动变形特性
度；
位变加速度（迁移加速度） 流动过程中流体由于速度随位置变化而引起的加速度。
流体力学_第三章_伯努利方程及动量方程
4根线具有能量 意义： 总水头线 测压管水头线 水流轴线 基准面线
23
第三节 恒定总流的伯努利方程
例 用直径d=100mm的水管从水箱引水，水管水面与
管道出口断面中心高差H=4m，水位保持恒定，水头 损失hw=3m水柱，试求水管流量，并作出水头线 解：以0-0为基准面，列1-1、2-2断面的伯努利方程
第三节 恒定总流的伯努利方程
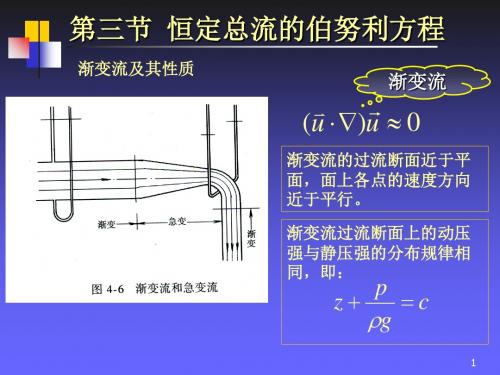
渐变流及其性质
渐变流
(u )u 0
渐变流的过流断面近于平 面，面上各点的速度方向 近于平行。 渐变流过流断面上的动压 强与静压强的分布规律相 同，即：
p z c g
1
第三节 恒定总流的伯努利方程
大小的变化 流速的变化 方向的变化
出现直线惯性力 压强沿流向变化
微小圆柱体的力平衡
p1dA ldA cos p2 dA l cos Z1 Z 2 p1 (Z1 Z 2 ) p2
Z1 p1 Z2 p2
4
第三节 恒定总流的伯努利方程
Z1 p1
Z2
p2
均匀流过流断面上压强 分布服从水静力学规 律
40
2
,
2
第三节 恒定总流的伯努利方程
( a )( z2 z1 ) ( a )( z2 z1 ) ( a )
单位体积气体所受有效浮力
v1 2 gh d1 1 d 2
4
4
2 1
2 1
30
第三节 恒定总流的伯努利方程
Q v1
4
d
2 1
4
d
2 1
2 gh d1 d 1 2
23
第三节 恒定总流的伯努利方程
例 用直径d=100mm的水管从水箱引水，水管水面与
管道出口断面中心高差H=4m，水位保持恒定，水头 损失hw=3m水柱，试求水管流量，并作出水头线 解：以0-0为基准面，列1-1、2-2断面的伯努利方程
第三节 恒定总流的伯努利方程
渐变流及其性质
渐变流
(u )u 0
渐变流的过流断面近于平 面，面上各点的速度方向 近于平行。 渐变流过流断面上的动压 强与静压强的分布规律相 同，即：
p z c g
1
第三节 恒定总流的伯努利方程
大小的变化 流速的变化 方向的变化
出现直线惯性力 压强沿流向变化
微小圆柱体的力平衡
p1dA ldA cos p2 dA l cos Z1 Z 2 p1 (Z1 Z 2 ) p2
Z1 p1 Z2 p2
4
第三节 恒定总流的伯努利方程
Z1 p1
Z2
p2
均匀流过流断面上压强 分布服从水静力学规 律
40
2
,
2
第三节 恒定总流的伯努利方程
( a )( z2 z1 ) ( a )( z2 z1 ) ( a )
单位体积气体所受有效浮力
v1 2 gh d1 1 d 2
4
4
2 1
2 1
30
第三节 恒定总流的伯努利方程
Q v1
4
d
2 1
4
d
2 1
2 gh d1 d 1 2
流体力学 第三章 流体动力学
按周界性质： ①总流四周全部被固体边界限制——有压流。如 自来水管、矿井排水管、液压管道。 ②总流周界一部分为固体限制，一部分与气体接 触——无压流。如河流、明渠。 ③总流四周不与固体接触——射流。如孔口、管 嘴出流。
7 流量、断面平均流速 a.流量：单位时间通过某一过流断面的流体量。流
量可以用体积流量Qv（m3/s）、质量流量Qm（kg/s） 表示。显然，对于均质不可压缩流体有
元流体积流量 总流的体积流量
Qm Qv
dQv vdA
Qv
dQ vdA vA
b.断面平均流速：总流过流断面上各点的流速v一般
不相等，为了便于计算，设过流断面上各点的速度
都相等，大小均为断面平均流速v。以v计算所得的
流量与实际流量相同。
vAQv
vdA
A
8 均匀流与非均匀流
流管——在流场中任意取不与流线重合的封 闭曲线，过曲线上各点作流线，所构成的管 状表面
流束——流管内的流体
5.过流断面——在流束上作出与流线正交的横断面
1
例：
注意：只有均匀流的过流断面才是平面
2
1
Hale Waihona Puke 1处过流断面2处过流断
2
面
6.元流与总流 元流——过流断面无限小的流束 总流——过流断面为有限大小的流束，它由无数元流构成
线上各点速度矢量与曲线相切
v1
v2
性质：一般情况下不相交、不折转
流线微分方程： 流线上任一点的切线方向 (dr)与该点速度矢量 (v)一致
i jk drv dx dy dz0
dx dy dz vx vy vz
vx vy vz
——流线微分方程
（2）迹线——质点运动的轨迹 迹线微分方程：对任一质点
7 流量、断面平均流速 a.流量：单位时间通过某一过流断面的流体量。流
量可以用体积流量Qv（m3/s）、质量流量Qm（kg/s） 表示。显然，对于均质不可压缩流体有
元流体积流量 总流的体积流量
Qm Qv
dQv vdA
Qv
dQ vdA vA
b.断面平均流速：总流过流断面上各点的流速v一般
不相等，为了便于计算，设过流断面上各点的速度
都相等，大小均为断面平均流速v。以v计算所得的
流量与实际流量相同。
vAQv
vdA
A
8 均匀流与非均匀流
流管——在流场中任意取不与流线重合的封 闭曲线，过曲线上各点作流线，所构成的管 状表面
流束——流管内的流体
5.过流断面——在流束上作出与流线正交的横断面
1
例：
注意：只有均匀流的过流断面才是平面
2
1
Hale Waihona Puke 1处过流断面2处过流断
2
面
6.元流与总流 元流——过流断面无限小的流束 总流——过流断面为有限大小的流束，它由无数元流构成
线上各点速度矢量与曲线相切
v1
v2
性质：一般情况下不相交、不折转
流线微分方程： 流线上任一点的切线方向 (dr)与该点速度矢量 (v)一致
i jk drv dx dy dz0
dx dy dz vx vy vz
vx vy vz
——流线微分方程
（2）迹线——质点运动的轨迹 迹线微分方程：对任一质点
工程流体力学-第三章
三、流管、流束和总流
1. 流管：在流场中任取一不是流 线的封闭曲线L，过曲线上的每 一点作流线，这些流线所组成的 管状表面称为流管。 2. 流束：流管内部的全部流体称 为流束。 3. 总流：如果封闭曲线取在管道 内部周线上，则流束就是充满管 道内部的全部流体，这种情况通 常称为总流。 4. 微小流束：封闭曲线极限近于 一条流线的流束 。
ax
dux dt
dux (x, y, z,t) dt
ux t
ux
ux t
uy
ux t
uz
ux t
ay
du y dt
duy (x, y, z,t) dt
u y t
ux
u y t
uy
u y t
uz
u y t
az
du z dt
duz (x, y, z,t) dt
x x(a,b,c,t)
y y(a,b,c,t)
z z(a,b,c,t)
欧拉法中的迹线微分方程
速度定义
u dr (dr为质点在时间间隔 dt内所移动的距离) dt
迹线的微分方程
dx dt
ux (x, y, z,t)
dy dt uy (x, y, z,t)
dz dt uz (x, y, z,t)
说明： （1）体积流量一般多用于表示不可压缩流体的流量。 （2）质量流量多用于表示可压缩流体的流量。
(3) 质量流量与体积流量的关系
Qm Q
(4) 流量计算 单位时间内通过dA的微小流量
dQ udA
通过整个过流断面流量
Q dQ udA A
流体力学 第三章
无数微元流束的总和称为总流。自然界和工程中所遇到 的管流或渠流都是总流。根据总流的边界情况，可以把总流 流动分为三类：
（1）有压流动 总流的全部边界受固体边界的约束， 即流体充满流道，如压力水管中的流动。
（2）无压流动 总流边界的一部分受固体边界约束，另 一部分与气体接触，形成自由液面，如明渠中的流动。
图 3-1 流体的出流
一、定常流动和非定常流动
这种运动流体中任一点的流体质点的流动参数(压强和 速度等)均不随时间变化，而只随空间点位置不同而变化的 流动，称为定常流动。
现将阀门A关小，则流入水箱的水量小于从阀门B流出的 水量，水箱中的水位就逐渐下降，于是水箱和管道任一点流 体质点的压强和速度都逐渐减小，水流的形状也逐渐向下弯 曲。
（2）如果流体是定常的，则流出的流体质量必然等于流 入的流体质量。
二、微元流束和总流的连续性方程 在工程上和自然界中，流体流动多数都是在某些周界
所限定的空间内沿某一方向流动，即一维流动的问题。 所谓一维流动是指流动参数仅在一个方向上有显著的
变化，而在其它两个方向上的变化非常微小，可忽略不计。 例如在管道中流动的流体就符合这个条件。在流场中取一 微元流束如图所示。
图 3-6 流场中的微元流束
假定流体的运动是连续、定 常的，则微元流管的形状不随时 间改变。根据流管的特性，流体 质点不能穿过流管表面，因此在 单位时间内通过微元流管的任一 过流断面的流体质量都应相等， 即
ρ1v1dA1=ρ2v2dA2=常数 dA1 、dA2—分别为1、2两个过 图 3-6 流场中的微元流束 流断面的面积，m2；
§ 3-1描述流体运动的两种方法
连续介质模型的引入，使我们可以把流体看作为由无 数个流体质点所组成的连续介质，并且无间隙地充满它所 占据的空间。
（1）有压流动 总流的全部边界受固体边界的约束， 即流体充满流道，如压力水管中的流动。
（2）无压流动 总流边界的一部分受固体边界约束，另 一部分与气体接触，形成自由液面，如明渠中的流动。
图 3-1 流体的出流
一、定常流动和非定常流动
这种运动流体中任一点的流体质点的流动参数(压强和 速度等)均不随时间变化，而只随空间点位置不同而变化的 流动，称为定常流动。
现将阀门A关小，则流入水箱的水量小于从阀门B流出的 水量，水箱中的水位就逐渐下降，于是水箱和管道任一点流 体质点的压强和速度都逐渐减小，水流的形状也逐渐向下弯 曲。
（2）如果流体是定常的，则流出的流体质量必然等于流 入的流体质量。
二、微元流束和总流的连续性方程 在工程上和自然界中，流体流动多数都是在某些周界
所限定的空间内沿某一方向流动，即一维流动的问题。 所谓一维流动是指流动参数仅在一个方向上有显著的
变化，而在其它两个方向上的变化非常微小，可忽略不计。 例如在管道中流动的流体就符合这个条件。在流场中取一 微元流束如图所示。
图 3-6 流场中的微元流束
假定流体的运动是连续、定 常的，则微元流管的形状不随时 间改变。根据流管的特性，流体 质点不能穿过流管表面，因此在 单位时间内通过微元流管的任一 过流断面的流体质量都应相等， 即
ρ1v1dA1=ρ2v2dA2=常数 dA1 、dA2—分别为1、2两个过 图 3-6 流场中的微元流束 流断面的面积，m2；
§ 3-1描述流体运动的两种方法
连续介质模型的引入，使我们可以把流体看作为由无 数个流体质点所组成的连续介质，并且无间隙地充满它所 占据的空间。
4流体力学第三章流动阻力与能量损失
二、能量损失的计算公式—长期工程经验总结
液体：沿程水头损失（达西公式）：
L v hf d 2g
均流速
2
(3-1)
λ—沿程阻力系数；Ｌ—管道长度；d—管道直径；v—平
v2 局部水头损失： hj 2g
气体：沿程压强损失： 局部压强损失： 核心问题： 和 的计算。
(3-2)
L v pf d 2
第一节 流动阻力与能量损失的两种 形式
一、流动阻力和能量损失的分类 根据流动的边界条件，能量损失分：沿程能量损失 和局部能量损失 ㈠沿程阻力及沿程能量损失 ◆沿程阻力—当束缚流体流动的固体边壁沿程不变, 流动为均匀流时,流层与流层之间或质点之间只存 在沿程不变的切应力，称为沿程阻力。 ◆沿程能量损失—沿程阻力作功引起的能量损失称 之这沿程能量损失。特点：沿管路长度均匀分布， 即沿程水头损失hf ∝ l。
层流区 不稳定区
紊流区
二、沿程水头损失与流态的关系
层流区：
紊流区：
hf v
hf v
1.75: 2.0
不稳定区：关系不稳定。
三、流动型态的判断标准
●雷诺数： 雷诺等人进一步实验表明：流态不仅和流速v有关， 还和管径d、流体的动力粘度μ和密度ρ有关。 以上四个参数组合成一个无因次数，叫雷诺数，用 Re表示。
㈡时均化
紊流运动要素围绕它上下波动的平均值称为时均值。 时均速度的定义：
u x AT u x Adt
0
T
1 T u x u x dt T 0
瞬时速度
(3-20)
' x
ux ux u
二、紊流阻力
由两部分组成： ①流体各层因时均流速不同而存在相对运动，故 流层间产生因粘滞性所引起的摩擦阻力。 粘性切应力τ1按牛顿内摩擦定律计算。 ②由于脉动现象，流层间质点的动量交换形成的 紊流附加切应力τ2。 其大小由普朗特的混合长度理论计算。见式 (3-21)。 Re较小时，τ1为主要； Re足够大时,τ2为主要。
流体力学第3章
得出涡量输运方程：
DΩ 2 (Ω )u Ω Dt
第3章
涡量与环量的一般原理
1. 旋度
旋转运动是用旋转角速度 来表征。源自在流体力学中，把两倍的旋转角速度矢 量定义为旋度，即
rotu u 2
式中，符号 rot 和 均表示求旋度， 速度的旋度为矢量。
2. 涡量
涡量就是速度的旋度，即
Ω u
有旋运动也称为涡量 Ω 不为零的运动。
式中， dA 为微分面积矢量。
这样，可通过分析速度环量研究 旋涡运动，Γ＝0 表示平面无旋运动； Γ≠ 0 则为有旋运动。
A
5. N－S 方程的替代形式与涡量输运方程
（1） N－S 方程的替代形式 利用下列表达式：
矢量恒等式 u2 (u )u ( ) u ( u ) 2 f Π 质量力有势 1 p － p ( ) 均质不可压缩流体
可将 N－S 方程化为兰姆型方程：
u p u2 2 ( Π ) u Ω u t 2
（2） 涡量输运方程
对兰姆型方程两端作“取旋度”运算， 并考虑到：
u Ω ( ) t t p
u2 ( Π )0 2 (u Ω ) ( Ω )u (u ) Ω 2 2 ( u ) Ω
3. 环量
在流场中任取一封闭曲线 L，把 速度矢量沿 L的线积分定义为速度 环量Γ，即 Γ L u dL L u x dx u y dy u z dz
式中， dL 为有向微分弧长，习惯上取反
时针回路为正向。
4.斯托克斯定理
斯托克斯定理 是将涡量与速度 环量联系起来的定理，即 Γ Ω dA
计算流体力学第三章
Axx 2Bxy Cyy D
方程的类型
The type of the equation are
B 2 AC 0 B 2 AC 0 B 2 AC 0
双曲型 Hyperbolic 抛物型 Parabolic 椭圆型 Elliptic
对于超音速流动（V>a），因为：
整理得
rewritten
dy tg ( ) c dx c dy tg ( ) c dx c
c 和 c 表示特征线的斜率。
c and
the slopes of the characteristic curves denote c
dy dx c
VxVy a
2
Vx2 Vy2 a
2
1
Vx2 1 2 a
利用速度三角形关系及马赫角定义
Using the velocity triangle relations and the mach angle of supersonic flow
Vx V cos Vy V sin 1 sin Ma
dy B B AC ( ) dx A
2
dy B B 2 AC ( ) dx A
x , y 沿特征线的变化规律 物理面特征线确定 The characteristic lines determine the change regulation of the velocity components
一、速度势方程
Equation of velocity potential function
二维轴对称流动的速度势方程
流体力学-第3章流体运动学
第3章流体运动学选择题：【3.1】 用欧拉法表示流体质点的加速度a 等于：（a ）22d d t r ；（b ）v t ∂∂；（c ）()v v ⋅∇；（d ）()t ∂+⋅∇∂vv v。
解：用欧拉法表示的流体质点的加速度为()d d t t∂==+∇∂v va v v （d ） 【3.2】 恒定流是：（a ）流动随时间按一定规律变化；（b ）各空间点上的运动要素不随时间变化；（c ）各过流断面的速度分布相同；（d ）迁移加速度为零。
解：恒定流是指用欧拉法来观察流体的运动，在任何固定的空间点若 流体质点的所有物理量皆不随时间而变化的流动.（b ）【3.3】 一元流动限于：（a ）流线是直线；（b ）速度分布按直线变化；（c ）运动参数是一个空间坐标和时间变量的函数；（d ）运动参数不随时间变化的流动。
解：一维流动指流动参数可简化成一个空间坐标的函数。
（c ）【3.4】 均匀流是：（a ）当地加速度为零；（b ）迁移加速度为零；（c ）向心加速度为零；（d ）合加速度为零。
解：按欧拉法流体质点的加速度由当地加速度和变位加速度（亦称迁移加速度）这两部分组成，若变位加速度等于零，称为均匀流动 （b ）【3.5】 无旋运动限于：（a ）流线是直线的流动；（b ）迹线是直线的流动；（c ）微团无旋转的流动；（d ）恒定流动。
解：无旋运动也称势流，是指流体微团作无旋转的流动，或旋度等于零的流动。
（d ） 【3.6】 变直径管，直径1320mm d =，2160mm d =，流速1 1.5m/s V =。
2V 为：（a ）3m/s ；（b ）4m/s ；（c ）6m/s ；（d ）9m/s 。
解：按连续性方程，22112244V d V d ππ=，故2212123201.56m/s160d V V d ⎛⎫⎛⎫==⨯= ⎪ ⎪⎝⎭⎝⎭（c ）【3.7】 平面流动具有流函数的条件是：（a ）理想流体；（b ）无旋流动；（c ）具有流速势；（d ）满足连续性。
3工程流体力学 第三章流体运动学基础
总流： 由无数元流构成的大的流束，包括整
个流动区域上的所有质点的流动。
§3-3 迹线、流线和染色线，流管（续16）
三、湿周、水力半径
1.湿周x 在总流过流断面上，液体与固体相接触的线
称为湿周。用符号x 表示。
2.水力半径R
总流过流断面的面积A与湿周的比值称为水Βιβλιοθήκη 力半径。R A x
注意：水力半径与几何半径是完全不同的两个概念。
这是两个微分方程，其中 t 是参数。 可求解得到两族曲面，它们的交线就是 流线族。
§3-3 迹线、流线和染色线，流管（续10）
例3-1 已知直角坐标系中的速度场 u=x+t； v= -y+t；w=0,
试求t = 0 时过 M(-1,-1) 点的流线。
解：由流线的微分方程：
dx d y dz u vw
§3-3 迹线、流线和染色线，流管（续5）
因为u不随t变，所以同一点的流线 始终保持不变。即流线与迹线重合。
某点流速的方向是
流线在该点的切线方向 A
B
流速的大小由流 线的疏密程度反映
uA=uB ?
§3-3 迹线、流线和染色线，流管（续6）
迹线与流线方程 采用拉格朗日方法描述流动时，质
点的运动轨迹方程:
试求t = 0 时过 M(-1,-1) 点的迹线。
解：由迹线的微分方程：
dx d y dz dt u vw
u=x+t；v=-y+t；w=0
dx xt dt
d y y t
dt
求解
x C1 et t 1
t = 0 时过 M(-1,-1)：C1 = C2 = 0 y C2 et t 1 x= -t-1 y= t-1 消去t，得迹线方程： x+y = -2
个流动区域上的所有质点的流动。
§3-3 迹线、流线和染色线，流管（续16）
三、湿周、水力半径
1.湿周x 在总流过流断面上，液体与固体相接触的线
称为湿周。用符号x 表示。
2.水力半径R
总流过流断面的面积A与湿周的比值称为水Βιβλιοθήκη 力半径。R A x
注意：水力半径与几何半径是完全不同的两个概念。
这是两个微分方程，其中 t 是参数。 可求解得到两族曲面，它们的交线就是 流线族。
§3-3 迹线、流线和染色线，流管（续10）
例3-1 已知直角坐标系中的速度场 u=x+t； v= -y+t；w=0,
试求t = 0 时过 M(-1,-1) 点的流线。
解：由流线的微分方程：
dx d y dz u vw
§3-3 迹线、流线和染色线，流管（续5）
因为u不随t变，所以同一点的流线 始终保持不变。即流线与迹线重合。
某点流速的方向是
流线在该点的切线方向 A
B
流速的大小由流 线的疏密程度反映
uA=uB ?
§3-3 迹线、流线和染色线，流管（续6）
迹线与流线方程 采用拉格朗日方法描述流动时，质
点的运动轨迹方程:
试求t = 0 时过 M(-1,-1) 点的迹线。
解：由迹线的微分方程：
dx d y dz dt u vw
u=x+t；v=-y+t；w=0
dx xt dt
d y y t
dt
求解
x C1 et t 1
t = 0 时过 M(-1,-1)：C1 = C2 = 0 y C2 et t 1 x= -t-1 y= t-1 消去t，得迹线方程： x+y = -2
流体力学第3章
相应的流体静压强增加dp，压强的增量取决于质量力。
22.04.2021
12
二、流体平衡条件
对于不可压缩均质流体，有
dpfxdxfydyfzdz
上式的左边是全微分，它的右边也必须是全微分。由数学
分析知：该式右边成为某一个函数全微分的充分必要条
件是
f y f z z y
f z f x x z
f x f y y x
22.04.2021
15
第三节 重力场中流体的平衡帕斯卡原理
一、重力作用下的静力学基本方程式
P0
P2 P1 Z1 Z2
推导静力学基本方程式用图
22.04.2021
16
作用在液体上的质量力只有重力G=mg，其单位质 量力在各坐标轴上的分力为 fx=0，fy=0，fz=-g
代入压强差公式，得
dpgdz
及烟囱的底部等处的绝对压强都低于当地大气压强，这些地
方的计示压强都是负值，称为真空或负压强，用符号pv表示，
则
pv pa p
如以液柱高度表示，则
hv
pv
g
pa p
g
式中hv称为真空高度。
22.04.2021
29
（1）当地大气压强是某地气压表上测得的压强值， 它随着气象条件的变化而变化，所以当地大气压强 线是变动的。
M点的绝对压强为 p=pa+ρ2gh2-ρ1gh1
M点的计示压强为 pe=p-pa=ρ2gh2-ρ1gh1
于是，可以根据测得的h1和h2以及已知的ρ1和ρ2计 算出被测点的绝对压强和计示压强值。
22.04.2021
37
• (2) 被测容器中的流体压强小于大气压强(即p<pa)：
流体力学第三章流体动力学(1)
（2）流线的作法
流线的作法如下：在流速场中任取一点1（如下图），绘出
在某时刻通过该点的质点的流速矢量u1，再在该矢量上取距
点1很近的点2处，标出同一时刻通过该处的另一质点的流速
矢量u2……如此继续下去，得一折线1 2 3 4 5 6……，若
折线上相邻各点的间距无限接近，其极限就是某时刻流速场 中经过点1的流线。
(b)非恒定流
mt1 流线 mt2
迹线 mt3
且与迹线重合。
3. 均匀流和非均匀流 划分依据：按流速的大小和方向是否沿程变化
（1）均匀流
流速沿程不变的流动称为均匀流
在均匀流时不存在迁移加速度，即 auuo s
其流线为彼此平行的直线
例：等直径直管中的液流或者断面形状和水深不变的长直渠道中的水流 都是均匀流。
ux
uz x
uy
uz y
uz
uz z
质点的加速度由两部分组成：
auuu t s
欧拉加速度
ax
ux t
ux
ux x
uy
ux y
uz
ux z
ay
uy t
ux
uy x
uy
uy y
uz
uy z
az
uz t
ux
பைடு நூலகம்
uz x
uy
uz y
uz
uz z
①时变加速度（当地加速度）——流动过程中液体由于速度 随时间变化而引起的加速度； ——等号右边第一项是时变 加速度 ②位变加速度（迁移加速度）——流动过程中液体由于速度 随位置变化而引起的加速度。 ——后三项是位变加速度
（1） （a,b,c）=Const , t为变数，可以得出某个指定质点在任意时刻 所处的位置。 （2） （a,b,c）为变数, t =Const ，可以得出某一瞬间不同质点在空 间的分布情况。
环境流体力学第三章随流扩散
第三章 随流扩散
第一节 随流扩散方程
第一节 随流扩散方程
设流体质点具有瞬时流速矢量 在x、y、z直角坐标上的分量分 别为u、v、w ： y， v
u uu
'
x， u
z，w
v v v'
w w w'
直角坐标系下的瞬时流速分量
随流扩散：由于水体的平均运动（包括时间平均和空间平均） 使污染物质发生输移的现象。 对层流: u′、 v′、w′为零，水体的平均运动指的是空间平均 运动，在这种情况下的物质的迁移就是分子扩散和随流输 移的叠加。
( 3-2-11 )
若Dx = Dy = D，有：
( x ut )2 y 2 Mz c( x, y , t ) exp 4 Dt 4 Dt
( 3-2-12 )
上两式均满足瞬时无限长线源无界空间的定解条件 初始条件：c(x，y，0)= Mzδ(r)， r =(x2+y2)1/2 边界条件：c(±∞， y， t )=c(x，±∞， t )=0
( 3-2-10 )
边界条件：c(±∞, t )=0
均匀流条件下瞬时点源的随流-扩散
例：一条无限长的顺直矩形断面渠道，水面 宽 B= 5m，水深 h= 2m，在其中间断面瞬时 投入 M= 10kg 的污染物，渠道的流速恒定， U= 0.2m/s，扩散系数 D= 0.075m2/s。求经过 时间t= 50s，100s 后，在投入点下游 10m 处污 染物的浓度。
第一节 随流扩散方程
1.一维随流扩散方程
设v=w=0，只有u分量（沿x轴）
c Q f D 分子扩散通量： x
污染物随流输移的通量：
Fick定律
qf qs
第一节 随流扩散方程
第一节 随流扩散方程
设流体质点具有瞬时流速矢量 在x、y、z直角坐标上的分量分 别为u、v、w ： y， v
u uu
'
x， u
z，w
v v v'
w w w'
直角坐标系下的瞬时流速分量
随流扩散：由于水体的平均运动（包括时间平均和空间平均） 使污染物质发生输移的现象。 对层流: u′、 v′、w′为零，水体的平均运动指的是空间平均 运动，在这种情况下的物质的迁移就是分子扩散和随流输 移的叠加。
( 3-2-11 )
若Dx = Dy = D，有：
( x ut )2 y 2 Mz c( x, y , t ) exp 4 Dt 4 Dt
( 3-2-12 )
上两式均满足瞬时无限长线源无界空间的定解条件 初始条件：c(x，y，0)= Mzδ(r)， r =(x2+y2)1/2 边界条件：c(±∞， y， t )=c(x，±∞， t )=0
( 3-2-10 )
边界条件：c(±∞, t )=0
均匀流条件下瞬时点源的随流-扩散
例：一条无限长的顺直矩形断面渠道，水面 宽 B= 5m，水深 h= 2m，在其中间断面瞬时 投入 M= 10kg 的污染物，渠道的流速恒定， U= 0.2m/s，扩散系数 D= 0.075m2/s。求经过 时间t= 50s，100s 后，在投入点下游 10m 处污 染物的浓度。
第一节 随流扩散方程
1.一维随流扩散方程
设v=w=0，只有u分量（沿x轴）
c Q f D 分子扩散通量： x
污染物随流输移的通量：
Fick定律
qf qs
第三章流体力学
因为时间∆ 极短，所以a 因为时间∆t极短，所以a1b1和a2b2 是两段极短的位移， 是两段极短的位移，在每段极短的位移 压强p 截面积S和流速v 中，压强p、截面积S和流速v都可看作 不变。 不变。设p1、S1、v1和p2、S2、v2分别是 a b 1 1 处流体的压强、 a1b1与a2b2处流体的压强、截面积和流 p v 2 则后面流体的作用力是p S1， 速，则后面流体的作用力是p1S1，位移S2 1 所作的正功是p 是v1 ∆t，所作的正功是p1S1v1 ∆t ，而 h1 前面流体作用力作的负功是前面流体作用力作的负功是-p2S2v2 ∆t ， 由此， 由此，外力的总功是
A
3、流线 、
A
vB
B
在流体内做一微小的闭合曲线， 在流体内做一微小的闭合曲线，通 过其上各点的流线围成的管状区域称为流管。 过其上各点的流线围成的管状区域称为流管。 因为流线不可相交， 因为流线不可相交，则 在任意时刻， 在任意时刻，流体质点 只能在流管内部或流管 表面流动， 表面流动，而不能穿越 流管。 流管。
vS
v1
S2
§3.2 伯努利方程
伯努利方程是流体动力学的基本定律， 伯努利方程是流体动力学的基本定律，它说明了 理想流体在管道中作稳定流动时， 理想流体在管道中作稳定流动时，流体中某点的压 流速v和高度h 强p、流速v和高度h三个量之间的关系为 ρv2 p + + ρ gh = 常量
2
式中ρ是流体的密度，g是重力加速度。试用功能 式中ρ是流体的密度， 是重力加速度。 a1 b1 原理导出伯努利方程。 原理导出伯努利方程。 我们研究管道中一段流体的p2 S2 v 1 运动。设在某一时刻， 运动。设在某一时刻，这段 a2 流体在a 位置， 流体在a1a2位置，经过极短 b2 h1 时间∆ 时间∆t后，这段流体达到 v h2 p S 2 b1b2位置 2 2
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
空间各点只要有一个运动要素随时间变化，流体运动称为非恒 定流。
二 均匀流和非均匀流 渐变流和急变 流
按各点运动要素（主要是速度）是否随位置变化，可将流体 运动分为均匀流和非均匀流。在给定的某一时刻，各点速度 都不随位置而变化的流体运动称均匀流。均匀流各点都没有 迁移加速度，表示为平行流动，流体作匀速直线运动。反之， 则称为非均匀流。
按限制总流的边界情况，可将流体运动分为有压流、无压流和射 流。
边界全为固体的流体运动称为有压流或有压管流。 边界部分为固体、部分为气体，具有自由表面的液体运动称为 无压流或明渠流。 流体经由孔口或管嘴喷射到某一空间，由于运动的流体脱离了 原来限制他的固体边界，在充满流体的空间继续流动的这种流 体运动称为射流。
四 三维流（三元流）、二维流（二元流）、一维流（一元流）
按决定流体的运动要素所需空间坐标的维数或空间坐标变量的 个数，可将流体运动分为三维流、二维流、一维流。
若流体的运动要素是空间三个坐标和时间t的函数，这种流体运 动称为三维流或三元流。
若流体的运动要素是空间两个坐标和时间t的函数，这种流体运 动称为二维流或二元流。
拉格朗日法来研究流体运动，就归结为求出函数x（a, b, c, t）, y (a, b, c, t), z (a, b, c, t)。（1）由于流体运动的复杂，要想求 出这些函数是非常繁复的，常导致数学上的困难。（2）在大多 数实际工程问题中，不需要知道流体质点运动的轨迹及其沿轨迹 速度等的变化。（3）测量流体运动要素，要跟着流体质点移动 测试，测出不同瞬时的数值，这种测量方法较难，不易做到。
3 脉线
脉线又称染色线，在某一段时间内先后流过同一空间点的所 有流体质点，在既定瞬时均位于这条线上。
在恒定流时，流线和流线上流体质点的迹线以及脉线都相互 重合。
第二节 描述流体运动的一些基本概念
一 流管 流束 过流断面 元流 总流
在流场中，任意取一非流线且不自相交的封闭曲线。从这封 闭曲线上各个点绘出流线，组成封闭管状曲面，称为流管。流 管内的流体称为流束。沿流体流动方向，在流束上取一横断面， 使它在所有各点上都和流线正交。这一横断面称过流断面。过 流断面面积无限小的流束称元流；相应的流管称微元流管。过 流断面面积具有一定大小的有限尺寸的流束称总流。总流可以 看出是由流动边界内无数元流所组成的总和
二 欧拉法： 运动流体占据的空间，称流场。欧拉法以流场为研究对象， 以空间点为着眼点。 欧拉法是从分析通过流场中某固定空间点的流体质点的运动 着手，设法描述出每一个空间点上流体质点运动随时间变化 的规律。
x, y, z都应看作自变量，它们和t一起都被称为欧拉变数。
流体质点的加速度由两部分组成，一是由于时间过程而使空间 点上的质点速度发生变化的加速度，称当地加速度（或时变加 速度）；另一是流动过程中质点由于位置占据不同的空间点而 发生速度变化的加速度，称迁移加速度（或位变加速度）。
连续性介质假定，在流体力学中，组成流体的最小基元是流 体质点，将流体视为由无穷多流体质点所组成的一种连续介 质。 要从宏观上研究流体的运动规律，必须在数学上对流体质点 的运动特征给出描述。描述流体质点运动，常采用两种方法： 拉格朗日法（Lagrange）法和欧拉法（Euler）。
一 拉格朗日法： 拉格朗日法是从分析流体质点的运动着手，设法描述出每一 个流体质点自始至终的过程，即它们的位置随时间的变化。
第三章 流体运动学 凡表征流体运动的各种物理量，如速度、加速度等，都称流体 的运动要素。
本章暂不涉及引起流体运动的动力要素—力。
研究流体运动就是研究流体的运动要素随时间和空间的变化以 及建立它们之间的关系式。
流体运动学是研究流体运动而不涉及力的规律及其在工程上的 应用。
第一节 描述流体运动的两种方法：拉格朗日法和欧拉法
消去时间t后，即得在直角坐标系中的迹线方程，为一迹线族。 给定（a, b, c）就可以得到以x, y, z表示的该流体质点（a, b, c）的迹线。
1 迹线 欧拉法
建立迹线方程：迹线微小段ds即代表流体质点在dt时段内的位 移，dx, dy, dz代表ds在坐标轴上的投影，所以
迹线的微分方程
或
2 流线 在欧拉法中，是以速度场来描述流体运动的。
在实际流体运动中，常难于遇到符合上述定义的均匀流。 按沿流程各个过流断面上位于同一流线上的点，称相应点的速 度（大小、方向）是否相等，可将流体运动分为均匀流和非均 匀流。均匀流的所有流线都是平行直线，非均匀流的所有流线 不是一组平行直线。
按各流线是否接近于平行直线，又可将非均匀流分为渐变流和 急变流。
为全加速度，又称随体导数或质点导数，即流 体质 点速度随时间的变化率。 为当地加速度，又称时变导数。
为迁移加速度，又称位变导数。
工程流体力学中常用欧拉法。（1）在大多数的实际工程问题中， 只要知道在通过空间任意固定点时有关的流体质点诸运动要素 随时间的变化。（2）在欧拉法中，数学方程的求解较拉格朗日 法为易。（3）量测流体运动要素，用欧拉法时可将测试仪固定 在指定的空间点上，这种量测方法是容易做到的。
拉格朗日法是一种质点系法，是理论力学中质点模型在流体 运动上的直接应用，和研究固体质点系的方法是一样的。
由于质点是连续分布的，要研究每一个质点的运动，必须用 某种数学方法来区分不同的流体质点。通常采用的方法是以 起始时刻t=t0时，各质点的空间坐标（a, b, c）作为区别不同 质点的标志。
由于每一个质点在t=t0时刻的坐标值（a, b, c）不一样，所以 每一个质点在任何时刻的空间位置，在直角坐标系中将是a, b, c, t的单值连续函数。
在元流同一过流断面上各点的运动要素如速度、压强等可认为是 相等的。总流同一过流断面上各点的运动要素如速度、压强等不 一定相等。
二 流量 断面平均流速
单位时间内通过某一过流断面的流体数量称为流量。可以用体积 流量、重量流量和质量流量表示，单位分别是m3/s, kN/s, kg/s
元流
总流
二 流量 断面平均流速
通常称a、b、c为自变量，它们和t称为拉格朗日变数。
式中a、b、c为初始时刻任意流体质点的坐标，即不同的a、 b、c代表不同的流体质点。 (1)对于某个确定的流体质点，a、b、c为常数，而t为变量，
则得到流体质点的运动规律。
(2)对于某个确定的时刻，t为常数，而a、b、c为变量，得到
某一时刻不同流体质点的位置分布。 (3)若（a，b，c）、t均为变数，可得任意流体质点在任何时 刻的运动情况，方程式所表达的是任意质点运动的轨迹。
连续性介质假定，在流体力学中，组成流体的最小基元是流 体质点，将流体视为由无穷多流体质点所组成的一种连续介 质。
拉格朗日法
着眼于流体质点，跟踪 质点描述其运动历程
欧拉法
是描述液体运动 常用的一种方法。
着眼于空间点，研究 质点流经空间各固定 点的运动特性
第一节 描述流体运动的两种方法：拉格朗日法和欧拉法
பைடு நூலகம்
流体质点的速度 流体质点的加速度
二 欧拉法： 运动流体占据的空间，称流场。欧拉法以流场为研究对象， 以空间点为着眼点。 欧拉法是从分析通过流场中某固定空间点的流体质点的运动 着手，设法描述出每一个空间点上流体质点运动随时间变化 的规律。
欧拉法又称流场法。采用欧拉法，就可利用场论的知识。如 果场的物理量不随时间而变化，为稳定场；随时间而变化， 则为非稳定场。在工程流体力学中，将上述的流体运动分别 称恒定流和非恒定流。如果场的物理量不随位置而变化，为 均匀场；随位置而变化，则为非均匀场。
各流线之间的夹角很小，即各流线几乎是平行的，且各流线的 曲率半径很大，即各流线几乎是直线的流体运动称为渐变流。 所有流线是一组几乎平行的直线，所以渐变流的过流断面可认 为是一平面。均匀流是渐变流的极限情况。
各流线之间的夹角很大，或者各流线的曲率半径很小的流体运 动称为急变流。
三 有压流（有压管流）、无压流（明渠流）、射流
2 流线
（1）在一般情况下，流线不能相交，因在相交处将出现两个速 度矢量，而每个流体质点在某一时刻只能有一个速度矢量，所 以通过一点只能有一条流线。
（2）在流场内，速度为零的点（称驻点或停滞点）和速度为无 穷大的点（称奇点）以及流线相切的点是例外，通过上述点不 只有一条流线。
（3）流线亦不能转折，因为转折处同样会出现有两个速度矢量 的问题。流体是连续介质，各运动要素在空间是连续
上式除以dxdydzdt后可得，可压缩流体的连续性微分方程
表达了任何可能实现的流体运动所必须满足的连续性条件， 即质量守恒条件。
不可压缩均质流体
上式即为不可压缩均质流体的连续性微分方程，它适用于恒 定流和非恒定流。 物理意义：流体的体积变形率为零，即它的体积不会发生变 化。
速度场是矢量场，可以用它的矢线来形象地描述它。
速度场的矢线就是流线。 流线是同一时刻不同质 点所组成的曲线，它给 出该时刻不同流体质点 的速度方向。
在流线AB上取一微小段ds，速度矢量 u与流线微小段ds重合，方向余弦为
流线的微分方程
流线是指某一指定时刻的曲线，所以时间t不应作为自变量， 只能作为一个参变量出现。 欲求某一指定时刻的流线，需把t当作常数代入上式，然后进 行积分。
若流体的运动要素仅是空间一个坐标和时间t的函数，这种流体 运动称为一维流或一元流。元流同一过流断面上的运动要素可 认为是相等的，所以元流中任意点的运动要素只与流程坐标s有 关，即为一维流。总流按一维流来分析处理，实际是以总流的 过流断面的运动要素平均值来代替该过流断面上各点的运动要 素。
第四节 流体运动的连续性方程
一 系统 控制体
流体系统的边界有以下几个特点：
（1）系统的边界随流体一起运动，系统的体积边界面的形状和 大小可随时间而变化;
（2）在系统的边界处没有质量的交换，即没有流体流进或流出 系统的边界;
二 均匀流和非均匀流 渐变流和急变 流
按各点运动要素（主要是速度）是否随位置变化，可将流体 运动分为均匀流和非均匀流。在给定的某一时刻，各点速度 都不随位置而变化的流体运动称均匀流。均匀流各点都没有 迁移加速度，表示为平行流动，流体作匀速直线运动。反之， 则称为非均匀流。
按限制总流的边界情况，可将流体运动分为有压流、无压流和射 流。
边界全为固体的流体运动称为有压流或有压管流。 边界部分为固体、部分为气体，具有自由表面的液体运动称为 无压流或明渠流。 流体经由孔口或管嘴喷射到某一空间，由于运动的流体脱离了 原来限制他的固体边界，在充满流体的空间继续流动的这种流 体运动称为射流。
四 三维流（三元流）、二维流（二元流）、一维流（一元流）
按决定流体的运动要素所需空间坐标的维数或空间坐标变量的 个数，可将流体运动分为三维流、二维流、一维流。
若流体的运动要素是空间三个坐标和时间t的函数，这种流体运 动称为三维流或三元流。
若流体的运动要素是空间两个坐标和时间t的函数，这种流体运 动称为二维流或二元流。
拉格朗日法来研究流体运动，就归结为求出函数x（a, b, c, t）, y (a, b, c, t), z (a, b, c, t)。（1）由于流体运动的复杂，要想求 出这些函数是非常繁复的，常导致数学上的困难。（2）在大多 数实际工程问题中，不需要知道流体质点运动的轨迹及其沿轨迹 速度等的变化。（3）测量流体运动要素，要跟着流体质点移动 测试，测出不同瞬时的数值，这种测量方法较难，不易做到。
3 脉线
脉线又称染色线，在某一段时间内先后流过同一空间点的所 有流体质点，在既定瞬时均位于这条线上。
在恒定流时，流线和流线上流体质点的迹线以及脉线都相互 重合。
第二节 描述流体运动的一些基本概念
一 流管 流束 过流断面 元流 总流
在流场中，任意取一非流线且不自相交的封闭曲线。从这封 闭曲线上各个点绘出流线，组成封闭管状曲面，称为流管。流 管内的流体称为流束。沿流体流动方向，在流束上取一横断面， 使它在所有各点上都和流线正交。这一横断面称过流断面。过 流断面面积无限小的流束称元流；相应的流管称微元流管。过 流断面面积具有一定大小的有限尺寸的流束称总流。总流可以 看出是由流动边界内无数元流所组成的总和
二 欧拉法： 运动流体占据的空间，称流场。欧拉法以流场为研究对象， 以空间点为着眼点。 欧拉法是从分析通过流场中某固定空间点的流体质点的运动 着手，设法描述出每一个空间点上流体质点运动随时间变化 的规律。
x, y, z都应看作自变量，它们和t一起都被称为欧拉变数。
流体质点的加速度由两部分组成，一是由于时间过程而使空间 点上的质点速度发生变化的加速度，称当地加速度（或时变加 速度）；另一是流动过程中质点由于位置占据不同的空间点而 发生速度变化的加速度，称迁移加速度（或位变加速度）。
连续性介质假定，在流体力学中，组成流体的最小基元是流 体质点，将流体视为由无穷多流体质点所组成的一种连续介 质。 要从宏观上研究流体的运动规律，必须在数学上对流体质点 的运动特征给出描述。描述流体质点运动，常采用两种方法： 拉格朗日法（Lagrange）法和欧拉法（Euler）。
一 拉格朗日法： 拉格朗日法是从分析流体质点的运动着手，设法描述出每一 个流体质点自始至终的过程，即它们的位置随时间的变化。
第三章 流体运动学 凡表征流体运动的各种物理量，如速度、加速度等，都称流体 的运动要素。
本章暂不涉及引起流体运动的动力要素—力。
研究流体运动就是研究流体的运动要素随时间和空间的变化以 及建立它们之间的关系式。
流体运动学是研究流体运动而不涉及力的规律及其在工程上的 应用。
第一节 描述流体运动的两种方法：拉格朗日法和欧拉法
消去时间t后，即得在直角坐标系中的迹线方程，为一迹线族。 给定（a, b, c）就可以得到以x, y, z表示的该流体质点（a, b, c）的迹线。
1 迹线 欧拉法
建立迹线方程：迹线微小段ds即代表流体质点在dt时段内的位 移，dx, dy, dz代表ds在坐标轴上的投影，所以
迹线的微分方程
或
2 流线 在欧拉法中，是以速度场来描述流体运动的。
在实际流体运动中，常难于遇到符合上述定义的均匀流。 按沿流程各个过流断面上位于同一流线上的点，称相应点的速 度（大小、方向）是否相等，可将流体运动分为均匀流和非均 匀流。均匀流的所有流线都是平行直线，非均匀流的所有流线 不是一组平行直线。
按各流线是否接近于平行直线，又可将非均匀流分为渐变流和 急变流。
为全加速度，又称随体导数或质点导数，即流 体质 点速度随时间的变化率。 为当地加速度，又称时变导数。
为迁移加速度，又称位变导数。
工程流体力学中常用欧拉法。（1）在大多数的实际工程问题中， 只要知道在通过空间任意固定点时有关的流体质点诸运动要素 随时间的变化。（2）在欧拉法中，数学方程的求解较拉格朗日 法为易。（3）量测流体运动要素，用欧拉法时可将测试仪固定 在指定的空间点上，这种量测方法是容易做到的。
拉格朗日法是一种质点系法，是理论力学中质点模型在流体 运动上的直接应用，和研究固体质点系的方法是一样的。
由于质点是连续分布的，要研究每一个质点的运动，必须用 某种数学方法来区分不同的流体质点。通常采用的方法是以 起始时刻t=t0时，各质点的空间坐标（a, b, c）作为区别不同 质点的标志。
由于每一个质点在t=t0时刻的坐标值（a, b, c）不一样，所以 每一个质点在任何时刻的空间位置，在直角坐标系中将是a, b, c, t的单值连续函数。
在元流同一过流断面上各点的运动要素如速度、压强等可认为是 相等的。总流同一过流断面上各点的运动要素如速度、压强等不 一定相等。
二 流量 断面平均流速
单位时间内通过某一过流断面的流体数量称为流量。可以用体积 流量、重量流量和质量流量表示，单位分别是m3/s, kN/s, kg/s
元流
总流
二 流量 断面平均流速
通常称a、b、c为自变量，它们和t称为拉格朗日变数。
式中a、b、c为初始时刻任意流体质点的坐标，即不同的a、 b、c代表不同的流体质点。 (1)对于某个确定的流体质点，a、b、c为常数，而t为变量，
则得到流体质点的运动规律。
(2)对于某个确定的时刻，t为常数，而a、b、c为变量，得到
某一时刻不同流体质点的位置分布。 (3)若（a，b，c）、t均为变数，可得任意流体质点在任何时 刻的运动情况，方程式所表达的是任意质点运动的轨迹。
连续性介质假定，在流体力学中，组成流体的最小基元是流 体质点，将流体视为由无穷多流体质点所组成的一种连续介 质。
拉格朗日法
着眼于流体质点，跟踪 质点描述其运动历程
欧拉法
是描述液体运动 常用的一种方法。
着眼于空间点，研究 质点流经空间各固定 点的运动特性
第一节 描述流体运动的两种方法：拉格朗日法和欧拉法
பைடு நூலகம்
流体质点的速度 流体质点的加速度
二 欧拉法： 运动流体占据的空间，称流场。欧拉法以流场为研究对象， 以空间点为着眼点。 欧拉法是从分析通过流场中某固定空间点的流体质点的运动 着手，设法描述出每一个空间点上流体质点运动随时间变化 的规律。
欧拉法又称流场法。采用欧拉法，就可利用场论的知识。如 果场的物理量不随时间而变化，为稳定场；随时间而变化， 则为非稳定场。在工程流体力学中，将上述的流体运动分别 称恒定流和非恒定流。如果场的物理量不随位置而变化，为 均匀场；随位置而变化，则为非均匀场。
各流线之间的夹角很小，即各流线几乎是平行的，且各流线的 曲率半径很大，即各流线几乎是直线的流体运动称为渐变流。 所有流线是一组几乎平行的直线，所以渐变流的过流断面可认 为是一平面。均匀流是渐变流的极限情况。
各流线之间的夹角很大，或者各流线的曲率半径很小的流体运 动称为急变流。
三 有压流（有压管流）、无压流（明渠流）、射流
2 流线
（1）在一般情况下，流线不能相交，因在相交处将出现两个速 度矢量，而每个流体质点在某一时刻只能有一个速度矢量，所 以通过一点只能有一条流线。
（2）在流场内，速度为零的点（称驻点或停滞点）和速度为无 穷大的点（称奇点）以及流线相切的点是例外，通过上述点不 只有一条流线。
（3）流线亦不能转折，因为转折处同样会出现有两个速度矢量 的问题。流体是连续介质，各运动要素在空间是连续
上式除以dxdydzdt后可得，可压缩流体的连续性微分方程
表达了任何可能实现的流体运动所必须满足的连续性条件， 即质量守恒条件。
不可压缩均质流体
上式即为不可压缩均质流体的连续性微分方程，它适用于恒 定流和非恒定流。 物理意义：流体的体积变形率为零，即它的体积不会发生变 化。
速度场是矢量场，可以用它的矢线来形象地描述它。
速度场的矢线就是流线。 流线是同一时刻不同质 点所组成的曲线，它给 出该时刻不同流体质点 的速度方向。
在流线AB上取一微小段ds，速度矢量 u与流线微小段ds重合，方向余弦为
流线的微分方程
流线是指某一指定时刻的曲线，所以时间t不应作为自变量， 只能作为一个参变量出现。 欲求某一指定时刻的流线，需把t当作常数代入上式，然后进 行积分。
若流体的运动要素仅是空间一个坐标和时间t的函数，这种流体 运动称为一维流或一元流。元流同一过流断面上的运动要素可 认为是相等的，所以元流中任意点的运动要素只与流程坐标s有 关，即为一维流。总流按一维流来分析处理，实际是以总流的 过流断面的运动要素平均值来代替该过流断面上各点的运动要 素。
第四节 流体运动的连续性方程
一 系统 控制体
流体系统的边界有以下几个特点：
（1）系统的边界随流体一起运动，系统的体积边界面的形状和 大小可随时间而变化;
（2）在系统的边界处没有质量的交换，即没有流体流进或流出 系统的边界;