结构力学——渐进法
清华大学结构力学第8章渐进法分析

A
i
B
A
M AB iA
M BA iA
A
i
B
A
CAB
M BA M AB
1 2
CAB
M BA M AB
0
CAB
M BA M AB
1
在上面的讨论中可知,远端弯矩等于近端弯
矩乘传递系数,即 MBA CAB M。AB 清华大学结构力学第8章渐进法分 析
四、单结点力矩分配
MB=60kN.m
200kN
A
EI
3m
B
3m
20kN/m
EI C
6m
a)
200kN MB 60kN.m 20kN/m
B
A
B
150kN.m -90kN.m 150kN.m 150kN.m 90kN.m C
b)
用位移法解图a)所示结构时,首先在结点B加上 附加转动约束,锁住B使之不能转动。其产生的 反力矩MB等于各杆端固端力矩的代数和,见图 b)。
0.571
BC
3 7
0.429
M
F AB
1 8
2006Biblioteka 150kN.mMF BC
1 20 62 8
90kN.m
结点B约束力矩为:
M
F BA
1 8
200
6
150kN.m
结点B分配力矩为:
MB (150 90)清华6大0学k结N构.m力学第8章渐进M法分B 60kN.m
析
3)运算格式
分配系数 固端弯矩 分配传递
A
-150
-17.13
杆端弯矩 -167.13
BA BC
0.571 0.429
150 -90 -34.26 -25.74
结构力学教程——第12章 渐进法和超静定结构的影响线

性质,可得到柱子两端弯矩。
知识点 12.5-3
柱间有水平荷载作用时的计算
I=∞
A
C
q
i1 h1
B
i2 h2 D
I=∞
A
C
q
i1 h1
i2 h2
B
+
D
A
i1 h1 B
I=∞ C
i2 h2 D
P 单跨梁计算
P 力矩分配法
知识点
12.6 用机动法绘制连续梁的影响线
力法基本方程
11 Z1 1P 0
SBA 1 5
CBA 1
例2:作图示刚架的弯矩图
解 (1)固端弯矩
M
F AB
M
F BA
1 4 kN 3.3m 2
= 6.6kN m
M
F BC
M
F CB
1 (4 8.5)kN 3.6m 2
= 22.5kN m
(2)分配系数
SBA iBA 3.5 SBC iBC 5 SBE 3iBE 162
(http://structuremechanics/index1.htm)
1. 课程导入
连续梁桥
q
多跨连续梁
2. 结点力矩下单结点力矩分配
2.1 力矩分配法概念的提出 回顾位移法
例1:若梁线刚度 i 相同,求梁各杆端弯矩。
M
M
B
A
MBA MBC
M BA 4iB
B
θB
C
M AB 2iB
M BC 3iB
SCB 4 SCF 2 SCD 3
CB 0.445 CD 0.333 CF 0.222
解(1)转动刚度和分配系数
EI0=1
结构力学教案第9章用渐进法计算超静定梁和刚架

结构力学教案第9章用渐进法计算超静定梁和刚架第九章用渐进法计算超静定梁和刚架9.1 力矩分配法的基本概念一、力矩分配法中使用的几个名词 1、转动刚度(S ij )使等截面直杆某杆端旋转单位角度?=1时,在该端所需施加的力矩。
2.传递系数(C ij )远端弯矩与近端弯矩之比称为传递系数,用C ij 表示。
3、分配系数(μi j )杆ij 的转动刚度与汇交于i 结点的所有杆件转动刚度之和的比值。
(a )MBM ACADM(a )A BS AB=3EI/lBS AB =EI/l(c )(d )(b )S=0二、用力矩分配法计算具有一个结点铰位移的结构 1、解题思路2、解题步骤(1)在刚结点上加上刚臂(想象),使原结构成为单跨超静定梁的组合体,计算分配系数。
(2)计算各杆的固端弯矩,进而求出结点的不平衡弯矩。
(3)将不平衡弯矩(固端弯矩之和)反号后,按分配系数、传递系数进行分配、传递。
(4)将各杆的固端弯矩、分配弯矩、传递弯矩相加,即得各杆的最后弯矩。
3、例题: 例9?1 试作图示连续梁的弯矩图。
各杆EI 为常数。
M BM f BC M f BACB A (b)A(a)例9?2 试作图示刚架的弯矩图。
9.2用力矩分配法计算连续梁和无侧移刚架一、基本概念1、力矩分配法是一种渐近法。
2、每次只放松一个结点。
3、一般从不平衡弯矩绝对值较大的结点算起。
二、计算步骤1、确定各结点处杆端力矩的分配系数、传递系数。
2、计算个杆端的固端弯矩。
3、逐次循环放松各结点,以使结点弯矩平衡,直至结点上的传递弯矩小到可以略去不计为止。
4、将各杆端的固端弯矩与历次分配弯矩、传递弯矩相加,即得各杆端的最后弯矩。
B 120kN 89.8三、例题: 试用弯矩分配法计算图示连续梁,绘弯矩图。
M 图(kN.m)A300kN30kN/m160kNM图(kN.m)例9?4用力矩分配法计算图9?8(a)所示的刚架,并绘M图。
9.3 无剪力分配法一、无剪力分配法的应用条件刚架中除两端无相对线位移的杆件外,其余杆件都是剪力静定杆件。
理学结构力学渐进法

§9-2 力矩分配法的基本原理
力矩分配法:适用于连续梁和无结点线位移的刚架计算。
一、转动刚度S: SAB=4i
1
4i
1
转动刚度 (劲度系数) 杆件AB(如图)的A端转动单 位角时,A端(近端)的弯矩 MAB称为该杆端的劲度系数,用 SAB表示。
转动刚度 (劲度系数)标志该杆端 抵抗转动能力的大小。与杆件 的线刚度有关,与杆件另一端 (远端)的支承情况有关。
取一半结构计算,如图d。
由于假设H点无水平位移,此时竖杆均为无侧移杆,所有横梁都是剪 力静定杆→可用无剪力分配法求解。
§9-4 无剪力分配法
计算过程如图a。
§9-4 无剪力分配法
弯矩图如图b。
求F点的竖向位移时,静定的基本体系如图c。
ΔFy
1 EI
Fl [ 1523l 10000 2
1 3
2l 3
§9-4 无剪力分配法 • 用于计算有侧移刚架。 • 要求刚架仅由剪力静定杆和无侧移杆组成。
无侧移杆
无侧移杆
剪力静定杆
剪力静定杆
无侧移杆
剪力静定杆
§9-4 无剪力分配法
剪力静定杆的转动刚度、传递系数和固端弯矩
剪力静定 杆
M
F AB
ql 2 3
;SLeabharlann A iMF BAql 2 6
CBA 1
剪力静定杆可看成一端固定,一端滑动的单跨超静定梁
配并传递,如图。
§9-3 用力矩分配法计算连续梁和无侧移刚架
例9-2 试用力矩分配法计算图a 所示连续梁,并绘制弯矩图。
解:EF的内力是 静定可去掉。
1、计算分配系数 设i=2EI/8m。
DC BC
4i 0.625 4i 3 0.8i
结构力学-渐近法

M1 图
4
M 1Fj — —将不平衡力矩变号后, 按劲度系数大小的比例,
分配给各近端;
M 12 — —节点转动 Z 1 角产生的弯矩 分配弯矩 F M 12 — —固端弯矩
F M 14 M 14 M 14
F 同理: M 13 M 13 M 13
远端弯矩(传递弯矩):
i1 l1
4P
1500
2500
C
B
5 P 3 E
2500
A
D
CB
BA 0.625, BC 0.375。 0.5, CD 0.5, DC 0.706, DE 0.294。
A
0.625 0.375 B
1500 -938 -562
0.5 0.5 C
-281 883 -301 -301 29 54 -42 -42
30kN/m B i=1
10m 0.5
160kN C
3m 0.5 +112.5
D i=1
5m
+250.0 -187.5
+32.0 -47.3 -47.3 +4.8 -2.4 -2.4 +0.3 -0.2 -0.2 +237.4 -237.4
B点一次分、传 0.0 C点一次分、传 B点二次分、传 0.0 C点二次分、传 B点三次分、传 0.0 C点第三次分配 最后弯矩 0.0
F
1
1
3 3
2 2
3i12 Z1=1 3i12 Z1=1 2i13 2i13 3
1
1 4i13
3
4i13
M1 图
4 4
i4i14 14
4i14
结构力学计算题经典(有答案)
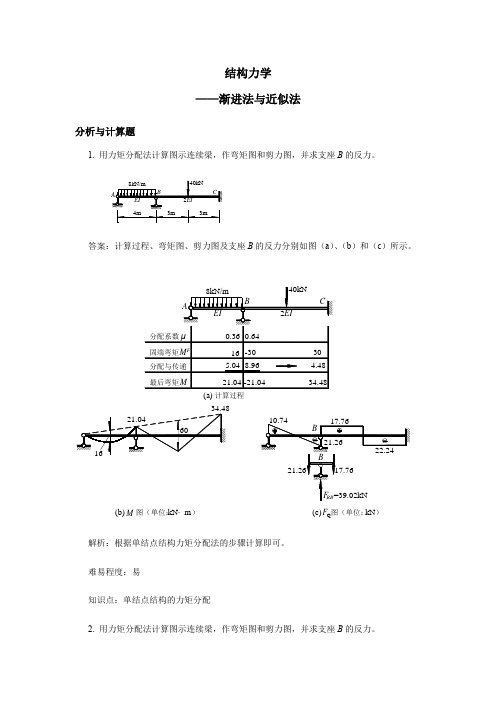
结构力学 ——渐进法与近似法分析与计算题1. 用力矩分配法计算图示连续梁,作弯矩图和剪力图,并求支座B 的反力。
答案:计算过程、弯矩图、剪力图及支座B 的反力分别如图(a )、(b )和(c )所示。
解析:根据单结点结构力矩分配法的步骤计算即可。
难易程度:易知识点:单结点结构的力矩分配2. 用力矩分配法计算图示连续梁,作弯矩图和剪力图,并求支座B 的反力。
A60kN 40kN·m EIEI B C4m4m6m(b)M 图(单位: )kN·m 图(单位: )(c)kNQ F (a)计算过程答案:图(a )为求解结点B 约束力矩的受力分析图。
计算过程、弯矩图、剪力图及支座B 的反力分别如图(b )、(c )和(d )所示。
解析:根据单结点结构力矩分配法的步骤计算即可。
难易程度:中知识点:单结点结构的力矩分配3. 用力矩分配法计算图示连续梁,作弯矩图和剪力图,并求支座B 的反力。
答案:CD 段为静定悬臂梁,将其截开并暴露出截面C 的弯矩,用力矩分配法计算如图(a )所示结构。
弯矩图和剪力图如图(b )、(c )所示。
BCEIN/m2EI m3m3m40kN(b)计算过程F BM (a)图(单位: )(c)M kN·m图(单位: )Q F (d)kN10kN20kN12kN/m ABCDEI 2EI 2m 4m4m解析:根据单结点结构力矩分配法的步骤计算即可。
本题中悬臂段CD 若不切除,则可按B 、C 两个刚结点的结构进行计算。
难易程度:中知识点:单结点结构的力矩分配4. 用力矩分配法计算图示连续梁,作弯矩图和剪力图,并求支座B 的反力。
答案:AB 段为静定悬臂梁,将其截开并暴露出截面B 的弯矩,用力矩分配法计算过程如图(a )所示。
弯矩图和剪力图图(b )、(c )所示。
kNQ F (c)图(单位: )m M 图(单位: )(b)RB F =63.02kN ( )计算过程(a)mkN·10kN/m 60kN EI 2IB CD2m6m2m解析:根据单结点结构力矩分配法的步骤计算即可。
结构力学 渐进法

EI=1 6m
D
iBC iCD
M F -60
1 2 S 4 BA 6 3 S 4 1 1 BC 4
1 6 2 1 8 4 1 6
B
分 14.7 配 与 传 1.5 递
0.2
Mij -43.6 43.6 A 21.9
0.3
92.6 -92.6 92.6 B
B
F
CB 0.445 CF 0.222 0.333 CD
单独使用时对连续梁和无结点线位移刚架的 计算特别方便。
一、基本概念
(1)转动刚度(S): 使杆端发生单位转角时需要施加的杆端弯矩。 SAB=4i
A B
SAB=3i
1
A B
1
SAB=i
A B
SAB=0
A
B
1
SAB=4i SAB与杆的i(材料的性质、横截面 的形状和尺寸、杆长)及远端支承 有关, 而与近端支承无关。
F 21 2
A
q 12kN / m
M1
1
M2
2
B
28.6
50
6.1
100
-28.6 -57.1 -42.9
21.4
-9.2 -12.2
1.8 1.8
-6.1
6.1 3.5 2.6
放松结点1(结点2固定):
S12 4i S1 A 3i 12 0.571 1 A 0.429
… … ...
41.3
-41.3
0
2 3 0.4 BA 2 1 3 0.6 BC 1 S 4 1 CB 4 S 3 1 1 CD 6 2
结构力学 第九章07 渐近法

显然, 结点各杆的分配系数总和恒等于1 显然, A结点各杆的分配系数总和恒等于1。
分配力矩:将A结点的不平衡力矩改变符号, 结点的不平衡力矩改变符号, 分配力矩: 乘以交汇于该点各杆的分配系数, 乘以交汇于该点各杆的分配系数,所得到的杆端 弯矩称为该点各杆的分配力矩(分配弯矩)。 弯矩称为该点各杆的分配力矩(分配弯矩)。 传递系数:三类位移法基本杆件AB,当仅 传递系数:三类位移法基本杆件AB, 其一端产生转角位移时, 其一端产生转角位移时,远端的杆端弯矩和近 端的杆端弯矩的比值,称为该杆的传递系数, 端的杆端弯矩的比值,称为该杆的传递系数, 记作C 例如对位移法三类等直杆 记作CAB 。 C AB = 1 / 2 C AB = 0 C AB = −1 i A B A i B A i B 显然,传递系数也仅与远端约束有关。 显然,传递系数也仅与远端约束有关。
C ij =
4iφA EI A φA 3iφA EI A φA l iφA EI A φA l B l 0 B -iφA B 2iφA
M ji M ij
CAB=2iϕA/ 4iϕA=1/2 CAB=0/ 3iϕA=0
CAB=-iϕA/ iϕA=-1
二、举例说明力矩分配法的基本原理
解题思路: 1、解题思路: P
1、确定各结点处杆端力矩的分配系数、传递系数。 确定各结点处杆端力矩的分配系数、传递系数。 计算个杆端的固端弯矩。 2、计算个杆端的固端弯矩。 3、逐次循环放松各结点,以使结点弯矩平衡,直至结点 逐次循环放松各结点,以使结点弯矩平衡, 上的传递弯矩小到可以略去不计为止。实际应用时, 上的传递弯矩小到可以略去不计为止。实际应用时, 一般只进行二、三轮的分配和传递。 一般只进行二、三轮的分配和传递。 将各杆端的固端弯矩与历次分配弯矩、传递弯矩相加, 4、将各杆端的固端弯矩与历次分配弯矩、传递弯矩相加, 即得各杆端的最后弯矩。 即得各杆端的最后弯矩。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)放松结点。在结点上加上一个反号的不平衡力矩, 计算各近端的分配弯矩及各远端的传递 弯矩。
(3)各杆端弯矩。近端=固端弯矩+分配弯矩; 远端=固端弯矩+传递弯矩
§9-2 力矩分配法的基本原理
例9-1 试作图a所示刚架的弯矩图。
解:(1)计算各杆端分配系数。
§9-2 力矩分配法的基本原理
传递系数:远端(B端)弯矩与近端(A端)弯矩的比值,用
CAB表示。
CAB
M BA M AB
等截面直杆的劲度系数和传递系数
远端支承情况 固定 铰支 滑动
自由或轴向支杆
劲度系数S 4i 3i i 0
传递系数C 0.5 0 -1
§9-2 力矩分配法的基本原理
图a所示刚架用位移法计算时,只有一个结点转角Z1, 其典型方程为
3、计算杆端最后弯矩,作弯矩图如图c。
§9-3 用力矩分配法计算连续梁和无侧移刚架
例9-3 试用力矩分配法计算图a所示刚架。
解:这是一个对称结构,承受正对称荷载,取一半结构如图b。 设:EI/8m=1, 各杆线刚度如图上 圆圈中所注。
§9-3 用力矩分配法计算连续梁和无侧移刚架
计算过程如图c。
校核各结点处的杆端弯矩是否满足平衡条件: M Bj 54.4 4.7 59.1 0 MCj 27.5 12.2 15.3 0
§9-2 力矩分配法的基本原理
由叠加法 M M P M1Z1 各杆近端弯矩为
M12
M
F 12
S12 ( S1 j
M 1Fj
)
M
F 12
12 (
M
F 1j
)
M13
M
F 13
S13 ( S1 j
M
F 1j
)
M
F 13
13 (
M
F 1j
)
(a)
M12
M
F 14
S14 ( S1 j
3 7
如图所示连续梁 各杆件线刚度为i
固端弯矩为
M
F 01
300kN
m,M
F 10
300kN
mMF 12来自600kNm,M
F 21
600kN
m
M
F 23
450kN
m,M
F 32
0
§9-3 用力矩分配法计算连续梁和无侧移刚架
计算过程如下图
1、放松结点1,其 不平衡力矩为 -300kN·m,反号分 配并传递,如图。
(
M
31
M
F 31
C13[ 13 (
M
F 1j
)
M
F 21
C12[12
(
M
F 1j
)]
M
F 1j
)]
(b)
M
41
M
F 41
C14[14 (
M1Fj )]
(b)式的第一项为固端弯矩; 第二项是将各近端的分配弯矩以传递系数的比例 传到各远端→传递弯矩。
§9-2 力矩分配法的基本原理
力矩分配法的步骤
2、放松结点2,其 不平衡力矩为 150+75=225kN·m, 反号分配并传递, 如图。
如此反复将各结点的不平衡力矩进行分 配和传递,直到传递弯矩的数值小到可以略 去,停止计算。
3、结点1有了新的 不平衡力矩 -64kN·m,反号分 配并传递,如图。
§9-3 用力矩分配法计算连续梁和无侧移刚架
例9-2 试用力矩分配法计算图a 所示连续梁,并绘制弯矩图。
M 1Fj
)
M
F 14
14 (
M
F 1j
)
(a)式的第一项为固端弯矩,荷载产生的; 第二项相当于把不平衡力矩反号后按劲度系数大 小的比例分配给各近端→分配弯矩。
1 j
S1 j S1 j
分配系数
同一结点
1 j 1
§9-2 力矩分配法的基本原理
各杆远端弯矩为
M
21
M
F 21
C12S12 S1 j
4m
75kN m
M
F DA
50kN 8
4m
25kN
m
§9-2 力矩分配法的基本原理
(3)进行力矩的分配和传递。结点A的不平衡力矩为 计算过程如图b。
M
F Aj
(40
75)kN m
35kN m
§9-2 力矩分配法的基本原理
(4)计算杆端最后弯矩。并作弯矩图如图c。
近端弯矩=固端弯矩+分配弯矩 远端弯矩=固端弯矩+传递弯矩
第 九章 渐进法
§9-1 概述 §9-2 力矩分配法的基本原理 §9-3 用力矩分配法计算连续梁和无侧移刚架 §9-4 无剪力分配法 §9-5 剪力分配法
§9-1 概 述
位移法
计算超静定结构→
→组成和解算典型方程
力法
力矩分配法 无剪力分配法 →位移法的变体 →避免组成和解算典型方程
迭代法
易于掌握,适合手算,可不计算结点位移而直接求得杆端弯矩。
§9-3 用力矩分配法计算连续梁和无侧移刚架
一半刚架的弯矩图如图d。
原刚架的弯矩图可利用对称性作出。(略)
r11Z1 R1P 0
MP、M1 图如图b、c
R1P M1F2 M1F3 M1F4 M1Fj
→刚臂反力矩或结点上的不平衡力矩
r11 4i12 3i13 i14 S12 S13 S14 S1 j
→汇交于结点1的各杆端劲度系数总和
解典型方程得
Z1
R1P r11
M1Fj S1 j
§9-3 用力矩分配法计算连续梁和无侧移刚架
对于具有多个结点转角但无侧移的结构,需先固定所有 结点,然后各结点轮流放松。把各结点的不平衡力矩轮流地 进行分配、传递,直到小到可以停止。
分配系数为
10
4i 4i 4i
1 2
,12
4i 4i 4i
1 2
21
4i 4i 3i
4 7
,23
3i 4i 3i
§9-2 力矩分配法的基本原理
力矩分配法:适用于连续梁和无结点线位移的刚架计算。
劲度系数 杆件AB(如图)的A断转动单 位角时,A端(近端)的弯矩 MAB称为该杆端的劲度系数,用 SAB表示。
劲度系数标志该杆端抵抗 转动能力的大小,又称为转动 刚度。与杆件的线刚度有关, 与杆件另一端(远端)的支承 情况有关。
(2)计算固端弯矩,查表计算。
令iAB=iAC =EI/4=1,则iAD=2。
AB
41 41 31
2
4 9
0.445
AC
3 9
0.333
AD
2 9
0.222
M
F BA
30kN / m (4m)2 12
40kN m
M
F AB
30kN / m (4m)2 12
40kN m
M
F AD
3 50kN 8
解:EF的内力是 静定可去掉。
1、计算分配系数 设i=2EI/8m。
DC BC
4i 0.625 4i 3 0.8i
DE BA 0.375
2、计算固端弯矩
各固端弯矩及计算过程如图b
M
F DE
2kN m
M
F DC
5.62kN m
M
F CD
9.38kN m
§9-3 用力矩分配法计算连续梁和无侧移刚架
