高考文科立体几何证明专题

合集下载

立体几何(点到面的距离)

立体几何（文科综合）1．如图, 在四棱锥P ABCD 中,四边形ABCD 是直角梯形, DC 2AD 2AB 2，DAB ADC 90 , PB 2，PDC 为等边三角形.1）证明：PD BC ；2）求点B到平面PCD的距离.答案】（1）略；（2）632．如图，圆锥PO中，AB是圆O的直径，C是底面圆O上一点，且CAB ，点D为半径OB的中6（Ⅰ）求证：CD 平面APB ；（Ⅱ）当APB是边长为4的正三角形时，求点A到平面PBC的距离. 【答案】（Ⅰ）见证明；（Ⅱ）h 4 1553．如图，已知在直四棱柱ABCD A1 B1C1D1 中，AD DC ，AB/ /DC ，DC DD1 2AD 2AB 2 ．（1）求证：DB 平面B1BCC1 ；（2）求点A1到平面C1BD 的距离．【答案】（1）证明见解析；（2）3. 4．如图，四棱锥的底面是直角梯形，点，。

1）证明：平面2）求点到平面的距离。

答案】（ 1 ）见解析；（ 2 ）1）证明：平面平面2）求点到平面的距离.答案】（1）见解析（2）6．如图所示，在三棱锥D－ABC中，AC，BC，CD两两垂直，AC＝CD＝1，＝，O为AB 的中点．平面的中5．如图，在三棱柱，是边的中点.中（底面为正三角形），平面说明点 M ， N 的位置（不要求证明）；（2）求点 C 到平面 ABD 的距离．【答案】（ 1）见解析；（ 2）（1）求证： CF ∥平面；（2）求三棱锥 C －的高．【答案】（ 1）见解析；（ 2）求证：平面平面，求点到平面的距离与平面 ACD 平行，且与棱 DB ，CB 分别相交于 M ， N ，在图中画出该截面多边形，并在的条件下，若，求与平面所成角的正切值的侧棱 AA1⊥底面 ABC ，∠ACB ＝90°， E 是棱的中点， F 是 AB 的中点，8．已知四棱锥的底面是菱形，底面是上的任意一点7．如图，三棱柱 ABC －答案】（ 1）见解析（ 2）（3）9．如图，已知平面，为矩形，、分别为、的中点，1）求证：平面；2）求证：面平面3）求点到平面的距离 .答案】（ 1）证明见解析；（2）证明见解析；（3） .1）证明：平面答案】（ 1）证明见解析；（2）11．在长方体 ABCD A 1BC 1 1D 1 中，底面 ABCD 是边长为 2的正方形， AA 1=2 3，E 是 AB 的中点， F10．如图，在四棱锥点 Q 在棱 AB中，平面的体积为，求点 B 到平面 PDQ 的距离 .是 BB 1 的中点1）求证：EF / / 平面A1DC1；2）求点A到平面A1DC1 的距离.答案】（1）见解析（2） 2 217ADFC是边长为2的正方形，点M 是棱EF 的中点.2）若三棱锥B DEF 的体积为4，求点B到平面ADFC 的距离.答案】（1）见解析（2）613．已知四棱锥P ABCD的底面为菱形，且ABC 60 ，AB PC 2,AP BP 2 .1）求证：平面PAB 平面ABCD ；2）求点D 到平面APC的距离.答案】（1）证明见解析；（2） 2 21714．如图，在等腰梯形ABCD中，AB/ /CD ，AD DC CB CF ，ABC 60 ，四边形ACFE为平行四边形，FC 平面ABCD ，点M 为线段EF 中点.1）求证： BC ⊥平面 ACFE ；2）若 AD 2，求点 A 到平面 MBC 的距离答案】（ 1）详见解析；（ 2） 4 21 .715．如图所示，在梯形 ABCD 中， AD ∥ BC ，AB ⊥BC ，AB BC 1， PA ⊥平面 ABCD ， CD ⊥2）若 PA AD ，求点 B 到平面 PAC 的距离．答案】（ 1）见解析（ 2） 16．如图，在直三棱柱 ABC-A 1B 1C 1 中， ABC 为正三角形， AB=AA=1 2 ， M 是 A 1C 的中点， N 是 A 1B 1 的中点1）证明：MN ∥ 平面 BCC 1B 1 ； 2）求点 M 到平面 ACB 1的距离 .PAC ；【答案】（ 1）见证明；（2） 21717．如图，在底面是正方形的四棱锥P ABCD 中， PA 平面 ABCD ， BD 交 AC 于点 E , F 是 PA 的中点， G 为 AC 上一动点．1）求证： BD FG ；2）若 G 是AE 的中点， PA AB 4，求点 P 到平面 FGD 的距离. 答案】（1）证明见解析；（2） 2 14.718．如图，四面体 ABCD 中， O 、 E 分别是 BD 、BC 的中点，1）求证： AO 平面 BCD ；2）求异面直线 AB 与 CD 所成角的余弦值； 3）求点 E 到平面 ACD 的距离。

2020高三数学立体几何专项训练文科

2020高三数学立体几何专项训练文科1.在四棱锥P-ABCD中，底面ABCD为矩形，PA垂直于平面ABCD，E是PD的点。

Ⅰ) 证明PB平行于平面AEC。

Ⅱ) 设AP=1，AD=3，求三棱锥P-ABD的体积V和A点到平面PBD的距离。

2.在四棱锥P-ABCD中，AB平行于CD且AB等于2CD，E为PB的中点。

1) 证明CE平行于平面PAD。

2) 是否存在一点F在线段AB上，使得平面PAD平行于平面CEF？若存在，证明结论；若不存在，说明理由。

3.在四棱锥P-ABCD中，平面PAC垂直于平面ABCD，且PA垂直于AC且等于AD等于2，四边形ABCD满足BC平行于AD，AB垂直于AD且等于1，点E和F分别为侧棱PB和PC上的点，且PEPF等于λ(λ不等于0)。

1) 证明EF平行于平面PAD。

2) 当λ等于2时，求点D到平面AFB的距离。

4.四棱柱ABCD-A1B1C1D1的底面ABCD是正方形。

1) 证明平面A1BD平行于平面CD1B1.2) 若平面ABCD与平面B1D1C相交于直线l，证明B1D1平行于l。

5.在平行四边形ABCD外一点P，PC的中点为M，在DM上取一点G，过G与AP作平面交平面BDM于H。

证明AP平行于GH。

6.在四棱锥P-ABCD中，PA垂直于底面ABCD，AB垂直于AD，AC垂直于CD，且∠ABC等于60度，PA等于AB等于BC，E是PC的中点。

证明：1) CD垂直于AE；2) PD垂直于平面ABE。

7.在四棱锥P-ABCD中，平面PAB垂直于平面ABCD，四边形ABCD为正方形，△PAB为等边三角形，E是PB的中点，平面AED与棱PC交于点F。

1) 证明AD平行于EF；2) 证明PB垂直于平面AEFD；3) 设四棱锥P-AEFD的体积为V1，四棱锥P-ABCD的体积为V2，求V1和V2的值。

8.在四棱锥P-ABCD中，底面ABCD是边长为a，∠DAB 等于60度的菱形，侧面PAD为正三角形，其所在平面垂直于底面ABCD，G为AD的中点。

高考数学立体几何专题：证明

PA AD ， EF AD PA // EF 。
根据直线与平面平行的判定定理得到：
PA // EF ， EF 平面 BEF 直线 PA // 平面 BEF 。
跟踪训练一：已知：在四棱柱 ABCD A1B1C1D1 中： E 为 C1D1 上一点， C1EB1 A1D1C1 。求证：直线 B1E // 平面 A1 ADD1 。
跟踪训练一：已知：在三棱柱 ABC A1B1C1 中： O 为 AB 边上一点。证明：直线 B1C1 // 平面 OBC 。
跟踪训练二：已知：在四棱柱 ABCD A1B1C1D1 中： E 为 BB1 的中点。证明：直线 AD // 平面 A1 D1E 。
题型二：棱柱的所有侧棱都平行。
例题：已知：在三棱柱 ABC A1B1C1 中， O 为 A1C1 的中点。证明：直线 AA1 // 平面 OBB1 。
例题一：已知：在四棱锥 P ABCD 中， E 为 AB 上一点， DEA EDC 。证明：直线 CD // 平面 PAB 。
证明：如下图所示：
根据内错角相等，两条直线平行得到：
DEA EDC AB // CD 。
根据直线与平面平行的判定定理得到：
AB // CD ， AB 平面 PAB 直线 CD // 平面 PAB 。
（4）直棱柱：所有侧面都为矩形；斜棱柱：所有侧面都是平行四边形。
举例：在直三棱柱 ABC A1B1C1 中：侧面 A1 ABB1 为矩形；侧面 A1 ACC1 为矩形；侧面 B1BCC1 为矩形。
举例：在斜三棱柱 ABC A1B1C1 中：侧面 A1 ABB1 为平行四边形；侧面 A1 ACC1 为平行四边形；侧面 B1BCC1 为平行四边形。
（2）两条有中点的线段没有公共端点，则两个中点的连线不是中位线。得到中位线平行于底边，是否可以证明直线与平面平行？

立体几何文科常考证明题汇总

立体几何证明题1. 正方体1111ABCD-A B C D ，1AA =2，E 为棱1CC 的中点． (Ⅰ) 求证：11B D AE ⊥； (Ⅱ) 求证：//AC 平面1B DE ；（Ⅲ）求三棱锥A-BDE 的体积．2.已知正方体1111ABCD A BC D -，O 是底ABCD 对角线的交点.求证：(１) C 1O ∥面11AB D ；(2)1AC ⊥面11AB D ．3．如图，PA ⊥矩形ABCD 所在平面，M 、N 分别是AB 和PC 的中点. （Ⅰ）求证：MN ∥平面PAD ；（Ⅱ）求证：MN CD ⊥；（Ⅲ）若45PDA ∠=，求证：MN ⊥平面PCD .NM PDBA A11A EC D 1ODBAC 1B 1A 1C4. 如图（1），ABCD 为非直角梯形，点E ，F 分别为上下底AB ，CD 上的动点，且EF CD ⊥。

现将梯形AEFD 沿EF 折起，得到图（2）（1）若折起后形成的空间图形满足DF BC ⊥，求证：AD CF ⊥；（2）若折起后形成的空间图形满足,,,A B C D 四点共面，求证：//AB 平面DEC ；5．如图，在五面体ABCDEF 中，FA ⊥平面ABCD, AD//BC//FE ，AB ⊥AD ，M 为EC 的中点， N 为AE 的中点，AF=AB=BC=FE=12AD (I) 证明平面AMD ⊥平面CDE ； (II) 证明//BN 平面CDE ；6．在四棱锥P －ABCD 中,侧面PCD 是正三角形,且与底面ABCD 垂直,已知菱形ABCD 中∠ADC ＝60°, M 是P A 的中点，O 是DC 中点. （1）求证：OM // 平面PCB ；（2）求证:P A ⊥CD ；（3）求证:平面P AB ⊥平面COM .A B C D E F 图（1） EBCF DA 图（2）A FEBC DMN PDABCOM7．如图，在四棱锥P—ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点，作EF⊥PB交PB于点F.（1）证明P A//平面EDB；（2）证明PB⊥平面EFD8.正四棱柱ABCD-A1B1C1D1的底面边长是3，侧棱长是3，点E，F分别在BB1，DD1上，且AE⊥A1B，AF⊥A1D．(1)求证：A1C⊥面AEF；(2)求二面角A-EF-B的大小；(3)点B1到面AEF的距离.1．已知直线l、m、平面α、β，且l⊥α，m⊂β，给出下列四个命题：（1）α∥β，则l⊥m （2）若l⊥m，则α∥β（3）若α⊥β，则l∥m （4）若l∥m，则α⊥β其中正确的是__________________.2. m、n是空间两条不同直线，αβ、是空间两条不同平面，下面有四个命题：①,;m n m nαβαβ⊥⇒⊥,　②,,;m n m nαβαβ⊥⊥⇒③,,;m n m nαβαβ⊥⇒⊥④,,;m m n nααββ⊥⇒⊥其中真命题的编号是________（写出所有真命题的编号）。

高考文科立体几何题汇总（含答案）

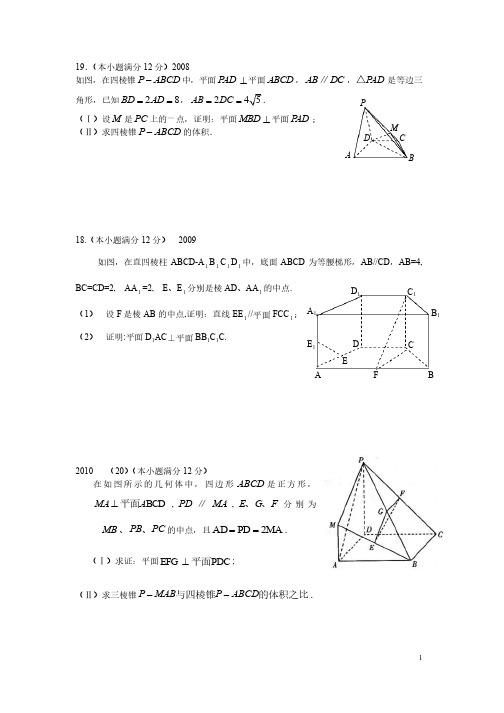
19．（本小题满分12分）2008 如图，在四棱锥P ABCD -中，平面PAD ^平面ABCD ，AB DC ∥，P AD △是等边三角形，已知28BD AD ==，245AB DC ==．（Ⅰ）设M 是PC 上的一点，证明：平面MBD ^平面PAD ；（Ⅱ）求四棱锥P ABCD -的体积．的体积．18.（本小题满分12分）分） 2009 如图，在直四棱柱ABCD-A 1B 1C 1D 1中，底面ABCD 为等腰梯形，AB//CD ，AB=4, BC=CD=2, AA 1=2, E 、E 1分别是棱AD 、AA 1的中点. （1）设F 是棱AB 的中点,证明：直线EE 1//平面FCC 1；（2）证明:平面D 1AC ⊥平面BB 1C 1C. 2010 （20）（本小题满分12分）分）在如图所示的几何体中，四边形ABCD 是正方形，BCD A MA 平面^,PD ∥MA ,E G F 、、分别为MB 、PC PB 、的中点，且2MA PD AD ==．（Ⅰ）求证：平面PDC EFG 平面^; （Ⅱ）求三棱锥的体积之比与四棱锥ABCD P MAB P --．A B C M P D EA B C F E 1 A 1 B 1 C 1 D 1 D 2011 19．（本小题满分12分）分）如图，在四棱台1111ABCD A B C D -中，1D D ^平面ABCD ，底面ABCD 是平行四边形，AB=2AD ，11AD=A B ，BAD=Ð60° （Ⅰ）证明：1AA BD ^；（Ⅱ）证明：11CC A BD ∥平面．2012 (19) ( (本小题满分本小题满分12分)如图，几何体E ABCD -是四棱锥，△ABD 为正三角形，,CB CD EC BD =^. (Ⅰ)求证：BE DE =；(Ⅱ)若∠120BCD =°，M 为线段AE 的中点，的中点，求证：DM ∥平面BEC .53238545545523163 ACM PDOEA B C F 1 1 C 1 D 1 D F 1 EC 1 1 C 1 D 1 D 所以CC 1⊥AC,因为底面ABCD 为等腰梯形，AB=4, BC=2, F 是棱AB 的中点,所以CF=CB=BF ，△BCF 为正三角形，为正三角形， 60BCF Ð=°,△ACF 为等腰三角形，且30ACF Ð=°所以AC ⊥BC, 又因为BC 与CC 1都在平面BB 1C 1C 内且交于点C, 所以AC ⊥平面BB 1C 1C,而AC Ì平面D 1AC, 所以平面D 1AC ⊥平面BB 1C 1C. 2010 （20）本小题主要考查空间中的线面关系，考查线面垂直、）本小题主要考查空间中的线面关系，考查线面垂直、面面垂直的判定及几面面垂直的判定及几何体体积的计算，考查试图能力和逻辑思维能力。

完整)高中立体几何证明平行的专题

完整)高中立体几何证明平行的专题在此文章中，存在一些格式错误和明显有问题的段落，需要进行修改和删除。

修改后的文章如下：立体几何——平行的证明例1】如图，四棱锥P-ABCD的底面是平行四边形，点E、F分别为棱AB、PD的中点。

求证：AF∥平面PCE。

分析：取PC的中点G，连EG，FG，则易证AEGF是平行四边形。

例2】如图，已知直角梯形ABCD中，AB∥CD，AB⊥BC，AB=1，BC=2，CD=1+3，过A作AE⊥CD，垂足为E，G、F分别为AD、CE的中点，现将△ADE沿AE折叠，使得DE⊥EC。

Ⅰ）求证：BC⊥面CDE；（Ⅱ）求证：FG∥面BCD。

分析：取DB的中点H，连GH、HC，则易证FGHC是平行四边形。

例3】已知直三棱柱ABC-A1B1C1中，D、E、F分别为A1A、C1C、AB的中点，M为BE的中点，AC⊥BE。

求证：（Ⅰ）C1D⊥BC；（Ⅱ）C1D∥平面B1FM。

分析：连EA，易证C1EAD是平行四边形，于是MF//EA。

例4】如图所示，四棱锥P-ABCD底面是直角梯形，BA⊥AD，CD⊥AD，CD=2AB，E为PC的中点。

证明：EB//平面PAD。

分析：取PD的中点F，连EF、AF，则易证ABEF是平行四边形。

例5】如图，已知E、F、G、M分别是四面体的棱AD、CD、BD、BC的中点，求证：AM∥平面EFG。

分析：连MD交GF于H，易证EH是△AMD的中位线。

例6】如图，ABCD是正方形，O是正方形的中心，E是PC的中点。

求证：PA∥平面BDE。

AEBGMFCD例7】如图，三棱柱ABC-A1B1C1中，D为AC的中点。

求证：AB1//面BDC1.分析：连B1C交BC1于点E，易证ED是△B1AC的中位线。

例8】如图，平面ABEF⊥平面ABCD，四边形ABEF与ABCD都是直角梯形，∠BAD=∠FAB=90，BC//AD，BE//AF，G、H分别为FA、FD的中点。

Ⅰ）证明：四边形BCHG是平行四边形；Ⅱ）C、D、F、E四点是否共面？为什么？例9】正方体ABCD-A1B1C1D1.例10：在四棱锥P-ABCD中，AB∥CD，AB=DC，E为PD中点。

高中立体几何证明题

高中立体几何证明题一、线面平行的证明题1已知正方体ABCD - A_{1}B_{1}C_{1}D_{1}，E，F分别是AB，BC的中点，求证：EF∥平面A_{1}C_{1}D。

解析1. 连接AC。

- 在 ABC中，因为E，F分别是AB，BC的中点，所以EF∥ AC。

2. 正方体ABCD - A_{1}B_{1}C_{1}D_{1}中：- AC∥ A_{1}C_{1}。

- 由EF∥ AC和AC∥ A_{1}C_{1}可得EF∥ A_{1}C_{1}。

- 又A_{1}C_{1}⊂平面A_{1}C_{1}D，EFnot⊂平面A_{1}C_{1}D。

- 根据线面平行的判定定理，所以EF∥平面A_{1}C_{1}D。

题2在三棱柱ABC - A_{1}B_{1}C_{1}中，D是AB的中点，求证：AC_{1}∥平面CDB_{1}。

解析1. 连接BC_{1}，交B_{1}C于点E。

- 在三棱柱ABC - A_{1}B_{1}C_{1}中，E为BC_{1}的中点。

2. 因为D是AB的中点：- 所以在 ABC_{1}中，DE∥ AC_{1}。

- 又DE⊂平面CDB_{1}，AC_{1}not⊂平面CDB_{1}。

- 根据线面平行的判定定理，可得AC_{1}∥平面CDB_{1}。

二、线面垂直的证明题3在四棱锥P - ABCD中，底面ABCD是正方形，PA = PB = PC = PD，求证：PA⊥平面ABCD。

解析1. 连接AC，BD交于点O，连接PO。

- 因为底面ABCD是正方形，所以O为AC，BD中点。

- 又PA = PC，PB = PD，根据等腰三角形三线合一的性质：- 可得PO⊥ AC，PO⊥ BD。

- 而AC∩ BD = O，AC⊂平面ABCD，BD⊂平面ABCD。

- 根据直线与平面垂直的判定定理，所以PO⊥平面ABCD。

- 又PA = PB = PC = PD，AO = BO = CO = DO，所以 PAO≅ PBO≅ PCO ≅ PDO。

2024届高考二轮复习文科数学课件：立体几何中的证明与计算

∵BC⊥EB,PE,BE⊂平面PEB,PE∩BE=E,∴BC⊥平面PEB.∵EM⊂平面PEB,
∴EM⊥BC,由PE=EB,PM=MB知EM⊥PB.又BC,PB⊂平面PBC,BC∩PB=B,
∴EM⊥平面PBC,又EM⊂平面EMN,∴平面EMN⊥平面PBC.
1
·
2
(2)解 ∵点 N 为 BC 的中点,∴△EBN 与正方形 EBCD 的面积之比为
1
4
知 HM= PD= ,所以三棱锥 C-ABH 的体积就等于三棱锥 H-ABC 的体积,所
3
3
1
以所求体积是
3
×
1
1
AB·
AD·
HM=
2
3
×
1
4
×1×1×
2
3
=
2
.
9
2.(2023陕西渭南一模)如图,在直三棱柱ABC-A1B1C1中,点E为A1C1的中点,
AB=BC=2,C1F⊥AB.
(1)求证:AB⊥BC;
(1)证明连接 CO1 并延长交 AB 于点 H,连接 O2H.
∵△ABC 为底面圆 O1 的内接正三角形,∴CH⊥AB.∵AB∥DE,∴CH⊥DE.
∵四边形 DEFG 为圆柱 O1O2 的轴截面,∴O1O2⊥圆面 O1.∵DE⊂圆面 O1,
∴O1O2⊥DE.∵O1O2∩CH=O1,∴DE⊥平面 CHO2.∵DE∥FG,∴FG⊥平面
成的角.因为 EG=1,BE=2,所以 BG= 5.在 Rt△AOB 和 Rt△BEG 中,易知∠

·
4×2
EBG=∠OAB,所以 Rt△AOB∽Rt△BEG,所以 = ,即 AO=
=
=

8 5

文科数学高考立体几何考点总结学习资料

C
B
D
A
【例 7】如图所示的多面体是由底面为 ABCD 的长方体被截面 AEC1F 所截面而得到的，其
中 AB 4, BC 2,CC1 3, BE 1. （Ⅰ）求 BF 的长；（Ⅱ）求点 C 到平面 AEC1F 的距离.
F D
A
C1
C E B
【例 8】 P ABCD中，ABC BAD 90 ，BC 2AD, PAB与PAD 都是边长为 2 等边三角
【例 13】如图，直三棱柱 ABC -A1B1C1 中，D，E 分别是 AB，BB1 的中点． (1)证明：BC1∥平面 A1CD； (2)设 AA1＝AC＝CB＝2，AB＝2 2，求三棱锥 C -A1DE 的体积．
二、角度、距离问题计算
【例 1】.如图，在正方体 ABCD A1B1C1D1 中，M、N 分别是 CD ，CC1 的中点，则异面直线 A1M 与 DN 所成的角的大小是____________.
【例 2 】如图，三棱柱 ABC A1B1C1 中，侧面 AA1C1C 底面 ABC ，
AA1 A1C AC 2, AB BC ,且 AB BC ,O 为 AC 中点.
在 BC1 上是否存在一点 E ，使得 OE // 平面 A1AB ，若不存在，说明理由；若存在，确定点 E
【例 2】如图，边长为 4 的正方形 ABCD 所在平面与正三角形 PAD 所在平面互相垂直， M，Q 分别为 PC，AD 的中点． (1)求四棱锥 P-ABCD 的体积； (2)求证：PA∥平面 MBD； (3)试问：在线段 AB 上是否存在一点 N，使得平面 PCN⊥平面 PQB？若存在，试指出点 N 的位置，并证明你的结论；若不存在，请说明理由．

高考二轮复习文科数学课件高考保分大题3立体几何中的证明与计算

(1)证明:MN∥平面C1DE;
(2)求三棱锥N-C1DE的体积.
(1)证明连接ME,B1C.
∵点E,M分别为BC,BB1中点,
∴ME为△B1BC的中位线,
∴ME∥B1C且ME=
1
B1C,
2
又点N为A1D的中点,A1D∥B1C,A1D=B1C,
∴ND∥B1C,ND=
1
B C,
21
∴ME∥ND,ME=ND,∴四边形MNDE为平行四边形,
又CM=B1M,∴B1F=3CF.
∵AB1∥PF,B1F=3CF,∴AP=3PC,
∴点P是线段AC上靠近点C的四等分点.
(2)如图,取AB的中点O,连接OC,OA1.
∵四边形ABB1A1为边长为2的菱形,∠A1AB=60°,
∴△AA1B为等边三角形,
∴OA1⊥AB.
又∵平面 ABB1A1⊥平面 ABC,且两平面的交线为 AB,∴OA1⊥平面 ABC,又
∴AD⊥平面 A1C1D.
(2)解连接
2
=1 +2
π
π
2
2
2
AB1,∵∠ABB1= ,AB=1,BB1=2,A1 =AB +B1 -2AB·
BB1cos
3
3
1
-2×1×2×2=3,
2
∴B12 =AB2+A12 ,∴AB1⊥AB,且 AB1= 3.
∵AC⊥平面 AA1B1B,∴AC⊥AB1.
∴MN∥DE,又MN⊄平面C1DE,DE⊂平面C1DE,
∴MN∥平面C1DE.
(2)解由(1)得 MN∥平面 C1DE,
∴-1 = -1 = -1 .
连接 C1M,ME.在矩形 BCC1B1 中,

《几何证明》高中文科数学专题复习

B1B C1A CA1D 高考复习专题《几何证明》17分知识点1：线面平行线面平行判定定理：线面平行性质定理：基础练习：1. 三棱柱ABC —A 1B 1C 1中，若D 为BB 1上一点， M 为AB 的中点，N 为BC 的中点.求证：MN ∥平面A 1C 1D ；2、如图，在底面为平行四边形的四棱锥 P —ABCD 中，点 E 是 PD 的中点. 求证：PB//平面 AEC ；3．四棱锥P －ABCD 中，底面ABCD 是矩形，M 、N 分别是AB 、PC 的中点，求证：MN ∥平面PAD ；4．在四棱锥P —ABCD 中，底面ABCD 是矩形，M ，N 分别是AB ，PC 的中点．求证：MN ∥平面PAD ；第4题第5题ABC DE Py P AB C D M NAB C D E FP 5、如图，在三棱柱ABC —A 1B 1C 1中， D 是 AC 的中点。

求证：AB 1//平面DBC 16、如图，在正方体ABCD ——A 1B 1C 1D 1中，O 是底面ABCD 对角线的交点.求证：C 1O//平面AD 1B 1.第6题第7题7．正四棱锥S ABCD -中，E 是侧棱SC 的中点.求证：直线SA //平面BDE8. 已知四棱锥P-ABCD 中，底面ABCD 是矩形，E 、F 分别是AB 、PD 的中点．求证：AF//平面PEC第8题第9题9 在三棱柱ABC -A 1B 1C 1中，M ，N 分别是CC 1，AB 的中点．求证：CN //平面AB 1M ．10．ABCD-A 1B 1C 1D 1是正四棱柱，E 是棱BC 的中点。

求证：BD 1//平面C 1DE第10题第11题11.在三棱柱111ABC A B C -中， D 为BC 中点.求证：1//A B 平面1ADC ；ABCD C 1A 1B 1N M C 1B 1A 1CB A知识点2：面面平行面面平行的判定面面平行的性质基础练习：1.如图，已知四棱锥P-ABCD 中,地面ABCD 为平行四边形,点M,N,Q 分别为PA,BD,PD 上的中点,求证:平面MNQ ∥平面PBA第1题第2题 2.在长方体ABCDA 1B 1C 1D 1中，E 、F 、E 1、F 1分别是AB 、CD 、A 1B 1、C 1D 1的中点．求证：平面A 1EFD 1∥平面BCF 1E 1.3.在正方体ABCD-A 1B 1C 1D 1中，E 、F 、G 、P 、Q 、R 分别是所在棱AB 、BC 、BB '、A 'D '、D 'C '、DD '的中点，求证：平面PQR ∥平面EFG 。

(完整版)高考文科立体几何证明专题

图 4立体几何专题1．如图4，在边长为1的等边三角形ABC 中，,D E 分别是,AB AC 边上的点，AD AE =，F 是BC 的中点，AF 与DE 交于点G ，将ABF∆沿AF 折起，得到如图5所示的三棱锥A BCF -，其中BC =． (1) 证明：DE //平面BCF ； (2) 证明：CF ⊥平面ABF ；(3) 当23AD =时，求三棱锥F DEG -的体积F DEG V -．【解析】（1）在等边三角形ABC 中，AD AE =AD AEDB EC∴=,在折叠后的三棱锥A BCF -中也成立，//DE BC ∴ ,DE ⊄Q 平面BCF ，BC ⊂平面BCF ，//DE ∴平面BCF ；（2）在等边三角形ABC 中，F 是BC 的中点，所以AF BC ⊥①，12BFCF ==. Q 在三棱锥A BCF -中，2BC =，222BC BF CF CF BF ∴=+∴⊥② BF CF F CF ABF ⋂=∴⊥Q 平面；（3）由（1）可知//GE CF ，结合（2）可得GEDFG ⊥平面.111111132323323324F DEG E DFGV V DG FG GF --⎛⎫∴==⋅⋅⋅⋅=⋅⋅⋅⋅⋅= ⎪ ⎪⎝⎭【解析】这个题是入门级的题，除了立体几何的内容，还考查了平行线分线段成比例这个平面几何的内容.2．如图5所示，在四棱锥P-ABCD 中,AB ⊥平面PAD,AB CD,PD=AD,E 是PB 的中点，F 是DC 上的点且DF=21AB,PH 为∆PAD 中AD 边上的高．（1）证明：PH ⊥平面ABCD ；（2）若PH=1，AD=2,FC=1，求三棱锥E-BCF 的体积；（3）证明：EF ⊥平面PAB ．解：(1)ABCDPH PAD PAD AB PAD 平面所以平面，面又中的高为⊥=⋂⊥∴⊂⊥⊥∴∆AAD AB AB PH PH AD PH PH Θ(2):过B 点做BG G CD BG ，垂足为⊥；连接HB,取HB 中点M ，连接EM ，则EM 是BPH ∆的中位线ABCD )1(平面知：由⊥PH ΘABCD 平面⊥∴EM BCF 平面ＥＭ⊥∴即EM 为三棱锥B CF -E 底面上的高BG FC •=∆21S BCF =222121=⨯⨯2121=PH ＥＭ＝12221223131=⨯⨯=••=-EMS V BCF BCF E（3）：取AB 中点N ，PA 中点Q ，连接EN ，FN ，EQ ，DQ NFN EN FN AB NADF AB 21DF //EN PAB EN PAD PAD AB PAD ,//=⋂⊥∴∴=⊥∴∴∆⊥∴⊂⊥∴⊥是距形四边形又的中位线是又平面，平面平面ΘΘΘENAB PA PAAB PA CD CD AB3、如图，已知三棱锥A —BPC 中，AP ⊥PC ， AC ⊥BC ， M 为AB 中点，D 为PB 中点，且△PMB 为正三角形。

(完整版)高考文科立体几何证明专题

立体几何专题1．如图 4，在边长为 1 的等边三角形 ABC 中， D , E 分别是 AB, AC 边上的点， AD AE ，F 是 BC 的中点， AF 与 DE 交于点G ，将 ABF 沿 AF 折起，获取如图5 所示的三棱锥A BCF ，其中 BC2 ．2(1) 证明： DE // 平面 BCF ；(2) 证明： CF 平面 ABF ；(3) 2时，求三棱锥 FDEG 的体积 V F DEG ．当 AD3ADGEBFC图 4【剖析】（ 1）在等边三角形ABC 中， ADAEAD AE ,A BCF 中DB在折叠后的三棱锥EC也成立， DE / / BC ,Q DE平面 BCF ，BC 平面 BCF ，DE / / 平面 BCF ；AGEDFCB图 5（2 ）在等边三角形ABC 中， F 是 BC 的中点，所以 AFBC 1 ①， BF CF.2Q 在三棱锥 ABCF 中， BC2， BC 2 BF 2 CF 2 CF BF ②2Q BF CF F CF 平面 ABF ；（）由（）可知 GE / /CF ，结合（ 2）可得 GE平面 DFG.3 1VF DEGV E1 11 1 1 1 3 13 DFG3 DG FG GF2 3 3 2332423【剖析】这个题是入门级的题，除了立体几何的内容，还观察了平行线分线段成比率这个平面几何的内容 .2．如图 5 所示，在四棱锥P-ABCD 中,AB平面PAD,AB CD,PD=AD,E是PB的中点，F是 DC 上的点且 DF= 1AB,PH 为PAD 中 AD 边上的高．2（1）证明： PH 平面 ABCD ；（2）若PH=1，AD= 2 ,FC=1，求三棱锥E-BCF 的体积；（3）证明：EF平面PAB．解： (1)PH 为PAD中的高PH AD又 AB面PAD，PH平面PADPH ABAB AD A所以PH平面ABCD(2):过 B 点做 BG BG CD ，垂足为 G ；连接 HB, 取 HB 中点 M ，连接 EM ，则 EM 是BPH 的中位线由(1)知： PH平面ABCDEM平面 ABCDＥＭ平面 BCF即 EM 为三棱锥E - BCF底面上的高ＥＭ＝1PH1 22SBCF 1FC ? BG =11 22 222 1V E BCF? S BCF ? EM1 2 13 2 2212.（3）：取 AB 中点 N， PA 中点 Q，连接 EN ， FN ，EQ， DQ AB // CD , CD平面PADAB平面PAD，PA平面PADAB PA又EN 是 PAB 的中位线EN // PAAB EN1又DF AB四边形NADF是距形AB FNEN FN NAB平面NEF又 EF平面NEFEF AB四边形NADF是距形AB NF 3、如图，已知三棱锥 A —BPC 中，AP ⊥ PC ， AC ⊥ BC ，M为 AB 中点， D 为 PB 中点，且△ PMB 为正三角形。

高考数学最新真题专题解析—立体几何(文科)

高考数学最新真题专题解析—立体几何（文科）考向一线面夹角【母题来源】2022年高考全国甲卷（文科）【母题题文】在长方体1111ABCD A B C D -中，已知1B D 与平面ABCD 和平面11AA B B 所成的角均为30，则（） A. 2AB AD =B. AB 与平面11AB C D 所成的角为30C. 1AC CB =D. 1B D 与平面11BB C C 所成的角为45︒ 【答案】D【试题解析】【详解】如图所示：不妨设1,,AB a AD b AA c ===，依题以及长方体的结构特征可知，1B D 与平面ABCD 所成角为1B DB ∠，1B D 与平面11AA B B 所成角为1DB A ∠，所以11sin 30c b B D B D==，即b c =，22212B D c a b c ==++2a c =．对于A ，AB a ，AD b ，2AB AD =，A 错误；对于B ，过B 作1BE AB ⊥于E ，易知BE ⊥平面11AB C D ，所以AB 与平面11AB C D 所成角为BAE ∠，因为2tan c BAE a ∠==30BAE ∠≠，B 错误；对于C ，223AC a b c =+=，2212CB b c c =+=，1AC CB ≠，C 错误；对于D ，1B D 与平面11BB C C 所成角为1DB C ∠，112sin 22CD a DB C B D c ∠===，而1090DB C <∠<，所以145DB C ∠=．D 正确．故选：D ．【命题意图】本题主要考查直线与平面夹角，是一道容易题.【命题方向】这类试题在考查题型上选择题、填空题、解答题形式出现，试题难度不大，多为中低档题，重点考查线面夹角的求法问题. 【得分要点】（1）找斜线在平面中的射影；（2）求斜线与其射影的夹角；考向二线面平行、垂直的证明【母题来源】2022年高考全国乙卷（文科）【母题题文】如图，四面体ABCD 中，,,AD CD AD CD ADB BDC ⊥=∠=∠，E 为AC 的中点．（1）证明：平面BED ⊥平面ACD ；（2）设2,60AB BD ACB ==∠=︒，点F 在BD 上，当AFC △的面积最小时，求三棱锥F ABC -的体积．【试题解析】【小问1详解】由于AD CD =，E 是AC 的中点，所以AC DE ⊥.由于AD CD BD BD ADB CDB =⎧⎪=⎨⎪∠=∠⎩，所以ADB CDB ≅△△，所以AB CB =，故AC BD ⊥，由于DE BD D ⋂=，,DE BD平面BED ，所以AC ⊥平面BED ，由于AC ⊂平面ACD ，所以平面BED ⊥平面ACD . 【小问2详解】依题意2AB BD BC ===，60ACB ∠=︒，三角形ABC 是等边三角形，所以2,1,3AC AE CE BE ====由于,AD CD AD CD =⊥，所以三角形ACD 是等腰直角三角形，所以1DE =.222DE BE BD +=，所以DE BE ⊥，由于AC BE E ⋂=，,AC BE ⊂平面ABC ，所以DE ⊥平面ABC . 由于ADB CDB ≅△△，所以FBA FBC ∠=∠，由于BF BF FBA FBC AB CB =⎧⎪∠=∠⎨⎪=⎩，所以FBA FBC ≅，所以AF CF =，所以EF AC ⊥，由于12AFCS AC EF =⋅⋅，所以当EF 最短时，三角形AFC 的面积最小值.过E 作EF BD ⊥，垂足为F ，在Rt BED △中，1122BE DE BD EF ⋅⋅=⋅⋅，解得32EF =，所以223131,2222DF BF DF ⎛⎫=-==-= ⎪ ⎪⎝⎭，所以34BF BD =. 过F 作FH BE ⊥，垂足为H ，则//FH DE ，所以FH ⊥平面ABC ，且34FH BF DE BD ==，所以34FH =,所以11133233324F ABC ABCV SFH -=⋅⋅=⨯⨯=【命题意图】本题考查线面平行、垂直的证明.【命题方向】这类试题在考查题型多以解答题形式出现，多为中档题，是历年高考的必考题型．常见的命题角度有：（1）线面平行的证明；（2）线面垂直的证明；（3）面面平行的证明；（4）面面垂直的证明. 【得分要点】（1）利用线面、面面平行的判定定理与性质定理；（2）利用线面、面面垂直的判定定理与性质定理. 真题汇总及解析一、单选题1．（2022·内蒙古·乌兰浩特一中模拟预测（文））已知,αβ为空间的两个平面，直线,l ααβ⊄⊥，那么“l ∥α”是“l β⊥”的（）条件 A ．必要不充分 B ．充分不必要C ．充分且必要D ．不充分也不必要【答案】A 【解析】【分析】根据空间线面位置关系，结合必要不充分条件的概念判断即可. 【详解】当直线,l ααβ⊄⊥，l ∥α，则l β//，l 与β相交，故充分性不成立；当直线l α⊄，且αβ⊥，l β⊥时，l ∥α，故必要性成立， ⸫“l ∥α”是“l β⊥”的的必要不充分条件. 故选：A.2．（2022·贵州·贵阳一中模拟预测（文））在正方体1111ABCD A B C D -中，M 为1A D 的中点，则直线CM 与11A C 所成的角为（） A ．π2B ．π3C ．π4D ．π6【答案】D 【解析】【分析】11AC AC ∥，所求角为ACM∠，利用几何体性质，解CMA 即可【详解】设正方体棱长为1，连接11,,AC AC AC CM ∴与11A C 所成角即是CM 与AC 所成角，22222221162,,1,2222AC AM CM AM CM AC ⎛⎫⎛⎫===++=∴+= ⎪ ⎪⎝⎭⎝⎭，CMA ∴为Rt △，1πsin ,26AM ACM ACM AC ∠∠==∴= 故选：D3．（2022·青海·模拟预测）已知四面体ABCD 的所有棱长都相等，其外接球的6π，则下列结论错误的是（） A ．四面体ABCD 的棱长均为2 B ．异面直线AC 与BD 2 C ．异面直线AC 与BD 所成角为60︒D ．四面体ABCD 的内切球的体积等于6π27【答案】C 【解析】【分析】对于A, 设该四面体的棱长为a ，表示出高，根据其外接球的体积等于6π，求得外接球半径，即可求得a ,判断A;对于B, 分别取BD,AC 的中点为E,F ,连接EF ,求得EF 的长，即可判断；对于C ，证明线面垂直即可证明异面直线AC 与BD 互相垂直，即可判断;对于D ，利用等体积法求得内切球半径，即可求得内切球体积，即可判断. 【详解】如图示，设该四面体的棱长为a ，底面三角形BCD 的重心为G ,该四面体的外接球球心为O ，半径为R ，连接AG ,GB,OB ,AG 为四面体的高，O 在高AG 上，在Rt AGB △中，2223336,()33BG AG a a ===-, 在Rt OGB △中，22263()()R R =-+，解得6R = ， 6π，即34π6π3R ,故336R =故38,2a a == ，故A 正确；分别取BD,AC 的中点为E,F ,连接EF ,正四面体ABCD 中，AE=EC ,故EF AC ⊥ ,同理EF BD ⊥, 即EF 为AC,BD 的公垂线，而3232CE =⨯= , 则2222(3)12EF CE CF =-=-= ,故B 正确；由于,AE BD CE BD ⊥⊥ , AE CE ⊂，平面ACE ,故BD ⊥平面ACE , 又AC ⊂平面ACE ,所以BD AC ⊥，即异面直线AC 与BD 所成角为90︒ ，故C 错误；设四面体内切球的半径为r ,而263AG =,故11433BCDBCDSr SAG ⨯⨯⨯=⨯⨯，故646AG r a ==，所以四面体ABCD 的内切球的体积等于3344666ππ()π3327r a ==，故D 正确，故选：C4．（2022·湖北·华中师大一附中模拟预测）如图，正方体1111ABCD A B C D -中，P 是1A D 的中点，则下列说法正确的是（）A ．直线PB 与直线1A D 垂直，直线PB ∥平面11B DC B ．直线PB 与直线1D C 平行，直线PB ⊥平面11AC D C ．直线PB 与直线AC 异面，直线PB ⊥平面11ADC B D ．直线PB 与直线11B D 相交，直线PB ⊂平面1ABC【答案】A 【解析】【分析】根据空间的平行和垂直关系进行判定. 【详解】连接11111,,,,DB A B D B D C B C ；由正方体的性质可知1BA BD =，P 是1A D 的中点，所以直线PB 与直线1A D 垂直；由正方体的性质可知1111//,//DB D B A B D C ，所以平面1//BDA 平面11B D C ，又PB ⊂平面1BDA ，所以直线PB ∥平面11B D C ，故A 正确；以D 为原点，建立如图坐标系，设正方体棱长为1，()111,1,,0,1,122PB D C ⎛⎫==- ⎪⎝⎭显然直线PB 与直线1D C 不平行，故B 不正确；直线PB 与直线AC 异面正确，()1,0,0DA =，102PB DA ⋅=≠，所以直线PB 与平面11ADC B 不垂直，故C 不正确；直线PB与直线B D异面，不相交，故D不正确；11故选：A.5．（2022·安徽·合肥市第八中学模拟预测）下列四个命题，真命题的个数为（）（1）如果一条直线垂直于一个平面内的无数条直线，则这条直线垂直于该平面；（2）过空间一定点有且只有一条直线和已知平面垂直；（3）平行于同一个平面的两条直线平行；（4）a与b为空间中的两条异面直线，点A不在直线a，b上，则过点A有且仅有一个平面与直线a，b都平行．A．0 B．1 C．2 D．3【答案】B【解析】【分析】根据线面垂直的定义即可判断命题(1)；根据线面垂直的性质定理即可判断命题(2)；根据空间中线面的位置关系即可判断命题(3)；结合图形即可判断命题(4). 【详解】命题(1)：由直线垂直平面的定义可知，若直线垂直于一个平面的任意直线，则该直线垂直于该平面，故命题(1)错误；命题(2)：由直线与平面垂直的性质定理可知，过空间一定点有且只有一条直线与已知平面垂直，故命题(2)正确；命题(3)：平行于同一个平面的两条直线，可能平行，可能相交，也可能异面，故命题(3)错误；命题(4)：如图，当点A在如图上底面时，不存在平面同时平行于直线a、b；点A不在异面直线a、b上，若点A在直线a、b之间，则可以确定一个平面同时平行于直线a、b；若点A在直线a、b的外侧，也可以确定一个平面同时平行于直线a、b，故命题(4)错误.故选：B.6．（2022·河南安阳·模拟预测（文））如图，在四面体ABCD中，90BCD AB∠=︒⊥，平面BCD，AB BC CD==，P为AC的中点，则直线BP与AD所成的角为（）A．π6B．π4C．π3D．π2【答案】D【解析】【分析】根据给定条件，证明BP⊥平面ACD即可推理计算作答.【详解】在四面体ABCD中，AB⊥平面BCD，CD⊂平面BCD，则AB CD⊥，而90BCD∠=︒，即BC CD⊥，又AB BC B⋂=，,AB BC⊂平面ABC，则有CD⊥平面ABC，而BP⊂平面ABC，于是得CD BP ⊥，因P 为AC 的中点，即AC BP ⊥，而AC CD C =，,AC CD ⊂平面ACD ，则BP ⊥平面ACD ，又AD ⊂平面ACD ，从而得BP AD ⊥，所以直线BP 与AD 所成的角为π2. 故选：D7．（2022·四川成都·模拟预测）如图，网格纸上小正方形的边长为1，粗实线画出的是某三棱锥的三视图，A ，B ，C ，D 是该三棱锥表面上四个点，则直线AC 和直线BD 所成角的余弦为（）A ．0B ．13C ．13-D 22【答案】A 【解析】【分析】由三视图还原几何体，根据线面垂直的判定有BG ⊥面AGD ，线面垂直的性质可得BG AC ⊥，再由线面垂直的判定和性质得AC BD ⊥，即可得结果. 【详解】由三视图可得如下几何体：BG AG ⊥，BG DG ⊥，AG DG G =，则BG ⊥面AGD ，又AC ⊂面AGD ，则BG AC ⊥，而AC GD ⊥，由BG GD G ⋂=，则AC ⊥面BGD ，又BD ⊂面BGD ，所以AC BD ⊥，故直线AC 和直线BD 所成角的余弦为0. 故选：A8．（2022·山东潍坊·三模）我国古代数学名著《九章算术》中给出了很多立体几何的结论，其中提到的多面体“鳖臑”是四个面都是直角三角形的三棱锥．若一个“鳖臑”的所有顶点都在球O 的球面上，且该“鳖臑”的高为2，底面是腰长为2的等腰直角三角形．则球O 的表面积为（） A ．12π B ．43π C ．6π D ．26π【答案】A 【解析】【分析】作出图形，设在三棱锥A BCD -中，AB ⊥平面BCD ，BC CD ⊥且2BC CD ==，2AB =，证明出该三棱锥的四个面均为直角三角形，求出该三棱锥的外接球半径，结合球体表面积公式可得结果. 【详解】如下图所示：在三棱锥A BCD -中，AB ⊥平面BCD ，BC CD ⊥且2BC CD ==，2AB =，因为AB ⊥平面BCD ，BC 、BD 、CD ⊂平面BCD ，则AB BC ⊥，AB BD ⊥，CD AB ⊥，CD BC ⊥，AB BC B ⋂=，CD平面ABC ，AC ⊂平面ABC ，AC CD ∴⊥，所以，三棱锥A BCD -的四个面都是直角三角形，且2222BD BC CD =+=，2223AD AB BD =+=，设线段AD 的中点为O ，则12OB OC AD OA OD ====，所以，点O 为三棱锥A BCD -的外接球球心，设球O 的半径为R ，则132R AD ==，因此，球O 的表面积为2412R ππ=. 故选：A. 二、填空题9．（2022·四川成都·模拟预测（理））如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的表面积为________.【答案】816283++ 【解析】【分析】根据三视图可知这是一个四面体，根据长度即可根据三角形面积公式求每一个面的面积，进而可得表面积. 【详解】该几何体的直观图是正方体中的四面体ABCD ，4,42,43AB AD BD BC CD AC ======，()21113448,44282,44282,42832224ABD ABC ADC DBCS S SS =⨯⨯==⨯⨯==⨯⨯==⨯= 故答案为： 816283++.10．（2022·上海普陀·二模）已知一个圆锥的侧面积为2π，若其左视图为正三角形，则该圆锥的体积为________. 3π3 【解析】【分析】由圆锥侧面积公式求得底面半径12r =3.【详解】由题设，令圆锥底面半径为r ，则体高为3r ，母线为2r ，所以12222r r ππ⨯⨯=，则12r =，故圆锥的体积为2133324r r ππ⨯⨯=. 故答案为：324π 11．（2022·黑龙江·佳木斯一中模拟预测（理））如图，在正方体1111ABCD A B C D -中，点F 是棱1AA 上的一个动点，平面1BFD 交棱1CC 于点E ，则下列正确说法的序号是___________.①存在点F 使得11A C ∥平面1BED F ； ②存在点F 使得1B D ∥平面1BED F ； ③对于任意的点F ，都有EF BD ⊥；④对于任意的点F 三棱锥1E FDD -的体积均不变. 【答案】①③④ 【解析】【分析】①，找到点F 为1AA 的中点时，满足11A C ∥平面1BED F ；②，证明出11,BD B D 相交，得到不存在点F 使得1B D ∥平面1BED F ；③，作出辅助线，证明线面垂直，进而得到线线垂直； ④，得到三棱锥1E FDD -的体积等于正方体体积的16，为定值. 【详解】当点F 为1AA 的中点，此时点E 为1CC 的中点，此时连接EF ，可得：11A C EF ，因为11A C ⊄平面1BED F ，EF ⊂1BED F ，所以11A C ∥平面1BED F ，①正确；连接11,BD B D ，因为11//BB DD ，且11BB DD =，所以四边形11BB D D 为平行四边形，所以11,BD B D 相交，因为1BD ⊂平面1BED F ，所以不存在点F 使得1B D ∥平面1BED F ，②错误连接AC ，BD ，则AC ⊥BD ，又1AA ⊥平面ABCD ，BD ⊂平面ABCD ，所以1AA ⊥BD ，因为1AA AC A =，所以BD ⊥平面11AAC C ，因为EF ⊂平面11AAC C ，所以BD ⊥EF ，③正确；连接DF ，EF ，ED ，则无论点F 在1A A 的何处，都有1112DFD SDD AD =⋅，是定值，为正方形11ADD A 面积的一半，又高等于CD ，故体积也为定值，为正方体体积的16，④正确.故选：①③④12．（2022·甘肃·武威第六中学模拟预测（文））如图，在长方体1111ABCD A B C D -中，E ，F 是棱CD 上的两个动点，点E 在点F 的左边，且满足122EF DC BC ==，给出下列结论：①11B D ⊥平面1B EF ；②三棱锥11D B EF -的体积为定值； ③1A A //平面1B EF ； ④平面11A ADD ⊥平面1B EF . 其中所有正确结论的序号是______. 【答案】②④ 【解析】【分析】根据线面位置关系、面面位置关系判断命题①③④，由棱锥体积公式判断②．【详解】11B D 与11D C 显然不垂直，而11//EF C D ，因此11B D 与EF 显然不垂直，从而11B D ⊥平面1B EF 是错误的，①错；1111D B EF B D EF V V --=，三棱锥11B D EF -中，平面1D EF 即平面11CDD C ，1B 到平面11CDD C 的距离为11B C 是定值，1D EF 中，EF 的长不变，1D 到EF 的距离不变，面积为定值，因此三棱锥体积是定值，②正确；平面1B EF 就是平面11B A DC ，而1AA 与平面11B A DC 相交，③错；长方体中CD ⊥平面11A D DA ，CD ⊂平面11B A DC ，所以平面11A D DA ⊥平面11B A DC ，即平面11A ADD ⊥平面1B EF ，④正确．故答案为：②④．三、解答题13．（2022·四川成都·模拟预测（文））如图，四棱锥P ABCD -中，四边形ABCD 为直角梯形，,PB PD 在底面ABCD 内的射影分别为,AB AD ，222PA AB AD CD ．(1)求证：PC BC ⊥； (2)求D 到平面PBC 的距离．【答案】(1)证明见解析 3【解析】【分析】（1）由题意可证AD PA ⊥、AB PA ⊥，则可得PA ⊥面ABCD ，即可知PA BC ⊥，又AC BC ⊥则可得BC ⊥面PAC ，即可证PC BC ⊥.（2）分别计算出BCD S 与PBC S ，再利用等体积法D PBC P BCD V V --=即可求出答案. (1)因为PB 在底面ABCD 内的射影为AB ，所以面PAB ⊥面ABCD ，又因为AD AB ⊥，面PAB ⋂面ABCD AB =，AD ⊂面ABCD 所以AD ⊥面PAB ，又因PA ⊂面PAB 因此AD PA ⊥，同理AB PA ⊥，又AB AD A ⋂=,AD ⊂面ABCD ,AB 面ABCD 所以PA ⊥面ABCD ，又BC ⊂面ABCD ,所以PA BC ⊥，连接AC ，易得2AC =45BAC ∠=，又2AB =，故AC BC ⊥，又PA AC A =,PA ⊂面PAC ,PA ⊂面PAC 因此BC ⊥面PAC ，又PC ⊂面PAC 即PC BC ⊥；(2)在RT PAC 中426PC =+=在RT ACB 中422BC =-把D 到平面PBC 的距离看作三棱锥D PBC -的高h ，由等体积法得，D PBC P BCD V V --=，故1133PBC BCD S h S PA ，即123213622BCD PBCS PA h S ，故D 到平面PBC 的距离为33． 14．（2022·青海·海东市第一中学模拟预测（文））如图，在四棱锥P ABCD -中，平面PCD ⊥平面ABCD ，PCD 为等边三角形，22CD AB ==，2AD =，90BAD ADC ∠=∠=︒，M 是棱PC 上一点．(1)若2MC MP =，求证：//AP 平面MBD ．(2)若MC MP =，求点P 到平面BDM 的距离．【答案】(1)证明见解析22 【解析】【分析】（1）连接AC ，记AC 与BD 的交点为H ，连接MH ，先证明//AP MH ，再由线面平行的判定定理即可证明.（2）由等体积法B DMP P BMD V V --=，即可求出点P 到平面BDM 的距离.(1)连接AC ，记AC 与BD 的交点为H ，连接MH ．由90BAD ADC ∠=∠=︒，得//AB CD ，12AB AH CD HC ==，又12PM MC =，则AH PM HC MC =， ∴//AP MH ，又MH ⊂平面MBD ，PA ⊄平面MBD ，∴//AP 平面MBD ．(2) 由已知易得3BD DM ==，3BM =，所以在等边BMD 中，BM 边上的高为32h =，所以BMD 的面积为13333224BMD S =⨯⨯=△，易知三棱锥B PDM -的体积为116132326B DMP V -=⨯⨯⨯⨯=，又因为B DMP P BMD V V --=，所以点P 到平面BDM 的距离为3223P BMD BMD V d S -==△． 15．（2022·贵州·贵阳一中模拟预测（文））如图，四棱锥P ABCD -中，平面,PAB ABCD ⊥平面,AB CD ∥,AB AD ⊥3,3,2,60AB AD AP CD PAB ====∠=︒.M 是CD 中点，N 是PB 上一点.(1)若3,BP BN =求三棱锥P AMN -的体积；(2)是否存在点N ,使得MN 平面PAD ,若存在求PN 的长；若不存在，请说明理由.【答案】(1)1；(2)存在，73=PN . 【解析】【分析】（1）证得点M 到平面PAB 的距离是3AD =，进而可求出结果；（2）证得//MN PE ，进而可证出MN //平面PAD ，从而可求出PN 的长.(1)P AMN M PAN V V --=，由面PAB ⊥面ABCD 且交线是AB ，又DA AB ⊥，DA ⊂面PAB ，所以DA ⊥平面PAB ，又MD //AB ， ∴点M 到平面PAB 的距离是3AD =，又3BP BN =，则22123sin603332APN APB S S ==⨯⨯⨯⨯=， ∴三棱锥P AME -的体积13313=⨯⨯=. (2)存在.//,3,2AB DC AB CD==，连接BM并延长至于AD交于点E，//DM AB，∴在EAB中：13 EM DMEB AB==，∴在PBE△中：在PB上取点N，使得23 BN BMBP BE==，而13PN PB=，则//MN PE，又MN⊄平面PAD，PE⊂平面PAD，MN∴//平面PAD，在PAB△中，2212322372PB=+-⨯⨯⨯=7PN∴=。