比的意义和基本性质例题
比与比例的知识点与练习题

比与比例的知识点与练习题比例的意义和性质比的意义和性质1.比的意义:两个数相除叫做比。
冒号“:”是比号,读作“比”。
比号前面的数叫做比的前项,比号后面的数叫做比的后项。
比的前项除以后项所得的商,叫做比值。
比的前项相当于被除数,后项相当于除数,比值相当于商。
比值通常用分数表示,也可以用小数表示,有时也可能是整数。
比的后项不能是零。
比的前项相当于分子,后项相当于分母,比值相当于分数值。
2.比的性质:比的前项和后项同时乘上或者除以相同的数(除外),比值不变,这叫做比的基本性质。
比的化简可以根据比的基本性质进行,结果必须是一个最简比。
比例的意义和性质1.比例的意义:表示两个比相等的式子叫做比例。
组成比例的四个数,叫做比例的项。
两端的两项叫做外项,中间的两项叫做内项。
2.比例的基本性质:在比例里,两个外项的积等于两个内项的积。
3.解比例:根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个数比例中的另外一个未知项。
求比例中的未知项,叫做解比例。
练比例的意义和性质练题1.填空。
1) 两个比相等的式子叫做比例。
2) 组成比例的四个数叫做比例的项。
两端的两项叫做外项,中间的两项叫做内项。
3) 在比例里,两个外项的积等于两个内项的积。
4) 求比例中的未知项,叫做解比例。
5) 比值相等的两个比就相等。
2.按要求写比例。
1) 例如:1:2可以表示为2:4.2) 3:5=6:10.3) 1:2和2:1:10.4) 3:2:5:12.5) 17:3/5=68:12,所以比例为17:3/5=68:12.6) 2/3:6/2=4:9.3.按要求转化。
1) 6:8=3:4,8:6=4:3,24:6=4:1,2:3=8:12.2) 7:8=14:16,7:16=14:32,8:7=16:14,16:7=32:14.3) 7a=6b,a:b=6:7.4) 3/5a=4/9b,a:b=4:5/27.5.如果甲数的4/5与乙数的7/9相等,则甲数与乙数的比是多少?解:设甲数为4x,乙数为5y,则有:4x/(5y) = 7/9解得:x/y = 35/36因此甲数与乙数的比为4x/5y = 140/180 = 7/96.男生人数的5/8与女生人数的5/9相等,那么女生人数与男生人数的比是多少?解:设男生人数为5x,女生人数为8y,则有:5x/(8y) = 5/9解得:x/y = 8/9因此女生人数与男生人数的比为8y/5x = 72/25选择题:1.比例5:3=15:9的内项3增加6,要使比例成立,外项9应该增加多少?解:内项3增加6,变为9,比例变为5:3=15:9+6,即5:3=21:15因此,外项9应该增加6,变为15.答案:⑴62.把2千克盐加入15千克水中,盐与盐水重量的比是多少?解:盐水总重量为17千克,盐的重量为2千克,因此盐与盐水重量的比为2:17.答案:⑶2:173.下面的比中能与3:8组成比例的是多少?解:3:8的比值为0.375,只有1.5:4的比值也为0.375,因此1.5:4能与3:8组成比例。
比的意义及比的基本性质

2、比与除法、分数又有什 么不同?
比和除法、分数的联系和区别
联
比
系(相
当
于)
区 别
一种 关系
一种 运算 一种 数
比的前项 :比号 比的后项 比值 ÷除号
—分数线
除法 被除数
分数 分 子
除数
商
分母 分数值
比的后项可以是0吗?
• 做一做: • 1、小敏和小亮在文具店买同样的本子。小 敏买了6本,花了1.8元。 小亮买了8本,花 了2.4元。 小敏和小亮买的练习本之比是 • ( ):( ),比值是( ) ,花钱 数之比是( ) :( ),比值是( )。
• ( ): ( )
• 0.75:2 =(0.75×100): (2×100) • =75:200=( ): ( )
• 例如:15
﹕
3 10 = 15÷10= 2
• 前项 比号 后项 比值 • 根据分数与除法的关系,两个数的比也可以写成 分数形式。例如:15:10也可以写成 15 • 仍读作“15 比10”。 10
比值通常用分数表示,能 除尽时也可以用小数表示, 能整除时就用整数表示。
想一想:
1、比的前项、后项和比值 分别相当于除法算式和分 数中的什么?
• 6 :8= (6×2) • 6 :8 = (6÷2)
: (8×2) =12 : 16 : (8÷2) = 3 : 4
• 6÷8 = (6÷2) : (8÷2) =3 ÷4 • 你能根据比和分数的关系研究比的规律吗?
比的前项和后项同时乘或除以相同的数 (0除外)比值不变。
• 这叫做比的基本性质 • 根据比的基本性质,可以把比化成最简单 的整数比。
比的应用题典型题归类

比的应用题典型题归类一、比的概念及基本性质比是数学中常用的一种比较两个数量大小关系的方法。
在解决实际问题时,经常会遇到涉及到比的应用题。
比的应用题主要包括比例、百分数、倍数等类型。
下面将对这些典型题目进行分类和归纳,以便更好地理解和掌握比的应用。
二、比例问题1. 比例问题一:已知一个长度为a的线段与一个长度为b的线段的比是m:n,求第一个线段的长度。
解析:根据比例关系可以得到 a/b = m/n,求解得到 a = mb/n。
2. 比例问题二:已知一个物体的重量与其体积的比是m:n,求该物体的质量。
解析:根据比例关系可以得到 m/n = p/V,其中p为物体的密度,V 为物体的体积,求解得到 m = p * V。
三、百分数问题1. 百分数问题一:某商品原价100元,现折扣20%,求折后价格。
解析:原价100元,折扣20%,即折扣为100 * 20% = 20元,所以折后价格为100 - 20 = 80元。
2. 百分数问题二:某数增加了p%,求增加前的数。
解析:设增加前的数为x,则增加了p%后的数为x + x * p% = x(1 + p/100),所以增加前的数为x = (增加后的数)/(1 + p/100)。
四、倍数问题1. 倍数问题一:某任务A需要3个小时完成,任务B比A多完成1/3的工作,求任务B完成所需的时间。
解析:设任务B完成所需的时间为x小时,则任务A完成的工作量为1,任务B完成的工作量为1 + 1/3。
根据工作量和时间的关系可得到:3/1 = x / (1 + 1/3),求解得到 x = 2小时。
2. 倍数问题二:某矿井A挖掘一定数量的煤需要9天,矿井B比A 快1/4,求矿井B挖掘同样数量的煤需要多少天。
解析:设矿井B挖掘同样数量的煤需要x天,则矿井A的挖掘速度为1,矿井B的挖掘速度为1 + 1/4。
根据速度和时间的关系可得到:9/1 = x / (1 + 1/4),求解得到 x = 6天。
13比的意义、比的基本性质、比的应用

学科教师辅导讲义学生姓名:年级:六课时数:3辅导科目:数学辅导教师:辅导内容:比辅导日期:教学目标:(1)理解并掌握比的意义,会正确读与写。
记住比各部分的名称,并会正确求比值。
(2)通过主动发现的讨论式学习,激发合作意识,理解并正确掌握比与除法、分数之间的联系,明确比的后项不能为零的道理。
同时懂得事物之间是互相联系的。
(3)理解掌握比的基本性质与应用【同步知识讲解】知识点1:比的意义知识点概念梳理比的意义是两个数相除又叫做两个数的比,比是表示两个数相除,有两项;例题1:六年级一班40名同学共植树120棵.则植树棵数与植树人数的比是________,化成最简整数比是________.()A.40:120,1:2 B.140:60,4:1 C.10:300,1:3 D.120:40,3:1【分析】40名同学共植树120棵.则植树棵数与植树人数的比是120:40,再根据比的基本性质化简即可.【点评】本题主要考查了比的意义及化简比的方法.例题2:用100克药粉和1千克水配制成一种药水.药粉和药水的比是()A.100:1 B.1:100 C.1:10 D.1:11【分析】1千克=1000克,把100克药粉溶解在1000克水中,药水是1100克,进而根据题意求出药粉和药水的比;据此选择.【点评】此题考查了比的意义,应明确:药粉+水=药水.变式1:一杯糖水,糖与水的比是1:16,喝掉一半后,糖与水的比是()A.1:8 B.1:32 C.1:16 D.无法比较【分析】一杯糖水,糖与水的比是1:16,说明含糖率为×100%≈5.9%;喝掉一半后,剩下的糖水中的含糖率不变,也就是糖与水的比仍然是1:16.【点评】解决此题关键是理解整杯糖水和半杯糖水的含糖率不变,也就是糖与水的比不变.变式2:一杯糖水,糖与水的比是1:16,喝掉一半后,剩下的糖水中糖与水的比是()A.1:16 B.1:8 C.1:32 D.无法确定【分析】一杯糖水,糖与水的比是1:16,说明含糖率为×100%≈5.9%;喝掉一半后,剩下的糖水中的含糖率不变,也就是糖与水的比仍然是1:16.【点评】解决此题关键是理解整杯糖水和半杯糖水的含糖率不变,也就是糖与水的比不变.变式3:从学校走到电影院甲用了8分钟,乙用了9分钟.甲乙的速度比是()A.8:9 B.9:8 C.17:9【分析】把从学校走到电影院的路程看作单位“1”,根据“路程÷时间=速度”分别求出甲和乙的速度,进而根据题意求比即可选择.【点评】解答此题用到的知识点:(1)比的意义;(2)路程、时间和速度三者之间的关系.变式4:两个圆锥的高都是8cm,若它们的底面半径之比是4:5,则它们的体积之比是()A.4:5 B.16:25 C.5:4【分析】根据两个圆锥的它们的底面半径之比是4:5,设一个半径是4r,则另一个半径是5r,由圆锥的体积公式s=πr2h,带入数求比,即可得解.【点评】此题主要考查圆锥的体积计算方法,明确圆锥的体积大小是由它的底面积和高两个条件决定的.等高的圆锥的体积之比是底面半径比的平方变式5:某校男生和女生人数的比是5:4,男生人数比女生人数多________,男生人数是全部学生的________.【分析】(1)假设男生有5人,则女生有4人,求男生人数比女生人数多几分之几,把女生人数看作单位“1”,根据“(大数-小数)÷单位”1“的量”进行解答即可;(2)假设男生有5人,则女生有4人,则全班就有(5+4)=9人,求男生人数是全部学生的几分之几,根据求一个数是另一个数的几分之几,用除法解答即可.【点评】解答此题的关键是运用假设法,设出男生的人数,进而得出女生的人数,进而求出全班的人数,进而根据题意,进行比即可.知识点2:比的读写知识点概念梳理两个数相除又叫两个数的比。
比的意义和基本性质

比的意义和基本性质比的意义和基本性质1.比的意义:两个数的比表示两个数相除。
2.比的各部分名称。
(1)比号:“:”叫做比号,读作:“比”。
(2)比的前项和后项:在两个数的比中,比号前面的数叫做比的前项,比号后面的数叫做比的后项。
(3)比值:比的前项除以后项所得的商,叫做比值。
3.比和比值的关系:2既可以表示2:3,又可以表示联系:比和比值都可以用分数形式表示,如32:3的比值。
区别:比表示两个数量的倍数关系;比值是一个具体的数,可以是分数,也可以是小数或整数。
温馨提示:当比的后项为1时,1不能省略不写。
如2:1不能写成2,写成2就是2:1的比值。
4.比与分数、除法的关系。
(1)联系:比的前项相当于分数的分子、除法中的被除数;比号相当于分数的分数线、除法中的除号;比的后项相当于分数的分母、除法中的除数;比值相当于分数的分数值、除法中的商。
(2)区别:比表示两个数量的倍数关系,分数是一个数,除法是一种运算。
5.比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变。
6.化简比:把两个数的比化成最简单的整数比。
(1)整数比的化简方法:比的前项和后项同时除以它们的最大公因数。
(2)分数比的化简方法:比的前项和后项同时乘它们分母的最小公倍数,先转化成整数比,再进行化简;也可以利用求比值的方法化简。
(3)小数比的化简方法:先用恰当的方法转化成整数比,再进行化简。
【诊断自测】1.填空。
(1)甲是乙的23,甲和乙的比是(),乙和甲的比是()。
(2)5÷8=():()=()()(3)比的后项不能为()。
(4)把43:1.125化成最简单的整数比是(),比值是()。
(5)把25克糖放入100克水中,糖和糖水的质量比为()。
2.求比值。
53:411.2:3.61.5t:240kg 12:1513.求下列各比中的未知数。
113:x=3x:0.6=1099:x=434.化简下面各比。
9:126.5:1.354:1580.3:920.75:2【考点突破】类型一:已知一个数的几分之几等于另一个数的几分之几,求这两个数的比。
比的认识知识点及练习

比的认识知识点及练习比是数学中常见的一个概念,用于对两个或多个事物进行大小、数量的比较。
在实际生活中,比的概念广泛应用于各个领域,比如商品的价格比较、车辆的速度比较、学生的成绩比较等等。
对比的认识及掌握,对我们理解和应用数学知识都有很大的帮助。
本文将介绍比的基本概念、比的表示方法、比的性质以及比的练习题目。
首先,我们来了解比的基本概念。
比的基本思想就是将两个事物进行对比,找出它们之间大小的关系。
比的结果可以是相等、大于或小于。
我们用冒号“:”来表示比,例如用a:b表示a与b之间的比。
如果两个事物相等,比的结果就是1:1;如果a大于b,比的结果就是a:b,其中a大于b;如果a小于b,比的结果就是a:b,其中a小于b。
其次,比的表示方法也有一定的规则。
比的表示方法可以是分数形式,也可以是小数形式。
通常用分数形式表示的比更直观,例如2:3可以表示为2/3。
而用小数形式表示比更便于计算和比较,例如2:3可以表示为0.67。
除此之外,在比的表示中,我们还可以通过相似表示法将若干个比进行组合。
例如,如果有a:b和c:d两个比,我们可以将它们表示为(a:b):(c:d)。
这种相似表示法可以帮助我们更直观地比较复杂的数值关系。
第三,比有一些基本的性质。
比的性质主要包括比的对称性、比的传递性和比的替代性。
比的对称性表示,如果a:b,那么b:a也成立;比的传递性表示,如果a:b,b:c,那么a:c也成立;比的替代性表示,如果a:b,那么若a等于或有一个等于a的数与b成比例,则a与这个数成比例。
这些性质的掌握有助于我们在比较中灵活运用比的知识。
最后,为了更好地掌握比的应用,我们需要进行一些比的练习。
下面是几道比的练习题:1. 一个教室里有24个男生和32个女生,男生人数与女生人数的比是多少?2. 一支队伍有60人,其中男生和女生人数的比是2:3,那么女生的人数是多少?3. 小明家里有橘子和苹果,橘子和苹果的比是3:4,如果小明有21个苹果,他家有多少个水果?通过这些练习题,我们可以巩固对比的概念和原理的理解,提高比的运用能力。
六年级比的意义和基本性质练习题
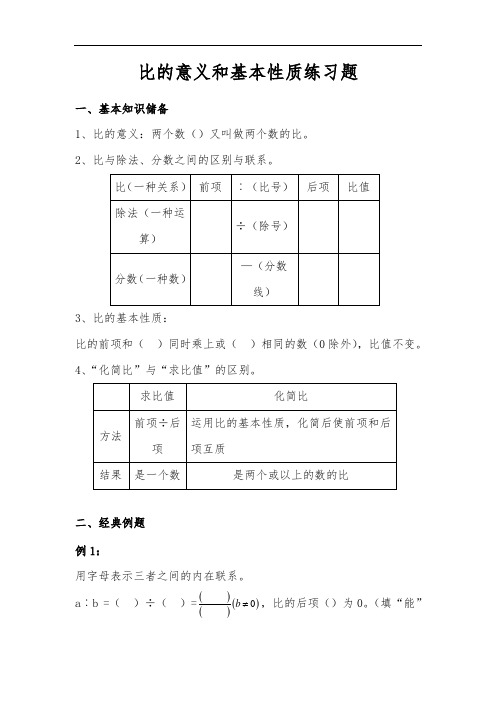
比的意义和基本性质练习题一、基本知识储备1、比的意义:两个数()又叫做两个数的比。
2、比与除法、分数之间的区别与联系。
3、比的基本性质:比的前项和( )同时乘上或( )相同的数(0除外),比值不变。
4、“化简比”与“求比值”的区别。
二、经典例题 例1:用字母表示三者之间的内在联系。
a ︰b =( )÷( )=()()()0b ≠,比的后项()为0。
(填“能”或“不能”)举一反三1:一袋洗衣粉重320克,一块香皂重80克。
洗衣粉与香皂的重量比是(),比值是();香皂与洗衣粉的重量比是(),比值是()。
例2:盐与水的比是1︰10,则盐︰盐水=(︰),水︰盐=(︰),盐水︰水=(︰)。
举一反三2:两个正方形边长比是1︰3,这两个正方形的周长比是(︰)面积比是(︰)。
例3:男生与女生的人数比是3︰4,男生比女生少() ()。
举一反三3:1、某班有男生20人,女生30人,男生与全班人数的比是(),女生比男生多() ()。
2、甲数除以乙数的商是43,甲数与乙数的比是()。
例4:易错题分析1、在4︰9中,如果比的前项加上8,要使比值不变,后项应加上()。
易错题分析2、A ︰B=2︰3,B ︰C=4︰5,那么A ︰B ︰C=(︰︰)。
易错题分析3、一项工程,甲单独完成需要6小时完成,乙单独完成需要5小时完成,甲、乙工作效率之比是(︰)。
举一反三4:1、在3︰8中,如果比的前项加上15,要使比值不变,后项应加上()。
2、A ︰B=3︰4,B ︰C=5︰6,那么A ︰B ︰C =(︰︰)。
3、一辆汽车从甲地开往乙地,3小时到达,返回时4小时到达,前往速度与返回速度的比是(︰)。
三、迁移拓展 例1、如果532CB A ==(其中A 、B 、C 都不等于0),那么A ︰B ︰C=(︰︰)。
举一反三7:如果2A=3B=4C (其中A 、B 、C 都不等于0),那么A ︰B ︰C=(︰︰)。
例2、有两个重叠的正方形,大正方形的边长是5厘米,小正方形的边长是4厘米,重叠部分的面积是9平方厘米,求阴影部分面积。
比的意义及比的基本性质

第十讲 比的意义及比的基本性质【典型例题1】求下列各式的比值:(1)4.5:217; (2)312:611 (3)36分:0.4时.解析:(1)4.5:217= 4.5÷7.5=0.6;或 4.5:217=29÷215=29×152=53.(2)312:611=37÷67=37×76=2.(3)0.4时=0.4×60=24分; 36分:0.4时=36分÷24分=211点评:此题考查的是比与比值的概念;掌握正确、熟练地求比值的方法. 【知识点】1.比a 、b 是两个数或两个同类的量,为了把b 和a 相比较,将a 与b 相除,叫做a与b 的比.记作a:b ,或写成ba,其中b ≠0;a 叫做比的前项,b 叫做比的后项.2.比值 比的前项除以比的后项所得的商叫做比值。
求比值时注意: (1)得到的结果是一个数(分数或小数,有时是整数). (2)求两个同类量的比值时,如果单位不同,必须把这两个量化成相同的单位. (注意:比是解决同类量之比). 【基本习题限时训练】1. 求54:45的比值,结果正确的是:( ) A 、2516 B 、1625 C 、16﹕25 D 、 25﹕16【解】A2. 求2周: 5天的比,结果正确的是:( )A 、14:5B 、542 C 、5:14 D 、 2.8【解】C3. 某中学预备(2)的学生人数为40人,其中男生17人,则该班男生人数与女生人数的比值是:( )A 、4017B 、1723C 、17﹕23D 、 2317【解】D 【拓展题1】一项工程,甲队用15天完成,乙队用18天完成,求甲队与乙队的工作效率的比值.【解析】(1÷15) ﹕(1÷18)= 151:181=151÷181=151×18=115【点评】把这项工程看成整体“1”,工作效率=工作总量÷工作时间,所以甲队和乙队的工作效率分别是151和181【拓展题2】如图,在ΔABC 中BC=10厘米,BD 是BC 的52,求ΔABD 和ΔABC 的面积之比.【解析】BD=10×52=4厘米;BC=10厘米;BD 上高的长=BC 上高的长;ΔABD 的面积:ΔABC 的面积=(21×BD ×BD 上高):(21×BC ×BC 上高)=(21×4):(21×10)=2:5.【点评】 三角形的面积公式是21×底边长×底边长上的高,而ΔABD 和ΔABC的边长可以取B D 、BC 它们底边上的高是同一条高,由已知条件只要求出B D 长就可以求出这两个三角形的面积比.【典型例题2】已知41:x=213,求x.解析:因为41:x=213;所以41÷x=213;由 x=41÷213;可得x=41×72;所以x=141.点评:要求正确理解分数、除法、比的关系和区别,从而求出所求的未知数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
比的意义和性质
☆知识要点:
(1)比的意义:两个数相除,又叫两个数的比.例如:
某车间有男工人15人,女工人有11人.求男工是女工的几倍可以写成15÷11,也可以说男工与女工人数的比是15∶11.求女工是男工的几分之几,可以写成11÷15,也可写成女工和男工人数的比是11∶15.
比号前面的数叫比的前项,比号后面的数叫比的后项.注意:
写比时要认真审题,弄清谁与谁相比,确定哪个量作比的前项,哪个量作比的后项前项和后项的位置不能颠倒.
(2)比和除法,分数的关系.
比和除法,分数之间既有联系,又有区别.
因为比与分数有一定的联系,所以比也可以写成分数形式,例如,3比2,可以写成3∶2
也可以写成3
2
,仍读3比2.
区别:
比,除法,分数,意义不一样
除法是一种运算,除号是运算符号.
分数是一种数,分数线有除号,比号,括号的作用.
比是两个数相除,表示两数的关系,比号是关系的符号.
比值:比的前项除以比的后项,所得的商叫做比值.
(3)比的基本性质:
比的前项和后项同时乘以或者同时除以相同的数,(零除外)比值不变.
应用比的基本性质,可以把比化成最简单的整数比.
例如①300∶=3000∶32=125∶2.
先把它们化成整数比,然后再化简,使比的前项和后项互质,
例如②:3小时∶18分.
有单位名称的要先统一单位名称,然后去掉单位名称,再化简成最简单的整数比,
3小时∶18分=180分∶18分=180∶18=10∶1
(4)求比值和化简比的区别.
①意义不同:求比值是用比的前项除以比的后项所得的商.化简比是把一个比化成最简单的整数比,使比的前项和后项成为互质数.
②结果不同, 求比值,结果是商,它是一个数,这个数可以是整数,也可以是小数或分数.
化简比结果仍是一个比,写成比的形式,也可以写成分数形式.注:化简比也可以用求比值的方法.
☆基础练习:
练习: 1、求比值:
3、填空:
4填空:
①5只羊重280千克,写出羊的总重量与羊的只数的最简单的整数比是().
②甲数比乙数少20%,乙数与甲数的比是().
③甲数与乙数的比是9∶4,甲比乙多()%.
④20克糖加200克水,溶成糖水,糖和糖水的比是().
⑩
如图:甲乙两个三角形重叠部分的面积相当于甲三角形的面积的,相当于乙三角形的,甲乙两三角形面积的比是()。
