中考数学每日一练:特殊角的三角函数值练习题及答案_2020年解答题版
2020年人教版九年级数学下册 同步练习《特殊角的三角函数值》(含答案)

2020年人教版九年级数学下册同步练习特殊角的三角函数值一、选择题1.如图,点A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( )A.B.C.D.2.在Rt△ABC中,∠C=90°,BC=3,AB=4,则sinA的值为()A. B.C.D.3.如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是( )A.2B.C.D.4.3tan 30°的值为( )A. B.C.D.5.如图,已知Rt△ABC中,∠C=90°,AC=6,BC=8,则tanA的值为()A.0.6B.0.8C.0.75D.6.计算2sin30°﹣sin245°+tan30°的结果是()A.+3B.+C.+D.1﹣+7.计算:cos245°+sin245°=()A. B.1 C.D.8.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.若AC=,BC=2,则sin∠ACD的值为()A.B.C.D.9.2cos45°的值等于()A. B. C.D.10.tan60°的值等于()A.1B.C. D.211.3tan60°的值为()A.B.C.D.312.如图,已知△ABC的三个顶点均在格点上,则cosA的值为()A.B.C.D.二、填空题13.计算: +(﹣4)0+cos60°﹣|﹣2|=14.如图,若点A的坐标为,则sin∠1= .15.如图,菱形ABCD的边长为10cm,DE⊥AB,sinA=,则这个菱形的面积= cm2.16.如图,∠BAC位于6×6的方格纸中,其中A,B,C均为格点,则tan∠BAC= .17.菱形的两条对角线长分别为16和12,较长的对角线与菱形的一边的夹角为θ,则cos θ=________.18.在△ABC 中,∠A 、∠B 都是锐角,若sinA=23,cosB=21,则∠C=________. 三、计算题 19.计算:(1)3tan30°+cos 245°-2sin60°; (2)tan 260°-2sin45°+cos60°.20.计算:21.计算:22.计算:23.计算:sin30°+cos60°-tan45°-tan60°tan30°.24.计算:25.计算:26.计算:27.先化简,再求代数式的值,其中a=tan60°﹣6sin30°.28.已知α是锐角,且sin(α+15°)=,计算:﹣4cosα﹣(π﹣ 3.14)0+tanα+()﹣1的值.29.先化解,再求值:,已知,.30.先化简,再求值:,其中x=2(tan45°-cos30°)参考答案1.C.2.C.3.B.4.B.5.D.6.B.7.B.8.A.9.B.10.C.11.D.12.D.13.答案为:2.514.答案为:.15.菱形的面积=DE•AB=6×10=60(cm2).16.答案为:1.5.17.答案为:0.8. 18.答案为:60°.19.解:(1)原式=0.5.(2)原式=227.20.解原式=2.21.原式=22.原式==223.解:原式=-1.24.原式=3-6+2+1=025.略26.原式==27.解:原式=÷=×=﹣,当a=tan60°﹣6sin30°=﹣6×=﹣3时,原式=﹣=﹣.28.∵sin60°=,∴α+15°=60°,∴α=45°,则原式=2﹣4×﹣1+1+3=3.29.解:原式=x=3,y=1原式=30.解:∵(tan45°-cos30°)∴原式====第41 页共41 页。
三角函数练习题(含答案)

三角函数练习题及答案(一)选择题1、在直角三角形中,各边都扩大2倍,则锐角A 的正弦值与余弦值都( )A 、缩小2倍B 、扩大2倍C 、不变D 、不能确定12、在Rt △ABC 中,∠C=900,BC=4,sinA=45,则AC=( ) A 、3 B 、4 C 、5 D 、6 3、若∠A 是锐角,且sinA=13,则( )A 、00<∠A<300B 、300<∠A<450C 、450<∠A<600D 、600<∠A<9004、若cosA=13,则A A AA tan 2sin 4tan sin 3+-=( ) A 、47B 、 13C 、 12D 、0 5、在△ABC 中,∠A :∠B :∠C=1:1:2,则a :b :c=( )A 、1:1:2B 、1:1:√2C 、1:1:√3D 、1:1:√226、在Rt △ABC 中,∠C=900,则下列式子成立的是( )A 、sinA=sinB B 、sinA=cosBC 、tanA=tanBD 、cosA=tanB7.已知Rt △ABC 中,∠C=90°,AC=2,BC=3,那么下列各式中,正确的是( )A .sinB= 23B .cosB= 23C .tanB= 23D .tanB=32 8.点(-sin60°,cos60°)关于y 轴对称的点的坐标是( ) A .(32,12) B .(-32,12) C .(-32,-12) D .(-12,-32)9.每周一学校都要举行庄严的升国旗仪式,让我们感受到了国旗的神圣.某同学站在离旗杆12米远的地方,当国旗升起到旗杆顶时,他测得视线的仰角为30°,若这位同学的目高1.6米,则旗杆的高度约为( )A .6.9米B .8.5米C .10.3米D .12.0米10.王英同学从A 地沿北偏西60º方向走100m 到B 地,再从B 地向正南方向走200m 到C 地,此时王英同学离A 地 ( )(A )350m (B )100 m (C )150m (D )3100m11、如图1,在高楼前D点测得楼顶的仰角为300,向高楼前进60米到C点,又测得仰角为450,则该高楼的高度大约为()A.82米B.163米C.52米D.70米12、一艘轮船由海平面上A地出发向南偏西40º的方向行驶40海里到达B地,再由B地向北偏西10º的方向行驶40海里到达C地,则A、C两地相距().(A)30海里(B)40海里(C)50海里(D)60海里(二)填空题1.在Rt△ABC中,∠C=90°,AB=5,AC=3,则sinB=_____.2.在△ABC中,若BC=2,AB=7,AC=3,则cosA=________.3.在△ABC中,AB=2,AC=2,∠B=30°,则∠BAC的度数是______.4.如图,如果△APB绕点B按逆时针方向旋转30°后得到△A'P'B,且BP=2,那么PP'的长为________. (不取近似值. 以下数据供解题使用:sin15°=,cos15°=624+)5.如图,在甲、乙两地之间修一条笔直的公路,从甲地测得公路的走向是北偏东48°.甲、乙两地间同时开工,若干天后,公路准确接通,则乙地所修公路的走向是南偏西___________度.6.如图,机器人从A点,沿着西南方向,行了个42单位,到达B 点后观察到原点O在它的南偏东60°的方向上,则原来A的坐标为___________结果保留根号).7.求值:sin260°+cos260°=___________.8.在直角三角形ABC中,∠A=090,BC=13,AB=12,那么tan B=___________.9.根据图中所给的数据,求得避雷针CD的长约为_______m(结果精确的到0.01m).(可用计算器求,也可用下列参考数据求:sin43°≈0.6802,sin40°≈0.6428,cos43°≈0.7341,cos40°≈0.7660,tan43°≈0.9325,tan40°≈0.8391)10.如图,自动扶梯AB 段的长度为20米,倾斜角A 为α,高度BC 为___________米(结果用含α的三角比表示).11.如图2所示,太阳光线与地面成60°角,一棵倾斜的大树与地面成30°角,这时测得大树在地面上的影子约为10米,则大树的高约为________米.(保留两个有效数字,2≈1.41,3≈1.73)三、简答题:1,计算:sin cos cot tan tan 3060456030︒+︒-︒-︒⋅︒分析:可利用特殊角的三角函数值代入直接计算;2计算:22459044211(cos sin )()()︒-︒+-︒+--π分析:利用特殊角的三角函数值和零指数及负整数次幂的知识求解。
九上数学每日一练:特殊角的三角函数值练习题及答案_2020年综合题版

九上数学每日一练:特殊角的三角函数值练习题及答案_2020年综合题版答案解析答案解析答案解析答案解析2020年九上数学:图形的变换_锐角三角函数_特殊角的三角函数值练习题1.(2020建湖.九上期末) 如图,在等腰中, ,, 是 上一点,若 .(1) 求的长;(2) 求 的值.考点: 勾股定理;特殊角的三角函数值;2.(2020泰兴.九上期末) 对钝角α,定义三角函数值如下:sinα=sin(180°-α),cosα=-cos(180°-α).(1) 求sin120°,cos120°的值;(2) 若一个钝角三角形的三个内角比是1:1:4,点A ,B 是这个三角形的两个顶点,sinA ,cosB 是方程4x -mx -1=0的两个不相等的实数根,求m 的值及∠A 和∠B 的度数.考点: 一元二次方程根的判别式及应用;特殊角的三角函数值;3.(2020长兴.九上期末) 如图是某学校体育看台侧面的示意图,看台AC 的坡比i 为1:2,看 高度BC 为12米,从顶棚的D 处看E 处的仰角a=18°,CD 距离为5米,E 处到观众区底端A 处的水平距离AF 为3米。
(sin18°≈0.31,tan18°≈0.32,结果精确到0.1米)(1) 求AB 的长;(2)求AB 的长;(3) 求EF 的长。
(4) 求EF的长。
考点: 特殊角的三角函数值;解直角三角形的应用﹣坡度坡角问题;4.(2019海门.九上期末)(1) 计算:;(2) 先化简,再求代数式的值: ,其中 .考点: 实数的运算;利用分式运算化简求值;特殊角的三角函数值;5.(2019宜阳.九上期末) 如图,AB 是⊙O 的直径,弦DE 交AB 于点F ,⊙O 的切线BC 与AD 的延长线交于点C ,连接AE .2答案解析(1) 试判断∠AED 与∠C 的数量关系,并说明理由;(2) 若AD=3,∠C=60°,点E 是半圆AB 的中点,则线段AE 的长为.考点: 圆周角定理;特殊角的三角函数值;解直角三角形的应用;2020年九上数学:图形的变换_锐角三角函数_特殊角的三角函数值练习题答案1.答案:2.答案:3.答案:4.答案:5.答案:。
专题25 含特殊角三角函数值的混合运算中考最新模拟30道(解析版)

专题25 含特殊角三角函数值的混合运算中考最新模拟30道1.计算:()1013tan30132π-⎛⎫+︒--- ⎪⎝⎭;2()101 3.14tan 603π-⎛⎫---︒ ⎪⎝⎭.3.计算101(2)1tan602π-︒⎛⎫---- ⎪⎝⎭4.计算:1001()3tan 30(13π---+ 【答案】﹣55.计算:(1)sin45°·cos45°+tan60°·sin60°;(2)sin30°-tan 245°+34tan 230°-cos60°.6114cos 45()|2|2-︒++-7.计算:101()2cos 451(3.14)4π-︒-+-+-.8.计算:201345(20171)--- .45(2017-9.计算:201(24602sin π-⎛⎫-+︒ ⎪⎝⎭.10.计算:2022cos6012( 3.14)π--+--.11.计算:2sin45°0(2019)π+-【点睛】此题主要考查了实数运算,正确化简各数是解题关键.12.计算:011)6sin30-︒-13.计算 101(12cos302-︒⎛⎫++⋅ ⎪⎝⎭14.计算:04sin 60|1|1)︒--+15.计算:0212tan 60( 3.14)()2π--︒--+-16.计算:(12)﹣1﹣2tan45°+4sin60°17.计算:101()(1)2cos6092π-++-+2cos609+18.计算:140111 1.414)2sin 602-︒⎛⎫-++-- ⎪⎝⎭19101()2cos60(2π)2---︒+-.20.计算:0|3|(3)tan 45π-+-︒【答案】3.【分析】根据有理数的绝对值,特殊角的三角函数值,负整数指数幂,二次根式一一计算即可得出答案.【详解】原式31213=+-+=【点睛】本题考查实数的混合运算,解题关键是熟练掌握运算法则.21.计算:1145tan 603-⎛⎫+-- ⎪⎝⎭°°22.计算:021(2020)sin 45()2︒--+- 【答案】-2【分析】根据零次幂的定义,特殊角的三角函数值,负整数指数幂分别化简后再相加减.12sin 45(2︒-【点睛】此题考查计算能力,掌握零次幂的定义,特殊角的三角函数值,负整数指数幂是解题的关23.计算:222cos602sin 45tan 60sin 303︒-︒+︒-︒.24.计算:0112sin 45(2)()3π-︒+--.2520112cos30()2-+︒+-.26.计算:1201tan 452cos60(2)2π-⎛⎫︒-︒+--- ⎪⎝⎭27.计算:(13)﹣2﹣(π02|+4tan60°.28.计算)2013460.2cos -⎛⎫+--︒ ⎪⎝⎭29.计算()01cot 3012sin 60cos60tan 30︒--︒+︒+︒.30.计算:2tan 452sin60cot 302cos 45︒-︒︒-︒.。
2020年中考数学压轴题每日一练(含答案)
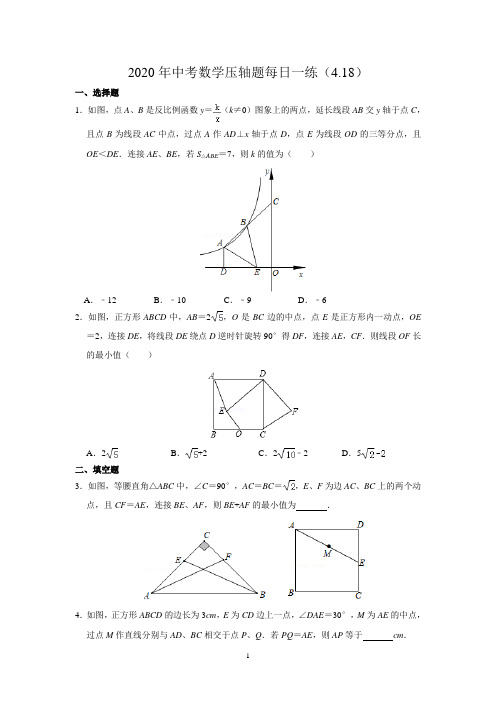
2020年中考数学压轴题每日一练(4.18)一、选择题1.如图,点A、B是反比例函数y=(k≠0)图象上的两点,延长线段AB交y轴于点C,且点B为线段AC中点,过点A作AD⊥x轴于点D,点E为线段OD的三等分点,且OE<DE.连接AE、BE,若S△ABE=7,则k的值为()A.﹣12 B.﹣10 C.﹣9 D.﹣62.如图,正方形ABCD中,AB=2,O是BC边的中点,点E是正方形内一动点,OE =2,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE,CF.则线段OF长的最小值()A.2B.+2 C.2﹣2 D.5二、填空题3.如图,等腰直角△ABC中,∠C=90°,AC=BC=,E、F为边AC、BC上的两个动点,且CF=AE,连接BE、AF,则BE+AF的最小值为.4.如图,正方形ABCD的边长为3cm,E为CD边上一点,∠DAE=30°,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q.若PQ=AE,则AP等于cm.三、解答题5.如图,矩形ABCD中,AB=a,BC=b,动点P从A点出发,按A→B→C的方向在AB 和BC上移动,记P A=x,点D到直线P A的距离为y,且y关于x的函数图象大致如图:(1)a=,b=;(2)求y关于x的函数关系式,并直接写出x的取值范围;(3)当△PCD的面积是△ABP的面积的时,求y的值.6.如图,以D为顶点的抛物线y=﹣x2+bx+c交x轴于点A,B(3,0),交y轴于点C(0,3).(1)求抛物线的解析式;(2)在直线BC上有一点P,使PO+P A的值最小,求点P的坐标;(3)在x轴上是否存在一点Q,使得以A,C,Q为顶点的三角形与△BCD相似?若存在,请求出点Q的坐标;若不存在,请说明理由.【答案与解析】一、选择题1.【分析】设A(m,),C(0,n),则D(m,0),E(m,0),由AB=BC,推出B(,),根据点B在y=上,推出•=k,可得mn=3k,连接EC,OA.因为AB=BC,推出S△AEC=2•S△AEB=14,根据S△AEC=S△AEO+S△ACO﹣S△ECO,构建方程即可解决问题;【解答】解:设A(m,),C(0,n),则D(m,0),E(m,0),∵AB=BC,∴B(,),∵点B在y=上,∴•=k,∴k+mn=4k,∴mn=3k,连接EC,OA.∵AB=BC,∴S△AEC=2•S△AEB=14,∵S△AEC=S△AEO+S△ACO﹣S△ECO,∴14=•(﹣m)•+•n•(﹣m)﹣•(﹣m)•n,∴14=﹣k﹣+,∴k=﹣12.故选:A.2.【分析】连接DO,将线段DO绕点D逆时针旋转90°得DM,连接OF,FM,OM,证明△EDO≌△FDM,可得FM=OE=2,由条件可得OM=5,根据OF+MF≥OM,即可得出OF的最小值.【解答】解:如图,连接DO,将线段DO绕点D逆时针旋转90°得DM,连接OF,FM,OM,∵∠EDF=∠ODM=90°,∴∠EDO=∠FDM,∵DE=DF,DO=DM,∴△EDO≌△FDM(SAS),∴FM=OE=2,∵正方形ABCD中,AB=2,O是BC边的中点,∴OC=,∴OD=,∴OM=,∵OF+MF≥OM,∴OF≥.故选:D.二、填空题3.如图,等腰直角△ABC中,∠C=90°,AC=BC=,E、F为边AC、BC上的两个动点,且CF=AE,连接BE、AF,则BE+AF的最小值为.【分析】如图,作点C关于直线AB的对称点D,连接AD,BD,延长DA到H,使得AH=AD,连接EH,BH,DE.想办法证明AF=DE=EH,BE+AF的最小值转化为EH+EB 的最小值.【解答】解:如图,作点C关于直线AB的对称点D,连接AD,BD,延长DA到H,使得AH=AD,连接EH,BH,DE.∵CA=CB,∠C=90°,∴∠CAB=∠CBA=45°,∵C,D关于AB对称,∴DA=DB,∠DAB=∠CAB=45°,∠ABD=∠ABC=45°,∴∠CAD=∠CBD=∠ADC=∠C=90°,∴四边形ACBD是矩形,∵CA=CB,∴四边形ACBD是正方形,∵CF=AE,CA=DA,∠C=∠EAD=90°,∴△ACF≌△DAE(SAS),∴AF=DE,∴AF+BE=ED+EB,∵CA垂直平分线段DH,∴ED=EH,∴AF+BE=EB+EH,∵EB+EH≥BH,∴AF+BE的最小值为线段BH的长,BH==,∴AF+BE的最小值为,故答案为.4.如图,正方形ABCD的边长为3cm,E为CD边上一点,∠DAE=30°,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q.若PQ=AE,则AP等于2或1cm.【分析】根据题意画出图形,过P作PN⊥BC,交BC于点N,由ABCD为正方形,得到AD=DC=PN,在直角三角形ADE中,利用锐角三角函数定义求出DE的长,进而利用勾股定理求出AE的长,根据M为AE中点求出AM的长,利用HL得到三角形ADE与三角形PQN全等,利用全等三角形对应边,对应角相等得到DE=NQ,∠DAE=∠NPQ =30°,再由PN与DC平行,得到∠PF A=∠DEA=60°,进而得到PM垂直于AE,在直角三角形APM中,根据AM的长,利用锐角三角函数定义求出AP的长,再利用对称性确定出AP′的长即可.【解答】解:根据题意画出图形,过P作PN⊥BC,交BC于点N,∵四边形ABCD为正方形,∴AD=DC=PN,在Rt△ADE中,∠DAE=30°,AD=3cm,∴tan30°=,即DE=cm,根据勾股定理得:AE=2cm,∵M为AE的中点,∴AM=AE=cm,在Rt△ADE和Rt△PNQ中,,∴Rt△ADE≌Rt△PNQ(HL),∴DE=NQ,∠DAE=∠NPQ=30°,∵PN∥DC,∴∠PF A=∠DEA=60°,∴∠PMF=90°,即PM⊥AF,在Rt△AMP中,∠MAP=30°,cos30°=,∴AP===2cm;由对称性得到AP′=DP=AD﹣AP=3﹣2=1cm,综上,AP等于1cm或2cm.故答案为:1或2.三、解答题5.如图,矩形ABCD中,AB=a,BC=b,动点P从A点出发,按A→B→C的方向在AB 和BC上移动,记P A=x,点D到直线P A的距离为y,且y关于x的函数图象大致如图:(1)a=3,b=4;(2)求y关于x的函数关系式,并直接写出x的取值范围;(3)当△PCD的面积是△ABP的面积的时,求y的值.【分析】(1)根据函数的图象,即可得出a、b的值;(2)分点P在线段AB上跟点P在线段BC上讨论,依据相似三角形的性质,即可得出y与x之间的关系;(3)由等高三角形的面积比等于底边长之比,可得出BP的长,根据勾股定理得出x的值,代入到(2)中的关系式中即可求出y的值.【解答】解:(1)当点P在线段AB上时,D到AB的距离为AD,由函数图象可看出,AD=4,即BC=b=4,当点P运动到线段BC上时,D到AB的距离出现变化,由函数图象可看出,AB=3=a.故答案为:3;4.(2)①当点P在线段AB上时,有0≤AP≤AB,即0≤x≤3,此时y=4.②当点P在线段BC上时,连接AC,过点D作DE⊥AP于点E,如图,由勾股定理可得:AC==5.∵此时P点过B点向C点运动,∴AB<AP≤AC,即3<x≤5.∵AD∥BC,∴∠DAE=∠APB,又∵∠ABP=∠DEA=90°,∴△DAE∽△APB,∴=,即=,∴y=.综合①②得:y=.(3)∵△PCD的面积是△ABP的面积的,且两三角形等高,∴BP=3PC,∵BP+PC=BC=4,∴BP=3,由勾股定理可得:x==3,将x=3代入,得y==2.故当△PCD的面积是△ABP的面积的时,y的值为2.6.如图,以D为顶点的抛物线y=﹣x2+bx+c交x轴于点A,B(3,0),交y轴于点C(0,3).(1)求抛物线的解析式;(2)在直线BC上有一点P,使PO+P A的值最小,求点P的坐标;(3)在x轴上是否存在一点Q,使得以A,C,Q为顶点的三角形与△BCD相似?若存在,请求出点Q的坐标;若不存在,请说明理由.【分析】(1)根据点B,C的坐标,利用待定系数法可求出抛物线的解析式;(2)利用二次函数图象上点的坐标特征可得出点A的坐标,由点B,C的坐标可得出直线BC的解析式,作O关于BC的对称点O′,则点O′的坐标为(3,3),由两地之间线段最短可得出当A,P,O′共线时,PO+P A取最小值,由点O′,A的坐标可求出该最小值,由点A,O′的坐标,利用待定系数法可求出直线AO′的解析式,联立直线AO′和直线BC的解析式成方程组,通过解方程组可求出点P的坐标;(3)由点B,C,D的坐标可得出BC,BD,CD的长,由CD2+BC2=BD2可得出∠BCD=90°,由点A,C的坐标可得出OA,OC的长度,进而可得出=,结合∠AOC=∠DCB=90°可得出△AOC∽△DCB,进而可得出点Q与点O重合时△AQC∽△DCB;连接AC,过点C作CQ⊥AC,交x轴与点Q,则△ACQ∽△AOC∽△DCB,由相似三角形的性质可求出AQ的长度,进而可得出点Q的坐标.综上,此题得解.【解答】解:(1)将B(3,0),C(0,3)代入y=﹣x2+bx+c,得:,解得:,∴抛物线的解析式为y=﹣x2+2x+3.(2)当y=0时,﹣x2+2x+3=0,解得:x1=﹣1,x2=3,∴点A的坐标为(﹣1,0).∵点B的坐标为(3,0),点C的坐标为(0,3),∴直线BC的解析式为y=﹣x+3.如图1,作O关于BC的对称点O′,则点O′的坐标为(3,3).∵O与O′关于直线BC对称,∴PO=PO′,∴PO+P A的最小值=PO′+P A=AO′==5.设直线AO′的解析式为y=kx+m,将A(﹣1,0),Q′(3,3)代入y=kx+m,得:,解得:,∴直线AO′的解析式为y=x+.联立直线AO′和直线BC的解析式成方程组,得:,解得:,∴点P的坐标为(,).(3)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴点D的坐标为(1,4).又∵点C的坐标为(0,3),点B的坐标为(3,0),∴CD==,BC==3,BD==2,∴CD2+BC2=BD2,∴∠BCD=90°.∵点A的坐标(﹣1,0),点C的坐标为(0,3),∴OA=1,OC=3,∴==.又∵∠AOC=∠DCB=90°,∴△AOC∽△DCB,∴当Q的坐标为(0,0)时,△AQC∽△DCB.如图2,连接AC,过点C作CQ⊥AC,交x轴与点Q.∵△ACQ为直角三角形,CO⊥AQ,∴△ACQ∽△AOC.又∵△AOC∽△DCB,∴△ACQ∽DCB,∴=,即=,∴AQ=10,∴点Q的坐标为(9,0).综上所述:当Q的坐标为(0,0)或(9,0)时,以A,C,Q为顶点的三角形与△BCD相似.。
2020年中考数学第一轮复习 第十九讲 解直角三角形 知识点+真题

2020年中考数学第一轮复习教案第三章图形的认识与三角形第十九讲解直角三角形【基础知识回顾】一、锐角三角函数定义:在Rt△ABC中,∠C=900, ∠A、∠B、∠C的对边分别为a、b、c,则∠A的正弦可表示为:sinA= ,∠A的余弦可表示为cosA= ∠A的正切:tanA= ,它们统称为∠A的锐角三角函数注意:1、sinA、∠cosA、tanA表示的是一个整体,是两条线段的比,没有单位,这些比值只与有关,与直角三角形的无关2、取值范围<sinA< ,cosA< ,tanA>注意:1、三个特殊角的三角函数值都是根据定义应用直角三角形性质算出来的,要在理解的基础上结合表格进行记忆2、正弦和正切值随着角度的增大而余弦值随着角度的增大而3、几个特殊关系:⑴sinA+cos2A= ,tanA=sin A()⑵若∠A+∠B=900,则sinA= ,tanA·tanB=三、解直角三角形:1、定义:由直角三角形中除直角外的个已知元素,求出另外个未知元素的过程叫解直角三角形2、解直角三角形的依据:Rt∠ABC中,∠C=900 三边分别为a、b、c⑴三边关系:⑵两锐角关系⑶边角之间的关系:sinA cosA tanAsinB cosB tanB注意:解直角三角形中已知的两个元素应至少有一个是当没有直角三角形时应注意构造直角三角形,再利用相应的边角关系解决3、解直角三角形应用中的有关概念⑴仰角和俯角:如图:在图上标上仰角俯角 ⑵坡度坡角:如图:斜坡AB 的垂直度h 和水平宽度l 的比叫做坡度,用i 表示,即i= 坡面与水平面得夹角为 用字母α表示,则i=tanα=hl。
⑶方位角:是指南北方向线与目标方向所成的小于900的水平角 如图:OA 表示 OB 表示 OC 表示OD 表示 (也可称东南方向)3、 利用解直角三角形知识解决实际问题的一般步骤:⑴把实际问题抓化为数学问题(画出平面图形,转化为解直角三角形的问题)⑵根据条件特点,选取合适的锐角三角函数去解直角三角形 ⑶解出数学问题答案,从而得到实际问题的答案注意:在解直角三角形实际应用中,先构造符合题意的三角形,解题的关键是弄清在哪个直角三角形中用多少度角的哪种锐角三角函数解决【中考真题考点例析】考点一:锐角三角函数的概念例1 (2019年威海)如图,一个人从山脚下的A 点出发,沿山坡小路AB 走到山顶B 点。
中考数学每日一练:特殊角的三角函数值练习题及答案_2020年单选题版

中考数学每日一练:特殊角的三角函数值练习题及答案_2020年单选题版答案答案答案答案答案2020年中考数学:图形的变换_锐角三角函数_特殊角的三角函数值练习题~~第1题~~(2020松江.中考模拟) 如图,两条宽度都为1的纸条,交叉重叠放在一起,它们的夹角为锐角,它们重叠部分(阴影部分)的面积是1.5,那么 的值为( ) A . B . C . D .考点: 菱形的性质;特殊角的三角函数值;~~第2题~~(2020哈尔滨.中考模拟) 在△ABC 中,∠C=90°,sinA= ,则cosB 的值是( )A . 1B .C .D . 考点: 特殊角的三角函数值;~~第3题~~(2020虹口.中考模拟) 若cosα= ,则锐角α的度数是( )A . 30°B . 45°C . 60°D . 90°考点: 特殊角的三角函数值;~~第4题~~(2020迁安.中考模拟) 如图,在矩形ABCD 中,AD=3,M 是CD 上的一点,将△ADM 沿直线AM 对折得到△ANM,若AN 平分∠MAB ,则DM 的长为( )A . 3B .C .D . 1考点: 角平分线的性质;翻折变换(折叠问题);特殊角的三角函数值;~~第5题~~(2020长兴.中考模拟) 如图,AB 为☉O 的直径,P 为弦BC 上的点,∠ABC=30°,过点P 作PD ⊥OP 交☉O 于点D ,过点D 作DE∥AB 交AB 的延长线于点E.若点C 恰好是 的中点,BE=6,则PC 的长是( )A . -8B . -3C . 2D . 12-考点: 等边三角形的判定与性质;圆周角定理;特殊角的三角函数值;答案答案答案答案答案~~第6题~~(2020绍兴.中考模拟) 按如图所示的运算程序,能使输出的y 值为的是()A . α=60°,β=45°B . α=30°,β=45°C . α=30°,β=30°D . α=45°,β=30°考点: 特殊角的三角函数值;~~第7题~~(2018建邺.中考模拟) 若锐角三角函数tan55°=a ,则a 的范围是( )A . 0<a <1B . 1<a <2C . 2<a <3D . 3<a <4考点: 特殊角的三角函数值;~~第8题~~(2018大庆.中考真卷) 2cos60°=( )A . 1B .C .D .考点: 特殊角的三角函数值;~~第9题~~(2019三明.中考模拟) 如图,A ,B ,C 是小正方形的顶点,且每个小正方形的边长为1,则tan ∠BAC 的值为( )A .B . 1C .D .考点: 勾股定理;勾股定理的逆定理;特殊角的三角函数值;~~第10题~~(2018沧州.中考模拟) 若关于x 的方程x ﹣x+sina=0有两个相等的实数根,则锐角a 为( )A . 75°B . 60°C . 45°D . 30°考点: 一元二次方程根的判别式及应用;特殊角的三角函数值;2020年中考数学:图形的变换_锐角三角函数_特殊角的三角函数值练习题答案1.答案:C2.答案:A3.答案:C4.答案:B5.答案:A6.答案:C7.答案:B8.答案:A9.答案:B10.答案:D 2。
初中特殊角三角函数值和解直角三角形练习题(含答案)

特殊角三角函数值和解直角三角形练习题一、 真空题:1、在Rt △ABC 中,∠B =900,AB =3,BC =4,则sinA= 4/52、在Rt △ABC 中,∠C =900,AB =,35cm BC cm =,则SinA= 515 cosA=5103、Rt △ABC 中,∠C =900,SinA=54,AB=10,则BC = 84、α是锐角,若sin α=cos150,则α= 75°若sin53018\=0.8018,则cos36042\= 0.80185、∠B 为锐角,且2cosB -1=0则∠B = 60°6、在△ABC 中,∠C =900,∠A ,∠B ,∠C 所对的边分别为a ,b ,c ,a =9,b =12,则sinA= 9/13 sinB= 12/137、Rt △ABC 中,∠C =900,tanA=0.5,则cotA= 28、在Rt △ABC 中,∠C =900,若b a 32=则9.等腰三角形中,腰长为5cm ,底边长8cm ,则它的底角的正切值是 3/4 10、若∠A 为锐角,且tan 2A+2tanA -3=0则∠A = 45°11、Rt △ABC 中,∠A =600,c=8,则a b = 4/1612、在Rt △ABC 中,若32=c ,b =3,则面积S13、在Rt △ABC 中,∠C =900,AC :BC =1:3,AB =6,∠B =30°,AC =3/,BC 14、在△ABC 中,∠B =900,AC 边上的中线BD =5,AB =8,则tan ∠ACB= 4/3二、选择题1、在Rt △ABC 中,各边的长度都扩大2倍,那么锐角A 的正弦、余弦值 ( C ) A 、都扩大2倍 B 、都扩大4倍 C 、没有变化 D 、都缩小一半2、若∠A 为锐角,且cotA <3,则∠A ( B )A 、小于300B 、大于300C 、大于450且小于600D 、大于600 3、在Rt △ABC 中,已知a 边及∠A ,则斜边应为 ( B ) A 、asinA B 、Aa sin C 、acosA D 、A a cos4、等腰三角形底边与底边上的高的比是2:3,则顶角为( A ) A 、600 B 、900 C 、1200 D 、15005、在△ABC 中,A ,B 为锐角,且有sinA =cosB ,则这个三角形是( B ) A 、等腰三角形 B 、直角三角形 C 、钝角三角形 D 、锐角三角形6、有一个角是300的直角三角形,斜边为1cm ,则斜边上的高为( C ) A 、41cm B 、21cm C 、43cm D 、23cm 三、求下列各式的值1、sin 2600+cos 26002、sin600-2sin300cos300 3. sin300-cos 2450=1 =0 =04. 2cos450+|32-|5. 0045cos 360sin 2+6. 130sin 560cos 300-=3 =6 =17. 2sin 2300·tan300+cos600·cot300 8. sin 2450-tan 2300 =332 =-5/2四、解答下列各题1、在Rt △ABC 中,∠C =900,,AB =13,BC =5,求sinA, cosA, tanA, cotA 答案:sinA=5/13, cosA=12/13, tanA=5/12, cotA=12/52. 在Rt △ABC 中,∠C =900,若1312sin =A 求cosA, sinB, cosB 答案:cosA=5/13, sinB=5/13, cosB=12/133. 在Rt △ABC 中,∠C =900,b=17, ∠B=450,求a, c 与∠A 答案:a=17,c=172,∠A=450四、根据下列条件解直角三角形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考数学每日一练:特殊角的三角函数值练习题及答案_2020年解答题版答案答案答案答案2020年中考数学:图形的变换_锐角三角函数_特殊角的三角函数值练习题
~~第1题~~(2020郑州.中考模拟)
先化简,再求值: ÷( ﹣x+1),其中x=sin30°+2+ .
考点: 实数的运算;利用分式运算化简求值;特殊角的三角函数值;
~~第2题~~
(2020长兴.中考模拟) 将一副直角三角尺如图放置,A ,E ,C 在一条直线上,边AB 与DE 交于点F ,已知∠B=60°,∠D =45°
,AD=AC= ,求DF 的长.
考点: 平行线分线段成比例;特殊角的三角函数值;~~第3题~~
(2019太原.中考模拟) 清代诗人高鼎的诗句“儿童散学归来早,忙趁东风放纸鸢”描绘出一幅充满生机的春天景象。
小明制作了一个风筝,如图1所示,AB 是风筝的主轴,在主轴AB 上的D 、E 两处分别固定一根系绳,这两根系绳在C 点处打结并与风筝线连接。
如图2,根据试飞,将系绳拉直后,当∠CDE =75°,∠CED =60°时,放飞效果佳。
已知D 、
E 两点之间的
距离为20cm ,求两根系绳CD 、CE 的长。
(结果保留整数,不计打结长度。
参考数据: )
考点: 等腰直角三角形;特殊角的三角函数值;~~
第4题~~
(2019徐汇.中考模拟) 计算:
.考点: 特殊角的三角函数值;~~第5题~~
(2019.中考模拟) 在平面直角坐标系中,O 为原点,点
A (1,0),点
B (0,
),把△ABO 绕点O 顺时针旋转,得A′
B′O ,记旋转角为α.
(Ⅰ)如图①,当α=30°时,求点B′的坐标;
(Ⅱ)设直线AA′与直线BB′相交于点M.
①如图②,当α=90°时,求点M 的坐标;
②点C (﹣1,0),求线段CM 长度的最小值.(直接写出结果即可)﹣1
考点:等腰直角三角形;旋转的性质;锐角三角函数的定义;特殊角的三角函数值;
答案2020年中考数学:图形的变换_锐角三角函数_特殊角的三角函数值练习题答案
1.答案:
2.答案:
3.答案:
4.答案:
5.答案:。
