Minimal Rectangular Partitions of Digitized Bolbs
• By L.FERRARI, P.V. SANKAR, AND J.SKLANSKY, 1984
Introduction
Contents
1. What is the minimum number? Theorem One: P = N – L + 1 2. How to produce the partition with minimum number? Theorem Two: Max Matching equal no augmenting path.
• A rectilinear polygon R has a minimum number of N – L + 1 rectangular partitions where, N = Total number of concave vertices L = Maximum number of nonintersecting chords that can be drawn between cogrid concave vertices.
Proof: P<= N – L + 1
Proof : P <= N – L + 1
Part 2 : P >= N – L + 1
• Given a rectilinear polygon B and one of its possible partitions. The set of nonintersecting cogrid points contains a maximum number of L rectangle. • Prove that at least N – L + 1 rectangles are needed to cover the whole polygon.
Only circles of even vertices
Finding a maximum matching
• We can always find a maximum matching by reversing the augmenting path. • Bipartite Matching(G;M)
Contents
1. What is the minimum number? Theorem One: P = N – L + 1 2. How to produce the partition with minimum number? Theorem Two: Max Matching equals no augmenting path.
Proof Schedule
P <= N – L + 1
Construction of a solution with N – L + 1 rectangles By Lemma One P >= N – L + 1 Every partition must have at least N - L + 1 rectangles
• C is the set of cogrid concave chords. • C’ is the maximum set of nonintersecting cogrid concave chords. C’ contains L chords. • C’’ is the set of C – C’. Lemma 2 In the (L + 1) subregions divided by C’, treating the cogrid concave points forming the chords in C’’ as noncogrid points will not increase the number of rectangles.
Lemma 1
• For a rectilinear polygon whose boundary contains N noncogrid concave vertices, the minimum number of rectangular partition is N+1.
Proof of Lemma One
Some observations
• A is an important point. • A point is concave if it has an inner angle of 270° • Chord: a chord is a line segment separating the polygon A
From Maximum Matching to Vertex Cover
• Partition the vertices of G into subsets Si as follows: (1) S0 consist of all vertices unmatched by M. (2) For integer j >= 0, let S2j+1 be the set of vertices that: a. are adjacent to vertices in S2j via some edge e ∈E|M. b. have not been included in any previously-defined set Sk, k < j. Remark : Each vertex v∈S2j+1much be adjacent to another vertex u via an edge e ∈ M。 (3) S2j+2 contain these adjacent vertices (4) If there are no vertices adjacent to S2j , arbitrarily pick an unused vertex and continue in S2j+1. Vertices in odd levels form a vertex cover.
Illustration
Matching
• A matching M of G(V,E) is a subset of the edges E, such that no vertex in V is incident to more than one edge in M.
• Maximum matching
Theorem 2. Part 2
• Part 2 : If M is not maximum then there is an augmenting path w.r.t. M. • M is the maximum Matching, N is non-Maximum Matching • The components of union of M (solid) and N (dashed) can be classified as (|M| < |N|)
1. For every vertex in L, start DFS. 2. DFS() If current vertex is in L follow an matched edge else follow a free edge. If at any point we find an augmenting path, reverse it and continue with unmatched vertices.
a,b are boundary line defining A. Two chords (c,d) can be drawn from A α,β are arbitrarily small rectangles defined by (a,c) and (b,d) 1. α and β cannot be in the same rectangle. 2. Either c or d must exist to separate α and β. 3. Each noncogrid vertex will increase the total number of rectangles by at least one.
Alternating Path
• A path is alternating w.r.t. a matching if its edges are alternating between free and matched edges.
• Three types of alternating paths • 1. Between two matched vertices • 2. Between two free vertices (Augmenting Path) • 3. Between a matched vertex and a free v is not a maximum matching if and only if there exists an augmenting path w.r.t M. • Part One : If there exists an augmenting path, the matching is not maximum. • Proof : A reverse of matched and free edges can produce a matching with M+1.
P >= N – L + 1
• (3) Q: the total number of noncogrid concave vertices in the S subregions Q = N – 2L’ – 2L1’ – L2 P = min {L’ + 1 + M1 + M2 + M3+(N – 2L’ – 2L1– L2 )} = min {N – L’ + 1 + (M1-2L1) + (M2 – L2) + M3 } =N–L+1
压缩映像原理翻译部分
部分1.文摘结果主题和概括。
压缩映像原理是一种研究非线性程最有用的工具，比如代数程，积分或微分程。
原则是一个不动点定理，证明了完备度量空间的压缩映像本身有一个独特的固定 点通过反复图像的映射下任意起始点的空间获得极限的定义。
因此，这是一个建设性的不动点定理并且可以实现定点的数值计算。
从古代数学（即计算古代数字平根的古代案）以来，迭代格式一直被使用并且在牛顿法求解多项式或代数程组和皮卡德的迭代过程求解初值和边值非线性常微分程的问题变得特别实用(见,[58],[59])。
在完整的赋线性空间中，这个原理首先被巴拿赫5证明在收缩映射（在巴拿赫的多结果请看[60]）。
同时，豪斯多夫为完备度量空间的收缩映射（来自Caccioppoli 17， [75]）提供了总体框架原则，介绍了一个抽象的度量空间的概念。
它出现在各种文本实际分析(前一个注释,[56])在这些记录中，我们用不同的形式开发压缩映像原理并且提供不同数学文献中的多应用程序。
我们的目的是向读者介绍一些关于已经发现有用的原则在不同区域的分析。
我们会讨论这些分析：牛顿法的收敛；如确定分形是固定的点集值压缩迭代函数系统；积极使用希尔伯特的度量矩阵的门阶-弗罗贝尼乌斯定理和这个无限维空间的拓展(定理Krein-Rutman)； 常微分程的存在性和唯一性定理的基本理论（Picard-Lindel 定理）和各种相关的结果；Abel-Liouville 类型的积分程理论的应用程序；隐函数定理；变分不等式的基本存在和唯一性定理；非对称二次形式的Lax-Milgram 类型结果；Cauchy-Kowalevsky 基本存在性定理的偏微分程的分析条件。
这些记录已经收集了几年,最近，被用来作为研讨会中VIGRE 项目的一个部门基础部分。
我们在这里要感那些参加了研讨会的本科学生,给了我们有价值的反馈。
2．完备度量空间在本节中,我们短暂回顾大多数本科生数学课程中一些非常基本的概念。
压缩映像定理 数分
压缩映像定理数分
压缩映像定理（Compression Mapping Theorem）在数学中，特别是泛函分析和度量空间理论中具有重要意义。
该定理又称Banach不动点定理，它揭示了压缩映射在完备距离空间中的性质。
压缩映像定理的表述如下：
设（X，P）是一个完备的距离空间，T是（X，P）到其自身的一个压缩映射，则T在X上存在唯一的不动点。
这里，完备的距离空间指的是一个具有完备性质的度量空间，即其中的所有基本列都是收敛列。
压缩映射是指映射T将空间X映射到其自身，并且满足T（X）⊆X。
压缩映像定理在数学分析中有很多应用，例如零点存在性定理、三大中值定理等。
这些定理中的映射都可以看作是压缩映射的特殊情况。
在实际应用中，压缩映像定理也有广泛的应用，如在解方程、微分方程、最优化问题等领域。
此外，压缩映像定理在数字图像和视频压缩中也发挥着重要作用。
通过将图像或视频信号压缩到其极限，可以实现更高的压缩比和更好的质量。
总之，压缩映像定理是数学中一个重要的定理，它在理论研究和实际应用中都有着广泛的意义。
无取样受限波尔兹曼机的图像重建研究
可 见 单 元 固 定为 已 知 数 据 的 值 时 ，模 型 平 衡 状 态 时 可 见 单 元 与 隐 单 元 值 的 乘 积 。 而
＜ ｖ ｉ ｈ ｊ ＞ ｍｏ ｄ ｅ ｌ 代表 模型 的期 望 ，即对 模型 没 有
２ ０ ０ ２年 Ｈ ｉ ｎ ｔ ｏ ｎ 提 出Ｒ Ｂ Ｍ 的快 速学 习算 法
对 比散度 （ ｃ ｏ ｎ ｓ ｔ ｒ ａ ｓ ｔ ｉ ｖ ｅ Ｄｉ ｖ ｅ ｒ ｇ ｅ ｎ ｃ ｅ ，Ｃ Ｄ） ， ２ ０ ０ ６年 Ｈｉ ｎ ｔ ｏ ｎ等提 出 了 一 种 深 度 信 念 网 络 【 ５ ］（ Ｄｅ ｅ ｐＢｅ ｌ ｉ ｅ ｆ Ｎｅ ｔ ｓ ，ＤＢ Ｎ）。 实 践 表 明 ， Ｒ ＢＭ 是一种有 效 的特征提 取方法 ， 已成功 应 用于分类 、回归 、图像特征提取 、协同过滤等
图像与多媒体技术 ・ Ｉ ｍａ ｇ ｅ＆Ｍｕ ｌ ｔ ｉ ｍｅ ｄ ｉ ａ Ｔ ｅ ｃ ｈ ｎ ｏ ｌ ｏ ｇ ｙ
无取样 受限波尔兹 曼机 的图像 重建研 究
文／ 姜 倩 盼
本 丈分 析 了受 限玻 尔兹 曼机 用 于 重 建 的 不 足 ， 提 出 了一 种 无 取样 受限玻 尔兹曼机 的图像 重建 新 方 法 ，应 用 Ｍ Ｎ Ｉ Ｓ Ｔ数 据 集 证 明
对Ｒ ＢＭ 原理 分析 表 明 ，Ｒ ＢＭ 的 训 练过 程 可 以构成 一种 效果 很好 的重 建 过程 。基 于 Ｒ ＢＭ 的强大 功 能 ，预 期基 于 ＲＢ Ｍ 的重建 过
ｐ （ ｈ ｊ ＝ １ Ｉ Ｖ ） ＝ （ ＋ ∑ ） …
其中 （ ｘ ） 为ｓ ｉ ｇ ｍ ｏ ｉ ｄ函数 １ ／ （ １ ＋ ｅ ｘ ｐ （ 一 ｘ ） ） 。
（ Ｒ ｅ ｓ ｔ ｒ ｉ ｃ ｔ ｅ ｄ Ｂ ｏ ｌ ｔ ｚ ｍａ ｎ ｎ Ｍａ ｃ ｈ ｉ ｎ ｅ ｓ ，Ｒ ＢＭ）。Ｌ ｅ Ｒ ｏ ｕ ｘ和 Ｂ ｅ ｎ ｇ ｉ ｏ从理论上 证 明，只要 隐单元 的 数 目足够 多 ，ＲＢ Ｍ 能够 拟合任 意离散 分布 。
【计算机应用研究】_软件测试_期刊发文热词逐年推荐_20140723
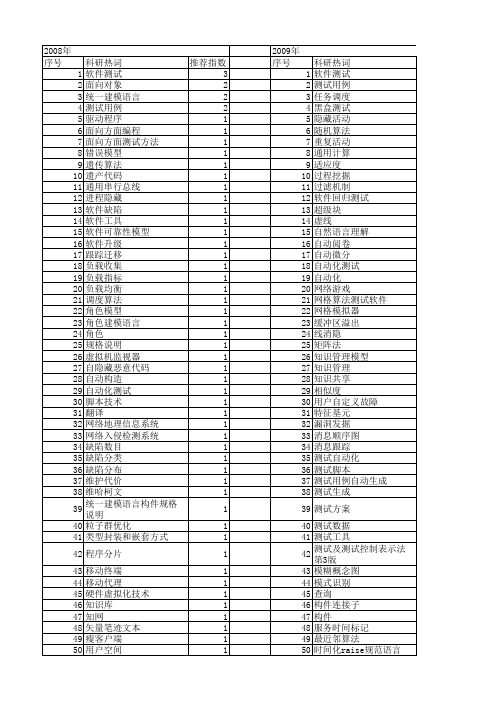
测试监控 测试用例复杂性 测试模型 测试数据 测试指标 测试执行顺序 测试执行管理 测试场景 测试准则 正则表达式 横切行为 模式匹配 检索 构件行为模型 构件 期望最大化算法 最小可恢复状态集 普适计算 显示及排版 文本断行 数据集成/融合 支持向量机 搜索引擎 控制流图 扩展元数据交换 性能优化 序列图 并行工程 并列复句 嵌入式软件 实时系统 字母选形 字母拉长 多层混合检查点 回归自动测试 回归测试 可靠性 变体测试 单字识别 单字分类 协议识别 动态自适应 分类器 关联性 信号量 依赖关系 优先级继承 优先级反转 仿真测试 仿真 专家系统 web信息抽取 loadrunner java
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
科研热词 推荐指数 软件测试 3 面向对象 2 统一建模语言 2 测试用例 2 驱动程序 1 面向方面编程 1 面向方面测试方法 1 错误模型 1 遗传算法 1 遗产代码 1 通用串行总线 1 进程隐藏 1 软件缺陷 1 软件工具 1 软件可靠性模型 1 软件升级 1 跟踪迁移 1 负载收集 1 负载指标 1 负载均衡 1 调度算法 1 角色模型 1 角色建模语言 1 角色 1 规格说明 1 虚拟机监视器 1 自隐藏恶意代码 1 自动构造 1 自动化测试 1 脚本技术 1 翻译 1 网络地理信息系统 1 网络入侵检测系统 1 缺陷数目 1 缺陷分类 1 缺陷分布 1 维护代价 1 维哈柯文 1 统一建模语言构件规格说明 1 粒子群优化 1 类型封装和嵌套方式 1 程序分片 1 移动终端 1 移动代理 1 硬件虚拟化技术 1 知识库 1 知网 1 矢量笔迹文本 1 瘦客户端 1 用户空间 1 特征 1 片变体测试 1
外文翻译---基于离散混沌映射的图像加密并行算法
3.转换
3.1.A-转换
在A转换中，A代表加，能被形式化的定义如下：
a+b=c(1)
加法被定义为按位与操作
转换A有三个基本性质：
(2.1)a+a=0
(2.2)a+b=b+a(2)
(2.3)(a+b)+c=a+(b+c)
在并行模式计算时，许多的PE可以同时读取或写入相同的内存区域（即临界区），
这往往会导致意想不到的执行程序。因此，有必要在关键区域使用一些并行技术管理。
2.2.并行图像的加密框架
为了满足上述要求，我们提出了一个并行图像加密的框架，这是一个四个步骤的过程：
步骤1：整个图像被划分成若干块。
步骤2：每个PE负责确定数量块。一个区域内的像素可以充分使用有效的混乱和扩散进行操作加密。
附件C：译文
基于离散混沌映射的图像加密并行算法
摘要：
最近，针对图像加密提出了多种基于混沌的算法。然而，它们都无法在并行计算环境中有效工作。在本文中，我们提出了一个并行图像加密的框架。基于此框架内，一个使用离散柯尔莫哥洛夫流映射的新算法被提出。它符合所有并行图像加密算法的要求。此外，它是安全、快速的。这些特性使得它是一个很好的基于并行计算平台上的图像加密选择。
这个框架可以非常有效的实现整个图像的扩散。但是，它是不适合在并行计算环境中运行。这是因为当前像素的处理无法启动直到前一个像素已加密。即使有多个处理元素（PE），这种计算仍然是在一个串行模式下工作。此限制了其应用平台，因为许多基于FPGA / CPLD或者数字电路的设备可以支持并行处理。随着并行计算技术的应用，加密速度可以大大加快。
用vasp计算硅的能带结构
用vasp计算硅的能带结构在最此次仿真之前，因为从未用过vasp软件，所以必须得学习此软件及一些能带的知识。
vasp是使用赝势和平面波基组，进行从头量子力学分子动力学计算的软件包。
用vasp计算硅的能带结构首先要了解晶体硅的结构，它是两个嵌套在一起的FCC布拉菲晶格，相对的位置为(a/4,a/4,a/4), 其中a=5.4A是大的正方晶格的晶格常数。
在计算中，我们采用FCC的原胞，每个原胞里有两个硅原子。
VASP计算需要以下的四个文件：INCAR（控制参数）, KPOINTS（倒空间撒点）, POSCAR（原子坐标）, POTCAR（赝势文件）为了计算能带结构，我们首先要进行一次自洽计算，得到体系正确的基态电子密度。
然后固定此电荷分布，对于选定的特殊的K点进一步进行非自洽的能带计算。
有了需要的K点的能量本征值，也就得到了我们所需要的能带。
步骤一.—自洽计算产生正确的基态电子密度：以下是用到的各个文件样本:INCAR 文件：SYSTEM = SiStartparameter for this run:NWRITE = 2; LPETIM=F write-flag & timerPREC = medium medium, high lowISTART = 0 job : 0-new 1-cont 2-samecutICHARG = 2 charge: 1-file 2-atom 10-constISPIN = 1 spin polarized calculation?Electronic Relaxation 1NELM = 90; NELMIN= 8; NELMDL= 10 # of ELM stepsEDIFF = 0.1E-03 stopping-criterion for ELMLREAL = .FALSE. real-space projectionIonic relaxationEDIFFG = 0.1E-02 stopping-criterion for IOMNSW = 0 number of steps for IOMIBRION = 2 ionic relax: 0-MD 1-quasi-New 2-CGISIF = 2 stress and relaxationPOTIM = 0.10 time-step for ionic-motionTEIN = 0.0 initial temperatureTEBEG = 0.0; TEEND = 0.0 temperature during runDOS related values:ISMEAR = 0 ; SIGMA = 0.10 broadening in eV -4-tet -1-fermi 0-gausElectronic relaxation 2 (details)Write flagsLWAVE = T write WAVECARLCHARG = T write CHGCARVASP给INCAR文件中的很多参数都设置了默认值，所以如果你对参数不熟悉，可以直接用默认的参数值。
基于小波包变换和奇异值分解的机加工表面纹理特征提取
Ｔｅ ｔ ｒ ａ ｕ ｅ Ｅｘ ｒ ｃｉ ｎ ｏ ａ ｈ ｎ ｄ Ｓ ｒ ａ ｅ Ｂａ ｅ ｎ Ｗ ａ ｅｅ ｐ ｃ ｅ ｘ ｕ ｅ Ｆｅ ｔ ｒ ｔ ａ ｔｏ ｆＭ ｃ ｉ ｅ ｕ ｆ ｃ ｓ ｄ ｏ ｖ ｌｔ ａ ｋ ｔ
Ｔｒ ｎ ｆ ｒ ｎｄ Ｓ ｎ ｕ ａ ｉｙ Ｖａ ｕ ｃ ｍ ｐ ｓｔｏ ａ ｓ ｏ ｍ ａ ｉ ｇ ｌ ｒ ｔ ｌ ｅ Ｄｅ ｏ ｏ ｉｉ ｎ
ａ ｄ ｔ ｅ ｓｎ ｕ ａ ｔ ａｕ ｅ ｏ ｏ ｉ ｏ ｒｔ ｍｅｉ ｒ ｎｒ ｄ ｃ ｄ． ｅ ｃ ａ ａ ｔｒｓｉ ａ ａ ｔｒ ｌａ ｄ ｋ ｒ ｅ ｎ ｄ ｎ ｈ ｉｇ ｌｒ ｙｖ ｌ ｅ ｄ ｃ ｍｐ ｓｔ ｎ ａ ｈ ｔ ｗｅｅ ｉ ｔｏ ｕ ｅ Ｔｈ ｈ ｒ ｃｅ ｔ ｐ ｒ ｍｅｅｓ ｋ ｎ ２ｗｅｅ ｄ ｆ ｅ ｉ ｉ ｉ ｃ ｉ ｃ ｉ ｂ ｓｄ ｏ ａ ｎ ａ ａ ｃ ｆｔｅ ｓｎ ｕ ａ ａｕ ｈ ｒ ｃｅ ｓｉ ｅ ｔｒ Ｔ ｅ ｒｌｔｏ ｓｂ ｔ ｅ ｈ ｈ ｒｃｅ ｓｉ ａａ ｔｒ ａ ｅ ｎ ｍｅ ｎ ａ ｄ ｖ ｒ ｎ ｅｏ ｉｇ ｌｒｖ ｌ ｅｃ ａ ａ ｔｒ ｔ ｖ ｃｏ ． ｈ ｅａｉｎ ｅｗｅ ｎ ｔ ｅｃ ａ ａ ｔｒ ｔ ｐ ｍｅｅ ｓ ｉ ｈ ｉ ｃ ｉ ｃ ｒ
超像素分割算法(SLIC算法)
超像素分割算法（SLIC算法）
SLIC算法的核心思想是将图像空间和颜色空间相结合，通过将像素点聚类为超像素，实现图像的分割。
算法的流程如下：
1.初始化：选择超像素数量K，并进行初始位置的选择。
一种常用的初始化方法是均匀地将图像分成K个网格，并选取每个网格的中心点作为初始位置。
2. 迭代优化：对每个超像素中心点，使用k-means算法将其周围的像素分类到该超像素。
这里的距离度量不仅包括欧氏距离，还考虑了颜色相似性和空间距离的权重。
同时，还计算了每个像素点到最近超像素中心点的距离，用于后续的超像素合并操作。
3.超像素合并：根据像素点到最近超像素中心点的距离和相邻超像素之间的相似性，进行超像素的合并操作。
这样可以将尺寸较小的超像素合并为更大的超像素，使得图像分割更加连贯。
4.迭代优化：重复步骤2和步骤3，直到达到预设的迭代次数或者收敛为止。
SLIC算法有以下特点：
1. 快速有效：SLIC算法通过使用k-means算法进行迭代聚类，使得算法具有较高的效率。
同时，由于使用了颜色和空间信息，也能够获得更好的分割效果。
2.参数少：SLIC算法只需要设置一个参数，即超像素数量K，此外，还可以根据需要设置聚类的迭代次数。
3.保持图像边界：由于考虑了颜色相似性和空间距离的权重，在进行超像素合并操作时能够较好地保持图像的边界。
4.可扩展性：SLIC算法可以很容易地扩展到多通道的图像，同时也可以用于视频超像素分割。
总的来说，SLIC算法是一种快速有效的超像素分割算法，具有较好的分割效果。
通过合适的初始化和迭代次数，可以在保持图像细节的同时实现图像的快速分割。
Acoustic Camera手册说明书
CHALLENGEResidents living in Welzow near the mining bridge were complaining about environmental noise. In order to reduce noise pollution, the acoustic sources of the bucket-wheel excavator needed to be localized. SOLUTIONThe Acoustic Camera as a mobile system allows high flexibility for outdoor measurements. Fast measurement and quick analysis enables users to easily identify sources as well as additional measurement positions of interest. With complete measurement set-up and postprocessing of the data, it takes only a few hours to completely identify the loudest sources on large machinery. The sound sources on the excavator can be precisely identified without stopping its operation. Once these sound sources are localized, they can be eliminated to reduce the effects of noise pollution.gfai tech GmbH Volmerstraße 3 12489 Berlin | Germany Ph.: +49 30 814563-750Fax: +49 30 814563-755E-Mail:****************www.gfaitech.de2D Outdoor MeasurementTHE ACOUSTIC CAMERA FOR ENVIRONMENTAL NOISE ANALYSIS AND HEAVY EQUIPMENTBENEFITS• Fast and easy set-up• No expensive machine downtime• Long distance measurement capability• Mobile system for flexible measurement locations• Advanced algorithms for precise localizationMEASUREMENT Measurement Object Microphone Array SoftwareData Acquisition Strip mining excavator Star48 AC Pro NoiseImage 4 Acoustic Photo 2D Recorder Spectral Photo Advanced Algorithms Data Recorder mcdRecThe Acoustic Camera was set up as a mobile system for full flexibility using a Star Array with 48 microphone channels. After an overview measurement from 150 meters away, the acoustic hot spots were localized. After the quick overview analysis, additional measurements were conducted closer to the sound sources for a more detailed analysis.www.gfaitech.de Page 2/2RESULTFor a reliable sound analysis, background noise was minimized by applying A-weighting to all data. In the first measurement from 150 meters distance, the main sources could be easily identified. In Fig. 1, the powerhouse and the derrick jib clearly stand out as the loudest areas.The second measurement was conducted closer to the derrick jib. As result of this measurement, the redirection point of the jib was identified as one of the loudest sources. A third measurement was made from a position on the bank with direct view to the jib. Several additional measurements were conducted from that position. A detailed analysis in the frequency domain was conducted using advanced algorithms in NoiseImage.The analysis using the HDR algorithm (High Dynamic Range) shows different sources and reflections on the ground within a dynamic of 35 dB(A). In the spectrogram (Fig. 3), the “banging” sounds are clearly visible. In order to find their location, these areas are simply marked as basis for the calculation region of the acoustic photo. The sound sources can be precisely identifiedas showninFig. 4. The broadband rattle sounds were produced by theshovel guidesimpacting the guide blockjust below the point of redirection.Fig. 1, left: powerhouse and derrick jib,right: derrick jibFig. 2direct view of the derrick jibFig. 3 Acoustic photo and spectrogram with a marked frequency range of 700 Hz - 1,1kHzFig. 4Acoustic photo and spectrogram withE-Mail:****************。
3GPP TS 36.331 V13.2.0 (2016-06)
3GPP TS 36.331 V13.2.0 (2016-06)Technical Specification3rd Generation Partnership Project;Technical Specification Group Radio Access Network;Evolved Universal Terrestrial Radio Access (E-UTRA);Radio Resource Control (RRC);Protocol specification(Release 13)The present document has been developed within the 3rd Generation Partnership Project (3GPP TM) and may be further elaborated for the purposes of 3GPP. The present document has not been subject to any approval process by the 3GPP Organizational Partners and shall not be implemented.This Specification is provided for future development work within 3GPP only. The Organizational Partners accept no liability for any use of this Specification. Specifications and reports for implementation of the 3GPP TM system should be obtained via the 3GPP Organizational Partners' Publications Offices.KeywordsUMTS, radio3GPPPostal address3GPP support office address650 Route des Lucioles - Sophia AntipolisValbonne - FRANCETel.: +33 4 92 94 42 00 Fax: +33 4 93 65 47 16InternetCopyright NotificationNo part may be reproduced except as authorized by written permission.The copyright and the foregoing restriction extend to reproduction in all media.© 2016, 3GPP Organizational Partners (ARIB, ATIS, CCSA, ETSI, TSDSI, TTA, TTC).All rights reserved.UMTS™ is a Trade Mark of ETSI registered for the benefit of its members3GPP™ is a Trade Mark of ETSI registered for the benefit of its Members and of the 3GPP Organizational PartnersLTE™ is a Trade Mark of ETSI currently being registered for the benefit of its Members and of the 3GPP Organizational Partners GSM® and the GSM logo are registered and owned by the GSM AssociationBluetooth® is a Trade Mark of the Bluetooth SIG registered for the benefit of its membersContentsForeword (18)1Scope (19)2References (19)3Definitions, symbols and abbreviations (22)3.1Definitions (22)3.2Abbreviations (24)4General (27)4.1Introduction (27)4.2Architecture (28)4.2.1UE states and state transitions including inter RAT (28)4.2.2Signalling radio bearers (29)4.3Services (30)4.3.1Services provided to upper layers (30)4.3.2Services expected from lower layers (30)4.4Functions (30)5Procedures (32)5.1General (32)5.1.1Introduction (32)5.1.2General requirements (32)5.2System information (33)5.2.1Introduction (33)5.2.1.1General (33)5.2.1.2Scheduling (34)5.2.1.2a Scheduling for NB-IoT (34)5.2.1.3System information validity and notification of changes (35)5.2.1.4Indication of ETWS notification (36)5.2.1.5Indication of CMAS notification (37)5.2.1.6Notification of EAB parameters change (37)5.2.1.7Access Barring parameters change in NB-IoT (37)5.2.2System information acquisition (38)5.2.2.1General (38)5.2.2.2Initiation (38)5.2.2.3System information required by the UE (38)5.2.2.4System information acquisition by the UE (39)5.2.2.5Essential system information missing (42)5.2.2.6Actions upon reception of the MasterInformationBlock message (42)5.2.2.7Actions upon reception of the SystemInformationBlockType1 message (42)5.2.2.8Actions upon reception of SystemInformation messages (44)5.2.2.9Actions upon reception of SystemInformationBlockType2 (44)5.2.2.10Actions upon reception of SystemInformationBlockType3 (45)5.2.2.11Actions upon reception of SystemInformationBlockType4 (45)5.2.2.12Actions upon reception of SystemInformationBlockType5 (45)5.2.2.13Actions upon reception of SystemInformationBlockType6 (45)5.2.2.14Actions upon reception of SystemInformationBlockType7 (45)5.2.2.15Actions upon reception of SystemInformationBlockType8 (45)5.2.2.16Actions upon reception of SystemInformationBlockType9 (46)5.2.2.17Actions upon reception of SystemInformationBlockType10 (46)5.2.2.18Actions upon reception of SystemInformationBlockType11 (46)5.2.2.19Actions upon reception of SystemInformationBlockType12 (47)5.2.2.20Actions upon reception of SystemInformationBlockType13 (48)5.2.2.21Actions upon reception of SystemInformationBlockType14 (48)5.2.2.22Actions upon reception of SystemInformationBlockType15 (48)5.2.2.23Actions upon reception of SystemInformationBlockType16 (48)5.2.2.24Actions upon reception of SystemInformationBlockType17 (48)5.2.2.25Actions upon reception of SystemInformationBlockType18 (48)5.2.2.26Actions upon reception of SystemInformationBlockType19 (49)5.2.3Acquisition of an SI message (49)5.2.3a Acquisition of an SI message by BL UE or UE in CE or a NB-IoT UE (50)5.3Connection control (50)5.3.1Introduction (50)5.3.1.1RRC connection control (50)5.3.1.2Security (52)5.3.1.2a RN security (53)5.3.1.3Connected mode mobility (53)5.3.1.4Connection control in NB-IoT (54)5.3.2Paging (55)5.3.2.1General (55)5.3.2.2Initiation (55)5.3.2.3Reception of the Paging message by the UE (55)5.3.3RRC connection establishment (56)5.3.3.1General (56)5.3.3.1a Conditions for establishing RRC Connection for sidelink communication/ discovery (58)5.3.3.2Initiation (59)5.3.3.3Actions related to transmission of RRCConnectionRequest message (63)5.3.3.3a Actions related to transmission of RRCConnectionResumeRequest message (64)5.3.3.4Reception of the RRCConnectionSetup by the UE (64)5.3.3.4a Reception of the RRCConnectionResume by the UE (66)5.3.3.5Cell re-selection while T300, T302, T303, T305, T306, or T308 is running (68)5.3.3.6T300 expiry (68)5.3.3.7T302, T303, T305, T306, or T308 expiry or stop (69)5.3.3.8Reception of the RRCConnectionReject by the UE (70)5.3.3.9Abortion of RRC connection establishment (71)5.3.3.10Handling of SSAC related parameters (71)5.3.3.11Access barring check (72)5.3.3.12EAB check (73)5.3.3.13Access barring check for ACDC (73)5.3.3.14Access Barring check for NB-IoT (74)5.3.4Initial security activation (75)5.3.4.1General (75)5.3.4.2Initiation (76)5.3.4.3Reception of the SecurityModeCommand by the UE (76)5.3.5RRC connection reconfiguration (77)5.3.5.1General (77)5.3.5.2Initiation (77)5.3.5.3Reception of an RRCConnectionReconfiguration not including the mobilityControlInfo by theUE (77)5.3.5.4Reception of an RRCConnectionReconfiguration including the mobilityControlInfo by the UE(handover) (79)5.3.5.5Reconfiguration failure (83)5.3.5.6T304 expiry (handover failure) (83)5.3.5.7Void (84)5.3.5.7a T307 expiry (SCG change failure) (84)5.3.5.8Radio Configuration involving full configuration option (84)5.3.6Counter check (86)5.3.6.1General (86)5.3.6.2Initiation (86)5.3.6.3Reception of the CounterCheck message by the UE (86)5.3.7RRC connection re-establishment (87)5.3.7.1General (87)5.3.7.2Initiation (87)5.3.7.3Actions following cell selection while T311 is running (88)5.3.7.4Actions related to transmission of RRCConnectionReestablishmentRequest message (89)5.3.7.5Reception of the RRCConnectionReestablishment by the UE (89)5.3.7.6T311 expiry (91)5.3.7.7T301 expiry or selected cell no longer suitable (91)5.3.7.8Reception of RRCConnectionReestablishmentReject by the UE (91)5.3.8RRC connection release (92)5.3.8.1General (92)5.3.8.2Initiation (92)5.3.8.3Reception of the RRCConnectionRelease by the UE (92)5.3.8.4T320 expiry (93)5.3.9RRC connection release requested by upper layers (93)5.3.9.1General (93)5.3.9.2Initiation (93)5.3.10Radio resource configuration (93)5.3.10.0General (93)5.3.10.1SRB addition/ modification (94)5.3.10.2DRB release (95)5.3.10.3DRB addition/ modification (95)5.3.10.3a1DC specific DRB addition or reconfiguration (96)5.3.10.3a2LWA specific DRB addition or reconfiguration (98)5.3.10.3a3LWIP specific DRB addition or reconfiguration (98)5.3.10.3a SCell release (99)5.3.10.3b SCell addition/ modification (99)5.3.10.3c PSCell addition or modification (99)5.3.10.4MAC main reconfiguration (99)5.3.10.5Semi-persistent scheduling reconfiguration (100)5.3.10.6Physical channel reconfiguration (100)5.3.10.7Radio Link Failure Timers and Constants reconfiguration (101)5.3.10.8Time domain measurement resource restriction for serving cell (101)5.3.10.9Other configuration (102)5.3.10.10SCG reconfiguration (103)5.3.10.11SCG dedicated resource configuration (104)5.3.10.12Reconfiguration SCG or split DRB by drb-ToAddModList (105)5.3.10.13Neighbour cell information reconfiguration (105)5.3.10.14Void (105)5.3.10.15Sidelink dedicated configuration (105)5.3.10.16T370 expiry (106)5.3.11Radio link failure related actions (107)5.3.11.1Detection of physical layer problems in RRC_CONNECTED (107)5.3.11.2Recovery of physical layer problems (107)5.3.11.3Detection of radio link failure (107)5.3.12UE actions upon leaving RRC_CONNECTED (109)5.3.13UE actions upon PUCCH/ SRS release request (110)5.3.14Proximity indication (110)5.3.14.1General (110)5.3.14.2Initiation (111)5.3.14.3Actions related to transmission of ProximityIndication message (111)5.3.15Void (111)5.4Inter-RAT mobility (111)5.4.1Introduction (111)5.4.2Handover to E-UTRA (112)5.4.2.1General (112)5.4.2.2Initiation (112)5.4.2.3Reception of the RRCConnectionReconfiguration by the UE (112)5.4.2.4Reconfiguration failure (114)5.4.2.5T304 expiry (handover to E-UTRA failure) (114)5.4.3Mobility from E-UTRA (114)5.4.3.1General (114)5.4.3.2Initiation (115)5.4.3.3Reception of the MobilityFromEUTRACommand by the UE (115)5.4.3.4Successful completion of the mobility from E-UTRA (116)5.4.3.5Mobility from E-UTRA failure (117)5.4.4Handover from E-UTRA preparation request (CDMA2000) (117)5.4.4.1General (117)5.4.4.2Initiation (118)5.4.4.3Reception of the HandoverFromEUTRAPreparationRequest by the UE (118)5.4.5UL handover preparation transfer (CDMA2000) (118)5.4.5.1General (118)5.4.5.2Initiation (118)5.4.5.3Actions related to transmission of the ULHandoverPreparationTransfer message (119)5.4.5.4Failure to deliver the ULHandoverPreparationTransfer message (119)5.4.6Inter-RAT cell change order to E-UTRAN (119)5.4.6.1General (119)5.4.6.2Initiation (119)5.4.6.3UE fails to complete an inter-RAT cell change order (119)5.5Measurements (120)5.5.1Introduction (120)5.5.2Measurement configuration (121)5.5.2.1General (121)5.5.2.2Measurement identity removal (122)5.5.2.2a Measurement identity autonomous removal (122)5.5.2.3Measurement identity addition/ modification (123)5.5.2.4Measurement object removal (124)5.5.2.5Measurement object addition/ modification (124)5.5.2.6Reporting configuration removal (126)5.5.2.7Reporting configuration addition/ modification (127)5.5.2.8Quantity configuration (127)5.5.2.9Measurement gap configuration (127)5.5.2.10Discovery signals measurement timing configuration (128)5.5.2.11RSSI measurement timing configuration (128)5.5.3Performing measurements (128)5.5.3.1General (128)5.5.3.2Layer 3 filtering (131)5.5.4Measurement report triggering (131)5.5.4.1General (131)5.5.4.2Event A1 (Serving becomes better than threshold) (135)5.5.4.3Event A2 (Serving becomes worse than threshold) (136)5.5.4.4Event A3 (Neighbour becomes offset better than PCell/ PSCell) (136)5.5.4.5Event A4 (Neighbour becomes better than threshold) (137)5.5.4.6Event A5 (PCell/ PSCell becomes worse than threshold1 and neighbour becomes better thanthreshold2) (138)5.5.4.6a Event A6 (Neighbour becomes offset better than SCell) (139)5.5.4.7Event B1 (Inter RAT neighbour becomes better than threshold) (139)5.5.4.8Event B2 (PCell becomes worse than threshold1 and inter RAT neighbour becomes better thanthreshold2) (140)5.5.4.9Event C1 (CSI-RS resource becomes better than threshold) (141)5.5.4.10Event C2 (CSI-RS resource becomes offset better than reference CSI-RS resource) (141)5.5.4.11Event W1 (WLAN becomes better than a threshold) (142)5.5.4.12Event W2 (All WLAN inside WLAN mobility set becomes worse than threshold1 and a WLANoutside WLAN mobility set becomes better than threshold2) (142)5.5.4.13Event W3 (All WLAN inside WLAN mobility set becomes worse than a threshold) (143)5.5.5Measurement reporting (144)5.5.6Measurement related actions (148)5.5.6.1Actions upon handover and re-establishment (148)5.5.6.2Speed dependant scaling of measurement related parameters (149)5.5.7Inter-frequency RSTD measurement indication (149)5.5.7.1General (149)5.5.7.2Initiation (150)5.5.7.3Actions related to transmission of InterFreqRSTDMeasurementIndication message (150)5.6Other (150)5.6.0General (150)5.6.1DL information transfer (151)5.6.1.1General (151)5.6.1.2Initiation (151)5.6.1.3Reception of the DLInformationTransfer by the UE (151)5.6.2UL information transfer (151)5.6.2.1General (151)5.6.2.2Initiation (151)5.6.2.3Actions related to transmission of ULInformationTransfer message (152)5.6.2.4Failure to deliver ULInformationTransfer message (152)5.6.3UE capability transfer (152)5.6.3.1General (152)5.6.3.2Initiation (153)5.6.3.3Reception of the UECapabilityEnquiry by the UE (153)5.6.4CSFB to 1x Parameter transfer (157)5.6.4.1General (157)5.6.4.2Initiation (157)5.6.4.3Actions related to transmission of CSFBParametersRequestCDMA2000 message (157)5.6.4.4Reception of the CSFBParametersResponseCDMA2000 message (157)5.6.5UE Information (158)5.6.5.1General (158)5.6.5.2Initiation (158)5.6.5.3Reception of the UEInformationRequest message (158)5.6.6 Logged Measurement Configuration (159)5.6.6.1General (159)5.6.6.2Initiation (160)5.6.6.3Reception of the LoggedMeasurementConfiguration by the UE (160)5.6.6.4T330 expiry (160)5.6.7 Release of Logged Measurement Configuration (160)5.6.7.1General (160)5.6.7.2Initiation (160)5.6.8 Measurements logging (161)5.6.8.1General (161)5.6.8.2Initiation (161)5.6.9In-device coexistence indication (163)5.6.9.1General (163)5.6.9.2Initiation (164)5.6.9.3Actions related to transmission of InDeviceCoexIndication message (164)5.6.10UE Assistance Information (165)5.6.10.1General (165)5.6.10.2Initiation (166)5.6.10.3Actions related to transmission of UEAssistanceInformation message (166)5.6.11 Mobility history information (166)5.6.11.1General (166)5.6.11.2Initiation (166)5.6.12RAN-assisted WLAN interworking (167)5.6.12.1General (167)5.6.12.2Dedicated WLAN offload configuration (167)5.6.12.3WLAN offload RAN evaluation (167)5.6.12.4T350 expiry or stop (167)5.6.12.5Cell selection/ re-selection while T350 is running (168)5.6.13SCG failure information (168)5.6.13.1General (168)5.6.13.2Initiation (168)5.6.13.3Actions related to transmission of SCGFailureInformation message (168)5.6.14LTE-WLAN Aggregation (169)5.6.14.1Introduction (169)5.6.14.2Reception of LWA configuration (169)5.6.14.3Release of LWA configuration (170)5.6.15WLAN connection management (170)5.6.15.1Introduction (170)5.6.15.2WLAN connection status reporting (170)5.6.15.2.1General (170)5.6.15.2.2Initiation (171)5.6.15.2.3Actions related to transmission of WLANConnectionStatusReport message (171)5.6.15.3T351 Expiry (WLAN connection attempt timeout) (171)5.6.15.4WLAN status monitoring (171)5.6.16RAN controlled LTE-WLAN interworking (172)5.6.16.1General (172)5.6.16.2WLAN traffic steering command (172)5.6.17LTE-WLAN aggregation with IPsec tunnel (173)5.6.17.1General (173)5.7Generic error handling (174)5.7.1General (174)5.7.2ASN.1 violation or encoding error (174)5.7.3Field set to a not comprehended value (174)5.7.4Mandatory field missing (174)5.7.5Not comprehended field (176)5.8MBMS (176)5.8.1Introduction (176)5.8.1.1General (176)5.8.1.2Scheduling (176)5.8.1.3MCCH information validity and notification of changes (176)5.8.2MCCH information acquisition (178)5.8.2.1General (178)5.8.2.2Initiation (178)5.8.2.3MCCH information acquisition by the UE (178)5.8.2.4Actions upon reception of the MBSFNAreaConfiguration message (178)5.8.2.5Actions upon reception of the MBMSCountingRequest message (179)5.8.3MBMS PTM radio bearer configuration (179)5.8.3.1General (179)5.8.3.2Initiation (179)5.8.3.3MRB establishment (179)5.8.3.4MRB release (179)5.8.4MBMS Counting Procedure (179)5.8.4.1General (179)5.8.4.2Initiation (180)5.8.4.3Reception of the MBMSCountingRequest message by the UE (180)5.8.5MBMS interest indication (181)5.8.5.1General (181)5.8.5.2Initiation (181)5.8.5.3Determine MBMS frequencies of interest (182)5.8.5.4Actions related to transmission of MBMSInterestIndication message (183)5.8a SC-PTM (183)5.8a.1Introduction (183)5.8a.1.1General (183)5.8a.1.2SC-MCCH scheduling (183)5.8a.1.3SC-MCCH information validity and notification of changes (183)5.8a.1.4Procedures (184)5.8a.2SC-MCCH information acquisition (184)5.8a.2.1General (184)5.8a.2.2Initiation (184)5.8a.2.3SC-MCCH information acquisition by the UE (184)5.8a.2.4Actions upon reception of the SCPTMConfiguration message (185)5.8a.3SC-PTM radio bearer configuration (185)5.8a.3.1General (185)5.8a.3.2Initiation (185)5.8a.3.3SC-MRB establishment (185)5.8a.3.4SC-MRB release (185)5.9RN procedures (186)5.9.1RN reconfiguration (186)5.9.1.1General (186)5.9.1.2Initiation (186)5.9.1.3Reception of the RNReconfiguration by the RN (186)5.10Sidelink (186)5.10.1Introduction (186)5.10.1a Conditions for sidelink communication operation (187)5.10.2Sidelink UE information (188)5.10.2.1General (188)5.10.2.2Initiation (189)5.10.2.3Actions related to transmission of SidelinkUEInformation message (193)5.10.3Sidelink communication monitoring (195)5.10.6Sidelink discovery announcement (198)5.10.6a Sidelink discovery announcement pool selection (201)5.10.6b Sidelink discovery announcement reference carrier selection (201)5.10.7Sidelink synchronisation information transmission (202)5.10.7.1General (202)5.10.7.2Initiation (203)5.10.7.3Transmission of SLSS (204)5.10.7.4Transmission of MasterInformationBlock-SL message (205)5.10.7.5Void (206)5.10.8Sidelink synchronisation reference (206)5.10.8.1General (206)5.10.8.2Selection and reselection of synchronisation reference UE (SyncRef UE) (206)5.10.9Sidelink common control information (207)5.10.9.1General (207)5.10.9.2Actions related to reception of MasterInformationBlock-SL message (207)5.10.10Sidelink relay UE operation (207)5.10.10.1General (207)5.10.10.2AS-conditions for relay related sidelink communication transmission by sidelink relay UE (207)5.10.10.3AS-conditions for relay PS related sidelink discovery transmission by sidelink relay UE (208)5.10.10.4Sidelink relay UE threshold conditions (208)5.10.11Sidelink remote UE operation (208)5.10.11.1General (208)5.10.11.2AS-conditions for relay related sidelink communication transmission by sidelink remote UE (208)5.10.11.3AS-conditions for relay PS related sidelink discovery transmission by sidelink remote UE (209)5.10.11.4Selection and reselection of sidelink relay UE (209)5.10.11.5Sidelink remote UE threshold conditions (210)6Protocol data units, formats and parameters (tabular & ASN.1) (210)6.1General (210)6.2RRC messages (212)6.2.1General message structure (212)–EUTRA-RRC-Definitions (212)–BCCH-BCH-Message (212)–BCCH-DL-SCH-Message (212)–BCCH-DL-SCH-Message-BR (213)–MCCH-Message (213)–PCCH-Message (213)–DL-CCCH-Message (214)–DL-DCCH-Message (214)–UL-CCCH-Message (214)–UL-DCCH-Message (215)–SC-MCCH-Message (215)6.2.2Message definitions (216)–CounterCheck (216)–CounterCheckResponse (217)–CSFBParametersRequestCDMA2000 (217)–CSFBParametersResponseCDMA2000 (218)–DLInformationTransfer (218)–HandoverFromEUTRAPreparationRequest (CDMA2000) (219)–InDeviceCoexIndication (220)–InterFreqRSTDMeasurementIndication (222)–LoggedMeasurementConfiguration (223)–MasterInformationBlock (225)–MBMSCountingRequest (226)–MBMSCountingResponse (226)–MBMSInterestIndication (227)–MBSFNAreaConfiguration (228)–MeasurementReport (228)–MobilityFromEUTRACommand (229)–Paging (232)–ProximityIndication (233)–RNReconfiguration (234)–RNReconfigurationComplete (234)–RRCConnectionReconfiguration (235)–RRCConnectionReconfigurationComplete (240)–RRCConnectionReestablishment (241)–RRCConnectionReestablishmentComplete (241)–RRCConnectionReestablishmentReject (242)–RRCConnectionReestablishmentRequest (243)–RRCConnectionReject (243)–RRCConnectionRelease (244)–RRCConnectionResume (248)–RRCConnectionResumeComplete (249)–RRCConnectionResumeRequest (250)–RRCConnectionRequest (250)–RRCConnectionSetup (251)–RRCConnectionSetupComplete (252)–SCGFailureInformation (253)–SCPTMConfiguration (254)–SecurityModeCommand (255)–SecurityModeComplete (255)–SecurityModeFailure (256)–SidelinkUEInformation (256)–SystemInformation (258)–SystemInformationBlockType1 (259)–UEAssistanceInformation (264)–UECapabilityEnquiry (265)–UECapabilityInformation (266)–UEInformationRequest (267)–UEInformationResponse (267)–ULHandoverPreparationTransfer (CDMA2000) (273)–ULInformationTransfer (274)–WLANConnectionStatusReport (274)6.3RRC information elements (275)6.3.1System information blocks (275)–SystemInformationBlockType2 (275)–SystemInformationBlockType3 (279)–SystemInformationBlockType4 (282)–SystemInformationBlockType5 (283)–SystemInformationBlockType6 (287)–SystemInformationBlockType7 (289)–SystemInformationBlockType8 (290)–SystemInformationBlockType9 (295)–SystemInformationBlockType10 (295)–SystemInformationBlockType11 (296)–SystemInformationBlockType12 (297)–SystemInformationBlockType13 (297)–SystemInformationBlockType14 (298)–SystemInformationBlockType15 (298)–SystemInformationBlockType16 (299)–SystemInformationBlockType17 (300)–SystemInformationBlockType18 (301)–SystemInformationBlockType19 (301)–SystemInformationBlockType20 (304)6.3.2Radio resource control information elements (304)–AntennaInfo (304)–AntennaInfoUL (306)–CQI-ReportConfig (307)–CQI-ReportPeriodicProcExtId (314)–CrossCarrierSchedulingConfig (314)–CSI-IM-Config (315)–CSI-IM-ConfigId (315)–CSI-RS-Config (317)–CSI-RS-ConfigEMIMO (318)–CSI-RS-ConfigNZP (319)–CSI-RS-ConfigNZPId (320)–CSI-RS-ConfigZP (321)–CSI-RS-ConfigZPId (321)–DMRS-Config (321)–DRB-Identity (322)–EPDCCH-Config (322)–EIMTA-MainConfig (324)–LogicalChannelConfig (325)–LWA-Configuration (326)–LWIP-Configuration (326)–RCLWI-Configuration (327)–MAC-MainConfig (327)–P-C-AndCBSR (332)–PDCCH-ConfigSCell (333)–PDCP-Config (334)–PDSCH-Config (337)–PDSCH-RE-MappingQCL-ConfigId (339)–PHICH-Config (339)–PhysicalConfigDedicated (339)–P-Max (344)–PRACH-Config (344)–PresenceAntennaPort1 (346)–PUCCH-Config (347)–PUSCH-Config (351)–RACH-ConfigCommon (355)–RACH-ConfigDedicated (357)–RadioResourceConfigCommon (358)–RadioResourceConfigDedicated (362)–RLC-Config (367)–RLF-TimersAndConstants (369)–RN-SubframeConfig (370)–SchedulingRequestConfig (371)–SoundingRS-UL-Config (372)–SPS-Config (375)–TDD-Config (376)–TimeAlignmentTimer (377)–TPC-PDCCH-Config (377)–TunnelConfigLWIP (378)–UplinkPowerControl (379)–WLAN-Id-List (382)–WLAN-MobilityConfig (382)6.3.3Security control information elements (382)–NextHopChainingCount (382)–SecurityAlgorithmConfig (383)–ShortMAC-I (383)6.3.4Mobility control information elements (383)–AdditionalSpectrumEmission (383)–ARFCN-ValueCDMA2000 (383)–ARFCN-ValueEUTRA (384)–ARFCN-ValueGERAN (384)–ARFCN-ValueUTRA (384)–BandclassCDMA2000 (384)–BandIndicatorGERAN (385)–CarrierFreqCDMA2000 (385)–CarrierFreqGERAN (385)–CellIndexList (387)–CellReselectionPriority (387)–CellSelectionInfoCE (387)–CellReselectionSubPriority (388)–CSFB-RegistrationParam1XRTT (388)–CellGlobalIdEUTRA (389)–CellGlobalIdUTRA (389)–CellGlobalIdGERAN (390)–CellGlobalIdCDMA2000 (390)–CellSelectionInfoNFreq (391)–CSG-Identity (391)–FreqBandIndicator (391)–MobilityControlInfo (391)–MobilityParametersCDMA2000 (1xRTT) (393)–MobilityStateParameters (394)–MultiBandInfoList (394)–NS-PmaxList (394)–PhysCellId (395)–PhysCellIdRange (395)–PhysCellIdRangeUTRA-FDDList (395)–PhysCellIdCDMA2000 (396)–PhysCellIdGERAN (396)–PhysCellIdUTRA-FDD (396)–PhysCellIdUTRA-TDD (396)–PLMN-Identity (397)–PLMN-IdentityList3 (397)–PreRegistrationInfoHRPD (397)–Q-QualMin (398)–Q-RxLevMin (398)–Q-OffsetRange (398)–Q-OffsetRangeInterRAT (399)–ReselectionThreshold (399)–ReselectionThresholdQ (399)–SCellIndex (399)–ServCellIndex (400)–SpeedStateScaleFactors (400)–SystemInfoListGERAN (400)–SystemTimeInfoCDMA2000 (401)–TrackingAreaCode (401)–T-Reselection (402)–T-ReselectionEUTRA-CE (402)6.3.5Measurement information elements (402)–AllowedMeasBandwidth (402)–CSI-RSRP-Range (402)–Hysteresis (402)–LocationInfo (403)–MBSFN-RSRQ-Range (403)–MeasConfig (404)–MeasDS-Config (405)–MeasGapConfig (406)–MeasId (407)–MeasIdToAddModList (407)–MeasObjectCDMA2000 (408)–MeasObjectEUTRA (408)–MeasObjectGERAN (412)–MeasObjectId (412)–MeasObjectToAddModList (412)–MeasObjectUTRA (413)–ReportConfigEUTRA (422)–ReportConfigId (425)–ReportConfigInterRAT (425)–ReportConfigToAddModList (428)–ReportInterval (429)–RSRP-Range (429)–RSRQ-Range (430)–RSRQ-Type (430)–RS-SINR-Range (430)–RSSI-Range-r13 (431)–TimeToTrigger (431)–UL-DelayConfig (431)–WLAN-CarrierInfo (431)–WLAN-RSSI-Range (432)–WLAN-Status (432)6.3.6Other information elements (433)–AbsoluteTimeInfo (433)–AreaConfiguration (433)–C-RNTI (433)–DedicatedInfoCDMA2000 (434)–DedicatedInfoNAS (434)–FilterCoefficient (434)–LoggingDuration (434)–LoggingInterval (435)–MeasSubframePattern (435)–MMEC (435)–NeighCellConfig (435)–OtherConfig (436)–RAND-CDMA2000 (1xRTT) (437)–RAT-Type (437)–ResumeIdentity (437)–RRC-TransactionIdentifier (438)–S-TMSI (438)–TraceReference (438)–UE-CapabilityRAT-ContainerList (438)–UE-EUTRA-Capability (439)–UE-RadioPagingInfo (469)–UE-TimersAndConstants (469)–VisitedCellInfoList (470)–WLAN-OffloadConfig (470)6.3.7MBMS information elements (472)–MBMS-NotificationConfig (472)–MBMS-ServiceList (473)–MBSFN-AreaId (473)–MBSFN-AreaInfoList (473)–MBSFN-SubframeConfig (474)–PMCH-InfoList (475)6.3.7a SC-PTM information elements (476)–SC-MTCH-InfoList (476)–SCPTM-NeighbourCellList (478)6.3.8Sidelink information elements (478)–SL-CommConfig (478)–SL-CommResourcePool (479)–SL-CP-Len (480)–SL-DiscConfig (481)–SL-DiscResourcePool (483)–SL-DiscTxPowerInfo (485)–SL-GapConfig (485)。