(完整版)整体法和隔离法典型例题
整体法与隔离法
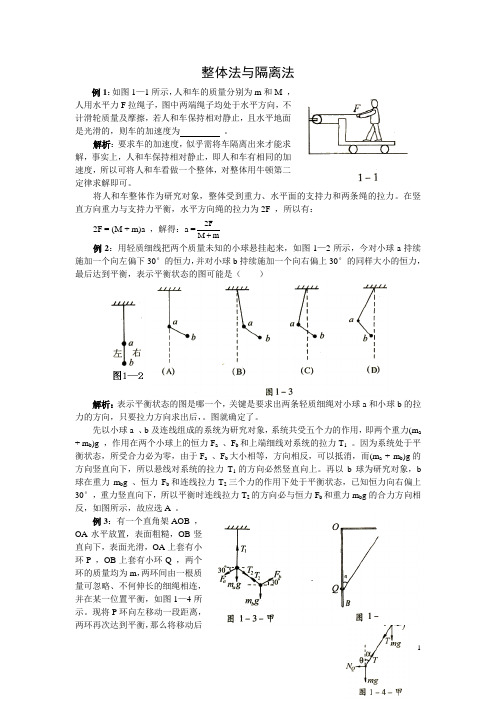
整体法与隔离法例1:如图1—1所示,人和车的质量分别为m 和M ,人用水平力F 拉绳子,图中两端绳子均处于水平方向,不计滑轮质量及摩擦,若人和车保持相对静止,且水平地面是光滑的,则车的加速度为 。
解析:要求车的加速度,似乎需将车隔离出来才能求解,事实上,人和车保持相对静止,即人和车有相同的加速度,所以可将人和车看做一个整体,对整体用牛顿第二定律求解即可。
将人和车整体作为研究对象,整体受到重力、水平面的支持力和两条绳的拉力。
在竖直方向重力与支持力平衡,水平方向绳的拉力为2F ,所以有:2F = (M + m)a ,解得:a =2F M m例2:用轻质细线把两个质量未知的小球悬挂起来,如图1—2所示,今对小球a 持续施加一个向左偏下30°的恒力,并对小球b 持续施加一个向右偏上30°的同样大小的恒力,最后达到平衡,表示平衡状态的图可能是( )解析:表示平衡状态的图是哪一个,关键是要求出两条轻质细绳对小球a 和小球b 的拉力的方向,只要拉力方向求出后,。
图就确定了。
先以小球a 、b 及连线组成的系统为研究对象,系统共受五个力的作用,即两个重力(m a + m b )g ,作用在两个小球上的恒力F a 、F b 和上端细线对系统的拉力T 1 。
因为系统处于平衡状态,所受合力必为零,由于F a 、F b 大小相等,方向相反,可以抵消,而(m a + m b )g 的方向竖直向下,所以悬线对系统的拉力T 1的方向必然竖直向上。
再以b 球为研究对象,b 球在重力m b g 、恒力F b 和连线拉力T 2三个力的作用下处于平衡状态,已知恒力向右偏上30°,重力竖直向下,所以平衡时连线拉力T 2的方向必与恒力F b 和重力m b g 的合力方向相反,如图所示,故应选A 。
例3:有一个直角架AOB ,OA 水平放置,表面粗糙,OB 竖直向下,表面光滑,OA 上套有小环P ,OB 上套有小环Q ,两个环的质量均为m ,两环间由一根质量可忽略、不何伸长的细绳相连,并在某一位置平衡,如图1—4所示。
(完整版)整体法和隔离法专题(带答案)
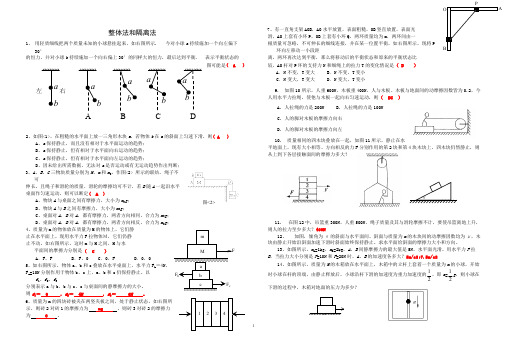
n e i n g整体法和隔离法1、用轻质细线把两个质量未知的小球悬挂起来,如右图所示.今对小球a 持续施加一个向左偏下30°的恒力,并对小球b 持续施加一个向右偏上30°的同样大的恒力,最后达到平衡. 表示平衡状态的图可能是( A )2、如图<1>,在粗糙的水平面上放一三角形木块a ,若物体b 在a 的斜面上匀速下滑,则( A )A 、a 保持静止,而且没有相对于水平面运动的趋势;B 、a 保持静止,但有相对于水平面向右运动的趋势;C 、a 保持静止,但有相对于水平面向左运动的趋势;D 、因未给出所需数据,无法对a 是否运动或有无运动趋势作出判断;3、A 、B 、C 三物块质量分别为M 、m 和m 0,作图<2> 所示的联结. 绳子不可伸长,且绳子和滑轮的质量、滑轮的摩擦均可不计. 若B 随A 一起沿水平桌面作匀速运动,则可以断定( A )A 、物块A 与桌面之间有摩擦力,大小为m 0g ;B 、物块A 与B 之间有摩擦力,大小为m 0g ;C 、桌面对A ,B 对A ,都有摩擦力,两者方向相同,合力为m 0g ;D 、桌面对A ,B 对A ,都有摩擦力,两者方向相反,合力为m 0g ;4、质量为m 的物体放在质量为M 的物体上,它们静止在水平面上。
现用水平力F 拉物体M,它们仍静止不动。
如右图所示,这时m 与M 之间,M 与水平面间的摩擦力分别是( C ) A .F ,F B .F ,0 C .0,F D .0,05、如右图所示,物体a 、b 和c 叠放在水平桌面上,水平力F b =4N 、F c =10N 分别作用于物体b 、c 上,a 、b 和c 仍保持静止。
以f 1、f 2、f 3分别表示a 与b 、b 与c 、c 与桌面间的静摩擦力的大小。
则f 1= 0 ,f 2= 4N ,f 3= 6N 。
6、质量为m 的四块砖被夹在两竖夹板之间,处于静止状态,如右图所示,则砖2对砖1的摩擦力为 mg 。
牛顿运动定律 典型例题 参考答案

牛顿运动定律典型例题参考答案一、连接体问题(整体法与隔离法):1.二体连接问题例题1:F=(M+m)g F=(M+m)g F=(M+m)g F=(M+m)g例题2:例题3:2.多体连接问题:例题4:例题5:二、 超失重问题:例题1:BC例题2:A 例题3:C 例题4:A例题5:D三、 等环境问题(力的质量分配原则):例题1.例题2.D四、 临界值问题: 例题1. 解析:(1)ma sin N cos T =α-αmg cos N sin T =α+α当g 31a =时,N=68.4(N ) T=77.3(N ) (2) 若N=0,则有'm a cos T =αm g sin T =α )s /m (17g 3gctg 'a ==α=例题2.五、 瞬时值问题:例题1:解析:分析物体在某一时刻的瞬时加速度,关键是分析瞬时前后的受力情况及运动状态,再由牛顿第二定律求出瞬时加速度。
此类问题应注意两种模型的建立。
先分析剪断细线前两个物体的受力如图2,据平衡条件求出绳或弹簧上的弹力。
可知,F mg 2=,F F mg mg 122=+='。
剪断细线后再分析两个物体的受力示意图,如图2,绳中的弹力F 1立即消失,而弹簧的弹力不变,找出合外力据牛顿第二定律求出瞬时加速度,则图2剪断后m 1的加速度大小为2g ,方向向下,而m 2的加速度为零。
例题2:C例题3,D 例题4: (a=gsinθ ,a=gtanθ ) 例题5、BD 六、 分离问题:例题1:例题2:设物体与平板一起向下运动的距离为x 时,物体受重力mg ,弹簧的弹力F=kx 和平板的支持力N 作用。
据牛顿第二定律有:mg-kx-N=ma 得N=mg-kx-ma ,当N=0时,物体与平板分离,所以此时ka g m x )(-= 因为221at x =,所以kaa g m t )(2-= 例题3:七、 相对滑动问题:例题1:例题2:BC 例题3:ABC例题4:例题5:例题6:例题7:八、 传送带问题:例题1:D例题2:解析: 物体放上传送带以后,开始一段时间,其运动加速度2m/s 10cos sin =+=m mg mg a θμθ。
物理整体法隔离法解决物理试题题20套(带答案)

(M+2m)g, C 错误.
D、B 与斜面体间的正压力 N′=2mgcosθ,对 B 分析,根据共点力平衡有
F=mgsinθ+μmgcosθ+f′,则 B 与斜面间的动摩擦因数
f N
F -mgsin mgcos 2mgcos
,故
D
正确.
故选 BD
11.如图所示,电源电动势为 E,内阻为 r,电压表 V1、V2、V3 为理想电压表,R1、R3 为定 值电阻,R2 为热敏电阻(其阻值随温度升高而减小),C 为电容器,闭合开关 S,电容器 C 中 的微粒 A 恰好静止.当室温从 25 ℃升高到 35 ℃的过程中,流过电源的电流变化量是 ΔI, 三只电压表的示数变化量是 ΔU1、ΔU2 和 ΔU3.则在此过程中( )
A.大小为零 C.方向水平向左 【答案】A 【解析】 【详解】 对斜面体进行受力分析如下图所示:
B.方向水平向右 D.无法判断大小和方向
开始做匀速下滑知压力与摩擦力在水平方向上的分力相等,当用力向下推此物体,使物体
加速下滑,虽然压力和摩擦力发生了变化,但摩擦力 f 始终等于 FN 。知两力在水平方向
滑动,小灯泡的阻值可视为不变,下列说法正确的是( )
A.小灯泡 L1 变暗,V1 表的示数变小,V2 表的示数变大 B.小灯泡 L1 变亮,V1 表的示数变大,V2 表的示数变小 C.小灯泡 L2 变暗,V1 表的示数变小,V2 表的示数变大 D.小灯泡 L2 变亮,V1 表的示数变大,V2 表的示数变大
ma Fb ,F
为负值,b
对a
为推力;若
mb Fa ma Fb ,F 为正值,则 b 对 a 为拉力;若 mb Fa ma Fb ,F 为零.故 C 正确,A、
B、D 错误.故选 C.
专题整体法和隔离法的应用

a=MFAA=MFBB=9-3 2t=3+6 2t 故分离前的运动时间为 t=2.5 s,则分离时的速度 v=at≈3.3 m/s. (3)位移 s=12at2≈4.2 m. 答案:(1)初速度为零的匀加速直线运动 (2)3.3 m/s,43 m/s2 (3)4.2 m
变式训练3-1 如右图所示,在劲度系数为k旳弹簧 下端挂有质量为m旳物体,开始用托盘托住物体,使弹簧 保持原长,然后托盘以加速度a匀加速下降(a<g),求经过 多长时间托盘与物体分离.
解析:当托盘以加速度a匀加速下降时,托盘与物体 具有相同旳加速度,在下降过程中,物体所受旳弹力逐渐 增大,支持力逐渐减小,当托盘与物体分离时,支持力为 零.设弹簧旳伸长量为x,以物体为研究对象,根据牛顿 第二定律,有:
(2)设分离前两物体之间的正压力为 F′ 由 a=9-2Mt-A F′=F′+M3B+2t,得 t=0,F′=5 N 由于 FA 随 t 的增加而减小,FB 随 t 的增加而增加,可以 断定,分离前随着时间的增加,两物体之间的正压力 F′逐 渐减小,分离时两者之间的正压力 F′为零. 分离时两者的速度和加速度相等,加速度仍为 a=43 m/s2. 此时两者之间的作用力为零,由加速度相等得:
变式训练1-1 质量分别为m1、m2、m3、m4旳四个 物体彼此用轻绳连接,放在光滑旳桌面上,拉力F1、F2分 别水平地加在m1、m4上,如图所示.求物体系旳加速度a 和连接m2、m3轻绳旳张力T.(F1>F2)
解析:由于物体系具有相同的向左加速度,所以可把 它们当成一个整体(或看作一个质点),整个系统在水平方向 受到外力F1、F2,有:
【解析】 当小球和斜面接触,但两者之间刚好无压 力时,设滑块旳加速度为a′,此时小球受力如图所示,由 水平和竖直方向状态可列方程分别为:
高中物理整体法隔离法解决物理试题题20套(带答案)

高中物理整体法隔离法解决物理试题题20套(带答案)一、整体法隔离法解决物理试题1.两倾斜的平行杆上分别套着a 、b 两相同圆环,两环上均用细线悬吊着相同的小球,如图所示。
当它们都沿杆向下滑动,各自的环与小球保持相对静止时,a 的悬线与杆垂直,b 的悬线沿竖直方向,下列说法正确的是A .a 环与杆有摩擦力B .d 球处于失重状态C .杆对a 、b 环的弹力大小相等D .细线对c 、d 球的弹力大小可能相等 【答案】C 【解析】 【详解】对c 球单独进行受力分析,受力分析图如下,c 球受重力和绳的拉力F ,物体沿杆滑动,因此在垂直于杆的方向加速度和速度都为零,由力的合成及牛顿第二定律可知物体合力1=mg sin a=ma a=gina F ⇒,因a 和c 球相对静止,因此c 球的加速度也为gsina ,将a 和c 球以及绳看成一个整体,在只受重力和支持力的情况下加速度为gsina ,因此a 球和杆的摩擦力为零,故A 错误;对球d 单独进行受力分离,只受重力和竖直方向的拉力,因此球d 的加速度为零,因为b 和d 相对静止,因此b 的加速度也为零,故d 球处于平衡状态,加速度为零,不是失重状态,故B 错;细线对c 球的拉力cos c T mg a =,对d 球的拉力d T mg =,因此不相等,故D 错误;对a 和c 整体受力分析有()cos na a c F m m g a =+,对b 和d 整体受力分析()cos nb b d F m m g a =+,因a 和b 一样的环,b 和d 一样的球,因此受力相等,故C 正确。
2.如图所示,R 0为热敏电阻(温度降低,其电阻增大),D 为理想二极管(正向电阻为零,反向电阻无穷大),平行板电容器中央有一带电液滴刚好静止,M 点接地,开关S 闭合.下列各项单独操作时可使带电液滴向上运动的是( )A .滑动变阻器R 的滑动触头P 向上移动B .将热敏电阻R 0的温度降低C .开关S 断开D .电容器的上极板向上移动 【答案】C 【解析】 【详解】A.当滑动变阻器的滑动触头P 向上移动时,滑动变阻器接入电路的电阻减小,则总电流增大,内电压及R 0两端的电压增大,则路端电压和滑动变阻器两端的电压都减小,由于二极管具有单向导电性,电荷不会向右流出,所以电容器两端的电势差不变,故A 项不合题意;B.当热敏电阻温度降低时,其阻值增大,则由闭合电路欧姆定律可知,滑动变阻器两端的电压减小,液滴仍然静止,故B 项不合题意;C.开关S 断开时,电容器直接接在电源两端,电容器两端电压增大,则液滴向上运动,故C 项符合题意;D.若使电容器的上极板向上移动,即d 增大,则电容器电容C 减小,由于二极管具有单向导电性,电荷不会向右流出,所以电容器两端的电势差增大,由于Q U C =,4S C kdεπ=,U E d =,所以4kQE Sπε=,由于极板上的电荷量不变,而场强E 与极板之间的距离无关,所以场强E 不变,液滴仍然静止,故D 项不合题意. 3.a 、b 两物体的质量分别为m 1、m 2,由轻质弹簧相连。
整体法与隔离法例题

变式4:有一个直角支架AOB,AO水平放置,表面粗糙,OB竖直向下,表面光滑,AO上套有小环P,OB上套有小环Q,两环质量均为m,两环间有一根质量可忽略,不可伸长的细绳相连,并在某一位置平衡,如图3所示,现将P环向左移一小段距离,两环再次达到平衡,那么将移动后的平衡状态和原来的平衡状态相比较,AO杆对P环的支持力 和 如图所示,光滑的金属球B放在纵截面为等腰三角形的物体A与竖直墙壁之间,恰好匀速下滑,已知物体A的重力是B的重力的6倍,不计球跟斜面和墙壁之间摩擦,问:物体A与水平面之间的动摩擦因数μ是多少?
( )
2、如图所示,质量为M的直角三棱柱A放在水平地面上,三棱柱的斜面是光滑的,且斜面倾角为θ。质量为m的光滑球放在三棱柱和光滑竖直墙壁之间,A和B都处于静止状态,求地面对三棱柱支持力和摩擦力各为多少?
(1)运动过程中轻绳与水平方向夹角θ;
(2)木块与水平杆间的动摩擦因数μ.
变式6:如图所示,一个底面粗糙,质量为m的斜面体静止在水平地面上,斜面体的斜面部分是光滑的,倾角为30°。现用一端固定的轻绳系一质量也为m的小球,小球静止时轻绳与斜面的夹角也是30°。试求:⑴当斜面体静止时绳的拉力大小?⑵若地面对斜面体的最大静摩擦力等于地面对斜面体支持力的k倍,为了使整个系统始终保持静止状态,k值必须满足什么条件?
A. 不变, 变大;
B. 不变, 变小;
C. 变大, 变大;
D. 变大, 变小。
变式5:如图所示,用轻质绝缘细线把两个带等量异种电荷的小球悬挂起来.今将该系统移至与水平方向成30”角斜向右上方向的匀强电场中,达到平衡时,表示平衡状态的图可能是( )
整体法与隔离法练习

整体法与隔离法的应用通常在分析外力对系统的作用时,用整体法;在分析系统内各物体(各部分)间相互作用时,用隔离法.解题中应遵循“先整体、后隔离”的原则。
【例1】 在粗糙水平面上有一个三角形木块a ,在它的两个粗糙斜面上分别放有质量为m1和m2的两个木块b 和c ,如图所示,已知m1>m2,三木块均处于静止,则粗糙地面对于三角形木块A .有摩擦力作用,摩擦力的方向水平向右B .有摩擦力作用,摩擦力的方向水平向左C .有摩擦力作用,但摩擦力的方向不能确定D .没有摩擦力的作用【解析】由于三物体均静止,故可将三物体视为一个物体,它静止于水平面上,必无摩擦力作用,故选D .【例2】如图所示,设A 重10N ,B 重20N ,A 、B 间的动摩擦因数为0.1,B 与地面的摩擦因数为0.2.问:(1)至少对B 向左施多大的力,才能使A 、B 发生相对滑动?(2)若A 、B 间μ1=0.4,B 与地间μ2=0.l ,则F 多大才能产生相对滑动?【解析】(1)设A 、B 恰好滑动,则B 对地也要恰好滑动,选A 、B为研究对象,受力如图,由平衡条件得:F=f B +2T 选A 为研究对象,由平衡条件有T=f A f A =0.1×10=1N f B =0.2×30=6N F=8N 。
(2)同理F=11N 。
【3】如图所示,重为8N 的球静止在与水平面成370角的光滑斜面上,并通过定滑轮与重4N 的物体A 相连,光滑挡板与水平而垂直,不计滑轮的摩擦,绳子的质量,求斜面和挡板所受的压力(sin370=0.6)。
【解析】分别隔离物体A 、球,并进行受力分析,如图所示:由平衡条件可得: T=4N Tsin370+N 2cos370=8N 2sin370=N 1+Tcos370得 N 1=1N N 2=7N 。
【4】如图所示,光滑的金属球B 放在纵截面为等边三角形的物体A 与坚直墙之间,恰好匀速下滑,已知物体A 的重力是B 重力的6倍,不计球跟斜面和墙之间的摩擦,问:物体A 与水平面之间的动摩擦因数μ是多少?【解析】首先以B 为研究对象,进行受力分析如图由平衡条件可得: N 2=m B gcot300 ①再以A 、B 为系统为研究对象.受力分析如图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
匀变速直线运动
难点1.概念、规律、推论之间的联系与区别
(1)一个重要概念:加速度0
t v v v a t t
-∆==
∆ (2)三个重要规律: ①速度-时间规律:0t v v at =+
②位移-时间规律:201
2
x v t at =+
③速度-位移规律:22
2t v v ax -= (3)三个重要推论:
①相邻相等时间内的位移差是定值,即:2x aT ∆= ②中间时刻的瞬时速度等于生程的平均速度,即:02
2
t
t v v v +=
③中间位置的瞬时速度等于初速度与末速度的方均根值,即:2
x v =(4)五个二级结论(仅适用于初速度为零的匀变速直线运动,请注意推导过程) ①第1s 、第2s 、…第ns 的速度之比
12::
:1:2:
:n v v v n =
②前1s 、前2s 、…前ns 的位移之比
22212::
:1:2:
:n x x x n =
③第1s 、第2s 、…第ns 的位移之比
::
:1:3:
:(21)N x x x n I =-
④前1m 、前2m 、…前nm 所用时间之比
12:::1:2:
:n t t t n =
⑤第1m 、第2m 、…第nm 所用时间之比
:::1:(21):
:(1)N t t t n n I =---
7、用电火花计时器(或电磁打点计时器)研究匀变速直线运动(A )(经常考试的实验)
1、实验步骤:
(1)把附有滑轮的长木板平放在实验桌上,将打点计时器固定在平板上,并接好电路 (2)把一条细绳拴在小车上,细绳跨过定滑轮,下面吊着重量适当的钩码. (3)将纸带固定在小车尾部,并穿过打点计时器的限位孔
(4)拉住纸带,将小车移动至靠近打点计时器处,先接通电源,后放开纸带. (5)断开电源,取下纸带
(6)换上新的纸带,再重复做三次 2、常见计算:
(1)2B AB BC T υ+=,2C BC CD
T υ+=
(2)2
C B C
D BC
a T T υυ--==
整体法和隔离法典型例题
1.(2011·天津理综·T2)如图所示,A 、B 两物块叠放在一起,在粗糙的水平面上保持相对静止地向右做匀减速直线运动,运动过程中B 受到的摩擦力( )
A. 方向向左,大小不变
B. 方向向左,逐渐减小
C. 方向向右,大小不变
D. 方向向右,逐渐减小 【答案】选A .
2.如图8所示,质量为M 的斜劈形物体放在水平地面上,质量为m 的粗糙物块,以某一初速度沿劈的斜面向上滑,至速度为零后又加速返回,而物体M 始终保持静止,则在物块m 上、下滑动的整个过程中 【 】
(A )地面对物体M 的摩擦力方向没有改变 (B )地面对物体M 的摩擦力先向左后向右
(C )物块m 上、下滑动时的加速度大小相同 (D )地面对物体M 的支持力总小于g m M )(+
本题的正确答案是AD
3.如图,质量为M 的楔形物块静置在水平地面上,其斜面的倾角为θ.斜面上有一质量为m 的小物块,小物块与斜面之间存在摩擦.用恒力F 沿斜面向上拉小物块,使之匀速上滑.在小物块运动的过程中,楔形物块始终保持静止.地面对楔形物块的支持力为( ) A .(M +m )g
B .(M +m )g -F
C .(M +m )g +F sin θ
D .(M +m )g -F sin θ
m F
M θ • • •
• •
• O A B C D E
3.07 12.38
27.87
49.62.
77.40
图2-5
4.有一个直角支架AOB ,AO 水平放置,表面粗糙, OB 竖直向下,表面光滑.AO 上套有小环
P ,OB 上套有小环Q ,两环质量均为m ,两环由一根质量可忽略、不可伸长的细绳相连,并
在某一位置平衡,如图所示.现将P 环向左移一小段距离,两环再次达到平衡,那么将移动后的平衡状态和原来的平衡状态比较,AO 杆对P 环的支持力F N 和摩擦力f 的变化情况是 ( )
A .F N 不变,f 变大
B .F N 不变,f 变小
C .F N 变大,f 变大
D .F N 变大,f 变小
5(09年安徽卷)在2008年北京残奥会开幕式上,运动员手拉绳索向上攀登,最终点燃了主火炬,体现了残疾运动员坚忍不拔的意志和自强不息的精神。
为了探究上升过程中运动员与绳索和吊椅间的作用,可将过程简化。
一根不可伸缩的轻绳跨过轻质的定滑轮,一端挂一吊椅,另一端被坐在吊椅上的运动员拉住,如图所示。
设运动员的质量为65kg ,吊椅的质量为15kg ,不计定滑轮与绳子间的摩擦。
重力加速度取g =10m/s2。
当运动员与吊椅一起正以加速度a =1m/s2上升时,试求
(1)运动员竖直向下拉绳的力;(440N) (2)运动员对吊椅的压力。
(275N)
6、如图所示,光滑水平面上放置质量分别为m 和2m 的四个木块,其中两个质量为m 的木块间用一不可伸长的轻绳相连,木块间的最大静摩擦力是μmg 。
现用水平拉力F 拉其中一个质量为2m 的木块,使四个木块以同一加速度运动,则轻绳对m 的最大拉力为( ) A 、3μmg/5 B 、3μmg/4 C 、3μmg/2 D 、3μmg
7、物体B 放在物体A 上,A 、B 的上下表面均与斜面平行(如图)。
当两者以相同的初速度靠惯性沿光滑固定斜面C 向上做匀减速运动时( )
A.A 受到B 的摩擦力沿斜面方向向上
B.A 受到B 的摩擦力沿斜面方向向下
C.A 、B 之间的摩擦力为零
D.A 、B 之间是否存在摩擦力取决与A 、B 表面的性质 [答案]C
8、 如图,在倾角为α的固定光滑斜面上,有一用绳子拴着的长木板,木板上站着一只猫。
已知木板的质量是猫的质量的2倍。
当绳子突然断开时,猫立即沿着板向上跑,以保持其相对斜面的位置不变。
则此时木
F
m 2m
m 2m
A B C
O
B P
Q
板沿斜面下滑的加速度为()
A.gsinα/2 B.GsinαC.3gsinα/2 D.2gsinα答案:C。
