动态规划作业完整修订稿
动态规划1(qh)

4 1 C3
B2
2
2
C2 3
5 B1 4
3 C1 3
D3 5
E2
3
2
D2
4
F
4
2 E1
D1
A
B
C
D
E
F
动态规划的函数方程(DP)
建立DP函数方程是指确定过 程的阶段及阶段数,规定状态变 量和决策变量的取法,给出各阶 段的状态集合,允许决策集合, 状态转移方程和指标函数等。
在上面的计算过程中,利用了第 k阶段与第k+1阶段的关系:
f3(C1)=MIN r(C1,D1)+ f4(D1) r(C1,D2)+ f4(D2)
=MIN(3+6,3+5)=8 最短路线: C1——D2——E2——F 最优解: d3*(C1)= D2
4 A3
4 1 C3
B2
2
2
C2 3
5 B1 4
3 C1 3
D3 5
E2
3
2
D2
4
F
4
2 E1
D1
A
B
C
D
4
F
4
2 E1
D1
A
B
C
D
E
F
d1
r (S 1,d 1 (S 1))+ f2(S 2) f 1(S 1) d 1 (S 1)
S1
B1
B2
A
15
14
14
B2
4 A3
4 1 C3
B2
2
2
C2 3
5 B1 4
3 C1 3
D3 5
E2
3
第3章 动态规划_作业-3.22

0.36
0 1 2 3
1 0.24
2
3
4
5
6 1
0
1
2
3
4
5
6
0
0.6
0.18
1
0
0.36
0.09
2
1 2
0
0.31
0.13 0.56
3 4 0.3 0.42
2 3
4
5 6 7
0
4 4
0
4
5
6 7
5 5
0
0.06
5 6
k 3 : C ( 3, 2 ) C ( 4 , 4 ) C ( 3,4) m in k 4 : C ( 3 , 3 ) C ( 5 ,4 )
式1 式2
C(i, j)=min{C(i, k-1)+C(k+1, j)+w(i,j)} (1≤i≤j≤n, i≤k≤j) =min{C(i, k-1)+C(k+1, j)}+w(i,j) (1≤i≤j≤n, i≤k≤j) 式3
0 1 0.24 2 3 4 5 6 1 2 0.09 3 0.13 4 0.3 5 0.06 6 7 0 1 2 3 4 5 6
s
0 0.18 0.42 0.6
C(i, i-1)=0 (1≤i≤n+1) C(i, i)=pi (1≤i≤n)
式1 式2
C(i, j)=min{C(i, k-1)+C(k+1, j)+w(i,j)} (1≤i≤j≤n, i≤k≤j) =min{C(i, k-1)+C(k+1, j)}+w(i,j) (1≤i≤j≤n, i≤k≤j) 式3
动态规划(完整)

主要内容:
§7.1多阶段决策问题 §7.2 动态规划的基本概念和基本原理
§7.3 动态规划应用举例
例 求解最短路问题
A1 2 Q 4 3 A3 A2 6 3 7 4 B1 1 4 2 4 4 1 5 6 B2 3 B3 3 3 C2 C1 3 4 T
Ⅰ
Ⅱ
Ⅲ
Ⅳ
分阶段的最短路径
• • • • • • • Ⅳ : C1—T Ⅲ --Ⅳ : B1—C1—T Ⅱ--Ⅲ--Ⅳ :A2—B1—C1—T Ⅰ--Ⅱ--Ⅲ --Ⅳ: Q—A2—B1—C1—T Q--A3—B1—C1—T Q--A3—B2—C2—T 3 4 7
决策为 xk 时的指标,则它就是第 k 段指标函
数,简记为vk 。 (2)过程指标函数(也称目标函数) 用f(sk , xk)表示第k子过程的指标函数。表
示处于第 k 段 sk 状态且所作决策为xk时,
从 sk 点到终点的距离。由此可见, f(sk , xk)
不仅跟当前状态 sk 有关,
还跟该子过程策略 pk(sk) 有关,严格说来,应
(6) 指标函数
用来衡量策略或子策略或决策的效果的 某种数量指标,就称为指标函数。它是定义 在全过程或各子过程或各阶段上的确定数量 函数。对不同问题,指标函数可以是诸如费 用、成本、产值、利润、产量、耗量、距离、 时间、效用,等等。
(1)阶段指标函数(也称阶段效应)
用vk(sk , xk)表示第 k 段处于状态 sk且所作
资规划, 排序问题和生产过程的最优控制
等问题;
§7.2 动态规划的基本概念和基本思想
一、基本概念
使用动态规划方法求解决策问题首先要将 问题改造成符合动态规划求解要求的形式, 要涉及以下概念: (1)阶段 (3)决策与策略 (2)状态 (4)状态转移方程
动态规划习题详解
动态规划动态规划是运筹学的一个分支,它是解决多阶段决策过程最优化问题的一种方法。
该方法是由美国数学家贝尔曼(R.Bellman)等人在本世纪50年代初提出的。
他们针对多阶段决策问题的特点,提出了解决这类问题的“最优化原理”,并成功地解决了生产管理、工程技术等方面的许多实际问题,从而建立了运筹学的一个新分支——动态规划。
他的名著《动态规划》于1957年出版,该书是动态规划的第一本著作。
动态规划是现代企业管理中的一种重要决策方法,在工程技术、经济管理、工农业生产及军事及其它部们都有广泛的应用,并且获得了显著的效果。
动态规划可用于解决最优路径问题、资源分配问题、生产计划与库存问题、投资分配问题、装载问题、设备更新与维修问题、排序问题及生产过程的最优控制等。
由于它所具有独特的解题思路,在处理某些优化问题时,常常比线性规划或非线性规划方法更有效。
第一节动态规划的基本方法多阶段决策的实际问题很多,下面通过具体例子,说明什么是动态规划模型及其求解方法。
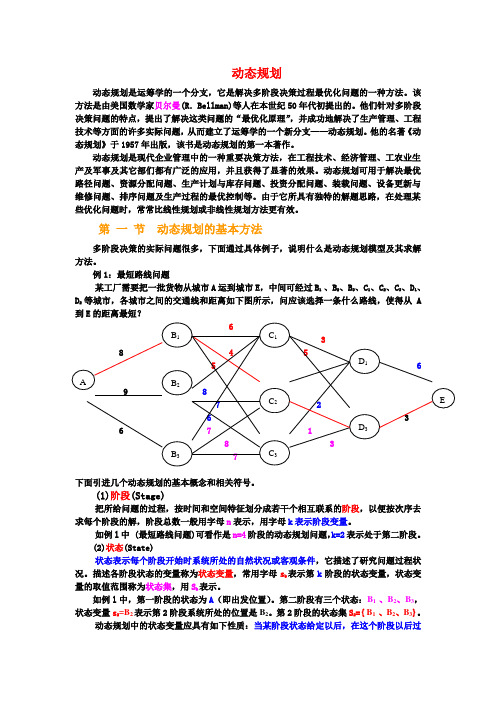
例1:最短路线问题某工厂需要把一批货物从城市A运到城市E,中间可经过B1 、B2、B3、C1、C2、C3、D1、D2等城市,各城市之间的交通线和距离如下图所示,问应该选择一条什么路线,使得从A到E的距离最短?下面引进几个动态规划的基本概念和相关符号。
(1)阶段(Stage)把所给问题的过程,按时间和空间特征划分成若干个相互联系的阶段,以便按次序去求每个阶段的解,阶段总数一般用字母n表示,用字母k表示阶段变量。
如例l中 (最短路线问题)可看作是n=4阶段的动态规划问题,k=2表示处于第二阶段。
(2)状态(State)状态表示每个阶段开始时系统所处的自然状况或客观条件,它描述了研究问题过程状况。
描述各阶段状态的变量称为状态变量,常用字母sk表示第k阶段的状态变量,状态变量的取值范围称为状态集,用Sk表示。
如例l中,第一阶段的状态为A(即出发位置)。
第二阶段有三个状态:B1 、B2、B3,状态变量s2=B2表示第2阶段系统所处的位置是B2。
动态规划算法作业

动态规划算法作业动态规划是一种解决多阶段决策问题的优化方法。
在这种方法中,我们将问题划分为多个子问题,并通过解决这些子问题来求解原始问题的最优解。
动态规划可以应用于各种领域,如经济学、制造业、计算机科学等,在优化问题中经常被使用。
1.状态定义:确定问题的子问题以及每个子问题的状态。
状态是问题的关键属性,这些属性在问题的不同阶段保持不变。
2.状态转移方程:表示问题的子问题之间的关系。
它描述了如何从一个子问题转移到下一个子问题。
通过状态转移方程,我们可以推导出子问题的最优解。
3.初始条件:定义问题的起始状态。
这通常是问题的边界条件,如在第一个阶段的子问题中,我们需要定义初始状态。
4.最优解的计算:通过迭代计算,我们可以逐步解决子问题,并最终求解出原始问题的最优解。
这通常通过填充一个表或者使用递归函数来实现。
为了更好地理解动态规划算法的应用,我们可以考虑以下两个经典问题。
1.背包问题:有一个容量为C的背包和一组物品。
每件物品有一个重量和价值。
我们的目标是选择物品,使其总重量不超过背包的容量,同时价值最大化。
我们可以使用动态规划来解决这个问题。
我们定义一个二维表,其中每一行表示一个物品,每一列表示背包的容量。
通过填充这个表,我们可以计算出每个子问题的最优解,并最终得出最优解。
2.最长公共子序列问题:给定两个字符串,求它们的最长公共子序列。
子序列在原字符串中不一定是连续的,但保持原有顺序。
我们可以使用动态规划来解决这个问题。
我们定义一个二维表,其中每个单元格表示两个字符串的子问题。
通过填充这个表,我们可以逐步计算出更长子序列的最优解,并最终得出最长公共子序列。
动态规划算法的优点是可以减少问题的重复计算,并且可以避免使用递归导致的堆栈溢出。
然而,这种算法也存在一些局限性。
首先,动态规划算法需要定义子问题以及状态转移方程,这在一些问题中可能会很困难。
其次,动态规划算法的时间复杂度通常较高,特别是对于一些大规模问题。
动态规划作业完整

动态规划作业1、1、设某工厂自国外进口一部精密机器,由机器制造厂至出口港有三个港口可供选择,而进口港又有三个可供选择,进口后可经由两个城市到达目的地,其间的运输成本如图中所标的数字,试求运费最低的路线?把A看作终点,该问题可分为4个阶段。
f k(S k)表示从第K阶段点S k到终点A的最短距离。
f4(B1)=20,f4(B2)=40,f4(B3)=30f3(C1)=min[d3(C1,B1)+ f4(B1), d3(C1,B2)+ f4(B2), d3(C1,B3)+ f4(B3) ]=70,U3(C1)= B2 或B3f3(C2)=40 ,U3(C2)= B3f3(C3)=80 ,U3(C3)= B1或B2 或B3f2(D1)=80 ,U2(D1)= C1f2(D2)=70 ,U2(D2)= C2f1(E)=110 ,U1(E)= D1或D2所以可以得到以下最短路线,E→D1→C1→B2 / B3→AE→D2→C2→B3→A2、习题4-2解:1)将问题按地区分为三个阶段,三个地区的编号分别为1、2、3;2)设Sk表示为分配给第k个地区到第n个地区的销售点数,Xk表示为分配给第k个地区的销售点数,S k+1=S k-X kPk(Xk)表示为Xk个销售点分到第k个地区所得的利润值fk(Sk)表示为Sk个销售点分配给第k个地区到第n个地区的最大利润值3)递推关系式:fk(Sk)=max[ Pk(Xk)+ f k+1(S k-X k) ] k=3,2,1f4(S4)=04)从最后一个阶段开始向前逆推计算第三阶段:设将S3个销售点(S3=0,1,2,3,4)全部分配给第三个地区时,最大利润值为:f3(S3)=max[P3(X3)] 其中X3=S3=0,1,2,3,4表1第二阶段:设将S2个销售点(S2=0,1,2,3,4)分配给乙丙两个地区时,对每一个S2值,都有一种最优分配方案,使得最大盈利值为:f2(S2)=max[ P2(X2)+ f3(S2-X2) ]其中,X2=0,1,2,3,4表2第一阶段:设将S1个销售点(S1=4)分配给三个地区时,则最大利润值为:f1(S1)=max[ P1(X1)+ f2(4-X1) ]其中,X1=0,1,2,3,4表3然后按计算表格的顺序反推,可知最优分配方案有两个:最大总利润为531)由X1*=2,X2*=1,X3*=1。
运筹学 动态规划-作业及答案
1
第五章 动态规划作业题及答案
1.用动态规划法求解求最短路径
从起点A 到终点E 之间各点的距离如图所示。
求A 到E 的最短路径。
B A
C B
D B C D E
C 21
23
12
31
2
5
11214
10610
41312113
96
5810
5
2
2.用动态规划法求解资源分配问题
有资金4万元,投资A 、B 、C 三个项目,每个项目的投资效益与投入该项目的资金有关。
三个项目A 、B 、C 的投资效益(万吨)和投入资金(万元)的关系见下表:
用动态规划法求解对三个项目的最优投资分配,使总投资效益最大。
3.用动态规划法求解生产库存问题
一个工厂生产某种产品,1~7月份生产成本和产品需求量的变化情况如下表:
为了调节生产生产和需求,工厂设有一个产品仓库,库容量H=9。
已知期初库存量为2,要求期末(七月低)库存量为0。
每个月生产的产品在月末入库,月初根据当月需求发货。
求七个月的生产量,能满足各月的需求,并使生产成本最低。
4.用动态规划法求解背包问题
第i 种每件价值c 1=65,c 2=85,c 3=40元; 第i 种物品每件重量为:w 1=2,w 2=3,w 3=1公斤;现有一只可装载重量为5公斤的背包,求各种物品应各取多少件放入背包,使背包中物品的价值最高。
动态规划——流水作业调度问题

动态规划——流⽔作业调度问题问题:n个作业 N={1,2,…,n}要在2台机器M1和M2组成的流⽔线上完成加⼯。
每个作业须先在M1上加⼯,然后在M2上加⼯。
M1和M2加⼯作业i 所需的时间分别为 ai 和bi,每台机器同⼀时间最多只能执⾏⼀个作业。
流⽔作业调度问题要求确定这n个作业的最优加⼯顺序,使得所有作业在两台机器上都加⼯完成所需最少时间。
最优调度应该是:1. 使M1上的加⼯是⽆间断的。
即M1上的加⼯时间是所有ai之和,但M2上不⼀定是bi之和。
2. 使作业在两台机器上的加⼯次序是完全相同的。
则得结论:仅需考虑在两台机上加⼯次序完全相同的调度。
为了得到最优⼦解结构(⽐较重要~~~~ ⽼师说期末考试会考到这个):—>机器M1开始加⼯S中作业时,机器M2还在加⼯其他作业,要等时间 t 后才可利⽤,则: 1. 则完成S中作业所需的最短时间记为T(S,t) 2. 完成所有作业所需的最短时间为T(N,0) 3. T(N,0)=min{ai + T(N-{i}, bi)}, i∈N。
ai:选⼀个作业i先加⼯,在M1的加⼯时间。
T(N-{i},bi}:剩下的作业要等bi时间后才能在M2上加⼯。
注意这⾥函数的定义,因为⼀开始⼯作i是随机取的,M1加⼯完了ai之后,要开始加⼯bi了,这⾥M1是空闲的可以开始加⼯剩下的N-i个作业了,但此时M2开始加⼯bi,所以要等bi时间之后才能重新利⽤,对应到上⾯函数T(s,t)的定义的话,这⾥就应该表⽰成T(N-{i},bi), 所以最优解可表⽰为T(N,0)=min{ai + T(N-{i}, bi)}, i∈N,即我们要枚举所有的⼯作i,使这个式⼦取到最⼩值。
这⾥顺便吐槽⼀句:算法中会利⽤很多数学知识,⼀定要搞清楚函数的意义以及每个数学符号所代表的含义,这样不⾄于各种懵⽐。
继续分析T(S,t)可得: T(S,t)={ai + T(S-{i}, bi+max{t-ai,0})}, i∈S 其中:T(S-{i}, bi+max{t-ai,0}):剩下的作业等bi+max{t-ai,0}才能在M2加⼯,⾄于这⾥是怎么推导出来的呢?见下⾯推导:最优⼦结构的证明(问题最优解包括⼦问题最优解):最优⼦结构:设π是N的⼀个最优调度,其加⼯顺序为π1,…, πn,其所需的加⼯时间为 aπ1+T’(即第⼀个作业π1在M1上加⼯的时间和其它的加⼯时间)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
动态规划作业完整 WEIHUA system office room 【WEIHUA 16H-WEIHUA WEIHUA8Q8-动态规划作业1、1、设某工厂自国外进口一部精密机器,由机器制造厂至出口港有三个港口可供选择,而进口港又有三个可供选择,进口后可经由两个城市到达目的地,其间的运输成本如图中所标的数字,试求运费最低的路线?把A看作终点,该问题可分为4个阶段。
f k(S k)表示从第K阶段点S k到终点A的最短距离。
f4(B1)=20,f4(B2)=40,f4(B3)=30f3(C1)=min[d3(C1, B1)+ f4(B1), d3(C1, B2)+ f4(B2), d3(C1, B3)+f4(B3) ]=70,U3(C1)= B2 或B3f3(C2)=40 ,U3(C2)= B3f3(C3)=80 ,U3(C3)= B1或B2 或B3f2(D1)=80 ,U2(D1)= C1f2(D2)=70 ,U2(D2)= C2f1(E)=110 ,U1(E)= D1或D2所以可以得到以下最短路线,E→D1→C1→B2 / B3→AE→D2→C2→B3→A2、习题4-2解:1)将问题按地区分为三个阶段,三个地区的编号分别为1、2、3;2)设Sk表示为分配给第k个地区到第n个地区的销售点数,Xk表示为分配给第k个地区的销售点数,S k+1=S k-X kPk(Xk)表示为Xk个销售点分到第k个地区所得的利润值fk(Sk)表示为Sk个销售点分配给第k个地区到第n个地区的最大利润值3)递推关系式:fk(Sk)=max[ Pk(Xk)+ f k+1(S k-X k) ] k=3,2,1f4(S4)=04)从最后一个阶段开始向前逆推计算第三阶段:设将S3个销售点(S3=0,1,2,3,4)全部分配给第三个地区时,最大利润值为:f3(S3)=max[P3(X3)] 其中X3=S3=0,1,2,3,4表1第二阶段:设将S2个销售点(S2=0,1,2,3,4)分配给乙丙两个地区时,对每一个S2值,都有一种最优分配方案,使得最大盈利值为:f2(S2)=max[ P2(X2)+ f3(S2-X2) ]其中,X2=0,1,2,3,4表2第一阶段:设将S1个销售点(S1=4)分配给三个地区时,则最大利润值为:f1(S1)=max[ P1(X1)+ f2(4-X1) ]其中,X1=0,1,2,3,4表3然后按计算表格的顺序反推,可知最优分配方案有两个:最大总利润为531)由X1*=2,X2*=1,X3*=1。
即得第一个地区分得2个销售点,第二个地区分得1个销售点,第三个地区分得1个销售点。
2)由X1*=3,X2*=1,X3*=0。
即得第一个地区分得3个销售点,第二个地区分得1个销售点,第三个地区分得0个销售点。
3、某施工单位有500台挖掘设备,在超负荷施工情况下,年产值为20万元/台,但其完好率仅为,在正常负荷下,年产值为15万元/台,完好率为。
在四年内合理安排两种不同负荷下施工的挖掘设备数量,使第四年年末仍有160台设备保持完好,并使产值最高。
试求出四年内使得产值最高的施工方案和产值数。
解:1)该问题分成四个阶段,k 表示年度,k =1,2,3,4 2)设Sk 表示为分配给第k 年初拥有的完好挖掘设备数量, Uk 表示为第k 年初分配在超负荷下施工的挖掘设备数量, Dk (Sk)={ Uk|0≤Uk ≤Sk }Sk -Uk 表示为第k 年初分配在正常负荷下施工的挖掘设备数量。
状态转移方程:S k +1= +(Sk -Uk), S1=500台 3)设vk(sk,uk)为第k 年度的产量,则 vk =20Uk +15(Sk -Uk)故指标函数为V1,4= f k (Sk)表示由资源量Sk 出发,从第k 年开始到第4年结束时所生产的产量最大。
4)递推关系式:f k (Sk)=MAX{20 Uk +15(Sk -Uk)+ f k+1[ +(Sk -Uk)]} k=1,2,3,45)从第4阶段开始,向前逆推计算∑=41k )U ,(S V k k k当k=4时,S5=160, +(S4-U4)=160 2S4-U4=400 U4=2S4-400f4(S4)=MAX{20 U4 +15(S4-U4)+ f5[ +(S4-U4)]} =MAX{5 U4 +15S4}=25S4-2000当k=3时,f3(S3)=MAX{20 U3 +15(S3-U3)+ f4[ +(S3-U3)]} = MAX{5U3+15S3+25 =MAX{-5U3 +35S3-2000} 故得最大解U3*=0所以f3(S3)=35 S3-2000依次类推,可求得:U2*=0,f2(S2)=43S2-2000U1*=0,f1(S1)=因为S1=500台,故f1(S1)=22700台最优策略为U1*=0,U2*=0,U3*=0,U4*=112 已知S1=500,S2= *+(S1-U1*)==400S3= *+(S2-U2*)==320S4= *+(S3-U3*)==256U4=2S4-400=112 S4-U4=256-112=144即前三年应把年初全部完好的挖掘设备投入正常负荷下施工,第四年应把年初112台全部完好的挖掘设备投入超负荷下施工,144台投入正常负荷下施工。
这样最高产量为22700台。
4、某电视机厂为生产电视机而需生产喇叭,生产以万只为单位。
根据以往记录,一年的四个季度需要喇叭分别是3万、2万、3万、2万只。
设每万只存放在仓库内一个季度的存储费为万元,每生产一批的装配费为2万元,每万只的生产成本费为1万元。
问应该怎样安排四个季度的生产,才能使总的费用最小?再生产点性质,Xi Xi hi Xi nXi Xi Xi Ci 2.0)(00,2,12)(=⎩⎨⎧==+= C(1,1)=C(3)+h(0)=5 C(1,2)=C(5)+h(2)= C(1,3)=C(8)+h(5)+h(3)= C(1,4)=C(10)+h(7)+h(5)+h(2)=C(2,2)=C(2)+h(0)=4 C(2,3)=C(5)+h(3)= C(2,4)=C(7)+h(5)+h(2)=C(3,3)=C(3)+h(0)=5 C(3,4)=C(5)+h(2)= C(4,4)=C(2)+h(0)=4 f0=0 f1=f0+ C(1,1)=5 j(1)=1f2=min{f0+ C(1,2),f1+ C(2,2)}=min{0+,5+4}= j(2)=1 f3= min{f0+ C(1,3),f1+ C(2,3),f2+ C(3,3)} =min{0+,5+,+5}= j(3)=1F4= min{f0+ C(1,4),f1+ C(2,4),f2+ C(3,4), f3+ C(4,4)}=min{0+,5+,+,+4}= j(4)=1,3当j(4)=1,X1=d1+d2+d3+d4=10,X2=0,X3=0,X4=0 当j(4)=3,X3=d3+d4=5,X4=0,X1=d1+d2=5,X2=0。
5、某工厂生产三种产品,各产品重量与利润关系如下表所示,现将此三种产品运往市场出售,运输能力总重量不超过6吨。
问如何安排运输使总利润最大。
解:(){}{()}()()}{2180,60max 3463180max )2130180max(3180max 62221,036343f f x f x x x x f x x ++=-+=++==≤(){}{()}()()()}{}{01260260,210,240max 0260,3130,60max 2362130max )180max(2130max 611112,1,026232===+++=-+=+==≤x f f f x f x x x f x x (){}{()}()1180********max )180max(2130max 211022232===-+=+==≤x f x f x x x f x x()}{13,02,113,22,01260260,260max63========xxxxxxf6、某工厂在一年进行了A、B、C三种新产品试制,由于资金不足,估计在年内这三种新产品研制不成功的概率分别为、、,因而都研制不成功的概率为××=。
为了促进三种新产品的研制,决定增援2万元的研制费,并要资金集中使用,以万元为单位进行分配。
其增援研制费与新产品不成功的概率如下表所示。
试问如何分配费用,使这三秤新产品都研制不成功的概率为最小。
解:1) (1分)将问题按产品A、B、C分为三个阶段,k=1、2、3;2) (6分)设Sk表示第k阶段可分配给第k个产品到第n个产品的研制费,S1=2Xk设为决策变量,表示第k阶段分配给第k个产品的研制费。
状态转移方程为Sk+1=Sk-Xk允许决策集合:Dk(Sk)={ Xk∣0≤Xk≤Sk,Xk为整数}Pk(Xk)表示为第k个产品失败的概率fk(Sk)表示为Sk万元研制费分配给第k个产品到第n个产品的最小的失败概率3)(4分)递推关系式:f k(Sk)=min[ Pk(Xk)×f k+1(Sk-Xk) ] k=3,2,1边界条件: f4(S4)=14)(11分)从最后一个阶段开始向前逆推计算第三阶段:设将S3万元研制费(S3=0,1,2)全部分配给C产品时,最小的失败概率为:f3(S3)=min[P3(X3)] 其中X3=S3=0,1,2X3*表示使得f3(S3)为最大值时的最优决策。
第二阶段:设将S2万元研制费(S2=0,1,2)分配给B、C产品时,最小的失败概率为:f2(S2)=min[ P2(X2)×f3(S2-X2) ]其中,X2=0,1,2第一阶段:设将S1万元研制费(S1=2)分配给三个产品时,最小的失败概率为:f1(S1)=min[ P1(X1)×f2(S1-X1) ]其中,X1=0,1,25)即分配给A产品1万元,B产品0万元,C产品1万元,可使三个小组都失败的概率减小到。
