45道动态规划题目分析
动态规划练习试题和解答

动态规划练习题[题1] 多米诺骨牌(DOMINO)问题描述:有一种多米诺骨牌是平面的,其正面被分成上下两部分,每一部分的表面或者为空,或者被标上1至6个点。
现有一行排列在桌面上:顶行骨牌的点数之和为6+1+1+1=9;底行骨牌点数之和为1+5+3+2=11。
顶行和底行的差值是2。
这个差值是两行点数之和的差的绝对值。
每个多米诺骨牌都可以上下倒置转换,即上部变为下部,下部变为上部。
现在的任务是,以最少的翻转次数,使得顶行和底行之间的差值最小。
对于上面这个例子,我们只需翻转最后一个骨牌,就可以使得顶行和底行的差值为0,所以例子的答案为1。
输入格式:文件的第一行是一个整数n(1〈=n〈=1000〉,表示有n个多米诺骨牌在桌面上排成一行。
接下来共有n行,每行包含两个整数a、b(0〈=a、b〈=6,中间用空格分开〉。
第I+1行的a、b分别表示第I个多米诺骨牌的上部与下部的点数(0表示空)。
输出格式:只有一个整数在文件的第一行。
这个整数表示翻动骨牌的最少次数,从而使得顶行和底行的差值最小。
[题2] Perform巡回演出题目描述:Flute市的Phlharmoniker乐团2000年准备到Harp市做一次大型演出,本着普及古典音乐的目的,乐团指挥L.Y.M准备在到达Harp市之前先在周围一些小城市作一段时间的巡回演出,此后的几天里,音乐家们将每天搭乘一个航班从一个城市飞到另一个城市,最后才到达目的地Harp市(乐团可多次在同一城市演出).由于航线的费用和班次每天都在变,城市和城市之间都有一份循环的航班表,每一时间,每一方向,航班表循环的周期都可能不同.现要求寻找一张花费费用最小的演出表.输入: 输入文件包括若干个场景.每个场景的描述由一对整数n(2<=n<=10)和k(1<=k<=1000)开始,音乐家们要在这n个城市作巡回演出,城市用1..n标号,其中1是起点Flute市,n是终点Harp市,接下来有n*(n-1)份航班表,一份航班表一行,描述每对城市之间的航线和价格,第一组n-1份航班表对应从城市1到其他城市(2,3,...n)的航班,接下的n-1行是从城市2到其他城市(1,3,4...n)的航班,如此下去.每份航班又一个整数d(1<=d<=30)开始,表示航班表循环的周期,接下来的d个非负整数表示1,2...d天对应的两个城市的航班的价格,价格为零表示那天两个城市之间没有航班.例如"3 75 0 80"表示第一天机票价格是75KOI,第二天没有航班,第三天的机票是80KOI,然后循环:第四天又是75KOI,第五天没有航班,如此循环.输入文件由n=k=0的场景结束.输出:对每个场景如果乐团可能从城市1出发,每天都要飞往另一个城市,最后(经过k天)抵达城市n,则输出这k个航班价格之和的最小值.如果不可能存在这样的巡回演出路线,输出0.样例输入: 样例输出:3 6 4602 130 150 03 75 0 807 120 110 0 100 110 120 04 60 70 60 503 0 135 1402 70 802 32 0 701 800 0[题3] 复制书稿(BOOKS)问题描述:假设有M本书(编号为1,2,…M),想将每本复制一份,M本书的页数可能不同(分别是P1,P2,…PM)。
动态规划专项练习题解

另一种方法
• 将原串与原串的倒序做一次LCS—最长公 共子序列,用原串长度减去LCS长度,即 为需要插入字符的个数 • 例如:ab3bd与 db3ba • LCS(‘ab3bd’, ‘db3ba’)=‘b3b’ • 因此, ans=Len(‘ab3bd’)-Len(‘b3b’)=2
LCS的求法
• 最长公共子串(LCS),有三种情况: 1. 公共子串的元素必须相邻. 2. 公共子串的元素可以不相邻 3. 求多个字符串而不是两个字符串的最长公共 子串 • 动归4中,我们讲了求情况2的LCS序列。下面我们 来讨论情况1的做法。
• 任务:对于任意一个字符串,输出将这个字符串 变为回文串需要插入的最少字符个数,比如, ab3bd只需要插入2个字符就可以变为一个回文串. • 0<n<=1992,n为字符串长度。
分析
• ab3bd • 只需变为adb3bda即可,在前面插入d,在 后面插入a; • 我们分几种情况讨论:
– 若A形如 ?A?,(问号代表任意一个相同字符, 下同)则只需将A变为回文串。 – 若A形如?A再在A的后面插入一个”?” – 若A形如A ?再在A的前面插入一个”?”
分析
• 性质:青蛙遍历的路径不会相交。
• 上图中图2的路径比图1要短。 • 证明:图1: D1=d(1,3)+d(2,3)+d(2,4) 图2: D2=d(1,2)+d(2,3)+d(3,4) 要证明D1>D2,只要证明d(1,3) +d(2,4)>d(1,2)+d(3,4) 连接两边,见图3,由三角形的三边关系定理即可证明。
动态规划
• 设f(i,j)为将Ai..Aj变为回文串的最小代价,则
f (i 1, j 1), 若a[i] a[ j ] f (i, j ) min f (i 1, j ) 1, 若a[i] a[ j ],后插一个字符 f (i, j - 1) 1,若a[i] a[ j ],前插一个字符
动态规划的具体应用例题

动态规划的具体应用例题3.1 最长不降子序列(1)问题描述设有由n个不相同的整数组成的数列,记为:a(1)、a(2)、……、a(n)且a(i)<>a(j) (i<>j)例如3,18,7,14,10,12,23,41,16,24。
若存在i1<i2<i3< … < ie 且有a(i1)<a(i2)< … <a(ie)则称为长度为e的不下降序列。
如上例中3,18,23,24就是一个长度为4的不下降序列,同时也有3,7,10,12,16,24长度为6的不下降序列。
程序要求,当原数列给出之后,求出最长的不下降序列。
(2)算法分析根据动态规划的原理,由后往前进行搜索。
1· 对a(n)来说,由于它是最后一个数,所以当从a(n)开始查找时,只存在长度为1的不下降序列;2· 若从a(n-1)开始查找,则存在下面的两种可能性:①若a(n-1)<a(n)则存在长度为2的不下降序列a(n-1),a(n)。
②若a(n-1)>a(n)则存在长度为1的不下降序列a(n-1)或a(n)。
3· 一般若从a(i)开始,此时最长不下降序列应该按下列方法求出: 在a(i+1),a(i+2),…,a(n)中,找出一个比a(i)大的且最长的不下降序列,作为它的后继。
4.用数组b(i),c(i)分别记录点i到n的最长的不降子序列的长度和点i后继接点的编号(3) 程序如下:(逆推法)program li1;const maxn=100;var a,b,c:array[1..maxn] of integer;fname:string;f:text;n,i,j,max,p:integer;beginreadln(fname);assign(f,fname);reset(f);readln(f,n);+for i:=1 to n dobeginread(f,a[i]);b[n]:=1;c[n]:=0;end;for i:= n-1 downto 1 dobeginmax:=0;p:=0;for j:=i+1 to n doif (a[i]<a[j]) and (b[j]>max) then begin max:=b[j];p:=j end;if p<>0 then begin b[i]:=b[p]+1;c[i]:=p endend;max:=0;p:=0;for i:=1 to n doif b[i]>max then begin max:=b[i];p:=i end;writeln('maxlong=',max);write('result is:');while p<>0 dobegin write(a[p]:5);p:=c[p] end;end.3.2 背包问题背包问题有三种1.部分背包问题一个旅行者有一个最多能用m公斤的背包,现在有n种物品,它们的总重量分别是W1,W2,...,Wn,它们的总价值分别为C1,C2,...,Cn.求旅行者能获得最大总价值。
45道动态规划题目分析

分析
• d[i,j]表示是否有可能i和j相遇, 则第i个人能 取得最后的胜利当且仅当d[i,i]为true • 状态转移: 考虑相遇前的最后一步, 则d[I,j] 为true当且仅当
– 能找到一个k, 使得i能遇k, k能遇到j, 且 – i或者j能打败k
• 状态有O(n2)个, 转移有O(n)个, 共O(n3)
• 状态O(kn2)个, 决策O(n), 转移时间O(1)(先预处理), 总时间O(kn3)
机器人的名字
• 考虑一种基于重复子串的压缩方法 • 用[St]k表示k个相同的子串St(其中St称为重复子串, k是一个单字节整数,只占一个字符位置) • 如果这k个子串并没有连在一起,则可以在[St]k的 后面加上{S1}t1{S2} t2…{Sr} tr(1<ti<k,ti<ti+1), 表示在第ti个St的后面放置Si,Si称为插入子串 • St和Si也都可以是压缩后的字符串 • 比如I_am_WhatWhat_is_WhatWhat的压缩结果 为I_am_[What]4{_is_}2,长度为19 (例子中的空 格用下划线“_”表示,数字2和4实际上是用单字 节二进制表示的) • 名字不会以空格开始或结尾,大小写敏感
• 原棋盘上每一格有一个分值,一块矩形棋 盘的总分为其所含各格分值之和。现在需 要把棋盘按上述规则分割成n块矩形棋盘, 并使各矩形棋盘总分的均方差最小。
(a) 允许的分割方案
(b) 不允许的分割方案
分析
• 变形均方差公式
n n 1 1 n 2 2 ( n( x ) 2 x i 2 2 x x i ) x i ( x ) 2 n n i 1 i 1 i 1
– d[k-1,x1,y1,a,y2]+s[a+1,y1,x2,y2] – d[k-1,a+1,y1,x2,y2]+s[x1,y1,a,y2] – 其中x1<=a<=x2
动态规划-例题众多-详细讲解

步骤2:状态转移方程:
步骤3:以自底向上的方法来计算最优解
12
程序的实现
BuyTicks(T, R)
1 n ← length[T]
2 f[0] ← 0
3 f[1] ← T[1]
4 for i ← 2 to n do
5
f[i] ← f[i-2]+R[i-1]
6
if f[i] > f[i-1]+T[i] then
n 0 1 2 3 4 5 6 7 8 9 10 F(n) 1 1 2 3 5 8 13 21 34 55 89
2
递归 vs 动态规划
递归版本:
F(n)
1 if n=0 or n=1 then
2
return 1
3 else
4
return F(n-1) + F(n-2)
太慢!
动态规划:
F(n)
1 A[0] = A[1] ← 1
这里是某支股票的价格清单: 日期 1 2 3 4 5 6 7 8 9 10 11 12 价格 68 69 54 64 68 64 70 67 78 62 98 87 最优秀的投资者可以购买最多4次股票,可行方案中的一种是: 日期 2 5 6 10 价格 69 68 64 62 输入 第1行: N (1 <= N <= 5000),股票发行天数 第2行: N个数,是每天的股票价格。 输出 输出文件仅一行包含两个数:最大购买次数和拥有最大购买次数的方案数(<=231) 当二种方案“看起来一样”时(就是说它们构成的价格队列一样的时候),这2种方 案被认为是相同的。
你的任务是,已知所有N位同学的身高,计算最少需要 几位同学出列,可以使得剩下的同学排成合唱队形。
动态规划习题详解
动态规划动态规划是运筹学的一个分支,它是解决多阶段决策过程最优化问题的一种方法。
该方法是由美国数学家贝尔曼(R.Bellman)等人在本世纪50年代初提出的。
他们针对多阶段决策问题的特点,提出了解决这类问题的“最优化原理”,并成功地解决了生产管理、工程技术等方面的许多实际问题,从而建立了运筹学的一个新分支——动态规划。
他的名著《动态规划》于1957年出版,该书是动态规划的第一本著作。
动态规划是现代企业管理中的一种重要决策方法,在工程技术、经济管理、工农业生产及军事及其它部们都有广泛的应用,并且获得了显著的效果。
动态规划可用于解决最优路径问题、资源分配问题、生产计划与库存问题、投资分配问题、装载问题、设备更新与维修问题、排序问题及生产过程的最优控制等。
由于它所具有独特的解题思路,在处理某些优化问题时,常常比线性规划或非线性规划方法更有效。
第一节动态规划的基本方法多阶段决策的实际问题很多,下面通过具体例子,说明什么是动态规划模型及其求解方法。
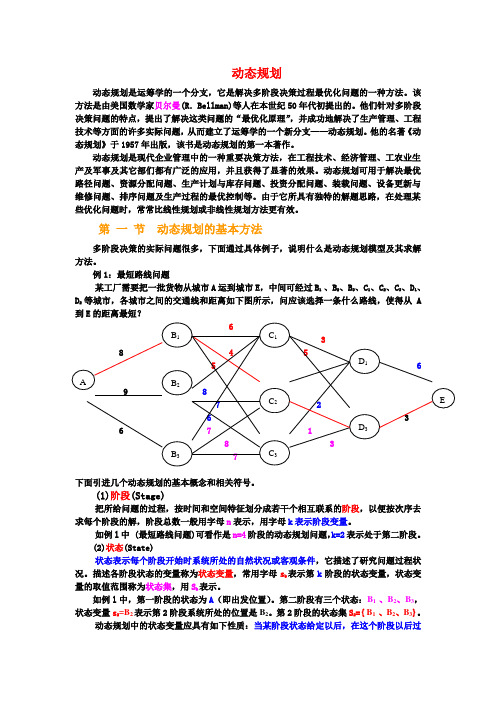
例1:最短路线问题某工厂需要把一批货物从城市A运到城市E,中间可经过B1 、B2、B3、C1、C2、C3、D1、D2等城市,各城市之间的交通线和距离如下图所示,问应该选择一条什么路线,使得从A到E的距离最短?下面引进几个动态规划的基本概念和相关符号。
(1)阶段(Stage)把所给问题的过程,按时间和空间特征划分成若干个相互联系的阶段,以便按次序去求每个阶段的解,阶段总数一般用字母n表示,用字母k表示阶段变量。
如例l中 (最短路线问题)可看作是n=4阶段的动态规划问题,k=2表示处于第二阶段。
(2)状态(State)状态表示每个阶段开始时系统所处的自然状况或客观条件,它描述了研究问题过程状况。
描述各阶段状态的变量称为状态变量,常用字母sk表示第k阶段的状态变量,状态变量的取值范围称为状态集,用Sk表示。
如例l中,第一阶段的状态为A(即出发位置)。
第二阶段有三个状态:B1 、B2、B3,状态变量s2=B2表示第2阶段系统所处的位置是B2。
动态规划总结经典题目(经典中的经典)

动态规划总结——经典问题总结本文着重讨论状态是如何表示,以及方程是怎样表示的。
当然,还附上关键的,有可能作为模板的代码段。
但有的代码的实现是优化版的。
经典问题总结最长上升子序列(LIS)问题描述如下:设L=<a1,a2,…,an>是n个不同的实数的序列,L的递增子序列是这样一个子序列Lin=<aK1,ak2,…,akm>,其中k1<k2<…<km且aK1<ak2<…<akm。
求最大的m值。
这里采用的是逆向思维的方法,从最后一个开始想起,即先从A[N](A数组是存放数据的数组,下同)开始,则只有长度为1的子序列,到A[N-1]时就有两种情况,如果a[n-1] < a[n] 则存在长度为2的不下降子序列a[n-1],a[n];如果a[n-1] > a[n] 则存在长度为1的不下降子序列a[n-1]或者a[n]。
有了以上的思想,DP方程就呼之欲出了(这里是顺序推的,不是逆序的):DP[I]=MAX(1,DP[J]+1)J=0,1,...,I-1但这样的想法实现起来是)O(n^2)的。
本题还有更好的解法,就是O(n*logn)。
利用了长升子序列的性质来优化,以下是优化版的代码://最长不降子序const int SIZE=500001;int data[SIZE];int dp[SIZE];//返回值是最长不降子序列的最大长度,复杂度O(N*logN)int LCS(int n) { //N是DATA数组的长度,下标从1开始int len(1),low,high,mid,i;dp[1]=data[1];for(i=1;i<=n;++i) {low=1;high=len;while( low<=high ) { //二分mid=(low+high)/2;if( data[i]>dp[mid] ) {low=mid+1;}else {high=mid-1;}}dp[low]=data[i];if( low>len ) {++len;}}return len;}最长公共子序列(LCS)给出两个字符串a, b,求它们的最长、连续的公共字串。
动态规划经典题目分析

寻宝游戏
SAMPLE INPUT 55 00010 10000 01000 00020 00000 6 101211 SAMPLE OUTPUT 3 数据范围 2≤N、M≤100,1≤Len≤250。表格和数列中的每一项都小于100。
分析
设F[i,x,y]表示ai与表格中位于(x,y)的数向对 应,且数列{ai}的前1~i-1项与表格中所有bi 位置为(x,y)的数列的最小接近程度。 B1和B2~Bn是有点不一样的。 因为B2~Bn都和前面的数有位置关系,而 B1没有。 所以初始化条件为 F[1,x,y]=(a[1]-table[x,y])2
代码
program CQF_CMI; var value,last:array[0..200000] of longint; n:longint; procedure init; var i,j:longint; begin readln(n); for i:=1 to n do read(value[i]); readln; end;
数字游戏
小W发明了一个游戏,他在黑板上写出了一行 数字a1,a2,a3,……,an,然后给你M个回合 的机会,每会回你可以从中选择一个数字擦去它, 接着剩下来的每个数字ai都要递减一个值bi。如此 重复m个回合,所有你擦去的数字之和就是你所 得的分数。 小W和他的好朋友小Y玩了这个游戏,可是他 发现,对于每个给出的a和b序列,小Y的得分总 比他高,所以他就很不服气。于是他想让你帮他 算算,对于每个a和b序列,可以得到的最大得分 是多少。
算法
建立一个数组last。 Last[i]表示长度为i的子序列中最小的最后一 个数。 特别的last[0]=负无穷 假如现在已经处理了前i-1个数,考虑加入 第i个数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
跳舞机
• DDR的主要内容是用脚来踩 踏板。踏板有4个方向的箭 头,用1,2,3,4来代表 • 每首歌曲有一个箭头序列, 游戏者必须按照这个序列依 次用某一只脚踩相应的踏板。 在任何时候,两只脚都不能 在同一个踏板上,但可以同 时待在中心位置0。
跳舞机
• 每一个时刻,必须移动而且只能移动一只 脚去踩相应的箭头,另一只脚不许移动。 • 跳DDR会消耗体力。从中心移动到任何一 个箭头耗费2单位体力,从任何一个箭头移 动到相邻箭头耗费3单位体力,移动到相对 的箭头(1和3相对,2和4相对)耗费4单位 体力,而留在原地再踩一下只需要1单位。 • 给定一首舞曲, 每个箭头应该用哪只脚踩才 能使体力消耗最少呢?例如对于序列LLUR, 用LLRR脚去踩,总的体力耗费为2 + 1 + 2 + 3 = 8单位
分析
• 模型:在一个2×N的矩阵中,找出K个子矩 阵。矩阵的每个元素有两个值V和F。题目 要让K个子矩阵的V值和其他矩阵的F值之和 最小,而如果我们令W=V-F,则目标转换 为让K个子矩阵元素的W值之和最小 • 矩阵可以重叠,这给解题带来不便。我们 可以不考虑重叠情况,如图所示
L L
R S(1,2,2,4) S’(1,3,1,6) S(1,2,2,4) S’(1,5,1,6) 图 1-43 重叠情况转化为不重叠情况
决斗
• 编号为1~n的n个人按逆时针方向排成一圈, 他们要决斗n-1场。每场比赛在某相邻两人 间进行,败者退出圈子,紧靠败者右边的 人成为与胜者直接相邻的人。 • 任意两人之间决斗的胜负都将在一矩阵中 给出(如果A[i,j]=1则i与j决斗i总是赢,如果 A[i,j]=0则i与j决斗时i总是输), • 求出所有可能赢得整场决斗的人的序号
索引
• • • • • • • • 【UVAxxx】最长上升子序列问题 【UVAxxx】最优二分检索树问题 【POJ1180】任务调度问题 【AOA】序列分割问题 【AOA】多排列的LCS 【POJ1159】回文词 【AOA】友好城市 【POJ1160】邮局
索引
• • • • • 【AOA】基因串 【POJ1946】奶牛转圈 【AOA】元件折叠 【AOA】 DNA序列 【AOA】最优布车方案
《算法艺术与信息学竞赛》 45道动态规划题目
刘汝佳
索引
• • • • • • • • 【POJ1141】括号序列 【POJ1191】棋盘分割 【SPOJ196】决斗 【AOA】跳舞机 【AOA】积木游戏 【AOA】艺术馆的火灾 【AOA】机器人的名字 【UVa10559】方块消除
索引
• • • • • • • • 【AOA】公路巡逻 【POJ1074】并行期望值 【AOA】高性能计算机 【AOA】模板匹配 【AOA】不可解码的编码 【AOA】青蛙的烦恼 【AOA】排列问题 【AOA】最优排序二叉树
– g: 本来是三维的O(L3)的, 但注意到在每个式子 里b参量没有发生变化, 故以b为阶段递推, 只需 要O(L2)的空间 – 预处理结果: 如果用h[a,b,c]表示是否有S[a, a+c-1]=S[b, b+c-1], 则又是三维的. 可以用链式 存储, 用next[a,b]表示子串S[a,b]的下一个相同 子串的开始位置, 则只需要O(L2)的空间
– (, [, ], )(, ([()
• 现在,给出一些由‘(’,‘)’,‘[’,‘]’构成的序 列,请添加尽量少的括号,得到一个规则序列。
分析
• d[i,j]: 子串i…j最少需要添加的括号数 • 状态转移
– S形如(S’)或者[S’]: d[i+1,j-1] – S形如(S’或者[S’: d[i+1,j]+1 – S形如S’)或者S’]: d[i,j-1]+1 – 长度大于1: d[i,k]+d[k+1,j] (i<=k<=j-1)
• 状态O(kn2)个, 决策O(n), 转移时间O(1)(先预处理), 总时间O(kn3)
机器人的名字
• 考虑一种基于重复子串的压缩方法 • 用[St]k表示k个相同的子串St(其中St称为重复子串, k是一个单字节整数,只占一个字符位置) • 如果这k个子串并没有连在一起,则可以在[St]k的 后面加上{S1}t1{S2} t2…{Sr} tr(1<ti<k,ti<ti+1), 表示在第ti个St的后面放置Si,Si称为插入子串 • St和Si也都可以是压缩后的字符串 • 比如I_am_WhatWhat_is_WhatWhat的压缩结果 为I_am_[What]4{_is_}2,长度为19 (例子中的空 格用下划线“_”表示,数字2和4实际上是用单字 节二进制表示的) • 名字不会以空格开始或结尾,大小写敏感
索引
• • • • • • • • 【POJ1038】 Bugs公司 【UVa10531】迷宫统计 【AOA】贪吃的九头龙 【AOA】快乐的蜜月 【AOA】移动机器人 【UVa10271】佳佳的筷子 【AOA】偷懒的工人 【AOA】铁路调度
索引
• • • • • • • • 【POJ1691】平板涂色 【POJ1947】道路重建 【ZJUxxx】圆和多边形 【AOA】铁球落地 【UVA10118】免费糖果 【AOA】丢三落四的老鼠 【AOA】最长公共子序列问题 【UVA10635】排列的LCS问题
• 原棋盘上每一格有一个分值,一块矩形棋 盘的总分为其所含各格分值之和。现在需 要把棋盘按上述规则分割成n块矩形棋盘, 并使各矩形棋盘总分的均方差最小。
(a) 允许的分割方案
(b) 不允许的分割方案
分析
• 变形均方差公式
n n 1 1 n 2 2 ( n( x ) 2 x i 2 2 x x i ) x i ( x ) 2 n n i 1 i 1 i 1
• 平均值是一定的(等于所有方格里的数的 和除以n) • 只需要让每个矩形总分的平方和尽量小
分析
• 考虑左上角坐标为(x1,y1),右下角坐标为 (x2,y2)的棋盘,设它把切割k次以后得到的 k+1块矩形的总分平方和最小值为 d[k,x1,y1,x2,y2] • 状态转移: 沿着某横线切或者竖线切,然后 选一块继续切, 如横着切的两类决策是
• 状态O(n2), 转移O(n), 共(n3)
ቤተ መጻሕፍቲ ባይዱ
棋盘分割
• 将一个8×8的棋盘进行如图所示的分割: 将原棋盘割下一块矩形棋盘并使剩下部分 也是矩形,再将剩下的部分继续如此分割, 这样割了(n-1)次后,连同最后剩下的矩形 棋盘共有n(n<15)块矩形棋盘(每次切割 都只能沿着棋盘格子的边进行)。
棋盘分割
括号序列
• 定义如下规则序列(字符串):
– 空序列是规则序列; – 如果S是规则序列,那么(S)和[S]也是规则序列; – 如果A和B都是规则序列,那么AB也是规则序列。
• 例如,下面的字符串都是规则序列:
– (), [], (()), ([]), ()[], ()[()]
• 这几个则不是规则序列:
积木游戏
• 有N块编号依次为1,2,…,N的长方体积木。每 块积木有三条不同边分别称为a、b、c边
a c
b
• 从积木中选出若干块分成M堆, 每堆至少有1块积 木,并且第K堆中任意一块积木的编号要大于第 K+1堆中任意一块积木的编号
积木游戏
• 每一堆积木要垂直摞成一根柱子,并满足
– 除最顶上的一块积木外,任意一块积木的上表 面同且仅同另一块积木的下表面接触,并且要 求下面积木的上表面能包含上面的积木的下表 面,也就是说,要求下面积木的上表面两对边 的长度分别大于等于上面积木两对边的长度。 – 对于任意两块上下表面相接触的积木,下面积 木的编号要小于上面积木的编号
分析
• 边界条件
g[a, b, c] d [ a , b ] 3 b a 1 2 c b a 1 或者 S[a, a c 1] S[b c 1, b] c b a 1
• d[a,b]的状态转移方程
分析
• g[a,b,c]表示将串S[a,b], 选择长度为c的重复 子串进行压缩得到的最短长度. 枚举插入串 (可能为空)的下一个位置i, 状态转移方程为
g[i, b, c] i a c g[a, b, c] min a c i b c 1 g[i, b, c] d[a c, i 1] 3 i a c S [ a ,a c 1] S [i ,i c 1]
分析
• 令d[a,b]表示以a, b为起止位置的串(记为 S[a,b])的最短压缩长度, 则目标为d[1,L] • 状态转移
– 连接: d[a,b] = min{d[a,i] + d[i+1,b]}, a<=i<b – 压缩: 需要确定重复子串. 当重复子串很多时, 决策枚举的代价较大
• 压缩决策可以通过动态规划来枚举!
min{d[a, i] d[i 1, b]} a i b d[a, b] min 1min1{g[a, b, i]} i b a
• 如何较快的判断是否有S[a, a+c-1]=S[i, i+c-1]? 从c=1开始递推, 总O(L3)
分析
• 时间: 预处理O(L3), 核心O(L4), 共O(L4) • 空间
• 状态O(n2m)个, 决策O(1), 总时间O(n2m)
艺术馆的火灾
• 艺术馆着火了. 这是一幢两层的小楼,每层有N个 房间,用两个数分别表示艺术品价值和火势.
40/50 30/40 50/40 30/50 30/50 40/20 60/70 20/30
• 灭火器最多只能发射K次,每次发射将覆盖一个 矩形的区域(矩形的高度可以是1也可以是2), 所到之处不但火焰会被扑灭,艺术品也被摧毁。 • 你需要决定灭火器每次应该怎样发射,才能将这 次火灾的损失降到最低限度。损失等于摧毁的艺 术品总价值加上剩余的火势总值
