分式章节测试题(二)

合集下载

分式单元测试题及答案

分式单元测试题学生______ 日期_______ 得分_______一、填空题（每小题2分，共24分）1．将2()a b c ÷-写成分式的形式：________.2．用22,,1a x -+中的任意两个代数式组成一个分式：________.3．当x ________时，分式12x 有意义. 4．若2x =-，则分式22x-=________. 5．当x ________时，分式1x x -无意义. 6．当x ________时，分式32x x-的值为零. 7．计算：b a a b⋅=________. 8．化简：222a ab a=+________. 9．计算：232233-⎛⎫⎛⎫⋅= ⎪ ⎪⎝⎭⎝⎭________. 10．计算：511212x x+=________. 11．用科学记数法表示：0.0000056-=____________________.12．写成不含有分母的式子，323()a b a b -=- ________. 二、选择题（每小题3分，共12分）13．下列各式中，是分式的是（）．（A ）12；（B ）23a ；（C ）222x x + ；（D ）212x x +．14．下列方程中，2x =不是它的一个解的是（）（A ）152x x +=；（B ）240x -=；（C ）2122x x x +=--；（D ）22032x x x -=++．15．下列分式中，是最简分式的是（）．（A ）x xy 2；（B ）a xy 2；（C ）221++x x ；（D ）222yxy y x ++ ．16．下列化简过程正确的是（）．（A ）421262x x x =；（B ）y x y x y x +=-+122；（C ）x x x x x 3123222+=+ ；（D ）2362+=---x x x x ．三、计算题（每小题7分，共28分）17．22226543425x x x x x x x -++⋅+-- ． 18．22562321x x x x x x -+-÷+++ ．19．223123x x x ----2223x x x +--221223x x x -+--． 20．221x x y x y --+．四、解方程（每小题7分，共28分）21．213121x x =+-． 22．5155x x x -+=++．23．23856x x x -=-+2456x x x --+． 24．12x x -=+23x x -+．五、应用题（共8分）25．小丽、小明练习打字，小丽打字速度是小明的1.2倍，同样打600个字，小丽比小明少用1分钟，问小丽每分钟打字多少个？答案：1． 2a b c - .2． 2a -等. 3． 0x ≠. 4． 12. 5．1x =. 6．3x =. 7．1.8． 11b +. 9． 23 .10． 12x.11． 65.610--⨯ .12． 1323()a b a b ----. 13．（D ）． 14．（C ）． 15．（B ）． 16．（D ）．17．5x x + ． 18．32x x -+ ．19．23x x --． 20．22y x y -． 21．3x =． 22．无解． 23．无解．24．12x =-． 25．小丽每分钟打字120个．。

分式章节测试(附答案)

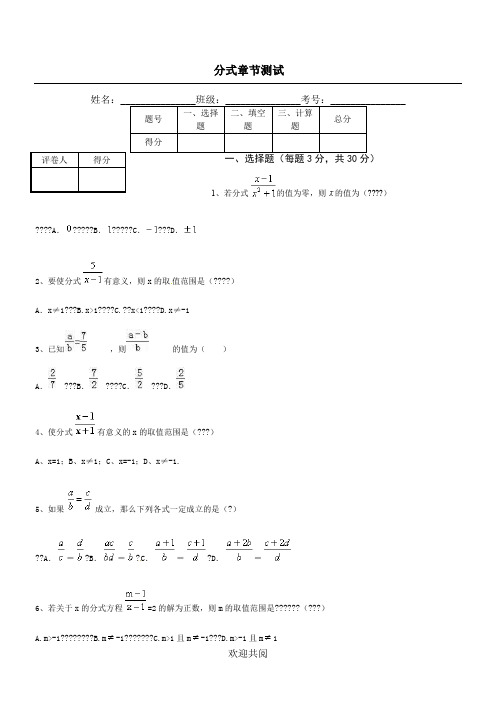
分式章节测试姓名：1、若分式????A ．?????B ．?????C ．???D ．2、要使分式有意义，则x 的取值范围是（????）A ．x ≠1???B.x>1????C.??x<1????D.x ≠-13、已知A ．．．???D ． 4、使分式A 、x=1；B 5、如果??A ．＝?B ．＝?C ．＝?D ．＝6、若关于x 的分式方程=2的解为正数，则m 的取值范围是??????（???）A.m>-1????????B.m -1???????C.m>1且m -1???D.m>-1且m 17、若代数式有意义，则实数x的取值范围是（）A．x≠1B．x≥0C．x＞0D．x≥0且x≠18、若分式的值为0，则等于（????）A.－1?????????????B.1??????C.－1或1???????????D.1或29、若则下列式子正确的是(???)．A．???B ．????C ．．10、分式可变形为（??）．?????????D．5分，共30分）其中分式共有_______个。

、若分式的值为13、当分式的值为零时，x的值为????????????.14、若分式的值为负数，则x的取值范围是__________。

15、如果分式的值为零，则a的值为____________16、当a＝????时，分式的值为－4．三、计算题（17题、18题各8分，19题、20题各10分，21题、22题各12分，共计60分）17、通分：，．18、约分：．19、先化简，再求值：，其中．20、先化简，再求值；21、已知、互为负倒数，且，试求的值。

22、请你先将分式化简，再求出当a=9999时，该代数式的值．??1、D?2、A37、D【分析】根据二次根式的性质和分式的意义，被开方数大于或等于0，分母不等于0，可以求出x的范围．【解答】解：根据题意得：，解得：x≥0且x≠1．故选D．【点评】本题考查的知识点为：分式有意义，分母不为0；二次根式的被开方数是非负数．8、A9、B10、D；二、填空题11、?2?12、-1???13、?314、x＜???15、216、1；三、计算题17、【考点】通分．【解答】解：?=，=2）凡出现18、原式=19、解：原式．当，时，原式．20、化简结果：?计算结果：21、解：∵、互为相反数，∴，即???又∵、互为负倒数，∴????????????????????????∴22、解：原式=???????=??????=???????????=．?。

_鲁教版(五四制)数学八年级上册第二章分式与方程式同步测试题

初中数学鲁教版八年级上册第二章测试题一、选择题1.若xy =34，则下列各式中不正确的是()A. x+yy =74B. yy−x=4 C. x−yy=14D. x+2yx=1132.要使分式x+2x−1有意义，x必须满足的条件是()A. x≠0B. x≠1C. x≠−2D. x≠−2且x≠13.已知分式x−b2x+a当x=2时，分式的值为零；当x=−2时，分式没有意义，则分式有意义时，a+b的值为()A. −2B. 2C. 6D. −64.分式2m−1m+1为0的条件是()A. m=−1B. m=1C. m=12D. m=05.下列运算正确的是()A. (−a3)2=−a6B. 2a2+3a2=6a2C. 2a2⋅a3=2a6D. (−b22a )3=−b68a36.化简m−1m ÷m−1m2的结果是()A. mB. 1m C. m−1 D. 1m−17.下列计算结果的错误的是()A. 3xx2⋅x3x=1xB. 8a2b2⋅(−3a4b2)=−6a3C. aa2−1÷a2a2+a=1a−1D. a÷b⋅1b=a8.化简x÷xy ⋅1x的结果是()A. 1B. xyC. yx D. xy9.如果|a|a +|b|b+|c|c=1，则|abc|abc的值为()A. −1B. 1C. ±1D. 不确定10.计算a−1a +1a，正确的结果是()A. 1B. 12C. a D. 1a11. 已知分式A =4x 2−4，B =1x+2+12−x ，其中x ≠±2，则A 与B 的关系是( )A. A =BB. A =−BC. A >BD. A <B12. 如果a 2+2a −1=0，那么代数式(a −4a )⋅a 2a−2的值是( )A. −3B. −1C. 1D. 313. 河南省将在2020年底前实现县城以上城区5G 全覆盖.5G 网络峰值速率为4G 网络峰值速率的10倍，在峰值速率下传输500兆数据，5G 网络比4G 网络快45秒，求这两种网络的峰值速率．设5G 网络的峰值速率为每秒传输x 兆数据，依题意，可列方程是( )A.500x −50010x =45 B. 500x−5000x =45 C. 50010x −500x=45D.5000x−500x=4514. 关于x 的分式方程2x−3+x+m 3−x=2有增根，则m 的值是( )A. m =−1B. m =0C. m =3D. m =0或m =315. 施工队要铺设一段全长2000米的管道，因在中考期间需停工两天，实际每天施工需比原计划多50米，才能按时完成任务，求原计划每天施工多少米．设原计划每天施工x 米，则根据题意所列方程正确的是( )A. 2000x −2000x+50=2B. 2000x+50−2000x =2C.2000x−2000x−50=2D. 2000x−50−2000x=216. 若分式方程x+1x−4=2+ax−4有增根，则a 的值为( )A. 5B. 4C. 3D. 0二、填空题17. 当x ______时，分式x+2x−2有意义． 18. 计算：yx 2−y 2÷yx+y 的结果是． 19. 已知m −1m =√6，则m +1m 的值为______． 20. 分式的12y 2,−15xy 最简公分母为______．21. 有五张正面分别标有数0，1，2，3，4，5的不透明卡片，它们除了数字不同外其余全部相同．现将它们背面朝上，洗匀后从中任取一张，将卡片上的数记为a ，则使关于x 的方程1−axx−2+2=12−x 有正整数解的概率为______22.已知关于x的分式方程xx−1−2=m1−x的解是正数，则m的取值范围是______．三、解答题23.已知分式1−mm2−1÷(1+1m−1).(1)请对分式进行化简；(2)如图，若m为正整数，则该分式的值对应的点落在数轴上的第______段上．(填写序号即可)24.为迎接“五一”国际劳动节，某商场计划购进甲、乙两种品牌的T恤衫共100件，已知乙品牌每件的进价比甲品牌每件的进价贵30元，且用120元购买甲品牌的件数恰好是购买乙品牌件数的2倍．(1)求甲、乙两种品牌每件的进价分别是多少元？(2)商场决定甲品牌以每件50元出售，乙品牌以每件100元出售．为满足市场需求，购进甲种品牌的数量不少于乙种品牌数量的4倍，请你确定获利最大的进货方案，并求出最大利润．25.在国家精准扶贫的政策下，某村企生产的黑木耳获得了国家绿色食品标准认证，绿标的认证，使该村企的黑木耳在市场上更有竞争力，今年每斤黑木耳的售价比去年增加了20元．预计今年的销量是去年的3倍，年销售额为360万元．已知去年的年销售额为80万元，问该村企去年黑木耳的年销量为多少万斤？26. 已知分式A =(a +1−3a−1)÷a 2−4a+4a−1．(1)化简这个分式；(2)当a >2时，把分式A 化简结果的分子与分母同时加上3后得到分式B ，问：分式B 的值较原来分式A 的值是变大了还是变小了？试说明理由． (3)若A 的值是整数，且a 也为整数，求出符合条件的所有a 值的和．答案和解析1.【答案】C【解析】解：A 、x+y y=74⇒3k+4k 4k=74，故正确；B 、yy−x =4⇒4k4k−3k =4，故正确； C 、x−y y=14⇒3k−4k 4k=−14，故错误； D 、x+2y x=113⇒3k+8k 3k=113，故正确．故选：C ．设x =3k ，y =4k.代入选项计算结果，排除错误答案．已知几个量的比值时，常用的解法是：设一个未知数，把题目中的几个量用所设的未知数表示出来，实现消元．2.【答案】B【解析】解：要使分式有意义，则x −1≠0，解得x ≠1，故选：B ．要使分式有意义，分式的分母不能为0．解此类问题，只要令分式中分母不等于0，求得字母的值即可．3.【答案】C【解析】解：∵x =2时，分式的值为零， ∴2−b =0，解得b =2．∵x =−2时，分式没有意义， ∴2×(−2)+a =0，解得a =4．∴a +b =4+2=6．故选：C ．根据分式的值为0，即分子等于0，分母不等于0，从而求得b 的值；根据分式没有意义，即分母等于0，求得a的值，从而求得a+b的值．考查了分式的值为零的条件，分式有意义的条件，注意：分式的值为0，则分子等于0，分母不等于0；分式无意义，则分母等于0．4.【答案】C【解析】解：分式2m−1m+1为0的条件是：2m−1=0，m+1≠0，解得：m=12，故选：C．直接利用分式有意义和方式的值为0的条件分析得出答案．此题主要考查了分式的值为零的条件，正确把握分式有意义的条件是解题关键．5.【答案】D【解析】解：A、(−a3)2=a6，此选项错误；B、2a2+3a2=5a2，此选项错误；C、2a2⋅a3=2a5，此选项错误；D、(−b22a )3=−b68a3，此选项正确；故选：D．分别根据幂的乘方、合并同类项法则、同底数幂的乘法及分式的乘方逐一计算即可判断．本题主要考查整式的运算，解题的关键是掌握幂的乘方、合并同类项法则、同底数幂的乘法及分式的乘方的运算法则．6.【答案】A【解析】【分析】此题考查了分式的乘除法，熟练掌握运算法则是解本题的关键．原式利用除法法则变形，约分即可得到结果．【解答】解：原式=m−1m ⋅m2 m−1=m．故选A．【解析】解：(B)原式=a×1b ⋅1b=ab2，故选：D．根据分式的运算法则即可求出答案．本题考查分式的运算，解题的关键是熟练运用分式的运算法则，本题属于基础题型．8.【答案】C【解析】【分析】本题主要考查了分式乘除混合运算，关键是理解法则把乘除的混合运算统一成乘法运算．首先统一成乘法运算，然后约分即可．【解答】解：原式=x⋅yx ⋅1 x=yx．故选C．9.【答案】A【解析】解：由|a|a +|b|b+|c|c=1可得a、b、c中必有两正一负，故设a、b为正，c为负，则|abc|abc =−abcabc=−1．故选：A．由|a|a +|b|b+|c|c=1可得a、b、c中必有两正一负，设a、b为正，c为负，从而可得出答案．本题考查了分式的化简求值及绝对值的知识，难度不大，确定a、b、c的正负情况是关键．【解析】解：原式=a−1+1a=1．故选：A．直接利用分式的加减运算法则计算得出答案．此题主要考查了分式的加减运算，正确掌握相关运算法则是解题关键．11.【答案】B【解析】解：∵B=x−2−x−2(x+2)(x−2)=−4x2−4，∴A和B互为相反数，即A=−B．故选：B．先把B式进行化简，再判断出A和B的关系即可．本题考查的是分式的加减法，先根据题意判断出A和B互为相反数是解答此题的关键．12.【答案】C【解析】【分析】本题考查分式的化简求值，解答本题的关键是明确分式化简求值的方法．根据分式的减法和乘法可以化简题目中的式子，然后对a2+2a−1=0变形即可解答本题．【解答】解：(a−4a )⋅a2a−2=a2−4a⋅a2a−2=(a+2)(a−2)a⋅a2a−2=a(a+2)=a2+2a，∵a2+2a−1=0，∴a2+2a=1，∴原式=1，故选：C．13.【答案】D【解析】解：∵5G网络的峰值速率为每秒传输x兆数据，∴4G网络的峰值速率为每秒传输x10兆数据．依题意，得：500x10−500x=45，即5000x −500x=45．故选：D．由5G网络的峰值速率为每秒传输x兆数据，可得出4G网络的峰值速率为每秒传输x10兆数据，根据在峰值速率下传输500兆数据时5G网络比4G网络快45秒，即可得出关于x的分式方程，此题得解．本题考查了由实际问题抽象出分式方程，找准等量关系，正确列出分式方程是解题的关键．14.【答案】A【解析】【分析】本题考查了分式方程的增根，增根问题可按如下步骤进行：①让最简公分母为0确定增根；②化分式方程为整式方程；③把增根代入整式方程即可求得相关字母的值．方程两边都乘以最简公分母(x−3)，把分式方程化为整式方程，再根据分式方程的增根就是使最简公分母等于0的未知数的值求出x的值，然后代入进行计算即可求出m的值．【解答】解：方程两边都乘以(x−3)得，2−x−m=2(x−3)，∵分式方程有增根，∴x−3=0，解得x=3，∴2−3−m=2×(3−3)，解得m=−1．故选A．15.【答案】A【解析】解：设原计划每天施工x米，则实际每天施工(x+50)米，根据题意，可列方程：2000x −2000x+50=2，故选：A．设原计划每天铺设x米，则实际施工时每天铺设(x+50)米，根据：原计划所用时间−实际所用时间=2，列出方程即可．本题考查了由实际问题抽象出分式方程，关键是读懂题意，找出合适的等量关系，列出方程．16.【答案】A【解析】【分析】此题考查了分式方程的增根，增根确定后可按如下步骤进行：①化分式方程为整式方程；②把增根代入整式方程即可求得相关字母的值．将分式方程去分母转化为整式方程，由分式方程有增根，求出x的值，代入整式方程计算即可求出a的值．【解答】解：去分母得：x+1=2x−8+a，由分式方程有增根，得到x−4=0，即x=4，把x=4代入整式方程得：a=5，故选A．17.【答案】≠2【解析】解：若分式有意义，则x−2≠0，解得：x≠2．故答案为x≠2．分式有意义的条件是分母不为0．本题考查的是分式有意义的条件：当分母不为0时，分式有意义．18.【答案】1x−y【解析】本题主要考查的是分式的除法的有关知识，由题意利用分式除法的计算法则，除以一个分式等于乘以这个分式的倒数进行求解即可．【解答】解：原式=y(x+y)(x−y)×x+yy=1x−y．故答案为1x−y．19.【答案】±√10【解析】解：∵m−1m=√6，∴(m−1m )2=m2+1m2−2=6，即m2+1m2=8，∴(m+1m )2=m2+1m2+2=8+2=10，则m+1m=±√10．故答案为：±√10．利用完全平方公式的结构特征计算即可求出所求．此题考查了分式的化简求值，以及完全平方公式，熟练掌握公式及运算法则是解本题的关键．20.【答案】10xy2【解析】解：分式的12y2,−15xy的分母分别是2y2、5xy，则它们的最简公分母是10xy2．故答案是：10xy2．确定最简公分母的方法是：(1)取各分母系数的最小公倍数；(2)凡单独出现的字母连同它的指数作为最简公分母的一个因式；(3)同底数幂取次数最高的，得到的因式的积就是最简公分母．本题主要考查了最简公分母，利用最简公分母的定义求解即可．21.【答案】16【解析】本题考查概率的基本计算，用到的知识点为：概率等于所求情况数与总情况数之比．易得分式方程的解，看所给6个数中，能使分式方程有整数解的情况数占总情况数的多少即可．【解答】解：解分式方程得：x=2，2−a∵分式方程的解为正整数，∴2−a>0，∴a<2，∴a=0，1，∵分式方程的解为正整数，当a=1时，x=2不合题意，∴a=0，∴使关于x的分式方程有正整数解的概率为1，6．故答案为：1622.【答案】m>−2且m≠−1【解析】解：方程两边同时乘以x−1得，x−2(x−1)=−m，解得x=m+2．∵x为正数，∴m+2>0，解得m>−2．∵x≠1，∴m+2≠1，即m≠−1．∴m的取值范围是m>−2且m≠−1．故答案为m>−2且m≠−1．先利用m表示出x的值，再由x为正数求出m的取值范围即可．本题考查的是分式方程的解，熟知求出使分式方程中令等号左右两边相等且分母不等于0的未知数的值，这个值叫方程的解是解答此题的关键．23.【答案】②【解析】解：(1)原式=1−m(m+1)(m−1)÷mm−1=1−m(m+1)(m−1)⋅m−1m=1−1m+1=m+1m+1−1m+1=mm+1；(2)∵m≠±1且m≠0，∴取m=2，则原式=22+1=23，∴该分式的值对应的点落在数轴上的第②段上，故答案为：②．(1)根据分式的混合运算顺序和运算法则化简原式即可得；(2)根据分式有意义的条件排除不能取到的m的值，再任取一个正整数m，代入计算，从而得出答案．本题主要考查分式的混合运算，解题的关键是熟练掌握分式的混合运算顺序和运算法则．24.【答案】解：(1)设甲品牌每件的进价为x元，则乙品牌每件的进价为(x+30)元，120 x =2×120x+30，解得，x=30经检验，x=30是原分式方程的解，∴x+30=60，答：甲品牌每件的进价为30元，则乙品牌每件的进价为60元；(2)设该商场购进甲品牌T恤衫a件，则购进乙品牌T恤衫(100−a)件，利润为w元，∵购进甲种品牌的数量不少于乙种品牌数量的4倍，∴a≥4(100−a)解得，a≥80w=(50−30)a+(100−60)(100−a)=−20a+4000，∵a≥80，∴当y=80时，w取得最大值，此时w=2400元，100−a=20，答：获利最大的进货方案是：购进甲品牌T恤衫80件，购进乙品牌T恤衫20件，最大利润是2400元．【解析】(1)根据乙品牌每件的进价比甲品牌每件的进价贵30元，且用120元购买甲品牌的件数恰好是购买乙品牌件数的2倍，可以列出相应的分式方程，从而可以求得甲、乙两种品牌每件的进价分别是多少元；(2)根据题意，可以求得购买甲种品牌的T恤衫数量的取值范围，然后列出利润与甲种品牌的T恤衫数量的函数关系，再根据一次函数的性质，即可得到获利最大的进货方案，并求出最大利润．本题考查一次函数的应用、分式方程的应用、一元一次不等式的应用，解答本题的关键是明确题意，列出相应的分式方程和一次函数关系式，利用一次函数的性质和不等式的性质解答，注意分式方程要检验．25.【答案】解：设该村企去年黑木耳的年销量为x万斤，则今年黑木耳的年销量为3x 万斤，依题意，得：3603x −80x=20，解得：x=2，经检验，x=2是原方程的解，且符合题意．答：该村企去年黑木耳的年销量为2万斤．【解析】设该村企去年黑木耳的年销量为x万斤，则今年黑木耳的年销量为3x万斤，根据单价=总价÷数量结合今年每斤黑木耳的售价比去年增加了20元，即可得出关于x 的分式方程，解之经检验后即可得出结论．本题考查了分式方程的应用，找准等量关系，正确列出分式方程是解题的关键．26.【答案】解：(1)A=a2−1−3a−1÷(a−2)2a−1=(a+2)(a−2)a−1⋅a−1(a−2)2=a+2a−2；(2)变小了，理由如下：A−B=a+2a−2−a+5a+1=(a+2)(a+1)−(a+5)(a−2)(a+1)(a−2)=12(a−2)(a+1)，∵a>2，∴a−2>0，a+1>0，∴A−B=12(a−2)(a+1)>0，即A>B；(3)A=a+2a−2=1+4a−2，根据题意，a−2=±1、±2、±4，则a=1、0、−2、3、4、6，又a≠1，∴0+(−2)+3+4+6=11，即：符合条件的所有a值的和为11．【解析】(1)根据分式混合运算顺序和运算法则化简即可得；(2)根据题意列出算式A−B=a+2a−2−a+5a+1，化简可得A−B=12(a−2)(a+1)，结合a的范围判断结果与0的大小即可得；(3)由A=a+2a−2=1+4a−2知a=±1、±2、±4，结合a的取值范围可得．本题主要考查分式的混合运算，解题的关键是熟练掌握分式的混合运算顺序和运算法则．。

人教版八年级数学上册第十五章《分式》单元测试题(含答案)

人教版八年级数学上册第十五章《分式》单元测试题（含答案）一、选择题（每小题3分，共24分）1．在式子x y 3，πa ，13+x ，31+x ，a a 2中，分式有（） A ．1个 B ．2个 C ．3个 D ．4个2．分式32+x x 无意义的条件是（） A ．x≠—3 B ． x=－3 C ．x=0 D ．x=33．下列各分式中与分式ba a --的值相等是（） A ．b a a -- B ．b a a +- C ．a b a - D ．—a b a - 4．计算（2-a a —2+a a ）·a a 24-的结果是（） A ． 4 B ．－4 C ．2a D ．－2a5．分式方程2114339x x x +=-+-的解是（） A ．x=－2 B ．x=2 C ． x=±2 D ．无解6．把分式(0)xy x y x y+≠+中的x ,y 都扩大3倍，那么分式的值（） A ．扩大为原来的3倍 B ．缩小为原来的13C ．扩大为原来的9倍D ．不变 7．若分式34922+--x x x 的值为0，则x 的值为（） A ．3 B ．3或－3 C ．－3 D ．08.某厂接到加工720件衣服的订单，预计每天做48件，正好按时完成，后因客户要求需提前5 天交货.设每天应多做x 件，则x 应满足的方程为（）A ．72072054848x -=+ B ．72072054848x+=+ C ．720720548x -= D ．72072054848x -=+ 二、填空题（每小题4分，共32分）9．当x= 时，分式22x x --值为零.10．计算．2323()a b a b --÷= .11．用科学记数法表示0.002 014= . 12．分式222439x x x x --与的最简公分母是____ ______. 13．若方程322x m x x-=--无解,则m =__________________. 14．已知a 1－b 1=21，则b a ab -的值为________________. 15．若R 1=11R +21R （R 1≠R 2），则表示R 1的式子是________________. 16.（2013年泰安）某电子元件厂准备生产4600个电子元件，甲车间独立生产一半后，由于要尽快投入市场，乙车间也加入了该电子元件的生产.若乙车间每天生产的电子元件个数是甲车间的1.3倍，结果用33天完成任务.问：甲车间每天生产电子元件多少个？在这个问题中设甲车间每天生产电子元件x 个，根据题意可得方程为________________.三、解答题（共64分）17．（14分）计算：（1）（2x －3y 2）－2÷（x －2y ）3；（2）21+-x x ÷41222-+-x x x +11-x .18．(8分)先化简，再求值：211122x x x -⎛⎫-÷ ⎪++⎝⎭，其中2x =.19．(8分)解方程21124x x x -=--.20．（10分）先仔细看（1）题，再解答（2）题.（1）a 为何值时，方程 3x x -= 2 + 3a x -会产生增根？解：方程两边乘（x-3），得x = 2（x-3）+a①.因为x=3是原方程的增根，•但却是方程①的解，所以将x=3代入①，得3=2×（3-3）+a ，所以a=3.（2）当m 为何值时，方程1y y --2m y y -=1y y-会产生增根？25．（12分）贵港市在旧城改造过程中，需要整修一段全长2400米的道路，为了尽量减少施工对城市交通所造成的影响，实际工作效率比原计划提高了20%，结果提前8小时完成任务，求原计划每小时修路的长度.26．（12分）荷花文化节前夕，我市对观光路工程招标时，接到甲、乙两个工程队的投标书，甲、乙施工一天的工程费用分别为1.5万元和1.1万元，市政局根据甲、乙两队的投标书测算，有三种施工方案．（1）甲队单独做这项工程刚好如期完成.（2）乙队单独做这项工程，要比规定日期多5天.（3）若甲、乙两队合作4天后，余下的工程由乙队单独做，也正好如期完成.在确保如期完成的情况下，你认为哪种方案最节省工程款，通过计算说明理由.第十五章分式测试题参考答案一、1. C 2. B 3. C 4. B 5. B 6. A 7. C 8. D二、9．-2 10．a 4b 6 11．-2.014×10-3 12．x(x+3)(x-3) 13．114．－2 15.R 1=RR RR -22 16.333.123002300=++x x x 三、17．（1）7124yx . （2）1. 18.原式=11-x .代入x=2，得原式=1. 19．x=－23. 20．解：方程两边乘y （y-1），得y 2-m=（y-1）2.化简，得m=2y －1.因为y=0和y=1都是原方程的的增根，但却是化简后整式方程的解.故将y=0和y=1分别代入m=2y －1，得m=－1或m=1.所以m =±1.21．解：设原计划每小时修路x 米，根据题意，得8%)201(24002400=+-xx . 解得50=x .经检验．x=50是原方程的解，且符合题意.答：原计划每小时修路50米.22．解：设工程期为x 天，则甲队单独完成用x 天，乙队单独完成用（x ＋5）天. 根据题意，得415x x x +=+. 解得x=20.经检验，x=20是原方程的解,且符合题意.所以在不耽误工期的情况下,有方案(1)和方案(3)两种方案合乎要求.方案(1)需工程款1.5×20=30(万元)，方案(3)需工程款1.5×4＋1.1×20=28(万元). 故方案(3)最节省工程款且不误期.人教版八年级上册第十五章分式单元检测（含答案）一、单选题1．在5x ，38a ，2π，1x a -中，属于分式的个数为（） A ．0个B ．1个C ．2个D ．3个 2．下列分式为最简分式的是（）A ．11a a --B ．235xy y xy -C ．22m n n m +-D ．22a b a b++ 3．下列各式中，变形不正确的是（）A ．2233x x=-- B ．66a a b b -=- C ．3344x x y y -=- D ．5533n n m m --=- 4．计算322b b 1·a a b⎛⎫⎛⎫÷ ⎪ ⎪⎝⎭⎝⎭的值为 ( ) A ．222b a B ．6ab 2 C ．8a D ．15．计算:22m-1m -1m m÷的结果是 ( ) A ．m m 1+ B ．1m C ．m-1 D ．1m-16．若111u v f+=，则用u 、v 表示f 的式子应该是（） A ．u v uv + B ．uv u v + C ．v u D ．u v7．若234a b c ==，则2222232a bc c a ab c-+--的值是( ) A ．13 B ．13- C ．12 D ．12- 8．纳米材料多被应用于建筑、家电等行业，实际上，纳米(nm)是一种长度的度量单位：1纳米＝0.000000001米，用科学记数法表示0.12纳米应为( )A.0.12×10－9米B.0.12×10－8米C.1.2×10－10米D.1.2×10－8米 9．计算20140的结果是（）A ．1B ．0C ．2014D ．﹣1 10．当m 为何值时，方程会产生增根( ) A.2 B.－1 C.3 D.－311．下列各式中，是分式方程的是（）A.x+y=5B.C.D.12．已知一汽船在顺流中航行46千米和逆流中航行34千米，共用去的时间，正好等于它在静水中航行80千米用去的时间，且水流速度是2千米/时，求汽船在静水中的速度，若设汽船在静水中速度为x 千米/时，则所列方程正确的是（） A.+= B.+= C.=－ D.=+二、填空题13．当x ＝_________时，分式242x x -+的值为0． 14．当x ＝__________时，分式3x x-无意义． 15．若a+b=1，且a ∶b=2∶5,则2a-b=____________.16．计算：（12）﹣2+（﹣2）3﹣20110=__________．三、解答题17．解方程：(1)233011x x x +-=--；(2)1433162x x -=--. 18．计算：①()223·14a aa a a ----； ②211a a a ---； ③225611x x x x x+⎛⎫-÷ ⎪--⎝⎭ 19．22322222244(82)25356a b ab b b a b b ab a b ab a ++-÷⋅---+，其中12a =-，14b =. 20．某书商去图书批发市场购买某本书，第一次用12000元购书若干本，并把该书按定价7元/本出售，很快售完，由于该书畅销，书商又去批发市场采购该书，第二次购书时，每本书批发价已比第一次提高了20%，他用15000元所购书数量比第一次多了100本. （1）求第一次购书的进价是多少元一本？第二次购进多少本书？（2）若第二次购进书后，仍按原定价7元/本售出2000本时，出现滞销，书商便以定价的n 折售完剩余的书，结果第二次共盈利100m 元（n 、m 为正整数），求相应的n 、m 的值.答案1．C 2．D 3．D 4．C 5．A 6．B 7．C 8．C 9．A10．C 11．D 12．B 13．2 14．315．-1 716．﹣517．（1）x＝0；（2）23 x=.18．①11aa-+;②11a-;③-5x19．242a ba b+-+，020．（1）第一次购书的进价为5元/本，且第二次买了2500本；（2）当n=4时，m=4；当n=6时，m=11；当n=8时，m=18人教版八年级上数学第十五章分式单元测试（解析）一、选择题(每小题3分,共24分)1.若代数式在实数范围内有意义,则实数x的取值范围是( )A.x<3B.x>3C.x≠3D.x=32.下列等式成立的是( )A.+=B.=C.=D.=-3.下列运算结果为x-1的是( )A.1-B.·C.÷D.4.化简+的结果是( )A.m+nB.n-mC.m-nD.-m-n5.当x=6,y=3时,代数式·的值是( )A.2B.3C.6D.96.计算÷-的结果为( )A. B. C. D.a7.甲、乙两人同时从A地出发到B地,如果甲的速度v保持不变,而乙先用v的速度到达中点,再用2v的速度到达B地,则下列结论中正确的是( )A.甲、乙同时到达B地B.甲先到达B地C.乙先到达B地D.谁先到达B地与v有关8.(2016黑龙江龙东中考)关于x的分式方程=3的解是正数,则字母m的取值范围是( )A.m>3B.m<3C.m>-3D.m<-3二、填空题(每小题3分,共24分)9.某种电子元件的面积大约为0.000 000 69平方毫米,将0.000 000 69这个数用科学记数法表示为.10.当x= 时,分式的值为0.11.某市为治理污水,需要铺设一段全长600 m的污水排放管道.铺设120 m后,为加快施工速度,后来每天比原计划增加20 m,结果共用11天完成这一任务,求原计划每天铺设管道的长度.如果设原计划每天铺设x m管道,那么根据题意,可列方程: .12.计算:÷= .13.如图15-4-1,点A、B在数轴上,它们所对应的数分别是-4、,且点A、B到原点的距离相等,则x= .图15-4-114.甲、乙二人做某种机械零件,已知甲是技术能手,每小时比乙多做3个,甲做30个所用的时间与乙做20个所用的时间相等,那么甲每小时做个零件.15.计算(x+1)的结果是.16.若a2+5ab-b2=0,则-的值为.三、解答题(共52分)17.(4分)化简:-.18.(5分)计算:÷.19.(6分)(2016山东菏泽中考)列方程或方程组解应用题:为了响应“十三五”规划中提出的绿色环保的倡议,某校文印室提出了每个人都践行“双面打印,节约用纸”.已知打印一份资料,如果用A4厚型纸单面打印,总质量为400克,将其全部改成双面打印,用纸将减少一半;如果用A4薄型纸双面打印,这份资料的总质量为160克.已知每页薄型纸比厚型纸轻0.8克,求A4薄型纸每页的质量.(墨的质量忽略不计)20.(6分)先化简,再求值:÷·,其中a=-,b=.21.(7分)解分式方程:(1)(2016广西贵港中考)+1=-;(2)(2016湖北天门中考)=-1.22.(6分)(2015四川广元中考)先化简:÷,然后解答下列问题:(1)当x=3时,求代数式的值;(2)原代数式的值能等于-1吗?为什么?23.(8分)(2016辽宁铁岭中考)先化简,再求值:÷-,其中a=(3-)0+-.24.(10分)(2016新疆乌鲁木齐中考)某商场用24 000元购入一批空调,然后以每台3 000元的价格销售,因天气炎热,空调很快售完;商场又以52 000元的价格再次购入该种型号的空调,数量是第一次购入的2倍,但购入的单价上调了200元,每台的售价也上调了200元.(1)商场第一次购入的空调每台进价是多少元?(2)商场既要尽快售完第二次购入的空调,又要在这两次空调销售中获得的利润率不低于22%,打算将第二次购入的部分空调按每台九五折出售,最多可将多少台空调打折出售?第十五章分式答案解析满分：100分；限时：60分钟一、选择题(每小题3分,共24分)1.若代数式在实数范围内有意义,则实数x的取值范围是( )A.x<3B.x>3C.x≠3D.x=3答案 C 由分式有意义的条件得x-3≠0,解得x≠3.故选C.2.下列等式成立的是( )A.+=B.=C.=D.=-答案 C +=,所以A错误;=不成立,所以B错误;==,所以C正确;=-,所以D错误,故选C.3.下列运算结果为x-1的是( )A.1-B.·C.÷D.答案 B 选项A的运算结果为,选项B的运算结果为x-1,选项C的运算结果是,选项D的运算结果为x+1.故选B.4.化简+的结果是( )A.m+nB.n-mC.m-nD.-m-n答案 A +=-==m+n,故选A.5.当x=6,y=3时,代数式·的值是( )A.2B.3C.6D.9答案 C ·=·=.当x=6,y=3时,原式==6.6.计算÷-的结果为( )A. B. C. D.a答案 C ÷-=÷-=×-=-=,故选C.7.甲、乙两人同时从A地出发到B地,如果甲的速度v保持不变,而乙先用v的速度到达中点,再用2v的速度到达B地,则下列结论中正确的是( )A.甲、乙同时到达B地B.甲先到达B地C.乙先到达B地D.谁先到达B地与v有关答案 B 设从A地到B地的距离为2s,∵甲的速度v保持不变,∴甲所用时间为,∵乙先用v的速度到达中点,再用2v的速度到达B地,∴乙所用时间为+=+,∵s>0,v>0,∴+>,故甲先到达B地.8.(2016黑龙江龙东中考)关于x的分式方程=3的解是正数,则字母m的取值范围是( )A.m>3B.m<3C.m>-3D.m<-3答案D解分式方程,得x=-3-m,∵方程的解为正数,∴-3-m>0,解得m<-3,∵x+1≠0,∴x≠-1,∴-3-m≠-1,解得m≠-2,∴m<-3,故选D.二、填空题(每小题3分,共24分)9.某种电子元件的面积大约为0.000 000 69平方毫米,将0.000 000 69这个数用科学记数法表示为.答案 6.9×10-7解析0.000 000 69=6.9×10-7.10.当x= 时,分式的值为0.答案 2解析分式的值为0,则即所以当x=2时,原分式的值为0.11.某市为治理污水,需要铺设一段全长600 m的污水排放管道.铺设120 m后,为加快施工速度,后来每天比原计划增加20 m,结果共用11天完成这一任务,求原计划每天铺设管道的长度.如果设原计划每天铺设x m管道,那么根据题意,可列方程: .答案+=11解析根据题意,可列方程为+=11.12.计算:÷= .答案解析原式=a4b2c-2÷=a4b2c-2÷=b6c-2=.13.如图15-4-1,点A、B在数轴上,它们所对应的数分别是-4、,且点A、B到原点的距离相等,则x= .图15-4-1答案解析由题意,得=4,解得x=,经检验,x=是方程=4的解.14.甲、乙二人做某种机械零件,已知甲是技术能手,每小时比乙多做3个,甲做30个所用的时间与乙做20个所用的时间相等,那么甲每小时做个零件. 答案9解析设甲每小时做x个零件,则乙每小时做(x-3)个零件,根据题意可得=,解得x=9.经检验,x=9是方程的解,且符合题意.因此甲每小时做9个零件.15.计算(x+1)的结果是.答案x解析(x+1)=(x+1)=(x+1)=x.16.若a2+5ab-b2=0,则-的值为.答案 5解析由a2+5ab-b2=0,得b2-a2=5ab,∴-===5.三、解答题(共52分)17.(4分)化简:-.解析原式=-=-==1.18.(5分)计算:÷.解析原式=·=·=·=.19.(6分)(2016山东菏泽中考)列方程或方程组解应用题:为了响应“十三五”规划中提出的绿色环保的倡议,某校文印室提出了每个人都践行“双面打印,节约用纸”.已知打印一份资料,如果用A4厚型纸单面打印,总质量为400克,将其全部改成双面打印,用纸将减少一半;如果用A4薄型纸双面打印,这份资料的总质量为160克.已知每页薄型纸比厚型纸轻0.8克,求A4薄型纸每页的质量.(墨的质量忽略不计)解析设A4薄型纸每页的质量为x克,则厚型纸每页的质量为(x+0.8)克.根据题意,得×=.解得,x=3.2.经检验,x=3.2是原分式方程的根,且符合题意.答:A4薄型纸每页的质量为3.2克.20.(6分)先化简,再求值:÷·,其中a=-,b=.解析÷·=··=··=.当a=-,b=时,原式==-6.21.(7分)解分式方程:(1)(2016广西贵港中考)+1=-;(2)(2016湖北天门中考)=-1.解析(1)去分母,得x-3+x-2=-3,移项,得x+x=-3+3+2,合并同类项,得2x=2,系数化为1,得x=1,经检验,x=1为原分式方程的根,∴分式方程的解为x=1.(2)两边同时乘(x+1)(x-1),得3(x-1)=x(x+1)-(x+1)(x-1),解得x=2. 检验:当x=2时,(x+1)(x-1)=(2+1)(2-1)=3≠0,∴原方程的解为x=2.22.(6分)(2015四川广元中考)先化简:÷,然后解答下列问题:(1)当x=3时,求代数式的值;(2)原代数式的值能等于-1吗?为什么? 解析原式=·=·=.(1)当x=3时,原式=2.(2)不能.理由:如果=-1,那么x+1=-x+1,则x=0,当x=0时,原代数式中的除式=0,矛盾, ∴原代数式的值不能等于-1.23.(8分)(2016辽宁铁岭中考)先化简,再求值:÷-,其中a=(3-)0+-.解析原式=÷- =×- =- =,∵a=(3-)0+-=1+3-1=3,∴原式===-.24.(10分)(2016新疆乌鲁木齐中考)某商场用24 000元购入一批空调,然后以每台3 000元的价格销售,因天气炎热,空调很快售完;商场又以52 000元的价格再次购入该种型号的空调,数量是第一次购入的2倍,但购入的单价上调了200元,每台的售价也上调了200元.(1)商场第一次购入的空调每台进价是多少元?(2)商场既要尽快售完第二次购入的空调,又要在这两次空调销售中获得的利润率不低于22%,打算将第二次购入的部分空调按每台九五折出售,最多可将多少台空调打折出售? 解析 (1)设第一次购入的空调每台进价是x 元,依题意,得=2×,解得x=2 400,经检验,x=2 400是原方程的解.答:第一次购入的空调每台进价为2 400元.(2)第一次购进空调的数量为24 000÷2 400=10台,总收入为3 000×10=30 000元, 第二次购进空调的数量为52 000÷(2 400+200)=20台,不妨设打折售出y 台空调, 则总收入为(3 000+200)·(20-y)+(3 000+200)·0.95y=(64 000-160y)元.两次空调销售的总利润为[30 000+(64 000-160y)]-(24 000+52 000)=(18 000-160y)元, 依题意,得18 000-160y≥(24 000+52 000)×22%,解得y≤8.答:最多可将8台空调打折出售.人教版八年级上第十五章《分式》单元检测卷（含答案）一、选择题(每题3分，共30分)1．(2019·常州)若代数式x ＋1x －3有意义，则实数x 的取值范围是( )A ．x ＝－1B ．x ＝3C ．x ≠－1D ．x ≠3 2.如果把xy x y+中的x 与y 都扩大10倍，那么这个代数式的值（） A ．不变 B ．扩大20倍C ．扩大10倍D ．缩小为原来的110 3.计算22x y y y x x -⎛⎫÷⋅ ⎪⎝⎭的结果是（） A ．2x y B ．y x C ．2x y - D ．－x4.已知a ＝2－2，b ＝1)0，c ＝(－1)3，则a ，b ，c 的大小关系是（）A .a ＞b ＞cB .b ＞a ＞cC .c ＞a ＞bD .b ＞c ＞a5.花粉的质量很小，一粒某种植物花粉的质量约为0.000037毫克，已知1克＝1000毫克，那么0.000037毫克可以用科学记数法表示为( )A .3.7×10－5克B .3.7×10－6克C .3.7×10－7克D .3.7×10－8克6.若（244a -＋12a-）⋅w ＝1，则w ＝（） A .a ＋2(a ≠－2) B .－a ＋2(a ≠2)C .a －2(a ≠2)D .－a －2(a ≠－2)7.分式方程11x -－21x +＝211x -的解是（） A .x ＝0 B .x ＝－1 C .x ＝±1 D .无解 8.若分式22-x 与1互为相反数，则x 的值为( ) A .2B .－2C .1D .－19.(2019·十堰)十堰即将跨入高铁时代，钢轨铺设任务也将完成．现还有6000米的钢轨需要铺设，为确保年底通车，如果实际施工时每天比原计划多铺设20米，就能提前15天完成任务．设原计划每天铺设钢轨x 米，则根据题意所列的方程是( )A.6000x －6000x ＋20＝15 B.6000x ＋20－6000x ＝15 C.6000x －6000x －15＝20 D.6000x －15－6000x＝20 10.已知关于x 的方程22x m x +-＝3的解是正数，则m 的取值范围为( ) A .m ＜－6B .m ＞－6C .m ＞－6且m ≠－4D .m ≠－4二、填空题(每题3分，共18分)11.如果分式11x x +-的值为0，那么x 的值为______. 12.某中学图书馆添置图书，用240元购进一种科普书，同时用200元购进一种文学书.由于科普书的单价比文学书的单价高出一半，因此学校所购买的文学书比科普书多4本.求文学书的单价.设这种文学书的单价为x 元，则根据题意，所列的方程是______.13.计算：(－2xy －1)－3＝______.14．(2019·绥化)当a ＝2018时，代数式⎝⎛⎭⎫a a ＋1－1a ＋1÷a －1（a ＋1）2的值是________． 15.若(x －y －2)2＋│xy ＋3│＝0，则(3x x y -－2x x y -)÷1y的值是. 16.(2019·齐齐哈尔)关于x 的分式方程2x －a x －1－11－x＝3的解为非负数，则a 的取值范围为_____________．三、解答题(共52分)17.（12分）(1)计算1－2a b a b -+÷222244a b a ab b -++；(2) (2019·枣庄)先化简，再求值:x 2x 2－1÷⎝⎛⎭⎫1x －1＋1，其中x 为整数且满足不等式组⎩⎪⎨⎪⎧x －1＞1，5－2x ≥－2.18.(12分)解方程：(1)32x x +＋22x -＝3；(2)241x -＋21x x +-＝－1.19.(8分)先化简2249xx--÷（1－13x-）,再从不等式2x－3＜7的正整数解中选一个使原式有意义的数代入求值.20.（8分）(2019·黄冈)为了对学生进行革命传统教育，红旗中学开展了“清明节祭扫”活动．全校学生从学校同时出发，步行4000米到达烈士纪念馆．学校要求九(1)班提前到达目的地，做好活动的准备工作．行走过程中，九(1)班步行的平均速度是其他班的1.25倍，结果比其他班提前10分钟到达．分别求九(1)班、其他班步行的平均速度．21.(12分)一项工程，甲队单独做需40天完成，若乙队先做30天后，甲、乙两队一起合做20天恰好完成任务，请问：(1)乙队单独做需要多少天才能完成任务?（2）现将该工程分成两部分，甲队做其中一部分工程用了x天，乙队做另一部分工程用了y天，若x，y都是正整数，且甲队做的时间不到15天，乙队做的时间不到70天，那么两队实际各做了多少天?参考答案1.D2.A3.D4.B5.D6.D7.D8.D9.A 10.C 11.－112.45.1240200=-xx 13.－338xy 14.201915.－23 16.a ≤4且a ≠3 17.(1)－b a b+. (2)由⎩⎪⎨⎪⎧x －1＞1，5－2x ≥－2得2＜x ≤72. ∵x 为整数，∴x ＝3，∴x 2x 2－1÷⎝⎛⎭⎫1x －1＋1＝x 2()x ＋1()x －1÷1＋x －1x －1＝x 2()x ＋1()x －1×x －1x ＝x x ＋1＝34. 18.(1)x ＝4.(2)x ＝31.19.答案不唯一，略20.解:设其他班步行的平均速度为x 米/分，则九(1)班步行的平均速度为1.25x 米/分．依题意，得4000x －40001.25x＝10，解得x ＝80，经检验，x ＝80是原方程的解，且符合题意，∴1.25x ＝100.答:九(1)班步行的平均速度为100米/分，其他班步行的平均速度为80米/分．21. (1)乙队单独做需要100天才能完成任务.(2)甲、乙两队实际分别做了14天和65天.。

分式方程精选试题

测试题（一）一、解分式方程（1）11322x x x -=--- (2)512552x x x=--- （3）255522-++x x x =1 (4) 2223-=---xx x（5）（6）21162-x 2312x x x -=--- （7）2212525x x x -=-+ (8) 2124111x x x +=+--(9)114112=---+x x x （10）11322x x x-+=---（11）30120021200=--xx （12）2213211x x x x --=--243111xx x-+=--(13) 2227461x x x x x +=+-- (14) 223433x x x x +-=+(15) 6165122++=-+x x x x （16）3513+=+x x ；测试题（二）1.若分式方程52)1()(2-=--x a a x 的解为3=x ,则a = .2.若关于x 的方程81=+xax 的解为41=x ,则a = .3.若方程xx x --=+-34731无解,则增根为 . 4.若方程3323-+=-x x x 无解,则增根为 .5.分式方程121mx x =-+无解，则增根为 .6.关于x 的方程12144a xx x-+=--无解，则a = .7.关于x 的方程1122kx x +=--无解，则k 的值为 .8.若分式方程201m xm x ++=-无解,则m 的取值是 .9.关于x 的方程21326x m x x -=--无解，则m 的值 .10.当a ，关于x 的分式方程311x a x x--=-无解.11.当m ,解方程115122-=-++x mx x 无解.12.若关于x 的方程313292-=++-x x x m 无解, m 的值 .13.已知关于x 的方程323-=--x mx x 解为正数,则m 的取值范围 . 14.若方程kx x +=+233有负数根,求k 的取值范围 .15.关于x 的方程12-=-+x mx 的解大于零, 求m 的取值范围 .。

鲁教版八年级数学上册第二章分式与分式方程单元测试

鲁教版八年级数学上册第二章分式与分式方程单元测试第二章分式与分式方程单元测试一.单选题（共10题；共30分）1. 当分式的值为0时，x的值是（）A. 0B. 1C. －1D. －22.在,，，，a+中，分式的个数有（）A. 2个B. 3个C. 4个D. 5个3.在式子、、、中，分式的个数是（）A. 1个B. 2个C. 3个D. 4个4.使分式有意义的x的取值范围是（）A. x≠2B. x≠-2C. x>-2D. x<25.下列各式中，正确的是（）A. B. =a+b C. D.6.要使分式有意义，x必须满足的条件是（）A. B. C. D. 且7.若的值为零，则m等于（）A. a+bB. a﹣bC. （a+b）2D. （a﹣b）28.计算的结果为（）A. B. - C. -1 D. 29.已知﹣=，则的值为（）A. B. - C. 2 D. -210.已知，则的值是（）A. B. C. 1 D.二.填空题（共8题；共27分）11.若分式无意义，则x的取值为________.12.化简=________.13.不改变分式的值，使分式的分子，分母的最高次项系数都是正数，则=________．14.分式除以分式，把除式的分子、分母________ 位置后，与被除式________ ；15.若分式的值为零，则x的值为________．16.若关于x的方程无解，则m的值是________．17.若分式方程=5+ 有增根，则a的值为________．18.分式方程：1+ = 的解是________．三.解答题（共6题；共42分）19.（2015?莱芜）先化简，再求值：（1﹣）÷，其中x=320.当x满足什么条件时，分式的值①等于0？②小于0？21.有一项工程，若甲队单独做，恰好在规定日期完成，若乙队单独做要超过规定日期3天完成；现在先由甲、乙两队合做2天后，剩下的工程再由乙队单独做，也刚好在规定日期完成，问规定日期多少天？22.列方程或方程组解应用题：为了培育和践行社会主义核心价值观，引导学生广泛阅读古今文学名著，传承优秀传统文化，我区某校决定为初三学生购进相同数量的名著《三国演义》和《红岩》．其中《三国演义》的单价比《红岩》的单价多28元．若学校购买《三国演义》用了1200元，购买《红岩》用了400元，求《三国演义》和《红岩》的单价各多少元．23.比邻而居的蜗牛神和蚂蚁王相约，第二天上午8时结伴而行，到相距16米的银树下参加探讨环境保护的微型动物首脑会议．蜗牛神想到“笨鸟先飞”的古训，于是给蚂蚁王留下一纸便条后，提前2小时独自先行，蚂蚁王按既定时间出发，结果它们同时到达．已知蚂蚁王的速度是蜗牛神的4倍，求它们各自的速度．24.2016年“母亲节”前夕，宜宾某花店用4000元购进若干束花，很快售完，接着又用4500元购进第二批花，已知第二批所购花的束数是第一批所购花束数的1.5倍，且每束花的进价比第一批的进价少5元，求第一批花每束的进价是多少？答案解析部分一.单选题1.【答案】B【考点】分式的值为零的条件【解析】【分析】根据分式值为零的条件可得x-1=0，x+2≠0，解可得答案．【解答】由题意得：x-1=0，x+2≠0，解得：x=1，故选：B．【点评】此题主要考查了分式值为零的条件：是分子等于零且分母不等于零．注意：“分母不为零”这个条件不能少．2.【答案】B【考点】分式的定义【解析】【分析】判断分式的依据是看分母中是否含有字母，如果分母中含有字母则是分式，如果分母中不含有字母则不是分式．【解答】，，a+这三个式子分母中含有字母，因此是分式．其它式子分母中均不含有字母，是整式，而不是分式．故选B．【点评】本题主要考查分式的概念，分式与整式的区别主要在于：分母中是否含有字母．3.【答案】B【考点】分式的定义【解析】【分析】判断分式的依据是看分母中是否含有字母，如果含有字母则是分式，如果不含有字母则不是分式．【解答】，，分母中均不含有字母，因此它们是整式，而不是分式．，分母中含有字母，因此是分式．故选B．【点评】本题主要考查分式的定义，特别注意π不是字母，是常数，所以不是分式，是整式．【考点】分式有意义的条件【解析】【分析】根据分式有意义的条件：分母不等于0，即可求解．【解答】根据题意得：x+2≠0，解得：x≠-2．故选B．【点评】本题主要考查了分式有意义的条件，正确理解条件是解题的关键．5.【答案】D【考点】分式的基本性质【解析】【分析】正确，其他都错误。

初中数学北师大版八年级下册期末-章节测试习题(2)

章节测试题1.【题文】（1）计算（2)解不等式组，并写出不等式组的非负整数解。

（3）解分式方程：【答案】①+2；②0、1；③原方程无解【分析】（1）首先计算负指数次幂，0次幂，二次根式的混合运算，去掉绝对值符号，化简二次根式，然后合并同类二次根式即可求解；（2）首先解每个不等式，两个不等式解集的公共部分就是不等式组的解集．（3）中因为x2-4=（x+2）（x-2），所以最简公分母为（x+2）（x-2），确定方程的最简公分母后，方程两边乘最简公分母，把分式方程转化为整式方程求解．．【解答】解（1）原式=3-1-（1-）+-1=3-1-1++2-1=+2（2）解不等式①得，x≤1，解不等式②得，x＜4，所以不等式组的解集是x≤1，所以不等式组的非负整数解是0、1．故答案为：0、1．（3）方程两边同乘（x+2）（x-2），得：（x-2）2=（x+2）2+16，整理解得x=-2．经检验x=-2是增根，故原方程无解．2.【题文】已知，求的值. 【答案】-【分析】将分式通分、化简，再将已知条件变形，整体代入．【解答】解：=-÷=-=-∵∴1-即1-=1-∴-=-∴原式=-3.【题文】对x，y定义一种新运算T，规定：T（x，y）＝（其中a，b均为非零常数），这里等式右边是通常的四则运算，例如：T（0，1）＝＝b，已知T（1，1）＝2.5，T（4，-2）＝4．（1）求a，b的值；（2）若关于m的不等式组恰好有2个整数解，求实数P的取值范围．【答案】（1）a，b的值分别为3和2；（2）实数P的取值范围是≤p＜2【分析】（1）根据题意把T（1，1）＝2.5，T（4，-2）＝4代入T（x，y）＝即可求出ab的值；（2）根据题意列出关于m的不等式，分别解出来再根据m有两个整数解来确定p的取值.【解答】（1）根据题意得：，①+②得：3a＝9，即a＝3，把a＝3代入①得：b＝2，故a，b的值分别为3和2；（2）根据题意得：，由①得：m≤，由②得：m＞p-3，∴不等式组的解集为p-3＜m≤，∵不等式组恰好有2个整数解，即m＝0，1，∴-1≤p-3＜0，解得≤p＜2，即实数P的取值范围是≤p＜2．4.【题文】如图所示，已知△ABC的三个顶点的坐标分别为A（-2，3）、B（-6，0）、C（-1，0），（1）请直接写出点A关于原点O对称的点的坐标；（2）将△ABC绕坐标原点O逆时针旋转90°，求出A′点的坐标。

人教版八年级数学上《第15章分式》单元测试(2)含答案解析

《第15章分式》一、选择题（本题共8小题，每小题3分，共24分）1． 20100的值是（）A．2010 B．0 C．1 D．﹣12．计算（﹣3a﹣1）﹣2的结果是（）A．6a2B．C．D．9a23．下列算式中，你认为错误的是（）A． B．C．D．4．如果把分式中x和y都扩大10倍，那么分式的值（）A．扩大10倍B．缩小10倍C．扩大2倍 D．不变5．关于分式，当x=﹣a时，（）A．分式的值为零 B．当时，分式的值为零C．分式无意义D．当时，分式无意义6．已知非零有理数x，y满足x2﹣6xy+9y2=0，则=（）A．B．C．D．7．若，则（）A．m=6，n=1 B．m=4，n=1 C．m=2，n=1 D．m=2，n=08．一项工程，甲单独做需m小时完成，若与乙合作20小时可以完成，则乙单独完成需要的时间是（）A．小时B．小时C．小时D．小时二、填空题9．当x 时，分式有意义；当x 时，分式的值为零．10．成人体内成熟红细胞的平均直径一般为0.00000725m，用科学记数法可以表示为m．11．化简= ．12．计算： = ．13．方程的解是．14．关于x的方程的解为2，则k的值为．15．若的值是．16．轮船顺水航行40km所需的时间和逆水航行30km所需的时间相同．已知水流速度为3km/h，设轮船在静水中的速度为xkm/h，可列方程为．三、解答题17．化简：．18．解方程：．19．先化简，再求值：，其中x=5．20．已知方程的解是关于x的方程x2﹣2kx=0的解，求k的值．21．列方程或方程组解应用题：某市在旧城改造过程中，需要整修一段全长2400米的道路．为了尽量减少施工对城市交通所造成的影响，实际工作效率比原计划提高了20%，结果提前8小时完成任务．求原计划每小时修路的长度．22．节日里，姐妹两人在50米的跑道上进行短路比赛，两人从出发点同时起跑，姐姐到达终点时，妹妹离终点还差3米，已知姐妹两人的平均速度分别为a米/秒、b米/秒．（1）如果两人重新开始比赛，姐姐从起点向后退3米，姐妹同时起跑，两人能否同时到达终点？若能，请求出两人到达终点的时间；若不能，请说明谁先到达终点．（2）如果两人想同时到达终点，应如何安排两人的起跑位置？请你设计两种方案．《第15章分式》参考答案与试题解析一、选择题（本题共8小题，每小题3分，共24分）1．20100的值是（）A．2010 B．0 C．1 D．﹣1【考点】零指数幂．【专题】计算题．【分析】根据任何非0数的0次幂都是1，即可求解．【解答】解：20100=1，故选C．【点评】任何非0的数的0次幂是1，而0的0次幂无意义．2．计算（﹣3a﹣1）﹣2的结果是（）A．6a2B．C．D．9a2【考点】负整数指数幂．【分析】根据积的乘方的性质以及负整数指数次幂等于正整数指数次幂的倒数进行计算即可得解．【解答】解：（﹣3a﹣1）﹣2=（﹣3）﹣2（a﹣1）﹣2=a2．故选B．【点评】本题主要考查了积的乘方的性质，负整数指数次幂等于正整数指数次幂的倒数的性质，熟记性质是解题的关键．3．下列算式中，你认为错误的是（）A． B．C．D．【考点】分式的乘除法；分式的加减法．【专题】计算题．【分析】A、利用同分母分式的加法法则计算得到结果，即可做出判断；B、利用除以一个数等于乘以这个数的倒数将除法运算化为乘法运算，约分得到结果，即可做出判断；C、原式通分并利用同分母分式的减法法则计算得到结果，即可做出判断；D、原式约分得到结果，即可做出判断．【解答】解：A、原式==1，本选项正确；B、原式=1××=，本选项错误；C、原式==﹣，本选项正确；D、原式=•=，本选项正确．故选B．【点评】此题考查了分式的乘除法，分式的乘除法的关键是约分，约分的关键是找公因式．4．如果把分式中x和y都扩大10倍，那么分式的值（）A．扩大10倍B．缩小10倍C．扩大2倍 D．不变【考点】分式的基本性质．【专题】探究型．【分析】先把分式中的x、y用10x、10y代替，得出代替后的分式与原分式进行比较即可．【解答】解：分式中的x、y用10x、10y代替得， =．故选D．【点评】本题考查的是分式的基本性质，即分式的分子、分母扩大相同的倍数，分式的值不变．5．关于分式，当x=﹣a时，（）A．分式的值为零 B．当时，分式的值为零C．分式无意义D．当时，分式无意义【考点】分式的值；分式有意义的条件；分式的值为零的条件．【分析】根据分式有意义的条件是分母不等于零；分式无意义的条件是分母等于零；分式值为零的条件是分子等于零且分母不等于零即可判断．【解答】解：A、当x=﹣a=时，分式无意义，故本选项错误；B、当x+a=0且x≠时，即当时，分式的值为零，故本选项正确；C、当x=﹣a≠时，分式有意义，故本选项错误；D、当a=时，分式有意义，故本选项错误；故选B．【点评】本题考查了分式有意义、分式无意义的条件及分式值为零的条件，是基础知识，需熟练掌握．6．已知非零有理数x，y满足x2﹣6xy+9y2=0，则=（）A．B．C．D．【考点】分式的值．【分析】由x2﹣6xy+9y2=0，根据完全平方公式得出x=3y，再代入，计算即可求出其值．【解答】解：∵x2﹣6xy+9y2=0，∴（x﹣3y）2=0，∴x=3y，∴==．故选C．【点评】本题考查了完全平方公式及分式的值，由完全平方公式得出x=3y是解题的关键．7．若，则（）A．m=6，n=1 B．m=4，n=1 C．m=2，n=1 D．m=2，n=0【考点】分式的乘除法．【专题】计算题．【分析】利用单项式除以单项式法则计算，根据结果相等求出m与n的值即可．【解答】解：x m y n÷x3y=x m﹣3y n﹣1=x﹣1，∴m﹣3=﹣1，n﹣1=0，解得：m=2，n=1．故选C．【点评】此题考查了分式的乘除法，分式的乘除法的关键是约分，约分的关键是找公因式．8．一项工程，甲单独做需m小时完成，若与乙合作20小时可以完成，则乙单独完成需要的时间是（）A．小时B．小时C．小时D．小时【考点】列代数式（分式）．【专题】工程问题．【分析】设工作总量为1，甲乙合作20小时可以完成，那么甲乙合作的工效是，甲单独做需m小时完成，甲的工效为，则乙的工效为：（），由时间=工作量÷工效列式．【解答】解：设工作总量为1，那么甲乙合作的工效是，甲单独做需m小时完成，甲的工效为，乙单独完成需要的时间是1÷（）=1÷=小时．故选A．【点评】本题考查工作量=工效×时间这个等量关系，如果没有工作总量，通常把工作总量看成1．二、填空题9．当x ≠时，分式有意义；当x =﹣1 时，分式的值为零．【考点】分式的值为零的条件；分式有意义的条件．【分析】分式有意义：分母不等于零；分式的值等于零：分子等于零，且分母不等于零．【解答】解：当分母3x﹣2≠0，即x≠时，分式有意义；当分子x+1=0且3x﹣2≠0，即x=﹣1时，分式的值为零．故答案是：；﹣1．【点评】本题考查了分式有意义的条件，分式的值为零的条件．若分式的值为零，需同时具备两个条件：（1）分子为0；（2）分母不为0．这两个条件缺一不可．10．成人体内成熟红细胞的平均直径一般为0.00000725m，用科学记数法可以表示为7.25×10﹣6m．【考点】科学记数法—表示较小的数．【分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10﹣n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．【解答】解：将0.00000725用科学记数法表示为：7.25×10﹣6．故答案为：7.25×10﹣6．【点评】本题考查用科学记数法表示较小的数，一般形式为a×10﹣n，其中1≤|a|＜10，n为由原数左边起第一个不为零的数字前面的0的个数所决定．11．化简= x﹣1 ．【考点】约分．【专题】计算题．【分析】将分式分子因式分解，再将分子与分母公共的因式约分，即可求解．【解答】解： ==x﹣1．故答案为：x﹣1．【点评】此题主要考查了分式的约分，分子与分母能因式分解的必须首先因式分解再约分是解决问题的关键．12．计算： = 1 ．【考点】分式的加减法．【专题】计算题．【分析】因为分式的分母相同，所以只要将分母不变，分子相加即可．【解答】解： =．故答案为1．【点评】此题比较容易，是简单的分式加法运算．13．方程的解是x=2 ．【考点】解分式方程．【专题】计算题．【分析】观察可得最简公分母是x（x+2），方程两边乘最简公分母，可以把分式方程转化为整式方程求解．【解答】解：方程的两边同乘x（x+2），得2x=x+2，解得x=2．检验：把x=2代入x（x+2）=8≠0．∴原方程的解为：x=2．故答案为：x=2．【点评】本题考查了分式方程的解法，注：（1）解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．（2）解分式方程一定注意要验根．14．关于x的方程的解为2，则k的值为 3 ．【考点】分式方程的解．【专题】计算题．【分析】将x=2代入方程计算求出k的值，检验即可．【解答】解：将x=2代入方程得：﹣1=0，解得：k=3，经检验k=3是方程的解．故答案为：3．【点评】此题考查了分式方程的解，方程的解即为能使方程左右两边相等的未知数的值．15．若的值是11 ．【考点】完全平方公式．【专题】计算题．【分析】把x﹣=3利用完全平方公式两边平方展开，整理即可得解．【解答】解：∵x﹣=3，∴（x﹣）2=9，即x2﹣2+=9，解得x2+=9+2=11．故答案为：11．【点评】本题主要考查了完全平方公式的运用，利用好乘积二倍项不含字母是解题的关键．16．轮船顺水航行40km所需的时间和逆水航行30km所需的时间相同．已知水流速度为3km/h，设轮船在静水中的速度为xkm/h，可列方程为=．【考点】由实际问题抽象出分式方程．【分析】根据静水中的速度为xkm/h，则顺水速度为（x+3）km/h，逆水速度为（x﹣3）km/h，根据关键语句“轮船顺水航行40km所需的时间和逆水航行30km所需的时间相同．”列出方程即可．【解答】解：设轮船在静水中的速度为xkm/h，则顺水速度为（x+3）km/h，逆水速度为（x﹣3）km/h，由题意得：=，故答案为： =．【点评】此题主要考查了由实际问题抽象出分式方程，关键是正确理解题意，抓住关键语句，列出方程．三、解答题17．（2013•嘉峪关校级一模）化简：．【考点】分式的混合运算．【分析】根据分式混合运算的法则进行计算即可．【解答】解：原式=•﹣=﹣=0．【点评】本题考查的是分式的混合运算，在解答此类题目时要注意通分及约分的灵活应用．18．解方程：．【考点】解分式方程．【分析】观察可得最简公分母是（x﹣1），方程两边乘最简公分母，可以把分式方程转化为整式方程求解．【解答】解：原方程可化为：﹣=x，方程的两边同乘（x﹣1），得1﹣x=x（x﹣1），解得x=±1．检验：把x=1代入（x﹣1）=0，x=1是方程的增根；把x=﹣1代入（x﹣1）=﹣2≠0，x=﹣1是方程的根．故原方程的解为：x=﹣1．【点评】本题考查了分式方程的解法，注意：（1）解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．（2）解分式方程一定要验根．19．先化简，再求值：，其中x=5．【考点】分式的化简求值．【分析】先根据分式混合运算的法则把原式进行化简，再把x的值代入进行计算即可．【解答】解：原式=•﹣=﹣﹣=﹣=﹣=，当x=5时，原式==﹣．【点评】本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．20．已知方程的解是关于x的方程x2﹣2kx=0的解，求k的值．【考点】解分式方程；一元二次方程的解．【分析】先求出方程的解，再将分式方程的解代入方程x2﹣2kx=0，即可求出k的值．【解答】解：，方程的两边同乘2（x﹣1），得2=x﹣1，解得x=3．经检验：x=3是原方程的根．将x=3代入方程x2﹣2kx=0，得9﹣6k=0，解得k=．【点评】本题考查了分式方程的解法及一元二次方程的解的定义，正确求出分式方程的解是解题的关键，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．21．（2013•潮阳区模拟）列方程或方程组解应用题：某市在旧城改造过程中，需要整修一段全长2400米的道路．为了尽量减少施工对城市交通所造成的影响，实际工作效率比原计划提高了20%，结果提前8小时完成任务．求原计划每小时修路的长度．【考点】分式方程的应用．【专题】应用题．【分析】本题的关键语是：“提前8小时完成任务”；等量关系为：原计划用的时间﹣实际所用的时间=8．而工作时间=工作总量÷工作效率．【解答】解：设原计划每小时修路x米．依题意得：．解得：x=50．经检验：x=50是所列方程的解，且符合实际问题的意义．答：原计划每小时修路50米．【点评】列分式方程解应用题与所有列方程解应用题一样，重点在于准确地找出相等关系，这是列方程的依据．22．（2007•大连一模）节日里，姐妹两人在50米的跑道上进行短路比赛，两人从出发点同时起跑，姐姐到达终点时，妹妹离终点还差3米，已知姐妹两人的平均速度分别为a米/秒、b米/秒．（1）如果两人重新开始比赛，姐姐从起点向后退3米，姐妹同时起跑，两人能否同时到达终点？若能，请求出两人到达终点的时间；若不能，请说明谁先到达终点．（2）如果两人想同时到达终点，应如何安排两人的起跑位置？请你设计两种方案．【考点】分式方程的应用．【专题】行程问题．【分析】（1）姐妹两人在相同时间内所走的路程之比为：50：47，可得两人的速度之比为50：47，设出其中一人的速度，得到另一人的速度，分别算出两人到底终点的时间，比较即可得到谁先到达终点；（2）①若妹妹在起跑线不动，表示出同时到终点所用时间，所以姐姐应该后退的米数为姐姐的速度乘以到达的时间数﹣50；②同理，若姐姐在起跑线不动，则妹妹只需向前3米，便可与姐姐同时到达终点．【解答】解：（1）姐妹两人在相同时间内所走的路程之比为：50：47，可得两人的速度之比为50：47，设姐姐的速度为50k米/秒，则妹妹的速度为47k米/秒，姐姐所用的时间为：秒，妹妹所用的时间为：秒，﹣==＜0，∴姐姐先到；（2）若安排姐姐后退，则两人同时到达的时间为妹妹跑50米用的时间为，此时姐姐跑的米数为：×50k=米，后退的米数为：﹣50=米；若安排妹妹前进，则两人同时到达的时间为姐姐跑50米用的时间为=，此时妹妹跑的米数为：×47k=47m，需前进的米数为50﹣47=3米；答：姐姐后退米或妹妹前进3米．【点评】考查行程问题的相关的知识点；判断出姐妹两人的速度之比是解决本题的突破点．。

人教版八年级数学上册第 15 章《分式》单元测试题(配套练习附答案)

【答案】，
【解析】
【分析】
原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，将x的值代入计算即可求出值．
【详解】解：原式
当x=1时，原式= ．
【点睛】本题考查了分式的化简求值，解题的关键是熟练的掌握分式的化简求值.
19.开学初，小芳和小亮去学校商店购买学习用品，小芳用30元钱购买钢笔的数量是小亮用25元钱购买笔记本数量的2倍，已知每支钢笔的价格比每本笔记本的价格少2元
11.当a=______时，的值为零．
【答案】﹣1．
【解析】
【分析】
根据分式的值为零的条件列式计算即可．
【详解】由题意得：a2﹣1=0，a﹣1≠0，
解得：a=﹣1．
故答案为：﹣1．
【点睛】本题考查了分式的值为零的条件．若分式的值为零，需同时具备两个条件：①分子为0；②分母不为0．这两个条件缺一不可．
（1）求每支钢笔和每本笔记本各是多少元；
（2）学校运动会后，班主任再次购买上述价格的钢笔和笔记本共50件作为奖品，奖励给校运动会中表现突出的同学，总费用不超过200元．请问至少要买多少支钢笔？
【答案】（1）每支钢笔3元，每本笔记本5元；（2）至少要买25支钢笔．
【解析】
【分析】
（1）根据小芳用30元钱购买钢笔的数量是小亮用25元钱购买笔记本数量的2倍，已知每支钢笔的价格比每本笔记本的价铬少2元，可以得到相应的方程，解方程即可求得每支钢笔和每本笔记本各是多少元；
2018-2019年人教版八年级数学上册第 15 章《分式》经典题型单元测试题
第Ⅰ卷（选择题）
一．选择题（每小题3分，共10小题）
1.若把变形为，则下列方法正确的是
A.分子与分母同时乘 B.分子与分母同时除以

《第十五章分式》单元测试卷含答案(共6套)

《第十五章分式》单元测试卷（一）（本检测题满分：100分，时间：90分钟）一、选择题（每小题3分，共30分） 1.下列各式中，分式的个数为（），，，，，，.A. B. C. D. 2.要使分式有意义，则应满足（）A ．≠-1B ．≠2C ．≠±1D ．≠-1且≠23.化简：（）A.0B.1C.D.4.将分式中的，的值同时扩大到原来的2倍，则分式的值（）A.扩大到原来的倍B.缩小到原来的C.保持不变D.无法确定5.若分式的值为零，则的值为( )A.或B.C.D.6.某工厂现在平均每天比原计划多生产50台机器，现在生产600台机器所需时间与原计划生产450台机器所需时间相同.设原计划平均每天生产x 台机器，根据题意，下面所列方程正确的是（） A. B. C.D. 3x y -21a x -3a b -12x y +12x y +2123x x =-+5432211x xx x -=--x 1x x -2x x y +x y 221122+--x x x 60045050x x =+60045050x x =-60045050x x =+60045050x x =-7.对于下列说法，错误的个数是（）①是分式；②当时，成立；③当时，分式的值是零；④；⑤；⑥. A.6 B.5 C.4 D.3 8.把，，通分的过程中，不正确的是（） A ．最简公分母是（-2）（+3）2 B ． C ． D ．9.下列各式变形正确的是（）A. B. C.D.10.若，则w=（） A. B. C. D.二、填空题（每小题3分，共24分） 11.化简的结果是 . 12.将下列分式约分：(1) ；(2).13.计算= .14. 有一个分式，三位同学分别说出了它的一些特点，甲：分式的值不可能为0；乙：分式有意义时的取值范围是≠±1；丙：当=-2时，分式的值为1.请你写出满足上述全部特点的一个分式： .15.已知，则________.1x ≠2111x x x -=+-33x x +-11a b a a b ÷⨯=÷=2a a a x y x y +=+3232x x-⋅=-x y x y x y x y -++=---22a b a bc d c d--=++0.20.03230.40.0545a b a b c d c d --=++a b b ab c c b--=--241142w a a ⎛⎫+⋅= ⎪--⎝⎭2(2)a a +≠-2(2)a a -+≠2(2)a a -≠2(2)a a --≠-2211121x x x x +⎛⎫+÷ ⎪--+⎝⎭258xx 22357mnn m -2223362cab b c b a ÷222n m m n m n n m m ---++16.若，则=_____________.17.代数式有意义时，应满足的条件是_____________. 18.为改善生态环境,防止水土流失,某村拟在荒坡地上种植960棵树, 由于青年团员的支持,每日比原计划多种20棵,结果提前4天完成任务,问原计划每天种植多少棵树?设原计划每天种植棵树，根据题意可列方程__________________.三、解答题（共46分）19.（6分）约分：（1）；（2）.20.（4分）通分：，. 21.（10分）计算与化简：（1）；（2）；（3）；（4）；（5）． 22.（5分）先化简，再求值：,其中，. 23.（6分）若, 求的值.24.（9分）解下列分式方程：（1）；（2）；（3）. 25.（6分）“母亲节”前夕，某商店根据市场调查，用3 000元购进第一批盒装花，上市后很快售完，接着又用5 000元购进第二批这种盒装花．已知第二批所购花的盒数是第一批所购花的盒数的2倍，且每盒花的进价比第一批的进价少50544≠==zy x z y x y x 32+-+11x -x 22444a a a --+22211m m m -+-21x x -2121x x --+222x y y x ⋅22211444a a a a a --÷-+-22142a a a ---211a a a ---()()222142y x x y xy x y x +-÷⋅-222693bab a aba +--x1y 1y xy x y xy x ---+2232730100+=x x 132543297=-----x x x x 21212339x x x -=+--元．求第一批盒装花每盒的进价.参考答案1.C 解析：由分式的定义，知，，为分式，其他的不是分式.2. D 解析：要使分式有意义，则（+1）（-2）≠0，∴ +1≠0且-2≠0， ∴ ≠-1且≠2．故选D ．3. C 解析：原式=－== =x .点拨：此题考查了同分母分式相减，分母不变，分子相减.4.A 解析：因为，所以分式的值扩大到原来的2倍.5.C 解析：若分式的值为零，则所以6. A 解析：若原计划平均每天生产x 台机器，则现在每天可生产（x +50）台，根据现在生产600台机器所需时间与原计划生产450台机器所需时间相同，从而列出方程. 7.B 解析：不是分式，故①不正确；当时，成立，故②正确；当时，分式的分母，分式无意义，故③不正确；④，故④不正确；，故⑤不正确；，故⑥不正确.8. D 解析：A.最简公分母为（-2）（+3）2，正确； B.(分子、分母同乘，通分正确； C.(分子、分母同乘)，通分正确；D.通分不正确，分子应为2×（-2）=2-4.故选D ．9.D 解析：，故A 不正确；，故B 不正确；，故C 不正确；，故D 正确.21a x -3ab-12x y +()()y x x y x x y x x y x x +⨯=+=+=+22222224222122+--x x x 60045050x x=+1x ≠2111x x x -=+-33x x +-10. D 解析：∵ ， ∴ .11.x -1 解析：原式=÷ =× =x -1.12.（1）（2）解析：(1)；(2). 13. 解析： 14.（答案不唯一）解析：由题意，可知所求分式可以是，，等，答案不唯一.15. 解析：因为，所以，所以16.解析：设则所以17.x ≠±1 解析：由题意知分母不能为0，∴ |x |-1≠0,∴ ，则x ≠±1.18. 解析：根据“原计划完成任务的天数实际完成任务的天数”列方程即可．依题意列方程为． 19.解：（1）；（2） ()()()()41211222222a w w w a a a a a a ⎛⎫-++⋅=⋅=-⋅=⎪⎪-+--++⎝⎭()22w a a =---≠83x n m5-258x x 83x 22357mn nm -nm5-c b a 323.36262322223322233cb a abc b c b a c ab b c b a =⋅=÷79n m 34=()()()()()()()()n m n m m n m n m n m n n m n m n m m n m m n m n n m m -+--+++-+-=---++2222()()()().799734342222222==⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛+=-+=-+-++-=n n n n n n n n m n m n n m n m m n mn mn m 118544≠===k z y x .11811815844432==+-+=+-+k k k k k k k z y x y x 420960960=+-x x 420960960=+-x x 22444a a a --+()22)2(222-+=-+-=a a a a a ）（22211m m m-+-()().111)1()1(1)1()1(22m m m m m m m m +-=+--=+--=20.解：因为与的最简公分母是所以； . 21.解：（1）原式=．（2）原式=．（3）原式==．（4）原式====．（5）原式=． 22.解：当，时，原式23.解：因为所以所以24.解：（1）方程两边都乘，得. 解这个一元一次方程，得. 检验：把代入原方程，左边右边. 所以，是原分式方程的根.21x x -2121x x --+21x x-()211)1(1--=-=x x x x x 2121x x --+()221)1(1--=--=x x x x 4y()()()()()2221112a a a a a a +--⋅+--()()212a a a +=+-()()()()()()2222222222a a a a a a a a a a +---=-+-+-+()()21222a a a a -=-++2111a a a +--()()2111a a a a -+--2211a a a -+-11a -()()()12222xy x y x y y x y x x y +-⋅⋅=-+--()().3336932222b a ab a b a a b ab a ab a -=--=+--.49162498212483==---=-ba ax 1y 1().41422342)(322232=--=--+-=--+-=---+xy xy xy xy xy xy xy y x xy y x y xy x y xy x（2）方程两边都乘，得. 整理，得.解这个一元一次方程，得. 检验：把代入原方程，左边右边. 所以，是原分式方程的根. （3）方程两边都乘，得. 整理，得.解这个一元一次方程，得. 检验可知，当时，.所以，不是原分式方程的根，应当舍去.原分式方程无解. 25. 解：设第一批盒装花的进价是x 元/盒，则 2×=，解得 x =30. 经检验，x =30是原分式方程的根．答：第一批盒装花每盒的进价是30元．点拨：本题考查了分式方程的应用．注意：分式方程需要验根，这是易错的地方．《第十五章分式》单元测试卷（二）一、选择题：（每小题3分，共30分）二、1．下列各式，，，，，中，是分式的共有（）A.1个B.2个C.3个D.4个2．如果分式的值等于0，那么（）A. B. C. D.x 000 350005-x 2b a -x x 3+πy +5()1432+x b a b a -+)(1y x m-242--x x 2±=x 2=x 2-=x 2≠x3．与分式相等的是（） A. B. C. D. 4．若把分式中的x 和y 都扩大3倍，那么分式的值（） A ．扩大3倍 B ．不变 C ．缩小3倍 D ．缩小6倍5．化简的结果是（）A.B. C. D. 6．下列算式中，你认为正确的是( ) A ．B. C ． D ． 7．甲乙两个码头相距千米，某船在静水中的速度为a 千米/时，水流速度为b 千米/时，则船一次往返两个码头所需的时间为（）小时. A.B. C. D. 8．甲、乙两班学生参加植树造林，已知甲班每天比乙班多植5棵树，甲班植80棵树所用的天数与乙班植70棵树所用的天数相等，若设甲班每天植树棵，则根据题意得出的方程是（）A ．B ．C ．D ． 9．分式方程若有增根，则增根可能是（） A ．1 B ． C ．1或 D ．010．若三角形三边分别为a 、b 、c ，且分式的值为0，则此三角形一定是（）A. 不等边三角形B. 腰与底边不等的等腰三角形C. 等边三角形D. 直角三角形二、填空题：（每空2分，共18分）ba ba --+-b a b a -+b a b a +-b a b a -+-ba b a +--xyyx 2+2293m mm --3+m m 3+-m m 3-m m m m-31-=---a b a b a b 11=⨯÷baa b 3131aa -=b a b a b a b a +=--⋅+1)(1222s b a s +2b a s -2b s a s +ba sb a s -++x 80705x x =-80705x x =+80705x x =+80705x x =-214111x x x +-=--1-1-ca b bc ac ab --+-211．当x ________时,分式有意义． 12．利用分式的基本性质填空：（1）（2） 13．计算：__________． 14. 计算：＝ . 15. 分式的最简公分母是． 16. 当x= 时，分式的值等于 .17. 生物学家发现一种病毒的长度约为0.000 043毫米，用科学记数法表示为_____________米. 18. 已知，则分式的值为 ___ ．三、解答题：（每题5分，共25分） 19.计算：（1）（2）（3）（4）20. 先化简，再求值：，其中．xx2121-+())0(,10 53≠=a axy xy a ()1422=-+a a =+-+3932a a a abba b ab -÷-)(2abb a 65,43,322x x +-5121311=-y x yxy x yxy x ---+2232x y y x y x y x -+-+-+212222222)(ab a ab b ab a a ab -⋅+-÷-1111-÷⎪⎭⎫ ⎝⎛--x x x 32232)()2(b a c ab ---÷x x x x x x 11132-⋅⎪⎭⎫ ⎝⎛+--2=x四、解分式方程：（每题6分，共12分） 21. 22.五、列方程解应用题：（每题6分，共12分）23. 某工人原计划在规定时间内恰好加工1500个零件，改进了工具和操作方法后，工作效率提高为原来的2倍，因此加工1500个零件时，比原计划提前了5小时，问原计划每小时加工多少个零件？24. 学校在假期内对教室内的黑板进行整修，需在规定期限内完成．如果由甲工程小组做，恰好如期完成；如果由乙工程小组做，则要超过规定期限3天．结果两队合作了2天，余下部分由乙组独做，正好在规定期限内完成，问规定期限是几天？六、解答题：（共3分） 25．为何值时，关于的方程会产生增根．答案：1、C2、C3、B4、C5、B6、D7、D8、D9、C 10、B87176=-+--x x x 1412112-=-++x x x m x 223242mx x x x +=--+11、 12、（1）（2） 13、 14、 15、 16、 -117、 18、19、（1）0 （2）（3） 1 （4） 20、 21、822、是增根，原方程无解。

八年级下数学第二章《分式》测验题

湘教版八年级下数学第二章《分式》测验题•填空题（20分） 1•用科学记数法表示0.00009=0.1x +0.3y =0.5x -0.02y 25x - y3.当x 时分式—_2有意义.x 3x 2 _164. 当 x 时分式 ------ =0.x -45计算： 4—(—2)2_3 2 十(—2)= _______________的最大值为18•化简x J,选择题（30分）把答案填在下表中1.若方程汙=亡有增根’则的值为（）10.我们知道：6是没有意义的，9•计算 x 4y • (x )请你写出一个一定有意义的分式2.填写适当的多项式6•化简a 2 ab a 2 -b 2亠（丄）2y•计算题（30 分）A . -3x 2B . x-2 x-1C x-1D . x - -1x 6x 3 x-2x 36 . 计算：—9(1 — - ) X 12— 32的结果是( )23A . 4B . — 14C . —26D . —10儿若启？=缶+三则A'B 的值分别为（10.已知：x --1 =3则x 2 + &等于（x x A . — 1B . 1C . 3) D . 9B .1C .2D . -22.下列各式变形正确的是（)2A x xA .—二——B . b=(-)2C .x _ xy~2 y xyaay y3.下列各数中是质数的是（A . 35B . 36C . )37D . 3832・aA . n 2B . 2nC .(2n+1)2 —1D . 2 n+1 B . 2'—1C. — 1' — 3D . — 2' — 38 . 下列正确的是（)A . 0 ” a =1 —2B . 3=— 9 C . —25 . 6X 0 =560 D . 1 —2(-)2 = 25 5 9 . 已知： 4 M=—— ,N = 1 1 + 贝 M'N的关系是（a -4a 2 2 -aA . M = NB . M XN=1 C.M + N = 0 D.不能确定4.当n 为正整数时，下列各式能被 4整的除是（5 .将分式:化简的结果是（A . 1' 3•计算题（30 分）x 2y +y - x x - y y -x2 22a_ x b 3 5b a 32.7a 3b 228a J b10.已知：x --1 =3则x 2 + 2等于（x x A . — 1B . 1C . 3) D . 95.比-x+1A .M = NB . M XN=1 C.M + N = 0D.不能确定六.某项工程，甲、乙两队合作8天可以完成。

鲁教版2019—2020八年级数学第二章分式与分式方程单元测试题2(附答案详解)

鲁教版2019—2020八年级数学第二章分式与分式方程单元测试题2（附答案详解）1．要使分式的值为0,则x的值为( )A．3或-3 B．3 C．-3 D．22．下列各式中，正确的是()A．－=B．－＝C．＝D．－＝3．某单位向一所希望小学赠送1080件文具，现用A，B两种不同的包装箱进行包装，已知每个B型包装箱比A型包装箱多装15件文具，单独使用B型包装箱比单独使用A型包装箱可少用12个，设B型包装箱每个可以装x件文具，根据题意列方程为( )A．B．C．D．4．化简的结果是（）A．B．C．D．5．空气的密度(单位体积内空气的质量)是0.00129g/cm3，用科学记数法表示0.00129为( ) A．1.29×10-3B．0.129×10-3C．0.129×10-2D．1.29×10-26．在，，，中，分式的个数为（）A．B．C．D．7．若关于x的方程有增根，则m的值是（）.A．B．C．D．8．下列等式成立的是( )A．=0 B．=-1 C．-D．=09．计算的结果是()A．B．C．D．10．下列运算正确的是（）A．B．C．D．11．计算：________．12．对于实数，b定义一种新运算“”：，例如，.则方程的解是_______.13．若关于x的分式方程有增根，则m的值为___．14．若有增根，则m=______15．计算﹣22×（2018﹣2019）0÷2﹣2的结果是_____．16．计算：﹣（﹣2）+2﹣2＝_____．17．某项工程限期完成，甲单独做提前1天完成，乙单独做延期2天完工，现两人合作1天后，余下的工程由乙队单独做，恰好按期完工，求该工程限期___________天.18．关于x的分式方程的解不小于1，则m的取值范围是_____．19．分式的最简公分母是________20．若关于x的方程的解为整数，且不等式组无解，则所有满足条件的非负整数a的和为_____．21．服装厂准备为某中学加工470套运动装，在加工完200套后，采用了新技术，使得工作效率比原计划提高了20%，结果共用了17天完成任务，问原计划每天加工服装多少套？22．已知，求代数式的值.23．解下列分式方程：（1）（2）．24．先化简，再求值：，其中25．(1)解方程：. (2)求不等式组：.26．计算：2﹣1+|﹣3|﹣（1﹣）027．已知，有一组不为零的数 a ，b ，c ，d ，e ，f ，m ，满足，求解：∵a=bm ，c=md ，e=fm∴利用数学的恒等变形及转化思想，试完成：（1）244，333，422的大小关系是________；（2）已知 a ，b ，c 不相等且不为零，若，求的值．28．先化简，再求值：24511(1)()1a a a a a a -+-÷---，其中a 是不等式组2133211(1)()323x x x x +<+⎧⎪⎨-≤+⎪⎩的一个非负整数解．参考答案1．C【解析】【分析】要使分式为0，需分母不为0，分子为0，故-9=0，-+60.【详解】依题意，得x=3，x2，x3，∴x=-3.【点睛】此题主要考察分式为0的条件.2．D【解析】【分析】根据等式的性质即可一一判断．【详解】A、-=，故本选项不符合题意；B、-=，故本选项不符合题意；C、=，故本选项不符合题意；D、－=，故本选项符合题意；故选：D．【点睛】本题考查等式的性质，解题的关键是记住：分式的分子与分母同乘（或除以）一个不等于0的整式，分式的值不变．3．B【解析】【分析】充分理解题意，列出方程，要使列出的方程能充分表达题意.【详解】根据题意，得：=−12，故答案选B.【点睛】本题考查的知识点是由实际问题抽象出分式方程，解题的关键是熟练的掌握由实际问题抽象出分式方程.4．B【解析】【分析】根据分式的运算法则即可求出答案．【详解】解：原式==故选：B．【点睛】本题考查分式的运算法则，解题的关键是熟练运用分式的运算法则，本题属于基础题型．5．A【解析】【分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10－n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．【详解】解：0.00129这个数用科学记数法可表示为1.29×10－3．故选：A．【点睛】本题考查用科学记数法表示较小的数，一般形式为a×10－n，其中1≤|a|＜10，n为由原数左边起第一个不为零的数字前面的0的个数所决定．6．B【解析】【分析】利用分式的定义：分母中含有字母，判断即可得到结果．【详解】解：在所列的个代数式中，分式的是和这个，故选：B．【点睛】此题考查了分式的定义，熟练掌握分式的定义是解本题的关键．7．B【解析】【分析】方程两边都乘以最简公分母（x-3），把分式方程化为整式方程，再根据分式方程的增根就是使最简公分母等于0的未知数的值求出x的值，然后代入进行计算即可求出m的值．【详解】方程两边都乘以(x−3)得，2−x−m=2(x−3)，∵分式方程有增根，∴x−3=0，解得x=3，∴2−3−m=2(3−3)，解得m=−1.故选:B.【点睛】考查分式方程的增根，掌握增根的概念，写出方程的增根是解题的关键.8．B【解析】【分析】根据分式的性质来计算、约分即可.【详解】A. =1，故错误；B. =-1，故正确；C. -，故错误；D. =，故错误；选B.【点睛】此题主要考察分式的运算.9．D【解析】【分析】根据分式的运算法则进行计算即可.【详解】，故选D.【点睛】本题主要考查分式的运算，熟练掌握分式的运算法则是解答的关键.10．C【解析】【分析】根据负整数指数幂，同底数幂的除法，幂的乘方，零指数幂的运算法则计算即可判断．【详解】3-1=，A错误；a5÷a-2=a7，B错误；（a-1）-3=a3，C正确；（-20）0=1，D错误；故选：C．【点睛】本题考查了负整数指数幂，同底数幂的除法，幂的乘方，零指数幂的运算，掌握它们的运算法则是解题的关键．11．【解析】【分析】根据负整数指数幂的意义计算即可.【详解】.故答案为：.【点睛】本题考查了负整数指数幂的运算，任何不等于0的数的-p（p是正整数）次幂，等于这个数的p次幂的倒数，即（a≠0，p是正整数）；0的负整数指数幂没有意义.12．x=5【解析】【分析】根据：，把转化为分式方程求解即可.【详解】∵，∴可变为：，解之得x=5.经检验x=5符合题意，∴方程的解是x=5.【点睛】本题考查了新定义运算，熟练掌握分式方程的解法是解答本题的关键，其基本思路是把方程的两边都乘以各分母的最简公分母，化为整式方程求解，求出x的值后不要忘记检验. 13．1.【解析】【分析】增根是化为整式方程后产生的不适合分式方程的根．所以应先确定增根的可能值，让最简公分母x-3=0，得到x=3，然后代入化为整式方程的方程算出m的值．【详解】方程两边都乘x﹣3，得x﹣3m＝2m（x﹣3）∵原方程有增根，∴最简公分母x﹣3＝0，解得x＝3，当x＝3时，m＝1故m的值是1，故答案为：1.【点睛】本题考查了分式方程的增根．增根问题可按如下步骤进行：①让最简公分母为0确定增根；②化分式方程为整式方程；③把增根代入整式方程即可求得相关字母的值．14．-2【解析】【分析】增根是分式方程化为整式方程后产生的使分式方程的分母为0的根．有增根，最简公分母x-3=0，所以增根是x=3，把增根代入化为整式方程的方程即可求出未知字母的值．【详解】方程两边都乘（x-3），得x-2（x-3）=1-m，∵方程有增根，∴最简公分母x-3=0，即增根是x=3，把x=3代入整式方程，得m=-2．故答案是：-2.【点睛】解决增根问题的步骤：①确定增根的值；②化分式方程为整式方程；③把增根代入整式方程即可求得相关字母的值．15．-16【解析】【分析】原式利用零指数幂、负整数指数幂法则计算即可求出值．【详解】原式＝﹣4×1÷＝﹣16，故答案是：﹣16【点睛】考查了实数的运算，熟练掌握运算法则是解本题的关键．16．214．【解析】【分析】根据有理数的运算法则和负指数幂意义进行分析即可. 【详解】﹣（﹣2）+2﹣2＝2+14＝214．故答案为：214．【点睛】考核知识点：负指数幂运算.理解运算法则是关键.17．x=4【解析】【分析】设该工期限期天，根据“两队合作1天后，余下的工程由乙队单独做，恰好按期完工”可列出；接下来根据分式方程的解法解分式方程即可得到答案，注意分式方程要验根检验.【详解】设该工期限期天，根据题意得，解得，经检验是原方程的解.故该工期限期4天.故答案为：.【点睛】本题考查了分式方程的应用，熟练掌握分式方程的应用是本题解题的关键.18．m≥5且m≠.【解析】【分析】分式方程去分母转化成整式方程，表示出整式方程的解，根据分式方程的解不小于1结合分式有意义的条件即可求出m的取值范围.【详解】方程两边同时乘以（x+3）（x-2），得：x2﹣2x﹣x2﹣4x﹣3＝x﹣2m，解得：x＝，由方程的解不小于1，得到≥1且≠2，解得：m≥5且m≠，故答案为：m≥5且m≠.【点睛】本题考查了解分式方程，解一元一次不等式组，正确理解分式方程的解是解题的关键. 19．12x3yz【解析】【分析】确定最简公分母的方法是：（1）取各分母系数的最小公倍数；（2）凡单独出现的字母连同它的指数作为最简公分母的一个因式；（3）同底数幂取次数最高的，得到的因式的积就是最简公分母．【详解】因为三分式中常数项的最小公倍数12，x的最高次幂为3，y、z的最高次幂都为1，所以最简公分母是12x3yz．故答案为：12x3yz．【点睛】本题考查了最简公分母的定义及求法．通常取各分母系数的最小公倍数与字母因式的最高次幂的积作公分母，这样的公分母叫做最简公分母．一般方法：①如果各分母都是单项式，那么最简公分母就是各系数的最小公倍数，相同字母的最高次幂，所有不同字母都写在积里．②如果各分母都是多项式，就可以将各个分母因式分解，取各分母数字系数的最小公倍数，凡出现的字母（或含字母的整式）为底数的幂的因式都要取最高次幂．20．7【解析】【分析】先把a当常数解分式方程，x=，再将a当常数解不等式组，根据不等式组无解得：a≤5，找出当a为非负整数时，x也是整数的值时，确定a的值并相加即可．【详解】解：，去分母，方程两边同时乘以x﹣3，ax＝3+a+x，x＝，且x≠3，，由①得：x＞5，由②得：x＜a，∵不等式组无解，∴a≤5，当a＝0时，x＝＝﹣3，当a＝1时，x＝无意义，当a＝2时，x＝＝5，当a＝3时，x＝＝3分式方程无解，不符合题意，当a＝4时，x＝＝，当a＝5时，x＝＝2，∵x是整数，a是非负整数，∴a＝0，2，5，所有满足条件的非负整数a的和为7，故答案为：7【点睛】考查了解分式方程、一元一次不等式组的解的情况，求出分式方程和不等式组的解是解本题的关键，要注意分式方程有意义，即分母不为0．21．原计划每天加工服装25套【解析】【分析】设原计划每天加工x套，则采用了新技术之后，每天加工1.2x套，根据题中等量关系可列方程．【详解】.解：设原计划每天加工服装x套，根据题意得解得：x=25经检验: x=25是原方程的解并且符合题意.答:原计划每天加工服装25套.【点睛】考查分式方程的应用，读懂题目，找出题目中的等量关系是解题的关键.22．4.【解析】【分析】原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，把已知等式变形后代入计算即可求出值．【详解】，，，，，，∵∴∴原式【点睛】此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．23．（1）；（2）分式方程无解【解析】【分析】（1）先根据分式的基本性质把分子、分母化整，然后分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解；（2）去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．【详解】（1）方程整理得：﹣＝40，去分母得：40x＝30，解得：x＝，经检验x＝是分式方程的解；（2）去分母得：2+2x＝5x+5，移项合并得：3x＝﹣3，解得：x＝﹣1，经检验x＝﹣1是增根，分式方程无解．【点睛】本题考查了分式方程的解法，其基本思路是把方程的两边都乘以各分母的最简公分母，化为整式方程求解，求出x的值后不要忘记检验.24．【解析】【分析】先算括号内的，再算除法，最后把a、b的值代入进行计算即可．【详解】原式=当时，原式=【点睛】本题考查的是分式的化简求值，在解答此类题目时要注意把分式化为最简形式，以简化计算．25．(1)x＝1；(2)﹣1≤x＜1【解析】【分析】(1)根据解分式方程的步骤解方程即可,注意检验.(2)可先根据一元一次不等式的解法分别解不等式，找出解集的公共部分即可.【详解】解：(1)(x+1)(x-2)+x=x(x-2)解得：x＝1；检验：x=1是原方程的根(2)解①x≥﹣1，②x＜1，∴原不等式组的解集是﹣1≤x＜1.【点睛】考查分式方程的解法以及解一元一次不等式组，掌握它们的解题步骤是解题的关键.26．3【解析】【分析】直接利用负指数幂的性质以及零指数幂的性质、绝对值的性质分别化简进而得出答案．【详解】＝+3﹣1＝4﹣1＝3．【点睛】考查了实数运算，正确化简各数是解题关键．27．（1）333＞244=422；（2）【解析】【分析】（1）先将各式转化成幂相同的指数式，再来比较大小.（2）根据题意可得a+b=3ab，b+c=4bc，a+c=5ac，即（a+b）c=3abc，（b+c）a=4abc，（a+c）b=5abc，再把三个式子相加、计算即ab+bc+ac=6abc，从而即可得证.【详解】（1）解（1）∵244=（24）11=1611，333=（33）11=2711，422=（42）11=1611，∴2711＞1611=1611，即333＞244=422.故答案为：333＞244=422.（2）解：∵∴a+b=3ab ，b+c=4bc ，a+c=5ac ， ∴（a+b ）c=3abc ，（b+c ）a=4abc ，（a+c ）b=5abc ，即ac+bc=3abc ，ab+ac=4abc ，ab+bc=5abc ，∴2（ab+bc+ac ）=12abc ，即ab+bc+ac=6abc ， ∴.【点睛】本题主要考查了幂的大小比较的方法，以及分式的运算，解题的关键是熟练运用分式的运算法则，一般说来，比较几个幂的大小，或者把它们的底数变得相同，或者把它们的指数变得相同，再分别比较它们的指数或底数．28．a(a ﹣2)；3，8或15．【解析】【分析】本题应该分成两个部分来完成，先对分式进行化简，再根据不等式组求出其非负整数解，最后进行代入求值即可．【详解】 24511(1)()1a a a a a a -+-÷--- ＝(1)(1)451111(1)(1)a a a a a a a a a a ⎡⎤+---⎡⎤-÷-⎢⎥⎢⎥----⎣⎦⎣⎦＝a(a ﹣2)，又由不等式组2133211(1)()323x x x x +<+⎧⎪⎨-≤+⎪⎩可得25x x >-⎧⎨≤⎩，即该不等式组的解集为﹣2＜x≤5，∵a 是该不等式组的一个非负整数解，而由上式化简过程可知a≠0，a ﹣1≠0，a ﹣2≠0，∴a≠0，1，2，故在解集﹣2＜x≤5中可取a＝3，4，5，若a＝3，得a(a﹣2)＝3×1＝3；若a＝4，t得a(a﹣2)＝4×2＝8；若a＝5，得a(a﹣2)＝5×3＝15故上式的值可以是3，8或15．。

八年级数学(下)第二章分式测试题

湘教版八年级数学（下）第二章分式测试题班级________ 姓名一、选择题（每题3分，共18分）学号成绩1、4y 3x x2 -1 x2 _ xy y2分式4a x4-1匚单中,ab - 2b 最简分式有（）C、3个2、若代数式（X _ 2）（x x-1二"的值为0，则x的取值应为（B、x = -13、X _1所得正确结果是（xC、D、一14、5、计算1 -< 1—a 丿212 -1的正确结果是a -1 a -1a a纳米技术是21世纪新兴技术，纳米是一个长度单位, 纳米等于D、-- -----a1米的10亿分之一，关系式1纳米=10 4米中，n应该是（）A、10B、9C、8D、一106、甲、乙两人合修一台机床，2小时完成，已知甲单独修，需要2 2 2方程1，方程左边的代数式：3 xA、工作效率之和二、填空题（每空3小时，设乙单独修需要x小时，可得7、分式一J -x -3x9、3B、工作量之和3分，共18分）2壬一表示（）xC、工作时间之和D、以上说法都不对与-22x不改变分式的值，使的最简公分母是______________ 。

-93x 3yJ的分子与分母中各项系数都为整数，最简单的结果为3x- y2计算：（3-皿）0(1f--I< 3丿10、计算：8x2y =5a丄十X—1(m —1)(m —3)曲/古亠__________ 时，分式 -------- ------ 的值为0。

m -3m +2(每题8分，共64分)x17、关于x 的分式方程一x — 3 3 — x=2，当m 为何值时，会产生增根?18、甲、乙两地相距19千米，某人从甲地到乙地，先步行 7千米，然后改骑自行车，到达乙地共用 2小时，已知这人骑自行车的速度是步行速度的4倍，求这人步行的速度。

19、甲、乙两人合做一项工作，4小时后，甲因另有工作离开，剩下的工作由乙单独做 6小时完成。

已知甲做4小时的工作乙需要做 5小时，问甲、乙单独做完这项工作各需要多少小时？12、计算: a 2 -1 ~2 a 14、计算: 16、先化简：, 2a 113、计算:x 2 xy x — y xy15、解方程一4 15-x 1 - 2x3 + ------- x —4x -1再求值：—x一x -2x，其中*=—2x -4211、当 m三、解答题。

《分式》单元测试题

宜宾市八中2011级数学《分式》单元测试题姓名：分数：一．选择题（每小题3分，共30分）1．下列各式中，分式的个数为（）3x y -，21a x -，1x π+，3ab -， 12x y +，12x y +，2123x x =-+； A 、2个； B 、3个； C 、4个； D 、5个； 2．下列各式正确的是（） A 、c c a b a b =----； B 、；c ca b a b =--++C 、c c a b a b =---+； D 、c ca b a b-=----；3． -0.0000077用科学记数法表示为（）A 、-57.710-⨯； B 、-67710-⨯； C 、57710-⨯； D 、-67.710-⨯； 4．下列分式是最简分式的是（）A 、22x y x y -+；B 、11m m --；C 、3xy yxy-； D 、6132m m -；5．将分式2x x y+中的x 、y 的值同时扩大2倍，则扩大后分式的值（） A 、扩大2倍； B 、缩小2倍； C 、保持不变； D 、无法确定； 6、方程112212-=-x x 的解是（）A ．无解； B. 1- C. 0 ； D. 1.7、解方程4223=-+-xx x 时，去分母后得（） A.)2(43-=-x x ； B. )2(43-=+x x ； C.4)2()2(3=-+-x x x ； D.43=-x8、已知1)1(0=-x ，则 ( ) A. 1=x ； B. 1-=x ； C. 1≠x ； D. x 为任意实数；9、要修一条公路，甲单修路需a 小时完成，乙单独需b 小时完成，那么甲乙两人合修需要（）小时完成． A .ab b a + B.b a ab + C. ab 1 D ba 11+ 10、若31=+-xx ，则=+-22x x （）A. 9；B. 8； C . 7； D. 6 二．填空题（每小题3分，共30分） 11．若分式33x x --的值为零，则x = ； 12．分式2x y xy +，23y x ，26x y xy -的最简公分母为； 13．计算：201()( 3.14)3π--+-= ；14、解分式方程275-=x x 其根为________； 15、用小数表示：-3101.3-⨯= ； 16、将式子3233)()(--ab a 化为不含负整数指数的形式是； 17、计算：=-+-mn mn m n ； 18、已知311=-a b ，则2322a a b ba ab b+---= ； 19、若)3)(2(4232-+-=-++x x x x B x A 则A+B= ； 20、汽艇顺流而下行驶60千米以后返回，共用5小时10分。

分式全章测试题含答案

第十六章分式测试1 分式课堂学习检测一、选择题1．在代数式32,252,43,32,1,32222-++x x x x xy x x 中，分式共有( )． (A)2个 (B)3个(C)4个(D)5个2．下列变形从左到右一定正确的是( )．(A)22--=b a b a(B)bc ac b a =(C)ba bx ax =(D)22ba b a =3．把分式yx x+2中的x 、y 都扩大3倍，则分式的值( )． (A)扩大3倍(B)扩大6倍 (C)缩小为原来的31(D)不变4．下列各式中，正确的是( )． (A)y x yx y x y x +-=--+-(B)y x yx y x y x ---=--+-(C)yx yx y x y x -+=--+-(D)yx yx y x y x ++-=--+-5．若分式222---x x x 的值为零，则x 的值为( )．(A)－1 (B)1(C)2(D)2或－1二、填空题6．当x ______时，分式121-+x x 有意义． 7．当x ______时，分式122+-x 的值为正．8．若分式1||2--x xx 的值为0，则x 的值为______．9．分式22112mm m -+-约分的结果是______． 10．若x 2－12y 2＝xy ，且xy ＞0，则分式yx yx -+23的值为______．11．填上适当的代数式，使等式成立：(1)ba b a b ab a +=--+)(22222；(2)xxx x 2122)(2--=-；(3)a b b a b a-=-+)(11； (4))(22xy xy =．综合、运用、诊断三、解答题12．把下列各组分式通分：(1);65,31,22abca b a - (2)222,b a aab a b --．13．把分子、分母的各项系数化为整数：(1);04.03.05.02.0+-x x(2)b a ba -+32232．14．不改变分式的值，使分式的分子与分式本身不含负号：(1)yx yx ---22；(2)ba b a +-+-2)(．15．有这样一道题，计算))(1()12)((2222x x x x x x x --+-+，其中x ＝2080．某同学把x ＝2080错抄成x ＝2008，但他的计算结果是正确的．你能解释其中的原因吗?拓展、探究、思考16．已知311=-y x ，求分式yxy x y xy x ---+2232的值．17．当x 为何整数时，分式2)1(4-x 的值为正整数．18．已知3x －4y －z ＝0，2x ＋y －8z ＝0，求yz xy z y x +-+222的值．测试2 分式的运算课堂学习检测一、选择题1．下列各式计算结果是分式的是( )．(A)b a m n ÷(B)n m m n 23.(C)xx 53÷(D)3223473y x y x ÷2．下列计算中正确的是( )．(A)(－1)0＝－1 (B)(－1)－1＝1 (C)33212aa=-(D)4731)()(aa a =-÷- 3．下列各式计算正确的是( )． (A)m ÷n ·m ＝m(B)m nn m =⋅÷1(C)11=⋅÷m m m(D)n ÷m ·m ＝n4．计算54)()(ab a a b a -⋅-的结果是( )． (A)－1(B)1(C)a1(D)ba a--5．下列分式中，最简分式是( )．(A)21521y xy(B)y x y x +-22(C)yx y xy x -+-.222(D)y x y x -+226．下列运算中，计算正确的是( )． (A))(212121b a b a +=+ (B)acbc b a b 2=+ (C)aa c a c 11=+-(D)011=-+-ab b α 7．ab a b a -++2的结果是( )．(A)a2-(B)a4(C)ba b --2(D)ab- 8．化简22)11(yx xy y x-⋅-的结果是( )． (A)y x +1(B)yx +-1(C)x －y (D)y －x二、填空题9．2232)()(yx y x -÷＝______．10．232])[(x y -＝______．11．a 、b 为实数，且ab ＝1，设1111,11+++=+++=b a Q b b a a P ，则P ______Q (填“＞”、“＜”或“＝”)． 12．aa a -+-21422＝______． 13．若x ＜0，则|3|1||31---x x ＝______．14．若ab ＝2，a ＋b ＝3，则ba 11+＝______．综合、运用、诊断三、解答题15．计算：)()()(432b a ba ba -÷-⋅-．16．计算：⋅-+-++222244242x y yx y x y y x17．计算：⋅-÷+--+11)1211(22x x x x18．已知2222222y x y x N yx xy M -+=-=、，用“＋”或“－”连结M 、N ，有三种不同的形式：M ＋N 、M －N 、N －M ，请你任选其中一种进行计算，并化简求值，其中x ∶y ＝5∶2．19．先化简，再求值：1112+---x xx x ，其中x ＝2． 20．已知x 2－2＝0，求代数式11)1(222++--x x x x 的值．拓展、探究、思考21．等式⋅-++=-++236982x Bx A x x x 对于任何使分母不为0的x 均成立，求A 、B 的值．22．A 玉米试验田是边长为a m 的正方形减去边长为1m 的蓄水池后余下部分，B 玉米试验田是边长为(a －1)m 的正方形，两块试验田的玉米都收获了500kg ． (1)哪种玉米田的单位面积产量高?(2)高的单位面积产量是低的单位面积产量的多少倍?测试3 分式方程课堂学习检测一、选择题 1．方程132+=x x 的解为( )．(A)2 (B)1 (C)－2 (D)－12．解分式方程12112-=-x x ，可得结果( )． (A)x ＝1 (B)x ＝－1(C)x ＝3(D)无解3．要使54--x x 的值和xx--424的值互为倒数，则x 的值为( )． (A)0 (B)－1 (C)21(D)14．已知4321--=+-y y x x ，若用含x 的代数式表示y ，则以下结果正确的是( )． (A)310+=x y (B)y ＝x ＋2(C)310xy -=(D)y ＝－7x －25．若关于x 的方程xkx --=-1113有增根，则k 的值为( )． (A)3(B)1(C)0(D)－16．若关于x 的方程323-=--x mx x 有正数解，则( )． (A)m ＞0且m ≠3 (B)m ＜6且m ≠3(C)m ＜0 (D)m ＞67．完成某项工作，甲独做需a 小时，乙独做需b 小时，则两人合作完成这项工作的80％，所需要的时间是( )． (A))(54b a +小时 (B))11(54ba +小时 (C))(54b a ab+小时(D)ba ab+小时 8．a 个人b 天可做c 个零件(设每人速度一样)，则b 个人用同样速度做a 个零件所需天数是( )．(A)c a 2(B)2ac(C)a c 2(D)2c a 二、填空题9．x ＝______时，两分式44-x 与13-x 的值相等． 10．关于x 的方程324+=-b xa 的解为______． 11．当a ＝______时，关于x 的方程4532=-+x a ax 的根是1． 12．若方程114112=---+x x x 有增根，则增根是______． 13．关于x 的方程11=+x a的解是负数，则a 的取值范围为____________． 14．一艘轮船在静水中的最大航速为20千米/时，它在江水中航行时，江水的流速为v 千米/时，则它以最大航速顺流航行s 千米所需的时间是______．综合、运用、诊断三、解方程15．.32121=-+--xx x16．⋅+=+--1211422x xx x x 17．⋅-+=+-xx x x x 25316四、列方程解应用题18．甲工人工作效率是乙工人工作效率的212倍，他们同时加工1500个零件，甲比乙提前18个小时完工，问他们每人每小时各加工多少个零件?19．甲、乙两地相距50km ，A 骑自行车，B 乘汽车，同时从甲城出发去乙城．已知汽车的速度是自行车速度的2.5倍，B 中途休息了0.5小时还比A 早到2小时，求自行车和汽车的速度．拓展、探究、思考20．面对全球金融危机的挑战，我国政府毅然启动内需，改善民生．国务院决定从2009年2月1日起，在全国范围内实施“家电下乡”，农民购买入选产品，政府按原价购买总．．额的．．13．．％．给予补贴返还．某村委会组织部分农民到商场购买入选的同一型号的冰箱、电视机两种家电，已知购买冰箱的数量是电视机的2倍，且按原价购买冰箱总额为40000元、电视机总额为15000元．根据“家电下乡”优惠政策，每台冰箱补贴返还的金额比每台电视机补贴返还的金额多65元，求冰箱、电视机各购买多少台?(2)列出方程(组)并解答．参考答案第十六章分式测试1 分式1．B ． 2．C ． 3．D ． 4．A ． 5．A ． 6．21≠． 7．21-<． 8．0． 9．⋅+--11m m 10．1．11．(1)a ＋2b ； (2)2x 2； (3)b ＋a ； (4)x 2y 2．12．(1);65,62,632223bca abc a bc bc a c a - (2)⋅-+-++))((,))(()(2b a b a a a b a b a a b a b 13．(1);2152510+-x x (2)⋅-+ba ba 6491214．(1);22x y y x -- (2)⋅-+ba ba 215．化简原式后为1，结果与x 的取值无关． 16．⋅53 17．x ＝0或2或3或－1． 18．⋅23 测试2 分式的运算1．A ． 2．D ． 3．D ． 4．D ． 5．D ． 6．D ． 7．C ． 8．B ．9．x 4y ． 10．⋅612x y11．＝． 12．⋅+21a 13．⋅-922x x 14．⋅2315．⋅6ba 16．⋅+y x x 22提示：分步通分．17．2x ．18．选择一：y x y x N M -+=+，当x ∶y ＝5∶2时，原式37= 选择二：y x x y N M +-=-，当x ∶y ＝5∶2时，原式⋅-=73选择三：y x yx M N +-=-，当x ∶y ＝5∶2时，原式73=．注：只写一种即可． 19．化简得1)1(+--x x ，把x ＝2代入得31-．20．原式112+-+=x x x∵x 2－2＝0，∴x 2＝2，∴原式112+-+=x x ，∴原式＝121．A ＝3，B ＝5．22．(1)A 面积(a 2－1)米2，单位产量15002-a 千克/米；B 玉米田面积(a －1)2米2，单位产量是2)1(500-a 千克/米2，22)1(5001500-<-a a ，B 玉米的单位面积产量高； (2)11-+a a 倍．测试3 分式方程1．A ． 2．D ． 3．B ． 4．C ． 5．A. 6．B ． 7．C ． 8．A ．9．x ＝－8． 10．⋅--=462b a x 11．⋅-=317a12．x ＝1． 13．a ＜1且a ≠0． 14．20+v s小时．15．无解． 16．⋅-=21x 17．无解．18．设乙的工作效率为x 个/时，甲的工作效率为x 25个/时．182515001500+=x x ．50=x ．经检验，x ＝50是原方程的根．答：甲每小时加工125个，乙每小时加工50个．19．设自行车速度为x 千米/时，汽车速度为2.5x 千米/时．xx 502215.250=++．x ＝12．经检验x ＝12是原方程的根．答：自行车的速度为12km/时，汽车的速度为30km/时． 20．(1)2x ，40000×13％，x2%1340000⨯，15000×13％，x %1315000⨯；(2)冰箱、电视机分别购买20台、10台．第十六章分式全章测试一、填空题1．在代数式222232,3221,12,1,2,3,1,43abx x x b a a y x x b a --+++-中，分式有_________． 2．当x ______时，分式2+x x 没有意义；当x ______时，分式112+x 有意义；当x ______时，分式113-+x x 的值是零．3．不改变分式的值，把分式的分子和分母各项系数都化成整数：b a ba 3.051214.0+-＝______．4．计算：--32m m m －3＝______．5．若x ＝－4是方程311+=-x x a 的解，则a ＝______． 6．若332-+x x 与35+x 的值互为相反数，则满足条件的x 的值是______． 7．当x ______时，等式512)5(2222+-=+-x x x x x x 成立．8．加工一批产品m 件，原计划a 天完成，今需要提前b 天完成，则每天应生产______件产品．9．已知空气的单位体积质量为0.001239g/cm 3，那么100单位体积的空气质量为______g/cm 3．(用科学记数法表示) 10．设a ＞b ＞0，a 2＋b 2－6ab ＝0，则ab ba -+的值等于______．二、选择题11．下列分式为最简分式的是( )．(A)ab 1533(B)a b b a --22(C)xx 32(D)y x y x ++2212．下列分式的约分运算中，正确的是( )．(A)339x xx =(B)bac b c a =++ (C)0=++ba ba (D)1=++ba ba 13．分式11,121,1122-+-+x x x x 的最简公分母是( )． (A)(x 2＋1)(x －1) (B)(x 2－1)(x 2＋1) (C)(x －1)2(x 2＋1)(D)(x －1)214．下列各式中，正确的个数有( )．①2－2＝－4； ②(32)3＝35； ③2241)2(xx -=--； ④(－1)－1＝1． (A)0个 (B)1个(C)2个(D)3个15．使分式x326--的值为负数的条件是( )．(A)32<x (B)x ＞0 (C)32>x(D)x ＜016．使分式1||-x x有意义的条件是( )．(A)x ≠1(B)x ≠－1 (C)x ≠1且x ≠－1(D)x ≠017．学完分式运算后，老师出了一道题“化简42232--+++x xx x ”．小明的做法是：原式＝424)2)(3(22-----+x x x x x ；小亮的做法是：原式＝(x ＋3)(x －2)＋(2－x )＝x 2＋x －6＋2－x ＝x 2－4；小芳的做法是：原式＝.12132123)2)(2(223=+-+=+-++=-+---+x x x x x x x x x x 其中正确的是( )． (A)小明 (B)小亮(C)小芳(D)没有正确的 18．如果分式)(3)(b a b a a ++的值是零，那么a ，b 满足的条件是( )． (A)a ＝－b(B)a ≠－b (C)a ＝0(D)a ＝0且a ≠－b 19．若关于x 的分式方程11+=+x m x x 无解，则m 的值为( )． (A)1 (B)0 (C)－1 (D)－220．有一项工程需在规定日期内完成，如果甲队去做，恰能如期完成；如果乙队去做，要超过规定日期3天．现由甲、乙两队合作2天后，余下的工程由乙队单独去做，恰好在规定日期内完成．如果设规定日期为x 天，下列关于x 的方程中错误的是( )． (A)132=++x x x (B)332+=x x (C)1)2(312)311(=-++⨯++x x x x (D)1311=++x x 三、化简下列各题 21．⋅+----112223x x xx x x 22．⋅-÷+--24)22(x x x x x x23．⋅--÷-++--+)64121()622322(222x x x x x x x x四、解方程24．⋅++=+-312132x x x 25．⋅--+=--2163524245m m m m ．五、列方程解应用题26．A ，B 两地相距80千米，一辆大汽车从A 地开出2小时后，又从A 地开出另一辆小汽车，已知小汽车的速度是大汽车速度的3倍，结果小汽车比大汽车早40分钟到达B 地，求两辆汽车每小时各走多少千米．参考答案第十六章分式全章测试1．⋅-++2232,12,1,1ab x x b a x 2．＝－2，取任意实数，⋅-=31． 3．⋅+-b a b a 3254 4．⋅-39m 5．5． 6．－4． 7．≠0． 8．⋅-ba m 9．1.239×10－1． 10．.2- 11．D ． 12．D ． 13．C ．14．A ． 15．A ． 16．C ． 17．C ． 18．D ． 19．C ． 20．D ． 21．2x －1． 22．⋅+21x 23．⋅+-x x 1 24．⋅-=31x 25．m ＝2是增根，无解．26．小汽车每小时60千米，大汽车每小时20千米．。

苏科版八年级下学期数学《分式》章节测试题(含解析)

苏科版八年级下学期数学《分式》章节测试题（含解析）一．选择题（共10小题）1．若分式的值为0，则（）A．x=﹣2 B．x=0 C．x=1 D．x=1或﹣22．若分式，则分式的值等于（）A．﹣B．C．﹣D．3．若关于x的分式方程无解，则m的值为（）A．0 B．2 C．0或2 D．±24．已知a2+b2=6ab，则的值为（）A．B．C．2 D．±25．分式，，的最简公分母是（）A．（a2﹣1）2B．（a2﹣1）（a2+1）C．a2+1 D．（a﹣1）46．在，，，，中分式的个数有（）A．1个B．2个C．3个D．4个7．若分式的值为0，则x的值为（）A．2 B．﹣2 C．2或﹣2 D．2或38．某次列车平均提速vkm/h，用相同的时间，列车提速前行驶skm，提速后比提速前多行驶50km．设提速前列车的平均速度为xkm/h，则列方程是（）A．=B．= C．=D．=9．已知关于x的分式方程﹣=1的解为负数，则k的取值范围是（）A．k＞或k≠1 B．k＞且k≠1 C．k＜且k≠1 D．k＜或k≠110．如果a、b、c是非零实数，且a+b+c=0，那么的所有可能的值为（）A．0 B．1或﹣1 C．2或﹣2 D．0或﹣2二．填空题（共8小题）11．计算：﹣=．12．分式方程的解是．13．某快递公司的分拣工小王和小李，在分拣同一类物件时，小王分拣60个物件所用的时间与小李分拣45个物件所用的时间相同．已知小王每小时比小李多分拣8个物件，设小李每小时分拣x个物件，根据题意列出的方程是．14．已知a＞b＞0，a2+b2=3ab，则的值为．15．当a=2016时，分式的值是．16．已知关于x的方程的解是负数，则m的取值范围为．17．若分式方程的解为x=0，则a的值为．18．一个容器装有1升水，按照如下要求把水倒出：第1次倒出升水，第2次倒出的水量是升的，第3次倒出的水量是升的，第4次倒出的水量是升的，…按照这种倒水的方法，倒了10次后容器内剩余的水量是．三．解答题（共9小题）19．先化简，再求值：﹣÷，其中x=﹣1．20．化简：（a+1﹣）•．21．先化简，再求值：（﹣）+，其中a=2，b=．22．A、B两地相距200千米，甲车从A地出发匀速开往B地，乙车同时从B地出发匀速开往A地，两车相遇时距A地80千米．已知乙车每小时比甲车多行驶30千米，求甲、乙两车的速度．23．某商店用1050元购进第一批某种文具盒，很快卖完．又用1440元购进第二批该种文具盒，但第二批每只文具盒的进价是第一批进价的1.2倍，数量比第一批多了10只．（1）求第一批每只文具盒的进价是多少元？（2）卖完第一批后，第二批按24元/只的价格销售，恰好销售完一半时，根据市场情况，商店决定对剩余的文具盒全部按同一标准一次性打折销售，但要求这批文具盒利润不得少于288元，问最低可打几折？24．“五一”期间，我市某商场举行促销活动，活动期间规定：商场内所有商品按标价的80%出售；同时，当顾客在该商场消费满一定金额后，按如下方案获得相应金额的奖券：消费金额p（元）的范围200≤p＜400400≤p＜500500≤p＜700700≤p＜900…获得奖券金额（元）3060100130…根据促销方法，顾客在该商场购物可获得双重优惠．例如，购买标价为450元的商品，则消费金额为450×0.8=360（元），获得优惠额为：450×0.2+30=120（元）．设购买商品的优惠率=．试问：（1）购买一件标价为800元的商品，顾客得到的优惠率是多少？（2）若一顾客购买了一套西装，得到的优惠率为，已知该套西装的标价高于700元，低于850元，该套西装的标价是多少元？25．甲车从A地驶往B地，同时乙车从B地驶往A地，两车相向而行，匀速行驶，甲车距B地的距离y （km）与行驶时间x（h）之间的函数关系如图所示，乙车的速度是60km/h（1）求甲车的速度；（2）当甲乙两车相遇后，乙车速度变为a（km/h），并保持匀速行驶，甲车速度保持不变，结果乙车比甲车晚38分钟到达终点，求a的值．26．某服装店购进一批甲、乙两种款型时尚T恤衫，甲种款型共用了7800元，乙种款型共用了6400元，甲种款型的件数是乙种款型件数的1.5倍，甲种款型每件的进价比乙种款型每件的进价少30元．（1）甲、乙两种款型的T恤衫各购进多少件？（2）商店进价提高60%标价销售，销售一段时间后，甲款型全部售完，乙款型剩余一半，商店决定对乙款型按标价的五折降价销售，很快全部售完，求售完这批T恤衫商店共获利多少元？27．某汽车销售公司经销某品牌A款汽车，随着汽车的普及，其价格也在不断下降．今年5月份A款汽车的售价比去年同期每辆降价1万元，如果卖出相同数量的A款汽车，去年销售额为100万元，今年销售额只有90万元．（1）今年5月份A款汽车每辆售价多少万元？（2）为了增加收入，汽车销售公司决定再经销同品牌的B款汽车，已知A款汽车每辆进价为7.5万元，B款汽车每辆进价为6万元，公司预计用不多于105万元且不少于99万元的资金购进这两款汽车共15辆，有几种进货方案？（3）如果B款汽车每辆售价为8万元，为打开B款汽车的销路，公司决定每售出一辆B款汽车，返还顾客现金a万元，要使（2）中所有的方案获利相同，a值应是多少？此时，哪种方案对公司更有利？参考答案与试题解析一．选择题（共10小题）1．若分式的值为0，则（）A．x=﹣2 B．x=0 C．x=1 D．x=1或﹣2【分析】根据分式的值为0的条件列出关于x的不等式组，求出x的值即可．【解答】解：∵分式的值为0，∴，解得x=1．故选：C．【点评】本题考查的是分式的值为0的条件，即分式值为零的条件是分子等于零且分母不等于零，根据此条件列出关于x的不等式组是解答此题的关键．2．若分式，则分式的值等于（）A．﹣ B．C．﹣ D．【分析】根据已知条件，将分式整理为y﹣x=2xy，再代入则分式中求值即可．【解答】解：整理已知条件得y﹣x=2xy；∴x﹣y=﹣2xy将x﹣y=﹣2xy整体代入分式得====．故答案为B．【点评】由题干条件找出x﹣y之间的关系，然后将其整体代入求出答案即可．3．若关于x的分式方程无解，则m的值为（）A．0 B．2 C．0或2 D．±2【分析】根据解分式方程的方法和关于x的分式方程无解，可以求得相应的m的值，本题得以解决．【解答】解：方程两边同乘以x，得x﹣m=mx﹣x解得，x=∵关于x的分式方程无解，∴x=0或2﹣m=0，解得m=0或m=2，故选C．【点评】本题考查分式方程的解，解题的关键是明确分式方程什么时候无解．4．已知a2+b2=6ab，则的值为（）A．B．C．2 D．±2【分析】首先由a2+b2=6ab，即可求得：（a+b）2=8ab，（a﹣b）2=4ab，然后代入即可求得答案．【解答】解：∵a2+b2=6ab，∴a2+b2+2ab=8ab，a2+b2﹣2ab=4ab，即：（a+b）2=8ab，（a﹣b）2=4ab，a+b=±2，a﹣b=±2，∴当a+b=2，a﹣b=2时，=；当a+b=2，a﹣b=﹣2时，=﹣；当a+b=﹣2，a﹣b=2时，=﹣；当a+b=﹣2，a﹣b=﹣2时，=．故选：B．【点评】本题主要考查完全平方公式．注意熟记公式的几个变形公式，还要注意整体思想的应用．5．分式，，的最简公分母是（）A．（a2﹣1）2B．（a2﹣1）（a2+1）C．a2+1 D．（a﹣1）4【分析】利用最简公分母就是各系数的最小公倍数，相同字母或整式的最高次幂，所有不同字母或整式都写在积里求解即可．【解答】解：=，，=，所以分式，，的最简公分母是（a﹣1）2（a+1）2．即（a2﹣1）2故选：A．【点评】本题主要考查了最简公分母，解题的关键是熟记最简公分母的定义．6．在，，，，中分式的个数有（）A．1个 B．2个 C．3个 D．4个【分析】一般地，如果A，B表示两个整式，并且B中含有字母，那么式子叫做分式．【解答】解：分母不含字母，不是分式；是分式；是分式；π是数字不是字母，不是分式，是分式．故选C．【点评】本题主要考查的是分式的定义，掌握分式的定义是解题的关键．7．若分式的值为0，则x的值为（）A．2 B．﹣2 C．2或﹣2 D．2或3【分析】分式值为零的条件是分子等于零且分母不等于零．【解答】解：∵分式的值为0，∴|x|﹣2=0．解得：x=±2．当x=2时，x2﹣4x+4=0，分式无意义，当x=﹣2时，x2﹣4x+4=16≠00，分式有意义．∴x的值为﹣2．故选：B．【点评】本题主要考查的是分式值为零的条件，掌握分式值为零的条件是解题的关键．8．某次列车平均提速vkm/h，用相同的时间，列车提速前行驶skm，提速后比提速前多行驶50km．设提速前列车的平均速度为xkm/h，则列方程是（）A．=B．=C．=D．=【分析】首先根据行程问题中速度、时间、路程的关系：时间=路程÷速度，用列车提速前行驶的路程除以提速前的速度，求出列车提速前行驶skm用的时间是多少；然后用列车提速后行驶的路程除以提速后的速度，求出列车提速后行驶s+50km用的时间是多少；最后根据列车提速前行驶skm和列车提速后行驶s+50km时间相同，列出方程即可．【解答】解：列车提速前行驶skm用的时间是小时，列车提速后行驶s+50km用的时间是小时，因为列车提速前行驶skm和列车提速后行驶s+50km时间相同，所以列方程是=．故选：A．【点评】此题主要考查了由实际问题抽象出分式方程问题，解答此类问题的关键是分析题意找出相等关系，（1）在确定相等关系时，一是要理解一些常用的数量关系和一些基本做法，如行程问题中的相遇问题和追击问题，最重要的是相遇的时间相等、追击的时间相等．（2）列分式方程解应用题要多思、细想、深思，寻求多种解法思路．9．已知关于x的分式方程﹣=1的解为负数，则k的取值范围是（）A．k＞或k≠1 B．k＞且k≠1 C．k＜且k≠1 D．k＜或k≠1【分析】首先根据解分式方程的步骤，求出关于x的分式方程﹣=1的解是多少；然后根据分式方程的解为负数，求出k的取值范围即可．【解答】解：由﹣=1，可得（x+k）（x﹣1）﹣k（x+1）=x2﹣1，解得x=1﹣2k，∵1﹣2k＜0，且1﹣2k≠1，1﹣2k≠﹣1，∴k＞且k≠1．故选：B．【点评】此题主要考查了分式方程的解，要熟练掌握，解答此题的关键是要明确：在解方程的过程中因为在把分式方程化为整式方程的过程中，扩大了未知数的取值范围，可能产生增根，增根是令分母等于0的值，不是原分式方程的解．10．如果a、b、c是非零实数，且a+b+c=0，那么的所有可能的值为（）A．0 B．1或﹣1 C．2或﹣2 D．0或﹣2【分析】根据a、b、c是非零实数，且a+b+c=0可知a，b，c为两正一负或两负一正，按两种情况分别讨论代数式的可能的取值，再求所有可能的值即可．【解答】解：由已知可得：a，b，c为两正一负或两负一正．①当a，b，c为两正一负时：；②当a，b，c为两负一正时：．由①②知所有可能的值为0．应选A．【点评】本题考查了分式的化简求值，涉及到绝对值、非零实数的性质等知识点，注意分情况讨论未知数的取值，不要漏解．二．填空题（共8小题）11．计算：﹣=．【分析】同分母分式加减法法则：同分母的分式相加减，分母不变，把分子相加减；再分解因式约分计算即可求解．【解答】解：﹣===．故答案为：．【点评】考查了分式的加减法，注意通分是和约分是相反的一种变换．约分是把分子和分母的所有公因式约去，将分式化为较简单的形式；通分是分别把每一个分式的分子分母同乘以相同的因式，使几个较简单的分式变成分母相同的较复杂的形式．12．分式方程的解是x=﹣1．【分析】根据解分式方程的方法可以求得分式方程的解，记住最后要进行检验，本题得以解决．【解答】解：方程两边同乘以2x（x﹣3），得x﹣3=4x解得，x=﹣1，检验：当x=﹣1时，2x（x﹣3）≠0，故原分式方程的解是x=﹣1，故答案为：x=﹣1．【点评】本题考查分式方程的解，解题的关键是明确解分式方程的解得方法，注意最后要进行检验．13．某快递公司的分拣工小王和小李，在分拣同一类物件时，小王分拣60个物件所用的时间与小李分拣45个物件所用的时间相同．已知小王每小时比小李多分拣8个物件，设小李每小时分拣x个物件，根据题意列出的方程是．【分析】先求得小王每小时分拣的件数，然后根据小王分拣60个物件所用的时间与小李分拣45个物件所用的时间相同列方程即可．【解答】解：小李每小时分拣x个物件，则小王每小时分拣（x+8）个物件．根据题意得：．故答案为：．【点评】本题主要考查的是分式方程的应用，根据找出题目的相等关系是解题的关键．14．已知a＞b＞0，a2+b2=3ab，则的值为．【分析】先依据完全平方公式得到（a+b）2=5ab，（a﹣b）2=ab，然后由=求解即可．【解答】解：∵a2+b2=3ab，∴（a+b）2=5ab，（a﹣b）2=ab．∵a＞b＞0，∴＞0．∴===．故答案为：．【点评】本题主要考查的是求分式的值，依据完全平方公式求得=是解题的关键．15．当a=2016时，分式的值是2017．【分析】首先化简分式，然后把a=2016代入化简后的算式，求出算式的值是多少即可．【解答】解：当a=2016时，=﹣===a+1=2016+1=2017．故答案为：2017．【点评】此题主要考查了分式求值问题，要熟练掌握，求分式的值可以直接代入、计算．如果给出的分式可以化简，要先化简再求值．16．已知关于x的方程的解是负数，则m的取值范围为m＞﹣8且m≠﹣4．【分析】求出分式方程的解x=﹣，得出﹣＜0，求出m的范围，根据分式方程得出﹣≠﹣2，求出m，即可得出答案．【解答】解：，2x﹣m=4x+8，﹣2x=8+m，x=﹣，∵关于x的方程的解是负数，∴﹣＜0，解得：m＞﹣8，∵方程，∴x+2≠0，即﹣≠﹣2，∴m≠﹣4，故答案为：m＞﹣8且m≠﹣4．【点评】本题考查了分式方程的解和解一元一次不等式，关键是得出﹣＜0和﹣≠﹣2，题目具有一定的代表性，但是有一定的难度．17．若分式方程的解为x=0，则a的值为5．【分析】根据方程的解的定义，把x=0代入方程即可得到一个关于a的方程，从而求得a的值．【解答】解：把x=0代入方程得：=1，解得：a=5，故答案是：5．【点评】解题关键是要掌握方程的解的定义，由已知解代入原方程得到新方程，然后解答．18．一个容器装有1升水，按照如下要求把水倒出：第1次倒出升水，第2次倒出的水量是升的，第3次倒出的水量是升的，第4次倒出的水量是升的，…按照这种倒水的方法，倒了10次后容器内剩余的水量是．【分析】根据题意，易知倒出的水的规律，第n次倒出的水=，然后从1升水中逐次减去每一次倒的水，再进行计算即可．【解答】解：根据题意可知第一次倒出：，第二次倒出：，第三次倒出：，…第n次倒出：，∴第10次倒出：，∴倒了10次后容器内剩余的水量=1﹣（++…+）=1﹣（+﹣+﹣+…+﹣）=1﹣（1﹣）=．故答案是．【点评】本题考查了分式的混合运算，解题的关键是注意寻找规律，如：第n次倒出：；以及=﹣．三．解答题（共9小题）19．先化简，再求值：﹣÷，其中x=﹣1．【分析】先化简分式，再把x=﹣1代入求解即可．【解答】解：﹣÷=﹣•，=﹣，=，当x=﹣1时原式=．【点评】本题主要考查了分式的化简求值，解题的关键是正确的化简．20．化简：（a+1﹣）•．【分析】先对括号内的式子进行化简，再根据分式的乘法进行化简即可解答本题．【解答】解：（a+1﹣）•====2a﹣4．【点评】本题考查分式的混合运算，解题的关键是明确分式的混合运算的计算方法．21．先化简，再求值：（﹣）+，其中a=2，b=．【分析】先对所求式子进行化简，然后根据a=2，b=可以求得化简后式子的值，本题得以解决．【解答】解：（﹣）+===，当a=2，b=时，原式=．【点评】本题考查分式的化简求值，解题的关键是会对所求的式子化简并求值．22．A、B两地相距200千米，甲车从A地出发匀速开往B地，乙车同时从B地出发匀速开往A地，两车相遇时距A地80千米．已知乙车每小时比甲车多行驶30千米，求甲、乙两车的速度．【分析】根据题意，可以设出甲、乙的速度，然后根据题目中的关系，列出相应的方程，本题得以解决．【解答】解：设甲车的速度是x千米/时，乙车的速度为（x+30）千米/时，解得，x=60，经检验，x=60是分式方程的根，则x+30=90，即甲车的速度是60千米/时，乙车的速度是90千米/时．【点评】本题考查分式方程的应用，解题的关键是明确题意，找出所求问题需要的条件，发现题目中的数量关系，列出相应的方程．23．某商店用1050元购进第一批某种文具盒，很快卖完．又用1440元购进第二批该种文具盒，但第二批每只文具盒的进价是第一批进价的1.2倍，数量比第一批多了10只．（1）求第一批每只文具盒的进价是多少元？（2）卖完第一批后，第二批按24元/只的价格销售，恰好销售完一半时，根据市场情况，商店决定对剩余的文具盒全部按同一标准一次性打折销售，但要求这批文具盒利润不得少于288元，问最低可打几折？【分析】（1）设第一批文具盒的进价是x元，则第二批的进价是每只1.2x元，根据两次购买的数量关系建立方程求出其解即可；（2）设最低可以打m折，根据这批文具盒利润不得少于288元列出一元一次不等式求解．【解答】解：（1）设第一批每只文具盒的进价是x元．根据题意得：，解之得x=15，经检验，x=15是方程的根答：第一批文具盒的进价是15元/只．（2）设最低可打m折（24﹣15×1.2）××+（24×﹣15×1.2）××≥288，m≥8，答：最低可打8折．【点评】本题考查了列分式方程解实际问题的运用，列一元一次不等式解实际问题的运用，解答时找到题意中的等量关系及不相等关系建立方程及不等式是解答的关键．24．“五一”期间，我市某商场举行促销活动，活动期间规定：商场内所有商品按标价的80%出售；同时，当顾客在该商场消费满一定金额后，按如下方案获得相应金额的奖券：消费金额p（元）的范围200≤p＜400400≤p＜500500≤p＜700700≤p＜900…获得奖券金额（元）3060100130…根据促销方法，顾客在该商场购物可获得双重优惠．例如，购买标价为450元的商品，则消费金额为450×0.8=360（元），获得优惠额为：450×0.2+30=120（元）．设购买商品的优惠率=．试问：（1）购买一件标价为800元的商品，顾客得到的优惠率是多少？（2）若一顾客购买了一套西装，得到的优惠率为，已知该套西装的标价高于700元，低于850元，该套西装的标价是多少元？【分析】（1）由800元×80%得出消费金额，再根据表中规定应享受100元优惠．则根据题目提供的优惠计算方法即可求出优惠额，从而得到优惠率；（2）因为西服标价低于850，所以其消费额最大为850×0.8=680（元），低于700元，因此获得的奖券金额为100元，设西服标价x元，根据题意可列出方程=，解方程即可．【解答】解：（1）消费金额为800×0.8=640（元），获得优惠额为：800×0.2+100=260（元），所以优惠率为=0.325=32.5%；（2）设西服标价x元，根据题意得=，解之得x=750经检验，x=750是原方程的根．答：该套西装的标价为750元．【点评】本题考查了分式方程的应用，列分式方程解应用题与所有列方程解应用题一样，重点在于准确地找出相等关系，这是列方程的依据．要注意题中给出的判断条件．此题关键是套用优惠率的公式．25．甲车从A地驶往B地，同时乙车从B地驶往A地，两车相向而行，匀速行驶，甲车距B地的距离y （km）与行驶时间x（h）之间的函数关系如图所示，乙车的速度是60km/h（1）求甲车的速度；（2）当甲乙两车相遇后，乙车速度变为a（km/h），并保持匀速行驶，甲车速度保持不变，结果乙车比甲车晚38分钟到达终点，求a的值．【分析】（1）根据函数图象可知甲2小时行驶的路程是（280﹣120）km，从而可以求得甲的速度；（2）根据第（1）问中的甲的速度和甲乙两车相遇后，乙车速度变为a（km/h），并保持匀速行驶，甲车速度保持不变，结果乙车比甲车晚38分钟到达终点，可以列出分式方程，从而可以求得a的值．【解答】解：（1）由图象可得，甲车的速度为：=80km/h，即甲车的速度是80km/h；（2）相遇时间为：=2h，由题意可得，=，解得，a=75，经检验，a=75是原分式方程的解，即a的值是75．【点评】本题考查分式方程的应用、函数图象，解题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答问题．26．某服装店购进一批甲、乙两种款型时尚T恤衫，甲种款型共用了7800元，乙种款型共用了6400元，甲种款型的件数是乙种款型件数的1.5倍，甲种款型每件的进价比乙种款型每件的进价少30元．（1）甲、乙两种款型的T恤衫各购进多少件？（2）商店进价提高60%标价销售，销售一段时间后，甲款型全部售完，乙款型剩余一半，商店决定对乙款型按标价的五折降价销售，很快全部售完，求售完这批T恤衫商店共获利多少元？【分析】（1）可设乙种款型的T恤衫购进x件，则甲种款型的T恤衫购进1.5x件，根据甲种款型每件的进价比乙种款型每件的进价少30元，列出方程即可求解；（2）先求出甲款型的利润，乙款型前面销售一半的利润，后面销售一半的亏损，再相加即可求解．【解答】解：（1）设乙种款型的T恤衫购进x件，则甲种款型的T恤衫购进1.5x件，依题意有+30=，解得x=40，经检验，x=40是原方程组的解，且符合题意，1.5x=60．答：甲种款型的T恤衫购进60件，乙种款型的T恤衫购进40件；（2）=160，160﹣30=130（元），130×60%×60+160×60%×（40÷2）﹣160×[1﹣（1+60%）×0.5]×（40÷2）=4680+1920﹣640=5960（元）答：售完这批T恤衫商店共获利5960元．【点评】本题考查了列分式方程解实际问题的运用，分式方程的解法的运用，分析题意，找到关键描述语，找到合适的等量关系是解决问题的关键．27．某汽车销售公司经销某品牌A款汽车，随着汽车的普及，其价格也在不断下降．今年5月份A款汽车的售价比去年同期每辆降价1万元，如果卖出相同数量的A款汽车，去年销售额为100万元，今年销售额只有90万元．（1）今年5月份A款汽车每辆售价多少万元？（2）为了增加收入，汽车销售公司决定再经销同品牌的B款汽车，已知A款汽车每辆进价为7.5万元，B款汽车每辆进价为6万元，公司预计用不多于105万元且不少于99万元的资金购进这两款汽车共15辆，有几种进货方案？（3）如果B款汽车每辆售价为8万元，为打开B款汽车的销路，公司决定每售出一辆B款汽车，返还顾客现金a万元，要使（2）中所有的方案获利相同，a值应是多少？此时，哪种方案对公司更有利？【分析】（1）求单价，总价明显，应根据数量来列等量关系．等量关系为：今年的销售数量=去年的销售数量．（2）关系式为：99≤A款汽车总价+B款汽车总价≤105．（3）方案获利相同，说明与所设的未知数无关，让未知数x的系数为0即可；多进B款汽车对公司更有利，因为A款汽车每辆进价为7.5万元，B款汽车每辆进价为6万元，所以要多进B款．【解答】解：（1）设今年5月份A款汽车每辆售价m万元．则：，解得：m=9．经检验，m=9是原方程的根且符合题意．答：今年5月份A款汽车每辆售价9万元；（2）设购进A款汽车x辆．则：99≤7.5x+6（15﹣x）≤105．解得：6≤x≤10．∵x的正整数解为6，7，8，9，10，∴共有5种进货方案；（3）设总获利为W万元，购进A款汽车x辆，则：W=（9﹣7.5）x+（8﹣6﹣a）（15﹣x）=（a﹣0.5）x+30﹣15a．当a=0.5时，（2）中所有方案获利相同．此时，购买A款汽车6辆，B款汽车9辆时对公司更有利．【点评】本题考查分式方程和一元一次不等式组的综合应用，找到合适的等量关系及不等关系是解决问题的关键．。

2020年北师大八年级下第五章《分式与分式方程》单元测试题及答案 (2)

《分式与分式方程》单元检测一、选择题（每小题4分，共10小题，满分40分）1.下列各式-3x，，，-，，，中，分式的个数为（）A．1 B．2 C．3 D．4【考点】分式的定义．【分析】判断分式的依据是看分母中是否含有字母，如果含有字母则是分式，如果不含有字母则不是分式．【解答】解：-3x，，的分母中均不含有字母，因此它们是整式，而不是分式．-，，，分母中含有字母，因此是分式．故选：D．2.若分式的x和y均扩大为原来各自的10倍，则分式的值（）A．不变B．缩小到原分式值的C．缩小到原分式值的D．缩小到原分式值的【解答】解：式的x和y均扩大为原来各自的10倍，得==，故选：C．3.化简的结果是（）A．B．C．D．【考点】分式的乘除法．【专题】计算题．【分析】原式利用除法法则变形，约分即可得到结果．【解答】解：原式==．故选A．4.计算a3（）2的结果是（）A．a B．a5C．a6D．a8【考点】分式的乘除法．【专题】计算题．【分析】原式先计算乘方运算，再计算乘法运算即可得到结果．【解答】解：原式=a3=a，故选A5.若m个人完成某项工程需要a天，则（m+n）个人完成此项工程需要的天数（）A．a+m B．C．D．【解答】解：因为m个人完成某项工程需要a天，所以工作总量为ma，所以（m+n）个人完成此项工程需要的天数为．故选B．6.若分式方程=a无解，则a的值（）A．1 B．-1 C．±1D．0【解答】解：在方程两边同乘（x+1）得：x-a=a（x+1），整理得：x（1-a）=2a，当1-a=0时，即a=1，整式方程无解，当x+1=0，即x=-1时，分式方程无解，把x=-1代入x（1-a）=2a得：-（1-a）=2a，解得：a=-1，故选：C．7.化简的结果是（）A．x-1 B．C．x+1 D．【考点】分式的加减法．【专题】计算题；分式．【分析】原式变形后，通分并利用同分母分式的减法法则计算即可得到结果．【解答】解：原式===，故选B8.已知，则的值是（）A．9 B．11 C．7 D．1【考点】分式的乘除法．【分析】根据已知式左边右边都平方，可得所求式的形式，可得答案．【解答】解：∵，（m+）2=m2+2+=9，∴m2+=9-2=7，故选：C．9.如果，，那么等于（）A．1 B．2 C．3 D．4【考点】分式的化简求值．【分析】所求分式涉及字母a、c，故要消除b，根据两个已知等式中b的倒数关系消除b，再把所得等式变形即可．【解答】解：由已知得=1-a，b=1-，两式相乘，得（1-a）（1-）=1，展开，得1--a+=1去分母，得ac+2=2a两边同除以a，得c+=2．故选B．10.对于非零的两个实数a，b，规定a*b=-，若5*（3x-1）=2，则x的值为（）A．B．C．D．-【考点】解分式方程．【专题】新定义．【分析】根据规定5*（3x-1）可化成-，再根据解分式方程的步骤即可得出答案．【解答】解：根据题意得：-=2，解得：x=；经检验x=是原方程的解；故选B．二、填空题11.x的值为-1 时，分式无意义．【考点】分式有意义的条件．【分析】根据分母不为零分式有意义，可得答案．【解答】解：由分式无意义，得x+1=0，解得x=-1，12.计算： = -1 ．【解答】解：原式=-==-1．故答案为：-1．13.化简（）的结果是x+2 ．【解答】解：原式===x+2．故答案为：x+2．14.已知关于x的方程的解是负数，则m的取值范围为m＞-8且m≠-4 ．【解答】解：，2x-m=4x+8，-2x=8+m，x=-，∵关于x的方程的解是负数，∴-＜0，解得：m＞-8，∵方程，∴x+2≠0，即-≠-2，∴m≠-4，故答案为：m＞-8且m≠-4．15. 当x= 1 时，分式=0．【解答】解：由题意可得x-1=0且x+2≠0，解得x=1．故答案为x=1．16. 关于x的方程=-1无解，则m= -1或-．【考点】分式方程的解．【专题】计算题．【分析】先按照一般步骤解方程，用含m的代数式表示x，然后根据原方程无解，即最简公分母为0，求出m的值．【解答】解：化为整式方程得：3-2x-2-mx=3-x整理得x（1+m）=-2当此整式方程无解时，1+m=0即m=-1；当最简公分母x-3=0得到增根为x=3，当分式方程无解时，把增根代入，得m=-．故m=-1或-．17. 某园林队计划由6名工人对180平方米的区域进行绿化，由于施工时增加了2名工人，结果比计划提前3小时完成任务，若每人每小时绿化面积相同，求每人每小时的绿化面积．设每人每小时的绿化面积．设每人每小时的绿化面积为x平方米，请列出满足题意的方程是-=3 ．【考点】由实际问题抽象出分式方程．【分析】设每人每小时的绿化面积为x平方米，等量关系为：6名工人比8名工人完成任务多余3小时，据此列方程即可．【解答】解：设每人每小时的绿化面积为x平方米，由题意得， -=3．故答案为： -=3．18.某工厂原计划生产7200顶帐篷，后来有一个地区突然发生地震，要求工厂生产的帐篷比原计划多20%，并且需提前4天完成任务．已知实际生产时比原计划多生产720顶帐篷，设实际每天生产x顶帐篷，根据题意可列方程为-=720 ．【解答】解：设实际需要x天完成生产任务．根据题意得： -=720，故答案为： -=720．三、解答题19.先化简，再求值：÷（-x-2），其中x为-1≤x≤3的整数．【考点】分式的化简求值．【分析】先根据分式混合运算的法则把原式进行化简，再选出合适的x的值代入进行计算即可．【解答】解：原式=÷==，∵x为2时，原代数式无意义，∴x=-1或0或1或3，当x=-1时，原式=-．20. 先化简，再求值：，其中x是不等式组的一个整数解．【解答】解：原式===-（x+2）（x-1）=-x2-x+2，解不等式组，由①得x≤2，由②得x＞-1，所以不等式组的解集为-1＜x≤2，其整数解为0，1，2，由于x不能取1和2，所以当x=0时，原式=-0-0+2=2．21. 先化简：，并从0，-1，2中选一个合适的数作为a的值代入求值．【考点】分式的化简求值．【专题】计算题；开放型．【分析】首先把括号的分式通分化简，后面的分式的分子分解因式，然后约分化简，接着计算分式的乘法，最后代入数值计算即可求解．【解答】解：=×，=×=-，当a=0时，原式=1．22. 先化简，再求值：（ -）÷（-），其中x=，y=1．【考点】分式的化简求值．【分析】先根据分式混合运算的法则把原式进行化简，再把x=，y=1代入进行计算即可．【解答】解：原式=[-][-] ===-，当x=，y=1是，原式=-=2-3．23. 材料阅读：将分式拆分成一个整式与一个分式（分子为整数）的和（差）的形式．解：由分母为x+3，可设x2+2x-5=（x+3）（x+a）+b，则由x2+2x-5=（x+3）（x+a）+b=x2+ax+3x+3a+b=x2+（a+3）x+（3a+b）．∵对于任意x，上述等式均成立，∴，解得．∴==-=x-1-这样，分式就被拆分成一个整式与一个分式（分子为整数）的和（差）的形式．（1）将分式拆分成一个整式与一个分式（分子为整数）的和（差）的形式；（2）将分式拆分成整式与一个分式（分子为整数）的和（差）的形式．【解答】解：（1）由分母为x-1，可设x2+3x+6=（x-1）（x+a）+b，则x2+3x+6=（x-1）（x+a）+b=x2+（a-1）x+（b-a）．∵对于任意x，上述等式均成立，∴，解得，∴==x+4+；（2）由分母为-x2+1，可设-2x4-x2+5=（-x2+1）（2x2+a）+b，则由-2x4-x2+5=（-x2+1）（2x2+a）+b=-2x4+2x2-ax2+a+b=-2x4+（2-a）x2+（a+b）．∵对于任意x，上述等式均成立，∴，解得，，∴==2x2+3+．24. 【阅读】我们分析解决某些数学问题时，经常要比较两个数或代数式的大小，而解决问题的策略一般要进行一定的转化，其中“作差法”就是常用的方法之一．所谓“作差法”：就是通过作差、变形，并利用差的符号确定他们的大小，即要比较代数式M、N的大小，只要作出它们的差M-N，若M-N＞0，则M＞N；若M-N=0，则M=N；若M-N＜0，则M＜N．【运用】利用“作差法”解决下列问题：（1）小丽和小颖分别两次购买同一种商品，小丽两次都买了m千克商品，小颖两次购买商品均花费n元，已知第一次购买该商品的价格为a元/千克，第二次购买该商品的价格为b 元/千克（a，b是整数，且a≠b），试比较小丽和小颖两次所购买商品的平均价格的高低．（2）奶奶提一篮子玉米到集贸市场去兑换大米，每2kg玉米兑换1kg大米，商贩用秤称得连篮子带玉米恰好20kg，于是商贩连篮子带大米给奶奶共10kg，在这个过程中谁吃了亏？并说明理由．【考点】列代数式（分式）．【分析】（1）根据题意分别表示出小丽和小颖两次所购买商品的平均价格，利用作差法比较即可；（2）设篮子的质量为xkg，根据题意可得奶奶有的玉米数量为（20-x）kg，小贩给小莲的大米数量为（10-）kg，再根据玉米大米兑换比例即可得解．【解答】解：（1）∵=， =，∴-==＞0。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

7新人教版诚信教育学校分式章节测试题】若分式士有总义，则X 的取值范盹）三对于分式詩，当时，下列辨析正确的是（①分式值一定为0；②分式一定有意义；③a*—专时，分式值为a ④当x=如寸，分式无意义•3卜•列运算中，错误的是（44. 若角表示一个整数则幣数X 可取的值的个数是X-1A. 3B. 4 C ・ 5 D ・ 6主一的值为零，则X 的值是（A -3A- x^l B. x>lC. X=1 D- x<lAl 个B2个 C.3个 D4个a ac , 、 —a —b A(唧)E 石石C 0 5"b 5a + 10b 0 2a-0 3b 2a-3bX —y y —X x+y y+x(A) ±1-B 1.C. —1 •D 不存在.若 X-x-2 = 0 • 则的值等于（）（X" — X ）* — 1 + jy3.^3C. yjyD. 或邑n+c如果一3<n<-2.则卄;n+3 . n &八上 H ,肘+讨的值是（rd n n —1 己知心，Kl=—, N=—P=；^,则M 、N 、P 的大小关系为（A M>N>PB M>P>NC PAM>ND P>N>M 710卞列各式中，变形不正确的是（U 化简：Zmn +缶iir - 4irTC — Y — 213若分式I 的值为0,则X 的值等于X* + 2X + 114己知a b 为实数，且ab=b a 农1,设14=命+缶，N=^4-^ 15. 在下列三个不为零的式子x--<x--2x.x--4x+4任选两个你喜欢的式子组成一个分式•把这个分式化简所得的结JR 是16. 已知丄-丄=3,则代数式竺土空二空的值为X y x-2xy- y17己知当时分式云牙的值为0：当x=l 时.分式无总义-则a —b=・(Y — a ) 2^ Z V — 1 \ 2 -4-118已知r —5x —2009=0.则代数式 ——的值为I,若分式占的值是正整数，则整数X 的值是x3 — X* 1 — x'20请你先化简•再选一个使原式有意义，而你又喜爱的数值代入求值： -----------X" - X X+15 4-h9已知—妙且2a-3b = 0,那么代数式冷的值是（C -128 或一 12 —cnA 3y 3yB 二^=工C 丑=-丸—6x 6x —4y4y—8x 8x 3y -3y填空题（每小题2分，共20分）时，分式丄没有意义.X则M-N 的值等于X —2解答题（共60分）11-当 X3 2 — aa — 2 35 —X（本题8分）若分式百的值是负数，试求X 的取值范K11Y口56分）先化简（右一寸）.左=然后从不等式组——x<l 2 的整数解中选 3X+1 2X-1 5 ----------- <- 4 3 6取一个你认为合适的数作为X 的值代入求值• •23X* _ 2X （ 2x —4、（本题7分）求代数式的值；■-茶y.，其中24 2x+ 2（木题7分）如图•点A, B 在数轴上，它们所对应的数分别是一4, ------ ,且点AB 到原点的距3x-5离相等，求X 的值25 （本题8分）已知=0,求（岳-启隹的值.2627.（木题9分〉方案设计问题某市粮店出售某种人米，上半月的l^^价为每公斤a元，下半月的价为每公斤b元，冇一餐饮业老板毎个J］要向该店采购两次人米，且上半月购买一次，下半刀购买一次・该老板结合市场米价情况，设计两套釆购方案：A.每次购买100公斤人米；B.每次购买100元钱的犬米•请你运用所学知识分析一下・该老板采用哪种方式购买较划算•28 （本题9分）福兴商场文具专柜以每枝a （a为整数）元的价格购进一批”英tr牌钢笔，决定每枝加价 2元销售-由于这种胡牌的钢笔价格优、质量好、外观美•很快就销何一空-结账时•售货员发现这批钢笔的销俗总额为399a+805 （元）•你能根据上面的信息求出文人专柜共购进多少枝钢笔及每枝钢笔的进价a是多少元吗?鑫考答案基础知识回放①分母、②原来相等的同分母、③公因式、④最高次帚、⑤益、（§銓中考效能测试1.A【解析】木题考査的是分式有总义的条件若使分式有总义，必须保证分母X— 1的值不等于0所以对12.B【解析】本题考査的是使分式冇意义与无意义的条件根据是分式值为零的条件：3x+a=0且2x— 1却.所以aH-丰.对于①②说法不正确；对于③④就町以使分式有总义了答案为B3.D【解析】本题考査的是分式的基本性质对于A分式的分子与分母同时乘以一个不为0的C,符合分式的基本性质S而B在分式成立的条件下，分子与分母同时除以a+b也成立：C中分子与分母同时乘以 10使分子与分母的系数都为整数，也正确；D的结果应该等于一错课.4.D【解析】本题考査的是整除性首先考虑能够整除4的整数有±1, ±2> ±4o所以X —1=±1, ±2, ±4.所以X的值有6个5.C【解析】本题考查的是分式值为0的条件若使分式值为0必须保证分子的值等于0而分母的值不为 0因为闵一1=0・所以x=±l,但x=l时x'+2x—3=0,所以x=—12 /7 6.AI解析】本题考資的是整体代入法首先把r—x-2=0转化成r—x=2,然后整体代入经计算等于竺i37. A【解析】木题考查的足分式化简TT先根据n的范尉去折［绝对值，然后利用分式约分进行化简。

答案S. B【解析】本题考竇的是分式小的比较首先比较M与P的人小。

W为n-l<n+l,所以m>R其次比较M与N的人小因为n>n-l.n-l<n.所以m>n.^后比较N与P的大小采用做差法N-P=^丄一誌斤丽书V0,所以F>N所以B正确9. A【解析】本题考查的是分式求值•本题月三种方法：一釆用特殊值代入•这种方法对填空题和选择题很适用，例如取a=3, b=2代入可得结果为8二足用b表示a・即ajb,然后直接代入也训\三是把原分式化成含有辛的形式，即:U，然后把2a-3b = 0化成壽等代入10.D【解析】本题考査的是利用分式的符号法则变形在分式的分子.分母与分式本身的三处符号中如果改变其中两处分式的侑不变根据这个法则D改变了三处符号.D错误二、填空H11. xP 【解析】本题考査的是分式无意义的条件如果一个分式的分母值等于6则该分式没有意义 2. 黯【解析】本题考査的是分式约分先把分子与分母因式分解，然后约去公因式原式 1 (m-2n) (in+2n) ~m+2n13・2【解析】本题考査的是分式值为0的条件若使分式值为0必须保证分子的值等于0而分母的值不为14. 0【解析】木题考査的是分式求值首先计算M 的值。

M#y+b ；厂a ；ab + b ；n ）L +占同理N=l,所以M —N=0其次直接计算也可，但麻烦15.答案不唯一：务学或丘驚：^壽等【解析】本题考査的是分式化简答案不唯一 16. 4【解析】本题考査的是整体代入求值首先把原式转化成町以用;一：表示的形式，然后幣体代入原式呀14 ■ iin *■ ■ xy -17. -4［解析】本题考査的是使分式值为0和分时没有意义的条件市题意的2+a=0,即a=-2・又x=l 时分式没右•意义■所以2—b=0,所以b=2所以a —b=—4（X —r ）（X —1 ） •+!18. -2［解析】本题考査的是分式求值首先对——= ------- 进行化简，然后根据化简结果采的值跟X 的収值没令关系.20-提示：X 不能取0, -b 1答案不唯一.三、解答题 21.解：原式=4a-l + —^•^^ = 4a -l-a =3a-12-a 1原式r-亠。

22.原*一"-DE 二(x-l)(x + l)X X(m-2n) ■ m-2n0因为x^—X —2=0・所以x=2. x= b 但 x=—1 时 x^+2x+l=0t 所以 x=2取适当的方法代入求值（1）2-（L1） 2+1 &X+4/+X1+1 -2X+4x ・2_ =—2,根据化简町得本题中X-—X-2 X —2——x<l2得-2<x<3 3x+l 2x-l 5——<- 3 6 / X 为幣数 •: x=—1.0丄2 Tx 不能取±1.0 /. x=2a'—4—+a a + 2 a(a +2) 2 a —4 a —4 a + 2a (a + 2) • a—4 a (a + 2) a"4-2a因为 a-+2a-l=O,所以 a= + 2a = b 所以p?a 十/解不等式组2 23.解:X* - 2x X* - 2x x + 2 x+2 =(x-2)(x + 2)・-2只 "x-2当x=2 + JI 时原式占¥24.解: 由题意得,2x+2 ----- =4 , 3x-5 解得X=—.5经检验，x=¥是原方程的解. ・•• X 的值为2.a ra — 1 a —4 (a+2)沪ZT3(a —2) (a + 2) a (a —1) a + 2a (a+2)-3 (a + 2) a —4 2a 15—x>0 (5—xVO ®lx-3<0 或®1—>0解不等式组①，得XV3,解不等式组②，得x>5・此时X 的取值范由是x<3或x>5・试根据以上内容,解答下列问逼当分式m 的值是正数时，求次的范闾解当分式m 的值是正数时，则有:X S解不等式组①，得3<x<5：解不等式组②，得X 无解.此时X 的取值范用是3<x<5.27.解：若按方案A 购买，则平均每公斤大米的价格为（元）.200 若按方案B 购买，则平均毎公斤人米的价格为100 100 200 _ 2ab - 100b + 100a (兀人 ab • •a+b_ (a+b) ? • 丁 =2 (a+b) ' a+b —2 (a+b)'2ab 4ab又T (a+b) --4ab= (a-b) ->0 (当且仅当 a=b 时. (a-b) "=0), 学2鵲（当且仅当E 时，申=熬）.即当a=b 时，两种方案一样，当aHb 时，按方案B 购买较划算.399a+ 805 399a+80528.分析：依题意，知购进钢笔的枝数为a+.，显然，仅仅通过a + r 不能求出a.因此，挖掘条件中的内涵是解决问题的关键-这里a 为正整数・399a 严05也是正整数. 解：设文具专柜共购进钢笔y 枝，则竹399a+805 399a+798+7 399 (a + 2) +7 , 7 y=——= zm = =399+肓三・a+2 a +2 Ta>0且为整数，y 为正整数.•••a+2是7的约数••••a + 2=7 或 a +2=l ・ •'•a = 5, a = — 1 (不合题盘)• 当a = 5时・y=400-故文具专柜共购进钢笔400枝，每枝进价5元. 窗-QO 或閱-xVOx-3>0 X 一 3V0。