九年级上第四单元易错题集合(含答案)
2022-2023学年牛津译林版九年级英语上册Units4-5易错题含答案

牛津译林版英语9A Units4-5易错题一、单项选择。
( ) 1. How can _______ man like him be recommended as ______ leader of our hospital?A. the; /B. a; aC. the; theD. a; /( )2. important information it is! I’d tell to my mum.A.What an, itB.How, themC.What, itD.How, it( ) 3. _____ learning more and more about music, Tan Dun decided to use the sounds of nature in his works ______ musical instruments.A. Because; insteadB. Since; insteadC. As; instead ofD. Because of; instead of( ) 4. —Your spoken English is all very good. How do you improve it?—Thanks. Mrs. Wang always ask us to ____ conversations in our English classes.A. take upB. turn upC. make upD. end up( ) 5. --- Did you have fun camping on that hill?---Actually not. It’s not easy to find a suitable place to our tents.A. make upB. put upC. turn upD. stay up( )6. You’d better _______ here _______ the heavy rain.A. not to leave; becauseB. not leave ; becauseC. not leave; because ofD. not to leave; because of( )7The clothes need_______ but you_______ do that by yourself.A. to wash; needn’tB. washing; needn’t toC. washing; needn’tD. to wash; don’t ne ed to( )8 ________ everyone is here, let’s begin our meeting.A. SinceB. WhenC. ForD. Though( )9 When Mr Fang smelt the food, he stopped ___________.A. paintB. to paintC. paintingD.to painting( )10.---Oh,so many people are standing outside the hall.______will the film start? ---_______seven o’clock.A. How soon; Not untilB. How long; Not untilC. How soon; UntilD. How long; Until( )11. __________ musical talent Tan dun has!A. How amazingB. What amazedC. How amazedD. What amazing( )12.---Do you think this film is worth watching again?---_________. I’ve never seen a better one.A. I disagreeB. Yes, I think soC. That’s a good ideaD. It’s hard to say二、用所给单词的适当形式填空1 Lily and Rose are good friends and always keep their secrets to _____________(them).2 He was too angry. He ___________(简直是) didn’t know what to say.3 As a teacher, I want to see all my students __________________(成功).4 Could you tell me which league ________________(成功) in the end?5. The Dragon Boat Festival and the Mid-Autumn Festival are both _________(传统的)Chinese festival.6. Beethoven was born in Germany in 1770, and he was one of the most famous _________ (music) in history.7. All the countries in the world should work together to keep _________ (last) peace.8. He practices ____________(play) the piano.9. If you want to have a ________(last) change in your life, you need to eat healthy food.10. The reporter will write down the _________(win) names.三、阅读理解On a hot summer day, ice-cold watermelons serve up a delicious treat. Sure, the rosy flesh (果肉) quenches your thirst (解渴). But now there are more reasons than ever for people to reach for a slice of watermelon.Meet Dr Alison Edwards. She is a scientist at the Agricultural Research Service. Scientists are people who come up with new ideas called theories (理论). They usually do scientific research to test their new theories. That’s how they find out if a new idea is a go od one, or if the new idea will bring an even better idea.At her lab, Dr Edwards recently learned more about the secrets of why watermelons are good for you!Dr Edwards has known for a long time that watermelons have vitamin C. But recently she learned that watermelons also have lycopene(番茄红素). It is something that gives tomatoes and watermelons their rosy red colour.What’s so special about the lycopene in watermelons?Dr Edwards says that watermelons and tomatoes both have lots of lycopene. It seems that your body can use the lycopene from watermelons more easily than the lycopene from raw(生的) tomatoes. In fact, the lycopene from tomatoes is more easily absorbed (吸收) inside your body once they have been cooked.( ) 1. The watermelon is a kind of .A. drinkB. fruitC. medicineD. vitamin( ) 2. How does a scientist usually test a theory?A. By practising it in daily life.B. By doing scientific research.C. By discussing it with other scientists.D. By looking into many scientific reports.( ) 3. Lycopene is something that gives tomatoes and watermelons their colour.A. redB. greenC. blackD. yellow( ) 4. To make full use of tomatoes, we’d better .A. eat them rawB. not peel theC. cook them firstD. make them into juice( ) 5. Which of the following is TRUE according to the passage?A. Our bodies cannot absorb lycopene.B. Watermelons are good for us in hot summer.C. Tomatoes have more lycopene than watermelons do.D. Lycopene in watermelons is hard for our bodies to absorb.四. 任务型阅读Playing is serious business for children. In fact, it’s what they do best! Ask them why they do it, and kids will probably say, “Because it’s fun!” But it’s much more than that. It’s also good for them.Studies show that from birth babies begin learning through play. They use their five senses to get to know their new world. Touching allows them to discover how different things feel. Brightly coloured toys and clothing help develop a baby’s sense of sight (视觉). When small children choose which toy to play with, they begin developing their abilities in making decisions. Children love toys that allow them to use their imagination (想象力). Sometimes an empty box is more fun than a high-tech (高科技) toy. That’s because a box can become anything to a child. Crayons, paints and Play-Doh (彩色塑泥) are also good because they allow children to create. Traditional building blocks teach important pre-math skills.Playing doesn’t become any less important once children start school. Many valuable lessons about life are learned on the school playground. Kids learn how to share, take turns and play by the rules.Children’s (1)_______________The (2) _______________ of playingPlaying with brightly coloured toys It is good for (3) _______________ a baby’s sense of sight.(4) _______________ which toy to play with Children can learn how to make (5) _______________.Playing with an (6) _______________boxChildren can use their (7) _______________.Playing with crayons, paints andPlay-DohChildren can be (8) _______________ to create.Playing on the playground Children can learn many (9) _______________ lessons about life, such as how to share, (10) _______________ turns and play by the rules.根据所给提示,请你用英语完成短文。
(易错题)初中数学九年级数学上册第四单元《圆》检测(包含答案解析)
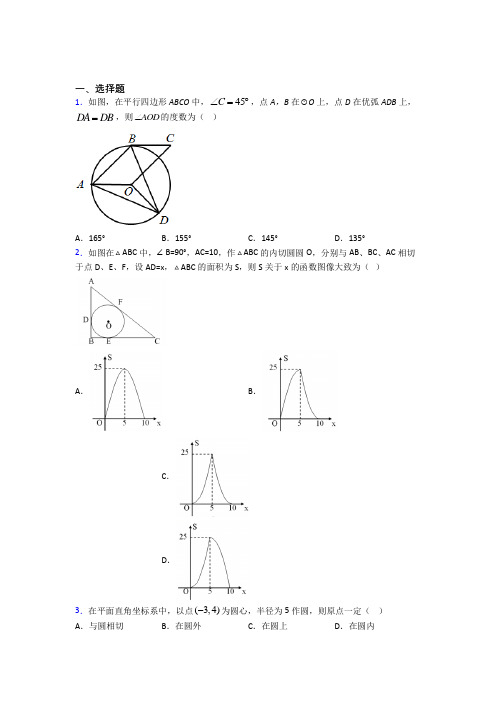
一、选择题1.如图,在平行四边形ABCO 中,45C ∠=︒,点A ,B 在⊙O 上,点D 在优弧ADB 上,DA DB =,则AOD ∠的度数为( )A .165°B .155°C .145°D .135°2.如图在ABC 中,∠B=90°,AC=10,作ABC 的内切圆圆O ,分别与AB 、BC 、AC 相切于点D 、E 、F ,设AD=x ,ABC 的面积为S ,则S 关于x 的函数图像大致为( )A .B .C .D .3.在平面直角坐标系中,以点()3,4-为圆心,半径为5作圆,则原点一定( ) A .与圆相切 B .在圆外 C .在圆上 D .在圆内4.下列事件属于确定事件的为( )A .氧化物中一定含有氧元素B .弦相等,则所对的圆周角也相等C .戴了口罩一定不会感染新冠肺炎D .物体不受任何力的时候保持静止状态 5.若圆锥的底面半径为5cm ,侧面积为265cm π,则该圆锥的高是( ) A .13cmB .12cmC .11cmD .10cm 6.如图,O 的半径为5,弦AB 的长为8,M 是弦AB 上的一个动点,则线段OM 可取的整数值有( )个A .1B .2C .3D .47.如图△ABC 中,∠C =90°,∠B =28°,以C 为圆心,CA 为半径的圆交AB 于点D ,则AD 的度数为( )A .28°B .56 °C .62°D .112° 8.已知AB 是经过圆心O 的直线,P 为O 上的任意一点,则点P 关于直线AB 的对称点P '与O 的位置关系是( ) A .点P '在⊙○内B .点P '在O 外C .点P '在O 上D .无法确定 9.如图,AB 是⊙的直径,DB 、DE 分别切⊙O 于点B 、C ,若∠ACE =35°,则∠D 的度数是( )A .65°B .55°C .60°D .70°10.如图,四边形ABCD 内接于O ,若108B ∠=︒,则D ∠的大小为( )A .36°B .54°C .62°D .72°11.如图,⊙O 是四边形 ABCD 的内切圆,连接 OA 、OB 、OC 、OD .若∠AOB =110°,则∠COD 的度数是( )A .60°B .70°C .80°D .45° 12.在扇形中,∠AOB =90°,面积为4πcm 2,用这个扇形围成一个圆锥的侧面,这个圆锥的底面半径为 ( )A .1cmB .2cmC .3n cmD .4cm 二、填空题13.如图,PA 、PB 是⊙O 的切线,切点分别为A 、B ,若OA=2,∠P=60°,则AB 的长为________14.如图,已知AB 是O 的直径,点C ,D 在O 上,2BC =,30CDB ∠=︒,则O 的半径为_____.15.在矩形ABCD 中,43AB =6BC =,若点P 是矩形ABCD 上一动点,要使得60APB ∠=︒,则AP 的长为__________.16.如图,O 是正方形ABCD 的外接圆,2,AB =点E 是劣弧AD 上的任意一点,连接BE ,作CF BE ⊥于点F ,连接,AF 则当点E 从点A 出发按顺时针方向运动到点D 时,AF 长的取值范围为________________.17.在平面直角坐标系xOy 中,A (5,6),B (5,2),C (3,0),△ABC 的外接圆的圆心坐标为____.18.如图,ABC 是等边三角形,180BAD BCD ∠+∠=︒,8BD =,2CD =,则AD =________.19.已知圆心O 到直线l 的距离为5,⊙O 半径为r ,若直线l 与⊙O 有两个交点,则r 的值可以是________.(写出一个即可)20.如图,ABC 内接于半径为10的半圆,AB 为直径,点M 是弧AC 的中点,连结BM 交AC 于点E ,AD 平分∠CAB 交BM 于点D ,∠ADB =_____°,当点D 恰好为BM 的中点时,BM 的长为____.三、解答题21.如图,已知正方形ABCD 的边长为1,正方形BEFG 中,点E 在AB 的延长线上,点G 在BC 上,点O 在线段AB 上,且AO BO ≥.以OF 为半径的O 与直线AB 交于点M 、N .(1)如图1,若点O为AB中点,且点D,点C都在O上,求正方形BEFG的边长.(2)如图2,若点C在O上,求证:以线段OE和EF为邻边的矩形的面积为定值,并求出这个定值.⊥.(3)如图3,若点D在O上,求证:DO FO22.如图,AB是⊙O的弦,点C在AB上,点D是AB的中点.将AC沿AC折叠后恰好经过点D,若⊙O的半径为25,AB=8.则AC的长是_______.=,以BC为直径的O交AB于点O,过点D作23.已知:如图,ABC中,BC AC⊥于点E,交BC的延长线于点F.DE AC=,(2)DF是O的切线.求证:(1)AD BD24.如图,已知直线l与⊙O相离,过圆心O画OA⊥l于点A,交⊙O于点P且OA=5,点B为⊙O上一点BP的延长线交直线l于点C且AB=AC.(1)判断AB与⊙O有怎样的位置关系,并说明理由;PC=⊙O的半径.(2)若525.已知△ABC,请按以下要求完成本题:(1)请作出△ABC的外接圆⊙O(尺规作图,保留作图痕迹);(2)若在△ABC中,∠ABC=70°,∠ACB=40°,⊙O的直径AD交CB于E,则∠DEC= .26.如图,OA、OB、OC分别是⊙O的半径,且AC=CB,D、E分别是OA、OB的中点.CD与CE相等吗?为什么?【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【分析】连接OB,根据平行四边形的性质可得∠OAB=∠C=45°,再根据等腰三角形的等边对等角得∠OBA=∠OAB=45°,则∠AOB=90°,由DA=DB得∠AOD=∠BOD,进而可求得∠AOD的度数.【详解】解:连接OB,∵四边形ABCO是平行四边形,∴∠OAB=∠C=45°,∵OA=OB,∴∠OBA=∠OAB=45°,∴∠AOB=90°,∵DA=DA ,∴∠AOD=∠BOD=12(360°﹣90°)=135°, 故选:D .【点睛】本题考查平行四边形的性质,等腰三角形的性质,圆心角、弧、弦的关系等知识,熟练掌握平行四边形的性质和等腰三角形的性质,熟知等弦所对的圆心角相等是解答的关键. 2.A解析:A【分析】连接OD 、OE ,根据三角形内切圆证得四边形DBEO 是正方形,在根据勾股定理即可得解;【详解】连接OD 、OE ,如图,O 的半径为r ,∵△ABC 的内切圆O 分别于AB 、BC 、AC 相切与点D 、E 、F ,∴⊥OD AB ,OE BC ⊥,AF=AD=x ,CE=CF=10-x , 易得四边形DBEO 是正方形,∴DB BE OD r ===,∵()()2△1110101022ABC S r AB BC AC r x r r x r r =++=+++-+=+,∵222AB BC AC +=,∴()()2221010x r x r ++-+=, ∴221010r r x x +=-+,∴()2210525S x x x=-+=--+(0<x<10).故答案选A.【点睛】本题主要考查了切线的性质,三角形的内切圆与圆心,函数图像,准确分析判断是解题的关键.3.C解析:C【分析】设点(-3,4)为点P,原点为点O,先计算出OP的长,然后根据点与圆的位置关系的判定方法求解.【详解】解:∵设点(-3,4)为点P,原点为点O,∴OP5,而⊙P的半径为5,∴OP等于圆的半径,∴点O在⊙P上.故选:C.【点睛】本题考查了点与圆的位置关系:点的位置可以确定该点到圆心距离与半径的关系,反过来已知点到圆心距离与半径的关系可以确定该点与圆的位置关系.4.A解析:A【分析】根据确定事件的概念,可知需找出必然事件或不可能事件即可.【详解】A、氧化物是含有两种元素其中一种是氧元素的化合物,必然事件;B、在同圆或等圆中,弦相等所对的圆周角相等或互补,不确定事件;C、戴了口罩一定不会感染新冠肺炎,不确定事件;D、物体不受任何力的时候保持静止状态或匀速运动,不确定事件.故选A.【点睛】本题考查事件的划分,必然事件和不可能事件统称为确定事件,确定事件中,必然出现的事情称为必然事件;不可能出现的事情称为不可能事件.5.B解析:B【分析】先根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形面积公式得到12•2π•5•OA=65π,可求出OA=13,然后利用勾股定理计算圆锥的高.【详解】解:根据题意得12•2π•5•OA=65π,解得:OA=13,所以圆锥的高=2213512.故选:B.【点睛】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.6.C解析:C【分析】当M与A或B重合时,达到最大值;当OM⊥AB时,为最小,从而确定OM的取值范围即可解决问题.【详解】解:如图所示,过O作OM′⊥AB,连接OA,∵过直线外一点与直线上的所有连线中垂线段最短,∴当OM于OM′重合时OM最短,∵AB=8,OA=5,∴AM′=12×8=4,∴在Rt△OAM′中,222254OA AM=--'=3,∴线段OM长的最小值为3,最大值为5.所以,OM的取值范围是:3≤OM≤5,故线段OM长的整数值为3,4,5,共3个.故选:C.【点睛】本题考查的是勾股定理和最值.本题容易出现错误的地方是对点M的运动状态不清楚,无法判断什么时候会为最大值,什么时候为最小值.7.B解析:B【分析】连接CD,如图,利用互余计算出∠A=62°,则∠A=∠ADC=62°,再根据三角形内角和定理计算出∠ACD=56°,然后根据圆心角的度数等于它所对弧的度数求解.【详解】解:连接CD,如图,∵∠C=90°,∠B=28°,∴∠A=90°-28°=62°,∵CA=CD,∴∠A=∠ADC=62°,∴∠ACD=180°-2×62°=56°∴AD的度数为56°;故选:B.【点睛】本题考查了同圆的半径相等、直角三角形的两锐角互余、等腰三角形的性质,熟练进行逻辑推理是解题关键.8.C解析:C【分析】圆是轴对称图形,直径所在的直线就是对称轴,从而得到圆上的点关于对称轴对称的点都在圆上求解.【详解】解:∵圆是轴对称图形,直径所在的直线就是对称轴,∴点P关于AB的对称点P′与⊙O的位置为:在⊙O上,故选:C.【点睛】本题考查了点与圆的位置关系,利用了圆的对称性求解.9.D解析:D【分析】连结BC,则由已知可以求得∠BCD与∠CBD的度数,最后由三角形的内角和定理可以得到∠D 的度数.【详解】解:如图,连结BC ,则由弦切角定理可知:∠ABC=∠ACE=35°,∵DB 与⊙O 相切,∴∠CBD=90°-∠ABC=90°-35°=55°,∵AB 是⊙的直径,∴∠ACB=90°,∴∠BCD=180°-∠ACE-∠90°=55°,∴∠D=180°-∠BCD-∠CBD=70°,故选D .【点睛】本题考查圆的应用,灵活运用直线与圆相切的性质求解是解题关键.10.D解析:D【分析】运用圆内接四边形对角互补计算即可.【详解】∵四边形ABCD 内接于⊙O ,∠B =108°,∴∠D =180°−∠B =180°−108°=72°,故选:D .【点睛】本题主要考查了圆内接四边形的性质,熟练掌握圆内接四边形对角互补是解答此题的关键.11.B解析:B【分析】设四个切点分别为E 、F 、G 、H ,分别连接切点和圆心,利用切线性质和HL 定理可以得到4对全等三角形,进而可得∠1=∠2,∠3=∠4,∠5=∠6,∠7=∠8,根据8个角之和为360°即可求解.【详解】解:设四个切点分别为E 、F 、G 、H ,分别连接切点和圆心,则OE ⊥AB ,OF ⊥BC ,OG ⊥CD ,OH ⊥AD ,OE=OF=OG=OH ,在Rt △BEO 和△BFO 中,OE OF OB OB =⎧⎨=⎩, ∴Rt △BEO ≌△BFO (HL )∴∠1=∠2,同理可得:∠3=∠4,∠5=∠6,∠7=∠8,∴∠1+∠8=∠2+∠7,∠4+∠5=∠3+∠6,∵∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8=360°,∴∠1+∠8+∠4+∠5=180°,即∠AOB+∠COD=180°,∵∠AOB=110°,∴∠COD=180°﹣∠AOB=180°﹣110°=70°,故选:B .【点睛】本题考查了圆的切线性质、全等三角形的判定与性质,利用圆的的切线性质,添加辅助线构造全等三角形是解答的关键.12.A解析:A【分析】圆锥的底面周长等于侧面展开图的扇形弧长,因而要先求扇形的弧长,根据扇形的面积公式2360n R S π=,可以求出扇形的半径,就可以求出弧长. 【详解】 解:根据扇形的面积公式2360n R S π=得到:2904360R ππ=; ∴R=4,则弧长9042180cm ππ⋅==, 设圆锥的底面半径为r ,则2π=2πr ;∴r=1cm .故选:A .【点睛】 本题综合考查有关扇形和圆锥的相关计算.解题思路:解决此类问题时要紧紧抓住两者之间的两个对应关系:(1)圆锥的母线长等于侧面展开图的扇形半径;(2)圆锥的底面周长等于侧面展开图的扇形弧长.正确对这两个关系的记忆是解题的关键.二、填空题13.【分析】连接AB并延长BO交圆于C连接ACPAPB是⊙O的切线由切线长定理知PA=PB;又∠P=60°则等腰三角形APB是等边三角形则有∠ABP=60°BC是直径;由直径对的圆周角是直角得∠PBC=解析:23【分析】连接AB,并延长BO交圆于C,连接AC,PA、PB是⊙O的切线,由切线长定理知PA=PB;又∠P=60°,则等腰三角形APB是等边三角形,则有∠ABP=60°,BC是直径;由直径对的圆周角是直角得∠PBC=90°,则在Rt△ABC中,有∠ABC=30°,进而可知AB的长.【详解】解:连接AB,并延长BO交圆于C,连接AC,∵PA、PB是⊙O的切线,∴PA=PB,又∵∠P=60°,∴∠PBA=60°;又∵BC是圆的直径,∴CB⊥PB,∠BAC=90°,∴∠ABC=30°,而BC=4,∴在Rt△ABC中,cos30°=AB BC,∴323故答案为:3【点睛】本题利用了切线长定理,等边三角形的判定和性质,弦切角定理,直角三角形的性质,正弦的概念求解.注意本题的解法不唯一.掌握相关知识是解题的关键.14.2【分析】根据圆周角定理得出∠A=∠CDB∠ACB=90°根据含30°角的直角三角形的性质得出AB=2BC求出AB再求出半径即可【详解】解:∵∴∠A=∠CDB∵∠CDB=30°∴∠A=30°∵AB为解析:2【分析】根据圆周角定理得出∠A=∠CDB,∠ACB=90°,根据含30°角的直角三角形的性质得出AB=2BC,求出AB,再求出半径即可.【详解】解:∵=BC BC∴∠A=∠CDB,∵∠CDB=30°,∴∠A=30°,∵AB为⊙O的直径,∴∠ACB=90°,∵BC=2,∴AB=2BC=4,∴⊙O的半径是142⨯=,2故答案为:2.【点睛】本题考查了圆周角定理,含30°角的直角三角形的性质等知识点,能根据圆周角定理得出∠A=∠CDB和∠ACB=90°是解此题的关键.15.或4或8【分析】取CD中点P1连接AP1BP1由勾股定理可求AP1=BP1=4即可证△AP1B是等边三角形可得∠AP1B=60°过点A点P1点B作圆与ADBC各有一个交点即这样的P点一共3个再运用勾解析:43或4或8.【分析】取CD中点P1,连接AP1,BP1,由勾股定理可求AP1=BP1=43,即可证△AP1B是等边三角形,可得∠AP1B=60°,过点A,点P1,点B作圆与AD,BC各有一个交点,即这样的P 点一共3个.再运用勾股定理求解即可.【详解】解:如图,取CD中点P1,连接AP1,BP1,如图1,∵四边形ABCD 是矩形∴AB =CD =43,AD =BC =6,∠D =∠C =90°∵点P 1是CD 中点∴CP =DP 1=23∴AP 1=221AD DP +=43, BP 1=221BC CP +=43 ∴AP 1=P 1B =AB∴△APB 是等边三角形∴∠AP 1B =60°,过点A ,点P 1,点B 作圆与AD ,BC 的相交,∴这样的P 点一共有3个当点P 2在AD 上时,如图2,∵四边形ABCD 是矩形,∴3,43,90AB A CD AD =∠===︒∵260,AP B ∠=︒∴221,2P A P B = 即222,P B P A =在2Rt P AB ∆中,22222,P B P A AB -=∴222222(43),P A P A -=∴24AP =;当点P 3在BC 上时,如图3,∵四边形ABCD 是矩形,∴∠B=90°∵∠360,AP B =︒∴∠3390906030,P AB AP B =︒-∠=︒-︒=︒ ∴331,2BP AP = 在3Rt ABP ∆中,22233,AP BP AB -=222331()(43),2AP AP -= 23348,4AP = ∴8,AP =综上所述,AP 的长为:34或8. 故答案为:34或8.【点睛】本题考查了矩形的性质,勾股定理,等边三角形的判定和性质,灵活运用这些性质进行推理是本题的关键.16.【分析】首先根据题意可知当点与点重合时最长的最大值为;再证明点的运动轨迹为以为直径的通过添加辅助线连接交于点连接由线段公理可知当点与点重合时最短的最小值为即可得解【详解】解:∵由题意可知当点与点重合 512AF ≤≤【分析】首先根据题意可知,当点F 与点B 重合时AF 最长,AF 的最大值为2;再证明点F 的运动轨迹为以BC 为直径的'O ,通过添加辅助线连接'AO 交'O 于点M ,连接'O F ,由线段公理可知,当点F 与点M 重合时AF 最短,AF 51.即可得解.【详解】解:∵由题意可知,当点F 与点B 重合时AF 最长∴此时2AF AB ==,即AF 的最大值为2∵CF BE ⊥∴90CFB ∠=︒∴点F 的运动轨迹为以BC 为直径的'O ,连接'AO 交'O 于点M ,连接'O F ,如图:∵2AB = ∴11'122BO BC AB === ∴在'Rt ABO 中,22''5AO AB BO =+=∴''51AM AO O M =-=∴由两点之间,线段最短可知,当点F 与点M 重合时AF 最短∴AF 51 ∴512AF ≤≤.【点睛】本题考查了正多边形和圆的动点问题、90︒的圆周角所对的弦为直径、勾股定理、线段公理等知识点,解题的关键是确定AF 取最大值和最小值时点F 的位置,属于中考常考题型,难度中等.17.(14)【分析】如图作AB 和BC 的垂直平分线它们的交点为△ABC 的外接圆的圆心然后直接读出△ABC 的外接圆的圆心坐标【详解】解:如图所示:点P 即为所求;所以点P 的坐标为(14)故答案为(14)【点睛解析:(1,4)【分析】如图,作AB 和BC 的垂直平分线,它们的交点为△ABC 的外接圆的圆心,然后直接读出△ABC 的外接圆的圆心坐标.【详解】解:如图所示:点P 即为所求;所以点P 的坐标为(1,4).故答案为(1,4).【点睛】本题主要考查了三角形的外接圆与外心,掌握三角形外接圆的圆心是三角形三条边垂直平分线的交点是解答本题的关键.18.6【分析】在线段BD 上取一点E 使得BE=CD 连接AE 由四点共圆得∠再证明△是等边三角形得再由线段的和差关系可得结论【详解】解:在线段BD 上取一点E 使得BE=CD 连接AE ∵∴四点共圆∴∠∴∠∵△是等边解析:6【分析】在线段BD 上取一点E ,使得BE=CD ,连接AE ,由,,,A B C D 四点共圆得∠ABE ACD =∠,再证明ABE ACD ≅∆,△ADE 是等边三角形,得AD DE AE ==,再由线段的和差关系可得结论.【详解】解:在线段BD 上取一点E ,使得BE=CD ,连接AE ,∵180BAD BCD ∠+∠=︒∴,,,A B C D 四点共圆,∴∠ABD ACD =∠∴∠ABE ACD =∠∵△ABC 是等边三角形,∴AB AC BC ==,60DAE ∠=︒,∴△ABE ACD ≅∆,∠60BAE CAF +∠=︒,∴,BAE CAD BAF CAD ∠=∠∠=∠,∴∠60CAD CAE +∠=︒,即60DAE ∠=︒,∴△ADE 是等边三角形,∴AD DE AE ==,∵=8BD ,2CD =,∴6DE BD BE BD CD =-=-=,∴6AD DE ==.【点睛】此题主要考查了全等三角形的判定与性质,以及四点共圆的判定,证明∠ABE ACD =∠是解答此题的关键.19.答案不唯一如516等(满足即可)【分析】根据直线与圆的位置关系可得出圆的半径与圆心距之间的关系再取r 的值即可【详解】解:∵直线l 与⊙O 有两个交点圆心O 到直线l 的距离为5∴∴在此范围内取值即可如516解析:答案不唯一,如5.1,6等(满足5r >即可)【分析】根据直线与圆的位置关系可得出圆的半径与圆心距之间的关系,再取r 的值即可.【详解】解:∵直线l 与⊙O 有两个交点,圆心O 到直线l 的距离为5,∴5r >∴在此范围内取值即可,如5.1,6等.【点睛】此题主要考查了直线与圆的位置关系---相交,熟知直线与圆相交满足的条件是解答此题的关键.20.【分析】(1)根据直径所对的圆周角是可得到再根据弧的中点定义同弧所对的圆周角相等角平分线定义可推导出最后有三角形的内角和定理即可求得答案;(2)在(1)的基础上结合已知条件添加辅助线连接从而构造出等解析:135【分析】(1)根据直径所对的圆周角是90︒可得到90CAB CBA ∠+∠=︒,再根据弧的中点定义、同弧所对的圆周角相等、角平分线定义可推导出45DAB DBA ∠+∠=︒,最后有三角形的内角和定理即可求得答案;(2)在(1)的基础上,结合已知条件添加辅助线“连接AM ”,从而构造出等腰Rt ADM △,利用勾股定理解Rt ABM 即可求得答案.【详解】解:(1)∵AB 是直径∴90ACB ∠=︒∴90CAB CBA ∠+∠=︒∵点M 是弧AC 的中点∴AM CM =∴CBM ABM ∠=∠∵AD 平分CAB ∠∴CAD BAD ∠=∠ ∴()1452DAB DBA CAB CBA ∠+∠=∠+∠=︒ ∴()180135ADB DAB DBA ∠=︒-∠+∠=︒.(2)连接AM ,如图:∵AB 是直径∴90AMB ∠=︒∵18045ADM ADB ∠=︒-∠=︒∴AM DM = ∵点D 为BM 的中点∴DM DB =∴2BM AM =∴设AM x =,则2BM x =∵10∴210AB =∵在Rt ABM 中,222AM BM AB +=∴22440x x +=∴122x =222x =-∴22AM =∴42BM =.【点睛】本题考查了直径所对的圆周角是90︒、弧的中点定义、同弧所对的圆周角相等、角平分线定义、三角形的内角和定理、线段的中点定义、利用勾股定理解直角三角形、解一元二次方程等知识点,通过添加辅助线构造直角三角形解决问题的关键,难度中等,属于中考常考题型.三、解答题21.(1)12;(2)见解析;12;(3)证明见解析【分析】(1)连接OC,设BE=EF=x,则OE=x+12,得出(x+12)2+x2=(12)2+12,解得:x=12,则答案求出;(2)连接OC,设OB=y,BE=EF=x,同(1)可得,OE2+EF2=OF2,OB2+BC2=OC2,得出x2+(x+y)2=y2+12,即x(x+y)=12,则结论可得证;(3)连接OD,设OA=a,BE=EF=b,则OB=1-a,则OE=1-a+b,可得出12+a2=(1-a+b)2+b2,得出a=b,则OA=EF,证明Rt△AOD≌Rt△EFO(HL),则得出∠FOE=∠ODA,结论得出.【详解】解:(1)连接OC∵四边形ABCD和四边形BEFG为正方形,∴AB=BC=1,BE=EF,∠OEF=∠ABC=90°,∵点O为AB中点,∴OB=12AB=12,设BE=EF=x,则OE=x+12,在Rt△OEF中,∵OE2+EF2=OF2,∴(x+12)2+x2=OF2,在Rt△OBC中,∵OB2+BC2=OC2,∴(12)2+12=OC2,∵OC,OF为⊙O的半径,∴OC=OF,∴(x+12)2+x2=(12)2+12,解得:x=12,∴正方形BEFG的边长为12;(2)证明:如图2,连接OC,设OB=y,BE=EF=x,同(1)可得,OE2+EF2=OF2,OB2+BC2=OC2,∴OF2=x2+(x+y)2,OC2=y2+12∵OC,OF为⊙O的半径,∴OC=OF,∴x2+(x+y)2=y2+12,∴2x2+2xy=1,∴x2+xy=12,即x(x+y)=12,∴EF×OE=12,∴以线段OE和EF为邻边的矩形的面积为定值,这个定值为12.(3)证明:连接OD,设OA=a,BE=EF=b,则OB=1-a,则OE=1-a+b,∵∠DAO=∠OEF=90°,∴DA2+OA2=OD2,OE2+EF2=OF2,∴12+a2=OD2,(1-a+b)2+b2=OF2,∵OD=OF,∴12+a2=(1-a+b)2+b2,∴(b+1)(a-b)=0,∵b+1≠0,∴a-b=0,∴a=b,∴OA=EF,在Rt△AOD和Rt△EFO中,OD OF OA EF ⎧⎨⎩==, ∴Rt △AOD ≌Rt △EFO (HL ),∴∠FOE=∠ODA ,∵∠DAO=90°,∴∠ODA+∠AOD=90°,∴∠FOE+∠AOD=90°,∴∠DOF=90°,∴DO ⊥FO .【点睛】本题是圆的综合题,考查了圆的性质,正方形的性质,全等三角形的判定与性质,矩形的面积等知识,熟练运用方程的思想是解题的关键.22.【分析】延长BO 交⊙O 于E ,连接AE ,OA ,OD ,OC ,BC ,作CH ⊥AB 于H .首先证明∠CAE=∠CAH=45°,推出∠BOC=90°,推出,设AH=CH=x ,则BH=8-x ,在Rt △BCH 中,根据222CH BH BC +=,构建方程求出x 即可解决问题【详解】解:如图,延长BO 交⊙O 于E ,连接AE ,OA ,OD ,OC ,BC ,作CH ⊥AB 于H . ∵AD =DB ,∴OD ⊥AB ,∴∠ADO =90°,∵OA =AD =DB =4,∴OD2,∵BE 是直径,∴∠BAE =90°,∵AD =DB ,EO =OB ,∴OD//AE ,AE =2OD =4,∴AE =AD ,∴AD AE =,∴EC CD =,∴∠CAE =∠CAH =45°,∴∠BOC =2∠CAB =90°,∴BCOC =,∵CH ⊥AB ,∴∠CAH =∠ACH =45°,∴AH =CH ,设AH =CH =x ,则BH =8﹣x ,在Rt △BCH 中,∵222CH BH BC +=,∴()()2228210x x +-=, ∴x =6或2(舍弃),在Rt △ACH 中,∵AC =22AH CH +,∴AC =62.故答案为:62.【点睛】本题考查圆周角定理、垂径定理、勾股定理、解直角三角形等知识,综合性比较强,作出辅助线,构造直角三角形是解题的关键.23.(1)证明见解析;(2)证明见解析.【分析】(1)如图(见解析),先根据圆周角定理可得90BDC ∠=︒,再根据等腰三角形的三线合一即可得证;(2)先根据等腰三角形的三线合一可得ACD BCD ∠=∠,再根据等腰三角形的性质可得ODC BCD ∠=∠,从而可得ACD ODC ∠=∠,然后根据平行线的判定与性质可得OD DF ⊥,最后根据圆的切线的判定即可得证.【详解】(1)如图,连接CD ,BC 是O 的直径,90BDC ∴∠=︒,即CD AB ⊥,又BC AC =,CD ∴是AB 边上的中线(等腰三角形的三线合一),AD BD ∴=;(2)如图,连接OD ,,BC AC CD AB =⊥,ACD BCD ∴∠=∠,OC OD =,ODC BCD ∴∠=∠,ACD ODC ∴=∠∠,//∴,OD AC⊥,DE AC⊥,即DF AC∴⊥,OD DF又OD是O的半径,DF∴是O的切线.【点睛】本题考查了等腰三角形的三线合一、圆周角定理、圆的切线的判定等知识点,较难的是题(2),熟练掌握圆的切线的判定定理是解题关键.24.(1)AB与⊙O相切,理由见解析;(2)3【分析】(1)连接OB,由题意易得∠ACB =∠ABC,∠OAC=90°,则有∠APC=∠OBP,进而可证OB⊥AB,则问题可证;(2)设⊙O的半径为x,由(1)得OP = OB = x,则有PA = 5-x,然后根据勾股定理可进行求解.【详解】解:(1)AB与⊙O相切,理由:连接OB,如图所示:∵AB=AC,∴∠ACB =∠ABC,又∵OA⊥l,∴∠OAC=90°,∴∠ACB +∠APC =90°,又∵OP=OB,∴∠O PB=∠OBP,∵∠OPB=∠APC,∴∠APC=∠OBP,∴∠OBP +∠ABC =90°,即OB⊥AB,∵点B 是半径OB 的外端点,∴AB 是⊙O 的切线;(2)设⊙O 的半径为x ,∴OP = OB = x又∵OA = 5,25PC =∴ PA = 5-x在Rt △ACP 中∴ AC 2 =PC 2 -PA 2 =()()222255105x x x --=-+-, 在Rt △OAB 中∴ AB 2 =OA 2 -OB 2 =222525x x -=-又∵AB = AC∴2225105x x x -=-+-,解得:x =3∴⊙O 的半径为3.【点睛】本题主要考查切线的判定定理,熟练掌握切线的判定定理是解题的关键.25.(1)见解析;(2)60°【分析】(1)分别作出AB 与AC 的垂直平分线,进而得出圆心的位置,再利用圆心到三角形顶点的距离为半径得出圆O 即可;(2)连接BD .根据圆周角定理求出∠ABD=90°,∠D=∠ACB=40°,则∠DBC=∠ABD-∠ABC=20°,再利用三角形外角的性质即可求出∠DEC .【详解】解:(1)如图所示:(2)连接BD .∵AD 是直径,∴∠ABD=90°,∴∠DBC=∠ABD-∠ABC=90°-70°=20°,又∵∠D=∠ACB=40°,∴∠DEC =∠D+∠DBC=40°+20°=60°.【点睛】本题主要考查了三角形外接圆的作法,圆周角定理,三角形外角的性质,熟练掌握相关的定理是解题关键.26.CD=CE .见解析.【分析】由题意易得OD=OE ,由等弧所对的圆心角相等可得DOC EOC ∠=∠,进而由全等三角形的判定证得△CDO ≌△CEO ,进而求证结论.【详解】CD=CE .∵ D 、E 分别是OA 、OB 的中点, ∴12OD OA ,12OE OB =, ∴OD=OE ,∵AC CB =.∴DOC EOC ∠=∠,又∵OC=OC ,∴△CDO ≌△CEO ,∴CD=CE .【点睛】本题主要考查圆圆周角定理、全等三角形的判定和性质,解题的关键是由等弧所对的圆心角相等求得DOC EOC ∠=∠.。
(易错题)初中数学九年级数学上册第四单元《圆》检测卷(答案解析)

解析:D
【分析】
利用垂径定理可对A进行判断;根据圆周角定理得到∠AOC=2∠D=60°,则△OAC为等边三角形,根据等边三角形的性质和垂径定理可计算出 ,则可对B进行判断;利用AB=AC=OA=OC=OB可对C进行判断;通过判断△AOB为等边三角形,再根据扇形的面积公式可对D进行判断.
【详解】
24.如图,在平面直角坐标系中,点A的坐标为 ,点B的坐标为 .
(1)画出将绕点O顺时针旋转 后的图形,记为 ;
(2)在题(1)旋转过程中线段OA扫过的面积为_______(直接写出答案)
25.如图, 中, , , 与 交于点 .求证 .
26.已知:如图, 是 的直径,弦 于点 , 是 上一点, 与 的延长线交于点 .
∵OB=OA,
∴∠ABO=∠BAO= (180°﹣∠AOB)=36°,
故选:C.
【点睛】
本题考查了圆周角定理,圆心角、弧、弦之间的关系,等腰三角形的性质和三角形的内角和定理等知识点,能求出圆心角∠AOB的度数是解此题的关键.
3.B
解析:B
【分析】
设AC=a,BC=b,由勾股定理可求得a2+b2=102,由三角形的面积公式和圆的面积公式分别求出空白部分图形面积和阴影部分图形面积,利用阴影部分图形面积之和是空白部分图形面积之和的3倍可求得ab,进而可求得△ABC的面积.
【分析】
根据切线的性质得到∠OPB=90°,证出OP//BC,根据平行线的性质得到∠POB=∠CBD,于是得到结果.
【详解】
∵AB是⊙O的切线,
∴∠OPB=90°,
∵∠ABC=90°,
∴OP//BC,
∴∠CBD=∠POB=40°,
故选D.
【点睛】
九年级上册英语9AUnit4 Growing up单元易错题整理(含答案)

9AU4 Growing up易错题整理一、单项填空1.He graduated fromuniversity this summer and got_________unusual job luckily.A. a; anB. an; aC. a; aD. an; an2. ---Would you mind telling me something about the two ?---.They are exchange students from England.A. Frenchmen; Of courseB. Frenchmans; That's all rightC. Germans; Not at allD. German; All right3.Before the local government ___________ him, he stayed in a primary school for 10 years.A.got away fromB. took notice ofC. tried out forD. cheered up4. ---Waiter, $22 for dinner, right?---I’m afraid $25, sir, for drinks are ________.A.freeB. highC. spareD. extra5. The washing machine requires _________. I’m uncertain if I can fix it myself.A.to repairB. to be repairedC. repairingD. both B and C6.一I am away, would you please look after my pet cats?一With pleasure.A.WhileB. AfterC. BeforeD. Until7. — Is your uncle in his _______?— Yes. His_______ birthday is coming next week.A.forty; forty-firstB. forties; forty-firstC. forties; forty-oneD. forty; forty-first8.______ he is not rich,_____ he is very happy.A. Though; butB. Though; /C. Although; butD. Because; so9. — How much difficulty did you havethis problem?—. It's quite easy.A.to solve; NothingB. to solve; NoneC. solving; NothingD. solving; None10. He never gives up,____ he has made _____progress in his study.A.although;muchB. although;littleC.but;muchD. but;a little11.The shop ________ at 9:00 a.m. and it ________ for ten hours every day.A.opens; is openB. is opened; opensC. is open; has openedD. opened; opens12.It was raining outside, but the boy remained ______football.A.to be playedB.playsC.playingD.play13. —When shall I hand in my report?—As soon as it_________ next week.pletesB.is completedC.will completeD.will be completed14.After reading the texts, the students were asked to go on ____________.A.to practise to listenB.practising to listenC.to practise listeningD.practising listening15.The thing that_______ is not whether you fail or not, but whether you try your best or not.A.mindsB.caresC.mattersD.considers16.Nowadays we can learn a great deal about the world not only___books but also ___ the Internet.A.in;onB.in;throughC.from;throughD.through;from17.—When will you go shopping with me? —_______________.A. Until my housework is finishedB. Not until my housework is finishedC.After my housework will be finishedD. As soon as my housework will be finished18. I’ll go to visit my aunt in England ________ the summer holidays start.A. whileB. sinceC. untilD. as soon as19. _______ you have problems, you can call me.A. WhateverB. UntilC. WheneverD. While20. I don’t like driving. I do it __________ because I have to get to work each day.A. easilyB. simplyC. easyD. simple21. His mum wants to have him________the radio, but he has had it _______already.A. repair; repairB. to repair; repairC. repaired; to repairD. repair; repaired22. Tommy will stop showing off, if no notice of him.A. is takenB. will be takenC. takesD. has taken23. The show he paid much attention tosuccessful at last.A. provedB. proveC. provingD. proves24. ---Do you know Lily’s grandma?---Yes.She is a kind woman, but she has____for about a month since she____in the accident.A.been dead ; killedB. died ; killedC.died ; was killedD. been dead; was killed25.There are no ways she can come up ________ her out.A.to helpingB. to helpC. with helpingD. with to help26. ---How long do you think it'll beI can go back to school?---Well, you will be feeling much better by next weekend.A. beforeB. whenC. sinceD. after27. ---did you leave the classroom?---I saw my daughter sit down and read her book.A. How long; AfterB. When; AfterC. How long; UntilD. When; Until28. We visited Huaxi Village last Sunday and had some photosthere.A. tookB. takingC. takenD. to take二、词汇运用1. The lovely cat’s sudden___________ (die) was a great hit to the twin sisters.2. You can ask for help ______________(无论何时) you need it.3. We ____________(简直) can’t wait for the fashion show tomorrow.4. Whichever way you look at it,an Olympic gold medal is a great_______(成就)for one so young.5. It’s such a good suggestion that no one is ____________ (反对)it.6. Now more and more__________(大学) students can make money to support their daily lives.7. Please write down the______________(德国人) names in this form.8. Our school_____________(success) held the art festival last week.9. The kind man ____________(successfully) in helping them out of the trouble in the end.10. Many people were __________(强迫) to move to other countries because of the war.11. They have__________(保持不变) in touch with the old couple for more than 5 years.12. I’d like to listen to your ___________(think), boys and girls.13. My professor is in her __________ (50).14. Lost in the mountain for weeks, the two students were(final) saved by the local police.15.He had his car(repair) on his way to the party,so he was late that day.三、阅读填空I have lived in France for nine years, but I cannot walk down the street without being recognized(认出) as an Englishman from 50 metres away before I open my mouth. Why?In France, the quickest way to recognize an Englishman is that he'll be the one with the belly(肚子) and the shirt hanging out. Englishmen often wear shapeless black T-shirts, either too big or too small. However. Frenchmen are more formal in dressing. Their T-shirts have collars(领子). Shorts have buttons and zips rather than drawstrings(拉绳). Shoes look expensive.Englishmen think of lunchtime as 1 p.m. but for Frenchmen it is 12 o'clock, one hour earlier. This may explain the sad looks if an Englishman arrives at a local restaurant at 1:30 p.m. At that time most restaurants don't have waiters. All the cooking and serving may be done by the boss and his wife. When you arc shown to your table, just sit there and wait. Don't wave your hands to the waiters. Englishmen think guests should do something to make the waiters pay attention to them. But in France some bread and water will come first, then the waiters will take your order according to the rhythm(节奏) of the restaurant. Have enough patience!Some 1 between Englishmen and FrenchmenFrenchmen Englishmen参考答案单项选择ACBDD ABBDB ACBCC CBDCBDAADD ABC词汇运用death whenever simply achievement against university Germans’successfully succeeded forced remained thoughts fifties finally repaired 阅读填空differences cost waiter’s/waiters less patient。
(易错题)初中数学九年级数学上册第四单元《圆》检测卷(包含答案解析)
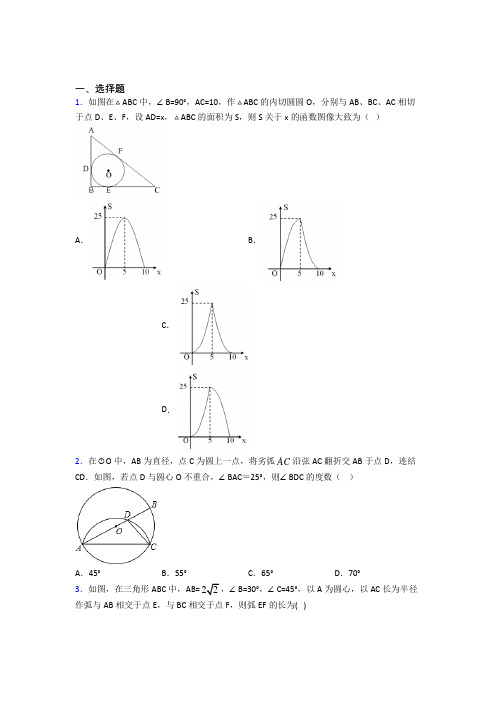
一、选择题1.如图在ABC中,∠B=90°,AC=10,作ABC的内切圆圆O,分别与AB、BC、AC相切于点D、E、F,设AD=x,ABC的面积为S,则S关于x的函数图像大致为()A.B.C.D.2.在⊙O中,AB为直径,点C为圆上一点,将劣弧AC沿弦AC翻折交AB于点D,连结CD.如图,若点D与圆心O不重合,∠BAC=25°,则∠BDC的度数()A.45°B.55°C.65°D.70°3.如图,在三角形ABC中,AB=2,∠B=30°,∠C=45°,以A为圆心,以AC长为半径作弧与AB相交于点E,与BC相交于点F,则弧EF的长为( )A .6πB .2πC .23πD .π4.下列事件属于确定事件的为( )A .氧化物中一定含有氧元素B .弦相等,则所对的圆周角也相等C .戴了口罩一定不会感染新冠肺炎D .物体不受任何力的时候保持静止状态 5.给出下列说法:①圆是轴对称图形,对称轴是圆的每一条直径;②三角形的外心到三角形各顶点的距离相等;③经过三个点一定可以画一个圆;④平分弦的直径垂直于弦;⑤垂直于弦的直径平分弦,并且平分弦所对的两条弧.正确的有( )A .4B .3C .2D .16.如图,不等边ABC 内接于O ,下列结论不成立的是( )A .12∠=∠B .14∠=∠C .2AOB ACB ∠=∠D .23ACB ∠=∠+∠ 7.已知O 的半径为5,若4PO =,则点P 与O 的位置关系是( ) A .点P 在O 内 B .点P 在O 上 C .点P 在O 外 D .无法判断 8.如图,在⊙O 中,AB 是直径,弦AC=5,∠BAC=∠D .则AB 的长为( )A .5B .10C .52D .1029.如图,O 的半径为5,弦AB 的长为8,M 是弦AB 上的一个动点,则线段OM 可取的整数值有( )个A.1 B.2 C.3 D.410.如图,AB是⊙的直径,DB、DE分别切⊙O于点B、C,若∠ACE=35°,则∠D的度数是()A.65°B.55°C.60°D.70°11.下列说法中,正确的是()A.三点确定一个圆B.在同圆或等圆中,相等的弦所对的圆周角相等C.平分弦的直径垂直于弦D.在同圆或等圆中,相等的圆心角所对的弦相等12.在扇形中,∠AOB=90°,面积为4πcm2,用这个扇形围成一个圆锥的侧面,这个圆锥的底面半径为 ( )A.1cm B.2cm C.3n cm D.4cm二、填空题13.如图,四边形ABCD是O的内接四边形,对角线AC,BD交于点E,且AC BD AB==,若70∠=︒,则AOBAEB∠等于______︒.14.如图,有一半径为6cm的圆形纸片,要从中剪出一个圆心角为60︒的扇形ABC,AB,AC为⊙O的弦,那么剪下的扇形ABC(阴影部分)的面积为 ___________.15.如图,⊙O 的直径16AB =,半径OC AB ⊥,E 为OC 的中点, DE OC ⊥,交⊙O 于点D ,过点D 作DF AB ⊥于点F .若 P 为直径AB 上一动点,则PC PD +的最小值为 ________ .16.如图,正六边形ABCDEF 的边长为2,分别以点A ,D 为圆心,以AB ,DC 为半径作扇形ABF ,扇形DCE .则图中阴影部分的面积是______.17.如图,若∠BOD =140°,则∠BCD=___________ .18.如图,正方形 ABCD 中,点 E 是 CD 边上一点,连接 AE ,过点 B 作 BG ⊥AE 于点 G , 连接 CG 并延长交 AD 于点 F ,当 AF 的最大值是 2 时,正方形 ABCD 的边长为______.19.如图,直线33y x =+x 轴于点A ,交y 轴于点B .以A 为圆心,以AB 为半径作弧交x 轴于点A 1;过点A 1作x 轴的垂线,交直线 AB 于点B 1,以A 为圆心,以AB 1为半径作弧交x 轴于点 A 2;…,如此作下去,则点n A 的坐标为___________;20.如图,已知空间站A 与星球B 距离为a ,信号飞船C 在星球B 附近沿圆形轨道行驶,B ,C 之间的距离为b .数据S 表示飞船C 与空间站A 的实时距离,那么S 的最小值________.三、解答题21.如图,已知AB 是O 的一条弦,DE 是O 的直径且DE AB ⊥于点C . (1)若3,5OC OA ==,求AB 的长;(2)求证:EAO BAD ∠=∠.22.如图,已知圆内接四边形ABDC 中,∠BAC =60°,AB =AC ,AD 为它的对角线. 求证:AD =BD+CD .23.如图,已知AB 为O 的直径,点C 、D 在O 上,CD BD =,E 、F 是线段AC 、AB 的延长线上的点,并且EF 与O 相切于点D .(1)求证:2A BDF ∠=∠;(2)若3AC =,5AB =,求CE 的长.24.如图,已知在△ABC 中,∠A =90°.(1)作∠ABC 的角平分线交AC 于点P ,以点P 为圆心,PA 长为半径作⊙P ,则⊙P 与BC 的位置关系是 .(2)在(1)的条件下,若AB=3,BC=5,求⊙P 的面积.25.对于平面直角坐标系xOy 中的点P 和C ,给出如下定义:如果C 的半径为r ,C 外一点P 到C 的切线长小于或等于2r ,那么点P 叫做C 的“离心点”. (1)当C 的半径为1时,①在点())12313,0,2,5,02P P P ⎛- ⎝⎭中,C 的“离心点”是_____________; ②点P(m ,n)在直线3y x =-+上,且点P 是O 的“离心点”,求点P 横坐标m 的取值范围; (2) C 的圆心C 在y 轴上,半径为2,直线132y x =-+与x 轴.y 轴分别交于点A 、B .如果线段AB 上的所有点都是C 的“离心点”,请直接写出圆心C 纵坐标的取值范围. 26.已知,AB 是O 的直径,点P 在弧AB 上(不含点A 、B ),把AOP 沿OP 对折,点A 的对应点C 怡好落在O 上.(1)当P 、C 都在AB 上方时(如图1),判断PO 与BC 的位置关系是______; (2)当P 在AB 上方而C 在AB 下方时(如图2),(1)中结论还成立吗?证明你的结论:(3)当P 、C 都在AB 上方时(如图3),过C 点作CD ⊥直线AP 于D ,且CD 是O 的切线,证明:4AB PD =.【参考答案】***试卷处理标记,请不要删除一、选择题1.A解析:A【分析】连接OD 、OE ,根据三角形内切圆证得四边形DBEO 是正方形,在根据勾股定理即可得解;【详解】连接OD 、OE ,如图,O 的半径为r ,∵△ABC 的内切圆O 分别于AB 、BC 、AC 相切与点D 、E 、F ,∴⊥OD AB ,OE BC ⊥,AF=AD=x ,CE=CF=10-x ,易得四边形DBEO 是正方形,∴DB BE OD r ===, ∵()()2△1110101022ABC S r AB BC AC r x r r x r r =++=+++-+=+,∵222AB BC AC +=,∴()()2221010x r x r ++-+=, ∴221010r r x x +=-+, ∴()2210525S x x x =-+=--+(0<x <10). 故答案选A .【点睛】本题主要考查了切线的性质,三角形的内切圆与圆心,函数图像,准确分析判断是解题的关键.2.C解析:C【分析】连接BC ,求出∠B =65°,根据翻折的性质,得到∠ADC+∠B =180°,进而得到∠BDC=∠B =65°.【详解】解:连接BC ,∵AB 是直径,∴∠ACB =90°,∵∠BAC =25°,∴∠B =90°﹣∠BAC =90°﹣25°=65°,根据翻折的性质,AC 所对的圆周角为∠B ,ABC 所对的圆周角为∠ADC ,∴∠ADC+∠B =180°,∴∠BDC=∠B =65°,故选:C .【点睛】本题考查了圆周角定理及其推论,根据题意添加适当辅助线是解题关键.3.A解析:A【分析】过A 作AD ⊥BC ,连接AF ,求出∠FAE ,再利用弧长计算公式计算EF 的长即可.【详解】解:过A 作AD 垂直BC ,连接AF ,如图,∵2,30,45AB B C =∠=︒∠=︒,可得2∴AC=2,∵AC=AF∴∠AFC=∠C=45°,∴∠FAE=∠AFC-∠B=45°-30°=15°∴EF 的长为:152180π⨯=6π 故选:A【点睛】此题主要考查了弧长的计算,关键是掌握弧长计算公式. 4.A解析:A【分析】根据确定事件的概念,可知需找出必然事件或不可能事件即可.【详解】A 、氧化物是含有两种元素其中一种是氧元素的化合物,必然事件;B 、在同圆或等圆中,弦相等所对的圆周角相等或互补,不确定事件;C 、戴了口罩一定不会感染新冠肺炎,不确定事件;D 、物体不受任何力的时候保持静止状态或匀速运动,不确定事件.故选A.【点睛】本题考查事件的划分,必然事件和不可能事件统称为确定事件,确定事件中,必然出现的事情称为必然事件;不可能出现的事情称为不可能事件.5.C解析:C【分析】根据对称轴是一条直线,即可判断①;根据外心的性质即可判断②;利用确定圆的条件即可判断③;根据弦不是直径时,平分弦的直径才垂直于弦,即可判断④;根据垂径定理的推论,即可判断⑤.【详解】∵圆是轴对称图形,直径所在直线是它的对称轴,∴①错误;∵三角形的外心到三角形的三个顶点的距离相等,∴②正确;∵经过不在同一直线上的三点确定一个圆,∴③错误;∵平分弦(弦不是直径)的直径垂直于弦,∴④错误;∵垂直于弦的直径平分弦,且平分弦所对的弧,∴⑤正确;综上,正确的是②⑤,共2个,故选:C.【点睛】本题考查了垂径定理及其推论,三角形的外接圆与外心等知识点的应用,正确把握相关定义是解题关键.6.B解析:B【分析】利用OB=OC可对A选项的结论进行判断;由于AB≠BC,则∠BOC≠∠AOB,而∠BOC=180°-2∠1,∠AOB=180°-2∠4,则∠1≠∠4,于是可对B选项的结论进行判断;根据圆周角定理可对C选项的结论进行判断;利用∠OCA=∠3,∠1=∠2可对D选项的结论进行判断.【详解】解:∵OB=OC,∴∠1=∠2,所以A选项的结论成立;∵OA=OB,∴∠4=∠OBA,∴∠AOB=180°-∠4-∠OBA=180°-2∠4,∵△ABC为不等边三角形,∴AB≠BC,∴∠BOC≠∠AOB,而∠BOC=180°-∠1-∠2=180°-2∠1,∴∠1≠∠4,所以B选项的结论不成立;∵∠AOB与∠ACB都对弧AB,∴∠AOB=2∠ACB,所以C选项的结论成立;∵OA=OC,∴∠OCA=∠3,∴∠ACB=∠1+∠OCA=∠2+∠3,所以D选项的结论成立.故选:B.【点睛】本题考查了三角形的外接圆与外心:三角形外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心.也考查了圆周角定理和等腰三角形的性质.7.A解析:A【分析】已知圆O的半径为r,点P到圆心O的距离是d,①当r>d时,点P在⊙O内,②当r=d 时,点P在⊙O上,③当r<d时,点P在⊙O外,根据以上内容判断即可.【详解】∵⊙O的半径为5,若PO=4,∴4<5,∴点P与⊙O的位置关系是点P在⊙O内,故选:A.【点睛】本题考查了点与圆的位置关系的应用,注意:已知圆O的半径为r,点P到圆心O的距离是d,①当r>d时,点P在⊙O内,②当r=d时,点P在⊙O上,③当r<d时,点P在⊙O外.8.C解析:C【分析】根据圆周角定理得出∠D=∠B,得出△ABC是等腰直角三角形,进而解答即可.【详解】∵AC=AC,∴∠D=∠B,∵∠BAC=∠D,∴∠B=∠BAC,∴△ABC是等腰三角形,∵AB是直径,∴△ABC是等腰直角三角形,∵AC=5,∴AB=52,故选:C.【点睛】本题考查了圆周角定理,等腰直角三角形的判定和性质,勾股定理的应用,关键是根据圆周角定理得出∠D=∠B.9.C解析:C【分析】当M与A或B重合时,达到最大值;当OM⊥AB时,为最小,从而确定OM的取值范围即可解决问题.【详解】解:如图所示,过O作OM′⊥AB,连接OA,∵过直线外一点与直线上的所有连线中垂线段最短,∴当OM于OM′重合时OM最短,∵AB=8,OA=5,∴AM′=1×8=4,2∴在Rt△OAM′中,O M′=2222-'=3,OA AM=-54∴线段OM长的最小值为3,最大值为5.所以,OM的取值范围是:3≤OM≤5,故线段OM长的整数值为3,4,5,共3个.故选:C.【点睛】本题考查的是勾股定理和最值.本题容易出现错误的地方是对点M的运动状态不清楚,无法判断什么时候会为最大值,什么时候为最小值.10.D解析:D【分析】连结BC,则由已知可以求得∠BCD与∠CBD的度数,最后由三角形的内角和定理可以得到∠D的度数.【详解】解:如图,连结BC,则由弦切角定理可知:∠ABC=∠ACE=35°,∵DB与⊙O相切,∴∠CBD=90°-∠ABC=90°-35°=55°,∵AB是⊙的直径,∴∠ACB=90°,∴∠BCD=180°-∠ACE-∠90°=55°,∴∠D=180°-∠BCD-∠CBD=70°,故选D .【点睛】本题考查圆的应用,灵活运用直线与圆相切的性质求解是解题关键.11.D解析:D【分析】根据确定圆的条件、垂径定理、圆周角定理一一判断即可.【详解】解:A、任意三点确定一个圆;错误,应该的不在同一直线上的三点可以确定一个圆,不符合题意;B 、在同圆或等圆中,相等的弦所对的圆周角相等或互补,错误,不符合题意;C 、平分弦的直径垂直于弦,错误,此弦不是直径,不符合题意;D 、在同圆或等圆中,相等的圆心角所对的弦相等,正确,符合题意;故选:D .【点睛】本题考查确定圆的条件、垂径定理、圆周角定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.12.A解析:A【分析】圆锥的底面周长等于侧面展开图的扇形弧长,因而要先求扇形的弧长,根据扇形的面积公式2360n R S π=,可以求出扇形的半径,就可以求出弧长. 【详解】 解:根据扇形的面积公式2360n R S π=得到:2904360R ππ=; ∴R=4,则弧长9042180cm ππ⋅==, 设圆锥的底面半径为r ,则2π=2πr ;∴r=1cm .故选:A .【点睛】 本题综合考查有关扇形和圆锥的相关计算.解题思路:解决此类问题时要紧紧抓住两者之间的两个对应关系:(1)圆锥的母线长等于侧面展开图的扇形半径;(2)圆锥的底面周长等于侧面展开图的扇形弧长.正确对这两个关系的记忆是解题的关键.二、填空题13.125【分析】根据题意先求出∠ABE=∠BAE=55°然后由等腰三角形的定义和三角形的内角和定理求出∠C=625°即可求出的度数【详解】解:根据题意∵在圆中有∴∴∴在△ABE 中∴在等腰△ABC 中则∴解析:125【分析】根据题意,先求出∠ABE=∠BAE=55°,然后由等腰三角形的定义和三角形的内角和定理,求出∠C=62.5°,即可求出AOB ∠的度数.【详解】解:根据题意,∵在圆中,有AC BD AB ==,∴AC BD =,∴AD BC =,∴ABD BAC ∠=∠,在△ABE 中,70AEB ∠=︒, ∴1(18070)552ABD BAC ∠=∠=⨯︒-︒=︒, 在等腰△ABC 中,AC AB =则1(18055)62.52C ∠=⨯︒-︒=︒, ∴2125AOB C ∠=∠=︒;故答案为:125.【点睛】本题考查了圆内接四边形的性质,圆周角定理,三角形的内角和定理,等腰三角形的定义,解题的关键是熟练掌握所学的知识,正确的进行解题.14.【分析】如图(见解析)先根据等边三角形的判定与性质可得再根据圆周角定理可得然后根据垂径定理勾股定理可得BC 的长从而可得AB 的长最后利用扇形的面积公式即可得【详解】如图连接OBOCBC 过点O 作于点D 由 解析:218cm π【分析】如图(见解析),先根据等边三角形的判定与性质可得AB BC =,再根据圆周角定理可得120BOC ∠=︒,然后根据垂径定理、勾股定理可得BC 的长,从而可得AB 的长,最后利用扇形的面积公式即可得.【详解】如图,连接OB 、OC 、BC ,过点O 作OD BC 于点D ,由题意得:,60,6AB AC A OB OC cm =∠=︒==,ABC ∴是等边三角形,AB BC ∴=,由圆周角定理得:2120BOC A ∠=∠=︒,OD BC ⊥,160,22BOD BOC BC BD ∴∠=∠=︒=, 30OBD ∴∠=︒,在Rt BOD 中,13,2OD OB cm BD ====,2AB BC BD ∴===,则剪下的扇形ABC (阴影部分)的面积为()()22606318360cm ππ⨯=, 故答案为:218cm π.【点睛】本题考查了等边三角形的判定与性质、圆周角定理、垂径定理、扇形的面积公式等知识点,通过作辅助线,利用到垂径定理是解题关键.15.【分析】延长CO 交⊙O 于G 连接GD 交AB 于P 根据两点之间线段最短可知PC+PD 的最小值为GD 由勾股定理分别求得DEDG 即可解答【详解】解:延长CO 交⊙O 于G 连接GD 交AB 于P 则PC+PD 的最小值为G解析:83【分析】延长CO 交⊙O 于G ,连接GD 交AB 于P ,根据两点之间线段最短可知PC+PD 的最小值为GD ,由勾股定理分别求得DE 、DG 即可解答.【详解】解:延长CO 交⊙O 于G ,连接GD 交AB 于P ,则PC+PD 的最小值为GD ,连接OD ,则OD=OG=OC= 12AB=8, ∵E 为OC 的中点,∴OE=12OC=4, ∴EG=4+8=12,∵DE OC ⊥,∴在Rt △OED 中,==,在Rt △GED 中,==故答案为:【点睛】本题考查勾股定理、最短路径问题、圆的有关概念与性质,熟练掌握勾股定理和圆的性质是解答的关键.16.﹣【分析】根据题意和图形可知阴影部分的面积是正六边形的面积减去两个扇形的面积从而可以解答本题【详解】解:∵正六边形ABCDEF 的边长为2∴正六边形ABCDEF 的面积是:6××22=∠FAB =∠EDC解析:83π 【分析】根据题意和图形可知阴影部分的面积是正六边形的面积减去两个扇形的面积,从而可以解答本题.【详解】解:∵正六边形ABCDEF 的边长为2,∴正六边形ABCDEF 的面积是:2=,∠FAB =∠EDC =120°, ∴图中阴影部分的面积是:2×21202360π⋅⋅=83π,故答案为:83π. 【点睛】本题考查正多边形和圆、扇形面积的计算,解答本题的关键是明确题意,利用数形结合的思想解答. 17.【分析】如图(见解析)先根据圆周角定理可得再根据圆内接四边形的性质即可得【详解】如图在优弧上取一点E 连接BEDE 由圆内接四边形的性质得:故答案为:【点睛】本题考查了圆周角定理圆内接四边形的性质熟练掌 解析:110︒【分析】如图(见解析),先根据圆周角定理可得70BED ∠=︒,再根据圆内接四边形的性质即可得.【详解】如图,在优弧BD 上取一点E ,连接BE 、DE ,140BOD ∠=︒,1702BED BOD ∠∴∠==︒, 由圆内接四边形的性质得:180110BC ED D B ∠=︒-∠=︒,故答案为:110︒.【点睛】本题考查了圆周角定理、圆内接四边形的性质,熟练掌握圆周角定理是解题关键. 18.8【分析】以AB 为直径作圆O 则∠AGB=90º当CF 与圆O 相切时AF 最大AF=2由切线长定理的AF=FGBC=CG 过F 作FH ⊥BC 与H 则四边形ABHF 为矩形AB=FHAF=BH=2设正方形的边长为x解析:8.【分析】以AB 为直径作圆O ,则∠AGB=90º,当CF 与圆O 相切时,AF 最大,AF=2,由切线长定理的AF=FG ,BC=CG ,过F 作FH ⊥BC 与H ,则四边形ABHF 为矩形,AB=FH ,AF=BH=2,设正方形的边长为x ,在Rt △FHC 中,由勾股定理得x 2+(x-2)2=(x+2)2解之即可.【详解】以AB 为直径作圆O ,∵AB 为直径,∴∠AGB=90º,当CF 与圆O 相切时,AF 最大,AF=2,由切线长定理的AF=FG ,BC=CG ,过F 作FH ⊥BC 与H ,则四边形ABHF 为矩形,AB=FH ,AF=BH=2,设正方形的边长为x ,则HC=x-2,FC=2+x ,FH=x ,在Rt △FHC 中,由勾股定理得,x 2+(x-2)2=(x+2)2,整理得:x 2-8x=0,解得x=8,x=0(舍去),故答案为:8.【点睛】本题考查圆的切线问题,涉及切线长,直径所对的圆周角,引辅助圆与辅助线,正方形的性质,矩形的性质与判定,能综合运用这些知识解决问题特别是勾股定理构造分析是解题关键.19.(2n﹣10)【分析】根据题意先求出点AB的坐标再利用勾股定理求出AA1AA2AA3……AAn的长可得到点A1A2A3……An的坐标找到规律即可解答【详解】解:当x=0时y=当y=0时x=﹣1∴A(解析:(2n﹣1,0)【分析】根据题意,先求出点A、B的坐标,再利用勾股定理求出AA1、AA2、AA3……AA n的长,可得到点A1、A2、A3……A n的坐标,找到规律即可解答.【详解】解:当x=0时,3y=0时,x=﹣1,∴A(﹣1,0),B(03,∴AA122++=,则点A1(1,0),B1(1,3,(01)(3)2∴AA2=AB122++=,则点A2(3,0),B2(3,3,(11)(23)4∴AA3=AB222++=,则点A3(7,0),B3(7,3,(31)(43)8……∴可以得到A n的坐标为(2n﹣1,0),故答案为:(2n﹣1,0).【点睛】本题考查了一次函数图象上的点的坐标特征、图形的规律探究、圆的基本知识、勾股定理,解答的关键是利用勾股定理求得AA1、AA2、AA3……AA n的长,进而得到A1、A2、A3……A n的坐标的变化规律.20.a-b【分析】根据圆外一点到圆的最大距离是过圆心的直线与圆相交的最远的点到圆的最小距离是点与圆心的连线与圆相交的最近点求解即可【详解】解:空间站A与星球B飞船C在同一直线上时S取到最小值a-b故答案解析:a-b根据圆外一点到圆的最大距离是过圆心的直线与圆相交的最远的点,到圆的最小距离是点与圆心的连线与圆相交的最近点求解即可.【详解】解:空间站A与星球B、飞船C在同一直线上时,S取到最小值a-b.故答案为:a-b.【点睛】本题考查了圆外一点到圆的最大距离和最短距离,最大距离和最短距离都在过圆心的直线上.属于基础知识.三、解答题AB=;(2)见解析21.(1)8【分析】(1)由DE⊥AB,得∠OCA=90°,OC=3,OA=5,通过勾股定理即可求出AC;由DE是⊙O的直径,所以DE平分AB,得到AB=2AC,即可得到AB;(2)由OA=OE,得∠EAO=∠E,而直径DE⊥AB,则AD BD=,所以∠E=∠BAD,由此得到∠EAO=∠BAD.【详解】(1)∵DE⊥AB∴∠OCA=90°,则OC2+AC2=OA2又∵OC=3,OA=5,∴AC=4,∵DE是⊙O的直径,且DE⊥AB,∴AB=2AC=8(2)证明∵ EO=AO,∴∠E=∠EAO又∵DE是⊙O的直径,且DE⊥AB,∴AD BD=,∴∠E=∠BAD∴∠EAO=∠BAD.【点睛】本题考查了圆周角定理.在同圆或等圆中,同弧和等弧所对的圆周角相等,一条弧所对的圆周角是它所对的圆心角的一半.同时考查了垂径定理以及勾股定理.22.见解析.【分析】连接BC,证明∠ADB=∠ADC=60°,在AD上取点E、F,使DE=DB、DF=DC,连接BE、CF,证明△BDE、△CDF为正三角形,再证明∠AEB=∠CFA=120°,∠EAB=∠FCA,证明△ABE≌△CAF,可得AE=CF,从而可得结论.解:连接BC , ∠BAC =60°,AB =AC ,∴ △ABC 为等边三角形,∴ ∠ABC =∠ACB =60°,,,AC AC AB AB ==∴ ∠ADC =∠ABC 60,=︒ ∠ADB =∠ACB 60,=︒在AD 上取点E 、F ,使DE =DB 、DF =DC ,连接BE 、CF ,∴△BDE 、△CDF 为等边三角形,∴∠DEB =∠DFC =60°,,,DE BD CF DC ==∴∠AEB =∠CFA =120°,又∠FAC+∠FCA =∠DFC =60°、∠FAC+∠EAB =∠BAC =60°,∴∠EAB =∠FCA ,在△ABE 和△CAF 中,∵EAB FCA AEB CFA AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABE ≌△CAF (AAS ),∴AE =CF ,∴AD =DE+AE =BD+FC =BD+CD .【点睛】本题考查的是等边三角形的性质与判定,全等三角形的判定与性质,圆周角定理,掌握以上知识是解题的关键.23.(1)见解析;(2)1【分析】(1)如图连接AD ,,先证明CD BD =可得∠1=∠2,根据圆周角定理得到∠ADB=90°,再根据切线的性质得到OD EF ⊥即3490∠+∠=°,最后证明∠1=∠4即可;(2)如图,连接BC 交OD 于,由圆周角定理得到∠ACB=90°,由CD BD =得到OD BC ⊥,则CF=BF ,进而求得OF 、DF ,然后证明四边形CEDH 为矩形即可解答.【详解】(1)证明:连接AD ,如图,CD BD =,∴CD BD =,12∠∠∴=,∵AB 为直径,90ADB ∴∠=︒,190ABD ∴∠+∠=︒,∵EF 为切线,∴OD EF ⊥,∴3490∠+∠=°,∵OD OB =,3OBD ∴∠=∠,14∴∠=∠,2A BDF ∴∠=∠;(2)解:连接BC 交OD 于F ,如图,∵AB 为直径,90ACB ∴∠=︒,∵CD BD =,∴OD BC ⊥,∴CF BF =, ∴1322OF AC ==, ∴53122DF =-=, ∵ACB 90∠=︒,OD BC ⊥,OD EF ⊥∴四边形CEDF 为矩形,∴1CE DF ==.【点睛】本题主要考查了切线的性质、圆周角定理以及矩形的判定与性质,灵活应用相关知识点成为解答本题的关键.24.(1)相切;(2)94π 【分析】(1)先利用角平分线的性质得到点P 到BC 的距离等于PA ,然后根据直线与圆的位置关系进行判断.(2)由全等三角形的性质,先求出CD=2,由勾股定理求出AC=4,再利用勾股定理求出PD 的长度即可.【详解】解:(1)作PD ⊥BC ,交BC 于点D ,如图:∵PB 平分∠ABC ,∴点P 到BC 的距离等于PA ,∴PA=PD ,∴BC 为⊙P 的切线.故答案为:相切.(2)由(1)可知,易得△ABP ≌△DBP ,∴BD=AB=3,∴CD=5-3=2,∵在直角△ABC 中,由勾股定理,得22534AC =-=,设PA PD r ==,∴4PC r =-,在直角△PDC 中,由勾股定理,则()22242r r -=+, 解得:32r =, ∴圆的面积为:223924S r πππ==•=(). 【点睛】 本题考查了圆的定义,勾股定理,角平分线的性质,全等三角形的判定和性质,解题的关键是熟练掌握所学的知识,正确的进行解题.25.(1)①23,P P ;②12m ≤≤;(2)圆心C 的纵坐标满足34y <≤或1515y -≤<-【分析】(1) ①分别计算123OP OP OP ,,的长,判断P 到C 的切线长是否小于或等于2r ,即可解题;②设(),3P m m -+,根据题意,当过点P 的切线长为2时,OP=5,列出相应的一元二次方程,解方程即可;(2) 分类讨论,当C 在y 轴的正半轴上时,当点C 在y 轴的负半轴上时,当圆C 与直线112y x =-+相切时,画出相应的图形,结合全等三角形的判定与性质解题. 【详解】①()()12313,,0,2,5,022P P P ⎛⎫- ⎪ ⎪⎝⎭ 1231,2,5OP OP OP ===所以点1P 不在圆上,不符合题意;因为过点2P 的切线长为2213=-=,32<所以2P 是圆的离心点因为过3P 的切线长为5122=-==所以3P 是离心点;故答案为23,P P ;②如图设(),3P m m -+当过点P 的切线长为2时,OP=5,所以22(3)5m m +-+=解得m=1或m=2观察图像得12m ≤≤(2)如图2,当C 在y 轴的正半轴上时,经过点B(1,0),A(2,0)当AC=5A 是离心点,此时C(0,4);观察图像知圆的纵坐标满足34y <≤,线段AB 上所有的点都是离心点;如图3,当点C 在y 轴的负半轴上时,25BC =,点B 是离心点,此时C(0, 125-)如图4,当圆C 与直线112y x =-+相切时,设切点为N , 如图,由题意得CNB AOB ∆≅∆5CB NB ==(0,15C ∴,观察图像得当圆C 的纵坐标满足1515y -≤<-AB 上的所有点都是离心点; 综上所述,圆C 的纵坐标满足34y <≤或1515y -≤<-【点睛】本题考查直线与圆的位置关系、切线等知识,是重要考点,难度中等,掌握相关知识是解题关键.26.(1)平行;(2)PO ∥BC ,理由见详解;(3)见详解.【分析】(1)由折叠的性质可得∠AOP=∠POC ,则有∠AOC=2∠B ,进而可得∠AOP=∠B ,则问题可得;(2)由题意及折叠的性质可得∠APO=∠CPO ,∠A=∠APO ,则有∠A=∠PCB=∠CPO ,进而问题可证;(3)由题意易得AD ∥OC ,则有∠APO=∠POC ,由∠AOP=∠POC 可得∠APO=∠AOP ,进而可得△AOP 是等边三角形,然后可得四边形AOCP 是菱形,∠A=∠DPC=60°,最后根据含30°角的直角三角形的性质可求证.【详解】解:(1)由折叠的性质可得∠AOP=∠POC ,∵OC=OB ,∴∠B=∠OCB ,∴∠AOC=2∠B ,∴∠AOP=∠B ,∴PO ∥BC ,故答案为平行;(2)PO ∥BC ,理由如下:由折叠的性质可得∠APO=∠CPO ,∵OA=OP ,∴∠A=∠APO ,∴∠A=∠CPO ,∵∠A=∠PCB ,∴∠PCB=∠CPO ,∴PO ∥BC ;(3)证明:∵CD 是⊙O 的切线,∴OC ⊥CD ,∵CD ⊥AP ,∴AP ∥OC ,∴∠APO=∠POC ,∵∠AOP=∠POC ,∴∠APO=∠AOP ,∴AP=AO=OP ,∴△AOP 是等边三角形,∴∠A=60°,AP=AO=OC=PC ,∴四边形AOCP 是菱形,∴∠DPC=∠A=60°,∴∠DCP=30°,∴2PC PD =,即2AO PD =,∵AB=2AO ,∴4AB PD =.【点睛】本题主要考查切线的性质定理及含30°角的直角三角形的性质、菱形的性质与判定,熟练掌握切线的性质定理及含30°角的直角三角形的性质、菱形的性质与判定是解题的关键.。
【易错题】湘教版九年级数学上册《第四章锐角三角函数》单元检测试卷含答案解析.doc

【易错题解析】湘教版九年级数学上册 第四章 锐角三角函数 单元检测试卷 .单选题(共10题;共30分)1 •在 RtA ABC 中,ZC=90°, AC=1, BC=3,则ZA 的正切值为(2•如图,在 RtA ABC 中,ZC=90°, BC=3, AC=4,则 sinA 的值是5•已知Rf ABC 中,ZA=90。
,则黑ZB 的(A1 7.如图,为一颗折叠的小桌支架完全展开后支撑在地血的示意图,此吋ZABC=90°,固定点A 、C 和活动点 0处于同一直线上,且AO : 0C=2: 3,在支架的向内折叠收拢过程中(如箭头所示方向),AABC 边形为 则完全展开后ZBAC 的正切值为()A. 3B-3c 迺10D 迴10B.PC. PD 丄 xA. B(3, 0)3•在 RtA ABC 中,ZC=90% >48=10, AC 二& 则 sin A 的值是()D.D4•如图,在RtA ABC 中, ZC=90°, AC=3, AB 二5, 则cosB 的值为(c-iA.正切;B.余切; 6.如图CD 是RtA ABC 斜边上的高,AC=4, BC=3,C ・正弦; 则cosZBCD 的值是D •余弦c-5・53 48•如图,将ZAOB 放置在5x5的正方形网格屮,则tanZAOB 的值是()C 匹13则cosA 的值为(D 上1310.—艘在南北航线上的测量船,于A 点处测得海岛B 在点A 的南偏东30。
方向,继续向南航行30海里到 达C点时,测得海岛B 在C 点的北偏东15。
方向,那么海岛B 离此航线的最近距离是()(结果保留小 数点后两位)(参考数据:V3 « 1.732, V2 « 1.414)A. 4.64海里B. 5.49海里C. 6.12海里D. 6.21海里二、填空题(共10题;共30分)14. _____________________________________________________________________________________ 如图,点A (3, t )在第一象限,0A 与x 轴所夹的锐角为a, tana= | ,则t 的值是 ______________________________ . 15. _____________________________________________________________________________________ 如图,在AABC 中,ZACB=90°, CD 丄AB 于 D,若 AC=4, AB=5,贝lj cosZBCD 的值为 _______________________ ・在直角三角形中,一个锐角为57。
Module 4 Home alone 单元测试卷(含答案)
Module 4 学情评估英语九年级上册(WY版)时间:45分钟满分:100分一、单项选择。
( 每小题2分, 共20分)1. [易错题]Amanda feels ____ because she is new here, so I try ____ friends with her.A. alone; to makeB. lonely; makeC. lonely; to makeD. alone; make2. The teachers hope all of us can hand ____ our homework ____ time every day.A. up; inB. out; onC. on; inD. in; on3. The ice cream is ____ delicious ____ everyone in the house wants to enjoy it.A. such; thatB. too; toC. so; thatD. enough; to4. [易错题] —I'm a big fan of the famous girl.—____ Thanks to her, foreigners now know more about Chinese culture.A. So I am.B. So am I.C. Neither I am.D. Neither am I.5. Although they feel tired, ____ they still go on working.A. andB. butC. soD. /6. The Yunnan Museum is such an interesting place that many kids have fun ____ it.A. visitB. visitingC. to visitD. visited7. It's time to ____ the TV and go to bed.A. turn onB. turn offC. turn downD. turn up8. Most of the students went out of the classroom. Only ____ boys are waiting foryou.A. couple ofB. lot ofC. a littleD. a couple of9. There isn't ____ in the classroom. All the students are having a PE lesson in theplayground.A. anybodyB. somebodyC. nobodyD. everybody10. —I'll go to Hainan for my winter holiday.—____.A. Not at allB. Thank youC. Have a good tripD. Good job二、完形填空。
【易错题】青岛版九年级数学上册《第四章一元二次方程》单元检测试题(含解析).doc
【易错题解析】青岛版九年级数学上册第四章一元二次方程 单元检测试题一、单选题(共10题;共30分)2.方程X 2=25的解为( )4•下列方程是关于x 的一元二次方程的是()C. (30-x ) (100-2X )=200二、填空题(共10题;共30分)11. 一元二次方程x 2=・3x 的解是 _______ .12. 已知关于%的方程x 2-x + m = 0的一个根是1,则另一个根为 ________________ •13. ________________________________________ 两个连续负奇数的积是143,则这两个数是 • 14. 若(x 2+y 2) (1 - x 2 - y 2) +6=0,则 x 2+y 2 的值是 ________ .15. 己知关于x 的一元二次方程(a - 2) x 2+x+a 2 - 4=0的一个根是0,则a 的值为 ___________ • 16. 如果关于x 的方程X?・3x+k=0有两个相等的实数根,那么实数k 的值是 ________ • 17. ______________________ 方程x 2+x-l=0的根是 o18. 已知关于x 的一元二次方程:x —3x ・2 (m ・:l ) =0的两个实数根是xi 和X2 ,且|x 】・ x 2|=7,那么mA. x=5B. x= - 65C. x=±5 2•—元二次方程2* -3x + 1 A.有两个不相等的实数根3.已知 D. x=±V25 0根的情况是()B.有两个相等的实数根C.只有一个实数根D.没有实数根A.2 x= —1是方程x 2+ mx + 1 = 0的一个根,则m= B.-2C.0A. ax 2+bx+c=0C. X 2+2X =X 2 - 1D. 3 (x+1) J2 (x+1)5•己知关于x 的方程x<6x+m-l=0有两个不相等的实数根, 则m 的取值范圉是()• A. m < 10B. m = 10C. m > 10D. m > 10 6. 若一元二次方程ax 2+ bx + c = 0中的a = 2,b = 0,c =-1,则这个一元二次方程是() A. 2%24- 1 = 0B. 2x 2- 1 = 0C. 2x 2+ x = 07. 用配方法解一元二次方程6x=-5的过程中,配方正确的是( A. (x+3) 2=1B. (x ・ 3) 2=1C. (x+3) $二4D. D. 2x 2- x = 0(x - 3) 2=48. —元二次方程X 2+4X -3=0的两根为X ]、仝,则 乃的值是( C. 3 A. 4B.-49.方程x 2+ax+l=0和/xan 有一个公共根,贝U a 的值是()D.・3 B. 1 C. 2D. 3A. 010.某商店购进一种商品,单价为30元.试销中发现这种商品每天的销售量P (件)与每件的销售价x (元) 满足关系:P=100-2x.若商店在试销期间每天销售这种商品获得200元的利润,根据题意,下面所列方程正 确的是()・A. (x-30) (100-2x) =200B. x (100-2x) =200 D. (x-30) (2x-100) =200的值是 _______ .19. ___________________________________________________________________________ 若关于x 的方程x 2 + 5x+m = 0的两个根分别为为Xi , x 2 ,且* + *=:1,则m= ____________________________ .X1 x 220. 合肥大建设再创新高潮,继“高架时代〃后合肥即将边入"地铁时代〃,2015年合肥市投入200亿元用于地下轨道交通建设,并计划2016年、2017年两年累计再投入528亿元用于地下轨道交通建设,若设这两年 中投入资金的年平均增长率为X,则可列方程为 _______________三、解答题(共8题;共60分)22. 己知关于x 的方程kx?+ (2k+l ) x+2=0. 求证:无论k 取任何实数时,方程总有实数根.23. 学完一元二次方程后,在一次数学课上,同学们说出了一个方程的特点: ① 它的一般形式为ax 2+bx+c=0 (a^ b 、c 为常数,a*0) ② 它的二次项系数为5③ 常数项是二次项系数的倒数的相反数你能写出一个符合条件的方程吗?24. 如图,邻边不等的矩形花ISJABCD,它的一边AD 利用已有的围墙,另外三边所围的栅栏的总长度是6m.若 矩形的面积为4n?,请你计算AB 的长度(可利用的围墙长度超过6m ).25. —海关缉私艇发现在正北方45海里处有一艘可疑船只,测得它以60海里/时的速度向正东方向航行, 立即调整方向,以75海里/时的速度准备将其拦截,问经过多少时间能拦截上?26. (2017・巴中)巴中市某楼盘准备以每平方米5000元的均价对外销售,由于有关部门关于房地产的新政 策出台后,部分购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平 方米4050元的均价开盘销售,若两次下调的百分率相同,求平均每次下调的百分率.27. 某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调 查:每个玩具按480元销售时,每天可销售160个;若销售单价每降低元,每天可多售出2个.已知每 个玩具的固21•解下列方程(1) 22-=0(2) X 2-4X=4定成本为360元,问这种玩具的销售单价为多少元时,厂家每天可获利润20000元?28.已知:如图,AABC是边长3cm的等边三角形,动点P、Q同吋从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是lcm/s,当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t (s), 解答问题:当t为何值时,APBCl是直角三角形?【易错题解析】青岛版九年级数学上册第四章一元二次方程单元检测试题一、单选题(共10题;共30分)L方程X2=25的解为( )A. x=5B. x= - 65C. x=±5D. x=±V25【答案】C【考点】直接开平方法解一元二次方程【解析】【解答】解:X2=25,x=±5;故选C.【分析】直接开方即可得出答案.2.—元二次方程2妒一3尢+ 1 = 0根的情况是()A.有两个不相等的实数根B.有两个相等的实数根C.只有一个实数根D.没有实数根【答案】A【考点】根的判别式【解析】【解答】解:*•* a=2z b=-3,c=l・•・△ =b2-4ac=(-3)2-4x2xl=l>0;・••方程有两个不相等的实数根。
河南省九年级语文上册第四单元易错题集锦
河南省九年级语文上册第四单元易错题集锦单选题1、下面这些话说得不简明的一句是()A.你这种做法是错误的,要把它改正过来。
B.学校里出现了空前的学习热潮。
C.用不干净的抹布擦碗,越擦越不干净,越擦越脏。
D.这份资料正在打印,明天就可以发到学生手中。
答案:CC 越擦越不干净与越擦越脏意思重复。
A、B、D正确。
故答案为:C【点睛】本题考查学生用语的简明性。
2、下列横线上依次填入词语正确的一项是()然而我又不愿意他们因为要一气,都如我的_______而生活,也不愿意他们都如闰土的_______而生活,也不愿意都如别人的_______而生活。
他们应该有_______的生活,为我们所未经生活过的。
A.辛苦展转辛苦恣睢新B.辛苦麻木辛苦恣睢新C.辛苦展转辛苦麻木与众不同D.辛苦恣睢辛苦麻木与众不同答案:B结合文义,应知“我”离别故乡,辗转各地;闰土已麻木,失去往日的活力;如杨二嫂等的“别人”,已变得自私刻薄,放纵贪婪,所以是“恣睢”的生活。
“我”希望下一代能有“新”的生活,是与父辈充满人与人的隔膜完全不一样的生活。
这种“新”体现在人与人的关系平等、自由的精神世界中。
故答案为:B【点睛】说话和写作时要正确使用词语,注意词语的搭配和组合;正确理解词语在具体语言环境中的意义;注意词语使用过程中的感情色彩的变化;加强对教材注释和课文后列出的字词背诵积累等。
3、选出下列词语中没有错别字的一组( )A.阴侮影像心绪谋食B.蓬隙寓所獾猪愕然C.潮汛打拱装弶惶恐D.熟识惘然箫索寒噤答案:CC项正确。
其余三项是同音字、形近字弄错,A项“侮”应为“晦”;B项“蓬”应为“篷”;D项“箫”应为“萧”。
【点睛】本题考查学生对课文中重点词语的正确书写。
平时读书,写作时要注意区别同音字、形近字。
4、下列词语中加横线字的注音有误的一项是( )A.祭祀(sì) 刺猹(chá) 五行缺土(xínɡ)B.嗤笑(chī)瓦楞(lènɡ)禁不住(jīn)C.鄙夷(bǐ)断茎(jīnɡ)厚障壁(zhànɡ)D.髀间(bì) 脚踝(huái) 小毡帽(zhān)答案:BB项注音有误,“楞”应读lénɡ。
【易错题】浙教版九年级数学上册《第四章相似三角形》单元测试卷含答案解析.doc
【易错题解析】浙教版九年级数学上册第四章相似三角形单元测试卷一、单选题(共10题;共30分)1•已知「夕,则?的值是()3 4 y2. 如图1, A ABC和4GAF是两个全等的等腰直角三角形,图屮相似三角形(不包括全等)共有()A. 1对B. 2对C. 3对D. 4对3. 图中的两个三角形是位似图形,它们的位似中心是()A.点PB.点OC.点MD.点N4. 在ZiABC 和△ DEF 屮,ZA=40°, ZD=60°, ZE=80°,字=器,那么ZB 的度数是()AC FEA.40°B.60°C.80°D.100°5. 如图,锐角AABC的高CD和BE相交于点0,图中与△ ODB相似的三角形有()6. 如图,在平行四边形ABCD中,AE: AD=2: 3,连接BE交AC于点F,若△ ABF和四边形CDEF的面积分别记为Si , S2 ,贝iJSi: S2% ()A. 2: 3B.4: 9C. 6: 11D. 6: 137. 如图,在AABC中,点D, E分别是AB, C的中点,则S AADE:S A ABC=()A. 1: 2B. 1: 3C. 1: 4D. 1: 58. (2017*淄惮)如图,在RtA ABC 中,ZABC=90°, AB=6, BC=8, ZBAC, ZACB 的平分线相交于点E,过点E作EF〃BC交AC于点F,则EF的长为()9.如图,点D是AABC的边AC的上一点,且ZABD=ZC;如果= |,那么譽=()CD 3 D LF八…! f►•10.如图,RtA ABC 中,BC=2V3 ,ZACB=90°, ZA=30°, 6 是斜边 AB 的中点,过 6 作 DiEi 丄AC 于 Ei二、填空题(共10题;共30分)AB=4, CD=3, OD=2,那么线段OA 的长为22.如果两个相似三角形周长的比是2:3 ,那么它们面积的比是 ____________ •13. 如图,已知直线 I] || l 2 II $,分别交直线 m 、n 于点 A^ C^ D 、E 、F, AB = 5cm, AC=15cm, DE = 3cm,则EF 的长为 ________ cm.14. ________________________________________________________________________________ 已知AABCsADEF,相似比为3:5, A ABC 的周长为6,则△ DEF 的周长为 ___________________________________ .15. ________________________________________________________________________________________________ 已知△ ABC^ADEF, △ ABC 的周长为1, △ DEF 的周长为3,则厶ABC 与氐DEF 的面积之比为 _________________ .16. 若两个相似三角形的周长之比为2:3,较小三角形的面积为8crY?,则较大三角形面积是 ____________ cm 2 . 17. 如图,在矩形ABCD 中,E 是边AB 的中点,连接DE 交对角线4C 于点F ,若AB = 4 f18. 如图,已知ZAOB=60。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
九年级英语上第四单元易错题集合一、单项选择。
( )1. She spends ______ money on clothes every year.A. a number ofB. a great deal ofC. the number ofD. many of( )2. Nobody _______him to leave China.A.suggestedB.madeC.hopedD.got( )3. When will you come back to Beijing?A.After three daysB.Until next weekC.Not until May 1D.In three days( )4. Hard work is the only way to ______ in business.A. successB.successfullyC. succeedD.successful( )5. We visited Huaxi Village last Sunday and had some photos _______there.A. tookB.takingC.takenD.to take( )6. I hearone of his shoes is lost. Tell me where his ________ shoe is.A. anotherB. the otherC. otherD. others( )7. His father looks young, but ______ fact he is________.A. in;in the fortiesB.in;in his fortiesC. in the;in his fortiethD.in the;in the forties ( )8. Are you sure you don’t mind if I ask you to look after my birds while I______ here?A. leaveB.leavingC. am leavingD.am away from( )9. They _______each other since they_______.A. have loved;have firstmetB.loved;first metC. have loved;first metD.loved;have first met( )10. We ______ not ______in the area because it’s too dangerous.A. asked;remainB.are asked;remainC. asked;to remainD.are asked;to remain( )11. When ______the meeting, remember ______ your computer.A. to enter;to takeB. entering;takingC. attended;takingD. attending;to take( )12 .—Dad,I’m wondering whe n Mum _______. I miss her very much.—She will return when she _____ her task.A. returns;finishesB. returns;will finishC. will return;finishesD. will return;will finish()13. Linda was strongly ______ choosing John as the Best Student of the Term, as he took no notice of her when she was once in trouble.A. againstB. forC. downD. up()14. —Which one of these do you want? —_______. Either will do.A. Go aheadB. I don’t mindC. No problemD. I’m sure( )15. Simon is ________ honest boy. Now he is studying at ________university.A. a;anB. an;aC. the;aD. the; a( )16. More and more people have a low-C life and the air is getting _______ cleaner than aFew years ago.A.manyB.moreC.muchD.quite()17. ________ mysurprise,________ of us was given a present at the party.A. To;every oneB.With;every oneC. To;everyoneD.With;everyone()18. —How long do you think it’ll be ______ I can go back to school?—Well, you will be feeling much better by next weekend.A. beforeB. whenC.sinceD.after()19. —______ did you leave the classroom?—______ I saw my daughter sit down and read her book.A. How long;AfterB.When;AfterC. How long;UntilD.When;Until()20. ______ the day went on, the weather got worse.A. WhileB. SinceC.AsD.With()21. The song reminded me of the old golden days as soon as it _______.A. playedB. playsC. is playedD.was played()22. —Do you knowwhere Mary is? I can’t find her anywhere.—Well. She ______ go far一her coat is still here.A. shouldn’tB. mustn’tC.can’tD.won’t()23. Please don’t stand up in class until you______.A. are toldB. will be toldC.will tellD.are told to ()24.—What’s the matter ______ him?—He is worrying about his job.The job______ more _____ him thananythingelseA. with;matters;withB. with;matters;toC. to;matter;withD. to;matter;to()25. —Would you mind telling me something about the two_____?—______. They are exchange students from England.A. Frenchmen;Of courseB. Frenchmans;That’s all rightC. Germans;Not at allD. German;All right()26.—I’m so happy that you could come to England with us for the holidays.—______. It’s the first time for me to be out of China.A. I think notB. All rightC. Thank youD. Me too二、单词拼写。
1. He ______ (保持不变)the manager of the company until the end of last year.2. ______ (尽管)it’s hard for you, you can’t give it up.3.So far, we’ve______ (成功)in saving thousands of people in danger.4.Fraser ______ (得分)again in the second half.5.All the Asians are proud of Li Na’s challenging ______ (精神).6.Books allow me to learn about people in different ______ (时期)and places.7.The computer is used to ______ (记录)the tickets which we buy.8.—I heard Jack was punished by our school. Is that true?—Yes, it’s true. He did something ________ our school rules.9.—Millie has decided to ______ out for the singing competition.—She is a really good singer. I bet she will get the first prize.10.—I’m afraid your grandma’s life became really hard after your grandpa’s______. —Yes, she was so sad that she refused to see anyone.11.I finally finished my report on wild animals________ (凭借)hard work.12.Three bad men broke in and the shopkeeper was________ (迫使)to hand over all his money.13.I hope the results of my ________ (调查)will be of some value to you.14.Her face showed________ (惊奇)at the good news.三、翻译句子。
