spss的数据分析案例
论文spss数据分析100例子
论文spss数据分析100例子对比使用翻转课堂和不使用翻转课堂对学生成绩的影响；对比使用新药品和不使用新药品对病人血压的影响；当然，我们不一定必须有一组干预才能使用独立样本t检验，也可以为了比较两个不同群体而使用独立样本t检验。
例如：对比男生和女生的身高差异；对比南方人与北方人的体重差异；什么是独立样本t检验？概念：独立样本t检验用于分析两组不同群组直接定量数据的差异情况，是差异性检验的一种方法。
自变量：定类数据因变量：定量数据什么时候使用独立样本t检验？独立样本t检验的适用范围：1.适用于自变量为定类数据且仅为两组时；2.适用于因变量为定量数据；3.各个观察值相互独立，不能相互影响，即满足独立性。
这个一般根据专业背景考察，如遗传性疾病、传染性疾病的数据就可能存在非独立性问题，也就是不同数据会相互影响，而不同学生身高可认为相互独立，彼此不相互影响；4.各个样本均来自正态分布的总体，即满足正态性。
独立样本t建议对于数据资料的正态性存在一定的耐受能力，一般认为样本量大于30即可满足正态分布。
5.各个样本所在总体方差相等，即满足方差齐性。
很多同学对于这个概念不太了解，这没有关系，在SPSS进行独立样本t检验时，自动会进行使用Levene’s检验来方差齐性，我们只需要根据相应结果解读数据即可。
案例我们通过一个案例来深入了解独立样本t检验如何进行。
研究问题与数据某老师了解到翻转课堂的教学模型，希望研究翻转课堂是否能对学生成绩产生影响，于是进行了一项教学实验，在某年级1班使用翻转课堂的教学模式进行教学，在2班使用传统教学模式进行教学，一个学期之后收集了两个班的成绩进行分析。
我们初步收集到的数据如下：然而，如果我们把这些数据导入SPSS，并没有办法进行分析，我们首先需要做数据的预处理。
数据预处理变量划分为了能让SPSS进行分析，我们需要把数据处理成自变量和因变量分别用不同列表示的方式，即一列为班级，一列为成绩，数据如下：。
spss案例分析
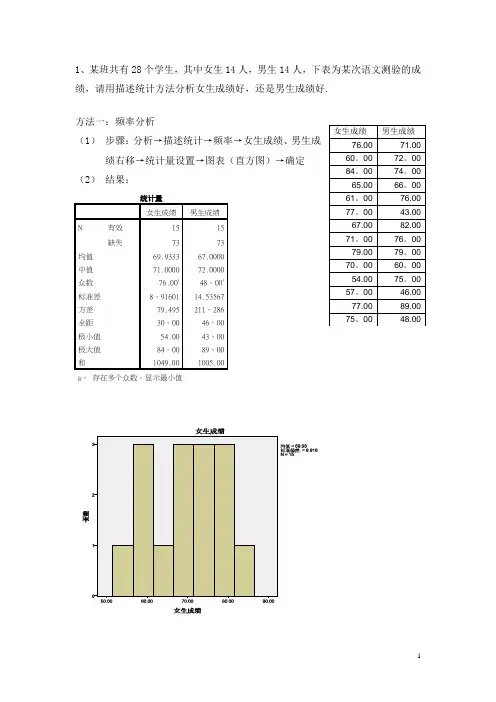
1、某班共有28个学生，其中女生14人，男生14人，下表为某次语文测验的成绩，请用描述统计方法分析女生成绩好，还是男生成绩好. 方法一：频率分析（1） 步骤：分析→描述统计→频率→女生成绩、男生成绩右移→统计量设置→图表（直方图）→确定 （2） 结果：统计量女生成绩男生成绩N有效 1515 缺失73 73 均值 69.9333 67.0000 中值 71.0000 72.0000 众数 76.00a48。
00a标准差 8。
91601 14.53567 方差 79.495 211。
286 全距 30。
00 46。
00 极小值 54.00 43。
00 极大值 84。
00 89。
00 和1049.001005.00a 。
存在多个众数。
显示最小值(3）分析：由统计量表中的均值、标准差及直方图可知，女生成绩比男生成绩好。
方法二:描述统计（1）步骤:分析→描述统计→描述→女生成绩、男生成绩右移→选项设置→确定（2）结果：描述统计量N 极小值极大值均值标准差方差女生成绩15 54。
00 84。
00 69.9333 8.91601 79。
495 男生成绩15 43.00 89.00 67.0000 14.53567 211.286 有效的 N （列表状态）15（3）分析：由描述统计量表中的均值、标准差、方差可知，女生成绩比男生成绩好。
2、某公司经理宣称他的雇员英语水平很高，现从雇员中随机随出11人参加考试，得分如下：80、81、72、60、78、65、56、79、77、87、76,请问该经理的宣称是否可信？（1）方法：单样本T检验H 0：u＝u,该经理的宣称可信H 1:u≠u,该经理的宣称不可信(2)步骤：①输入数据:(80，81，…76）②分析→比较均值→单样本T检验→VAR00001右移→检验值（75)→确定(3）结果：单个样本统计量N 均值标准差均值的标准误VAR00001 11 73.73 9。
551 2.880（4）分析：由单个样本检验表中数据知t＝0。
spss的数据分析报告范例
spss的数据分析报告范例一、引言数据分析是科学研究过程中不可或缺的一部分。
针对一项研究项目，本报告将借助SPSS软件对收集的数据进行详尽分析，并提供相关结果和结论。
本报告的目的是帮助读者更好地理解数据，提供决策和制定战略所需的支持。
二、研究方法本研究的数据来源于一份问卷调查，共收集了500份有效问卷。
在问卷设计中，我们采用了随机抽样的方法，以保证样本的代表性。
该问卷包括了参与者的基本背景信息、满意度评价等方面的问题。
三、数据分析1. 受访者基本背景首先，我们对受访者的基本背景信息进行了统计分析。
其中包括性别、年龄、教育水平和职业等因素。
以下是相关结果的总结：（1）性别分布：男性占65%，女性占35%。
（2）年龄分布：年龄在18-24岁的受访者占40%；25-34岁的占30%；35-44岁的占20%；45岁及以上的占10%。
（3）教育水平：高中或以下占20%；本科占50%；研究生及以上占30%。
（4）职业：学生占25%；职员占40%；自由职业者占20%；其他占15%。
2. 满意度评价为了了解受访者对某产品的满意度，我们设计了一套评价体系。
通过SPSS软件进行数据分析，得到以下结果：（1）整体满意度：根据赋分制度，平均满意度得分为4.2（满分为5），表明受访者对该产品整体上持较高满意度。
（2）各项指标：通过因子分析，我们得到了几个影响满意度的关键因素。
其中，产品质量、价格和售后服务被认为是受访者最关注的方面。
3. 相关性分析在数据分析过程中，我们还进行了一些相关性分析，以探究不同变量之间的关系。
以下是一些值得关注的相关性结果：（1）性别与满意度之间的关系：经过卡方检验，我们发现性别与满意度之间存在一定的相关性（p < 0.05），女性对产品的满意度略高于男性。
（2）年龄与满意度之间的关系：通过相关系数分析，我们发现年龄与满意度呈现出弱相关关系（r = 0.15，p < 0.05），年龄越小，满意度越高。
SPSS典型相关分析案例
SPSS典型相关分析案例典型相关分析（Canonical Correlation Analysis，CCA）是一种统计方法，用于研究两组变量之间的相关性。
它可以帮助研究人员了解两组变量之间的关系，并提供有关这些关系的详细信息。
在SPSS中，可以使用典型相关分析来探索两个或多个变量之间的关系，并进一步理解这些变量如何相互影响。
下面我们将介绍一个典型相关分析的案例，以展示如何在SPSS中执行该分析。
案例背景：假设我们有一个医学研究数据集，包含30名患者的多个生物标记物和他们的疾病严重程度评分。
我们希望了解这些生物标记物与疾病严重程度之间的关系，并查看是否可以建立一个线性模型来预测疾病严重程度。
以下是执行这个案例的步骤：第1步：准备数据首先，我们需要准备数据，确保所有变量都是数值型。
在SPSS中，我们可以通过检查数据集的描述性统计信息或查看变量视图来做到这一点。
第2步：导入数据在SPSS中，我们可以通过选择菜单中的"File"选项，然后选择"Open"来导入数据集。
我们应该选择包含待分析数据的文件，并确保正确指定变量的类型。
第3步：执行典型相关分析要执行典型相关分析，我们可以选择菜单中的"Analyze"选项，然后选择"Canonical Correlation"。
在弹出的对话框中，我们应该选择我们希望研究的生物标记物变量和疾病严重程度评分变量。
然后，我们可以选择一些选项，如方差-协方差矩阵、相关矩阵和判别系数，并点击"OK"执行分析。
第4步：解释结果完成分析后，SPSS将提供几个输出表。
我们应该关注典型相关系数和标准化典型系数，以了解两组变量之间的关系。
我们可以使用这些系数来解释生物标记物如何与疾病严重程度相关联，并找到最重要的变量。
此外，我们还可以使用SPSS提供的其他统计结果来进一步解释模型的效果和预测能力。
大学生spss数据分析案例
大学生spss数据分析案例在大学生活中，数据分析是一项非常重要的技能，尤其是对于学习社会科学的学生来说。
SPSS（Statistical Package for the Social Sciences）是一个非常常用的统计分析软件，它可以帮助我们对数据进行分析和处理。
在本文中，我们将以一个实际案例为例，介绍大学生如何运用SPSS进行数据分析。
首先，我们需要明确我们的研究目的和问题。
假设我们想要研究大学生的学习成绩和课堂参与度之间的关系。
我们收集了一份包括学习成绩和课堂参与度的数据，接下来我们将使用SPSS进行分析。
第一步，我们需要导入数据。
在SPSS软件中，我们可以通过导入Excel文件的方式将我们收集到的数据导入到软件中。
一旦数据导入完成，我们就可以开始进行数据的清洗和整理工作。
我们需要检查数据是否存在缺失值或异常值，并进行处理。
接着，我们可以进行描述性统计分析。
通过SPSS，我们可以轻松地计算出数据的均值、标准差、最大值、最小值等统计指标，从而更好地了解我们的数据特征。
比如，我们可以计算出学习成绩和课堂参与度的平均值、标准差，以及两者之间的相关性。
然后，我们可以进行相关性分析。
通过SPSS的相关性分析功能，我们可以计算出学习成绩和课堂参与度之间的相关系数，从而判断它们之间是否存在显著的相关关系。
通过相关性分析，我们可以更好地理解两个变量之间的关系，为后续的研究提供参考。
最后，我们可以进行回归分析。
通过SPSS的回归分析功能，我们可以建立一个模型，来预测学习成绩和课堂参与度之间的关系。
我们可以通过回归系数和显著性检验来判断模型的拟合程度，并进行模型的诊断和改进。
通过以上的数据分析过程，我们可以得出结论，进一步探讨学习成绩和课堂参与度之间的关系。
这个案例不仅可以帮助大学生更好地理解SPSS软件的使用方法，还可以帮助他们在日常学习和研究中更好地运用数据分析方法。
希望本文能对大学生们有所帮助，引发更多关于数据分析的思考和讨论。
spss案例分析报告(精选)
spss案例分析报告（精选）本文通过分析一份 SPSS 数据，展示 SPSS 在统计分析中的应用。
数据概述本数据为一家咖啡馆的销售数据，共有 200 条记录，包括 7 个变量：日期、时间、收银员、商品名、销售价格、数量和总价。
SPSS 分析1. 描述性统计使用 SPSS 的描述性统计功能，可以获取数据的基本信息，如均值、标准偏差、最大值、最小值等。
其中，销售价格的均值为 44.71 元，标准偏差为 13.29 元，最小值为 23 元，最大值为 78 元。
数量的均值为 1.62 个，标准偏差为 0.51 个，最小值为 1 个，最大值为3 个。
总价的均值为 73.25 元，标准偏差为 21.89 元，最小值为 23 元，最大值为 156 元。
2. 单样本 t 检验假设一杯咖啡的平均售价为 50 元，我们可以使用单样本 t 检验对这个假设进行检验。
首先，我们需要用 SPSS 的数据透视表功能，计算出每杯咖啡的平均售价。
然后，使用单样本 t 检验功能，输入样本均值、假设的总体均值（50 元）、样本标准差、样本大小以及置信度水平。
在这个数据集中，单样本 t 检验得出的 t 值为 -2.36，P 值为 0.019，显著性水平为 0.05，因此我们可以拒绝原假设，认为该咖啡馆的咖啡售价不是 50 元。
4. 相关分析假设我们想要了解商品数量和销售额之间的关系，我们可以使用 SPSS 的相关分析功能来进行分析。
首先，我们需要使用数据透视表功能，计算出每个订单的总价和数量。
然后，使用相关分析功能，输入这两个变量的值，得出相关系数和显著性水平。
在这个数据集中，商品数量和销售额之间的相关系数为 0.749，P 值为 0，显著性水平非常显著。
因此，我们可以认为商品数量和销售额之间存在极强的正相关关系。
结论本文通过 SPSS 对一份咖啡馆销售数据进行分析，展示了 SPSS 在统计分析中的应用。
通过描述性统计、单样本 t 检验、双样本 t 检验和相关分析等功能，我们可以获得数据的基本信息，检验假设，分析变量之间的关系，从而帮助企业更好地决策和管理。
SPSS数据分析案例-信度效度-调节效应-中介效应
样本的基本计数统计：年龄、艺考科目、准备时间、年级、性别、是否独生、是否寄宿、家庭类型对于变量年龄，年龄为16的频数是72(占17.2%)，年龄为17的频数是224(占53.5%)，年龄为18的频数是123(占29.4%)；对于变量艺考科目，艺考科目为体育的频数是57(占13.6%)，艺考科目为美术的频数是208(占49.6%)，艺考科目为舞蹈的频数是86(占20.5%)，艺考科目为音乐的频数是68(占16.2%)；对于变量准备时间，准备时间为高二的频数是362(占86.4%)，准备时间为高三的频数是57(占13.6%)；对于变量年级，年级为高二的频数是75(占17.9%)，年级为高三的频数是344(占82.1%)；对于变量性别，性别为男的频数是153(占36.5%)，性别为女的频数是266(占63.5%)；对于变量是否独生，是否独生为是的频数是303(占72.3%)，是否独生为否的频数是116(占27.7%)；对于变量是否寄宿，是否寄宿为是的频数是275(占65.6%)，是否寄宿为否的频数是144(占34.4%)；对于变量家庭类型，家庭类型为双亲家庭的频数是301(占71.8%)，家庭类型为组合家庭的频数是118(占28.2%)。
变量年龄、艺考科目、准备时间、年级、性别、是否独生、是否寄宿、家庭类型的计数统计频数百分比年龄16 72 17.217 224 53.518 123 29.4艺考科目体育57 13.6美术208 49.6舞蹈86 20.5音乐68 16.2 准备时间高二362 86.4高三57 13.6 年级高二75 17.9高三344 82.1 性别男153 36.5女266 63.5 是否独生是303 72.3否116 27.7 是否寄宿是275 65.6否144 34.4 家庭类型双亲家庭301 71.8变量年龄、艺考科目、准备时间、年级、性别、是否独生、是否寄宿、家庭类型的计数统计频数百分比组合家庭118 28.2变量反向编码因为变量q11_2、q11_5、q11_6、q11_12、q11_11、q11_14、q11_16、q11_17、q11_18、q11_20是反向计分的，为了和其他题目保持相同的计分方式，并且能够与其他题目合成，我们需要对这些题目进行反向计分，也就是把分数进行转换使得高分变成低分，低分变成高分。
大学生spss数据分析案例
大学生spss数据分析案例大学生SPSS数据分析案例。
在大学教育中，数据分析是一个非常重要的环节，尤其是对于社会科学和商业管理专业的学生来说。
SPSS（Statistical Package for the Social Sciences）是一个专业的统计分析软件，广泛应用于学术研究和商业决策中。
本文将以一个大学生SPSS数据分析案例为例，介绍如何使用SPSS进行数据分析。
案例背景：某大学社会科学专业的学生对大学生活满意度进行了调查，并收集了相关数据，包括学生的性别、年级、专业、宿舍类型、课程质量、宿舍环境、社交活动等方面的信息。
现在需要对这些数据进行分析，以了解不同因素对大学生活满意度的影响。
数据准备：首先，需要将调查所得的数据录入SPSS软件中，确保数据的准确性和完整性。
在录入数据时，要注意将不同的变量分别录入不同的列中，以便后续的分析和处理。
数据分析：1. 描述统计分析。
首先，可以对各个变量进行描述统计分析，包括计算均值、标准差、频数分布等。
通过描述统计分析，可以直观地了解各个变量的分布情况，为后续的分析提供基础。
2. 相关性分析。
接下来，可以进行各个变量之间的相关性分析，通过相关系数的计算来了解不同变量之间的关联程度。
例如，可以分析学生的性别、年级、专业与大学生活满意度之间的相关性，以及宿舍类型、课程质量、社交活动等因素对大学生活满意度的影响程度。
3. 方差分析。
针对分类变量，可以进行方差分析，比较不同组别之间的均值差异是否显著。
例如，可以分析不同年级、不同专业的学生对大学生活满意度的差异情况，以及不同宿舍类型对大学生活满意度的影响是否显著。
4. 回归分析。
最后，可以利用回归分析来探讨不同因素对大学生活满意度的影响程度。
通过建立回归模型，可以了解各个自变量对因变量的影响情况，以及它们之间的关系强度和方向。
结论与建议：通过以上的数据分析，可以得出不同因素对大学生活满意度的影响程度，为学校和相关部门提供决策建议。
SPSS案例分析(2020年7月整理).pdf
某道路弯道处53车辆减速前观测到的车辆运行速度，试检验车辆运行速度是否服从正态分布。
这道题目的解答可以先通过绘制样本数据的直方图、P-P图和Q-Q图坐车粗略判断，然后利用非参数检验的方法中的单样本K-S检验精确实现。
一、初步判断1.1绘制直方图（1）操作步骤在SPSS软件中的操作步骤如图所示。
（2）输出结果通过观察速度的直方图及其与正态曲线的对比，直观上可以看到速度的直方图与正太去线除了最大值外，整体趋势与正态曲线较吻合，说明弯道处车辆减速前的运行速度有可能符合正态分布。
1.2绘制P-P图（1）操作步骤在SPSS软件中的操作步骤如图所示。
（2）结果输出根据输出的速度的正态P-P 图，发现速度均匀分布在正态直线的附近，较多部分与正态直线重合，与直方图的结果一致，说明弯道处车辆减速前的运行速度可能服从正态分布。
二、单样本K-S 检验2.1单样本K-S 检验的基本思想K-S 检验能够利用样本数据推断样本来自的总体是否服从某一理论分布，是一种拟合优的检验方法，适用于探索连续型随机变量的分布。
单样本K-S 检验的原假设是：样本来自的总体与指定的理论分布无显著差异，即样本来自的总体服从指定的理论分布。
SPSS 的理论分布主要包括正态分布、均匀分布、指数分布和泊松分布等。
单样本K-S 检验的基本思路是：首先，在原假设成立的前提下，计算各样本观测值在理论分布中出现的累计概率值F(x)，；其次，计算各样本观测值的实际累计概率值S(x)；再次，计算实际累计概率值与理论累计概率值的差D(x)；最后，计算差值序列中的最大绝对值差值，即）（）（i i x F x S max D −=通常，由于实际累计概率为离散值，因此D 修正为：）（）（1i i x F x S max D −=−D 统计量也称为K-S 统计量。
在小样本下，原假设成立时，D 统计量服从Kolmogorov 分布。
在大样本下，原假设成立时，D n 近似服从K(x)分布：当D 小于0时，K(x)为0；当D 大于0时，）2-（exp ）1-（）（22x j x K j ∑∞−∞==容易理解，如果样本总体的分布与理论分粗的差异不明显，那么D 不应较大。
统计学课SPSS数据分析实战案例
统计学课SPSS数据分析实战案例SPSS（统计分析系统）是一款常用的统计软件，被广泛应用于社会科学、商业、医学等领域的数据分析工作中。
通过这个案例，我们将运用SPSS软件进行数据分析，以展示统计学课的实战应用。
案例背景假设你是一位市场研究员，你的公司正在调查消费者对某产品的满意度。
你已经收集了一份随机抽样的数据集，包含了消费者的满意度评分以及他们的一些个人信息。
你的任务是对这些数据进行分析，以了解消费者满意度与个人信息之间是否存在关联。
数据集说明数据集包括了500个消费者的信息，具体变量如下：1. 变量1：满意度评分（连续变量，取值范围从1到10）；2. 变量2：性别（分类变量，取值为男性和女性）；3. 变量3：年龄（连续变量）；4. 变量4：收入水平（分类变量，取值为低、中、高三个层次）；5. 变量5：购买次数（连续变量，表示过去一年内购买该产品的次数）。
数据分析步骤以下是对这份数据集进行分析的步骤：1. 数据清洗和准备首先，我们需要检查数据集中是否存在缺失值或异常值，并进行数据清洗。
在SPSS中，我们可以使用数据查看和数据清洗的功能来完成这一步骤。
确保数据集中的每一列都没有缺失值，并且所有的异常值已经得到恰当的处理。
2. 描述性统计分析接下来，我们可以使用SPSS的描述性统计分析功能，对数据集进行描述性统计分析。
我们可以计算满意度评分、年龄和购买次数的平均值、标准差、最小值、最大值，并生成频数分布表和柱状图。
3. 相关性分析为了确定满意度评分与其他个人信息变量之间的关联性，我们可以使用SPSS的相关性分析功能。
通过计算满意度评分与性别、年龄、收入水平和购买次数之间的相关系数，我们可以评估它们之间的相关性。
4. 单因素方差分析我们可以使用SPSS进行单因素方差分析，以了解不同收入水平的消费者在满意度评分上是否存在显著差异。
通过观察方差分析表和显著性水平，我们可以得出初步结论。
5. 多元线性回归分析最后，我们可以使用SPSS的多元线性回归分析功能来建立一个回归模型，以预测满意度评分。
spss数据分析报告案例
SPSS数据分析报告案例1. 研究背景本研究旨在调查大学生是否存在晚睡现象，并探究晚睡与健康问题之间的关系。
通过采集大学生的睡眠时间、就寝时间以及健康状况等数据，利用SPSS软件进行数据分析，进一步了解大学生的睡眠状况与健康问题的关联。
2. 数据概况本研究共收集了200名大学生的数据，其中包括性别、年级、每晚睡眠时间、平均就寝时间、是否存在健康问题等变量。
下面是对数据的描述统计分析结果：•性别分布：男性占50%，女性占50%。
•年级分布：大一占25%，大二占30%，大三占25%，大四占20%。
•每晚睡眠时间：平均睡眠时间为7.8小时，标准差为1.2小时。
最小值为5小时，最大值为10小时。
•平均就寝时间：平均就寝时间为23:30，标准差为0.5小时。
最早就寝时间为22:00，最晚就寝时间为01:00。
•健康问题：共有45%的大学生存在健康问题。
3. 数据分析结果3.1 性别与睡眠时间的关系首先，我们探究性别与睡眠时间之间的关系。
利用独立样本T检验，得出以下的结果：•假设检验：男性和女性的睡眠时间是否存在显著差异？•结果：独立样本T检验显示，男性平均睡眠时间为7.6小时，女性平均睡眠时间为8.0小时。
T值为-2.14，P值为0.034，意味着男性和女性的睡眠时间存在显著差异。
3.2 年级与睡眠时间的关系我们进一步探究年级与睡眠时间的关系。
使用单因素方差分析（ANOVA），得出以下结果：•假设检验：各年级的睡眠时间是否存在显著差异？•结果：单因素方差分析显示，大一、大二、大三和大四的平均睡眠时间分别为7.7小时、7.9小时、8.1小时和7.6小时。
F值为2.75，P值为0.043，说明各年级之间的睡眠时间存在显著差异。
3.3 睡眠时间与健康问题的关系最后，我们分析睡眠时间与健康问题之间的关系。
利用相关分析，得出以下结果：•假设检验：睡眠时间与健康问题之间是否存在相关性？•结果：相关分析结果显示，睡眠时间和健康问题之间存在显著负相关（r = -0.25，P值 = 0.001），即睡眠时间越少，存在健康问题的可能性越大。
spss数据分析案例
spss数据分析案例SPSS数据分析案例。
在实际的数据分析工作中，SPSS（Statistical Product and Service Solutions）是一个非常常用的统计分析软件。
它提供了强大的数据处理和分析功能，可以帮助研究人员快速、准确地进行数据处理和分析。
本文将通过一个实际的案例，介绍如何使用SPSS进行数据分析，并展示分析结果。
案例背景：某公司想要了解员工满意度与工作绩效之间的关系，为了达到这个目的，他们进行了一项调查，收集了员工的满意度评分和绩效评分数据。
现在，他们希望通过这些数据，利用SPSS进行分析，找出员工满意度和工作绩效之间的关系。
数据收集：首先，我们收集了100名员工的满意度评分和绩效评分数据。
满意度评分采用了1-5的五级评分制，绩效评分采用了1-100的百分制评分。
数据导入：将收集到的数据导入SPSS软件中，创建一个新的数据集，并将员工的满意度评分和绩效评分数据分别录入到不同的变量中。
数据描述统计分析：首先，我们对数据进行描述性统计分析，包括计算满意度评分和绩效评分的均值、标准差、最大值、最小值等。
这些统计量可以帮助我们更好地了解数据的分布情况。
相关性分析：接下来，我们使用SPSS进行相关性分析，探索员工满意度评分和绩效评分之间的相关关系。
通过相关性分析，我们可以计算出两个变量之间的相关系数，进而判断它们之间是否存在显著的相关性。
回归分析：在确定了员工满意度评分和绩效评分之间存在相关性的基础上，我们可以进一步进行回归分析，建立员工满意度评分对绩效评分的预测模型。
通过回归分析，我们可以得到员工满意度评分对绩效评分的影响程度，以及其他可能影响绩效评分的因素。
结论：通过SPSS数据分析，我们发现员工满意度评分与绩效评分之间存在显著的正相关关系，即员工满意度评分越高，其绩效评分也越高。
这为公司提高员工绩效提供了重要的参考依据，可以通过提升员工满意度来提高整体绩效水平。
总结：在本案例中，我们利用SPSS软件进行了员工满意度和绩效之间的数据分析。
基于SPSS软件的临床数据分析实例
06
结果可视化与报告撰写
结果可视化技巧和方法
01
02
03
图表类型选择
根据数据类型和分析目的 选择合适的图表类型，如 柱状图、折线图、散点图 等。
色彩搭配
合理运用色彩，突出重要 信息，提高图表的可读性 和美观度。
标注与说明
在图表中添加必要的标注 和说明，帮助读者更好地 理解数据和分析结果。
应的干预措施。
生存分析及其在临床研究中的应用
生存分析概念
生存分析是一种用于研究事件发生时间及其 相关因素的统计方法，尤其适用于存在删失 数据的情况。在临床研究中，生存分析常用 于评估患者生存时间、疾病复发时间等。
在临床研究中的应用
生存分析可用于评估不同治疗方案对患者生 存时间的影响，以及识别影响患者生存时间 的危险因素。例如，在肿瘤临床试验中，可 以通过生存分析比较不同治疗组的患者生存 曲线，评估治疗方案的疗效。同时，还可以 结合多因素分析，探讨患者年龄、性别、病
数据来源及特点
01
医学实验数据
通常来源于临床试验、观察性研究或医学调查，具有样本量小、变量多
、数据结构复杂等特点。
02
电子病历数据
从医院信息系统中提取，包含患者基本信息、诊断、治疗、检查等多方
面的数据，具有数据量大、信息丰富、结构化和非结构化并存等特点。
03
生物信息学数据
如基因表达、蛋白质组学等高通量数据，具有数据维度高、噪声大、需
聚类分析及其在临床研究中的应用
聚类分析概念
聚类分析是一种无监督学习方法，用于将相 似的对象归为一类，使得同一类内的对象尽 可能相似，而不同类间的对象尽可能不同。
在临床研究中的应用
spss数据分析简单案例
spss数据分析简单案例SPSS数据分析简单案例。
在社会科学研究中，SPSS（统计分析软件包）被广泛应用于数据分析。
本文将通过一个简单的案例来介绍如何使用SPSS进行数据分析。
首先，我们收集了一份关于学生学习成绩的数据，包括学生的性别、年龄、每周学习时间和期末考试成绩。
我们的研究问题是探讨性别、年龄和每周学习时间对学习成绩的影响。
我们首先打开SPSS软件，导入我们收集的数据。
然后，我们可以使用SPSS 的数据编辑功能对数据进行清洗和整理，确保数据的准确性和完整性。
接下来，我们可以使用SPSS的描述性统计功能对数据进行分析。
我们可以计算每个变量的均值、标准差、最大值和最小值，从而对数据的分布和特征有一个直观的了解。
然后，我们可以使用SPSS的相关分析功能来探讨不同变量之间的相关性。
我们可以计算不同变量之间的皮尔逊相关系数，从而了解它们之间的线性关系。
在接下来的分析中，我们可以使用SPSS的回归分析功能来探讨性别、年龄和每周学习时间对学习成绩的影响。
我们可以建立一个多元线性回归模型，从而探讨不同变量对学习成绩的预测作用。
最后，我们可以使用SPSS的图表功能来进行数据可视化分析。
我们可以绘制散点图、柱状图和折线图，从而直观地展示不同变量之间的关系和趋势。
通过以上步骤，我们可以利用SPSS对学生学习成绩的数据进行全面的分析，从而回答我们的研究问题。
在实际研究中，我们还可以进一步探讨其他统计分析方法，如方差分析、卡方检验等，以深入挖掘数据的内在规律。
总之，SPSS作为一款功能强大的统计分析软件，为社会科学研究提供了重要的数据分析工具。
通过本文的简单案例，希望读者能够对SPSS的数据分析功能有一个初步的了解，并能够在实际研究中灵活运用，从而为研究工作提供有力的支持。
spss的数据分析案例
精心整理关于某公司474名职工综合状况的统计分析报告一、数据介绍：本次分析的数据为某公司474名职工状况统计表，其中共包含^一变量，分别是：id （职工编号），gender（性别），bdate（出生日期），edcu （受教育水平程度），jobcat （职务等级），salbegin （起始工资），salary （现工资），jobtime（本单位工作经历＜月＞），prevexp（以前工作经历＜月＞），minority（民族类型），age（年龄）＜通过运用spss统计软件，对变量进行频数分析、描述性统计、方差分析、相关分析、I ■以了解该公司职工上述方面的综合状况，并分析个变量的分布特点及相互间的关系。
二、数据分析■■ ] I ■.1、频数分析。
基本的统计分析往往从频数分析开始。
通过频数分析能够了解变量的取值状况，对把握数据的分布特征非常有用。
此次分析利用了某公司474名职工基本状况的统计数据表，在gender（性别）、edcu （受教育水平程度）、不同的状况下的频数分析，从而了解该公司职工的男女职工数量、受教育状况的基本分布。
精心整理上表说明，在该公司的474名职工中，有216名女性，258名男性，男女比例分别为45.6%和54.4%,该公司职工男女数量差距不大，男性略多于女性。
/ 「’--了/其次对原有数据中的受教育程度进行频数分析，结果如下表：Educati on alLevel(years).4 .4 99.8 20 2上表及其直方图说I I明，被调查的474名职工中，受过12年教育的职工是该组频数最高的，为190人，占 总人数的40.1%，其次为15年，共有116人，占中人数的24.5%。
且接受过高于20年的 教育的人数只有1人，比例很低。
2、描述统计分析。
再通过简单的频数统计分析了解了职工在性别和受教育水平• J ' P t ，- J上的总体分布状况后，我们还需要对数据中的其他变量特征有更为精确的认识， 这就需要通过计算基本描述统计的方法来实现。
2024版SPSS数据案例分析
SPSS数据案例分析目录CATALOGUE•数据导入与预处理•数据分析方法介绍•SPSS 软件操作指南•案例一：医学领域数据分析应用举例•案例二：社会科学领域数据分析应用举例•总结与展望01CATALOGUE数据导入与预处理SPSS 可以导入多种格式的数据，如Excel 、CSV 、TXT 等。
支持多种格式通过“文件”菜单中的“打开”选项，选择要导入的数据文件，设置相关参数，即可将数据导入SPSS 。
步骤简单在导入数据后，需要对数据进行初步检查，以确保数据的完整性和准确性。
数据检查缺失值处理对于数据中的缺失值，可以选择删除、填充或插值等方法进行处理。
异常值处理通过箱线图、散点图等方法识别异常值，并进行相应的处理，如删除或替换。
数据筛选根据需要，对数据进行筛选，以保留符合特定条件的数据。
变量转换对数据进行变量转换，如计算新变量、变量重编码等。
数据标准化将数据按照一定比例进行缩放，以消除量纲对数据分析的影响。
数据离散化将连续型数据转换为离散型数据，以便于进行某些统计分析。
数据描述性统计频数分析对数据进行频数分析，了解数据的分布情况。
描述性统计量计算数据的均值、中位数、众数、方差、标准差等描述性统计量。
图表展示通过直方图、饼图、散点图等图表展示数据的分布情况。
02CATALOGUE数据分析方法介绍做出决策根据检验统计量的值和显著性水平，决定是否拒绝原假设。
利用SPSS 软件计算检验统计量的值。
确定显著性水平根据研究需求，选择合适的显著性水平，如0.05或0.01。
提出假设根据研究问题，提出原假设和备择假设。
选择检验方法根据数据类型和分布，选择合适的假设检验方法，如t 检验、卡方检验等。
假设检验方差齐性检验在进行方差分析前，需要对数据进行方差齐性检验，以确保数据满足方差分析的前提条件。
单因素方差分析研究一个自变量对一个因变量的影响，通过比较不同组间的均值差异来判断自变量对因变量是否有显著影响。
多因素方差分析研究多个自变量对一个因变量的影响，通过比较不同组间的均值差异来判断哪些自变量对因变量有显著影响。
spss的数据分析报告范例
spss的数据分析报告范例SPSS数据分析报告范例一、引言数据分析是现代科学研究的重要环节，在统计学中，SPSS作为一种广泛应用的数据分析软件，为研究人员提供了丰富的功能和工具。
本报告旨在使用SPSS对某项研究的数据进行分析，并整理并呈现结果，以帮助读者深入了解数据的含义，并得出有关数据的结论。
二、研究背景与目的在这一部分，我们将简要介绍研究的背景和目的。
本次研究旨在调查大学生的学习焦虑水平与其学业成绩之间的关系。
通过收集相关数据并使用SPSS进行分析，我们希望能够揭示大学生学习焦虑对学业成绩的影响程度，并为教育管理者和辅导员提供数据支持。
三、研究设计与方法在这一部分，我们将介绍研究的设计和采用的方法。
本研究采用问卷调查的形式，使用了由专家设计的学习焦虑量表和学业成绩评估表。
我们在某大学的三个院系中选取了500名大学生作为样本，并通过邮件方式发送问卷，并以匿名方式收集数据。
四、数据分析与结果本节将展示SPSS分析后的数据结果。
首先，我们将进行数据清洗和描述性统计分析。
然后，我们将使用相关性分析和回归分析来探究学习焦虑与学业成绩之间的关系。
1.数据清洗和描述性统计针对收集到的数据，我们进行了数据清洗，包括去除不完整或无效数据。
然后，我们进行了描述性统计分析，包括计算样本量、均值、标准差和分布情况。
2.相关性分析为了探究学习焦虑与学业成绩之间的关系，我们进行了相关性分析。
根据SPSS的输出结果，我们发现学习焦虑与学业成绩之间存在显著的负相关关系（r=-0.35, p<0.05），表明学习焦虑水平越高，学业成绩越低。
3.回归分析为了更深入地了解学习焦虑对学业成绩的影响程度，我们进行了回归分析。
回归分析结果显示，学习焦虑是预测学业成绩的显著因素（β=-0.25, p<0.05）。
这表明学习焦虑对学业成绩有着一定的负向影响。
五、讨论与结论根据数据分析的结果，我们得出以下结论：1.学习焦虑与学业成绩之间存在显著的负相关关系，即学习焦虑水平越高，学业成绩越低。
大学生spss数据分析案例
大学生spss数据分析案例SPSS数据分析是大学生在进行学术研究和毕业论文撰写过程中常常需要掌握的技能之一。
本文将以一个实际案例为例，介绍如何使用SPSS软件进行数据分析，以帮助大学生更好地理解和运用SPSS进行数据处理和分析。
首先，我们需要明确案例研究的背景和目的。
假设我们要研究大学生学习成绩与每周学习时间的关系，我们收集了一批大学生的学习成绩和每周学习时间的数据，现在需要用SPSS进行分析。
第一步，我们需要导入数据。
在SPSS软件中，点击“文件”-“导入数据”-“从数据库导入数据”，选择相应的文件并导入数据。
第二步，进行数据清洗。
在数据清洗过程中，我们需要检查数据是否存在缺失值、异常值等情况，可以使用SPSS中的数据查看功能和描述统计功能进行检查和处理。
第三步，进行描述性统计分析。
在SPSS中，我们可以使用“描述统计”功能来计算学习成绩和每周学习时间的均值、标准差、频数分布等统计指标，以便对数据有一个整体的了解。
第四步，进行相关性分析。
我们可以使用SPSS中的“相关分析”功能来计算学习成绩和每周学习时间之间的相关系数，以判断它们之间是否存在显著的相关性。
第五步，进行回归分析。
如果我们想进一步探究学习成绩与每周学习时间之间的因果关系，可以使用SPSS中的“线性回归”功能来进行回归分析，得出它们之间的回归方程和相关系数。
最后，我们需要对分析结果进行解释和总结。
在解释和总结过程中，我们需要使用清晰、准确的语言对分析结果进行解释，并结合案例研究的背景和目的进行合理的总结和结论。
通过以上案例分析，我们可以看到，SPSS软件作为一款专业的统计分析工具，能够帮助我们快速、准确地进行数据分析，为我们的学术研究和毕业论文撰写提供了有力的支持。
希望本文能够对大学生在SPSS数据分析方面有所帮助，引起大家对SPSS数据分析的重视和学习兴趣。
spss的数据分析报告范例1
关于某地区361个人旅游情况统计分析报告一、数据介绍：本次分析的数据为某地区361个人旅游情况状况统计表，其中共包含七变量，分别是：年龄，为三类变量；性别，为二类变量（0代表女，1代表男）；收入，为一类变量；旅游花费，为一类变量；通道，为二类变量（0代表没走通道，1代表走通道）；旅游的积极性，为三类变量（0代表积极性差，1代表积极性一般，2代表积极性比较好，3代表积极性好 4代表积极性非常好）；额外收入,一类变量。
通过运用spss统计软件，对变量进行频数分析、描述性统计、方差分析、相关分析，以了解该地区上述方面的综合状况，并分析个变量的分布特点及相互间的关系。
二、数据分析1、频数分析。
基本的统计分析往往从频数分析开始。
通过频数分地区359个人旅游基本状况的统计数据表，在性别、旅游的积极性不同的状况下的频数分析，从而了解该地区的男女职工数量、不同积极性情况的基本分布。
统计量积极性性别N 有效359 359缺失0 0首先，对该地区的男女性别分布进行频数分析，结果如下性别频率百分比有效百分比累积百分比有效女198 55.2 55.2 55.2男161 44.8 44.8 100.0合计359 100.0 100.0表说明，在该地区被调查的359个人中，有198名女性，161名男性，男女比例分别为44.8%和55.2%，该公司职工男女数量差距不大，女性略多于男性。
其次对原有数据中的旅游的积极性进行频数分析，结果如下表：积极性频率百分比有效百分比累积百分比有效差171 47.6 47.6 47.6一般79 22.0 22.0 69.6比较好79 22.0 22.0 91.6好24 6.7 6.7 98.3非常好 6 1.7 1.7 100.0合计359 100.0 100.0其次对原有数据中的积极性进行频数分析，结果如下表：其次对原有数据中的是否进通道进行频数分析，结果如下表：Statistics通道N Valid 359Missing 0通道Frequency Percent Valid Percent Cumulative PercentValid 没走通道293 81.6 81.6 81.6通道66 18.4 18.4 100.0Total 359 100.0 100.0这说明，在该地区被调查的359个人中，有没走通道的占81.6%，占绝大多数。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
关于某公司474名职工综合状况的统计分析报告
一、数据介绍：
本次分析的数据为某公司474名职工状况统计表，其中共包含十一变量，分别是：id（职工编号），gender(性别)，bdate(出生日期)，edcu（受教育水平程度），jobcat（职务等级），salbegin（起始工资），salary（现工资），jobtime(本单位工作经历<月>)，prevexp(以前工作经历<月>)，minority(民族类型)，age(年龄)。
通过运用spss统计软件，对变量进行频数分析、描述性统计、方差分析、相关分析、以了解该公司职工上述方面的综合状况，并分析个变量的分布特点及相互间的关系。
二、数据分析
1、频数分析。
基本的统计分析往往从频数分析开始。
通过频数分析能够
了解变量的取值状况，对把握数据的分布特征非常有用。
此次分析利用了某公司474名职工基本状况的统计数据表，在gender(性别)、edcu（受教育水平程度）、不同的状况下的频数分析，从而了解该公司职工的男女职工数量、受教育状况的基本分布。
Statistics
首先，对该公司的男女性别分布进行频数分析，结果如下：
上表说明，在该公司的474名职工中，有216名女性，258名男性，男女比例分别为45.6%和54.4%，该公司职工男女数量差距不大，男性略多于女性。
其次对原有数据中的受教育程度进行频数分析，结果如下表：
Educational Level (years)
14 6 1.3 1.3 52.5
15 116 24.5 24.5 77.0
16 59 12.4 12.4 89.5
17 11 2.3 2.3 91.8
18 9 1.9 1.9 93.7
19 27 5.7 5.7 99.4
20 2 .4 .4 99.8
21 1 .2 .2 100.0
Tot
474 100.0 100.0
al
上表及其
直方图说明，被调查的474名职工中，受过12年教育的职工是该组频数最高的，为190人，占总人数的40.1%，其次为15年，共有116人，占中人数的24.5%。
且接受过高于20年的教育的人数只有1人，比例很低。
2、描述统计分析。
再通过简单的频数统计分析了解了职工在性别和受教
育水平上的总体分布状况后，我们还需要对数据中的其他变量特征有更为精确的认识，这就需要通过计算基本描述统计的方法来实现。
下面就对各个变量进行描述统计分析，得到它们的均值、标准差、片度峰度等数据，以进一步把我数据的集中趋势和离散趋势。
Descriptive Ststistics
如表所示，以起始工资为例读取分析结果，474名职工的起始工资最小值为＄9000，最大值为＄79980，平均起始工资为＄17016，标准差为＄7870.638，偏度系数和峰度系数分别为2.853和12.390。
其他数据依此读取，则该表表明474名职工的受教育水平、起始工资、现工资、先前工作经验、现在工作经验的详细分布状况。
3、Exploratory data analysis。
（1）交叉分析。
通过频数分析能够掌握单个变量的数据分布情况，但是在实际分析中，不仅要了解单个变量的分布特征，还要分析多个变量不同取值下的分布，掌握多个变量的联合分布特征，进而分析变量之间的相互影响和关系。
就本数据而言，需要了解现工资与性别、年龄、受教育水平、起始工资、本单位工作经历、以前工作经历、职务等级的交叉分析。
现以现工资与职务等级的列联表
分析为例，读取数据（下面数据分析表为截取的一部分）：
单因素分析用来研究一个控制变量的不同水平是否对观测变量产生了显着影响。
下面我们把受教育水平和起始工资作为控制变量，现工资为观测变量，通过单因素方差分析方法研究受教育水平和起始工资对现工资的影响进行分析。
分析结果如下：
上表是起始工资对现工资的单因素方差分析结果。
可以看出：F统计量的观测值为33.040，对应的概率P值近似等于0，如果显着性水平为0.05，由于概率值P小于显着性水平q，则应拒绝原假设，认为不同的起始工资对现工资产生了显着影响。
同理，上表是受教育水平对现工资影响的单因素分析结果，其结果亦为拒绝原假设，所以不同的受教育水平对现工资产生显着影响。
4、相关分析。
相关分析是分析客观事物之间关系的数量分析法，明确客
观事物之间有怎
样的关系对理解和运用相关分析是极其重要的。
函数关系是指两事物之间的一种一一对应的关系，即当一个变量X取一定值时，另一个变量函数Y可以根据确定的函数取一定的值。
另一种普遍存在的关系是统计关系。
统计关系是指两事物之间的一种非一一对应的关系，即当一个变量X取一定值时，另一个变量Y无法根据确定的函数取一定的值。
统计关系可分为线性关系和非线性关系。
事物之间的函数关系比较容易分析和测度，而事物之间的统计关系却不像函数关系那样直接，但确实普遍存在，并且有的关系强有的关系弱，程度各有差异。
如何测度事物之间的统计关系的强弱是人们关注的问题。
相关分
析正是一种简单易行的测度事物之间统计关系的
具。
上表是对本次分析数据中，现工资、起始工资、本单位工作时间、以前工作时间、年龄五个变量间的相关分析，表中相关系数旁边有两个星号（**）的，表示显着性水平为0.01时，仍拒绝原假设。
一个星号（*）表示显着性水平为0.05是仍拒绝原假设。
先以现工资这一变量与其他变量的相关性为例分析，由上表可知，现工资与起始工资的相关性最大，相关系数为0.880，而与在本单位的工作时间相关性最小，相关系数为0.084。
5、参数检验。
首先对现工资的分布做正态性检验，结果如下：
由上图可知，现工资的分布可近似看作符合正态分布，现推断现工资变量的平均值是否为$3,000,0，因此可采取单样本t检验来进行分析。
分析如下：
One-Sample Statistics
One-Sample Test
由One-Sample Statistics可知，474名职工的现工资平均值为￥34,419.57，标准差为$17,075.661，均值标准误差为$784.311。
图表One-Sample Test 中，第二列是t统计量的观测值为5.635；第三列是自由度为473（n-1）；第四列是t统计量观测值的双尾概率值；第五列是样本均值和检验值的差；第六列和第七列是总体均值与原假设值差的95%的置信区间为（$2,878.40 , 5,960.73）。
该问题的t值等于5.635对应的临界置信水平为0，远远小于设置的0.05，因此拒绝原假设，表明该公司的474名职工的现工资与$3,000,0存在显着差异。
6、非参数检验。
对本数据中的年龄做正态分布检验，结果如下：
由上图两图可知，474名职工的年龄分布并不完全符合正态分布，所以现推断其职工年龄的平均数在40-45岁之间，可对其采用非参数检验的方法进行检验。
检验结果如下：
Chi-Square Test
上面的第一个表为卡方检验的频率表，输出有关频率统计。
从表中可知，职工年龄为40岁的有41名，期望值为23.5，残差为17.5，其余读取方式相同。
第二个表是卡方检验统计表，显示检验的卡方值，自由度和渐进显着性水平分别是28.489、5、0。
因为显着性水平0小于0.05，因此拒绝原假设，即474名职工的平均年龄不在40到45岁之间。