统计学练习题(计算题)
统计学计算题例题(含答案)
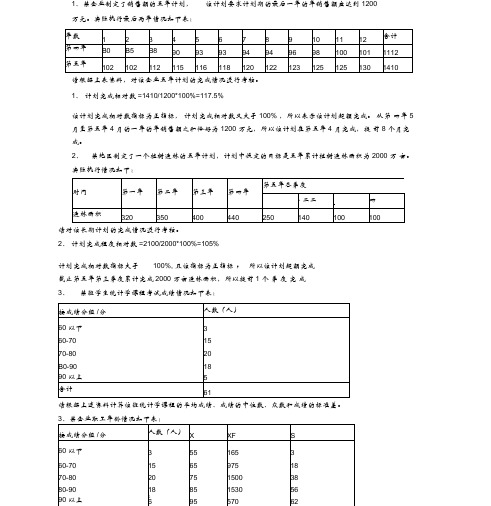
1、某企业制定了销售额的五年计划, 该计划要求计划期的最后一年的年销售额应达到 1200万元。
实际执行最后两年情况如下表:请根据上表资料,对该企业五年计划的完成情况进行考核。
1、 计划完成相对数 =1410/1200*100%=117.5%该计划完成相对数指标为正指标, 计划完成相对数又大于 100% ,所以表示该计划超额完成。
从第 四年 5 月至第五年 4 月的一年的年销售额之和恰好为 1200 万元,所以该计划在第五年 4 月完成,提 前 8 个月完成。
2、 某地区制定了一个植树造林的五年计划,计划中设定的目标是五年累计植树造林面积为 2000 万 亩。
实际执行情况如下:请对该长期计划的完成情况进行考核。
2、 计划完成程度相对数 =2100/2000*100%=105%计划完成相对数指标大于100%, 且该指标为正指标 , 所以该计划超额完成截止第五年第三季度累计完成 2000 万亩造林面积,所以提前 1 个 季 度 完 成3、某班学生统计学课程考试成绩情况如下表:请根据上述资料计算该班统计学课程的平均成绩、成绩的中位数、众数和成绩的标准差。
3、某企业职工年龄情况如下表:X 二三于=4740/62=76.45 (分)Me=70+ (62/2-18) *10/20=76.5 (分)Mo=70+(20 J5)70/[(2CM5)+(2CM8)]=77 」4 (分)G-7(55-76.45f *3 +⋯⋯+ (95^76.45f *6/62=10.45 (分)4、某学校有5000 名学生,现从中按重复抽样方法抽取250 名同学,调查其每周观看电视的小时数的情况,获得资料如下表:请根据上述资料,以95% 的概率保证程度对全校学生每周平均收看电视时间进行区间估计。
4> 样本平均数X= Sxf/Sf-l250/250-5样 ______________ __________二>/ 刀(好予f/(工f—1 )二V 1136/249 二2. 14抽样平均误差U 二s/ Vn=0.14因为 F (t) =95%, 所以日.96抽样极限误差△ 二t U 二 1. 96*0. 14=0. 27 区间下限=5-0. 27=4. 73 区间上限二5+0. 27-5. 27全校学生每周平均收看电视的吋间在( 4.73,5.27) 小时之间,概率保证程度为95%5 、某企业对全自动生产线上的产品随机抽取1000 件进行检验,发现有45 件是不合格的,设定允许的极限误差为1.32% 。
统计学练习题

统计学练习题(计算题)第四章----第一部分总量指标与相对指标:(1)某企业产值计划完成程度为105%,比上年增长7%,试计算计划规定比上年增长多少(2)单位产品成本上年为420元,计划规定今年成本降低5%,实际降低6%,试确定今年单位成本的计划数字和实际数字,并计算出降低成本计划完成程度指标。
(3)按计划规定,劳动生产率比上年提高10%,实际执行结果提高了12%,劳动生产率计划完成程度是多少:某市三个企业某年的下半年产值及计划执行情况如下:要求:[1]试计算并填写上表空栏,并分别说明(3)、(5)、(6)、(7)是何种相对数;[2]丙企业若能完成计划,从相对数和绝对数两方面说明该市三个企业将超额完成计划多少:我国2008年-2013年国内生产总值资料如下:单位:亿元根据上述资料,自行设计表格:(1)计算各年的第一产业、第二产业、第三产业的结构相对指标和比例相对指标;(2)计算我国国内生产总值、第一产业、第二产业、第三产业与上年对比的增长率;(3)简要说明我国经济变动情况。
:某公司下属四个企业的有关销售资料如下:根据上述资料:(1)完成上述表格中空栏数据的计算;(2)若A能完成计划,则公司的实际销售额将达到多少比计划超额完成多少(3)若每个企业的计划完成程度都达到B企业的水平,则公司的实际销售额将达到多少比计划超额完成多少第四章-----第二部分平均指标与变异指标:已知某地区各工业企业产值计划完成情况以及计划产值资料如下:要求:(1)根据上述资料计算该地区各企业产值计划的平均完成程度。
(2)如果在上表中所给资料不是计划产值而是实际产值,试计算产值计划平均完成程度。
、:已知某厂三个车间生产不同的产品,其废品率、产量和工时资料如下:计算:(1)三种产品的平均废品率;(2)假定三个车间生产的是同一产品,但独立完成,产品的平均废品率是多少;(3)假定三个车间是连续加工某一产品,产品的平均废品率是多少。
:对某车间甲、乙两工人当日产品中各抽取10件产品进行质量检查,得资料如下:试比较甲乙两工人谁生产的零件质量较稳定。
统计学计算题
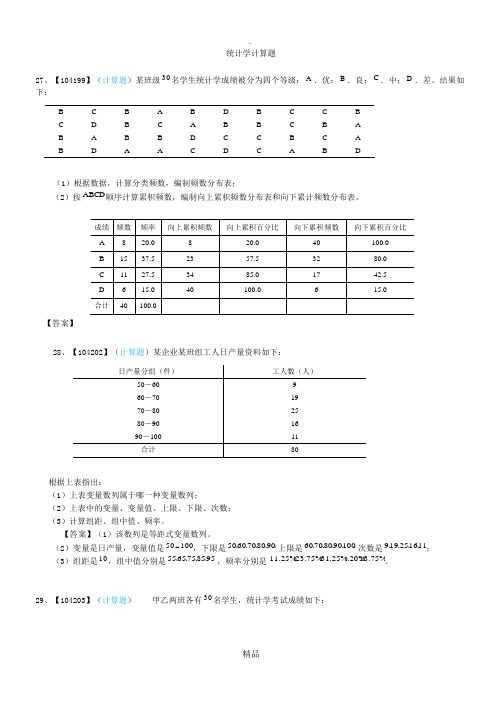
统计学计算题27、【104199】(计算题)某班级30名学生统计学成绩被分为四个等级:A .优;B .良;C .中;D .差。
结果如下:B C B A B D B C C B C D B C A B B C B A B A B B D C C B C A BDAACDCABD(1)根据数据,计算分类频数,编制频数分布表;(2)按ABCD 顺序计算累积频数,编制向上累积频数分布表和向下累计频数分布表。
【答案】28、【104202】(计算题)某企业某班组工人日产量资料如下:根据上表指出:(1)上表变量数列属于哪一种变量数列;(2)上表中的变量、变量值、上限、下限、次数; (3)计算组距、组中值、频率。
【答案】(1)该数列是等距式变量数列。
(2)变量是日产量,变量值是50-100,下限是,、、、、9080706050上限是,、、、、10090807060次数是111625199、、、、; (3)组距是10,组中值分别是 9585756555、、、、,频率分别是13.75%31.25%.20%23.75%11.25% 、、。
29、【104203】(计算题) 甲乙两班各有30名学生,统计学考试成绩如下:(1)根据表中的数据,制作甲乙两班考试成绩分类的对比条形图; (2)比较两班考试成绩分布的特点。
【答案】乙班学生考试成绩为优和良的比重均比甲班学生高,而甲班学生考试成绩为中和差的比重比乙班学生高。
因此乙班学生考试成绩平均比乙班好。
两个班学生都呈现出"两头大,中间小"的特点,即考试成绩为良和中的占多数,而考试成绩为优和差的占少数。
30、【104205】(计算题)科学研究表明成年人的身高和体重之间存在着某种关系,根据下面一组体重身高数据绘制散点图,说明这种关系的特征。
体重(Kg )5053 57 60 66 70 76 75 80 85 身高(cm ) 150155160165168172178180182185【答案】散点图:可以看出,身高与体重近似呈现出线性关系。
统计学期末考试练习题及参考答案

D、把多种产品的价格乘以报告期相应的数量,然后进行对比
答案:A
16、当变量值有一项为0时,不能计算
A、算术平均数B、中位数C、调和平均数D、众数
答案:C
17、标志变异系数的主要用途是()
A、反映一组数据的离散程度B、反映一组数据的平均水平
C、比较多组数据的离散程度D、比较多组数据的平均水平
答案:D
20、无交互作用的双因素方差分析是指用于检验的两个因素
A、对因变量的影响是有交互作用的;B、对自变量的影响是有交互作用的;
C、对自变量的影响是独立的;D、对因变量的影响是独立的;
答案:A
21、收入水平与受教育程度之间关系数为0.6314,这种相关肯定属于
A、显著相关;B、负相关;C、高度相关;D、正相关
答案:
3.研究表明,某地区机电行业的销售额与该地区汽本产量及建筑业的产值关系十分密切,搜集1996~2012年共17年的相关资料,利用Exe得到下面的国日结果(是著性》
a=0.05):
42074……
(1)将方差分析表中的所缺数值补齐。(保留到小数点后两位数字)
(2)写出该地区机电行业的销售额(单位:万元)与该地区汽车产量及建筑业的产值的多元线性回归方程,并解释各回归系数的意)
答案:单纯随机抽样系统抽样分层抽样整群抽样
7、统计学的基本方法有哪些?
答案:大量观察法统计推断法统计描述法
8、综合指数的编制原理?
答案:综合指数是设法将各个个体的数量先综合以后再通过两个时期的综合数值对比来计算的总指数。先综合、后对比
9、在应用平均指标分析说明社会经济现急时,应注意哪些问题?
答案:(1)注意所研究对象的同质性(2)用组平均数补充说明总平均数(3)用分配数列补充说明平均数(4)注意一般和个别相结合
统计学复习题题目——计算题
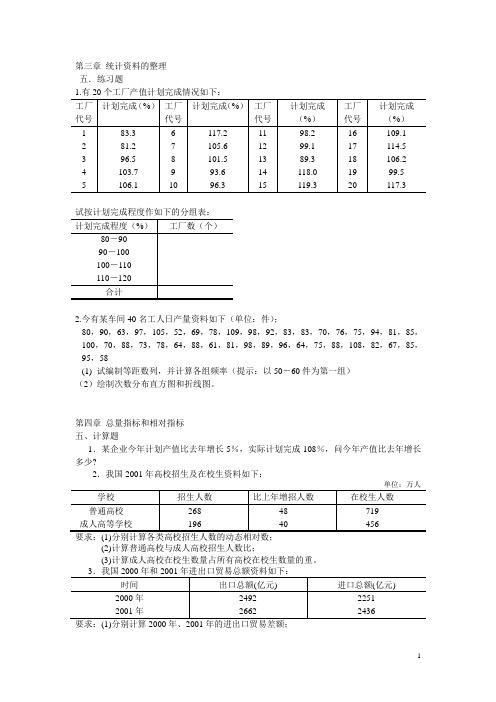
第三章 统计资料的整理 五.练习题试按计划完成程度作如下的分组表:2.今有某车间40名工人日产量资料如下(单位:件);80,90,63,97,105,52,69,78,109,98,92,83,83,70,76,75,94,81,85,100,70,88,73,78,64,88,61,81,98,89,96,64,75,88,108,82,67,85,95,58(1) 试编制等距数列,并计算各组频率(提示:以50-60件为第一组) (2)绘制次数分布直方图和折线图。
第四章总量指标和相对指标 五、计算题1.某企业今年计划产值比去年增长5%,实际计划完成108%,问今年产值比去年增长多少?2.我国2001年高校招生及在校生资料如下:(2)计算普通高校与成人高校招生人数比;(3)计算成人高校在校生数量占所有高校在校生数量的重。
(2)计算2001年进出口总额比例相对数及出口总额增长速度; (3)分析我国进出口贸易状况。
4.根据下列资料,计算强度相对数的正指标和逆指标,并根据正指标数值分析该地区5.某公司下属三个企业有关资料如下表,试根据指标之间的关系计算并填写表中所缺数第六章 动态数列习题五、计算题1.某公司某年9月末有职工250人,10月上旬的人数变动情况是:10月4日新招聘12名大学生上岗,6日有4名老职工退休离岗,8日有3名青年工人应征入伍,同日又有3名职工辞职离岗,9日招聘7名营销人员上岗。
试计算该公司10月上旬的平均在岗人数。
(2)分别计算该银行2005年第一季度、第二季度和上半年的平均现金库存额。
(2)计算该地区2001—2005年间的平均国民生产总值。
(3)计算2002—2005年间国民生产总值的平均发展速度和平均增长速度。
(2)计算该企业第四季度劳动生产率。
(2)应用最小平方法配合趋势直线,并计算各年的趋势值。
第七章统计指数习题五、计算题1.某市1999年第一季度社会商品零售额为36200万元,第四季度为35650万元,零售物价下跌0.5%,试计算该市社会商品零售额指数、零售价格指数和零售量指数,以及由于零售物价下跌居民少支出的金额。
统计学练习题(计算题)

统计学练习题(计算题)第四章----第一部分总量指标与相对指标:(1)某企业产值计划完成程度为105%,比上年增长7%,试计算计划规定比上年增长多少(2)单位产品成本上年为420元,计划规定今年成本降低5%,实际降低6%,试确定今年单位成本的计划数字和实际数字,并计算出降低成本计划完成程度指标。
(3)按计划规定,劳动生产率比上年提高10%,实际执行结果提高了12%,劳动生产率计划完成程度是多少:某市三个企业某年的下半年产值及计划执行情况如下:要求:[1]试计算并填写上表空栏,并分别说明(3)、(5)、(6)、(7)是何种相对数;[2]丙企业若能完成计划,从相对数和绝对数两方面说明该市三个企业将超额完成计划多少:我国2008年-2013年国内生产总值资料如下:单位:亿元根据上述资料,自行设计表格:(1)计算各年的第一产业、第二产业、第三产业的结构相对指标和比例相对指标;(2)计算我国国内生产总值、第一产业、第二产业、第三产业与上年对比的增长率;(3)简要说明我国经济变动情况。
:某公司下属四个企业的有关销售资料如下:根据上述资料:(1)完成上述表格中空栏数据的计算;(2)若A能完成计划,则公司的实际销售额将达到多少比计划超额完成多少(3)若每个企业的计划完成程度都达到B企业的水平,则公司的实际销售额将达到多少比计划超额完成多少第四章-----第二部分平均指标与变异指标:已知某地区各工业企业产值计划完成情况以及计划产值资料如下:要求:(1)根据上述资料计算该地区各企业产值计划的平均完成程度。
(2)如果在上表中所给资料不是计划产值而是实际产值,试计算产值计划平均完成程度。
、:已知某厂三个车间生产不同的产品,其废品率、产量和工时资料如下:计算:(1)三种产品的平均废品率;(2)假定三个车间生产的是同一产品,但独立完成,产品的平均废品率是多少;(3)假定三个车间是连续加工某一产品,产品的平均废品率是多少。
:对某车间甲、乙两工人当日产品中各抽取10件产品进行质量检查,得资料如下:试比较甲乙两工人谁生产的零件质量较稳定。
统计学计算题8个例题及答案

统计学计算题8个例题及答案
1.给定一组数据,X=(13,12,13,13,10,13,11),求它的众数:
答:13(众数是出现次数最多的值)
2.给定一组数据,X=(1,2,3,4,5,6,7),求它的中位数:
答:4(中位数是将一组数据按照大小顺序排列后位于正中间的一个数)
3.给定一组数据,X=(1,2,3,4,5,6,7),求它的样本标准差:
答:(样本标准差S=√ [(∑(Xi−X平均数)2)/ (n−1)],其中,Xi代表样本的每一项,X平均数是样本的平均值,n是样本的总观测值数量)
4.给定一组数据,X=(1,2,3,4,5,6,7,8,9),求它的方差:
答:(方差σ^2=∑(Xi−X平均数)^2/n,其中,Xi代表样本的每一项,X平均数是样本的平均值,n是样本的总观测值数量)
5.给定一组数据,X=(21, 25, 28, 31, 34, 37, 40),求它的算术平均数:
答:31(算术平均数是将样本中数据求和,再除以样本的个数得到的数)
6.给定一组数据,X=(1,2,3,4,5,6,7,8,9),求它的期望:
答:5(期望是一组数据根据概率分布定义出的一种数学期望)
7.给定一组数据,X=(3,4,5,7,12,15,18),求它的方差:
答:(方差σ^2=∑(Xi−X平均数)^2/n,其中,Xi代表样本的每一项,X平均数是样本的平均值,n是样本的总观测值数量)
8.给定一组数据,X=(7,7,7,7,8,8,9),求它的众数:
答:7(众数是出现次数最多的值)。
统计学计算习题
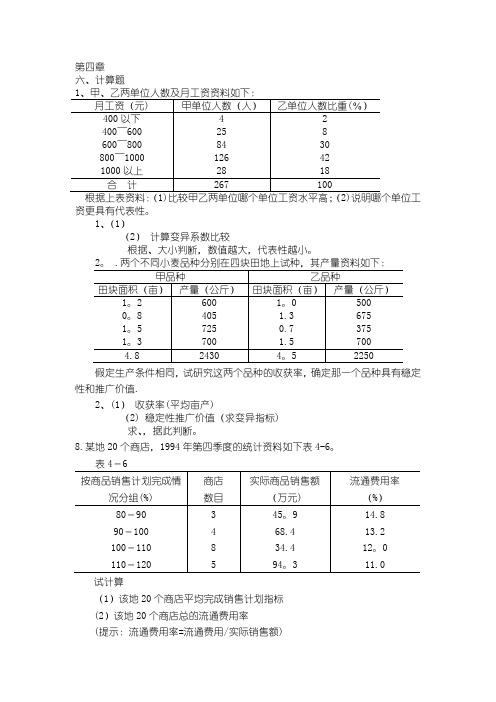
第四章六、计算题资更具有代表性。
1、(1)(2)计算变异系数比较根据、大小判断,数值越大,代表性越小。
假定生产条件相同,试研究这两个品种的收获率,确定那一个品种具有稳定性和推广价值.2、(1)收获率(平均亩产)(2) 稳定性推广价值(求变异指标)求、,据此判断。
8.某地20个商店,1994年第四季度的统计资料如下表4-6。
表4-6试计算(1)该地20个商店平均完成销售计划指标(2)该地20个商店总的流通费用率(提示:流通费用率=流通费用/实际销售额)8、(1)(2) 据提示计算:13、提示:(2)平均一级品率。
14、(1) (2)15.某生产小组有36名工人,每人参加生产的时间相同,其中有4人每件产品耗时5分钟,20人每件耗时8分钟,12人每件耗时10分钟。
试计算该组工人平均每件产品耗时多少分钟?如果每人生产的产品数量相同,则平均每件产品耗时多少分钟?15、(1) 设时间为t ,(2) 设产品数量为a ,16.为了扩大国内居民需求,银行为此多次降低存款利润,近5年年利润率分别为7%、5%、4%、3%、2%,试计算在单利和复利情况下5年的平均年利率。
16、(1) 单利:(2) 复利(几何平均法): 第五章2。
某企业1—7月份工人人数及总产值资料如表8-4:计算:(1)上半年平均月劳动生产率。
(2)上半年劳动生产率。
2、(1) 上半年平均月劳动生产率:(2) 上半年劳动生产率: 3.某企业第二季度有关资料如表8-5:试计算第二季度月平均流转次数及第二季度流转次数。
3、(1) 第二季度月平均流转次数: (2) 第二季度流转次数=4.设某地区1980年国民生产总值为125亿元,人口5000万。
据过去五年国民生产总值的增长速度计算,平均每年递增7.5%,试推算2000年的国民生产总值;若人口增加到6000万人问平均每人能否达到1000元?4、 求 据计算。
7、 计算方法类同9. 某地区对外贸易总额,l994年是1990年的135。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
请计算各种动态指标,并说明如下关系:⑴发展速度和增长速度;⑵定
基发展速度和环比发展速度;⑶逐期增长量与累计增长量;⑷平均发展 速度与环比发展速度;⑸平均发展速度与平均增长速度。 10、某厂职工人数及非生产人员数资料如下: 1月1日 2月1日 3月1日 4月1日 5月1日 6月1日 7月1日 职工人数 (人) 其中:非生 产人员数 (人) 4000 724 4040 716 4050 682 4080 694 4070 666 4090 666 4100 660
10、⑴第一季度非生产人员比重:17.4%; 第二季度非生产人员比重:16.4%; ∴第二季度指标值比第一季度少1%。 ⑵上半年非生产人员比重:16.9%。 ⒍yc=345.6+14.4x;y2008=417.6万吨 11、各指标计算见下表: 单位:万元 年份 2000 2001 2002 2003 2004 2005 发展 水平 258 327.5 391.2 413.8 562.8 580.8 增减量 累计 逐期 — 42.5 53.1 42.9 69.5 69.2 平 均 增减值 发展速度 (%) 定基 100.0 114.9 137.3 145.2 197.5 203.8 环比 — 114.9 119.5 105.8 136.0 103.2 增减速度 定基 — 14.9 37.3 45.2 97.5 103.8 环比 — 14.9 19.5 5.8 36.0 3.2
试根据上述资料,计算表中所缺的数字。
7、第一季度平均每月总产值=4400万元 第二季度平均每月总产值≈4856.7万元 第三季度平均每月总产值=5200万元 第四季度平均每月总产值=5500万元 全年平均每月总产值=4989.2万元 8、第一季度平均职工人数≈302人
第二季度平均职工人数≈310人 第三季度平均职工人数=322人 第四季度平均职工人数=344人 全年平均职工人数≈320人 9、计算结果如下表:
1 2 3 4 5
⑴=510(元); ⑵全距=690-375=315(元)
⑶=78(元); ⑷=102.1(元)⑸=15.29%; ⑹=20.02%
5、某班甲乙两个学习小组某科成绩如下: 甲小组 成绩 60分以下 60-70 70-80 80-90 90分以上 合计 乙小组 成绩 60分以下 60-70 70-80 80-90 90分以上 合计 人数 2 6 9 5 2 24 人数 3 5 10 4 2 24
7、某地区2005年各月总产值资料如下: 月份 1 2 3 4 5 6 总产值(万元) 4200 4400 4600 4820 4850 4900 月份 7 8 9 10 11 12 总产值(万元) 5000 5200 5400 5400 5500 5600
请计算各季平均每月总产值和全年平均每月总产值。 8、某企业2005年各月月初职工人数资料如下: 日期 1月 2月 3月 4月 5月 6月 7月 8月 9月 10 月 11 月 12 月
根据上表计算该商店售货员工资的全距,平均差和标准差,平均差 系数和标准差系数。 解: 工资额 (元)X 375 430 510 590 690 2595 售货员人数 (人) 4 3 7 3 3 20 Xf 1500 -135 1290 3570 1770 2070 10200 -80 0 80 180 — 540 240 0 240 540 1560 72900 19200 0 19200 97200 208500
3、甲乙两企业生产同种产品,1月份各批产量和单位产品成本资料 如下: 甲企业 单位产品成 产量比重 本 (%) (元) 1.0 10 1.1 1.2 20 70 乙企业 单位产品成 产量比重 本 (%) (元) 1.2 30 1.1 1.0 30 40
第一批 第二批ቤተ መጻሕፍቲ ባይዱ第三批
试比较和分析哪个企业的单位成本高,为什么?
— — 42.5 42.5 106.2 63.7 128.8 22.6 277.8 149.0 295.8 18.0
12、有三种商品的销量和售价资料如下 销 量 售价(元) 商品 q0 q1 p0 p1 甲 4000 5000 50 60 (件) 乙 1000 800 240 200 (台) 丙 2000 2500 100 80 (套)
14、某灯管厂生产10万只日光灯管,现采用简单随机不重复抽样方式抽 取1%灯管进行质量检验,测试结果如下: 耐用时间(小时) 灯管数(只) 800小时以下 800-900 900-1000 1000-1100 1100小时以上 合计 根据上述资料: 10 15 35 25 15 100
8月份 工人数 比重 (人)f (%)f/ 18 30 72 120 5.00 8.33 30.00 33.34 270 750 2520 5400
50-60 60以上 合计
55 65 —
42 12 360
11.67
2310
90 30 360
25.00 8.33 100.00
4950 1950 15840
3.33 780 100.00 13320
7月份平均每人日产量为:(件) 8月份平均每人日产量为:(件) 根据计算结果得知8月份比7月份平均每人日产量多7件。其原因是不 同组日产量水平的工人所占比重发生变化所致。7月份工人日产量在40 件以上的工人只占全部工人数的40%,而8月份这部分工人所占比重则 为66.67%。 2、某纺织厂生产某种棉布,经测定两年中各级产品的产量资料如 下: 产品等级 一级 二级 三级 合计 产量(万米) 2009年 200 40 10 250 2010年 270 24 6 300
试比较这两年产品的平均等级,并说明该厂棉布生产在质量上有何变化 及其因。
解: 2009年棉布的平均等级==1.24(级)
2010年棉布的平均等级==1.12(级) 可见该厂棉布产品质量2010年比2009年有所提高,其平均等级由 1.24级上升为1.12级。质量提高的原因是棉布一级品由80%上升为90%, 同时二级品和三级品分别由16%及4%下降为8%及2%。
要求:⑴计算第一季度和第二季度非生产人员比重,并进行比较;⑵ 计算上半年非生产人员比重。 11、某企业历年若干指标资料如下表: 单位:万元 发展水 年度 平 2000 2001 2002 2003 2004 2005 285 增减量 累计 — 106.2 45.2 136.0 3.2 逐期 — 平均增 减量 — 42.5 发展速度% 定基 — 环比 — 增减速度% 定基 — 环比 —
试比较甲乙两个学习小组该科平均成绩的代表性大小。
解:
甲小组 成绩 (分) 60分以下 60-70 70-80 80-90 90以上 合计 人数 3 5 10 4 2 24 组中值 55 65 75 85 95 —— xf 165 325 750 340 191 1770 18.75 8.75 1.25 11.25 21.25 —— 3513.56 76.56 1.56 126.56 451.56 —— 1054.69 382.81 15.63 506.25 903.13 2936.25
416.98 833.95 —— 2695.83
=74.58(分) =10.60(分) ×100%=14.21% 计算结果得知乙小组标准差系数小,所以乙小组平均成绩代表性大。
6、某机械厂铸造车间生产600吨铸件,合格540吨,试求平均合格 率,标准差及标准差系数。
解: 标准差×100%=30% 标准差系数
定基发展速度 % 环比发展速度 % 定基增长速度 % 环比增长速度 %
130.21 151.38 159.83 204.95 228.34 130.21 116.26 105.58 128.23 111.41 30.21 30.21 51.38 16.26 59.83 5.58 104.95 128.34 28.23 11.41
4、有四个地区销售同一种产品,其销售量和销售额资料如下: 地区 甲 乙 丙 丁 销售量(千件) 50 40 60 80 销售额(万元) 200 176 300 384
试计算各地区平均价格和此种商品在四个地区总的平均价格。
解: 总平均价格==46.09
5、某商店售货员的工资资料如下: 工资额(元) 375 430 510 590 690 售货员人数(人) 4 3 7 3 3
工业总产值 累计增长量 逐年增长量
单位 2000年 2001年 2002年 2003年 2004年 2005年 万元 343.3 447.0 519.7 548.7 703.6 783.9 万元 — 万元 — — — — — 103.7 103.7 176.4 72.7 205.4 29.0 360.3 154.9 440.6 80.3
—
—
—
—
计算分析销量和售价的变动对销售额变动的影响。
13、某企业职工人数和工资资料统计如下: 组别 技术人员 普通职工 人数(人) 基期f0 50 180 报告期f1 60 250 人均月收入(元) 基期x0 2500 1450 报告期x1 3200 1860
根据资料,从相对数和绝对数两个方面分析工人结构变化及各组平 均工资水平的变动对总体平均工资的影响。
职工人 数 300 300 304 306 308 314 312 320 320 340 342 345 (人) 请计算该企业2005年各季平均职工人数和全年平均职工人数。 9、2000年和第十个五年计划时期某地区工业总产值资料如下: 时期 工业总 产值 (万 元) 2000年 343.3 2001年 447.0 2002年 519.7 2003年 548.7 2004年 703.6 2005年 783.9
统计学练习题——计算题
1、某企业工人按日产量分组如下: 工人按日产量分组 20以下 20-30 30-40 40-50 50-60 60以上 合计 七月份 30 78 108 90 42 12 360
