最新初中数学全等三角形常见题目型训练基础测试卷

合集下载

三角形全等测试题及答案

三角形全等测试题及答案一、选择题1. 两个三角形全等的条件是（）A. 有两条边和它们的夹角对应相等B. 三条边对应相等C. 有两条边和其中一条边的对角对应相等D. 有两条边和其中一条边的邻角对应相等答案：B2. 如果两个三角形的对应角相等，那么这两个三角形（）A. 一定全等B. 可能相似C. 一定相似D. 无法确定答案：B二、填空题3. 已知三角形ABC与三角形DEF全等，且∠A=∠D，AB=DE，那么AC=______。

答案：EF4. 如果两个三角形的两边和夹角对应相等，那么这两个三角形是______。

答案：全等三、判断题5. 如果两个三角形的对应边成比例，那么这两个三角形一定全等。

（）答案：错误6. 如果两个三角形的两边和夹角对应相等，那么这两个三角形一定相似。

（）答案：正确四、解答题7. 如图所示，已知三角形ABC与三角形DEF全等，且AB=5cm，BC=7cm，∠A=∠D=90°，求DE的长度。

答案：DE=7cm8. 已知三角形ABC与三角形DEF相似，且AB=3cm，BC=4cm，DE=6cm，求AC的长度。

答案：AC=8cm五、证明题9. 已知三角形ABC与三角形DEF全等，且∠A=∠D，AB=DE，证明：AC=EF。

证明：由于三角形ABC与三角形DEF全等，根据全等三角形的性质，对应边相等，所以AC=EF。

10. 已知∠A=∠D，AB=DE，AC=DF，求证：三角形ABC≌三角形DEF。

证明：根据SAS（边角边）判定方法，已知∠A=∠D，AB=DE，AC=DF，所以三角形ABC≌三角形DEF。

全等三角形基础测试题

全等三角形基础测试题( 练习时间60分钟）班别姓名学号成绩（一）精心选一选6小题（每小题4分，共24分）1、使两个直角三角形全等的条件是（）Ａ.一锐角对应相等Ｂ.两锐角对应相等Ｃ.一条边对应相等Ｄ.两条边对应相等2、如图，AB 与CD 交于点O ，OA ＝OC ，OD ＝OB ，∠A=50°，∠B ＝30°，则∠D 的度数为（）.A ．50°B ．30°C ．80°D ．100°3、如图，在△ABC 和△DEF 中，给出以下六个条件中：① AB=DE ；②BC=EF ；③AC=DF ；④∠A=∠D ； ⑤∠B=∠E ；⑥∠C=∠F 。

以其中三个作为已知条件，不能判断△ABC 和△DEF 全等的是（）A ．①⑤②B 、①②③C 、④⑥①D 、②③④4、下列说法中不正确的是（）A.全等三角形一定能重合B.全等三角形的面积相等C.全等三角形的周长相等D.周长相等的两个三角形全等5、某同学把一块三角形的玻璃打碎成了3块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事方法是（） A ．带①去 B ．带②去 C ．带③去 D ．①②③都带去6、如图，∠B=∠C=90，M 是BC 的中点，DM 平分∠ADC ，∠CMD=35°，∠MAB 的度数是（） A ．35° B ．45° C ．55° D ．65°（二）细心填一填6小题（每小题4分，共24分）7、如图示，AC ，BD 相交于点O ，△AOB ≌△COD ，∠A=∠C ，则其它对应角分别为______________________，对应边分别为_____________________.8、已知，如图，AD =AC ，BD =BC ，O 为AB 上一点，那么，图中共有对全等三角形．9、△ABC 中，∠B ＝60°，∠C ＝80°，O 则∠OAC ＝______，∠BOC ＝________．10、将一张长方形纸片按如图所示的方式进行折叠，其中BC BD ，为折痕，则BCD ∠的度数为．OC BA第8题BD 第7题图ODACBABCE DF（第3题）DA BC M（第6题） O DCB A（第2题）11、EO ＝12＝ 13、(6分ACD ∵AD 平分∠BAC∴∠________＝∠_________（角平分线的定义）在△ABD 和△ACD 中∴△ABD ≌△ACD （）14、(6分)已知：如图，在直线MN 上求作一点P ，使点P 到∠AOB 两边的距离相等（要求写出作法，并保留作图痕迹，写出结论）15、(8分)已知：如图，点A 、E 、F 、C 在同一直线上，AD ∥BC ，AD=CB ，AE=CF 。

全等三角形基础测试卷及答案

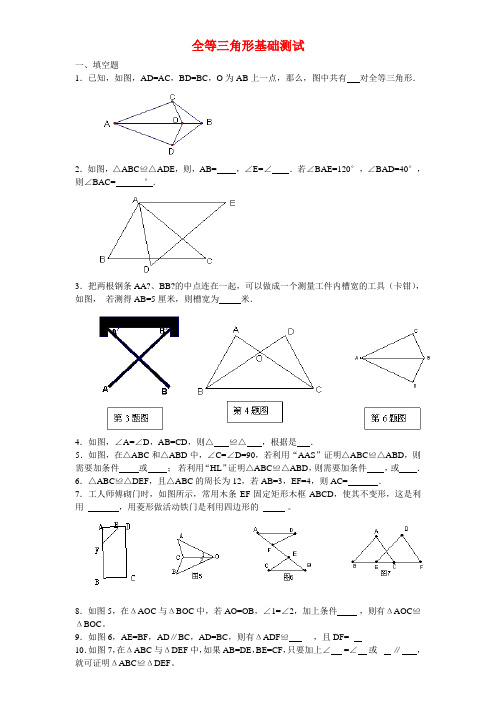
全等三角形基础测试一、填空题1．已知，如图，AD=AC，BD=BC，O为AB上一点，那么，图中共有对全等三角形．2．如图，△ABC≌△ADE，则，AB= ，∠E=∠．若∠BAE=120°，∠BAD=40°，则∠BAC= °．3．把两根钢条AA?、BB?的中点连在一起，可以做成一个测量工件内槽宽的工具（卡钳），如图，若测得AB=5厘米，则槽宽为米．4．如图，∠A=∠D，AB=CD，则△≌△，根据是．5．如图，在△ABC和△ABD中，∠C=∠D=90，若利用“AAS”证明△ABC≌△ABD，则需要加条件或；若利用“HL”证明△ABC≌△ABD，则需要加条件，或．6．△ABC≌△DEF，且△ABC的周长为12，若AB=3，EF=4，则AC= ．7．工人师傅砌门时，如图所示，常用木条EF固定矩形木框ABCD，使其不变形，这是利用，用菱形做活动铁门是利用四边形的。

8．如图5，在ΔAOC与ΔBOC中，若AO=OB，∠1=∠2，加上条件，则有ΔAOC≌ΔBOC。

9．如图6，AE=BF，AD∥BC，AD=BC，则有ΔADF≌，且DF=10．如图7，在ΔABC与ΔDEF中，如果AB=DE，BE=CF，只要加上∠ =∠或∥，就可证明ΔABC≌ΔDEF。

11．如图，BE=CF，AB=DE，添加下列哪些条件可以推证△ABC≌△DFE （）（A）BC=EF （B）∠A=∠D （C）AC∥DF （D）AC=DF12．已知，如图，AC=BC，AD=BD，下列结论，不正确的是（）（A）CO=DO（B）AO=BO （C）AB⊥BD （D）△ACO≌△BCO13．在△ABC内部取一点P使得点P到△ABC的三边距离相等，则点P应是△ABC 的哪三条线交点．（）（A）高（B）角平分线（C）中线（D）垂直平分线已知14．下列结论正确的是（）（A）有两个锐角相等的两个直角三角形全等；（B）一条斜边对应相等的两个直角三角形全等；（C）顶角和底边对应相等的两个等腰三角形全等；（D）两个等边三角形全等.15．下列条件能判定△ABC≌△DEF的一组是（）（A）∠A=∠D，∠C=∠F，AC=DF（B）AB=DE，BC=EF，∠A=∠D（C）∠A=∠D，∠B=∠E，∠C=∠F（D）AB=DE，△ABC的周长等于△DEF的周长16．已知，如图，△ABC中，AB=AC，AD是角平分线，BE=CF，则下列说法正确的有几个（）（1）AD平分∠EDF；（2）△EBD≌△FCD；（3）BD=CD；（4）AD⊥BC．（A）1个（B）2个（C）3个（D）4个1．如图，AB=DF，AC=DE，BE=FC，问：ΔABC与ΔDEF全等吗？AB与DF平行吗？请说明你的理由。

中考数学复习《全等三角形》专题训练-附带有答案

中考数学复习《全等三角形》专题训练-附带有答案一、选择题1．如图，△ABC≌△EFD，且AB＝EF，EC＝4，CD＝3，则AC等于（）A．3 B．4 C．7 D．82．某同学把一块三角形的玻璃打碎成了3块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事方法是（）A．带①去B．带②去C．带③去D．①②③都带去3．如图，为了测量B点到河对面的目标A之间的距离，在B点同侧选择了一点C，测得∠ABC=60°，∠ACB= 40°然后在BC的同侧找到点M使∠MBC=60°，∠MCB=40°，得到△MBC≌△ABC，所以测得MB的长就是A，B两点间的距离，这里判定△MBC≌△ABC的理由是（）A．SAS B．AAA C．SSS D．ASA4．如图，在△ABC中，BE是∠ABC的平分线，CE是外角∠ACM的平分线，BE与CE相交于点E，若∠A=60°，则∠BEC是（）A．15°B．30°C．45°D．60°5．如图，BP是∠ABC的平分线，AP⊥BP于P，连接PC，若△ABC的面积为1cm2则△PBC的面积为（）.A．0.4 cm2B．0.5 cm2C．0.6 cm2D．不能确定6．如图，OP平分∠AOB，PA⊥OA，PB⊥OB垂足分别为A，B，下列结论中不一定成立是（）A．PA=PB B．PO平分∠APBC．OA=OB D．AB垂直平分OP7．如图，△ABC中∠ACF、∠EAC的角平分线CP、AP交于点P，延长BA、BC，PM⊥BE，PN⊥BF.则下列结论中正确的个数（）①BP平分∠ABC ②∠ABC+2∠APC=180°③∠CAB=2∠CPB④S△PAC=S△MAP+S△NCP．A．1个B．2个C．3个D．4个8．如图，已知∠BAC的平分线与BC的垂直平分线相交于点D，DE⊥AB，DF⊥AC，垂足分别为E，F，AB＝6，AC＝3，则BE＝（）A．6 B．3 C．2 D．1.5二、填空题9．如图BA=BE，∠1=∠2要使△ABD≌△EBC还需添加一个条件是．（只需写出一种情况）10．如图，△ABC中，AB=AC，D是BC的中点，AC的垂直平分线分别交AC、AD、AB于点E、O、F，则图中全等的三角形的对数是．11．如图，在Rt△ABC，∠C=90°，E是AB上一点，且BE=BC，DE⊥AB于点E，若AC=8，则AD+DE的值为．12．如图，在△ABC中AB=AC，BF=CD，BD=CE，∠FDE=70°那么∠A的大小等于度．13．如图，在△ABC中，CD平分∠ACB交AB于点D，DE⊥AC交于点E，DF⊥BC于点F，且BC=4，DE=2，则△BCD的面积是．三、解答题14．如图，AD平分∠BAC，∠B=∠C.（1）求证：BD=CD；（2）若∠B=∠BDC=100°，求∠BAD的度数.15．如图，已知，EC＝AC，∠BCE＝∠DCA，∠A＝∠E.（1）求证：BC＝DC；（2）若∠A＝25°，∠D＝15°，求∠ACB的度数.16．如图，AB＝AC，AD＝AE，∠BAC＝∠DAE.（1）求证：△ABD≌△ACE；（2）若∠1＝25°，∠2＝30°，求∠3的度数.17．如图，△ABD、△AEC都是等边三角形，直线CD与直线BE交于点F．（1）求证：CD=BE；（2）求∠CFE的度数．18．如图，在△AOB和△COD中OA=OB，OC=OD，OA<OC，∠AOB=∠COD=36°连接AC、BD交于点M，连接OM．求证：（1）∠AMB=36°；（2）MO平分∠AMD．参考答案1．C2．C3．D4．B5．B6．D7．D8．D9．BD =BC 或∠A =∠E 或∠C =∠D （任填一组即可）10．411．812．4013．414．（1）证明：∵AD 平分∠BAC∴∠BAD =∠CAD .在△ABD 和△ACD 中{∠BAD =∠CAD ∠B =∠C AD =AD∴△ABD ≌△ACD(AAS)∴BD =CD .（2）解：由(1)得：△ABD ≌△ACD∴∠C =∠B =100°，∠BAD =∠CAD∵∠BAC +∠B +∠BDC +∠C =360°∴∠BAC =60°∴∠BAD =30°15．（1）证明：∵∠BCE ＝∠DCA∴∠BCE +∠ACE ＝∠DCA +∠ECA即∠BCA ＝∠DCE .在△BCA 和△DCE 中{∠BCA =∠DCE AC =EC ∠A =∠E∴△BCA ≌△DCE （ASA ）∴BC ＝DC ；（2）解：∵△BCA ≌△DCE∴∠B ＝∠D ＝15°.∵∠A ＝25°∴∠ACB ＝180°−∠A −∠B ＝140°.16．（1）证明：∵∠BAC ＝∠DAE∴∠BAC ﹣∠DAC ＝∠DAE ﹣∠DAC∴∠1＝∠EAC在△ABD 和△ACE 中{AB =AC ∠1=∠EAC AD =AE∴△ABD ≌△ACE （SAS ）（2）解：∵△ABD ≌△ACE∴∠ABD ＝∠2＝30°∵∠1＝25°∴∠3＝∠1+∠ABD ＝25°+30°＝55°.17．（1）证明：∵△ABD 、△AEC 都是等边三角形∴AD=AB ，AC=AE ，∠DAB=∠DBA=∠ADB=60°，∠CAE=60°∵∠DAB=∠DAC+∠CAB ，∠CAE=∠BAE+∠CAB∴∠DAC=∠BAE在△DAC 和△BAE 中{AD =AB ∠DAC =∠BAE AC =AE∴△DAC ≌△BAE∴CD=BE（2）解：∵△DAC ≌△BAE∴∠ADC=∠ABE∴∠CFE=∠BDF+∠DBF=∠BDF+∠DBA+∠ABF=∠BDF+∠DBA+∠ADC=∠BDA+∠DBA=60°+60°=120°18．（1）解：证明：∵∠AOB=∠COD=36°∴∠AOB+∠BOC=∠COD+∠BOC，即∠AOC=∠BOD 在△AOC和△BOD中{OA=OB ∠AOC=∠BOD OC=OD∴△AOC≌△BOD(SAS)∴∠OAC=∠OBD∵∠AEB是△AOE和△BME的外角∴∠AEB=∠AMB+∠OBD=∠AOB+∠OAC∴∠AMB=∠AOB=36°；（2）解：如图所示，作OG⊥AC于G，OH⊥BD于H∴OG是△AOC中AC边上的高，OH是△BOD中BD边上的高由（1）知：△AOC≌△BOD∴OG=OH∴点O在∠AMD的平分线上即MO平分∠AMD．。

中考数学复习《全等三角形》专项练习题-附带有答案

中考数学复习《全等三角形》专项练习题-附带有答案一、选择题1．下列选项中表示两个全等的图形的是（）A．形状相同的两个图形B．周长相等的两个图形C．面积相等的两个图形D．能够完全重合的两个图形2．如图，点D、E分别在线段AB、AC上，BE、CD相交于点O，AE＝AD，则不一定能使△ABE≌△ACD的条件是（）A．AB＝AC B．∠B＝∠CC．∠AEB＝∠ADC D．CD＝BE3．如图是用直尺和圆规作已知角的平分线的示意图，则说明∠CAD=∠DAB的依据是（）A．SAS B．ASA C．AAS D．SSS4．如图△ABC≌△DEC，点A和点D是对应顶点，点B和点E是对应顶点，过点A作AF⊥CD，垂足为点F，若∠BCE=65°，则∠CAF的度数为（）A．25°B．30°C．35°D．65°5．如图，在△ABC中，∠C＝90°，AD平分∠BAC，过点D作DE⊥AB，若BC＝7，BD＝4，则DE的长为（）A．5 B．4 C．3 D．26．如图，在△ABC中，点D在AC上，BD平分∠ABC，延长BA到点E，使得BE=BC，连接DE．若∠ADE=38°，则∠ADB的度数是（）A．68°B．69°C．71°D．72°7．如图∠ACB=90°，AC=BC，AD⊥CE，BE⊥CE，垂足分别是点D，E，若AD=3，BE=1则DE的长是（）A．2 B．5C．3 D．428．如图，∠C＝90°，AD平分∠BAC，DE⊥AB于点E，有下列结论：①CD＝ED；②AC+BE＝AB；③DA平分∠CDE；④∠BDE＝∠BAC；⑤S△ABD：S△ACD＝AB：AC．其中结论正确的个数有（）A．5个B．4个C．3个D．2个二、填空题9．如图，已知OB=OC，若以“SAS”为依据证明△AOB≌△DOC，还需要添加的条件是．10．如图，在△ABC中，已知AD=DE，AB=BE，∠A=80°，则∠CED=度．11．如图，已知△ABC中BD、CE分别是∠ABC、∠ACB的平分线，BD、CE交于点O，∠A=70°则∠BOE=．12．如图，已知∠B=∠C=90°，M是BC的中点，DM平分∠ADC，∠DAM=35°则∠MAB等于．13．如图∠ACB=90°，AC=BC，AD⊥CE于点D，BE⊥CE于点E.若AD=2.5cm，DE=1.7cm则BE= cm．三、解答题14．如图，AB＝CD，DE⊥AC，BF⊥AC，点E，F是垂足，AE＝CF，求证：（1）△ABF≌△CDE；（2）AB∥CD.15．如图，在Rt△ABC中，∠C＝90°，AD平分∠CAB交BC于点D，DE⊥AB于点E，且E为AB的中点．（1）求证：△ADE≌△BDE；（2）求∠B的度数．16．如图∠A=∠B，AE=BE点D在AC边上∠CED=∠AEB，AE交BD于点F.（1）求证：△AEC≌△BED；（2）求证：DE平分∠BDC.17．如图，已知△ABC，△ADE都是等腰直角三角形，连接BD，CE.（1）求证：△BAD≌△CAE；（2）若延长BD交CE于点F，试判断BF与CE的位置关系，并说明理由.18．如图，△ABC在平面直角坐标系中的位置如图，其中点A(0，a)，点B(b，0)分别在x轴和y轴上，且a和b满足：|a−1|+(b+3)2=0，若点C在第四象限∠BAC=90°，且AB=AC．（1）请直接写出点A和点B的坐标；（2）求点C的坐标；（3）若AC交x轴于M，BC交y轴于D，E是线段AC上一点，且CE=AM，连DE，求证：AD+DE=BM．参考答案1．D2．D3．D4．A5．C6．C7．A8．A9．OA=OD10．10011．55°12．35°13．0.814．（1）证明：∵AE＝CF∴AE+EF＝CF+EF，即AF＝CE又∵BF⊥AC，DE⊥AC∴∠AFB＝∠CED＝90°在Rt△ABF与Rt△CDE中∴Rt△ABF≌Rt△CDE（HL）（2）证明：∵Rt△ABF≌Rt△CDE∴∠C＝∠A∴AB∥CD15．（1）证明：∵DE⊥AB ∴∠AED＝∠BED＝90°∵E为AB的中点∴AE＝BE在△AED和△BED中{AE=BE∠AED=∠BEDDE=DE∴△AED≌△BED（SAS）（2）解：∵△AED≌△BED∴∠B＝∠DAE∵AD平分∠CAB∴∠CAD＝∠DAE∵∠C=90°∴∠B+∠CAD+∠DAE＝90°∴3∠B＝90°∴∠B＝30°．16．（1）证明：∵∠CED=∠AEB∴∠CED+∠AED=∠AEB+∠AED∴∴∠AEC=∠BED在△AEC和△BED中{∠A=∠BAE=BE ∠AEC=∠BED∴△AEC≌△BED（2）证明：∵△AEC≌△BED∴∠C=∠BDE，CE=DE∴∠C=∠EDC∴∠BDE=∠EDC∴DE平分∠BDC17．（1）证明：∵△ABC，△ADE都是等腰直角三角形∴AB=AC，∠BAC=∠DAE=90°，AD=AE∴∠BAC−∠DAC=∠DAE−∠DAC即∠BAD=∠CAE在△BAD和△CAE中∵AB=AC，∠BAD=∠CAE，AD=AE∴△BAD≌△CAE(SAS)（2）解：BF⊥CE，理由如下：如图，设AC与BF交于点G∵△BAD≌△CAE∴∠ABD=∠ACE∵∠AGB=∠CGF∴∠BFC=∠BAC=90°∴BF⊥CE.18．（1）A(0，1)（2）解：如图1，过A作MN⊥BM于M，MN⊥CN于N∴∠M=∠N=90°∵∠BAC=90°∴∠MAB+∠ABM=90°=∠MAB+∠CAN∴∠ABM=∠CAN∵∠M=∠N=90°，∠ABM=∠CAN，AB=AC∴△ABM≌△CAN(AAS)∴AN=BM=1，CN=AM=3∴C(1，−2)；（3）证明：如图2，过C作CF⊥AC，交y轴于F∴∠BAM=∠ACF=90°∵∠BAC=90°∴∠ABM+∠BAO=90°=∠CAF+∠BAO∴∠ABM=∠CAF∵∠BAM=∠ACF=90°，∠ABM=∠CAF，AB=AC ∴△ABM≌△CAF(AAS)∴AF=BM，AM=CF=CE∵∠BAC=90°，且AB=AC．∴∠ACB=45°=∠DCF∵CF=CE，∠ACB=∠DCF，CD=CD∴△CDF≌△CDE(SAS)∴DF=DE∴BM=AF=AD+DF=AD+DE∴AD+DE=BM．。

全等三角形测试题及答案

全等三角形测试题及答案一、选择题1. 下列选项中，哪两个三角形是全等的？A. ∠A=∠B，AB=BCB. ∠A=∠B，AC=BDC. ∠A=∠C，AB=ACD. ∠A=∠B，AB=BC，AC=BD2. 如果两个三角形的对应边成比例，且夹角相等，这两个三角形是：A. 相似但不全等B. 必然全等C. 不一定全等D. 无法判断二、填空题3. 根据全等三角形的性质，如果两个三角形的对应角相等，且对应边成比例，那么这两个三角形是_________。

4. SAS全等条件指的是_________。

三、判断题5. 如果两个三角形的三边对应相等，那么这两个三角形一定全等。

（）6. 根据HL全等条件，直角三角形中，如果斜边和一条直角边对应相等，那么这两个直角三角形全等。

（）四、解答题7. 已知三角形ABC和三角形DEF，其中∠A=∠D=90°，AB=DE，AC=DF，求证：三角形ABC全等于三角形DEF。

8. 如图所示，三角形ABC和三角形DEF在平面直角坐标系中，点A(2,3)，B(4,5)，C(1,1)，点D(-1,-2)，E(1,-1)，F(-2,-4)。

若AB=DE，AC=DF，∠BAC=∠EDF，请证明三角形ABC全等于三角形DEF。

五、综合题9. 在三角形ABC中，点D在BC上，若AD平分∠BAC，且BD=DC，求证：AB=AC。

10. 已知三角形ABC和三角形DEF，其中AB=DE，∠B=∠D，∠C=∠E，求证：三角形ABC全等于三角形DEF。

答案：一、选择题1. 答案：D2. 答案：A二、填空题3. 答案：相似4. 答案：边角边三、判断题5. 答案：正确6. 答案：正确四、解答题7. 解：由于∠A=∠D=90°，AB=DE，AC=DF，根据直角三角形的HL全等条件，我们可以得出三角形ABC全等于三角形DEF。

8. 解：由于AB=DE，AC=DF，∠BAC=∠EDF，根据SAS全等条件，我们可以得出三角形ABC全等于三角形DEF。

人教版数学八年级上册【全等三角形】基础测试题+答案

数学八年级上册【全等三角形】基础测试题+答案
基础巩固
1．下列说法中，不正确的是( )． A．形状相同的两个图形是全等形 B．大小不同的两个图形不是全等形 C．形状、大小都相同的两个三角形是全等三角形 D．能够完全ABD≌△BAC，B，C 和 A，D 分别是对应顶点，如果 AB＝4 cm， BD＝3 cm，AD＝5 cm，那么 BC 的长是( )．
A．5 cm B．4 cm C．3 cm D．无法确定
3．如图所示，△ABC≌△ADC，∠ABC＝70°，则∠ADC 的度数是( )
A．70°B．45° C．30° D．35° 4．如图所示，△ABC 与△DBE 是全等三角形，即△ABC≌△DBE，那么图中相等的角有( )
A．1 对 B．2 对 C．3 对 D．4 对 5．如图所示，△ABC 与△DEF 是全等三角形，即△ABC≌△DEF，图中相等的线段有( )．
4．D 点拨：因为△ABC≌△DBE，根据全等三角形的对应角相等，得∠A＝∠D，∠C ＝∠E，∠ABC＝∠DBE. 又由∠ABC＝∠DBE，得∠ABC－∠DBC＝∠DBE－∠DBC，即∠ABD＝∠CBE. 5．D 点拨：由全等三角形的对应边相等得三组对应边相等，即 AB＝DE，AC＝DF，BC＝EF. 又由 BC＝EF，得 BC－CF＝EF－CF，即 BF＝EC.
参考答案
1．A 点拨：选项 A 中，形状相同的两个图形，大小不一定相同，所以不一定是全等形．选项 B、C、D 均正确，只要两个图形形状、大小相同，放在一起能够完全重合，它们一定是全等形．全等三角形是全等形的特殊情形． 2．A 点拨：因为△ABD≌△BAC，所以 BC＝AD＝5 cm. 3．A 点拨：因为△ABC≌△ADC，所以∠ADC＝∠ABC＝70°.

第12章全等三角形(单元测试基础卷)(学生版)2024-2025学年八年级数学上册基础知识专项突破

第12章全等三角形（单元测试·基础卷）一、单选题（本大题共10小题，每小题3分，共30分）1．如图，已知ABC A BC ''≌ ，A C BC '' ，20C ∠=︒，则ABA '∠的度数是（）A ．15︒B ．20︒C ．25︒D ．30︒2．如图，小明书上的三角形被墨迹污染了一部分，很快他就根据所学知识画出一个与书上完全一样的三角形．他的依据是（）A ．SASB ．ASAC ．HLD ．SSS3．如图，点P 是BAC ∠平分线AD 上的一点，7AC =，3AB =，2PB =，则PC 的长不可能是（）A ．6B ．5C ．4D ．34．如图，CD AB ⊥于点D ，EF AB ⊥于点F ，AC BE =．证明Rt Rt ACD BEF ≌ 不是利用“HL ”的条件是（）A ．AD BF =B ．AC BE ∥C ．CD EF =D ．AF BD=5．如图，已知AB CD =．若添加一个条件后，可得ABC CDA △△≌，则在下列条件中，可以添加的是（）A ．B D∠=∠B ．AD BC ∥C ．AB CD D ．AC 平分BCD∠6．如图所示，在ABC 中，AC BC =，AE CD =，AE CE ⊥于点E ，BD CD ⊥于点D ，7AE =，2BD =，则DE 的长是()A ．7B ．5C ．3D ．27．如图，在Rt ABC △中，90C = ∠，以顶点A 为圆心，适当长为半径画弧，分别交AC ，AB 于点M ，N ，再分别以点M ，N 为圆心，大于12MN 的长为半径画弧，两弧交于点P ，作射线AP 交边BC 于点D ，若1CD =，4AB =，则ABD △的面积是（）A ．2B ．32C ．3D ．728．如图，由9个完全相同的小正方形拼接而成的33⨯网格，图形ABCD 中各个顶点均为格点，设ABC α∠=，BCD β∠=，BAD γ∠=，则αβγ--的值为（）A ．30︒B ．45︒C ．60︒D ．75︒9．如图，在平面直角坐标系中，点()0,2A 处有一激光发射器，激光照射到点()1,0B 处倾斜的平面镜上发生反射，使得反射光线照射到点C 处的接收器上，若入射角45α=︒，AB BC =，则点C 处的接收器到y 轴的距离为（）A ．1B ．2C ．3D ．410．如图，已知AC 平分DAB ∠，CE AB ⊥于E ，2AB AD BE =+，则下列结论①()12E A A A B D =+；②180DAB DCB ∠+∠=︒；③CD CB =；④ACE BCE ACD S S S -= ．其中，正确结论的个数（）A ．1个B ．2个C ．3个D ．4个二、填空题（本大题共8小题，每小题4分，共32分）11．如图，点A 、B 、C 、D 在同一条直线上，AB =CD ，AE =DF ，CE =BF ．若∠A =55°，∠E =84°，则∠DBF 的大小为12．如图，D ，E 是ABC 外两点，连接AD AE ，，有AB AD AC AE ==，，40BAD CAE ∠=∠=︒．连接CD，BE 交于点F ，则DFE ∠的度数为．13．如图，AB CF ，E 为DF 的中点，若7cm AB =，5cm CF =，则BD =cm ．14．如图，在ABC 中，CP 平分ACB ∠，AP CP ⊥于点P ，已知ABC 的面积为2，则阴影部分的面积为．15．如图，()()4,0,0,6A B ，以B 点为直角顶点在第一象限作等腰直角ABC ∆，则C 点的坐标为16．如图，在ABC ∆中，AB AC =．点D 为ABC ∆外一点，AE BD ⊥于E ．BDC BAC ∠=∠，3DE =，2CD =，则BE 的长为．17．如图，在四边形ABCD 中，E 是边BC 的中点，AE 平分BAD ∠，且90AED ∠︒＝，若2CD AB ＝，四边形ABCD 的周长为18，5BC =，则AB 的值为．18．如图，操场上有两根旗杆相距12m ，小强同学从B 点沿BA 走向A ，一定时间后他到达M 点，此时他测得CM 和DM 的夹角为90︒，且CM DM =，已知旗杆AC 的高为3m ，小强同学行走的速度为0.5m/s ．（1）另一旗杆BD 的高度为m ；（2）小强从M 点到达A 点还需要的时间是s ．三、解答题（本大题共6小题，共58分）19．（8分）如图，在ABC 中，90C ∠=︒，AD AC =，DE CE =，试猜想ED 与AB 的位置关系，并说明理由．20．（8分）如图，在ABC 中，AC BC =，直线l 经过顶点C ，过A ，B 两点分别作l 的垂线AE BF ，，E ，F 为垂足，且AE CF =；求证：(1)EAC FCB∠=∠(2)AC BC ⊥．21．（10分）如图，在ABC 中，90C ∠=︒，AD 是CAB ∠的角平分线，DE AB ⊥于E ，点F 在边AC 上，连接DF ．且DF DB =．（1）求证：CFD EBD ≌△△；（2）若40BAC ∠︒=，求AFD ∠的度数；22．（10分）如图，在ABC 中，90ACB ∠=︒，CD AB ⊥于点D ，BE 平分ABC ∠交AC 于点E ，交CD 于点F ，过点E 作EG CD ∥，交AB 于点G ，连接CG ．（1）求证：90A AEG ∠+∠=︒；（2）求证：EC EG =；23．（10分）（1）【模型建立】如图1，在Rt ABC △与Rt ADE △中，AB AC =，AD AE =，90BAC DAE ︒∠=∠=，求证：AEC ADB △≌△；（2）【模型应用】如图2，在ABC 与ADE V 中，AB AC =，AD AE =，90BAC DAE ︒∠=∠=，B D E 、、三点在一条直线上，AC 与BE 交于点F ，若点F 为AC 中点，①求BEC ∠的度数；②3CE =，求AEF △的面积；24．（12分）【阅读理解】定义：在同一平面内，点A ，B 分别在射线PM ，PN 上，过点A 垂直PM 的直线与过点B 垂直PN 的直线交于点Q ，则我们把AQB ∠称为APB ∠的“边垂角”．【迁移运用】（1）如图1，CD ，BE 分别是ABC 的两条高，两条高交于点F ，根据定义，我们知道DBE ∠是DCE ∠的“边垂角”或DCE ∠是DBE ∠的“边垂角”，DAE ∠的“边垂角”是______；（2）若AQB ∠是APB ∠的“边垂角”，则AQB ∠与APB ∠的数量关系是______；（3）若ACD ∠是ABD ∠的“边垂角”，且AB AC =．如图2，BD 交AC 于点E ，点C 关于直线BD 对称点为点F ，连接AF ，EF ，且45CAF ∠=︒，求证：BE CF CE =+．。

全等三角形判定基础练习(有答案)

全等三角形判定基础练习（有答案）一．选择题（共3小题）1．如图，已知AD=AE，添加下列条件仍无法证明△ABE≌△ACD的是（）A．AB=AC B．∠ADC=∠AEB C．∠B=∠C D．BE=CD2．判定两个三角形全等，给出如下四组条件：①两边和一角对应相等；②两角和一边对应相等；③两个直角三角形中斜边和一条直角边对应相等；④三个角对应相等；其中能判定这两个三角形全等的条件是（）A．①和②B．①和④C．②和③D．③和④3．如图，下列各组条件中，不能得到△ABC≌△BAD的是（）A．BC=AD，∠ABC=∠BAD B．BC=AD，AC=BDC．AC=BD，∠CAB=∠DBA D．BC=AD，∠CAB=∠DBA二．解答题（共6小题）4．如图，AB=CB，BE=BF，∠1=∠2，证明：△ABE≌△CBF．5．如图所示，有两个直角三角形△ABC和△QPA按如图位置摆放C，P，A在同一条直线上，并且BC=PA．当QP与AB垂直时，△ABC能和△QPA全等吗，请说明理由．6．如图，BE⊥AC于E，CF⊥AB于F，CF、BE相交于点D，且BD=CD．求证：AD平分∠BAC．7．如图，在直角三角形ABC中，∠ABC=90°，点D在BC的延长线上，且BD=AB，过B作BE⊥AC，与BD的垂线DE交于点E．求证：△ABC≌△BDE．8．如图，在△ABC中，AB=AC，点D、E在BC上，且BD=CE．求证：△ABE≌△ACD．9．如图，已知点D在AB上，点E在AC上，BE和CD相交于点O，AB=AC，∠B=∠C．求证：△ABE≌△ACD．全等三角形判定（孙雨欣）初中数学组卷参考答案与试题解析一．选择题（共3小题）1．如图，已知AD=AE，添加下列条件仍无法证明△ABE≌△ACD的是（）A．AB=AC B．∠ADC=∠AEB C．∠B=∠C D．BE=CD【分析】全等三角形的判定定理有SAS，ASA，AAS，SSS，看看条件是否符合判定定理即可．【解答】解：A、∵在△ABE和△ACD中，，∴△ABE≌△ACD（SAS），正确，故本选项错误；B、∵在△ABE和△ACD中，，∴△ABE≌△ACD（ASA），正确，故本选项错误；C、∵在△ABE和△ACD中，，∴△ABE≌△ACD（AAS），正确，故本选项错误；D、根据AE=AD，BE=CD和∠A=∠A不能推出△ABE和△ACD全等，错误，故本选项正确；故选D．【点评】本题考查了对全等三角形的判定定理的应用，注意：全等三角形的判定定理有SAS，ASA，AAS，SSS．2．判定两个三角形全等，给出如下四组条件：①两边和一角对应相等；②两角和一边对应相等；③两个直角三角形中斜边和一条直角边对应相等；④三个角对应相等；其中能判定这两个三角形全等的条件是（）A．①和②B．①和④C．②和③D．③和④【分析】认真分析各选项提供的已知条件，结合全等三角形判定方法对选项提供的已知条件逐一判断．【解答】解：①两边和一角对应相等不正确，应该是两边的夹角，故本选项错误，②两角和一边对应相等，符合AAS，故本选项正确，③两个直角三角形中斜边和一条直角边对应相等，符合SAS，故本选项正确，④三个角对应相等，可以相似不全等，故本选项错误，故选C．【点评】本题主要考查了对全等三角形的判定方法的理解及运用．常用的判定方法有AAS，SSS，SAS 等，难度适中．3．如图，下列各组条件中，不能得到△ABC≌△BAD的是（）A．BC=AD，∠ABC=∠BAD B．BC=AD，AC=BDC．AC=BD，∠CAB=∠DBA D．BC=AD，∠CAB=∠DBA【分析】根据图形可得公共边AB=AB，再加上选项所给条件，利用判定定理SSS、SAS、ASA、AAS分别进行分析即可．【解答】解：根据图形可得公共边：AB=AB，A、BC=AD，∠ABC=∠BAD可利用SAS证明△ABC≌△BAD，故此选项不合题意；B、BC=AD，AC=BD可利用SSS证明△ABC≌△BAD，故此选项不合题意；C、AC=BD，∠CAB=∠DBA可利用SAS证明△ABC≌△BAD，故此选项不合题意；D、BC=AD，∠CAB=∠DBA不能证明△ABC≌△BAD，故此选项符合题意；故选：D．【点评】本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．二．解答题（共7小题）4．如图，AB=CB，BE=BF，∠1=∠2，证明：△ABE≌△CBF．【分析】利用∠1=∠2，即可得出∠ABE=∠CBF，再利用全等三角形的判定SAS得出即可．【解答】证明：∵∠1=∠2，∴∠1+∠FBE=∠2+∠FBE，即∠ABE=∠CBF，在△ABE与△CBF中，，∴△ABE≌△CBF（SAS）．【点评】本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．5．如图所示，有两个直角三角形△ABC和△QPA按如图位置摆放C，P，A在同一条直线上，并且BC=PA．当QP与AB垂直时，△ABC能和△QPA全等吗，请说明理由．【分析】首先根据∠QAP=90°，AB⊥PQ可证出∠PQA=∠BAC，在加上条件BC=AP，∠C=∠QAP=90°，可利用AAS定理证明△ABC和△QPA全等．【解答】△ABC能和△QPA全等；证明：∵∠QAP=90°，∴∠PQA+∠QPA=90°，∵QP⊥AB，∴∠BAC+∠APQ=90°，∴∠PQA=∠BAC，在△ABC和△QPA中，，∴△ABC≌△QPA（AAS）．【点评】本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．6．如图，BE⊥AC于E，CF⊥AB于F，CF、BE相交于点D，且BD=CD．求证：AD平分∠BAC．【分析】要证AD平分∠BAC，只需证DF=DE．可通过证△BDF≌△CDE（AAS）来实现．根据已知条件，利用AAS可直接证明△BDF≌△CDE，从而可得出AD平分∠BAC．【解答】证明：∵BE⊥AC，CF⊥AB，∴∠BFD=∠CED=90°．在△BDF与△CDE中，，∴Rt△BDF≌Rt△CDE（AAS）．∴DF=DE，∴AD是∠BAC的平分线．【点评】本题考查了全等三角形的判定和性质，以及到角两边距离相等的点在角平分线上等知识．发现并利用△BDF≌△CDE是正确解答本题的关键．7．如图AB，CD相交于点O，AD=CB，AB⊥DA，CD⊥CB，求证：△ABD≌△CDB．【分析】首先根据AB⊥DA，CD⊥CB，可得∠A=∠C=90°，再利用HL定理证明Rt△ABD≌Rt△CBD即可．【解答】证明：∵AB⊥DA，CD⊥CB，∴∠A=∠C=90°，在Rt△ABD和Rt△CBD中，∴Rt△ABD≌Rt△CBD（HL）．【点评】本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．8．如图，在△ABC中，AB=AC，点D、E在BC上，且BD=CE．求证：△ABE≌△ACD．【分析】由AB=AC可得∠B=∠C，然后根据BD=CE可证BE=CD，根据SAS即可判定三角形的全等．【解答】证明∵AB=AC，∴∠B=∠C，∵BD=EC，∴BE=CD，在△ABE与△ACD中，，∴△ABE≌△ACD（SAS）．【点评】本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．9．如图，已知点D在AB上，点E在AC上，BE和CD相交于点O，AB=AC，∠B=∠C．求证：△ABE≌△ACD．【分析】根据全等三角形的判定定理ASA推出即可．【解答】证明：∵在△ABE和△ACD中，∴△ABE≌△ACD（ASA）．【点评】本题考查了全等三角形的判定定理的应用，注意：全等三角形的判定定理有SAS，ASA，AAS，SSS．10．如图，在直角三角形ABC中，∠ABC=90°，点D在BC的延长线上，且BD=AB，过B作BE⊥AC，与BD的垂线DE交于点E．求证：△ABC≌△BDE．【分析】利用已知得出∠A=∠DBE，进而利用ASA得出△ABC≌△BDE即可．【解答】证明：在Rt△ABC中，∵∠ABC=90°，∴∠ABE+∠DBE=90°，∵BE⊥AC，∴∠ABE+∠A=90°，∴∠A=∠DBE，∵DE是BD的垂线，∴∠D=90°，在△ABC和△BDE中，∵，∴△ABC≌△BDE（ASA）．【点评】此题主要考查了全等三角形的判定，三角形内角和定理的应用，正确发现图形中等量关系∠A=∠DBE是解题关键．。

八年级数学上册《全等三角形》专项测试卷及答案-人教版

八年级数学上册《全等三角形》专项测试卷及答案-人教版（考试时间：60分钟总分：100分）一、选择题（共8题，共40分）1.如图是两个全等三角形，则∠1的度数为( )A．48∘B．60∘C．62∘D．72∘2.如图，AD⊥BC，D为BC的中点，其中错误的结论是( )A．△ABD≌△ACD B．∠B=∠CC．AD平分∠BAC D．△ABC是等边三角形3.如图，在四边形ABCD中AB=AD，∠B+∠ADC=180∘，E，F分别是边BC，CD延∠BAD，若DF=1，BE=5则线段EF的长为( )长线上的点∠EAF=12A．3B．4C．5D．64.如图，点C是AB的中点，且AD=BE，CD=CE，则图中全等三角形共有( )A．2对B．3对C．4对D．5对5．如图，在△ABC中，AB＝3BC，BD平分∠ABC交AC于点D，若△ABD的面积为S1，△BCD的面积为S2，则关于S1与S2之间的数量关系，下列说法正确的是（）A．S1＝4S2B．S1＝3S2C．S1＝2S2D．S1＝S2 6．根据下列已知条件，能画出惟一的△ABC的是（）A．AB=3cm，BC=7cm，AC=4cmB．AB=3cm，BC=7cm，∠C=40°C．∠A=30°，AB=3cm，∠B=100°D．∠A=30°，∠B=100°，∠C=50°7．如图所示，DE⊥AB，DF⊥AC，AE＝AF，则下列结论成立的是（）A．BD＝CD B．DE＝DF C．∠B＝∠C D．AB＝AC 8．如图，已知△ABC中，AD=BD，AC=4，H是高AD和BE的交点，则线段BH的长度为（）A．√6B．4C．2 √3D．5二、填空题（共5题，共15分）9.如图，OB平分∠MON，A为OB的中点，AE⊥ON于点E，AE=4，D为OM上一点，BC∥OM交DA于点C，则CD的最小值为．10.如图所示AB=AC，AD=AE，∠BAC=∠DAE，∠1=22∘，∠2=34∘则∠3=．11.如图，△ABC和△DCE都是等腰直角三角形∠ACB=∠ECD=90∘，∠EBD=42∘则∠AEB=．12.如图，OC为∠AOB的平分线CM⊥OB，OC=5，OM=4则点C到射线OA的距离为．13.如图，四边形ABCD中∠ABC=∠ACD=90∘，AC=CD，BC=4cm，则△BCD的面积为cm2．三、解答题（共3题，共45分）14.如图，在平行四边形ABCD中，E，F分别是AB，DC边上的点，且AE=CF(1) 求证：△ADE≌△CBF．(2) 若∠DEB=90∘，求证四边形DEBF是矩形．15.如图，点B，C，E，F在同一条直线上∠B=∠E，AC∥DF，AB=DE．(1) 求证：AC=DF．(2) 若AM，DN分别是△ABC和△DEF的角平分线，求证：AM=DN．16.如图，在△ABC中∠A=90∘，AB=AC，BD平分∠ABC，CE⊥BD交BD的延长线于E，若CE=5cm，求BD的长．参考答案1. 【答案】D2. 【答案】D3. 【答案】B4. 【答案】C5．【答案】B6．【答案】C7．【答案】B8．【答案】D9. 【答案】810. 【答案】56°11. 【答案】132°12. 【答案】313. 【答案】 814. 【答案】(1) ∵ 四边形 ABCD 是平行四边形∴AD =CB ，∠A =∠C在 △ADE 和 △CBF 中{AD =CB,∠A =∠C,AE =CF,∴△ADE ≌△CBF （SAS ）．(2) ∵ 四边形 ABCD 是平行四边形∴AB =CD ，AB ∥CD∵AE =CF∴BE =DF∴ 四边形 DEBF 是平行四边形∵∠DEB =90∘∴ 四边形 DEBF 是矩形．15. 【答案】(1) ∵AC ∥DF∴∠ACB =∠DFE在 △ABC 和 △DEF 中{∠B =∠E,∠ACB =∠DFE,AB =DE,∴△ABC ≌△DEF∴AC =DF ．(2) 由（1）可知 △ABC ≌△DEF∴∠CAB =∠FDE又 ∵AM ，DN 分别是 △ABC 和 △DEF 的角平分线 ∴∠CAM =12∠CAB =12∠FDE =∠FDN又 ∵∠ACB =∠DFE ，AC =DF∴△AMC ≌△DNF∴AM =DN ．16. 【答案】延长 CE 与 BA 延长线交于点 F ． ∵∠BAC =90∘，CE ⊥BD∴∠BAC =∠DEC∵∠ADB =∠CDE∴∠ABD =∠DCE在 △BAD 和 △CAF 中 {∠BAD =∠CAF,AB =AC,∠ABD =∠DCE,∴△BAD ≌△CAF (ASA )∴BD =CF∵BD 平分 ∠ABC ，CE ⊥DB∴∠FBE =∠CBE在 △BEF 和 △BEC 中{∠FBE =∠CBE,∠BEF =∠BEC,BE =BE,∴△BEF ≌△BEC (AAS )∴CE=EF∴DB=2CE=10cm．。

初中数学：《全等三角形》测试题(含答案)

初中数学：《全等三角形》测试题(含答案)初中数学：全等三角形测试题一、选择题（共7小题，每小题3分，满分21分）1.如图，△ABC≌△DEC，∠A=70°，∠ACB=60°，则∠E的度数为（）A。

70°B。

50°C。

60°D。

30°2.如图，已知△ABC≌△DAE，BC=2，DE=5，则CE的长为（）A。

2B。

2.5C。

3D。

3.53.XXX不小心把一块三角形形状的玻璃打碎成了三块，如图①②③，他想要到玻璃店去配一块大小形状完全一样的玻璃，你认为应带（）A。

①B。

②C。

③D。

①和②4.如图，Rt△ABC，∠C=90°，AD平分∠CAB，DE⊥XXX于E，则下列结论中不正确的是（）A。

BD+ED=BCB。

DE平分∠ADBCC。

AD平分∠EDCD。

ED+AC＞AD5.如图，已知△ABC≌△EDF，点F，A，D在同一条直线上，AD是∠BAC的平分线，∠EDA=20°，∠F=60°，则∠DAC的度数是（）A。

50°B。

60°C。

100°D。

120°6.如图，射线OC是∠AOB的角平分线，P是射线OA上一点，DP⊥OA，DP=5，若点Q是射线OB上一个动点，则线段DQ长度的范围是（）A。

DQ＞5B。

DQ＜5C。

DQ≥5D。

DQ≤57.如图，在方格纸中，以AB为一边作△ABP，使之与△ABC全等，从P1，P2，P3，P4四个点中找出符合条件的点P，则点P有（）A。

1个B。

2个C。

3个D。

4个二、填空题（共6小题，每小题3分，满分18分）8.如图：在△ABC和△FED中，AD=FC，AB=FE，当添加条件BC=ED或∠A=∠F或AB∥EF时，就可得到△ABC≌△FED．（只需填写一个即可）9.如图，把两根钢条AA′、BB′的中点连在一起，可以做成一个测量工件内槽宽的工具（卡钳），若测得AB=5米，则槽宽为5米．10.在Rt△ABC中，∠C=90°，AD平分∠BAC交BC于D，若BC=15，且BD：DC=3：2，则D到边AB的距离是6．11.如图，已知△ABE≌△ACF，∠XXX∠F=90°，∠CMD=70°，则∠2=20度．12.如图，OP平分∠MON，PE⊥OM于E，PF⊥ON于F，OA=OB，则图中有3对全等三角形．故选：C．点评】本题考查的是全等三角形的性质，需要掌握全等三角形的对应边相等和对应角相等的知识．3．如图，已知△ABC≌△DEF，AB=3，BC=4，则EF的长为（）A．3.6B．4C．4.8D．6考点】全等三角形的性质．分析】根据全等三角形的性质求出DE=3，AC=4，进而得出EF的长．解答】解：∵△ABC≌△DEF。

七年级全等三角形测试题八套

全等三角形测试题一1.下图中全等的三角形是（）A.Ⅰ和ⅡB.Ⅱ和ⅣC.Ⅱ和ⅢD.Ⅰ和Ⅲ2.在△ABC和△A'B'C'中, 要使△ABC≌△A'B'C' , 需满足条件（）A.AB=A'B', AC=A'C', ∠B=∠B'B.AB =A'B', BC=B'C', ∠A=∠A'C.AC=A'C', BC=B'C', ∠C=∠C'D.AC=A'C', BC=B'C', ∠C=∠B'3.如图，AB∥CD，AC∥DB，AD与BC交于0，AE⊥BC．于E，DF⊥BC于F，那么图中全等的三角形有( )对A．5 B．6 C．7 D．84.如图，在△ABC中，AC=BC，∠ACB=90°．AD平分∠BAC，BE⊥AD交AC的延长线于F，E为垂足．则结论：①AD=BF；②CF=CD；③AC+CD=AB；④BE=CF；⑤BF=2BE，其中正确结论的个数是( ) A．1 B.2 C．3 D．45.如图,△ABD≌△ACE,则AB的对应边是_________,∠BAD的对应角是______．6.已知:如图,△ABE≌△ACD,∠B=∠C,则∠AEB=_______,AE=__ ______．7.如图，0A=0B，OC=OD，∠O=60°,∠C=25°,则∠BED等于8.在△ABC中，高AD和BE交于H点，且BH=AC，则∠ABC=9.如图，已知AE平分∠BAC，BE上AE于E，ED∥AC，∠BAE=36°，那么∠BED=10.如图，把△ABC绕点C顺时针旋转35度，得到△A′B′C, A′B′交AC乎点D，已知∠A′DC=90°，求∠A的度数11.已知：如图AB=CD,AD=BC 求证：AD∥BC.12.已知：如图, E, B, F, C四点在同一直线上, ∠A=∠D=90°, BE=FC, AB=DF．求证：∠E=∠C13.如图, AB BC于B , AD DC于D , 且CB=CD , AC , BD相交于O．求证：∠ABD=∠ADB14.已知：如图, AE , FC都垂直于BD , 垂足为E、F , AD=BC , BE=DF．求证：OA=OC.15.已知：如图, AB=CD , D、B到AC的距离DE=BF．求证：AB∥CD．16.已知：如图，∠A=∠D=90°，AC，BD交于O，AC=BD.求证：OB=OC．全等三角形测试题二1.如图，已知AB=AD，要使△ABC≌△ADC，可增加条件，理由是定理。

初中数学全等三角形常见题型训练基础测试卷

初中数学全等三角形常见题型训练基础测试卷一、单选题 (共 4 道，每道 25 分 )1.如图，在AB、 AC 上各取一点D、 E，使得AE=AD，连接CD、 BE 相交于点O，再连接AO．若∠ CAO=∠ BAO，则图中全等三角形共有（）A.3 对C.5 对B.4 对D.6 对2.如图 ,已知点 E 在△ ABC 地外部 ,点 D 在 BC 边上 ,DE 交 AC 于 F,若∠ 1=∠ 2=∠ 3,AC=AE.求证: △ABC≌△ ADE.证明 :∵∠ 1=∠2=∠ 3∴∠ 1+∠ DAC=∠ 2+∠ DAC即∠ BAC=∠ DAE又∵∠ 3=∠ B+,∠2=∠ B+∴∠ E=∠C在△ ABC和△ ADE中∴① ∠DAC,② ∠ E, ③∠ C, ④, ⑤, ⑥ △ABC≌△ ADE(ASA), ⑦△ ABC≌△ ADE(AAS),以上空缺处依次填写正确地顺序为()A. ①②⑤⑦B.②③⑤⑦C. ①③④⑥D.②③④⑥3. 如图 , 四边形 ABCD 为正方形 ,∠ ABE=∠ DCE=90°,AB=BC=CD=AD,E为BC 边上一点 , 且AE=DE,AE与对角线 BD 交于点 F,∠ ABF=∠ CBF,连接 CF,交 ED 于点 G.判断 CF 与 ED 地位置关系,并说明理由 .解: 垂直 .理由如下 :在△ ABF与△ CBF中∴∴∠ BAF=∠BCF在 Rt△ ABE和 Rt△ DCE中∴∴∠ BAE=∠ CDE∴∠ BCF=∠ CDE∵∠ CDE+∠ DEC=90°∴∠ BCF+∠ DEC=90°∴DE⊥CF①,②,③,④, ⑤ Rt△ ABE≌ Rt△ DCE(HL), ⑥△ ABE≌△ DCE(SAS), ⑦△ ABF≌△ C BF(SAS), ⑧△ ABF≌△ CBF(SSS),以上空缺处依次填写正确地顺序为()A. ①⑦④⑥B.②⑧③⑤C. ①⑦③⑤D.②⑧④⑥4.如图 ,四边形 ABCD中 ,AB=CD,BC=AD求.证 :∠ A=∠ C.证明 :如图 ,_________________在△ ABD 和△ CDB中________________∴________________∴∠ A=∠ C(全等三角形对应角相等)①作直线BD,②连接BD,③作射线BD, ④, ⑤, ⑥ △ ABD≌△ CDB(SSS),⑦△ AB D≌△ BCD(SSS),⑧△ABD≌△ CDB(SAS),以上空缺处依次填写正确地顺序为()A. ②⑤⑥B.②⑤⑦C. ①⑤⑧D.②⑤⑧。

八年级数学全等三角形测试题

八年级数学全等三角形测试题一、选择题（每题3分，共30分）1. 下列说法正确的是（）A. 全等三角形是指形状相同的两个三角形B. 全等三角形的周长和面积分别相等C. 全等三角形是指面积相等的两个三角形D. 所有的等边三角形都是全等三角形解析：选项A：全等三角形不仅形状相同，而且大小也相同，所以A错误。

选项B：全等三角形能够完全重合，所以它们的周长和面积分别相等，B正确。

选项C：面积相等的三角形不一定全等，比如一个底为4，高为3的三角形和一个底为6，高为2的三角形面积相等，但不全等，C错误。

选项D：所有等边三角形形状相同，但大小不一定相同，所以不是所有的等边三角形都是全等三角形，D错误。

2. 如图，已知△ABC≌△DEF，∠A = 50°，∠B = 70°，则∠F的度数为（）A. 50°B. 60°C. 70°D. 80°解析：在△ABC中，根据三角形内角和为180°，可得∠C=180°∠A ∠B = 180° 50°70° = 60°。

因为△ABC≌△DEF，全等三角形对应角相等，所以∠F = ∠C = 60°，答案为B。

3. 如图，在△ABC和△DEC中，已知AB = DE，还需添加两个条件才能使△ABC≌△DEC，不能添加的一组条件是（）A. BC = EC，∠B = ∠EB. BC = EC，AC = DCC. ∠B = ∠E，∠A = ∠DD. BC = DC，∠A = ∠D解析：选项A：AB = DE，BC = EC，∠B = ∠E，根据SAS（边角边）可判定△ABC≌△DEC。

选项B：AB = DE，BC = EC，AC = DC，根据SSS（边边边）可判定△ABC≌△DEC。

选项C：AB = DE，∠B = ∠E，∠A = ∠D，根据AAS（角角边）可判定△ABC≌△DEC。

(完整版)全等三角形基础练习及答案

全等三角形判断一、选择题1. AABC^A ^S'C'中，若AB= A'B', BC=3C',AC=HC'.则（）A.AAB（C^A A'C'B 1B. AAB（^A A'B'C'1. AABCC2A C'A1 B' D. AABCC2A C'B'A'2.如图，已知AB= CDD AD= BG则下列结论中错误的是（）A.AB/I DCB. ZB= Z DC. / A= Z CD.AB= BC3.下列判断正确的是（）A.两个等边三角形全等B.三个对应角相等的两个三角形全等C.腰长对应相等的两个等腰三角形全等D.直角三角形与锐角三角形不全等4.如图，AR CD EF相交于O,且被O点平分，D已CE, BF= AE,则图中全等三角形的对数共有（）A. 1对B. 2对C. 3对D. 4对5.如图，将两根钢条£引的中点o连在一起，使』且,，卫夕可以绕着点O自由转动，就做成了一个测量工件，则上田’的长等于内槽宽AB,那么判定△ OAB^A ◎月‘8’的理由是（）A.边角边B.角边角C.边边边D.角角边6 .如图，已知 AE^BD 于B, EDLBD 于D, AB= C 口 BC= EDD 以下结论不正确的是()二、填空题如图，AB= C 口 AC= DB, /ABD= 25° , Z AOB= 82°如图，AC= AD, CB= DB, Z 2=30° , / 3=26° ,则/ CBE=D.DC = CB7. 8. 9. 如图，在4ABC 和4EFD 中，AD= FC, BD 互相平分，则图中全等三角形共有AB= FE,当添加条件时，就可得△ AB 隼AEF[)( SSS10. 11. 如图，点 D 在AB 上，点E 在AC 上, CD 与 BE 相交于点 0,且 AD= AE, AB= AC,若/ B =20° ,则/CC.ED +AB =DB如图，在四边形ABCD43,对角线AG分析：要证AD// BG 只要证/ = 又需证叁. 证明：AB//CD (),/ _______ = / (), 在△ ______ 和△中，「 = (= _____ ( IA 色 A ()./ _____ = / ( ).// ( ) .AB= C 口 AC= BD,贝SABC^ ,AADC^三、解答题13 .已知：如图，四边形 ABCD43,对角线 AC BD 相交于 O, / ADC= Z BCDAD= BC,14 .已知：如图，AB// CD AB= CD,求证：AD// BC12.已知，如图,10.【答案】56 ;15.如图，已知 AB= DQ AC=DR BE=CE 求证：AE= DE.答案与解析一 .选择题1 .【答案】B;【解析】注意对应顶点写在相应的位置 .2 .【答案】Q【解析】连接AC 或BD 证全等.3 .【答案】Q4 .【答案】C;【解析】△ DO 四△COR ABOI^AAO^ ADOB2ACOA.5 .【答案】A;【解析】将两根钢条幺4, £3,的中点。

(必考题)初中八年级数学上册第十二章《全等三角形》基础卷(答案解析)

一、选择题1．如图，在△ABC 中，AB=AC ，AB ＞BC ，点D 在BC 边上，BD=12DC ，∠BED=∠CFD=∠BAC ，若S △ABC =30，则阴影部分的面积为（）A ．5B ．10C ．15D ．202．如图，△ACB ≌△A′C B′，∠ACB ＝70°，∠ACB′＝100°，则∠BCA′度数是（）A ．40°B ．35C ．30°D ．45° 3．下列命题的逆命题是真命题的是（）． A ．3的平方根是3B ．5是无理数C ．1的立方根是1D ．全等三角形的周长相等4．如图，在ABC 中，AB AC =，点D ，E 在BC 上，连接AD ，AE ，若只添加一个条件使DAB EAC ∠=∠，则添加的条件不能为（）A ．BD CE =B ．AD AE =C ．BE CD = D ．DA DE = 5．下列四个命题中，真命题是（）A ．如果 ab ＝0，那么a ＝0B ．面积相等的三角形是全等三角形C ．直角三角形的两个锐角互余D ．不是对顶角的两个角不相等6．如图，ABC 的面积为26cm ，AP 垂直B 的平分线BP 于P ，则PBC 的面积为（）A ．21cmB ．22cmC ．23cmD ．24cm 7．下列说法正确的是（）①近似数232.610⨯精确到十分位；②在2，()2--，38-，2--中，最小的是38-；③如图所示，在数轴上点P 所表示的数为15-+；④用反证法证明命题“一个三角形最多有一个钝角”时，首先应假设“这个三角形中有两个钝角”；⑤如图，在ABC 内一点P 到这三条边的距离相等，则点P 是三个角平分线的交点．A ．1B ．2C ．3D ．48．对于ABC 与DEF ，已知∠A=∠D ，∠B=∠E ，则下列条件：①AB=DE ；②AC=DF ；③BC=DF ；④AB=EF 中，能判定它们全等的有（）A ．①②B ．①③C ．②③D ．③④ 9．如图，已知∠A=∠D ， AM=DN ，根据下列条件不能够判定△ABN ≅△DCN 的是（）A ．BM ∥CNB ．∠M=∠NC ．BM=CND ．AB=CD 10．如图，AD 是△ABC 中∠BAC 的角平分线，DE ⊥AB 于点E ，S △ABC =7，DE =2，AB =4，则AC 长是（）A ．2.5B ．3C ．3.5D ．411．下列命题，真命题是（）A ．全等三角形的面积相等B ．面积相等的两个三角形全等C ．两个角对应相等的两个三角形全等D ．两边和其中一边的对角对应相等的两个三角形全等12．如图，△ACB ≌△A 'CB '，∠BCB '=25°，则∠ACA '的度数为（）A ．35°B ．30°C ．25°D ．20°13．如图，要判定△ABD ≌△ACD ，已知AB ＝AC ，若再增加下列条件中的一个，仍不能说明全等，则这个条件是（）A ．CD ⊥AD ，BD ⊥ADB ．CD ＝BDC ．∠1＝∠2D ．∠CAD ＝∠B AD 14．如图，AD 是ABC 的中线，E ，F 分别是AD 和AD 延长线上的点，且DE DF =，连结BF ，CE ．下列说法：①CE BF =；②ACE △和CDE △面积相；③//BF CE ；④BDF CDE ≌．其中正确的有（）A ．1个B ．2个C ．3个D ．4个15．如图，已知，CAB DAE ∠=∠，AC AD =．下列五个选项：①AB AE =，②BC ED =，③C D ∠=∠，④B E ∠=∠，⑤12∠=∠，从中任选一个作为已知条件，其中能使ABC AED ≌△△的条件有（）A ．2个B ．3个C ．4个D ．5个二、填空题16．如图，已知四边形,90,3,4,5,ABCD B AB BC AC ︒∠====180BAD CAD ︒∠+∠=，180BCD ACD ︒∠+∠=，则四边形ABCD 的面积是_________．17．如图，在ABC 中，=6AB ，=4AC ，点D ，E 分别在边AB ，AC 上，2BD AE CE ===，//CE AB 交DE 的延长线于点F ，则CF 的长为_____________．18．如图（1），已知AB AC =，D 为BAC ∠的角平分线上一点，连接BD ，CD ；如图（2），已知AB AC =，D ，E 为BAC ∠的角平分线上两点，连接BD ，CD ，BE ，CE ；如图（3），已知AB AC =，D ，E ，F 为BAC ∠的角平分线上三点，连接BD ，CD ，BE ，CE ，BF ，CF ；……，依此规律，第7个图形中有全等三角形的对数是________．19．如图，△ABE ≌△ADC ≌△ABC ，若∠1＝130°，则∠α的度数为________．20．如图，在Rt ABC △中，90C ∠=︒，以顶点A 为圆心，任意长为半径画弧，分别交AC ，AB 于点M ，N ，再分别以点M ，N 为圆心，大于12MN 的长为半径画弧，两弧交于点P ，作射线AP 交BC 于点D ．若3CD =，10AB =，则ABD △的面积是______．21．如图，在△ABC 中，∠ABC 的平分线与外角∠ACE 的平分线交于点D ，若∠D ＝20°，则∠A ＝_____．22．如图，AC//BD ，OA ，OB 分别平分BAC ∠和ABD ∠，OE AB ⊥，垂足为E ，如果OE 5=，那么AC 与BD 的距离是________23．如图，ABC 中，∠C ＝90°，AD 平分∠BAC ， AB ＝5，CD ＝2，则ABD △的面积是______24．如图所示，己知ABC ∆的周长是22,,OB OC 分别平分ABC ∠和ACB OD BC D ∠⊥，于,且3OD =，则ABC ∆的面积是__________．25．如图，在ABC 中，AD 平分BAC ∠，P 为线段AD 上的一个动点，PE AD ⊥交直线BC 于点E ．若35B ∠=︒，85ACB ∠=︒，则E ∠的度数为______．26．如图，AD 是ABC 中BAC ∠的平分线，DE AB ⊥交AB 于点E ，DF AC ⊥交AC 于点F ．若28ABC S =，4DE =，8AB =，则AC =_________．三、解答题27．如图，点A ，E ，F ，B 在直线l 上，AE BF =，//AC BD ，且AC BD =，求证：ACF BDE ≅△△．28．如图，直角梯形ABCD 中，//,,AD BC AB BC E ⊥是AB 上的点，且,DE CE DE CE =⊥，（1）证明：AB AD BC =+．（2）若已知AB a ，求梯形ABCD 的面积．29．如图，点E 在线段BD 上，已知,,AB AC AD AE BE CD ===．（1）求证：BAC EAD ∠=∠．（2）写出123∠∠∠、、之间的数量关系，并予以证明．30．如图，∠ACB 和∠ADB 都是直角，BC ＝BD ，E 是AB 上任意一点．（1）求证：△ABC ≌△ABD ．（2）求证：CE ＝DE ．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

初中数学全等三角形常见题目型训练基础
测试卷
初中数学全等三角形常见题型训练基础测试卷
一、单选题(共4道，每道25分)
1.如图，在AB、AC上各取一点D、E，使得AE=AD，连接CD、BE相交于点O，再连接AO．若∠CAO=∠BAO，则图中全等三角形共有（）
A.3对
B.4对
C.5对
D.6对
2.如图,已知点E在△ABC的外部,点D在BC边上,DE交AC于F,若
∠1=∠2=∠3,AC=AE。

求证:△ABC≌△ADE.
证明:∵∠1=∠2=∠3
∴∠1+∠DAC=∠2+∠DAC
即∠BAC=∠DAE
又∵∠3=∠B+ ,∠2=∠B+
∴∠E=∠C
在△ABC和△ADE中
∴
①∠DAC,②∠E,③∠C,④,⑤,⑥△ABC≌△ADE(ASA),⑦△ABC≌△ADE(AAS), 以上空缺处依次填写正确的顺序为()
A.①②⑤⑦
B.②③⑤⑦
C.①③④⑥
D.②③④⑥
3.如图,四边形ABCD为正方形,∠ABE=∠DCE=90°,AB=BC=CD=AD,E为BC边上一点,且AE=DE,AE与对角线BD交于点F,∠ABF=∠CBF,连接CF,交ED于点G.判断CF与ED的位置关系,并说明理由.
解:垂直.理由如下:
在△ABF与△CBF中
∴
∴∠BAF=∠BCF
在Rt△ABE和Rt△DCE中
∴
∴∠BAE=∠CDE
∴∠BCF=∠CDE
∵∠CDE+∠DEC=90°
∴∠BCF+∠DEC=90°
∴DE⊥CF
①,②,③,④
,⑤Rt△ABE≌Rt△DCE(HL),⑥△ABE≌△DCE(SAS),⑦△ABF≌△CBF(SAS),⑧△ABF≌△CBF(SSS), 以上空缺处依次填写正确的顺序
为()
A.①⑦④⑥
B.②⑧③⑤
C.①⑦③⑤
D.②⑧④⑥
4.如图,四边形ABCD中,AB=CD,BC=AD.求证:∠A=∠C.
证明:如图,_________________
在△ABD和△CDB中
________________
∴________________
∴∠A=∠C(全等三角形对应角相等)
①作直线BD,②连接BD,③作射线
BD,④,⑤,⑥△ABD≌△CDB(SSS),⑦△ABD≌△BCD(SSS),⑧△ABD≌△CDB(SAS), 以上空缺处依次填写正确的顺
序为()
A.②⑤⑥
B.②⑤⑦
C.①⑤⑧
D.②⑤⑧。