2018-2019学年华东师大版八年级数学上册《全等三角形中常见的辅助线的作法》专题练习及答案
2024八年级上《全等三角形》常见辅助线作法总结

全等三角形是初中数学中的重要概念,掌握全等三角形的判断和性质是解决三角形问题的关键。
常用的辅助线作法可以帮助我们更好地理解和应用全等三角形的知识。
下面将对2024八年级上《全等三角形》常见的辅助线作法进行总结。
一、三角形内部的辅助线作法:1.外切圆:对于一个三角形,可以在它的外面作出三个外接圆,然后通过外接圆的协调定理来判断和证明两个三角形全等。
2.角平分线:对于一个角,可以作出它的角平分线,然后利用角平分线的性质来判断和证明两个三角形全等。
3.中位线:对于一个三角形,可以连接它的两个顶点和中点,得到两条中位线。
根据中位线的性质,可以判断和证明两个三角形全等。
4.高线:对于一个三角形,可以分别作出它的三条高线,然后根据高线的性质来判断和证明两个三角形全等。
5.角高线和中线:对于一个锐角三角形,可以连接其中一个角的顶点和对边的中点,得到一条角高线和一条中线。
根据角高线和中线的性质,可以判断和证明两个三角形全等。
二、三角形外部的辅助线作法:1.外接圆和割线:对于一个三角形,可以通过外接圆和割线的性质来判断和证明两个三角形全等。
2.正弦定理和余弦定理:对于一个三角形,可以通过正弦定理和余弦定理来判断和证明两个三角形全等。
3.对称性和重叠法:对于一个三角形,可以利用对称性和重叠法来判断和证明两个三角形全等。
4.平移法和旋转法:可以通过平移法和旋转法来判断和证明两个三角形全等。
以上仅是2024八年级上《全等三角形》常见的辅助线作法的总结,实际问题中可能还会有其他的辅助线作法。
在解决三角形问题时,选择合适的辅助线作法可以简化问题,提高解题效率。
同时,还需要对全等三角形的基本知识进行深入理解和掌握,不仅要掌握判断全等三角形的条件,还要熟练运用全等三角形的性质和定理。
八年级上册数学辅助线技巧

八年级上册数学辅助线技巧
1.等腰三角形“三线合一”法:在遇到等腰三角形时,可以作底边上的高,利用
“三线合一”的性质进行解题。
2.倍长中线:通过倍长中线,使延长线段与原中线长相等,构造全等三角
形。
3.角平分线:在角平分线上添线,构造全等三角形。
4.垂直平分线:通过连接线段两端,构造全等三角形。
5.“截长法”或“补短法”:当遇到有二条线段长之和等于第三条线段的长时,可
以用这种方法来辅助解题。
6.图形补全法:如果有一个角为60度或120度,可以通过添线后构成等边三
角形。
这些辅助线技巧可以在解题时帮助你构造全等三角形,从而更容易地解答数学问题。
在做题时,你需要根据具体的问题和已知条件选择合适的辅助线技巧。
初中几何全等三角形常见辅助线作法

全等三角形常见辅助线作法【例1】.已知:如图6, 4BCE、△ACO分别是以8E、为斜边的直角三角形,且= ACDE是等边三角形.求证:△ A3c是等边三角形.【例2】、如图,已知BC>AB, AD=DCo BD 平分NABC。
求证:ZA+ZC=180°.线段的数量关系: 通过添加辅助线构造全等三角形转移线段到一个三角形中证明线段相等。
1、倍长中线法【例.3]如图,己知在△ABC中,ZC = 90°, ZB = 30°, A。
平分NB4C,交BC于点D.求证:BD = 2CD证明:延长DC到E,使得CE=CD,联结AEZC=90°A AC ± CDVCD=CEAD=AEVZB=30° ZC=90°ZBAC=60°YAD 平分NBACJ ZBAD=30°A DB=DA ZADE=60°VDB=DA:.BD=DE/. BD=2DC4B D笫3题•/ ZADE=60° AD=AEA △ ADE为等边三角形,AD=DE【例4.】如图,。
是AABC的边上的点,且CD = AB, ZADB = ZBAD, AE是AARD的中线。
求证:AC = 2AEo 证明:延长AE至IJ点F,使得EF=AE联结DF在4ABE和4FDE中BE=DEZAEB=ZFEDAE=FE/.△ABE 也AFDE (SAS) A AB=FD ZABE=ZFDE VAB=DCJ FD = DCZADC=ZABD+ZBAD ZADB = ZBAD,ZADC=ZABD+ZBDA VZABE=ZFDE・・・NADONADB+NFDE即ZADC= ZADF ffiAADF 和AADC 中AD=AD< ZADF= ZADC、DF =DC・•・△ ADF也ADC(SAS) AAF=ACAC=2AE【变式练习】、如图,AABC中,BD二DOAC, E是DC的中点,求证:AD平分NBAE.【小结】熟悉法一、法三“倍长中线”的辅助线包含的基本图形“八字型”和“倍长中线”两种基本操作方法, 倍长中线,或者倍长过中点的一条线段以后的对于解决含有过中点线段有很好的效果。
八年级数学《全等三角形五种常见的辅助线作法》
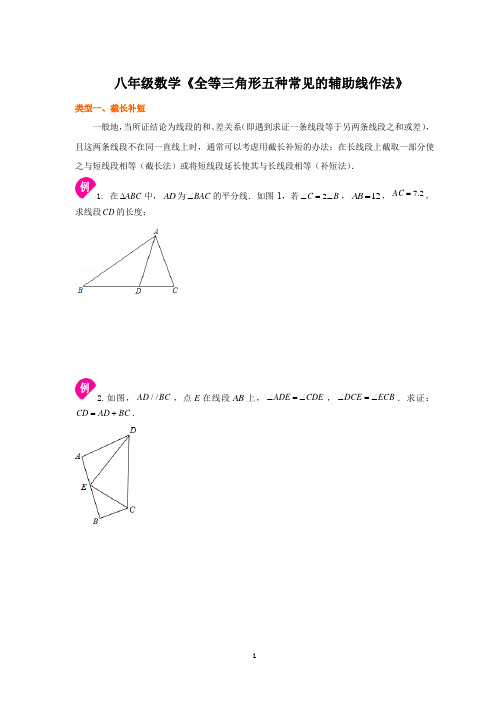
八年级数学《全等三角形五种常见的辅助线作法》 类型一、截长补短一般地,当所证结论为线段的和、差关系(即遇到求证一条线段等于另两条线段之和或差),且这两条线段不在同一直线上时,通常可以考虑用截长补短的办法:在长线段上截取一部分使之与短线段相等(截长法)或将短线段延长使其与长线段相等(补短法).1. 在ABC ∆中,AD 为BAC ∠的平分线.如图1,若2C B ∠=∠,12AB =,2.7=AC ,求线段CD 的长度;2.如图,//AD BC ,点E 在线段AB 上,ADE CDE ∠=∠,DCE ECB ∠=∠.求证:CD AD BC =+.举一反三【变式1】如图,在ABC∠、ACB∠.∠=︒,AD,CE分别平分BAC∆中,60ABC(1)求AOC∠的度数;(2)求证:AC AE CD=+.【变式2】在等边ABC∠=︒,∆中,E为BC边上一点,G为BC延长线上一点,过点E作60AEM交ACG∠的平分线于点M.(1)如图1,当点E在BC边的中点位置时,求证:AE EM=;(2)如图2,当点E在BC边的任意位置时(1)中的结论是否成立?请说明理由.类型二、倍长中线三角形问题中涉及中线(中点)时,将三角形中线延长一倍,构造全等三角形是常用的解题思路.3. 已知在ABCAC=,AD是BC边上的中线,则AD的取值范围(AB=,4∆中,3)A.34AD>D.0.5 3.5AD<<C.3<<ADAD<<B.174已知:在ABC=,延长BE交∆中,AD是BC边上的中线,E是AD上一点,且BE AC=.AC于F,求证:AF EF举一反三【变式1】已知:如图,()∆≠中,D、E在BC上,且DE ECABC AB ACDF BA=,过D作//交AE于点F,DF AC∠.=.求证:AE平分BAC【变式2】如图,已知:CD AB =,BAD BDA ∠=∠,AE 是ABD ∆的中线,求证:2AC AE =.类型三、作平行线当三角形问题中有相等的角或等腰等条件时,可通过作平行线将相等的角转换到某一个三角形中得到另外的等腰三角形或相等的角,从而为证明全等提供条件.5.已知,如图,在ABC ∆中,AB AC =,在AC 上取点E ,在AB 的延长线上取点D ,使BD EC =,连接DE 交BC 于点F .求证:DF EF =.举一反三【变式1】ABC∠=︒,AP平分BAC∠交C∠交BC于P,BQ平分ABC ∆中,60BAC∠=︒,40+=+.AC于Q,求证:AB BP BQ AQ类型四、补全图形在一些求证三角形问题中,延长某两条线段(边)相交,构成一个封闭的图形,可找到更多的相等关系,有助于问题的解决.6. 如图,在ABC∠的平分线,若A点到直线BD ∆中,AC BC∠=︒,BD为ABCC=,90的距离为a,则BE的长为.举一反三【变式1】已知:90BD CE=.⊥,垂足为E.求证:2=,BD平分ABCA∠=︒,AB AC∠,CE BD类型五、利用角的平分线对称构造全等角的平分线是角的对称轴,在证明全等过程中不仅提供了两个相等的角,还有一条公共边,利用角的平分线在角的两边上截取相等的线段,或向两边作垂线(双垂直),对称构造出全等三角形是常用的证明方法.7.如图,在ABC⊥于点E,点F在AC上,C∠,DE AB∆中,90∠=︒,AD平分CAB=.BE FC=.求证:BD DF举一反三【变式1】如图,90∠,将直角三角板的顶点P在射线OM上移动,∠=︒,OM平分AOBAOB两直角边分别与OA、OB相交于点C、D,问PC与PD相等吗?试说明理由.。
全等三角形问题中常见的8种辅助线的作法

全等三角形问题中常见的辅助线的作法(有答案)常见辅助线的作法有以下几种:最主要的是构造全等三角形,构造二条边之间的相等,二个角之间的相等。
1)遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题,思维模式是全等变换中的“对折”法构造全等三角形.2)遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角形,利用的思维模式是全等变换中的“旋转”法构造全等三角形.3)遇到角平分线在三种添辅助线的方法,(1)可以自角平分线上的某一点向角的两边作垂线,利用的思维模式是三角形全等变换中的“对折”,所考知识点常常是角平分线的性质定理或逆定理.(2)可以在角平分线上的一点作该角平分线的垂线与角的两边相交,形成一对全等三角形。
(3)可以在该角的两边上,距离角的顶点相等长度的位置上截取二点,然后从这两点再向角平分线上的某点作边线,构造一对全等三角形。
4)过图形上某一点作特定的平分线,构造全等三角形,利用的思维模式是全等变换中的“平移”或“翻转折叠”5)截长法与补短法,具体做法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,是之与特定线段相等,再利用三角形全等的有关性质加以说明.这种作法,适合于证明线段的和、差、倍、分等类的题目.6)已知某线段的垂直平分线,那么可以在垂直平分线上的某点向该线段的两个端点作连线,出一对全等三角形。
特殊方法:在求有关三角形的定值一类的问题时,常把某点到原三角形各顶点的线段连接起来,利用三角形面积的知识解答.一、倍长中线(线段)造全等例1、已知,如图△ABC 中,AB=5,AC=3,则中线AD 的取值范围是_________.例2、如图,△ABC 中,E 、F 分别在AB 、AC 上,DE ⊥DF ,D 是中点,试比较BE+CF 与EF 的大小.例3、如图,△ABC 中,BD=DC=AC ,E 是DC 的中点,求证:AD 平分∠BAE.应用:1、(09崇文二模)以ABC ∆的两边AB 、AC 为腰分别向外作等腰Rt ABD ∆和等腰Rt ACE ∆,90,BAD CAE ∠=∠=︒连接DE ,M 、N 分别是BC 、DE 的中点.探究:AM 与DE 的位置关系及数量关系.(1)如图① 当ABC ∆为直角三角形时,AM 与DE 的位置关系是 ,线段AM 与DE 的数量关系是 ;(2)将图①中的等腰Rt ABD ∆绕点A 沿逆时针方向旋转︒θ(0<θ<90)后,如图②所示,(1)问中得到的两个结论是否发生改变并说明理由.二、截长补短1、如图,ABC ∆中,AB=2AC ,AD 平分BAC ∠,且AD=BD ,求证:CD ⊥AC2、如图,AD ∥BC ,EA,EB 分别平分∠DAB,∠CBA ,CD 过点E ,求证;AB =AD+BC 。
八年级数学上册-全等三角形(常见辅助线)

Ⅴ.“周长问题”的转化 借助“角平分线性质”
1.如图,△ABC中,∠C=90o,AC=BC,AD平分∠ACB, DE⊥AB.若AB=6cm,则△DBE的周长是多少?
BE+BD+DE BE+BD+CD BE+BC BE+AC BE+AE AB
A E B C D
Ⅴ.“周长问题”的转化 借助“垂直平分线性质”
构造全等三角形
B E
C
M
D
Ⅰ.连结
典例3:如图,AB=AC,BD=CD, M、N分别是BD、CD 的中点,求证:∠AMB= ∠ANC A 连结AD
构造全等三角形
B M D N C
Ⅰ.连结
典例4:如图,AB与CD交于O, 且AB=CD,AD=BC, OB=5cm,求OD的长. C A 连结BD
构造全等三角形
过点D作DE⊥AB 构造了: 全等的直角三角形且距离相等
B E D C A
思考: 若AB=15cm,则△BED的周长是多少
?
Ⅱ.角平分线上点向两边作垂线段
典例3:如图,梯形中, ∠A= ∠D =90o, BE、CE均是角平分线, 求证:BC=AB+CD.
过点E作EF⊥BC 构造了: 全等的直角三角形且距离相等
AB+AC+BC
A1
B A O N C A2 M
A1 B+ A2 C+BC
A1 A2
Ⅴ.“周长问题”的转化 借助“垂直平分线性质”
4.如图, △ABC中,MN是AC的垂直平分线. 若AN=3cm, △ABM周长为13cm,求△ABC的周长.
AB+BC+AC AB+ BM+MC+6 AB+ BM+AM+6 13+6
2019年秋数学华东师大版八年级上册习题课件:第13章 探究专题 巧作辅助线构造等腰三角形
连接两点构造等腰三角形 4.如图,在△ABC 中,AB=AC,点 D、E、F 分别在边 BC、AB、AC 上, 且 BD=CF,BE=CD,G 是 EF 的中点.求证:DG⊥EF.
证明:连接 ED、FD.∵AB=AC,∴∠B=∠C.在△BDE 和△CFD 中,
B∠DB==C∠FC BE=CD
6.如图,D 是等边△ABC 的边 AC 的中点,F 在 AB 上,E 在 BC 的延长 线上,∠FDE=120°. (1)求证:DE=DF; (2)求证:CE+BF=12BC.
证明:(1)过点 D 作 DP∥BC 交 AB 于点 P,∵△ABC 是等边三角形,∴AB =AC=BC,∠ABC=∠ACB=∠ADP=∠APD=∠A=60°,∴△ADP 是等 边三角形,∴AD=DP=AP,∠DPF=∠DCE=∠PDC=120°,又∵D 是 AC 的中点,∴AD=CD=PD,又∵∠FDE=120°,∴∠PDF=∠CDE,∴ △DPF≌△DCE,∴DF=DE;
证明:易证∠AED=∠ADE=80°,AD=AE.在 AB 上截取 AM=AC,证△ AMD≌△ACD,CD=DM,∠AMD=∠C=100°,∠DME=∠DEM=80°, DM=DE=BE,∴AB=AE+BE=AD+CD.
作二倍角的平分线构造等腰三角形 2.如图,△ABC 中,∠BCA=2∠A,BC=12AC,求∠A 的度数.
初二数学-三角形问题中常见的辅助线作法总结
三角形问题中常见的辅助线的作法【三角形辅助线做法】图中有角平分线,可向两边作垂线。
也可将图对折看,对称以后关系现。
角平分线平行线,等腰三角形来添。
角平分线加垂线,三线合一试试看。
线段垂直平分线,常向两端把线连。
要证线段倍与半,延长缩短可试验。
三角形中两中点,连接则成中位线。
三角形中有中线,延长中线等中线。
1.等腰三角形“三线合一”法:遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题2.倍长中线:倍长中线,使延长线段与原中线长相等,构造全等三角形3.角平分线在三种添辅助线4.垂直平分线联结线段两端5.用“截长法”或“补短法”:遇到有二条线段长之和等于第三条线段的长6.图形补全法:有一个角为60度或120度的把该角添线后构成等边三角形7.角度数为30、60度的作垂线法:遇到三角形中的一个角为30度或60度,可以从角一边上一点向角的另一边作垂线,目的是构成30-60-90的特殊直角三角形,然后计算边的长度与角的度数,这样可以得到在数值上相等的二条边或二个角。
从而为证明全等三角形创造边、角之间的相等条件。
8.计算数值法:遇到等腰直角三角形,正方形时,或30-60-90的特殊直角三角形,或40-60-80的特殊直角三角形,常计算边的长度与角的度数,这样可以得到在数值上相等的二条边或二个角,从而为证明全等三角形创造边、角之间的相等条件。
常见辅助线的作法有以下几种:最主要的是构造全等三角形,构造二条边之间的相等,二个角之间的相等。
1)遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题,思维模式是全等变换中的“对折”法构造全等三角形.2)遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角形,利用的思维模式是全等变换中的“旋转”法构造全等三角形.3)遇到角平分线在三种添辅助线的方法,(1)可以自角平分线上的某一点向角的两边作垂线,利用的思维模式是三角形全等变换中的“对折”,所考知识点常常是角平分线的性质定理或逆定理.(2)可以在角平分线上的一点作该角平分线的垂线与角的两边相交,形成一对全等三角形。
全等三角形中的辅助线的作法
全等三角形中的辅助线的作法在《全等三角形》的解题中,在解决一些复杂的全等三角形问题中往往需要构造辅助线,本文将对添加辅助线的一些常用方法进行介绍,通常有连线构全等、截长补短法、倍长中线法、角平分线构全等等四种常见辅助线。
一、连线构全等例1:已知,如图,AD =BC ,AC =BD ,求证:D C ∠=∠分析:此题是一道易错的全等三角形证明题,很多学生会错误地认为需要证明的是ADO ∆和BCO ∆,但条件明显是不能证明的,所以本题的正确解法是连结AB (或者CD )构造ADB ∆和BCA ∆全等,再得到D C ∠=∠证明:连结AB在ADB ∆和BCA ∆中⎪⎩⎪⎨⎧===BA AB BD AC BC ADADB ∆∴≌BCA ∆ (SSS )D C ∠=∠∴练习1:如图,CD AB =,DC BC =,求证:D B ∠=∠.练习2:如图,CD AB //,CD AB =,求证:BC AD =练习3:如图,AB=AC ,BD=CD ,M 、N 分别是BD 、CD 的中点,求证:ANC AMB ∠=∠二、截长补短法截长补短法:在某条线段上截取一条线段与特定线段相等,或者将某条线段延长,使之与特定线段相等,再利用三角形全等的有关性质加以说明。
这种作法,适合于证明线段的和、差、倍、分等类的题目。
例2:已知在ABC ∆,B C ∠=∠2,21∠=∠,求证:CD AC AB +=分析:本题证明的是线段的和差问题,可考虑利用截长或补短法。
方法一(截长法):如图1,在AB 上截取AE=AC ,连结BE ,易证ADE ∆≌ADC ∆,从而得DC DE =,AED C ∠=∠,AC AE =又因为B C ∠=∠2所以得B AED ∠=∠2,又因为BDE B AED ∠+∠=∠所以得BDE B ∠=∠可得DE BE =从而得CD AC AB +=方法二(补短法):如图2,延长AC 到点E ,使得AE=AB ,易证ADE ∆≌ADB ∆,从而得AE AB =,E B ∠=∠又因为B ACB ∠=∠2所以得E ACB ∠=∠2,又因为E CDE ACB ∠+∠=∠所以得E CDE ∠=∠可得CE CD =从而得CD AC AB +=练习1:如图所示,已知BC AD //,AE 平分DAB ∠,BE 平分ABC ∠,线段CD 经过点E 交AD 于点D ,交BC 于点C ,求证:AB BC AD =+图1图2练习2:如图,在四边形ABDE 中,C 是BD 边的中点,若AC 平分BAE ∠,︒=∠90ACE ,猜想线段AE 、AB 、DE 的长度满足的数量关系,并证明。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
新课标-----最新华东师大版
华东师大版八年级数学上册 第13章 全等三角形 全等三角形问题中
常见的辅助线的作法 专题检测题
1.在△ABC中,AB=8,AC=6,则BC边上的中线AD的取值范围是( )
A.6<AD<8 B.2<AD<14 C.1<AD<7 D.无法确定
2.如图,在△ABC中,AD为BC上的中线,E为AC的一点,BE与AD交于点F,若AE=EF.求证:AC=BF.
3.如图,在△ABC中,AD交BC于点D,点E是BC的中点,EF∥AD交CA的延长线于点F,交AB于点G.
若BG=CF,求证:AD为△ABC的角平分线.
4.如图,CE,CB分别是△ABC,△ADC的中线,且AB=AC.求证:CD=2CE.
5.如图,在△ABC中,∠B=60°,∠BAC,∠ACB的平分线AD,CE交于点F,试猜想AE,CD,AC三条线段
之间的数量关系,并加以证明.
6.已知:如图,ABCD是正方形,∠FAD=∠FAE.求证:BE+DF=AE.
新课标-----最新华东师大版
7.如图,△ABC是边长为2的等边三角形,BD=CD,∠BDC=120°,E,F分别在AB,AC上,且∠EDF=60°.
(1) 证明:BE+CF=EF;
(2)求△AEF的周长.
三、过角平分线上一点向角两边作垂线
8.如图,在△ABC中,AC=BC,∠ACB=90°,BD平分∠ABC,求证:AB=BC+CD.
新课标-----最新华东师大版
9.如图,AB<BC,BD平分∠ABC,AD=DC,求证:∠BAD+∠BCD=180°.
10.如图,在△ABC中,∠C=2∠B,∠1=∠2,求证:AB=AC+CD.
11.如图,在△ABC中,∠B=2∠C,且AD⊥BC于D.求证:CD=AB+BD.
12.如图,在△DEF中,DE=DF,过EF上一点A作直线分别与DE,DF的延长线交于点B,C,且BE=CF.
新课标-----最新华东师大版
求证:AB=AC.
答案:
1. C
2.
证明:延长AD至G,使DG=AD,连结BG,
在△BDG和△CDA中,∵BD=CD∠BDG=∠CDADG=DA,
∴△BDG≌△CDA(S.A.S.),∴BG=AC,∠CAD=∠G,又∵AE=EF,∴∠CAD=∠AFE,又∠BFG=∠AFE,∴
∠CAD=∠BFG,∴∠G=∠BFG,∴BG=BF,∴AC=BF
3.
新课标-----最新华东师大版
延长FE,截取EH=EG,连结CH,∵E是BC中点,∴BE=CE,∴∠BEG=∠CEH,在△BEG和△CEH中,
BE=CE
∠BEG=∠CEH
GE=EH
,∴△BEG≌△CEH(S.A.S.),∴∠BGE=∠H,∴∠BGE=∠FGA=∠H,∵BG=CH,∵CF=BG,
∴CH=CF,∴∠F=∠H=∠FGA,∵EF∥AD,∴∠F=∠CAD,∠BAD=∠FGA,∴∠CAD=∠BAD,∴AD平分
∠BAC
4.
证明:延长CE到F,使EF=CE,连结FB.∵CE是△ABC的中线,∴AE=EB,又∵∠AEC=∠BEF,∴△AEC
≌△BEF(S.A.S.),∴∠A=∠EBF,AC=FB.∵AB=AC,∴∠ABC=∠ACB,∴∠CBD=∠A+∠ACB=∠EBF+
∠ABC=∠CBF,∵CB是△ADC的中线,∴AB=BD,又∵AB=AC,AC=FB,∴FB=BD,又∵CB=CB,∴△CBF
≌△CBD(S.A.S.),∴CD=CF=CE+EF=2CE
5. 在CA上取点G使得CG=CD,∵∠AFC=180°-12(∠BAC+∠ACB)=180°-12(180°-60°)=120°,∴∠AFE
=∠CFD=60°,∵在△GCF和△DCF中,FC=FC∠GCF=∠FCDCD=CG,∴△GCF≌△DCF(S.A.S.),∴∠GFC=∠CFD=60°,
CD=CG.∴∠AFG=120°-60°=60°=∠AFE,∵在△AEF和△AGF中,∠AFE=∠AFG∠EAF=∠GAFAF=AF,∴△AEF≌△
AGF(A.S.A.),∴AE=AG,∴AE+CD=AG+CG=AC
6.
新课标-----最新华东师大版
延长CB到G,使BG=DF,连结AG,∵四边形ABCD为正方形,∴AB=AD,AB∥CD,∠D=∠ABC=90°,∴
∠5=∠BAF=∠1+∠3,∠ABG=180°-∠ABC=90°,在△ABG和△ADF中,AB=AD∠ABG=∠ADF=90°,BG=DF∴△ABG
≌△ADF(S.A.S.),∴∠G=∠5,∠1=∠2=∠4,∴∠G=∠5=∠1+∠3=∠4+∠3=∠EAG,∴AE=GE
=BE+GB=BE+DF
7.
(1)延长AB到N,使BN=CF,连接DN,∵△ABC是等边三角形,∴∠ABC=∠ACB=60°,∵BD=CD,∠BDC
=120°,∴∠DBC=∠DCB=30°,∴∠ACD=∠ABD=30°+60°=90°=∠NBD,∵在△NBD和△FCD中,
BD=CD
∠NBD=∠FCD=90°,
BN=CF
∴△NBD≌△FCD(S.A.S.),∴DN=DF,∠NDB=∠FDC,∵∠BDC=120°,∠EDF=60°,
∴∠EDB+∠FDC=60°,∴∠EDB+∠BDN=60°,即∠EDF=∠EDN,在△EDN和△EDF中,DE=DE∠EDF=∠EDNDN=DF,
∴△EDN≌△EDF(S.A.S.),∴EF=EN=BE+BN=BE+CF,即BE+CF=EF
(2)∵△ABC是边长为2的等边三角形,∴AB=AC=2,∵BE+CF=EF,∴△AEF的周长为AE+EF+AF=AE
+EB+FC+AF=AB+AC=4
8.
新课标-----最新华东师大版
过点D作DE⊥AB于点E,∵BD平分∠ABC,
∴CD=DE,在△BCD与△BED中,
∠DBC=∠DBE
∠C=∠BED=90°
BD=BD
,∴△BCD≌△BED(A.A.S.),∴BC=BE,
∵△ABC是等腰直角三角形,∴∠A=45°,∴△ADE是等腰直角三角形,∴DE=AE=CD,∴AB=BE+AE=
BC+CD
9.
过点D作DE⊥AB交BA的延长线于E,DF⊥BC于F,∵BD平分∠ABC,DE⊥AB,DF⊥BC,∴DE=DF,∠AED
=∠CFD=90°,∵在△AED和△CFD中,AD=CDDE=DF,∴△AED≌△CFD(H.L.)∴∠DAE=∠BCD,∵∠BAD+∠
DAE=180°,∴∠BAD+∠BCD=180°
10.
方法1:在AB上取AE=AC,连接DE,∵AE=AC,∠1=∠2,且AD=AD,∴△ACD≌△AED(S.A.S.),∴ED
=CD,∠AED=∠C=2∠B,又∵∠AED=∠B+∠BDE,∴∠B=∠BDE,∴EB=ED,即△BED为等腰三角形.
∴BE=ED=CD,∴AB=AE+EB=AC+CD.
方法2:延长AC到E,使CE=CD,连接DE.则∠CDE=∠E,∴∠ACB=∠CDE+∠E=2∠E,∵∠ACB=2∠B,
∴∠B=∠E,∵∠1=∠2,AD=AD,∴△ABD≌△AED,∴AB=AE=AC+CD
新课标-----最新华东师大版
11.
如图,在DC上取DE=BD,∵AD⊥BC,∴AB=AE,∴∠B=∠AEB,在△ACE中,∠AEB=∠C+∠CAE,又∵
∠B=2∠C,∴2∠C=∠C+∠CAE,∴∠C=∠CAE,∴AE=CE,∴CD=CE+DE=AB+BD
12.
过B作BG∥CD,交EF于G,∵BG∥CD,∴BG∶DF=BE∶DE,∠AGB=∠AFC,又∵DE=DF,∴BG=BE,又
∵BE=CF,∴BG=CF,又∵∠GAB=∠FAC,∴△ACF≌△ABG,∴AB=AC
