云南师大附中2013届高三高考适应性月考卷(三)理科数学试题
云南师大附中2013届高考八模(理科)数学试卷及答案
云南师大附中2013届高考适应性月考卷（八）文科数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．参考公式： 样本数据12,,,n x x x 的标准差s =其中x 为样本平均数 柱体体积公式VSh =其中S 为底面面积，h 为高锥体体积公式13V Sh =其中S 为底面面积，h 为高球的表面积，体积公式24R S π=，334R V π=其中R 为球的半径第Ⅰ卷（选择题共60分）一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．复数11ii-+（i 是虚数单位）化简的结果是A ．i -B ．iC ．1D ．1-2．已知集合101x A xx ⎧-⎫=≥⎨⎬+⎩⎭，{}2|log (2)B x y x ==+，则A B ＝ A ．()2,1-- B ．()[)2,11,--+∞C ．[)1,+∞D ．()()2,11,---+∞3．已知两条直线,m n 和平面α，且m 在α内，n 在α外，则“n ∥α”是“m ∥n ”的A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件4．已知等差数列{}n a 中，39159a a a ++=，则数列{}n a 的前17项和17S ＝A ．102B ．51C ．48D ．36 5．阅读如图1所示的程序框图，则输出的S 的值是A ．910 B ．89 C ．78D ．67正视图 侧视图俯视图1 1 1 6．开学不久，学校从某班的学生中随机抽取25名学生进行学情调查，经过一段时间再次从该班的学生中随机抽取15名学生进行健康状况调查，发现有5名学生上次被抽查过，据此估计该班的学生人数为A ．75B ．65C ．60D ．50 7．某四面体的三视图如图2所示，该四面体的六条棱长中，长度最大的是ABCD ．8．设变量,x y 满足约束条件0,1,21,x y x y x y -≥⎧⎪+≤⎨⎪+≥⎩目标函数222z x x y =++，则z 的取值范围是A ．17,49⎡⎤⎢⎥⎣⎦B ．2⎤⎥⎣⎦C ．8,39⎡⎤⎢⎥⎣⎦D ．23⎡⎤⎢⎥⎣⎦9．定义在R 上的偶函数()f x 满足2(1)()f x f x +=-(()0)f x ≠，且(1)2013f =，则(2013)f ＝A ．12013B ．1C ．4D ．2013 10．已知方程ln 10x ax -+=（a 为实常数）有两个不等实根，则实数a 的取值范围是A ．()0,eB ．[]1,eC ．()0,1D ．[]0,111．在平面直角坐标系中，定义1212(,)||||d A B x x y y =-+-为两点11(,)A x y ，22(,)B x y 间的“折线距离”，在此定义下，给出下列命题：①到原点的“折线距离”为1的点的集合是一个正方形； ②到原点的“折线距离”为1的点的集合是一个圆；③到(1,0)M -，(1,0)N 两点的“折线距离”相等的点的轨迹方程是0x =． 其中，正确的命题有A ．3个B ．2个C ．1个D ．0个12．已知点P 在圆22:(3)1C x y +-=上，点Q 在双曲线22152x y -=的右支上，F 是双曲线的左焦点，则||||PQ QF +的最小值为A．1B．3+C．4+D ．5+第Ⅱ卷（非选择题共90分）注意事项：用钢笔或圆珠笔直接答在答题卡上．二、填空题：本大题共4小题，每小题5分，共20分，把答案填在题中横线上．13．已知1sin 3α=-，且,02πα⎛⎫∈- ⎪⎝⎭，则sin 2α＝ ． 14．直线cos sin 10x y θθ++=与圆221x y +=的位置关系为 ．15．已知向量AB 与AC 的夹角为30°，且||6AB =，则||AB AC -的最小值是 ． 16．已知函数*(1)()log (2)()m f m m m N +=+∈，令(1)(2)()f f f m k ⋅⋅⋅=，当[]1,2013m ∈，且*k N ∈时，满足条件的所有k 的值的和为 ．三、解答题：本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤．17．（本小题满分12分）已知数列{}n a 的前n 项和为n S ，点(,)n n a S 在直线34y x =+上． （1）求数列{}n a 的通项a ；（2）令*()n n b na n N =∈，试求数列{}n b 的前n 项和n T ．18．（本小题满分12分）如图3，在直三棱柱111ABC A B C -中，△ABC 为等腰直角三角形，90BAC ∠=，且1AB AA =，E 、F 分别为BC 、1CC 的中点．（1）求证：1B E ⊥平面AEF ；（2）当2AB =时，求点E 到平面1B AF 的距离．19．（本小题满分12分）在平面直角坐标系xOy 中，满足229x y +≤的点(,)P x y 组成的平面区域（或集合）记为Ω，现从Ω中随机取点(,)M x y ．（1）设,x Z y Z ∈∈，22x y ξ=+，求5ξ=的概率；（2）设,x R y R ∈∈，若直线(0)y x b b =-+>被圆229x y +=截得的弦长为，求ABCEF B 1C 1 A 1y x b ≥-+的概率．20．（本小题满分12分）已知抛物线的顶点在原点，准线方程为1x =，F 是焦点．过点(2,0)A -的直线与抛物线交于11(,)P x y ，22(,)Q x y 两点，直线PF ，QF 分别交抛物线于点M ，N ． （1）求抛物线的方程及12y y 的值；（2）记直线PQ ，MN 的斜率分别为1k ，2k ，证明：12k k 为定值． 21．（本小题满分12分）已知函数2()416mx f x x =+，||1()2x m g x -⎛⎫= ⎪⎝⎭，其中m R ∈且0m ≠．（1）判断函数()f x 的单调性；（2）设函数(),2,()(),2,f x x h xg x x ≥⎧=⎨<⎩当2m ≥时，若对于任意的[)12,x ∈+∞，总存在唯一的()2,2x ∈-∞，使得12()()h x h x =成立，试求m 的取值范围．请考生在第22、23、24三题中任选一题作答，如果多做，则按所做的第一题记分．作答时请写清题号． 22．（本小题满分10分）【选修4－1：几何选讲】 如图4，已知,AB CD 是圆O 的两条平行弦，过点A 引圆OP ，F 为CD 上的一点，弦,FA FB 分别与CD 交于点,GH ．（1）求证：GP GH GC GD ⋅=⋅；（2）若39AB AF GH ===，6DH =，求PA 的长． 23．（本小题满分10分）【选修4－4：坐标系与参数方程】 已知椭圆C 的极坐标方程为222123cos 4sin ρθθ=+，点1F ，2F 为其左右焦点．以极点为原点，极轴为x 轴的正半轴建立平面直角坐标系，直线l 的参数方程为2,2,2x y ⎧=+⎪⎪⎨⎪=⎪⎩（t为参数，t R ∈）．（1）求直线l 的普通方程和椭圆C 的直角坐标方程；（2）求点1F ，2F 到直线l 的距离之和．24．（本小题满分10分）【选修4－5：不等式选讲】 已知函数()2()log |1||5|1f x x x =-+--． （1）当5a =时，求函数()f x 的定义域；（2）若函数()f x 的值域为R ，求实数a 的取值范围．云南师大附中2013届高考适应性月考卷（八）文科数学参考答案第Ⅰ卷（选择题，共60分）一、选择题（本大题共12小题，每小题5分，共60分）【解析】 4．11717917()172a a S a +==，3915939a a a a ++==，93a =∴．故选B ． 5．依题意，知11,2,0,12i n S ===+⨯ 112,3,,1223i n S ===+⨯⨯ 1113,4,,122334i n S ===++⨯⨯⨯ ……，1111188,9,11223348999i n S ===++++=-=⨯⨯⨯⨯…. 故选B ． 6．设该班学生人数为n ，依题意知25515n =，75n =，故选A ． 7．由题图可知，几何体为如图1所示的三棱锥P ABC -， 其中1,,PA AC PA AC PA AB ==⊥⊥，由俯视图可知，AB BC =PB =D ．8．2222+2(1)1z x x y x y =+=++-，用线性规划，可求得22(1)x y ++的范围是17,49⎡⎤⎢⎥⎣⎦，所以8,39z ⎡⎤∈⎢⎥⎣⎦．故选C ． 9．22(4)()2(2)()f x f x f x f x +=-=-=+-，故()f x 为周期函数，周期4T =，(2013)(45031)(1)2013f f f =⨯+==∴．故选D ．10．ln 1=0ln =1x ax x ax -+⇔-，令12ln ,1y x y ax ==-，直线21y ax =-过定点(0,1)-，图1设直线21y ax =-与1y 的切点为00(,ln )x x ，由于11y x'=， 所以切线斜率0000ln 11,1,1x a x a x x +====∴， 当(0,1)a ∈时，直线21y ax =-与1y 的图象有2个交点．故选C. 11．设到原点的“折线距离”为1的点为(,)x y ，则||||1x y +=，其轨迹为如图2所示的正方形，所以①正确，②错误； 设到(1,0),(1,0)M N -两点的“折线距离”相等的点为(,)x y ， 则|1||||1|||,|1||1|x y x y x x ++=-++=-， 从而0x =，所以③正确．故选B ．12．设双曲线22152x y -=的右焦点为F '，则(0),0)F F '，由双曲线定义知||||QF QF '=+，||||||||QF PQ QF PQ '+=++ 当,,,C P Q F '共线时，min (||||)3QF PQ '+=，min (||||)3QF PQ +=+∴ C.第Ⅱ卷（非选择题，共90分）二、填空题（本大题共4小题，每小题5分，共20分）【解析】 15．如图3所示，点C 的轨迹为射线AC '（不含端点A ），当BC AC ⊥时，min min ||||3AB AC CB -==．16．234(1)(1)(2)()log 3log 4log 5log (2)m f f f m m +=+……2log (2)m k =+=，22k m =-，[1,2013],m k ∈∈*N ∵，101121024,22013=>，所以，k 值组成的集合为{2,3,4,5,6,7,8,9,10}，2391054++++=…．图3图2三、解答题（共70分．解答应写出文字说明、证明过程或演算步骤） 17．（本小题满分12分）解：（Ⅰ）因为点(,)n n a S 在直线34y x =+上，所以34n n S a =+，1134n n S a ++=+， 11133n n n n n a S S a a +++=-=-，化简得123n n a a +=，所以数列{}n a 为等比数列，公比32q =，由11134S a a ==+得12a =-， 故11132()2n n n a a qn --⎛⎫==-∈ ⎪⎝⎭*N ．……………………………………………（6分）（Ⅱ）因为 ()n n b na n =∈*N ， 所以12341n n n T b b b b b b -=++++++23213333321234(1)22222n n n n --⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+⨯+⨯+⨯++-⨯+⨯⎢⎥ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦，① 234133333332234(1)2222222n nn T n n -⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⨯=-+⨯+⨯+⨯++-⨯+⨯⎢⎥ ⎪ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦，② ①-②得23113333321+222222n nn T n -⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫-⨯=-++++-⨯⎢⎥ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦， ………（8分）2313333341+22222n nn T n -⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=++++-⨯⎢⎥ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦31332444(2)8()32212nn nn n n ⎛⎫- ⎪⎛⎫⎛⎫⎝⎭=⨯-⨯=--∈ ⎪ ⎪⎝⎭⎝⎭-*N ． ……………………（12分）18．（本小题满分12分）（Ⅰ）证明：在直三棱柱111ABC A B C -中，不妨设1||||=AB AA a =， ABC ∵△为等腰直角三角形，90BAC ∠=︒，11||BC B C =∴，∵E 、F 分别为BC 、1CC 的中点，222222113||||||2B E BE BB a a ⎫=+=+=⎪⎪⎝⎭∴， 22222213||||||44EF EC CF a a⎫=+=+=⎪⎪⎝⎭， 222222111119||||||244B F B C C F a a a =+=+=，有22222211339||||||244B E EF a a a B F +=+==，1B E EF ⊥∴，又1,AE BC B B ⊥⊥∵平面ABC ，1B E AE ⊥∴，AE EF E =，1B E ⊥∴平面AEF ．…………………………………………………………（6分）（Ⅱ）解：由条件知，1||||||||AE B E EF AF =，11||||3AB B F ==，…………………………………………………………（8分）AE EF ⊥∵，11||||22AEF S AE EF ==⨯△∴， 在1AFB △中，11cos sin B AF B AF ∠==∠=11111||||sin 322AB F S AB AF B AF =∠=⨯=△∴， ………………（10分）设点E 到平面1B AF 的距离为d ， 则11||AB F AEF d S B E S =△△，所以213d ==，即点E 到平面1B AF 的距离为1． ………………………………………………（12分）19．（本小题满分12分）解：（Ⅰ）当,x y ∈∈Z Z 时，圆229x y +=内共有29个点， 满足225x y +=的点有8个，所以8(5)29P ξ==． ……………………………………………………………（5分）（Ⅱ）当直线(0)y x b b =-+>被圆229x y +=截得的弦长为时， 设圆心O 到直线(0)y x b b =-+>的距离为d ，由22232d ⎛+= ⎝⎭，d =3b =． ………………………………（8分）满足y x b -+≥的(,)M x y位于弦长为的弓形内，所以y x b -+≥的概率为9π91142==9π42πS P S -=-弓形圆． ………………………（12分）20．（本小题满分12分）（Ⅰ）解：依题意，设抛物线方程为22(0)y px p =->， 由准线12px ==，得2p =， 所以抛物线方程为24y x =-．………………………………………………（2分）设直线PQ 的方程为2x my =-，代入24y x =-， 消去x ，整理得2480y my +-=， 从而128y y =-．………………………………………………………………（6分）（Ⅱ）证明：设3344(,),(,)M x y N x y ，则223434341121222122123434124444y y x x y y k y y y y y y k x x y y y y y y --+----=⨯=⨯=---+---． …………………（8分）设直线PM 的方程为1x ny =-，代入24y x =-， 消去x ，整理得2440y ny +-=， 所以134y y =-， 同理244y y =-．………………………………………………………………（10分）故3411221212124444182y y k y y k y y y y y y --++--=====++-，为定值． …………………………（12分）21．（本小题满分12分）解：（Ⅰ）依题意，22222(4)(2)(2)()4(4)4(4)m x m x x f x x x --+'==++，当0m >时，()022,()02f x x f x x ''>⇒-<<<⇒<-或2x >， 所以()f x 在(2,2)-上单调递增；在(,2),(2,)-∞-+∞上单调递减． 当0m <时，()022,()02f x x f x x ''<⇒-<<>⇒<-或2x >，所以()f x 在(2,2)-上单调递减；在(,2),(2,)-∞-+∞上单调递增． …………（6分） （Ⅱ）当2m ≥，1[2,)x ∈+∞时，11121()()416mx h x f x x ==+，由（Ⅰ）知1()h x 在[2,)+∞上单调递减， 从而1()(0,(2)]h x f ∈，即1()0,16m h x ⎛⎤∈ ⎥⎝⎦； ……………………………………（8分） 当2m ≥，22x <时，222||22111()()2222x m m x mx h x g x --⎛⎫⎛⎫⎛⎫====⋅ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭，在(,2)-∞上单调递增， 从而2()(0,(2))h x g ∈，即221()0,2m h x -⎛⎫⎛⎫∈ ⎪ ⎪ ⎪⎝⎭⎝⎭．……………………………（10分）对于任意的1[2,)x ∈+∞，总存在唯一的2(,2)x ∈-∞，使得12()()h x h x =成立， 只需21162m m -⎛⎫< ⎪⎝⎭，即210162m m -⎛⎫-< ⎪⎝⎭成立即可．记函数21()162m m H m -⎛⎫=- ⎪⎝⎭，易知21()162m m H m -⎛⎫=- ⎪⎝⎭在[2,)+∞上单调递增，且(4)0H =，所以m 的取值范围为[2,4)． …………………………………………………（12分）22．（本小题满分10分）【选修4−1：几何证明选讲】（Ⅰ）证明：∵PE 与圆O 切于点A ， ∴EAB BFA ∠=∠， ∵//AB CD ，∴EAB APD ∠=∠．在HGF △和AGP △中，,,HFG APG HGF AGP ∠=∠⎧⎨∠=∠⎩∴HGF △∽AGP △， ………………………………………………………………（2分）∴GH GP GF GA =．又∵GC GD GF GA =， ∴GP GH GC GD =． ……………………………………………………………（5分）（Ⅱ）解：∵AB AF =， ∴ABF AFB APH ∠=∠=∠． 又∵//AB CD ，∴四边形ABHP 为平行四边形， ………………………………………………（7分）∴9AB PH ==， ∴6GP PH GH =-=， ∴6329GP GH GC GD ⨯===， ∴4PC =．∵PA 是⊙O 的切线，∴2PA PC PD =，PA =．………………………………………………（10分）23．（本小题满分10分）【选修4−4：坐标系与参数方程】解：（Ⅰ）由l 的参数方程消去t ，得2y x =-， 故直线l 的普通方程为20x y --=． …………………………………………（2分）由22222123(cos )4(sin )123cos 4sin ρρθρθθθ=⇒+=+， 而cos ,sin ,x y ρθρθ=⎧⎨=⎩所以223412x y +=，即22143x y +=，故椭圆C 的直角坐标方程为22143x y +=．……………………………………（6分）（Ⅱ）由（Ⅰ）知，12(1,0),(1,0)F F -， 点1(1,0)F -到直线l的距离1d == 点2(1,0)F 到直线l的距离2d ==，12d d +=12,F F 到直线l的距离之和为 …………………（10分）24．（本小题满分10分）【选修4−5：不等式选讲】解：（Ⅰ） 当5a =时，要使函数2()log (|1||5|)f x x x a =-+--有意义， 需|1||5|50x x -+-->恒成立．1,15,5,|1||5|50210102110x x x x x x x <<⎧⎧⎧-+-->⇔⎨⎨⎨-+>->->⎩⎩⎩≤≥或或 11122x x ⇒<>或，所以函数()f x 的定义域为111,,22⎛⎫⎛⎫-∞+∞ ⎪ ⎪⎝⎭⎝⎭．……………………………（5分）（Ⅱ）函数()f x 的值域为R ，需要()|1||5|g x x x a =-+--能取到所有正数， 即min ()0g x ≤．由62,1,|1||5|4,15,26,5,x x x x x x x -<⎧⎪-+-=⎨⎪->⎩≤≤ 易知|1||5|4x x -+-≥，故min ()40g x a =-≤，得4a ≥，所以实数a 的取值范围为4a ≥．……………（10分）云南师大附中2013届高考适应性月考卷（八）·双向细目表文科数学。
云南师大附中高三高考适应性月考卷(三)理科数学试题 Word版.pdf
进球的概率分别是和．
（Ⅰ）如果以投篮得分的期望值高作为选择的标准，问该选手应该选择哪个区投篮？请说明理由；
（Ⅱ）求该选手在A区投篮得分高于在B区投篮得分的概率．
19．（本小题满分12分）
如图5甲，四边形ABCD中，E是BC的中点，DB=2, DC=1，BC=，AB=AD=．将（图甲）沿直线BD折起，使二面角A － BD
13．在区间[－6，6]，内任取一个元素xO ，若抛物线y=x2在x=xo处的切线的倾角为，则的概率为
。
14．在锐角△ABC中，角A、B、C所对的边分别为a、b、c，若b=2，
B=且sinA+sin(A+C)=sinB，则△ABC的面积为
。
15．正三棱锥A－BCD内接于球O，且底面边长为，侧棱长为2，则
A．B．（－3，0）C．（－3，1）D．（－3，－）
11．若在曲线f（x，y）=0上两个不同点处的切线重合，则称这条切线为曲线f（x，y）=0的“自公切线”。下列方
程：①；②，③；④对应的曲线中存在“自公切线”的有（ ）
A．①②B．②③C．①④D．③④
12．已知为R上的可导函数，且均有′（x），则有（ ）
（1）当0＜t＜时； （2）当t≥时， 所以 ………………………………………………………（6分） （Ⅱ）证明：由（Ⅰ）知，当时， 的最小值是，（当且仅当x=时取到最小值） 问题等价于证明， 设， 则，易得，（当且仅当x=1时取到最大值） 从而对一切，都有成立. ………………………………（12分） 21．（本小题满分12分） 解：（Ⅰ）当M的坐标为时， 设过M点的切线方程为，代入，整理得，① 令，解得， 代入方程①得，故得，. 因为M到AB的中点(0，1)的距离为2， 从而过三点的圆的标准方程为． 易知此圆与直线l：y=-1相切. ………………………………………………………（6分） （Ⅱ）设切点分别为、，直线l上的点为M， 过抛物线上点的切线方程为，因为， ， 从而过抛物线上点的切线方程为，又切线过点， 所以得，即. 同理可得过点的切线方程为，………………………（8分） 因为，且是方程的两实根， 从而， 所以， 当，即时， 直线上任意一点M均有MA⊥MB，…………………………………………………（10分） 当，即m≠1时，MA与MB不垂直. 综上所述，当m?=1时，直线上存在无穷多个点M，使MA⊥MB，当m≠1时，直线l 上不存在满足条件的点M.……………………………………………………………（12分） 22．（本小题满分10分）【选修4—1：几何证明选讲】 （Ⅰ）证明：，. 在正△中，，， 又，， △BAD≌△CBE，， 即，所以，，，四点共圆. …………………………（5分） （Ⅱ）解：如图6，取的中点，连结，则. ，， ，， △AGD为正三角形， ，即， 是△AED外接圆的圆心，且圆的半径为. 由于，，，四点共圆，即，，，四点共圆，其半径为.…（10分） 23.（本小题满分10分）【选修4—4：坐标系与参数方程】 解：（Ⅰ）由点M的极坐标为，得点M的直角坐标为， 所以直线OM的直角坐标方程为y?=?x.………………………………………………（4分） （Ⅱ）由曲线C的参数方程（α为参数）， 化成普通方程为：， 圆心为A(1，0)，半径为， 由于点M在曲线C外，
备战2014年高考数学全国统考区精选理科试题(详解)分类汇编2：函数
备战2014年高考之2013届全国统考区（甘肃、贵州、云南）精选理科试题（大部分详解）分类汇编2：函数一、选择题1 ．（云南省昆明三中2013届高三高考适应性月考（三）理科数学）定义域为R 的偶函数)(x f 满足对x R ∀∈，有)1()()2(f x f x f -=+，且当]3,2[∈x 时，18122)(2-+-=x x x f ，若函数)1|(|log )(+-=x x f y a 在),0(+∞上至少有三个零点，则a 的取值范围是 （ ）A ．)22,0(B ．)33,0(C ．)55,0(D ．)66,0( 【答案】B 【解析】因为函数是偶函数，所以(2)()(1)()(1)f x f x f f x f -+=--=-，即(2)(2)f x f x +=-+，所以函数()f x 关于直线2x =对称，又(2)(2)(2)f x f x f x +=-+=-，所以(4)()f x f x +=，即函数的周期是4.由()log (||1)0a y f x x =-+=得，()log (||1)a f x x =+，令()log (||1)a y g x x ==+，当0x >时，()log (||1)log (1)a a g x x x =+=+，过定点(0,1).由图象可知当1a >时，不成立.所以01a <<.因为(2)2f =-，所以要使函数)1|(|log )(+-=x x f y a 在),0(+∞上至少有三个零点，则有(2)2g >-，即2(2)log 32log a a g a -=>-=，所以23a -<，即213a <，所以03a <<，即a 的取值范围是(0,3，选B,如图 2 ．（云南省部分名校2013届高三第一次统一考试理科数学（玉溪一中、昆明三中、楚雄一中））函数()()ax x f a -=6log 在[]2,0上为减函数，则a 的取值范围是（ ）A.()1,0B.()3,1C.(]3,1D. [)+∞,3【答案】B 【解析】当02a ≤≤时，函数()6t g t ax ==-单调递减，所以要使函数()f x 为减函数，所以函数log a y x =为增函数，所以有1a >且(2)620g a =->，即13a <<，所以a 的取值范围是(1,3)，选B.3 ．（甘肃省兰州一中2013届高三上学期12月月考数学（理）试题）设()f x 是定义在R 上的增函数，且对任意x ，都有()()0f x f x -+=恒成立，如果实数,m n 满足不等式22(621)(8)0f m m f n n -++-<，那么22m n +的取值范围是.A （9，49） .B （13，49） .C （9，25） .D （3，7）【答案】A 【解析】对任意x ，都有()()0f x f x -+=恒成立，所以函数()f x 是奇函数，又因为()f x 是定义在R 上的增函数，所以由22(621)(8)0f m m f n n -++-<得：()222(621)(8)8f m m f n n f n n -+<--=-+，所以226218m m n n -+<-+，即()()22344m n -+-≤，所以22m n +的最大值为()22r +，即49；因此最小值为()22r -，即9，22m n +的取值范围是（9，49），故选A 。
6云南师大附中2013届高三高考适应性月考卷(三)
云南师大附中2013届高三适应性月考卷（三）数学（理）试题第Ⅰ卷（选择题，共60分）注意事项：1．答题前，考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号在答题卡上填写清楚，并请认真填涂准考证号．2．每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦擦干净后，再选涂其他答案标号．在试题卷上作答无效．一、选择题（本大题共12小题，每小题5分，共60分，在每个小题给出的四个选项中，只有一项是符合题目要求的）1．设集合{}{}|,|5,,A x x k N B x x x Q ==∈=≤∈则A B 等于（ ）A． {1,2,5} B．{l, 2，4, 5} C．{1，4, 5}D．{1，2，4}2．在复平面内，复数311i i+-对应的点位于（ ）A．第四象限 B．第三象限 C．第二象限 D．第一象限3．一个几何体的三视图如图l所示，其中正视图是一个正三角形，则该几何体的体积为（ ）A．1 334．下列函数中既不是奇函数也不是偶函数的是 （ ）A．||2x y = B．1(y g x =+C．22x x y -=+D．111y gx =+5.执行如图2所示的程序框图，则输出的x值是（ ）A．8B．6C．4D．36.已知条件2:340p x x --≤；条件22:690q x x m -+-≤若p 是q 的充分不必要条件，则m 的取值范围是（ ）A．[]1,1- B．[]4,4- C．(][),44,-∞-+∞D．(][),11,-∞-+∞7．如图3，直线y=2x 与抛物线y=3－x 2所围成的阴影部分的面积是（ ）A ．353B ．C ．2-D ．3238．对于函数11()(sin co s )|co s sin |22f x x x x x =+--，下列说法正确的是（ ）A．该函数的值域是[]1,1-B．当且仅当22()2k x k k Z πππ<<+∈时，()0f x >C．当且仅当2()2x k k Z ππ=+∈时，该函数取最大值1D．该函数是以π为最小正周期的周期函数9．实数对（x，y）满足不等式组20,250,20,x y x y y --≤⎧⎪+-≥⎨⎪-≤⎩则目标函数z=kx－y当且仅当x=3，y=1时取最大值，则k的取值范围是（ ）A ．[)1,1,2⎛⎫-∞-+∞ ⎪⎝⎭B ．1,|2⎛⎫-+∞ ⎪⎝⎭C ．1.12⎛⎫-⎪⎝⎭D ．(],1-∞-10．已知函数21,0,()1,0,x f x x x -≥⎧=⎨-<⎩则满足不等式2(3)(2)f x f x -<的x 的取值范围为（ ）A ．[)3,0-B ．（－3，0）C ．（－3，1）D ．（－311．若在曲线f （x ，y ）=0上两个不同点处的切线重合，则称这条切线为曲线f （x ，y ）=0的“自公切线”。
云南省昆明市2013届高三3月复习教学质量检测数学(理)试题 Word版含答案
云南昆明市2013届高三复习教学质量检测数学（理）试题本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分．考试结束后，将本试卷和答题卡一并交回．满分150分，考试用时120分钟 注意事项：1．答题前，考生务必用黑色碳素笔将自己的姓名．准考证号、考场号、座位号在答题卡上填写清楚，并认真核准条形码上的准考证号，姓名、考场号、座位号，在规定的位置贴好条形码．2．每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动用橡皮擦干净后，再选涂其它答案标号，答在试卷上的答案无效第I 卷（选择题，共60分）一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1．若复数z 满足31ii z-=+，i 是虚数单位，则z=A ．22i -B ．12i -C ．2i +D ．12i +2．某几何体的三视图如图所示，它的体积为A ．2B ．4C ．23D ．433．已知sin10,k =则sin 70°=A ．1—k 2B ．2k 2 —lC ．1—2k 2D ．1+2k 24．已知双曲线C 的中心在原点，焦点在坐标轴上，P （l ，-2）是C 上的点，且是C 的一条 渐近线，则C 的方程为A ．2212y x -=B ．22212y x -=C ．222212122y y x x -=-=或 D ．22221122y y x x -=-=或 5．若a<b<0，则下列不等式一定成立的是A ．11a b b>- B ．2a ab <C ．||||1||||1b b a a +<+ D ．n na b >6．函数()sin()(0)6f x x πωω=+>把函数f （x ）的图象向右平移6π个长度单位，所得图象的一条对称轴方程是x=,3πω则，的最小值是A ．lB ．2C ．4D ．327．已知某算法的流程图如图所示，则程序运行结束时输出的结果为 A ．19 B ．10 C ．-19 D ．-108．设不等式组544||1x y ππ⎧≤≤⎪⎨⎪≤⎩所表示的平面区域内为D ，现向区域D内随机投掷一点，且该点又落在曲线sin cos y x y x ==与围成的 区域内的概率是ABC．D．1π-9．函数21()ln ||8f x x x =+的图象大致是10．在直角三角形ABC 中，∠C ,2π=AC=3，取点D 、E ，使2,BD DA AB CD CA CE CA =⋅+⋅==3BE,那么=A ．3B ．6C ．-3D ．-611．已知三棱锥P-ABC 的四个顶点均在半径为1的球面上，且满足PA 、PB 、PC 两两垂直，当 PC·AB 的最大值时，三棱锥O —PAB 的高为 ABCD12．定义在R 上的函数f （x ）满足()(),()(4),f x f x f x f x -==-∈且已知x (1,-3]时，c o s ,(1,1](),()4()21|2|,(1,3]x xf xg x f x x x x π⎧∈-⎪==-⎨⎪--∈⎩则函数零点个数为A ．3B ．4C ．5D ．6第II 卷（非选择题，共90分）本卷包括必考题和选考题两部分，第（13）题～第（21）题为必考题，每个试题考生都必须做答，第（22）题～第（24）题为选考题，考生根据要求做答二、填空题：本大题共4小题，每小题5分，共20分把答案填在答题卡上． 13．等比数列{}n a 的前n 项和为4214,2,n S S a a a =则的值是 ； 14．将4名学生分配到3个学习小组，每个小组至少有1学生，则不同的分配方案共有 种（用数学作答）；15．已知直线22222:1(0)b x y y C a b a a b=-=>>与椭圆交于P 、Q 两点，F 是C 的右焦点，若|FQ|=2|FQ|，则C 的离心率为 。
【2013备考】各地名校试题解析分类汇编(一)理科数学：3导数1
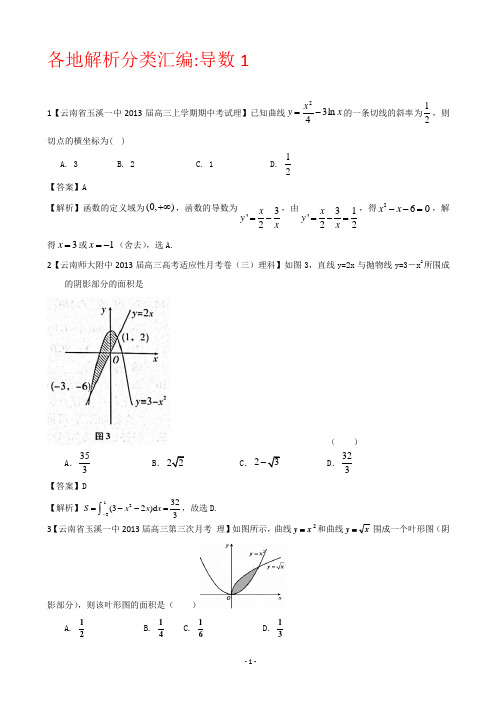
各地解析分类汇编:导数11【云南省玉溪一中2013届高三上学期期中考试理】已知曲线x x y ln 342-=的一条切线的斜率为21，则切点的横坐标为( ) A. 3 B. 2 C. 1 D.21【答案】A【解析】函数的定义域为(0,)+∞，函数的导数为3'2x y x =-，由31'22x y x =-=，得260x x --=，解得3x =或1x =-（舍去），选A.2【云南师大附中2013届高三高考适应性月考卷（三）理科】如图3，直线y=2x 与抛物线y=3－x 2所围成的阴影部分的面积是（ ）A ．353B ．C ．2D ．323【答案】D【解析】12332(32)d 3S x x x -=--=⎰，故选D. 3【云南省玉溪一中2013届高三第三次月考 理】如图所示，曲线2x y =和曲线x y =围成一个叶形图（阴影部分），则该叶形图的面积是（ ）A.21 B. 41 C. 61 D. 31【答案】D【解析】由2y xy ⎧=⎪⎨=⎪⎩，解得11x y =⎧⎨=⎩或0x y =⎧⎨=⎩，所以根据积分的应用可得阴影部分的面积为3123120021211)()33333x dx x x =-=-=⎰，选D. 4【山东省烟台市莱州一中2013届高三10月月考（理）】由直线2,21==x x ，曲线xy 1=及x 轴所谓成图形的面积为 A.415B.417C.2ln 21D. 2ln 2【答案】D【解析】根据积分的应用可知所求22112211ln ln 2ln2ln 22dx x x==-=⎰，选D. 5【云南师大附中2013届高三高考适应性月考卷（三）理科】已知()f x 为R上的可导函数，且,x R ∀∈均有()f x f>′（x），则有 （ ）A．20132013(2013)(0),(2013)(0)e f f f e f -<> B．20132013(2013)(0),(2013)(0)e f f f e f -<< C．20132013(2013)(0),(2013)(0)e f f f e f ->>D ．20132013(2013)(0),(2013)(0)e f f f e f -><【答案】A【解析】构造函数()()x f x g x=，则2()()()()()()()x x x x f x e e f x f x f x g x e e ''''--==，6【山东省烟台市莱州一中2013届高三10月月考（理）】曲线x e y 21=在点()2,4e处的切线与坐标轴所围三角形的面积为 A.2eB.24eC.22eD.229e 【答案】A【解析】121'2x y e =，所以在点()2,4e 的导数为142211'22y e e ⨯==，即切线斜率为212k e =，所以切线方程为221(4)2y e e x -=-，令0x =得，2y e =-，令0y =，得2x =.所以三角形的面积为22122e e ⨯⨯=，选A.7【云南省昆明一中2013届高三新课程第一次摸底测试理】函数22ln y x x e ==在处的切线与坐标轴所围成的三角形的面积为A ．292e B ．212Se =C ．22eD ．2e【答案】D【解析】212'2y x x x =⨯=，所以在2x e =处的切线效率为22k e =，所以切线方程为2224()y x e e-=-，令0x =，得2y =，令0y =，得2x e =-，所以所求三角形的面积为22122e e ⨯⨯=，选D.8【山东省烟台市莱州一中20l3届高三第二次质量检测 （理）】曲线()ln 2y x =+在点()1,0P -处的切线方程是 A.1y x =+ B.1y x =-+C.21y x =+D.21y x =-+【答案】A 【解析】1'2y x =+,所以在点P 处的切线斜率1112k ==-+，所以切线方程为(1)1y x x =--=+，选A.9【山东省烟台市莱州一中20l3届高三第二次质量检测 （理）】由直线2,,0sin 33x x y y x ππ====与所围成的封闭图形的面积为 A.12B.1C.2【答案】B【解析】由积分的应用得所求面积为2233332sin cos coscos 2cos 1333xdx xπππππππ=-=-+==⎰，选B. 10【天津市新华中学2012届高三上学期第二次月考理】 已知函数))((R x x f ∈满足1)1(=f ，且)(x f 的导函数21)('<x f ，则212)(+<x x f 的解集为 A. {}11<<-x x B. {}1-<x x C. {}11>-<x x x 或 D. {}1>x x【解析】设1()()()22xF x f x =-+, 则11(1)(1)()11022F f =-+=-=，1'()'()2F x f x =-，对任意x R ∈，有1'()'()02F x f x =-<，即函数()F x 在R 上单调递减，则()0F x <的解集为(1,)+∞，即212)(+<x x f 的解集为(1,)+∞，选D.11【山东省烟台市莱州一中20l3届高三第二次质量检测 （理）】函数()32f x x bx cx d =+++的大致图象如图所示，则2212x x +等于A.89B.109C.169D.289【答案】C【解析】函数过原点，所以0d =。
云南师大附中2013届高考适应性月考卷(五)理科数学
云南师大附中2013届高考适应性月考卷（五）理科数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．参考公式：样本数据12,,,n x x x 的标准差s =其中x 为样本平均数 柱体体积公式VSh =其中S 为底面面积，h 为高锥体体积公式13V Sh =其中S 为底面面积，h 为高球的表面积，体积公式24R S π=，334R V π=其中R 为球的半径第Ⅰ卷（选择题共60分）一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合{}|10A x ax =-=，{}3,4B =，且A B A = ，则a 的所有可能值组成的集合是A ．110,,34⎧⎫⎨⎬⎩⎭B ．11,34⎧⎫⎨⎬⎩⎭C ．13⎧⎫⎨⎬⎩⎭D ．{}02．设复数21z i=-（其中i 为虚数单位），则23z z +为 A ．2iB ．10i -C ．10iD ．62i --3．设向量sin ,2a α⎛⎫= ⎪ ⎪⎝⎭的模为2，则cos2α＝ A ．14-B ．12C ．12-D4．如图1，设D 是图中所示的矩形区域，E 是D 内函数cos y x =的图像上方的点构成的区域，向D 中随机投一点，则该点落入E （阴影部分）中的概率为A ．2πB ．1πC ．2ππ- D ．125．在同一个坐标系中画出函数xy a =，sin y ax =的部分图像，其中0a >且1a ≠，则下列所给图像中可能正确的是6．一个几何体的三视图如图2所示，其中俯视图是菱形，则该几何体的侧面积为A B CD 7．图3是某算法的程序框图，则程序运行后输出的T 是A ．1B ．2C ．3 D．48．函数sin()y x ωϕ=+（0ω>且||2πϕ<）在区间2,63ππ⎡⎤⎢⎥⎣⎦上单调递减，且函数值从1减小到－1，那么此函数图像与y 轴交点的纵坐标为A ．2B ．12C ．2D ．49．设a 、b 、c 、d R ∈，若,1,a b 成等比数列，且,1,c d 成等差数列，则下列等式恒成立的是A ．||2a b cd +≥B ．2a b cd +≥C ．||2a b cd +≤D ．2a b cd +≤10．P 是双曲线22221(0,0)x y a b a b-=>>上的点，1F 、2F 是其焦点，且120PF PF ⋅= ，若△12F PF 的面积是9，7a b +=，则双曲线的离心率为A ．74B ．54C D 11．如图4，已知O 、A 、B 是平面上三点，向量OA a = ，OB b =．在平面AOB 上，P 是线段AB 垂直平分线上任意一点，向量OP p = ，且||3a =，正视图 侧视图11111||2b = ，则()p a b ⋅-的值是A ．12 B ．32 C ．72D ．52 12．已知0a >且1a ≠，2()xf x x a =-，当(1,1)x ∈-时均有1()2f x <，则实数a 的取值范围是A ．[)10,2,2⎛⎤+∞ ⎥⎝⎦B ．(]1,11,22⎡⎫⎪⎢⎣⎭C ．(]1,11,44⎡⎫⎪⎢⎣⎭D ．[)10,4,4⎛⎤+∞ ⎥⎝⎦第Ⅱ卷（非选择题共90分）注意事项：用钢笔或圆珠笔直接答在答题卡上．二、填空题：本大题共4小题，每小题5分，共20分，把答案填在题中横线上．13．在△ABC 中，角A 、B 、C 所对的边分别为a 、b 、c ，且4cos 5A =)4A π-的值为 ． 14．若数列{}n a 满足112a =，2*12()n n a a a n a n N +++=∈ ，则数列{}n a 的前60项和为 ． 15．若不等式组0,34,34,x x y x y ≥⎧⎪+≥⎨⎪+≤⎩所表示的平面区域被直线43y kx =+分为面积相等的两部分，则k 的值为 ．16．如图5，已知球O 是棱长为1的正方体1111ABCD A B C D -的内切球，则以球心O 为顶点，以球O 被平面1ACD 所截得的圆为底面的圆锥的体积为 ．三、解答题：本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤．17．（本小题满分12分）已知等比数列{}n a 满足22a =，且3452a a a +=，0n a >． （1）求数列{}n a 的通项公式；（2）设(1)321nn n b a n =-++，数列{}n b 的前n 项和为n T ，求n T18．（本小题满分12分）在一次抢险救灾中，某救援队的50名队员被分别分派到四个不同的区（1）求这2（2）若这2人来自区域A ，D ，并记来自区域A 队员中的人数为ξ，求随机变量ξ的分布列及数学期望．19．（本小题满分12分）在如图6所示的几何体中，平面ACE ⊥平面ABCD ，四边形ABCD 为平行四边形，90ACB ∠=，EF ∥BC ，2AC BC EF ==，AC ==．（1）求证：AE ⊥平面BCEF ； （2）求二面角A BF C --的大小．20．（本小题满分12分）已知函数2()ln 8x f x x =-，[]1,3x ∈． （1）求()f x 的最大值与最小值；（2）若()4f x at <-对于任意的[]0,2t ∈恒成立，求实数a 的取值范围．21．（本小题满分12分）已知椭圆2222:1(0)x y C a b a b+=>>的离心率为2，连接椭圆的四个顶点得到的菱形的面积为 （1）求椭圆C 的方程；（2）若过点(2,0)的直线l 的与椭圆C 交于A 、B 两点，设P 为椭圆上一点，且满足OA OB tOP += （O 为坐标原点），当||PA PB -< t 的取值范围．请考生在第22、23、24三题中任选一题作答，如果多做，则按所做的第一题记分．作答时请写清题号． 22．（本小题满分10分）【选修4－1：几何选讲】如图7所示，PA 为O 的切线，A 为切点，PBC 是过点O 的割线，10PA =，5PB =，BAC ∠的平分线与BC 和O 分别交于点D 和E ．（1）求证：AB PAAC PC=； （2）求AD AE ⋅的值．23．（本小题满分10分）【选修4－4：坐标系与参数方程】已知曲线C 的极坐标方程是1ρ=，以极点为原点，极轴为x 轴的正半轴建立平面直角坐标系，直线l的参数方程为11,22,2x t y ⎧=+⎪⎪⎨⎪=+⎪⎩（t 为参数）．（1）写出直线l 的普通方程与曲线C 的直角坐标方程；（2）设曲线C 经过伸缩变换2,,x x y y '=⎧⎨'=⎩得到曲线C '，设曲线C '上任一点为(,)M x y，求x +的最小值．24．（本小题满分10分）【选修4－5：不等式选讲】 设函数()|1||1|f x x x =-+-． （1）若1a =-，解不等式()3f x ≥；（2）如果x R ∀∈，()2f x ≥，求a 的取值范围．云南师大附中2013届高考适应性月考卷（五）理科数学参考答案一、选择题，本题考查基础知识，基本概念和基本运算能力二、填空题．本题考查基础知识,基本概念和基本运算技巧 13． 14． 15． 16．三、解答题 17．云南师大附中2013届高考适应性月考卷（五）理科数学参考答案第Ⅰ卷（选择题，共60分）一、选择题（本大题共12小题，每小题5分，共60分）【解析】1．由= A B A 知⊆A B ，而{3,4}=B ，且0=a 时，=∅A ，适合= A B A ，故选A ． 2．2112i i=-=+z ，则223(12i)3(12i)10i +=+++=z z ，故选C. 3. 213sin 24+=α，则21sin 4=α，21cos212sin 2=-=αα，故选B ．4．=πD S ，22cos d 2ππ-=π-=π-⎰E S x x ，故选C ．5．0>a 且1≠a ，当22π=>πT a时，01<<a ，故选C. 6．该几何体是高为1，底面对角线长为2的菱形构成的四棱锥，1121222⎛⎫⎛=⨯+⨯= ⎪ ⎝⎭⎝S D ．7．第一次循环有1,1,2===a T k ，第二次循环有0,1,3===a T k ，第三次循环有0,1,4===a T k ，第四次循环有1,2,5===a T k ，第五次循环有1,3,6===a T k ，此时不满足条件，输出3=T ，故选C.8．12=T 2362πππ-=，=πT ，222ππ===πT ω，此时sin(2)=+y x ϕ，又函数过点,16π⎛⎫⎪⎝⎭，代入可得6π=ϕ，因此函数sin 26π⎛⎫=+ ⎪⎝⎭y x ，令0=x ，可得12=y ．故选B.9．212+⎛⎫= ⎪⎝⎭a b ab ≤，故2+a b ≥，又2+=c d ，故212+⎛⎫= ⎪⎝⎭c d cd ≤，即22cd ≥，故选A ．10． 设1=PF x ，2=PF y ，由题意得192=xy ，即18=xy ，又2224+=x y c ，故22()24-+=x y xy c ， 即229+=a c ，于是29=b ，即3=b ，又7+=a b ，所以4=a ，5=c ，54==c e a ，选B. 11．如图1，采用特殊化法，当点P 运动到线段AB 的中点M 这一特殊位置时，有1()2=+p a b ，所以22115()()()()222-=+-=-= p a b a b a b a b ，故选D.另解：设线段AB 的中点为M ，则1()2=-=-+ MP OP OM p a b ，又=- BA a b ，且⊥ MP BA ，所以1()()02⎡⎤-+-=⎢⎥⎣⎦p a b a b ，即22115()()()()222-=+-=-= p a b a b a b a b .12．原命题212⇔-<x x a ，在(1,1)∈-x 上恒成立，因为当(1,1)∈-x 时2111222--<x ≤，于是若1>a ，则x a 的最小值是1-a ，故112-a ≥，即2a ≤，此时12<a ≤，至此可选答案为B ；事实上若01<<a ，则x a 的最小值是a ，故12a ≥，此时1 1.2<a ≤（也可作出212=-y x 与=x y a 在(1,1)∈-x 上的简图，易知当1>a 时，112-a ≥；当01<<a 时，112a ≥，解之得B ．）第Ⅱ卷（非选择题，共90分）二、填空题（本大题共4小题，每小题5分，共20分）图1【解析】13．在ABC △中，由4cos 5=A ，得3sin 5=A 341sin cos 4555π⎛⎫-=-=-=- ⎪⎝⎭A A A ．14. 由题意知2=n n S n a ，当2n ≥时，211(1)--=-n n S n a ，两式相减得221(1)-=--n n n a n a n a ，即221(1)(1)--=-n n n a n a ，故111--=+n n a n a n ， 所以324112*********.23451(1)---===++n n n a a a a n n a a a a a a n n n n …… 又1a 也满足上式，故111(1)1==-++n a n n n n ，所以数列{}n a 的前60项和为16016161-=． 15．不等式组所表示的平面区域如图2阴影部分，易知40,3⎛⎫⎪⎝⎭B ，所以直线43=+y kx 过点B ，若=BDC BDA S S △△，则点D 为线段AC 的中点，由34,34,+=⎧⎨+=⎩x y x y 得(1,1)A ，又(0,4)C，所以15,22⎛⎫⎪⎝⎭D ，代入直线43=+y kx 中，解得73=k．16．如图3，O 为球心，也是正方体的中心，设球O 被平面1ACD 所截得的圆的半径为r ，AC 中点为M，则113==r D M ，球的半径12=R ，则O 到平面1ACD 的距离=h圆锥的体积213=πV r h ．三、解答题（共70分. 解答应写出文字说明，证明过程或演算步骤） 17．（本小题满分12分）解：（Ⅰ）设等比数列{}n a 的首项为1a ，公比为q ， 则12341112,2, =⎧⎪⎨+=⎪⎩a q a q a q a q ①②…（2分）把①代入②整理得220--=q q ，即1,2=-=q q ，0>n a ∵, 2=q ∴，代入①得11=a , ∴12-=n n a ． ……………（6分）图2图3（Ⅱ）1(1)321(1)3221-=-++=-++ n n n n n b a n n ∵13(2)21-=--++n n ， ……………（9分） 13[1248(2)][35721]-=--+-++-++++++ n n T n ,223[1(2)]2(2)2112---=++=-++-+n n n T n n n n ∴． ………………………………（12分）18．（本小题满分12分）解：（Ⅰ）记“这2人来自同一区域”为事件E ，那么22222010515250C C C C 2()C 7+++==P E ， 所以这2人来自同一区域的概率是27． …………………………………………（4分） （Ⅱ）随机变量ξ可能取的值为0，1，2，且215235C 3(0)C 17===P ξ，112201520223535C C C 6038(1),(2).C 119C 119======P P ξξ …………………………（8分） 所以ξ的分布列是：ξ的数学期望为360381368012.171191191197=⨯+⨯+⨯==E ξ……………………（12分） 19．（本小题满分12分）（Ⅰ）证明：如图4，∵平面⊥ACE 平面ABCD ， 平面 ACE 平面=ABCD AC ， 且⊥BC AC ，∴⊥BC 平面ACE，⊥BC AE ， …………………………………………………………………………（3分） 又==AC ，∴⊥AE EC ，而= BC EC C ，∴⊥AE 平面.BCEF ……………………………………………（6分）图4（Ⅱ）解：方法一：建立如图5所示的空间直角坐标系， 不妨设2==AC BC，则=AE EC ， 由题意得(0,0,0)A ，(2,2,0)-B ，(2,0,0)C ， (1,1,1)-F ，(2,2,0)=- AB ，(0,2,0)=BC ，(1,1,1)=-BF ， ……………………………………………………………………（8分） 设平面BFC 的法向量为111(,,)=m x y z ，由0= m BC ，且0=m BF ，得(1,0,1)= m ， 设平面ABF 的法向量为222(,,)=n x y z ，由0= n AB ，且0=n BF ，得(1,1,0)= n ， ……………………………………（10分） 所以1cos ,2⋅〈〉==m n m n m n ，∴二面角--A BF C 的大小为60︒. ………………………………………………（12分） 方法二：如图6，取AC 的中点N ，连接EN ， ∵平面⊥ACE 平面ABCD ，=AE EC ， ∴⊥EN 平面ABCD .取AB 的中点H ，连接FH ，NH ，由题意可知四边形EFHN 是平行四边形， 则//FH EN ，⊥FH 平面ABCD ， ∴平面ABF ⊥平面ABCD .连接CH ，∵=AC BC ，则⊥CH AB ，∴⊥CH 平面ABF . 过H 向BF 引垂线交BF 于R ，连接CR ，则⊥CR BF ，则∠HRC 为二面角--A BF C 的平面角. …………………………………………（9分） 由题意，不妨设2==AC BC，则=AB图5图6在Rt BHF △中，=HR，12=CH AB 所以在Rt △CHR中，tan ∠=CHHRC RH因此二面角--A BF C 的大小为60︒. ……………………………………………（12分） 20．（本小题满分12分）解：（Ⅰ）1(2)(2)()44+-'=-=x x x f x x x， 令()0'=f x ，得2=-x 或2=x .[1,3]∈x ∵，故当12<<x 时，()0'<f x ，当23<<x 时，()0'>f x ， …………………………………………………………（3分） ∴()f x 在2=x 处取得唯一极小值，也是最小值1(2)ln 22=-f ， 又1(1)8=f ，9(3)ln38=-f ，19ln 3ln 31088⎛⎫--=-> ⎪⎝⎭，即(1)(3)>f f ，∴()f x 的最大值为18， 最小值为1ln 22-． ………………………………………（6分）（Ⅱ）由（Ⅰ）知1()8f x ≤，所以()4<-f x at 对于任意的[0,2]∈t 恒成立，只要148->at ，即8310-<at 对任意[0,2]∈t 恒成立， ………………………（9分） 设()831=-g t at （[0,2]∈t ），则(0)0,(2)0,<⎧⎨<⎩g g 解得3116<a ，所以实数a 的取值范围是31,16⎛⎫-∞ ⎪⎝⎭． ……………………………………………（12分）21．（本小题满分12分）解：（Ⅰ）由2==c e a 得，222=a b，依题意1222⨯⨯=a b，即=ab解方程组222,⎧=⎪⎨=⎪⎩a b ab得=a 1=b ，所以椭圆C 的方程为2212+=x y . …………………………………………………（4分）（Ⅱ）依题意直线l 的斜率存在，设l ：(2)=-y k x ，11(,)A x y ，22(,)B x y ，(,)P x y ， 由22(2),1,2=-⎧⎪⎨+=⎪⎩y k x x y 得2222(12)8820+-+-=k x k x k ， 由422644(21)(82)0∆=-+->k k k ，得212<k ， 且2122812+=+k x x k ，21228212-=+k x x k ． ………………………………………………（6分）∵+=OA OB tOP ，1212(,)(,)++=x x y y t x y ∴，当0=t 时，0=k，2-== PA PB a ，∴0≠t ， 21228(12)+==+x x k x t t k ，1212214[()4](12)+-==+-=+y y k y k x x k t t t k ， ∵点P 在椭圆上，∴222222222(8)(4)22(12)(12)-+⋅=++k k t k t k ，即22216(12)=+k t k . …………………………………………………………（8分）∵-< PA PB12-<x ，即22121220(1)[()4]9++-<k x x x x ，∴422222648220(1)4(12)129⎡⎤-+-⋅<⎢⎥++⎣⎦k k k k k ， 即22(41)(1413)0-+>k k ，∴21.4>k ………………………………………………（10分）又212<k ，∴21142<<k ，则由222216881221==-++k t k k ，得2843<<t ，∴实数t的取值范围是2,2⎛⎫- ⎪ ⎪⎝⎭⎝⎭． …………………………（12分）22．（本小题满分10分）【选修4—1：几何证明选讲】（Ⅰ）证明：PA ∵为 O 的切线，∠=∠PAB ACP ∴， 又∠=∠P P ，PAB PCA ∴△∽△．.=AB PAAC PC∴…………………………………………………………………………（4分） （Ⅱ）解：如图7，∵P A 为 O 的切线，PBC 是过点O 的割线，2.=⋅PA PB PC ∴ ………………………………………………………………………（5分）又10,5,20,15,====PA PB PC BC ∵∴ 由（Ⅰ）知，12==AB PA AC PC ，∵BC 是 O 的直径， 22290,225,∠=︒+==CAB AC AB BC ∴∴==AC AB ∴ …………………………（7分）连接CE ，则∠=∠ABC E ，又∠=∠CAE EAB ，,ACE ADB △∽△ .=AB ADAE AC∴90.⋅=⋅=AD AE AB AC ∴ …………………………………………（10分）23．（本小题满分10分）【选修4—4：坐标系与参数方程】解：（Ⅰ）直线l20-+y ，曲线C 的直角坐标方程为：221+=x y ． …………………………………………（4分） （Ⅱ）∵2,,'=⎧⎨'=⎩x x y y ∴将,2'⎧=⎪⎨⎪'=⎩x x y y 代入C ，得'C ：22()()14''+=x y ， 即椭圆'C 的方程为2214+=x y ．设椭圆'C 的参数方程为2cos ,sin =⎧⎨=⎩x y ϕϕ（ϕ为参数），则π2cos 4sin 6⎛⎫+=+=+ ⎪⎝⎭x ϕϕϕ，∴+x 的最小值为 4.- …………………………………………………………（10分） 24．（本小题满分10分）【选修4—5：不等式选讲】解：（Ⅰ）方法一：当1=-a 时，()11=-++f x x x ， …………………………（1分） 由()3f x ≥得 113-++x x ≥，（ⅰ）当1-x ≤时，不等式化为113---x x ≥，即23-x ≥， 不等式组1,()3-⎧⎨⎩x f x ≤≥的解集为3,2⎛⎤-∞- ⎥⎝⎦；（ⅱ）当11-<x ≤时，不等式化为113-++x x ≥，不可能成立，图7不等式组11,()3-<⎧⎨⎩x f x ≤≥ 的解集为∅；（ⅲ）当1>x 时，不等式化为113-++x x ≥， 即23x ≥，不等式组1,()3>⎧⎨⎩x f x ≥的解集为3,2⎡⎫+∞⎪⎢⎣⎭，综上得，()3f x ≥的解集为33,,22⎛⎤⎡⎫-∞-+∞ ⎪⎥⎢⎝⎦⎣⎭. ……………………………（5分）方法二：当1=-a 时，()11=-++f x x x ，由()3f x ≥得113-++x x ≥，由绝对值的几何意义11-++x x 表示数轴上的点x 到1-与1的距离之和，而11-++x x 的最小值为2，所以当32-x ≤或32x ≥时，113-++x x ≥，所以不等式()3f x ≥的解集为33,,22⎛⎤⎡⎫-∞-+∞ ⎪⎥⎢⎝⎦⎣⎭． （Ⅱ）若1,()21==-a f x x ，不满足题设条件，若21,,1,()1,1,2(1),1,-++⎧⎪<=-<<⎨⎪-+⎩x a x a a f x a a x x a x ≤≥()f x 的最小值为1-a ；若21,1,1,()1,1,2(1),,-++⎧⎪>=-<<⎨⎪-+⎩x a x a f x a x a x a x a ≤≥ ()f x 的最小值为1-a ， …………………（8分）所以,()2∀∈x f x R ≥的充分条件是12-a ≥，从而a 的取值范围为(,1][3,)-∞-+∞ ． ………………………………………（10分）云南师大附中2013届高考适应性月考卷（五）·双向细目表 理科数学。
云南师大附中2013届高三高考适应性月考卷(三)理科综合试题 Word版
云南师大附中2013届高考适应性月考卷（三）理综试题本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，考试结后，请将本试卷和答题卡并交回。
满分300分，考试用时150分钟。
注意事项：1．答题茄子，考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号在答题卡上填写清楚，并请认真填涂准考证号。
2．每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑o如需改动，用橡皮擦擦干净后，再选涂其他答案标号。
在试题卷上作答无效。
以下数据可供解题时参考。
可能用到的相对原子质量：H-I C-12 N-14 0-16 Na-23 S-32 Fe-56第Ⅰ卷（选择题，共126分）一、选择题：本题共1 3小题，每小题6分o在每小题给出的四个选项中，只有一项是符合题目要求的。
1．下列关于生物体内化合物的叙述，正确的是A．肤岛素是在核糖体上合成并经高尔基体分泌的B．细胞内的单糖都可以作为生命活动的能源物质C．噬茵体和质粒的组成元素相同D．酶、载体蛋白在发挥作用后立即失去生物活性2．下列有关细胞生命历程的说法正确的是A．多细胞生物个体的长大，主要原因是细胞的生长B．细胞生物的生命历程中一定会发生细胞的分化C．被病原体感染的细胞的清除，是通过细胞凋亡完成的D．癌变细胞的细胞膜会发生改变，如糖蛋白、甲胎蛋白和癌胚抗原等会减少3．下列有关基因工程和酶的相关叙述，正确的是A．同种限制酶既可以切割目的基因又可以切割质粒，因此不具备专一性B．运载体的化学本质与载体蛋白相同C．限制酶不能切割烟草花叶病毒的核酸D．DNA连接酶可催化脱氧核苷酸链间形成氢键4．利用基因型为aabb与AABB的水稻作为亲本培育基因型为AAbb的新品种，有关叙述不正确的是A．操作最简便的是杂交育种，能明显缩短育种年限的是单倍体育种B．利用F1的花药进行离体培养可获得该新品种C．诱变育种不能定向获得该新品种D．若通过多倍体育种获得AAAAbbbb个体，和该新品种存在生殖隔离5．下列有关人类遗传病的叙述正确的是A．遗传病都是由致病基因引起的B．调查人群中，的遗传病时，最好选择发病率较高的单基因遗传病C．单基因遗传病是由一个致病基因控制的D．通过调查患病家族，可统计出某种遗传病在人群巾的发病率6．下列与生物进化相关的描述，正确的是A．生物的变异都能为生物进化提供原材料B．不是所有新物种的形成都需要经过隔离C．基因频率发生改变，说明生物进化了D．共同进化导致生物多样性的形成7．化学与科学、技术、社会、环境密切相关。
云南师大附中2013届高考适应性月考卷(一)理科数学
10分
极坐标与参数方程
中
24
解答题
10分
不等式
中
命题
思想
达成
目标
优秀率
及格率
平均分
5%
60%
90～97
检查基本知识、基本解题方法、常规方法的掌握，重点体现数形结合、分类讨论、特值思想数学命题思想
一、每次考试在选择题及填空题侧重于所复习内容。
二、大题、包括选考题每次考试按照高考考点分布滚动命题，8次考试将所有知识点，考点覆盖，达到全程复习、全程备考的目的。
云南师大附中2013届高考适应性月考卷（一）·双向细目表
理科数学
题号
题型
分值
试题内容
难易程度
备注
1
选择题
5分
集合
易
2
选择题
5分
复数
易
3
选择题
5分
向量
易
4
选择题
5分
函数
易
5
选择题
5分
三角函数
中
6
选择题
命题与函数
中
8
选择题
5分
数列与函数
中
9
选择题
5分
三角函数
中
10
选择题
5分
定积分、几何概型
中
11
选择题
5分
圆锥曲线
难
12
选择题
5分
函数
难
13
填空题
5分
立体几何
易
14
填空题
5分
排列组合、概率
易
15
填空题
5分
函数
中
16
云南省昆明市2013届高三复习适应性检测数学(理)试题
昆明市2013届高三复习适应性检测 理科数学试卷本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.第Ⅰ卷1至4页，第Ⅱ卷5至8页.考试结束后，将本试卷和答题卡一并交回.满分150分，考试用时120分钟.注意事项：1．答题前，考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号在答题卡上填写清楚，并认真核准条形码上的准考证号、姓名、考场号、座位号，在规定的位置贴好条形码.2．每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号，答在试卷上的答案无效.第Ⅰ卷（选择题，共60分）一、选择题：本大题共12小题，每小题5分，共60分. 在每小题给出的四个选项中，只有一项是符合题目要求的.（1）复数i i+12（i 是虚数单位）的虚部是（A ）i （B ）i - （C ）1 （D ）1-（2）对某班级50名学生学习数学与学习物理的成绩进行调查，得到如下表所示：由22()()()()()n ad bc K a b c d a c b d -=++++，解得2250(181967)11.525252426K ⨯⨯-⨯=≈⨯⨯⨯参照附表，得到的正确结论是（A）在犯错误的概率不超过000.1的前提下，认为“数学成绩与物理成绩有关”（B）在犯错误的概率不超过000.1的前提下，认为“数学成绩与物理成绩无关”（C）有00100的把握认为“数学成绩与物理成绩有关”（D）有0099以上的把握认为“数学成绩与物理成绩无关”（3）把边长为1的正方形ABCD沿对角线BD折起，连结AC，得到三棱锥C－ABD，其正视图与俯视图为全等的等腰直角三角形，如图所示，则侧视图的面积为（A）14（B）12（C）（D）1（4）已知等差数列{}na满足244a a+=，534a a=，则数列{}na的前10项的和等于（A）23 （B）95 （C）135 （D）138正视图俯视图（5）下列程序框图中，某班50名学生，在一次数学考试中，n a 表示学号为n 的学生的成绩，则（A ）P 表示成绩不高于60分的人数； （B ）Q 表示成绩低于80分的人数； （C ）R 表示成绩高于80分的人数；（D ）Q 表示成绩不低于60分，且低于80分人数.（6）设抛物线2:2(0)C y px p =>，直线l 过抛物线C 的焦点F ，且与C 的对称轴垂直，l 与C 交于Q R 、两点， S 为C 的准线上一点，若QRS △的面积为8，则p =（A（B ）2 （C） （D ）4（7）已知函数()2sin sin )1f x x x x =-+，若()f x ϕ-为偶函数，则ϕ的一个值为（A ）2π （B ）3π（C ）4π （D ）6π（8）命题1p ：若函数1()f x x a =-在(,0)-∞上为减函数，则(,0)a ∈-∞；命题2p ：(,)22x ππ∈-是()tan f x x =为增函数的必要不充分条件；命题3p ：“a 为常数，R x ∈∀，01)(22>++=ax x a x f ”的否定. 以上三个命题中，真命题的个数是（A ）3 （B ）2 （C ）1 （D ）0（9）三棱柱111ABC A B C -中，1AA 与AC 、AB 所成角均为60 ，90BAC ∠= ，且11AB AC AA ===，则1A B 与1AC 所成角的余弦值为（A ）1 （B ）1- （C） （D）（10）若函数113()22x x y e e x x -=---≤≤的图象上任意点处切线的倾斜角为α，则α的最小值是（A ）56π （B ）34π （C ）4π （D ）6π（11）过双曲线2222:1(0,0)x y C a b a b -=>>左焦点F 斜率为a b 的直线l 分别与C 的两渐近线交于点P 与Q ，若FP PQ =，则C 的渐近线的斜率为（A） （B ）2± （C ）1± （D）（12）设()f x 是定义在R 上的偶函数，x R ∀∈，都有(2)(2)f x f x -=+，且当[0,2]x ∈时，()22xf x =-，若函数()()log (1)a g x f x x =-+()0,1a a >≠在区间(1,9]-内恰有三个不同零点，则实数a的取值范围是（A）11(,)95（B）1(0,))9+∞（C）1(,1)(1,9（D）11(,)3)73第Ⅱ卷（非选择题，共90分）本卷包括必考题和选考题两部分.第（13）题～第（21）题为必考题，每个试题考生都必须做答.第（22）题～第（24）题为选考题，考生根据要求做答.二、填空题：本大题共4小题，每小题5分，共20分.把答案填在答题卡上（13）设yx,满足约束条件⎪⎩⎪⎨⎧≤--≥+-≥-+2211yxyxyx，若目标函数()0>+=ayaxz的最大值为10，则a=.（14）在71)x展开式中，不含2x的项的系数和是.（15）某一部件由四个电子元件按如图方式连结而成，已知每个元件正常工作的概率为p，且每个元件能否正常工作相互独立，那么该部件正常工作的概率为.（16）数列{}n a 的首项为1，数列{}n b 为等比数列且1n n n a b a +=，若10112b b ⋅=，则21a = .三、解答题：本大题共6小题，共70分. 解答应写出文字说明，证明过程或演算步骤.（17）在ABC ∆中，角A B C 、、所对的边分别为a b c 、、sin cC =，（Ⅰ）求A 的大小；（Ⅱ）若6=a ，求ABC ∆的周长的取值范围.（18）某种报纸，进货商当天以每份进价1元从报社购进，以每份售价2元售出。
云南师大附中2013届高考适应性月考卷(四)理科数学
甲 乙 9 0 86 5 5 4 1 3 5 5 71 2 2云南师大附中2013届高考适应性月考卷（四）理科数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．参考公式：样本数据12,,,n x x x 的标准差s =其中x 为样本平均数 柱体体积公式V Sh = 其中S 为底面面积，h 为高锥体体积公式13V Sh =其中S 为底面面积，h 为高 球的表面积，体积公式24R S π=，334R V π=其中R 为球的半径第Ⅰ卷（选择题共60分）一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．设全集U 为实数集R ，{}||2M x x =>，{}2|430N x x x =-+<，则图1中阴影部分所表示的集合是A ．{}|2x x <B ．{}|22x x -≤≤C ．{}|21x x -≤<D ．{}|12x x <≤2．已知i 为虚数单位，则复数133i i-+的虚部是A ．1-B ．1C ．iD ． i -3．命题“所有实数的平方都是正数”的否定为A ．所有实数的平方都不是正数B ．有的实数的平方是正数C ．至少有一个实数的平方不是正数D ．至少有一个实数的平方是正数4．已知(0,0)a b t a b +=>>，t 为常数，且a b 的最大值为2，则t ＝A ．2B ．4C．D．5．甲、乙两名运动员在某项测试中的6次成绩的茎叶图如图2所示，1x ，2x 分别表示甲乙两名运动员这项测试成绩的平均数，12,s s 分别表示甲乙两名运动员这项测试成绩的标准差，则有A ．1212,x x s s ><B ．1212,x x s s ==C ．1212,x x s s =<D ．1212,x x s s =>6．若二项式321nx x ⎛⎫+ ⎪⎝⎭的展开式中含有非零常数项，则正整数n 的最小值为A ．2B ．5C ．7D ．107．已知定义在R 上的函数2()sin x f x e x x x =+-+，则曲线()y f x =在点(0,(0))f 处的切线方程是A ．1y x =+B ．32y x =-C ． 21y x =-D ．23y x =-+8．如果实数,x y 满足不等式组1,10,220,x x y x y ≥⎧⎪-+≤⎨⎪--≤⎩则22x y +的最小值是A ．25B ．5C ．4D ．19．如图1给出的是计算111124620++++的值的一个程序框图，其中判断框内应填入的条件是A ．12?i >B ．11?i >C ．10?i >D ．9?i >10．已知一几何体的三视图如图3，主视图和左视图都是矩形，俯视图为正方形，在该几何体上任意选择4个顶点，以这4个点为顶点的几何形体可能是①矩形；②有三个面为直角三角形，有一个面为等腰三角形的四面体；③每个面都是直角三角形的四面体．A ．①②③B ．②③C ．①③D ．①②11．已知定义在R 上的奇函数()f x ，满足(4)()f x f x -=-，且在区间[]0,2上是增函数，若方程()(0)f x m m =>，在区间[]0,8上有四个不同的根1234,,,x x x x ，则1234x x x x +++＝A ．－12B ．－8C ．－4D ．412．设F 是双曲线22221(0,0)x y a b ab-=>>的右焦点，双曲线两条渐近线分别为12,l l ，过F 作直线1l 的垂线，分别交12,l l 于A 、B 两点，且向量BF与FA 同向．若||,||,||OA AB OB 成等差数列，则双曲线离心率e 的大小为主视图左视图俯视图A ．2 B．2C．2D．2第Ⅱ卷（非选择题共90分）注意事项：用钢笔或圆珠笔直接答在答题卡上．二、填空题：本大题共4小题，每小题5分，共20分，把答案填在题中横线上．13．如果随机变量2~(1,)N ξσ，且(31)0.4P ξ-≤≤-=，则(1)P ξ≥＝ ． 14．在直角坐标系xOy 中，有一定点(2,1)A ，若线段O A 的垂直平分线过抛物线22(0)y px p =>的焦点，则该抛物线的准线方程是 ．15．我们把平面内与直线垂直的非零向量称为直线的法向量，在平面直角坐标系中，利用求动点轨迹方程的方法，可以求出过点(3,4)A -，且法向量(1,2)n =-的直线（点法式）方程为1(3)(2)(4)0x y ⨯++-⨯-=，化简得2110x y -+=．类比以上方法，在空间直角坐标系中，经过点(1,2,3)A ，且法向量为(1,2,1)n =--的平面（点法式）方程为 ．16．已知数列{}n a 中121,2a a ==，当整数1n >时，1112()n n n S S S S +-+=+都成立，则15S ＝ ．三、解答题：本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤．17．（本小题满分12分）已知函数21()2cos 22f x x x =--，x R ∈．（1）求函数()f x 的最小正周期；（2）设ABC △的内角A 、B 、C 的对边分别为a 、b 、c ，且c =()9f C =，sin 2sin B A =，求,a b 的值．18．（本小题满分12分）班主任统计本班50名学生平均每天放学回家后学习时间的数据用图5所示条形图表示． （1）求该班学生每天在家学习时间的平均值；（2）假设学生每天在家学习时间为18时至23时，已知甲每天连续学习2小时，乙每天连续学小时)习3小时，求22时甲、乙都在学习的概率．19．（本小题满分12分）如图4，正三棱柱111ABC A B C -中，E 是A C 中点． （1）求证：平面1B E C ⊥平面11AC C A ；（2）若12A A AB=，求二面角1E BC C --的大小．20．（本小题满分12分）已知函数()ln b f x x a x x=-+在1x =处取得极值，且3a >（1）求a 与b 满足的关系式； （2）求函数()f x 的单调区间．21．（本小题满分12分）已知椭圆22221(0)x y a b ab+=>>的焦距为4，设右焦点为1F ，离心率为e ．（1）若2e =，求椭圆的方程；（2）设A 、B 为椭圆上关于原点对称的两点，1A F 的中点为M ，1BF 的中点为N ，若原点O 在以线段M N 为直径的圆上． ①证明点A 在定圆上； ②设直线A B 的斜率为k，若k ≥e 的取值范围．请考生在第22、23、24三题中任选一题作答，如果多做，则按所做的第一题记分．作答时请写清题号． 22．（本小题满分10分）【选修4－1：几何选讲】如图6，已知圆O 外有一点P ，作圆O 的切线PM ，M 为切点，过PM 的中点N ，作割线N A B ，交圆于A 、B 两点，连接P A 并延长，交圆O 于点C ，连续P B 交圆O 于点D ，若M C B C =．（1）求证：△A P M ∽△A B P ； （2）求证：四边形P M C D 是平行四边形．23．（本小题满分10分）【选修4－4：坐标系与参数方程】在极坐标系中，直线l 的极坐标方程为()3R πθρ=∈，以极点为原点，极轴为x 轴的正半轴建立ABCE B 1A 1C1平面直角坐标系，曲线C 的参数方程为2cos ,1cos ,x y αα=⎧⎨=+⎩（α为参数），求直线l 与曲线C 的交点P的直角坐标．24．（本小题满分10分）【选修4－5：不等式选讲】 已知函数2()log (|1||5|)f x x x a =-+--． （1）当2a =时，求函数()f x 的最小值；（2）当函数()f x 的定义域为R 时，求实数a 的取值范围．数学试题参考答案一、选择题，本题考查基础知识，基本概念和基本运算能力二、填空题．本题考查基础知识,基本概念和基本运算技巧 13．0.1 14．54x =-15．220x y z +--= 16．211三、解答题 17．云南师大附中2013届高考适应性月考卷（四）理科数学参考答案第Ⅰ卷（选择题，共60分）一、选择题（本大题共12小题，每小题5分，共60分）【解析】1．由集合运算得结果.2．原式=10i 10-，则复数13i 3i-+的虚部是1-.3．全称命题的否定是特称命题. 4．当0,0a b >>时，有2()4a b ab +≤.5．115x =，215x =，由茎叶图得12s s <. 6．展开式的通项公式是T r ＋1=C r nx3n −3r x −2r=C r nx3n −5r，若二项式321nx x ⎛⎫+ ⎪⎝⎭的展开式中含有非零常数项，则3n −5r = 0，即n 53r =(0r =，1，2，…，n )，故当3r =时，此时n 的最小值是5.7．令0x =，解得(0)1f =. 对()f x 求导，得()f x 'x e =+2x −1+cos x ，令0x =，解得(0)1f '=，故切线方程为1y x =+.8．在直角坐标系中画出不等式组1,10,220x x y x y ⎧⎪-+⎨⎪--⎩≥≤≤ 所表示的平面区域如图1所示的阴影部分，x 2+y 2的最小值即表示 阴影部分（包含边界）中的点到原点的距离的最小值的平 方，由图可知直线x −y +1=0与直线x =1的交点(1，2)到原 点最近，故x 2+y 2的最小值为12+22=5. 9．该程序框图为求和运算，得C 选项.10．以长方体1111ABCD A B C D -为几何体的直观图. 当选择的四个点为B 1、B 、C 、C 1时，可知①正确；当选择B 、A 、B 1、C 时，可知②正确；当选择A 、B 、D 、D 1时，可知③正确. 11．因为()f x 是定义在R 上的奇函数，满足(4)()f x f x -=-，所以(4)()f x f x -=-，由()f x 为奇函数，所以函数图象关于直线2x =-对称且(0)f =，由(4)()f x f x -=-知图1(8)()f x f x -=，所以函数是以8为周期的周期函数，又因为()f x 在区间[0，2]上是增函数，所以()f x 在区间[−2，0]上也是增函数. 如图2所示，那么方程()f x =m (m >0)在区间[−8，8]上有四个不同的根x 1，x 2，x 3，x 4，不妨设x 1<x 2<x 3<x 4，由对称性知1262x x +=-，即x 1+x 2 = −12，同理：x 3+x 4 = 4，所以x 1+x 2+x 3+x 4 = −12+4 = −8.12．设O A =m −d ，A B =m ，O B =m +d ，由勾股定理，得 (m −d )2+m 2=(m +d )2．解得m =4d ．设∠AOF =α，则cos2α=35OA OB=．cos α，所以，离心率e=1cos 2α=.第Ⅱ卷（非选择题，共90分）二、填空题（本大题共4小题，每小题5分，共20分）【解析】13．如果随机变量ξ～N (−1，σ2)，且P (−3≤ξ≤−1) = 0.4.∴P (ξ≥1) = P (ξ≤−3) = 0.5-0.4 = 0.1.14．OA 的垂直平分线的方程是y −12(1)2x =--，令y = 0得到x =54．所以该抛物线的准线方程为54x =-.15．设B (x ，y ，z )为平面内的任一点，由0AB n =得(1)(1)(2)(2)1(3)0x y z -⨯-+-⨯-+⨯-=，即220x y z +--=．16. 111()()22n n n n S S S S S +----==,即12(2)n n a a n +-=≥，数列{n a }从第二项起构成等差数列，15S =1+2+4+6+8+…+28=211.图2三、解答题（共70分. 解答应写出文字说明，证明过程或演算步骤） 17．（本小题满分12分）解：（Ⅰ）1cos 21π()2sin 212226xf x x x +⎛⎫=--=-- ⎪⎝⎭， 则()f x 的最小正周期是2ππ2T ==. ………………………………………………（6分）（Ⅱ）π()sin 2106f C C ⎛⎫=--= ⎪⎝⎭，则πsin 216C ⎛⎫-= ⎪⎝⎭， ∵0πC <<，∴022πC <<， ∴ππ11π2<666C -<-，∴ππ262C -=，∴3C π=，∵sin 2sin B A =，由正弦定理，得12a b =，①由余弦定理，得2222cos 3c a b ab π=+-，即223a b ab +-=， ②由①②解得1,2a b ==. ……………………………………………………………（12分） 18．（本小题满分12分）解：（Ⅰ）平均学习时间为20102103541.8()50⨯⨯+⨯+⨯=1+小时. ……………（6分）（Ⅱ）设甲开始学习的时刻为x ，乙开始学习的时刻为y ，试验的全部结果所构成的区域为Ω ={(x ，y )|18≤x ≤21，18≤y ≤20}，面积S Ω = 2×3=6.事件A 表示“22时甲、乙都在学习”，所构成的区域为A ={(x ，y )|20≤x ≤21，19≤y ≤20}，面积为111A S =⨯=，这是一个几何概型，所以P (A )A S S Ω==16. …………………………………………（12分）19．（本小题满分12分）（Ⅰ）证明：如图3，∵111ABC A B C -是正三棱柱， ∴1,AA ABC ⊥平面 ∴1BE AA ⊥.∵△ABC 是正三角形，E 是AC 中点， ∴,BE AC ⊥ ∴11BE ACC A ⊥平面.图3又∵1BE BEC ⊂平面，∴平面111BEC ACC A ⊥平面. …………………………………………………………（6分） （Ⅱ） 解：如图4，作1CF EC F ⊥于，1FG BC ⊥于G ，连CG . ∵平面111BEC ACC A ⊥平面， ∴1CF BEC ⊥平面，∴FG 是CG 在平面1BEC 上的射影. ∴根据三垂线定理得，1CG BC ⊥， ∴∠CGF 是二面角1E BC C --的平面角， 设AB a =，∵12A A AB=，则12A A =.在1Rt ECC △中，116EC CC CF EC ⋅==.在1Rt BCC △中，113BC CC CG BC ⋅==,在R t C FG △中，∵sin 2C F C G F C G∠==,∴45C G F ∠=︒.∴二面角1E BC C --的大小是45°. …………………………………………………（12分）20．（本小题满分12分）解：（Ⅰ）2()1a b f x x x'=--，由(1)0f '= 得1ba=-. ………………………（4分）（Ⅱ）函数()f x 的定义域为(0,)+∞，由（Ⅰ）可得22221(1)(1)[(1)]()1a a x ax a x x a f x x xxx-------'=--==．令()0f x '=，则11x =，21x a =-.3a >时，11a ->，图4所以单调递增区间为(0,1)，(1,)a -+∞，单调递减区间为(1,1)a -. ………（12分）21. （本小题满分12分）解：（Ⅰ）由2e =，c =2，得a =，b =2 ,所求椭圆方程为22184xy+=. ………………………………………………………（4分）（Ⅱ）设00(,)A x y ，则00(,)B x y --， 故00+222x y M ⎛⎫⎪⎝⎭，，00222x y N -⎛⎫-⎪⎝⎭，.① 由题意，得0OM ON =.化简，得22004x y +=，所以点A 在以原点为圆心，2为半径的圆上. ……………（8分）② 设00(,)A x y ，则002222200220022222222220000,1,111,(1)444y kx x k x x y k k a ba b a b x kx x y =⎧⎧⎪+=⎪⎪+=⇒⇒+=+⎨⎨⎪⎪+=⎩⎪+=⎩. 将2c e aa==，222244b ac e=-=-，代入上式整理，得2242(21)2 1.k e e e -=-+因为42210e e -+>，k 2>0，所以2210e ->， 所以 422221321e e ke -+=-≥．化简，得422840,210.e e e ⎧-+⎪⎨->⎪⎩≥解之，得2142e <-≤1,2e <≤故离心率的取值范围是12⎤⎥⎝⎦. ……………………………………………（12分）22.（本小题满分10分）【选修4—1：几何证明选讲】证明：（Ⅰ）∵P M 是圆O 的切线，N A B 是圆O 的割线，N 是P M 的中点，∴22,MN PN NA NB ==⋅ ∴,PN N A N B PN = 又∵,P N AB N P ∠=∠ ∴PN A △∽BN P △， ∴,A P NP B N ∠=∠ 即,A P M P B A ∠=∠ ∵,M C B C = ∴,M A C B A C ∠=∠∴,M AP PAB ∠=∠∴A P M △∽ABP △． …………………………………………………………………（5分） （Ⅱ）∵AC D PBN ∠=∠，∴AC D PBN APN ∠=∠=∠，即PC D C PM ∠=∠，∴//PM C D ，∵A P M △∽ABP △，∴PM A BPA ∠=∠，∵P M 是圆O 的切线，∴PM A M C P ∠=∠，∴PM A BPA M C P ∠=∠=∠，即,M C PD P C ∠=∠∴//,M C P D ∴四边形P M C D 是平行四边形． ……………………………………………………（10分）23．（本小题满分10分）【选修4—4：坐标系与参数方程】解：因为直线l 的极坐标方程为=()3θρπ∈R ，所以直线l 的普通方程为y =，① ………………………………………………（3分）又因为曲线C 的参数方程为2cos ,1cos 2x y αα=⎧⎨=+⎩ (α为参数)， 所以曲线C 的直角坐标方程为212y x =([2,2])x ∈-，② …………………………（6分）联立①②解方程组得0,0x y =⎧⎨=⎩ 或 6.x y ⎧=⎪⎨=⎪⎩根据x 的范围应舍去6,x y ⎧=⎪⎨=⎪⎩故P 点的直角坐标为(0，0). ………………………………………………………（10分）24．（本小题满分10分）【选修4—5：不等式选讲】解：（Ⅰ）函数的定义域满足：150x x a-+-->，即15x x a-+->，设()15g x x x=-+-，则()15g x x x=-+-=26,5, 4,15, 62,1,x xxx x-⎧⎪<<⎨⎪-⎩≥≤g (x)min= 4，f (x)min = log2 (4−2)=1. ………………………………………………（5分）（Ⅱ）由（Ⅰ）知，()15g x x x=-+-的最小值为4.150x x a-+-->，∴a<4，∴a的取值范围是(−∞，4). ………………………………………………（10分）。
云南师大附中2013届高三高考适应性月考卷(三)理综答案.pdf
云南师大附中2013届高考适应性月考卷（三） 理科综合参考答案 第Ⅰ卷（选择题，共126分） 一、选择题：本题共13小题，每小题6分。
题号12345678910111213答案ACCBBDCDADBCD二、选择题：本题共8小题，每小题6分。
在每小题给出的四个选项中，有的只有一项符合题目要求，有的有多项符合题目要求，全部选对的得6分，选对但不全的得3分，有选错的得0分。
题号1415161718192021答案AACDBBCBCDADBD【解析】 1．B项生物体内的单糖有多种，功能不同，如葡萄糖主要作用是为生物体供能，核糖和脱氧核糖则参与核酸的构成；C项噬菌体含蛋白质，含S元素，质粒是DNA，不含S；D项酶和载体蛋白发挥作用后仍保持活性。
故选A。
2．A项多细胞生物个体的长大，主要原因是细胞的增殖；B项单细胞生物生命历程中不会发生细胞的分化；D项癌变细胞的细胞膜会发生改变，如糖蛋白等会减少，有的产生甲胎蛋白和癌胚抗原等物质。
故选C。
3．A项一种限制酶只能识别一种特定的核苷酸序列，并在特定的切点上切割DNA分子，因此具有专一性；B项运载体有质粒、噬菌体和动植物病毒等，成分不单一，载体蛋白本质是蛋白质；D项DNA连接酶可催化黏性末端黏合后的磷酸二酯键形成。
故选C。
4．利用F1的花药离体培养获得单倍体植株后，还需人工诱导使染色体数目加倍才能选育出AAbb植株。
故选B。
5． A项遗传病不一定都是由致病基因引起的，如染色体异常遗传病；C项单基因遗传病是由一对等位基因控制的遗传病；D项通过调查患病家族，可以分析遗传病的传递方式和推算后代的再发风险率等，但不可用于统计某种遗传病在人群中的发病率。
故选B。
6．A项可遗传的变异为生物进化提供了原材料；B项所有新物种的形成都需要经过隔离（生殖隔离）；C项生物进化的实质是基因频率的定向改变。
故选D。
7．C项形成酸雨的主要原因是化石燃料燃烧产生的SO2。
8．A项应为 ；B项根据异性电荷相互吸引应为氧原子朝里，氢原子朝外；C项应 为氧化剂得电子，还原剂失电子。
云南师大附中2013届高考适应性月考卷(二)理科数学试卷
云南师大附中2013届高考适应性月考卷（二）理科数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．参考公式：样本数据的标准差其中为样本平均数柱体体积公式其中为底面面积，为高锥体体积公式其中为底面面积，为高球的表面积，体积公式，其中为球的半径第Ⅰ卷（选择题共60分）一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．设集合，，则＝A． B． C． D．2．复数满足，则＝A． B． C． D．3．下列函数中，既是奇函数又是增函数的是A． B． C． D．4．已知双曲线的一条渐近线方程为，则它的离心率是A． B． C． D．5．设满足则的最大值是A．2 B．3 C．12 D．136．设向量与平行，则＝A． B． C．0 D．1开始输入输入结束是否7．如果执行图1所示的程序框图，输入，则输出的值为A．2 B．0C．－1 D．8．在各项均为正数的等比数列中，，则＝A．12 B．10C．8 D．9．直线与圆相交于、两点，则弦的长度为A． B． C． D．110．下列命题①命题“存在实数，使得”的否定是“不存在实数，使得”；②若函数是定义在上的偶函数，且在上是增函数，，则；③要得到函数的图像，只需将函数的图像向左平移个单位．其中正确的命题个数是A．0 B．1 C．2 D．311．已知函数，若，，则A． B． C． D．12．已知函数是定义在上的增函数，函数的图像关于点对称，若对任意的，不等式恒成立，则当时，的取值范围是A． B． C． D．第Ⅱ卷（非选择题共90分）注意事项：用钢笔或圆珠笔直接答在答题卡上．二、填空题：本大题共4小题，每小题5分，共20分，把答案填在题中横线上．1 4 7 8 82 0 113．如图2是某学校一名篮球运动员在六场比赛中所得分数的茎叶图，则该运动员在这六场比赛中得分的方差是．14．设为展开式中含项的系数，则数列的前项和为．15．数列的通项公式，其前项和为，则等于．16．设函数，为的导函数，若成立的充分条件是，则实数的取值范围是三、解答题：本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤．17．（本小题满分12分）在△中，角、、对边分别为、、，且．（1）求角的大小；PABCED（2）若，，求，．18．（本小题满分12分）如图3，在四棱锥中，底面为平行四边形，平面⊥平面，且，是的中点．（1）求证：∥平面；（2）平面分棱锥为两部分，求这两部分中体积较小者与体积较大者的体积之比．19．（本小题满分12分）已知椭圆的离心率为，，分别是椭圆的左、右焦点，直线过点与椭圆交于、两点，且△的周长为．（1）求椭圆的标准方程；（2）是否存在直线使△的面积为？若存在，求出直线的方程；若不存在，请说明理由．20．（本小题满分12分）某学校为了研究学情，从高三年级抽取了20名学生三次测试的数学成绩和物理成绩，计算出了他们三次成绩的平均名次如下表：学生12345678910序号数学平均 1.312.325.736.7.50.367.749.052.040.034.3学生序号11121314151617181920数学平均名次78.350.065.766.368.095.090.787.7103.786.7物理平均名次49.746.783.359.750.0101.376.786.099.799.0次物理平均名次2.39.731.022.340.058.039.060.763.342.7学校规定平均名次小于或等于40.0者为优秀，大于40.0者为不优秀．（1）对名次优秀赋分2分，对名次不优秀赋分1分，从这20名学生中随机抽取两名学生，用表示这两名学生两科名次赋分的和，求的分布列和数学期望；（2）根据这次抽查数据，能否在犯错误的概率不超过0.025的前提下认为物理成绩与数学成绩有关？．附：，其中．0.500.400.250.150.100.050.0250.0100.0050.0010.4550.708 1.323 2.072 2.706 3.841 5.024 6.6357.87910.828 21．（本小题满分12分）已知函数．（1）讨论函数的单调区间；（2）若，求函数在上的最大值和最小值．请考生在第22、23、24三题中任选一题作答，如果多做，则按所做的第一题记分．作答时请写清题号．22．（本小题满分10分）【选修4－1：几何选讲】如图4，已知与外切于点，是两圆的外公切线，、为切点，与的延长线相交于点，延长交于点，点在的延长线上，且满足．ABO1CDFEO2（1）求证：；（2）若，，求的值．23．（本小题满分10分）【选修4－4：坐标系与参数方程】在平面直角坐标系中，曲线和的参数方程分别为（为参数，）与（为参数）．（1）化、的方程为普通方程，并说明它们分别代表什么曲线；（2）求曲线和的交点坐标．24．（本小题满分10分）【选修4－5：不等式选讲】设函数．（1）当时，解不等式；（2）若存在实数使得成立，求实数的取值范围．数学试题参考答案一、选择题，本题考查基础知识，基本概念和基本运算能力题号１23456789101112答案A C D A D C D B B B B C二、填空题．本题考查基础知识,基本概念和基本运算技巧13．514．15．16．三、解答题17．。
云南师大附中2013届高考适应性月考卷(四)(五)(六)理科数学及答案分析
甲 乙 9 0 86 5 5 4 1 3 5 5 71 2 2云南师大附中2013届高考适应性月考卷（四）理科数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．参考公式：样本数据12,,,n x x x 的标准差s =其中x 为样本平均数 柱体体积公式V Sh = 其中S 为底面面积，h 为高锥体体积公式13V Sh =其中S 为底面面积，h 为高 球的表面积，体积公式24R S π=，334R V π=其中R 为球的半径第Ⅰ卷（选择题共60分）一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．设全集U 为实数集R ，{}||2M x x =>，{}2|430N x x x =-+<，则图1中阴影部分所表示的集合是A ．{}|2x x <B ．{}|22x x -≤≤C ．{}|21x x -≤<D ．{}|12x x <≤2．已知i 为虚数单位，则复数133i i-+的虚部是A ．1-B ．1C ．iD ． i -3．命题“所有实数的平方都是正数”的否定为A ．所有实数的平方都不是正数B ．有的实数的平方是正数C ．至少有一个实数的平方不是正数D ．至少有一个实数的平方是正数4．已知(0,0)a b t a b +=>>，t 为常数，且a b 的最大值为2，则t ＝A ．2B ．4C．D．5．甲、乙两名运动员在某项测试中的6次成绩的茎叶图如图2所示，1x ，2x 分别表示甲乙两名运动员这项测试成绩的平均数，12,s s 分别表示甲乙两名运动员这项测试成绩的标准差，则有A ．1212,x x s s ><B ．1212,x x s s ==C ．1212,x x s s =<D ．1212,x x s s =>6．若二项式321nx x ⎛⎫+ ⎪⎝⎭的展开式中含有非零常数项，则正整数n 的最小值为A ．2B ．5C ．7D ．107．已知定义在R 上的函数2()sin x f x e x x x =+-+，则曲线()y f x =在点(0,(0))f 处的切线方程是A ．1y x =+B ．32y x =-C ． 21y x =-D ．23y x =-+8．如果实数,x y 满足不等式组1,10,220,x x y x y ≥⎧⎪-+≤⎨⎪--≤⎩则22x y +的最小值是A ．25B ．5C ．4D ．19．如图1给出的是计算111124620++++的值的一个程序框图，其中判断框内应填入的条件是A ．12?i >B ．11?i >C ．10?i >D ．9?i >10．已知一几何体的三视图如图3，主视图和左视图都是矩形，俯视图为正方形，在该几何体上任意选择4个顶点，以这4个点为顶点的几何形体可能是①矩形；②有三个面为直角三角形，有一个面为等腰三角形的四面体；③每个面都是直角三角形的四面体．A ．①②③B ．②③C ．①③D ．①②11．已知定义在R 上的奇函数()f x ，满足(4)()f x f x -=-，且在区间[]0,2上是增函数，若方程()(0)f x m m =>，在区间[]0,8上有四个不同的根1234,,,x x x x ，则1234x x x x +++＝A ．－12B ．－8C ．－4D ．412．设F 是双曲线22221(0,0)x y a b ab-=>>的右焦点，双曲线两条渐近线分别为12,l l ，过F 作直线1l 的垂线，分别交12,l l 于A 、B 两点，且向量BF与FA 同向．若||,||,||OA AB OB 成等差数列，则双曲线离心率e 的大小为主视图左视图俯视图A ．2 B．2C．2D．2第Ⅱ卷（非选择题共90分）注意事项：用钢笔或圆珠笔直接答在答题卡上．二、填空题：本大题共4小题，每小题5分，共20分，把答案填在题中横线上．13．如果随机变量2~(1,)N ξσ，且(31)0.4P ξ-≤≤-=，则(1)P ξ≥＝ ． 14．在直角坐标系xOy 中，有一定点(2,1)A ，若线段O A 的垂直平分线过抛物线22(0)y px p =>的焦点，则该抛物线的准线方程是 ．15．我们把平面内与直线垂直的非零向量称为直线的法向量，在平面直角坐标系中，利用求动点轨迹方程的方法，可以求出过点(3,4)A -，且法向量(1,2)n =-的直线（点法式）方程为1(3)(2)(4)0x y ⨯++-⨯-=，化简得2110x y -+=．类比以上方法，在空间直角坐标系中，经过点(1,2,3)A ，且法向量为(1,2,1)n =--的平面（点法式）方程为 ．16．已知数列{}n a 中121,2a a ==，当整数1n >时，1112()n n n S S S S +-+=+都成立，则15S ＝ ．三、解答题：本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤．17．（本小题满分12分）已知函数21()2cos 22f x x x =--，x R ∈．（1）求函数()f x 的最小正周期；（2）设ABC △的内角A 、B 、C 的对边分别为a 、b 、c ，且c =()9f C =，sin 2sin B A =，求,a b 的值．18．（本小题满分12分）班主任统计本班50名学生平均每天放学回家后学习时间的数据用图5所示条形图表示． （1）求该班学生每天在家学习时间的平均值；（2）假设学生每天在家学习时间为18时至23时，已知甲每天连续学习2小时，乙每天连续学小时)习3小时，求22时甲、乙都在学习的概率．19．（本小题满分12分）如图4，正三棱柱111ABC A B C -中，E 是A C 中点． （1）求证：平面1B E C ⊥平面11AC C A ；（2）若12A A AB=，求二面角1E BC C --的大小．20．（本小题满分12分）已知函数()ln b f x x a x x=-+在1x =处取得极值，且3a >（1）求a 与b 满足的关系式； （2）求函数()f x 的单调区间．21．（本小题满分12分）已知椭圆22221(0)x y a b ab+=>>的焦距为4，设右焦点为1F ，离心率为e ．（1）若2e =，求椭圆的方程；（2）设A 、B 为椭圆上关于原点对称的两点，1A F 的中点为M ，1BF 的中点为N ，若原点O 在以线段M N 为直径的圆上． ①证明点A 在定圆上； ②设直线A B 的斜率为k，若k ≥e 的取值范围．请考生在第22、23、24三题中任选一题作答，如果多做，则按所做的第一题记分．作答时请写清题号． 22．（本小题满分10分）【选修4－1：几何选讲】如图6，已知圆O 外有一点P ，作圆O 的切线PM ，M 为切点，过PM 的中点N ，作割线N A B ，交圆于A 、B 两点，连接P A 并延长，交圆O 于点C ，连续P B 交圆O 于点D ，若M C B C =．（1）求证：△A P M ∽△A B P ； （2）求证：四边形P M C D 是平行四边形．23．（本小题满分10分）【选修4－4：坐标系与参数方程】在极坐标系中，直线l 的极坐标方程为()3R πθρ=∈，以极点为原点，极轴为x 轴的正半轴建立ABCE B 1A 1C1平面直角坐标系，曲线C 的参数方程为2cos ,1cos ,x y αα=⎧⎨=+⎩（α为参数），求直线l 与曲线C 的交点P的直角坐标．24．（本小题满分10分）【选修4－5：不等式选讲】 已知函数2()log (|1||5|)f x x x a =-+--． （1）当2a =时，求函数()f x 的最小值；（2）当函数()f x 的定义域为R 时，求实数a 的取值范围．云南师大附中2013届高考适应性月考卷（四）理科数学参考答案第Ⅰ卷（选择题，共60分）一、选择题（本大题共12小题，每小题5分，共60分）【解析】1．由集合运算得结果.2．原式=10i 10-，则复数13i 3i-+的虚部是1-.3．全称命题的否定是特称命题. 4．当0,0a b >>时，有2()4a b ab +≤.5．115x =，215x =，由茎叶图得12s s <. 6．展开式的通项公式是T r ＋1=C r nx3n −3r x −2r=C r nx3n −5r，若二项式321nx x ⎛⎫+ ⎪⎝⎭的展开式中含有非零常数项，则3n −5r = 0，即n 53r =(0r =，1，2，…，n )，故当3r =时，此时n 的最小值是5.7．令0x =，解得(0)1f =. 对()f x 求导，得()f x 'x e =+2x −1+cos x ，令0x =，解得(0)1f '=，故切线方程为1y x =+.8．在直角坐标系中画出不等式组1,10,220x x y x y ⎧⎪-+⎨⎪--⎩≥≤≤ 所表示的平面区域如图1所示的阴影部分，x 2+y 2的最小值即表示 阴影部分（包含边界）中的点到原点的距离的最小值的平 方，由图可知直线x −y +1=0与直线x =1的交点(1，2)到原 点最近，故x 2+y 2的最小值为12+22=5. 9．该程序框图为求和运算，得C 选项.10．以长方体1111ABCD A B C D -为几何体的直观图. 当选择的四个点为B 1、B 、C 、C 1时，可知①正确；当选择B 、A 、B 1、C 时，可知②正确；当选择A 、B 、D 、D 1时，可知③正确. 11．因为()f x 是定义在R 上的奇函数，满足(4)()f x f x -=-，所以(4)()f x f x -=-，由()f x 为奇函数，所以函数图象关于直线2x =-对称且(0)f =，由(4)()f x f x -=-知(8)()f x f x -=，所以函数是以8为周期的周期函数，又因为()f x 在区间[0，2]上是增函数，所以()f x 在区间[−2，0]上也是增函数. 如图2所示，那么方程()f x =m (m >0)在区间[−8，8]上有四个不同的根x 1，x 2，x 3，x 4，不妨设x 1<x 2<x 3<x 4，由对称性知1262x x +=-，即x 1+x 2 = −12，同理：x 3+x 4 = 4，所以x 1+x 2+x 3+x 4 = −12+4 = −8.12．设O A =m −d ，A B =m ，O B =m +d ，由勾股定理，得 (m −d )2+m 2=(m +d )2．解得m =4d ．设∠AOF =α，则cos2α=35OA OB=．cos α，所以，离心率e=1cos 2α=.第Ⅱ卷（非选择题，共90分）二、填空题（本大题共4小题，每小题5分，共20分）图1图2【解析】13．如果随机变量ξ～N (−1，σ2)，且P (−3≤ξ≤−1) = 0.4.∴P (ξ≥1) = P (ξ≤−3) = 0.5-0.4 = 0.1.14．OA 的垂直平分线的方程是y −12(1)2x =--，令y = 0得到x =54．所以该抛物线的准线方程为54x =-.15．设B (x ，y ，z )为平面内的任一点，由0AB n =得(1)(1)(2)(2)1(3)0x y z -⨯-+-⨯-+⨯-=，即220x y z +--=．16. 111()()22n n n n S S S S S +----==,即12(2)n n a a n +-=≥，数列{n a }从第二项起构成等差数列，15S =1+2+4+6+8+…+28=211.三、解答题（共70分. 解答应写出文字说明，证明过程或演算步骤） 17．（本小题满分12分）解：（Ⅰ）1cos 21π()2sin 212226xf x x x +⎛⎫=--=-- ⎪⎝⎭， 则()f x 的最小正周期是2ππ2T ==. ………………………………………………（6分）（Ⅱ）π()sin 2106f C C ⎛⎫=--= ⎪⎝⎭，则πsin 216C ⎛⎫-= ⎪⎝⎭， ∵0πC <<，∴022πC <<， ∴ππ11π2<666C -<-，∴ππ262C -=，∴3C π=，∵sin 2sin B A =，由正弦定理，得12a b =，①由余弦定理，得2222cos 3c a b ab π=+-，即223a b ab +-=， ②由①②解得1,2a b ==. ……………………………………………………………（12分） 18．（本小题满分12分）解：（Ⅰ）平均学习时间为20102103541.8()50⨯⨯+⨯+⨯=1+小时. ……………（6分）（Ⅱ）设甲开始学习的时刻为x ，乙开始学习的时刻为y ，试验的全部结果所构成的区域为Ω ={(x ，y )|18≤x ≤21，18≤y ≤20}，面积S Ω = 2×3=6.事件A 表示“22时甲、乙都在学习”，所构成的区域为A ={(x ，y )|20≤x ≤21，19≤y ≤20}，面积为111A S =⨯=，这是一个几何概型，所以P (A )A S S Ω==16. …………………………………………（12分）19．（本小题满分12分）（Ⅰ）证明：如图3，∵111ABC A B C -是正三棱柱， ∴1,AA ABC ⊥平面 ∴1BE AA ⊥.∵△ABC 是正三角形，E 是AC 中点， ∴,BE AC ⊥ ∴11BE ACC A ⊥平面. 又∵1BE BEC ⊂平面， ∴平面1BE CA⊥平面. …………………………………………………………（6分）（Ⅱ） 解：如图4，作1CF EC F ⊥于，1FG BC ⊥于G ，连CG . ∵平面111BEC ACC A ⊥平面， ∴1CF BEC ⊥平面，∴FG 是CG 在平面1BEC 上的射影. ∴根据三垂线定理得，1CG BC ⊥， ∴∠CGF 是二面角1E BC C --的平面角， 设AB a =，∵12A A AB=，则12A A =.图3图4在1Rt ECC △中，116EC CC CF EC ⋅==.在1Rt BCC △中，113BC CC CG BC ⋅==,在R t C FG △中，∵sin 2C F C G F C G∠==,∴45C G F ∠=︒.∴二面角1E BC C --的大小是45°. …………………………………………………（12分）20．（本小题满分12分）解：（Ⅰ）2()1a b f x x x'=--，由(1)0f '= 得1ba=-. ………………………（4分）（Ⅱ）函数()f x 的定义域为(0,)+∞，由（Ⅰ）可得22221(1)(1)[(1)]()1a a x ax a x x a f x x xxx-------'=--==．令()0f x '=，则11x =，21x a =-.3a >时，11a ->，所以单调递增区间为(0,1)，(1,)a -+∞，单调递减区间为(1,1)a -. ………（12分）21. （本小题满分12分）解：（Ⅰ）由2e =c =2，得a =，b =2 ,所求椭圆方程为22184xy+=. ………………………………………………………（4分）（Ⅱ）设00(,)A x y ，则00(,)B x y --， 故00+222x y M ⎛⎫⎪⎝⎭，，00222x y N -⎛⎫-⎪⎝⎭，.① 由题意，得0OM ON =.化简，得22004x y +=，所以点A 在以原点为圆心，2为半径的圆上. ……………（8分）② 设00(,)A x y ，则002222200220022222222220000,1,111,(1)444y kx x k x x y k k a ba b a b x kx x y =⎧⎧⎪+=⎪⎪+=⇒⇒+=+⎨⎨⎪⎪+=⎩⎪+=⎩. 将2c e aa==，222244b ac e=-=-，代入上式整理，得2242(21)2 1.k e e e -=-+因为42210e e -+>，k 2>0，所以2210e ->， 所以 422221321e e k e -+=-≥．化简，得422840,210.e e e ⎧-+⎪⎨->⎪⎩≥解之，得2142e <-≤1,2e <≤故离心率的取值范围是12⎤⎥⎝⎦. ……………………………………………（12分）22.（本小题满分10分）【选修4—1：几何证明选讲】证明：（Ⅰ）∵P M 是圆O 的切线，N A B 是圆O 的割线，N 是P M 的中点， ∴22,MN PN NA NB ==⋅ ∴,PN N A N BPN=又∵,P N A B N P ∠=∠∴PN A △∽BN P △，∴,A P N PB N ∠=∠ 即,A P M P B A ∠=∠∵,M CB C =∴,M A CB AC ∠=∠∴,M AP PAB ∠=∠∴A P M △∽ABP △． …………………………………………………………………（5分） （Ⅱ）∵AC D PBN ∠=∠，∴AC D PBN APN ∠=∠=∠，即PC D C PM ∠=∠， ∴//PM C D ，∵A P M △∽ABP △，∴PM A BPA ∠=∠，∵P M 是圆O 的切线，∴PM A M C P ∠=∠， ∴PM A BPA M C P ∠=∠=∠，即,M C P D P C ∠=∠∴//,M CP D∴四边形P M C D 是平行四边形． ……………………………………………………（10分） 23．（本小题满分10分）【选修4—4：坐标系与参数方程】解：因为直线l 的极坐标方程为=()3θρπ∈R ，所以直线l的普通方程为y =，① ………………………………………………（3分） 又因为曲线C 的参数方程为2cos ,1cos 2x y αα=⎧⎨=+⎩ (α为参数)，所以曲线C 的直角坐标方程为212y x =([2,2])x ∈-，② …………………………（6分）联立①②解方程组得0,0x y =⎧⎨=⎩或 6.x y ⎧=⎪⎨=⎪⎩根据x的范围应舍去6,x y ⎧=⎪⎨=⎪⎩故P 点的直角坐标为(0，0). ………………………………………………………（10分） 24．（本小题满分10分）【选修4—5：不等式选讲】解：（Ⅰ）函数的定义域满足：150x x a -+-->， 即15x x a -+->， 设()15g x x x =-+-，则()15g x x x =-+-=26,5,4,15,62,1,x x x x x -⎧⎪<<⎨⎪-⎩≥≤g (x )min = 4，f (x )min = log 2 (4−2)=1. ………………………………………………（5分） （Ⅱ）由（Ⅰ）知，()15g x x x =-+-的最小值为4.150x x a -+-->，∴a <4，∴a 的取值范围是(−∞，4). ………………………………………………（10分）云南师大附中2013届高考适应性月考卷（五）理科数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．第Ⅰ卷（选择题共60分）一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合{}|10A x ax =-=，{}3,4B =，且A B A = ，则a 的所有可能值组成的集合是A ．110,,34⎧⎫⎨⎬⎩⎭B ．11,34⎧⎫⎨⎬⎩⎭C ．13⎧⎫⎨⎬⎩⎭D ．{}02．设复数21z i=-（其中i 为虚数单位），则23z z +为A ．2iB ．10i -C ．10iD ．62i --3．设向量sin ,2a α⎛= ⎪⎝⎭的模为2，则cos 2α＝ A ．14-B ．12C ．12-D24．如图1，设D 是图中所示的矩形区域，E 是D 内函数cos y x =的图像上方的点构成的区域，向D 中随机投一点，则该点落入E （阴影部分）中的概率为A ．2πB ．1πC ．2ππ-D ．125．在同一个坐标系中画出函数xy a =，sin y ax =的部分图像，其中0a >且1a ≠，则下列所给图像中可能正确的是6．一个几何体的三视图如图2所示，其中俯视图是菱形，则该几何体的侧面积为A ．B ．+正视图侧视图11111CD7．图3是某算法的程序框图，则程序运行后输出的T 是A ．1B ．2C ．3 D．48．函数sin()y x ωϕ=+（0ω>且||2πϕ<）在区间2,63ππ⎡⎤⎢⎥⎣⎦上单调递减，且函数值从1减小到－1，那么此函数图像与y 轴交点的纵坐标为A ．2B ．12C 2D 49．设a 、b 、c 、d R ∈，若,1,a b 成等比数列，且,1,c d 成等差数列，则下列等式恒成立的是A ．||2a b cd +≥B ．2a b cd +≥C ．||2a b cd +≤D ．2a b cd +≤10．P 是双曲线22221(0,0)x y a b ab-=>>上的点，1F 、2F 是其焦点，且120PF PF ⋅= ，若△12F P F 的面积是9，7a b +=，则双曲线的离心率为A ．74B ．54C 2D 211．如图4，已知O 、A 、B 是平面上三点，向量OA a = ，OB b =．在平面AO B 上，P 是线段A B 垂直平分线上任意一点，向量O P p = ，且||3a =，||2b = ，则()p a b ⋅-的值是A ．12B ．32C ．72D ．5212．已知0a >且1a ≠，2()xf x x a =-，当(1,1)x ∈-时均有1()2f x <，则实数a 的取值范围是A ．[)10,2,2⎛⎤+∞ ⎥⎝⎦B ．(]1,11,22⎡⎫⎪⎢⎣⎭C ．(]1,11,44⎡⎫⎪⎢⎣⎭D ．[)10,4,4⎛⎤+∞ ⎥⎝⎦第Ⅱ卷（非选择题共90分）注意事项：用钢笔或圆珠笔直接答在答题卡上．二、填空题：本大题共4小题，每小题5分，共20分，把答案填在题中横线上．13．在△ABC 中，角A 、B 、C 所对的边分别为a 、b 、c ，且4cos 5A =，则)4A π-的值为 ． 14．若数列{}n a 满足112a =，2*12()n n a a a n a n N +++=∈ ，则数列{}n a 的前60项和为 ．15．若不等式组0,34,34,x x y x y ≥⎧⎪+≥⎨⎪+≤⎩所表示的平面区域被直线43y kx =+分为面积相等的两部分，则k 的值为 ．16．如图5，已知球O 是棱长为1的正方体1111ABC D A B C D -的内切球，则以球心O 为顶点，以球O 被平面1A C D 所截得的圆为底面的圆锥的体积为 ．三、解答题：本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤．17．（本小题满分12分）已知等比数列{}n a 满足22a =，且3452a a a +=，0n a >． （1）求数列{}n a 的通项公式；（2）设(1)321nn n b a n =-++，数列{}n b 的前n 项和为n T ，求n T18．（本小题满分12分）在一次抢险救灾中，某救援队的50名队员被分别分派到四个不同的区域参加救援工作，其分布的情况如下表，从这50名队员中随机抽出2人去完成一项特殊任务．（1）求这2人来自同一区域的概率；（2）若这2人来自区域A ，D ，并记来自区域A 队员中的人数为ξ，求随机变量ξ的分布列及数学期望．19．（本小题满分12分）在如图6所示的几何体中，平面AC E ⊥平面A B C D ，四边形A B C D 为平行四边形，90ACB ∠= ，E F ∥B C ，2AC BC EF ==，AC ==．（1）求证：A E ⊥平面B C E F ； （2）求二面角A B F C --的大小． 20．（本小题满分12分）已知函数2()ln 8xf x x =-，[]1,3x ∈．（1）求()f x 的最大值与最小值；（2）若()4f x at <-对于任意的[]0,2t ∈恒成立，求实数a 的取值范围．21．（本小题满分12分）已知椭圆2222:1(0)x y C a b ab+=>>的离心率为2，连接椭圆的四个顶点得到的菱形的面积为． （1）求椭圆C 的方程；（2）若过点(2,0)的直线l 的与椭圆C 交于A 、B 两点，设P 为椭圆上一点，且满足OA OB tOP += （O 为坐标原点），当||3PA PB -< 时，求实数t 的取值范围．请考生在第22、23、24三题中任选一题作答，如果多做，则按所做的第一题记分．作答时请写清题号．22．（本小题满分10分）【选修4－1：几何选讲】如图7所示，P A 为O 的切线，A 为切点，PBC 是过点O 的割线，10P A =，5P B =，B A C ∠的平分线与B C 和O 分别交于点D 和E ． （1）求证：A B P AA CP C=；（2）求A D A E ⋅的值．23．（本小题满分10分）【选修4－4：坐标系与参数方程】已知曲线C 的极坐标方程是1ρ=，以极点为原点，极轴为x 轴的正半轴建立平面直角坐标系，直线l的参数方程为11,22,2x t y ⎧=+⎪⎪⎨⎪=+⎪⎩（t 为参数）．（1）写出直线l 的普通方程与曲线C 的直角坐标方程； （2）设曲线C 经过伸缩变换2,,x x y y '=⎧⎨'=⎩得到曲线C '，设曲线C '上任一点为(,)M x y，求x +的最小值．24．（本小题满分10分）【选修4－5：不等式选讲】 设函数()|1||1|f x x x =-+-． （1）若1a =-，解不等式()3f x ≥；（2）如果x R ∀∈，()2f x ≥，求a 的取值范围．云南师大附中2013届高考适应性月考卷（五）理科数学参考答案一、选择题，本题考查基础知识，基本概念和基本运算能力二、填空题．本题考查基础知识,基本概念和基本运算技巧三、解答题 17．云南师大附中2013届高考适应性月考卷（五）理科数学参考答案第Ⅰ卷（选择题，共60分）一、选择题（本大题共12小题，每小题5分，共60分）【解析】1．由= A B A 知⊆A B ，而{3,4}=B ，且0=a 时，=∅A ，适合= A B A ，故选A ． 2．2112i i=-=+z ，则223(12i)3(12i)10i +=+++=z z ，故选C.3. 213sin 24+=α，则21sin 4=α，21cos 212sin 2=-=αα，故选B ．4．=πD S ，22cos d 2ππ-=π-=π-⎰E S x x ，故选C ．5．0>a 且1≠a ，当22π=>πT a时，01<<a ，故选C.6．该几何体是高为1，底面对角线长为2的菱形构成的四棱锥，1121222⎛⎫⎛=⨯⨯+⨯⨯= ⎪ ⎝⎭⎝S D ．7．第一次循环有1,1,2===a T k ，第二次循环有0,1,3===a T k ，第三次循环有0,1,4===a T k ，第四次循环有1,2,5===a T k ，第五次循环有1,3,6===a T k ，此时不满足条件，输出3=T ，故选C. 8．12=T 2362πππ-=，=πT ，222ππ===πTω，此时sin(2)=+y x ϕ，又函数过点,16π⎛⎫⎪⎝⎭，代入可得6π=ϕ，因此函数sin 26π⎛⎫=+⎪⎝⎭y x ，令0=x ，可得12=y ．故选B.9．212+⎛⎫= ⎪⎝⎭a b ab ≤，故2+a b ≥，又2+=c d ，故212+⎛⎫= ⎪⎝⎭c d cd ≤，即22cd ≥，故选A ．10． 设1=PF x ，2=PF y ，由题意得192=xy ，即18=xy ，又2224+=x y c ，故22()24-+=x y xy c ，即229+=a c ，于是29=b ，即3=b ，又7+=a b ，所以4=a ，5=c ，54==c e a，选B.11．如图1，采用特殊化法，当点P 运动到线段AB 的中点M 这一特殊位置时，有1()2=+p a b ，所以22115()()()()222-=+-=-=p a b a b a b ab ，故选D.另解：设线段AB 的中点为M ， 则1()2=-=-+M P OP OM p a b ，又=- BA a b ，且⊥ MP BA ，所以1()()02⎡⎤-+-=⎢⎥⎣⎦p a b a b ，即22115()()()()222-=+-=-=p a b a b a b ab .12．原命题212⇔-<xx a，在(1,1)∈-x 上恒成立，因为当(1,1)∈-x 时2111222--<x ≤，于是若1>a ，则x a 的最小值是1-a ，故112-a ≥，即2a ≤，此时12<a ≤，至此可选答案为B ；事实上若01<<a ，则x a 的最小值是a ，故12a ≥，此时1 1.2<a ≤（也可作出212=-y x 与=xy a 在(1,1)∈-x 上的简图，易知当1>a 时，112-a ≥；当01<<a 时，112a ≥，解之得B ．）第Ⅱ卷（非选择题，共90分）二、填空题（本大题共4小题，每小题5分，共20分）【解析】13．在ABC △中，由4cos 5=A ，得3sin 5=A 341sin cos 4555π⎛⎫-=-=-=- ⎪⎝⎭A A A ．图114. 由题意知2=n n S n a ，当2n ≥时，211(1)--=-n n S n a ，两式相减得221(1)-=--n n n a n a n a ，即221(1)(1)--=-n n n a n a ，故111--=+n n a n a n ，所以324112311123211.23451(1)---===++n n n a a a a n n a a a a a a nn n n ……又1a 也满足上式，故111(1)1==-++n a n n nn ，所以数列{}n a 的前60项和为16016161-=．15．不等式组所表示的平面区域如图2阴影部分，易知40,3⎛⎫ ⎪⎝⎭B ，所以直线43=+y kx 过点B ，若=BDC BDA S S △△，则点D 为线段A C 的中点，由34,34,+=⎧⎨+=⎩x y x y 得(1,1)A ，又(0,4)C ，所以15,22⎛⎫ ⎪⎝⎭D ，代入直线43=+y kx 中，解得73=k ．16．如图3，O 为球心，也是正方体的中心，设球O 被平面1ACD 所截得的圆的半径为r ，AC 中点为M，则1136==r D M ，球的半径12=R ，则O 到平面1ACD的距离6==h圆锥的体积213108=π=V r h ．三、解答题（共70分. 解答应写出文字说明，证明过程或演算步骤） 17．（本小题满分12分）解：（Ⅰ）设等比数列{}n a 的首项为1a ，公比为q ， 则12341112,2,=⎧⎪⎨+=⎪⎩a q a q a q a q ①② …（2分）把①代入②整理得220--=q q ，即1,2=-=q q ，0>n a ∵, 2=q ∴，代入①得11=a , ∴12-=n n a ． ……………（6分） （Ⅱ）1(1)321(1)3221-=-++=-++ n n n n n b a n n ∵13(2)21-=--++n n ， ……………（9分）13[1248(2)][35721]-=--+-++-++++++ n n T n ,223[1(2)]2(2)2112---=++=-++-+nnn T n n n n ∴． ………………………………（12分）图2图318．（本小题满分12分）解：（Ⅰ）记“这2人来自同一区域”为事件E ，那么22222010515250C C C C 2()C 7+++==P E ，所以这2人来自同一区域的概率是27． …………………………………………（4分）（Ⅱ）随机变量ξ可能取的值为0，1，2，且215235C 3(0)C 17===P ξ，112201520223535C C C 6038(1),(2).C119C119======P P ξξ …………………………（8分）所以ξ的分布列是：ξ的数学期望为360381368012.171191191197=⨯+⨯+⨯==E ξ……………………（12分）19．（本小题满分12分）（Ⅰ）证明：如图4，∵平面⊥AC E 平面ABC D ， 平面 A C E 平面=ABC D AC ， 且⊥BC AC ，∴⊥BC 平面AC E ，⊥BC AE， …………………………………………………………………………（3分）又==AC ，∴⊥AE EC ，而= B C E C C ，∴⊥AE平面.B C E F ……………………………………………（6分） （Ⅱ）解：方法一：建立如图5所示的空间直角坐标系， 不妨设2==AC BC ，则==AE EC ， 由题意得(0,0,0)A ，(2,2,0)-B ，(2,0,0)C ，图4(1,1,1)-F ，(2,2,0)=- AB ，(0,2,0)=BC ，(1,1,1)=-BF ， ……………………………………………………………………（8分）设平面BFC 的法向量为111(,,)=m x y z ， 由0= m BC ，且0= m BF ，得(1,0,1)=m ， 设平面ABF 的法向量为222(,,)=n x y z ，由0=n AB ，且0= n BF ，得(1,1,0)=n ， ……………………………………（10分）所以1cos ,2⋅〈〉==m n m n m n，∴二面角--A BF C 的大小为60︒. ………………………………………………（12分） 方法二：如图6，取A C 的中点N ，连接E N ， ∵平面⊥AC E 平面ABC D ，=A E E C ， ∴⊥EN 平面ABC D .取AB 的中点H ，连接FH ，N H ，由题意可知四边形E F H N 是平行四边形， 则//FH EN ，⊥FH 平面ABC D ， ∴平面ABF ⊥平面ABC D .连接C H ，∵=AC BC ，则⊥C H AB ，∴⊥C H 平面ABF . 过H 向BF 引垂线交BF 于R ，连接C R ，则⊥C R B F ，则∠H R C 为二面角--A BF C 的平面角. …………………………………………（9分） 由题意，不妨设2==AC BC，则=AB ， 在R t BH F △中，3=H R，12==CH AB ,所以在R t △CHR中，tan ∠==C H H RC RH因此二面角--A BF C 的大小为60︒. ……………………………………………（12分）图5图620．（本小题满分12分）解：（Ⅰ）1(2)(2)()44+-'=-=x x x f x xx，令()0'=f x ，得2=-x 或2=x .[1,3]∈x ∵，故当12<<x 时，()0'<f x ，当23<<x 时，()0'>f x ， …………………………………………………………（3分） ∴()f x 在2=x 处取得唯一极小值，也是最小值1(2)ln 22=-f ，又1(1)8=f ，9(3)ln 38=-f ，19ln 3ln 31088⎛⎫--=-> ⎪⎝⎭，即(1)(3)>f f ，∴()f x 的最大值为18， 最小值为1ln 22-． ………………………………………（6分）（Ⅱ）由（Ⅰ）知1()8f x ≤，所以()4<-f x at 对于任意的[0,2]∈t 恒成立，只要148->at ，即8310-<at 对任意[0,2]∈t 恒成立， ………………………（9分）设()831=-g t at （[0,2]∈t ），则(0)0,(2)0,<⎧⎨<⎩g g 解得3116<a ，所以实数a 的取值范围是31,16⎛⎫-∞ ⎪⎝⎭． ……………………………………………（12分）21．（本小题满分12分）解：（Ⅰ）由2==c e a得，222=a b，依题意1222⨯⨯=a b=ab解方程组222,⎧=⎪⎨=⎪⎩a b ab得=a 1=b ，所以椭圆C 的方程为2212+=xy . …………………………………………………（4分）（Ⅱ）依题意直线l 的斜率存在，设l ：(2)=-y k x ，11(,)A x y ，22(,)B x y ，(,)P x y ，由22(2),1,2=-⎧⎪⎨+=⎪⎩y k x x y 得2222(12)8820+-+-=k x k x k ，由422644(21)(82)0∆=-+->k k k ，得212<k ，且2122812+=+kx x k，21228212-=+k x x k． ………………………………………………（6分）∵+=OA OB tOP ，1212(,)(,)++=x x y y t x y ∴，当0=t 时，0=k ，23-==>PA PB a ，∴0≠t ，21228(12)+==+x x kx tt k ，1212214[()4](12)+-==+-=+y y k y k x x k ttt k ，∵点P 在椭圆上，∴222222222(8)(4)22(12)(12)-+⋅=++k k t k t k ，即22216(12)=+k t k . …………………………………………………………（8分）∵3-<PA PB 123-<x 22121220(1)[()4]9++-<k x x x x ，∴422222648220(1)4(12)129⎡⎤-+-⋅<⎢⎥++⎣⎦k k k k k ， 即22(41)(1413)0-+>k k ，∴21.4>k ………………………………………………（10分）又212<k ，∴21142<<k ，则由222216881221==-++kt kk ，得2843<<t ，∴实数t 的取值范围是2,233⎛⎛⎫-- ⎪⎪⎝⎭⎝⎭． …………………………（12分） 22．（本小题满分10分）【选修4—1：几何证明选讲】（Ⅰ）证明：P A ∵为 O 的切线，∠=∠PAB AC P ∴， 又∠=∠P P ，PAB PC A ∴△∽△．.=AB PA ACPC∴…………………………………………………………………………（4分）（Ⅱ）解：如图7，∵P A 为 O 的切线，PBC 是过点O 的割线，2.=⋅PA PB PC ∴ ………………………………………………………………………（5分）又10,5,20,15,====PA PB PC BC ∵∴由（Ⅰ）知，12==AB PA ACPC，∵BC 是 O 的直径，22290,225,∠=︒+==CAB AC AB BC ∴∴==AC AB ∴…………………………（7分）连接CE ，则∠=∠ABC E ，又∠=∠C AE EAB ，,AC E AD B △∽△ .=AB AD AEAC∴90.⋅=⋅==AD AE AB AC ∴…………………………………………（10分）23．（本小题满分10分）【选修4—4：坐标系与参数方程】解：（Ⅰ）直线l20-+-=y ，曲线C 的直角坐标方程为：221+=x y ． …………………………………………（4分）（Ⅱ）∵2,,'=⎧⎨'=⎩x x y y ∴将,2'⎧=⎪⎨⎪'=⎩x x y y 代入C ，得'C ：22()()14''+=x y ， 即椭圆'C 的方程为2214+=xy ．设椭圆'C 的参数方程为2cos ,sin =⎧⎨=⎩x y ϕϕ（ϕ为参数），则π2cos 4sin 6⎛⎫+=+=+⎪⎝⎭x ϕϕϕ，∴+x 的最小值为 4.- …………………………………………………………（10分） 24．（本小题满分10分）【选修4—5：不等式选讲】解：（Ⅰ）方法一：当1=-a 时，()11=-++f x x x ， …………………………（1分） 由()3f x ≥得 113-++x x ≥，（ⅰ）当1-x ≤时，不等式化为113---x x ≥，即23-x ≥， 不等式组1,()3-⎧⎨⎩x f x ≤≥的解集为 3,2⎛⎤-∞-⎥⎝⎦；（ⅱ）当11-<x ≤时，不等式化为113-++x x ≥，不可能成立， 不等式组11,()3-<⎧⎨⎩x f x ≤≥ 的解集为∅；（ⅲ）当1>x 时，不等式化为113-++x x ≥，图7即23x ≥，不等式组1,()3>⎧⎨⎩x f x ≥的解集为3,2⎡⎫+∞⎪⎢⎣⎭，综上得，()3f x ≥的解集为33,,22⎛⎤⎡⎫-∞-+∞ ⎪⎥⎢⎝⎦⎣⎭ . ……………………………（5分）方法二：当1=-a 时，()11=-++f x x x ，由()3f x ≥得113-++x x ≥，由绝对值的几何意义11-++x x 表示数轴上的点x 到1-与1的距离之和，而11-++x x 的最小值为2，所以当32-x ≤或32x ≥时，113-++x x ≥，所以不等式()3f x ≥的解集为33,,22⎛⎤⎡⎫-∞-+∞ ⎪⎥⎢⎝⎦⎣⎭．（Ⅱ）若1,()21==-a f x x ，不满足题设条件，若21,,1,()1,1,2(1),1,-++⎧⎪<=-<<⎨⎪-+⎩x a x a a f x a a x x a x ≤≥()f x 的最小值为1-a ；若21,1,1,()1,1,2(1),,-++⎧⎪>=-<<⎨⎪-+⎩x a x a f x a x a x a x a ≤≥ ()f x 的最小值为1-a ， …………………（8分）所以,()2∀∈x f x R ≥的充分条件是12-a ≥，从而a 的取值范围为(,1][3,)-∞-+∞ ． ………………………………………（10分）云南师大附中2013届高考适应性月考卷（六） 理科数学参考答案第Ⅰ卷（选择题，共60分）一、选择题（本大题共12小题，每小题5分，共60分） 9【解析】1．{|11}=-A x x ≤≤，{|0}=>B y y ，{|0}∴=U B y y ≤ð，故()= U A B ð[1,0]-.2．由题可得i i 1i -=+z ，12i 2ii+∴==-z ，则复数z 的共轭复数是2i +.3．A 、B 、D 选项都是正确的，选项C 的逆命题是“若<a b ，则22<am bm ”，它是错误的，因为当0=m时，22=am bm.4．由题可得点G 是ABC △的重心，设BC 边的中点为D ，则2211()(22)3323==⨯+=+AG AD AB AC AE AF ，23∴==x y ，43∴+=x y .5．只有②③是正确的.6．直线l 的斜率211=-k m ≤，tan 1,∴α≤ ∴ππ0,,π42⎡⎤⎛⎫∈ ⎪⎢⎥⎣⎦⎝⎭ α. 7．设正四面体的棱长为a ，则体积311322312=⨯⨯⨯⨯==V a ，2∴=a ，而正四面体的左视图为一个三角形，如图1所示，∴122=⨯⨯=S .8．73ππ()sin πcos πsin cos 4444⎛⎫⎛⎫⎛⎫⎛⎫=++-=--+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭f x x x x xππππsin coscos sincos cossin sincos )4444=--+=-x x x x x x图1π2sin 4⎛⎫=- ⎪⎝⎭x ，故最小正周期是2π.令πππ,42-=+x k 则3ππ4=+x k 为函数()=y f x 的对称轴方程. 当1=-k 时，π4=-x .9．由题意得2log <a x x 在10,2⎛⎤∈ ⎥⎝⎦x 上恒成立，故在10,2⎛⎤∈ ⎥⎝⎦x 上2=log =a y x y x的图象在的下方，由图象知0<<1a . 当=log a y x 的图象过点11,24⎛⎫⎪⎝⎭时，1=16a ，故1,116⎛⎫∈ ⎪⎝⎭a 时满足题意.10．()||0==f x x，即||=x ，函数()f x没有零点，则=y 的图象与||=y x 的图象没有交点. 如图2，22(0)=+=y x y a y ≥，它表示以(0,0)||=y x的图象是端点为(0,的一条折线，当上半圆与||=y x 相切时，1=a ；当上半圆经过点(0,2=∴=a ；若两图象没有交点，则01>2<<a a 或.11．①由于点(,)P a b 与点(1,0)Q 在直线23+1=0-x y 的两侧，则23+10-<a b ；②0≠a 时，00-=-bb aa 可看作点(,)P ab 与原点的斜率，由图可知无最值；③011-=--bb a a 可看作点(,)P a b 与点(1,0)的斜率，由图可知1-ba ∈12,,+33⎛⎫⎛⎫-∞-∞ ⎪ ⎪⎝⎭⎝⎭ ；④可看作点(,)P a b 与原点的距离，而原点到直线的距离为13=，故存在正实数13=MM .12．设00(,)M x y ，则100200(,),(,)=---=--M F c x y M F c x y ，图22222222222222220120000022211.⎛⎫⎛⎫∴⋅=-+=-+-=--+=-+ ⎪ ⎪⎝⎭⎝⎭ x b c M F M F x c y x c b x c b x c b a a a0[,]∈- x a a ，∴当0=±x a 时，12⋅M F M F 有最大值2b ，2222,∴c b c ≤≤ 22222222,23,∴-∴c a c c c a c ≤≤≤≤2211,32∴ca ≤≤32∴∈⎣⎦e .第Ⅱ卷（非选择题，共90分）【解析】13．i 从1开始，依次取3，5，7，9．故输出27317=⨯+=S . 14．如图3所示，圆的方程可化为22(2)1,-+=x y抛物线的焦点(2,0)F ，准线 2.=-x由228=-⎧⎨=⎩y x y x ，，得21240-+=x x ，设直线与抛物线交于(,),(,)A A D D A x y D x y ， 则12+=A D x x .()()(1)(1)2+=-+-=-+-=+-AB CD AF BF DF CF AF DF AF DF ，由抛物线的定义得2,2=+=+A D AF x DF x ， 故()2214+=+-=++=A D AB CD AF DF x x .15．,01,()2,12,<⎧==⎨-⎩x x y f x x x ≤≤≤ 22,01,()2,12,⎧<⎪∴==⎨-⎪⎩x x y xf x x x x ≤≤≤图33312122220101d (2)d 133⎛⎫∴=+-=+-= ⎪⎝⎭⎰⎰xx S x x x x x x .16．1231531311121,(),(),()1213+==∴======++ n n a a f a a f a a f a a a .20102012= a a，20122010201020101,12∴==∴=+a a a a ，2010200820062004220081====1222∴==∴=+ a a a a a a 同理：，12345612132326∴+++++=+++=a a a a a a .[来源:学*科*网]三、解答题（共70分. 解答应写出文字说明，证明过程或演算步骤） 17．（本小题满分12分） 解：（Ⅰ）311π3ππ,π41264=-=∴= T T ，2π2∴==Tω.图象过点π,6⎛⎫ ⎪⎝⎭A ，ππππ22π,0,6226∴⨯+=+<<∴= k ϕϕϕ，π()sin 26⎛⎫∴=+ ⎪⎝⎭f x A x .又图象过点(0,1)，πsin1,26∴=∴=A A ，π()2sin 26⎛⎫∴=+ ⎪⎝⎭f x x .……………………………………………………………（6分）（Ⅱ）πππ()2sin 22sin 2463⎡⎤⎛⎫⎛⎫=-+=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦g x x x . 由πππ2π22π232--+k x k ≤≤得π5πππ1212-+k x k ≤≤，∴()=y g x 的单调递增区间是π5ππ,π1212⎡⎤-+⎢⎥⎣⎦k k . ………………………………（12分）18．（本小题满分12分）如图4，（Ⅰ）证明：取'A B 的中点G ，连接FG ，EG ，F 、G 分别是'A C 、'A B 的中点，12∴FGBC，又12D EBC，∴FG DE，∴四边形DEGF 为平行四边形， ∴//D F E G，又''⊄⊂D F A BE EG A BE 平面，平面，∴DF //'A B E平面. ……………………………………………………………………（4分）（Ⅱ）解：取BE 的中点H ，连接,'A H H C ，则'⊥A H BE ，='''⊥∴⊥ A BE BCDE A BE BCDE BE A H BCDE平面平面，平面平面，平面，''∴∠A CH A C BCDE 为与平面所成角，在△BCH中，由余弦定理得22252222222⎛=+-⨯⨯⨯= ⎪⎝⎭C H，2'=A H 又，tan =5''∴∠=A H A C H C H. ……………………………………………………………（8分）（Ⅲ）解：过点D 作⊥DM BE 于点M ，易证'⊥D M A B E 平面，在R t △DME中，sin 452=⋅︒=D M D EDF //'A B E 平面，∴F 到平面'A BE 的距离即为D 到平面'A BE 的距离，111132212''--∴==⨯⨯⨯⨯=F A BE D A BE V V . ……………………………………（12分）另解：''---=-F A BE A BEC F BEC V V V .（其他解法酌情给分） 19．（本小题满分12分） 解：（Ⅰ）茎叶图表示为图5.甲地树苗高度平均数=1920212325293233374128(cm )10+++++++++=，乙地树苗高度平均数=1026303034374446464735(cm )10+++++++++=，图4图5甲地树苗高度中位数=252927(cm )2+=，乙地树苗高度中位数=343735.5(cm )2+=， ………………………………………（4分）（Ⅱ） 都来自乙地的概率为：2527C 10C21=，∴至少有一株来自甲地的概率为：11021-=1121. ………………………………………（8分）（Ⅲ）Z 的可能取值为0，5，10，15，20，设Z=5y ，则1~4,2⎛⎫ ⎪⎝⎭Y B ，(0)=P Z =4411C 216⎛⎫= ⎪⎝⎭，(5)=P Z =41411C 24⎛⎫=⎪⎝⎭，(10)=P Z =42413C 28⎛⎫= ⎪⎝⎭，(15)=P Z =43411C 24⎛⎫=⎪⎝⎭，(20)=P Z =44411C 216⎛⎫=⎪⎝⎭，Z∴()E Z =5()E y=10.故该市绿化部门此次采购所需资金总额Z 的数学期望为10万元. …………（12分） 20．（本小题满分12分）解：（Ⅰ）22-=-∴=p p∴抛物线22(0)=>y px p 的焦点为02⎛⎫⎪ ⎪⎝⎭， 2∴=a ，又双曲线的一条渐近线过点12⎛⎫-- ⎪ ⎪⎝⎭，1∴=∴=b b a .。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
云南师大附中2013届高三适应性月考卷（三）数学（理）试题本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．考试结束后，请将本试卷和答题卡一并交回．满分150分，考试用时120分钟， 参考公式：样本数据x 1,x 2，…，x n 的标准差 锥体体积公式()()()222121n s x x x x x x n⎡⎤=-+-++-⎢⎥⎣⎦v=13Sh 其中x 为样本平均数 其中S 为底面面积，h 为高柱体体积公式 球的表面积，体积公式 V=ShS=42R π, V=343R π其中S 为底面面积，h 为高其中R 为球的半径第Ⅰ卷（选择题，共60分）注意事项：1．答题前，考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号在答题卡上填写清楚，并请认真填涂准考证号．2．每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦擦干净后，再选涂其他答案标号．在试题卷上作答无效．一、选择题（本大题共12小题，每小题5分，共60分，在每个小题给出的四个选项中，只有一项是符合题目要求的） 1．设集合{}{}|31,,|5,,A x x k k N B x x x Q ==+∈=≤∈则A B 等于 （ ）A ． {1,2,5}B ．{l, 2，4, 5}C ．{1，4, 5}D ．{1，2，4} 2．在复平面内，复数311i i+-对应的点位于（ ）A ．第四象限B ．第三象限C ．第二象限D ．第一象限3．一个几何体的三视图如图l 所示，其中正视图是一个正三角形，则该几何体 （ ）的体积为A ．1B ．33 C ．3D ．2334．下列函数中既不是奇函数也不是偶函数的是 （ ） A ．||2x y = B ．21(1)y g x x =++C ．22x x y -=+D ．111y gx =+5．执行如图2所示的程序框图，则输出的x 值是 （ ）A ．8B ．6C ．4D ．36．已知条件2:340p x x --≤；条件22:690q x x m -+-≤ 若p 是q 的充分不必要条件，则m 的取值范围是（ ） A ．[]1,1- B ．[]4,4- C ．(][),44,-∞-+∞D ．(][),11,-∞-+∞7．如图3，直线y=2x 与抛物线y=3－x 2所围成的阴影部分 的面积是（ ） A ．353B ．22C ．23-D ．3238．对于函数11()(sin cos )|cos sin |22f x x x x x =+--，下列说法正确的是 （ ）A ．该函数的值域是[]1,1-B ．当且仅当22()2k x k k Z πππ<<+∈时，()0f x >C ．当且仅当2()2x k k Z ππ=+∈时，该函数取最大值1D ．该函数是以π为最小正周期的周期函数9．实数对（x ，y ）满足不等式组20,250,20,x y x y y --≤⎧⎪+-≥⎨⎪-≤⎩则目标函数z=kx －y 当且仅当x=3，y=1时取最大值，则k的取值范围是（ ）A ．[)1,1,2⎛⎫-∞-+∞ ⎪⎝⎭B ．1,|2⎛⎫-+∞ ⎪⎝⎭C ．1.12⎛⎫- ⎪⎝⎭D ．(],1-∞-10．已知函数21,0,()1,0,x f x x x -≥⎧=⎨-<⎩则满足不等式2(3)(2)f x f x -<的x 的取值范围为 （ ）A ．[)3,0-B ．（－3，0）C ．（－3，1）D ．（－3，－3）11．若在曲线f （x ，y ）=0上两个不同点处的切线重合，则称这条切线为曲线f （x ，y ）=0的“自公切线”。
下列方程：①221x y -=；②2||y x x =-，③3sin 4cos y x x =+；④2||14x y +=-对应的曲线A ．①②B ．②③C ．①④D ．③④12．已知()f x 为R 上的可导函数，且,x R ∀∈均有()f x f >′（x ），则有 （ ）A ．20132013(2013)(0),(2013)(0)e f f f e f -<>B ．20132013(2013)(0),(2013)(0)e f f f e f -<<C ．20132013(2013)(0),(2013)(0)e f f f e f ->>D ．20132013(2013)(0),(2013)(0)e f f f e f -><第II 卷（非选择题，共90分）注意事项：本卷包括必考题和选考题两部分，第13~21题为必考题，每个试题考生都必须作答．第22~24题为选考题，考生根据要求作答，把答案填写在答题卡上相应的位置，在试题卷上作答无效． 二、填空题（本大题共4小题，每小题5分，共20分）13．在区间[－6，6]，内任取一个元素x O ，若抛物线y=x 2在x=x o 处的切线的倾角为α，则3,44ππα⎡⎤∈⎢⎥⎣⎦的概率为 。
14．在锐角△ABC 中，角A 、B 、C 所对的边分别为a 、b 、c ，若b=2， B=3π且sin2A+sin(A+C)=sinB ，则△ABC 的面积为 。
15．正三棱锥A －BCD 内接于球O ，且底面边长为3，侧棱长为2，则 球O 的表面积为____ ．16．如图4，椭圆的中心在坐标原点，F 为左焦点，A ，B 分别为长轴和短轴上的一个顶点，当FB ⊥AB 时，此 类椭圆称为“黄金椭圆”．类比“黄金椭圆”，可推出 “焚金双曲线”的离心率为 。
三、解答题（共70分，解答应写出文字说明，iiE 明过程或演算步骤） 17．（本小题满分12分）已知数列{a n }的前n 项和为S n ，且有a 1=2，3S n =11543(2)n n n a a S n ---+≥ （I ）求数列a n 的通项公式； （Ⅱ）若b n =n·a n ，求数列{b n }的前n 项和T n 。
18．（本小题满分12分）某班将要举行篮球投篮比赛，比赛规则是：每位选手可以选择在A 区投篮2次或选择在B 区投篮3次，在A 区每进一球得2分，不进球得0分；在B 区每进一球得3分，不进球得0分，得分高的选手胜出．已知某参赛选手在A 区和B 区每次投篮进球的概率分别是910和13． （Ⅰ）如果以投篮得分的期望值高作为选择的标准，问该选手应该选择哪个区投篮？请说明理由； （Ⅱ）求该选手在A 区投篮得分高于在B 区投篮得分的概率． 19．（本小题满分12分） 如图5甲，四边形ABCD 中，E 是BC 的中点，DB =2, DC=1，BC=5，AB =AD=2．将（图甲）沿直线BD 折起，使二面角A － BD －C 为60o （如图乙）． （Ⅰ）求证：AE ⊥平面BDC;（Ⅱ）求点B 到平面ACD 的距离．20．（本小题满分12分） 已知f (x) = xlnx. （I ）求f (x) 在[t ，t+2]（t>0）上的最小值；（Ⅱ）证明：(0,)x ∀∈+∞都有121x nx e ex>-。
21．（本小题满分12分）设抛物线C 的方程为x 2 =4y ，M 为直线l ：y=－m(m>0)上任意一点，过点M 作抛物线C 的两 条切线MA ，MB ，切点分别为A,B ．（Ⅰ）当M 的坐标为（0，－l ）时，求过M ，A ，B 三点的圆的标准方程，并判断直线l 与此圆的位置关系；(Ⅱ)当m 变化时，试探究直线l 上是否存在点M ，使MA ⊥MB?若存在，有几个这样的点，若不存在，请说明理由，请考生在第22、23、24三题中任选一题作答，如果多做，则按所做的第一题记分．作答时请写题号．22．（本小题满分10分）【选修4—1：几何证明选讲】 如图6，在正△ABC 中，点D,E 分别在边AC, AB 上，且AD=13AC ， AE= 23AB ，BD ，CE 相交于点F 。
（I ）求证：A ，E ，F ，D 四点共圆；（Ⅱ）若正△ABC 的边长为2，求，A ，E ，F ，D 所在圆的半径．23．（本小题满分10分）【选修4—4：坐标系与参数方程】在直角坐标平面内，以坐标原点O 为极点，x 轴的非负半轴为极轴建立极坐标系，已知点M 的极坐标为42,4π⎛⎫ ⎪⎝⎭，曲线C 的参数方程为12cos ,2sin x y αα⎧=+⎪⎨=⎪⎩（α为参数）．（I ）求直线OM 的直角坐标方程；（II ）求点M 到曲线C 上的点的距离的最小值．24．（本小题满分10分）【选修4—5：不等式选讲】 已知函数f （x ）=|2x+1|+|2x －3|． （I ）求不等式 f （x ）≤6的解集；（Ⅱ）若关于 x 的不等式 f （x ）< |a －1 |的解集非空，求实数a 的取值范围参考答案第Ⅰ卷（选择题，共60分）一、选择题（本大题共12小题，每小题5分，共60分） 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案BABDACDBCBBA【解析】1．当k =0时，x =1；当k =1时，x =2；当k =5时，x =4；当k =8时，x =5，故选B. 2．1i 22z =-对应的点是1122⎛⎫- ⎪⎝⎭，，故选A.3．由三视图可知，此几何体为三棱锥，如图1，其中正视图为PAC △，是边长为2的正三角形，PD ABC ⊥平面，且3PD =，底面ABC △为等腰直角三角形，2AB BC ==，所以体积为113322323V =⨯⨯⨯⨯=，故选B.4．根据奇偶性定义知，A 、C 为偶函数，B 为奇函数，D 定义域为{|1}x x >-不关于原点对称，故选D. 5．1211134242322k S k S ==+⨯===+⨯=当时，；当时，； 332233103428k S k x k ==+⨯====当时，；当时，输出.故选A.6．14p x -：≤≤，记33(0)33(0)q m x m m m x m m -++-：≤≤＞或≤≤＜， 依题意，03134m m m ⎧⎪--⎨⎪+⎩＞， ≤，≥或03134m m m ⎧⎪+-⎨⎪-⎩＜， ≤，≥，解得44m m -≤或≥.7．12332(32)d 3S x x x -=--=⎰，故选D. 8．sin sin cos ()cos sin cos x x x f x x x x ⎧=⎨⎩，＜，，≥，由图象知，函数值域为212⎡⎤-⎢⎥⎣⎦，，A 错；当且仅当π2π()x k k =+∈Z 时，该函数取得最大值2， C 错；最小正周期为2π，D 错. 图19. 不等式组所表示的区域如图2所示，直线z kx y y kx z =-⇒=-过(31)，时z 取最大值，即直线y kx z =-在y 轴上的截距z -最小，由图可得直线y kx z =-的斜率112k ⎛⎫∈- ⎪⎝⎭，，故选C. 10．由函数图象可知，不等式的解为23220x x x -><⎧⎨⎩，，即(30)x ∈-，，故选B. 11．画图可知选B.12．构造函数()()x f x g x e=，则2()()()()()()()x x x x f x e e f x f x f x g x e e ''''--==，因为x ∀∈R ，均有()()f x f x '>，并且0x e >，所以()0g x '<，故函数()()xf xg x e =在R 上单调递减，所以(2013)(0)(2013)(0)g g g g -><，，即20132013(2013)(2013)(0)(0)f f f f e e--><，，也就是20132013(2013)(0)(2013)(0)e f f f e f -><，，故选A.第Ⅱ卷（非选择题，共90分）二、填空题（本大题共4小题，每小题5分，共20分）题号 1314 15 16 答案1112 316π3152+ 【解析】13．当α∈π3π44⎡⎤⎢⎥⎣⎦，时，斜率1k ≥或1k -≤，又 2y x '=，所以012x ≥或012x -≤，所以P =1112.14．sin 2sin sin()2sin cos sin()sin()A B A C A A A C A C =--∴=+--，， 2sin cos 2cos sin .cos 0π13sin sin 22 3.322ABC A A A C ABC A A C A C B S ∴=∴≠∴====∴=⨯⨯⨯=△△是锐角三角形，，，即，15．如图3，设三棱锥A BCD -的外接球球心为O ，半径为r ，BC=CD=BD =3，AB=AC=AD =2，AM BCD ⊥平面，M 为正BCD △的中心，则DM =1，AM =3，OA=OD=r ，所以22(3)1r r -+=，解得2r =，所以2164ππS r ==. 图3图216．由图知，2222()()a c b c c +=++，整理得220c ac a --=，即210e e --=，解得152e ±=，故152e +=. 三、解答题（共70分. 解答应写出文字说明，证明过程或演算步骤） 17．（本小题满分12分）解：（Ⅰ）113354(2)n n n n S S a a n ---=-≥，1122n n n n aa a a --∴==，，………………（3分）又12a =，{}22n a ∴是以为首项，为公比的等比数列， ……………………………（4分） 1222n n n a -∴=⋅=. ……………………………………………………………………（5分）（Ⅱ）2n n b n =⋅， 1231222322n n T n =⋅+⋅+⋅++⋅，23121222(1)22n n n T n n +=⋅+⋅++-⋅+⋅.……………………………………………（8分）两式相减得：1212222n n n T n +-=+++-⋅，12(12)212n n n T n +-∴-=-⋅-1(1)22n n +=-⋅-，………………………………………（11分）12(1)2n n T n +∴=+-⋅.…………………………………………………………………（12分）18．（本小题满分12分）解：（Ⅰ）设该选手在A 区投篮的进球数为X ，则999~2()210105X B E X ⎛⎫=⨯= ⎪⎝⎭，，故， 则该选手在A 区投篮得分的期望为92 3.65⨯=.………………………………………（3分）设该选手在B 区投篮的进球数为Y ，则11~3()3133Y B E Y ⎛⎫=⨯= ⎪⎝⎭，，故， 则该选手在B 区投篮得分的期望为313⨯=.所以该选手应该选择A 区投篮.………………………………………………………（6分）（Ⅱ）设“该选手在A 区投篮得分高于在B 区投篮得分”为事件C ，“该选手在A 区投篮得4分且在B 区投篮得3分或0分”为事件D ，“该选手在A 区投篮得2分且在B 区投篮得0分”为事件E ，则事件C DE =，且事件D 与事件E 互斥. …………（7分）81483()1009275P D ⎛⎫=⨯+= ⎪⎝⎭， ………………………………………………………（9分） 1884()1002775P E =⨯=， ……………………………………………………………（11分） 3449()()P C P DE ==+=，＝ 故该选手在A 区投篮得分高于在B 区投篮得分的概率为4975. ……………………（12分） 19．（本小题满分12分）（Ⅰ）证明：如图4，取BD 中点M ，连接AM ，ME . 因为AB=AD =2，所以AM ⊥BD ，因为DB =2，DC =1，BC =5，满足：DB 2+DC 2=BC 2，所以△BCD 是以BC 为斜边的直角三角形，BD ⊥DC ， 因为E 是BC 的中点，所以ME 为△BCD 的中位线， ∴ME ∥12CD ， ∴ME ⊥BD ，ME =12，…………………………………………………………………（2分） ∴∠AME 是二面角A -BD -C 的平面角，AM E ∴∠=60°.A MB D ⊥，ME BD ⊥且AM 、ME 是平面AME 内两条相交于点M 的直线， BD AEM ∴⊥平面，AE ⊂平面AEM ，BD AE ∴⊥.………………………………（4分）2A B A D ==，2DB =， ABD ∴△为等腰直角三角形，112AM BD ∴==， 在△AME 中，由余弦定理得：22232cos 2AE AM ME AM ME AME AE =+-⋅⋅∠∴=，，2221AE ME AM AE ME ∴+==∴⊥，， BDME M BD BDC ME BDC =⊂⊂，平面，平面，AE BDC ∴⊥平面.………………………………………………………………………（6分）（Ⅱ）解法一：等体积法.解法二：如图5，以M 为原点，MB 所在直线为x 轴，ME 所在直线为y 轴，平行于EA的直线为z轴，建立空间直角坐标系， ………………………………………………（7分） 则由（Ⅰ）及已知条件可知B (1，0，0)，1002E ⎛⎫⎪⎝⎭，，，13022A ⎛⎫⎪ ⎪⎝⎭，，，D (100)-，，，C (110)-，，. 图5图4则131(010)22AB CD ⎛⎫=--=- ⎪ ⎪⎝⎭，，，，，， ……………………………………（8分） 13122AD ⎛⎫=--- ⎪ ⎪⎝⎭，，， 设平面ACD 的法向量为n =()x y z ，，，则13·0022·00n AD x y z n CD y ⎧⎧=---=⎪⎪⇒⎨⎨=⎪⎪⎩-=⎩，，，令3x =，则z =-2， (302)n ∴=-，，，…………………………………………………………………（10分） 记点B 到平面ACD 的距离为d ， 则AB n d n ⋅=，所以d 2230322173)0(2)++==++-(. …………………………（12分） 20．（本小题满分12分）（Ⅰ）解：()ln 1f x x =+'，令1()0f x x e='=，得.当10()0()x f x f x e ⎛⎫∈< ⎪'⎝⎭，，，单调递减；当1()0()x f x f x e ⎛⎫∈+∞> ⎪'⎝⎭，，，单调递增. …………………………………………（2分）因为10+22t t e＞，＞＞，（1）当0＜t ＜1e 时min 11()f x f e e ⎛⎫==- ⎪⎝⎭，；（2）当t ≥1e时，min ()()ln .f x f t t t ==所以min110()1ln .t e e f x t t t e ⎧-<<⎪⎪=⎨⎪⎪⎩，，，≥ ………………………………………………………（6分）（Ⅱ）证明：由（Ⅰ）知，当(0)x ∈+∞，时，()ln f x x x =的最小值是min 11()f x f e e ⎛⎫==- ⎪⎝⎭，（当且仅当x =1e 时取到最小值）问题等价于证明2ln x x x x e e>-， 设2()((0))x x m x x e e=-∈+∞，， 则1()x x m x e -='，易得max 1()(1)m x m e==-，（当且仅当x =1时取到最大值）从而对一切(0)x ∈+∞，，都有12ln x x e ex>-成立. ………………………………（12分） 21．（本小题满分12分） 解：（Ⅰ）当M 的坐标为(01)-，时，设过M 点的切线方程为1y kx =-，代入24x y =，整理得2440x kx -+=，①令2(4)440k ∆=-⨯=，解得1k =±，代入方程①得2x =±，故得(21)A ，，(21)B -，. 因为M 到AB 的中点(0，1)的距离为2，从而过M A B ，，三点的圆的标准方程为22(1)4x y +-=．易知此圆与直线l ：y =-1相切. ………………………………………………………（6分） （Ⅱ）设切点分别为11()A x y ，、22()B x y ，，直线l 上的点为M 00()x y ，，过抛物线上点11()A x y ，的切线方程为11()y y k x x -=-，因为2114x y =，12x k = ， 从而过抛物线上点11()A x y ，的切线方程为111()2x y y x x -=-，又切线过点00()M x y ，， 所以得2110024x x y x =-，即21010240x x x y -+=. 同理可得过点22()B x y ，的切线方程为22020240x x x y -+=，………………………（8分） 因为12MA x k =，22MB x k =且12x x ，是方程200240x x x y -+=的两实根， 从而，12012024x x x x x y +=⎧⎨=⎩，，所以12022MA MB x x k k y ⋅=⨯=，当01y =-，即1m =时， 直线l 上任意一点M 均有MA ⊥MB ，…………………………………………………（10分） 当01y ≠-，即m ≠1时，MA 与MB 不垂直.综上所述，当m =1时，直线l 上存在无穷多个点M ，使MA ⊥MB ，当m ≠1时，直线l 上不存在满足条件的点M .……………………………………………………………（12分）22．（本小题满分10分）【选修4—1：几何证明选讲】 （Ⅰ）证明：23AE AB =，∴13BE AB =. 在正△ABC 中，13AD AC =，∴AD BE =， 又AB BC =，BAD CBE ∠=∠，∴△BAD ≌△CBE ，∴ADB BEC ∠=∠，即πADF AEF ∠+∠=，所以A ，E ，F ，D 四点共圆. …………………………（5分） （Ⅱ）解：如图6，取AE 的中点G ，连结GD ，则12AG GE AE ==. 23AE AB =，∴1233AG GE AB ===， 1233AD AC ==，60DAE ∠=︒， ∴△AGD 为正三角形， ∴23GD AG AD ===，即23GA GE GD ===， 所以点G 是△AED 外接圆的圆心，且圆G 的半径为23. 由于A ，E ，F ，D 四点共圆，即A ，E ，F ，D 四点共圆G ，其半径为23.…（10分） 23.（本小题满分10分）【选修4—4：坐标系与参数方程】解：（Ⅰ）由点M 的极坐标为π424⎛⎫ ⎪⎝⎭，，得点M 的直角坐标为(44)，， 所以直线OM 的直角坐标方程为y = x .………………………………………………（4分）（Ⅱ）由曲线C 的参数方程12cos 2sin x y αα⎧=+⎪⎨=⎪⎩，（α为参数），化成普通方程为：2)1(22=+-y x ，圆心为A (1，0)，半径为2=r ，由于点M 在曲线C 外， 故点M 到曲线C 上的点的距离的最小值为 |MA| 52r -=-.……………………（10分）24.（本小题满分10分）【选修4—5：不等式选讲】解：（Ⅰ）原不等式等价于313222(21)(23)6(21)(23)6x x x x x x ⎧⎧>-⎪⎪⎨⎨⎪⎪++-+--⎩⎩，≤≤，或≤≤或12(21)(23)6x x x ⎧<-⎪⎨⎪-+--⎩，≤，解之得3131212222x x x <--<-≤或≤≤或≤， 即不等式的解集为{|12}x x -≤≤.……………………………………………………（5分） （Ⅱ）()2123(21)(23)4f x x x x x =++-+--=≥， 14a ∴->，解此不等式得35a a <->或.…………………………………………（10分）图6。